删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

煤系页岩瓦斯吸附?解吸迟滞效应核磁共振谱实验研究

本站小编 Free考研考试/2022-01-01


引 言


煤系页岩气俗称瓦斯, 是陆相页岩气的重要组成部分之一, 主要以吸附态和游离态形式存在. 页岩气单井产能并非恒定不变, 而是随着累计产量增加而不断递减[1], 初期单井产量高递减快, 以游离气为主; 后期产量稳定, 递减慢, 以吸附气为主[2], 随着煤系页岩瓦斯开采深度不断增加, 这一现象愈发明显, 而煤系页岩瓦斯吸附?解吸过程差异即吸附?解吸迟滞效应在这一现象中影响不可忽略, 因此通过实验和理论从微细观角度探究煤系页岩瓦斯吸附?解吸迟滞规律就显得格外重要.

煤系页岩瓦斯吸附过程中随着孔隙瓦斯压力不断增加, 瓦斯(甲烷)分子在煤系页岩基质和孔喉表面不断吸附直到平衡如图1(a)所示; 裂隙游离态瓦斯采出引起的裂隙和基质压力差使得基质表面吸附态瓦斯解吸[3], 直到解吸平衡此时仍有部分瓦斯由于孔喉、吸附质以及纳米孔隙变形等诸多因素影响而被阻塞或封闭在微孔隙和基质中如图1(b)所示, 与吸附平衡状态相比, 这些被阻塞和封闭瓦斯导致明显滞后现象[4].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-264-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
吸附?解吸迟滞效应示意图



Figure
1.
Schematic diagram of adsorption-desorption hysteresis



下载:
全尺寸图片
幻灯片


国内外****对页岩瓦斯迟滞效应进行大量理论和实验研究. Ekundayo等[5-6]研究发现高温高压条件下页岩甲烷吸附?解吸存在明显滞后现象且迟滞程度与黏土和有机质碳含量有关; Zapata和Sakhaee-Pour[7]认为页岩气吸附?解吸迟滞效应与孔隙毛细管冷凝以及吸附层厚度有关; Hazraa等[8]研究发现贫瘠黑页岩甲烷吸附?解吸迟滞曲线形状与高岭石含量相关; Elizabeth等[9]认为吸附?解吸过程纳米孔隙阻塞效应和孔隙弹性流体性质是产生迟滞效应原因; Mehmani和Prodanovi?[10]则认为页岩气吸附?解吸滞后效应与样品微孔隙结构喉道空间分布有关; Zhao等[11]发现甲烷吸附?解吸迟滞效应可能与页岩样品孔隙改变有关; Chen等[12]从分子动力学角度研究发现常温条件下, 页岩气吸附?解吸迟滞效应主要与孔喉尺寸变化有关, 毛细管冷凝影响较小; Xu等[13]通过采用玻尔兹曼法对页岩纳米孔气体吸附?解吸模拟发现解吸迟滞曲线形状高度依赖于孔隙形状和孔隙空间凸曲率; 关富佳等[14]研究发现页岩气解吸滞后程度与孔裂隙发育和页岩物性参数有关; 唐巨鹏等[15]通过核磁共振技术研究发现煤系页岩瓦斯吸附?解吸存在迟滞现象, 且存在临界滞后瓦斯压力; 周银波等[16]和陆壮等[17]分别从热效应和变质程度方面对煤粉吸附?解吸迟滞效应进行了定量研究.

通过国内外****大量理论和实验研究, 可以确定页岩中甲烷吸附?解吸迟滞效应的确存在, 但是相关研究还存在以下问题: 对页岩气吸附?解吸迟滞效应发生机理, 不同****研究结论相去甚远, 且缺乏适用于页岩气吸附?解吸迟滞效应微细观定量评价指标; 研究对象多为海相或海陆过渡相页岩气而对储量丰富煤系页岩瓦斯吸附?解吸迟滞效应研究甚少.

对于以上研究不足, 以双鸭山盆地东保卫煤矿三采区36# 煤层底板煤系页岩为研究对象, 提出了一种基于核磁共振谱理论煤系页岩瓦斯迟滞效应微细观定量评价指标; 结合煤系页岩瓦斯吸附?解吸迟滞效应核磁共振谱实验进一步研究了吸附态、游离态以及微细观方法测定的宏观瓦斯迟滞规律, 以期为双鸭山盆地深部煤系页岩开采提供理论基础和实验参考.


1.
煤系页岩瓦斯吸附?解吸迟滞效应微细观定量评价指标



1.1
低场核磁共振谱实验原理


低场核磁共振作为一种针对含H1流体(油/气/水)等新型无损检测技术, 在能源勘探领域应用日趋广泛. 由低场核磁共振弛豫原理[18-19]可知横向弛豫时间T2为







$$frac{1}{{{T_2}}} approx {
ho _2}frac{A}{V} = {F_{
m{S}}}frac{{{
ho _2}}}{r}$$
(1)

式中, ${F_{
m{S}}}$为几何形状因子, 无量纲; $r$平均孔隙半径, μm; $A$为表面积, μm2 ; $V$为多孔介质体积, μm3; $;{
ho _2}$为表面弛豫强度, μm/ms; T2为瓦斯横向弛豫时间, ms.

低场核磁共振谱技术探测的是煤系页岩孔裂隙甲烷中氢原子核(H1), 其核磁共振谱信号幅度与探测范围内的甲烷质量成正比[20], 单一孔裂隙煤系页岩瓦斯质量与T2谱纵坐标幅值相对应, 可以采用T2谱曲线纵坐标幅值积分表征煤系页岩孔裂隙瓦斯量. 煤系页岩多孔介质结构的存在使其孔裂隙甲烷核磁共振横向弛豫时间比自由态甲烷小得多, 多孔介质中不同孔径对应不同横向弛豫时间, 结合自由态瓦斯核磁共振谱特性试验, 可以在核磁共振T2谱定量划分微孔隙、中?大孔?裂隙以及不受限自由空间范围, 进而对T2谱纵坐标积分求得吸附态和游离态瓦斯[15].


1.2
迟滞效应微细观评价指标


煤系页岩瓦斯主要以吸附态和游离态形式存在, 有煤系页岩(80 ~ 100目页岩粉)瓦斯吸附?解吸核磁共振谱实验研究发现, 吸附态和游离态瓦斯解吸过程均有迟滞效应[15]. 国内外****在高分子聚合物、煤岩和土壤等领域研究从宏观角度给出了吸附?解吸迟滞效应定量评价指标, 如表1所示, HI(hysteresis index)为宏观定量评价指标, 但它们对于煤系页岩迟滞效应微细观评价并不完全适用. 在文献[25]基础上, 本文提出一种适用于煤系页岩瓦斯迟滞效应微细观定量评价指标, 评价模型如图2所示. $S$为煤系页岩瓦斯核磁共振T2谱幅值积分(煤系页岩瓦斯量).




表
1
迟滞效应宏观定量评价指标



Table
1.
Macro quantitative evaluation index of hysteresis



table_type2 ">
Evaluation indexFormulaParameterReference
Freundlich${S_{{
m{ad}}}} = {K_{{
m{ad}}}}{C_{{
m{ad}}}}^{1/{n_{{
m{ad}}}}}$,
${S_{{
m{de}}}} = {K_{{
m{de}}}}{C_{{
m{de}}}}^{1/{n_{{
m{de}}}}}$,
$HI = dfrac{{{n_{{
m{de}}}}}}{{{n_{{
m{ad}}}}}}$		${S_{{
m{ad}}}}$—equilibrium concentration of solid phase adsorption
${S_{{
m{de}}}}$—equilibrium concentration of solid phase desorption
K—adsorption parameter
C—equilibrium concentration of adsorbent
${n_{{
m{ad}}}}$—Freundlich adsorption index
${n_{{
m{de}}}}$ —Freundlich desorption index		[21-22]
slope$HI = dfrac{{{f_{{
m{ad}}}}^prime (C) - {f_{{
m{de}}}}^prime (C)}}{{{f_{{
m{ad}}}}^prime (C)}}$		${f_{{
m{ad}}}}^prime (C)$, ${f_{{
m{de}}}}^prime (C)$—first derivative of characteristic equation		[23]
solid phase concentration$HI = dfrac{{max ({S_{{
m{de}}}} - {S_{{
m{ad}}}})}}{{{S_{{
m{ad}}}}}}$,
$HI = {left. {dfrac{{max ({S_{{
m{de}}}} - {S_{{
m{ad}}}})}}{{{S_{{
m{ad}}}}}}}
ight|_{T,C}}$		${S_{{
m{ad}}}}$—equilibrium concentration of solid phase adsorption
${S_{{
m{de}}}}$—equilibrium concentration of solid phase desorption
C—equilibrium concentration of adsorbent
T—test temperature		[24]
area$HI = 100left(dfrac{{{A_{{
m{de}}}} - {A_{{
m{ad}}}}}}{{{A_{{
m{ad}}}}}}
ight)$		${A_{{
m{de}}}}$—area under desorption curve
${A_{{
m{ad}}}}$—area under adsorption curve		[25]





下载:
导出CSV
|显示表格




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-264-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
迟滞评价模型示意图



Figure
2.
Schematic diagram of hysteresis model



下载:
全尺寸图片
幻灯片


选取常用吸附?解吸模型分别拟合煤系页岩瓦斯核磁共振谱数据, 采用相关系数R2作为最优等温吸附?解吸表征模型选取参数. 在寻找到最优表征模型后, 根据微细观迟滞评价指标MHI (microscopic hysteresis index) 定量计算煤系页岩瓦斯迟滞效应, 如式(2) ~ 式(4)所示







$${A_{{
m{hy}}}} = int_{{sigma _{min }}}^{{sigma _{max }}} {{f_{{
m{de}}}}(sigma )} {
m{d}}sigma - int_{{sigma _{min }}}^{{sigma _{max }}} {{f_{{
m{ad}}}}(sigma )} {
m{d}}sigma $$
(2)







$${A_{{
m{hf}}}} = f({sigma _{max }})({sigma _{max }} - {sigma _{min }}) - int_{{sigma _{min }}}^{{sigma _{max }}} {{f_{{
m{ad}}}}(sigma )} {
m{d}}sigma $$
(3)







$$MHI = frac{{{A_{{
m{hy}}}}}}{{{A_{{
m{hf}}}}}} times 100{text{%}} $$
(4)

式中${sigma _{min }}$为积分起始边界压力, MPa; ${sigma _{min }}$为积分终止边界压力, MPa; ${A_{{
m{hf}}}}$为完全不可逆迟滞区域面积; ${A_{{
m{hy}}}}$为实验迟滞区域面积; ${f_{{
m{ad}}}}(sigma )$为最优等温吸附模型; ${f_{{
m{de}}}}(sigma )$为最优等温解吸模型; $f({sigma _{max }})$为压力为${sigma _{max }}$最优等温吸附/解吸模型对应煤系页岩瓦斯核磁共振T2谱幅值积分; $M({sigma _{max }},f({sigma _{max }}))$为最优等温吸附和解吸模型曲线交点. MHI准确反映了煤系页岩瓦斯微细观迟滞程度, 当吸附?解吸过程完全可逆时, 吸附和解吸曲线重合, 实验迟滞区域面积趋于零, 由式(4)可得MHI = 0; 当吸附?解吸过程完全不可逆时等温解吸曲线不存在, 此时${A_{{
m{hf}}}}$ = ${A_{{
m{hy}}}}$. 由式(4)可得MHI = 1.


2.
煤系页岩瓦斯吸附?解吸迟滞效应核磁共振谱实验



2.1
试样采集和实验设备



2.1.1
试样采集

双鸭山矿区煤系页岩瓦斯储量大且具有较高开采价值. 试样取自双鸭山盆地东保卫煤矿三采区36# 煤层底板煤系页岩, 埋深578 m, 物理参数如表2所示.

取未风化煤系页岩, 实验室粉碎研磨制取不同粒径页岩粉, 并将足量岩粉在烘干箱中105 °C烘干24 h. 冷却后将18.70 g (40 ~ 60目)粗岩粉、37.45 g (80 ~ 110目)细岩粉和3.15 g (30 ~ 40目)松香, 三者充分混合后在200 t压力实验机上压制成型, 试样直径为24.87 mm, 高度为50.12 mm, 型岩试样迅速用保鲜膜包裹, 胶带缠绕后, 进行蜡封.




表
2
页岩特征参数



Table
2.
Shale characteristic parameters



table_type1 ">
Nameρ/(g·cm?3)φ/%σbc/MPaE/GPa
shale2.431.6 ~ 5.03.0 ~ 18.713.5





下载:
导出CSV
|显示表格



2.1.2
实验设备

煤系页岩瓦斯吸附?解吸迟滞效应核磁共振谱现场实验如图3所示, 实验装置连接如图4所示: 主要有动力加载系统、压力调节系统、温度控制系统、MacroMR12-150H-1低场核磁共振测试分析仪和数据采集系统, 煤系页岩吸附气采用高纯度甲烷, 实验温度25 ± 0.5 °C.


2.2
实验步骤


为进一步研究煤系页岩瓦斯吸附?解吸迟滞效应, 对同一试样首次进行三维应力状态吸附?解吸迟滞效应全过程低场核磁共振谱实验, 力求能从微细观尺度对原位应力状态下煤系页岩瓦斯迟滞规律进行更为精细的实验表征.

试样和核磁共振夹持器上下压头之间存在微小空间, 实验过程中此空间内会充满来自甲烷气瓶的自由态瓦斯. 为了能够采用核磁共振T2谱方法计算吸附态和游离态瓦斯, 有必要先对夹持器空隙自由态瓦斯进行核磁共振谱特性实验, 再进行煤系页岩瓦斯吸附?解吸迟滞效应核磁共振谱实验.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-264-3.jpg'"
class="figure_img
figure_type2 ccc " id="Figure3" />



图
3
煤系页岩瓦斯吸附?解吸迟滞效应现场实验



Figure
3.
Field experiment on hysteresis effect of gas adsorption-desorption in coal shale



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-264-4.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4" />



图
4
煤系页岩瓦斯吸附?解吸迟滞效应实验装置连接示意图



Figure
4.
Connection diagram of gas adsorption-desorption hysteresis effect experiment device for coal shale



下载:
全尺寸图片
幻灯片



2.2.1
自由态瓦斯核磁共振谱特性实验

将外径25.10 mm、内径4.2 mm、高49.60 mm的聚四氟乙烯试样放入核磁共振夹持器中, 如图4所示连接好实验装置进行自由态瓦斯核磁共振谱特性实验.

首先用氦气驱除管线及核磁共振夹持器内其它干扰性吸附气体, 检查管线气密性, 用真空泵负压10 kPa连续抽真空30 min, 启动低场核磁共振分析仪进行数据采集.

氮气通过减压阀、压力表和恒温水浴箱进入轴压活塞腔内给试样施加轴压; 启动高压氟油循环温控系统(循环氟油温度25 ± 0.5 °C), 将高压氟油由核磁共振夹持器围压入口注入, 围压出口循环流出给试样施加围压, 同时给试样提供稳定温度场; 接通高压瓦斯瓶, 通过减压阀、水浴箱和压力表将瓦斯注入瓦斯参考缸中预热至25 °C, 预热后瓦斯经六通阀流入核磁共振夹持器实验腔体中, 给试样施加孔隙压力. 自由态瓦斯核磁共振T2谱标定实验方案如表3所示, 按顺序依次完成实验并采集和记录相关数据.




表
3
自由态瓦斯核磁共振谱特性实验方案



Table
3.
Experiment of free gas by NMR spectrums



table_type1 ">
No.Confining
pressure
/MPa		Axial
pressure
/MPa		Pore
pressure
/MPa
11.792.131.35
23.093.542.46
34.034.933.52
44.995.714.43
56.026.465.44
67.017.566.50
78.899.418.29





下载:
导出CSV
|显示表格



2.2.2
煤系页岩瓦斯吸附?解吸迟滞效应核磁共振谱实验

页岩埋深578 m, 综合考虑实验安全和非磁性核磁共振夹持器极限承载能力, 在这里采用地应力折减、瓦斯压力不折减的方法对模型施加地应力和瓦斯压力[25], 选取煤系页岩瓦斯压力比例尺Cρ = 1, 垂直地应力比例尺Cσ = 4, 侧压系数为1.2, 地层平均容重为25 kN/m3[26], 可得实验工况轴压为3.61 MPa, 围压为2.97 MPa, 实验甲烷压力为2.24 MPa. 同时对相邻和深部煤系页岩瓦斯进行实验室相似工况模拟, 模拟埋深分别为350 m, 550 m, 750 m, 850 m, 1050 m, 1200 m和1500 m. 自由态瓦斯标定实验结束后, 将直径24.87 mm、长度50.12 mm型页岩试样放入核磁共振夹持器中, 按图4所示重新连接实验装置, 进行煤系页岩瓦斯吸附?解吸迟滞效应核磁共振谱实验.

(1)吸附实验

首先用氦气对管线和夹持器腔体进行冲扫, 负压10 kPa连续抽真空120 min. 启动低场核磁共振分析仪进行数据采集, 压力加载顺序为轴压?围压?孔隙压力, 压力加载方式和自由态瓦斯标定实验相同, 具体实验方案如表4所示, 按顺序依次完成实验并采集和记录相关数据.




表
4
吸附过程核磁共振谱实验方案



Table
4.
Experimental adsorption of gas by NMR spectrums



table_type1 ">
No.Confining
pressure
/MPa		Axial
pressure
/MPa		Pore
pressure
/MPa
11.782.241.31
22.973.612.24
34.044.473.37
45.025.434.39
56.026.445.65
67.017.456.33
78.799.347.89





下载:
导出CSV
|显示表格



(2) 解吸实验

在煤系页岩瓦斯吸附实验结束后, 立即进行煤系页岩瓦斯解吸实验, 具体实验方案如表5所示, 按顺序依次完成实验并采集和记录相关实验数据.




表
5
解吸过程核磁共振谱实验方案



Table
5.
Experimental desorption of gas by NMR spectrums



table_type1 ">
No.Confining
pressure
/MPa		Axial
pressure
/MPa		Pore
pressure
/MPa
18.799.347.89
27.498.186.94
36.547.235.76
45.476.244.48
54.525.153.41
63.514.162.40
72.493.251.41
80.951.470.40





下载:
导出CSV
|显示表格



3.
实验结果


煤系页岩瓦斯吸附?解吸实验过程中, 核磁共振夹持器内测试样品同时受到轴压?围压?孔隙压力共同作用, 采用平均有效应力σe[27]表示三者对试样应力场综合作用效果, 相关实验结果如下.


3.1
自由态瓦斯核磁共振谱特性实验结果


自由态瓦斯核磁共振谱特性实验结果如图5所示, 随着平均有效应力增加, 自由态瓦斯横向弛豫时间T2逐渐增大, 当平均有效应力在1.76 ~ 8.98 MPa, 对应自由态瓦斯T2谱范围为93.00 ~ 2710.63 ms, 且T2谱曲线只有一个特征峰, 这与前人研究结论一致[28].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-264-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
自由态瓦斯T2谱



Figure
5.
T2 spectrum of free gas



下载:
全尺寸图片
幻灯片



3.2
煤系页岩瓦斯吸附?解吸迟滞效应核磁共振谱实验结果


煤系页岩瓦斯迟滞效应核磁共振谱实验结果如图6和图7所示.



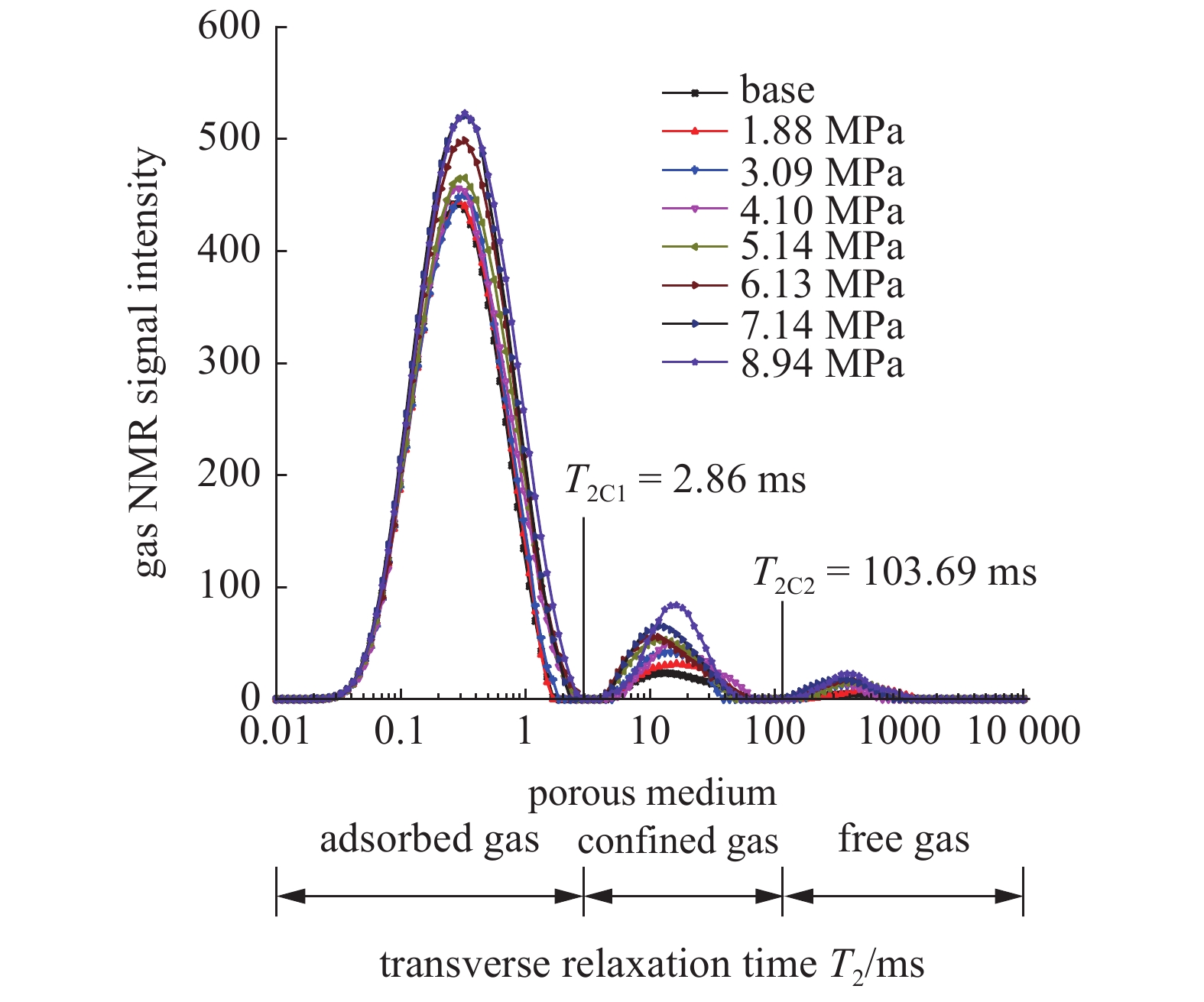onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-264-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
吸附过程T2谱



Figure
6.
T2 spectrum of shale gas adsorption



下载:
全尺寸图片
幻灯片




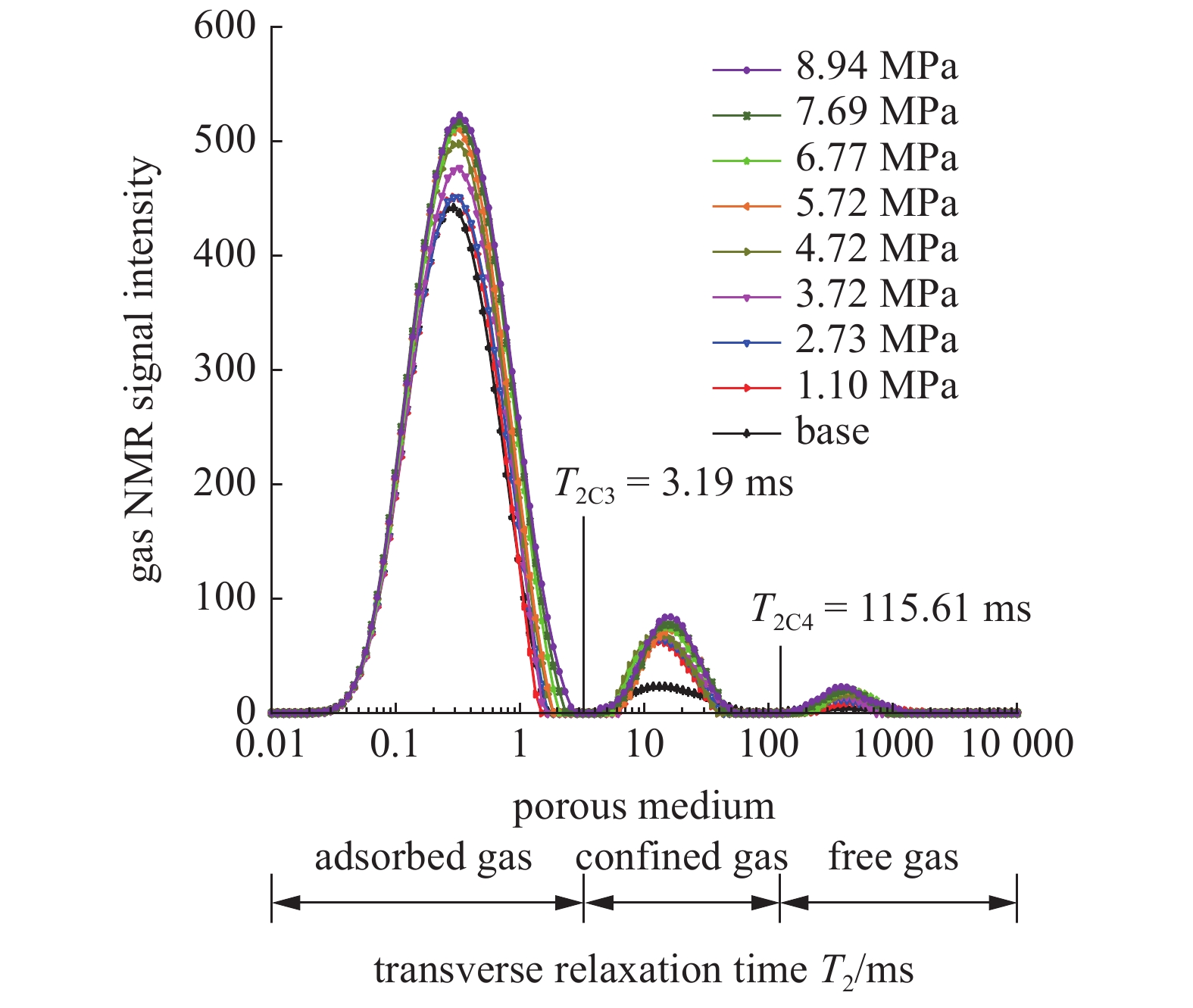onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-264-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
解吸过程T2谱



Figure
7.
T2 spectrum of shale gas desorption



下载:
全尺寸图片
幻灯片


由图5可以确定图6中横向弛豫时间T2大于103.69 ms部分为自由态瓦斯谱峰(> T2C2 = 103.69 ms). 由式(1)可知孔隙越小T2时间越短, 因此微孔隙横向弛豫时间要比中?大孔隙?裂隙横向弛豫时间短, 所以图6中横向弛豫时间T2小于2.86 ms部分为吸附态瓦斯谱峰(< T2C1 = 2.86 ms), 中间部分T2谱则为游离态瓦斯谱峰(T2C1 – T2C2). 同理可得图7解吸过程中自由态瓦斯T2谱峰(> T2C4 = 115.61 ms)、吸附态瓦斯T2谱峰(< T2C3 = 3.19 ms)和游离态瓦斯T2谱峰(T2C3 – T2C4), 这一划分方法与Yao等[19]研究相吻合.


4.
煤系页岩瓦斯吸附?解吸迟滞效应分析


由图6和图7可得吸附态和游离态瓦斯迟滞效应评价模型如图8和图9所示.



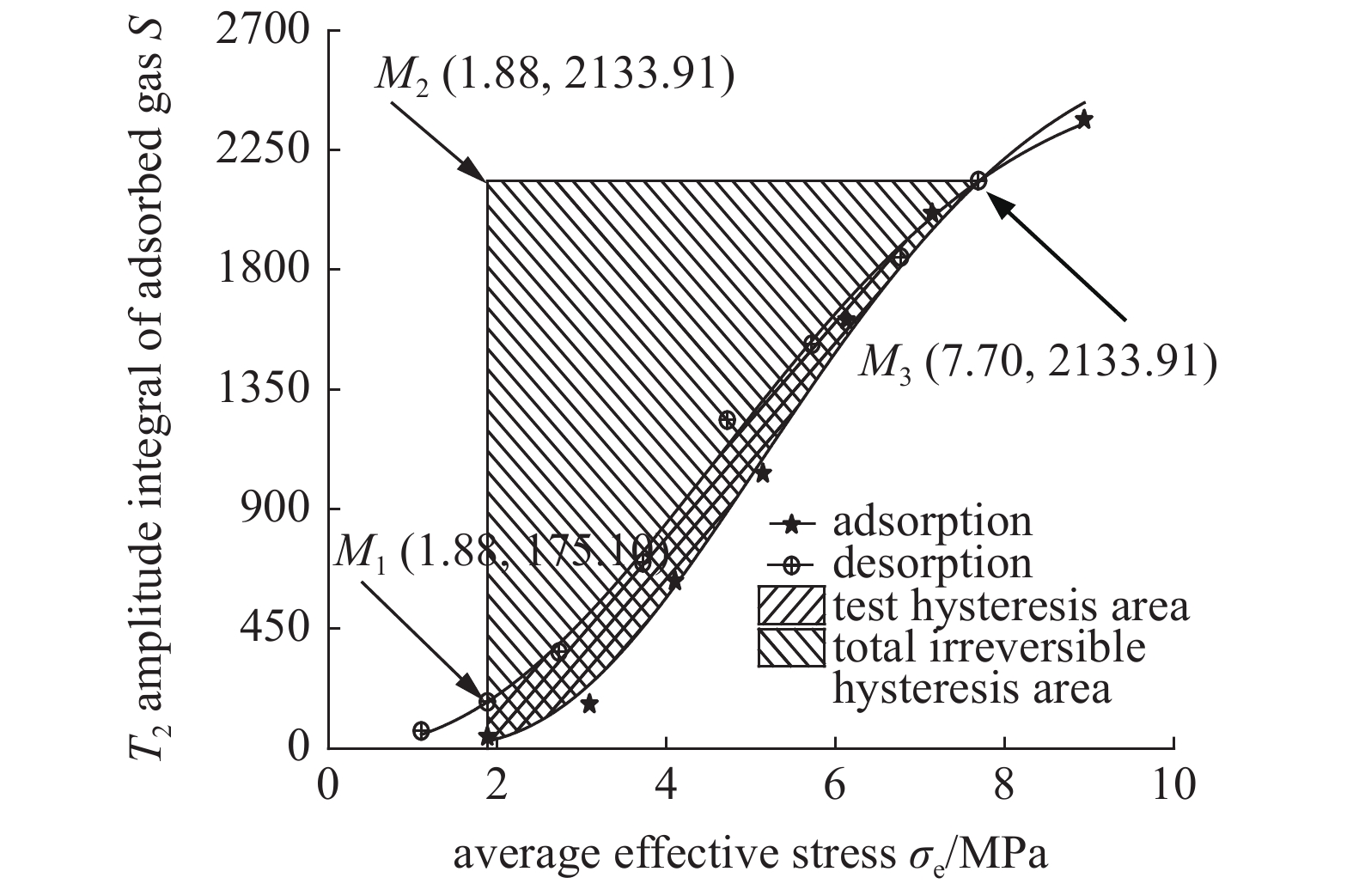onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-264-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
吸附态瓦斯迟滞效应评价模型



Figure
8.
Evaluation model for hysteresis effect of adsorbed gas



下载:
全尺寸图片
幻灯片




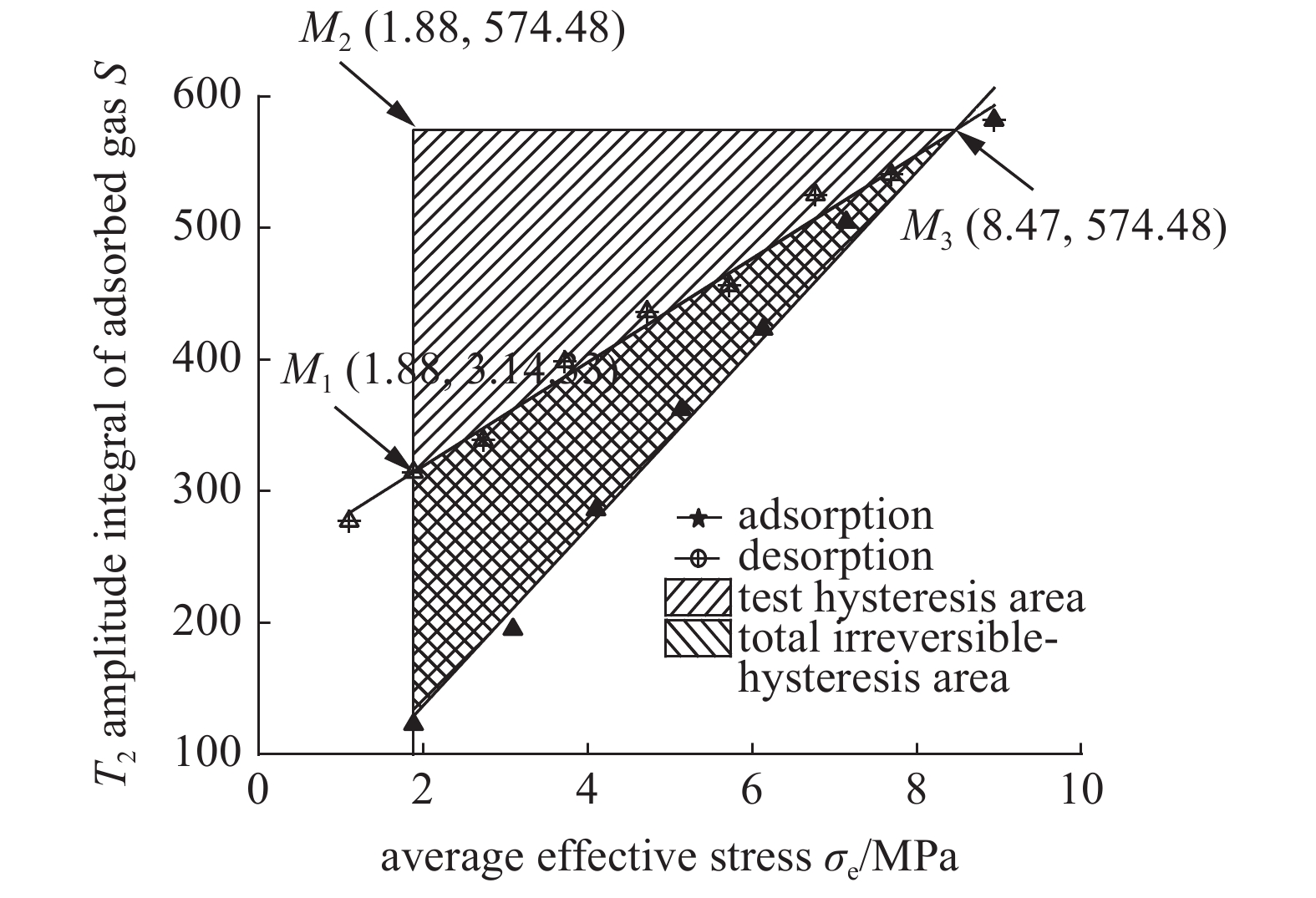onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-264-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
游离态瓦斯迟滞效应评价模型



Figure
9.
Evaluation model for hysteresis effect of porous medium-confined gas



下载:
全尺寸图片
幻灯片



4.1
吸附态瓦斯迟滞效应分析



4.1.1
吸附态瓦斯迟滞现象

由图8可知吸附态瓦斯量(吸附态瓦斯T2谱幅值积分S)与平均有效应力${sigma _{
m{e}}}$之间具有明显非线性特征, 使用D-A, D-R和BET等温模型对吸附态瓦斯吸附过程模拟时均需饱和蒸汽压力P0, 而实验温度25 ± 0.5 °C(甲烷临界温度?82.6 °C), 因此采用虚拟饱和蒸汽压力替代饱和蒸汽压力, 采用Dubinin算法[29]可得实验条件虚拟饱和蒸汽压力为11.24 MPa.

选取具有代表性的吸附和解吸模型, 分别模拟吸附态瓦斯吸附?解吸核磁共振谱实验数据, 模型公式及其相关系数R2如表6和表7所示. 由表6可得采用D-R模型拟合吸附态瓦斯吸附实验数据, 对应相关系数R2值为0.99475拟合程度最高; 由表7可得采用Weibull函数模型拟合吸附态瓦斯解吸实验数据, 对应相关系数R2值为0.996 6拟合程度最高; 因此选用D-R模型和Weibull函数模型分别作为吸附态瓦斯吸附和解吸过程最佳表征模型.




表
6
常用吸附模型



Table
6.
Common adsorption models



table_type1 ">
ModelModel expressionAdsorption R2
L $V = P{V_{
m{L}}}/({P_{
m{L}}} + P)$		 0.80002
F $V = {K_{
m{b}}}{P^m}$		 0.93634
E-L $V = {K_{
m{b}}}P{V_{
m{L}}}/(1 + {K_{
m{b}}}P + msqrt {{K_{
m{b}}}P} )$		 0.99038
T $V = {K_{
m{b}}}P{V_{
m{L}}}/{[1 + {({K_{
m{b}}}P)^m}]^{1/m}}$		 0.75002
B-BET $V = dfrac{{{V_{
m{m}}}CP}}{{({P^0} - P)[1 + (C - 1)(P/{P^0})]}}$		 0.76401
T-BET $V = dfrac{{{V_{
m{m}}}CP[1 - (n - 1)(P/{P^0}) + n{{(P/{P^0})}^{n + 1}}]}}{{({P^0} - P)[1 + (C - 1)(P/{P^0}) - C{{(P/{P^0})}^{n + 1}}]}}$		 0.93211
D-R $V = {V_0}exp [ - D{ln ^2}({P^0}/P)]$ 0.99475
D-A $V = {V_0}exp [ - D{ln ^m}({P^0}/P)]$ 0.56960
注: PL—Langmuir压力, MPa; VL—Langmuir体积, cm3/g; Vm—单层极限吸附量, cm3/g; P0—饱和蒸汽压力, MPa; C—吸附热常数; V0—最大吸附量, cm3/g; Kb—吸附经验常数; m—吸附剂非均质参数; n—模型参数; D—净吸附热常数.
Notes: PL—Langmuir pressure, MPa; VL—Langmuir volume, cm3/g; Vm—monolayer limit adsorption capacity, cm3/g; P0—saturated steam pressure, MPa; C—adsorption heat constant; V0—maximum adsorption capacity, cm3/g; Kb—adsorption empirical constant; m—adsorbent heterogeneity parameters; n—model parameter; D—final adsorption heat constant.





下载:
导出CSV
|显示表格






表
7
常用解吸模型



Table
7.
Common desorption models



table_type1 ">
ModelModel expressionDesorption R2
Weibull $V = {V_0}[1 - exp ( - b{p^q})]$ 0.99660
desorption function $V = dfrac{{abp}}{{1 + bp}} + c$ 0.97953
注: a—煤系页岩最大吸附量, cm3/g; b—吸附热、吸附速度与解吸速度综合函数, MPa?1; c—残余吸附量, cm3/g; V0—最大吸附量, cm3/g; b—吸附热常数; q—吸附质在孔隙表面的占位比.
Notes: a—maximum adsorption capacity of coal shale, cm3/g; b—comprehensive function of adsorption heat, adsorption rate and desorption rate, MPa?1; c—residual adsorption capacity, cm3/g; V0—maximum adsorption capacity, cm3/g; b—adsorption heat constant; q—occupation ratio of adsorbate on pore surface.





下载:
导出CSV
|显示表格



由图8可得吸附过程拟合曲线

S1(T2) = 2618.329exp$Big[ $?1.430ln2(11.24/${sigma _{
m{e}}}$)$Big] $, R2 = 0.99475

解吸过程拟合曲线

S2(T2) = 2543.331$Big[ $1 ? exp(?0.016 7${sigma _{
m{e}}}$2.3)$Big] $, R2 = 0.996 6

吸附过程S1(T2)与解吸过程S2(T2)在高应力阶段相交于M3点, 且存在临界滞后压力7.70 MPa. 当平均有效应力大于7.70 MPa, 吸附曲线S1(T2)比解吸曲线S2(T2)高, 无明显迟滞现象; 当平均有效应力在1.88 ~ 7.70 MPa, 解吸曲线S2(T2)在吸附曲线S1(T2)之上, 解吸过程具有明显滞后环.


4.1.2
吸附态瓦斯迟滞区域面积

由图8可知, 吸附过程发生在平均有效应力1.88 ~ 8.94 MPa范围内, 而解吸过程平均有效应力为1.10 ~ 8.94 MPa, 因此以${sigma _{{
m{e1}}}}$ = 1.88 MPa作为吸附态瓦斯迟滞起始边界, 并将其代入解吸曲线S2(T2) = 2543.331$Big[$1 ? exp(?0.016 7${sigma _{
m{e}}}$2.3)$Big]$, 求得S2(T2) = 175.10, 即解吸实验曲线模拟终点M1(1.88, 175.10); 吸附?解吸曲线交点横坐标为7.70 MPa, 对应吸附态瓦斯幅值积分为2133.91即M3(7.70, 2133.91); 吸附?解吸迟滞区域起始边界和上边界交点为M2(1.88, 2133.91). 在此边界条件结合式(2) ~ 式(3)可得吸附态瓦斯完全不可逆迟滞区域面积${A_{{
m{hf}} - {
m{ad}}}}$和实验迟滞区域面积${A_{{
m{hy}} - {
m{ad}}}}$如式(5) ~ 式(6)所示, ${sigma _{{
m{e}} - min }}$—积分起始边界压力, MPa







$${A_{{
m{hy}} - {
m{ad}}}} = int_{{sigma _{
m{e}}}_{ - min }}^{7.70} {{S_2}({T_2})} {
m{d}}{sigma _{
m{e}}} - int_{{sigma _{
m{e}}}_{ - min }}^{7.70} {{S_1}({T_2})} {
m{d}}{sigma _{
m{e}}};;;;;;;$$
(5)







$${A_{{
m{hf}} - {
m{ad}}}} = 2133.91 times (7.70 - {sigma _{{
m{e }}- min }}) - int_{{sigma _{
m{e}}}_{ - min }}^{7.70} {{S_1}({T_2})} {
m{d}}{sigma _{
m{e}}}$$
(6)


4.2
游离态瓦斯迟滞效应分析



4.2.1
游离态瓦斯吸附?解吸迟滞现象

由图9可得游离态瓦斯量(游离态瓦斯T2谱幅值积分S)与平均有效应力${sigma _{
m{e}}}$之间具有明显线性特征. 设游离态瓦斯吸附和解吸最佳表征模型均为S = K${sigma _{
m{e}}}$ + C, K为斜率, C为截距.

吸附过程拟合曲线

S3(T2) = 67.577${sigma _{
m{e}}}$ + 2.060, R2 = 0.98872

解吸过程拟合曲线

S4(T2) = 39.472${sigma _{
m{e}}}$ + 240.124, R2 = 0.98637

当平均有效应力大于8.47 MPa, 游离态瓦斯解吸曲线S4(T2)低于吸附曲线S3(T2), 无明显迟滞现象; 当平均有效应力在1.88 ~ 8.47 MPa范围内, 游离态瓦斯解吸曲线S4(T2)高于吸附曲线S3(T2), 游离态瓦斯解吸过程具有明显迟滞效应, 且存在临界迟滞压力8.47 MPa.


4.2.2
游离态瓦斯迟滞区域面积

由图9可知游离态瓦斯吸附过程发生在平均有效应力1.88 ~ 8.94 MPa范围内, 而解吸过程平均有效应力为1.10 ~ 8.94 MPa, 因此以${sigma _{{
m{e}}2}}$ = 1.88 MPa作为游离态瓦斯迟滞起始边界, 并将其代入解吸曲线S4(T2) = 39.472${sigma _{
m{e}}}$ + 240.124, 求得S4(T2) = 314.33, 即得游离态瓦斯解吸实验曲线模拟终点M1(1.88, 314.33); 游离态瓦斯吸附?解吸曲线交点横坐标为8.47 MPa, 对应幅值积分为574.48即M3(8.47, 574.48); 在此边界条件结合式(2) ~ 式(3)可得游离态瓦斯完全不可逆迟滞区域面积Ahf?pm和实验迟滞区域面积Ahy?pm如式(7) ~ 式(8)所示, ${sigma _{{
m{e}} - min }}$—积分起始边界压力, MPa







$${A_{{
m{hy}} - {
m{pm}}}} = int_{{sigma _{
m{e}}}_{ - min }}^{8.47} {{S_4}({T_2})} {
m{d}}{sigma _{
m{e}}} - int_{{sigma _{
m{e}}}_{ - min }}^{8.47} {{S_3}({T_2})} {
m{d}}{sigma _{
m{e}}};;;;;$$
(7)







$${A_{{
m{hf}} - {
m{pm}}}} = 574.48 times (8.47 - {sigma _{{
m{e}} - min }}) - int_{{sigma _{
m{e}}}_{ - min }}^{8.47} {{S_3}({T_2})} {
m{d}}{sigma _{
m{e}}}$$
(8)


4.3
煤系页岩瓦斯微细观迟滞规律


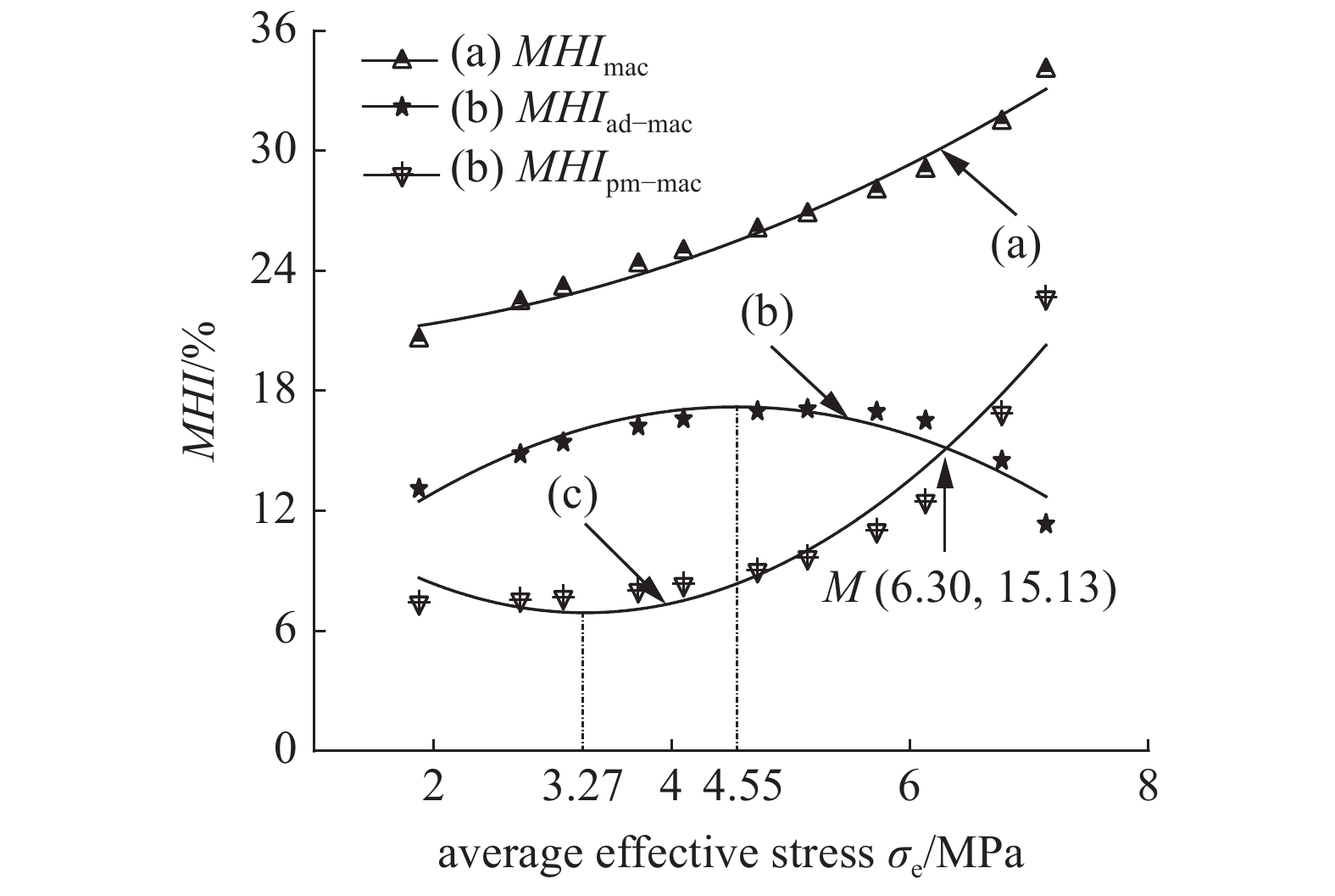
煤系页岩瓦斯主要以吸附态和游离态形式存在(忽略极少量基质固溶态瓦斯), 因此可以用吸附态和游离态瓦斯幅值积分之和, 近似表征吸附?解吸过程中煤系页岩瓦斯宏观吸附量和解吸量, 从微细观角度探究煤系页岩瓦斯宏观吸附?解吸迟滞规律. 结合式(2) ~ 式(8)可得煤系页岩瓦斯宏观迟滞系数MHImac, 以及吸附态和游离态瓦斯迟滞系数MHIad?mac和MHIpm?mac如式(9) ~ 式(11)所示, 并由此可得瓦斯迟滞系数与平均有效应力关系, 如图10所示







$$MH{I_{{
m{mac}}}} = 100{text{%}} times frac{{{A_{{
m{hy}} - {
m{ad}}}} + {A_{{
m{hy}} - {
m{pm}}}}}}{{{A_{{
m{hf}} - {
m{ad}}}} + {A_{{
m{hf}} - {
m{pm}}}}}}$$
(9)







$$MH{I_{{
m{ad}} - {
m{mac}}}} = 100{text{%}} times frac{{{A_{{
m{hy}} - {
m{ad}}}}}}{{{A_{{
m{hf}} - {
m{ad}}}} + {A_{{
m{hf}} - {
m{pm}}}}}}$$
(10)







$$MH{I_{{
m{pm}} - {
m{mac}}}} = 100{text{%}} times frac{{{A_{{
m{hy}} - {
m{pm}}}}}}{{{A_{{
m{hf}} - {
m{ad}}}} + {A_{{
m{hf}} - {
m{pm}}}}}}$$
(11)

由图10可得煤系页岩瓦斯宏观迟滞系数与平均有效应力具有明显幂函数关系. 宏观迟滞效应中由吸附态或游离态瓦斯引起的迟滞系数与平均有效应力均可采用二次多项式拟合, 且两曲线交于点M(6.30, 15.13).

当平均有效应力${sigma _{
m{e}}}$在高应力状态(6.30 ~ 7.14 MPa)游离态瓦斯迟滞系数曲线(b)在吸附态瓦斯迟滞系数曲线(c)之上且两曲线变化趋势相反, 游离态瓦斯对宏观瓦斯迟滞效应贡献大于吸附态瓦斯; 当平均有效应力${sigma _{
m{e}}}$在(1.88 ~ 6.30 MPa)游离态瓦斯迟滞系数曲线(b)在吸附态瓦斯迟滞系数曲线(c)之下, 此阶段宏观瓦斯迟滞效应受控于吸附态瓦斯迟滞效应.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-264-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
瓦斯迟滞系数与平均有效应力关系



Figure
10.
Relationship between hysteresis index of gas and average effective stress



下载:
全尺寸图片
幻灯片



4.3.1
煤系页岩瓦斯宏观迟滞规律

由核磁共振谱方法测定的煤系页岩瓦斯宏观迟滞系数MHImac = 0.23${sigma _{
m{e}}}^{2.021}$ + 20.407, R2 = 0.97708, 随着平均有效应力减小, 瓦斯宏观迟滞系数呈幂函数减小趋势如图10中(a)曲线所示, 当平均有效应力从7.14 MPa降低到1.88 MPa, 对应瓦斯宏观迟滞系数由34.02%降低到20.54%, 瓦斯宏观迟滞效应逐渐减小. 随着宏观迟滞系数减小, 煤系页岩瓦斯解吸量逐渐增大.


4.3.2
吸附态瓦斯迟滞规律

宏观迟滞效应中由吸附态瓦斯引起的迟滞系数MHIad?mac = ?0.664$sigma _{
m{e}}^2$ + 6.038${sigma _{
m{e}}}$ + 3.481, R2 = 0.82395.

随着平均有效应力降低, 吸附态瓦斯迟滞系数呈现出先增大后减小趋势如图10中(b)曲线所示. 当平均有效应力从7.14 MPa降低到4.55 MPa, 对应迟滞系数反而从11.35%增加到17.21%, 然而当平均有效应力从4.55 MPa降低到1.88 MPa, 对应迟滞系数则由17.21%逐渐降低到13.12%.

这一变化规律与煤系页岩原生微孔隙重新吸附和新生孔隙吸附有关. 煤系页岩微孔隙吸附态瓦斯处于吸附?解吸可逆动平衡状态, 卸压初始阶段(4.55 ~ 7.14 MPa)虽然平均有效应力有所降低, 但此时煤系页岩仍处于高应力状态, 当平均有效应力大于部分微孔隙端部应力强度因子, 微孔隙裂纹会继续扩展, 形成新微孔隙[30], 同时新生微孔隙也会使吸附态瓦斯扩散通道迂曲度变大, 吸附态瓦斯向外扩散受限. 此时解吸出的吸附态瓦斯一部分在高瓦斯浓度条件下重新在原生微孔隙表面吸附, 一部分则会在新生微孔隙吸附, 高平均有效应力阶段, 虽然平均有效应力降低36.27%, 但由吸附态瓦斯引起宏观迟滞系数反而增加51.63%.

随着继续卸压(1.88 ~ 4.55 MPa), 平均有效应力由4.55 MPa逐步减小, 新微孔隙产生速度减慢, 孔隙变形损伤减小. 同时随着游离态瓦斯不断采出, 孔裂隙瓦斯浓度梯度逐渐变大, 在瓦斯浓度梯度作用下吸附态瓦斯加速向中?大孔隙?裂隙结构扩散, 吸附态瓦斯引起的宏观迟滞效应逐渐变小, 吸附态瓦斯开始迅速大量解吸.


4.3.3
游离态瓦斯迟滞系数

宏观迟滞效应中由游离态瓦斯引起的迟滞系数MHIpm?mac = 0.895$sigma _{
m{e}}^2$ ? 5.856${sigma _{
m{e}}}$ + 16.499, R2 = 0.91806.

随着平均有效应力降低, 迟滞系数呈现先减小后增大趋势如图10中(c)曲线所示. 当平均有效应力从7.14 MPa降低到3.27 MPa, 对应迟滞系数由22.67%减小到6.92%, 但是当平均有效应力从3.27 MPa继续降低到1.88 MPa, 对应迟滞系数反而从6.92%增加到8.65%.

煤系页岩初始卸压阶段(3.27 ~ 7.14 MPa), 随着平均有效应力逐步减小中?大孔隙?裂隙损伤逐渐变大, 游离态瓦斯散失通道迂曲度增加. 但此时游离态瓦斯流动近似为达西流动且大部分处于超临界状态, 其渗透性远超出常温常压状态[31], 即使孔隙裂隙迂曲度增加游离态瓦斯仍然快速向井壁渗透, 游离态瓦斯引起的迟滞系数急速下降.

继续卸压进入低应力阶段(1.88 ~ 3.27 MPa), 中?大孔隙?微裂隙部分继续闭合, 游离态瓦斯向井壁散失通道进一步受限, 且此时游离态瓦斯压力在其临界压力4.59 MPa以下, 渗透性明显减弱, 游离态瓦斯渗透能力降低, 迟滞系数随着平均有效应力减小反而增加25.04%.


5.
迟滞效应对煤系页岩瓦斯开采影响


随着煤系页岩瓦斯开采深度不断增加, 受高渗透压、高地应力和高地温综合影响, 煤岩体中瓦斯高度聚集, 瓦斯压力急剧增大[32], 煤系页岩瓦斯深部原位赋存环境变得更为复杂. 由本文研究结论可知: 随着埋深增加平均有效应力逐渐变大, 煤系页岩瓦斯吸附?解吸迟滞系数呈幂函数增加趋势. 但深部煤系页岩在高地应力和高孔裂隙瓦斯压力作用下, 内部孔裂隙损伤会进一步加大, 进而加剧微孔隙吸附态瓦斯扩散受限和中?大孔隙?裂隙游离态瓦斯渗透阻力变大, 渗流路径迂曲度增加[33], 而这些会进一步加剧深部煤系页岩瓦斯迟滞效应, 使深部煤系页岩瓦斯解吸?扩散?渗流机理变得更为复杂. 因此建议使用三维应力状态煤系页岩瓦斯等温解吸模型去评估深部煤系页岩瓦斯可采储量, 替代常用一维(仅考虑瓦斯压力)等温吸附模型.

深部煤系页岩储层孔隙度和渗透率都很低, 同时受煤系页岩瓦斯吸附?解吸迟滞效应影响, 煤系页岩瓦斯自然采收率普遍偏低, 因此煤系页岩瓦斯商业化开采必须依赖于有效的水力压裂改造措施. 由上述研究可知煤系页岩瓦斯宏观迟滞效应中, 由吸附态或游离态瓦斯引起的迟滞系数与平均有效应力均具有明显二次多项式函数关系, 因此在煤系页岩瓦斯水力压裂开采过程中, 应该科学把控支撑剂充填时间节点和不同粒度充填剂合理配比, 同时尝试在高应力卸压阶段向微孔隙结构中输送和铺置粒径更小, 强度更高支撑剂, 以增加对煤系页岩微孔隙结构改造, 进一步减小吸附?解吸过程中由吸附态瓦斯引起的迟滞效应, 加速吸附态瓦斯解吸扩散, 提高煤系页岩瓦斯产量.


6.
结论


由煤系页岩瓦斯吸附?解吸迟滞效应核磁共振谱实验研究主要得出以下结论:

(1)吸附过程中吸附态瓦斯量与平均有效应力符合D-R模型而解吸过程Weibull函数模型拟合程度更高; 游离态瓦斯量和平均有效应力呈线性关系, 且解吸过程均有滞后性;

(2)宏观迟滞效应中由吸附态或游离态瓦斯引起的迟滞系数与平均有效应力均可采用二次多项式拟合; 而煤系页岩瓦斯宏观迟滞系数与平均有效应力则具有明显幂函数关系;

(3)煤系页岩瓦斯吸附?解吸迟滞效应变化规律与孔裂隙应力损伤以及微孔隙瓦斯扩散受限有关.

相关话题/实验 过程 瓦斯 图片 页岩
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 海陆过渡相页岩气藏不稳定渗流数学模型
    引言海陆过渡相页岩气沉积环境稳定,富有机质页岩大面积分布;发育微纳米级孔?缝体系,具备较好储集能力;富含石英等脆性矿物,有利于储集层压裂改造[1];页岩地层压力适中[2],含气量高[3];存在大量微小孔洞和裂隙,但整体渗透率较差.为高效开发页岩气藏,压裂技术的应用越来越广泛[4-6].与普通气藏相比 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 固体颗粒对沟槽湍流边界层影响的实验研究
    引言减阻沟槽作为一种被动的减阻方式因其不消耗能源的特点拥有广泛的应用前景.减阻沟槽起源于对于海豚表皮的仿生学研究[1],海豚和鲨鱼表皮存在着微小的,沿着水流方向排列的沟槽结构.这些结构与鲨鱼体表的清洁程度和快速游泳能力有较大的关系[2].顺流沟槽的研究始于20世纪80年代美国兰利研究所[3-5],之 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 挠性航天器太阳翼全局模态动力学建模与实验研究
    引言随着航天领域的发展,现代大型柔性航天器往往安装有诸如大型太阳翼等柔性结构,为了得到可持续的能源,其尺寸日益增大、结构重量越来越轻,太阳翼的弹性振动不可避免地与航天器主体平台的运动相互耦合,这种耦合效应随着太阳翼尺寸的增大显著增强.此时,单个太阳能帆板的模态(假设模态)并不能准确反映整个太阳翼在系 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 半结晶聚合物损伤演化的实验表征与数值模拟1)
    张毅,2),薛世峰,韩丽美,周博,刘建林,贾朋中国石油大学(华东),山东青岛266580EXPERIMENTALCHARACTERIZATIONANDNUMERICALSIMULATIONOFDAMAGEEVOLUTIONINSEMI-CRYSTALLINEPOLYMERS1)ZhangYi,2), ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 张拉整体结构的动力学等效建模与实验验证1)
    陈占魁,罗凯,2),田强北京理工大学宇航学院力学系,北京100081DYNAMICEQUIVALENTMODELINGOFTENSEGRITYSTRUCTURESANDEXPERIMENTALVERIFICATION1)ChenZhankui,LuoKai,2),TianQiangDepartmen ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 自由场空泡溃灭过程能量转化机制研究1)
    韩磊,张敏弟,2),黄国豪,黄彪,3)北京理工大学,北京100081ENERGYTRANSFORMATIONMECHANISMOFAGASBUBBLECOLLAPSEINTHEFREE-FIELD1)HanLei,ZhangMindi,2),HuangGuohao,HuangBiao,3)Beiji ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 滚波演化中聚合过程的数值模拟研究1)
    陈歆怡*,王晓亮,*,2),刘青泉*,张静?*北京理工大学宇航学院力学系,北京100081?江苏省常州市金坛区水利局,江苏常州213200NUMERICALSTUDYOFCOALESCENCEINROLLWAVEDEVELOPMENT1)ChenXinyi*,WangXiaoliang,*,2),L ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 湍流边界层等动量区演化机理的实验研究1)
    王超伟*,王康俊*,李彪辉*,姜楠,*,??,2)*天津大学机械工程学院力学系,天津300130??天津市现代工程力学重点实验室,天津300130EXPERIMENTALINVESTIGATIONONTHEEVOLUTIONMECHANISMOFUNIFORMMOMENTUMZONESINTURBU ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 返回舱高雷诺数再入过程底部流动稳定性1)
    朱德华,2),沈清,杨武兵中国航天空气动力技术研究院,北京100074BASEFLOWSTABILITYOFRETURNCAPSULEDURINGREENTRYPROCESSWITHHIGHREYNOLDSNUMBER1)ZhuDehua,2),ShenQing,YangWubingChinaAca ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 长编组高速列车的列车风动模型实验研究 1)
    郭易&,郭迪龙,&,2),杨国伟&,?,刘雯&,?*中国科学院力学研究所流固耦合系统力学重点实验室,北京100190?中国科学院大学工程科学学院,北京100190MOVINGMODELANALYSISOFTHESLIPSTREAMOFA ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.