海陆过渡相页岩气藏不稳定渗流数学模型

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

引言

海陆过渡相页岩气沉积环境稳定, 富有机质页岩大面积分布; 发育微纳米级孔?缝体系, 具备较好储集能力; 富含石英等脆性矿物, 有利于储集层压裂改造^[1]; 页岩地层压力适中^[2], 含气量高^[3]; 存在大量微小孔洞和裂隙, 但整体渗透率较差. 为高效开发页岩气藏, 压裂技术的应用越来越广泛^[4-6]. 与普通气藏相比, 海陆过渡相页岩常煤层、致密砂岩层互层, 形成页岩气、煤层气和致密砂岩气叠置成藏^[7], 储层连续性较差、横向变化快、非均质性强, 水力压裂技术是其获得经济产量的关键手段^[8]. 特别是海陆过渡相页岩气, 地层可采性和可压裂性良好, 具有较好的稳产能力, 开发前景较好^[9]. 然而, 目前缺乏有效的海陆过渡相页岩气藏不稳定渗流数学模型, 对其渗流特征分析及储层参数评价不利^[10-12]. 因此, 亟需开展海陆过渡相页岩气藏渗流模型的研究工作.

目前, 国内外一些****在页岩气藏的渗流理论方面取得了良好的进展. 1986年, Lee和Brockenbrough^[13]假设储层和裂缝之间的流动方式是三线性流, 建立了无限大均质地层有限导流垂直裂缝井的三线性渗流模型. 随后, Ozkan等^[14]将三线性流解析模型应用于压裂水平井试井分析中, 分析了非常规储层中的不稳定渗流特征. 进一步地, 许多****开展了页岩气藏的渗流理论工作^[15-26]. 例如, 高杰等^[27]考虑了页岩气吸附解吸和扩散机理页岩气压裂水平三线性流模型, 通过数值反演求得考虑井储和表皮系数的无因次井底压力解, 并绘制了压力响应特征曲线, 分析了页岩气藏不稳定渗流特征. 2016年, 肖聪^[28]针对页岩气藏中多级压裂水平井和体积压裂水平井裂缝网络模型, 综合考虑吸附、扩散、基质变形、天然裂缝应力敏感以及裂缝网络高速非达西等非线性流动效应的作用, 建立了考虑压裂裂缝和天然裂缝耦合条件下的页岩气藏气井渗流模型. 2018年, 任文希^[29]采用离散裂缝模型对水力裂缝进行显式处理, 并采用连续介质模型表征压裂区和未压裂区, 建立了考虑应力敏感、多组分渗流和多组分吸附的页岩气多级压裂水平井渗流模型. 2020年, Meng等^[12]基于渗流理论, 建立了页岩储层复杂裂缝网络系统条件下的渗流数学模型, 模型中考虑了压裂裂缝的非均匀性, 并分析了页岩储层的不稳定渗流特征. 同年, 吴明录和丁明才^[30]基于分形理论, 考虑到天然裂缝的方向、位置、开度和长度等几何规律, 建立了分形离散裂缝网络模型, 并采用嵌入式离散裂缝和有限差分相结合的方法求解模型, 得到了水平井井底压力响应特征及影响规律, 这些研究成果对页岩气藏渗流理论及特征研究具有十分重要作用. 然而, 由于海陆过渡相页岩储层的特殊物性^[31], 存在着渗透率极强非均质性, 其渗流数学模型未见报道, 不利于海陆过渡相页岩气藏渗流特征分析及储层参数评价.

针对这一问题, 本文考虑页岩气吸附解吸, 扩散, 裂缝特点, 以及海陆过渡相非均质性等特征, 建立并求解径向非均质页岩气藏压裂直井的不稳定渗流数学模型, 得到典型的页岩气藏不稳定渗流特征, 建立海陆过渡相页岩气井的储层参数评价方法, 并进行数值模拟验证, 最后针对鄂尔多斯盆地海陆过渡相典型页岩气井开展了实例分析应用, 可为同类页岩气藏的压裂评价提供理论支撑.

1.
海陆过渡相页岩气藏渗流数学模型

1.1
物理模型

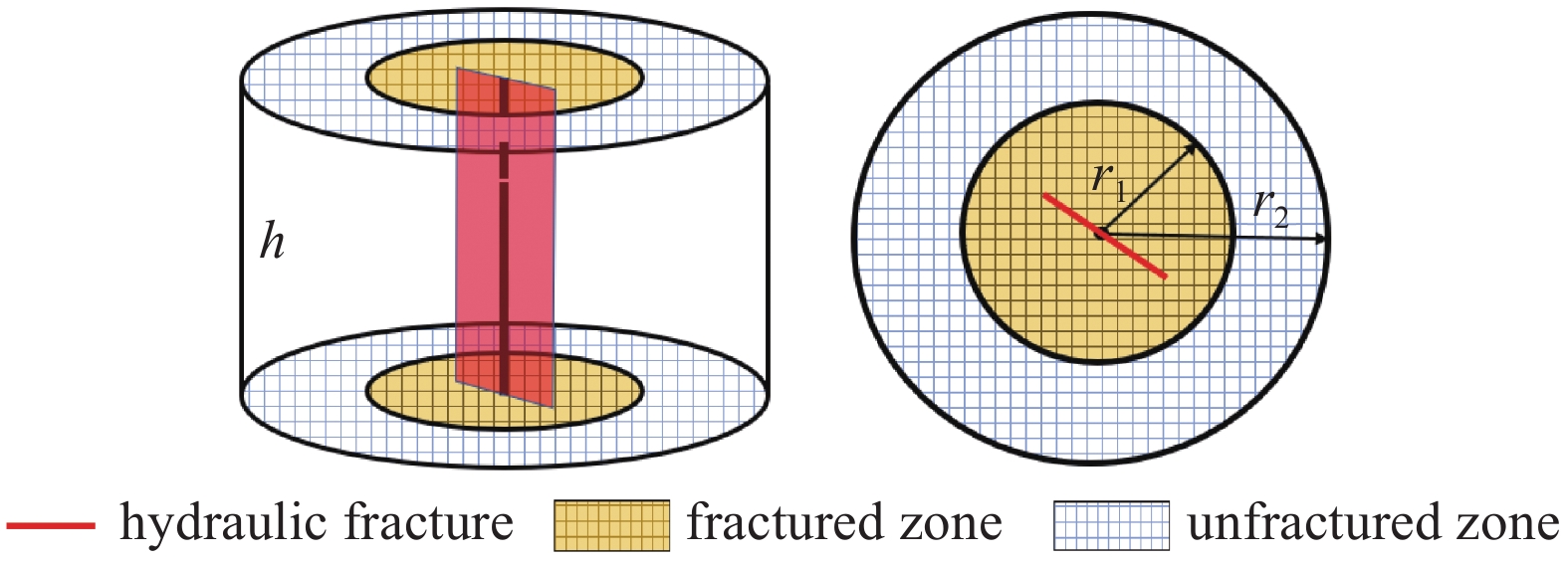
海陆过渡相页岩气藏的物理模型如图1所示, 考虑压裂施工和储层横向变化快, 物理模型考虑了压裂裂缝和渗透率的非均质性. 页岩气藏为圆形封闭水平等厚, 顶底为不渗透隔层; 利用双重介质模型描述页岩储层天然裂缝和基质系统; 考虑基质系统的页岩气吸附解吸特性, 利用Langmuir等温吸附曲线描述吸附气体压力与被吸附量的关系; 经过压裂后, 近井形成双翼水力裂缝, 水力裂缝为有限导流裂缝. 根据上述物理模型, 建立海陆过渡相页岩气藏压裂直井数学模型.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-271-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />

图
1
海陆过渡相页岩气压裂直井模型

Figure
1.
Fractured vertical well model

下载:
全尺寸图片
幻灯片

1.2
数学模型

由于页岩气藏存在吸附解吸, Langmuir方程为

$$V = frac{{{V_{
m{L}}}p}}{{{p_{
m{L}}} + p}}$$

(1)

其中, V为页岩气浓度, m³/kg; ${V_{
m{L}}}$

为吸附体积, m³/t; ${p_{
m{L}}}$

为解吸压力, MPa. 引入气体拟压力

$$psi = 2intlimits_0^p {frac{p}{{{mu _{
m{g}}}{z_{
m{g}}}}}{
m{d}}p} $$

(2)

(1)储层渗流方程为

$$begin{split} frac{{{partial ^2}{psi _1}}}{{partial {r^2}}} + frac{1}{r}frac{{partial {psi _1}}}{{partial r}} = frac{{{{left( {phi {mu _{
m{g}}}{c_{
m{g}}}}
ight)}_1}}}{{3.6{K_1}}}frac{{partial {psi _1}}}{{partial t}}+ frac{{T{p_{{
m{sc}}}}}}{{{K_1}{T_{{
m{sc}}}}}}frac{{partial V}}{{partial t}} end{split} $$

(3)

$$begin{split} frac{{{partial ^2}{psi _2}}}{{partial {r^2}}} + frac{1}{r}frac{{partial {psi _2}}}{{partial r}} = frac{{{{left( {phi {mu _{
m{g}}}{c_{
m{g}}}}
ight)}_2}}}{{3.6{K_2}}}frac{{partial {psi _2}}}{{partial t}} + frac{{T{p_{{
m{sc}}}}}}{{{K_2}{T_{{
m{sc}}}}}}frac{{partial V}}{{partial t}} end{split}$$

(4)

$$frac{1}{{l_{
m{m}}^2}}frac{partial }{{partial {l_{
m{m}}}}}left( {l_{
m{m}}^2Dfrac{{partial V}}{{partial {l_{
m{m}}}}}}
ight) = frac{{partial V}}{{partial t}};;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;$$

(5)

其中, 1表示内区; 2表示外区; D为扩散系数, m²/s; ${l_{
m{m}}}$

为基质块边长, m. 初始条件和内外边界条件为

$$left. begin{array}{l} {psi _1}left( {t = 0}
ight){
m{ = }}{psi _2}left( {t = 0}
ight){
m{ = }}{psi _i} {left. {rdfrac{{partial {psi _1}}}{{partial r}}}
ight|_{r; =; {r_{
m{w}}}}} = dfrac{{3.684 times {{10}^{ - 3}}{q_{{
m{sc}}}}}}{{{K_{{
m{f}}1}}h}}dfrac{{{p_{{
m{sc}}}}T}}{{{T_{{
m{sc}}}}}} {left. {dfrac{{{K_1}}}{mu }dfrac{{partial {psi _1}}}{{partial r}}}
ight|_{r; =; {r_{
m{f}}}}} = {left. {dfrac{{{K_2}}}{mu }dfrac{{partial {psi _2}}}{{partial r}}}
ight|_{r; =; {r_{
m{f}}}}} {left. {{psi _1}}
ight|_{r; =; {r_{
m{f}}}}} = {left. {{psi _2}}
ight|_{r; =; {r_{
m{f}}}}} {left. {dfrac{{partial {psi _2}}}{{partial r}}}
ight|_{r; =; {r_{
m{e}}}}} = 0 end{array}
ight}$$

(6)

式中, ${q_{{
m{sc}}}}$

为地面产量, m³/d; ${p_{{
m{sc}}}}$

为地面压力, MPa; ${T_{{
m{sc}}}}$

为地面绝对温度, K.

(2)压裂裂缝渗流方程为

$$frac{{{partial ^2}{psi _{
m{F}}}}}{{partial {x^2}}} + frac{{2{K_1}}}{{{W_{
m{F}}}{K_{
m{F}}}}}{left. {frac{{partial {psi _1}}}{{partial y}}}
ight|_{y ;=; frac{{{W_{
m{F}}}}}{2}}} = 0{
m{ }},;;;{0 < x < {L_{
m{F}}}} $$

(7)

式中, ${W_{
m{F}}}{K_{
m{F}}}$

为裂缝导流能力, mD·m; ${W_{
m{F}}}$

为裂缝宽度, m; ${K_{
m{F}}}$

为裂缝渗透率, mD. 初始条件和内外边界条件为

$$left. begin{array}{l} {psi _{
m{F}}}left( {x,y,t}
ight) = {psi _{{i}}} {K_{
m{F}}}displaystylemathop int limits_0^{frac{{{W_{
m{F}}}}}{2}} dfrac{{partial {psi _{
m{F}}}left( {0,y,t}
ight)}}{{partial x}}{
m{d}}y = dfrac{{{q_{
m{g}}}T}}{{2h{T_{{
m{sc}}}}}} dfrac{{partial {psi _{
m{F}}}left( {{L_{
m{F}}},y,t}
ight)}}{{partial x}} = 0 end{array}
ight}$$

(8)

(3)无因次渗流数学方程为

为使方程简洁, 引入无量纲量如附录A, 可得无因次的储层渗流数学模型

$$left. begin{array}{l} dfrac{{{partial ^2}{psi _{1{
m{D}}}}}}{{{partial ^2}{r_{
m{D}}}}} + dfrac{1}{{{r_{
m{D}}}}}dfrac{{partial {psi _{{
m{1D}}}}}}{{partial {r_{
m{D}}}}} = dfrac{1}{{{eta _{1{
m{D}}}}}}left[ begin{array}{l} omega dfrac{{partial {psi _{1{
m{D}}}}}}{{partial {t_{
m{D}}}}} + (1 - omega )dfrac{{partial {V_{
m{D}}}}}{{partial {t_{
m{D}}}}} end{array}
ight],qquad qquad varOmega in {varOmega _1} dfrac{{{partial ^2}{psi _{{
m{2D}}}}}}{{{partial ^2}{r_{
m{D}}}}} + dfrac{1}{{{r_{
m{D}}}}}dfrac{{partial {psi _{{
m{2D}}}}}}{{partial {r_{
m{D}}}}} = dfrac{1}{{{eta _{{
m{2D}}}}}}left[ begin{array}{l} omega dfrac{{partial {psi _{{
m{2D}}}}}}{{partial {t_{
m{D}}}}} + (1 - omega )dfrac{{partial {V_{
m{D}}}}}{{partial {t_{
m{D}}}}} end{array}
ight], qquad qquad varOmega in {varOmega _1} dfrac{1}{{l_{{
m{mD}}}^2}}dfrac{partial }{{partial {l_{{
m{mD}}}}}}left( {l_{{
m{mD}}}^2dfrac{{partial {V_{
m{D}}}}}{{partial {l_{{
m{mD}}}}}}}
ight) = dfrac{1}{{{D_{
m{D}}}}}dfrac{{partial {V_{
m{D}}}}}{{partial {t_{
m{D}}}}} {r_{
m{D}}}dfrac{{partial {psi _{{
m{1D}}}}}}{{partial {r_{
m{D}}}}}left| {_{{r_{
m{D}}} to 0} = - {q_{{
m{FD}}}}}
ight.,;;varOmega in {varOmega _1} {M_{1{
m{D}}}}dfrac{{partial {psi _{1{
m{D}}}}}}{{partial {r_{
m{D}}}}} = {M_{{
m{2D}}}}dfrac{{partial {psi _{{
m{2D}}}}}}{{partial {r_{
m{D}}}}},;;varGamma in {varGamma _1} {psi _{{
m{1D}}}} = {psi _{{
m{2D}}}},;;varGamma in {varGamma _1} dfrac{{partial {psi _{{
m{2D}}}}}}{{partial {r_{
m{D}}}}} ;=; 0,;;varGamma in {varGamma _{
m{2}}} {psi _{{
m{1D}}}}left| {_{{t_{
m{D}}} ;=; 0}}
ight. = {psi _{{
m{2D}}}}left| {_{{t_{
m{D}}} ;=; 0}}
ight. = 0 end{array}
ight}$$

(9)

式中, ${psi _{{
m{1,2D}}}}$

为内外区储层拟压力, 无因次. 同时, 可得无因次裂缝渗流数学模型

$$left. begin{array}{l} dfrac{{{partial ^2}{psi _{{
m{FD}}}}}}{{partial x_{
m{D}}^2}} + dfrac{2}{{{C_{{
m{FD}}}}}}{left. {dfrac{{partial {psi _{{
m{1D}}}}}}{{partial {y_{
m{D}}}}}}
ight|_{{y_{
m{D}}} ;=; frac{{{W_{{
m{FD}}}}}}{2}}} = 0 {left. {dfrac{{{
m{d}}{psi _{{
m{FD}}}}}}{{{
m{d}}{x_{
m{D}}}}}}
ight|_{{x_{
m{D}}} ;=; 1}} = 0 {left. {dfrac{{{
m{d}}{psi _{{
m{FD}}}}}}{{{
m{d}}{x_{
m{D}}}}}}
ight|_{{x_{
m{D}}} ;=; 0}} = - dfrac{{text{π}} }{{{C_{{
m{FD}}}}}} end{array}
ight} $$

(10)

式中, ${psi _{{
m{FD}}}}$

和${C_{{
m{FD}}}}$

分别为裂缝拟压力和裂缝导流能力, 无因次; ${q_{
m{F}}}$

为裂缝流量线密度, m³/(d·m); $q$

为裂缝中的流量, m³/d; ${q_{{
m{FD}}}}$

为裂缝流量线密度, 无因次.

1.3
模型求解

采用边界元方法对非均质油藏渗流模型进行求解. 首先对油藏基质渗流模型进行Laplace变换, 并利用微分算子进行简化表示, 同时考虑内区裂缝井生产状况, 可得:

(1)油藏基质渗流模型解

$$begin{split}& {nabla ^2}{overline psi _{{
m{1D}}}} - frac{{f(s)}}{{{eta _{{
m{1D}}}}}}{overline psi _{{
m{1D}}}} + &qquad delta ({{boldsymbol{r}}_{
m{D}}},{boldsymbol{r}}_{
m{D}}')left( {displaystylesumlimits_{j = 1}^{{n_{{
m{Fs}}}}} {displaystyleintlimits_l {{bar q_{{
m{FD,}}j}}{
m{d}}l} } }
ight) = 0,;;varOmega in {varOmega _1} end{split} $$

(11)

式中$ delta $

为Laplace算子, 无量纲.

同样可得

$${nabla ^2}{overline psi _{{
m{2D}}}} - frac{{f(s)}}{{{eta _{{
m{1D}}}}}}{overline psi _{2{
m{D}}}} = 0,;;varOmega in {varOmega _2}$$

(12)

对于控制方程式 (11), 引入Green方程

$$begin{split}& {overline G _1}({{boldsymbol{r}}_{
m{D}}},{boldsymbol{r}}_{
m{D}}';s) = &qquad frac{1}{{2{text{π}} {eta _{{
m{1D}}}}}} {K_0}left[ {sqrt {{{({x_{
m{D}}} - {x_{{
m{wD}}}})}^2} + {{({y_{
m{D}}} - {y_{{
m{wD}}}})}^2}} sqrt {frac{{f(s)}}{{{eta _{{
m{1D}}}}}}} }
ight] end{split} $$

(13)

很显然, 方程为无限大地层点源解, 满足

$$begin{split} {nabla ^2}{overline G _1}({{boldsymbol{r}}_{
m{D}}},{boldsymbol{r}}_{
m{D}}^{
m{'}};s) - frac{{f(s)}}{{{eta _{1{
m{D}}}}}}{overline G _1}({{boldsymbol{r}}_{
m{D}}},{boldsymbol{r}}_{
m{D}}';s) + delta ({{boldsymbol{r}}_{
m{D}}},{boldsymbol{r}}_{
m{D}}^{
m{'}}) = 0 end{split} $$

(14)

两边同乘${overline psi _{{
m{1D}}}}$

, 则可将上述方程变形为

$${overline psi _{1{
m{D}}}}{nabla ^2}{overline G _1} - frac{{f(s)}}{{{eta _{1{
m{D}}}}}}{overline psi _{1{
m{D}}}}{overline G _1} + {overline psi _{1{
m{D}}}}delta ({{boldsymbol{r}}_{
m{D}}},{boldsymbol{r}}_{
m{D}}') = 0$$

(15)

同样对式 (11) 两边同乘${overline G _1}$

得

$$begin{split}&{overline G _1}{nabla ^2}{overline psi _{{
m{1D}}}} - frac{{f(s)}}{{{eta _{{
m{1D}}}}}}{overline G _1}{overline psi _{{
m{1D}}}}+&qquad {overline G _1}delta ({{boldsymbol{r}}_{
m{D}}},{boldsymbol{r}}_{
m{D}}^{
m{'}})left( {sumlimits_{j = 1}^{{n_{{
m{Fs}}}}} {intlimits_l {{bar q_{{
m{FD,}}j}}{
m{d}}l} } }
ight) = 0,;;varOmega in {varOmega _1}end{split} $$

(16)

将式 (15) 减去式(16) 并在区域1内积分

$$begin{split}&intlimits_{{varOmega _1}} {Biggl[{20} {{{bar psi }_{{
m{1D}}}}{nabla ^2}{{bar G}_1} - {{bar G}_1}{nabla ^2}{{bar psi }_{{
m{1D}}}} + {{bar psi }_{1{
m{D}}}}delta ({{boldsymbol{r}}_{
m{D}}},{{boldsymbol{r}}_{{{
m{D}} }}^{
m{'}}}) - } } &qquadleft. {{{bar G}_1}delta ({{boldsymbol{r}}_{
m{D}}},{{boldsymbol{r}}_{
m{D}}^{
m{'}} })left( {sumlimits_{j = 1}^{{n_{{
m{Fs}}}}} {intlimits_l {{{bar q}_{{
m{FD}},{{j}}}}{
m{d}}l} } }
ight)}
ight]{
m{d}}varOmega = 0end{split}$$

(17)

根据$delta $

函数和格林函数的性质

$$left. begin{array}{l} displaystyleintlimits_varOmega {delta ({{boldsymbol{r}}_{
m{D}}},{boldsymbol{r}}_{
m{D}}^{
m{'}}){
m{d}}varOmega } = 1 displaystyleintlimits_varOmega {left( {v{nabla ^2}u - u{nabla ^2}v}
ight)} {
m{d}}varOmega = intlimits_varGamma {left( {vnabla u - unabla v}
ight)} cdot hat {boldsymbol{n}} {
m{d}}varGamma end{array}
ight}$$

(18)

式(17)可得

$$begin{split}& intlimits_{{varGamma _1}} {left( {{{overline psi }_{{
m{1D}}}}nabla {{overline G }_1} - {{overline G }_1}nabla {{overline psi }_{{
m{1D}}}}}
ight) cdot hat {boldsymbol{n}}{
m{d}}varGamma } + & qquad {overline psi _{1{
m{D}}}} - {intlimits_{varOmega _1}} {left( {sumlimits_{j = 1}^{{n_{{
m{Fs}}}}} {intlimits_l {{bar q_{{
m{FD,}}j}}{
m{d}}l} } }
ight)} {overline G _1}{
m{d}}{varOmega _1} = 0 [-12pt] end{split} $$

(19)

通过整理, 可得区域1无因次压力解

$$begin{split}& {overline psi _{{
m{1D}}}} = 2{text{π}} {eta _{1{
m{D}}}}{intlimits_{varOmega _1}} {left( {sumlimits_{j = 1}^{{n_{{
m{Fs}}}}} {intlimits_l {{bar q_{{
m{FD}},{{j}}}}{
m{d}}l} } }
ight){{overline G }_1}} {
m{d}}{varOmega _1} + &qquad {eta _{{
m{1D}}}}{intlimits_{varGamma _1}} {left( {{{overline G }_1}nabla {{overline psi }_{{
m{1D}}}} - {psi _{{
m{1D}}}}nabla {{overline G }_1}}
ight)} cdot hat {boldsymbol{n}}{
m{d}}varGamma [-8pt] end{split} $$

(20)

同样可得, 区域2无因次压力解

$$begin{split}& {overline psi _{{
m{2D}}}} = {eta _{{
m{2D}}}}{intlimits_{varGamma _1}} {left( {{{overline G }_2}nabla {{overline psi }_{{
m{2D}}}} - {psi _{{
m{2D}}}}nabla {{overline G }_2}}
ight)} cdot hat {boldsymbol{n}}{
m{d}}varGamma - &qquad {eta _{{
m{2D}}}}{intlimits_{varGamma _2}} {{{overline psi }_{{
m{2D}}}}nabla {{overline G }_2}} cdot hat {boldsymbol{n}}{
m{d}}varGamma [-9pt] end{split} $$

(21)

(2)连接面条件

$${M_{{
m{1D}}}}nabla {overline psi _{{
m{1D}}}} = - {M_{{
m{2D}}}}nabla {overline psi _{{
m{2D}}}},;;varGamma in {varGamma _1}$$

(22)

$${psi _{1{
m{D}}}} = {psi _{{
m{2D}}}},;;varGamma in {varGamma _1}$$

(23)

(3)压裂裂缝渗流模型解

对压裂裂缝渗流基本方程进行Laplace变换得

$$frac{{{partial ^2}{{overline psi }_{{
m{FD}}}}}}{{partial {y_{
m{D}}}^2}} - frac{{2{text{π}} {bar q_{{
m{FD}}}}}}{{{C_{{
m{FD}}}}}} = 0$$

(24)

$$frac{{partial {{overline psi }_{{
m{FD}}}}}}{{{y_{
m{D}}}}}left| {_{{y_{
m{D}}} ;=; {y_{{
m{dD}}}}} = frac{{2{text{π}} }}{{{C_{{
m{FD}}}}}}{bar q_{{
m{FwD}}}}}
ight.$$

(25)

$${bar q _{{
m{uD}}}}left| {_{{y_{
m{D}}} ;=; {y_{{
m{uD}}}}}}
ight. = {bar q _{{
m{FwD}}}} + {L_{{
m{FsD}}}}{bar q _{{
m{FD}}}}$$

(26)

利用积分方法可得

$$begin{array}{l} {overline psi _{{
m{FDu}}}} - {overline psi _{{
m{FDd}}}} = dfrac{{2{text{π}} }}{{{C_{{
m{FD}}}}}}displaystyleint_{{y_{{
m{dD}}}}}^{{y_{{
m{uD}}}}} {left[ {{bar q_{{
m{FD}}}}({y_{
m{D}}} - {y_{{
m{dD}}}}) + {bar q_{{
m{FwD}}}}}
ight]{
m{d}}{x_{
m{D}}}} end{array} $$

(27)

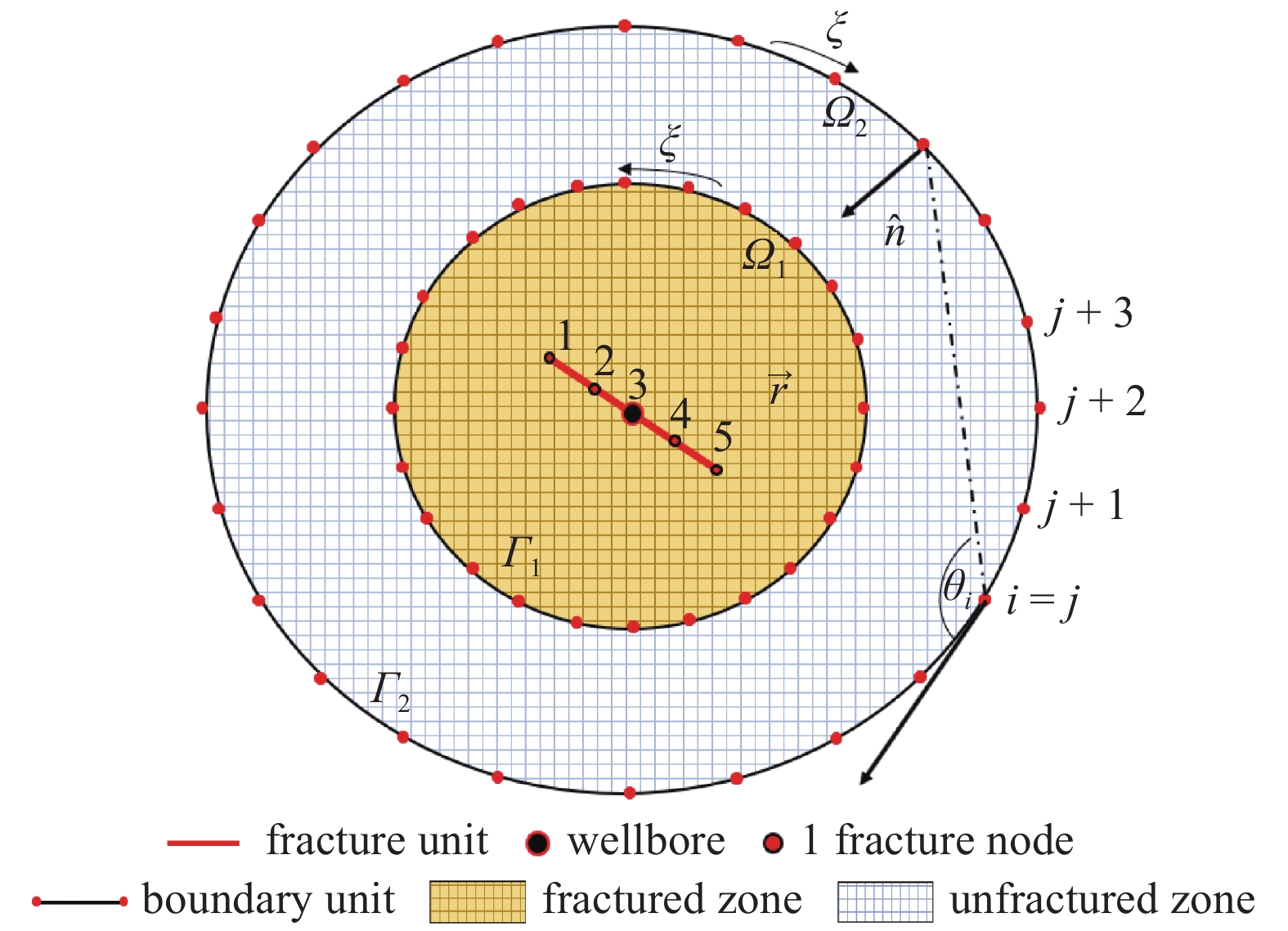
将边界和裂缝单元进行离散, 如图2. 假设边界线${varGamma _1}$

和${varGamma _2}$

分别被划分为${N_1}$

和${N_2}$

个边界单元, 裂缝被划分为${n_{{
m{Fs}}}}$

裂缝单元和${n_{{
m{Fv}}}}$

裂缝点, 如下图所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-271-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />

图
2
边界离散示意图

Figure
2.
Discretization of reservoir boundaries

下载:
全尺寸图片
幻灯片

根据离散边界单元的几何性质, 式(19) ~ 式(27)可离散为

①储层渗流模型解

$$begin{split}& frac{{{theta _i}}}{{2{text{π}} {eta _{1{
m{D}}}}}}{overline psi _{{
m{1D,}}i}} = 2{
m{{text{π}} }}left( {sumlimits_{j ;=; 1}^{{n_{{
m{Fs}}}}} {intlimits_l {{bar q_{{
m{FD,}}j}}{
m{d}}l} } }
ight){overline G _1} + &qquad sumlimits_{j ;=; 1}^{ {N_1}} {nabla {{overline psi }_{{
m{12,}}j}}}cdot {intlimits_{varGamma _{{
m{1,}}j}}} {{{overline G }_1} hat {boldsymbol{n}}{
m{d}}varGamma } - &qquad {
m{ }} sumlimits_{j ;=; 1}^{ {N_1}} {{{overline psi }_{{
m{12,}}j}}} hat {boldsymbol{n}}cdot{intlimits_{varGamma _{{
m{1,}}j}}} {nabla {{overline G }_1}{
m{d}}varGamma },;;i = 1,2,cdots,{N_1} [-12pt] end{split} $$

(28)

$$begin{split}& frac{{{theta _{{i}}}}}{{2{text{π}} {eta _{{
m{2D}}}}}}{overline psi _{{
m{2D,}}i}} = sumlimits_{j ;=; 1}^{ {N_1}} {nabla {{overline psi }_{{
m{21,}}j}}}cdot {intlimits_{varGamma _{{
m{1,}}j}}} {{{overline G }_2} hat {boldsymbol{n}}{
m{d}}varGamma } - &qquad sumlimits_{j ;=; 1}^{{N_1}} {{{overline psi }_{{
m{21,}}j}}} hat {boldsymbol{n}}cdot{intlimits_{{varGamma _{
m{1,}}j}}} {nabla {{overline G }_2}{
m{d}}varGamma } -&qquad {
m{ }} sumlimits_{j ;=; 1}^{ {N_2}} {{{overline psi }_{{
m{2,}}j}}} hat {boldsymbol{n}}cdot{intlimits_{varGamma _{{
m{2,}}j}}} {nabla {{overline G }_2}{
m{d}}varGamma },;;i = 1,2,cdots,{N_1} + {N_2} end{split} $$

(29)

②连接面条件

$$left. begin{array}{l} {overline psi _{{
m{12,}}j}} = {overline psi _{{
m{21,}}j}},;;j = 1,2,cdots,{N_{
m{1}}} {eta _{{
m{1D}}}}nabla {overline psi _{{
m{12,}}j}} = - {eta _{{
m{2D}}}}nabla {overline psi _{{
m{21,}}j}},;;j = 1,2,cdots,{N_{
m{1}}} end{array}
ight}$$

(30)

③压裂裂缝渗流模型解

$$begin{split}& {overline psi _{{
m{FD,}}k + 1}} - {overline psi _{{
m{FD}}k}} = & frac{{2{text{π}} }}{{{C_{{
m{FD}}k}}}}intlimits_{ - {L_{{
m{Fs}}k}}{
m{/}}2}^{{L_{{
m{Fs,}}k + 1}}/2} {left[ {({y_{
m{D}}} - {y_{{
m{D}}k}}){bar q_{{
m{FD}}k}} + {bar q_{{
m{FwD}}k}}}
ight]} {
m{d}}{y_{
m{D}}}, & k = 1,2,cdots,{n_{{
m{Fs}}}} end{split} $$

(31)

④辅助方程

利用质量守恒方程来考虑裂缝节点处流动, 同时考虑定产量生产条件, 则可得

$${({bar q _{{
m{FwD}}i}})_{{
m{in}}}} = left{ begin{array}{l} {({bar q _{{
m{FwD}}i}})_{{
m{out}}}},;;{{i}} = 1,2,.cdots,{n_{{
m{Fv}}}}{
m{ - 1}} {1 / s},;;i{
m{ = well}} end{array}
ight. $$

(32)

式(28) ~ 式(32)组成了一个$2{n_{{
m{Fv}}}} + {n_{{
m{Fs}}}} + 4{N_1} + {N_2}$

阶方程组. 而对应的未知量为${n_{{
m{Fv}}}}$

个裂缝节点压力${overline p _{{
m{FD}}}}$

, ${n_{{
m{Fv}}}}$

个裂缝节点出流量${bar q _{{
m{wD}}}}$

, ${n_{{
m{Fs}}}}$

个裂缝单元的单位长度流量${bar q _{{
m{FD}}}}$

, ${N_{12}}$

个边界单元节点压力$({overline psi _{12}}, $

$ {overline psi _{21}},;{overline psi _{
m{2}}})$

和${
m{2}}{N_1}$

边界单元压力梯度$(nabla {overline psi _{12}},nabla {overline psi _{21}})$

. 可以看出, 方程组是封闭的. 对方程组进行联立求解, 即可得到每一个裂缝节点压力${overline psi _{{
m{FD}}}}({r_{
m{D}}},s)$

, 包括井筒节点${overline psi _{{
m{wD}}}}$

. 考虑井筒储集效应及表皮效应, 进一步得到井底压力响应为

$${overline psi _{{
m{wCD}}}} = frac{{s{{overline psi }_{{
m{wD}}}} + S}}{{sBiggr[ {1 + s{C_{
m{D}}}( {s{{overline psi }_{{
m{wD}}}} + S} )} Biggr]}}$$

(33)

式中, ${overline psi _{{
m{wCD}}}}$

为包含井储效应和表皮效应的拉氏空间井底压力解, 无因次; ${C_{
m{D}}}$

为井筒储集系数, 无因次; $S$

为井筒表皮因子, 无因次. 最后运用stehfest数值反演^[31]即可得到实空间下的井底压力解.

2.
海陆过渡相页岩气藏不稳定渗流特征

2.1
不稳定渗流特征

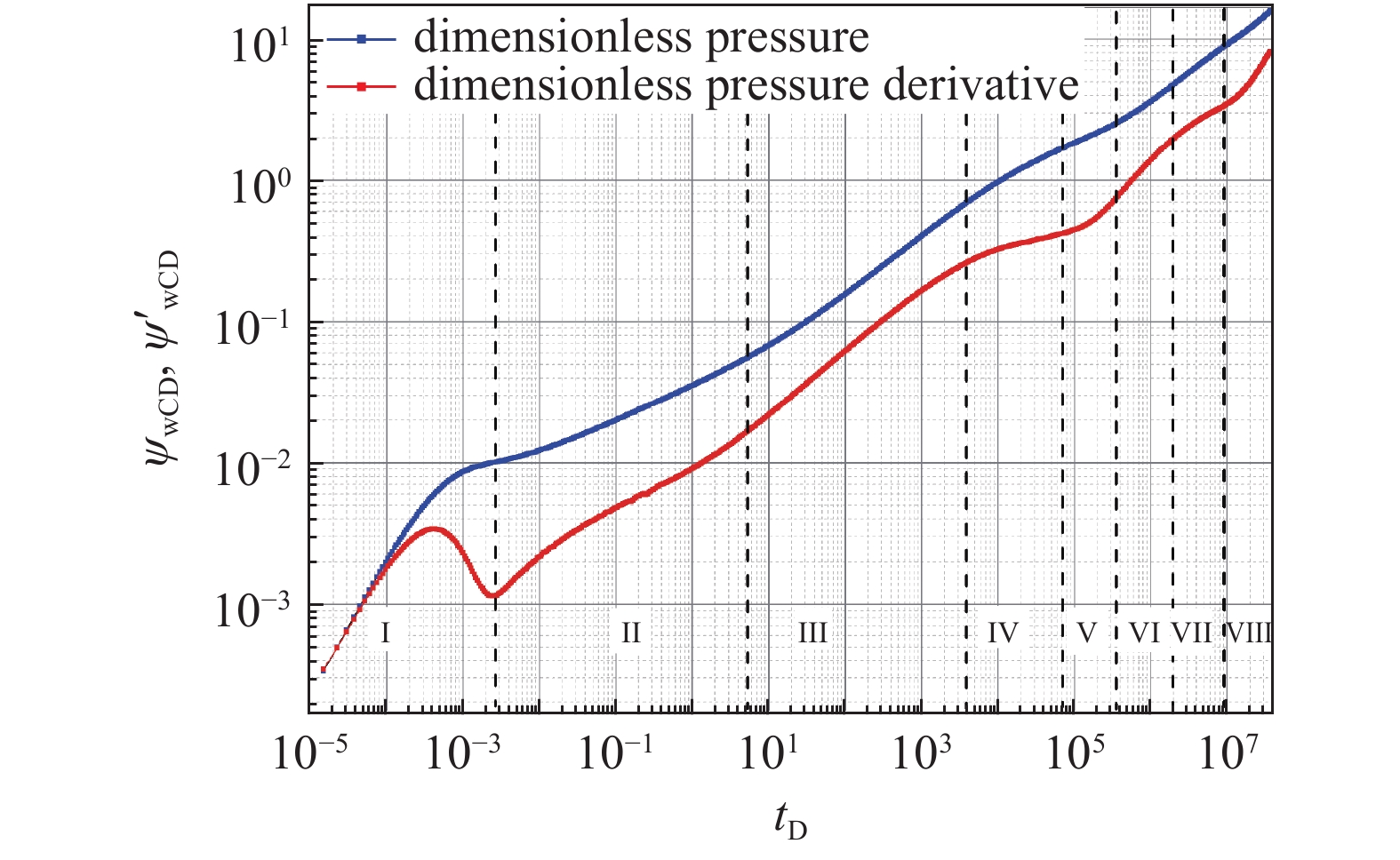
基于时间与井底压力和压力导数的双对数曲线特征, 可分析海陆过渡相页岩气藏不稳定渗流特征. 根据上述数学模型解, 取基础参数如表1所示, 绘制页岩气藏压裂井模型的时间与压力和压力导数的双对数曲线, 如图3所示. 从图可看出, 海陆过渡相页岩气藏不稳定渗流特征可分为以下阶段: I为流动早期阶段: 其受到井筒存储效应及表皮效应的影响, 在初期, 压力导数曲线表现为45°和隆起; II为双线性流阶段: 此阶段流体从地层线性流入裂缝, 裂缝流体线性流入生产井筒的阶段, 其压力导数曲线的斜率为1/4; III为线性流阶段: 此阶段是流体从地层线性流入有限导流裂缝的流动阶段, 压力导数曲线斜率为1/2; IV为径向流阶段: 压力导数曲线的值等于0.5的水平线, 达到内区径向流阶段; V为页岩气解吸阶段, 页岩气的解吸发生在该阶段, 压力导数出现下凹; VI为内外径向流过渡, 压力导数上升; VII为外区径向流阶段: 压力导数曲线的值等于0.5M的水平线; VIII为边界控制阶段, 该阶段主要受边界条件影响, 出现压力导数曲线上扬的情况.

表
1
径向复合气藏压裂直井模型参数取值表

Table
1.
Parameter table of fractured vertical well model in radial composite gas reservoir

table_type1 ">

Parameter	Value	Unit
well storage coefficient	0.05	m³/MPa
skin	0	dimensionless
fracture half length	30	m
conductivity	100	mD·m
porosity	5.38	%
permeability	0.02	mD
adsorption volume	1.06	m³·t^?1
desorption pressure	17	MPa

下载:
导出CSV
|显示表格

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-271-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />

图
3
海陆过渡相页岩气藏不稳定渗流特征

Figure
3.
Characteristics of unstable flow in marine-continental transitional shale gas reservoirs

下载:
全尺寸图片
幻灯片

2.2
不稳定渗流特征

为了更好的认识海陆过渡相页岩气藏不稳定渗流特征, 了解不同的参数对其影响, 运用控制变量法, 研究一系列参数对渗流特征的敏感性影响, 这些分析将为后续模型应用提供理论支撑.

2.2.1
裂缝半长的影响

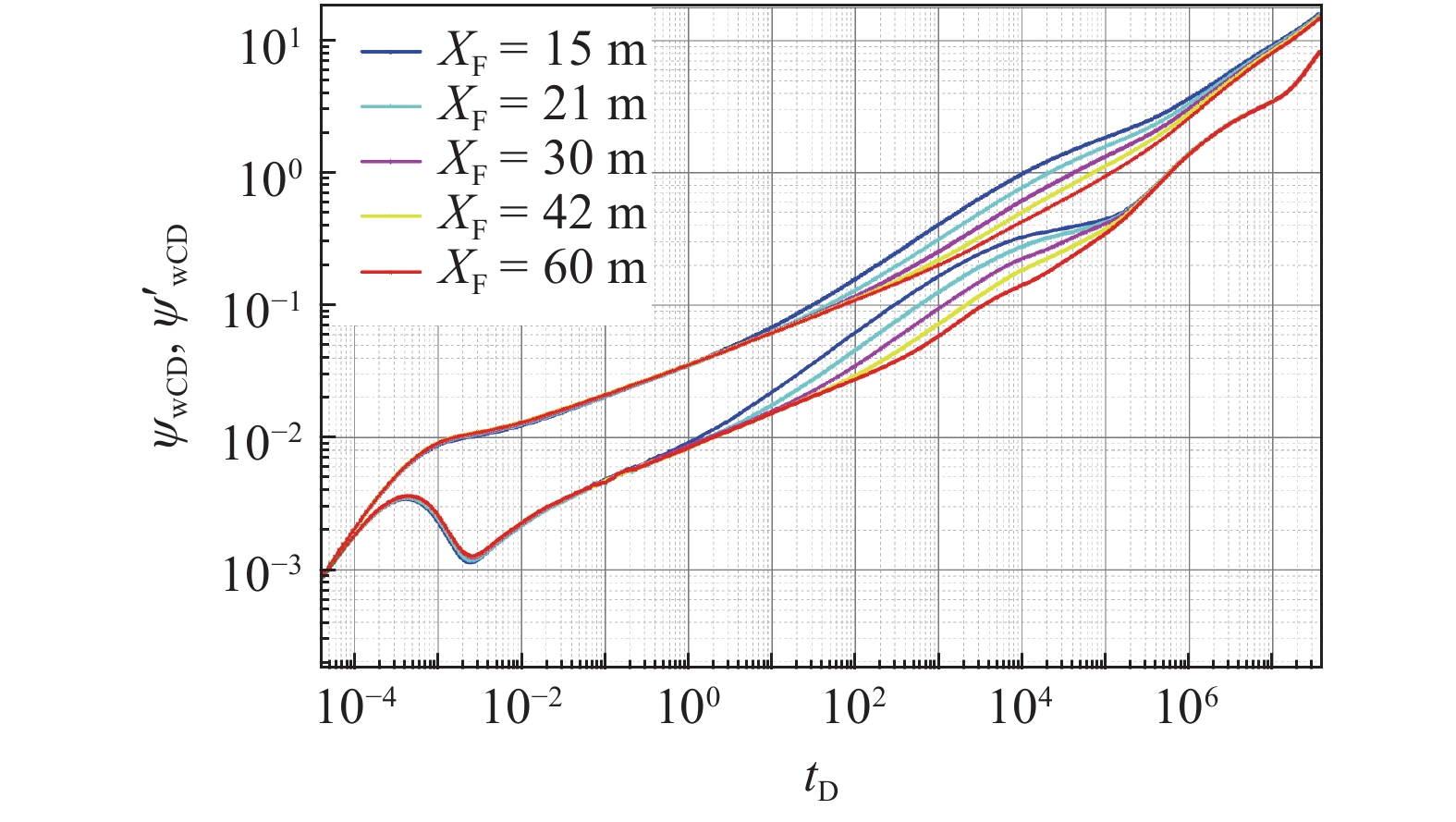
根据不同的裂缝半长, 分析对不稳定渗流特征影响, 如图4. 由图可知裂缝半长主要影响双线性流和线性流阶段, 随着裂缝半长的增大, 受影响的双线性流阶段结束时间推迟, 其持续时间变长. 同时, 由于裂缝更靠近内区边界, 使得压力波更早到达内区径向流阶段.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-271-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />

图
4
裂缝半长对不稳定渗流特征的影响

Figure
4.
Influence of fracture half-length on unstable flow characteristics

下载:
全尺寸图片
幻灯片

2.2.2
裂缝导流能力的影响

根据不同裂缝的导流能力, 分析对不稳定渗流特征影响, 如图5. 由图可知裂缝导流能力主要影响中期流动阶段, 随着裂缝导流能力增加, 图像整体下移, 压力降变小, 压力变化变缓, 裂缝导流能力的变化对流动晚期影响较小.

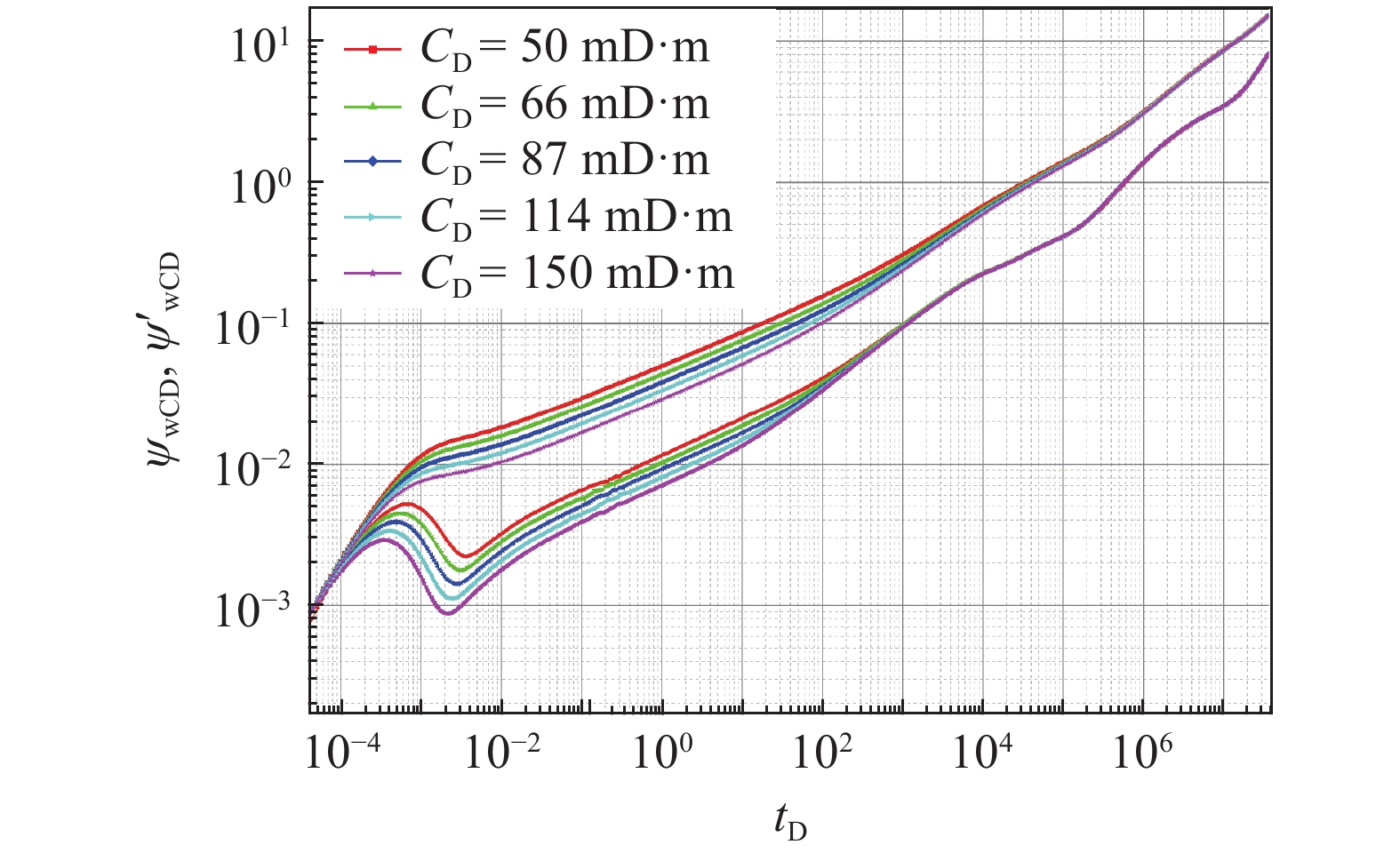onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-271-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />

图
5
裂缝导流能力对不稳定渗流特征的影响

Figure
5.
Influence of fracture conductivity on unstable flow characteristics

下载:
全尺寸图片
幻灯片

2.2.3
解吸压力的影响

根据不同解吸压力, 分析对不稳定渗流特征影响, 如图6. 由图可知解吸压力主要影响基质系统流体向天然裂缝系统的供给阶段. 随着临界解吸压力的增大, 曲线整体下移, 流体供给阶段的开始时间滞后, 同时下凹段越来越不明显, 直至逐渐消失.

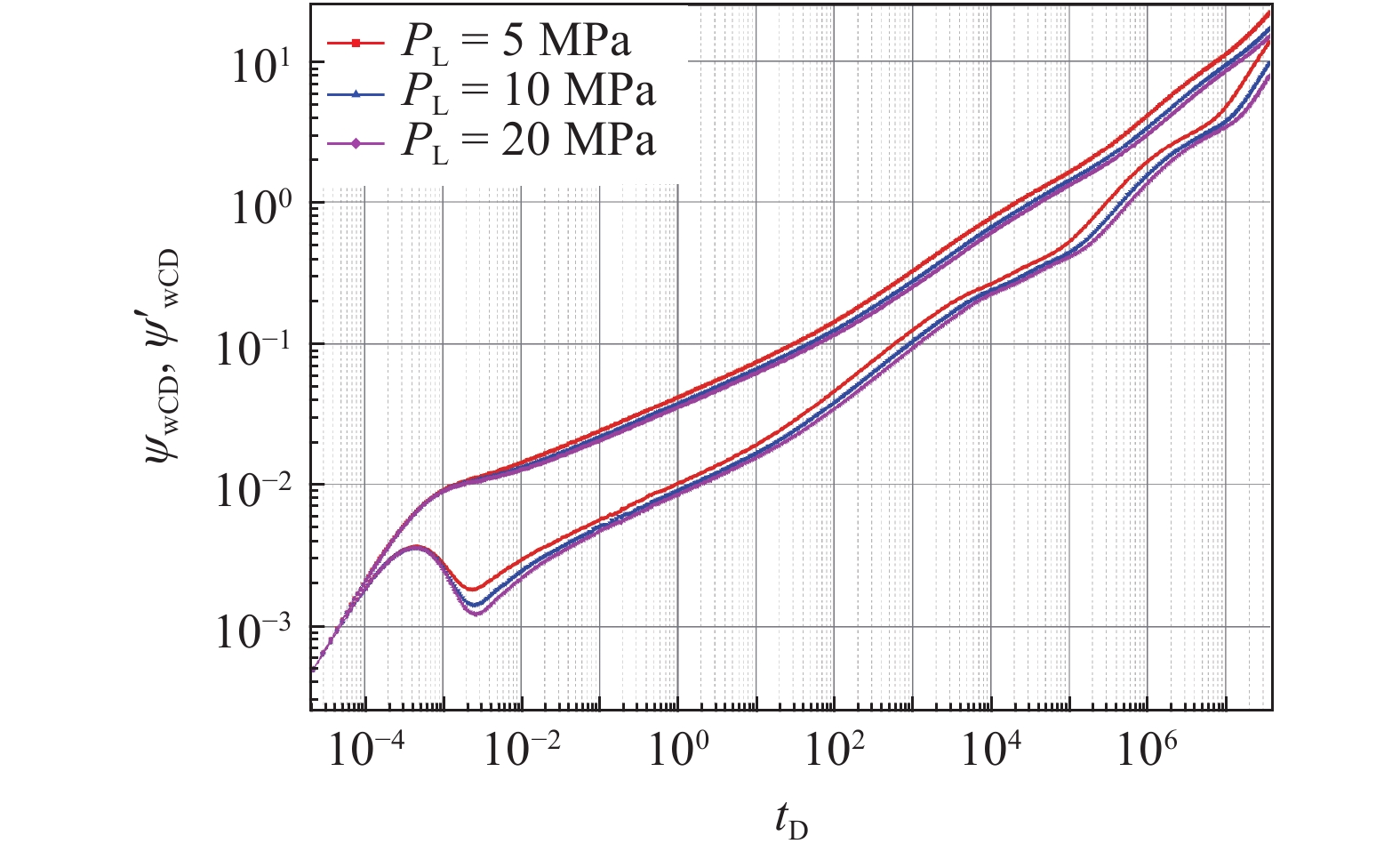onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-271-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />

图
6
临界解吸压力对不稳定渗流特征的影响

Figure
6.
Influence of critical desorption pressure on unstable flow characteristics

下载:
全尺寸图片
幻灯片

3.
模型验证

利用数值模拟方法对数学模型进行验证, 建立一口海陆过渡相压裂直井的数值模型(图7). 数值模型孔隙度为3.08%, 目的层储层温度68 °C, 原始地层压力为 22 MPa, 裂缝半长为30 m, 裂缝导流能力100 mD·m, 气藏厚度5.4 m. 压裂直井进行压降测试, 流量为1000 m³/d, 数值模拟测试数据见图8. 利用文中建立的数学模型与数值模型进行对比验证, 由模型验证参数表(表2)和结果对比图(图8)可知, 数学模型计算结果与数值模型结果基本一致.

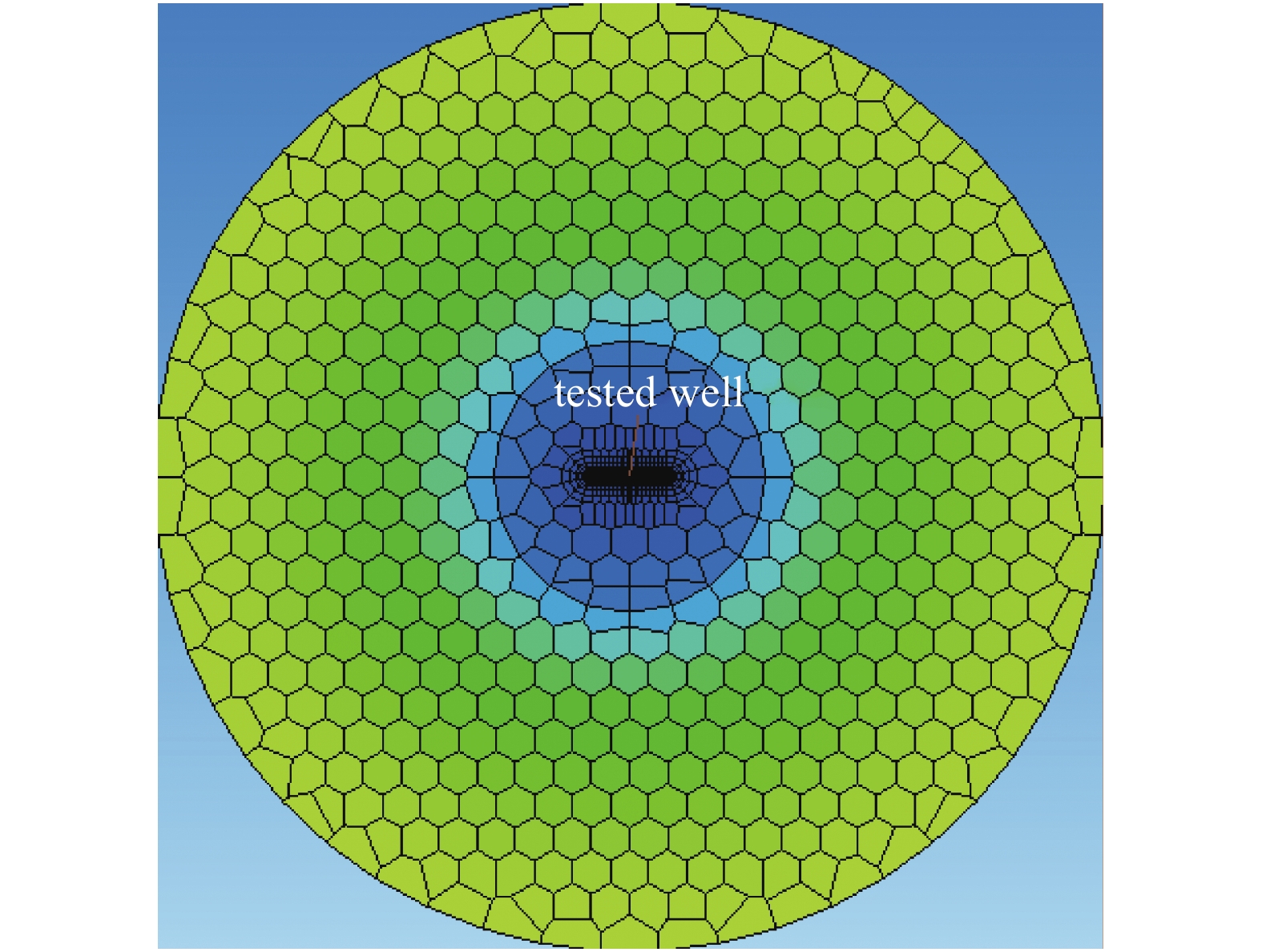onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-271-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />

图
7
海陆过渡相页岩气压裂直井数值模型

Figure
7.
Virtual well model

下载:
全尺寸图片
幻灯片

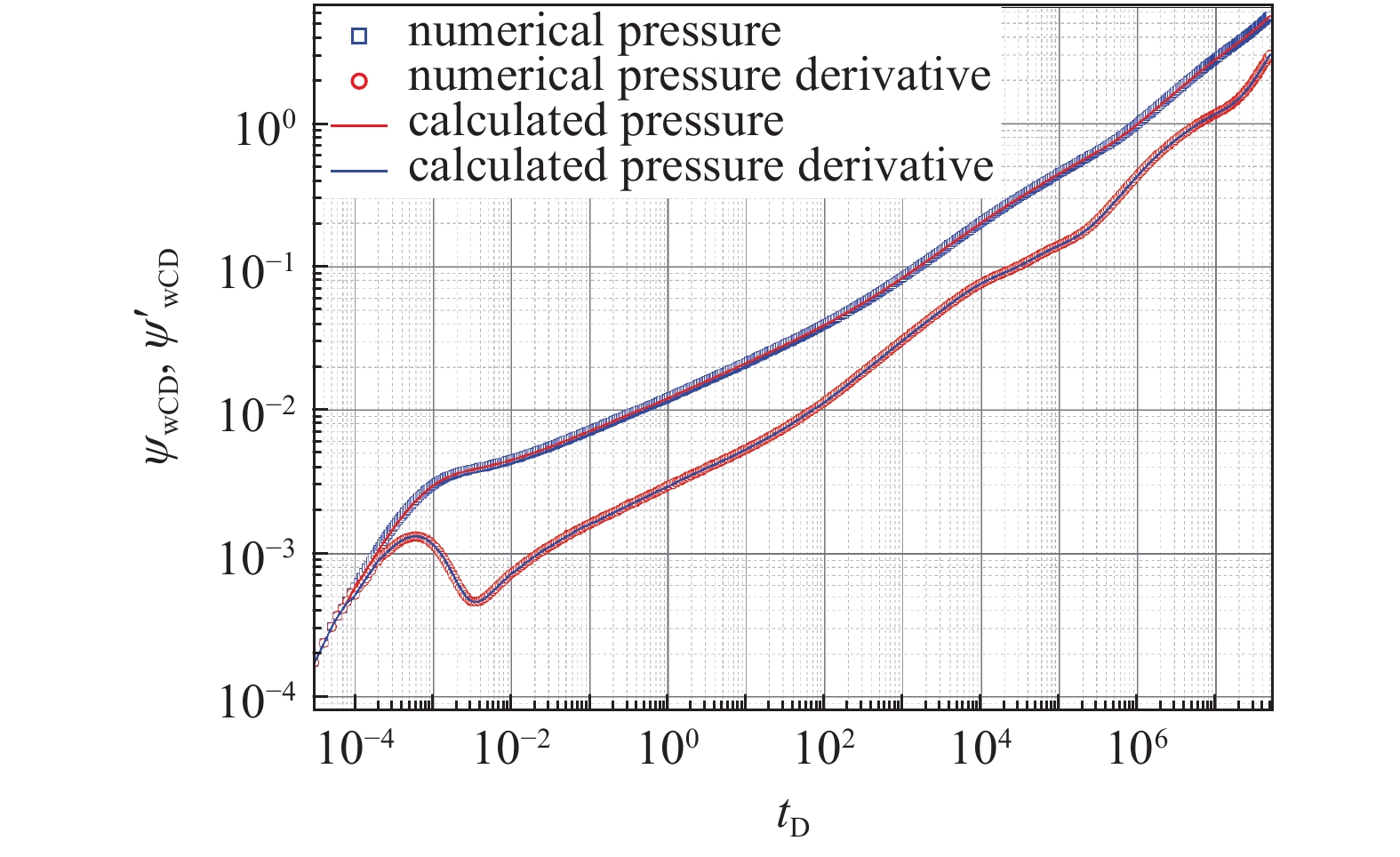onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-271-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />

图
8
文中计算结果与数值模拟结果对比验证

Figure
8.
Calculated results compared with the numerical simulation results

下载:
全尺寸图片
幻灯片

表
2
模型验证参数表

Table
2.
Model parameters

table_type1 ">

	Parameter	Value
fracture	fracture half length/m	30
fracture	fracture conductivity/(mD·m)	100
reservoir	pressure/MPa	30
	permeability/mD	0.2
	porosity/%	0.0538
wellbore	well storage coefficient/(m³·MPa^?1)	0.05
wellbore	skin	0.01
shale gas	adsorption volume/(m³·t^?1)	1.06
shale gas	desorption pressure/MPa	17

下载:
导出CSV
|显示表格

4.
模型应用

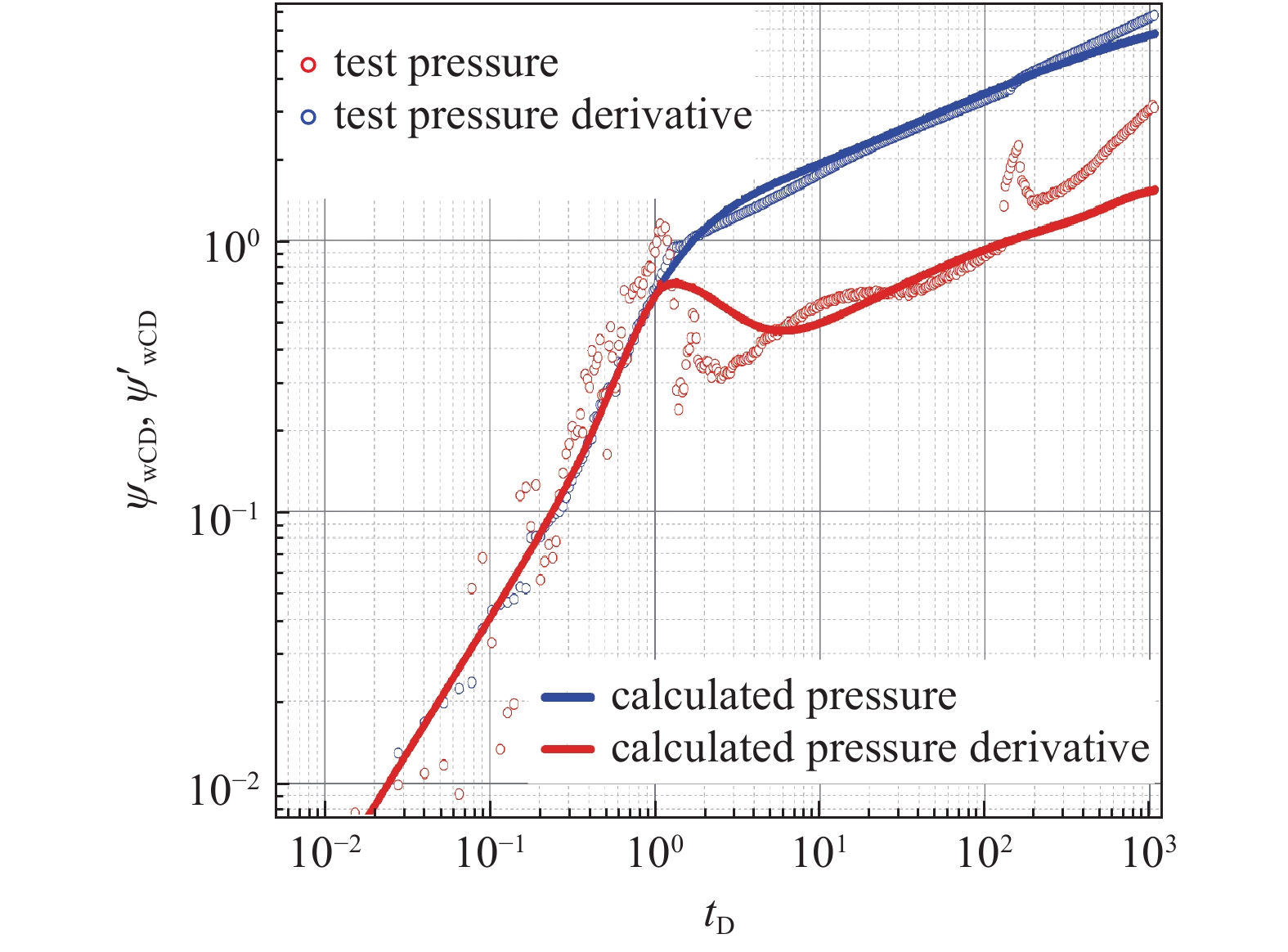
基于海陆过渡相页岩气藏不稳定渗流数学模型, 通过与实际矿场压力测试数据拟合分析^[3], 可评价储层及裂缝参数. DDJ井为 2017 年海陆过渡相页岩气藏完钻的一口压裂井. 为评价DDJ井的压裂裂缝参数, 开展了不稳定压力测试, 测试过程如图9. 连续测试阶段约进行了 1150 h, 测试阶段测试了 600 h, 测试时间相对比较长.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-271-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />

图
9
实际拟合压力测试数据

Figure
9.
Practical fitted pressure data

下载:
全尺寸图片
幻灯片

针对测试过程不稳定压力数据进行分析(图9), 发现存在不稳定流动特征的I, III, IV, V和VI阶段. 其中, 第I阶段为流动早期阶段, 其受到井筒存储系数以及表皮系数的影响; 第II阶段没有很明显出现, 主要是因为裂缝半长较短导致流体在裂缝中的流动时间较短; 第III阶段为线性流阶段, 流体从地层线性流入有限导流裂缝的流动阶段; 第IV阶段为径向流阶段, 达到内区径向流阶段; 第V阶段为页岩气解吸阶段, 页岩气的解吸发生在该阶段; 第VI阶段为内外径向流过渡. 利用建立的页岩气压裂井渗流数学模型, 对压力测试数据开展拟合分析(图9), 拟合分析和裂缝参数评价结果如表3. 分析发现, 经过压裂改造后, 典型井附近形成了主裂缝和改造区, 主裂缝为有限导流两翼缝, 裂缝半长为31 ~ 33 m, 导流能力为93 ~ 101 mD·m, 改造区半径为100 m, 改造区渗透率为0.2 ~ 0.3 mD. 典型井控制半径约为318 m, 控制可采储量约为8.52 × 10⁶ m³.

表
3
拟合分析参数结果表

Table
3.
Evaluated parameters using type-curve matching

table_type1 ">

	Parameter	Analysis result
fracture	fracture half length/m	31 ~ 33
fracture	fracture conductivity/(mD·m)	93 ~ 101
reservoir	permeability/mD	0.06
reservoir	radius/m	318
fractured zone	radius/m	100
fractured zone	permeability/mD	0.2 ~ 0.3
wellbore	storage coefficient/(m³·MPa^?1)	0.16
wellbore	skin	0.31
shale gas	adsorption volume/(m³·t^?1)	1.06 ~ 1.36
shale gas	desorption pressure/MPa	16.5 ~ 17.5

下载:
导出CSV
|显示表格

5.
结论

(1)考虑页岩气吸附解吸, 扩散, 裂缝特点, 以及海陆过渡相非均质性等特征, 建立并求解径向非均质的页岩气藏压裂直井不稳定渗流数学模型, 得到典型的页岩气压裂井试井曲线特征, 并进行了数值模拟验证, 最后针对鄂尔多斯盆地海陆过渡相典型页岩气井开展了实例分析应用, 可为同类页岩气藏的压裂评价提供一些理论支撑.

(2)海陆过渡相页岩气藏不稳定渗流特征可分为以下阶段: I为流动早期阶段: 其受到井筒存储效应以及表皮效应的影响, 在初期, 压力导数曲线表现为45°; II为双线性流阶段: 此阶段流体从地层线性流入裂缝, 裂缝流体线性流入生产井筒的阶段, 其压力导数曲线的斜率为1/4; III为线性流阶段: 此阶段是流体从地层线性流入有限导流裂缝的流动阶段, 压力导数曲线斜率为1/2; IV为径向流阶段: 压力导数曲线的值等于0.5的水平线, 达到内区径向流阶段; V为页岩气解吸阶段, 页岩气的解吸发生在该阶段, 压力导数出现下凹; VI为内外径向流过渡, 压力导数上升; VII为外区径向流, 压力导数曲线的值等于0.5M的水平线; VIII为边界控制阶段, 该阶段主要受边界条件影响, 出现压力导数曲线上扬.

附录$ ;$

无量纲量

引入储层渗流方程无量纲量如下

$${psi _{{
m{1,2D}}}} = frac{{{K_{1,2}}h{T_{{
m{sc}}}}}}{{3.684 times {{10}^{ - 3}}{q_{{
m{sc}}}}T{p_{{
m{sc}}}}}}left( {{psi _i} - {psi _{1,2}}}
ight)tag{A1}$$

$${t_{
m{D}}} = intlimits_0^t {frac{{{K_1}}}{{Lambda {mu _{
m{g}}}{r_{
m{w}}}^2}}{
m{d}}t},;;{
m{ }}varLambda = phi {c_{
m{g}}} + frac{{2{text{π}} {K_1}h}}{{{q_{{
m{sc}}}}{mu _{
m{g}}}}}tag{A2}$$

$${r_{
m{D}}} = frac{r}{{{r_w}}}tag{A3}$$

$${h_{
m{D}}} = frac{h}{{{r_{
m{w}}}}}tag{A4}$$

$${C_{
m{D}}} = frac{C}{{2{text{π}} hvarphi {C_{
m{t}}}{r_{
m{w}}}^2}}tag{A5}$$

$${D_{
m{D}}} = Dfrac{{mu varLambda }}{{{K_1}}}tag{A6}$$

$$omega {
m{ = }}frac{{phi {c_{
m{g}}}}}{varLambda }tag{A7}$$

其中, $omega $

为弹性储容比, 无量纲.

同时, 引入关于裂缝无因次量如下

$${psi _{{
m{FD}}}} = frac{{{K_1}h{T_{{
m{sc}}}}}}{{3.684 times {{10}^{ - 3}}{q_{{
m{sc}}}}T{p_{{
m{sc}}}}}}left( {{psi _{{i}}} - {psi _{
m{F}}}}
ight)tag{A8}$$

$${C_{{
m{FD}}}} = frac{{{K_{
m{F}}}{W_{
m{F}}}}}{{{K_1}{L_{
m{F}}}}}tag{A9} $$

$${q_{{
m{FD}}}}left( {{x_{
m{D}}},{t_{
m{D}}}}
ight) = frac{{2{L_{
m{F}}}{q_{
m{F}}}left( {x,t}
ight)}}{q}tag{A10}$$

式中, ${psi _{{
m{FD}}}}$

和${C_{{
m{FD}}}}$

分别为裂缝拟压力和裂缝导流能力, 无因次; ${q_{
m{F}}}$

为裂缝流量线密度, m³/(d·m); $q$

为裂缝中的流量, m³/d; ${q_{{
m{FD}}}}$

为裂缝流量线密度, 无因次.