删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

水中开孔腔流激振荡控制实验研究

本站小编 Free考研考试/2022-01-01


引言


空腔流激振荡是工程中常遇到的一类问题, 它是指流体在流经开口结构时, 边界层在开口前缘发生流动分离并形成不稳定的自由剪切层, 在满足一定的流速和几何特征条件下, 会引起剪切层发生稳定的自持振荡, 产生很强的周期脉动压力, 并通常引起高幅值纯音噪声辐射、附加阻力甚至是结构疲劳. 以往对空腔流激振荡的研究主要集中在流速较高的工程环境, 典型的如飞机弹舱[1]、起落架舱[2]、汽车侧窗[3]等开口结构都存在强烈的流激振荡现象. 近年来, 随着对水下噪声的重视, 众多研究发现即使对于水中空腔绕流这类极低马赫数的流动, 也存在明显的空腔流激振荡现象[4], 其工程问题则主要体现在舰船表面开孔的高幅值线谱噪声.

空腔流动研究的一个重要挑战是通过尽可能小的装置在尽可能大的流动条件下有效抑制空腔流激振荡, 并同时保证可靠性. 一般而言, 抑制空腔流激振荡最有效的途径是减弱或消除剪切层扰动, 其次是破坏或阻隔反馈环的形成[5]. 根据是否消耗外界能量, 空腔流激振荡控制可分为主动控制和被动控制, 典型的主动控制技术包括稳定或脉动射流技术[6]、电动或压电振荡翼片技术[7]、等离子体技术[8]和零质量射流[9]等, 这些主动控制技术的主要优点在于理论上可以在较大的流速范围内取得相对稳定的控制效果, 但由于消耗外界能量, 主动控制通常会带来较为可观的自噪声, 同时，主动控制的结构组成较为复杂，其可靠性在恶劣环境下(如海水环境)将成为一定挑战.

相较于主动控制, 被动控制方法的优势主要体现在结构简单易于应用, 在恶劣的环境中往往更为适用. 典型的被动控制方法包括改变前、后缘的几何形状[10]、设置前缘扰流体[11-12]、陷涡状上游表面[13]和上游凹槽[3]等, 都被证明在设计工况对空腔流激振荡有一定的抑制效果, 但大多数被动控制方法严重依赖于来流速度和雷诺数等流动条件, 控制效果随着流动偏离理想的设计状态而减弱. Mcgrath和Shaw[14]曾最先提出在开口前缘上方放置一横向流圆杆(也被称为“高频纯音发生器”), 可以在较大的流速范围内有效抑制空腔振荡. Marinez等[15]将这种横向流圆杆的作用机理归结为圆杆尾流中的卡门涡街与剪切层中的涡结构发生向更加无序状态的重组, 使得腔口剪切流趋于稳定, 但没有验证横向流圆杆在多个水流速度下的空腔振荡抑制效果.

纵观空腔流激振荡控制研究的发展历程可以发现, 无论是主动还是被动控制都已有丰富的研究成果, 但其中绝大部分都是针对空气介质空腔流, 而水中空腔流激振荡控制研究则要薄弱得多. 在为数不多的相关研究文献中, Arunajatesan和Sinha[16]和刘璐璐等[17]通过数值模拟探讨了格栅对水中空腔流激振荡的抑制效果, 但并未进一步开展实验研究; 张永昌[18]的研究结果表明, 格栅对空腔流激振荡的抑制效果极为有限; 邓玉清和张楠[19]对气动领域常用的射流控制技术对水中空腔流激振荡的抑制效果进行了数值研究, 但只开展了相关定性讨论, 并未探讨射流装置的结构组成; 张翰钦等[20]和汪利等[21]分别提出两种水中空腔流激振荡的主动控制装置, 但未见相关应用效果的探讨, 可见, 水中空腔流激振荡控制仍是亟需探索的领域.

作者在前期的研究工作中提出一种基于“分流”的空腔振荡抑制装置?前缘分流体(leading-edge flow splitter, LFS)[22], 数值模拟结果表明该装置对水中开孔腔流激振荡具有良好的抑制效果, 本文在此基础上进一步开展实验研究, 以水下航行器的表面开孔结构为对象设计了一种开孔腔模型, 并在循环水洞中开展空腔流激振荡控制实验, 通过测量腔底的壁面脉动压力, 评估前缘分流体在不同流速下对水中开孔腔流激振荡抑制效果. 研究结果对于抑制水下航行器表面开孔部位的流激振荡和噪声具有一定的应用潜力.


1.
实验设置



1.1
实验装置


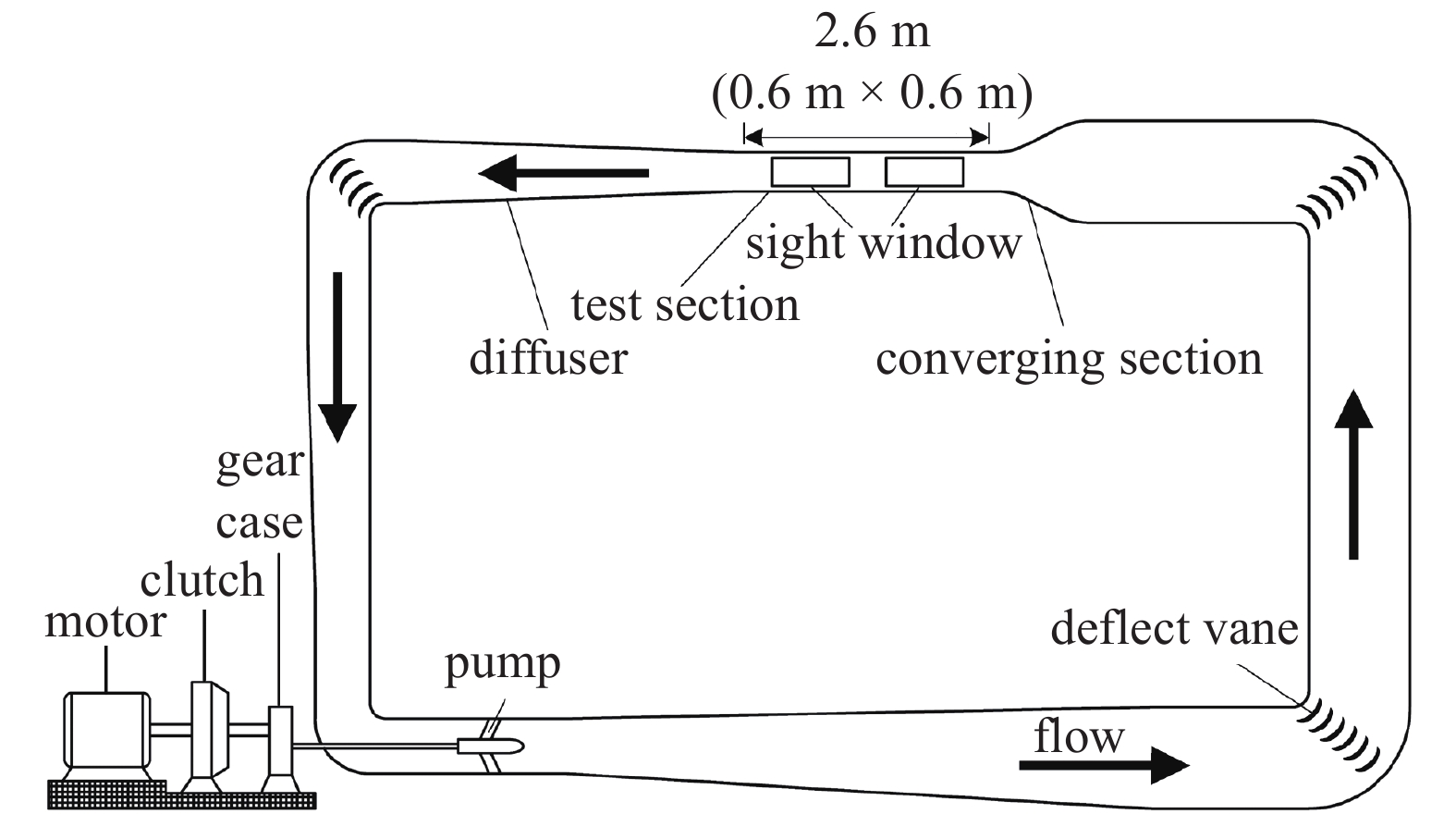
本实验在海军工程大学循环水洞实验室中开展, 循环水洞主要结构布置如图1所示. 循环水洞拥有尺寸为2.6 m × 0.6 m × 0.6 m的矩形截面工作段, 并分为两段长度相等的工作分段, 工作段的四周筒壁均为可拆卸的有机玻璃观察窗, 可用于安装实验模型和观察实验现象. 循环水洞内的水流由功率为133 kW的电机提供动力, 并通过变频柜控制电机转速来调整洞内水流速度, 水洞工作段内可实现的最大流速为5 m/s, 最小调整流速间隔为0.02 m/s, 流速通过皮托管进行测量. 为降低水洞工作段的湍流度, 在水洞转角处均设置有弧形整流片, 可以保证工作段核心区域湍流度小于0.5%. 实验过程中, 将开孔腔模型安装于水洞第二工作分段的上壁面, 以便于对开孔腔模型的调整和吊装, 同时降低收缩段的流体扰动.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
NUE循环水洞



Figure
1.
NUE water tunnel



下载:
全尺寸图片
幻灯片



1.2
实验模型


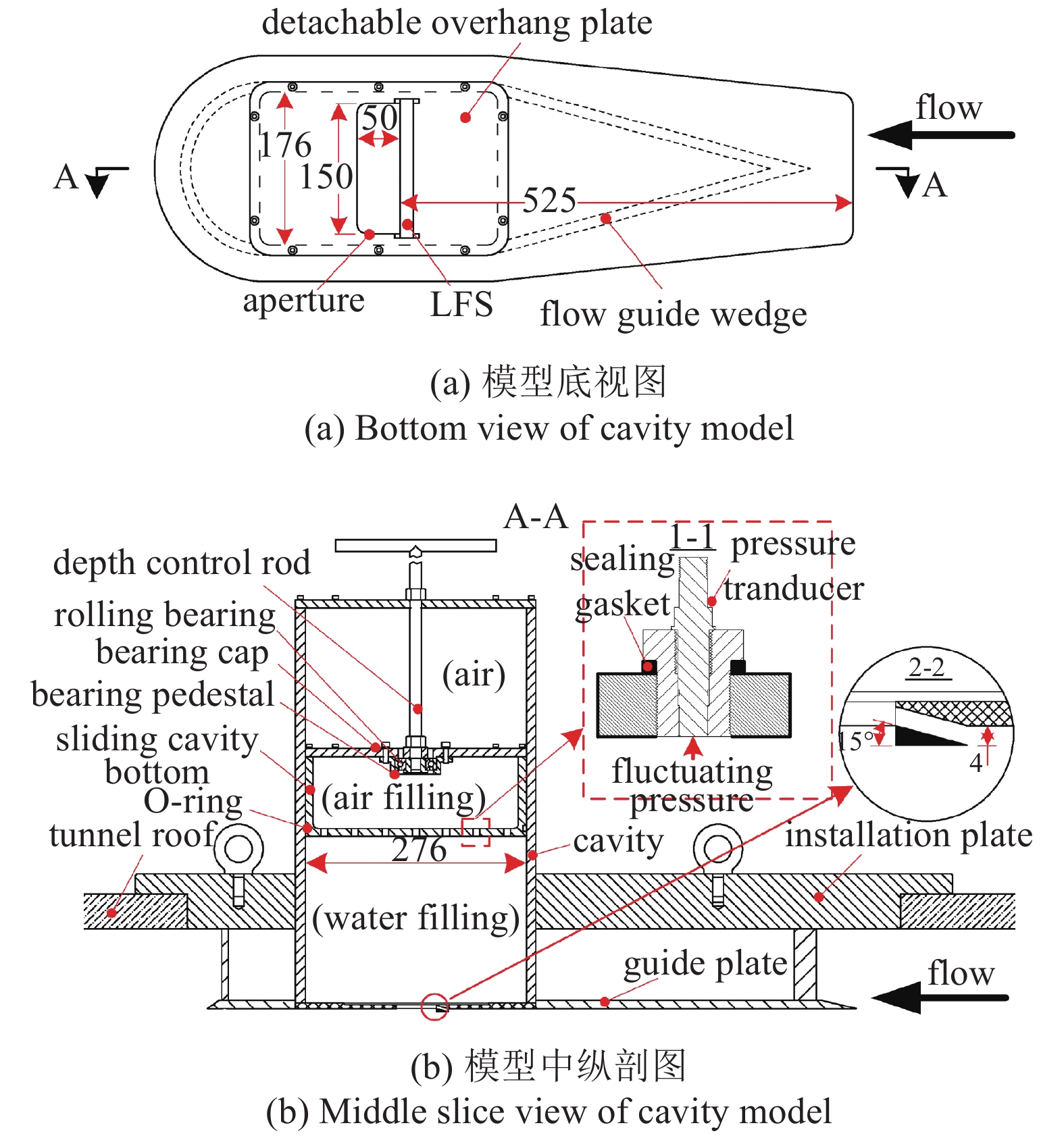
水下航行器的开孔形状、尺寸各异, 开孔腔深度不一, 为能够较为全面地针对水下航行器特点探究开孔腔流激振荡特性, 本实验设计了一种可拆开孔颈板的变腔深开孔腔模型, 其具体结构组成如图2所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
实验开孔腔模型及关键尺寸参数(单位: mm)

1-1—压力传感器安装; 2-2—前缘分流体安装



Figure
2.
The aperture-cavity model and key geometry parameters in experiments (unit: mm)

1-1—Installation of pressure transducers; 2-2—Installation of leading-edge flow splitter




下载:
全尺寸图片
幻灯片


如图2所示, 本实验的腔体模型为矩形腔, 截面尺度为276 mm × 176 mm (流向 × 展向), 空腔深度可以通过调深旋杆带动腔底沿腔体壁滑动实现在0 ~ 600 mm范围内的自由调整, 滑动腔底为半开式的矩形柱, 其底面设有13个螺纹孔, 用于安装实验所需的脉动压力传感器和水听器以及排气(保证腔体内完全充水), 中空部分为传感器的接线提供空间, 在滑动腔底底部设有开槽并放置有橡胶O型圈, 以保证实验过程中腔体的水密性. 实验腔体通过位于腔体中部的盖板安装于水筒上壁, 腔体开孔端面突出于腔体安装盖板120 mm, 以保证腔体孔口绕流位于水洞工作段核心区, 避免水洞洞壁对孔腔绕流场的干扰. 腔体开孔颈板采用可拆式设计, 便于控制装置的安装和其他类型开孔颈板的更换, 开孔颈板通过螺钉平齐内嵌于导流板内, 以保证孔口来流流场稳定, 同时为减小螺钉对孔口绕流的干扰, 实验采用埋头螺钉. 在导流板和腔体安装盖板之间设计有尖劈状的支撑板, 起到对腔体浸水部分的导流作用, 避免水流对腔体的直接冲刷而引起的腔体振动, 同时导流板的边缘也均设计为尖劈状, 尖劈角为13°, 以尽量降低来流与导流板边缘相互作用对孔口绕流场的干扰.

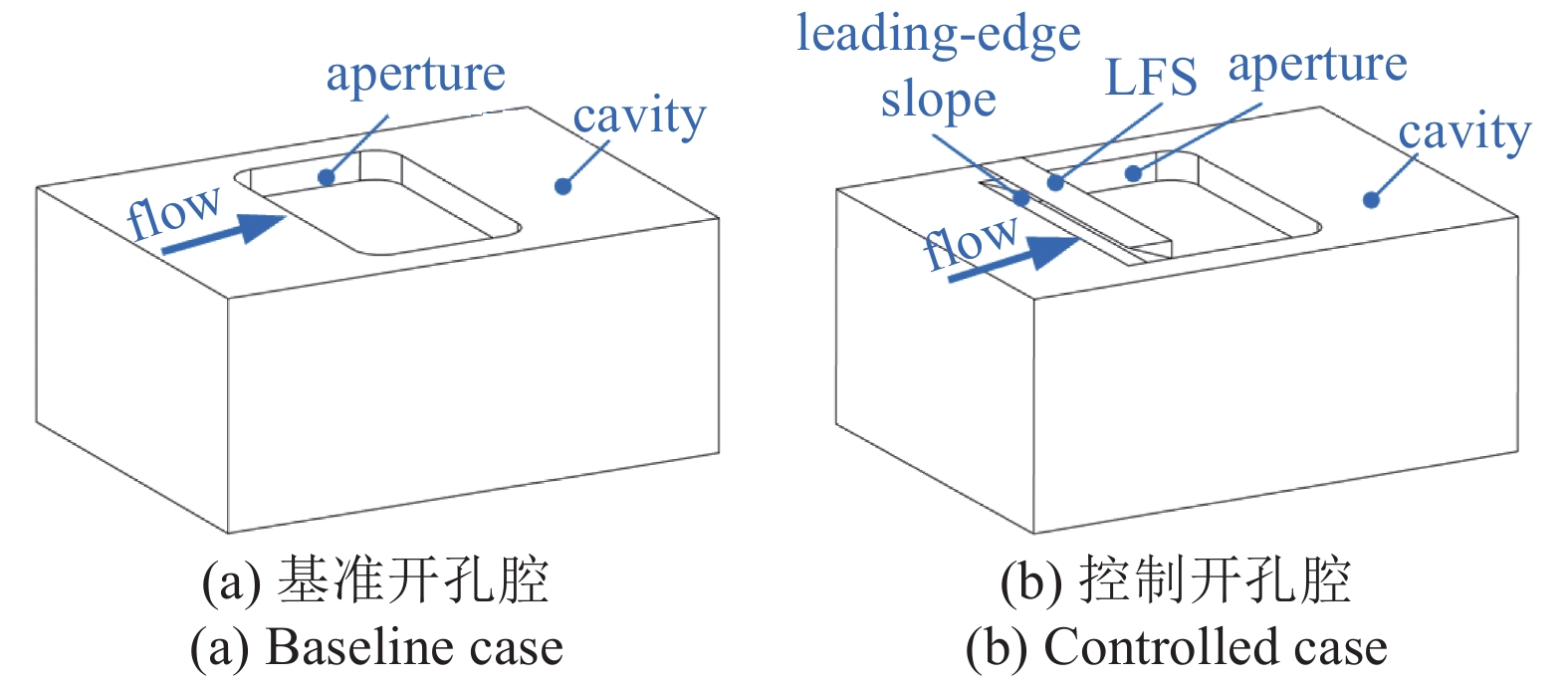
实验中的开孔腔模型三维结构示意图如图3所示, 其中, 基准开孔腔和控制开孔腔的区别在于后者安装了前缘分流体，而前者没有. 基准开孔腔的开孔尺寸为50 mm × 150 mm, 长宽比L/W =1/3, 较小的长宽比可以减小空腔流激振荡由孔口侧壁带来的三维效应, 空腔深度固定为100 mm, 长深比L/D=1/2, 开孔颈板厚度为10 mm. 本实验所研究的空腔振荡流动控制装置——前缘分流体, 为安装于开孔腔前缘上方的倒楔形块, 其流向剖面和三维形状分别如图2(b)和图3(b)所示, 分流体上表面与来流平行, 下表面与上表面成15°的分流角, 同时对控制开孔腔的前缘表面作等角度斜坡处理, 使分流体下表面与开孔前缘斜坡面相平行; 分流体后壁与开孔腔前缘平齐, 保证开孔的流向尺度不受影响; 分流体后壁高度与安装高度h保持一致, $h = delta /2$, $delta $为开孔前缘处的边界层厚度厚度. 边界层厚度根据文献[23]按下式进行计算



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
实验开孔腔模型三维示意图



Figure
3.
3D sketch maps of the aperture-cavities in experiments



下载:
全尺寸图片
幻灯片








$$delta {
m{ = }}frac{v}{{{u_*}}}{{
m{e}}^{0.41left( {sqrt {2/0.026;3} {Re} _x^{1/14} - 7.4}
ight)}}$$
(1)

式中, $nu $为水的运动黏度, 取${
m{1}}{
m{.5}} times {
m{1}}{{
m{0}}^{{
m{ - 6}}}}$ m2/s; ${{Re} _x} = $$ {U_infty }x/nu$为开孔前缘雷诺数, ${U_infty }$为来流速度, x=0.525 m; ${u_*}$为摩擦速度, ${u_*} = sqrt {{tau _w}/{
ho _0}} $, ${
ho _0}$=103 kg/m3, ${tau _w}$为绕流摩擦应力, 按照福尔科涅尔公式[23]计算: ${tau _w} = $$ 0.026;3{R{
m{e}}} _x^{ - 1/7} left( {{
ho _0}U_infty ^2/2}
ight)$.

前缘分流体的设计点流速为4 m/s, 根据式(1)计算可知该流速下的边界层厚度${delta _{{U_infty } = 4}} approx 8$ mm, 因而本实验中前缘分流体的安装高度h=4 mm. 文献[22]的研究表明, 前缘分流体的主要作用机理在于在空腔前缘处提前将一部边界层流体分流至腔内, 一方面可以降低腔口剪切层的速度梯度, 另一方面减少了剪切层内大尺度涡的分布, 进而减弱自由剪切层与空腔后缘的碰撞强度, 最终达到抑制开孔腔流激振荡的目的. 实验中的开孔腔模型安装如图4所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
开孔腔模型安装实物图



Figure
4.
Installation of the aperture-cavity model



下载:
全尺寸图片
幻灯片



1.3
传感器及测试系统


流激空腔振荡的直接物理表现主要为腔口剪切层的速度脉动和腔内流场作用于壁面的脉动压力, 其中, 前者的实验测量主要通过粒子成像测速(PIV)和激光多普勒测速(LDV)等方法进行, 后者则可通过动态压力传感器进行实验测量, 本文主要通过壁面脉动压力测量反映水中开孔腔的流激振荡特性.

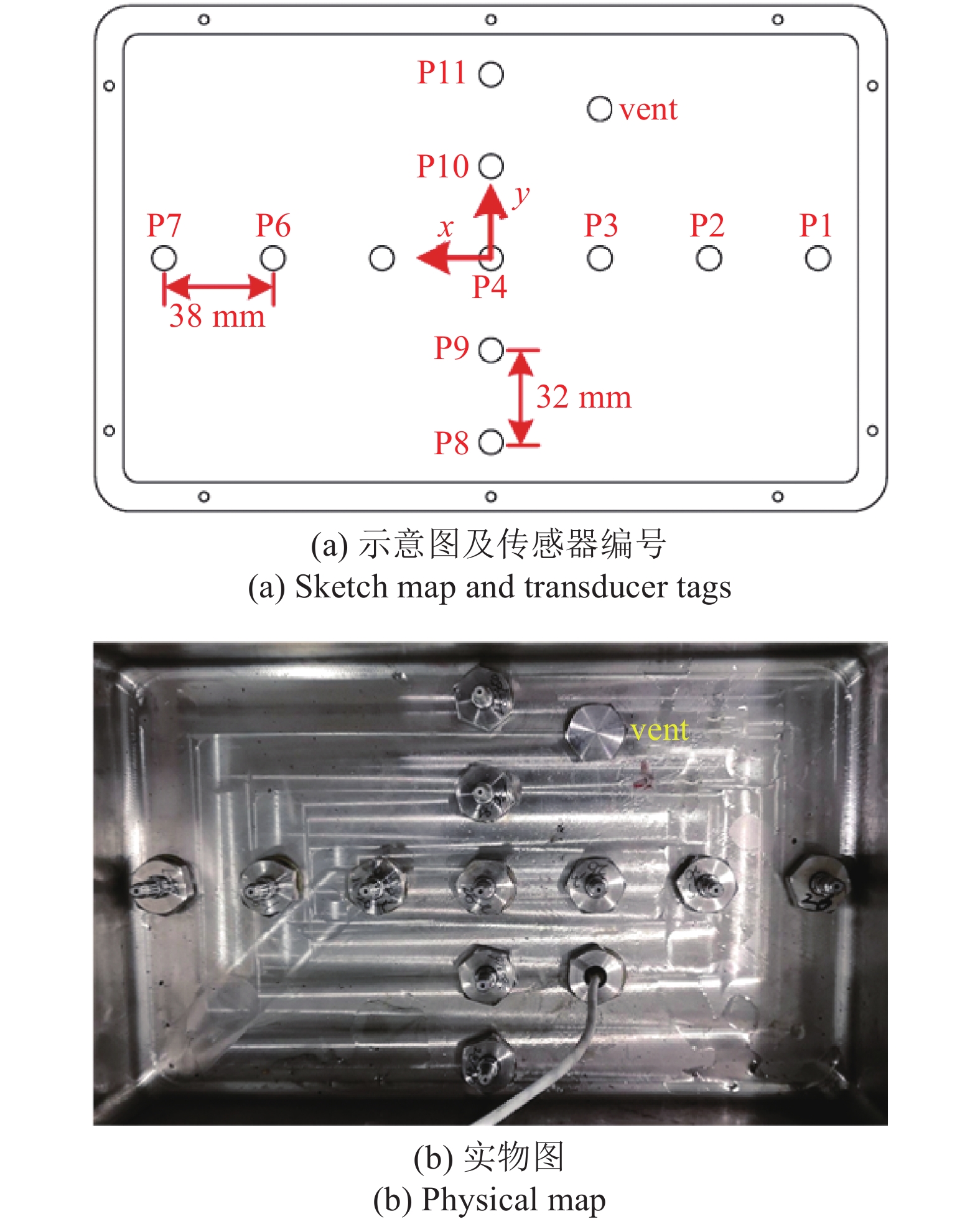
本实验中的传感器均通过螺钉内嵌安装于腔体模型的滑动腔底板, 并采用组合密封垫对传感器安装孔作水密处理, 如图2所示. 实验过程中, 在腔底流向中线和展向中线分别布置7个和5个压力传感器, 传感器测点布置及编号如图5所示, 传感器安装位置如表1所示, 其中, 传感器位置坐标原点位于腔底中心, 同时也正对于腔口中心. 动态压力传感器为美国PCB公司的113B28型压电式动态压力传感器, 其压力分辨率为1 mpsi, 量程为50 psi, 低频响应为0.5 Hz, 在实验中用于测量腔底的壁面压力脉动响应和压力分布, 并以此反映开孔腔流激振荡特性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
传感器测点布置



Figure
5.
Arrangements of transducers



下载:
全尺寸图片
幻灯片





表
1
腔底传感器安装位置



Table
1.
Location of the floor mounted transducers



table_type1 ">
TagsP1P2P3P4P5P6
x/L?2.28?1.52?0.7600.761.52
y/W000000
TagsP7P8P9P10P11
x/L2.280000
y/W0?0.43?0.210.210.43





下载:
导出CSV
|显示表格



实验采用丹麦B&K公司的LAN-XI 3660型数据采集模块对传感器信号进行采集, 其拥有12个数据传输通道, 单块LAN-XI 3660型数据采集模块即可完成本实验所涉及的全部11个传感器的信号采集工作, 实验数据记录和信号采集设置通过B&K公司的PULSE软件完成, 信号采样频率设定为32768 Hz, 信号分析有效最大频率为12.8 kHz, 单次采样时间设定为10 s. 为避免交流工频信号对实验采集数据的干扰, 实验过程中采用B&K公司的2831型直流电源模块对采集模块进行供电. 本实验的信号采集系统如图6所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
信号采集系统



Figure
6.
Set-up of signal collection system



下载:
全尺寸图片
幻灯片



2.
信号处理方法


由于传感器所采集的信号都是时域信号, 需要采用一系列数字信号处理手段对时域信号进行二次处理, 以更加全面地反映前缘分流体对水中开孔腔流激振荡的影响特性. 为分析本实验中开孔腔流激振荡的频率特性, 采用功率谱密度PSD描述采集的时域信号在频域上的能量分布, 在MATLAB软件中使用pwelch函数[24]对脉动压力时域信号做功率谱估计, 采用长度为2 s的Hamming窗对时域采样信号进行分段截取, 分段重叠度overlap设定为75%, 每段长度为10 s的时域采样信号共被截取为17个分段进行平均, 可有效平滑频谱曲线中的随机噪声分量; 分段计算频率点数和Hamming窗长所含的数据点数保持一致, 相应计算得到的频率分辨率$Delta f = 0.5;{
m{Hz}}$, 同时, 将脉动压力功率谱密度幅值做无量纲化, 用对数表示为声信号分析中常用的分贝值, 即功率谱密度级$PS{D^*}$(power spectra density level), 其计算式如下







$$PS{D^*} = 10lg left( {frac{{{P_{xx}}}}{{q_0^2}}}
ight)$$
(2)

式中, ${P_{xx}}$为脉动压力时域信号的自功率谱密度, 单位为Pa2; ${q_0}$为水声声压级计算参考值, 取1 ${text{μ}} {
m{Pa}}$. 本文的所有频谱图如在无特别说明的情况下, 其幅值都是功率谱密度级$PS{D^*}$.

由开孔腔流激振荡引起的脉动压力总能量和腔内有效压力载荷分别采用脉动压力总级$OASPL$和脉动压力均方根值${P_{{
m{rms}}}}$进行描述, 并同样对${P_{{
m{rms}}}}$作无量纲化, 将其表示为压力载荷系数${C_{{
m{prms}}}}$, OASPL和${C_{{
m{prms}}}}$的计算式如下







$$OASPL = 10lg left[ {Delta fsumlimits_{f = {f_0}}^{{f_{max }}} left({{{10}^{frac{{PSD_f^*}}{{10}}}}}
ight)}
ight]$$
(3)







$${C_{{
m{prms}}}} = dfrac{{sqrt {dfrac{1}{N}displaystylesumnolimits_0^{N - 1} {{{left[ {p(n) - overline p }
ight]}^2}} } }}{{{q_infty }}}$$
(4)

式中, $PSD_f^*$为各频率下的功率谱密度级, ${f_0}$为频带级起始计算频率, ${f_{max }}$为最大分析频率, Δf为频谱中的频率分辨率; $p(n)$为时域脉动压力幅值, $overline p $表示测量周期内时域压力信号平均值, ${q_infty }$为来流动压力, ${q_infty } =
ho U_infty ^2/2$. 开孔腔流激振荡控制前后的脉动压力载荷抑制效果采用脉动压力均方根值的相对变化量进行衡量, 按下式表示







$$% P_{{
m{rms}},{
m{reduction}}} = frac{{P_{{
m{rms}},{
m{baseline}}} - P_{{
m{rms}},{
m{controlled}}}}}{{P_{{
m{rms}},{
m{baseline}}}}} times 100% $$
(5)

互相关性(cross-correlation)可以反映两个不同信号在时域上的关联程度, 本文通过计算互相关系数${
ho _{{
m{pp}}}}$分析开孔腔不同位置脉动压力信号在时域的相互关联程度, 进而探讨前缘分流体对水中开孔腔流激振荡影响的空间分布特性, 互相关系数${;
ho _{{
m{pp}}}}$定义为







$${
ho _{{
m{pp}}}}({x_1},{x_2},tau ) = frac{{overline {p({x_1},t)p({x_2},t + tau )} }}{{sqrt {overline {{p^2}({x_1},t)} } sqrt {overline {{p^2}({x_2},t)} } }}$$
(6)

式中, $tau $为两个信号之间的时间延迟, $p({x_1},t)$和$p({x_2},t)$分别为不同位置测点的脉动压力时域信号, —表示变量在t在[0,$(N - 1){
m{d}}t$]时间范围内的算术平均, N为单个信号的数据点数, ${
m{d}}t$为信号采样时间间隔. ${
ho _{pp}}$为变化区间在为[?1, 1]的归一化系数.


3.
流激空腔振荡基本特性


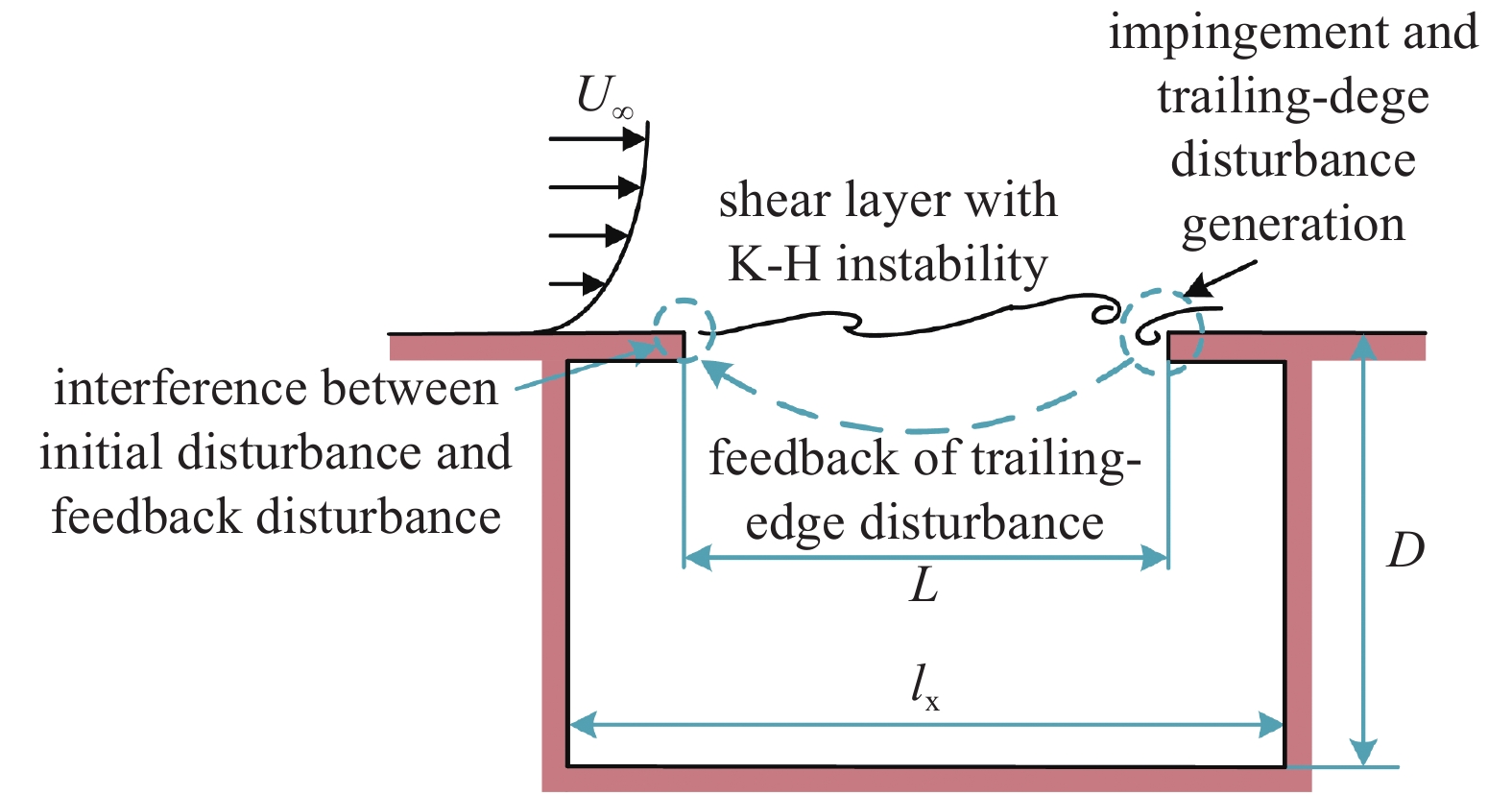
来流在流经空腔开口时, 边界层由于壁面缺失和速度梯度的影响, 会在开口处演化为具有Kelvin-Helmholtz不稳定性的剪切层, 剪切层在空腔前缘产生初始横向扰动, 且向下游传播的过程中, 剪切层扰动不断增大, 最终与空腔后缘抨击并产生一系列其他物理扰动, 如压力脉动、质量流、涡脱落和声波等, 这些扰动又向上游反馈, 当到达前缘的反馈扰动与剪切层的初始扰动同频同相时, 则发生最大增益叠加, 对腔口的剪切层流动产生调制作用, 引起腔口剪切层以特定频率发生自持振荡并辐射纯音噪声, 其物理进程如图7所示. 理想状态下, 空腔自持振荡满足以下相位关系







$$2{text{π}} frac{{{f_n}L}}{{{U_c}}} + phi = 2n{text{π}} - 2{text{π}} alpha, begin{array}{*{20}{c}} {}&{n = 1,2,3 ,cdots } end{array}$$
(7)

式中, $alpha $表示后缘抨击与反馈扰动之间的相位迟滞因子, 为与来流速度、空腔长深比等因素相关的经验常数; $phi $为扰动从后缘反馈至前缘的相位变化, 取决于具体的反馈路径和机制; ${U_c}$为腔口剪切层的平均对流速度, 约0.5倍的自由来流速度${U_infty }$; ${f_n}$即为剪切层自持振荡频率, n为振荡模态阶数.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
流激空腔振荡作用机制示意图



Figure
7.
Sketch map of the mechanism of flow-induced cavity oscillation



下载:
全尺寸图片
幻灯片


空腔绕流的自持振荡现象早在20世纪50年代便引起了关注[25], 此后大量实验结果表明空腔自持振荡频率随流速变化呈阶梯型线性分布规律[26], 与式(7)给出的理论分析规律相符, 但直到1964年Rossiter[27]提出“声反馈”机制, 给出了可以准确描述空腔绕流自持振荡频率特征的具体机理解释. 声反馈机制将腔口剪切层视为由一系列涡团组成, 涡团由来流边界层在前缘脱落而来, 向下游传播并最终与后缘碰撞激发声波, 声波向上游反馈又加剧了前缘的涡脱落, 从而形成剪切层自持振荡的反馈环, 自持振荡模态阶数n在具体的流动结构上即对应于剪切层内的涡团个数, 显然n取决于开口长度L和来流速度${U_infty }$, 这也被后续的流场显示实验所验证[28]. 在声反馈机制中, $phi = 2{text{π}} {f_n}L/{c_0}$, ${c_0}$为当地声速, $alpha $=0.25, 由此可得到被广泛用于流激空腔振荡频率预报的Rossiter方程







$$St = frac{{{f_n}L}}{{{U_infty }}} = frac{{n - 0.25}}{{Ma + {U_infty }/{U_c}}},begin{array}{*{20}{c}} {}&{n = 1,2,3, cdots } end{array}$$
(8)

式中, Ma为自由来流的马赫数, ${U_c} = 0.57{U_infty }$.

从式(8)和式(9)可知, 空腔自持振荡频率由来流速度${U_infty }$和开口长度L主导, 并且与反馈机制密切相关, 但需要注意的是, 空腔绕流的反馈机制同样受来流速度影响, 研究表明声反馈只在高亚马赫数和超音速空腔流动中与实际相吻合, 而在低速空腔流中则普遍认为以其他反馈机制为主导[29-30], 如Tuerke等[31]提出腔内循环回流反馈是不可压缩空腔流自持振荡的主要反馈机制.

当空腔绕流自持振荡频率与空腔的某一固有模态频率相近时, 则发生流激空腔振荡的另一形式?流激空腔共振, 两者的典型差异体现在幅值响应和频率响应上. 当空腔共振发生时, 产生的脉动压力要明显大于自持振荡, 幅值上常采用Q因子作为空腔共振的发生判据[32], $Q = {f_0}/({f_2} - {f_1})$, ${f_0}$为脉动压力频谱的峰值点频率, ${f_1}$和${f_2}$分别为峰值左、右侧半功率点对应的频率, 但$Q$因子并没有明确的临界取值定义, 而更为显著的区别为频率响应, 空腔共振具有明显的“频率锁定”现象[33], 即空腔共振时的振荡频率与流速将不再保持式(7)所示的线性关系, 几乎锁定在空腔本身的固有频率上.

流激空腔共振和自持振荡的本质区别在于形成机理不同, 前者是开口剪切层振荡与腔内流体运动、声模态甚至腔体结构振动强烈耦合的结果, 而后者与空腔腔体的关联较小. 根据共振机制的不同, Rockwell和Naudascher[34]将流激空腔共振归类为流体?声共振和流体?弹性共振, 流体?弹性共振即剪切层振荡与腔体结构振动相耦合的共振状态, 其振荡特性取决于结构的刚度大小, 而流体?声共振具体还包括声模态共振和Helmholtz共振, 前者为剪切层振荡与腔内声驻波相耦合的共振振荡, 开放式方腔的声模态频率的近似计算如式(9)所示, 显然声模态共振特性的主要影响因素为腔体在各方向的几何尺度; 对于“小开口、大腔体”一类的空腔, 如本文所研究的开孔腔, 更容易发生流激共振形式为Helmholtz共振, 理想Helmholtz共振腔的固有频率计算如式(10)所示, 可见, 空腔绕流的Helmholtz共振特性取决于空腔体积、开孔尺度以及声速.







$${f_m} = frac{{{c_0}}}{2}sqrt {{{left( {frac{{{m_x}}}{{{l_x}}}}
ight)}^2} + {{left( {frac{{{m_y}}}{{2{l_y}}}}
ight)}^2} + {{left( {frac{{{m_z}}}{{{l_z}}}}
ight)}^2}} $$
(9)







$${f_{HR}} = frac{{{c_0}}}{{2{text{π}} }}sqrt {frac{S}{{V{l_s}}}} $$
(10)

式中, ${f_m}$和${f_{HR}}$分别表示空腔的声模态频率和Helmholtz共振频率; ${m}_{x},;{m}_{y},;{m}_{z}$为正整数, 分别表示空腔各方向声模态阶数; ${l}_{x},;{l}_{y},;{l}_{z}$分别为腔体在流向、深度方向和展向的几何尺度; S为开孔面积, V为腔体体积, ${l_s}$为开孔颈部的有效长度.

对于水中空腔而言, 由于声速和结构刚度较大, 声共振和弹性共振往往难以单独产生, 但水中流体介质和结构材料的特性阻抗相近, 使得水中空腔通常存在较强的声?流?固耦合, 腔壁弹性会大大降低空腔的声共振频率. 周城光等[35]和高岩等[36]等曾分别对此进行了理论证明, 进而使得水中空腔也可能发生流激共振, 如Burroughs和Stinebring[4]在水中开孔腔流激振荡实验中发现, 在较高水流速度下, 开孔腔发生了流激共振现象, 并推测其为腔壁弹性影响下的Helmholtz共振. 厘清流激空腔振荡的具体机制对其控制具有重要意义, 例如针对空腔剪切层自持振荡, 首要抑制手段是破坏剪切层的不稳定性, 而对于流激空腔共振, 则应尽量减小腔体的放大效应.


4.
实验结果及分析


本实验在0 ~ 4.4 m/s流速范围内开展, 实验测试过程中的流速调整间隔为0.4 m/s, 每次调整流速后均在水洞内流动充分稳定后再进行数据采集, 为保证实验测试结果的准确性, 在实验前先对脉动压力信号采集系统进行标定, 即在水洞未运行时, 通过保证各传感器测得的脉动压力均方根值基本一致的方法标定脉动压力试验系统.


4.1
脉动压力频谱特性


为减小空间分布对开孔腔流激振荡频谱分析产生的影响, 鉴于测点布置及实验开孔腔模型的几何对称性, 以下频谱特性分析均基于腔底中心测点, 即图5中的P4脉动压力传感器采集的脉动压力数据, 根据本实验结果以及Burroughs和Stinebring[4]的水中空腔流动测试结果可以发现, 水中空腔流激振荡的主要频谱特征和能量都集中在200 Hz以内, 为分析的直观性, 本文只在200 Hz以内频段作频谱分析.

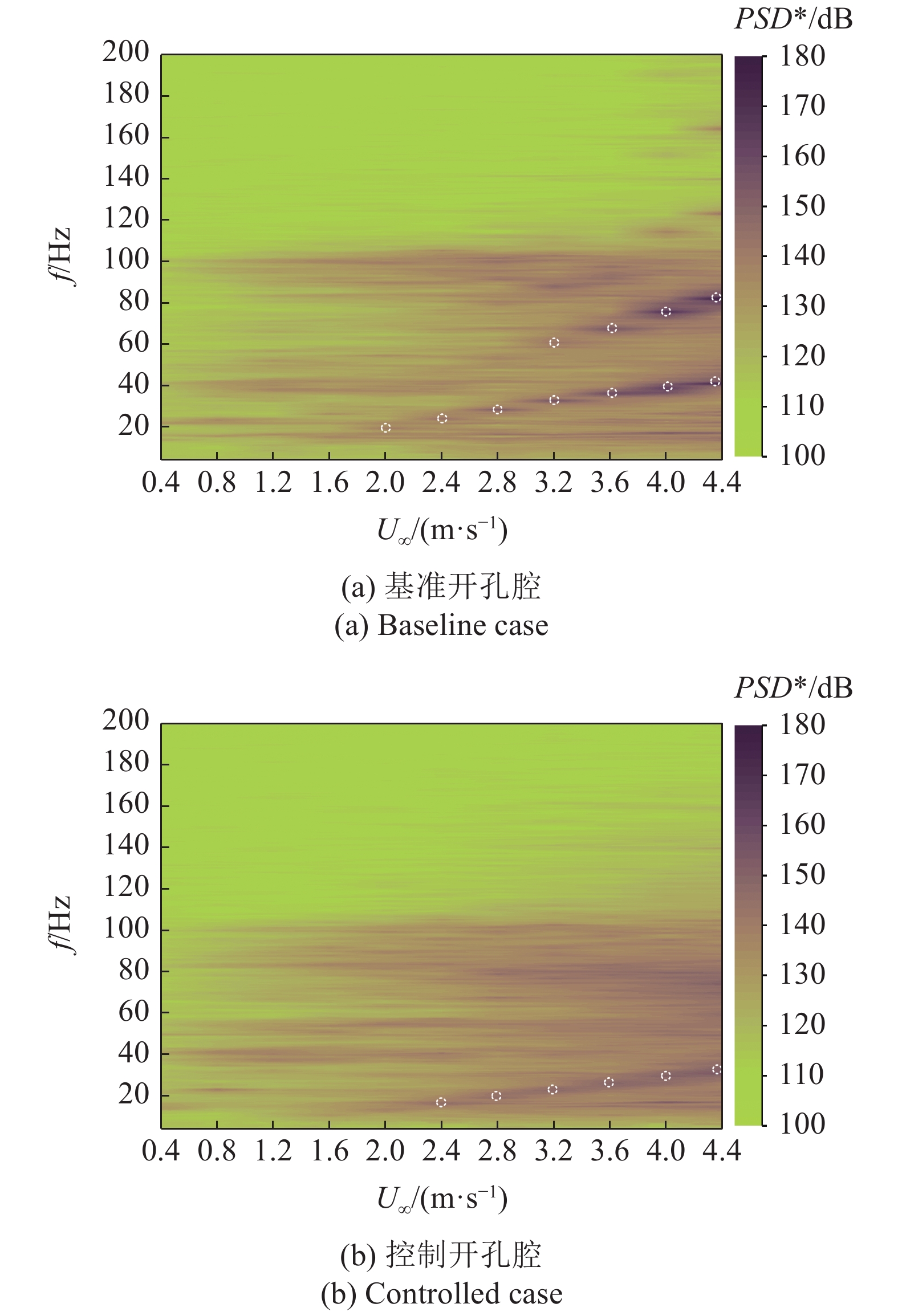
水中开孔腔在控制前后的壁面脉动压力频谱随流速变化云图如图8所示, 频谱中的壁面脉动压力幅值按式(2)所示的功率谱密度级PSD*表示. 从图中可以看出, 流速对水中开孔腔流激振荡特性具有显著影响. 在流速${U_infty }$<2 m/s时, 基准开孔腔的壁面脉动压力频谱较为平缓，没有产生突出的峰值, 表明较低流速并不会引起开孔腔产生周期性流激振荡. 随着流速升高, 频谱云图中陆续出现了一系列突出的离散窄带峰, 窄带峰值频率随流速近似呈线性增加, 这与众多在开放式方腔流动中观察到自持振荡特性相似, 且频谱峰值没有出现频率锁定现象, 表明开孔腔在实验流速范围内没有发生空腔共振, 只产生了剪切层自持振荡. 同时注意到, 来流速度的升高会使开孔腔产生新的高阶自持振荡模态, 如在${U_infty }$>3.2 m/s时, 壁面脉动压力频谱窄带峰值频率除了继续随流速升高而增大以外, 还在更高频处产生了新的窄带峰, 由原先的“单峰”频谱演变为“双峰”频谱.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
壁面脉动压力频谱随流速变化云图(白色圆圈对应于各流速下的频谱峰值)



Figure
8.
Spectral contour of wall pressure fluctuations as a function of freestream velocity (the white circles correspond to the peak of spectrum at different velocities)



下载:
全尺寸图片
幻灯片


与基准开孔腔相比, 安装了前缘分流体的控制开孔腔的自持振荡幅值得到显著抑制. 如图8所示, 在${U_infty }$>2.4 m/s时, 控制开孔腔的壁面脉动压力频谱中虽然具有频率随流速近似线性增长的离散窄带峰, 表明也产生一定程度的自持振荡, 但窄带峰值明显小于基准开孔腔. 从图9可以具体看出前缘分流体对开孔腔绕流自持振荡幅值的抑制效果: 在${U_infty }$=2.4 m/s时, 控制前和控制后的壁面脉动压力窄带峰值较为接近, 但随着流速的继续提升, 开孔腔的脉动压力窄带峰值在控制后得到了有效衰减, 且峰值衰减量随流速升高而增大, 在${U_infty }$=4.4 m/s时, 开孔腔壁面脉动压力窄带峰值经控制后的衰减量达到最大, 为25.3 dB.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-9.jpg'"
class="figure_img
figure_type2 ccc " id="Figure9" />



图
9
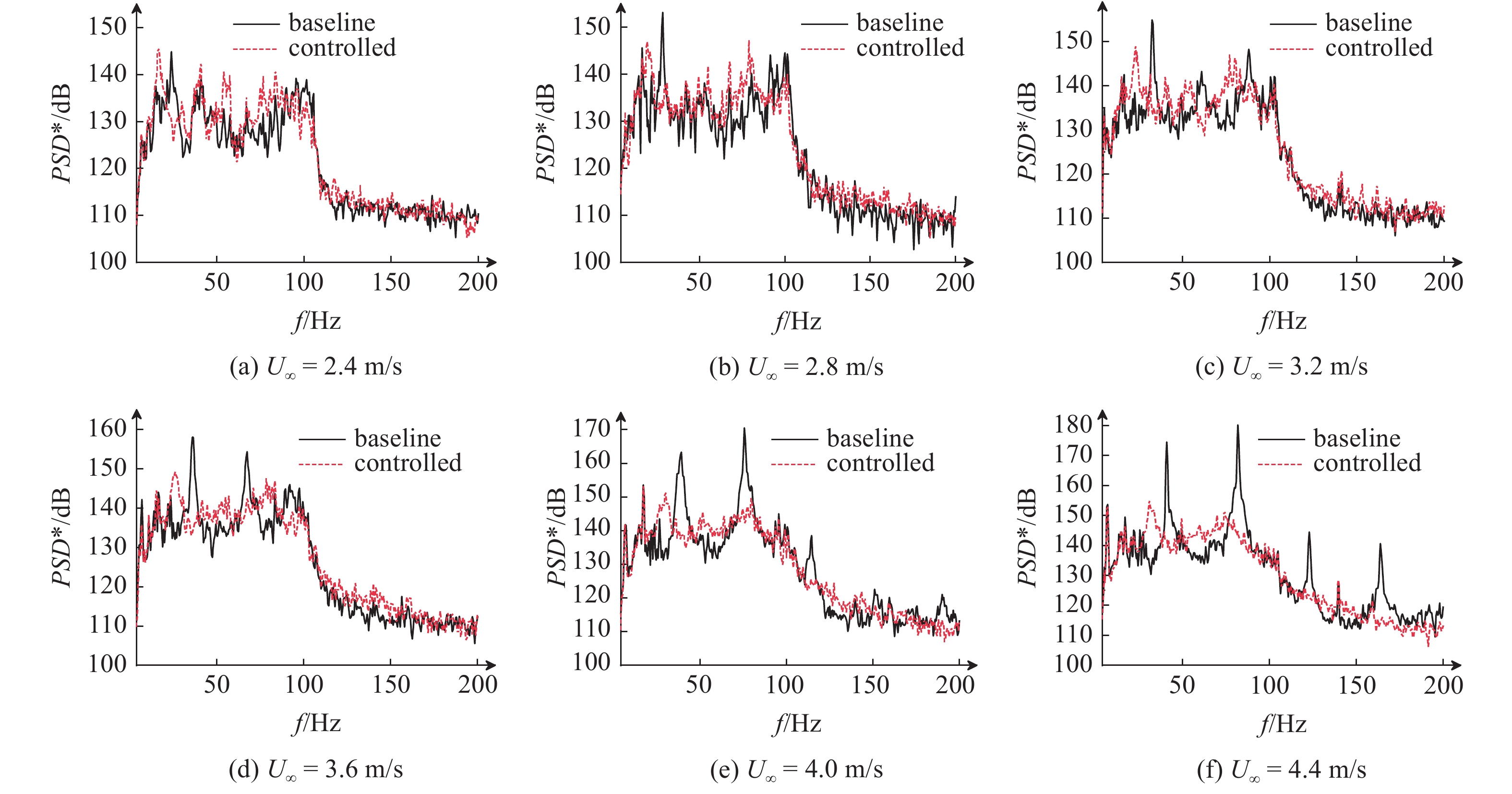
典型来流速度下壁面脉动压力PSD*



Figure
9.
PSD* of wall pressure fluctuations at typical freestream velocities



下载:
全尺寸图片
幻灯片


在实验流速范围内, 前缘分流体有效消除了水中开孔腔绕流自持振荡的二阶模态. 结合图8和图9可以发现, 在${U_infty }$=3.2 m/s时, 基准开孔腔在61 Hz频率处开始产生尚不突出的二阶自持振荡, 但随着流速增加, 基准开孔腔的二阶自持振荡迅速加强, 并在${U_infty }$=4.0 m/s时, 开孔腔绕流自持振荡的主导模态发生了由一阶向二阶的跃升, 而控制开孔腔除了具有幅值显著降低的一阶自持振荡外, 在实验流速范围几乎没有产生其他自持振荡模态, 这表明前缘分流体可以有效延缓高阶自持振荡模态的产生, 由于水中开孔腔的固有频率通常高于自持振荡频率, 这一特性有利于避免产生流激空腔共振.

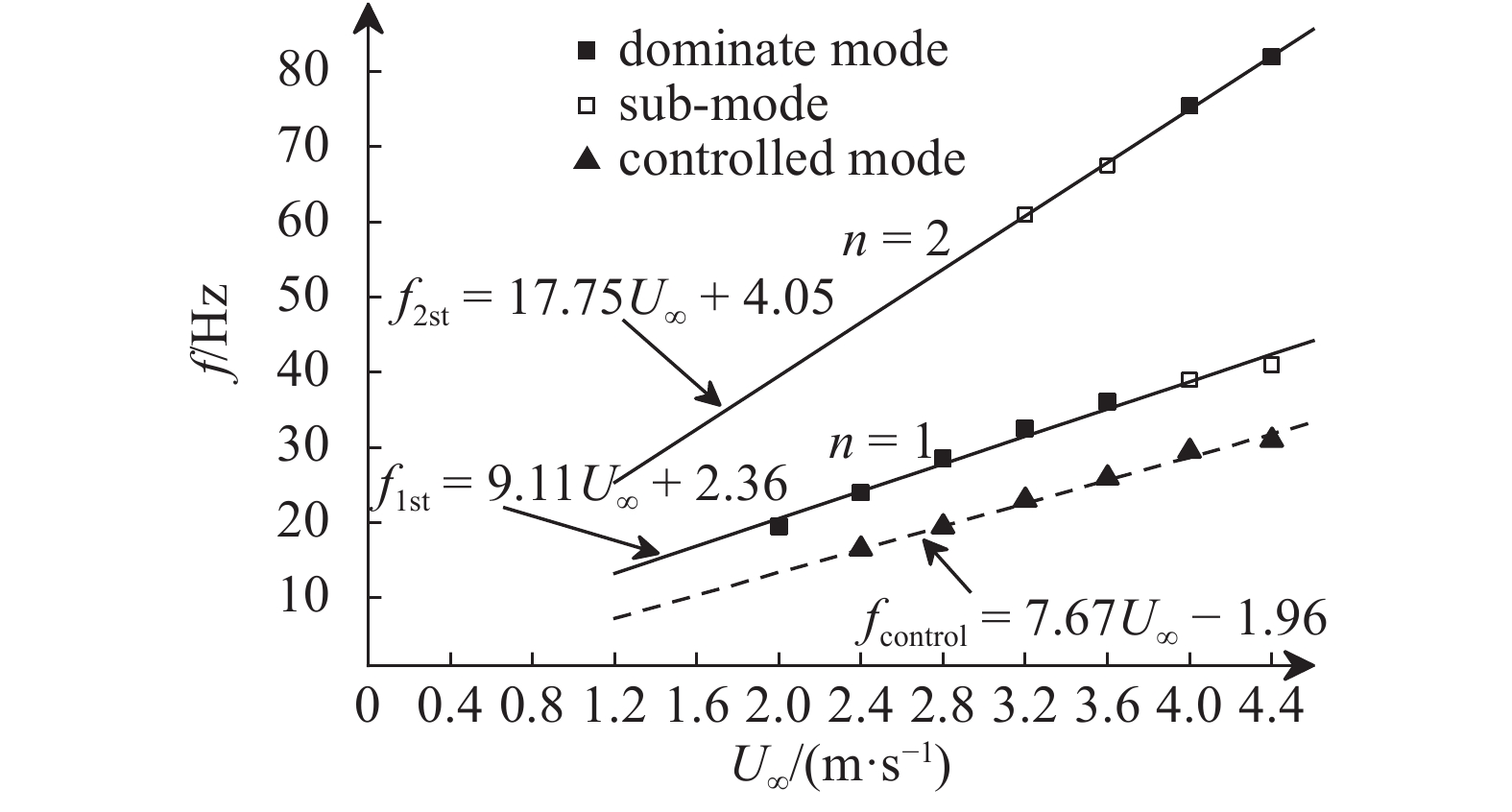
前缘分流体对开孔腔流激振荡具有良好的低频频移特性. 从壁面脉动压力频谱中提取开孔腔绕流的自持振荡频率, 并采用最小二乘法对各阶自持振荡的频率与来流速度关系作线性拟合, 如图10所示, 可以看出前缘分流体对开孔腔流激振荡的低频频移特性主要体现在两方面, 一是在实验流速范围内, 控制开孔腔的自持振荡频率均低于基准开孔腔, 二是控制开孔腔的自持振荡频率随流速的增长率要小于基准开孔腔, 具体表现为在${U_infty }$= 2.4 m/s时, 前缘分流体降低开孔腔自持振荡频率7.5 Hz, 在${U_infty }$= 4.4 m/s时, 开孔腔自持振荡的低频频移量则增大至10 Hz, 显然这一特性同样有益于避免流激空腔共振的发生. 由式(8)可知, 当腔口流向尺度L等效增加或对流速度${U_c}$等效降低时, 会使自持振荡频率向低频移动, 结合前缘分流体一个主要作用机理是通过将一部分来流边界层流体引入腔内, 进而降低腔口剪切流动的速度梯度, 因而可以推测前缘分流体对开孔腔流激振荡的低频频移特性的主要原因是降低了腔口剪切层的对流速度${U_c}$.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
不同流速下开孔腔绕流自持振荡频率分布(${f_{1{
m{st}}}}$和${f_{{
m{2nd}}}}$分别为基准开孔腔一阶和二阶自持振荡频率, ${f_{{
m{control}}}}$为控制开孔腔自持振荡频率)



Figure
10.
Frequencies of self-sustained oscillation of aperture-cavity flow versus freestream velocity (${f_{1{
m{st}}}}$&${f_{{
m{2nd}}}}$ are the frequencies of first and second self-sustained oscillation of baseline case, respectively; ${f_{{
m{control}}}}$ is the frequency of self-sustained oscillation of controlled case)



下载:
全尺寸图片
幻灯片


从图10中的自持振荡频率分布线性拟合线可以发现, 基准开孔腔的二阶自持振荡频率近似但略小于一阶自持振荡频率的倍频, 这与式(8)所体现的自持振荡频率分布规律相符, 但具体的频率值则存在的较大差异. 朱幼君[37]和张翰钦等[38]曾结合低速空气空腔流和水中开孔腔流动实验中测得自持振荡频率, 对Rossiter方程进行了修正, 分别得到可用于低速空腔流动自持振荡频率预报的修正公式, 如式(11)和式(12)所示







$$begin{split}&&{f_n} = dfrac{{{U_infty }}}{L} dfrac{{n - 0.25 times [1 - 0.22 times (1 - Ma)]}}{{Ma + 1/0.57}} end{split}$$
(11)






$$(n = 1,2,3, cdots )qquadqquadqquad$$







$${f_n} = dfrac{{{U_infty }}}{L} frac{{n - 0.028;6}}{{1/0.547;4}}begin{array}{*{20}{c}} {}&{(n = 1,2,3, cdots )} end{array}$$
(12)

将由式(11)和式(12)计算得到的自持振荡频率和本文的实验值进行对比, 如表2和表3所示, 可以发现, 朱幼君和张翰钦修正公式与本文的实验值仍存在一定偏差. 这表明单纯的在Rossiter方程的基础上进行经验修正已很难准确描述水中开孔腔的自持振荡频率特性, 其根本原因是声反馈机制并不适用于水中开孔腔流动, 本文实验结果进一步验证对水中开孔腔绕流自持振荡的准确预报需要从其他产生机理方面重新考量, 例如Tuerke等[31,39]提出的腔内循环回流反馈机制.




表
2
自持振荡一阶模态频率实验值和预测值对比



Table
2.
Comparison of 1st mode frequency of self-sustained oscillation between experimental values and predicted values



table_type2 ">
${U_infty }$/(m·s?1)${f_{1,exp }}$/Hz${f_{1,{
m{pre}}}}$(Eq. (12))
/Hz		${f_{1,{
m{pre}}}}$(Eq. (13))
/Hz		Error/%
Eq. (12)Eq. (13)
2.019.518.321.3?69.1
2.42422.025.5?8.36.4
2.828.525.729.8?104.5
3.232.529.334.?9.84.7
3.6363338.3?8.46.3
4.03936.642.5?69.1
4.44140.346.8?1.114.1





下载:
导出CSV
|显示表格






表
3
自持振荡二阶模态频率实验值和预测值对比



Table
3.
Comparison of 2nd mode frequency of self-sustained oscillation between experimental values and predicted values



table_type2 ">
${U_infty }$/(m·s?1)${f_{2,exp }}$/Hz${f_{2,{
m{pre}}}}$(Eq. (12))
/Hz		${f_{2,{
m{pre}}}}$(Eq. (13))
/Hz		Error/%
Eq. (12)Eq. (13)
3.26165.769.17.813.2
3.667.57477.79.615.1
4.075.582.286.38.814.3
4.48290.49510.215.8





下载:
导出CSV
|显示表格



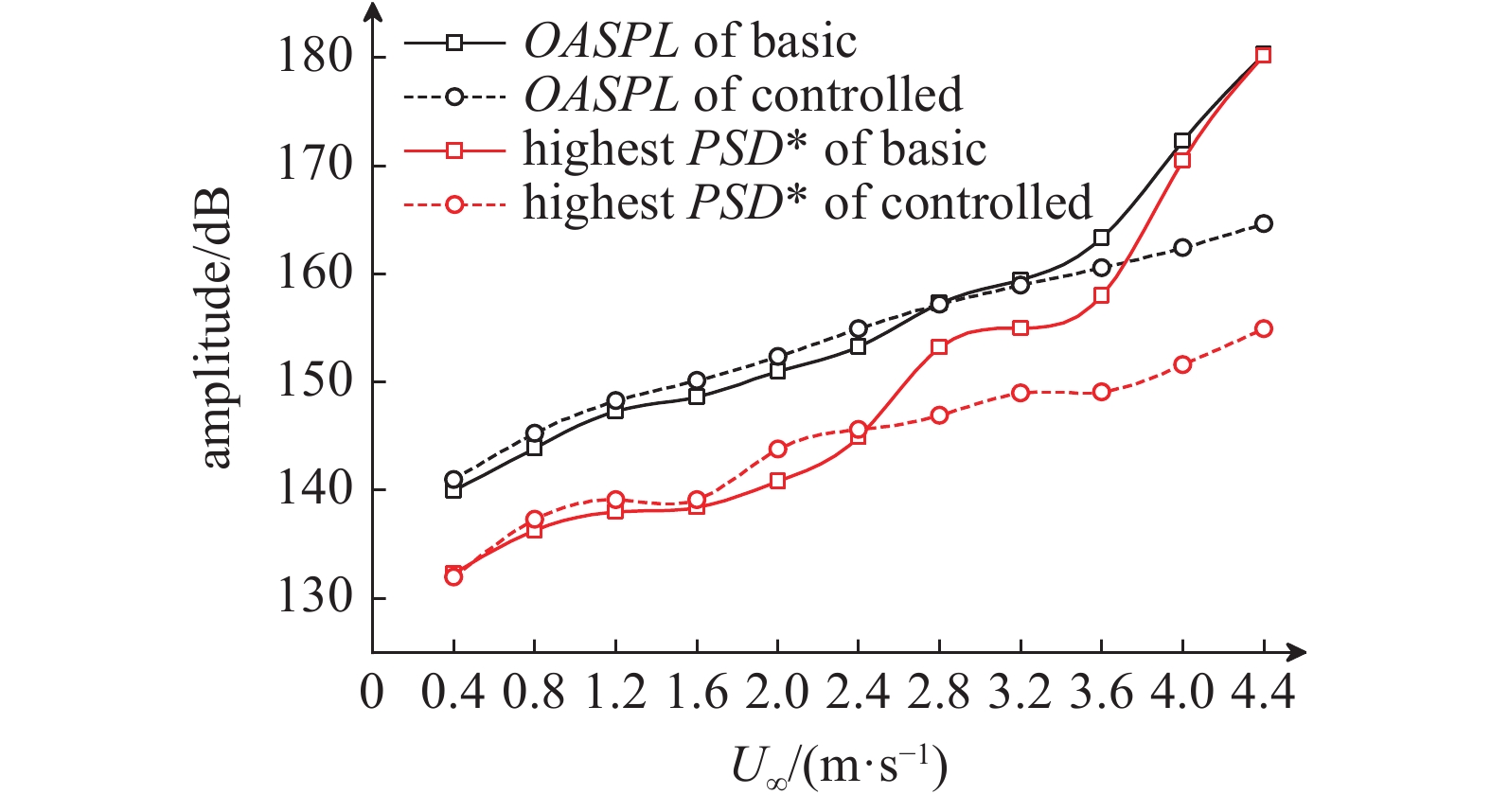
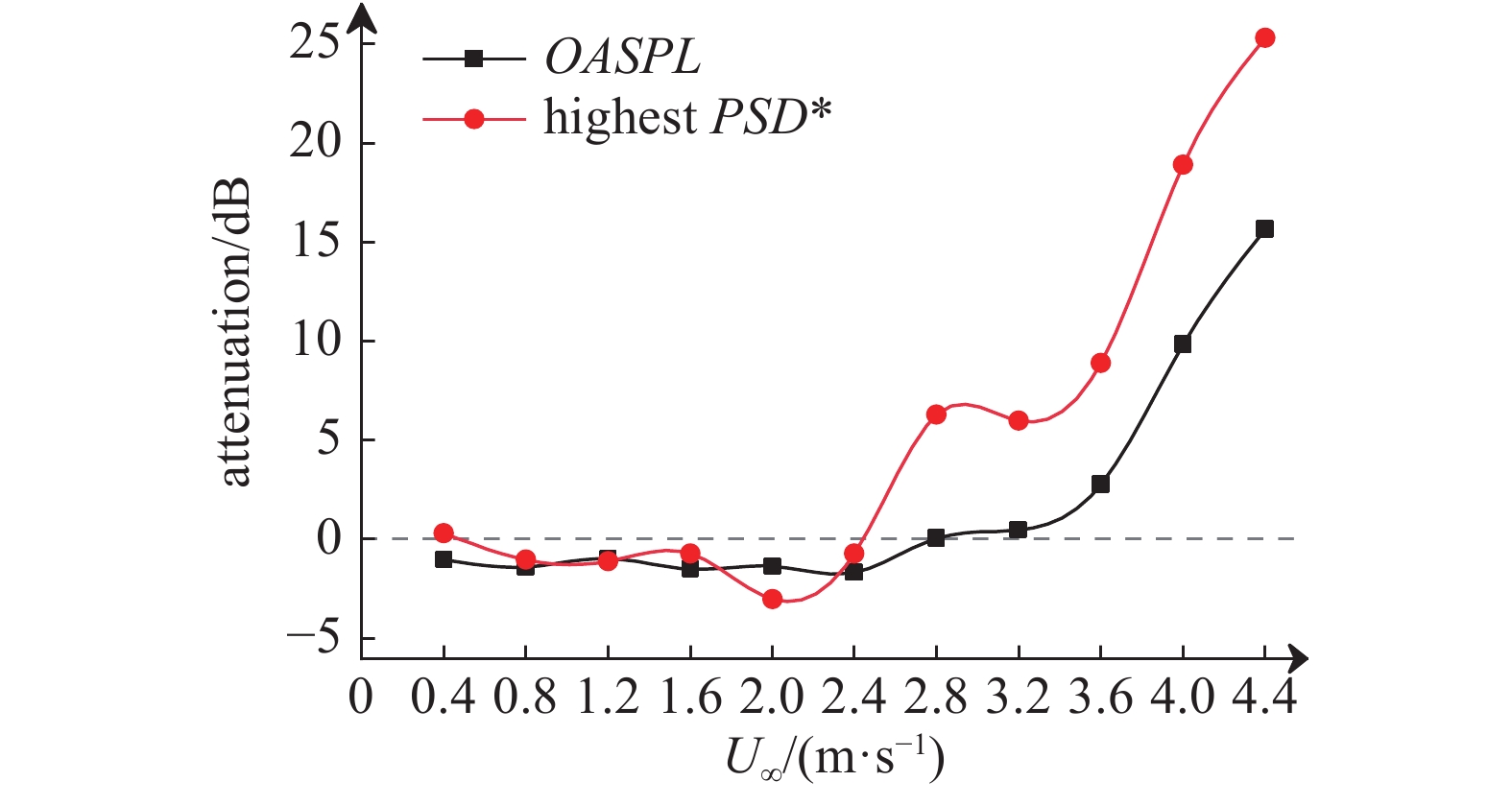
进一步探讨前缘分流体对水中开孔腔流激振荡的频谱幅值抑制效果, 根据式(3)计算脉动压力总级, 并绘制图11所示的壁面脉动压力总级和最大功率谱密度级随来流速度变化曲线. 从图中可以看出, 在发生稳定的自持振荡后, 基准开孔腔的最大脉动压力峰值呈现陡然上升趋势, 具体表现为从来流速度为2.4 m/s时的144.9 dB提高到4.4 m/s来流速度下的180.2 dB, 增幅超过35 dB, 且壁面脉动压力总级和最大功率谱密度级的逐渐接近, 表明腔内脉动压力能量逐渐集中于自持振荡主导模态的单一频率下, 在声学方面即意味着开孔腔流激噪声逐渐呈现明显的线谱特征. 采用前缘分流体进行流动控制后, 开孔腔内脉动压力总级和最大PSD*在整个流速范围内都保持相对一致的增长率随流速变化, 表明腔内流场声学环境得到改善. 从如图12所示的开孔腔脉动压力抑制量分布曲线可以看出, 前缘分流体对水中开孔腔流激振荡的抑制作用主要体现在发生自持振荡阶段, 在基准空腔还未发生稳定的自持振荡时(${U_infty }$< 2.4 m/s), 对水中开孔腔流激没有抑制效果, 甚至略微增大腔内脉动压力, 而在开孔腔绕流发生稳定的自持振荡后(${U_infty }$> 2.4 m/s), 随着流速的增加, 在自持振荡幅值显著上升的同时, 前缘分流体对水中开孔腔流激振荡抑制效果也明显增强, 在水流流速为4.4 m/s时, 前缘分流体对开孔腔脉动压力总级和最大PSD*抑制量分别达到了15.6 dB和25.3 dB.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
脉动压力总级和最大PSD*随流速变化曲线



Figure
11.
OASPL and PSD* of wall pressure fluctuation versus freestream velocity



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
脉动压力衰减量随流速变化曲线



Figure
12.
Attenuation of wall pressure fluctuation versus freestream velocity



下载:
全尺寸图片
幻灯片



4.2
脉动压力空间分布特性


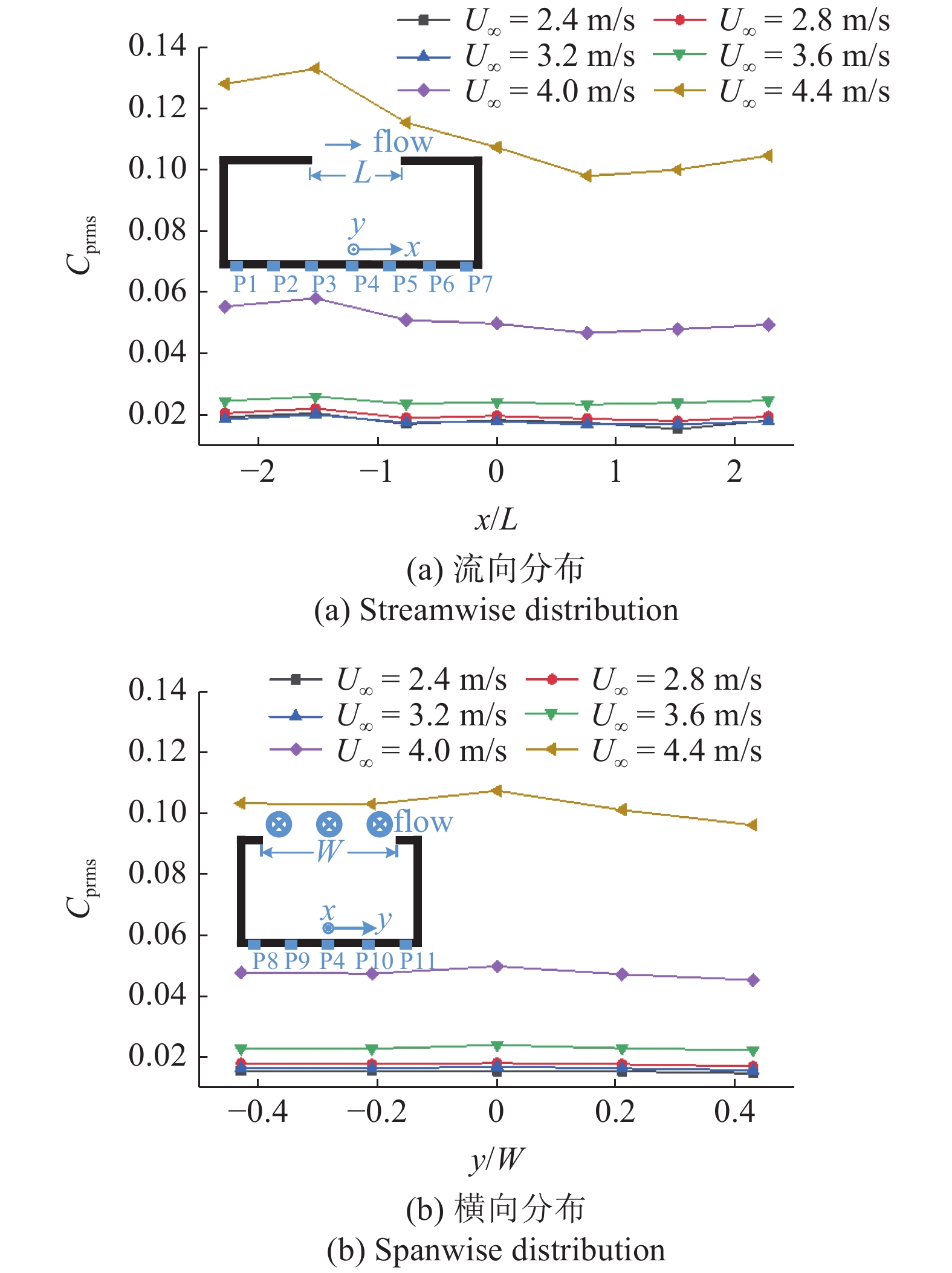
图13给出了基准开孔腔在不同流速下的腔底压力载荷空间分布曲线, 可以看出腔底压力载荷在流向上的分布规律受流速影响较大. 流速较低时, 开孔腔底压力载荷几乎呈现空间均匀分布, 随着流速增加, 腔底压力载荷在流向上逐渐呈现出在上游幅值较大、中部较小、下游又略有上升的“凹形”空间分布特点. 而在开放式空腔流动中, 腔底压力载荷的流向分布特点通常表现为沿下游方向单调增大[27, 40], 产生该差异的主要来源是由于开孔腔的后缘与腔体后壁不连续, 腔口剪切流与后缘碰撞后并不会沿腔体后壁向下运动, 而是沿后缘下方注入腔内, 并在腔内形成循环回流, 腔体前、后壁的约束作用使得在该区域的流体扰动增大, 从而引起腔底前、后部的压力载荷大于中部.

腔底压力载荷的横向空间分布波动较小, 只在流速较大时, 腔底中轴线处的压力载荷略为突出, 表明水中开孔腔的流激自持振荡表现出一定的三维效应, 这与Marsden等[41]和Zhang和Naguib[42]分别在开放式空腔流动实验中观察到的结果类似. 脉动压力空间分布结果也表明, 腔底中心处的脉动压力在反映开孔腔流激振荡整体特性上最具代表性, 选取腔底中心测点分析空腔振荡频谱特性是合理的.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
不同流速下腔底压力载荷系数空间分布



Figure
13.
Spatial distribution of ${C_{{
m{prms}}}}$ on the cavity floor at different freestream velocities



下载:
全尺寸图片
幻灯片


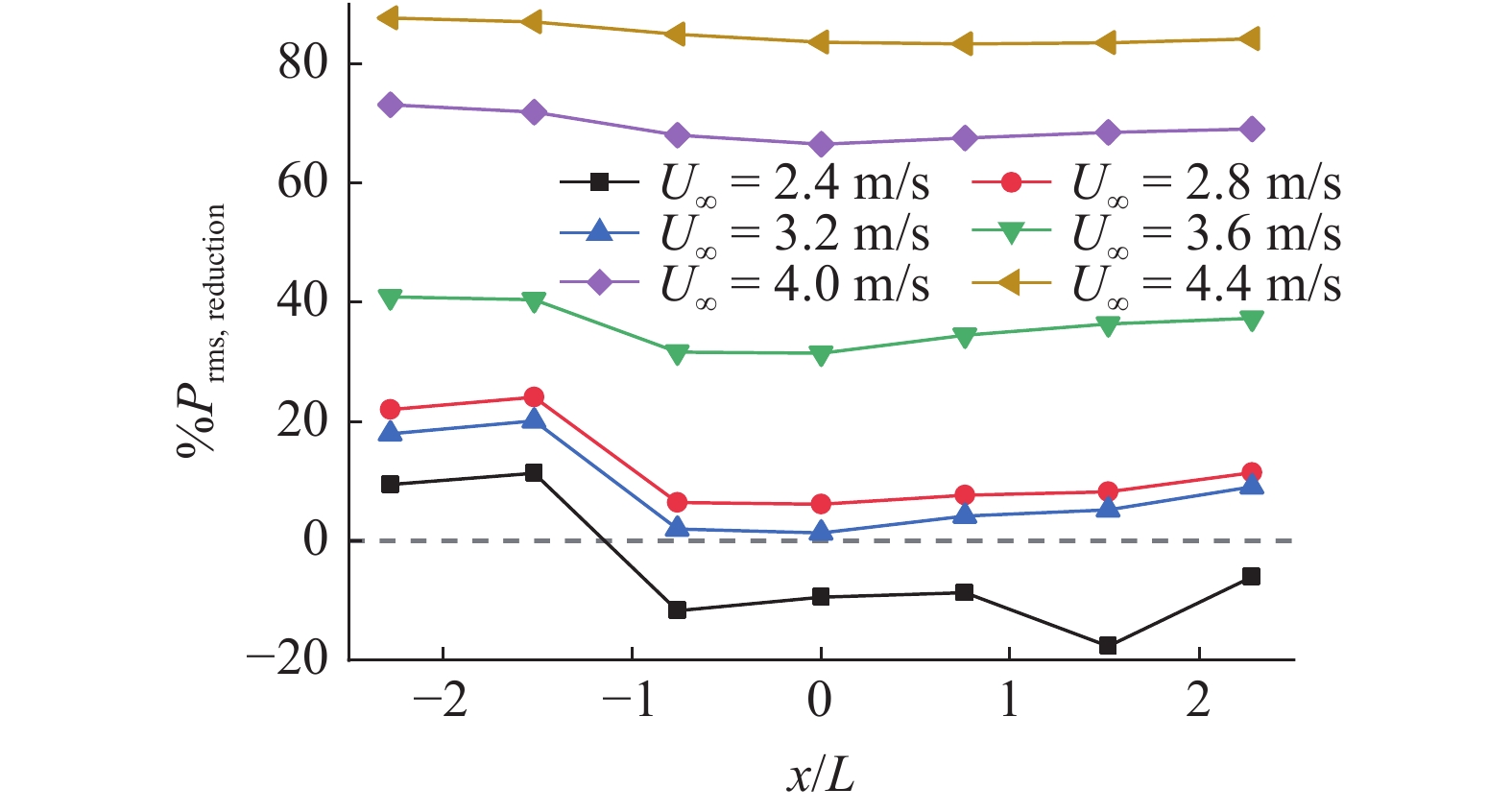
进一步讨论前缘分流体对开孔腔压力载荷的抑制效果, 由于压力载荷的横向分布波动较小, 仅对流向分布的腔底压力载荷抑制结果进行分析, 如图14所示. 从图14可以看出, 前缘分流体对水中开孔腔压力载荷的抑制效果与流速密切相关. 来流速度较低时, 前缘分流体对腔底压力载荷抑制效果不明显, 甚至可能增大开孔腔内压力载荷, 但随着流速的增加, 前缘分流体抑制腔底压力载荷效果显著提升, 在已发生强烈自持振荡的4.4 m/s流速下, 前缘分流体对腔底压力载荷抑制超过80%. 在空间分布规律方面, 前缘分流体对腔底压力载荷的抑制效果在流向上同样呈现“凹形”分布特点, 即对开孔腔内前部和后部的流体扰动的抑制效果要大于腔内中部, Ukeiley等[43]通过前缘挡块和横向流圆杆抑制空腔流激振荡的实验研究中也同样观察到类似的特点.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
腔底压力载荷抑制效果



Figure
14.
Suppression of pressure load on the cavity floor



下载:
全尺寸图片
幻灯片


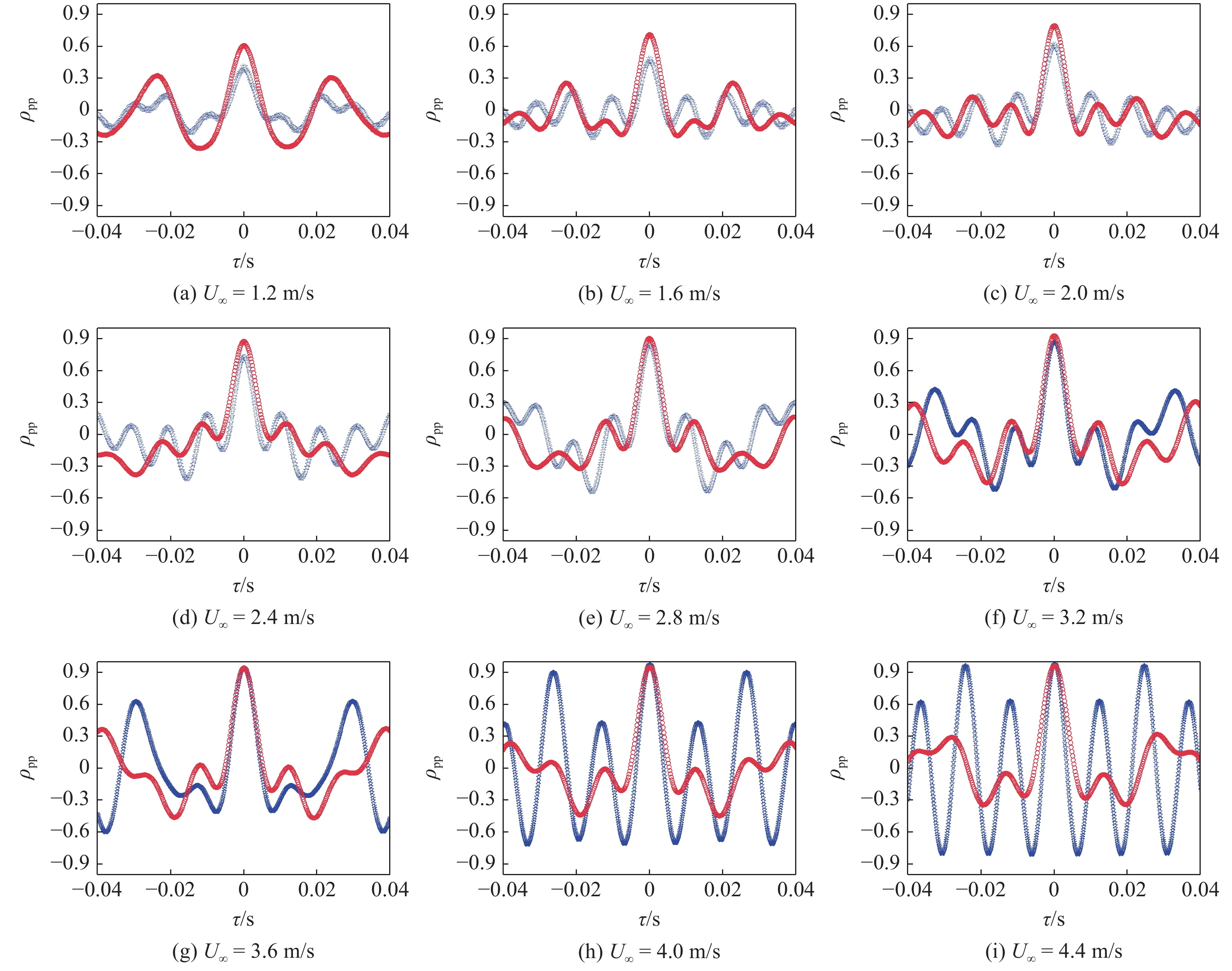
选取空间距离最远的最上游测点P1和最下游测点P7, 并对根据式(5)对这两个测点的脉动压力时域信号做互相关分析, 计算结果如图15所示, 从图中可以看出, 随着流速的增加, 基准空腔和控制空腔的最上游测点和最下游测点的脉动压力信号的相关性都同时增强, 表明前缘分流体没有改变腔内流场的相干结构, 腔内流场扰动激励源的一致性随流速的增加而增大, 但注意到基准空腔不同位置处脉动压力相关性的周期特征随流速增大而逐渐凸显, 在流速为4.0 m/s时, 互相关系数已呈现显著的周期波动, 表明此时腔内流场已经受到高度的周期调制作用, 而控制空腔不同位置处的脉动压力始终没有产生具有周期波动特征的互相关性, 表明前缘分流体有效破坏了腔内流场的周期扰动. 进一步分析互相关系数曲线相邻波峰之间的时间间隔可以发现, 其相邻波峰的时间间隔近似对应于脉动压力频谱分析中的主导模态频率, 由互相关分析估算得到的开孔腔流激振荡主导模态频率与频谱分析中的主导模态频率对比如表4所示, 可以发现, 随着脉动压力互相关系数的周期性增加, 主导模态频率的互相关分析估算结果与频谱分析结果也越接近, 腔内流场的受到的周期调制作用来源于开孔腔绕流自持振荡, 即前缘分流体对水中开孔腔流激振荡的抑制机理在于减缓了腔内流场的周期调制作用.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-143-15.jpg'"
class="figure_img
figure_type2 ccc " id="Figure15" />



图
15
P1测点和P7测点压力信号相关性分析(☆基准空腔, ○控制空腔)



Figure
15.
Cross-correlation analysis of pressure signals of P4 and P7 (☆baseline cavity, ○controlled cavity)



下载:
全尺寸图片
幻灯片





表
4
从互相关分析估算的自持振荡主导模态频率



Table
4.
Dominant mode frequencies of self-sustained oscillations estimated from cross-correlation analysis



table_type2 ">
${U_infty }$/(m·s?-1)Time lag/msEstimated ${f_{{
m{dom}}}}$
/Hz		${f_{{
m{dom}}}}$ obtained
from PSD/Hz
3.232.8730.4232.5
3.629.447433.9736
4.013.127476.1875.5
4.412.177482.1182





下载:
导出CSV
|显示表格



5.
结论


本文在循环水洞中对水中开孔腔流激振荡特性和控制效果进行了实验测试, 通过布置于开孔腔底的动态压力传感器测得的壁面脉动压力信号反映开孔腔流激振荡特征, 分别从壁面脉动压力的频率特性和空间分布特性两方面探讨前缘分流体对水中开孔腔流激振荡的抑制效果和作用机理, 并通过布置于腔内水听器分析了前缘分流体对开孔腔流激噪声的抑制效果, 得到以下结论:

(1)水中开孔腔绕流在流速较低的情况下, 如2.4 m/s, 就会产生稳定的自持振荡, 在其腔内壁面脉动压力频谱中形成突出的窄带峰, 而随着水流流速的升高, 自持振荡频率随之增大的同时, 腔内脉动压力幅值也急剧增加, 在自持振荡发生后流速增加2 m/s, 腔内壁面脉动压力峰值增加超过35 dB;

(2)前缘分流体对水下开孔腔流激振荡的抑制作用主要体现在发生稳定自持振荡阶段, 且随着开孔腔绕流自持振荡的加剧, 前缘分流体的抑制作用增强, 最大可降低腔内脉动压力载荷80%以上, 对开孔腔脉动压力总级和PSD*峰值的最大抑制量分别达到了15.6 dB和25.3 dB;

(3)前缘分流体有益于避免水中开孔腔流激共振的发生, 主要体现在前缘分流体使腔口绕流自持振荡模态频率向低频移动, 且有效消除了二阶自持振荡模态, 而腔口绕流自持振荡是流激空腔共振发生的主要激励源;

(4)前缘分流体抑制水中开孔腔流激振荡的主要作用机理在于减缓了腔内流场受到的周期性调制作用.

相关话题/实验 控制 信号 结构 图片
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • K<sub>0</sub>超固结结构性黏土的本构模型
    引言自然界存在的天然黏土通常是K0固结与结构性并存的状态[1-2],而K0固结又按照当前竖向应力是否大于先期固结压力而分为K0正常固结与K0超固结黏土.大量的室内试验以及现场测试表明,K0正常固结黏土由于初始固结为偏压固结,与等方向正常固结黏土相比,其在大主应力与先期固结压力一致的情况下,K0固结黏 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 倍频激励双转子振动同步机理与实验研究
    引言振动同步可以表征为运动系统根据内部子系统之间的耦合效应调整特征量的变化频率,并使子系统的位移、速度等变量具有一致性和统一性.近年来,由于同步在非线性耦合混沌系统[1-2]、复杂网络系统[3]、多轴控制系统[4-5]、振动筛系统[6-7]等工程技术中具有很高的应用价值和良好的应用前景,已成为国内外 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 倾斜吹吸控制下湍流边界层减阻的直接数值模拟
    引言湍流流动对流体质量、动量和能量的输运要远大于分子热运动产生的输运,湍流流动的控制(包括抑制和增强)是湍流研究领域的重要课题,如减阻控制等.湍流减阻控制研究能够在工程和国民经济领域发挥作用,如能够减少能量损失、减少环境污染、提高装置运行效率等.随着计算机水平的不断提高,数值模拟逐渐成为重要的湍流控 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 致密砂岩逆向渗吸作用距离实验研究
    引言随着常规油气资源的减少,致密油资源成为全球非常规油气勘探开发的热点[1-4],并且北美致密油开发已取得突破性进展[5-7].我国致密油资源丰富、分布广泛,致密油地质储量为2.0×1010t,技术可采储量为2.0×109~2.5×109t[8].我国多数致密油藏具有初始产油量低、产量递减快、衰竭采 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 压电超构材料及其波动控制研究: 现状与展望
    引言超构材料或超材料(metamaterials)是将精心设计的基本单元通过一定的空间排列来实现普通材料所不具有的奇异或反常性能,如带隙、波导、负折射、负模量、负密度、超透镜、声学聚焦、声学隐身和拓扑态等[1-2],已成为一个多学科交叉的前沿研究领域.过去几十多年来陆续出现的左手材料[3]、光子晶体 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 煤系页岩瓦斯吸附?解吸迟滞效应核磁共振谱实验研究
    引言煤系页岩气俗称瓦斯,是陆相页岩气的重要组成部分之一,主要以吸附态和游离态形式存在.页岩气单井产能并非恒定不变,而是随着累计产量增加而不断递减[1],初期单井产量高递减快,以游离气为主;后期产量稳定,递减慢,以吸附气为主[2],随着煤系页岩瓦斯开采深度不断增加,这一现象愈发明显,而煤系页岩瓦斯吸附 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 固体颗粒对沟槽湍流边界层影响的实验研究
    引言减阻沟槽作为一种被动的减阻方式因其不消耗能源的特点拥有广泛的应用前景.减阻沟槽起源于对于海豚表皮的仿生学研究[1],海豚和鲨鱼表皮存在着微小的,沿着水流方向排列的沟槽结构.这些结构与鲨鱼体表的清洁程度和快速游泳能力有较大的关系[2].顺流沟槽的研究始于20世纪80年代美国兰利研究所[3-5],之 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 挠性航天器太阳翼全局模态动力学建模与实验研究
    引言随着航天领域的发展,现代大型柔性航天器往往安装有诸如大型太阳翼等柔性结构,为了得到可持续的能源,其尺寸日益增大、结构重量越来越轻,太阳翼的弹性振动不可避免地与航天器主体平台的运动相互耦合,这种耦合效应随着太阳翼尺寸的增大显著增强.此时,单个太阳能帆板的模态(假设模态)并不能准确反映整个太阳翼在系 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 软材料粘接结构界面破坏研究综述
    引言因其特有的低模量和能量耗散等“软”的特性以及优异的“小激励大响应”等特征,多种多样的软材料,如水凝胶、介电弹性体以及聚甲基氧硅烷等被广泛应用在软机器人、生物医学和柔性电子等各个领域[1-4].近些年,软材料的力学行为已经成为学术界和工业界广泛关注的热点之一.在实际应用中,软材料一般需要粘附于某种 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于喷流拟序结构预测的SGS模型比较研究
    引言拟序结构普遍存在于湍流中[1–3],并影响湍流的发生、输运与耗散等过程,对湍流拟序结构的研究、对于理解湍流机理、分析流动相互作用有重要的意义.从大涡模拟来看,正确预测湍流拟序结构的关键就在于算法和亚网格尺度(sub-grid-scale,SGS)模型的准确性.在算法方面,传统的大涡模拟方法求解网 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.