引言

湍流流动对流体质量、动量和能量的输运要远大于分子热运动产生的输运, 湍流流动的控制(包括抑制和增强)是湍流研究领域的重要课题, 如减阻控制等. 湍流减阻控制研究能够在工程和国民经济领域发挥作用, 如能够减少能量损失、减少环境污染、提高装置运行效率等. 随着计算机水平的不断提高, 数值模拟逐渐成为重要的湍流控制研究手段^[1-2], 包括吹吸控制^[3-4]、添加减阻物控制^[5-6]、柔性覆层控制^[7-10]、沟槽控制^[11-12]等主动或被动控制方法结合数值模拟获得了丰富的研究成果.

Choi等^[3]使用反向控制方法通过抑制充分发展的湍流槽道流动近壁区的上抛及下扫事件, 获得了约25$ % $的流动减阻. 类似的主动控制方式, 还包括 Lee 等^[13-14], Fukagata和Kasagi^[15]的工作. Pamiés等^[16]提出了一种只在表面提供反向吹控制(blow-only opposition control, BOOC)的方法, 这种方法应用于湍流边界层流动, 最大可以获得60.8$ % $的减阻. 然而, 以上这些反向控制方式需要精确测量湍流流场内的流动信息, 因此增加了此类方法在应用上的难度和耗费.

一些研究者开发出了不需要流场信息的主动控制方式. Kametani和Fukagata^[17]通过在空间发展的湍流边界层流动中引入均匀吹(uniform blow, UB)或均匀吸(uniform suction, US)控制研究流动减阻, 发现UB能够获得减阻但增强了湍流强度, 而US虽然能够降低湍流强度但不能获得流动减阻. Min等^[18]在充分发展的湍流流动中引入了一种行波控制方法(通过在控制域下边界周期性吹吸), 这种控制方法在近壁区诱导出了负雷诺应力, 而且产生了明显的流动减阻效果.

Fukagata等^[19]通过对湍流平均运动方程在法向的三次积分开发出FIK恒等式, 给出了流动摩擦阻力系数与各贡献项的关系. 然而对边界层流动而言, 边界层外自由來流的速度是不变的, 在考察边界层流动时, 对平均运动方程的二次积分更能反映边界层流动自由來流速度不变的特点^[20-21].

对壁湍流而言, 雷诺应力($ leftlangle { uv }
ight
angle $)是重要的壁面摩擦阻力贡献项. 由于一般情况下, 流场中的平均雷诺应力是小于零的, 因此本文将小于零的雷诺应力称为正雷诺应力, 而将数值上大于零的雷诺应力定义为负雷诺应力. 在之前的研究中, 研究者们认为可以通过削弱流场内部的雷诺应力分布来获得流动减阻. 在此基础上, 前人基于物理直觉认为通过在壁面生成负雷诺应力进而影响流场内的雷诺应力分布的方式能够获得流动减阻, 并进行了相关研究^[22-25]. Fukagata 等^[25]在2008年提出了一种利用各向异性柔性覆层产生负雷诺应力的方法, 并将该覆层应用于槽道湍流减阻中. 通过该方法获得了约8$ % $的流动减阻, 并且在考察雷诺应力分布时, 部分控制算例流场内的雷诺应力出现了被抑制的现象; 然而, 在计算域条件发生变化时, 同样的覆层参数无法获得减阻. Xia等^[26]通过各向异性柔性覆层产生壁面生成负雷诺应力, 以此考察壁面生成负雷诺应力对湍流边界层流动减阻的影响, 发现壁面生成负雷诺应力的影响区域仅局限于极近壁区, 流场内部的雷诺应力分布不但没有被削弱反而因为控制而增强了, 并因此产生了流动增阻. 目前, 通过壁面产生负雷诺应力的方法来获得流动减阻仍然缺少相关共识.

本文采用DNS方法模拟壁面生成雷诺应力控制下的湍流边界层流动, 不仅考察了不同射流强度与射流频率对壁面摩擦阻力系数的影响, 还对比了壁面生成正或负雷诺应力的减阻效果, 分析了流动获得减阻的主要因素, 给出了各控制方式的收支比. 本文能够为壁湍流减阻控制研究提供新的借鉴和思路, 在工程领域也有一定的参考价值.

1.
物理模型及数值方法

本文针对零压力梯度平板边界层流动问题, 利用直接数值模拟方法开展了一系列研究. 流动的控制方程为不可压缩连续性方程(式(1))和N-S方程(式(2)). 公式中的流动变量通过外流速度$ U_infty $和主模拟区域进口处动量损失厚度$ theta_0 $无量纲化(“$ infty $”和“0”分别代表无穷远处和主模拟区域进口位置).

$$ frac{partial mathit u _i}{partial mathit x _i} = 0 $$

(1)

$$ frac{partial mathit u _i}{partial mathit t}+mathit u _j frac{partial mathit u _i}{partial mathit x _j} = -frac{partial mathit p}{partial mathit x _i}+ frac{1}{Re}frac{partial ^2 mathit u _i}{partial mathit x _j partial mathit x _j}$$

(2)

式中$ u_i $当i = 1, 2, 3时分别代表3个方向的速度分量$ u $, $ v $, $ w $; $ x_i $当i = 1, 2, 3时分别代表3个方向的坐标x, y, z; Re表示由流体运动黏度$ nu $、外流速度$ U_infty $以及主模拟区域进口动量损失厚度$ theta_0 $定义的流动雷诺数; $ p $表示压力. 式(1)和式(2)通过交错网格法和分数步法求解^[27].

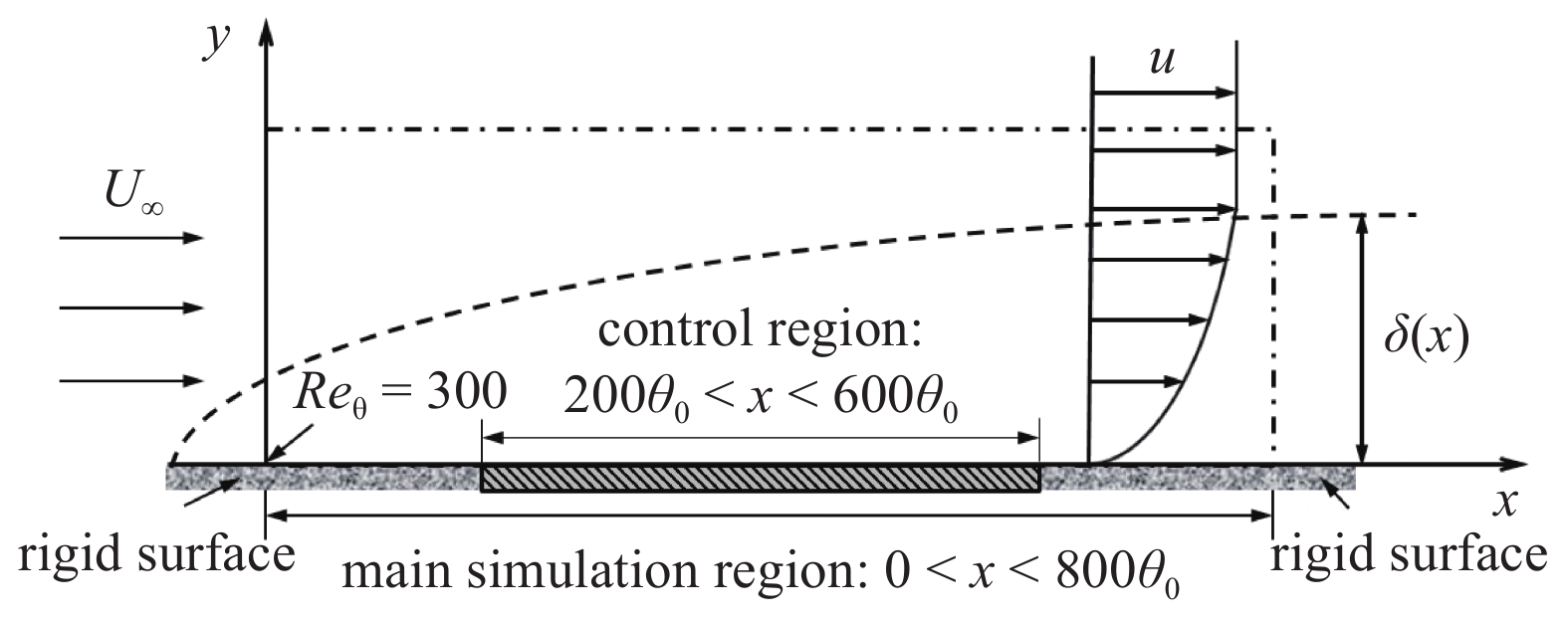
图1是湍流边界层流动的物理模型示意图, 图1中点划线区域包围的是主模拟区域范围, 该区域流向起始位置在Re$ _theta $ = 300处, 在流向、法向和展向的尺寸分别为800$ theta_0 $×60$ theta_0 $×40$ theta_0 $. 计算域下边界非控制区域的边界条件为无滑移条件、上边界为远场边界条件、展向为周期条件、出口为无反射条件. 主模拟区域进口边界条件为湍流速度入口边界条件, 速度入口数据从辅助计算模拟区域流向中间截面采集^[28]. 主计算域与辅助计算域网格的数量在3个方向分别为1024×96×128和128×96×128. 网格在流向和展向为均匀分布, 间距分别为12和5倍壁面尺度; 法向为非均匀分布, 最小网格间距为0.22倍壁面尺度. 更多的数值方法介绍可以参考作者之前的工作^{[26, 29]}.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
主模拟计算域示意图



Figure
1.
Sketch of the main simulation



下载:
全尺寸图片
幻灯片


前人根据物理直觉, 认为能够通过壁面生成的负雷诺应力来削弱流场中的雷诺应力分布, 从而获得流动减阻^[22-25]. Fukagata等^[25]提出了通过各向异性柔性覆层来获得负雷诺应力, 但是他们并没有在FIK公式中对壁面生成负雷诺应力进行考察. 式(3)反映的是对雷诺平均运动方程的法向二次积分后获得的壁面摩擦阻力系数($ C_{
m{f}} $)与其贡献项的关系, 在式(3)中摩擦阻力系数可以分解为5个部分^[26], 分别为: 代表黏性贡献的$ C_{
m{V}} $项、代表平均对流贡献的$ C_{
m{C}} $项、代表雷诺应力贡献的$ C_{
m{R}} $项、代表流向平均速度及脉动的导数贡献的$ C_{
m{D}} $项、代表壁面生成雷诺应力贡献的$ C_{
m{W}} $项. 通过式(3), 可以方便的考察各贡献项对边界层湍流壁面摩擦阻力系数的影响. 特别的, 通过考察式(3), 不难发现壁面生成负雷诺应力对摩擦阻力系数$ C_{
m{f}} $有正贡献, 是增阻的.

$$begin{array}{l} { {C_{ m{f}}}}=dfrac {2}{,, Re_ {delta },,}+2displaystyleint _0^1-leftlangle { {u'v'}} ight angle { m{ d}} y+ 2leftlangle { u_{ m{w}}'v_{ m{w}}'} ight angle+[-8pt]qquadunderbrace{}_{ C{_{ m{V}}}}, ;; ; underbrace{,quadquadqquad qquad}_{ C{_ { m{R}}}}quad underbrace{quadqquadquad}_{ C{_{ m{W}}}} 2displaystyleint _0^1 (1-y)left( {-dfrac {partial {UV}}{partial y}-dfrac{partial {UU}}{partial x}-dfrac 1{ ho}dfrac{partial P}{partial x}} ight){ m{d}} y+ [-8pt]underbrace{quadqquadqquadqquadqquadqquadqquad qquad qquad}_{ C{_ { m{C}}}} 2displaystyleint _0^1(1-y)left(dfrac 1{Re_{delta}}dfrac {partial ^2 U}{partial x ^2}-dfrac{partial leftlangle { u'u'} ight angle }{partial x} ight){ m{d}} y[-8pt] ,;; underbrace{;;quadqquadqquadqquadqquadqquadqquadqquad}_{ C{_ { m{D}}}}quad end{array} $$

(3)

式(3)中, $Re _delta $表示由流体运动黏度$ nu $、外流速度$ U_infty $以及边界层名义厚度$ delta $定义的流动雷诺数; 式中大写的变量为对应变量的平均量; $
ho $为流体密度, 在本文中恒为1.

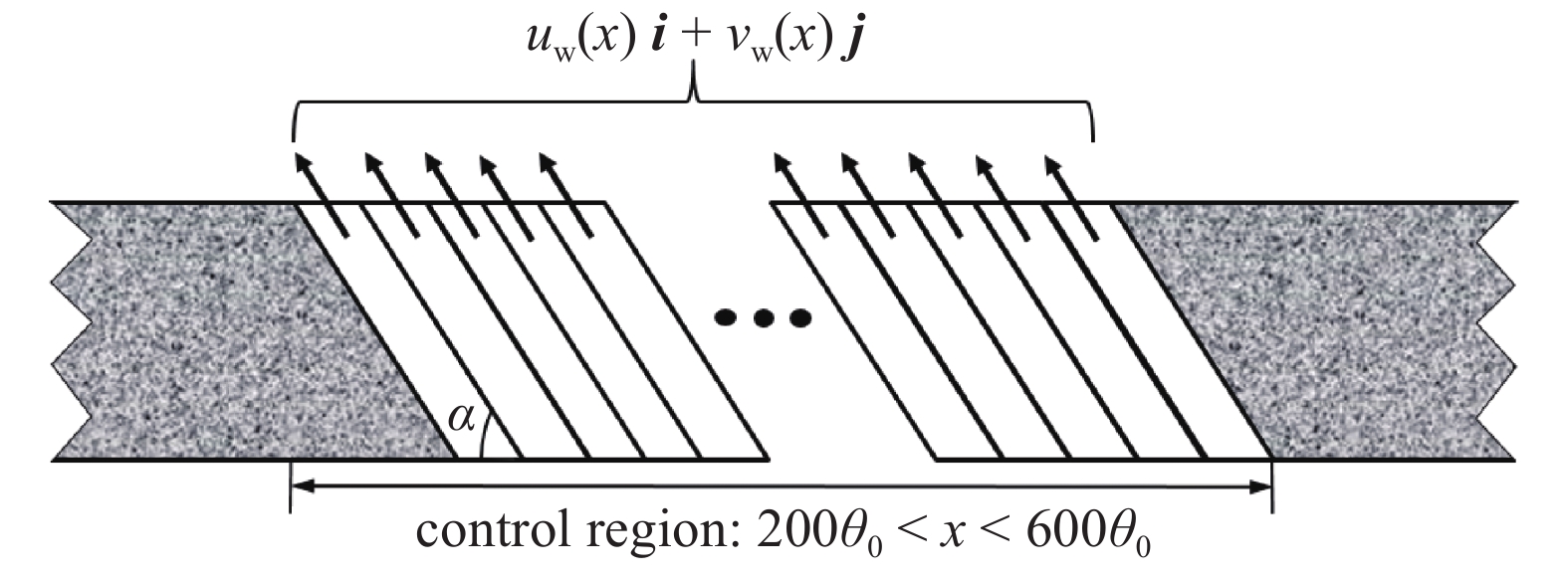
在流动控制区域下边界设置一系列与泵相连的倾斜狭缝, 并通过调节和控制泵吹/吸的强度、频率以及狭缝倾斜角度产生不同强度与频率的壁面生成雷诺应力. 如图2 所示, $ u_{
m{w}} $和$ v_{
m{w}} $分别表示狭缝中由吹吸形成的射流的流向及法向速度分量, 在控制区内倾斜狭缝沿流向顺序排列并充满流动的展向空间, 狭缝的上沿与非控制区域的固壁上表面在同一高度上, 狭缝底部同泵(用来提供周期性吹吸, 图中未示意)相连. 本文中, 流动控制区域处于流向200$ theta_0 $$ < $x$ < $600$ theta_0 $ 位置, 并且完全覆盖流动的展向空间. 为了获得最大的壁面生成雷诺应力, 狭缝倾斜角$ alpha $被设置为45°(或135°)对应生成正雷诺应力(或负雷诺应力). 在流动控制域内, 壁面射流的流向和法向速度分量$ u_{
m{w}} $和$ v_{
m{w}} $ 可分别表达为式(4)和式(5)

$$ {{ {u_{ m{w}}}}}({x}) = -{f}({x}){A}sin ({omega t})cos alpha ;,, $$

(4)

$$ {{ {v_{ m{w}}}}}({x}) = {f}({x}){A}sin ({omega t})sin alpha ;,, $$

(5)

$$ {f (x)} = left[1.0-{ m{e}}^{-({ x-L_{ m{S}}})^2 /{ L_{{ m{tr}}}} } ight]left[1.0-{ m{e}}^{-({ x-L_{ m{E}}})^2 /{ L_{{ m{tr}}}}} ight] $$

(6)

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
控制区域示意图



Figure
2.
Schematics of the lower boundary for control cases



下载:
全尺寸图片
幻灯片


其中, A代表流向或法向射流分量的强度, $ omega $代表射流的频率, $ f (x)$是过渡函数(见图3), $L_{
m{S}}$$ = 200{{theta_0}} $和$L_{
m{E}}$$ = 600{{theta_0}} $分别代表控制区域的流向开始位置和结束位置, $L_{{
m{tr}}}$为过渡段长度(本文中取$L_{{
m{tr}}} = 61{{theta_0}}$). 值得注意的是本文提出的控制区下边界条件在流向和展向上(控制区前后过渡段除外)是均匀的, 因此与通过行波获得流动减阻的控制方式不同^{[18, 30-32]}.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
控制区过渡函数的分布



Figure
3.
Distribution of transition function in control region



下载:
全尺寸图片
幻灯片


在式(4)和式(5)中, 当A不为零时, 在流动控制区域下边界将会产生正(或负)壁面雷诺应力. 在表1中, $ {A}_1^2, $ $ {A}_2^2 $和$ {A}_3^2 $在数值上等于无控制算例$ {x} = 400{theta}_0 $位置、法向高度分别为$ {y}^+ = 3 $, 7 和18倍壁面尺度处对应的$ leftlangle { uv }
ight
angle $的绝对值, 而设置$ {A_4} $和$ {A_5} $是为了考察更大射流强度的影响. 表1中的$ {omega_2} $等于无控制算例中在$ x = 400{theta_0} $位置湍流的特征频率(约为0.09^[29]), $ {omega_1} $ 取$ {omega_2} $的一半, $ {omega_3} $为$ {omega_2} $的2.5倍. 作者同样计算了更高控制频率的算例, 但是高频控制引起了流向压力梯度的急剧变化, 因此该部分内容未在本文中讨论. 表1中, 无控制算例、$ {u_{
m{w}}} $控制算例(${
m{u}}{
m{c}}$)和$ {v_{
m{w}}} $控制算例$( {
m{v}}{
m{c}}) $均作为参照算例. 以算例C31P为例, 第一个字母C表示算例(Case), 第一个数字3代表射流法向和流向分量的控制强度为$ A_3 $, 第二个数字1代表射流频率为$ {omega_1} $, 第二个字母P代表狭缝角度$ alpha $ 为45°时产生正雷诺应力(若第二个字母为N, 则表示狭缝角度$ alpha $ 为135°, 产生负雷诺应力). 表1中, $ mid $$leftlangle { u_{
m{w}}v_{
m{w}} }
ight
angle$$ mid $等于0.25$ A^2 $, 为壁面生成雷诺应力在时间平均后的绝对值, 能够反映壁面生成雷诺应力的强度.




表
1
算例参数表



Table
1.
Setup of the input parameters



table_type2 ">

Case	A & $omega$	A	$omega$	$alpha$	$mid leftlangle { {u_{ m{w}}} {v_{ m{w}}} } ight angle mid$$(times 10^3)$
C13N (P)	A1ω3	0.009	0.235	π/4 (3π/4)	0.02
C23N (P)	A2ω3	0.025	0.235	π/4 (3π/4)	0.15
C31N (P)	A3ω1	0.044	0.057	π/4 (3π/4)	0.48
C32N (P)	A3ω2	0.044	0.094	π/4 (3π/4)	0.48
C33N (P)	A3ω3	0.044	0.235	π/4 (3π/4)	0.48
C43N (P)	A4ω3	0.058	0.235	π/4 (3π/4)	0.84
C53N (P)	A5ω3	0.065	0.235	π/4 (3π/4)	1.06
uc	A3ω3	0.044	0.235	${text{π}}$/2	0.00
vc	A3ω3	0.044	0.235	0	0.00
NC	?	0	0	?	0.00

下载:
导出CSV
|显示表格

2.
结果与讨论

2.1
壁面生成正雷诺应力对湍流边界层流动的影响

图4(a)给出了无控制算例与频率为$ omega_3 $的壁面生成正雷诺应力控制算例的$ C_{
m{f}} $沿流向发展的情况. 如图4(a)所示, 相比无控制算例, 控制算例的$ C_{
m{f}} $在控制区域内均沿流向出现下降, 且射流强度越大的算例其$ C_{
m{f}} $沿流向下降的越显著; 在控制区域末端, 受过渡函数的影响, 控制算例的$ C_{
m{f}} $快速恢复到与无控制情形相接近的水平; 在控制区域下游, 存在一段(约40$ theta_0 $)$ C_{
m{f}} $的过冲区域, 随着流动继续向下游发展, 控制算例与无控制算例的$ C_{
m{f}} $差异逐渐减小. 在射流频率相同的情况下, 对比图4(a)中不同算例的$ C_{
m{f}} $曲线, 射流强度越大的控制算例所获得的减阻效果越好. 图4(b)给出了无控制算例与射流强度为$ A_3 $的控制算例的$ C_{
m{f}} $沿流向的发展情况. 图4(b)中, 在射流强度相同的情况下, 射流频率越大的算例获得的减阻效果越好. 在图4(a)和图4(b)中, 随着流动向下游发展, 所有控制算例在控制区内的$ C_{
m{f}} $均低于无控制算例, 表明壁面生成正雷诺应力控制可以获得流动减阻. 值得一提的是, 在射流强度的参照点同样取自缓冲区的情况下, 壁面生成正雷诺应力的控制效果要优于反向吹吸控制(减阻率25%)^[3]和只吹反向控制(减阻率60.8%)^[16]. 另外, 随着流动向下游发展, 射流强度较高的C33P, C43P和C53P算例在控制区后部出现了$ C_{
m{f}} $为负的情况, 表明以上3个算例在控制区后段的近壁区存在回流现象.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
摩擦阻力系数($C_{
m{f}}$)在壁面生成正雷诺应力控制下沿流向的分布



Figure
4.
Evolution of the skin friction coefficient in wall-generated positive RSS cases, $C_{
m{f}}$



下载:
全尺寸图片
幻灯片


图5显示了壁面生成正雷诺应力以及无控制算例在流向不同位置的平均雷诺应力沿法向分布的情况. 如图5(a)所示, 在流向位置$ x $ = 250处, 壁面生成正雷诺应力的影响区域大致为$ y^+ $$ < $0.6, 在此范围内控制算例的平均雷诺应力绝对值高于无控制算例, 在$ y^+ $$ > $0.6的区域内, 控制算例的平均雷诺应力曲线相比无控制算例作正向偏移, 表明流场内部的雷诺应力分布受到抑制, 并且射流强度越大的算例对应的平均雷诺应力的正向偏移越明显; 随着流动向下游发展, 在$ x $ = 400处, 壁面生成雷诺应力的影响区域降低至$ y^+ $$ < $0.2, 并且流场内部的平均雷诺应力分布曲线相比无控制算例出现更加明显的正向偏移, 射流强度较大的C43P和C53P 算例, 两者在流场内部的平均雷诺应力出现了大于零的情况; 在$ x $ = 550处, 壁面生成雷诺应力的影响区域进一步降低至$ y ^+ $ = 0.1附近, 流场内部平均雷诺应力曲线的正向偏移进一步增加, 包括C23P, C33P, C43P 和C53P等算例都出现了平均雷诺应力在流场内部大于零的情况. 如图5(b)所示, 在射流强度相同的情况下, 射流频率较低的算例其壁面生成正雷诺应力的影响区域较大, 如在$ x $ = 250处, 算例C13P的壁面生成正雷诺应力的影响范围能够达到$ y^+ $ = 2.0, 算例C23P的影响范围在$ y ^+$ = 1.0附近, 算例C33P的在$ y^+ $ = 0.6处, 并且在流动下游($ x $ = 400及$ x $ = 550处), 这一规律依然存在. 由此可见, 相对于高频控制, 低频控制产生的壁面生成雷诺应力的法向影响范围更高; 但是在整个流场内, 相对无控制算例, 频率较高的控制算例其平均雷诺应力的正向偏移更加明显.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
壁面生成正雷诺应力的各算例在不同流向位置的平均雷诺应力分布对比



Figure
5.
Profiles of the RSS at different streamwise locations



下载:
全尺寸图片
幻灯片


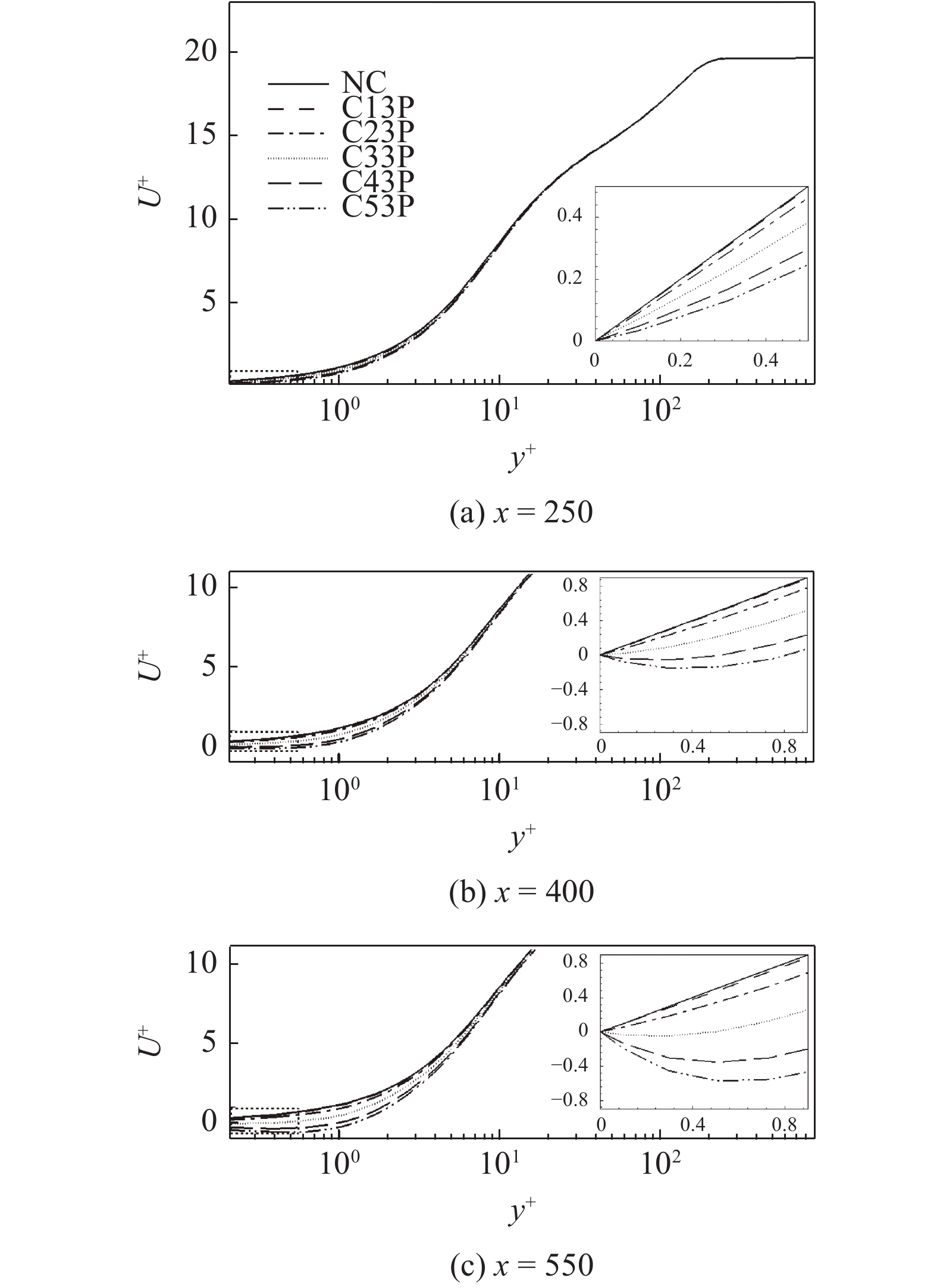
图6显示的是无控制算例以及壁面生成正雷诺应力算例(射流频率相同)的平均速度剖面在流向不同位置的分布, 图中平均速度由无控制算例对应位置的壁面摩擦速度无量纲化. 如图6(a)所示, 控制算例与无控制算例的平均速度剖面的区别主要出现在近壁区, 从放大图中可以发现, 随着射流强度的增加, 各控制算例在极近壁区的平均速度在$ y $方向的梯度逐渐减小, 反映流动摩擦阻力随着射流强度增加而减小(见图4(a)); 图6(b)中, 反映的极近壁区平均速度梯度与射流强度的关系的规律基本与图6(a)中所反映的一致, 但是在$ x $ = 400处, 算例C43P与C53P的平均速度出现了在极近壁区小于零且速度梯度为负的情况, 表明此时壁面摩擦阻力为负; 图6(c)中, 算例C33P也出现平均速度在极近壁区小于零的情况, 说明随着流动向下游发展, C33P算例也出现了壁面摩擦阻力为负的现象.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
壁面生成正雷诺应力的各算例在流向不同位置的平均速度剖面的对比



Figure
6.
Mean velocity profiles at different streamwise direction locations



下载:
全尺寸图片
幻灯片


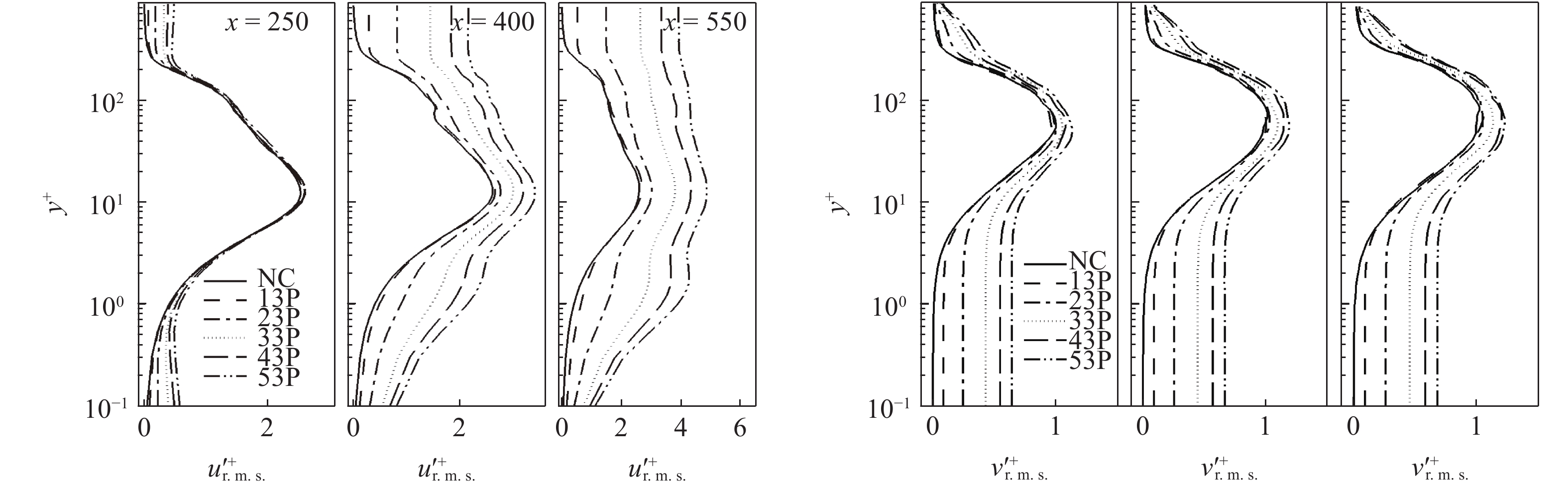
图7显示壁面生成正雷诺应力各算例的速度脉动均方根在流向不同位置的分布情况. 图7(a)中, $ x $ = 250处于控制区前部, 壁面控制对流动的影响仍未充分显现, 控制算例的流向速度脉动均方根只在近壁区和外流区与无控制算例的区别较为明显, 随着流动向下游发展, 控制算例的流向速度脉动均方根与无控制算例在整个法向方向都有着较为明显的区别, 在$ x $ = 550处这种情况表现的更为明显. 图7(b)中, 相比无控制算例, 控制算例的法向速度脉动量均方根从壁面处开始增强, 并延伸到流场内部, 随着流动向下游发展, 各算例法向脉动均方根在流场内部的分布稍有增强. 对比图7(a)和图7(b), 说明壁面生成正雷诺应力控制对流向速度脉动的影响相对较为显著.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
壁面生成正雷诺应力的各算例在不同流向位置脉动量均方根



Figure
7.
Profiles of the root mean square of $u^prime$ and $v^prime$ at different streamwise locations



下载:
全尺寸图片
幻灯片


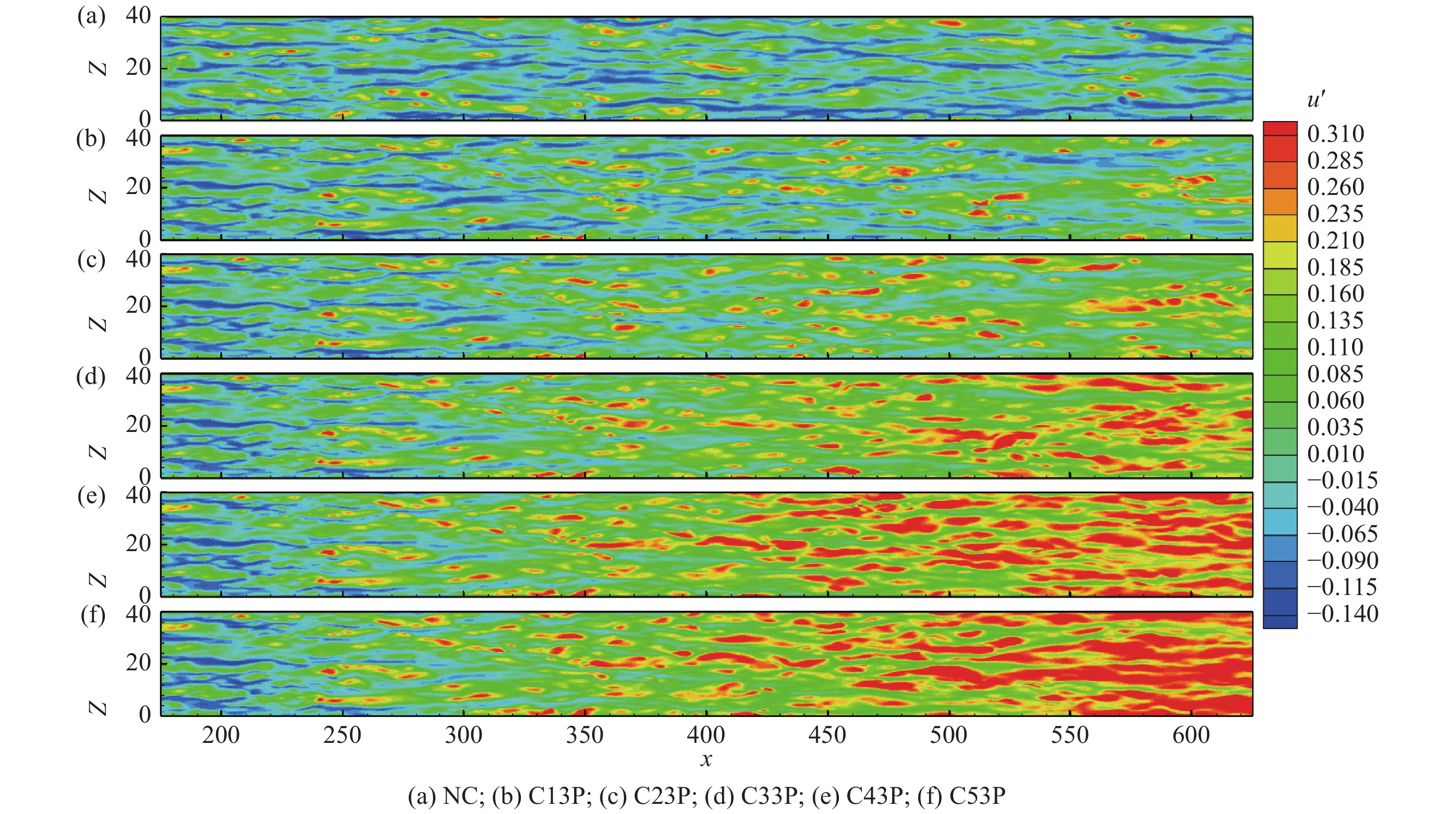
图8显示的是$ y^+ $ = 15平面的流向速度脉动云图, 控制算例截取时刻为$ t $ = 5350$ theta_0 /U_infty $, 由于无控制算例相同时刻的瞬时场数据丢失, 无控制算例截取时刻为$ t $ = 5450$ theta_0/U_infty $(图8中, 无控制算例瞬时场仅作为无控制条件下低速条带结构沿程发展状态的参照). 在无控制算例中能够看到明显的低速条带结构(见图8(a)), 当射流强度为$ A_1 $时(算例C13P)条带结构在控制区内仍明显存在, 在控制区后部条带结构受到抑制. 当射流强度增加, 相比无控制算例, C23P 算例的低速条带结构在控制区后部逐渐消失(见图8(c)), 随着射流强度进一步增加(图8(d) ~ 图8(f)), 在控制区前部仍能发现低速条带结构, 但在控制区中后部低速条带结构消失, 并且这种现象一直延续到控制区下游($ x $$ > $600).



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-8.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8" />



图
8
$ y^+ $ = 15平面的流向速度脉动云图



Figure
8.
Instantaneous of the streamwise velocity fluctuation $ u^prime $ at $ y^+ $ = 15



下载:
全尺寸图片
幻灯片

2.2
壁面生成负雷诺应力对湍流边界层流动的影响

图9(a)给出了无控制算例与射流频率为$ omega_3 $的所有壁面生成负雷诺应力控制算例的$ C_{
m{f}} $沿流向发展的情况. 如图9(a)所示, 相比无控制算例, 控制算例在控制区前部存在一段(约60$ theta_0 $)阻力增大的区域, 控制算例的$ C_{
m{f}} $在控制区前端沿流向方向快速增加, 在约$ x $ = 210$ theta_0 $位置达到峰值(该位置存在峰值原因是前部有过渡函数的影响, 否则此处应为单调下降), 随着流动向下游发展控制算例的$ C_{
m{f}} $迅速下降, 射流强度越大的算例其下降趋势越明显; 与正雷诺应力控制算例相似, 在控制区域后部, 负雷诺应力控制算例的$ C_{
m{f}} $快速恢复到与无控制情形相接近的水平; 在控制区域下游, 同样存在着一段(约40$ theta_0 $) $ C_{
m{f}} $的过冲区域, 随着流动继续向下游发展, 控制算例与无控制算例的$ C_{
m{f}} $差异逐渐减小. 对比图9(b)中无控制算例与3个射流强度相同($ A_3 $)的控制算例, 在控制区域前部流动增阻区别不明显, 但随着流动向下游发展, 射流频率越高的算例在控制区域中后部的壁面摩擦阻力系数越低, 即减阻效果越好.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
$C_{
m{f}}$在壁面生成负雷诺应力控制下的沿程发展



Figure
9.
Evolution of the $C_{
m{f}}$ in wall-generated negative RSS cases



下载:
全尺寸图片
幻灯片


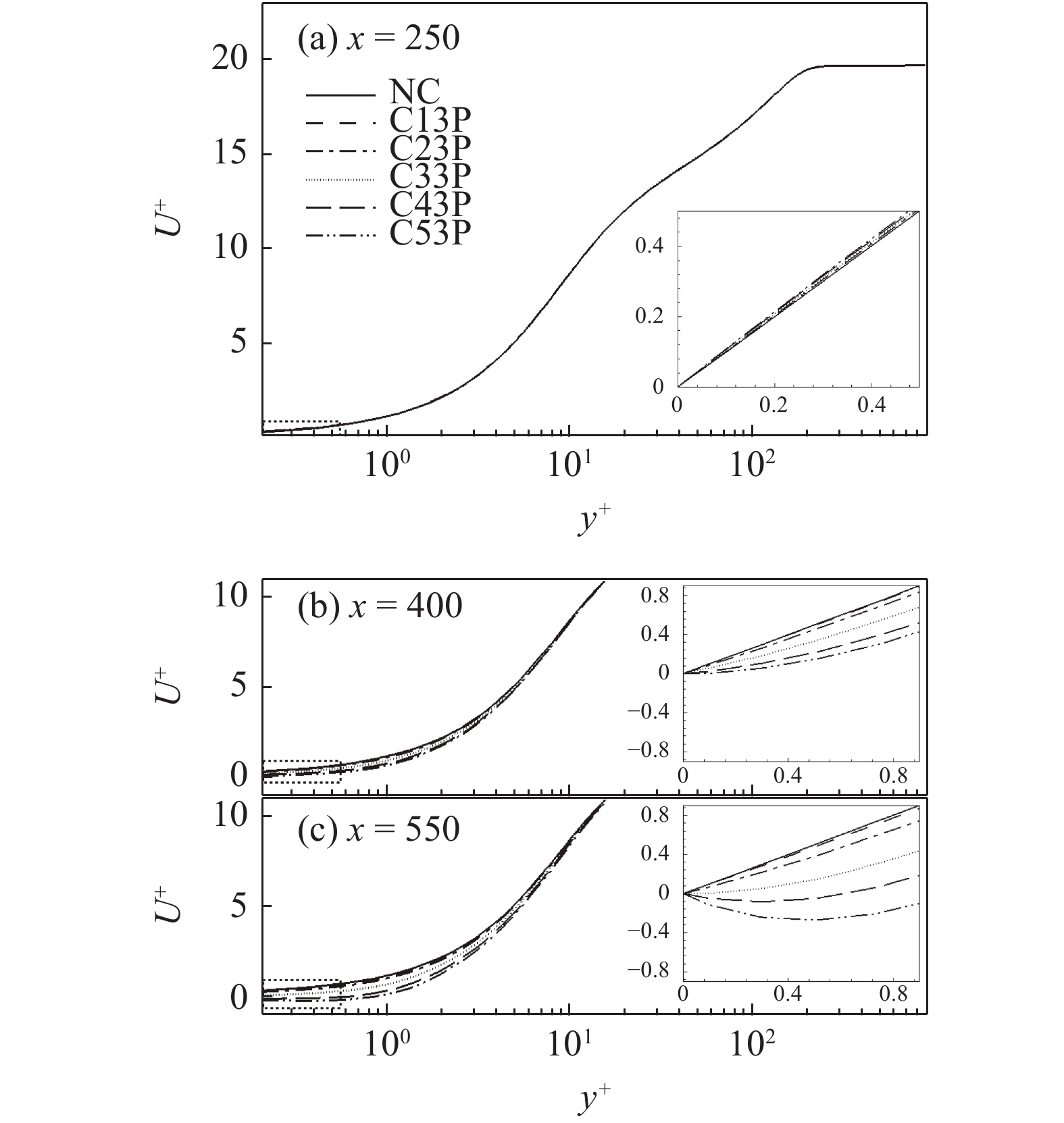
图10显示的是无控制算例以及壁面生成负雷诺应力算例(相同射流频率)的平均速度剖面在流向不同位置的对比, 图中平均速度由无控制算例对应位置的壁面摩擦速度无量纲化. 如图10(a)所示, 控制算例与无控制算例在流场内的平均速度剖面差异并不明显, 只有从放大图中才可以看出控制算例的平均速度剖面斜率相比无控制算例要高, 即控制算例在该位置存在增阻现象. 图10(b)中, 反映的极近壁区平均速度梯度与射流强度的关系的规律基本与图9(a)中所反映的一致; 在图10(c)中, 即$ x $ = 550处, 算例C43N与C53N的平均速度在极近壁区小于零, 且速度梯度为负, 表明这两个算例在此处的壁面摩擦阻力为负.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
壁面生成负雷诺应力控制各算例在流向不同位置的平均速度(U)剖面对比



Figure
10.
Profiles of mean streamwise velocity (U) in wall-generated negative RSS cases at different streamwise locations



下载:
全尺寸图片
幻灯片


图11显示壁面生成负雷诺应力各算例与无控制算例的平均雷诺应力在流向不同位置的分布情况. 图11(a)中, 在$ x $ = 250处, 在壁面生成负雷诺应力控制的影响下, 控制算例近壁区的平均雷诺应力相对无控制算例整体出现正向偏移, 并且控制算例的平均雷诺应力分布在整个流场内与无控制算例的区别均较为明显; 随着流动向下游发展, 控制算例的平均雷诺应力分布与无控制算例相比, 包括黏性底层在内的整个法向的平均雷诺应力的正向偏移愈加显著(见图11(a)中$ x $ = 400和$ x $ = 550处). 图11(b) 中, 在射流强度相同的情况下, 相比无控制算例, 射流频率较高的壁面生成负雷诺应力算例其平均雷诺应力在流场内出现的正向偏移相对更大. 通过图11, 发现壁面生成负雷诺应力的算例对流场内部的雷诺应力分布产生了明显的影响(射流强度较低的C13N算例除外), 并且这种影响从壁面一直延伸至流场内部直至外流区, 这与Xia等^[26]通过各向异性柔性覆层获得壁面负雷诺应力的影响无法深入流场内部不同.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
壁面生成负雷诺应力的各算例在不同流向位置处的平均雷诺应力分布对比



Figure
11.
Profiles of the mean RSS at different streamwise locations



下载:
全尺寸图片
幻灯片

2.3
壁面生成正或负雷诺应力控制的对比

为进一步研究壁面生成正或负雷诺应力对壁面摩擦阻力系数的影响, 选取C33P, C33N, $ {
m{u}}{
m{c}} $, $ {
m{v}}{
m{c}} $及NC, 5个算例进行对比, 其中各算例的控制参数均取$ A_3 $ 和$ omega_3 $.

图12(a)显示的是无控制算例与射流强度及射流频率分别为$ A_3 $和$ omega_3 $的控制算例的$ C_{
m{f}} $在流向的发展情况. 图中, 无控制算例与$ {
m{v}}{
m{c}} $控制算例基本重合, 反映$ {
m{v}}{
m{c}} $控制对壁面摩擦阻力系数的影响几乎可以忽略; $ {
m{u}}{
m{c}} $控制算例与C33N及C33P算例的摩擦阻力系数在控制区与无控制算例的$ C_{
m{f}} $分布曲线存在明显区别, 可以看出, 壁面生成正雷诺应力控制的减阻效果最好, $ {
m{u}}{
m{c}} $控制次之, 而壁面生成负雷诺应力控制的减阻效果最差. 为了进一步分析图12(a)中出现的流动减阻, 将壁面生成雷诺应力控制($ {u_{
m{w}}} $($ x $)${{{boldsymbol{i}}}}$+$ {v_{
m{w}}} $($ x $)${{{boldsymbol{j}}}}$控制, 见图(2))获得的流动减阻认为是由$ {{{u}}_{
m{w}}} $, $ {{{v}}_{
m{w}}} $以及壁面生成雷诺应力($ {{{u}}_{
m{w}}}{{{v}}_{
m{w}}} $)共同作用的结果. 考虑到在壁面生成雷诺应力控制算例中很难将上述三者的减阻效果区分开来, 因此假设壁面生成雷诺应力控制的减阻效果由$ {
m{u}}{
m{c}} $控制、$ {
m{v}}{
m{c}} $控制以及$ {u_{
m{w}}}{v_{
m{w}}} $线性叠加获得, 即使用$ {
m{u}}{
m{c}} $算例和$ {
m{v}}{
m{c}} $算例的减阻来分别代替C33P或C33N 算例中$ {u_{
m{w}}} $和$ {v_{
m{w}}} $两个壁面速度分量在湍流场中的减阻效果(下文将考察这一假设的可行性). 由此, 可以将壁面生成雷诺应力控制的减阻效果分解为

$$ {mathit DR}({mathit x}) = {mathit DR_{{ m{uc}}}}({mathit x})+{mathit DR_{{ m{vc}}}}({mathit x})+{mathit DR_{{ m{WRSS}}}}({mathit x}) $$

(7)

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
$C_{
m{f}}$及$C_{
m{w}}$沿流向发展情况



Figure
12.
Evolution of $C_{
m{f}}$ and $C_{
m{w}}$ in streamwise direction



下载:
全尺寸图片
幻灯片


其中, $ DR $为壁面生成雷诺应力控制所获得的流动减阻, $ DR_{{
m{uc}}} $为$ {
m{u}} {
m{c}}$控制所获得的流动减阻, $ DR_{{
m{vc}}} $为$ {
m{v}}{
m{c}} $控制所获得的流动减阻, $ DR_{{
m{WRSS}}} $为壁面生成的雷诺应力得到的流动减阻. 由等式(7)有

$$ {mathit DR_{{ m{WRSS}}}}({mathit x}) = {mathit DR}({mathit x})-{mathit DR_{{ m{uc}}}}({mathit x})-{mathit DR_{{ m{vc}}}}({mathit x})$$

(8)

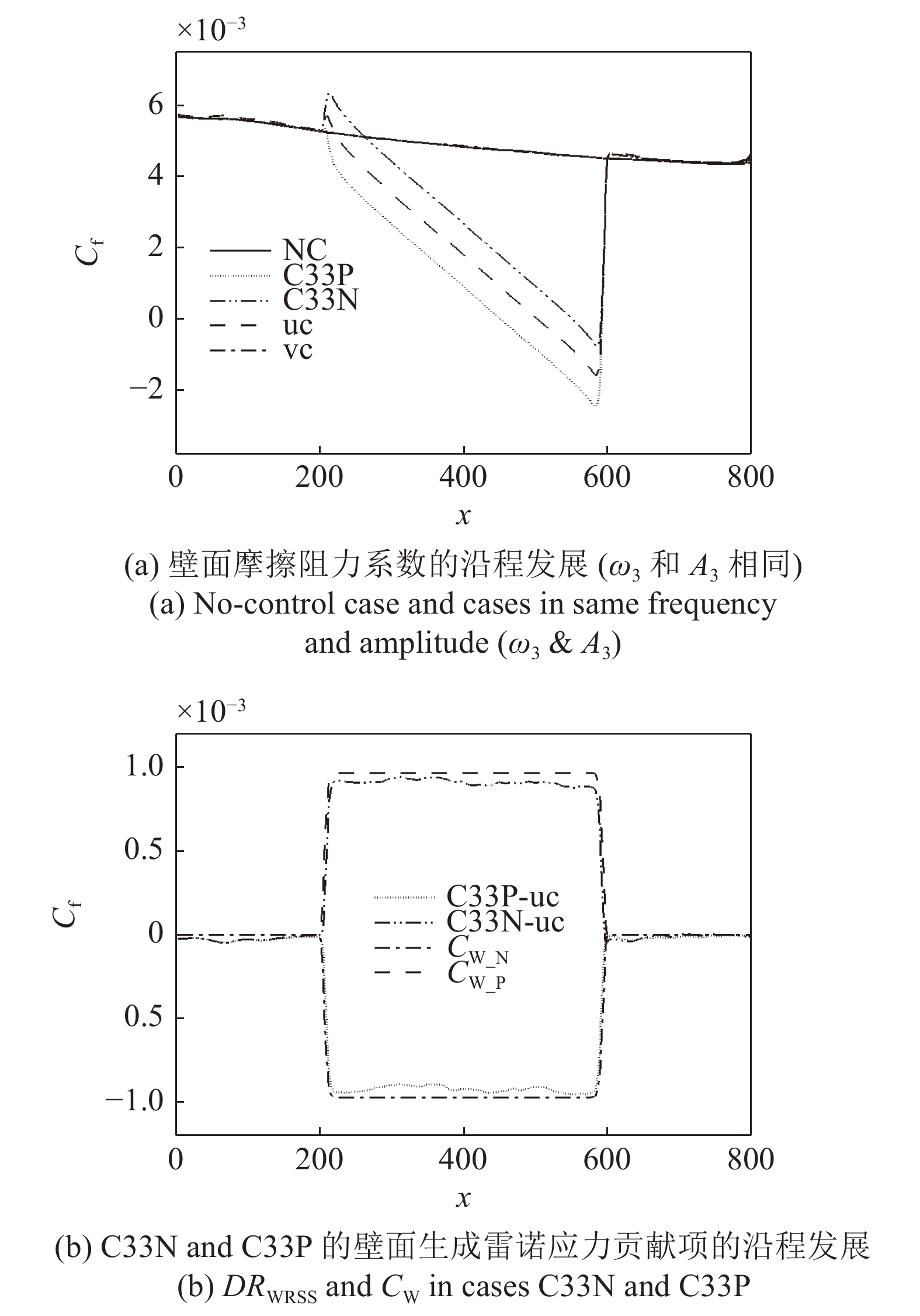
图12(b)显示的是$DR_{{
m{WRSS}}}$同等式(3)中$ C_{
m{W}} $项的对比情况, 图中的C33P(N)-$ {
m{uc}} $曲线是由式(8)得到的壁面生成雷诺应力对摩擦阻力系数的影响; 而$ C_{
m{W}} $曲线是式(3)中壁面雷诺应力贡献项沿流向的分布. 在图12(b)中, 两种途径得到的壁面雷诺应力对$ C_{
m{f}} $的贡献略有区别, 图中的壁面正雷诺应力曲线$C_{{{
m{W}}}-{
m{P}}}$ 和C33P-${
m{u}} {
m{c}}$($ {
m{P}} $代表数据来源于C33P算例)的最大差异约为10%, 而二者在控制区的平均差异小于8%, 图中壁面负雷诺应力曲线$C_{{
m{W}}-{
m{N}}}$和C33N-${
m{u}}{
m{c}}$($ {
m{N}} $代表数据来源于C33N算例)的差异略小, 反映上文中的线性叠加假设存在一定的合理性; 另外, 两种途径得到的壁面生成雷诺应力对$ C_{
m{f}} $的影响的趋势相同, 即壁面正雷诺应力产生减阻效果而壁面负雷诺应力产生增阻效果, 因此验证了式(3)中$ C_{
m{W}} $项对$ C_{
m{f}} $的影响. 此外, 通过式(7)可以在知晓某$ {
m{u}}{
m{c}} $ 控制的减阻效果的前提下, 结合$ C_{
m{W}} $项预估与$ {
m{u}}{
m{c}} $控制具有相同控制参数的壁面生成正或负雷诺应力控制的减阻效果.

图13显示了等式(3)中$ C_{
m{f}} $各贡献项在流向的发展情况, 在计算域后部由于受到流动出口条件的影响, 因此该区域的流动各贡献项的分布不作讨论. 图13(a) 中, 各算例$ C_{{
m{v}}} $项对$ C_{
m{f}} $项的贡献差别很小, 其中$ {
m{v}}{
m{c}} $控制与无控制算例无明显区别, 在计算域的下游, 算例C33P, C33N和$ {
m{u}}{
m{c}} $ 与无控制算例相比, 有约1.0 × 10^?5的增阻贡献, 这能够反映边界层厚度的变化(参见图14). 在图13(b)中, 除去几乎与无控制算例一致的$ {
m{v}}{
m{c}} $算例, C33P算例的$ C_{
m{C}} $ 项对$ C_{
m{f}} $的增阻贡献最大, 而C33N算例的$ C_{
m{C}} $增阻贡献最小; 在控制区下游, C33P, C33N和$ {
m{u}}{
m{c}} $算例的$ C_{
m{C}} $项先快速下降对$ C_{
m{f}} $产生减阻贡献, 之后又逐渐上升, 其中C33P算例的$ C_{
m{C}} $ 项对流动减阻的贡献最小. 图13(c)中, 相比无控制及vc控制算例, C33P, C33N 和$ {
m{u}}{
m{c}} $算例的$ C_{
m{D}} $项在控制区内对$ C_{
m{f}} $有减阻贡献, 在控制区下游, 各算例的$ C_{
m{D}} $项在经历一段快速增长并出现过冲的区域后, 迅速恢复到与无控制算例接近的水平. 图13(d)中, 在控制区起始段C33N和$ {
m{u}}{
m{c}} $算例的$ C_{
m{R}} $项出现增阻现象, 但随着流动向下游发展, 3个算例的$ C_{
m{R}} $项均对$ C_{
m{f}} $有减阻贡献, 结合放大图可以发现C33N算例的$ C_{
m{R}} $项减阻贡献最大, $ {
m{u}}{
m{c}} $算例的次之, 而C33P算例的$ C_{
m{R}} $项减阻贡献最小(比C33N 的$ C_{
m{R}} $项的减阻贡献少大约1.0 × 10^?4). 在图13(e)中, $C_{
m{W}}$项代表壁面生成雷诺应力对$ C_{
m{f}} $的贡献, 图中C33P的$ C_{
m{W}} $项有减阻贡献, 而C33N 的$ C_{
m{W}} $项为增阻贡献, 两者减阻贡献的差约为1.9 × 10^?3. 综合图13(a) ~ 图13(e), 并结合图12(a)和式(3), $ C_{
m{C}} $及$ C_{
m{D}} $项在控制区对$ C_{
m{f}} $ 的贡献相反, 并且C33P和C33N算例在这两项中的贡献差异仅有1.0 × 10^?4左右; 因此, C33P和C33N算例最大的减阻贡献来自于$ C_{
m{R}} $项, 而$ C_{
m{W}} $项是导致C33P和C33N算例的$ C_{
m{f}} $出现明显差异的主要原因.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-13-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
$C_{
m{f}}$各贡献项在流向的发展情况



Figure
13.
Streamwise evolution of the different terms on the right hand side of Eq. (3) for the no-control case and the control cases with same amplitude ($ A_3$) and frequency ($omega_3$)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
各算例边界层厚度沿流向的发展



Figure
14.
Evolution of the boundary layer thickness (99% velocity thickness)



下载:
全尺寸图片
幻灯片


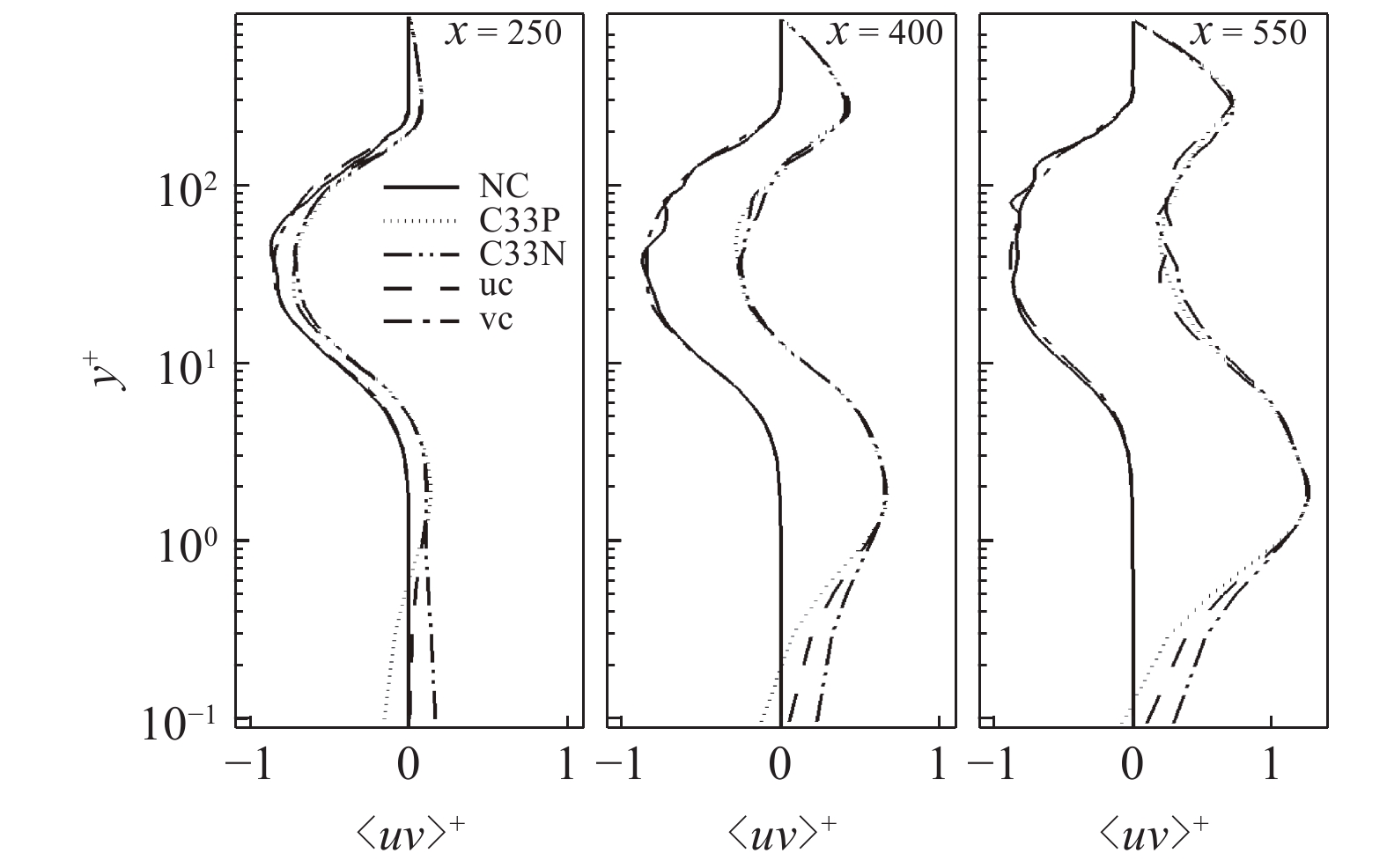
图15显示的是各个算例在流向不同位置的平均雷诺应力分布情况. 图15中, 在流向不同位置的$ y^+ $$ < $1区域, 可以发现C33P, C33N和$ {
m{u}}{
m{c}} $算例的平均雷诺应力分布均存在明显区别; 而在$ y^+ $$ > $1区域, 相对无控制及$ {
m{v}} {
m{c}}$控制算例, 上述3个算例的平均雷诺应力出现了显著的正向偏移, 且在流场内部壁面生成雷诺应力控制与$ {
m{u}}{
m{c}} $控制的平均雷诺应力分布趋近一致, 说明相比壁面生成雷诺应力$ ( {u_{
m{w}}} {v_{
m{w}}})$的影响, 壁面流向震荡对雷诺应力分布影响更大. 图13中, $ {
m{u}}{
m{c}} $算例主要的减阻贡献来自$ C_{
m{R}} $项($ C_{
m{C}} $项与$ C_{
m{D}} $ 项合并后对减阻的贡献很小, $C_{{
m{v}}}$项的贡献较$ C_{
m{R}} $项低一个量级, $ C_{
m{W}} $项为零), 结合图15, 可以认为壁面流向震荡主要通过改变雷诺应力在流场内的分布来获得流动减阻.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />



图
15
各算例的平均雷诺应力分布对比



Figure
15.
Profiles of the RSS at different streamwise locations



下载:
全尺寸图片
幻灯片

2.4
控制方法的收支比

为考察本文所用控制方式的收支比(即减阻收益同控制输入能量之比), 引入输入能量($ W_{{
m{in}}} $)、减阻率($ R $)以及能量收支比($ G $) 3个概念^[33]. 计算时忽略制动和气流入射过程中产生的机械能损失

$$ begin{split}&{W_{{ m{in}}}}(x) = Biggrlangle {frac{1}{2}v_{ m{w}}^2(x)left| {{v_{{{{ m{w}}y}}}}(x)} ight| + } &qquad{Delta {P_{{{{ m{w}}y}}}}(x){v_{{{{ m{w}}y}}}}(x) + Delta {P_{{{{ m{w}}x}}}}(x){v_{{{{ m{w}}x}}}}(x)} Biggr angle end{split}$$

(9)

$$ {mathit R}({mathit x}) = frac {{mathit C_{{ m{f}}_{ m{NC}}}}({mathit x})-{mathit C_{{ m{f}}_{ m{c}}}}({mathit x})}{mathit C_{{ m{f}}_{ m{NC}}}({mathit x})} $$

(10)

$${mathit G}({mathit x}) = frac {{mathit C_{{ m{f}}_{ m{NC}}}}({mathit x})-{mathit C_{{ m{f}}_{ m{c}}}}({mathit x})}{{mathit W_{{ m{in}}}}({mathit x})} $$

(11)

式(9)中, $ langle
angle $表示时间及展向平均, 下标$ {
m{w}} $代表该参数为壁面参量, $ v_{
m{w}} $, $ v_{{
m{w}}x} $和$ v_{{
m{w}}y} $分别表示壁面射流的合速度、$ x $方向分速度和$ y $方向分速度, $ Delta p_{{
m{w}}x} $和$ Delta p_{{
m{w}}y} $分别表示控制区下边界压力在$ x $和$ y $方向的压力梯度. 下标$ _{
m{NC}} $表示数据来自无控制算例, 下标$ _{
m{c}} $ 表示数据来自控制算例.

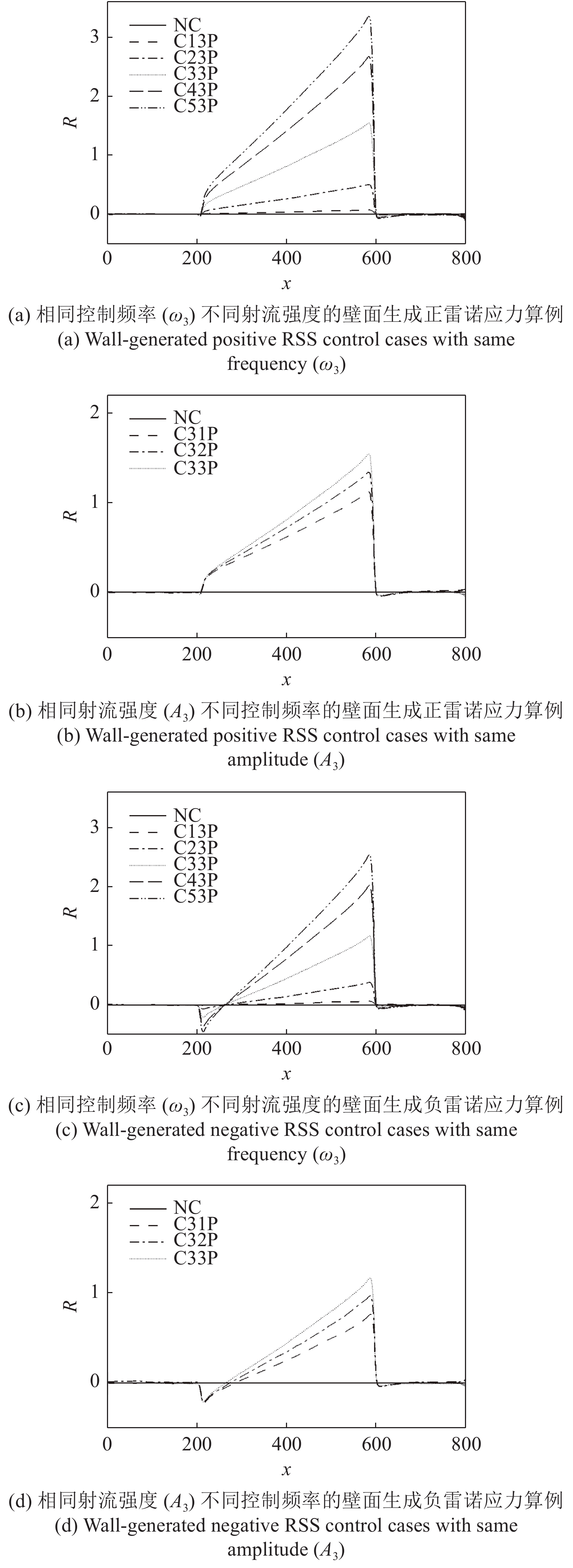
图16显示的是控制算例获得的流动减阻率的沿程发展情况. 图16(a)中, 随着流动向下游发展, 控制区内壁面生成正雷诺应力的控制算例的流动减阻率快速上升, 且射流强度越大的控制算例其流动减阻率越高, 算例C53P 在控制区后部的流动减阻率能够达到3.26; 图16(b) 中, 射流频率越高的控制算例的流动减阻率在控制区内沿流向的增长率越高; 图16(c) 中, 壁面生成负雷诺应力的控制算例在控制区前部出现了一段减阻率为负的区域, 随着流动向下游发展, 减阻率逐渐升高, 在控制区后部, C53N算例的减阻率最高能够达到2.53; 图16(d) 中, 不同射流频率的壁面生成负雷诺应力控制在前部同样出现了负减阻率的区域, 之后射流频率高的控制算例其流动减阻率沿流向增长率高. 对比图16(a) ~ 图16(d), 可以看出在射流频率与射流强度一致的情况下, 壁面生成正雷诺应力控制获得的流动减阻率要高于壁面生成负雷诺应力控制所获得的流动减阻率.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />



图
16
各算例控制算例沿程减阻率的变化



Figure
16.
Evolution of the drag reduction rate in streamwise direction



下载:
全尺寸图片
幻灯片


图17显示的是各控制算例的能量收支比的发展情况. 考察图17(a) ~ 图17(d), 可以发现本文所采用的控制算例均未能获得流动净收益, 获得的流动减阻最高也仅为输入的控制能量的0.38左右, 能量净收益为负; 其中壁面生成正雷诺应力控制在控制区内的能量收支比全程为正, 而壁面生成负雷诺应力控制在控制区前部出现了收支比为负的情况.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-223-17.jpg'"
class="figure_img
figure_type1 bbb " id="Figure17" />



图
17
各控制算例获得能量收支比的沿程发展情况



Figure
17.
Evolution of the cost-effectiveness ratio (gain) in streamwise direction



下载:
全尺寸图片
幻灯片

3.
结论

本文使用DNS方法主要考察了壁面生成雷诺应力控制对空间发展的零压力梯度湍流平板边界层流动的壁面摩擦阻力的影响. 文中采用沿流向阵列倾斜狭缝的方法生成正或负壁面雷诺应力. 通过对比不同算例的壁面摩擦阻力系数、雷诺应力分布、流向平均速度、近壁区流向速度脉动等物理量, 特别是通过对比控制频率和强度相同的壁面生成正负雷诺应力算例, 能够得到以下结论:

(1)壁面生成正或负雷诺应力控制均能够获得流动减阻, 当射流强度足够大时甚至能够在近壁区产生回流现象;

(2)壁面生成的正雷诺应力对壁面摩擦阻力有负贡献, 而壁面生成的负雷诺应力对壁面摩擦阻力有正贡献;

(3)相比壁面生成的雷诺应力对流动减阻的贡献, 更重要的减阻因素是由壁面流向速度$ u_{
m{w}} $引起的控制区下边界流向震荡, 且该因素在控制区的减阻贡献随流动向下游发展愈加显著;

(4)壁面生成的正雷诺应力仅在极近壁区对流场内的雷诺应力分布有影响, 在流场内部, 壁面雷诺应力的分布主要受壁面流向周期性震荡的影响;

(5)通过考察控制的收支比, 发现本文所采用的控制方法虽然能获得流动减阻, 但不能获得能量净收益.

致谢

本文的工作在清华大学探索100上计算, 得到清华信息科学与技术实验室支持. 感谢清华超算中心林皎老师在课题计算资源方面的帮助, 特别感谢清华大学航天航空学院黄伟希老师的帮助.