引 言
随着目前对于水下航行器的各方面研究不断深入, 人们逐渐将目光转向自然界中鱼类本身高效、灵活的运动方式上, 通过模仿自然界中鱼类的外形特征以及运动方式, 并将其成果应用在水下航行器研究中. 自仿生机器鱼成为国内外仿生学领域研究热点以来, 美国、日本、英国和中国等多个国家的研究机构相继研发成功具备不同鱼种特征的仿生机器鱼, 并已应用在许多不同的应用场景.
通过对2000年到2020年之间关于仿生机器鱼的研究进行调研, 当前关于仿生机器鱼的研究主要集中在两方面[1], 一方面通过观察自然界中鱼类运动的形式, 研究其运动机理并将成果应用在水下航行器中. 这一方面研究的主要方向可以分为两类, 一类是研究通过身体或尾鳍的摆动向前游动的鱼类, 这种鱼类的推进方式被称为BCF模式, 具有代表性的是美国东北大学使用形状记忆合金模仿鱼体摆动, 并成功研制了机器鳗鱼样机[2], 以及中国科学院自动化研究所李林等制作的鲹科模式仿生型水下航行器等[3-4]; 另一类是研究通过中间鳍或对鳍的摆动向前游动的鱼类, 这种推进方式被称为MPF推进模式[5-6]. 其中高帅[7]在2014年发表的仿生鳐鱼的结构设计与实验研究具有一定的代表性.
另一方面的研究则是从自然界中鱼类的形体特征出发[8], 研究其外观形状在其游动过程中所展现的流场特性及力学特征. 这一方面的研究成果不断涌现的原因是近年来随着计算机的不断发展, 三维建模技术以及CFD (computational fluid dynamics)技术也日趋成熟,这使得研究者可以使用计算机对自然界中鱼体的外形轮廓进行三维建模, 并使用CFD对模型进行仿真分析. 田晓洁等[9]以金枪鱼为仿生对象, 以金枪鱼在自然状态下处于直线型的鱼体特征为对象, 在Solid Works中进行了三维模型的建立, 并将其导入Ansys (Fluent模块)进行仿真, 分析了模型在定常流场下所呈现的力学特征, 说明了流线型鱼体在减阻方面的功能, 为仿生机器鱼的外形优化设计提供了支撑. 汤琳[10]以鲤鱼的外形为参照, 研发了一种BCF推进模式的机器鱼, 在Fluent中进行了一系列仿真实验, 探究了不同推进模式对于推进性能优劣的影响. 周澍欣和胡庆松[11]以鲤鱼为研究对象, 以其为原型建立了三维模型, 研究了该模型在定常流下不同部位对总和力的贡献度,结论表明在鲤鱼形机器鱼外形设计中, 升力以及运行阻力主要与鱼头部分以及前鳍的设计有关.
通过上述内容可以得出, 目前仿生机器鱼的研制虽然在理论方面有了较为深入的进展, 但是以上研究中所提到的仿生机器鱼模型在工程实际应用中仍然具有较大的缺陷. 对于以上研究中模仿自然界鱼类外形的机器鱼来说, 虽然都有良好的减阻性能, 但在工程实际中往往需要机器鱼的外形轮廓设计不仅要使其具有优良的减阻性, 而且需要考虑内部的容积是否合理, 体型是否利于传感器的安装等, 在某些特殊作业中, 还需要降低机器鱼行进过程中对周围环境的干扰以及提高机器鱼本身的隐蔽性等[12-13].
双髻鲨的头部外形独特, 作用如同一个水中翼, 帮助它在水中自由遨游, 而且分布在双髻鲨头部前侧的化学传感神经、电子传感神经和压力传感神经也对它的生存有很大帮助. 本文通过模仿双髻鲨(又称锤头鲨)的外形特征, 从仿生工程学的角度设计并提出了一种新的符合工程实际需求的仿生机器鱼外形, 通过与翼型壳体机器鱼体以及市场上常见的回转体型水下机器人进行对比[14-15], 利用Solid Works进行3种模型方案的三维建模和网格化, 分析了3种方案在来流为定常流时鱼体在给定流场下所呈现的力学特征, 从工程实际需求的角度出发, 分别从扰动性、减阻性等方面进行了评估和对比. 同时对该仿生机器鱼外形设计在流场中表现的特殊性质进行了探究和评价. 本文借助CFD技术采用数值模拟的方法, 结合具体设计参数进行了仿真实验, 研究了该机器鱼外形设计在流场中的特性, 为仿生水下航行器外形设计的优化提供了参考数据和新的思路[16-17].
1.
仿双髻鲨头部特征机器鱼模型建模
1.1
双髻鲨生物形态特征分析
双髻鲨, 其形态特征具有明显的特点, 头部一般呈扁平状, 具有一定的流线型特征, 头部向两侧延伸, 形成鎚状突出, 为“丁”字形, 故也称 “锤头鲨”, 其外形如图1所示. 头长约为全长的2/9 (幼体)至1/5. 身体狭长, 侧边偏扁, 整体呈亚圆筒形[18]. 由于双髻鲨的种类繁多, 本文选取了其中3种最具代表性的双髻鲨, 分别是锤头双髻鲨、丁字双髻鲨和窄头双髻鲨, 进行生物形体特征提取.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-160-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
双髻鲨外形图
Figure
1.
Shape image of a hammerhead shark
下载: 全尺寸图片
幻灯片
1.2
生物外形特征提取
本文从仿生工程学的角度出发, 将双髻鲨的头部形态特点与工程实际相结合, 从而设计了机器鱼模型. 采用生物外形特征提取技术[19-20], 利用CorelDRAW, Illustrator等软件对3种双髻鲨的3D扫描模型进行边缘点的检测、线条拟合等操作, 生成双髻鲨外形特征的轮廓曲线. 依据局部抽取优化法, 选取双髻鲨头部的曲线线条, 提取曲线结果如图2所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-160-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
3种双髻鲨头部轮廓曲线特征提取图
Figure
2.
Feature extraction of head profile curves of three species of hammerhead sharks
下载: 全尺寸图片
幻灯片
1.3
外形轮廓线条拟合
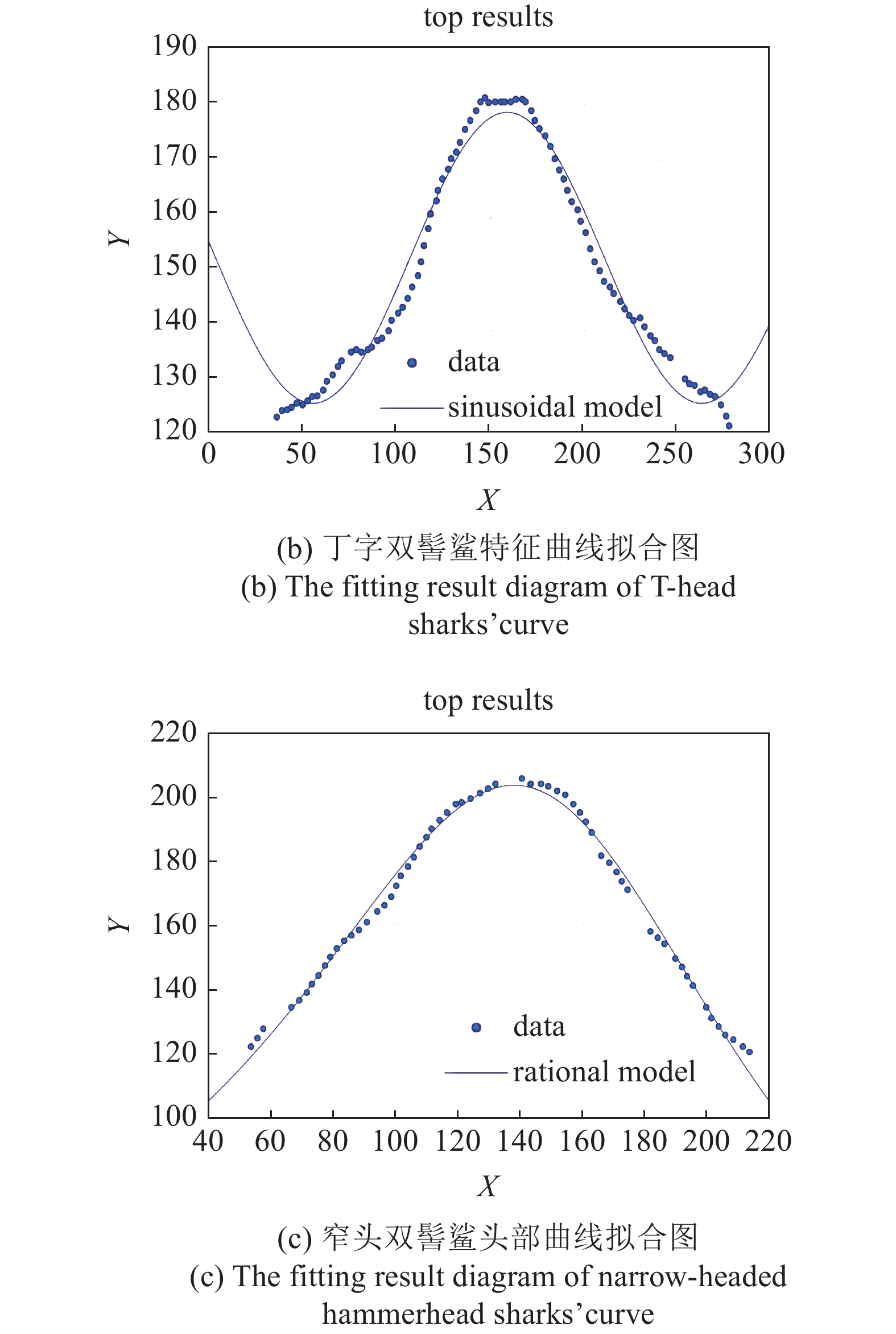
由于直接提取的头部特征曲线并不规则, 在工程实际中难以直接利用, 所以对头部特征曲线进行了平滑处理, 生成规则的曲线. 本文采用曲线插值拟合的方法, 先提取轮廓曲线上的关键点, 对点进行坐标化, 再对数据进行多种曲线拟合, 截取拟合效果最好的模型曲线. 拟合结果如图3所示, 图中散点为坐标化后的数据点, 曲线为拟合后的曲线. 表1为3种模型轮廓所用的曲线模型及方程, 表2所示为拟合曲线的方程参数.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-160-3-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure3-1" />
3
3种双髻鲨头部轮廓曲线拟合图
3.
Head contour curve fitting of three species of hammerhead
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-160-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
3种双髻鲨头部轮廓曲线拟合图 (续)
Figure
3.
Head contour curve fitting of three species of hammerhead (continued)
下载: 全尺寸图片
幻灯片
表
1
3种模型所用拟合曲线
Table
1.
Fitting curves used for the three models
table_type1 ">
| Name | Model | Equation |
| ① | exponential plus linear | $y = a + b{r^x} + cx$ |
| ② | sinusoidal | $y = a + bcos left( {cx + d} ight)$ |
| ③ | rational model | $y = dfrac{{a + bx}}{{1 + cx + d{x^2}}}$ |
下载: 导出CSV
|显示表格
表
2
3种曲线拟合的具体参数
Table
2.
Parameters of three fitting curves
table_type1 ">
| Model | Parameters |
| exponential plus linear | $ a=2.262;1times {10}^{3} $, $ b=-2.167;6times {10}^{3} $, $ c=-3.540;4 $, $ r=9.977;5times {10}^{-1} $ |
| sinusoidal | $ a=1.528;3times {10}^{2} $, $ b=2.565;7times {10}^{1} $, $ c=3.045;8times {10}^{-2} $, $ d=-4.847;0 $ |
| rational | $ a=7.266;1times {10}^{1} $, $ b=-1.210;4times {10}^{-1} $, $ c=-9.857;7times {10}^{-3} $, $ d=3.398;9times {10}^{-5} $ |
下载: 导出CSV
|显示表格
1.4
机器鱼头部特征曲线的选择
以3种双髻鲨头部的拟合曲线为驱动方程式, 建立具备其头部外轮廓特征的简易模型,参考文献[9]中的方法对模型进行仿真分析. 图4(b)中①②③, 分别代表锤头双髻鲨、丁字双髻鲨、窄头双髻鲨. 由图4(a)中3种简易模型在不同流速下的阻力值折线图所示, 其中3种简易模型在0 ~ 2 m/s流速下, 所受阻力相近, 但当流速大于2 m/s时, 丁字双髻鲨简易模型所受的阻力值明显大于锤头双髻鲨简易模型和窄头双髻鲨简易模型, 而锤头鲨轮廓模型与窄头鲨简易模型相比, 锤头鲨简易模型阻力略小与窄头鲨模型所受到的阻力, 即由锤头鲨头部外形轮廓制成的简易模型具有最优的减阻性; 图4(b)中流速云图中, 自上而下分别为在同等流速条件下的①锤头双髻鲨简易模型流速云图、②丁字双髻鲨简易模型流速云图、③为窄头双髻鲨简易模型流速云图, 可以得到在同样的流速场中, 远离模型的流场没有受到模型的干扰, 流场保持稳定; 当靠近模型时, 水流向两侧分离, 速度增加, 而模型后方流速较小, 从而形成尾迹. 由图①②③对比可得具有锤头双髻鲨头部轮廓特征的简易模型①相较于其他两种模型来说产生的尾迹更小, 对周围流场干扰更小, 周围流场更加稳定.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-160-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
3种模型在不同流速下的阻力值折线图及流速云图
Figure
4.
Line chart and cloud chart of resistance values of three models at different flow rates
下载: 全尺寸图片
幻灯片
经过以上分析, 锤头双髻鲨长宽比协调, 形体特征明显, 排流曲线斜率大, 且头部呈流线型, 减阻性能好、且对周围流场干扰性小, 故将锤头双髻鲨的拟合特征曲线作为机器鱼建模时的参照曲线最为优.
1.5
机器鱼体外形设计
参照文献[21]的内容, 以锤头双髻鲨头部的拟合曲线为驱动方程式, 在Solid Works软件中进行机器鱼体头部三维模型的构建, 并且在机器鱼头部顶端、机器鱼头部与身体连接处采用流线型过渡和平滑曲线过渡, 以减小机器鱼在水中行进时的阻力; 考虑到机器鱼应具有良好的工程适应性以及装配可行性, 鱼体中部应设计为规则形状且其内部应有足够的空间放置控制系统、驱动系统和传感器元件等功能装置, 故将鱼体中部设计为扁平状, 鱼体尾部设计为流线型过渡, 以减少尾流. 仿双髻鲨模型主要参数如表3所示.
表
3
模型尺寸参数
Table
3.
Size parameters of the model
table_type1 ">
| Name | Parameter descriptor | Value/m |
| $ {L}_{1} $ | the total length | 1.40 |
| $ {L}_{2} $ | the length of the head | 0.20 |
| $ {L}_{3} $ | the head width | 0.50 |
| $ {L}_{4} $ | the length of the tail | 0.20 |
| $ {L}_{5} $ | in the middle of length | 0.35 |
| $ {L}_{6} $ | middle minimum length | 0.85 |
| $ {L}_{7} $ | central maximum length | 0.90 |
| $ {L}_{8} $ | the length of the tail | 0.30 |
| $ {L}_{9} $ | height of model | 0.15 |
| $ {L}_{10} $ | the head height | 0.15 |
| $ {R}_{1} $ | side contour radius | 0.70 |
| ① | contour curve | controlled by Table 1 and Table 2 |
| ② | contour curve | |
| ③ | streamline curve | arc length 0.45, chord length 0.15 |
| ④ | streamline curve | arc length 0.45, chord length 0.15 |
下载: 导出CSV
|显示表格
通过对锤头双髻鲨的形体特征分析, 本文中将鱼体宽度设计为略小于双髻鲨头部宽度, 并推测在这样的设计中, 双髻鲨头部向两侧排开的“丁字”型结构可以对鱼体周围的流场创造低流速区域, 即水流通过机器鱼头部后, 由于头部和身体的宽度关系, 会在机器鱼头部后方一定范围内的鱼体的两侧产生低流速区域, 从而减少此区域内机器鱼体对周围流场的干扰性, 这种作用在工程实际中具有良好的利用价值, 可以极大地提高机器鱼体的可扩展性和隐蔽性. 如图5, 为仿生机器鱼模型设计细节和示意图.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-160-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
主要设计参数及细节
Figure
5.
Main design parameters and details
下载: 全尺寸图片
幻灯片
2.
数值计算
2.1
机器鱼网格划分
对于机器鱼体的流体仿真分析来说, 鱼体及其所处流场的网格划分结果直接关系到仿真结果的正确性和精确性, 所以根据鱼体的建模情况来正确地选择网格划分方法是十分有必要的. 精确度和求解所需的时间是计算流体动力学仿真中十分关键的问题, 这两个问题都依赖于网格的特点. 本次进行仿真模拟的3种模型方案表面并不规则且包含尖端部分, 需要不同类型的网格划分元素来求解各种几何形状和流态, 这其中不同类型的网格划分元素之间的过渡是必须要考虑的问题. 一般情况下过渡区通常依赖于非共形界面或四面体, 但这样处理可能会造成网格质量下降而且还伴随着生成过多的单元格从而导致求解时间变长的问题. 本文中使用了Ansys Mosaic 技术[22], 将不同类型的网格与一般多面体元素进行连接. Mosaic 网格具有数量更少、质量更好的单元格, 对于复杂外形的模型有非常好的适用性, 且具有划分效率高, 求解时间短的特点.
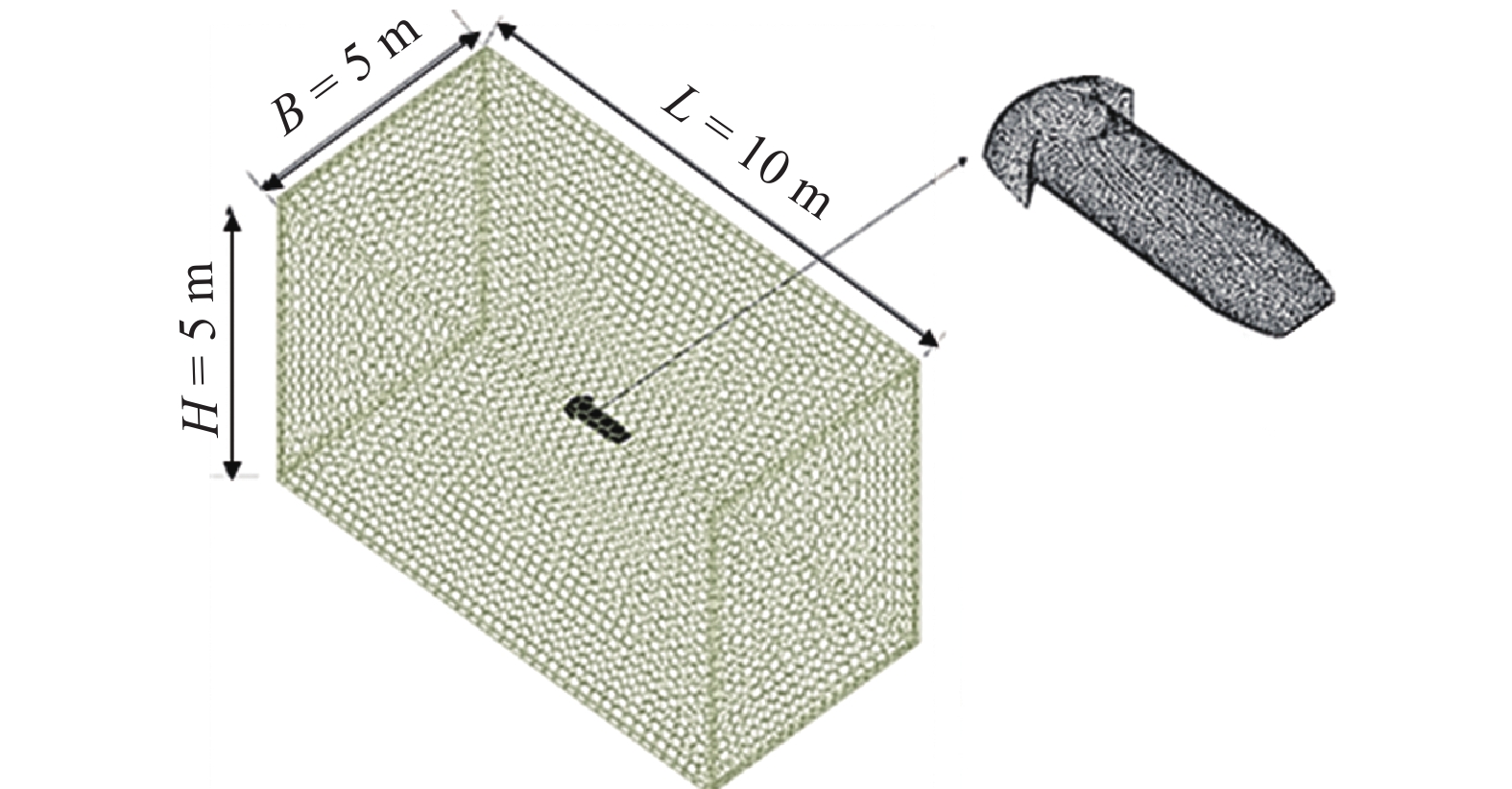
为了避免外流场边界引起的边界效应[9-10]对仿真结果造成影响, 设置计算域的尺寸为长L=10 m, 宽B = 5 m, 高H = 5 m, 鱼体置于计算域的中心位置. 流体域网格划分如图6所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-160-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
流域及鱼体网格划分
Figure
6.
Watershed and fish body grid division
下载: 全尺寸图片
幻灯片
2.2
湍流模型及初始条件的设置
本次仿真中, 考虑到流场进口来流速度较小, 且仿生鱼特征尺寸较小, 属于低雷诺数问题, 因此选择RNG k-ε模型作为本次仿真的湍流模型, RNG k-ε是标准k-ε模型的变形, 方程和系数来自解析解[23-28]. 标准k-ε模型是一种高雷诺数的模型, 其标准方程为湍流动能方程和扩散方程
动能方程
$$ begin{split}&frac{partial }{{partial t}}left( { ho k} ight) + frac{partial }{{partial {x_i}}}left( { ho k{u_i}} ight) =&quadquad frac{partial }{{partial {x_j}}}left[ {left( {mu + frac{{{mu _t}}}{{{sigma _k}}}} ight)frac{{partial k}}{{partial {x_j}}}} ight] + {G_k} + {G_b} - ho varepsilon - {Y_M} + {S_k}end{split} $$  | (1) |
扩散方程
$$begin{split} &frac{partial }{{partial t}}left( { ho varepsilon } ight) + frac{partial }{{partial {x_i}}}left( { ho varepsilon {u_i}} ight) = frac{partial }{{partial {x_j}}}left( {{alpha _varepsilon }{mu _{{ m{eff}}}}frac{{partial varepsilon }}{{partial {x_j}}}} ight) +&qquad {C_{1varepsilon }}frac{varepsilon }{k}left( {{G_k} + {C_{3varepsilon }}{G_b}} ight) - {C_{2varepsilon }} ho frac{{{varepsilon ^2}}}{k} - {R_varepsilon } + {S_varepsilon }end{split} $$  | (2) |
式中
RNG理论提供了一个考虑低雷诺数流动黏性的解析公式, RNG k-ε模型的方程为
$$ begin{split} &frac{partial }{{partial t}}left( { ho varepsilon } ight) + frac{partial }{{partial {x_i}}}left( { ho varepsilon {u_i}} ight) = frac{partial }{{partial {x_j}}}left( {{alpha _varepsilon }{mu _{{ m{eff}}}}frac{{partial varepsilon }}{{partial {x_j}}}} ight) +&qquad {C_{1varepsilon }}frac{varepsilon }{k}left( {{G_k} + {C_{3varepsilon }}{G_b}} ight) - {C_{2varepsilon }} ho frac{{{varepsilon ^2}}}{k} - {R_varepsilon } + {S_varepsilon }end{split} $$  | (3) |
$$ begin{split} &frac{partial }{{partial t}}left( { ho k} ight) + frac{partial }{{partial {x_i}}}left( { ho k{u_i}} ight) = &qquadfrac{partial }{{partial {x_j}}}left[ {left( {mu + frac{{{mu _t}}}{{{sigma _k}}}} ight)frac{{partial k}}{{partial {x_j}}}} ight] + {G_k} + {G_b} - ho varepsilon - {Y_M} + {S_k}end{split} $$  | (4) |
两种模型的区别在于RNG理论提供了
$$ {R_varepsilon } = frac{{{C_mu } ho {eta ^3}left( {1 - eta /{eta _0}} ight)}}{{1 + beta {eta ^3}}}frac{{{varepsilon ^2}}}{k} $$  | (5) |
这使得其比标准k-ε模型在低雷诺数的流动问题中有更高的可信度和精度, 通常用来预测中等强度的旋游和低雷诺数流动.
参照文献[9-10]考虑到仿生机器鱼被应用的场景通常为自然状态下的水域, 所以选择不可压缩模流模型; 由于本次仿真属于低速流动问题, 故选择分离求解器(即基于压力的求解器)比较适合, 默认采用Simple算法进行稳态计算. 设置流场的左侧边界为速度进口边界条件, 右侧为流出边界条件, 流场的其他面设置为壁面边界条件; 重力加速度设置为9.81 m/s2; 由于采用了Ansys Mosaic 技术, 网格划分中存在不同类型的网格单元, 流动的方向与网格并不对齐, 一阶的迎风格式会增大数值离散误差, 故选择离散格式为二阶迎风格式, 可以得到更为精确的计算结果. 经过对同类型的仿生机器鱼进行调研以及结合本文中仿真对象的速度考虑后, 设置入口来流速度分别为0.25 m/s, 0.5 m/s和1 m/s.
3.
仿真结果分析
3.1
阻力分析与计算结果对比
由于在仿生机器鱼的绝大多数作业环境中其鱼体下潜的深度都大于体长的1/3, 这时兴波阻力几乎为0, 故在阻力分析中, 不考虑兴波阻力, 仅考虑压差阻力以及黏性阻力. 利用Fluent在不同的来流速度下对三种模型进行阻力分析.
如图7所示, 综合3种模型在不同速度下的阻力分析得出, 在来流方向平行于鱼体直线的情况下, 随着机器鱼行进速度的增大, 压差阻力和黏性阻力都逐步增大. 随着速度的增大, 压差阻力占比越来越小, 黏性阻力占据主导因素. 3种模型中以翼型曲线为特征的机器鱼模型在行进过程中受到的阻力最大, 仿双髻鲨模型所受的阻力最小, 且流速越大差距越明显, 由此可得出仿双髻鲨模型相对于另两种模型具有更好的减阻性能, 能够有效的减少行进时产生的阻力. 表4为阻力计算结果.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-160-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
总阻力对比折线图与黏性阻力对比折线图
Figure
7.
Total resistance comparison line chart and viscous resistance comparison line chart
下载: 全尺寸图片
幻灯片
表
4
阻力计算结果
Table
4.
Drag calculation results
table_type1 ">
| Velocity /(cm·$ {mathrm{s}}^{-1} $) | Pressure drag/mN | Viscous drag /N | Total drag /N |
| 25 | 6 | 0.0712 | 0.0719 |
| 50 | 2.1 | 0.2604 | 0.2626 |
| 100 | 6.8 | 0.9238 | 0.9307 |
下载: 导出CSV
|显示表格
3.2
对周围流场的干扰性对比分析
为分析3种仿生机器鱼模型在相同流速条件下对周围流场干扰性的大小, 选取鱼体所在的中心平面为特征面进行分析. 当来流速度为1 m/s时3种模型在定常流环境下仿真结果如图8所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-160-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
流速分布云图(左侧为模型正视图, 右侧为俯视图)
Figure
8.
Velocity distribution nephogram (front view of the model on the left, top view on the right)
下载: 全尺寸图片
幻灯片
由流速分布云图可以得到, 3种模型在定常流下均会产生不同大小尾迹. 尾迹的形成是物体与流体发生相对运动时, 各层流体的速度发生了变化, 形成了一定的速度差使得物体后面的压强与流体其他部分的压强不同, 当中心的流速比四周的流速小, 在流场中的物体下游便形成尾迹[9]. (1)从图8中3种模型的正视流速云图(即①③⑤)看, 仿真结果显示仿双髻鲨头部特征的机器鱼(图8(b))相较于翼型机器鱼(图8(a))和回转体模型(如图8(c)), 在正视面对周围流场的影响更小, 其尾迹较小且对机器鱼体周围流场干扰范围为三者中最小; (2)从3种模型的俯视流速云图(即②④⑥)观察, 由于仿双髻鲨头部特征的机器鱼模型在机器鱼头部、尾部采用了流线型设计, 且整体采用扁平化结构, 这使得其在俯视面内的干扰性大大降低, 鱼头部和尾部对周围流场的影响范围和程度都优于翼型机器鱼和回转体模型, 为三者中最优.
综上所述, 可以得到仿双髻鲨头部特征的机器鱼外形在相同的流速条件下, 相较于翼型机器鱼和回转体模型干扰性更小, 表现在对周围流体流速的影响程度小、周围流体影响范围小以及产生的尾迹小这三方面.
3.3
仿双髻鲨头部特征的机器鱼周围流场特性
由图8中仿双髻鲨头部特征的机器鱼流速分布云图中③机器鱼周围流速分布形状推测: 当机器鱼迎流时, 流体经过仿锤头双髻鲨的头部特征后在机器鱼两侧形成了低流速区域, 在低流速区域内物体受到的流体阻力会更小, 且处于此区域内的物体不会对周围流场造成明显干扰, 同时对于鱼体隐蔽性的提升具有一定作用, 为证明此推测, 设置对比试验.
3.3.1
对比实验设置
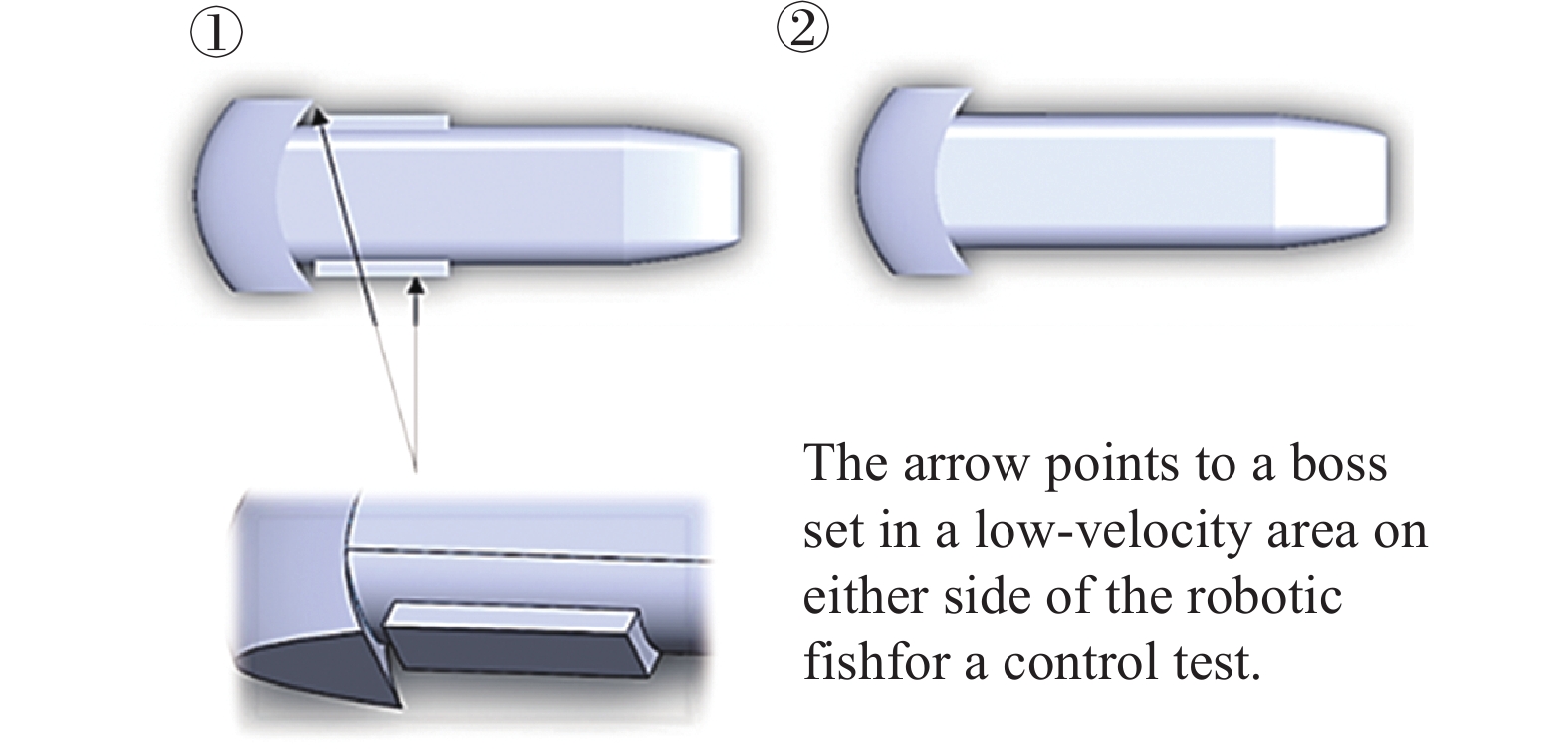
此实验为定性试验, 分别设置实验组和对照组, 在本次试验中, 对照组模型则不发生变化, 实验组的模型则设置为在对照组模型的基础上, 在机器鱼两侧头部突起后方设置长方形障碍物. 将两组试验模型导入Fluent中进行流体仿真, 以试验结果来对比长方形障碍物的存在是否会明显地影响鱼体周围的流场情况. 如图9所示, 实验组机器鱼与对照组机器鱼模型尺寸相同, 具体参数可参照表3, 机器鱼①为实验组模型, 在机器鱼头部后方的低流速区域内设置有长L=0.35 m, 宽B=0.1 m, 高H=0.05 m的长方形凸台作为障碍物; 机器鱼②为对照组实验模型, 尺寸同图5所示. 两组实验均在迎流速度为1 m/s的条件下进行.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-160-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
实验组模型与对照组模型
Figure
9.
Control group model and experimental group model
下载: 全尺寸图片
幻灯片
3.3.2
实验结果
利用同本文第2节相同的方法, 将两组实验组模型进行流体仿真分析, 结果如下.
(1) 实验结果
通过观察图10, 对比实验组机器鱼模型的流速云图和对照组模型流速云图, 在相同流速条件下, 在低流速区域增加障碍物后机器鱼周围流场的大体形状和范围并没有发生改变, 对周围流场影响的主要区域与对照组相同, 都集中在机器鱼头部以及流体流经机器鱼后在尾部后方产生的尾迹, 机器鱼两侧流场保持稳定. 通过对照发现, 实验组与对照组的尾迹基本相同, 这对有利于提高机器鱼的隐蔽性[29-31].
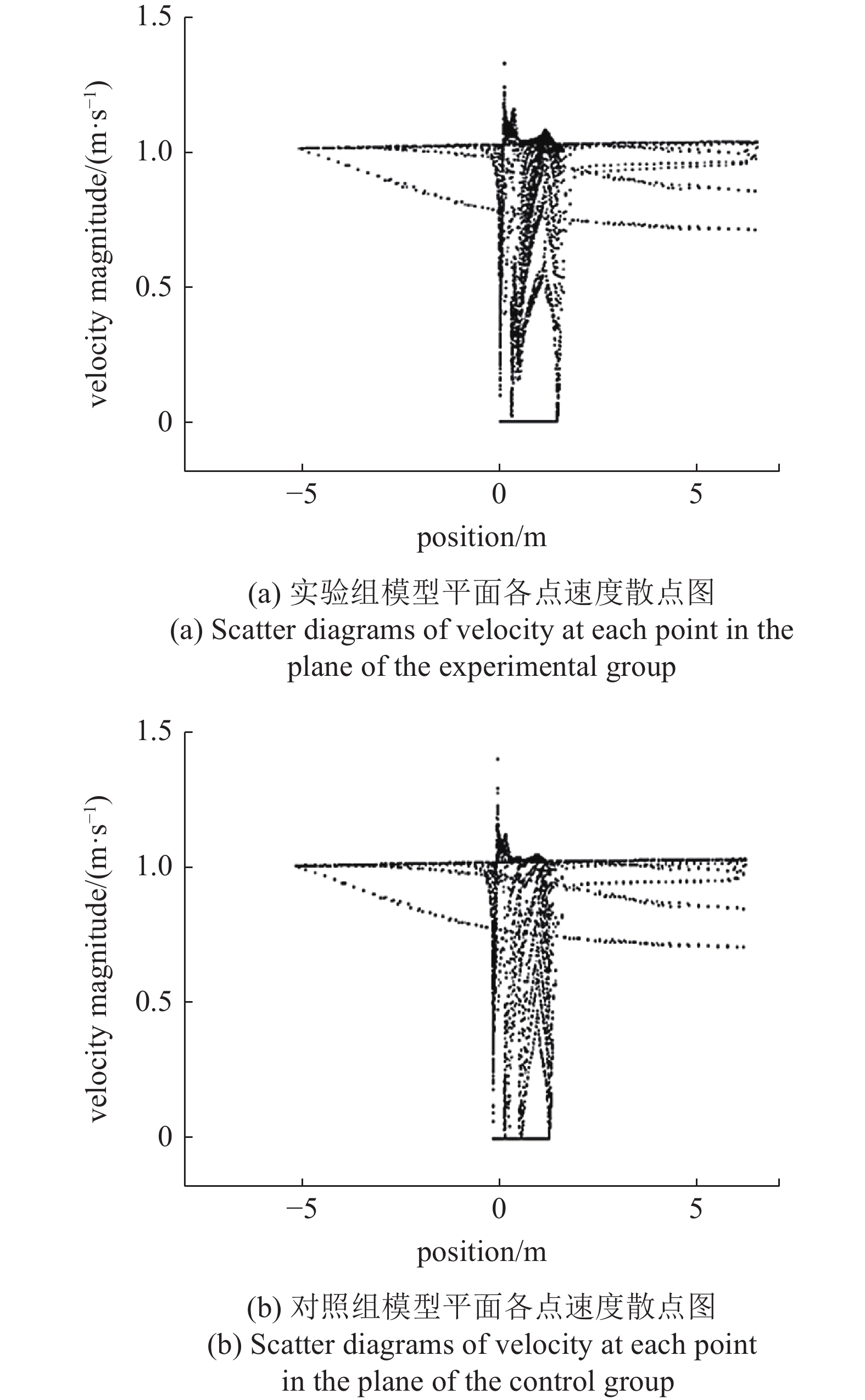
将机器鱼所在的平面设置为观测面, 监测该面内点的速度值大小, 结果如图11所示. 通过对比两图可得, 在计算域内, 原理机器鱼的地方, 对照组和实验组都未对流速数值产生影响, 在机器鱼模型周围, 两组实验模型速度数值分布形状大致相同, 并未发生太大变化.
综上所述, 该对比试验证实了前文中的推测, 即: 当机器鱼迎流时, 流体经过仿锤头双髻鲨的头部特征后在机器鱼两侧形成了低流速区域, 在低流速区域内物体受到的流体阻力会更小, 且处于此区域内的物体不会对周围流场造成明显干扰.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-160-10.jpg'" class="figure_img
figure_type1 bbb " id="Figure10" />
图
10
对照组模型与实验组流体流速分布云图
Figure
10.
Flow velocity distribution nephogram of control group model and experimental group
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-160-11.jpg'" class="figure_img
figure_type1 bbb " id="Figure11" />
图
11
流体平面速度分布对比图
Figure
11.
Comparison diagram of fluid plane velocity distribution
下载: 全尺寸图片
幻灯片
4.
结语
本文以双髻鲨为参照对象, 通过模仿其外形特征建立了符合工程实际需求的仿双髻鲨机器鱼模型, 重点从扰动性、减阻性等方面对模型进行评估. 利用了Ansys Mosaic 技术进行网格划分, 并依据工程实际场景设置了合理的流场边界条件. 基于RNG k-ε模型, 研究并对比与不同其他仿生机器鱼模型在特定流场下的力学特征及所受的阻力情况. 仿真结果表面, 仿双髻鲨机器鱼模型相较于以翼型机器鱼模型和广泛应用的回转体模型来说, 具有更好的减阻性及更小的扰动性, 可以有效减少仿生机器鱼在水下航行时对周围流场带来的扰动并提高推进效率, 并且探究了仿双髻鲨机器鱼模型周身流场的特殊性, 为仿生机器鱼的发展提供新的思路, 同时对水下机器人外形结构的优化设计提供依据.
