删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

考虑混凝土塑性耗散的CDM-XFEM裂缝计算方法

本站小编 Free考研考试/2022-01-01


引 言


混凝土结构是建筑、交通、水利等领域的重要基础材料, 其可塑性高、耐久性好是受广泛应用的主要原因. 但混凝土抗拉强度远低于抗压强度[1], 结构在服役期间受外界载荷的影响容易产生裂缝[2], 裂缝的出现不仅会降低结构刚度, 还为外部侵蚀介质的侵入提供了快捷通道, 从而加速内部钢筋锈蚀[3-4]、降低结构承载力. 因此, 采用准确的计算方法预测混凝土的裂缝发展是治理裂缝的基本前提, 也是保障结构安全的重要手段.

基于非线性断裂力学, 混凝土开裂大致分为以下三个过程[5-7]: (1)当材料拉伸应力接近抗拉强度时, 在断裂过程区会形成密集分布的微裂纹, 载荷?变形的关系不再具有线性斜率, 但材料的宏观响应仍然保持稳定; (2)由于载荷增大引起微裂纹的合并和交叉, 以及材料基体中骨料的脱黏, 材料的宏观响应变得不稳定, 载荷?变形的关系位于软化段中, 局部范围出现较大变形, 在应变场中形成了弱不连续性; (3)随着载荷继续增大, 断裂过程区黏聚力逐渐减小至零, 最终形成一个无黏聚应力裂纹的强不连续区域.

为模拟混凝土开裂的上述过程, 出现了较多的数值计算方法, 目前主流方法有三大类: 连续损伤力学方法(continuou damage method, CDM)、扩展有限单元法(mechanics-extended finite element method, XFEM)及两者相结合的方法(CDM-XFEM). 其中CDM方法是假定当等效应力达到抗力准则时, 开始发生初始断裂, 即在损伤单元中, 应力?应变关系会被有效应力?应变关系所取代, 因此, CDM方法只更新裂纹扩展过程中材料的本构关系, 其单元网格保持不变[8-9]. 如Vilppo等[10]从热力学的角度提出了各向异性损伤的本构模型, 分析了混凝土单轴受拉及受压情况下的破坏规律. Poliotti等[11]提出了考虑剪胀参数变化的塑性损伤模型, 分析了不同强度的混凝土受剪切作用下的受力状态. Pereira等[12]提出了一种与有效率相关的非局部损伤模型, 模拟了单切口混凝土受拉出现分叉裂缝的情况. 而XFEM方法是扩充带有不连续性质的形函数来代表计算区域内的间断, 在计算过程中, 不连续场的描述完全独立于网格边界[13-14]. 如Agathos等[15]在XFEM的基础上, 提出采用向量水平集的算法更新裂缝面的演化, 研究了三点受弯作用下含单切口混凝土的裂缝形态. Schatzer等[16]将显?隐式结合的水平集函数融入到XFEM方法中, 分析了含边缘裂口混凝土的裂缝张开度. 为提高裂缝的计算效率及稳定性, Haghani等[17] 开发了基于XFEM和α时间积分结合的混凝土裂缝扩展程序, 研究了振动作用下混凝土大坝的裂缝扩展规律.

相比而言, CDM和XFEM这两种方法各有利弊. CDM方法能够很好地描述裂缝扩展的第一个阶段, 但该方法不能描述离散的开裂面, 同时存在网格诱导偏差及虚假应力传递的弊端[18-20]. XFEM方法虽然能够很好的描述宏观裂纹的扩展, 但不能较好地描述第一阶段中密集分布的微裂纹, 计算出的裂纹分布与实际差异较大 [21]. 因此, 部分****提出将CDM及XFEM相结合的方法, 该方法基于能量等效原理, 建立CDM与XFEM黏聚裂缝的能量转化关系, 当损伤达到临界值时实现转换 [22]. 如Comi等[23]采用CDM-XFEM方法研究了含双切口的试件受竖向拉伸作用下的开裂情况, Jin等[24]采用该方法研究了含单切口混凝土梁受弯作用下的裂缝形态, Pandey等[25]采用该方法研究了高频疲劳载荷作用下混凝土裂缝的扩展规律.

采用CDM-XFEM准确计算裂缝的关键在于实现CDM与XFEM之间能量转化的平衡性. 首先要采用合适的牵引?分离函数模型描述裂缝张开的变化模式, 如直线型[26]、双折线型[27]、指数型函数[28]等, 其次是选取合适的能量转化点, 将宏观裂缝出现时损伤模型中的剩余能量全部转移到黏结裂缝模型中. 为此, Roth等[29]假定能量转化时, 两者能量等效的分割线为垂线, 且转化点的应力相等, 以此建立了能量平衡方程并求解了牵引?分离函数. Bobinski等[30]假定开裂时仅出现不可恢复变形, 不考虑材料刚度发生退化, 并自定义能量转化时的临界位移, 从而构建了两者能量的转化方程. Wang等[31]基于弹性损伤理论, 假定材料发生开裂时弹性能全部回弹, 从而建立了对应的能量平衡方程.

然而, 相关试验研究证明[32-33], 在实际情况下混凝土出现宏观裂纹时既存在刚度退化现象, 也存在不可逆变形的特征. 因此, 本文考虑CDM与XFEM之间断裂能转化时的塑性耗散, 重新构建能量转化方程, 采用广义逆的最小二乘法求解临界位移及牵引?分离函数的系数, 最终形成考虑混凝土塑性耗散的CDM-XFEM计算方法. 通过与双切口混凝土受剪拉开裂的试验进行对比验证, 结果表明采用考虑塑性耗散CDM-XFEM方法能够有效地预测混凝土裂缝的发展规律.


1.
考虑塑性耗散的CDM-XFEM计算方法



1.1
CDM-XFEM方法的计算过程


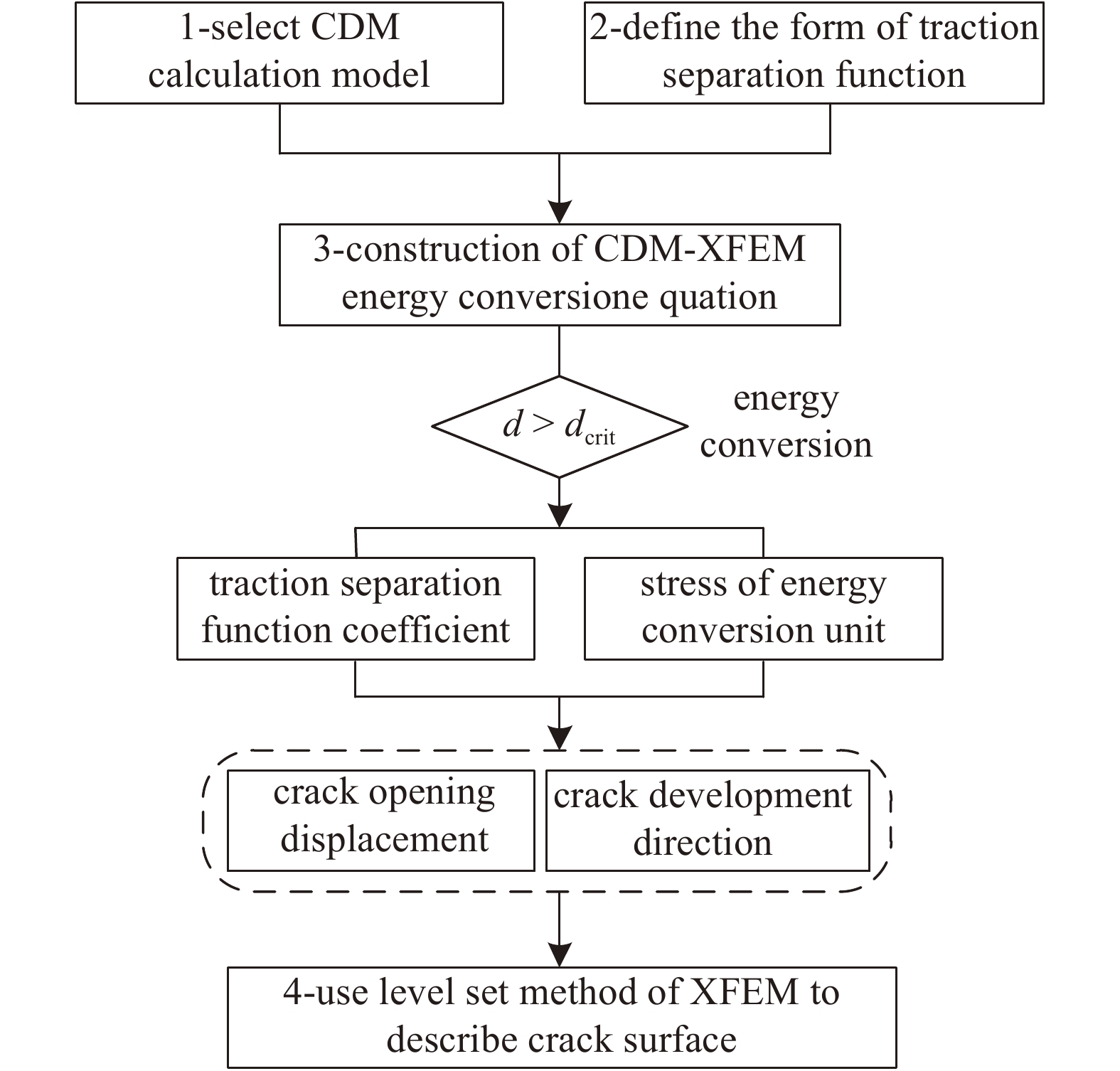
CDM-XFEM裂缝计算方法的过程为: 当损伤因子d小于临界值时, 基于连续损伤力学描述微裂缝的发展, 当损伤因子d大于临界值dcrit时, 将损伤模型所需耗散的剩余能量转移到黏结裂缝模型中, 采用扩展有限元单元法描述宏观裂缝的张开规律, 如图1所示, 其计算过程主要包含4个部分.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-272-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
CDM-XFEM方法计算过程示意图



Figure
1.
Calculation process CDM-XFEM method



下载:
全尺寸图片
幻灯片



1.2
混凝土受拉损伤及塑性应变的计算式


本文采用等效应变$ bar varepsilon $作为判定混凝土出现损伤的指标, 其计算公式为[34]







$$ left. begin{gathered}bar varepsilon > {r_0},begin{array}{*{20}{c}}{begin{array}{*{20}{c}}{}&{{
m{then}}} end{array}}&{D > 0} end{array} hfill bar varepsilon = sqrt {sumlimits_{i = 1}^3 {left( {{{leftlangle {varepsilon _i^{{
m{av}}}}
ight
angle }^2}{text{ + }}{{left( {{f_t}/{f_c}}
ight)}^2} cdot {{leftlangle { - varepsilon _i^{{
m{av}}}}
ight
angle }^2}}
ight)} } hfill end{gathered}
ight} $$
(1)

式中, $ varepsilon _i^{{
m{av}}} $表示单元平均应变, $ {f_t} $和$ {f_c} $表示混凝土抗拉强度和抗压强度.

受拉弹性损伤因子D的演化准则的计算式[35]为







$$ D = 1 - sqrt {frac{{{r_0}}}{{bar varepsilon }}exp Big[ { - Rleft( {bar varepsilon - {r_0}}
ight)} Big]} $$
(2)

式中, R为损伤演化参数, 其计算为 [29]







$$ R = frac{{2E{f_t}{l_{{
m{rve}}}}}}{{2E{G_F} - {f_t}{l_{{
m{rve}}}}}} $$
(3)

其中lrve为单元特征长度, 对于C3D8R单元, 一般取值0.02 m[36]. r0为混凝土的初始刚度, 计算式为







$$ {r_0} = frac{{{f_t}}}{E}qquadqquad $$
(4)

对于单次加载?卸载后出现塑性损伤的材料, Hatzigeorgioiu等[37]根据试验结果将弹性损伤因子D修正为Dk, 则变化后的弹性模量Ek表示为







$$ {E_k} = left( {1 - {D^k}}
ight)E $$
(5)

式中, E为初始弹性模量, 则总应变ε可由弹性应变εe和塑性应变εp表示为







$$ varepsilon = {varepsilon ^p} + {varepsilon ^e} = {varepsilon ^p} + frac{{left( {1 - D}
ight)Evarepsilon }}{{left( {1 - {D^k}}
ight)E}} $$
(6)

对于混凝土材料, Hatzigeorgioiu等[37]通过数值计算给出了最优值k = 2, 本文采用该数值, 代入式(6)可得出塑性应变的简化计算公式







$$ {varepsilon ^p} = frac{D}{{1{text{ + }}D}}varepsilon $$
(7)


1.3
黏结裂缝的牵引?分离函数形式


目前CDM-XFEM计算模型中均不考虑黏结裂缝单元的切向牵引力ts, 仅考虑黏结裂缝的法向牵引力tn, 在本文研究中同样只考虑裂缝间的法向牵引力, 其牵引?分离函数体现的是裂缝张开量与裂缝间牵引力的相互关系, 常用的牵引?分离函数主要包括: 线型、双折线型, 多项式型及指数型, 其计算为







$$ left. begin{gathered}{t_{n1}} = au hfill {t_{n2}} = au;(u < {u_0})begin{array}{*{20}{c}}{}&{{
m{or}}} end{array}begin{array}{*{20}{c}}{}&{{t_{n2}} = bu;(u > {u_0})} end{array} hfill {t_{n3}} = a{u^3} + b{u^2} + cu + d hfill {t_{n4}} = a{{
m{e}}^{bu}} hfill end{gathered}
ight} $$
(8)

由式(8)可知, 第1种函数求取的参数最少, 但相关研究表明, 采用线性函数表达牵引?分离法则计算得出的裂缝与实际裂缝相差较大[38]; 第2种和第3种函数需求取的未知变量数分别为3和4, 需引入较多的边界条件才能求取相应系数[39]; 第4种采用了指数型函数来表示, 既体现了裂缝张开与牵引力之间的非线性关系, 求解的未知变量也较少, 因此, 在本文的研究中也选择指数型函数来表达黏结裂缝的牵引?分离关系.


1.4
能量转化的基本假定条件


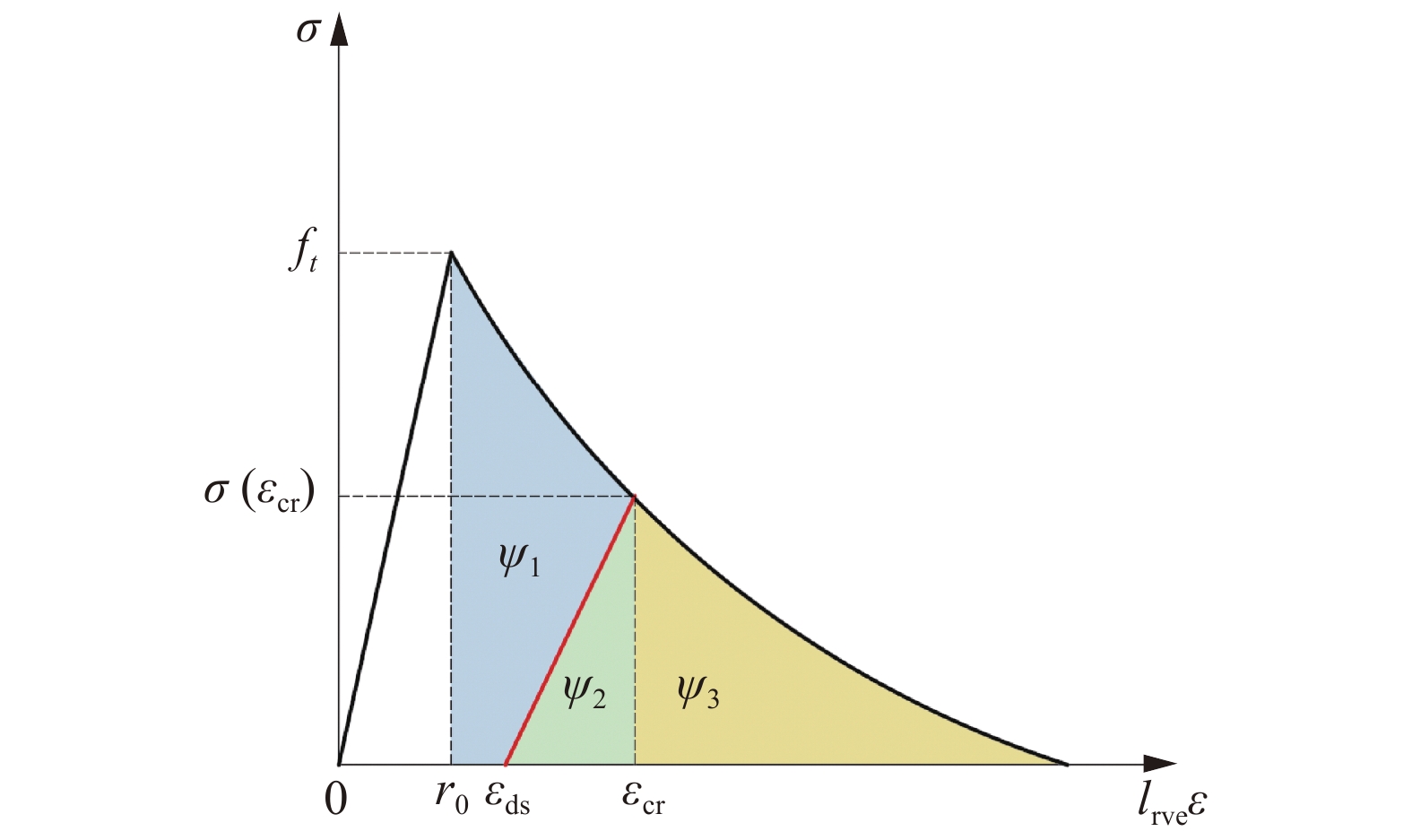
本文假定能量转化时 (D = Dcr) CDM模型中单元的最大拉应力等于XFEM中裂缝张开至ucr时的牵引力, 即 σ(εcr) = t(ucr), 此时产生的塑性应变为εds, 损伤消耗的能量 (当$ bar varepsilon $ > r0时开始出现损伤) 等于黏结裂缝张开至ucr的能量, 即图2中蓝色的面积等于图3中蓝色的面积; 同时, 损伤模型的剩余能量均全部转移到XFEM粘结裂缝模型中, 即图2中绿色和黄色的累计面积等于图3中黄色的面积, 其中‖u‖代表裂缝的总张开量.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-272-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
CDM的应力-应变曲线



Figure
2.
Stress-strain curve of CDM



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-272-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
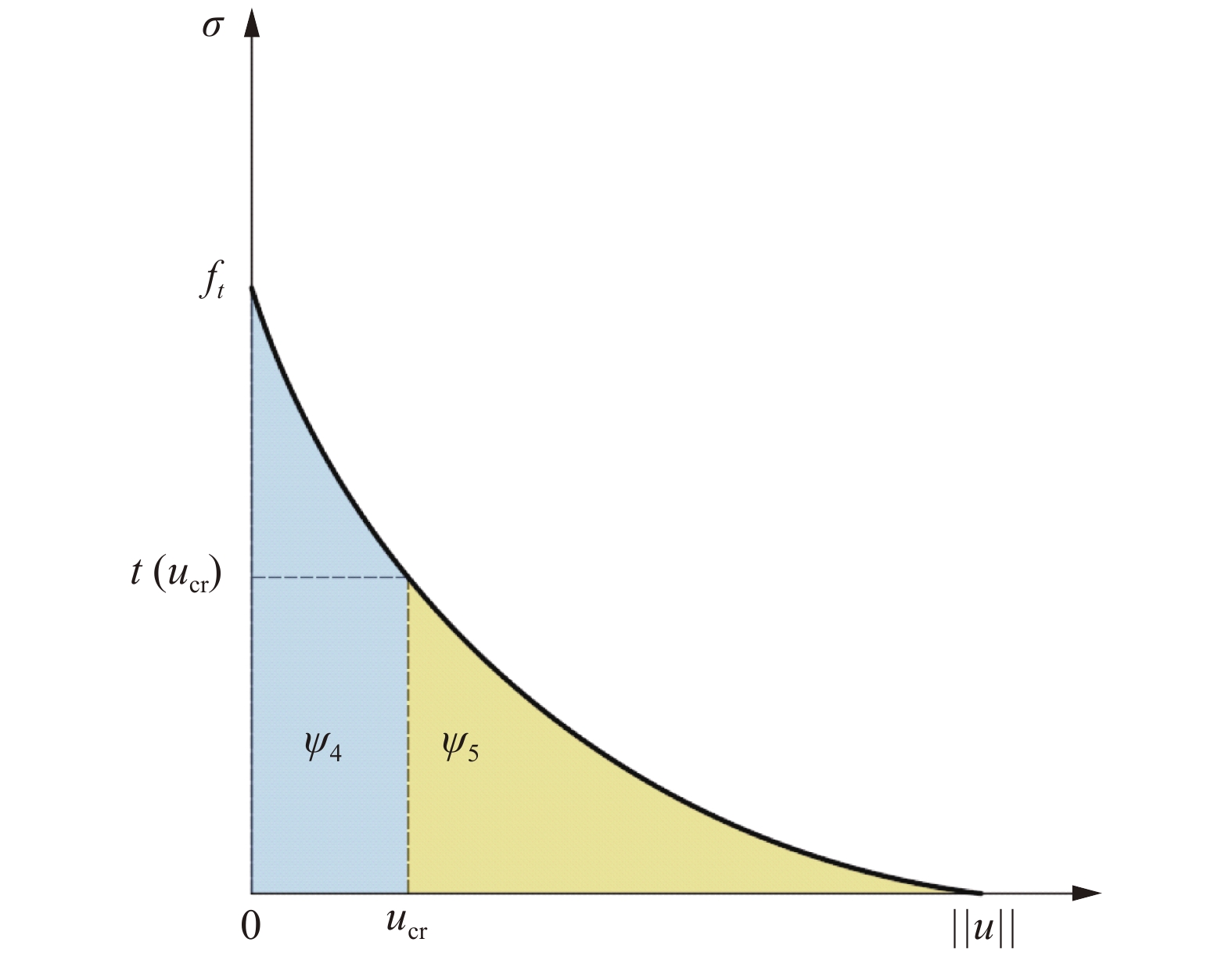
XFEM粘结裂缝的牵引-分离曲线



Figure
3.
Traction-separation curve of XFEM cohesive crack



下载:
全尺寸图片
幻灯片



1.5
能量转化方程


根据图3所示, 基于能量等效原理, 可得出关系式(9)和式(10)







$$ {varPsi _1} = {varPsi _4}qquad $$
(9)







$$ {varPsi _2}{text{ + }}{varPsi _3} = {varPsi _5} $$
(10)

式(9)中, 能量Ψ1可由r0到εcr的积分面积减去能量Ψ2的面积, 即







$$ {varPsi _1}{text{ = }}int_{{r_0}}^{{varepsilon _{cr}}} {sigma left( {bar varepsilon }
ight){
m{d}}} bar varepsilon - {varPsi _2} $$
(11)

根据应变等效原则[29], 即无损伤试件产生的应变ε等价于含损伤试件产生的应变$ bar varepsilon $, 则等效应力可表示为







$$ sigma left( {bar varepsilon }
ight) = E{left( {1 - D}
ight)^2}bar varepsilon $$
(12)

将式(2)、式(4)和式(12)代入到式(11)中, 则r0到εcr的积分面积可表示为







$$ begin{split} &int_{{r_0}}^{{varepsilon _{{
m{cr}}}}} {sigma left( {bar varepsilon }
ight){
m{d}}} bar varepsilon {text{ = }}int_{{r_0}}^{{varepsilon _{{
m{cr}}}}} {left{ {{l_{{
m{rve}}}}{f_t}left{ {frac{{{r_0}}}{{bar varepsilon }}exp left[ { - Rleft( {bar varepsilon - {r_0}}
ight)}
ight]}
ight}}
ight}{
m{d}}} bar varepsilon = &qquadexp left( {R{r_0}}
ight){f_t}{l_{{
m{rve}}}}{r_0}left( {Gamma left[ {R{r_0}}
ight] - Gamma left[ {R{varepsilon _{{
m{cr}}}}}
ight]}
ight) [-12pt]end{split}$$
(13)

式(10)中, 能量Ψ2可由为直角三角形面积表示, 即







$$ {varPsi _2}{text{ = }}frac{1}{2}{l_{{
m{rve}}}}sigma left( {{varepsilon _{{
m{cr}}}}}
ight) left( {{varepsilon _{{
m{cr}}}} - {varepsilon _{{
m{ds}}}}}
ight) $$
(14)

其中, ${varepsilon _{{
m{cr}}}} - {varepsilon _{{
m{ds}}}}$可表示为







$$ {varepsilon _{{
m{cr}}}} - {varepsilon _{{
m{ds}}}}{text{ = }}frac{{sigma left( {{varepsilon _{{
m{cr}}}}}
ight)}}{{{E_k}}} = frac{{E{{left( {1 - {D_{{
m{cr}}}}}
ight)}^2}left( {1 + {D_{{
m{cr}}}}}
ight)}}{{{D_{{
m{cr}}}}}} $$
(15)

将式(15)代入式(14), 则能量Ψ2的计算式表示为







$$ {varPsi _2}{text{ = }}frac{{f_t^2{l_{{
m{rve}}}}}}{{2r_0^2}}frac{{{{left( {1 - {D_{{
m{cr}}}}}
ight)}^4}left( {1 + {D_{{
m{cr}}}}}
ight)}}{{{D_{{
m{cr}}}}}}{varepsilon _{{
m{cr}}}} $$
(16)

为简化表示, 将损伤因子Dcr表示为关于εcr的函数$ Aleft( {{varepsilon _{{
m{cr}}}}}
ight) $, 则式(16)为







$$ left. begin{gathered}Aleft( {{varepsilon _{{
m{cr}}}}}
ight){text{ = }}sqrt {frac{{{r_0}}}{{{varepsilon _{{
m{cr}}}}}}exp Big[ { - Rleft( {{varepsilon _{{
m{cr}}}} - {r_0}}
ight)} Big]} hfill {varPsi _2}{text{ = }}frac{{f_t^2{l_{{
m{rve}}}}{varepsilon _{{
m{cr}}}}}}{{2r_0^2}} cdot frac{{{A^4}left( {{varepsilon _{{
m{cr}}}}}
ight)Big[ {{text{2}} - Aleft( {{varepsilon _{{
m{cr}}}}}
ight)} Big]}}{{1 - Aleft( {{varepsilon _{{
m{cr}}}}}
ight)}} hfill end{gathered}
ight} $$
(17)

将式(13)和式(17)代入到式(11), 可得到能量Ψ1的计算公式







$$ begin{split} &{varPsi _1}{text{ = }}exp left( {R{r_0}}
ight){f_t}{l_{{
m{rve}}}}{r_0}left( {Gamma left[ {R{r_0}}
ight] - Gamma left[ {R{varepsilon _{{
m{cr}}}}}
ight]}
ight) - &qquadfrac{{f_t^2{l_{{
m{rve}}}}{varepsilon _{{
m{cr}}}}}}{{2r_0^2}} cdot frac{{{A^4}left( {{varepsilon _{{
m{cr}}}}}
ight)Big[ {{text{2}} - Aleft( {{varepsilon _{{
m{cr}}}}}
ight)} Big]}}{{1 - Aleft( {{varepsilon _{{
m{cr}}}}}
ight)}} end{split}$$
(18)

式中, Γ(x)为伽马函数, 裂缝的牵引分离函数形式采用指数型函数, 即式(8)的tn4, 则能量Ψ4可表示为







$$ {varPsi _4}{text{ = }}int_0^{{u_{{
m{cr}}}}} {tleft( u
ight){
m{d}}} u = int_0^{{u_{{
m{cr}}}}} {alpha {{
m{e}}^{ - beta left( u
ight)}}{
m{d}}} u = frac{{alpha - alpha {{
m{e}}^{ - beta {u_{{
m{cr}}}}}}}}{beta } $$
(19)

将式(18)和式(19)代入到式(9), 则第1个能量等效方程可表示为







$$ begin{split} &exp left( {R{r_0}}
ight){f_t}{l_{{
m{rve}}}}{r_0}left( {Gamma left[ {R{r_0}}
ight] - Gamma left[ {R{varepsilon _{{
m{cr}}}}}
ight]}
ight) - hfill &qquadfrac{{f_t^2{l_{{
m{rve}}}}{varepsilon _{{
m{cr}}}}}}{{2r_0^2}} cdot frac{{{A^4}left( {{varepsilon _{{
m{cr}}}}}
ight)Big[ {{text{2}} - Aleft( {{varepsilon _{{
m{cr}}}}}
ight)} Big]}}{{1 - Aleft( {{varepsilon _{{
m{cr}}}}}
ight)}}{text{ = }}frac{{alpha - alpha {{
m{e}}^{ - beta {u_{{
m{cr}}}}}}}}{beta } end{split} $$
(20)

同理, 能量Ψ3和能量Ψ5的方程可表示为







$$ begin{split} {varPsi _3} = &int_{{varepsilon _{{
m{cr}}}}}^infty {sigma left( {bar varepsilon }
ight){
m{d}}} bar varepsilon hfill = { int_{{varepsilon _{{
m{cr}}}}}^infty {left{ {{l_{
m{rve}}}{f_t}left{ {frac{{{r_0}}}{{bar varepsilon }}exp Big[ { - Rleft( {bar varepsilon - {r_0}}
ight)} Big]}
ight}}
ight}{
m{d}}} bar varepsilon } =&{exp left( {R{r_0}}
ight){f_t}{l_{{
m{rve}}}}{r_0}Gamma left[ {R{varepsilon _{{
m{cr}}}}}
ight]} [-12pt]end{split} $$
(21)







$$ {varPsi _5} = int_{{u_{{
m{cr}}}}}^infty {sigma left( u
ight){
m{d}}} u = int_{{u_{{
m{cr}}}}}^infty {alpha {{
m{e}}^{ - beta left( u
ight)}}{
m{d}}} u = frac{{alpha {{
m{e}}^{ - beta {u_{{
m{cr}}}}}}}}{beta } $$
(22)

将式(17)、式(21)和式(22)代入到式(10), 则第2个能量等效方程可表示为







$$ begin{split} &frac{{f_t^2{l_{{
m{rve}}}}{varepsilon _{{
m{cr}}}}}}{{2r_0^2}} cdot frac{{{A^4}left( {{varepsilon _{{
m{cr}}}}}
ight)Big[ {{text{2}} - Aleft( {{varepsilon _{{
m{cr}}}}}
ight)} Big]}}{{1 - Aleft( {{varepsilon _{{
m{cr}}}}}
ight)}}{text{ + }} &qquadexp left( {R{r_0}}
ight){f_t}{l_{{
m{rve}}}}{r_0}Gamma left[ {R{varepsilon _{{
m{cr}}}}}
ight] = frac{{alpha {{
m{e}}^{ - beta {u_{{
m{cr}}}}}}}}{beta } end{split} $$
(23)

根据1.4节提出的应力等效假定条件, 除了满足能量等效, 转换时的应力条件也应该相等, 即







$$ left. begin{array}{l}tleft( {{u_{{
m{cr}}}}}
ight) = sigma left( {{varepsilon _{{
m{cr}}}}}
ight) alpha {{
m{e}}^{ - beta {u_{{
m{cr}}}}}} = {f_t}{A^{text{2}}}left( {{varepsilon _{{
m{cr}}}}}
ight) end{array}
ight} $$
(24)

联立方程式(20)、式(23)及式(24), 最终求出参数α, β和ucr.


2.
CDM-XFEM的数值求解算法



2.1
数值求解流程


本文采用ABAQUS软件的用户自定义扩展模块, 编写相应的用户单元子程序 UEL(user defined element). 计算流程总体分3个部分, 即

(1) 计算八节点六面体单元的应力及损伤因子, 以0.7作为临界损伤标准[29], 判定模型是否达到能量转化条件.

(2) 求解能量转化的临界位移, 计算牵引?分离函数的系数, 确定裂缝张开量.

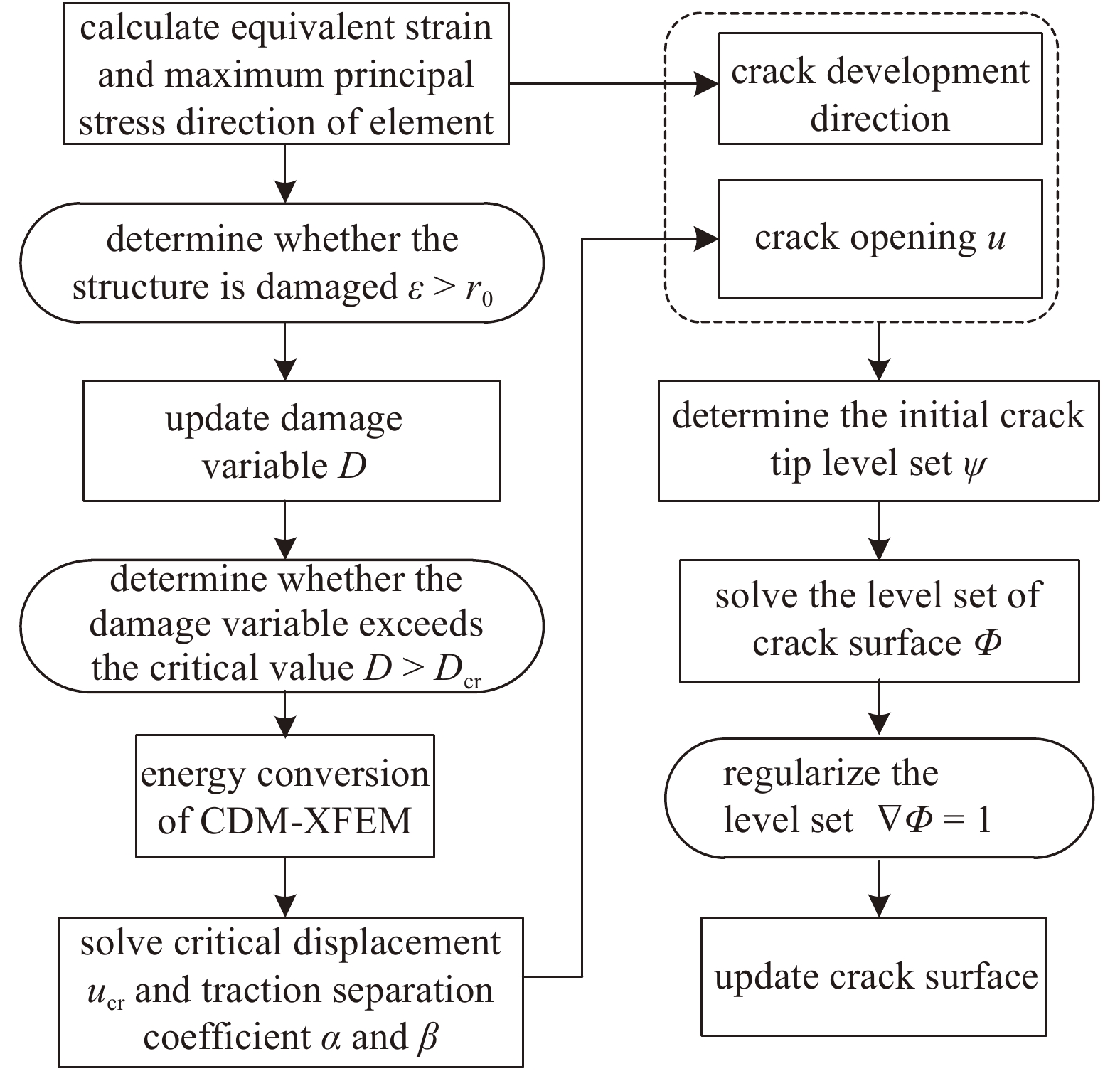
(3) 基于主应力确定裂缝的发展方向, 即裂缝的发展方向垂直于最大主应力方向, 更新裂缝尖端及裂缝面的水平集函数, 具体如图4所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-272-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
考虑混凝土塑性耗散的CDM-XFEM方法计算流程



Figure
4.
Calculation flow of CDM-XFEM method considered concrete plastic dissipation



下载:
全尺寸图片
幻灯片



2.2
能量转化系数求解方法


对于牵引?分离函数参数α, β和临界位移ucr, 采用广义逆的最小二乘法进行求解[40], 步骤为: 先将能量等效方程及应力等效方程转为3个待求的非线性方程, 即式(25), 然后对临界应变εcr设置初始值, 代入到式(26)和式(27)进行迭代求算, 最终求出最小范数解, 这里设置的最小范数的约束条件[29]为式(28)







$$ left. begin{gathered}{F_1} = exp left( {R{r_0}}
ight){f_t}{l_{{
m{rve}}}}{r_0}left( {Gamma left[ {R{r_0}}
ight] - Gamma left[ {R{varepsilon _{{
m{cr}}}}}
ight]}
ight) - hfill begin{array}{*{20}{c}}{}&{} end{array}frac{{f_t^2{l_{{
m{rve}}}}{varepsilon _{{
m{cr}}}}}}{{2r_0^2}} cdot frac{{{A^4}left( {{varepsilon _{{
m{cr}}}}}
ight)Big[ {{text{2}} - Aleft( {{varepsilon _{{
m{cr}}}}}
ight)} Big]}}{{1 - Aleft( {{varepsilon _{{
m{cr}}}}}
ight)}} - frac{{alpha - alpha {{
m{e}}^{ - beta {u_{{
m{cr}}}}}}}}{beta } hfill {F_2} = frac{{f_t^2{l_{{
m{rve}}}}{varepsilon _{{
m{cr}}}}}}{{2r_0^2}} cdot frac{{{A^4}left( {{varepsilon _{{
m{cr}}}}}
ight)Big[ {{text{2}} - Aleft( {{varepsilon _{{
m{cr}}}}}
ight)} Big]}}{{1 - Aleft( {{varepsilon _{{
m{cr}}}}}
ight)}}{text{ + }} hfill begin{array}{*{20}{c}}{}&{} end{array}exp left( {R{r_0}}
ight){f_t}{l_{{
m{rve}}}}{r_0}Gamma left[ {R{varepsilon _{{
m{cr}}}}}
ight] - frac{{alpha {{
m{e}}^{ - beta {u_{{
m{cr}}}}}}}}{beta } hfill {F_3} = alpha {{
m{e}}^{ - beta {u_{{
m{cr}}}}}} - {f_t}{A^{text{2}}}left( {{varepsilon _{{
m{cr}}}}}
ight) hfill end{gathered}
ight} $$
(25)







$$ - {left[ {begin{array}{*{20}{c}}{dfrac{{partial {F_1}}}{{partial alpha }}}&{dfrac{{partial {F_1}}}{{partial beta }}}&{dfrac{{partial {F_1}}}{{partial {u_{cr}}}}} {dfrac{{partial {F_2}}}{{partial alpha }}}&{dfrac{{partial {F_2}}}{{partial beta }}}&{dfrac{{partial {F_2}}}{{partial {u_{cr}}}}} {dfrac{{partial {F_3}}}{{partial alpha }}}&{dfrac{{partial {F_3}}}{{partial beta }}}&{dfrac{{partial {F_3}}}{{partial {u_{cr}}}}} end{array}}
ight]^{ - 1}}left{ {begin{array}{*{20}{c}}{{F_1}} {{F_2}} {{F_3}} end{array}}
ight} = left{ {begin{array}{*{20}{c}}{Delta alpha } {Delta beta } {Delta {u_{cr}}} end{array}}
ight} $$
(26)







$$ left. begin{array}{l}alpha {text{ = }}alpha {text{ + }}Delta alpha alpha {text{ = }}beta {text{ + }}Delta beta {u_{{
m{cr}}}}{text{ = }}{u_{{
m{cr}}}}{text{ + }}Delta {u_{{
m{cr}}}} end{array}
ight} $$
(27)







$$ left| M
ight| = sqrt {sumlimits_{i = 1}^n {F_i^2} } leqslant {10^{ - {text{8}}}} $$
(28)


2.3
裂缝尖端及裂缝面水平集更新


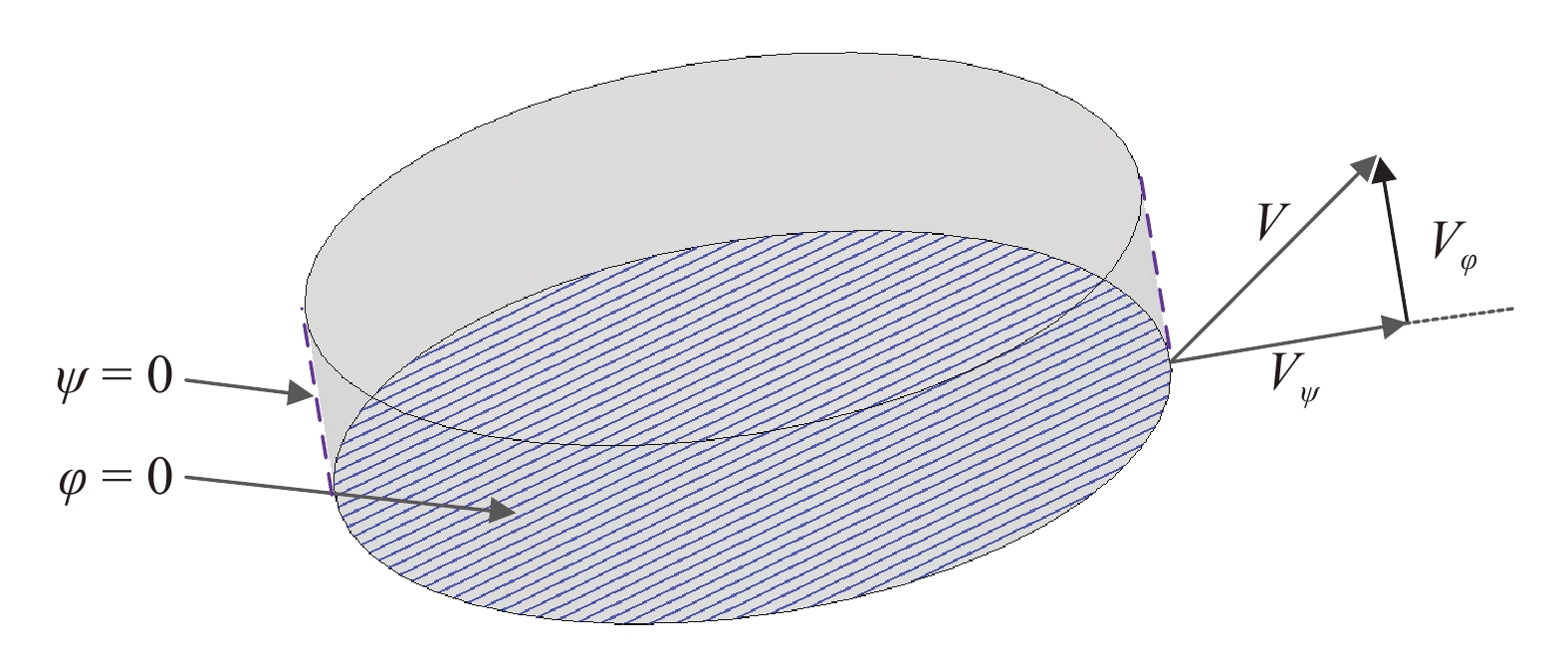
裂缝水平集更新的关键是将速度场从裂纹前缘扩展到整个水平集子域[41], 裂缝尖端和裂缝面水平集的速度分量如图5所示, 各个变量的关系式为







$$ V{text{ = }}{V_phi }{n_phi } times {V_psi }{n_psi } $$
(29)



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-272-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
裂缝水平集函数速度分量示意图



Figure
5.
Velocity component of crack level set function



下载:
全尺寸图片
幻灯片


裂缝水平集更新步骤主要如下:

(1) 对裂尖水平集进行初值化, 使其满足以下方程







$$ frac{{partial psi }}{{partial t}}{text{ + }}{V_psi }left| {nabla psi }
ight|{text{ = }}0 qquadqquad$$
(30)







$$ frac{{partial psi }}{{partial tau }}{text{ + sign}}left( psi
ight)left( {left| {nabla psi }
ight| - 1}
ight){text{ = }}0 $$
(31)

(2) 定义裂缝的初始扩展速度, 即式(32), 本文θ取值45°, R取值0.005 m[42], 再将1维的速度场扩展到3维的水平集子域, 进行正交延展, 即式(33)所示







$$ left. begin{gathered}{V_phi } = frac{1}{{Delta t}}2R sin Delta theta sin Delta theta ;; {V_psi } = frac{1}{{Delta t}}2R sin Delta theta cos Delta theta ;;end{gathered}
ight} $$
(32)







$$ left. begin{gathered}nabla {V_psi } cdot nabla psi {text{ = }}0 ;; nabla {V_psi } cdot nabla phi {text{ = }}0 ;; nabla {V_phi } cdot nabla phi {text{ = }}0 ;; nabla {V_phi } cdot nabla psi {text{ = }}0 ;; end{gathered}
ight}qquadqquad $$
(33)

根据Peng[43]的方法, 采用Hamilton–Jacobi方程对上述方程进行稳态求解, 使其满足方程式(34), 计算表达式为







$$ left. begin{gathered}frac{{partial {V_psi }}}{{partial tau }}{text{ + sign}}left( psi
ight)frac{{nabla psi }}{{left| {nabla psi }
ight|}} cdot nabla {V_psi }{text{ = }}0 ;; frac{{partial {V_psi }}}{{partial tau }}{text{ + sign}}left( phi
ight)frac{{nabla phi }}{{left| {nabla phi }
ight|}} cdot nabla {V_psi }{text{ = }}0 ;; frac{{partial {V_phi }}}{{partial tau }}{text{ + sign}}left( phi
ight)frac{{nabla phi }}{{left| {nabla phi }
ight|}} cdot nabla {V_phi }{text{ = }}0 ;; frac{{partial {V_phi }}}{{partial tau }}{text{ + sign}}left( psi
ight)frac{{nabla psi }}{{left| {nabla psi }
ight|}} cdot nabla {V_phi }{text{ = }}0 ;; end{gathered}
ight} $$
(34)

(3) 修正速度分量中裂纹面水平集的速度, 修正目的是保证裂缝面内($ psi < 0 $)的$ {overline V _phi } $为0, 使已生成裂缝不受水平集更新影响, 保证裂纹前缘平滑[44], 其中$ Hleft( psi
ight) $为阶跃函数, 修正方程为







$$ {overline V _phi } = Hleft( psi
ight)frac{{{V_phi }psi }}{{{V_psi }Delta t}}qquad;; $$
(35)







$$ Hleft( psi
ight){text{ = }}left{ begin{gathered}1,begin{array}{*{20}{c}}{}&{psi > 0} end{array} hfill 0,begin{array}{*{20}{c}}{}&{{
m{else}}} end{array} hfill end{gathered}
ight. $$
(36)

(4) 采用修正后的速度, 更新裂纹面水平集函数, 再对裂纹面水平集函数进行重初值化, 即







$$ frac{{partial phi }}{{partial t}}{text{ + }}{bar V_phi }left| {nabla phi }
ight|{text{ = }}0 $$
(37)







$$ frac{{partial phi }}{{partial tau }}{text{ + sign}}left( phi
ight)left( {left| {nabla phi }
ight| - 1}
ight){text{ = }}0 $$
(38)

(5) 更新裂尖水平集函数, 使其满足以下条件







$$ frac{{partial psi }}{{partial t}}{text{ + }}{V_psi }left| {nabla psi }
ight|{text{ = }}0 $$
(39)

(6) 对水平集函数进行正交化, 使其满足$ nabla phi cdot nabla psi {text{ = }}0 $, 并进行再初值化处理, 然而循环至第(2)步, 即







$$ frac{{partial psi }}{{partial tau }}{text{ + sign}}left( phi
ight)frac{{nabla phi }}{{left| {nabla phi }
ight|}} cdot nabla psi {text{ = }}0 $$
(40)







$$ frac{{partial psi }}{{partial tau }}{text{ + sign}}left( psi
ight)left( {left| {nabla psi }
ight| - 1}
ight){text{ = }}0 $$
(41)


3.
应用算例



3.1
双切口混凝土受剪拉作用开裂试验


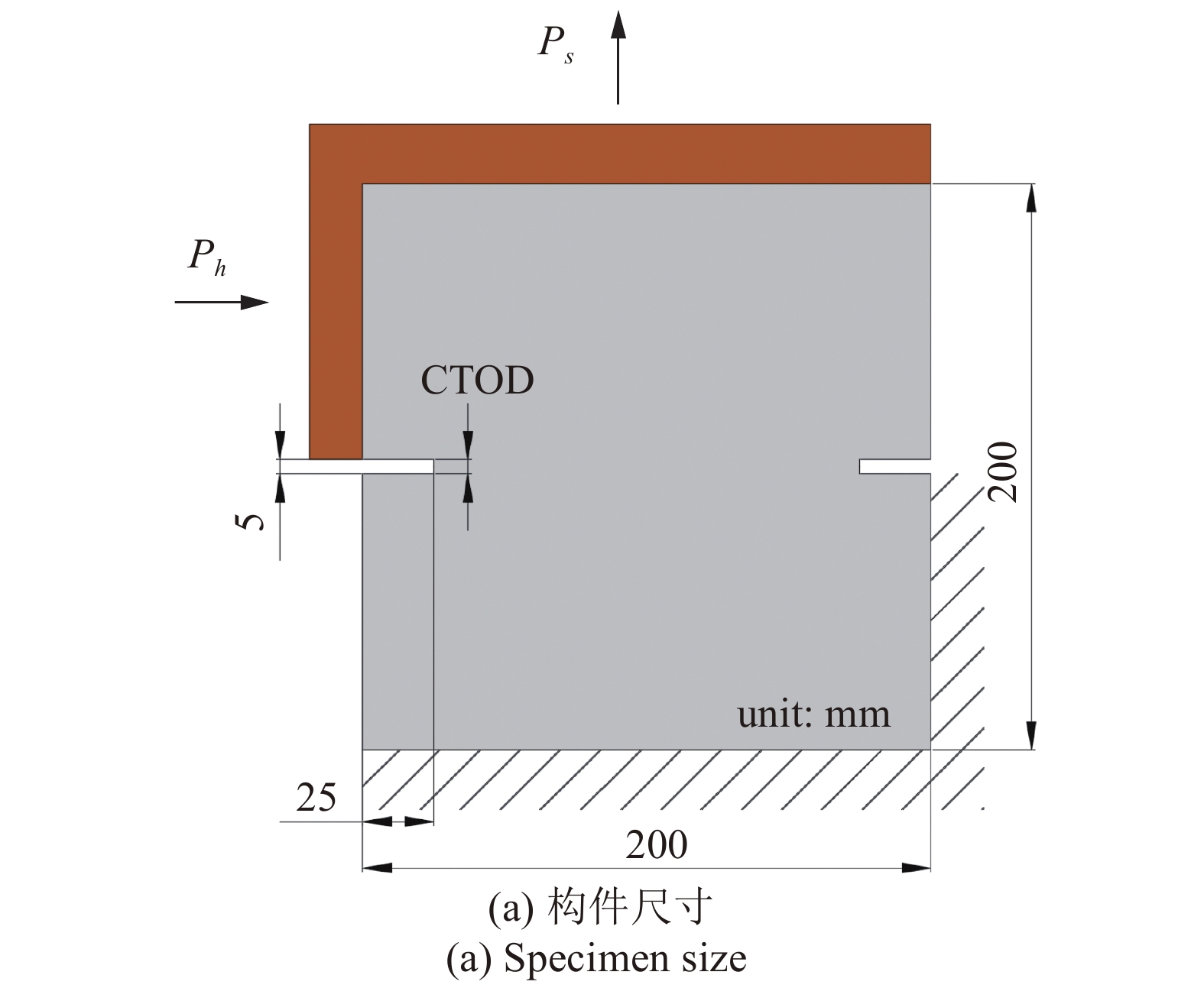
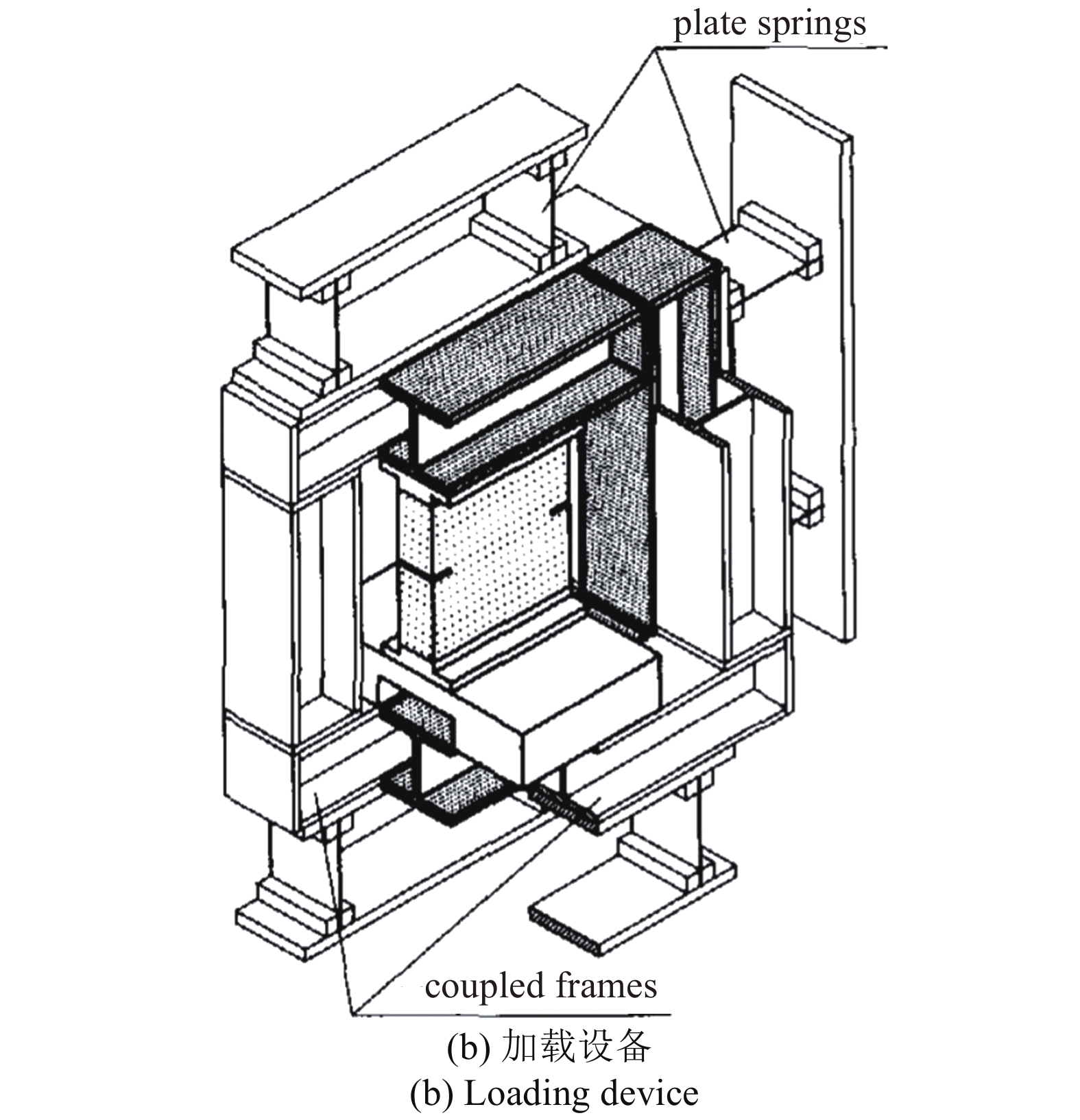
基于Nooru-Mohamed[45]的试验, 对比分析不同方法得出的混凝土受剪拉作用下的开裂情况. 如图6(a)所示, 混凝土试件的长度和高度均为200 mm, 厚度为50 mm, 切口位于混凝土两侧中心, 切口深度均为25 mm, 宽度为5 mm, 混凝土的强度为C30, 混凝土底部和右下侧部固定约束, 左上侧和顶部与钢框架连接, 加载钢框架的长度为220 mm, 宽度为120 mm, 如图6(b)所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-272-6-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-272-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
双切口混凝土受剪拉开裂试验[45]



Figure
6.
Shear tensile cracking test of concrete contained double notched[45]



下载:
全尺寸图片
幻灯片


试验时先在混凝土侧部施加水平力Ph分别到5 kN, 10 kN, 27.5 kN, 然后在顶端施加拉伸力Ps, 试验时在切口位置安装了位移计测试了位移变化情况, 即CTOD, 型号为WPS拉绳式位移计, 测试精度为0.01 mm.


3.2
裂缝分布对比


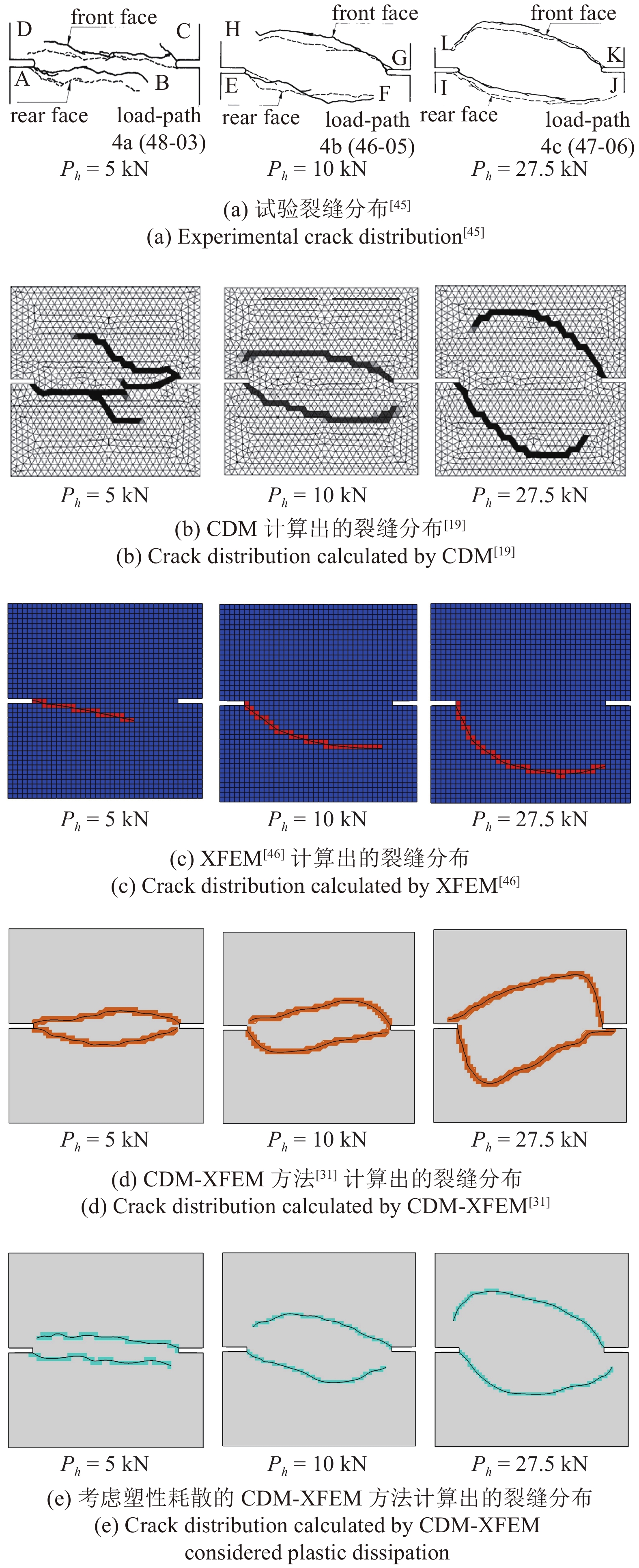
图7为试验及不同计算方法得出的裂缝分布对比图, 其中各种计算方法采用的最小网格尺寸为4 mm, 可看出采用CDM方法计算得出的裂缝形态在Ph = 5 kN时出现了分叉裂缝, 与试验差别较大, 且裂缝后期的走向还受到网格依耐的影响; 采用XFEM方法计算得出的裂缝仅为一条, 且均位于左端切口附近; 采用原有的CDM-XFEM方法计算得出的裂缝条数与试验相同, 但不同载荷阶段的弯曲程度与试验差距较大, 如Ph = 27.5 kN时试验从右切口延伸出的裂缝的拐点位于50 mm的位置, 但模拟得出裂缝的拐点却位于150 mm的位置. 采用考虑塑性耗散的CDM-XFEM方法计算得出的裂缝条数及走向与试验均较为接近, 虽然裂缝的弯曲程度与试验有部分差异, 但整体发展趋势一致. 以切口部位为中轴线, 裂缝距中轴线的最大垂直距离为H, 当Ph加载到27.5 kN时, 试验、CDM方法、XFEM方法、既有的CDM-XFEM方法、考虑塑性耗散的CDM-XFEM方法算出的H值分别为46.5 mm, 76.5 mm, 69.3 mm, 58.2 mm, 48.2 mm, 由此可知, 采用考虑塑性耗散CDM-XFEM计算出的混凝土裂缝形态与试验差异最小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-272-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
试验与各种方法算出的裂缝分布对比



Figure
7.
Comparison of crack distribution calculated by various methods and experiment



下载:
全尺寸图片
幻灯片


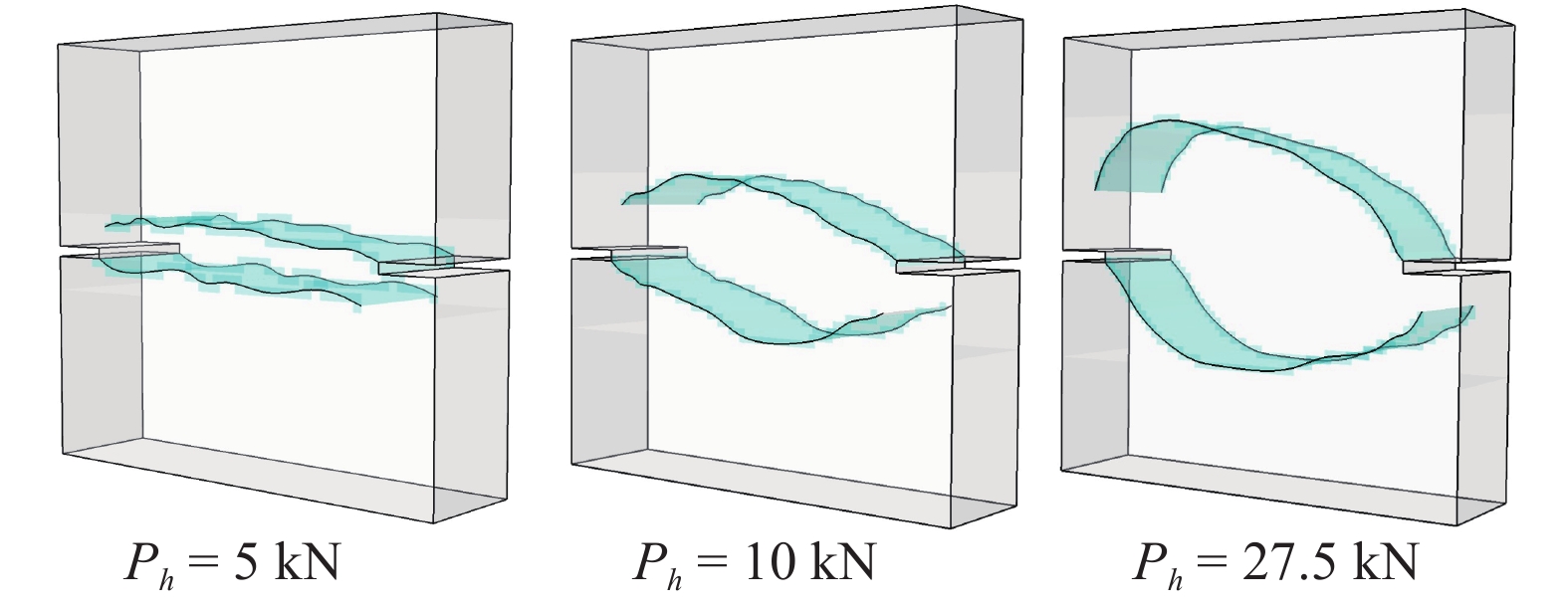
图8为考虑混凝土塑性耗散的CDM-XFEM方法算出的不同载荷下的三维裂缝面云图, 对比图7(a)可知, 数值计算出的裂缝形态在混凝土前部和后部的裂缝走向相同, 而试验的前部和后部的裂缝走向略有差异, 这是由于混凝土的开裂形态还受到内部骨料分布、骨料形态及ITZ界面力学性能等因素的影响[47-49].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-272-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
考虑塑性耗散的CDM-XFEM计算出的三维裂缝分布云图



Figure
8.
3D crack distribution calculated by CDM-XFEM considered plastic dissipation



下载:
全尺寸图片
幻灯片



3.3
拉力与切口位移关系曲线对比


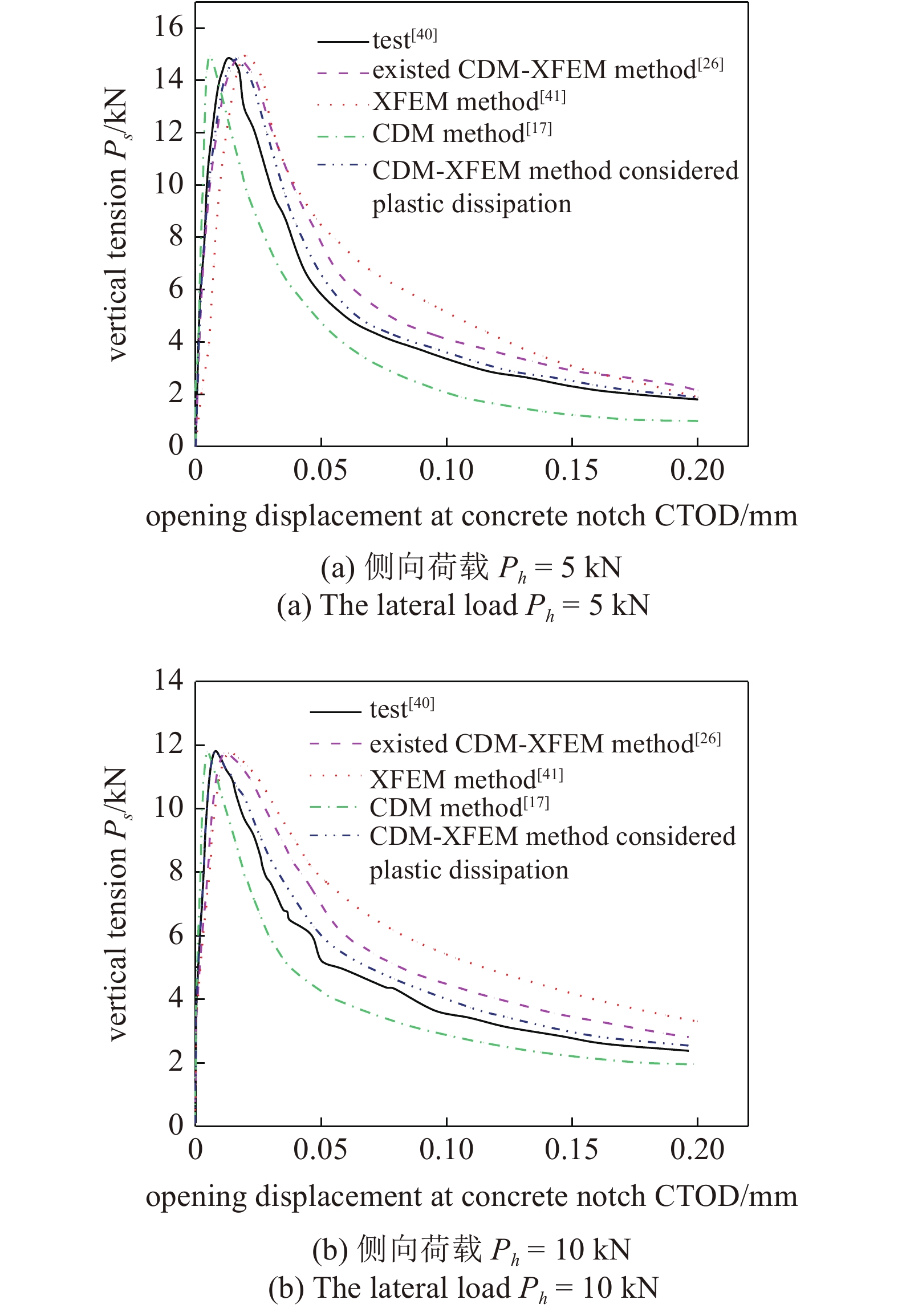
图9为侧向载荷Ph为5 kN和10 kN时, 试验与数值计算得出的混凝土切口处张开位移CTOD与竖向拉力Ps的关系曲线, 由图可知, 试验曲线出现拐点的位移分别为15 kN和12 kN, 采用CDM方法计算出的初始刚度大于试验数据, 而采用XFEM方法计算出的初始刚度远大于试验数据, 在后续的软化阶段, CDM或XFEM方法计算出的曲线均与试验差异较大, 原有的CDM-XFEM方法计算出的曲线虽然与试验走向基本一致, 但在软化阶段与试验的吻合程度不如考虑塑性耗散的CDM-XFEM方法计算的曲线. 在整个加载过程中, 试验与CDM方法、XFEM方法、原有的CDM-XFEM方法、考虑塑性耗散的CDM-XFEM方法计算得出的最大位移差值占比分别为26%, 20%, 14%, 8%, 说明采用考虑塑性耗散的CDM-XFEM方法分析混凝土的开裂规律是合理可行的.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-272-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
试验与各种方法算出的拉力-张开位移曲线对比



Figure
9.
Comparison of the tension-open displacement curves obtained by experiment and various calculation methods



下载:
全尺寸图片
幻灯片



4.
结 论


本文通过考虑能量转化时的塑性耗散, 选取裂缝的牵引?分离函数模式, 重新构建了能量转化方程, 最终提出了考虑混凝土塑性耗散的CDM-XFEM裂缝计算方法. 通过与双切口混凝土受剪拉开裂试验进行对比分析, 结果表明:

(1) 采用考虑塑性耗散的CDM-XFEM计算方法能有效模拟混凝土的开裂过程, 与其他计算方法相比, 在裂缝形态方面与试验差异最小;

(2) CDM和XFEM方法计算出的拉力-张开位移曲线均与试验差异较大, 原有的CDM-XFEM方法计算出的曲线虽然与试验走向基本一致, 但在软化阶段与试验的吻合程度不如考虑塑性耗散的CDM-XFEM方法. 说明采用考虑塑性耗散的CDM-XFEM方法分析混凝土的受力开裂是合理可行的.

相关话题/混凝土 计算 塑性 过程 图片
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 椭球颗粒体系剪切过程中自由体积的分布与演化
    引言颗粒物质是由大量离散固体相互作用而形成的复杂体系,在自然界和工业界广泛存在.以水利和岩土工程中的堆石体为例,由于取材方便,且对地形、地质条件有较强的适应性,在堆石坝、路堤、机场高填方地基等工程建设中得到广泛应用.这些工程一旦出现问题和隐患,将会严重威胁人民生命财产安全,因此迫切需要深入研究颗粒材 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 一种新的玻尔兹曼方程可计算模型构造与分析
    引言近年来,随着对临近空间战略意义认识的加深,各航空航天大国发展了众多临近空间飞行器.为满足长航时、大载荷、高超声速巡航等需求,这类临近空间飞行器通常整体尺寸较大,各部件间差异显著,飞行过程会出现多物理多场耦合、多流区共存的多尺度复杂流动现象,传统的数值模拟方法如基于宏观连续介质假设的纳维?斯托克斯 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 页岩凝析气藏相平衡的快速准确计算方法
    引言随着以煤炭、石油和木柴为代表的传统能源消耗带来的巨量的空气污染日益引起全社会的关注,天然气作为一种相对较为清洁的能源得到了广泛的重视[1].近年来在非常规油气藏勘探和开发技术上的迅猛发展,使得具有巨大潜在储量但一直得不到有效开发的以页岩气为代表的非常规油气资源成为了投资热点和研究焦点[2].中国 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于Darcy-Stokes耦合模型的多孔介质颗粒悬浮液等效黏性系数计算
    引言颗粒悬浮液广泛存在于自然界及工程应用领域,其黏性特征对悬浮液的流动行为有着重要的影响[1-4].早在1905年,Einstein[5]就研究了低浓度条件下球形固体颗粒对流体黏性的影响,给出了悬浮液等效黏度系数计算的一个强有力的理论框架,并得到了低浓度球形颗粒悬浮液的著名的Einstein黏性公式 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于主应变场的混凝土全表面开裂特征实时测量与分析
    引言混凝土结构服役过程中产生裂纹是不可避免的,而裂纹的扩展是混凝土结构承载能力、耐久性及防水性降低的主要原因.在实验室测试新型混凝土结构或混凝土材料时,测量裂纹发展过程对于揭示混凝土结构的破坏机理、评价混凝土结构的力学性能十分重要[1].目前在实验室检测混凝土表观裂纹仍以传统的人工方法为主,用马克笔 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • DVC中内部散斑质量评价及计算体素点的优化选择
    引言数字体图像相关方法(digitalvolumecorrelation,DVC)是二维数字图像相关方法(two-dimensionaldigitalimagecorrelation,2DDIC)在三维体图像上的拓展.通过比较体成像设备获取的被测试样变形前后数字体图像,该方法可测量物体内部三维全场变 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于人工弹簧模型的周期结构带隙计算方法研究1)
    冯青松*,杨舟*,郭文杰,*,2),陆建飞&,梁玉雄**华东交通大学铁路环境振动与噪声教育部工程研究中心,南昌330013&江苏大学土木工程与力学学院,江苏镇江212013RESEARCHONBANDGAPCALCULATIONMETHODOFPERIODICSTRU ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 自由场空泡溃灭过程能量转化机制研究1)
    韩磊,张敏弟,2),黄国豪,黄彪,3)北京理工大学,北京100081ENERGYTRANSFORMATIONMECHANISMOFAGASBUBBLECOLLAPSEINTHEFREE-FIELD1)HanLei,ZhangMindi,2),HuangGuohao,HuangBiao,3)Beiji ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于统一相场理论的早龄期混凝土化-热-力多场耦合裂缝模拟与抗裂性能预测1)
    吴建营,*,?,2),陈万昕?,黄羽立***华南理工大学亚热带建筑科学国家重点实验室,广州510641?华南理工大学土木工程系,广州510641**清华大学土木工程系,北京100084COMPUTATIONALMODELINGOFSHRINKAGEINDUCEDCRACKINGINEARLY-AGE ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.