引言

混凝土结构服役过程中产生裂纹是不可避免的, 而裂纹的扩展是混凝土结构承载能力、耐久性及防水性降低的主要原因. 在实验室测试新型混凝土结构或混凝土材料时, 测量裂纹发展过程对于揭示混凝土结构的破坏机理、评价混凝土结构的力学性能十分重要^[1]. 目前在实验室检测混凝土表观裂纹仍以传统的人工方法为主, 用马克笔在混凝土表面绘制裂纹的大致走向. 在测量混凝土裂纹的宽度时, 主要使用基于光学显微原理的裂纹测宽仪, 其测量精度较高, 但也只能得到裂纹某一点处的宽度.

近年来, 基于数字图像处理的表观裂纹测量方法得到了长足的发展. 相比于人工观察等传统方法, 基于图像的裂纹测量方法的效率大大提高, 其利用单幅图像中裂纹不同于背景的灰度特征, 将裂纹以整像素精度分割, 从而定位裂纹在图像中的位置. 基于空间域的裂纹识别算法利用阈值分割、边缘检测^[2]、裂纹种子识别^[3]等方法和思想测量裂纹; 基于频率域的裂纹识别算法利用小波变换^[4]、Beamlet变换^[5]、Contourlet变换^[6]等工具识别裂纹; 基于神经网络的裂纹识别算法在近年来得到了****的广泛关注^[7], 与传统的数字图像测量算法相比, 基于神经网络的算法在识别准确率方面有所提高. Ni等^[8]使用基于多尺度特征融合网络实现了对裂纹的整像素分割; Zou等^[9]基于SegNet网络提出了深度卷积神经网络 DeepCrack, 实现了复杂背景下的裂纹识别; Cha等^[10]利用卷积神经网络识别裂纹. 但是此方法一般需要用大量数据进行训练、监督学习, 计算成本较高. 基于图像的裂纹测量方法主要用于检测已开裂的桥梁、路面、房屋等建筑表观的裂纹, 可以识别出整像素的裂纹. 但受限于相机的视场和分辨率, 在测量微裂纹、尤其是成像不足一个像素的裂纹时, 基于数字图像的测量方法无法精确定位微裂纹并测量其宽度, 故而难以用于测量实验室中混凝土结构受载变形早期的裂纹扩展. 此外, 当被测物体表面过于灰暗或干扰较多时, 会对裂纹的准确识别造成很大影响, 基于图像本身的裂纹测量方法无法满足高精度的测量需求.

与上述基于图像本身的裂纹检测方法不同, 本文首先利用多相机数字图像相关方法(digital image correlation, DIC) 得到构件在载荷下丰富的全场变形数据, 再对变形场进行处理得到裂纹的信息. DIC自20世纪80年代初由美国的 Peters和Ranson^[11]和日本的Yamaguchi^[12]相互独立提出以来, 经过数十年的发展^[13-14], 以其非接触、无损、全场测量、精度较高的优点, 在土木工程、生物医学工程、材料科学等领域受到广泛关注^[15-17]. 文献[18-20]将DIC用于测量岩石、混凝土等材料的断裂过程, 但未能定量地得到完整的裂纹位置与宽度等信息. 本文进一步研究DIC在裂纹测量中的应用, 发现在试件变形并开裂的过程中, 裂纹附近的位移场出现较大梯度, 这导致基于位移场得到的主应变云图中开裂处的虚应变很大, 明显区别于未开裂处. 由于DIC在计算应变时的窗口作用, 裂纹法向的主应变场呈高斯分布的形式. 受用于提取激光条纹中心线的Steger算法^[21-23]的启发, 对主应变场进行处理以期实现对裂纹的定位, 用3次样条曲线拟合得到裂纹中心骨架. 根据裂纹中心骨架, 将裂纹两侧位于法线上点的张开位移向量之差做处理得到不同类型裂纹的宽度, 并基于高精度平移台设计模拟裂纹扩展的实验以验证裂纹宽度的测量精度. 本文基于DIC计算所得的裂纹处主应变场的特征, 结合Steger算法, 提出了一种全自动、实时裂纹扩展测量与分析方法, 为混凝土实验提供了一种可靠、精确的测量手段.

1.
研究方法

1.1
基于主应变场的裂纹检测

在三维DIC 中, 为了计算应变张量, 首先要建立局部坐标系. 使用计算点周围$(2M + 1) times (2M + 1)$个均匀分布的数据点拟合一个局部平面. 根据局部平面方程可以确定该局部平面的法向量, 再用世界坐标系的${X_{
m{W}}}$轴向局部平面投影即可确定局部平面的X轴. 最后将局部平面的法向量定为Z轴, 那么根据直角坐标系的关系可以确定Y轴. 确定了局部坐标系之后, 将三维位移从世界坐标系转换到局部坐标系中, 最后对转换过的平面位移进行差分求解应变, 或对平面位移用局部最小二乘方法以多项式拟合, 并用拟合系数表示应变^[24]. 当被测物体表面由于开裂使位移场出现梯度时, 开裂处的主虚应变会非常大, 明显区别于未开裂处. 如果能利用主应变场中的这种由于开裂而产生的特征, 就能实现裂缝的全场定位.

本文对计算点周围$7 times 7$的应变计算窗口以二维一次多项式拟合位移场, 位移场的形式为

$$u(x,y) = {a_0} + {a_1}x + {a_2}y$$

(1)

$$v(x,y) = {b_0} + {b_1}x + {b_2}y$$

(2)

其中, ${a_0}$, ${a_1}$, ${a_2}$, ${b_0}$, ${b_1}$和${b_2}$为拟合系数, (x, y)为窗口内某点的局部坐标, u, v分别为水平和竖直方向的位移分量, 用最小二乘法得到应变窗口的拟合公式. 根据弹性力学理论计算应变, 拉格朗日?格林应变分量的形式如式(3) ~ 式(5)所示. 得到某一点各方向的应变分量之后, 求其特征值和特征向量即可得到主应变场和各点主应变方向

$$begin{split}& {E_{xx}} = frac{{partial u}}{{partial x}} + frac{1}{2}left[ {{{left(frac{{partial u}}{{partial x}} ight)}^2} + {{left(frac{{partial v}}{{partial x}} ight)}^2}} ight] = &qquad {a_1} + frac{1}{2}left({a_1}^2 + {b_1}^2 ight) end{split}qquadqquad $$

(3)

$$begin{split}& {E_{yy}} = frac{{partial v}}{{partial y}} + frac{1}{2}left[ {{{left(frac{{partial u}}{{partial y}} ight)}^2} + {{left(frac{{partial v}}{{partial y}} ight)}^2}} ight] = &qquad{b_2} + frac{1}{2}left({a_2}^2 + {b_2}^2 ight) end{split} qquadqquad$$

(4)

$$begin{split}& {E_{xy}} = frac{1}{2}left(frac{{partial u}}{{partial x}} + frac{{partial v}}{{partial y}} ight) + frac{1}{2}left(frac{{partial u}}{{partial x}}frac{{partial u}}{{partial y}} + frac{{partial v}}{{partial x}}frac{{partial v}}{{partial y}} ight) = &qquad frac{1}{2}left({a_2} + {b_1} ight) + frac{1}{2}left({a_1}{a_2} + {b_1}{b_2} ight) end{split} $$

(5)

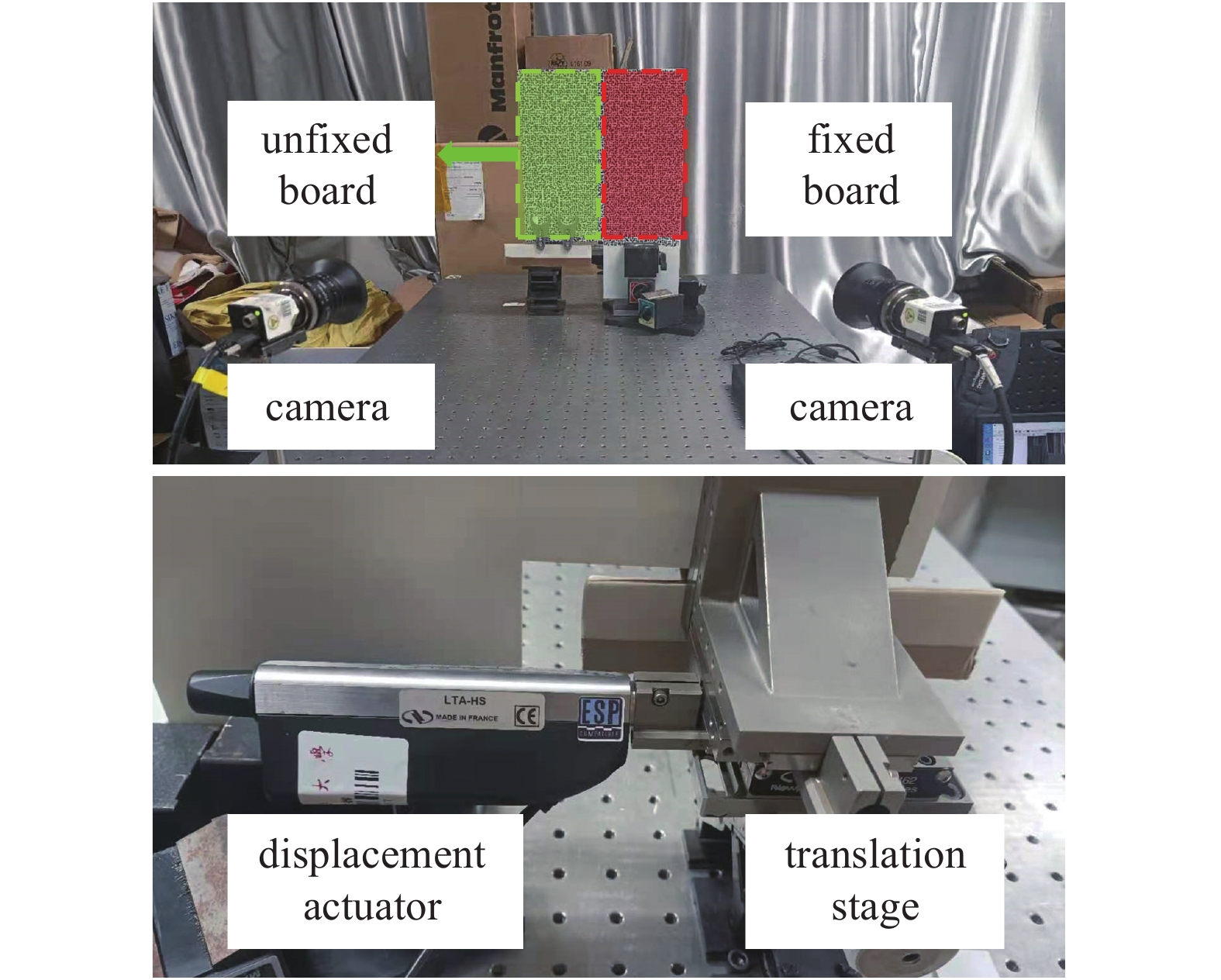
为了更直观地了解裂纹附近变形场的分布规律, 设计了模拟裂纹扩展的实验. 如图1所示, 在两块玻璃板的表面贴上优化的水转印数字散斑, 其中右侧的玻璃板固定在桌面不动, 左侧玻璃板固定在三轴平移台上, 平移台水平方向由型号为LTA-HS的高精度电动促动器驱动, 竖直方向和离面方向固定. 双目相机分辨率为2048 × 2048, 视场0.55 m × 0.55 m, 立体角${25^ circ }$, 物面比例为3.706像素每毫米. 驱动器驱动左侧玻璃板向左移动与右侧玻璃板分开, 模拟裂纹扩展过程. 每次步进5 μm, 步进10次. 标定相机并采集玻璃板移动前后的图像, 进行DIC分析.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-107-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
裂纹扩展模拟实验



Figure
1.
Simulation experiment of crack propagation



下载:
全尺寸图片
幻灯片


图2为左侧玻璃板分别平移不同距离时, 整体的变形场云图和实现裂缝定位的过程. 其中, DIC计算模板为21 × 21, 步长为3, 应变模板为7 × 7. 如图2中主应变场E1所示, 平板移动0.037像素、0.111像素、0.185像素时, 开裂处的虚应变随着裂纹的扩展而不断增大, 明显区别于未开裂处, 可以定性地表示裂纹的位置和大小. 但当平板移动0.019像素时, 由于移动太小, 应变噪声的干扰很大, 从图2中可以看出此时主应变场无法定性地表示完整的裂纹.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-107-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
基于主应变场的裂纹定位



Figure
2.
Crack location based on principal strain field



下载:
全尺寸图片
幻灯片


本实验中, DIC计算所得的主应变静态噪声标准差为2.5 × 10^?4, 平均值2.2 × 10^?4. 参考仪器检出限的定义, 检出限对应的响应值至少为噪声标准差的3 ~ 5倍. 且本文主要检测混凝土材料表面的裂纹, 其抗拉极限非常小. 考虑以上因素, 设置1.0 × 10^?3为应变阈值, 高于此阈值的主应变才被认为是由于开裂产生的, 使用阈值法去噪之后的主应变场进行下一步分析, 去噪后的主应变场如图2中E1′所示. 本实验中开始检测到完整的最小裂纹宽度为0.037像素.

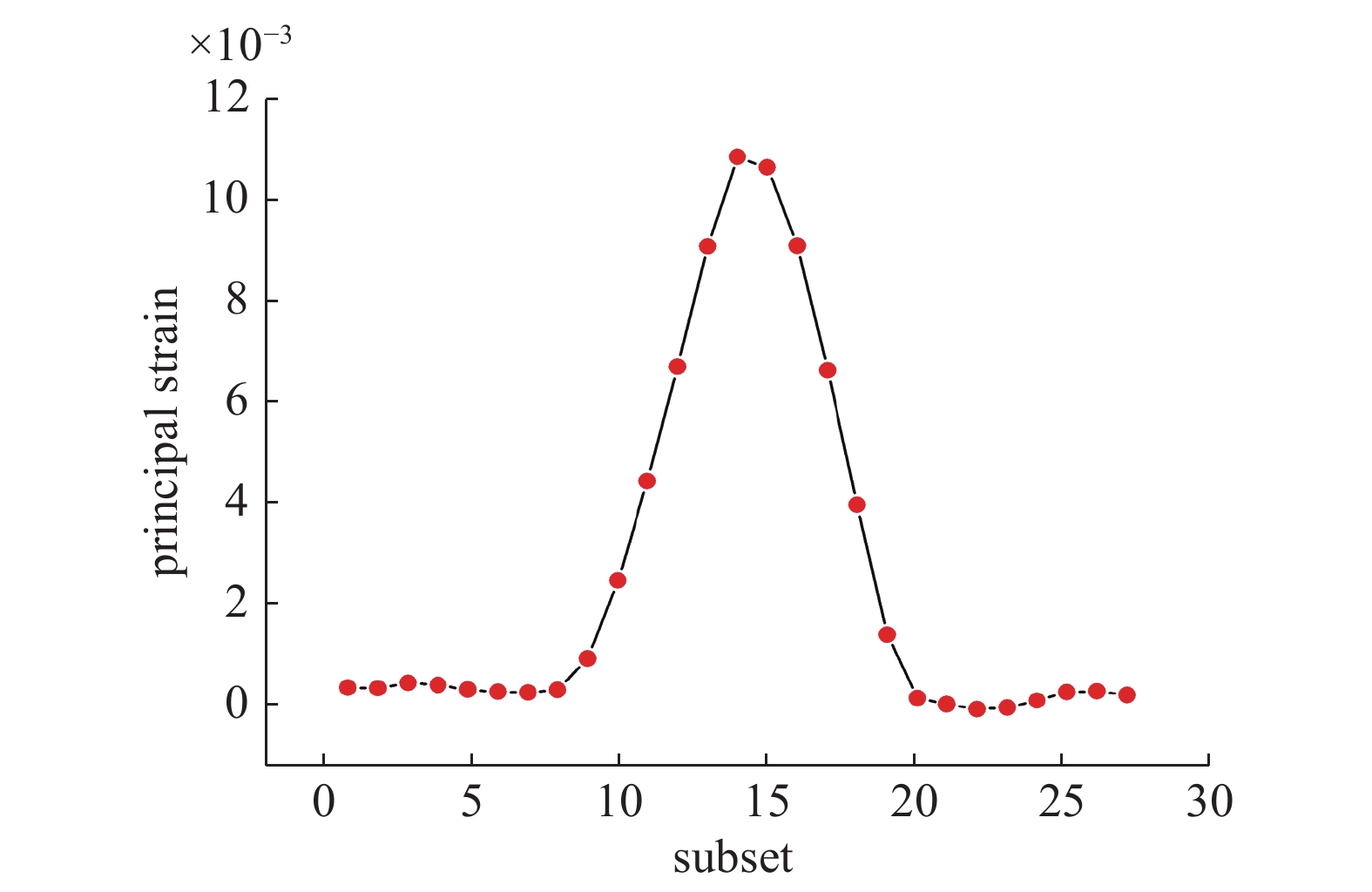
由于在计算应变时的窗口作用, 裂纹法线方向附近的虚应变分布类似高斯分布, 图3所示为平板移动0.185像素时, 裂纹附近水平方向的主应变分布, 这与激光条纹的灰度分布十分相似. 因此, 本文借鉴在激光条纹中心线定位中广泛采用的Steger算法, 对主应变场进行处理实现裂纹定位.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-107-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
裂纹法线方向附近主应变场分布



Figure
3.
Distribution of principal strain field around crack in normal direction



下载:
全尺寸图片
幻灯片


在Steger算法中, 高斯函数的均方差$sigma $是一个重要参数, 与最终的识别效果密切相关. $sigma $值越大图像平滑效果越好, 但若其过大会造成光条纹图像模糊虚化. $sigma $值的选取与光条的宽度密切相关, 文献[25]指出当光条宽度为$w$时, $sigma $的取值范围应为$sigma geqslant w/sqrt 3 $, 本文取$sigma = w/sqrt 3 $.

本文给出了估算主应变条纹宽度的方法. 若DIC计算时选择的模板宽度为${M_1}$, 步长为N, 约定ceil()为向正无穷方向取整, 考虑一维情况, 那么将裂纹包含在内的子区个数约为${
m{ceil}}({M_1}/N)$, 计算这些子区的位移时会受裂纹影响. 求出每个子区的位移后, 用${M_2} times {M_2}$大小的应变计算模板拟合位移场, 那么应变受到裂纹影响的点的个数为${M_2}{
m{ + ceil}}({M_1}/N)$. 以本文模拟裂纹扩展实验为例, 若模板大小取$21 times 21$, 步长为3, 应变模板为$7 times 7$, 估算主应变场光条宽度约为14. 图3中可以得到主应变值在1.0 × 10^?3以上的点共11个, 即条纹宽度为11, 与估计基本吻合.

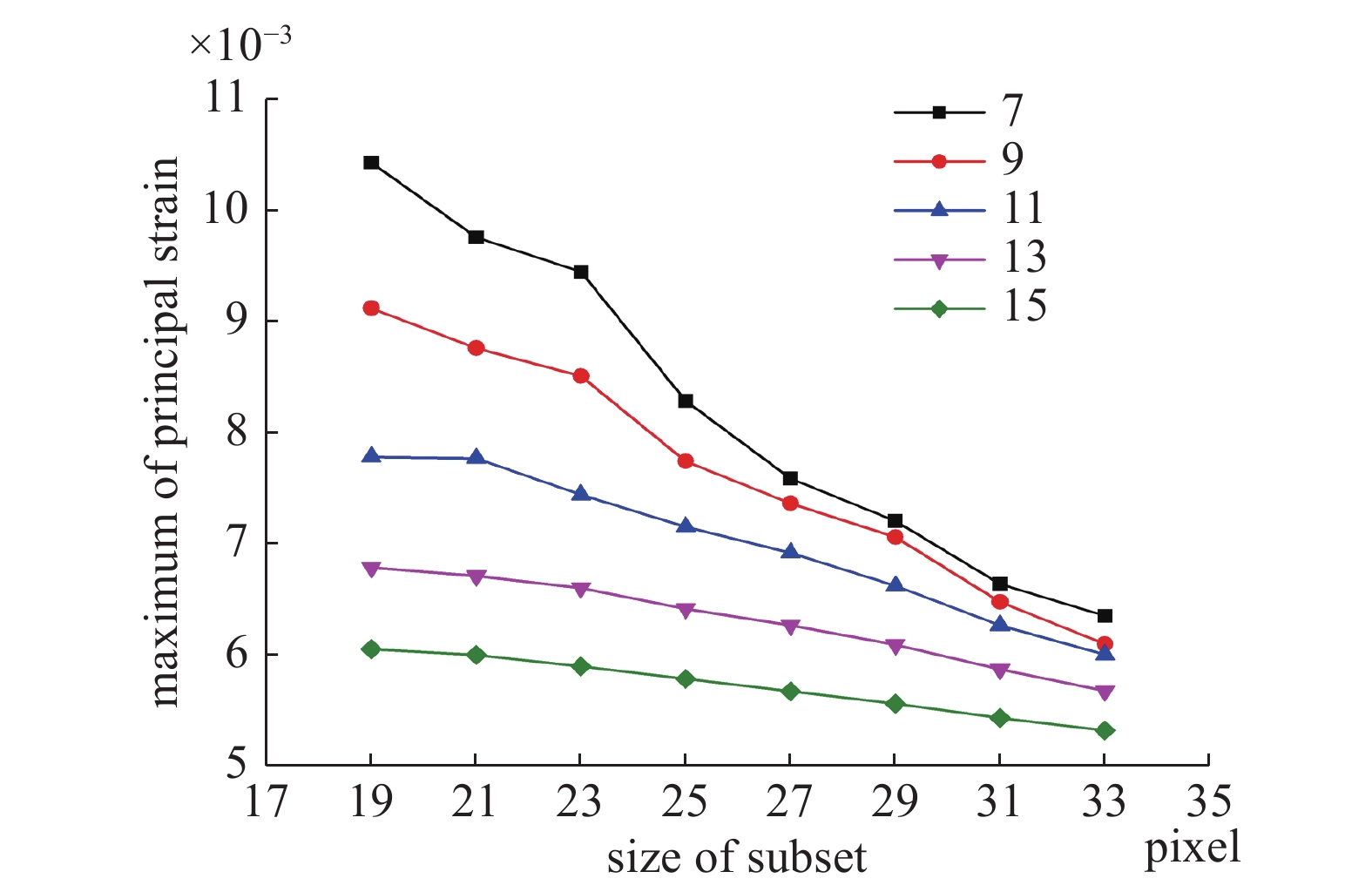
DIC应变计算结果依赖于子区大小的选择和应变计算窗口, 为研究裂纹附近主应变场的分布与子区大小和应变计算窗口的关系, 分别选用不同大小的子区和应变计算窗口来计算裂纹宽度为0.185像素时的主应变场. 随机选择20个裂纹上的点, 找出此点附近位于裂纹法线方向上的最大主应变值, 并取平均以减小随机误差, 结果如图4所示, 不同颜色的线表示选择不同的应变计算窗口. 当选择相同大小的子区时, 最大主应变随着应变计算窗口的增大而降低; 当选择相同大小的应变计算窗口时, 最大主应变随着模板的增大而降低. 这说明模板和子区的增大会对主应变场起平滑作用. 对于优化的数字散斑场, 选择文献中推荐的模板21 × 21^[26]. 考虑计算效率和裂纹上点的密度, 选择步长为3, 即大约每隔3个像素计算一个裂纹上的点. 在选择应变计算模板时, 希望能够使裂纹处的最大主应变尽可能大以区别于未开裂处, 所以应选择较小的应变计算模板, 本文选择应变模板为7 × 7. 同时, 如前文所述主应变场条纹宽度的估计值为${M_2}{
m{ + ceil}}({M_1}/N)$, 如果子区大小和应变计算窗口过大, 会使主应变场条纹宽度过大, 当有两条裂纹距离较近时, 会影响裂纹识别的效果.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-107-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
子区大小、应变窗口对最大主应变值的影响



Figure
4.
Influence of subset size and strain window on maximum principal strain



下载:
全尺寸图片
幻灯片


Steger算法基于Hessian矩阵, 能够实现截面处类似高斯分布的光条纹中心亚像素定位. Hessian矩阵由灰度图像与二维高斯微分核卷积得到, 二维高斯函数及其一、二阶微分, 任一点处Hessian矩阵的形式为

$$G(x,y) = frac{1}{{2{text{π}} {sigma ^2}}}{{ m{e}}^{^{ - frac{{{x^2} + {y^2}}}{{2{sigma ^2}}}}}}qquadqquadqquadqquadqquad;;$$

(6)

$${G_x} = frac{{partial G(x,y)}}{{partial x}} = - frac{x}{{2{text{π}} {sigma ^4}}}{{ m{e}}^{^{ - frac{{{x^2} + {y^2}}}{{2{sigma ^2}}}}}}qquadqquadqquadquad$$

(7)

$${G_y} = frac{{partial G(x,y)}}{{partial y}} = - frac{y}{{2{text{π}} {sigma ^4}}}{{ m{e}}^{^{ - frac{{{x^2} + {y^2}}}{{2{sigma ^2}}}}}}qquadqquadquadqquad$$

(8)

$${G_{xy}} = frac{{{partial ^2}G(x,y)}}{{partial xpartial y}} = - frac{y}{{2{text{π}} {sigma ^6}}}{{ m{e}}^{^{ - frac{{{x^2} + {y^2}}}{{2{sigma ^2}}}}}}qquadqquadqquad$$

(9)

$${G_{xx}} = frac{{{partial ^2}Gleft(x,y ight)}}{{partial {x^2}}} = - frac{1}{{2{text{π}} {sigma ^4}}}left(1 - frac{{{x^2}}}{{{sigma ^2}}} ight){{ m{e}}^{^{ - frac{{{x^2} + {y^2}}}{{2{sigma ^2}}}}}}qquad$$

(10)

$${G_{yy}} = frac{{{partial ^2}Gleft(x,y ight)}}{{partial {y^2}}} = - frac{1}{{2{text{π}} {sigma ^4}}}left(1 - frac{{{y^2}}}{{{sigma ^2}}} ight){{ m{e}}^{^{ - frac{{{x^2} + {y^2}}}{{2{sigma ^2}}}}}};;;;;;$$

(11)

$${boldsymbol{H}}(x,y) = left[ {begin{array}{*{20}{c}} {{G_{xx}}}&{{G_{xy}}} {{G_{xy}}}&{{G_{yy}}} end{array}} ight] otimes {boldsymbol{I}}(x,y) = left[ {begin{array}{*{20}{c}} {{r_{xx}}}&{{r_{xy}}} {{r_{xy}}}&{{r_{yy}}} end{array}} ight]$$

(12)

Hessian矩阵最大特征值对应的特征向量即对应于光条的法线方向, 用$({n_x},{n_y})$表示. 光条中心点的Hessian矩阵特征值相比其他位置更大, 所以可以设置阈值进行筛选. 若以点$({x_0},{y_0})$为光条中心整像素基准点, 在法线方向进行二阶泰勒展开. 二次多项式取极值时, 一阶导数过零点, 由此可得到极值点的亚像素位置. 光条中心的亚像素坐标为

$$({p_x},{p_y}) = ({x_0} + t{n_x},{y_0} + t{n_y})$$

(13)

其中

$$t = - frac{{{n_x}{r_x} + {n_y}{r_y}}}{{{n_x}^2{r_{xx}} + 2{n_x}{n_y}{r_{xy}} + {n_y}^2{r_{yy}}}}$$

(14)

为保证亚像素位置在选定的整像素基准点内, 还需满足$(t{n_x},t{n_y}) in left[ { - 0.5,0.5}
ight] times [ - 0.5,0.5]$.

算法的效果如图2裂纹定位所示. 裂纹扩展宽度为0.037像素、0.111像素和0.185像素时, 可以很好地识别裂纹.

1.2
基于位移场的裂纹宽度计算

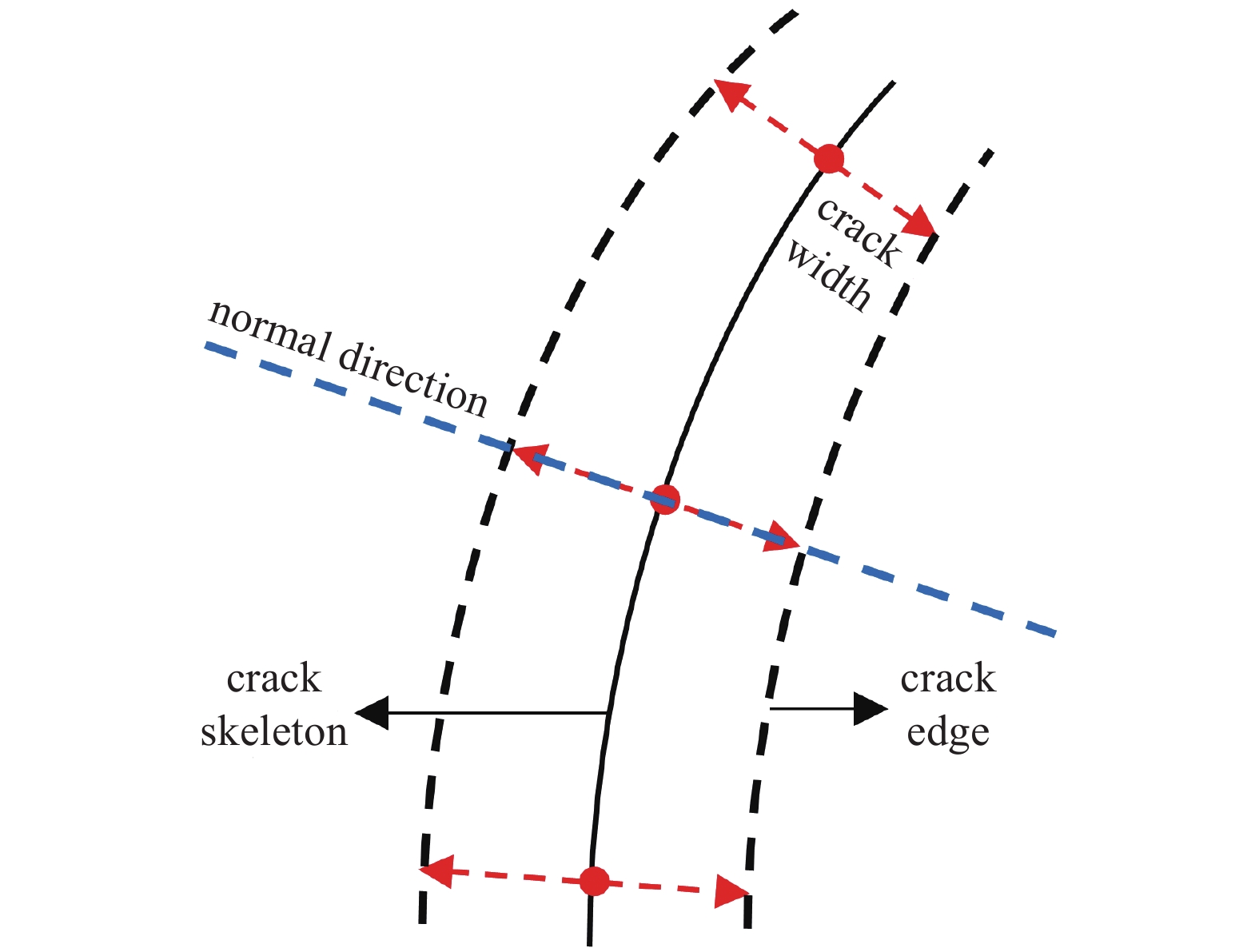
图5为模拟裂纹扩展实验中, 裂纹扩展为50 μm时某一段裂纹两侧的位移场, 位移场为每一个离散点的位移合集. 利用位移场在开裂处明显的梯度, 将裂纹法线方向上的两侧面内位移向量相减, 向量相减后沿法线方向上的投影即为Ⅰ型裂纹宽度, 沿法线垂线方向上的投影即为Ⅱ型裂纹宽度. 根据1.1节中得出的结论, 一维情况下将裂纹包含在内的子区个数约为${
m{ceil}}({M_1}/N)$. 如图5所示, 定位裂纹的中心位置后, 在法线方向远离中心位置至少${
m{ceil(}}({M_1}/N)/2)$个点开始, 取两侧$3 times 3$大小白色模板内的所有点, 求其位移分量的平均值以减小随机误差, 得到两侧的面内位移向量${{{boldsymbol{d}}_0}}$和${{{boldsymbol{d}}_1}}$, 若裂纹上此点的法线方向向量为${{boldsymbol{e}}_1}$, 垂直于法线的方向向量为${{boldsymbol{e}}_2}$, 则Ⅰ型裂纹宽度可以表示为$Delta {{{d}}}_{
m{?}}=left|({{boldsymbol{d}}_{0}}-{{boldsymbol{d}}_{1}})cdot {{boldsymbol{e}}}_{{}_{1}}
ight|$, Ⅱ型裂纹宽度可以表示为$Delta {{d}}_{
m{П}}=left|({{boldsymbol{d}}_{0}}-{{boldsymbol{d}}_{1}})cdot {{boldsymbol{e}}}_{2}
ight|$. 图6为Ⅰ型裂纹示意图, 用3次样条曲线插值出整条裂纹的中心骨架, 并在法线方向绘出每个点处裂纹的宽度, 最终得到完整的裂纹信息.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-107-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
裂纹附近位移场分布



Figure
5.
Distribution of displacement field around crack



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-107-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
裂纹示意图



Figure
6.
Diagram of crack



下载:
全尺寸图片
幻灯片

1.3
多相机三维数字图像相关

对于大尺寸混凝土梁的变形测量, 使用多相机组成的相机网络, 可以保证全场变形测量分辨率与测量精度^[27-28]. 本文使用基于外部标记的方法, 将一套双目视觉系统作为一个测量单元, 编码点作为外部标记^[29]. 利用近景摄影测量技术, 重构出物体表面的一组编码标记点的三维坐标^[30], 并将测量单元的局部坐标系统一到由编码点创建的全局坐标系中, 实现全场测量数据的拼接. 如图7所示, 双目系统A的视场为区域A, 利用相机标定和双目立体视觉原理, 重建区域A中编码点的三维坐标, 并建立局部坐标系, 从而求出整体坐标系和局部坐标系之间的转换矩阵${{boldsymbol{R}}_1}$和${{boldsymbol{T}}_1}$. 同理可以得到双目系统B相对于全局的转换矩阵, 两个区域之间无需有重合区域, 即可将外参统一.



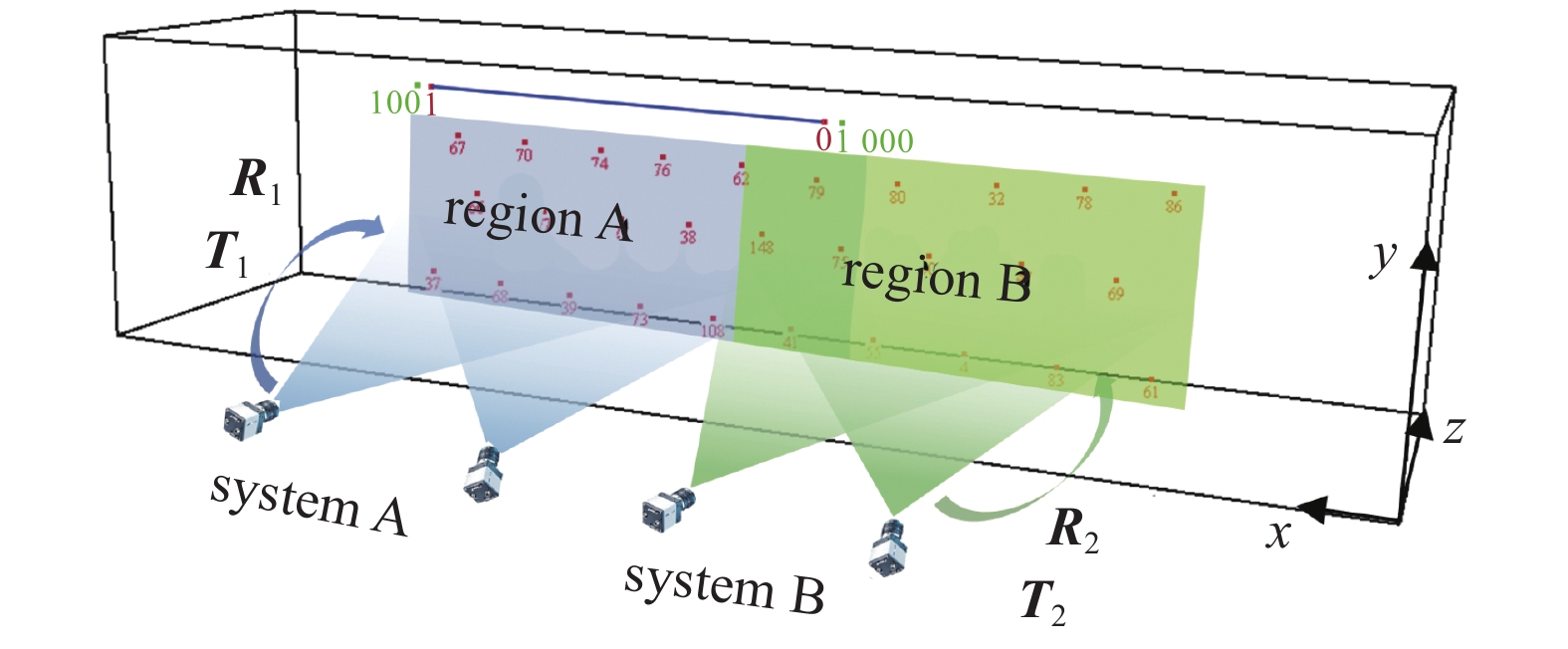onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-107-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
基于编码点的多相机外参统一



Figure
7.
Multi camera external parameters unification based on coded points



下载:
全尺寸图片
幻灯片

2.
结果与讨论

2.1
精度验证实验

在模拟裂纹扩展过程的实验中, 驱动器驱动左侧玻璃板与右侧玻璃板分开, 计算用本文所提方法测量出的裂纹宽度与实际裂纹宽度之间的误差, 评判此方法的精度. 左侧平板每次平移0.019像素, 平移10次. 进行DIC计算时, 设置模板为21 × 21, 步长为3, 应变计算窗口为7 × 7. 整条裂纹上共有233个控制点. 表1为233个控制点的平均测量宽度和测量误差、标准差, 均以像素为单位, 结果如表1所示, 发现法线裂纹的测量宽度与实际宽度基本一致.




表
1
裂纹宽度测量结果(像素)



Table
1.
Measurement results of crack (pixel)



table_type1 ">

Actual width	Measured width	Average error	Standard deviation
0.037	0.047	0.010	0.007
0.056	0.067	0.011	0.006
0.074	0.088	0.014	0.006
0.093	0.107	0.014	0.006
0.111	0.123	0.012	0.006
0.130	0.147	0.017	0.007
0.148	0.165	0.017	0.006
0.167	0.181	0.014	0.006
0.185	0.199	0.014	0.008

下载:
导出CSV
|显示表格



由于模拟裂纹开裂过程中没有滑移, 所以裂纹为Ⅰ型裂纹, 宽度可以表示为$Delta {d}_{
m{?}}=left|({{{boldsymbol{d}}}_{0}}-{{{boldsymbol{d}}}_{1}})cdot {{boldsymbol{e}}}_{{}_{1}}
ight|$. 根据误差传递理论, 可以得到宽度的测量误差为${e_{Delta d}} = left| {{e_{left| { {{{boldsymbol{d}}_0}} }
ight|}}}
ight| + left| {{e_{left| { {{{boldsymbol{d}}_1}} }
ight|}}}
ight|$. 一般认为DIC的精度为0.005 ~ 0.01像素, 因此裂纹的测量结果理论精度应为0.01 ~ 0.02像素. 表1中的实验数据表明, 在测量不同宽度的裂纹时, 本文提出的方法的测量误差在0.010 ~ 0.017像素之间, 与理论预测值相符. 测量标准差在0.006 ~ 0.008像素之间, 测量结果十分稳定.

值得注意的是, 在同等分辨率下基于数字图像的方法无法测量到裂纹的扩展. 如图8所示, 左图为白背景下玻璃板间裂纹的初始状态, 此时裂纹约占1个像素; 右图为裂纹扩展0.185像素时的裂纹图像, 与左图相比没有明显变化. 本文提出的基于DIC变形场的裂纹测量方法精度高于传统的基于数字图像本身的裂纹检测方法, 更加适用于土木工程实验中全场裂纹的精确识别与测量.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-107-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
裂纹扩展前后像素图



Figure
8.
Pixel image before and after crack propagation



下载:
全尺寸图片
幻灯片

2.2
混凝土梁抗弯实验

本文提出的方法主要利用裂纹处的虚应变明显大于未开裂处的应变这一特性, 成功实现了裂纹的检测. 但是对于一些延展性强的金属材料, 其表面应变很大时也没有裂缝出现; 或材料局部出现应力集中时, 由于应变过大, 也可能会被误认为是裂纹从而干扰测量结果. 而混凝土材料其抗拉极限很小, 考虑混凝土表面由于加载产生的应变和DIC本身的应变测量噪声, 设置1.0 × 10^?3为应变阈值, 大于此阈值的应变被认为是由于裂纹而产生的较大的虚应变. 本文提出的方法非常适合混凝土材料裂纹扩展的测量. 利用所提出的方法, 测量海水海沙?玄武岩纤维复合材料(BFRP)混凝土梁4点弯实验中梁表面的Ⅰ型裂纹扩展情况.

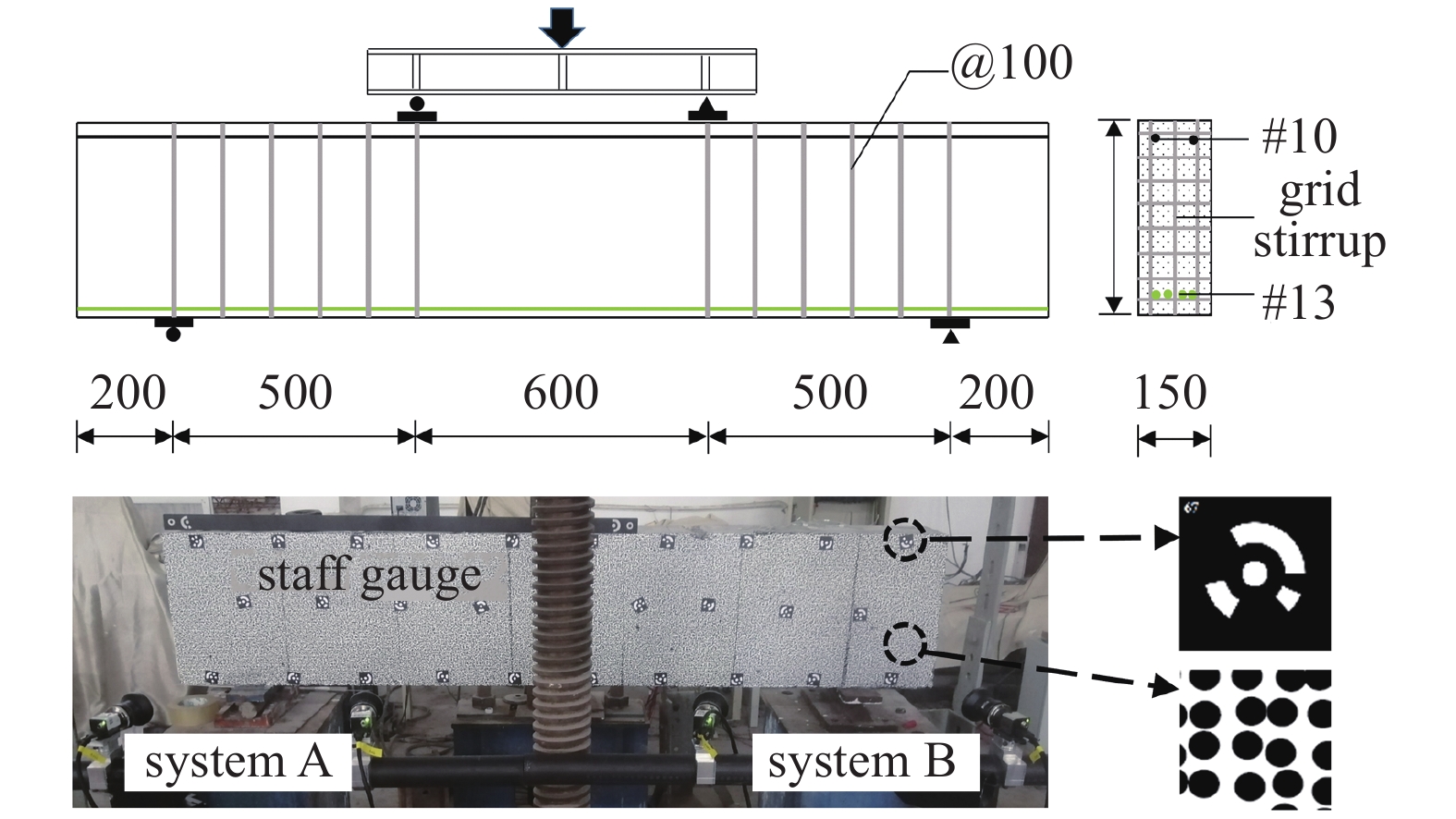
在现代建筑业中储量充足的海水海沙被认为是日益匮乏的淡水河沙最有可能的替代品, 但海水海沙中存留的氯离子会腐蚀混凝土结构中的钢筋^[31]. BFRP具有耐腐蚀、绝热等特殊性能, 不受氯离子的侵蚀, 可以取代混凝土梁中的钢筋. 为测量海水海沙?BFRP混凝土梁的承载能力, 进行4点弯加载试验. 图9中, 混凝土梁的尺寸为2000 mm × 150 mm × 400 mm, 底部放置4根直径为13 mm的玄武岩纤维增强复合材料受拉筋; 弯剪区箍筋间距为100 mm. 混凝土保护层厚度为30 mm, 受压区纵筋为两根10 mm的BFRP筋, 采用4点弯加载方式, 加载点对称布置, 弯剪段500 mm, 纯弯段600 mm. 在试件表面贴上水转印散斑, 然后按一定间隔贴编码点并放置标尺, 利用单反相机从不同角度拍摄梁表面的编码点并完成编码点坐标三维重构. 搭设两组双目系统A和B, 分别拍摄混凝土梁的左侧和右侧, 相机分辨率2048 × 2048, 搭配8 mm镜头, 每个相机视场约1.2 m. 双目系统拍摄编码点后将其撕下. 液压机以1 mm/min的速率加载, 同时相机以每秒2帧的速率采集变形中梁表面的散斑. 如图10所示, 图10(a)为梁在3个载荷级别下的主应变云图, 主应变云图能大致观察出裂纹的位置. 图10(b)为利用本文提出的方法得到的梁在3个载荷级别下的全场裂纹示意图, 各裂纹的宽度和长度均为真实比例, 通过对比发现, 全场裂纹识别的效果很好, 本文所提出方法可以非常直观地反映混凝土梁表面的裂纹扩展与发展情况.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-107-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
混凝土梁尺寸示意图及实验现场 (单位: mm)



Figure
9.
Concrete beam size diagram and experimental setup (unit: mm)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-107-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
混凝土梁表面全场裂纹分布图



Figure
10.
Crack distribution of the whole concrete beam surface



下载:
全尺寸图片
幻灯片


为了追踪裂纹在不同载荷下的形态和扩展, 图11(a)和图11(b)分别展示了跨中裂纹和左侧弯剪区斜裂纹随载荷的形态变化. 跨中裂纹在70 kN左右开始出现, 而左侧斜裂纹在200 kN左右才出现. 图中红色标记为裂纹最宽处, 均出现在大致同一位置.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-107-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
裂纹随荷载增加扩展



Figure
11.
Crack propagation with increasing load



下载:
全尺寸图片
幻灯片


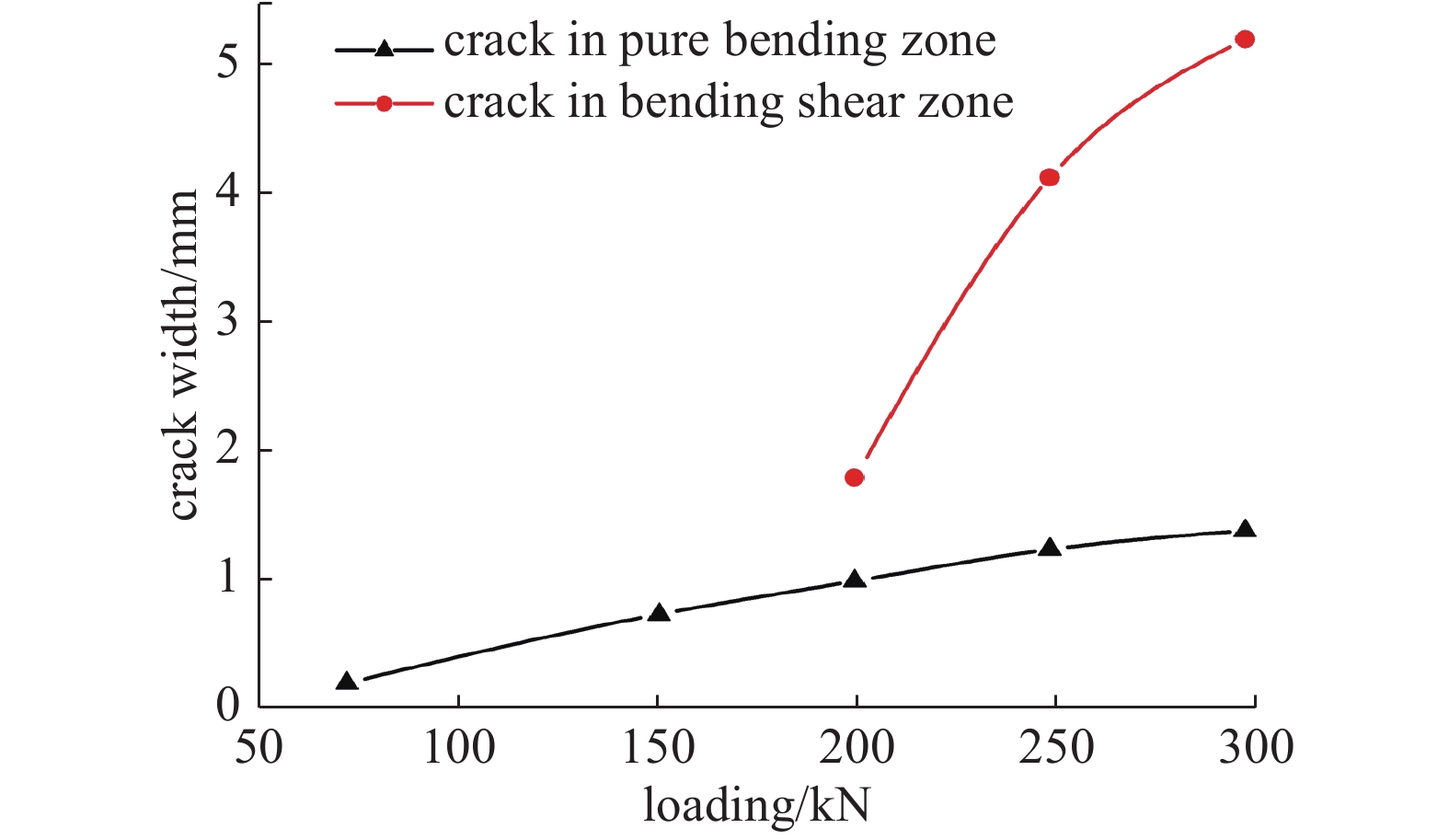
图12为各裂纹在不同载荷下最宽处的宽度值. 在相同载荷下, 梁弯剪区裂纹最宽值远大于梁跨中裂纹最宽值, 且扩展速度较快. 斜裂纹出现较晚且扩展迅速, 当加载到300 kN左右时, 斜裂纹处发生明显破坏, 试件失效, 斜裂纹是导致混凝土梁失效的主要原因.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-107-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
裂纹最大宽度变化图



Figure
12.
Variation diagram of maximum crack width



下载:
全尺寸图片
幻灯片

3.
结论

针对混凝土结构断裂力学性能分析的实际需求, 本文提出了一种基于虚主应变场的裂纹定位方法和基于裂纹张开位移的宽度测量方法, 结合多相机DIC技术可实现全场裂纹的全自动、高精度测量. 在分析子区大小、计算模板对裂纹附近主应变场分布的影响的基础上, 提出了适合本方法的子区大小、计算步长和计算模板. 实验结果表明, 本方法测量裂纹宽度的误差在0.010 ~ 0.017像素之间, 与理论预测相符, 且测量标准差在0.006 ~ 0.008像素之间, 测量结果十分稳定. 本文所提出的方法为土木工程混凝土实验提供了一种全面、可靠、精确的裂纹测量手段.