删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

椭球颗粒体系剪切过程中自由体积的分布与演化

本站小编 Free考研考试/2022-01-01


引言


颗粒物质是由大量离散固体相互作用而形成的复杂体系, 在自然界和工业界广泛存在. 以水利和岩土工程中的堆石体为例, 由于取材方便, 且对地形、地质条件有较强的适应性, 在堆石坝、路堤、机场高填方地基等工程建设中得到广泛应用. 这些工程一旦出现问题和隐患, 将会严重威胁人民生命财产安全, 因此迫切需要深入研究颗粒材料的物理力学特性.

由于颗粒材料具有结构异质性、各向异性和多尺度结构等特点, 其表现出复杂的物理力学特性, 如剪胀[1]、应变局部化[2], 固?液转变[3-4]等. 对岩土类颗粒材料, 自1963年Roscoe等[5]提出剑桥模型以来, 许多****根据颗粒材料的宏观应力变形特性发展了各种各样的本构理论[6-8]. 但目前还没有统一的理论能够解释颗粒材料所有的应力变形特性. 蒋明镜[9]指出这些基于唯象的土力学本构理论虽然在岩土工程实践中发挥了重要作用, 但是难以从机理上刻画岩土颗粒系统的非连续性、大变形、破坏等问题. 因此, 越来越多****尝试从细观尺度研究颗粒材料复杂力学行为的起源, 并试图将颗粒形状、表面摩擦、粒径分布等颗粒尺度的特性与宏观力学响应建立联系.

岩土颗粒材料的形状各异, 大量研究表明颗粒形状对颗粒材料的剪切强度[10-13]、塑性行为[14]以及堆积特性[15-16]等有显著影响. 深入研究颗粒形状对颗粒材料物理力学特性的影响, 剖析这些影响的细观机理, 对颗粒材料的理论研究和工程应用有重要意义. 受试验技术限制, 目前只能通过光弹试验技术[17]、X-ray断层扫描技术[18]等研究颗粒材料宏观力学响应的细观机理. 与此同时, 细观数值模拟方法在颗粒材料的宏细观力学特性研究方面得到广泛应用, 如离散单元法(discrete element method, DEM)[19]和连续离散耦合分析方法(combined finite and discrete element method, FDEM)[20-21]. 其中FDEM中将颗粒离散为有限元网格, 理论上可以考虑任意颗粒形状, 在模拟复杂颗粒形状方面具有显著优势.

虽然颗粒材料的结构特性与其物理力学性质的相关性已经得到大量研究证明[22-26], 但是具有复杂颗粒形状和宽粒径分布的颗粒材料的结构表征, 以及建立宏观力学响应和细观结构的联系仍是一个重大挑战. 基于该现状, 颗粒统计力学得到了快速发展, 例如Edwards等[27-28]建立了颗粒系统的体积系综理论(Edwards' volume ensemble), 用统计物理的框架来研究非平衡态的颗粒堆积问题. 该理论强调了局部自由体积(孔隙)在描述静态颗粒材料阻塞行为中的重要作用. 在工程中, 常采用孔隙率、孔隙比、体积分数等表征颗粒材料的密实程度, 但是这些表征量仅能提供宏观尺度的自由体积信息, 忽视了颗粒尺度自由体积的形态、分布和演化.

已有研究表明, 颗粒尺度的自由体积与颗粒材料的力学性能、变形特征等密切相关[29-30], 所以有必要探索颗粒材料的自由体积的统计分布特性及其在剪切过程中的演化规律. 将颗粒与其周围的自由体积组成一个局部元胞(以Voronoi元胞较为典型)用以定量分析颗粒材料自由体积特征是一种常见思路. 不少****研究了颗粒材料在特定状态下的局部自由体积[31-32]. 但是颗粒材料在剪切过程中会产生颗粒重排列现象, 颗粒材料的细观结构和自由体积会不断演化. 因此, 探索剪切过程非球颗粒材料的局部自由体积的演变规律, 可以为研究颗粒材料的宏细观多尺度力学特性提供新的思路.

本文将选择具有不同非球度的椭球颗粒体系为研究对象, 采用连续离散耦合分析方法进行三轴剪切数值模拟, 分析不同非球度的椭球颗粒试样在剪切过程中的宏细观力学响应, 并基于Voronoi元胞对椭球颗粒体系的局部自由体积进行定量分析, 探讨局部自由体积的分布特征和演化规律以及受颗粒形状的影响.


1.
椭球颗粒体系三轴剪切数值试验



1.1
FDEM基本理论


FDEM最早由Munjiza等[20]提出, 充分融合了有限元和离散元方法的优势. 颗粒的应力变形计算采用有限单元法, 颗粒运动和接触模型采用离散单元法. FDEM中颗粒均由有限元网格构成, 相比其他不连续数值模拟方法而言, 最吸引人的优点是能够考虑各种复杂形状[33-36].

有限元网格不仅定义了颗粒的形状和边界, 而且可以很方便进行接触检索以及引入接触模型. 在FDEM中, 罚函数法被用于颗粒间的接触分析, 假定接触力偶相互侵入, 根据重叠量在节点间产生分布式接触力. 切向力的最大值根据库仑摩擦定律控制. 本文采用线性接触模型计算颗粒间的接触力, 基于两个接触颗粒的相对速度, 通过阻尼力定律确定阻尼力. 接触力的计算公式如下







$${F_{
m{n}}} = {k_{
m{n}}}{delta _{
m{n}}} - 2{beta _{
m{n}}}sqrt {m{k_{
m{n}}}} {v_{{
m{rn}}}}qquadqquadqquad;;;$$
(1)







$${F_{
m{t}}} = min left( {left| {sum {{k_{
m{t}}}dot gamma Delta t - 2{beta _{
m{t}}}sqrt {m{k_{
m{t}}}} {v_{{
m{rt}}}}} }
ight|,mu {F_{
m{n}}}}
ight);;;$$
(2)







$${beta _{
m{n}}} = - ln {zeta _{
m{n}}}Bigr/sqrt {{{text{π}} ^2} + {{ln }^2}{zeta _{
m{n}}}} qquadqquadquad;;$$
(3)







$${beta _{
m{t}}} = - ln {zeta _{
m{t}}}Bigr/sqrt {{{text{π}} ^2} + {{ln^2 }}{zeta _{
m{t}}}} qquadqquadqquad$$
(4)

式中, ${k_{
m{n}}}$和${k_{
m{t}}}$分别为节点法向与切向接触刚度, 定义为${k_{
m{n}}}, = ;{p_{
m{n}}}{A_{{
m{node}}}}$, ${k_{
m{t}}}, = ;{p_{
m{t}}}{A_{{
m{node}}}}$, ${p_{
m{n}}}$和${p_{
m{t}}}$分别为法向和切向罚刚度, ${A_{{
m{node}}}}$为接触面上的节点控制区的面积, $dot gamma $为滑移率, $Delta t$为时间增量, ${delta _{
m{n}}}$为节点侵入量, $;{beta _{
m{n}}}$和$;{beta _{
m{t}}}$为法向与切向临界阻尼系数, ${zeta _{
m{n}}}$和${zeta _{
m{t}}}$为法向和切向恢复系数, $m$为节点质量.


1.2
颗粒形状与数值试验


Barrett[37]将颗粒形状量化分为形态、圆度和表面纹理3个层面. 本文重点关注形态, 故选取椭球颗粒体系作为研究对象. 共生成7种主轴长度不同的椭球颗粒, 颗粒的各种形态参数如图1所示. 其中L, I, S分别代表椭球长轴、中轴和短轴的长度. $alpha $为Domokos系数[38], 定义为$alpha {
m{ = (1/}}S{
m{ + 1/}}I{
m{ + 1/}}L{
m{)}} $$ sqrt {{S^2} + {I^2} + {L^2}} /sqrt 3$, 表征颗粒主轴各向异性, 在椭球形颗粒中可以反映颗粒的非球度. $psi $为球度, 定义为$psi = {{sqrt[3]{{36{text{π}} {V^2}}}} / A}$, 表征颗粒形状偏离圆球的程度, 式中A和V分别代表颗粒的表面积和体积. 后文分析中选取$alpha $作为椭球颗粒的形状量化指标.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
颗粒形状描述



Figure
1.
Particle shape descriptors



下载:
全尺寸图片
幻灯片


在立方体容器中生成等效半径(定义为等体积球体的半径)在6.8 ~ 10.2 mm范围内均匀分布的6394个颗粒, 颗粒位置和倾向均随机以避免产生初始各向异性. 采用各向同性压缩制样, 制样过程中颗粒间摩擦系数设为0.1, 六面无摩擦的刚性墙体缓慢压缩试样直至达到目标围压0.5 MPa. 图2为$alpha {
m{ ;=; }}3.394$的数值试样, 试 样 尺 寸为0.42 m × 0.42 m × 0.42 m. 采用常规三轴应力路径加载, 围压保持${sigma _2}{
m{ ;=; }}{sigma _3}{
m{ ;=; 0}}{
m{.5;MPa}}$, 控制顶部和底部两块刚性墙体以恒定速度相向移动.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
数值试样



Figure
2.
Numerical sample



下载:
全尺寸图片
幻灯片



1.3
细观参数率定


数值试验的可靠度很大程度取决于参数取值. 本试验中颗粒密度、弹性模量和泊松比参考天然砂砾石的自然属性. 根据岩石材料的回弹性质[39], 临界阻尼系数取0.03, 对应的恢复系数为0.9. Tatone和Grasselli[40]验证了当接触罚刚度设为10倍弹性模量时所得到的弹性响应与室内物理试验匹配较好, 故本试验接触罚刚度设为弹性模量的10倍. 通过颗粒柱坍塌物理试验和数值试验对比分析来率定颗粒摩擦系数. 具体步骤如图3所示: 选取粒径在6 ~ 10 mm均匀分布的砂砾石装入无底板圆筒, 随后缓慢抽离圆筒, 重复10次试验, 测得休止角均值为29.19°. 对物理试验中的砂砾石进行扫描, 通过主成分分析得到主轴长度, 在此基础上重构出形状相近的椭球颗粒. 调整颗粒摩擦系数进行颗粒柱坍塌数值试验, 使得休止角逼近物理试验的结果, 最终摩擦系数设为0.5时休止角为29.5°. FDEM数值模拟所需细观参数汇总于表1.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
颗粒柱坍塌试验



Figure
3.
Granular column collapse tests



下载:
全尺寸图片
幻灯片





表
1
FDEM数值模拟细观参数



Table
1.
Parameters used in the FDEM simulation



table_type1 ">
ParameterUnitValue
densitykg/m32600
friction coefficient?0.5
normal penaltyN/m34 × 1011
tangential penaltyN/m34 × 1011
Young’s modulusGPa40
Poisson’s ratio?0.2
normal critical damping fraction?0.03
tangential critical damping fraction?0.03





下载:
导出CSV
|显示表格



1.4
宏观力学响应


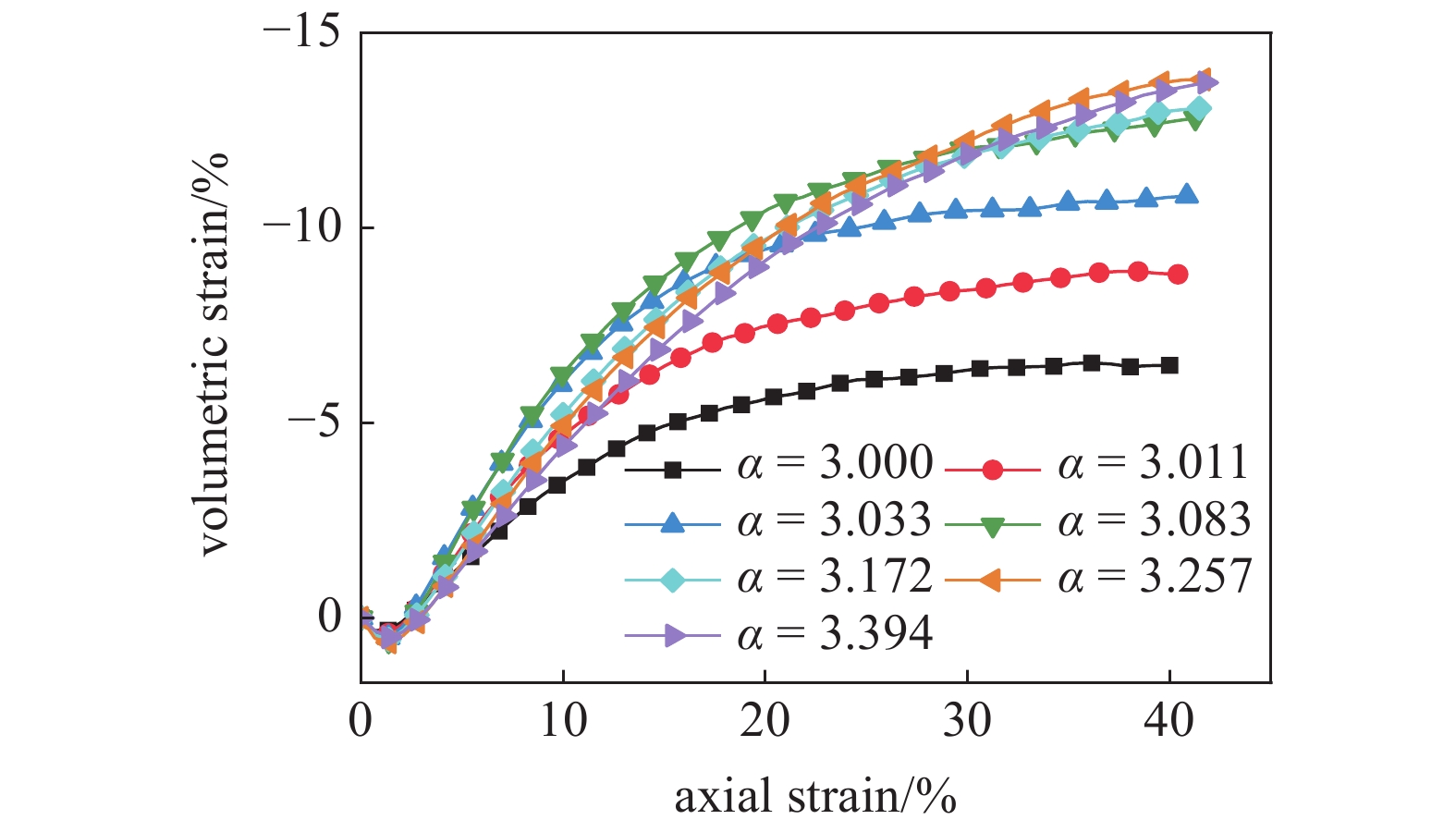
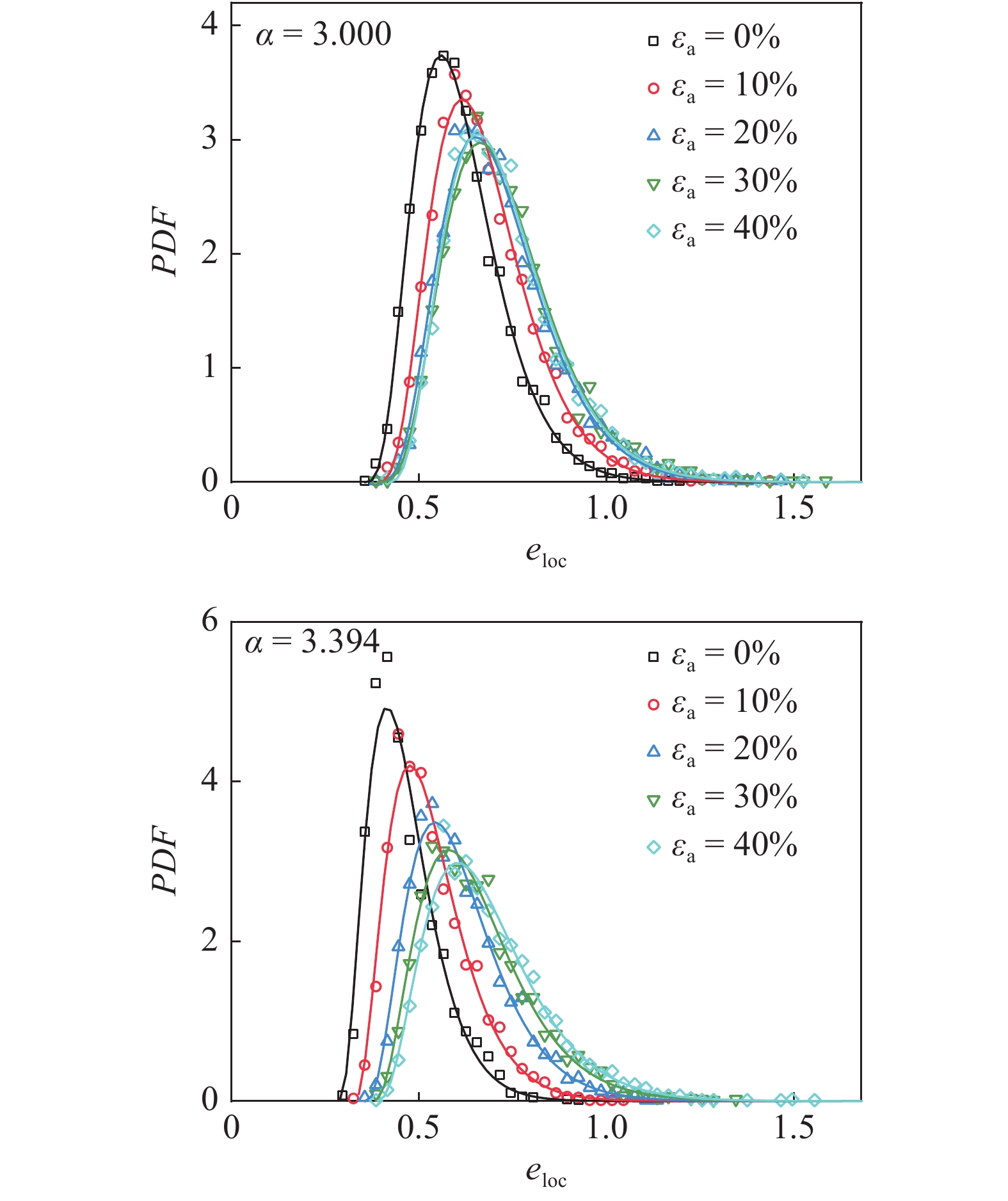
图4和图5分别为7组不同非球度的椭球颗粒试样的偏应力?轴向应变和体积应变?轴向应变关系曲线. 不同试样的宏观响应呈现相似的规律, 偏应力在加载初期迅速上升达到峰值, 随后开始下降, 呈现出明显的应变软化现象. 试样在加载初期有少量体积压缩, 随后发生明显的体胀. 在较大轴向应变时偏应力和体积应变都趋于稳定或呈缓慢变化趋势. 这种应力和体积响应在密实的无黏性颗粒材料中非常典型[6]. 随形状参数$alpha $增大, 即颗粒非球度增大, 试样的剪切强度明显增大, 并伴随着更加显著的剪胀. 目前普遍认为这种影响源自非球颗粒的互锁效应, 其增强了颗粒抵抗转动的能力[12,41].



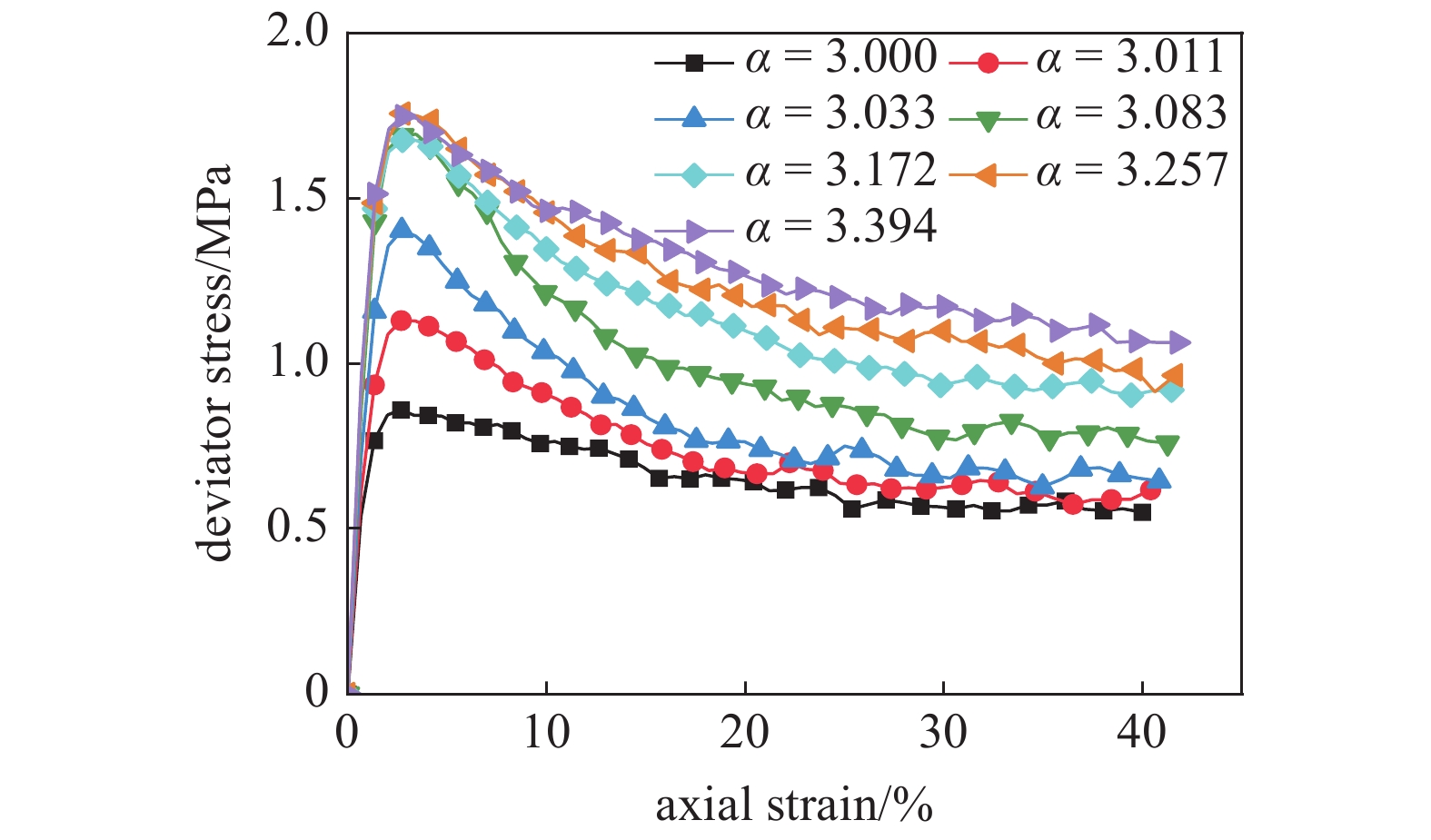onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
不同非球度的椭球颗粒偏应力?轴向应变



Figure
4.
Curves of deviatoric stress versus axial strain for ellipsoidal particles with different asphericity



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
不同非球度的椭球颗粒体积应变?轴向应变



Figure
5.
Curves of volumetric strain versus axial strain for ellipsoidal particles with different asphericity



下载:
全尺寸图片
幻灯片



2.
非球形颗粒的Voronoi剖分方法


Voronoi剖分作为一种基本几何结构划分方法, 将离散的颗粒在空间上划分, 利用所得到的空间结构来表征材料的细观结构, 目前已成为结构表征的一种常用手段. 其中圆球颗粒的Voronoi剖分被广泛应用, 计算软件也较为成熟(如Voro++[42]). 相比而言, 非球颗粒的Voronoi剖分由于实现困难, 在颗粒材料的计算分析中鲜有报道. 为实现非球颗粒的Voronoi剖分, Schaller等[43]提出了Set Voronoi剖分方法, 现已被成功运用于非球颗粒体系的细观结构分析[44-45]. 具体步骤如图6所示: (1)在颗粒表面均匀分布足够多的点, 得到每个颗粒表面的离散点集; (2)计算所有颗粒表面离散点的Voronoi元胞; (3)将属于同一颗粒的Voronoi元胞合并, 形成该颗粒的Voronoi元胞.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
Set Voronoi 剖分二维示意图



Figure
6.
Two-dimensional illustration of Set Voronoi tessellation



下载:
全尺寸图片
幻灯片


上述步骤适用于完全分离的非球颗粒体系. 然而在FDEM中, 由于颗粒间会相互侵入, 会造成局部计算失准. 为了避免这种情况, 在进行离散点的Voronoi剖分之前, 将每个颗粒表面离散点沿其法向方向收缩一定距离, 可在不影响Voronoi剖分结果的同时避免局部误差[43]. 图7为圆球颗粒和椭球颗粒的Voronoi元胞示意图, 可以看出圆球的Voronoi元胞是凸多面体, 而椭球的Voronoi元胞表面会存在凹面, 形态更加复杂.



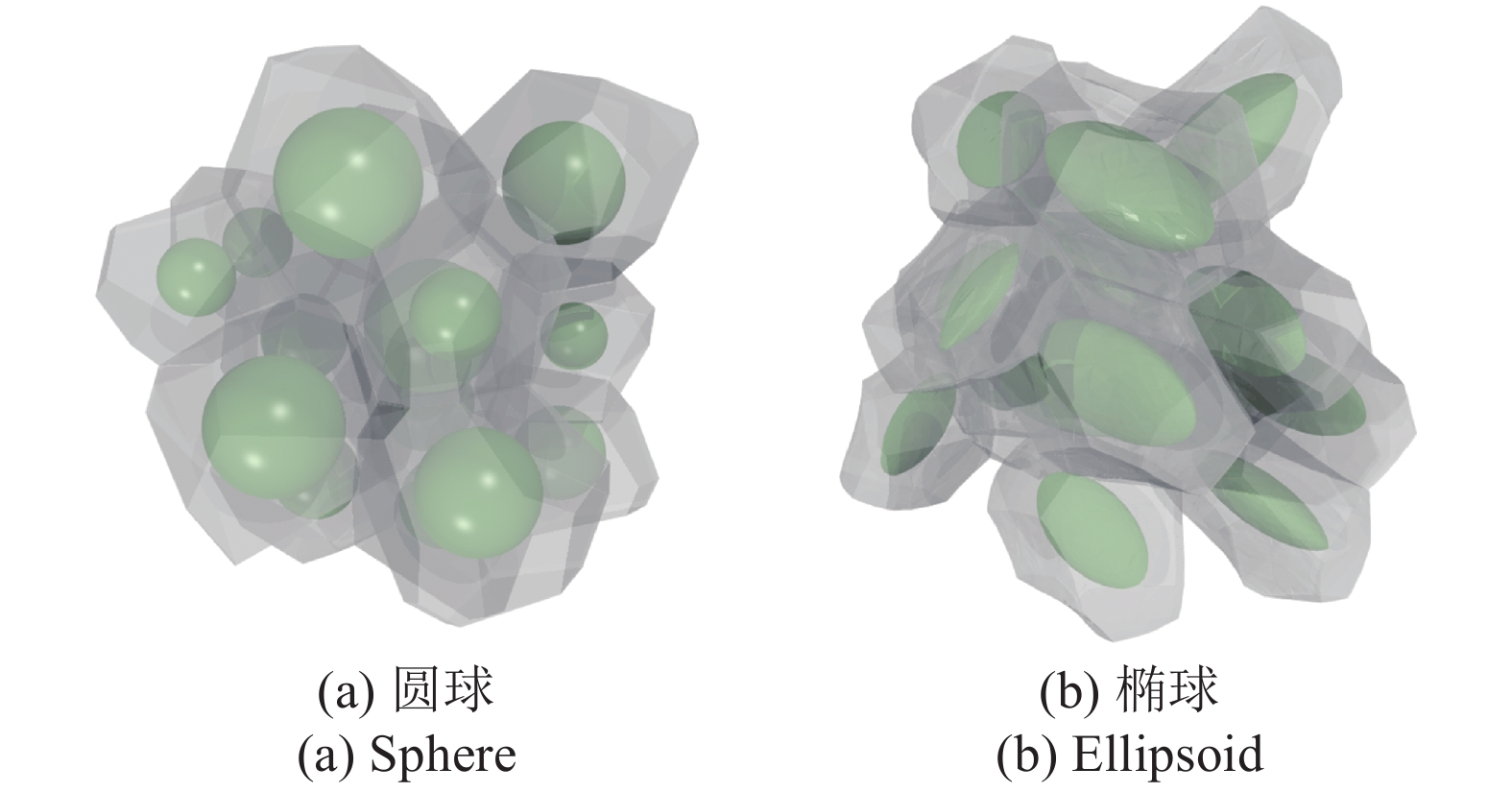onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
圆球和椭球颗粒的Voronoi元胞



Figure
7.
Voronoi cells of spherical and ellipsoidal particles



下载:
全尺寸图片
幻灯片



3.
Voronoi元胞的各向异性


对于颗粒材料而言, 即使是圆球颗粒体系, 在剪切过程中仍然会产生各向异性[46]. 由于各向异性与颗粒材料的力学性质密切相关, 相关研究受到广泛关注. 例如Ouadfel和Rothenburg[24]基于组构和接触力的各向异性张量, 推导了(stress-force-fabric, SFF)关系, 建立了组构各向异性、接触力各向异性与宏观应力比之间的关系. 组构和接触力是对接触状态的描述, 相比而言, Voronoi元胞是对颗粒局部空间的描述, 其形状的不规则程度可以用来量化局部空间各向异性. 由于Voronoi元胞本质上是一个多面体, 在量化其形状特性上可以借鉴于颗粒形状的描述指标. 引入最常见的球度, 描述Voronoi元胞形状偏离圆球(各向同性)的程度, 定义其为与元胞等体积球体的表面积与元胞表面积的比值







$${psi _{
m{c}}} = frac{{sqrt[3]{{36{text{π}} V_{
m{c}}^{
m{2}}}}}}{{{S_{
m{c}}}}}$$
(5)

式中, ${V_{
m{c}}}$和${S_{
m{c}}}$分别代表Voronoi元胞的体积与表面积.

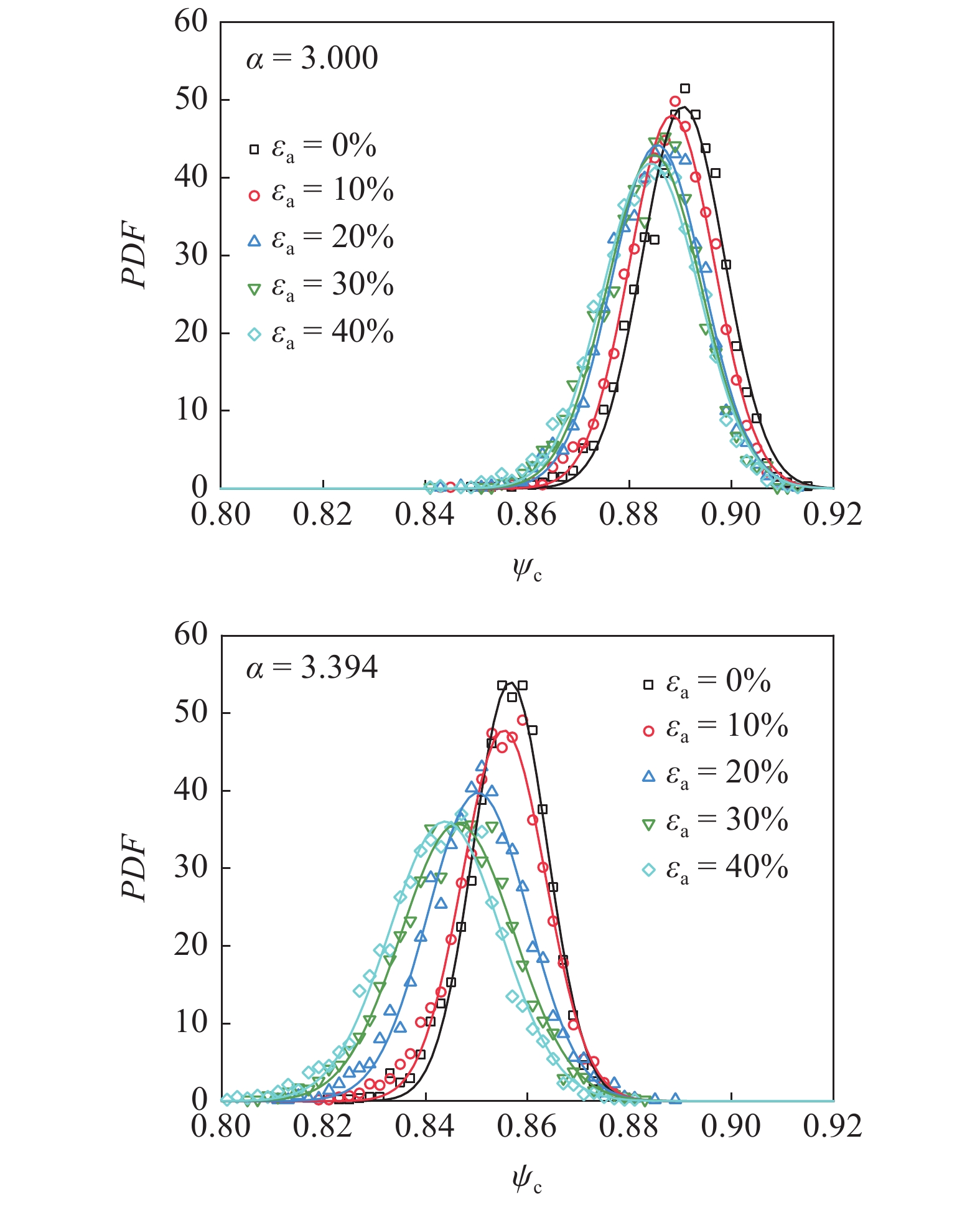
为了避免边界效应, 本文分析排除了在边界2倍平均粒径范围内的颗粒. 图8为不同非球度的椭球颗粒试样在不同加载阶段(${varepsilon _{
m{a}}}$为轴向应变)的Voronoi元胞球度${psi _{
m{c}}}$的概率密度分布函数(probability density function, PDF). 可以发现${psi _{
m{c}}}$呈现高斯分布, 图中实线为高斯分布函数拟合曲线. 在加载过程中${psi _{
m{c}}}$分布逐渐向左移动(均值降低), 且在加载到较大应变时趋于稳定. 这说明颗粒材料在剪切过程中, 局部空间的各向异性会逐渐增强直至系统达到临界状态, 且随颗粒非球度增大各向异性增强越明显, 这与组构各向异性和接触力各向异性的演化类似[41,47]. 在剪切过程中, ${psi _{
m{c}}}$分布的标准差也逐渐增大.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
不同非球度的椭球颗粒在不同加载阶段的Voronoi元胞球度概率密度分布



Figure
8.
Probability density distributions of sphericity of Voronoi cells at the different loading states for ellipsoidal particles with different asphericity



下载:
全尺寸图片
幻灯片


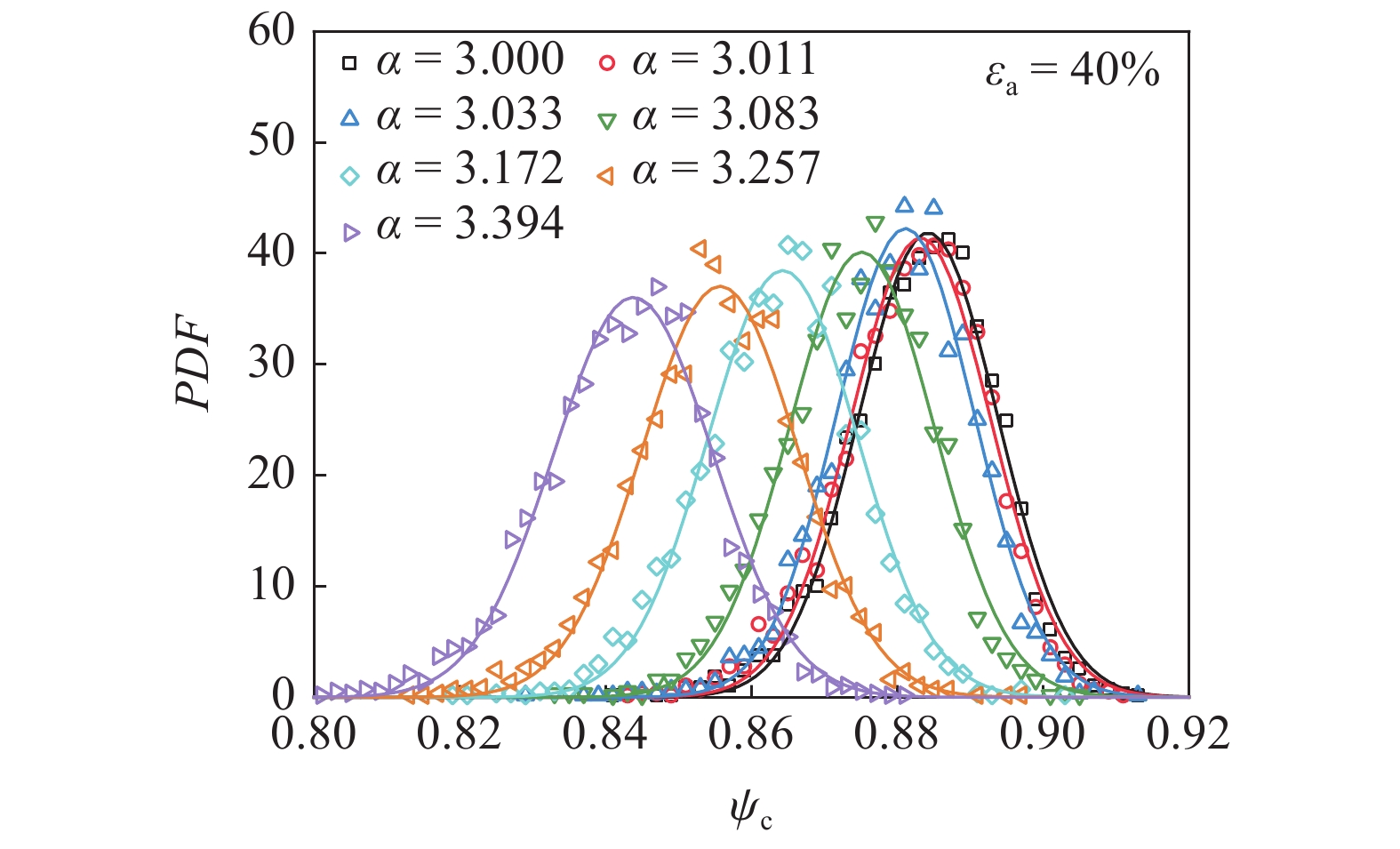
当颗粒材料充分剪切后, 会达到一个与初始状态无关的力学稳定态, 即临界状态. 颗粒材料在该状态时的力学性质受到广泛关注[7,11]. 本文试样虽未完全达到理想的临界状态, 但是在加载后期应力状态和体积已经趋近于稳定, 故选取轴向应变40%时为试样的“临界状态”, 代表充分剪切后的状态. 图9为不同非球度的椭球颗粒试样在临界状态的Voronoi元胞球度概率密度分布. 随形状参数$alpha $增大${psi _{
m{c}}}$分布向左平移, 分布更广. 图10展示了临界状态下Voronoi元胞球度与颗粒形状参数$alpha $的线性关系. 这说明局部各向异性的分布强烈依赖颗粒形状. 相比圆球, 椭球颗粒可以产生更为复杂的局部结构.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
不同非球度的椭球颗粒在临界状态的Voronoi元胞球度概率密度分布



Figure
9.
Probability density distributions of sphericity of Voronoi cells at critical state for ellipsoidal particles with different asphericity



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
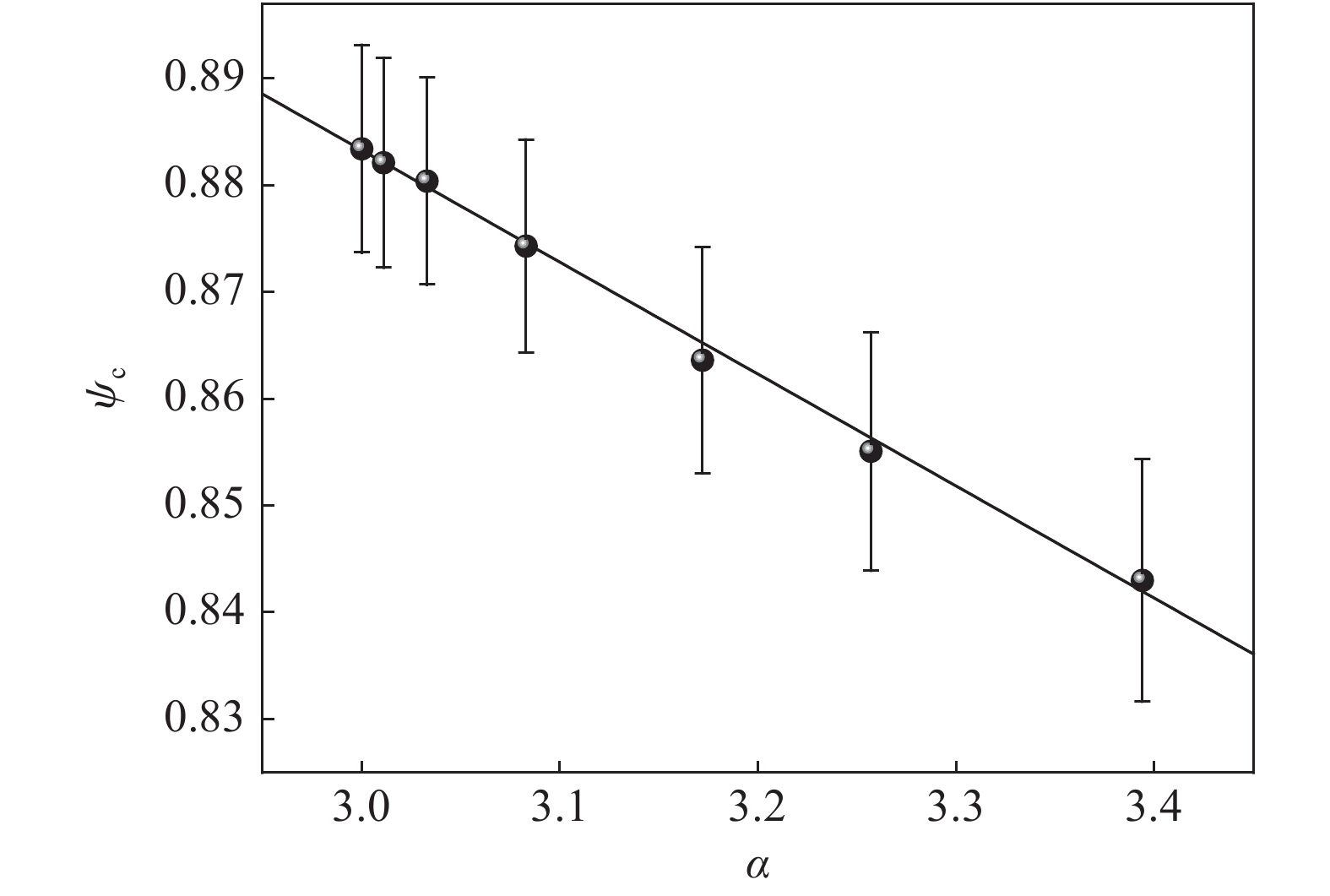
临界状态下Voronoi元胞球度与颗粒形状参数$alpha $的关系



Figure
10.
Relationship between Voronoi cell sphericity and shape parameter $alpha $ of particle at critical state



下载:
全尺寸图片
幻灯片



4.
局部自由体积分布及演化规律


为了量化颗粒尺度自由体积的大小, 引入局部孔隙比${e_{{
m{loc}}}} = ({V_{
m{c}}} - {V_{
m{p}}})/{V_{
m{p}}}$, 其中${V_{
m{p}}}$和${V_{
m{c}}}$分别为颗粒体积和其对应的Voronoi元胞体积. 图8展示了不同非球度的椭球颗粒试样在剪切过程中局部孔隙比${e_{{
m{loc}}}}$的概率密度分布. 局部孔隙比${e_{{
m{loc}}}}$呈现类高斯分布. 针对局部自由体积的统计分布特性已有一定报道, Schaller等[45]发现扁椭球颗粒局部体积分数$1/(1 + {e_{{
m{loc}}}})$近似服从高斯分布, Dong等[32]发现椭球颗粒和柱状颗粒局部孔隙比服从对数正态分布, Zhao等[30]认为局部孔隙率${e_{{
m{loc}}}}/(1 + {e_{{
m{loc}}}})$服从一个修改的对数正态分布. 此外, 还有一些研究发现圆球颗粒堆积体的局部体积分数的倒数(1+${e_{{
m{loc}}}}$)服从k?Γ分布[48-49]. 上述研究中以k?Γ分布的拟合参数最少, 其函数为







$${{PDF}}({e_{{
m{loc}}}}) = frac{{{k^k}}}{{Gamma (k)}}frac{{{{({e_{{
m{loc}}}} - {e_{min }})}^{k - 1}}}}{{{{({{bar e}_{{
m{loc}}}} - {e_{min }})}^k}}}exp left( - kfrac{{{e_{{
m{loc}}}} - {e_{min }}}}{{{{bar e}_{{
m{loc}}}} - {e_{min }}}}
ight)$$
(6)

式中, k为表示分布函数形状的参数, $Gamma $为伽马函数, ${e_{min }}$为当前堆积状态下最小局部孔隙比, ${bar e_{{
m{loc}}}}$为局部孔隙比的均值.

图11中实线为k?Γ函数拟合曲线. 虽然k?Γ分布是针对圆球颗粒体系提出的, 但是对于椭球颗粒体系仍然适用. 在加载过程中${e_{{
m{loc}}}}$分布逐渐向右移动, 峰值减小并且分布范围更宽, 这意味着颗粒在剪切过程中局部自由体积变大且分布更广. 在加载后期这种演变逐渐趋于稳定, 与试样先剪胀后达到临界状态的现象相吻合. 随非球度增大这种演变越明显, 这与图5中剪胀随$alpha $增强相对应.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
不同非球度的椭球颗粒在不同加载阶段的局部孔隙比概率密度分布



Figure
11.
Probability density distributions of local void ratio at the different loading states for ellipsoidal particles with different asphericity



下载:
全尺寸图片
幻灯片


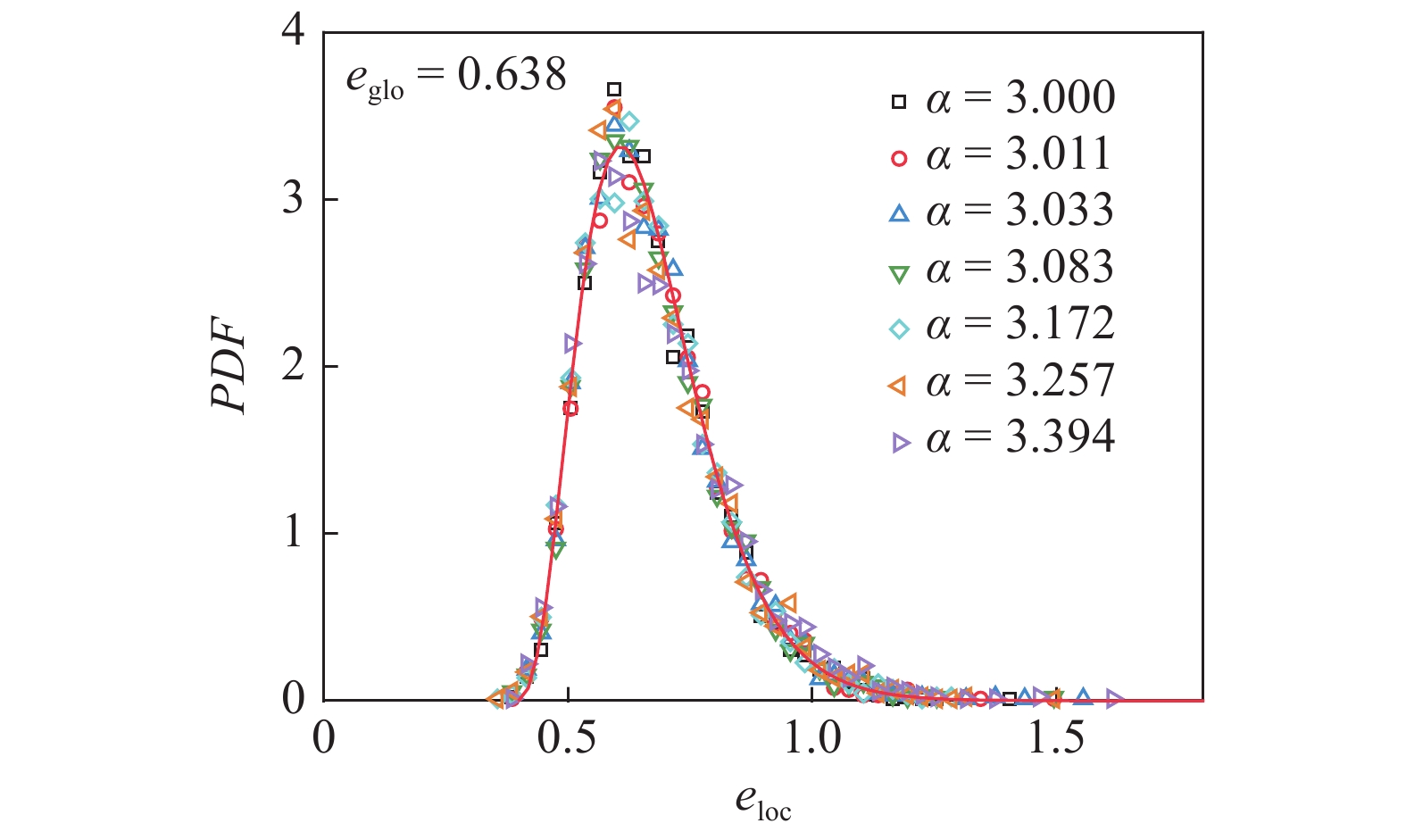
图12为全局孔隙比${e_{{
m{glo}}}} = 0.638$时不同非球度的椭球颗粒试样的局部孔隙比的概率密度分布, 此时7组试样剪切状态不同, 轴向应变分别为9.0%, 12.7%, 15.2%, 21.0%, 27.1%, 31.8%和37.7%. 可以发现不同非球度试样的局部孔隙比分布基本一致, 这说明颗粒局部孔隙比的分布仅与全局孔隙比相关, 不受颗粒形态和剪切状态的影响. 图13为不同非球度的椭球颗粒试样的局部孔隙比分布标准差$sigma ({e_{{
m{loc}}}})$与全局孔隙比${e_{{
m{glo}}}}$的关系. $sigma ({e_{{
m{loc}}}})$与${e_{{
m{glo}}}}$呈现明显的线性关系, 且这个线性关系不受颗粒形态影响, 进一步证明了颗粒局部孔隙比的分布仅受全局孔隙比控制.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
不同非球度的椭球颗粒在全局孔隙比相同时局部孔隙比概率密度分布



Figure
12.
Probability density distributions of local void ratio at the states as same global void ratio for ellipsoidal particles with different asphericity



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
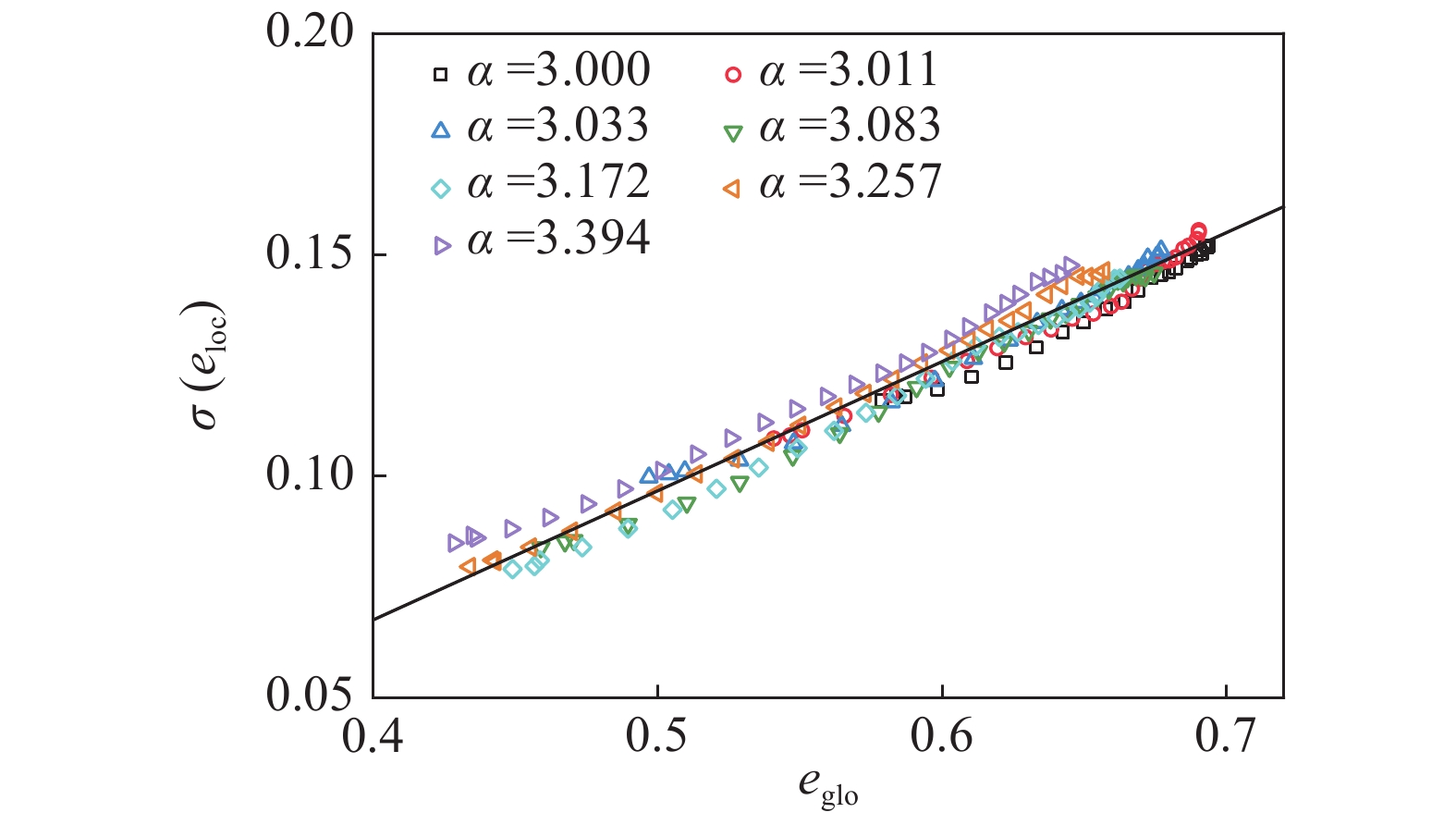
局部孔隙比的标准差与全局孔隙比的关系



Figure
13.
Relationship between standard deviation of local void ratio and global void ratio



下载:
全尺寸图片
幻灯片


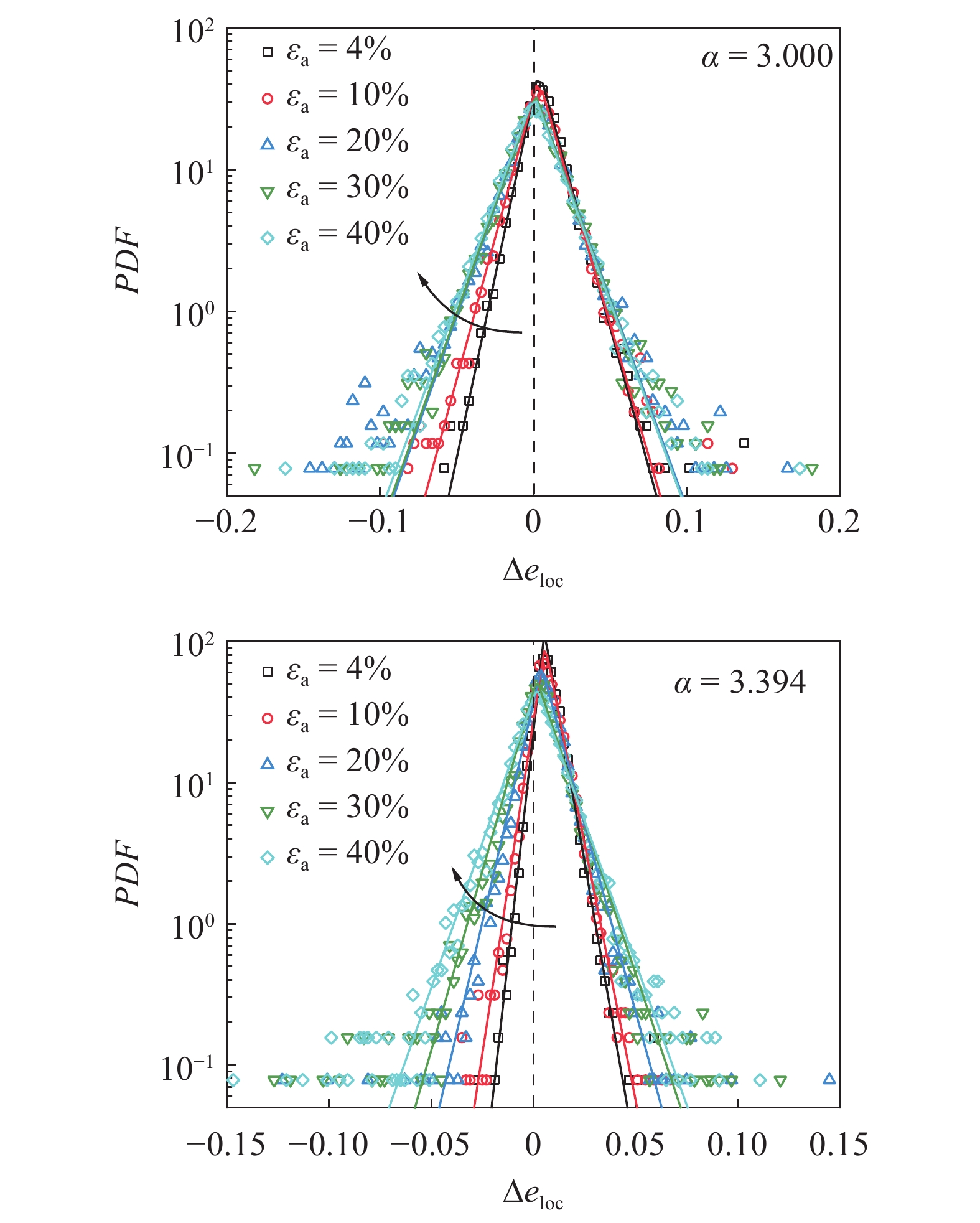
从局部孔隙比分布的演化可知剪切过程中局部自由体积的变化是非均匀的, 探索局部孔隙比波动可以帮助了解颗粒体系剪胀的细观机理. 选取了5个加载阶段(${varepsilon _{
m{a}}}$= 4%, 10%, 20%, 30%和40%), 分析不同非球度的椭球颗粒试样在应变窗口$Delta {varepsilon _{
m{a}}} approx 0.8 $%的局部孔隙比波动. 图14为不同非球度的椭球颗粒试样在不同加载阶段的局部孔隙比波动的概率密度分布. 局部孔隙比的波动呈现非对称拉普拉斯分布(asymmetric laplace distribution, ALD), 其函数为



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
不同非球度的椭球颗粒试样在不同加载阶段的局部孔隙比波动概率密度分布



Figure
14.
Probability density distributions of local void ratio fluctuations at the different loading states for particles with different shapes



下载:
全尺寸图片
幻灯片








$${{PDF(}}Delta {e_{{
m{loc}}}}{
m{) = }}frac{lambda }{{kappa + 1/kappa }}left{ begin{array}{l} exp Big[(lambda /kappa )(Delta {e_{{
m{loc}}}} - m)Big],;;{
m{ }}Delta {e_{{
m{loc}}}} < m exp Big[ - lambda kappa (Delta {e_{{
m{loc}}}} - m)Big],;;{
m{ }}Delta {e_{{
m{loc}}}} geqslant m end{array}
ight.$$
(7)

式中, $m$为分界点, $lambda $为尺度参数, $kappa $为非对称参数.

$Delta {e_{{
m{loc}}}}$的分布可以分为左右两个非对称的指数函数(在单对数坐标系下表现为斜率不一致的两段线性分布), 分界点在$Delta {e_{{
m{loc}}}} = 0$附近. 左右两侧分布的非对称性刻画了局部自由体积收缩和膨胀的博弈. 在加载初期(${varepsilon _{
m{a}}} = 4 $%)体积膨胀明显处于优势地位(图中图14(a)斜率绝对值小于图14(b)), 试样表现出明显的剪胀行为. 随形状参数$alpha $增大, 两侧斜率差异增大, 这意味着有更显著的体积膨胀, 与宏观体积响应相符合(图5). 随着剪切进行, 代表体积膨胀的图14(a)体积波动分布变化较小, 而图14(b)分布的斜率有明显下降, 两侧趋于对称, 即剪胀会随剪切过程逐渐停止.

ALD中非对称参数$kappa $为分布两侧斜率比值的平方, 描述了ALD的非对称程度, 也刻画了体积膨胀的强度. $kappa $越小体积膨胀越明显, $kappa = 1$时体积无变化. 如图15所示, $kappa $与全局孔隙比${e_{{
m{glo}}}}$呈现明显的线性关系, 并在$kappa = 1$附近截断. 这意味着体积膨胀的强度很大程度上取决于试样当前全局孔隙与临界全局孔隙比的差值, 故随$alpha $增大体胀更显著可以归因于椭球颗粒在相同固结条件下可以形成更密实的堆积.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-255-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />



图
15
非对称参数$kappa $与全局孔隙比的关系



Figure
15.
Relationship between asymmetric parameter $kappa $ and global void ratio



下载:
全尺寸图片
幻灯片



5.
结论


本文采用连续离散耦合分析方法, 对具有不同非球度的椭球颗粒试样进行了三轴剪切数值模拟. 基于Set Voronoi剖分技术对剪切过程中的颗粒试样进行Voronoi元胞分割, 研究了颗粒试样在剪切过程中局部自由体积的统计分布特性和演化规律, 以及颗粒形态的影响. 主要结论如下:

(1)不同椭球颗粒试样的Voronoi元胞的球度在剪切过程中均服从高斯分布, 但其均值降低, 标准差略有上升, 表明颗粒材料在剪切过程局部各向异性的逐渐增强. 局部各向异性程度与颗粒形态显著相关, 临界状态时Voronoi元胞球度随颗粒形态参数$alpha $线性减小.

(2)不同椭球颗粒试样的局部孔隙比均服从k?Γ分布, 且这个分布仅与全局孔隙比相关, 不受颗粒形态和剪切状态的影响. 非球度更大的颗粒在剪切过程中会产生更强烈的重排列, 导致局部孔隙比和Voronoi元胞球度在剪切过程中的变化随颗粒形状参数$alpha $的增大而增大.

(3)不同非球度的椭球颗粒试样的局部孔隙比波动均服从非对称拉普拉斯分布, 这种不对称性刻画了局部自由体积收缩和膨胀的博弈. 非对称参数与全局孔隙比呈现明显的线性关系, 表明体积膨胀的强度很大程度上取决于试样当前全局孔隙此与临界全局孔隙比的差值.

相关话题/材料 力学 图片 概率 结构
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于深度学习和细观力学的颗粒材料本构关系研究
    引言颗粒材料广泛存在于各类自然环境和工程活动中,人类几乎所有的基础设施都建造于岩土材料这类典型的颗粒材料上,理解和预测此类材料在外载作用下的力学响应具有重要的意义.岩土材料通常由粒径不一,形状各异的矿物颗粒以及颗粒之间的空隙组成.颗粒间的互相滑动会引起不可恢复的塑性变形,因而,颗粒材料在剪切作用下极 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 冲击载荷下颗粒材料临边界区域的波动行为及变形特征分析
    引言作为离散颗粒材料的土壤(或岩体),是日常生活中最常见的随机多孔介质,冲击载荷作用下材料的动力学响应对于工程实践和地质灾害防控有着重要的指导意义.注意到应力波的传播行为与介质性质密切相关,基于应力波的行为特征分析可提供一种非侵入式研究颗粒材料性质的途径.因此有非常多的****致力于研究冲击载荷作用 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 数据驱动印度洋海域全局动力学研究
    引言海洋系统天然受到多种环境因素(风速、温度、海水含盐量等)、人类活动和天体运动等不确定扰动的影响,导致其洋流运动复杂而多样[1-2].然而,一些观测和研究发现,其内部蕴含着能够对洋流的运动方向和趋势起限制和导向作用的复杂动力结构和特征,影响甚至主导了表面漂浮物的流动形式和演化路径.例如,经志友等[ ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 非常规油气资源渗流力学进展专题序
    石油和天然气在我国经济发展中起到了积极支撑作用.随着经济发展的后石油时代到来,我国油气资源对外依存度已超出了能源安全的警戒线.为保障国家能源安全,我国对非常规油气资源的开发力度大幅增加.自1996年以来,我国在页岩油气、煤层气、致密油气以及天然气水合物等非常规油气资源勘探开发领域取得了显著进展.作为 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 压电超构材料及其波动控制研究: 现状与展望
    引言超构材料或超材料(metamaterials)是将精心设计的基本单元通过一定的空间排列来实现普通材料所不具有的奇异或反常性能,如带隙、波导、负折射、负模量、负密度、超透镜、声学聚焦、声学隐身和拓扑态等[1-2],已成为一个多学科交叉的前沿研究领域.过去几十多年来陆续出现的左手材料[3]、光子晶体 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 含天然气水合物土微观力学特性研究进展
    引言天然气水合物(简称水合物)是由天然气分子与水分子在高压、低温环境下形成的非化学计量笼型结晶物质[1],广泛分布于全球近海大陆架及陆地永久冻土地带[2],资源储量巨大,被认为是21世纪最具潜力的替代能源之一[3].自20世纪开始,世界各国陆续成立了专门的水合物研究机构并开展了相关研究[4],在此基 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 挠性航天器太阳翼全局模态动力学建模与实验研究
    引言随着航天领域的发展,现代大型柔性航天器往往安装有诸如大型太阳翼等柔性结构,为了得到可持续的能源,其尺寸日益增大、结构重量越来越轻,太阳翼的弹性振动不可避免地与航天器主体平台的运动相互耦合,这种耦合效应随着太阳翼尺寸的增大显著增强.此时,单个太阳能帆板的模态(假设模态)并不能准确反映整个太阳翼在系 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 隧道开挖影响下地层-基础体系的接触力学响应分析
    引言在地层条件软弱、周围建筑物繁多的城市环境中进行隧道的施工,不可避免需要穿越和邻近施工,隧道施工扰动将对既有建(构)筑物的力学状态产生较大影响,进而导致建筑物的沉降、变形,甚至发生破坏[1-3].在城市运行高可靠度的要求下,隧道施工引起既有结构的工程响应预测与安全控制问题受到众多专家****与工程 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于T样条的变网格等几何薄板动力学分析
    引言随着柔性轻质结构在航天、汽车以及船舶工程等领域日益广泛的应用,柔性多体系统的动力学分析也愈加重要.然而,以线弹性小变形假设为基础的,将节点位移和转动作为坐标的传统有限单元不适合解决存在大位移、大变形的柔性多体系统的动力学问题.此外,对于传统结构有限元,将几何数据转换为有限元网格数据是困难且耗时的 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 软材料粘接结构界面破坏研究综述
    引言因其特有的低模量和能量耗散等“软”的特性以及优异的“小激励大响应”等特征,多种多样的软材料,如水凝胶、介电弹性体以及聚甲基氧硅烷等被广泛应用在软机器人、生物医学和柔性电子等各个领域[1-4].近些年,软材料的力学行为已经成为学术界和工业界广泛关注的热点之一.在实际应用中,软材料一般需要粘附于某种 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.