引言
在地层条件软弱、周围建筑物繁多的城市环境中进行隧道的施工, 不可避免需要穿越和邻近施工, 隧道施工扰动将对既有建(构)筑物的力学状态产生较大影响, 进而导致建筑物的沉降、变形, 甚至发生破坏[1-3]. 在城市运行高可靠度的要求下, 隧道施工引起既有结构的工程响应预测与安全控制问题受到众多专家****与工程人员的广泛关注[4-5]. 浅埋大刚度基础作为城市中低层民用建筑的重要基础形式之一, 在城市密集区隧道工程中较为常见. 因此, 准确预测浅埋隧道施工引起地层与基础结构的工程响应具有十分重大的工程意义.
隧道施工引起的地层变形及其传播是造成既有结构变形破坏的重要诱因, 因此隧道开挖引起的地层变形预测问题一直受到人们的关注[6]. 在城市地层变形理论预测研究方面, 目前相关****采用虚像法[7-8]、Airy应力函数法[9-10]、随机介质理论[11-12]和复变函数法[13-16]来预测不同隧道收敛模式、含隧道衬砌及土体重力效应影响等复杂条件下地层的位移和应力, 取得了诸多有价值的研究成果. 借助保角映射, 复变函数理论可将含复杂形状洞室的半平面映射到像平面内的圆环域, 建立边界方程, 并利用一般幂级数解法确定地层变形和应力, 其求解过程规范、能有效解决含复杂几何边界和力学边界的问题, 因而被广泛应用于岩土工程含隧洞问题的解析预测中. 上述理论成果只针对隧道施工引起地层变形和应力的预测, 尚没有考虑既有结构的存在.
在隧道开挖引起周围既有结构力学响应的理论研究方面, 目前普遍采用温克尔弹性地基梁模型考虑地层与既有结构间相互作用, 将地层视为一系列属性相同、彼此独立的线性弹簧系统[17]. Attewell等[18]将经典温克尔地基梁模型引入新建隧道施工对既有管线的影响研究中; 侯艳娟[19]基于温克尔模型, 结合等代荷载法将隧道开挖引起的基础支承弱化等效为作用于梁(基础)上的附加荷载, 给出了既有基础结构变形和内力的解答; Liu等[20]采用温克尔地基梁模型研究了新建隧道下穿施工既有隧道问题, 考虑了隧道开挖的附加荷载效应与地基支承弱化效应, 对既有隧道结构受力与变形进行了解析研究. 为处理温克尔地基模型无法考虑地层剪切特性的缺陷, 相关****通过新增剪切层的处理办法, 建立了双参数Pasternak模型和三参数Kerr模型等新地基模型, 并在隧道开挖对既有结构影响的理论研究方面取得了诸多成果[21-24].
总体来说, 目前关于隧道施工影响下地层与既有结构相互作用的解析理论基本将土体简化成弹簧系统, 而采用连续介质地基模型并考虑地层与既有结构间接触效应的解析理论鲜有报导. 此外, 城市隧道工程中地层与既有结构间存在复杂相互作用, 其本质是多体接触问题[25]. 因此, 本文将基于线弹性连续介质地基模型, 建立考虑多体接触作用的地层?基础体系力学响应解析预测方法, 研究隧道正交下穿引起的地层?基础体系接触力学响应, 以期为城市隧道下穿浅埋大刚度基础工程的设计与施工提供初步参考.
理论分析的基本假定如下:
(1)基础结构沿隧道轴向具有一定长度, 问题可看成关于竖轴对称的平面应变问题. 将地层视为各项同性均匀线弹性半平面, 忽略重力效应; 考虑大刚度浅基础, 将基础结构简化为作用于地表的刚性体;
(2)地层与基础结构间存在光滑接触作用, 仅考虑接触面法向压力;
(3)采用隧洞边界均匀径向位移u0的单圆收敛模式简单考虑隧道开挖效应;
(4)考虑小变形的情况, 忽略地层变形对隧道几何形位及计算点坐标的影响.
为方便描述, 本文做如下约定: 采用统一直角坐标系xoy, 坐标原点位于原始状态下的接触面中点, X轴、Y轴分别以向右、向上为正; 变量
1.
求解思路与力学模型
1.1
问题求解思路
依据基本假定, 隧道开挖引起的地层?基础体系力学平衡的演化过程如图1所示. 首先, 相比于无应力弹性半平面状态(原始状态), 基础单独作用于地层表面达到一次平衡(初始状态); 接下来, 基于初始状态, 于隧道边界施加增量位移u0, 一次平衡被打破并最终形成二次平衡(最终状态). 本文目标问题是确定最终状态的力学响应, 其关键是最终状态接触压力的求解. 由于最终状态接触力学响应是隧道开挖与接触效应耦合作用的结果, 难以直接确定, 故导致常规求解思路面临极大的困难.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-213-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
目标问题的常规求解过程
Figure
1.
General solving process of the target problem
下载: 全尺寸图片
幻灯片
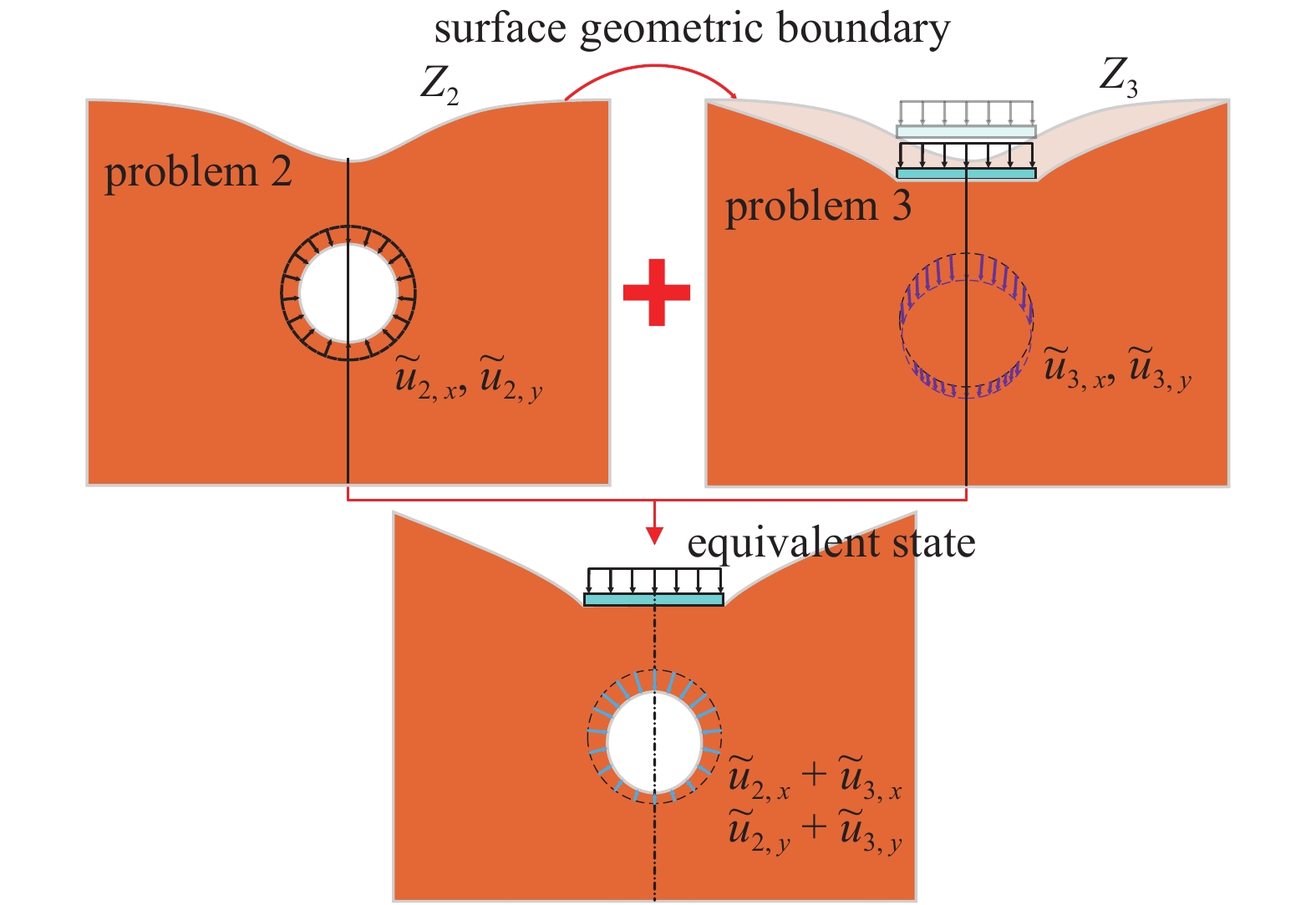
为处理以上困难, 本文依据弹性力学叠加性和应力路径无关性, 提出一种目标问题求解的新策略(见图2), 基于该求解策略形成的等效过程如下: 首先, 于隧道边界施加位移u0并确定地表竖向位移u2, y(x, 0); 接下来, 以曲线u2, y(x, 0)作为新半平面Z3的几何表面, 考虑理想条件下基础与其的接触, 采用接触理论获得接触压力的解答. 需要说明此处忽略了半平面中隧洞的存在对地层?基础体系接触压力计算结果的影响, 经试算, 当隧道埋深与隧道半径之比、隧道埋深与基础宽度之比均大于0.5时, 解析解具有较高的预测精度, 该简化具有合理性; 最后叠加第二、第三部分力学解答(含义见1.1节末问题描述), 得到等效状态力学解答(见图2). 对比图1和图2可知, 最终状态和等效状态的区别体现在隧道边界的位移表达式上. 由基础竖向力平衡可知, 初始状态与等效状态接触压力具有分布规律相似、合力相等的特性, 因此当隧道几何边界具有一定埋深时, 可用位移
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-213-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
目标问题的求解新策略
Figure
2.
New solving strategy for the target problem
下载: 全尺寸图片
幻灯片
基于以上求解新策略, 将原问题转化为求解3个子问题的过程, 并通过叠加对应的三部分解来获得最终解答(见图1和图2). 各子问题描述如下:
问题1: 弹性半平面Z1表面作用刚性基础, 基础上部作用均布荷载q, 接触范围外地表为自由应力边界. 半平面Z1的应力与位移解答对应第一部分解.
问题2: 含一圆形隧洞的弹性半平面Z2, 其隧道边界为均匀径向位移边界(值为u0), 半平面表面为自由应力边界. 半平面Z2的应力与位移解答对应第二部分解.
问题3: 以问题2确定的地表竖向变形曲线为表面几何边界的弹性半平面Z3, 其表面对称作用刚性基础, 基础上部作用均布荷载q, 接触范围外地表为自由应力边界. 半平面Z3的应力与位移解答对应第三部分解.
1.2
力学模型建立
根据以上内容, 针对本文待求的三个部分解答分别建立了以下力学模型.
图3(a)为第二部分解的力学模型. E和μ分别代表地层的杨氏模量和泊松比; 隧道埋深与半径分别用h与R表示; u0为隧道边界均匀径向位移值.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-213-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
力学分析模型
Figure
3.
Mechanical analysis models
下载: 全尺寸图片
幻灯片
图3(b)为最终状态的接触分析模型. L代表基础半宽度; 其余符号含义见下文接触压力的理论推导部分.
图3(c)为第一、第三部分解的力学模型. V(x)代表作用于地表的竖向分布荷载, 其作用范围为(x1, x2).
图3(d)为基础结构的力学分析模型. Mf(x0), Qf(x0)分别代表基础x0断面处的弯矩和剪力.
接下来, 基于以上力学模型, 分别针对各部分解答展开理论推导, 详细推导过程见本文第2章.
2.
解析方法
2.1
隧道均布收敛下地层响应解答
基于图3(a)所示力学分析模型, 本文采用复变函数理论开展第二部分解答的推导. 目前, 相关****已针对此类问题开展大量研究, 本文直接引用相关成果[15, 26-28]. 根据复变函数理论, 地层应力与位移分量均可由复平面Z2内两个解析函数φ1(z)和ψ1(z)表示, 其中地层应力的表达为
$$left. begin{array}{l} {sigma _{2,x}} = { m{Re}} left[ {2{{varphi '}_1}({textit{z}}) - overline {textit{z}} {{varphi ''}_1}({textit{z}}) - {{psi '}_1}({textit{z}})} ight] {sigma _{2,y}} = { m{Re}} left[ {2{{varphi '}_1}({textit{z}}) + overline {textit{z}} {{varphi ''}_1}({textit{z}}) + {{psi '}_1}({textit{z}})} ight] {tau _{2,xy}} = { m{Im}} left[ {overline {textit{z}} {{varphi ''}_1}({textit{z}}) + {{psi '}_1}({textit{z}})} ight] end{array} ight}$$  | (1) |
地层位移可表示为
$$left. begin{array}{l} 2G{u_{2,x}} = { m{Re}} [kappa {varphi _1}({textit{z}}) - {textit{z}}overline {{{varphi '}_1}({textit{z}})} - overline {{psi _1}({textit{z}})} ] 2G{u_{2,y}} = { m{Im}} [kappa {varphi _1}({textit{z}}) - {textit{z}}overline {{{varphi '}_1}({textit{z}})} - overline {{psi _1}({textit{z}})} ] end{array} ight}$$  | (2) |
式中, z为复平面Z2内任意点, z = x + iy; κ是材料常数, 对于平面应变问题κ = 3?4μ, μ为地层泊松比; G为地层剪切模量, G = E/[2(1 + μ)]; 上标“—”表示对复数取共轭.
采用保角映射[13]ω(ζ)将物理平面Z2映射成象平面ζ内的内、外半径分别为α, 1的单位圆环域
$${textit{z}} = omega (zeta) = - { m{i}}hfrac{{1 - {alpha ^2}}}{{1 + {alpha ^2}}}frac{{1 + zeta }}{{1 - zeta }}$$  | (3) |
式中, α (0 < α < 1)由方程R/h = 2α/(1 + α2)确定; ζ为单位圆环内任意点, ζ = ξ + iη = ρeiθ, α ≤ ρ ≤ 1.
利用式结合解析函数φ1(z), ψ1(z)中单值解析部分的Laurent级数展开特性, 得原解析函数在ζ平面内的表达如下
$$left. begin{array}{l} varphi (zeta) = {varphi _1}(omega (zeta)) = {e_0}ln zeta + displaystylesumlimits_{k = 0}^{{N_1}} {{a_k}} {zeta ^k} + displaystylesumlimits_{k = 1}^{{N_1}} {{b_k}} {zeta ^{ - k}} psi (zeta) = {psi _1}(omega (zeta)) = - kappa overline {{e_0}} ln zeta + displaystylesumlimits_{k = 1}^{{N_1}} {{c_k}} {zeta ^k} + displaystylesumlimits_{k = 1}^{{N_1}} {{d_k}} {zeta ^{ - k}} end{array} ight}$$  | (4) |
式中ak, bk, ck, dk及e0均为待定复系数. 在计算过程中, φ(ζ), ψ(ζ)的ζ最高正(负)幂次分别取为N1, N1 + 2, 因此解析函数中共有4N1 + 6个待定复系数.
依据复合函数求导法则, 解析函数φ1(z), ψ1(z)的各阶导数在ζ平面内的表达式如下
$$left. begin{array}{l} {{varphi '}_1}({textit{z}}) = dfrac{{varphi '(zeta)}}{{omega '(zeta)}} {{varphi ''}_1}({textit{z}}) = dfrac{{omega '(zeta)varphi ''(zeta) - omega ''(zeta)varphi '(zeta)}}{{{{omega '(zeta)}^3}}} {{psi '}_1}({textit{z}}) = dfrac{{psi '(zeta)}}{{omega '(zeta)}} end{array} ight}$$  | (5) |
本文采用基于频域分析的求解方法来确定待定复系数, 具体解析理论与求解过程可参考文献[29-30]. 首先, 利用单位圆环外边界的自由应力条件建立两个正交应力分量方程, 并用单位圆环内边界的切向、法向位移条件建立两个正交位移分量的方程; 然后根据频域分析法, 利用Fourier变换将4个边界方程转化到频域中进行分析, 取前N1 + 2阶频率(不包括零阶频率)可建立含8N1 + 20个方程的线性方程组; 此外, 取(± 100, 0)作为地层竖向位移的零位移参考点来建立2个附加方程; 进而联立8N1 + 22个线性方程确定4N1 + 6个待定复系数; 最后, 将式(3) ~ 式(5)带入式(1)和式(2)分别确定第二部分解答中地层的应力分量(σ2, x, σ2, y, τ2, xy)和位移分量(u2, x, u2, y).
2.2
地层与基础间接触压力解答
2.2.1
弹性接触理论基本方程
在直角坐标系xoy下, 根据弹性接触理论[31], 弹性半平面表面一定范围内地层的受力与变形之间满足关系
$$left. begin{array}{l} dfrac{{partial {{tilde u}_x}}}{{partial x}} = dfrac{{(1 - 2mu)(1 + mu)}}{E}V(x) - dfrac{{2(1 - {mu ^2})}}{{{text{π}} E}}displaystyleint_{{x_1}}^{{x_2}} {dfrac{{H(s)}}{{x - s}}} { m{d}}s - dfrac{{partial {{tilde u}_y}}}{{partial x}} = dfrac{{2{{(1 - mu)}^2}}}{{{text{π}} E}}displaystyleint_{{x_1}}^{{x_2}} {dfrac{{V(s)}}{{x - s}}} { m{d}}s + dfrac{{(1 - 2mu)(1 + mu)}}{E}H(x) end{array} ight}$$  | (6) |
式(6)即为接触控制方程. 式中, H(x)和V(x)分别表示弹性半平面表面的水平和竖向分布力, 其作用范围为(x1, x2), 方向分别沿X轴和Y轴正向;
依据本文假定, 考虑光滑接触, 第一部分解的核心是确定均布荷载q作用下地层与基础间的接触压力p1(x), 该问题与顶部光滑的刚性冲头垂直压入弹性半平面问题具有相同的解答, 依据文献[31], 其接触压力p1(x)的解析式为
$${p_1}(x) = - frac{{2qL}}{{{text{π}} {{({L^2} - {x^2})}^{{1 / 2}}}}},;;;x in ( - L,L)$$  | (7) |
2.2.2
最终状态接触压力p3(x)
由问题3定义可知, 需采用u2, y(x, 0)曲线来刻画半平面Z3表面几何边界. 由于竖向位移u2, y(x, 0)为级数解, 为方便p3(x)的数学推导, 本文采用Sagaseta[7]建议的公式来描述由地层损失引起的地表沉降值, 其表达式为
$$S(x) = - frac{{{S_{max }}}}{{{{(1 + {x^2}/{h^2})}^{{alpha _1}}}}}$$  | (8) |
式中, Smax为最大地表沉降的绝对值; α1为待定的常数, 本文中可通过接触范围内u2, y(x, 0)的数值采用最小二乘法计算.
观察图3(b)中浅色部分基础与地层间的几何关系, 结合式(8)不难看出基础与地表间的间隙函数表达式如下
$$g(x) = S(x) - S(L)$$  | (9) |
在接触范围(?L, L)内, 基础几何边界与地表竖向变形间存在如下几何关系
$${u_{3,y}}(x,0) + g(x) = {delta _2}, ;;;- L < x < L$$  | (10) |
式中, u3, y(x, 0)为接触范围内地表竖向位移; δ2 (δ2 < 0)为基础竖向位移, 此问题中为一常数.
依据假设, 将式(8) ~ 式(10)带入式(6), 令H(x) = 0, 得接触压力p3(x)的积分控制方程
$$frac{{2(1 - {mu ^2})}}{{{text{π}} E}}int_{ - L}^L {frac{{{p_3}(s)}}{{x - s}}{ m{d}}s = !frac{{2{alpha _1}{h^{2{alpha _1}}}{S_{max }}x}}{{{{({x^2} + {h^2})}^{{alpha _1} + 1}}}}} ,;; - L < x < L$$  | (11) |
利用? = x/L, T = s/L及P(?) = p3(x)的代换将式(11)标准化, 得
$$int_{{ m{ - }}1}^1 {frac{{P(T)}}{{varsigma - T}}} { m{d}}T = frac{{{text{π}} E{alpha _1}{h^{2{alpha _1}}}L{S_{max }}varsigma }}{{(1 - {mu ^2}){{({L^2}{varsigma ^2} + {h^2})}^{{alpha _1} + 1}}}},;; - 1 < varsigma < 1$$  | (12) |
式(12)在T = ?处奇异, 本文直接引用该类“奇异积分方程”的相关成果[32], 其解为
$$begin{split} P(varsigma) = &- frac{A}{{{{text{π}} ^2}{{(1 - {varsigma ^2})}^{{1 / 2}}}}}int_{ - 1}^1 {frac{{{{(1 - T)}^{{1 / 2}}}}}{{varsigma - T}}frac{T}{{{{({T^2} + {a^2})}^{{alpha _1} + 1}}}}} { m{d}}T +&frac{{{C_1}}}{{{{text{π}} ^2}{{(1 - {varsigma ^2})}^{{1 / 2}}}}},;;; - 1 < varsigma < 1 [-15pt]end{split} $$  | (13) |
式中
$$left. begin{array}{l} A = {text{π}} E{alpha _1}{h^{2{alpha _1}}}{{ m{S}}_{max }}/[(1 - {mu ^2}{ m{)}}{L^{2{alpha _1} + 1}}{ m{]}} a = h/L {C_1} = {text{π}} displaystyleint_{ - 1}^1 {P(T)} { m{d}}T end{array} ight}$$  | (14) |
$$left. {begin{array}{*{20}{l}} {f(T){ m{ = }}displaystylesumlimits_{n = 0}^{{N_2}} {{B_n}} {T^{2n}},;;; - 1 < T < 1} {{B_n} = left{ begin{array}{l} {a^{ - 2({alpha _1} + 1)}},;;;n = 0 dfrac{{{{( - 1)}^n}{a^{ - 2({alpha _1} + n + 1)}}displaystyleprodlimits_{k = 1}^n {({alpha _1} + k)} }}{{n!}},;;;n = 1,2, cdots, {N_2} end{array} !!!!! ight.} end{array}} ight}$$  | (15) |
忽略余项, 考虑a > 1的情况, 采用式中麦克劳林展开的前N2 + 1项替代式(13)中的
$$begin{split} P(varsigma) = &- frac{A}{{{{text{π}} ^2}{{(1 - {varsigma ^2})}^{{1 / 2}}}}}sumlimits_{n = 0}^{{N_2}} {{B_n}{I_{2n + 1}}} (varsigma) +&frac{{{C_1}}}{{{{text{π}} ^2}{{(1 - {varsigma ^2})}^{{1 / 2}}}}},;;; - 1 < varsigma < 1 end{split}$$  | (16) |
式中
m{d}}T$
$$begin{split}{I_{2n + 1}}(varsigma ) =& {text{π}} left[ {{varsigma ^{2n + 2}} - frac{1}{2}{varsigma ^{2n}} - frac{1}{8}{varsigma ^{2n - 2}} - cdots } - ight.&left. { frac{{1 cdot 3cdot; cdots ;cdot(2n - 1)}}{{2 cdot 4 cdot;cdots;cdot (2n + 2)}}} ight],;;n = 0,1,2 , cdotsend{split}$$  | (17) |
至此, P(?)表达式中只有常数C1未知. 对式(11)而言, 利用第一类奇异积分方程一般解可得p3(x)表达式中对应常数C2的结果, 再结合代换? = x/L, P(?) = p3(x), 建立常数C1和C2的关系式如下
$${C_2}{ m{ = }}{text{π}} int_{ - L}^L {p(s){ m{d}}s = } {text{π}} Lint_{ - 1}^1 {P(T){ m{d}}T} = L{C_1}$$  | (18) |
考虑基础结构竖向力平衡, 有
$$int_{ - L}^L {p(s){ m{d}}s} = - int_{ - L}^L {q(s){ m{d}}s} = - 2qL$$  | (19) |
联立式(18)、式(19)求得C1, 再将式(14)、式(15)及式(17)带入式(16)确定P(?)表达, 最后结式P(?) = p3(x), 最终得第三部分解中接触压力p3(x)的解析表达为
$${p_3}(x) = - frac{L}{{{{text{π}} ^2}{{({L^2} - {x^2})}^{{1 / 2}}}}}left[Asumlimits_{n = 0}^{{N_2}} {{B_n}{I_{2n + 1}}} left(dfrac{x}{L} ight) + 2{text{π}} q ight]$$  | (20) |
式中各未知参数表达见前文, x∈(?L, L).
2.3
第一、第三部分解答
利用2.2节中的式(7)和式(20)可分别确定地层?基础体系的初始状态接触压力p1(x)和最终状态接触压力p3(x). 接下来, 通过Flamant基本解的积分可计算地层中任意点的应力和位移分量值, 进而获得本文第一、第三部分解答.
地层中各点正应力与剪应力表达式为
$$left. begin{array}{l} {sigma _{xx}} = - dfrac{2}{{text{π}} }displaystyleint_{{x_1}}^{{x_2}} { {dfrac{{y{{(x - s)}^2}V(s)}}{{{{[{{(x - s)}^2} + {y^2}]}^2}}} + dfrac{{{{(x - s)}^3}H(s)}}{{{{[{{(x - s)}^2} + {y^2}]}^2}}}} } { m{d}}s {sigma _{yy}} = - dfrac{2}{{text{π}} }displaystyleint_{{x_1}}^{{x_2}} { {dfrac{{{y^3}V(s)}}{{{{[{{(x - s)}^2} + {y^2}]}^2}}} + dfrac{{{y^2}(x - s)H(s)}}{{{{[{{(x - s)}^2} + {y^2}]}^2}}}} } { m{d}}s {tau _{xy}} = - dfrac{2}{{text{π}} }displaystyleint_{{x_1}}^{{x_2}} { {dfrac{{{y^2}(x - s)V(s)}}{{{{[{{(x - s)}^2} + {y^2}]}^2}}} + dfrac{{y{{(x - s)}^2}H(s)}}{{{{[{{(x - s)}^2} + {y^2}]}^2}}}} } { m{d}}s end{array} ight}$$  | (21) |
各点位移表达式为
$$!!!!!!!!!!left. {begin{array}{*{20}{l}}begin{array}{l}{u_x} = displaystyleint_{{x_1}}^{{x_2}} { { - left[ {dfrac{{(1 - 2mu )(1 + mu )}}{{{text{π}} E}}arctan dfrac{{x - s}}{y} - } ight.} } ;;;;;;left. {dfrac{{1 + mu }}{{{text{π}} E}}dfrac{{(x - s)y}}{{{{(x - s)}^2} + {y^2}}}} ight]V(s) - ;left{ {dfrac{{1 - {mu ^2}}}{{{text{π}} E}}ln left[{{(x - s)}^2} + {y^2} ight] - } ight. {left. {;;;;;;dfrac{{1 + mu }}{{{text{π}} E}}dfrac{{{{(x - s)}^2}}}{{{{(x - s)}^2} + {y^2}}}} ight}H(s)} { m{d}}s + {A_1}end{array} begin{array}{l}{u_y} = displaystyleint_{{x_1}}^{{x_2}} { { - left{ {dfrac{{1 - {mu ^2}}}{{{text{π}} E}}ln left[{{(x - s)}^2} + {y^2} ight] + } ight.} } left. {;;;;;;;dfrac{{1 + mu }}{{{text{π}} E}}dfrac{{{{(x - s)}^2}}}{{{{(x - s)}^2} + {y^2}}}} ight}V(s) + left[ {dfrac{{(1 - 2mu )(1 + mu )}}{{{text{π}} E}}} ight.cdot {;;;;;;;;arctan dfrac{{x - s}}{y} + left. {dfrac{{1 + mu }}{{{text{π}} E}}dfrac{{(x - s)y}}{{{{(x - s)}^2} + {y^2}}}} ight]H(s)} { m{d}}s + {A_2}end{array}end{array}} ight}$$  | (22) |
式中A1和A2分别表征水平和竖向刚体位移, 需选定零位移参考点确定. 依据问题对称性, A1 = 0, A2选定(?100, ?200)点为竖向零位移点计算确定.
基于图3(c)的力学模型, 将式(23)带入式(21)和式(22)可得第一部分解的应力分量(σ1, x, σ1, y, τ1, xy)和位移分量(u1, x, u1, y)
$$begin{split} V(x) = {p_1}(x),;;H(x) = 0,;;{x_1} = - L,;;{x_2} = Lend{split}$$  | (23) |
对于第三部分解的地层应力分量(σ3, x, σ3, y, τ3, xy)和位移分量(u3, x, u3, y), 可通过将式(24)带入式(21)和式(22)计算确定
$$V(x) = {p_3}(x),;;H(x) = 0,;;{x_1} = - L,;;{x_2} = L$$  | (24) |
2.4
最终状态地层与基础的响应解答
根据本文提出的目标问题求解新策略, 采用等效状态替代最终状态, 并叠加第二、第三部分解答确定等效状态的应力与位移分量如下
$$left. begin{array}{l} {sigma _x} = {sigma _{2,x}} + {sigma _{3,x}},;;{sigma _y} = {sigma _{2,y}} + {sigma _{3,y}} {tau _{xy}} = {tau _{2,xy}} + {tau _{3,xy}} {u_x} = {u_{2,x}} + {u_{3,x}},;;{u_y} = {u_{2,y}} + {u_{3,y}} end{array} ight}$$  | (25) |
工程中重点关注的由隧道开挖引起的地层与既有结构的附加位移为
$$left. begin{array}{l} {U_x} = {u_{2,x}} + {u_{3,x}} - {u_{1,x}} {U_y} = {u_{2,y}} + {u_{3,y}} - {u_{1,y}} end{array} ight}$$  | (26) |
基于图3(d)的力学模型, 对基础进行受力分析, 得基础x断面处弯矩Mf和剪力Qf表达式如下
$$left. begin{array}{l} {M_{ m{f}}}(x) = displaystyleint_{ - L}^x {(s - x)[{p_3}(s) + q]} { m{d}}s {Q_{ m{f}}}(x) = - displaystyleint_{ - L}^x {[{p_3}(s) + q]} { m{d}}s end{array} ight}$$  | (27) |
本文解析结果均依据上文解析方法采用程序计算确定, 实际计算中为保证计算结果精度, 取参数N1 = 100, N2 = 50.
3.
解析验证
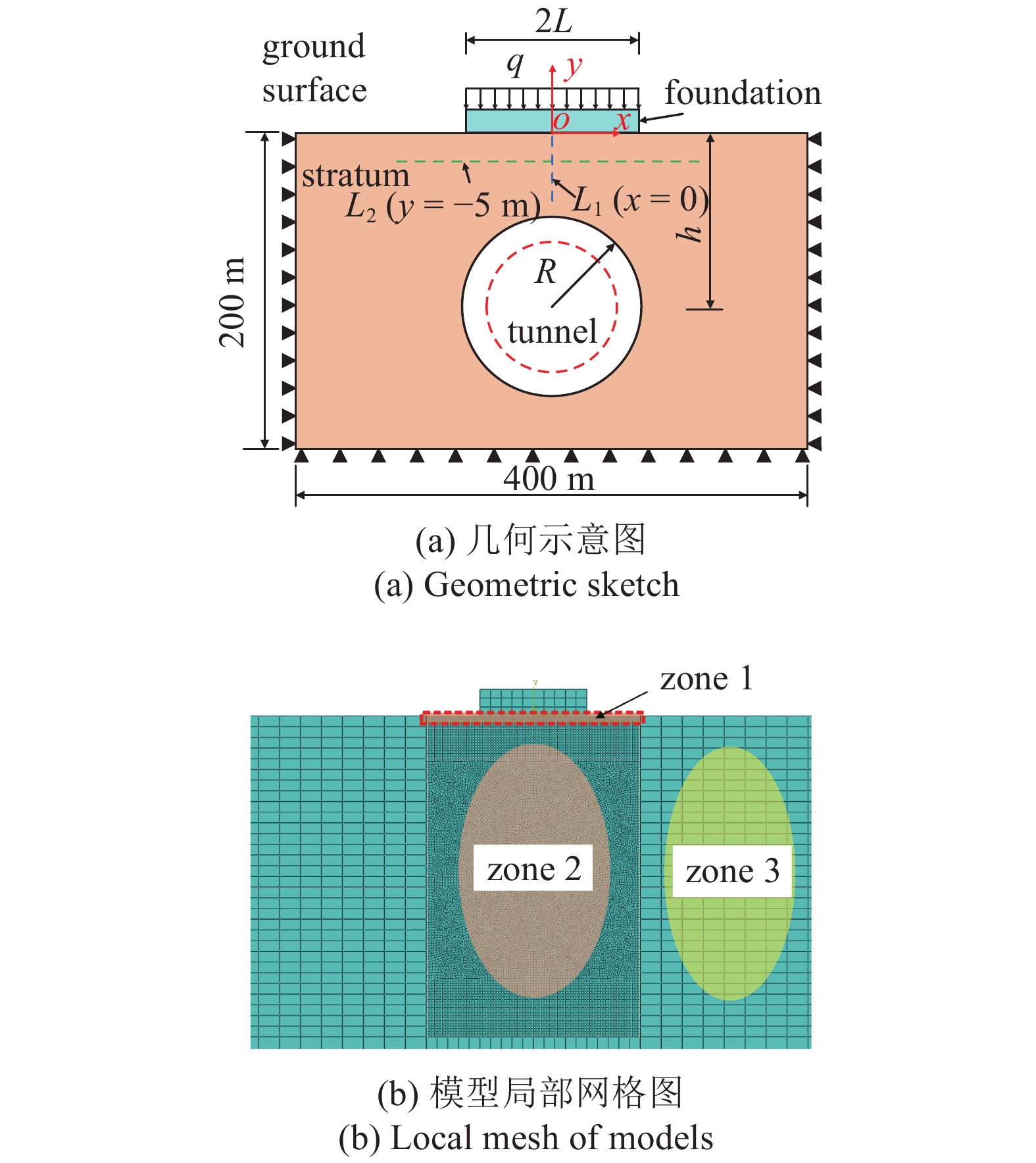
为验证本文解析理论正确性, 引入ABAQUS有限元软件进行计算分析. 按图4(a)所示示意图建立平面数值模型, 该模型为由400 m × 200 m的地层和20 m × 5 m的基础组成的整体, 地层为均匀各向同性线弹性体, 基础为刚性体, 地层与基础结构间接触采用ABAQUS中计算精度高且稳定性好的“面对面接触”算法模拟, 接触类型依据光滑接触假定定义为无摩擦接触. 为优化数值计算精度与单元数量间匹配性, 利用ABAQUS非协调网格技术实现对隧道及基础周围地层单元的局部加密处理, 并最终形成如图4(b)所示的分区加密计算网格, 其中各区域网格控制尺寸选定如下: 区域1网格控制尺寸(记为Ms)取0.05 m, 区域2, 3分别取0.5 m, 4 m. 数值模拟过程分以下两个步骤进行: 第1步, 施加约束条件, 并于基础上表面作用竖向均布荷载q, 计算保存; 第2步, 在第1步的基础上, 先冻结隧道边界内单元, 不考虑衬砌作用, 并在隧道边界上施加均匀径向增量位移u0, 计算最终状态的力学响应.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-213-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
数值模型的几何示意和计算网格
Figure
4.
Geometric sketch and computational mesh of numerical models
下载: 全尺寸图片
幻灯片
本文所有计算模型及其对应的计算参数见表1, 表中所有参数符号含义同上文, 此外所有计算模型的隧道半径R和基础半宽度L分别取为6 m和10 m.
表
1
模型计算参数
Table
1.
Computational parameters of models
table_type1 ">
| Group no. | Model no. | E /MPa | μ | h /m | u0 /mm | q /(kN·m?1) |
| 1 | 1 | 30 | 0.3 | 30 | ?60 | 20 |
| 2 | 35 | |||||
| 3 | 40 | |||||
| 4 | 45 | |||||
| 5 | 50 | |||||
| 2 | 6 | 40 | 0.25 | 30 | ?60 | 20 |
| 3 | 0.3 | |||||
| 7 | 0.35 | |||||
| 8 | 0.4 | |||||
| 3 | 9 | 40 | 0.3 | 23 | ?60 | 20 |
| 10 | 24 | |||||
| 11 | 25 | |||||
| 12 | 28 | |||||
| 3 | 30 | |||||
| 4 | 13 | 40 | 0.3 | 20 | ?20 | 20 |
| 14 | ?25 | |||||
| 15 | ?30 | |||||
| 16 | ?35 | |||||
| 17 | ?40 | |||||
| 5 | 18 | 40 | 0.3 | 20 | ?60 | 30 |
| 19 | 35 | |||||
| 20 | 40 | |||||
| 21 | 45 | |||||
| 22 | 50 |
下载: 导出CSV
|显示表格
为较全面地分析、验证解析方法的正确性, 采用该方法计算表1中第2, 3组参数模型解析解, 同时借助ABAQUS计算对应数值解, 并重点对比分析了模型3的地层位移场(ux, uy)以及不同参数下测线(L1, L2, 位置见图4(a))上各点竖向位移uy的解析解和数值解, 结果示于图5.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-213-5.jpg'" class="figure_img
figure_type2 ccc " id="Figure5" />
图
5
不同工况解析解与数值解对比分析
Figure
5.
Comparisons of analytical solution and numerical solution under different conditions
下载: 全尺寸图片
幻灯片
为方便对比分析, 取位移分量与均匀径向位移绝对值|u0|的比值, 对位移进行归一化处理. 图5(a)、图5(b)分别给出了模型3地层归一化竖向位移场、水平位移场的解析解与数值解对比结果, 可以发现位移解析解与数值解均关于Y轴对称, 两者具有较高的吻合度. 为探究不同参数下解析解的准确性, 图5(c) ~ 图5(f)对比分析了不同泊松比μ与埋深h情况下地层归一化竖向位移uy/|u0|的解析解和数值解, 可以看出在参数改变时, 解析解均保持较高的准确度. 以上对比结果说明了本文新求解策略的合理性, 同时也验证了本文解析方法的正确性.
需注意, 当泊松比较大或隧道埋深较小时, uy/|u0|解析解与数值解间的差异相对明显(最大约2%), 且数值上近乎相差一个常数(见图5(c), 图5(f)), 这是由积分法求解位移过程中“零”位移基准点选取的偏差造成的, 但可以通过优化“零”位移基准点的选取来获得精度更高的解答. 对于一般情况, 可以期望本文的解析理论给出较高精度的解答.
接触力学响应无疑是接触类问题的核心. 在本文数值计算中, 区域1网格控制尺寸大小对计算结果精度具有较大影响. 图6展示了在模型3的参数条件下, 改变Ms时接触压力的数值结果, 同时给出了接触压力的解析值. 从图中局部放大部分可知, 随着Ms不断减小, 更精细的模型显著提升了接触压力的计算精度, 且数值解与解析解间的误差也越来越小. 因此, 本文解析理论为此类问题接触压力的确定提供了一种准确、高效的计算方法, 同时也为此类问题中地层与基础结构相互作用的解耦分析提供了理论基础.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-213-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
网格尺寸Ms对接触压力计算结果的影响
Figure
6.
Influence of mesh size, Ms, on calculation results of the contact pressure
下载: 全尺寸图片
幻灯片
4.
参数分析
实际工程中, 地层与基础间接触压力、基础结构内力以及由隧道开挖引起的地层?基础体系的附加位移等的分布是工程人员重点关注的内容, 同时也是工前结构设计与施工中安全状态评估的重要依据. 基于本文解析方法, 计算地层?基础体系的接触压力p3(x)、地表附加竖向位移Uy(x, 0)以及基础结构弯矩Mf(x)和剪力Qf(x), 并重点讨论了地层杨氏模量E、地层泊松比μ、隧道埋深h、隧道边界均匀径向位移u0以及基础外荷载集度q的影响.
4.1
地层参数的影响
地层作为向基础结构传递隧道施工影响的关键媒介, 其力学参数无疑对隧道施工扰动下地层?基础系统力学响应有着重要影响.
(1) 地层杨氏模量E的影响
选取30, 35, 40, 45和50 MPa 五种地层杨氏模量, 具体参数见表1第1组参数, 计算结果示于图7. 从图7中可以看出, 对于本对称问题, 接触压力、基础弯矩分布均关于Y轴对称, 基础剪力则关于原点呈中心对称分布; 基础弯矩峰值位于基础中点处, 而基础剪力峰值则对称地出现在距基础端部约0.3L位置处, 因此工程中应注重满足基础中部抗弯能力及基础端部附近抗剪能力的要求. 具体到地层杨氏模量E的影响, 观察图7(a)可以发现随着E的增加, 接触压力表现出基础中部区域逐渐释放、两端进一步集中的变化规律, 表明基础受力状态正在逐步恶化. 不仅如此, 杨氏模量的改变会进一步加剧基础结构的内力集中. 例如, 对于Mf, 当E = 30 MPa时, 基础弯矩峰值为412.59 kN·m (x = 0 m); 当E = 50 MPa时, 基础弯矩峰值为506.72 kN·m (x = 0 m), 相比于30 MPa, 基础弯矩峰值增长了约22.8%. 以上结果表明, 杨氏模量的变化对地层?基础体系接触状态和基础结构受力状态具有显著影响.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-213-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
地层杨氏模量E的影响
Figure
7.
Influence of the Young’s modulus of stratum (E)
下载: 全尺寸图片
幻灯片
通过计算还发现, E的改变对地表附加竖向位移Uy(x, 0)的分布几乎没有影响, 但不同E对应的地表竖向位移uy(x, 0)会有所差别. 以上分析表明, 地层杨氏模量的变化更倾向于造成接触压力和基础内力的改变, 而对地表附加竖向位移则影响甚微.
(2) 地层泊松比μ的影响
选取0.25, 0.3, 0.35和0.4 四种地层泊松比, 具体计算参数见表1第2组参数, 主要计算结果如图8所示. 从图中可以看出改变地层泊松比, Uy(x, 0)和Qf的分布形态没有变化, 其中Uy(x, 0)分布呈平底“V”型, 并未呈现常规的槽型分布, 表明接触面附近地层附加竖向位移受接触作用的影响显著, 且地表各点Uy(x, 0)值整体上随着μ的增大而减小(见图8(a)). 不同于地层杨氏模量的影响, 地层泊松比μ的变化对Uy(x, 0)的影响效果更明显, 而对接触压力和基础内力分布的影响程度较小. 以上结果表明, 地层泊松比的改变对地表附加竖向位移具有一定程度的影响, 但对接触压力和基础受力的影响水平较低.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-213-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
地层泊松比μ的影响
Figure
8.
Influence of the Poisson’s ratio of stratum (μ)
下载: 全尺寸图片
幻灯片
4.2
隧道埋深h的影响
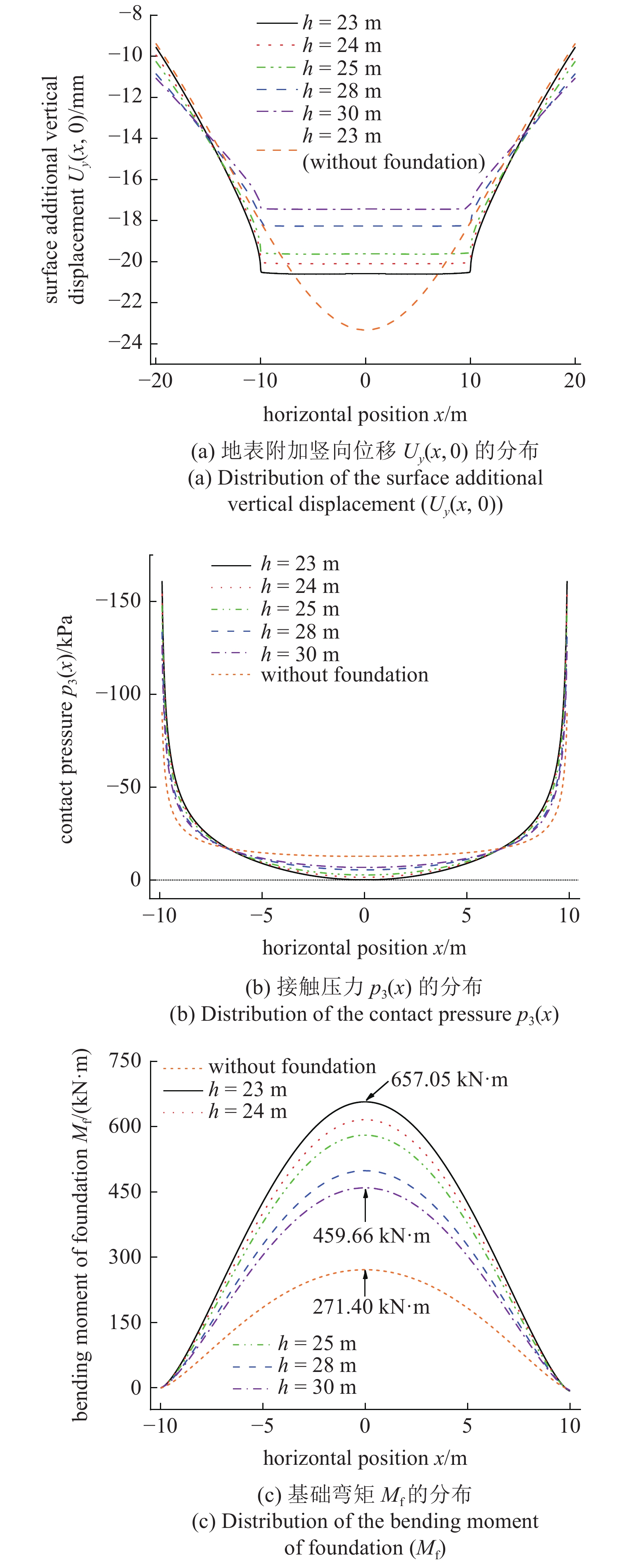
地层变形向周围传播具有随距离增大逐渐衰减的特性, 因此隧道埋深与地层?基础体系的力学响应密切相关. 选取23, 24, 25, 28和30 m 五种隧道埋深, 其余参数见表1第3组参数, 计算结果见图9. 可以看出隧道埋深h对地表附加竖向位移Uy(x, 0)的影响规律表现出区域差异性(见图9(a)), 在[?15, 15]范围内Uy(x, 0)随着h减小而增大, 在此范围外则表现出相反的变化规律. 不仅如此, 当h = 23 m时, 观察图9(a)中有、无基础情况下Uy(x, 0)的分布可知, 两种情况下的Uy(x, 0)值亦在[?15, 15]范围内差异明显, 此范围外两者的地表附加竖向位移值近乎相等. 以上结果表明, 地层变形是隧道开挖扰动与地层?基础接触效应耦合作用的结果, 该耦合作用在远离接触区域时逐渐表现出隧道开挖扰动影响占主导地位的趋势, 由此可见基础的存在对地层变形分布的显著影响区域有限, 验证了本文采用等效状态替代最终状态的合理性.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-213-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
隧道埋深h的影响
Figure
9.
Influence of the tunnel buried depth (h)
下载: 全尺寸图片
幻灯片
对于接触压力p3(x) (见图9(b)), 相比于无隧道情况, 隧道开挖扰动下的接触压力产生了显著的中部释放、端部集中的重分布现象, 且其重分布程度随着隧道埋深的减小而加剧, 说明隧道施工扰动造成基础接触及受力状态的恶化, 这从基础弯矩峰值的大幅增长可以看出(见图9(c)). 此外, 隧道埋深减小将导致基础中部接触压力值逐渐降为零, 当接触面无承拉能力时, 地层?基础体系将产生竖向位移不连续的脱空接触现象, 这是强烈的接触作用结果, 在地层?基础体系力学响应的预测中应予以充分考虑. 以上分析表明隧道埋深对地层?基础体系各方面力学响应均有着显著的影响.
4.3
洞周均匀径向位移u0的影响
洞周均匀径向位移u0也直接决定了隧道施工扰动的剧烈程度. 选定?20, ?25, ?30, ?35和?40 mm五种洞周均匀径向位移, 并与无隧道开挖情况计算结果作对比, 具体计算参数见表1第4组参数. 图10(a)和图10(b)分别绘制了Uy(x, 0)和p3(x)的分布. 对于地表附加竖向位移Uy(x, 0), |u0|的增大导致地表各点处Uy(x, 0)值的整体增大, 这与前文h减小时所表现的区域性影响略有差别. 对于接触压力p3(x), |u0|的增大与h的减小对p3(x)分布规律的影响相似, 同时可以看出当|u0|增大到一定程度后亦会引起地层?基础体系中部脱空接触现象的发生. 隧道边界均匀径向位移u0及隧道埋深h均与隧道施工扰动程度关系密切, 因此两者对地层?基础体系力学响应的影响规律相似.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-213-10.jpg'" class="figure_img
figure_type1 bbb " id="Figure10" />
图
10
均匀径向位移u0的影响
Figure
10.
Influence of the uniform radial displacement (u0)
下载: 全尺寸图片
幻灯片
4.4
外荷载集度q的影响
以上分析主要讨论了地层物理力学参数及隧道相关参数的影响, 本节考虑基础上覆荷载集度q的影响. 选定30, 35, 40, 45和50 kN/m 五种外荷载集度, 其余计算参数见表1中第5组参数. 图11(a)绘制了仅改变q时接触压力的分布情况. 从图中可以看出, 高荷载集度对应的接触压力整体量值大, 但低荷载集度下接触压力中部释放、两端集中的程度更严重. 观察图11(b), 图11(c)所示的基础弯矩、剪力分布情况可知, 虽然高荷载集度减弱了接触压力的重分布程度, 但基础内力仍表现出“集度高, 内力大”的变化规律.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-213-11.jpg'" class="figure_img
figure_type1 bbb " id="Figure11" />
图
11
外荷载集度q的影响
Figure
11.
Influence of the intensity of external loads (q)
下载: 全尺寸图片
幻灯片
此外, 通过对Uy(x, 0)计算结果的分析发现: q的大小只影响地层竖向位移uy(x, 0)的值, 而对地表附加竖向位移Uy(x, 0)则几乎无影响(未画出), 该结果表明从源头上控制隧道施工扰动可有效控制地层?基础体系的附加位移响应, 但高荷载集度下的变形控制措施要求更加严格.
5.
结论
本文基于平面应变假设, 将地层视为线弹性半平面, 通过引入弹性接触理论考虑地层?基础体系的接触作用, 并针对接触压力求解这一核心问题提出了以“隧道开挖与基础作用换序求解”为关键的新解析策略, 最终建立了浅埋隧道开挖扰动下地层?基础体系力学响应的耦合解析方法. 通过解析解与ABAQUS数值解对比结果的高度吻合验证了该解析方法的正确性. 基于此进行了影响因素分析, 获得以下主要结论:
(1)隧道开挖扰动对地层?基础体系地表附加竖向位移、接触压力、基础弯矩与剪力均存在不同程度影响. 在接触作用影响下, 隧道开挖引起的地表附加竖向位移呈现平底“V”型分布, 相比于传统沉降槽分布表现出显著的接触相关性; 接触压力发生不同程度的“中间释放、端部集中”的重分布现象, 并会造成基础弯矩、剪力峰值的大幅增长, 一定程度上劣化了基础的受力状态.
(2)地层杨氏模量变化对隧道开挖引起的地层?基础体系的接触压力和基础内力有一定程度的影响, 但几乎不改变地表附加竖向位移的大小; 与之相比, 地层泊松比的影响则更侧重于地表附加竖向变形的改变, 而对接触压力和基础内力的影响甚微.
(3)隧道埋深和隧道边界均匀收敛变形的改变直接决定隧道施工扰动的强弱程度, 二者均对地层?基础体系各力学响应有着显著影响. 当隧道埋深减小或隧道边界均匀径向收敛变形增大到一定程度时, 强烈的接触作用会造成地层与基础间产生变形不连续的脱空接触现象, 同时伴随着应力的高度集中, 实际工程中应及时采取加固措施避免此类情况的出现; 尽管高荷载集度可在一定程度上减弱接触压力“中部释放、端部集中”的程度, 但基础内力仍表现出“集度高, 内力大”的变化规律.
(4)本文解析方法可量化描述地层与基础间的接触力学行为, 同时也为地层?基础体系接触压力的预测提供了可靠的理论方法. 研究成果为浅埋隧道正交下穿影响下地层?基础体系的接触力学行为描述及力学响应预测提供科学参考.
