删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于T样条的变网格等几何薄板动力学分析

本站小编 Free考研考试/2022-01-01


引言


随着柔性轻质结构在航天、汽车以及船舶工程等领域日益广泛的应用, 柔性多体系统的动力学分析也愈加重要. 然而, 以线弹性小变形假设为基础的, 将节点位移和转动作为坐标的传统有限单元不适合解决存在大位移、大变形的柔性多体系统的动力学问题. 此外, 对于传统结构有限元, 将几何数据转换为有限元网格数据是困难且耗时的[1]. 据估计, 在航空航天、船舶制造和汽车工业中, 大约80%的分析时间用于网格生成[2]. 在计算机辅助工程(CAE)领域, 有限单元只是计算机辅助设计(CAD)几何模型的近似表示而非精确描述. 这种CAE网格与CAD几何之间的区别将会导致精确性问题, 例如在壳分析中, 随着几何缺陷的增加, 屈曲荷载有相当大的降低[2].

为了准确刻画柔性体大位移、大变形的动力学行为, 研究者将弹性力学与有限元方法和多体动力学理论相结合, 形成了绝对节点坐标方法(ANCF). ANCF利用梯度代替转角对柔性体位移场进行插值并与多体系统动力学理论相结合, 使得其具备描述柔性体大变形、大转动的能力, 从而成为多柔体系统动力学领域的研究热点[3]. 此外, 研究者又发现其与计算机辅助分析软件中的非均匀有理B样条(NURBS)几何体家族之间存在线性转化关系, 从而可以实现从几何模型到ANCF单元网格之间的快速转换, 避免了网格划分的步骤. 相关的研究始于缆索单元与B样条曲线之间的转化关系[4], 并延伸至有理的ANCF缆索单元与NURBS曲线间关系[5]. 相关研究深刻揭示了二者在几何体形状描述、连续性控制等方面的高度相似性[6-7]. 此后, ****们将研究拓展至ANCF双参数单元[8-9]. 研究结果表明, 当单元维数升高, NURBS几何体张量积形式的参数方程会引入冗余自由度, 从而需要对ANCF单元进行改造从而使其与之匹配. 例如增加混合梯度向量, 或在板单元中间添加额外节点等. 这一问题在三维单元中更加严重. Yu和Cui[10]提出了一种48自由度的八节点实体梁单元, 可以精确离散使用相同的基函数阶次Bézier体所代表的几何模型. Ma等[11]研究了一种基于三次有理Bézier体积的三维有理绝对节点坐标公式(RANCF)流体单元, 准确描述初始曲线形状的液柱.

对计算机辅助工程和计算机辅助设计进行整合的另外一个方向就是由Hughes等[2]于2005年提出的等几何分析(IGA), 其概念是将CAD和有限元分析(FEA)两个领域统一起来, 使用相同的基础进行几何描述和分析[12]. IGA方法因为具有实现无缝整合设计和分析的潜力[13]而受到了力学领域的关注[2]. ****们进行了很多针对壳体和板的等几何分析[14-17], 这些研究多是基于当前CAD系统的行业标准NURBS. 然而, 由于NURBS控制点呈矩形网格分布, 从而导致其拓扑结构中存在大量冗余控制点[18], 进而导致分析效率降低. 此外, 修剪后的NURBS表面不可避免地存在间隙和重叠是影响CAD, CAM和CAA系统互操作性的最严重的障碍之一[19]. 为了克服NURBS的这些缺点, Sederberg等[20]提出了T样条. 与NURBS曲面相比, T样条曲面的一个优点是允许局部细化. 由于T交叉点(T-junction)的存在使得T样条允许控制点局部插入到控制网格中, 而非整行或整列地增加控制点[20], 从而大大减少了多余控制点的数量[18]. T样条的另一个优点是T样条模型是水密的. 多个NURBS补丁可以合并成一个单一的水密T样条, 任何修剪过的NURBS对象都可以转换为未修剪的T样条[21]. 因此, T样条被认为是未来CAD行业的新标准, 将在CAD与CAE的集成中发挥重要作用. Casquero等[22]利用适合分析的任意度T样条曲面进行了完全非线性薄壳的结构分析. Casquero等[23]还利用适合分析的T样条来解决Kirchhoff?Love壳问题. Dimitri等[24]提出了一种基于T样条的等几何分析方法, 应用于大变形条件下变形体间的无摩擦接触问题.

在实际应用中, 由于ANCF单元使用梯度作为节点向量, 其建模过程较为复杂. 另外, 如果将一个薄板离散为几个ANCF薄板单元, 其单元边界上的梯度不连续, 因此格林?拉格朗日应变也是不连续的. 而使用IGA方法可以直接使用CAD软件对分析对象进行几何建模, 而且几何模型的连续性条件可以自然得通过结点重复性保证. 为此, 本文将在等几何分析的框架下, 开展基于T样条曲面单元的基尔霍夫薄板动力学分析方法研究. 本文的主要贡献在于:

(1)基于可局部细化的T样条曲面, 提出局部细化策略解决动力学分析中局部应变变化较大的问题, 并根据T样条曲面几何模型的局部细化算法创建变自由度系统动力学方程的求解算法;

(2)通过变网格柔性薄板与刚性球的碰撞问题, 展示所提出局部细化T样条曲面单元在接触碰撞问题中的应用价值.


1.
基于T样条的等几何基尔霍夫薄板



1.1
T样条曲面


T样条可视为控制网格上带有T交叉点的NURBS曲面[25], 可以通过控制点与T样条基函数${T_i}left( {u,v}
ight)$相乘得到. T样条曲面的定义式如下[26]







$${{boldsymbol{S}}_{
m{T}}}(u,v) = sumlimits_{i = 1}^n {{{boldsymbol{P}}_i}{T_i}(u,v)} $$
(1)

式中, ${{boldsymbol{S}}_{
m{T}}}$为T样条曲面上物质坐标为$left( {u,v}
ight)$的点的全局坐标, ${{boldsymbol{P}}_i} = left( {{x_i},{y_i},{z_i}}
ight)$为第$i$个控制点的全局坐标, $n$为控制点的数量, ${T_i}$为第$i$个控制点所对应的有理T样条基函数, 其表达式为







$${T_i}(u,v) = frac{{{omega _i}{B_i}(u,v)}}{{displaystylesumlimits_{i = 1}^n {{omega _i}{B_i}(u,v)} }}{
m{ = }}frac{{{omega _i}{N_i}(u){R_i}(v)}}{{W(u,v)}}$$
(2)

式中, 混合函数${B_i}$为B样条基函数${N_i}left( u
ight)$和${R_i}left( v
ight)$的乘积. ${omega _i}$是第$i$个控制点所对应的权重, $W$为权值与基函数的乘积之和.

与NURBS不同的是, 每一个T样条基函数都是基于局部结点矢量而不是全局结点矢量来计算的. 局部结点矢量的建立依赖于T网格和锚点的建立, 根据这两者可以得到T样条曲面上每一个控制点所对应的局部结点矢量${{boldsymbol{u}}_i} = left[ {{u_1},{u_2}, cdots ,{u_{p + 2}}}
ight]$和${{boldsymbol{v}}_i} = left[ {{v_1},{v_2}, cdots ,{v_{q + 2}}}
ight]$. T网格和锚点的具体定义参见文献[26-27], 并可依据参考文献[28]得到三次T样条基函数以及其导数的表达式.


1.2
T样条薄板的运动学描述


由于基尔霍夫薄板忽略横向剪切变形, 法向量始终垂直于中性层, 其运动学描述可以简化为其中性层的运动学描述. 为此, 首先需要采用T样条单元对薄板中性层进行运动学描述.

T样条单元是由T样条基函数的简化连续线构成的物理区域[29]. 在等几何分析中, 利用IEN数组可以确定每个样条单元的连接关系. IEN中的I表示数组是整数值, EN是“element nodes”的首字母缩写, 表示“单元节点”, 该数组可以将局部基函数号和单元号映射到相应的全局控制点号[29]. 对于第$i$个T样条单元而言, 其形函数以及单元节点向量${{boldsymbol{e}}_i}$可以表示为







$${{boldsymbol{e}}_i} = {left[ {begin{array}{*{20}{c}} {{{boldsymbol{P}}_{{
m{IEN}}left( 1
ight)}}}&{{{boldsymbol{P}}_{{
m{IEN}}left( 2
ight)}}}& cdots &{{{boldsymbol{P}}_{{
m{IEN}}left( j
ight)}}}& cdots &{{{boldsymbol{P}}_{{
m{IEN}}left( n
ight)}}} end{array}}
ight]^{
m{T}}}$$
(3)







$$begin{split} {{boldsymbol{S}}_i}left( {u,v}
ight) = &left[ {{T_{{
m{IEN}}left( 1
ight)}}left( {u,v}
ight){boldsymbol{I}}}qquad{{T_{{
m{IEN}}left( 2
ight)}}left( {u,v}
ight){boldsymbol{I}}}qquad cdots
ight. &left. {{T_{{
m{IEN}}left( j
ight)}}left( {u,v}
ight){boldsymbol{I}}}qquad cdots qquad{{T_{{
m{IEN}}left( n
ight)}}left( {u,v}
ight){boldsymbol{I}}}
ight] end{split};;;; $$
(4)

式中, $n$是一个T样条单元中包含的控制点的个数, ${
m{IEN}}left( j
ight)$为该T样条单元的IEN数列中的第$j$项, ${{boldsymbol{P}}_{{
m{IEN}}left( j
ight)}}$为第${
m{IEN}}left( j
ight)$个控制点的坐标, ${boldsymbol{I}}$为$3 times 3$的单位矩阵, ${T_{{
m{IEN}}left( j
ight)}}left( {u,v}
ight)$为第${
m{IEN}}left( j
ight)$个控制点所对应的有理T样条基函数.

综上所述, 基尔霍夫薄板的运动学描述为







$${boldsymbol{r}}left( {u,v}
ight) = {{boldsymbol{S}}_i}left( {u,v}
ight) cdot {{boldsymbol{e}}_i}$$
(5)

式中, $left( {u,v}
ight)$为当前构型下物质点${boldsymbol{r}}$的参数坐标, ${{boldsymbol{e}}_i}$为参数$left( {u,v}
ight)$所属的第$i$个T样条单元的单元节点向量, ${{boldsymbol{S}}_i}left( {u,v}
ight)$是第$i$个T样条单元的形函数.


1.3
T样条薄板的弹性模型


基于T样条曲面的基尔霍夫薄板的总弹性能可表示为[30]







$$U = {U_{{
m{mid}}}} + {U_{
m{kappa }}} = frac{1}{2}intlimits_V {{boldsymbol{varepsilon}} _{{
m{mid}}}^{
m{T}}{boldsymbol{E}}{{boldsymbol{varepsilon}} _{{
m{mid}}}}{
m{d}}V} + frac{1}{2}intlimits_V {{{boldsymbol{kappa}} ^{
m{T}}}{boldsymbol{Ekappa}} {
m{d}}V} $$
(6)

式中, ${U_{{
m{mid}}}}$为只与中性层应变${{boldsymbol{varepsilon}} _{{
m{mid}}}}$有关的薄板中性层的能量, ${U_{
m{kappa }}}$为只与弯曲应变${boldsymbol{kappa}} $有关的弯曲应变能. ${boldsymbol{E}}$为各向同性线弹性材料的广义胡克定律弹性系数矩阵. 根据文献[31], ${{boldsymbol{varepsilon}} _{{
m{mid}}}}$和${boldsymbol{kappa}} $可以表示为






$$begin{split}&{{boldsymbol{varepsilon}} _{{
m{mid}}}}{
m{ = }}&dfrac{1}{2}{boldsymbol{T}}_0^{
m{T}}left( {left[ {begin{array}{*{20}{c}} {dfrac{{partial {boldsymbol{r}}}}{{partial u}} cdot dfrac{{partial {boldsymbol{r}}}}{{partial u}}}!!&!!{dfrac{{partial {boldsymbol{r}}}}{{partial u}} cdot dfrac{{partial {boldsymbol{r}}}}{{partial v}}} {dfrac{{partial {boldsymbol{r}}}}{{partial v}} cdot dfrac{{partial {boldsymbol{r}}}}{{partial u}}}!!&!!{dfrac{{partial {boldsymbol{r}}}}{{partial v}} cdot dfrac{{partial {boldsymbol{r}}}}{{partial v}}} end{array}}
ight] - left[ {begin{array}{*{20}{c}} {dfrac{{partial {{boldsymbol{r}}_0}}}{{partial u}} cdot dfrac{{partial {{boldsymbol{r}}_0}}}{{partial u}}}!!&!!{dfrac{{partial {{boldsymbol{r}}_0}}}{{partial u}} cdot dfrac{{partial {{boldsymbol{r}}_0}}}{{partial v}}} {dfrac{{partial {{boldsymbol{r}}_0}}}{{partial v}} cdot dfrac{{partial {{boldsymbol{r}}_0}}}{{partial u}}}!!&!!{dfrac{{partial {{boldsymbol{r}}_0}}}{{partial v}} cdot dfrac{{partial {{boldsymbol{r}}_0}}}{{partial v}}} end{array}}
ight]}
ight){{boldsymbol{T}}_0} &{boldsymbol{kappa}} =& {
m{ - }}z{boldsymbol{T}}_0^{
m{T}}left( {left[ {begin{array}{*{20}{c}} {dfrac{{{partial ^2}{boldsymbol{r}}}}{{partial {u^2}}} cdot {boldsymbol{n}}}!!&!!{dfrac{{{partial ^2}{boldsymbol{r}}}}{{partial upartial v}} cdot {boldsymbol{n}}} {dfrac{{{partial ^2}{boldsymbol{r}}}}{{partial upartial v}} cdot {boldsymbol{n}}}!!&!!{dfrac{{{partial ^2}{boldsymbol{r}}}}{{partial {v^2}}} cdot {boldsymbol{n}}} end{array}}
ight] !-! left[ {begin{array}{*{20}{c}} {dfrac{{{partial ^2}{{boldsymbol{r}}_0}}}{{partial {u^2}}} cdot {{boldsymbol{n}}_0}}!!&!!{dfrac{{{partial ^2}{{boldsymbol{r}}_0}}}{{partial upartial v}} cdot {{boldsymbol{n}}_0}} {dfrac{{{partial ^2}{{boldsymbol{r}}_0}}}{{partial upartial v}} cdot {{boldsymbol{n}}_0}}!!&!!{dfrac{{{partial ^2}{{boldsymbol{r}}_0}}}{{partial upartial v}} cdot {{boldsymbol{n}}_0}} end{array}}
ight]}
ight){{boldsymbol{T}}_0}end{split}$$

式中, ${boldsymbol{r}}$和${{boldsymbol{r}}_0}$分别表示当前构型和初始构型中, 薄板中性层上任意点${boldsymbol{P}}left( {u,v}
ight)$的坐标. ${boldsymbol{n}} = dfrac{{{{boldsymbol{r}}_u} times {{boldsymbol{r}}_v}}}{{left| {{{boldsymbol{r}}_u} times {{boldsymbol{r}}_v}}
ight|}}$表示中性层的单位法向量. ${{boldsymbol{T}}_0}$表示中性层的局部笛卡尔坐标系${left( {{{boldsymbol{e}}_0}}
ight)_1}{
m{ - }}{left( {{{boldsymbol{e}}_0}}
ight)_2}{
m{ - }}{left( {{{boldsymbol{e}}_0}}
ight)_3}$与曲面坐标系${left( {{{boldsymbol{g}}_0}}
ight)_1}{
m{ - }}{left( {{{boldsymbol{g}}_0}}
ight)_2}{
m{ - }}{{boldsymbol{n}}_0}$的变换矩阵, 其表达式为







$$ left. {begin{array}{*{20}{l}}{left({boldsymbol{g}}_{0}
ight)}_{1}=dfrac{partial {boldsymbol{r}}_{0}}{partial u}begin{array}{c},end{array}{left({boldsymbol{g}}_{0}
ight)}_{{2}}=dfrac{partial {boldsymbol{r}}_{0}}{partial v} {boldsymbol{n}}_{0}=dfrac{{left({boldsymbol{g}}_{0}
ight)}_{1}times {left({boldsymbol{g}}_{0}
ight)}_{2}}{left|{left({boldsymbol{g}}_{0}
ight)}_{1}times {left({boldsymbol{g}}_{0}
ight)}_{2}
ight|}end{array}}
ight}$$
(7)







$$left. {begin{array}{*{20}{l}} {{{left( {{{boldsymbol{e}}_0}}
ight)}_1} = {{left( {{{boldsymbol{g}}_0}}
ight)}_1}} {{{left( {{{boldsymbol{e}}_0}}
ight)}_{
m{3}}} = {{boldsymbol{n}}_0}} {{{left( {{{boldsymbol{e}}_0}}
ight)}_{
m{2}}} = {{left( {{{boldsymbol{e}}_0}}
ight)}_{
m{3}}} times {{left( {{{boldsymbol{e}}_0}}
ight)}_{
m{1}}}} end{array}}
ight}$$
(8)







$$;;;{{boldsymbol{T}}_0} = {left[ {begin{aligned} {{{left( {{{boldsymbol{g}}_0}}
ight)}_1} cdot {{left( {{{boldsymbol{e}}_0}}
ight)}_1}} quad {{{left( {{{boldsymbol{g}}_0}}
ight)}_1} cdot {{left( {{{boldsymbol{e}}_0}}
ight)}_2}} {{{left( {{{boldsymbol{g}}_0}}
ight)}_2} cdot {{left( {{{boldsymbol{e}}_0}}
ight)}_1}} quad {{{left( {{{boldsymbol{g}}_0}}
ight)}_2} cdot {{left( {{{boldsymbol{e}}_0}}
ight)}_2}} end{aligned}}
ight]^{ - {
m{T}}}}$$
(9)

弹性力${{boldsymbol{Q}}_{
m{s}}}$是弹性能$U$的相对于单元节点向量${boldsymbol{e}}$的导数. 对于一个基于T样条曲面单元的薄板系统, 其弹性力表达式为







$${{boldsymbol{Q}}_{
m{s}}} = frac{{partial U}}{{partial {boldsymbol{e}}}}{
m{ = }}int_V {{boldsymbol{varepsilon}} _{{
m{mid}}}^{
m{T}}{boldsymbol{E}}frac{{partial {{boldsymbol{varepsilon}} _{{
m{mid}}}}}}{{partial {boldsymbol{e}}}}} {
m{d}}V{
m{ + }}int_V {{{boldsymbol{kappa}} ^{
m{T}}}{boldsymbol{E}}frac{{partial {boldsymbol{kappa}} }}{{partial {boldsymbol{e}}}}} {
m{d}}V$$
(10)

切线刚度矩阵${boldsymbol{J}}{{boldsymbol{Q}}_{
m{s}}}$是弹性力${{boldsymbol{Q}}_{
m{s}}}$对${boldsymbol{e}}$的导数, 其表达式为







$$begin{split} {boldsymbol{J}}{{boldsymbol{Q}}_{
m{s}}} =& int_V {left( {{{dfrac{{partial {{boldsymbol{varepsilon}} _{{
m{mid}}}^{
m{T}}}}}{{partial {{boldsymbol{e}}_j}}}}}{boldsymbol{E}}dfrac{{partial {{boldsymbol{varepsilon}} _{{
m{mid}}}}}}{{partial {{boldsymbol{e}}_i}}} + {boldsymbol{varepsilon}} _{{
m{mid}}}^{
m{T}}{boldsymbol{E}}dfrac{{{partial ^2}{{boldsymbol{varepsilon}} _{{
m{mid}}}}}}{{partial {{boldsymbol{e}}_j}partial {{boldsymbol{e}}_i}}}}
ight){
m{d}}V} + & int_V {left( {{{dfrac{{partial {boldsymbol{kappa}}^{
m{T}} }}{{partial {{boldsymbol{e}}_j}}}}}{boldsymbol{E}}dfrac{{partial {boldsymbol{kappa}} }}{{partial {{boldsymbol{e}}_i}}} + {{boldsymbol{kappa}} ^{
m{T}}}{boldsymbol{E}}dfrac{{{partial ^2}{boldsymbol{kappa}} }}{{partial {{boldsymbol{e}}_j}partial {{boldsymbol{e}}_i}}}}
ight){
m{d}}V} end{split} $$
(11)

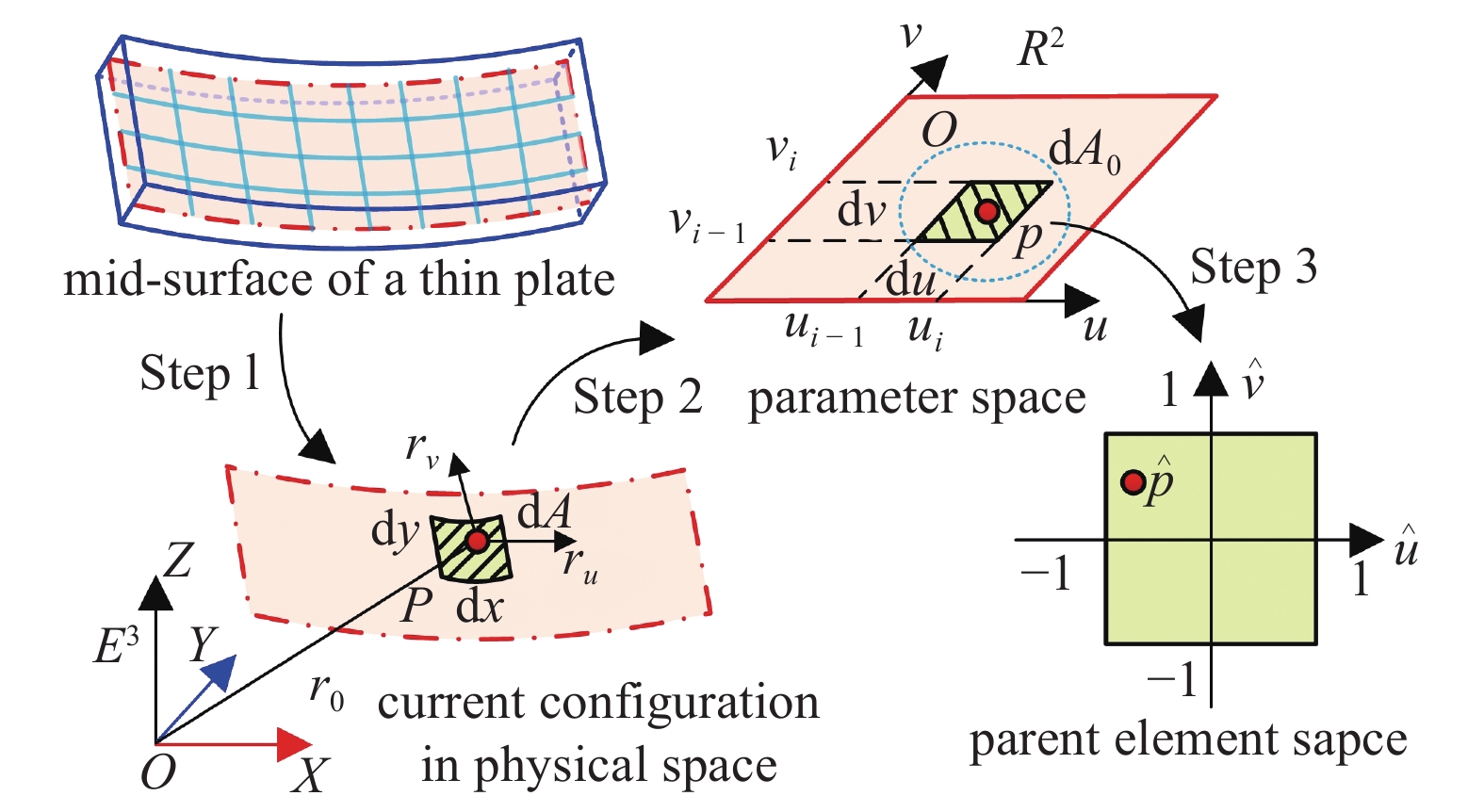
图1给出了等几何基尔霍夫薄板的转换示意图. 首先, 体积积分简化为厚度$h$与中性层面积分的乘积. 然后, 当前构型下物理空间中的面微元${
m{d}}A$被映射到参数空间中的面微元${
m{d}}{A_0}$, 其定义为







$${
m{d}}A{
m{ = }}left| {{{boldsymbol{r}}_u} times {{boldsymbol{r}}_v}}
ight|{
m{d}}{A_0} = {J_2}{
m{d}}{A_0}$$
(12)

最后, 对薄板的积分表达式可以写为







$$int_V f {
m{d}}V = h{J_2}int_0^v {int_0^u {f{
m{d}}u{
m{d}}v = } } {J_1}{J_2}hsumlimits_{j = 1}^m {sumlimits_{i = 1}^n {{omega _i}{omega _j}fleft( {hat u,hat v}
ight)} } $$
(13)

式中, ${omega _i}$和${omega _j}$是积分点$hat u$和$hat v$所对应的积分系数; ${J_1}$是参数空间到父单元的转换矩阵的行列式值, ${J_1}$的表达式为







$${J_1} = frac{{{u_i} - {u_{i - 1}}}}{2} cdot frac{{{v_i} - {v_{i - 1}}}}{2}$$
(14)



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
等几何基尔霍夫薄板积分过程



Figure
1.
The process of isogeometric Kirchhoff thin plate integration



下载:
全尺寸图片
幻灯片



2.
网格局部细化


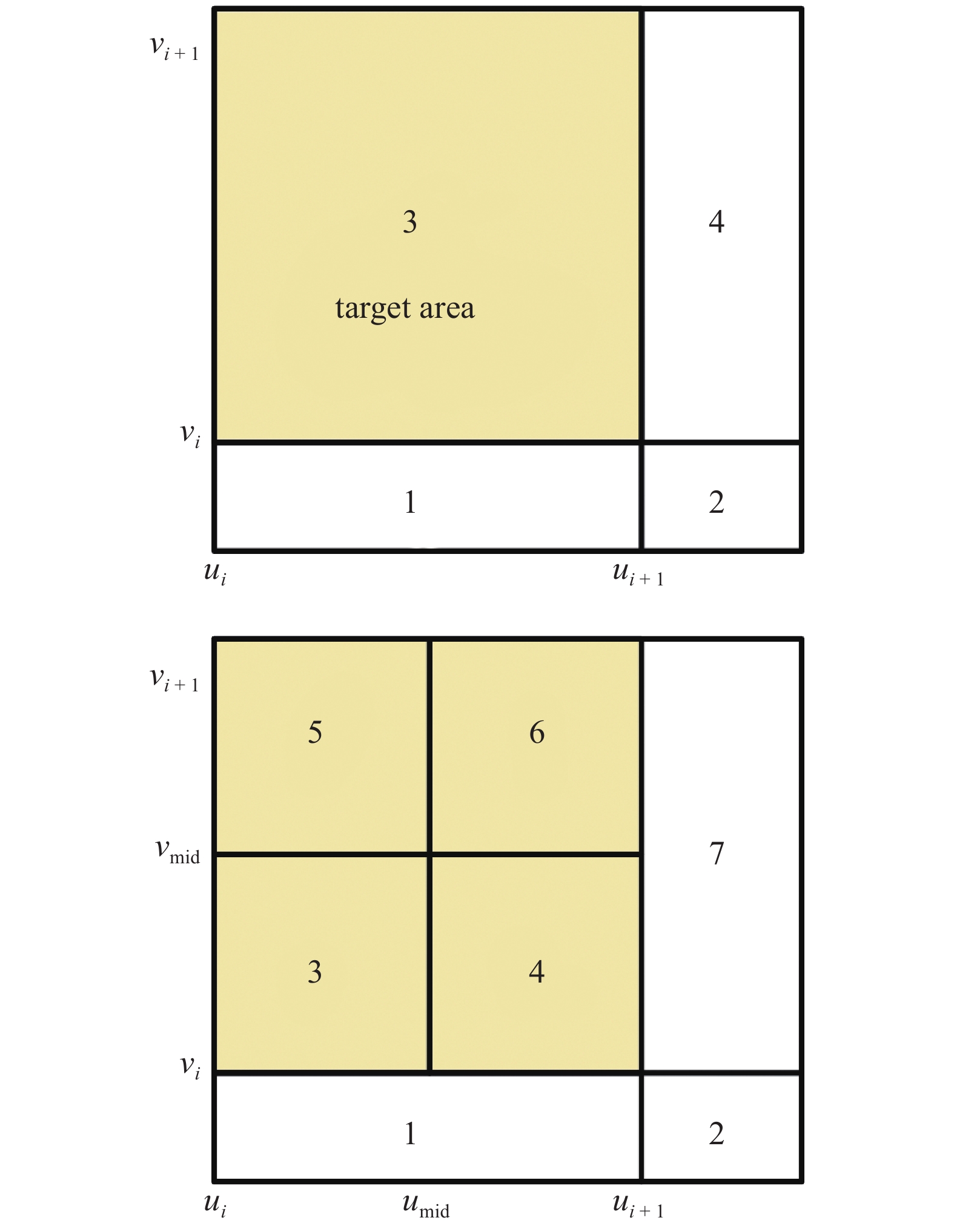
与NURBS单元网格相比, T样条允许在局部细化单元网格. 在处理碰撞接触等局部发生应变的剧烈变化的问题时具有优势. 本节将讨论T样条薄板的网格局部细分及新控制点的计算方法.

如图2所示, 一个边界为$left[ {{u_i},{u_{i + 1}}}
ight] times left[ {{v_i},{v_{i + 1}}}
ight]$的T样条单元被均匀分为4个单元, 将会产生两个新的结点, ${u_{{
m{mid}}}} = {{left( {{u_i} + {u_{i + 1}}}
ight)} / 2}$和${v_{{
m{mid}}}} = {{left( {{v_i} + {v_{i + 1}}}
ight)} / 2}$. 细化后, 初始T样条单元的区域将被4个新的子单元所替换, 其单元边界分别为$left[ {u_i}, {u_{{
m{mid}}}}
ight] times left[ {{v_j},{v_{{
m{mid}}}}}
ight]$, $left[ {u_{{
m{mid}}}},
ight. $$ left.{ u _{i + 1}}
ight] times left[ {{v_j},{v_{{
m{mid}}}}}
ight]$, $left[ {{u_i},{u_{{
m{mid}}}}}
ight] times left[ {{v_{{
m{mid}}}},{v_{j + 1}}}
ight]$以及 $left[ {{u_{{
m{mid}}}},{u_{i{
m{ + }}1}}}
ight] $$ times left[ {{v_{{
m{mid}}}},{v_{j + 1}}}
ight]$. 每一个T样条单元可以被循环细化直到达到停止细化的指标.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
局部细化策略的示意图



Figure
2.
Schematic diagram of local refinement strategy



下载:
全尺寸图片
幻灯片


曲面$H$初始由一个双三次T样条${S_1}$表示, 它的控制点数量为$m$, 笛卡尔空间中的控制点矩阵${boldsymbol{P}}$的表达式在式(15)中给出. 由于T网格中一个交点对应一个控制点, 细化后的几何模型将生成新的控制点, 所以细化后的曲面${S_2}$中控制点个数增至$n$, 其控制点坐标为$tilde {boldsymbol{P}}$. 初始T样条曲面${S_1}$被称为是细化后的T样条曲面${S_2}$的子空间(表示为${S_1} subset {S_2}$)







$${boldsymbol{P}} = {left[ {begin{array}{*{20}{c}} {{boldsymbol{P}}_1^{
m{T}}}&{{boldsymbol{P}}_2^{
m{T}}}& cdots &{{boldsymbol{P}}_i^{
m{T}}}& cdots &{{boldsymbol{P}}_m^{
m{T}}} end{array}}
ight]^{
m{T}}}$$
(15)

根据参考文献[18], 可以得到T样条混合函数的局部细化算法: 初始T样条曲面上任意控制点${{boldsymbol{P}}_i}$的局部结点矢量为${{boldsymbol{u}}_i} = left[ {u_i^0,u_i^1,u_i^2,u_i^3,u_i^4}
ight]$和${{boldsymbol{v}}_i} = left[ v_i^0,v_i^1,v_i^2,
ight. $$ left.v_i^3,v_i^4
ight]$, 则由${{boldsymbol{u}}_i}$和${{boldsymbol{v}}_i}$得到的B样条基函数${N_i}left( u
ight)$和${R_i}left( v
ight)$分别为${N_i}left[ {u_i^0,u_i^1,u_i^2,u_i^3,u_i^4}
ight]left( u
ight)$和${R_i}left[ {v_i^0,v_i^1,v_i^2,v_i^3,v_i^4}
ight]left(v
ight)$, 所以其混合函数${B_i}$可表示为${B_i} = {N_i}left( u
ight) cdot {R_i}left( v
ight)$. 如图2所示, 初始T样条曲面被细化后, 两个新的结点$hat u = {u_{{
m{mid}}}}$和$hat v = {v_{{
m{mid}}}}$被插入到原始单元的边界上. 控制点${{boldsymbol{P}}_i}$所对应的基函数${N_i}left( u
ight)$和${R_i}left( v
ight)$将使用插入$hat u$和$hat v$的新的局部结点矢量表示. 因此, 基函数${N_i}left( u
ight)$可以写作${{c_1}}tilde N_i^1left( u
ight)$与${c_2}tilde N_i^2left( u
ight)$之和, ${R_i}left( v
ight)$可以写作${d_{ 1}}tilde R_i^1left( v
ight)$与${d_2}tilde R_i^2left( v
ight)$之和. 一个初始控制点${{boldsymbol{P}}_i}$的混合函数${B_i}$可以由$tilde N_i^sleft( u
ight)$和$tilde R_i^rleft( v
ight)$表示







$${B_i}left( {u,v}
ight){
m{ = }}sumlimits_{s = 1}^2 {sumlimits_{r = 1}^2 {left( {{c_s} cdot {d_r}}
ight)tilde N_i^stilde R_i^r} } {
m{ = }}sumlimits_{t = 1}^4 {f_i^ttilde B_i^tleft( {u,v}
ight)} $$
(16)

式中, 初始T样条曲面${S_1}$中的第$i$个混合函数${B_i}$被分解为四个新混合函数$tilde B_i^t$与其对应系数$f_i^t$乘积之和. 如果$tilde B_i^t$等于细化后T样条曲面第$j$个混合函数${tilde B_j}$, 即$tilde B_i^t{
m{ = }}{tilde B_j}$, 那么${S_1}$中的混合函数${B_i}$可以被写作${S_2}$中混合函数${tilde B_j}$的线性组合







$${B_i}left( {u,v}
ight) = sumlimits_{j = 1}^n {f_i^j{{tilde B}_j}left( {u,v}
ight)} $$
(17)

因为${S_1} subset {S_2}$, 由参数$left( {u,v}
ight)$定义的${S_1}$上的点${{boldsymbol{r}}_1}$和${S_2}$上的点${{boldsymbol{r}}_2}$是相等的, 也就是${{boldsymbol{r}}_1}left( {u,v}
ight) equiv {{boldsymbol{r}}_2}left( {u,v}
ight)$. 根据式(1)和式(2), ${{boldsymbol{r}}_1}$和${{boldsymbol{r}}_2}$可表示为







$$left. {begin{array}{*{20}{l}} {{{boldsymbol{r}}_1}left( {u,v}
ight){
m{ = }}displaystylesumlimits_{i = 1}^m {frac{{{{boldsymbol{P}}_i}{omega _i}{B_i}left( {u,v}
ight)}}{{Wleft( {u,v}
ight)}}} } {{{boldsymbol{r}}_2}left( {u,v}
ight){
m{ = }}displaystylesumlimits_{j = 1}^n {frac{{{{tilde {boldsymbol{P}}}_j}{{tilde omega }_j}{{tilde B}_j}left( {u,v}
ight)}}{{tilde Wleft( {u,v}
ight)}}} } end{array}}
ight}$$
(18)

根据${B_i}$与${tilde B_j}$之间的转换关系, 可得到$tilde {boldsymbol{P}}_j^4$和${boldsymbol{P}}_i^4$之间的转换关系, 转换方程如式(19)和式(20)所示







$$sumlimits_{i = 1}^m {c_i^j{boldsymbol{P}}_i^4 = tilde {boldsymbol{P}}_j^4} $$
(19)

式中, 带有上标4的${boldsymbol{P}}_i^4$和$tilde {boldsymbol{P}}_j^4$表示包括四维空间中的齐次坐标







$$left.begin{split}&{boldsymbol{P}}_i^4 = {{boldsymbol{P}}_i}{omega _i} = left( {{omega _i}x,{omega _i}y,{omega _i}z,{omega _i}}
ight)& {{tilde {boldsymbol{P}}}^4} = {{boldsymbol{M}}_{
m{m}}}{{boldsymbol{P}}^4} & {{boldsymbol{P}}^4}{
m{ = }}{left[ {begin{array}{*{20}{c}} {{boldsymbol{P}}_1^4}&{{boldsymbol{P}}_2^4}& cdots &{{boldsymbol{P}}_i^4}& cdots &{{boldsymbol{P}}_m^4} end{array}}
ight]^{
m{T}}} & {{tilde {boldsymbol{P}}}^4}{
m{ = }}{left[ {begin{array}{*{20}{c}} {tilde {boldsymbol{P}}_1^4}&{tilde {boldsymbol{P}}_2^4}& cdots &{tilde {boldsymbol{P}}_j^4}& cdots &{tilde {boldsymbol{P}}_n^4} end{array}}
ight]^{
m{T}}} end{split}
ight} $$
(20)

式中, ${{boldsymbol{P}}^4}$和${tilde {boldsymbol{P}}^4}$是分别由控制点${boldsymbol{P}}_i^4$和$tilde {boldsymbol{P}}_j^4$组成的矩阵. 对于转换矩阵${{boldsymbol{M}}_{
m{m}}}$, 其第$j$行第$i$列为式(17)中的系数$f_i^j$.

根据式(20), 可以得到细化后T样条的齐次坐标矩阵${tilde {boldsymbol{P}}^4}$. 然而, 本文中T样条单元的节点向量是由控制点笛卡尔坐标构成的而非齐次坐标. 因此, 控制点${tilde {boldsymbol{P}}_j}$的笛卡尔坐标和权重的计算表达示为







$$left. {begin{array}{*{20}{l}} {tilde {boldsymbol{omega}} = {{boldsymbol{M}}_{
m{m}}}{boldsymbol{omega}} } {{{tilde {boldsymbol{P}}}_j} = {{tilde {boldsymbol{P}}_j^4} / {{omega _j}}}} end{array}}
ight}$$
(21)

式中${boldsymbol{omega}} $和$tilde {boldsymbol{omega}} $分别为初始T样条和细化后T样条中全部控制点的权重向量, ${tilde omega _j}$为向量$tilde {boldsymbol{omega}} $的第$j$项, ${tilde {boldsymbol{P}}_j}$是$tilde {boldsymbol{P}}$的第$j$项. 至此, 计算细化后T样条的新控制点的目标得以完成.

综上所述, 根据本节给出的局部细化策略和算法, 可以根据原T样条曲面和插入的结点得到细化后的T样条曲面, 实现几何模型拓扑结构的变化.


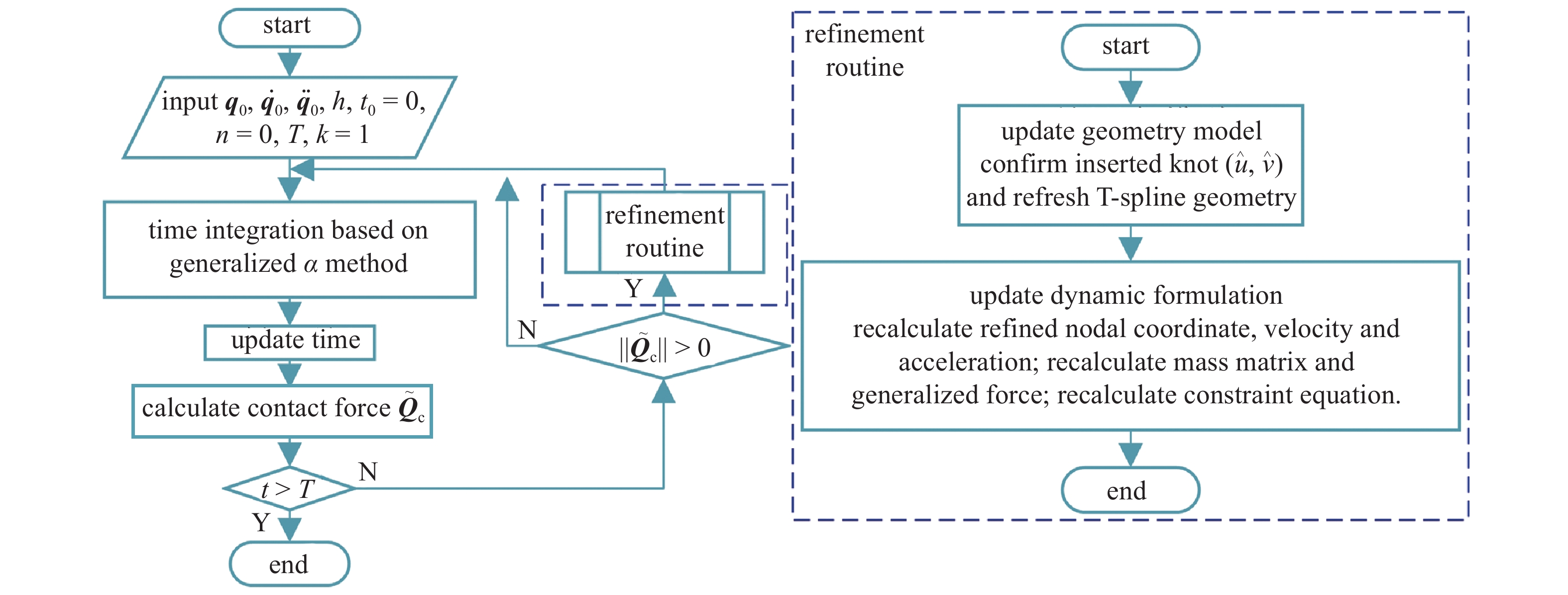
3.
变网格T样条薄板的求解算法


本文中基于T样条的柔性等几何薄板系统的动力学方程可表示为







$$tilde {boldsymbol{M}}ddot {boldsymbol{q}} + {tilde {boldsymbol{Q}}_{
m{s}}} - {tilde {boldsymbol{Q}}_{
m{e}}} = {bf{0}}$$
(22)

式中, $tilde {boldsymbol{M}}$表示缩减自由度之后的系统质量阵, $ddot {boldsymbol{q}}$表示广义加速度, ${tilde {boldsymbol{Q}}_{
m{s}}}$和${tilde {boldsymbol{Q}}_{
m{e}}}$表示自由度缩减后的系统广义弹性力与包含接触力的广义外力. 需要指出的是, 引入了基于T样条的网格细化算法后, 式(22)所含有的自由度数量是时变的, 因此, 需要对现有求解方法进行改进, 以考虑拓扑结构的变化. 图3给出了变网格T样条薄板系统动力学分析的求解算法流程图, 图中${{boldsymbol{q}}_0}$, ${dot {boldsymbol{q}}_0}$和${ddot {boldsymbol{q}}_0}$分别为初始系统的广义坐标、广义速度和广义加速度. 当接触力${tilde {boldsymbol{Q}}_{
m{c}}}$被检测为非零向量时, 执行细化子程序对接触区域施加进行网格局部细化操作.

在细化子程序中, 当前时刻$t$的收敛结果${boldsymbol{q}}_{n + 1}^{left( {k + 1}
ight)}$, $dot {boldsymbol{q}}_{n + 1}^{left( {k + 1}
ight)}$, $ddot {boldsymbol{q}}_{n + 1}^{left( {k + 1}
ight)}$为细化程序的输入变量. 首先, 模型的几何形状需要更新. 确定被插入结点$left( {hat u,hat v}
ight)$后, 可得到转换矩阵${{boldsymbol{M}}_{
m{m}}}$以计算细化后的T样条控制点, 此时系统自由度由$m$增加为$n$. 为了计算新系统的广义节点坐标、速度和加速度, 首先按照式(23)将初始系统的广义变量${boldsymbol{q}}_{n + 1}^{left( {k + 1}
ight)}$, $dot {boldsymbol{q}}_{n + 1}^{left( {k + 1}
ight)}$和$ddot {boldsymbol{q}}_{n + 1}^{left( {k + 1}
ight)}$还原为初始系统的节点坐标${boldsymbol{e}}$, 节点速度$dot {boldsymbol{e}}$和节点加速度$ddot {boldsymbol{e}}$







$$left. {begin{array}{*{20}{l}} {{{boldsymbol{e}}_{{
m{temp}}}} = {{boldsymbol{e}}_0} + {boldsymbol{q}}_{n + 1}^{left( {k + 1}
ight)} cdot {boldsymbol{B}}} {{{dot {boldsymbol{e}}}_{{
m{temp}}}} = {{dot {boldsymbol{e}}}_0} + dot {boldsymbol{q}}_{n + 1}^{left( {k + 1}
ight)} cdot {boldsymbol{B}}} {{{ddot {boldsymbol{e}}}_{{
m{temp}}}} = {{ddot {boldsymbol{e}}}_0} + ddot {boldsymbol{q}}_{n + 1}^{left( {k + 1}
ight)} cdot {boldsymbol{B}}} end{array}}
ight}$$
(23)

然后根据转换矩阵${{boldsymbol{M}}_{
m{m}}}$得到细化后新系统的节点坐标$tilde {boldsymbol{e}}$, 节点速度${dot {tilde {boldsymbol{e}}}}$和节点加速度${ddot {tilde {boldsymbol{e}}}}$, 如下式(24)所示







$$left. {begin{array}{*{20}{l}} {{{tilde {boldsymbol{e}}}_{{
m{temp}}}} = frac{{{{boldsymbol{M}}_{
m{m}}} cdot {{boldsymbol{e}}_{{
m{temp}}}}}}{{tilde {boldsymbol{omega}} }}} {{{dot {tilde {boldsymbol{e}}}}_{{
m{temp}}}} = frac{{{{boldsymbol{M}}_{
m{m}}} cdot {{dot {boldsymbol{e}}}_{{
m{temp}}}}}}{{tilde {boldsymbol{omega}} }}} {{{ddot {tilde {boldsymbol{e}}}}_{{
m{temp}}}} = frac{{{{boldsymbol{M}}_{
m{m}}} cdot {{ddot {boldsymbol{e}}}_{{
m{temp}}}}}}{{tilde {boldsymbol{omega}} }}} end{array}}
ight}$$
(24)

同理可得新系统在$t = 0$时刻的节点变量${tilde {boldsymbol{e}}_0}$, ${{dot {tilde {boldsymbol{e}}}}_0}$和${{ddot {tilde {boldsymbol{e}}}}_0}$.

更新几何模型后, 约束方程也会发生变化, 所以将会得到新的布尔矩阵$tilde {boldsymbol{B}}$. 根据$tilde {boldsymbol{B}}$可以得到新系统的广义坐标$tilde {boldsymbol{q}}_{n + 1}^{left( {k + 1}
ight)}$、广义速度${dot {tilde {boldsymbol{q}}}}_{n + 1}^{left( {k + 1}
ight)}$和广义加速度${ddot{ tilde {boldsymbol{q}}}}_{n + 1}^{left( {k + 1}
ight)}$, 其计算公式如下







$$left. {begin{array}{*{20}{l}} {tilde {boldsymbol{B}} cdot tilde {boldsymbol{q}}_{n + 1}^{left( {k + 1}
ight)} = {{tilde {boldsymbol{e}}}_{{
m{temp}}}} - {{tilde {boldsymbol{e}}}_0}} {tilde {boldsymbol{B}} cdot {dot {tilde {boldsymbol{q}}}}_{n + 1}^{left( {k + 1}
ight)} = {{dot {tilde {boldsymbol{e}}}}_{{
m{temp}}}} - {{dot {tilde {boldsymbol{e}}}}_0}} {tilde {boldsymbol{B}} cdot {ddot{ tilde {boldsymbol{q}}}}_{n + 1}^{left( {k + 1}
ight)} = {{ddot {tilde {boldsymbol{e}}}}_{{
m{temp}}}} - {{ddot {tilde {boldsymbol{e}}}}_0}} end{array}}
ight}$$
(25)

获取了上述变量之后, 系统动力学方程中的变量将会得到更新. 通过与$tilde {boldsymbol{B}}$的乘积, 将会得到新系统的广义质量阵$tilde {boldsymbol{M}}$, 广义外力${tilde {boldsymbol{Q}}_{
m{e}}}$, 广义弹性力${tilde {boldsymbol{Q}}_{
m{s}}}$和广义接触力${tilde {boldsymbol{Q}}_{
m{c}}}$. 将更新后的动力学方程输入到广义α算法中进行求解, 便可得到网格局部细化、自由度增加后的新系统下一时间步的广义变量$tilde {boldsymbol{q}}_{n + 1}^{left( {k + 1}
ight)}$, ${dot {tilde {boldsymbol{q}}}}_{n + 1}^{left( {k + 1}
ight)}$和${ddot{ tilde {boldsymbol{q}}}}_{n + 1}^{left( {k + 1}
ight)}$, 实现了对变自由度系统动力学方程的求解.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-3.jpg'"
class="figure_img
figure_type2 ccc " id="Figure3" />



图
3
变网格系统动力学分析流程图



Figure
3.
Dynamic analysis flow chart of variable mesh system



下载:
全尺寸图片
幻灯片



4.
数值算例



4.1
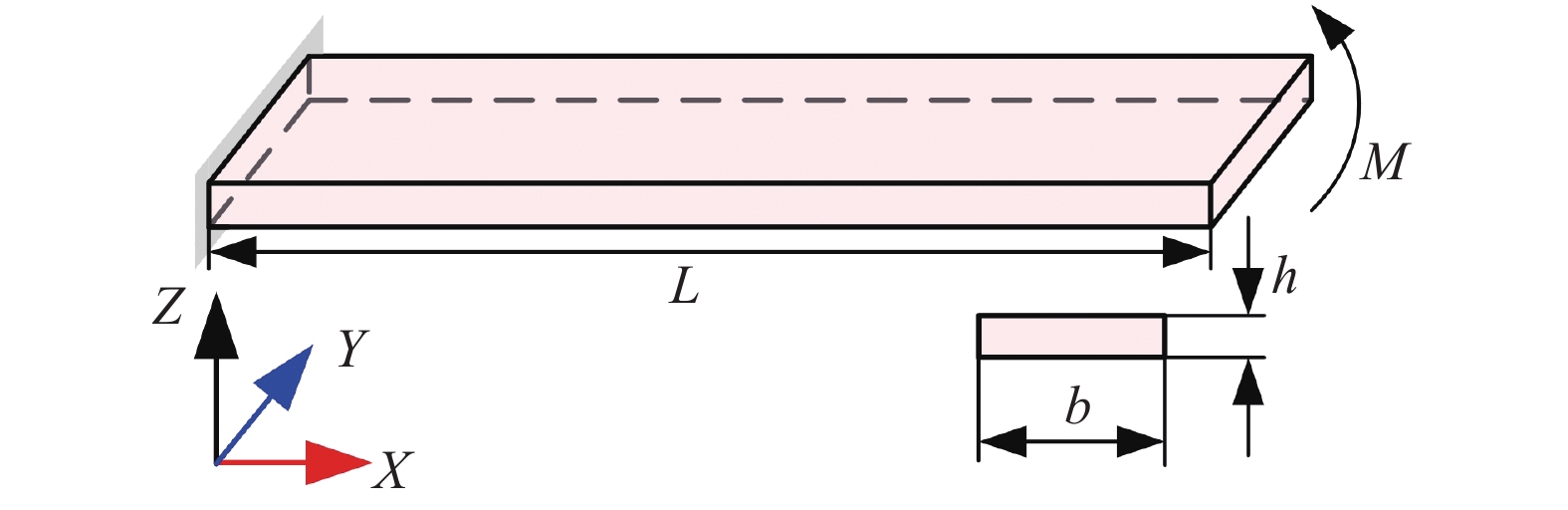
受端弯矩作用的悬臂薄板


图4为一末端受弯矩$M$的悬臂薄板. 该薄板长度$L{
m{ = }}12;{
m{m}}$, 宽度$b = 1;{
m{m}}$, 厚度$h{
m{ = }}0.1;{
m{m}}$, 弹性模量$E{
m{ = }}1.2;{
m{MPa}}$, 泊松比$nu {
m{ = }}0$, 惯性矩$I = dfrac{{b{h^3}}}{{12}}$. 图5给出了不同端弯矩下的薄板构型图.

根据文献[32]可知, 取最大弯矩为${M_0}{
m{ = }}dfrac{{2{
m{{text{π}} }}EI}}{L}$, 当末端所受弯矩$M = {M_0}$, 此时薄板将弯曲成一个半径为$R = dfrac{{EI}}{M} = dfrac{L}{{2{
m{{text{π}} }}}}$的圆. 当末端所受弯矩为$M = 0.75{M_0}$, $0.5{M_0}$和$0.25{M_0}$时, 薄板的端截面转角分别为$1.5{
m{{text{π}} }}$, ${
m{{text{π}} }}$和$0.5{
m{{text{π}} }}$.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
受端弯矩作用的悬臂薄板



Figure
4.
Cantilever subjected to end bending moment



下载:
全尺寸图片
幻灯片




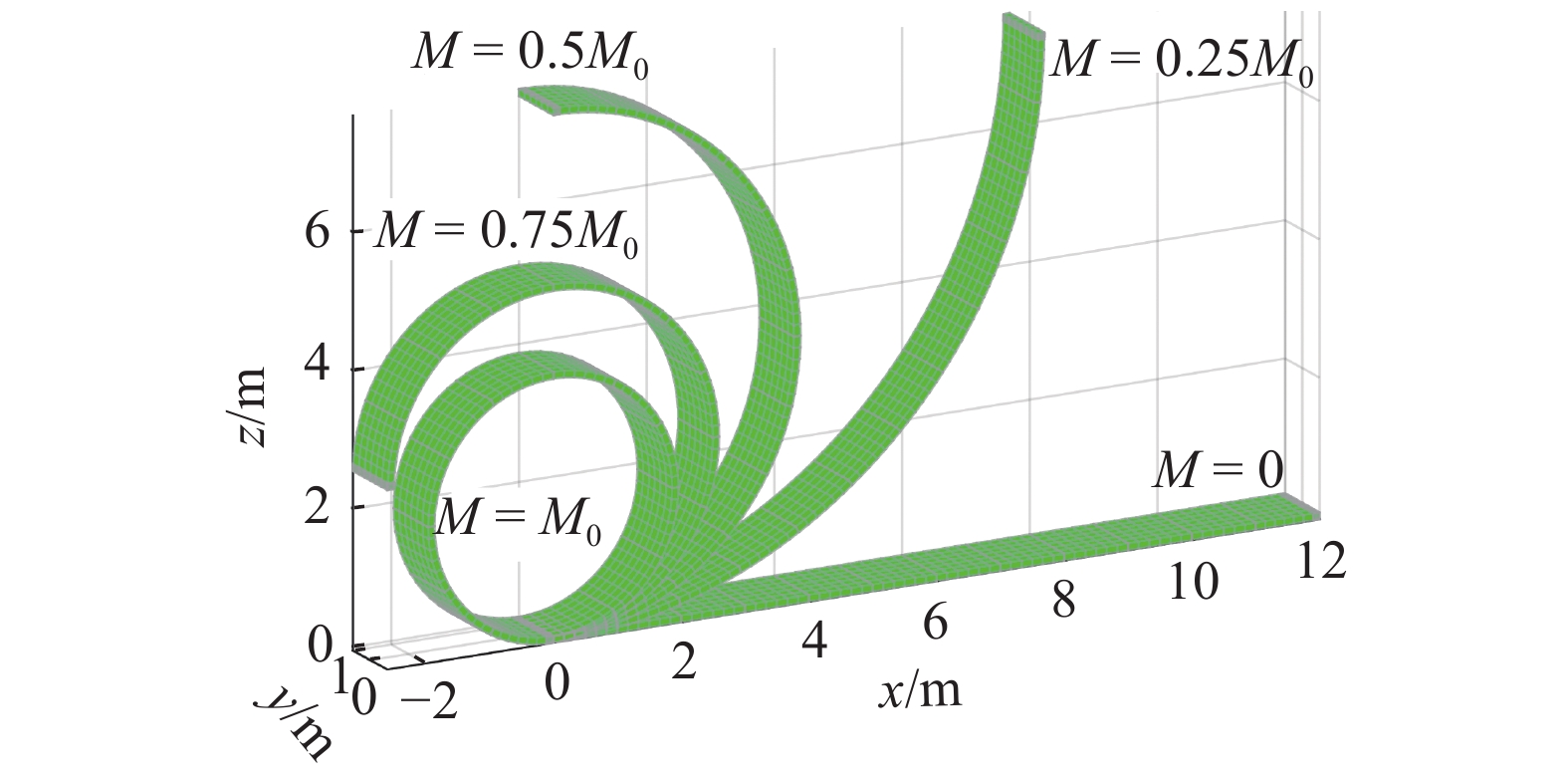onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
端弯矩作用下, 变形后悬臂梁的构形图



Figure
5.
Configuration of deformed cantilever under external moments



下载:
全尺寸图片
幻灯片



4.2
受内压圆环


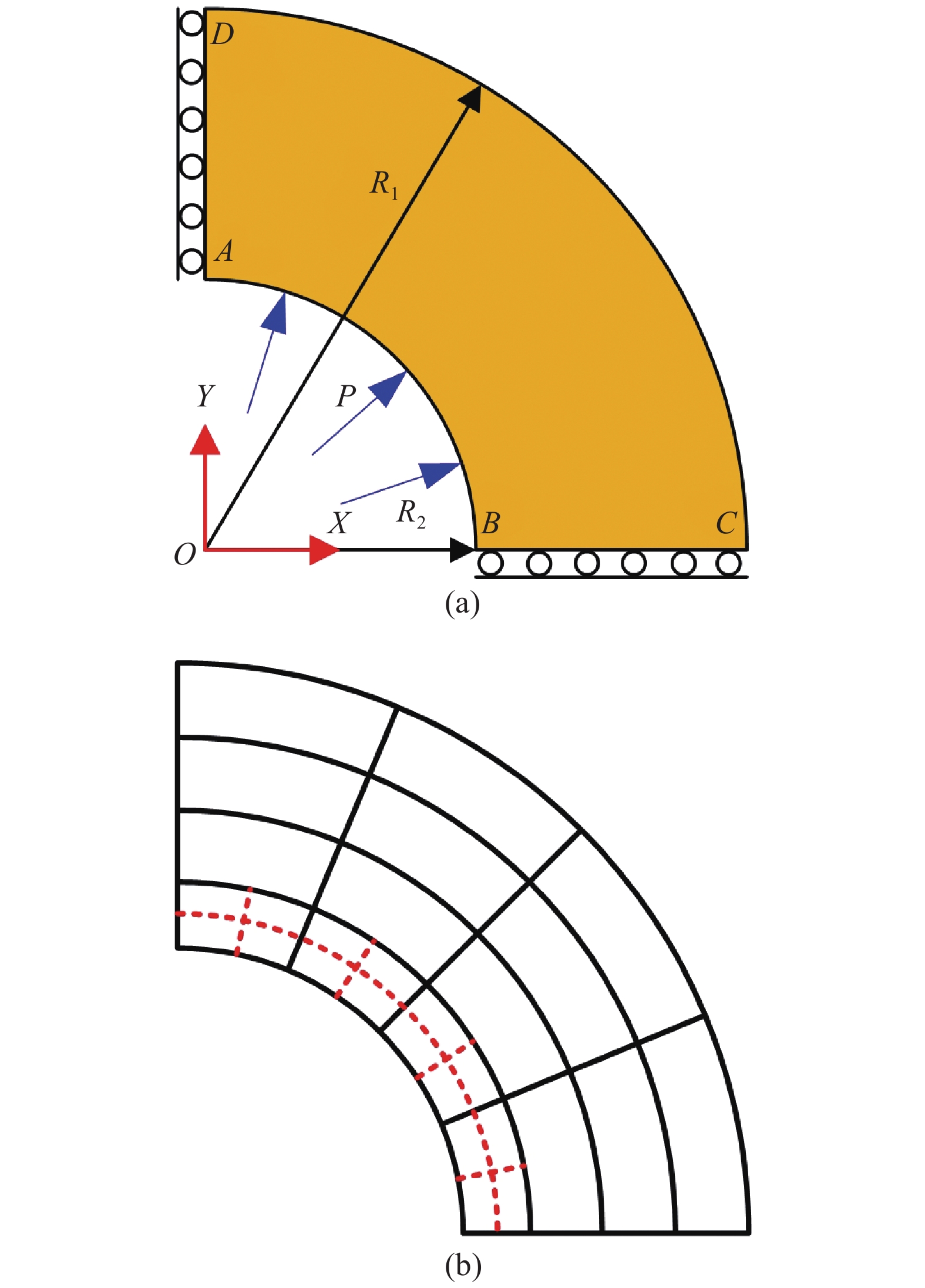
一平面圆环构件, 在其中心孔边缘受沿半径向外方向的均布载荷$P = 10;{
m{MPa}}$. 根据对称性, 取圆环构件的四分之一并在两侧施加滑动边界约束, 如图6(a)所示. 圆环构件的内与外径分别为${R_1}{
m{ = }}1;{
m{m}}$和${R_2} $= 2 m, 厚度$h $= 0.1 m. 材料密度$;
ho; {
m{ = }};7800;$kg/m3, 杨氏模量$E = 210;$GPa, 泊松比$nu = $0.3.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
四分之一圆环构件及其局部细化示意图



Figure
6.
Diagram of a quarter of circular thin plate and its local refinement diagram



下载:
全尺寸图片
幻灯片


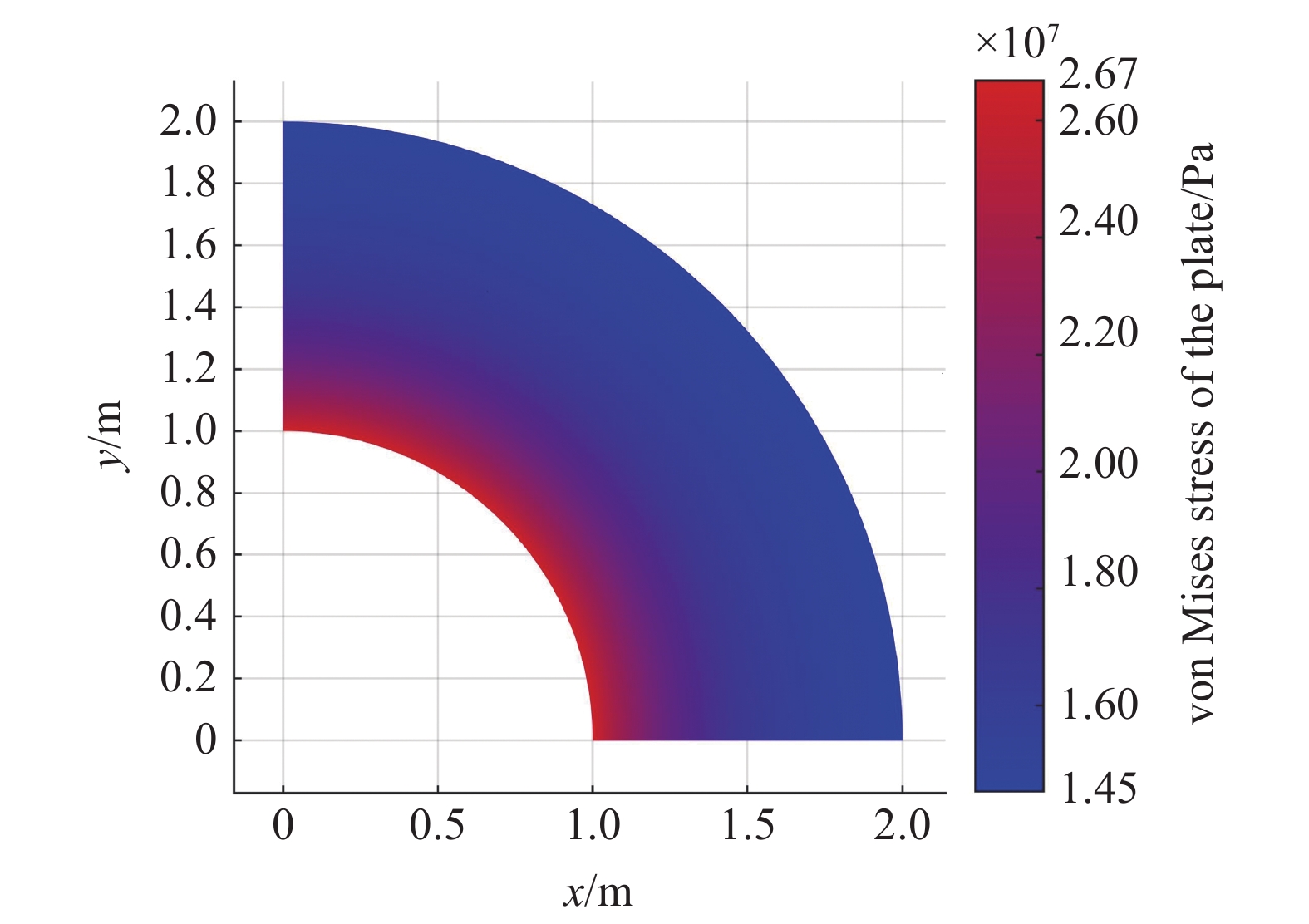
采用T样条曲面单元对构件离散, 单元网格分布图如图6(b)所示. 因为最大米塞斯应力出现在AB边界附近, 内部区域被局域细化. 模型共含有28个单元和72个控制点. 图7给出了局部细化后构件的米塞斯应力云图.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
局部细化后构件米塞斯应力云图



Figure
7.
von-Mises stress nephogram after local refinement



下载:
全尺寸图片
幻灯片


因为该算例属于平面问题, 所以轴向应力${sigma _{{z}}} = 0$. 根据拉美方程可以得到圆环在任意半径r处米塞斯应力${sigma _{
m{s}}}$的理论解







$$left. {begin{array}{*{20}{l}} {{sigma _{{theta }}}{{ = }}dfrac{{{{{P}}_0}{K^2}}}{{{K^2} - 1}}left( {1 - dfrac{{R_2^2}}{{{r^2}}}}
ight)} {{sigma _{{r}}}{{ = }}dfrac{{{{{P}}_0}{K^2}}}{{{K^2} - 1}}left( {1 + dfrac{{R_2^2}}{{{r^2}}}}
ight)} {{sigma _{{s}}} = sqrt {dfrac{1}{2}left[ {{{left( {{sigma _{{r}}} - {sigma _{{theta }}}}
ight)}^2} + {{left( {{sigma _{{r}}} - {sigma _{{z}}}}
ight)}^2} + {{left( {{sigma _{{theta }}} - {sigma _{{z}}}}
ight)}^2}}
ight]} } end{array}}
ight}$$
(26)

式中, ${sigma _{{r}}}$为径向应力, ${sigma _{
m{theta }}}$为环向应力, K为圆环外径与内径之比, $K = {R_2}:{R_1}$.

在有限元软件ANSYS中采用SHELL63单元运行相同算例并对比构件中最大和最小应力结果如表1所示. 可以看出, 相较于ANSYS结果, IGA结果更加接近于理论解而且与理论解的误差小于1‰.




表
1
圆环构件最小和最大米塞斯应力



Table
1.
Minimum and maximum von-Mises stress on circular thin plate



table_type1 ">
${sigma _{min }}$/MPa${sigma _{max }}$/MPa
theoretical solution14.5326.67
ANSYS solution (200 elements)14.4526.37
IGA solution (28 elements)14.5226.68





下载:
导出CSV
|显示表格



4.3
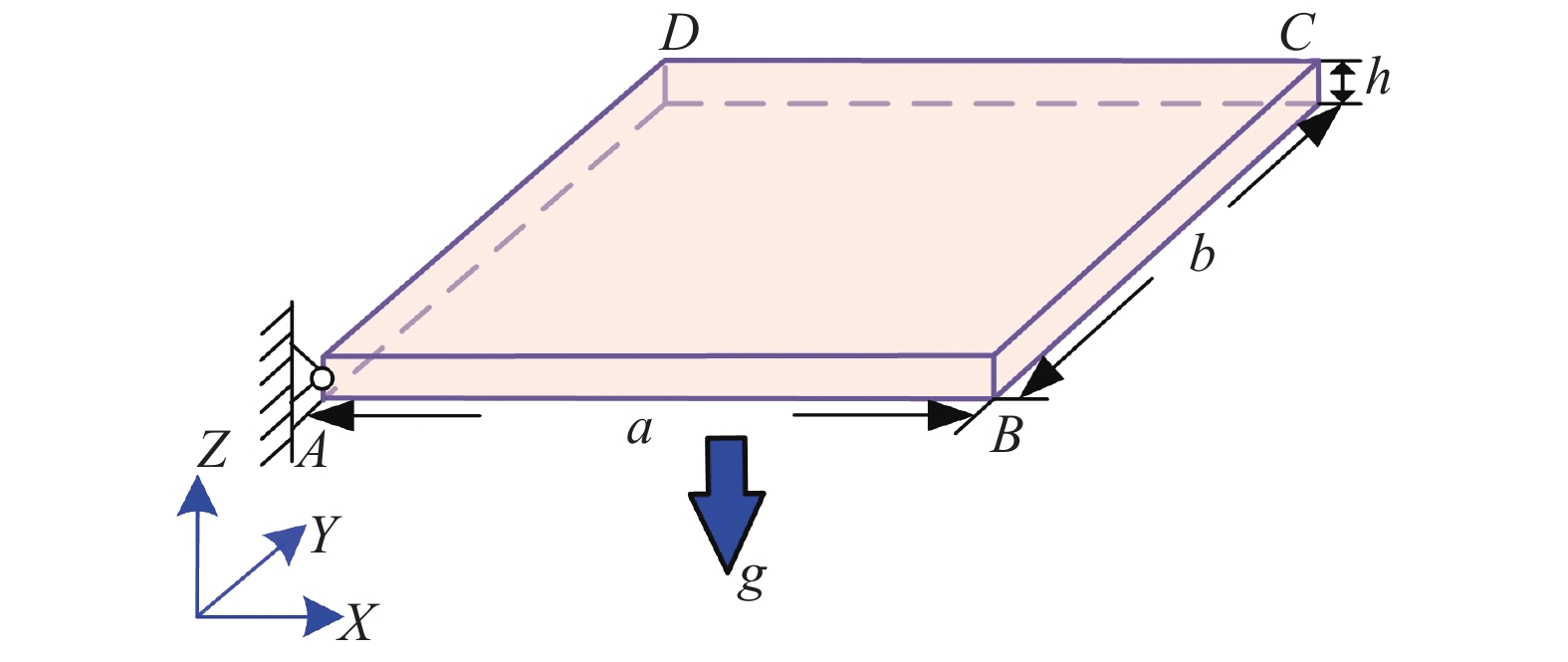
柔性单摆


该算例测试了基于T样条的等几何薄板的动力学特性. 如图8所示, 一个柔性单摆铰接固定在A处. 柔性薄板单摆在重力加速度$g = 9.81;{
m{m}}/{{
m{s}}^2}$的作用下坠落. 薄板的参数在表2中给出.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
一端铰接的柔性薄板单摆



Figure
8.
Flexible thin plate pendulum



下载:
全尺寸图片
幻灯片





表
2
材料参数



Table
2.
Material parameters



table_type1 ">
ParameterValue
length $a$/m 2
width $b$/m 2
height $h$/m 0.01
density $
ho $/(kg?m?3)		 7850
young’s modulus $E$/MPa 2
poisson ratio $mu $ 0.3





下载:
导出CSV
|显示表格



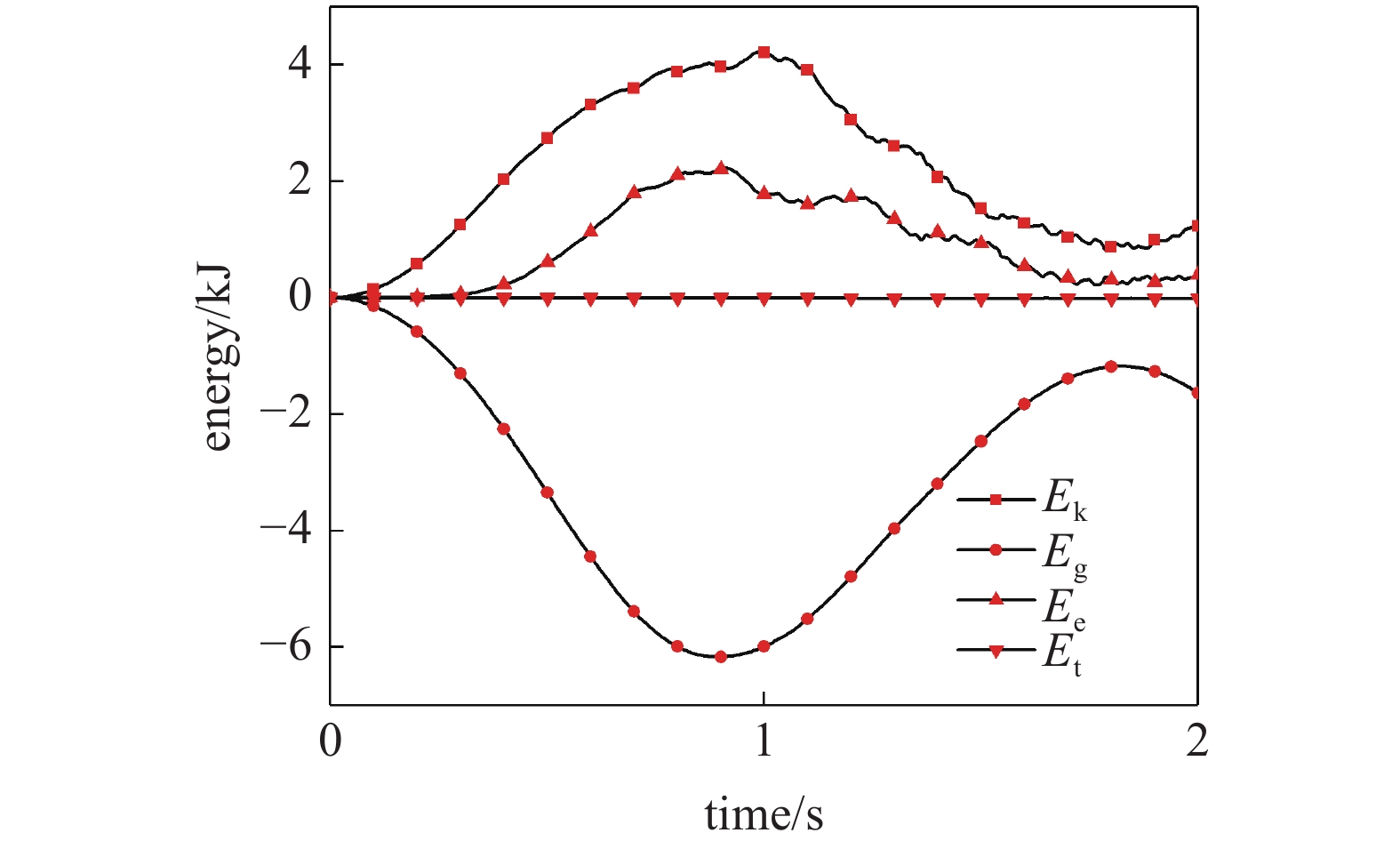
图9给出了含有2 × 2个T样条单元的薄板在1 s内动能${E_{
m{k}}}$、重力势能${E_{
m{g}}}$、弹性势能${E_{
m{e}}}$及总能量${E_{
m{t}}}$的变化情况. 可以看出, 基于T样条的等几何薄板满足能量守恒定律. 为了检验本文提出的方法的收敛性, 分别使用2 × 2, 4 × 4和8 × 8的T样条曲面单元对图8所示的单摆进行离散. 图10给出了单摆自由端C的z向位移曲线. 可以看出, 基于T样条的等几何薄板具有较好的收敛性. 图11给出了含有2 × 2个T样条单元的单摆在1 s内的连续构型.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
能量曲线



Figure
9.
The energy balance curve



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
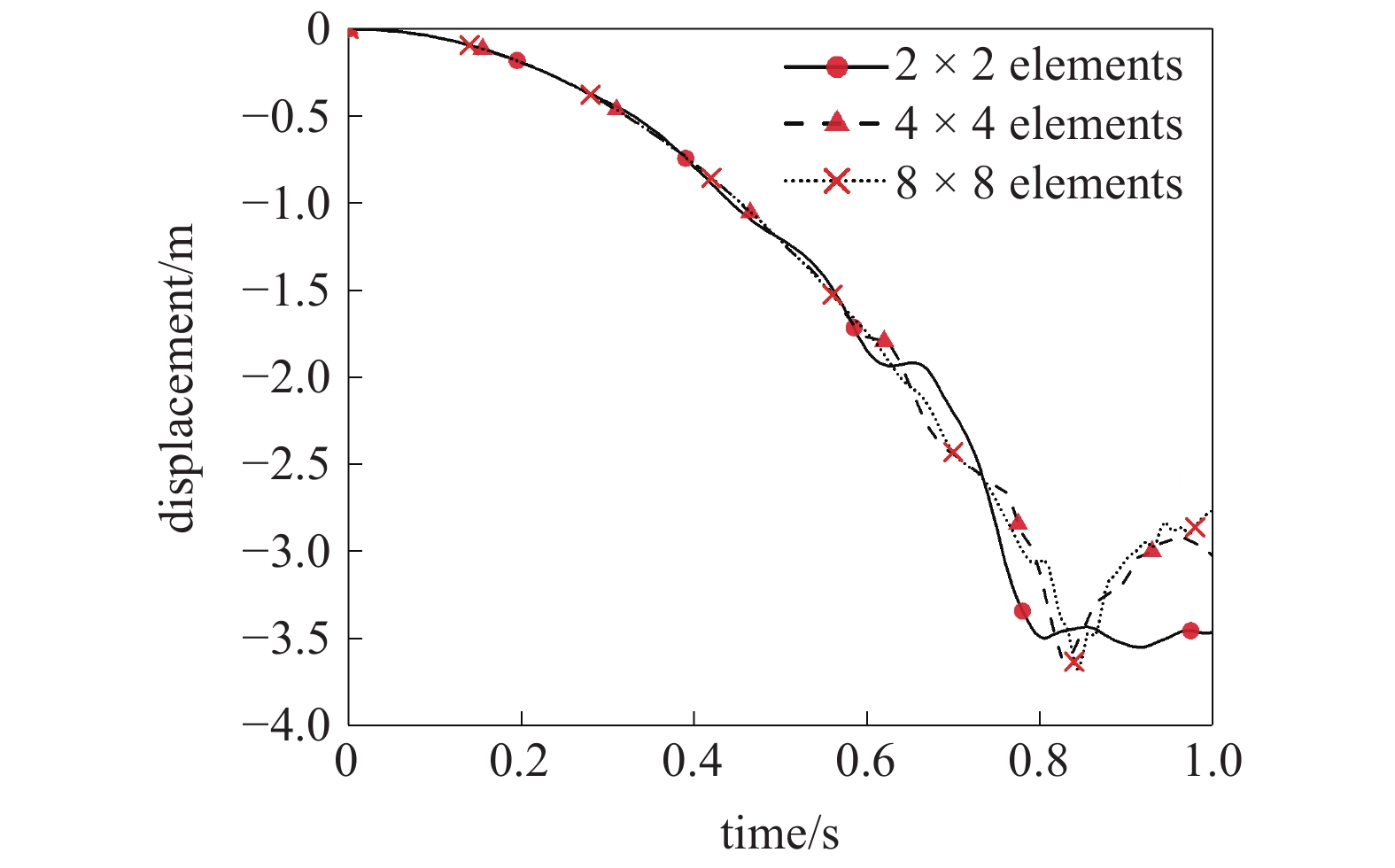
等几何薄板中T样条单元的收敛性



Figure
10.
Convergence of T-spline element in thin plate



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
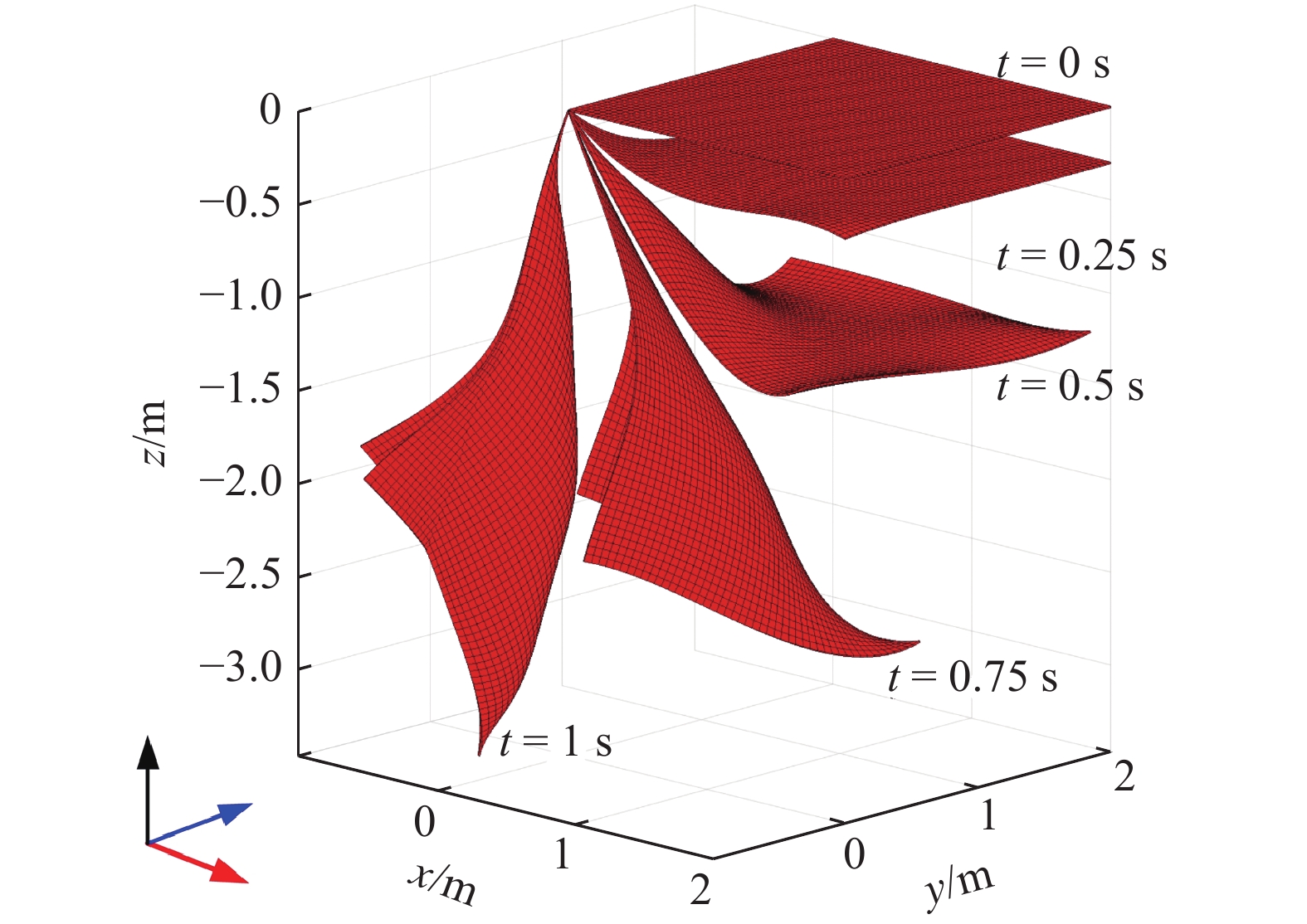
含有2 × 2个T样条单元的单摆的连续构型



Figure
11.
Configuration of the pendulum with 2 × 2 T-spline elements



下载:
全尺寸图片
幻灯片



4.4
刚性球与柔性板的接触


本算例将T样条局部细化算法应用于柔体动力学分析中. 如图12所示, 一个刚性球从四边固定的薄板中心正上方自由下落. 接触发生后, 对薄板中心受冲击区域进行局部细化. 刚性球与板的参数表3中给出.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
自由坠落刚性球与柔性薄板的碰撞



Figure
12.
The collision between a rigid ball and a flexible thin plate



下载:
全尺寸图片
幻灯片





表
3
接触算例的参数



Table
3.
Parameters of the contact example



table_type1 ">
ParameterNameValue
the flexible
thin plate		 length $a$/m 2
width $b$/m 2
height $h$/m 0.04
density $;{
ho _1}$/(kg?m?3)		 7850
Young’s modulus $E$/MPa 20
Poisson ratio $mu $ 0.3
the rigid ball radius $R$/m 0.1
density $;{
ho _2}$/(kg?m?3)		 1500
initial position ${{boldsymbol{P}}_{
m{b}}}$		 (1,1,0.2)





下载:
导出CSV
|显示表格



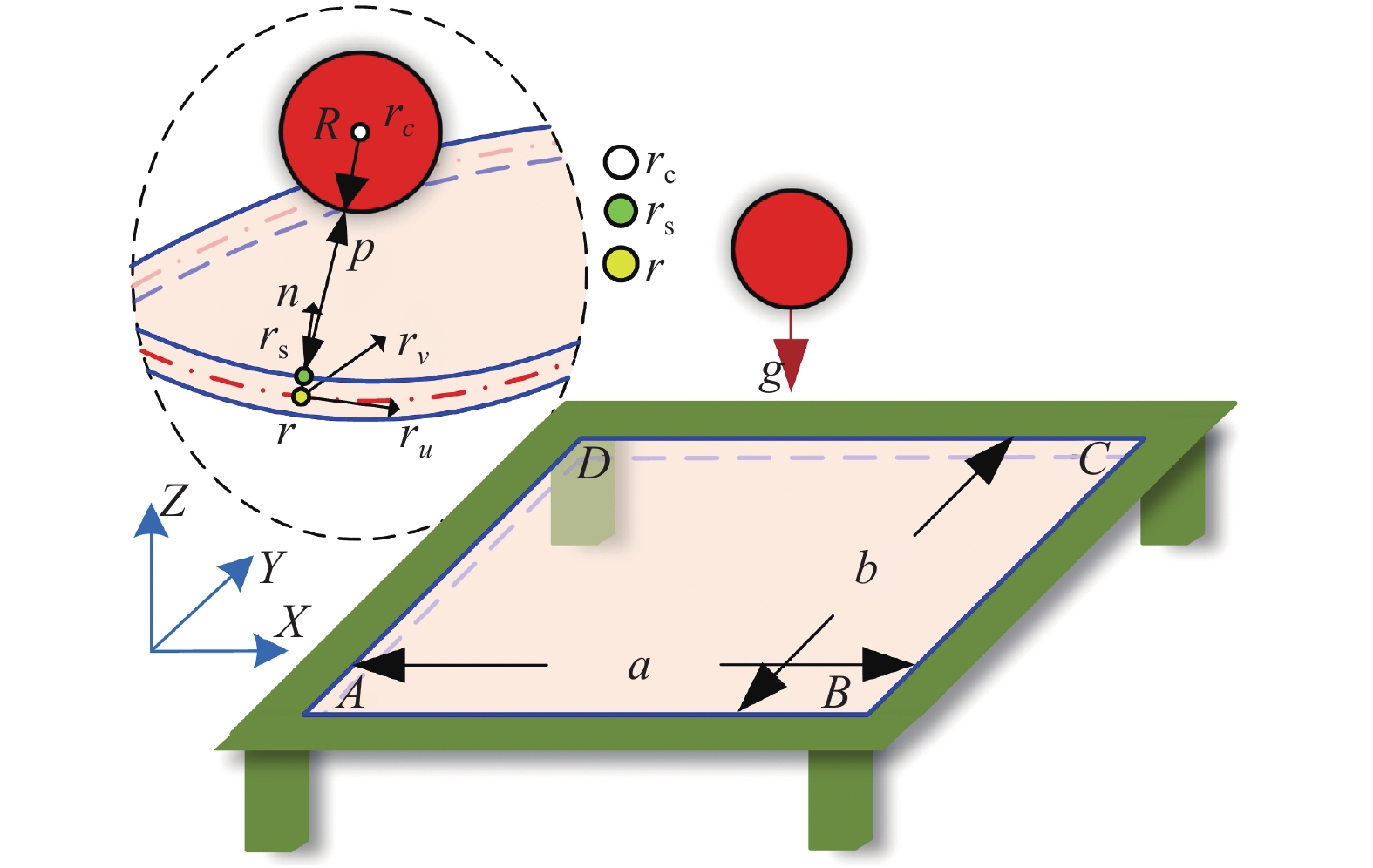
在本算例中, 采用罚值法来完成刚体球与柔性板的接触实现. 在每个T样条单元中, 刚体球与均匀检测点的距离用式(27)表示







$$left. {begin{array}{*{20}{l}} {{{boldsymbol{r}}_{
m{s}}} = {boldsymbol{r}}left( {u,v}
ight) + {boldsymbol{n}} cdot dfrac{h}{2}} {p = left| {{{boldsymbol{r}}_{
m{s}}} - {{boldsymbol{r}}_{
m{c}}}}
ight| - R} {{boldsymbol{n}} = dfrac{{{{boldsymbol{r}}_u} times {{boldsymbol{r}}_v}}}{{left| {{{boldsymbol{r}}_u} times {{boldsymbol{r}}_v}}
ight|}}} end{array}}
ight}$$
(27)

式中, $p$为嵌入深度, ${boldsymbol{r}}left( {u,v}
ight)$为薄板中性层上的接触检测点, ${{boldsymbol{r}}_{
m{s}}}$为任意点检测点在薄板上表面所对应的物质点, ${{boldsymbol{r}}_{
m{c}}}$为球心位置, $h$为薄板厚度, $R$为球心半径, ${boldsymbol{n}}$表示接触检测点的单位法向量.

一旦小球与薄板发生接触, 开始计算薄板所受的接触力. 计算切向接触力时, 采用文献[33]中计及临界滑动速度${v_{
m{0}}}$的平滑化库伦摩擦模型. 接触探测点$i$的法向接触力${boldsymbol{F}}_{
m{n}}^i$和切向接触力${boldsymbol{F}}_{
m{t}}^i$表达式分别为







$${boldsymbol{F}}_{
m{n}}^i = -left( {k{p^{1.5}} + c{v_{
m{p}}}left| p
ight|}
ight) cdot {boldsymbol{n}}$$
(28)







$$begin{split} &{boldsymbol{F}}_{
m{t}}^i = left{ {begin{array}{*{20}{l}} {{
m{ - }}mu left| {{boldsymbol{F}}_{
m{n}}^i}
ight|{{boldsymbol{v}}_{{
m{et}}}}},&{left| {{{boldsymbol{v}}_{
m{t}}}}
ight| < {{{v}}_0}} {{
m{ - }}dfrac{{left| {{{boldsymbol{v}}_{
m{t}}}}
ight|}}{{{{{v}}_0}}}mu left| {{boldsymbol{F}}_{
m{n}}^i}
ight|{{boldsymbol{v}}_{{
m{et}}}}},&{left| {{{boldsymbol{v}}_{
m{t}}}}
ight| geqslant {{{v}}_0}} end{array}}
ight.&{{boldsymbol{v}}_{{
m{et}}}} = dfrac{{{{boldsymbol{v}}_{
m{t}} }}}{{left| {{{boldsymbol{v}}_{
m{t}}}}
ight|}}end{split}$$
(29)

式中, ${{{v}}_{
m{p}}}$为嵌入速度, $k$和$c$表示刚度系数与阻尼系数. 在式中, $mu $为薄板与球之间的摩擦系数, ${{boldsymbol{v}}_{
m{t}}}$为切向接触速度, ${{{v}}_0}$为假定的临界滑动速度, ${{boldsymbol{v}}_{{
m{et}}}}$为单元切向接触速度.

图13介绍了三种网格构型图. 网格1和网格2都对表面进行了均匀的网格细化, 其单元数量分别为14 × 14和10 × 10. 网格3的初始网格较为粗糙, 含有10 × 10个单元. 当接触发生后, 薄板的接触区域被局部细化, 单元数量由100变为112个. 三组薄板的详细信息见表4.



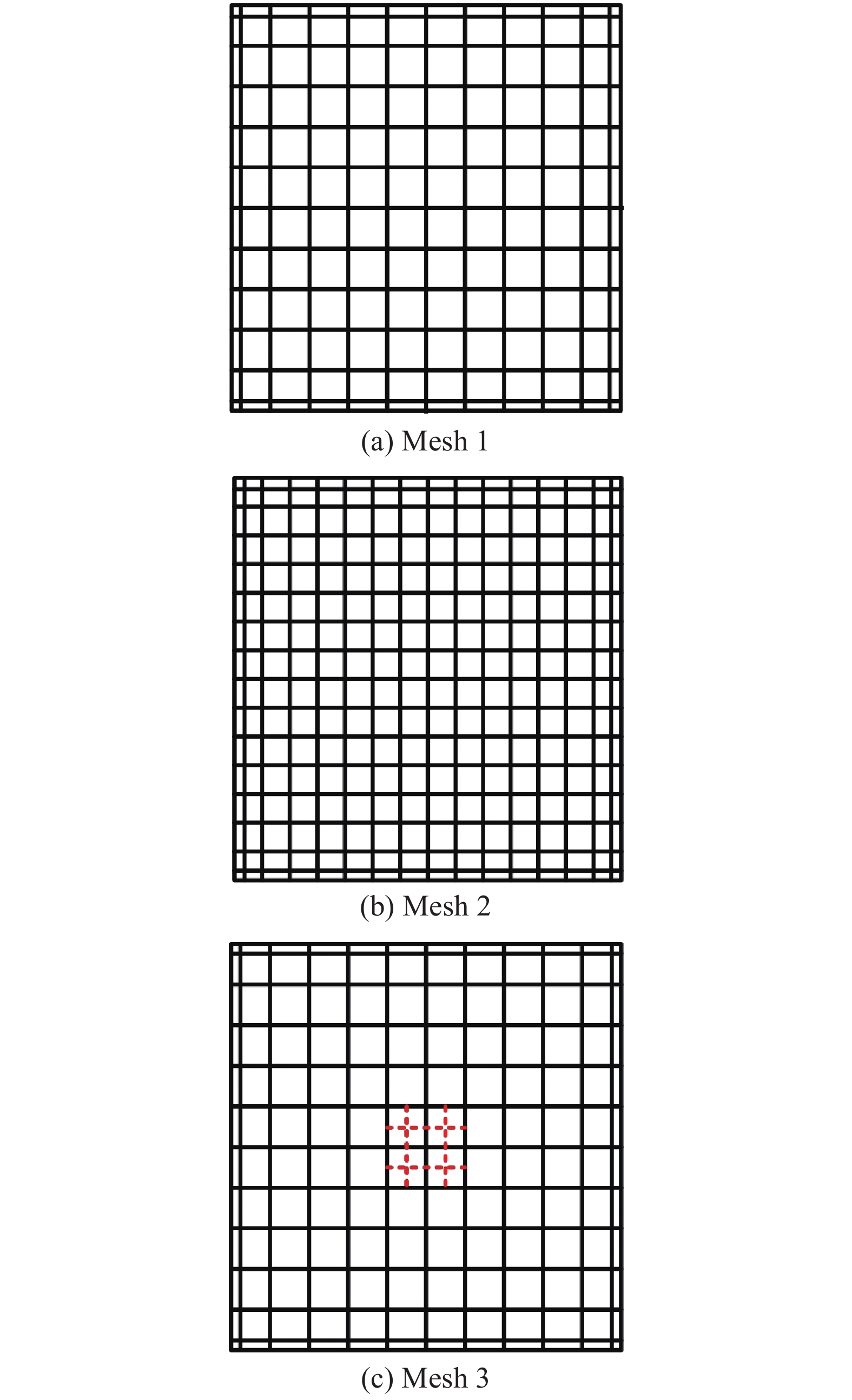onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
三组不同的网格构型



Figure
13.
The mesh refinement for three groups



下载:
全尺寸图片
幻灯片





表
4
三组薄板的详细信息



Table
4.
The detailed information of three groups



table_type1 ">
GroupNumber of
control point		Number of
element		Element
size/m2
mesh 12891961/7 × 1/7 (all region)
mesh 21691001/5 × 1/5 (all region)
mesh 31851121/10 × 1/10 (contact region)





下载:
导出CSV
|显示表格



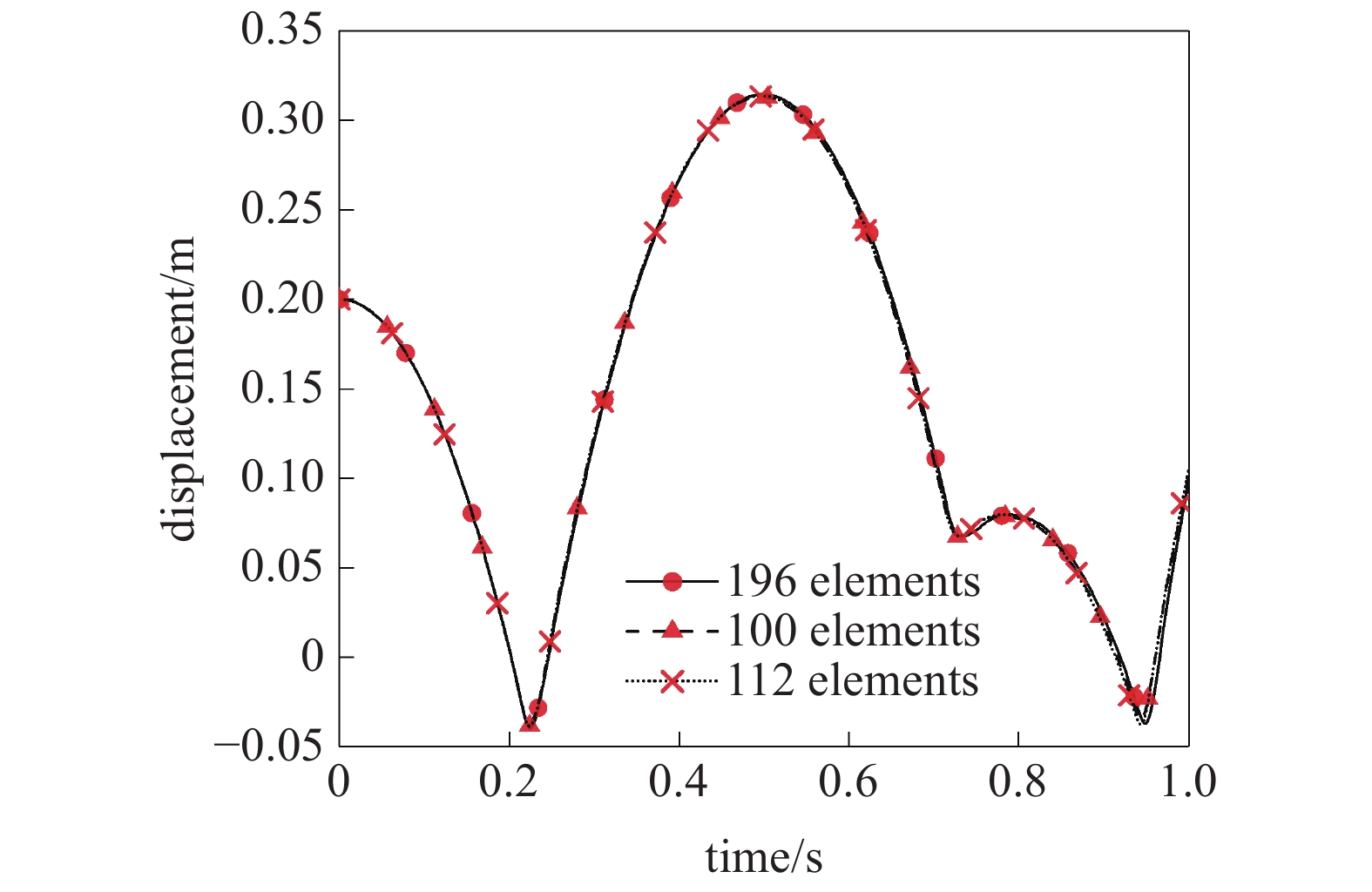
图14给出了三组小球球心在1 s内的z向位移曲线. 图15和图16则为三组薄板的质心z向位移曲线与弹性能曲线及其局部放大图. 在$t = 0.216;{
m{s}}$时, 刚性球与柔性板首次接触, 对薄板进行如图13所示的3种不同网格细化策略. 三组球的质心垂直位移具有较好的一致性, 薄板质心的垂直位移曲线在1 s内也呈现相似的趋势. 从薄板的质心位移与弹性能计算结果来看, 允许局部网格细化的T样条等几何薄板可以达到与退化为NURBS曲面的均匀网格板相同的计算精度, 且相较于网格2, 局部细化的网格3所对应曲线的变化趋势更接近网格1.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
球心z向位移



Figure
14.
Vertical displacement of the center of the ball



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />



图
15
薄板质心的z向位移



Figure
15.
Vertical displacement of the plate’s centroid



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />



图
16
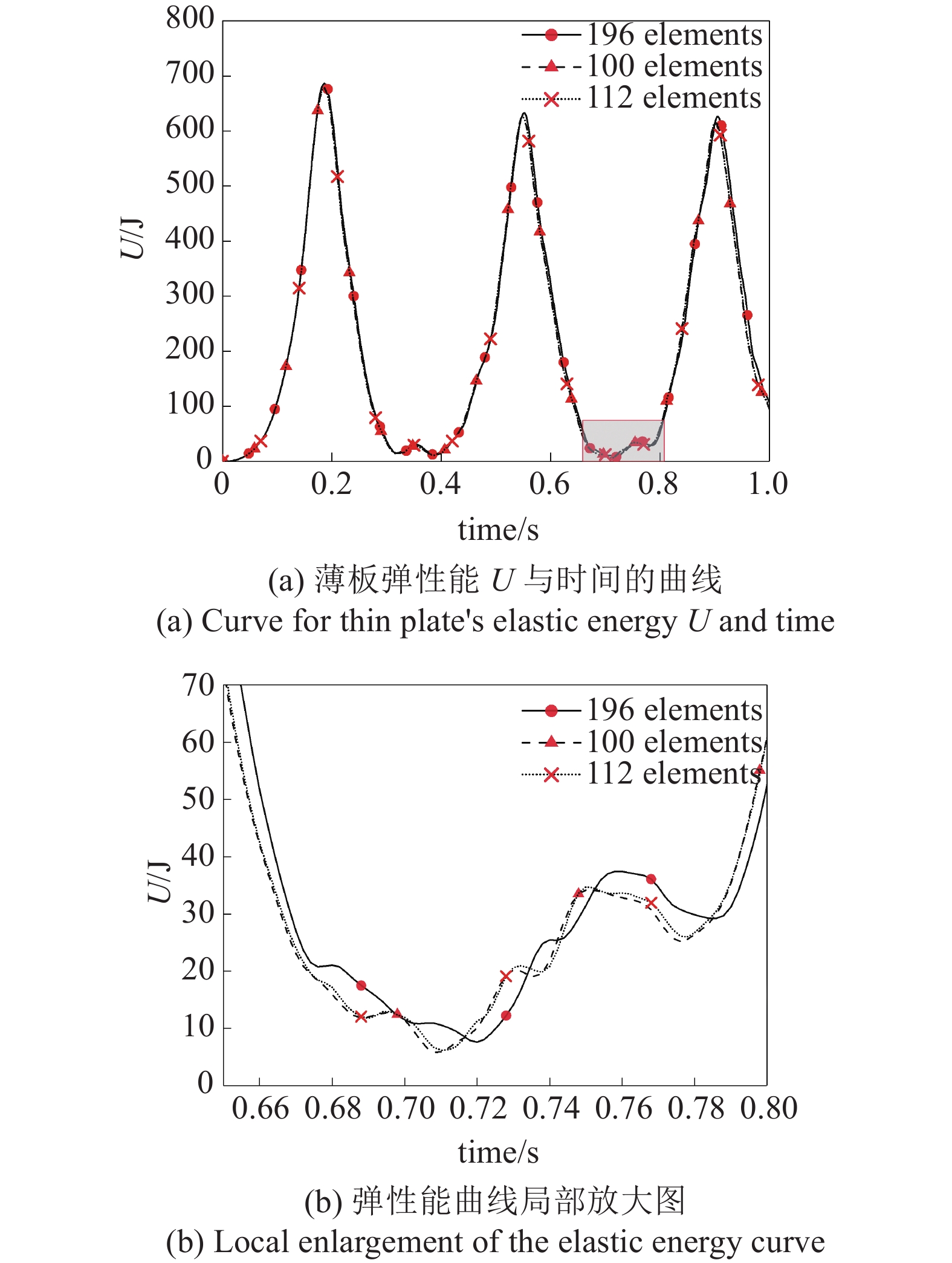
薄板弹性能曲线



Figure
16.
The elastic energy curve of thin plate



下载:
全尺寸图片
幻灯片


为了比较不同网格构型的薄板对计算效率的影响, 图17给出了三组薄板的仿真时间柱状图.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-17.jpg'"
class="figure_img
figure_type1 bbb " id="Figure17" />



图
17
计算消耗时间



Figure
17.
Time consumption for three groups



下载:
全尺寸图片
幻灯片


三组算例均是在配备Intel Core i5 CPU和8GB RAM的笔记本电脑上执行的. 由图17可知, 网格2与网格3用时接近, 约为网格1计算用时的一半. 值得注意的是, 由于在接触区域附近执行了网格细化, 使得求解收敛更快, 网格3虽然自由度数略多于网格2, 用时反而更少. 这也进一步体现了T样条单元网格局部细化的优势.

图18展示了带有112个T样条单元局部细化薄板在不同时刻的米塞斯应力云图, 分别为$t = 0.18;{
m{s}}$接触前的薄板发生最大变形, $t = 0.218;{
m{s}}$发生接触后首次使用细化后模型的时刻, $t = 0.548;{
m{s}}$接触后的发生最大变形的时刻以及仿真结束时刻$t = 1;{
m{s}}$.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-199-18.jpg'"
class="figure_img
figure_type2 ccc " id="Figure18" />



图
18
局部细化薄板的米塞斯应力云图



Figure
18.
von-Mises stress distribution of the locally refined thin plate



下载:
全尺寸图片
幻灯片



5.
结论


本文提出了一种基于T样条曲面的等几何分析方法, 建立了使用T样条曲面单元离散的基尔霍夫薄板模型. 单元基函数和节点坐标分别为T样条基函数和控制点坐标, 无需网格划分, 既保证模型的几何精确, 又能在没有约束方程的情况下保证期望的连续性条件. 给出了基于T样条的薄板运动学模型、弹性力模型及其雅克比矩阵的计算方法. 为了体现T样条局部细化特性在减少单元数目、提高计算效率方面的优势, 提出了一种基于T样条单元的局部网格细化算法, 包括单元网格拓扑的改变和相应的新控制点坐标计算方法. 将该细化算法与广义α法相结合, 建立了带有网格局部细化的变自由度系统动力学方程的求解算法. 通过受端弯矩的悬臂薄板以及环形构件受内压的静力学算例证明了T样条单元弹性力模型的正确性. 柔性摆算例验证了T样条单元在动力学问题中的收敛性和机械能守恒特性. 最后, 为验证T样条局部细化特性在模拟接触碰撞等柔性体局部发生应变剧烈变化等问题中的优势, 建立了刚性球落在柔性板上的动力学实例并进行了仿真. 首先, 采用10 × 10单元网格对柔性板进行离散. 接触发生后, 对冲击区域进行局部细化, 得到112个单元的网格. 对10 × 10和14 × 14两种网格进行了仿真, 并将仿真结果作为基准. 可以看到, 112单元网格的计算结果与14 × 14网格具有良好的一致性, 但所消耗的时间只有其1/2. 以上算例证明了基于T样条的局部网格细化等几何薄板在柔性多体系统动力学分析中的应用价值.

相关话题/控制 系统 图片 计算 结构
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 软材料粘接结构界面破坏研究综述
    引言因其特有的低模量和能量耗散等“软”的特性以及优异的“小激励大响应”等特征,多种多样的软材料,如水凝胶、介电弹性体以及聚甲基氧硅烷等被广泛应用在软机器人、生物医学和柔性电子等各个领域[1-4].近些年,软材料的力学行为已经成为学术界和工业界广泛关注的热点之一.在实际应用中,软材料一般需要粘附于某种 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于喷流拟序结构预测的SGS模型比较研究
    引言拟序结构普遍存在于湍流中[1–3],并影响湍流的发生、输运与耗散等过程,对湍流拟序结构的研究、对于理解湍流机理、分析流动相互作用有重要的意义.从大涡模拟来看,正确预测湍流拟序结构的关键就在于算法和亚网格尺度(sub-grid-scale,SGS)模型的准确性.在算法方面,传统的大涡模拟方法求解网 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 旋转振荡板尾流的控制研究
    引言桥梁颤振是结构从气流中吸取的能量大于结构阻尼所消耗的能量时发生的扭转(或扭、弯耦合)振动,其振动的振幅随时间不断加大,形成发散的自激振动,使结构遭受直接破坏.提出适应现代越来越轻型化的新型桥梁的颤振控制方法,为今后桥梁建设提供技术储备很有必要.Larsen和Larose[1]研究了Tacoma大 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于Darcy-Stokes耦合模型的多孔介质颗粒悬浮液等效黏性系数计算
    引言颗粒悬浮液广泛存在于自然界及工程应用领域,其黏性特征对悬浮液的流动行为有着重要的影响[1-4].早在1905年,Einstein[5]就研究了低浓度条件下球形固体颗粒对流体黏性的影响,给出了悬浮液等效黏度系数计算的一个强有力的理论框架,并得到了低浓度球形颗粒悬浮液的著名的Einstein黏性公式 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 新型负刚度吸能结构力学特性分析
    引言在冲击载荷作用下,吸能材料的应用具有重要的工程意义.传统的减振吸能方法主要有两种:其一,利用材料的塑性变形实现能量吸收耗散[1],如汽车保险杠和轻型自行车头盔均是基于这一原理进行结构以及超材料设计,然而破坏性的塑性变形使得材料无法重复利用;其二,利用材料的黏弹特性[2-3],实现重复性的能量吸收 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • DVC中内部散斑质量评价及计算体素点的优化选择
    引言数字体图像相关方法(digitalvolumecorrelation,DVC)是二维数字图像相关方法(two-dimensionaldigitalimagecorrelation,2DDIC)在三维体图像上的拓展.通过比较体成像设备获取的被测试样变形前后数字体图像,该方法可测量物体内部三维全场变 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 一类新型仿生起竖结构设计及其动力学分析
    引言随着科学技术的不断发展,机器人的应用范围越来越广泛,应用场景也越来越多样化.为了进行灾后搜救、管道清理、未知区域探索等任务,机器人需要能在有限的工作空间和不规则的地形下移动并完成任务.于是,许多****以蚯蚓等蠕虫为仿生对象,设计了一系列仿蠕虫机器人[1-8].受到蚯蚓的运动来源于体节的轴向变形 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于分数阶磁流变液阻尼器模型的车辆悬架组合控制
    引言磁流变液阻尼器是利用磁流变液提供可控阻尼力的装置,已广泛应用在车辆悬架[1]、汽车座椅[2]、斜拉索[3]等结构的振动控制中.磁流变液阻尼器通过改变阻尼线圈中的电流强度来改变其磁场强度,能够快速响应并且输出阻尼力.描述磁流变液的力学模型主要有Bingham模型[4-5]、Sigmoid模型[6] ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于高温气体效应的磁流体流动控制研究进展1)
    罗凯*,&,汪球,*,2),李逸翔*,&,李进平*,赵伟*,&*中国科学院力学研究所高温气体动力学国家重点实验室,北京100190&中国科学院大学工程科学学院,北京100049RESEARCHPROGRESSONMAGNETOHYDRO ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于数据驱动的流场控制方程的稀疏识别1)
    江昊,王伯福,卢志明,2)上海大学,力学与工程科学学院,上海市应用数学和力学研究所,上海200072DATA-DRIVENSPARSEIDENTIFICATIONOFGOVERNINGEQUATIONSFORFLUIDDYNAMICS1)JiangHao,WangBofu,LuZhiming,2)S ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.