冲击载荷下颗粒材料临边界区域的波动行为及变形特征分析

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

引言

作为离散颗粒材料的土壤(或岩体), 是日常生活中最常见的随机多孔介质, 冲击载荷作用下材料的动力学响应对于工程实践和地质灾害防控有着重要的指导意义. 注意到应力波的传播行为与介质性质密切相关, 基于应力波的行为特征分析可提供一种非侵入式研究颗粒材料性质的途径. 因此有非常多的****致力于研究冲击载荷作用下颗粒材料的动力学响应.

在过去几十年中, 一维颗粒链中的波传播行为一直是一个备受关注的话题^[1-3]. 在研究过程中, 研究人员通常在边界处设置传感器, 从多方面研究颗粒材料中的波特性^[4], 但很少讨论边界区的情况^[5-6]. 对于更复杂的塑性接触问题, 研究者们构建了具有弹性和塑性特性的理想颗粒材料模型, 研究不同的载荷条件下单分散的弹性和弹塑性颗粒链的动力学响应, 给出了波传播过程中能量衰减的机制^[7-9]. Hayden等^[10]开发了弹塑性球体动态压缩力?位移模型来研究由金属球体组成的系统对撞击的响应, 模拟中使用大型周期性颗粒晶体, 以确定材料中应力波速的控制因素. 除了天然材料之外, 基于颗粒物质的超材料设计一直是一个充满活力的研究领域, 它结合了材料科学, 非线性动力学和凝聚态物理等学科的思想^[11]. 迄今为止大多数研究都集中讨论一维晶体中的现象, 基本回避了边界问题^[12].

对于二维、三维的情况, 研究人员利用不同的方法研究了波在颗粒材料中的传播行为^[13-14], 修晨曦和楚锡华^[15]基于微形态模型研究了颗粒材料中波的频散特性. Mouraille 等^[16]利用周期性边界条件, 探讨了应力波在颗粒材料中的传播机制, 分析了波速和频散关系, 并与基于宏细观转化的理论结果进行了对比. Awasthi等^[17]采用数值方法研究了材料中压缩波的各向异性和传播速度的影响. Chotiros和Isakson^[18]发现在颗粒介质中的剪切波传播会涉及与晶粒旋转相关的能量. Huang等^[19]基于球形粒子模型, 计算了砂土中剪切波速度的计算公式, 其计算结果与现场测量数据非常吻合. Yang和Sutton^[20]通过数值和实验方法研究了非线性波在密排颗粒通道中的传播, 证明了颗粒旋转动力学的重要性. Lisyansky等^[21]研究了主脉冲在未压缩的二维密排颗粒晶体中的传播, 通过降阶模型描述了强定位主脉冲的空间演化. Keki和Van?Gorder^[22]对具有赫兹相互作用势的一维颗粒晶体中的孤波进行了研究, 在界面两侧设置不同的相互作用势, 孤立波显示出不同的反射和透射特性, 并根据准粒子碰撞解释了界面处的波传播效应. Hua和Van?Gorder^[23]研究了在赫兹接触定律下二维球形晶体中的波传播, 讨论了边界处的波反射, 尽管边界的反复反射将使系统长时间陷入混乱状态, 但有许多有趣的波结构和模式会以瞬态的形式出现. 除了对界面处波反射问题的简单研究之外, Li等^[24]研究了波之间的相互作用, 得到了波前速度和力幅值之间的通用关系.

颗粒材料中波传播特性的一个重要研究目标是材料定制(即超材料设计), 如何设计出具有特定导波特性的人工材料一直是研究者们努力的方向. Leonard等^[25]采用微型三轴加速度计来确定面内外碰撞所产生的应力波特性, 研究了未压缩不锈钢球的二维方形堆积的动力响应. Leonard等^[26]还通过选取不同的材料组合, 对应力波传播过程中的波前形状进行了调节. 他们还通过试验和数值模拟的方法, 研究了颗粒质量和刚度比的系统变化对应力波波前形状的改变. 在这些颗粒系统中控制应力波前特性的能力可以用来研发新的波定制材料^[27]. 这些结果为设计有效的减震结构开辟了道路, 并为颗粒物质中波传播的机理提供了新的见识^[28]. Xu和Zheng^[29]基于正方形密堆积和六角密堆积研究了二维布基球(buckyball C60)晶格的应力波行为, 其计算结果与分子动力学模拟的结果非常吻合. Galich等^[30]分析了弹性波在层状介质中的传播, 分析了不同频率范围内带隙的具体情况. Zhou等^[31]从基本波动方程出发, 得出了二维固体声子晶体带隙的影响因素, 并分析了波速比, 声阻抗比以及泊松比对带隙的影响.

以上诸多研究工作主要从两方面着手研究颗粒材料中的波传播行为: (1)通过建立更精准的接触本构模型(如弹塑性接触模型), 使计算所得的结果更符合实际. (2)通过人工设计颗粒材料内部结构, 主动控制波在材料中的传播行为. 事实上在波传播过程中, 由于边界的存在, 边界处应力波的反射、吸收等都把问题复杂化, 目前的研究工作中只有极少一部分考虑了材料边界对波传播的影响; 对边界附近区域的设计也是超材料设计中极为重要的一部分, 它往往比材料内部设计更有挑战性. 本研究从一维颗粒链中的波传播出发, 根据边界的影响范围, 给出了临边界区域的定义; 然后对不同颗粒排列方式下, 不同形状的临边界区域中波的传播行为和颗粒材料的变形特征进行了分析.

1.
临边界区域的定义

一维颗粒链模型由101个半径为0.5 mm的颗粒组成, 最右端设置刚性墙面, 计算过程中时间步长dt设为0.01 μs, 运动阻尼设为0.05. 计算中使用了两种常用的接触本构模型, 即线性接触模型和赫兹接触模型, 接触摩擦系数μ和接触阻尼系数β_n均为0.5. 其他参数如法/切向接触刚度, 剪切模量以及泊松比等见表1.

表
1
计算参数

Table
1.
Parameters used in the simulation

table_type2 ">

$ ho $ /(kg·m^?3)	${v_0}$ /(m·s^?1)	k_n /(N·m^?1)	k_s /(N·m^?1)	G /Pa	ν
2600	1.0	6.0 × 10⁷	6.0 × 10⁷	1.0 × 10⁹	0.3

下载:
导出CSV
|显示表格

在模型最左端施加冲击载荷, 指定ID为1的颗粒有沿x方向的初速${v_0} = 1.0$

m/s, 分别记录沿着初速度方向的若干观测点处, 波传播过程中颗粒的速度, 波速采用平均速度的定义, 即波传播距离$l$

时, 耗时为$t$

, 则平均波速$v = {l / t}$

, 如图1、图2所示. 在靠近边界的局部区域, 除正常沿程衰减(摩擦)的部分动能之外, 颗粒能够得到的最大动能(速度)明显小于其他区域, 颗粒的运动状态与远离边界处有明显不同, 图2中也表现出同样的速度变化规律. 因此将距离边界10倍颗粒尺度的区域定义为临边界区域, 以下分析主要限定在该区域中进行.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />

图
1
颗粒速度随加载时间的变化(线性接触模型)

Figure
1.
Particle velocity variation with loading time (linear contact model)

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />

图
2
颗粒速度随加载时间的变化(赫兹接触模型)

Figure
2.
Particle velocity variation with loading time (Hertz contact model)

下载:
全尺寸图片
幻灯片

2.
不同形状边界处波的反射

为探究边界处波的反射, 按照边界墙体形状的不同, 分为以下3类, 如图3所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />

图
3
计算模型

Figure
3.
Simulation model

下载:
全尺寸图片
幻灯片

对于A, B类θ范围从0每隔15°变化到75°, 对于C类θ范围从0每隔5°变化到45°. 此外, 变换颗粒排列方式, 即单粒径密排, 单粒径(r)随机排列, 均匀粒径(r_lo?r_hi)随机排列, 如图3(a)所示. 在涉及颗粒材料中波传播的研究当中, 相比线性接触模型, 非线性的Hertz接触模型能更好地反映波在颗粒材料内的传播特性. 因此在下面的研究中, 颗粒之间的接触本构均采用Hertz接触, 分别设置不同形状的边界, 边界与颗粒之间接触力的计算也采用Hertz模型, 得到多组样本, 相关尺寸参数见表2, 具体计算参数同表1.

表
2
二维样本尺寸参数

Table
2.
Size parameters for 2-D specimen

table_type1 ">

Size/mm	r/mm	r_lo/mm	r_hi/mm
75 × 150	0.5	0.25	0.75

下载:
导出CSV
|显示表格

对A类密排颗粒样本, 以θ = 0和θ = 60°为例, 图4显示了不同时刻应力波在样本中的传播情况.

由图4可以看出, 波传播初期, 在主波形之后的次级波表现出了明显的方向性图4(b) ~ 图4(f), 不同方向上传播速度的差异. 图4(c)中明显可以看到在距离激励源相同远近的下边界和右边界处, 波前到达边界的时间有较大差异, 沿y方向的速度明显更快. 将图4(c)单独画出, 见图5. 根据图中所示可以估算出横向速度与纵向速度之间的比约为${{{v_x}} / {{v_y}}} = $

$ 0.93$

, 从竖向变化到横向, 随着速度方向与x轴正向夹角变小, 波传播速度变小.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />

图
4
波前形状随时间演化θ = 0

Figure
4.
Wavefront shape evolves over time (θ = 0)

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />

图
5
波前形状分析示意图

Figure
5.
Schematic diagram of wavefront shape analysis

下载:
全尺寸图片
幻灯片

根据之前的研究工作^[32], 在单一粒径密排颗粒样本中, 波前形状随时间演化可以用以下式子来描述

$$left. {begin{array}{*{20}{l}} {{{left( {x - {a_c}}
ight)}^2} + {y^2} = {{left( {{L_x} - {a_c}}
ight)}^2},;;x > {L_theta }cos {theta '}} {{y^2} + dfrac{{L_y^2 - {{left( {{L_theta }cos {theta '}}
ight)}^2}}}{{{L_theta }sin {theta '}}}x - L_y^2 = 0,;;0 leqslant x leqslant {L_theta }cos {theta '}} end{array}}
ight}$$

(1)

其中${a_c} = dfrac{1}{2}left[ {{L_x} + {L_theta }cos {theta '} - dfrac{{{{left( {{L_theta }sin {theta '}}
ight)}^2}}}{{{L_x} - {L_theta }cos {theta '}}}}
ight]$

, ${L_x}$

, ${L_y}$

, ${L_theta }$

由相应的计算公式来确定, 具体算法可参考文献[32].

在之前的研究中没有考虑边界处的反射效应, 此处将边界的影响纳入其中. 图6显示了边界处反射之后波传播的情况, 图中黑色虚线是无限大体中的波前形状按下边界进行镜面对称而得, 黄色虚线是按左右边界进行镜面对称而得; 红色长点划线表示经下边界反射后实际的波前形状, 黑色实线表示经左右边界反射后实际的波前形状. 由图可知下边界与左右边界处的反射有明显的不同. 为便于分析, 仍然假设反射之后实际的波前形状(红色长点划线)近似为圆弧, 从图中可以看出反射后的圆弧半径明显小于未经边界反射的圆弧半径. 通过对波在时空中的演化过程进行细致分析, 可以得出结论: 下边界处的反射会使波前形状(圆弧)的半径逐渐变小, 这反映出反射后速度在不同方向上的分布呈现出中间高两边低的规律. 左右两边反射后的波前形状基本上为直线(黑色实线), 即半径为无穷大. 这与下边界的规律不一致, 导致这种差异的主要原因是边界处颗粒的排列方式不同.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />

图
6
边界处应力波的反射

Figure
6.
Reflection of stress wave at the boundary

下载:
全尺寸图片
幻灯片

假设颗粒在边界处的速度反射如图7所示, 与边界平行的速度分量不发生改变, 与边界垂直的速度分量反向. 分别观察下边界和右边界的细部图可以看到, 下边界处颗粒与墙体接触“紧密”, 局部孔隙率(考虑边界两层颗粒)为0.137 6. 右边界处颗粒与墙体接触“松散”, 局部孔隙率为0.319 8. 尽管颗粒的排列方式仍然规则, 但经边界反射之后, 速度在样本中的重分配会在孔隙处出现弱化(相同速度碰撞边界的条件下, 黄色颗粒获得的动能将小于下边界处绿色颗粒的动能), 这在宏观上表现为图6中黄色虚线向内收缩逐渐转化为黑色直线的现象.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />

图
7
边界反射细部图

Figure
7.
Details of boundary reflection

下载:
全尺寸图片
幻灯片

对于θ = 60°的A类样本, 波前随时间演化如图8所示, 应力波在边界处的反射效果虽然不明显, 但仍然能看到反射后的波在样本中的传播情况, 图中标示了波前在样本中的大致位置. 除了能观测到主波在边界处反射之外, 在图8(e)中还能观察到次级波在边界处的反射(绿色波形), 这个反射点与主波最初的反射点8(b)位置一致.

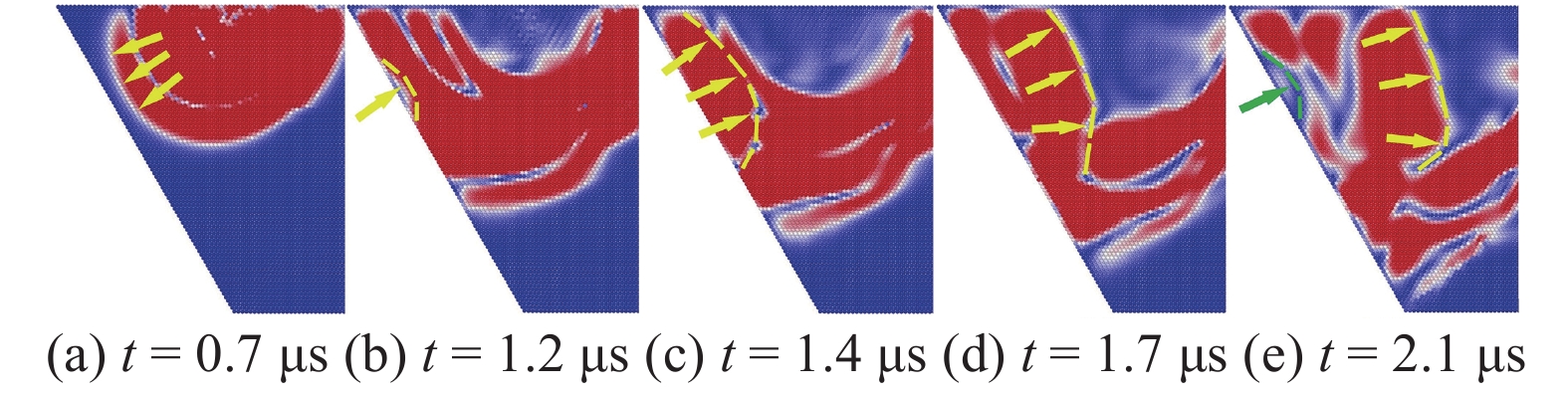onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />

图
8
波前形状随时间演化θ = 60°

Figure
8.
Wavefront shape evolves over time (θ = 60°)

下载:
全尺寸图片
幻灯片

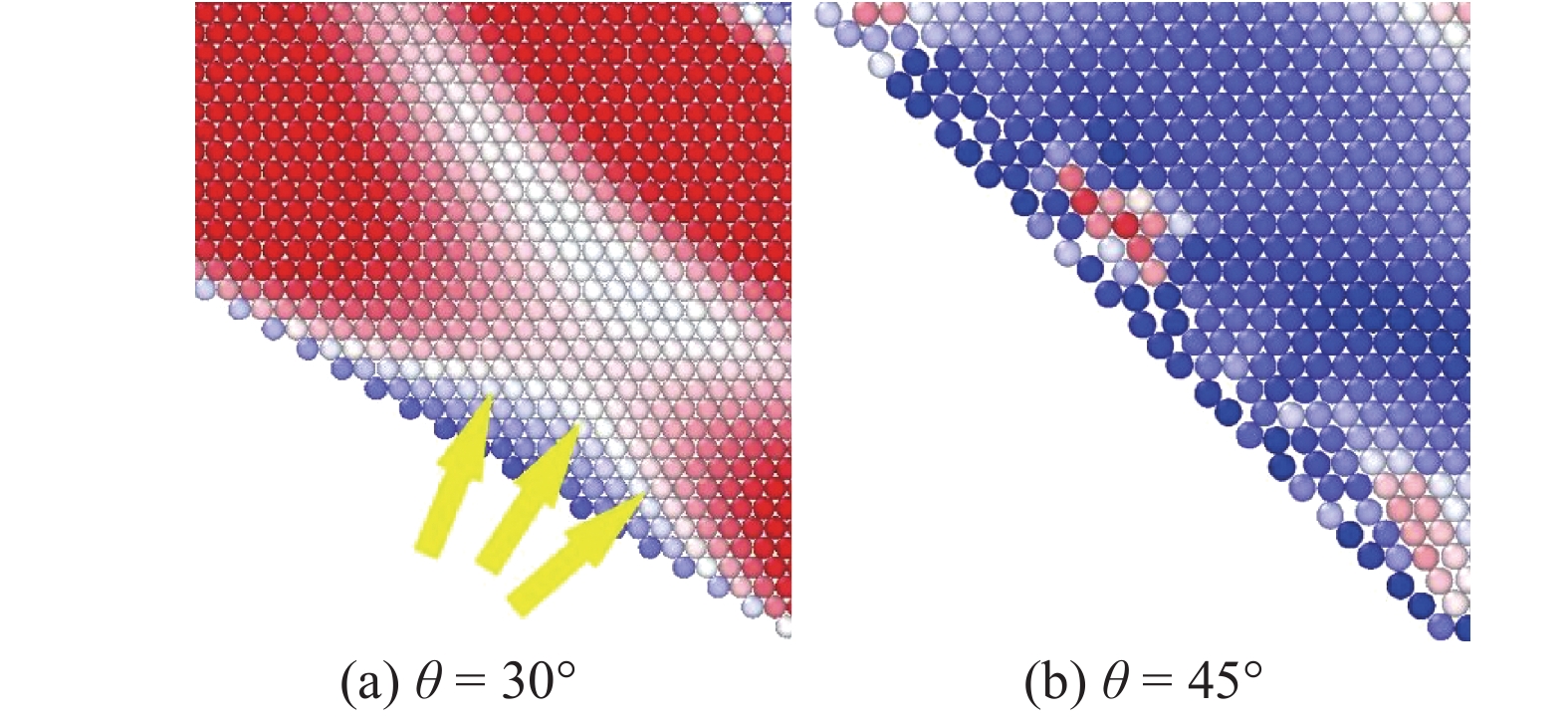
由于此时墙体角度与颗粒排列取向一致, 可以得到形如图9(c)的规整边界, 图中还展示了θ = 30°和 θ = 45°时边界细部情况, 可以看到由于在靠近边界处颗粒排列方式的细微差异, 导致波在边界处的反射表现出不同的形式. 与θ = 0的情况相比, 图8(b)和图10(a)经边界反射后的波前形状不明显; 对于局部孔隙率更大的θ = 45°边界图9(b), 甚至很难直接在临边界区内观察到主波的反射现象. 这是由于大孔隙的存在使临边界区内的颗粒有更多的“活动空间”, 使颗粒携带的动能更容易分散到临边界区域中去, 能量更易弥散开, 而不是像图6所示的那样朝着某个特定的方向传播.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />

图
9
边界细部图

Figure
9.
Details of boundary

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />

图
10
边界反射图

Figure
10.
Reflection at the boundary

下载:
全尺寸图片
幻灯片

为了验证上面所得的结论, 将样本排列方式替换为单粒径随机排列和均匀分布多粒径随机排列, 其他参数保持不变, 这里仍然以θ = 0°为例进行说明. 如图11所示, 当样本受到冲击载荷作用, 波前形状在到达边界之前, 基本保持为圆弧形, 这反映出随机排列样本的各向同性性质. 当主波到达边界后, 由于临边界区域内孔隙率较大, 主波动能在临边界区发生了弥散, 从而导致反射后的波前形状很难直接观察到.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />

图
11
随机排列样本中波前演化图. 上: 单粒径, 下: 均匀分布多粒径

Figure
11.
Wavefront evolution in randomly arranged specimens. Top: single-size particles, bottom: uniform distribution of multi-size particles

下载:
全尺寸图片
幻灯片

对于图3中B类对称边界, 由于密排颗粒取向的特殊性, 在边界与x轴夹角为0° (图6), 30°, 60°时波前形状随时间的演化如图12所示. 对于其他夹角的情况则几乎很难直接观察到波前在边界处的反射, 这是由于在临边界区域内部, 孔隙率较大, 颗粒动能发生弥散, 这一现象还可以通过图12上左2以及下左2观察到, 当主波动能扩散到边界时并没有立刻发生反射, 视觉上好像能量被临边界区域吸收了一样, 这部分能量将和后续次级波所携带的能量一起发生反射. 随着次级波的不断传播, 原先主波携带的能量已经远离边界, 次级波在边界处发生反射, 如图12下右2所示.

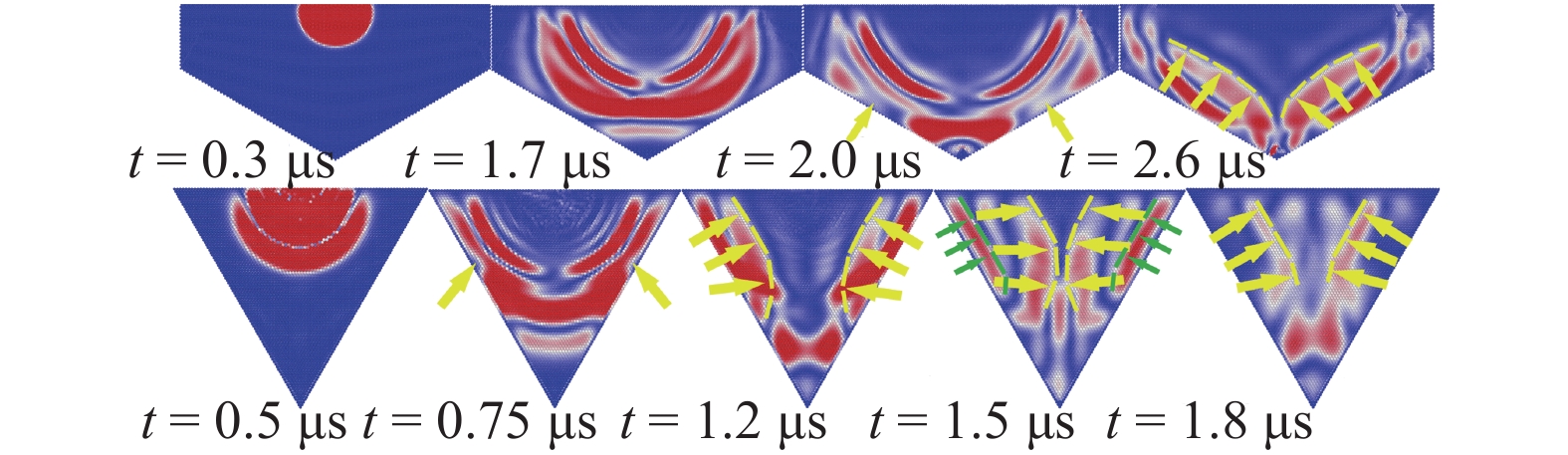onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />

图
12
波前形状随时间演化. 上: θ = 30°, 下: θ = 60°

Figure
12.
Wavefront shape evolves over time. Top: θ = 30°, bottom: θ = 60°

下载:
全尺寸图片
幻灯片

对于反射波形的分析可以分为两部分, 在临边界区域内, 反射波形主要受颗粒间的相互作用(方向)影响, 表现为与颗粒排布方向一致的现象, 如图13所示: 在临边界区反射波的波前形状基本呈直线, 并且与水平方向夹角约为顺时针60°; 在临边界区外(即材料中心区域), 反射波形主要受应力波传播速度的影响, 波形会随着时间不断发生变化, 在图13所示的时刻, 可以看到中心区域的波形近似为两段直线, 第一段与水平方向夹角约为逆时针60°, 第二段与边界平行. 对于折线边界的情况, 研究发现当θ > 30° (如θ=60°, 图12下左2)时, 应力波从边界一点处开始反射, 反射波离开临边界区域时逐渐不与边界平行, 随着角度增大, 这种现象表现更加明显.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />

图
13
B类边界θ = 30°波前形状分析示意图

Figure
13.
Schematic diagram of wavefront shape analysis of type B boundary θ = 30°

下载:
全尺寸图片
幻灯片

对于图3中C类对称边界, 密排颗粒样本很难保证临边界区域中较高的孔隙率, 因此能直接观察到的波反射现象并不明显. 与光或者声音的反射进行类比, 圆弧边界应当具有汇聚效应, 汇聚效应的强弱由圆弧边界的半径大小决定. 临边界区域颗粒排列相对松散, 这将使应力波反射的汇聚效应弱化. 这两个因素(边界形状和临边界区颗粒排列方式)共同影响应力波经材料边界反射后的波前形状. 两个因素是竞争关系, 当圆弧半径较大时, 临边界区颗粒排列方式占据主导地位, 临边界区域反射现象不明显; 随着圆弧半径减小, 边界形状的影响逐渐增强, 经材料边界反射后的波向圆心附近汇聚, 如图14下右1所示.

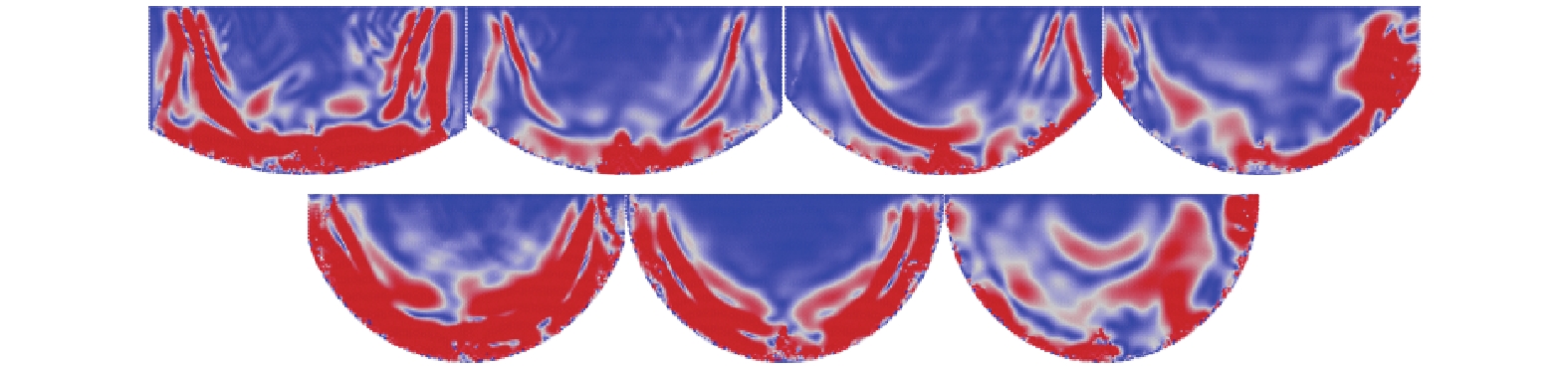onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />

图
14
C类边界样本中应力波的反射

Figure
14.
Reflection of stress wave at type C boundary

下载:
全尺寸图片
幻灯片

分别将样本排列方式替换为单粒径随机排列和均匀分布多粒径随机排列, 其他参数保持不变, 经边界反射之后波在样本中的传播如图15和图16所示, 观察到的现象与前面所得的结论一致.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />

图
15
单粒径随机排列样本波前形状图

Figure
15.
Wavefront shape in randomly arranged samples of single-size particles

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />

图
16
均匀分布多粒径随机排列样本波前形状图

Figure
16.
Wavefront shape in randomly arranged samples of uniformly distributed multi-size particles

下载:
全尺寸图片
幻灯片

3.
材料临边界区域的变形特征

下面从材料临边界区域内颗粒之间的接触关系和相对运动出发, 分析应力波反射过程中材料的变形特征. 这里主要分析密排颗粒样本, A类边界θ = 0°时, 下边界附近区域中颗粒之间的力链如图17所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-17.jpg'"
class="figure_img
figure_type1 bbb " id="Figure17" />

图
17
临边界区域力链随时间的演化

Figure
17.
Evolution of force chain in the pro-border zone over time

下载:
全尺寸图片
幻灯片

注意: 由于材料中颗粒按密排方式排列, 每个颗粒都与周围的6个颗粒发生接触, 初始接触力为0. 随着材料受到点冲击作用, 产生的应力波随着时间由激励点向四周传播, 颗粒之间发生相对位移, 于是接触力链的结构发生改变. 这才是真实的波最前端, 第二部分显示的波形状是由速度分布来表示的. 根据颗粒振动规律, 真实波前应当比图中所显示的略大, 在之前的工作^[33]中已经比较过应力波传播范围和颗粒运动(等效应变)之间的关系, 并定义了“激活区”. 事实上最准确的波前形状应当由颗粒之间接触力网络的变化来确定, 但是由于接触力链的拓扑关系(连接或断开)的改变, 无法有效区分初始波和反射波, 所以力链图适合用来研究未经扰动的无限大体中波的传播问题.

力链图的优点是提供了接触力的方向, 如图18所示, 当应力波刚刚进入临边界区时, 激活区中间部分颗粒之间的力链网络胞元为菱形, 主要接触力的贡献在竖直方向; 激活区其余部分颗粒之间的力链网络胞元为正六边形(或正三角形), 根据后续传播路径(图17)判断, (以右半为例)主要接触力的贡献在正六边形的右和右下分枝. 于是力链网络整体表现为中间向下, 两边向下向外扩展的形式, 这与第2节中波传播速度以及动能分布是一致的.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-18.jpg'"
class="figure_img
figure_type1 bbb " id="Figure18" />

图
18
应力波进入临边界区时力链网络

Figure
18.
Force chain network when stress wave enters the pro-border zone

下载:
全尺寸图片
幻灯片

图19显示了应力波经过边界反射之后, 临边界区域的力链分布图. 也分为两个不同的区域: 中间区域, 力链胞元为菱形; 两翼区域, 力链胞元为正六边形. 似乎与反射前的力链分布(图18)没有区别, 但仔细观察临边界区域力链随时间的演化图17, 发现中间区域和两翼区域的分界线的凸向发生了改变: 当应力波刚刚进入临边界区域时, 分界线上凸; 当应力波经边界反射之后, 分界线下凸.

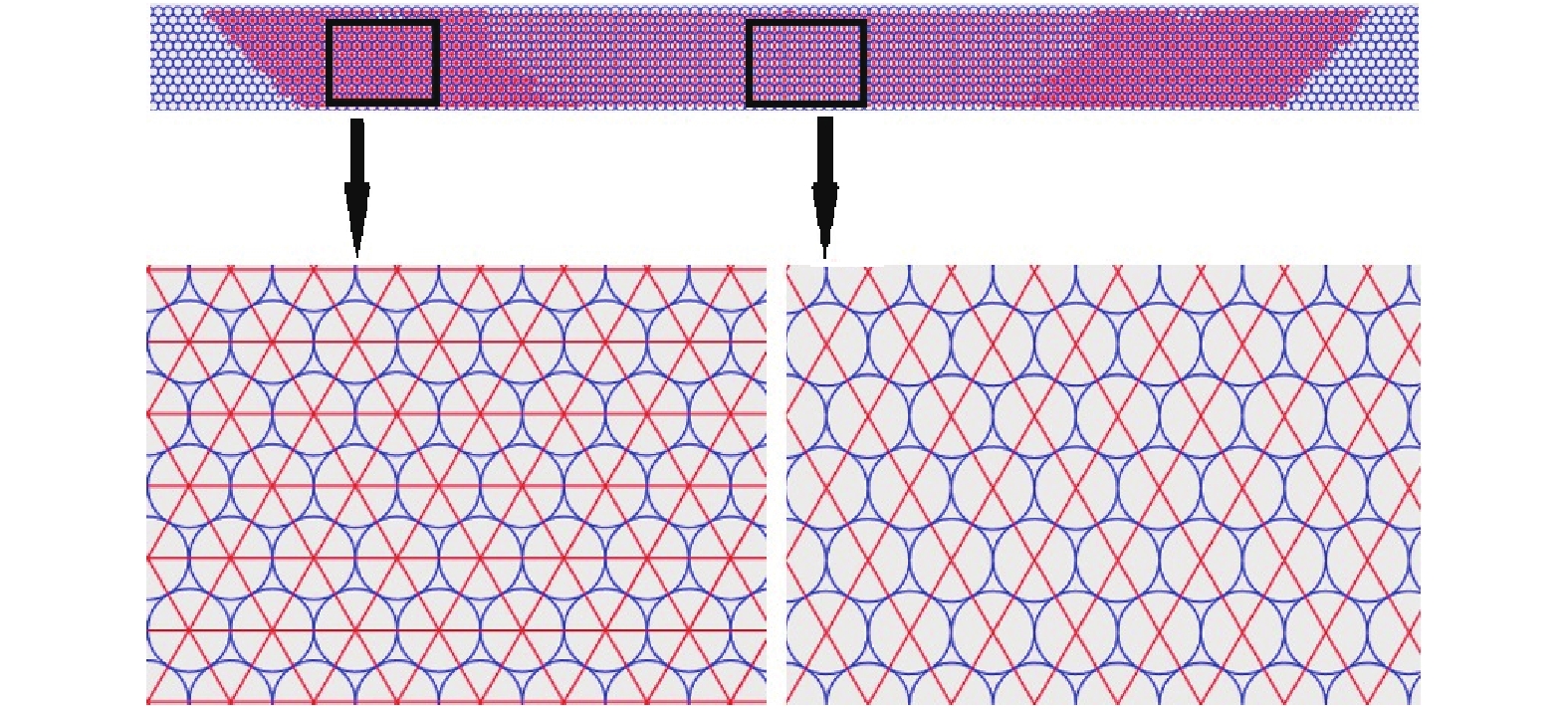onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-19.jpg'"
class="figure_img
figure_type1 bbb " id="Figure19" />

图
19
应力波反射后临边界区力链网络

Figure
19.
Force chain network in the pro-border zone after stress wave reflection

下载:
全尺寸图片
幻灯片

下面结合动能分布图来进一步说明, 如图20所示, 分别显示了应力波反射前后临边界区域颗粒动能的分布. 由图可知, 两翼部分具有最大动能, 动能等值线的最大梯度方向与波前形状的分布是一致的. 此外, 从动能分布上能直观反映出“反射滞后”现象, 临边界区域内颗粒与边界接触并反弹的过程对应着能量(动能)的存储和释放.

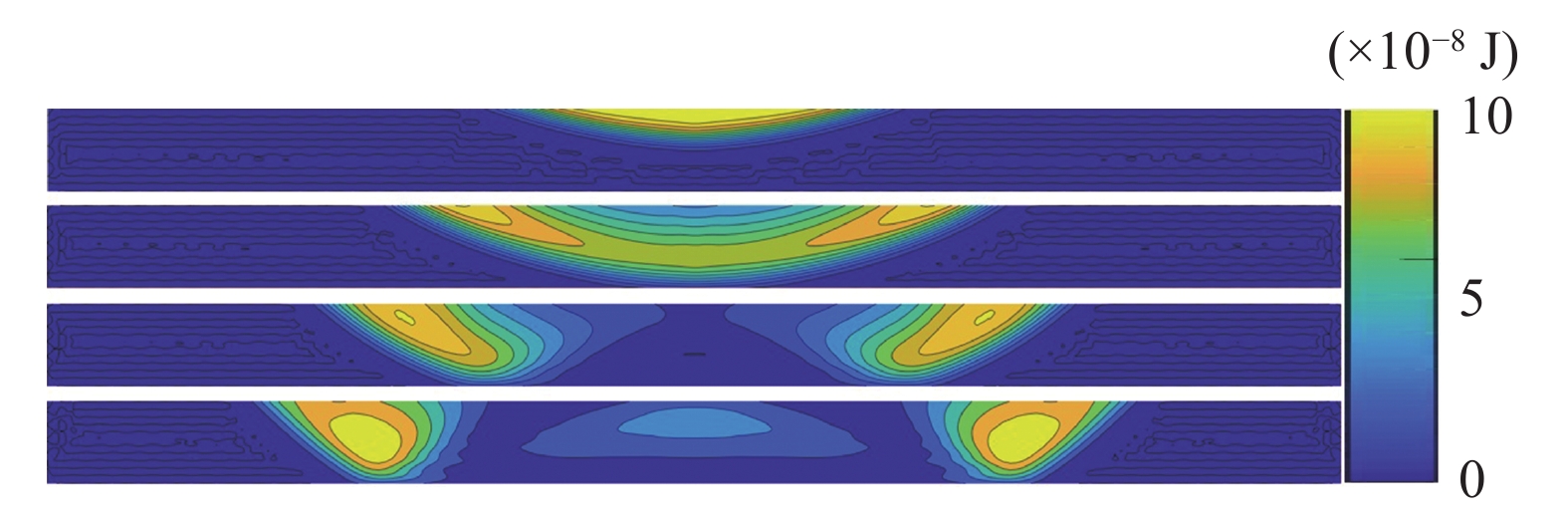onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-242-20.jpg'"
class="figure_img
figure_type1 bbb " id="Figure20" />

图
20
应力波反射前后临边界区颗粒动能分布

Figure
20.
Distribution of particle kinetic energy in the pro-border zone before and after stress wave reflection

下载:
全尺寸图片
幻灯片

4.
结论

本文首先从一维颗粒链中应力波的传播出发, 考虑离散元计算中常用的两种接触本构关系, 定义了临边界区域的范围. 然后讨论了不同边界形状条件下, 二维颗粒样本受冲击载荷作用时的动力响应, 对波在临边界区域中的传播进行了细致的分析, 得出如下结论:

(1) 颗粒排列方式和边界形状是影响边界反射的两个重要因素. 二维密排颗粒样本在水平边界处的反射表现为逐渐收缩的圆弧; 在竖直边界处的反射表现为直线波前形状.

(2) 临边界区颗粒排列方式的影响可以概括为两方面: 颗粒的相对位置和局部孔隙率. 临边界区内应力波的反射可以进行简化, 反射后的应力波直接以边界形状在临边界区内传播. 该结论在边界情况越复杂(高局部孔隙率, 颗粒无序随机排列)时, 越准确. 中心区域(临边界区域外)的波前形状主要由波速决定.

(3) 应力波在临边界区域中传播时会出现“反射滞后”现象, 颗粒与边界接触并反弹的过程对应着能量(动能)的存储和释放. 经过临边界区域的弥散作用, 主波动能通常会和紧随其后的次级波动能一起发生反射.

(4) 圆边界的汇聚作用和临边界区域内颗粒的排列方式是两个竞争因素, 共同决定临边界区域内波的反射过程.