引 言

颗粒材料广泛存在于各类自然环境和工程活动中, 人类几乎所有的基础设施都建造于岩土材料这类典型的颗粒材料上, 理解和预测此类材料在外载作用下的力学响应具有重要的意义. 岩土材料通常由粒径不一, 形状各异的矿物颗粒以及颗粒之间的空隙组成. 颗粒间的互相滑动会引起不可恢复的塑性变形, 因而, 颗粒材料在剪切作用下极易发生体积收缩或膨胀(剪胀性或者剪缩性). 在外载荷作用下, 颗粒材料主要通过颗粒之间的接触力来传递和平衡外力, 内部常常形成高度复杂的力链网络结构(非均匀性)^[1]. 这种力链网络的稳定性来源于颗粒间的摩擦强度和形状引起的互锁效应, 宏观上体现出颗粒材料的抗剪强度和刚度随着压应力的增加而增大(压硬性和摩擦性). 除此以外, 颗粒材料的力学响应还和应力路径, 材料初始各向异性等因素相关^[2-3]. 这些复杂的特性使得预测颗粒材料的应力?应变关系成为一个极具挑战的科学问题^[4-7].

在过去几十年间, 基于唯象假设建立应力?应变增量之间的解析关系一直是岩土等颗粒材料本构问题中最主流的研究方式, 然而发展一个统一的应力?应变理论模型仍然存在许多困难. 并且, 许多现有的本构模型数学形式复杂, 需要借助精细的室内实验来标定数十个自由参数, 对一般工程师而言学习和使用成本过高. 由于理论发展和实践应用的不相适应, 尽管各类高级模型层出不穷, 大量的岩土从业人员仍然使用基于线弹性理想塑性的摩尔?库伦等简单本构模型开展工程问题分析.

除唯象模型以外, 一些****也在寻找新的研究范式来研究本构问题. 在层级多尺度模拟方法中, 有限元等连续计算模型不再使用唯象的本构模型, 而是通过低尺度的离散元模拟来得到材料的应力?应变关系^[8]. 在有限元的计算过程中, 每个高斯点的位移梯度或者应变信息实时传递给离散元作为边界条件; 离散元计算后, 又将对应的应力响应或者切向刚度矩阵实时传递给有限元. 然而, 此种多尺度计算方法中每个高斯点均需要有对应的离散元模型, 计算成本过高, 很难真正应用到工程尺度问题的研究中.

另外一种代表性的方案是采用神经网络从大量实验数据中训练代理本构模型. 这种模型无需标定自由参数, 在有限元等宏观计算方法中使用方便, 并且随着新数据的不断增加, 其预测精度可以不断提高, 相比传统本构模型有独特的优势. 使用神经网络来训练岩土材料本构模型的思想可以追溯到20世纪90年代^[9-12]. 近年来, 随着深度学习技术的突破性进展, 基于神经网络的本构模型再次得到广泛的重视. Wang等^[13-15]结合博弈论和强化学习模型研究了颗粒材料的界面张力和位移的本构关系以及应力?应变关系; Zhang等^[16]使用长短期记忆模型(LSTM)预测了颗粒材料的循环剪切行为; Karapiperis等^[17]在有限元模型中实施了基于离散元数据训练得到的神经网络本构模型. Qu等^[18]基于离散元数据探索了3类不同的颗粒材料本构训练策略. 尽管深度学习模型已经被证明能有效捕捉特定工况下的颗粒材料力学响应, 但是要将此类纯粹的数据驱动模型发展成为可靠可用的, 适用于多种加载工况的本构模型仍有较远的距离.

解析模型和数据模型作为两种不同的科学研究范式具有不同的优缺点. 解析模型基于一些假设条件, 利用理论方法构造整个预测模型. 此种范式的优点是模型在自由参数得到标定后具有一定的预测能力, 但是受限于假设条件的约束, 面对复杂荷载工况时往往预测与实际存在不少出入. 数据模型不需要任何假设, 完全利用经验数据来构造预测模型. 然而一个纯粹的数据驱动模型需要大量且覆盖全面的训练样本, 对于本构问题来说, 获取大量的材料应力?应变数据并不容易. 另外, 当数据模型遇到超出经验样本以外的情况时, 往往预测能力有限. 本文拟尝试结合理论模型和数据驱动模型两种不同的研究范式, 通过将客观的力学规律与应力?应变数据经验结合起来, 发展颗粒材料的数据驱动本构模型训练方法.

本文首先基于Vogit假设推导小应变条件下颗粒材料的应力?应变解析关系, 利用此关系识别出一组与颗粒材料本构响应相关的重要变量. 通过有向图的方式, 将所有与本构响应相关的重要变量包含到从应变到应力的预测中, 变量间的映射关系通过时序的深度学习模型来描述. 采用离散元常规三轴以及真三轴数值试验生成颗粒材料应力?应变数据用于训练, 验证和测试本文提出的深度学习模型.

1.
基于深度学习的数据驱动本构模型

1.1
基本原理

深度学习是机器学习算法中的一类, 主要指基于多层人工神经网络结构的代理模型方法. 数学形式上, 神经网络是由线性的矩阵运算和非线性的激活函数构成的复合函数, 这类代理函数具有强大的表示能力, 已经被证明能够以任意的精度来估计任何一个定义在实数空间中的有界闭集函数^[19-20].

一个问题是否适合深度学习方法, 主要有3个基本前提: (1)问题本身包含某种确定的模式或者规律; (2)无法在数学上找到精确的解析方法来描述这种模式; (3)有包含这个问题所有自变量和因变量的完备数据. 对于颗粒材料而言, 本构关系由材料自身物理性质所决定, 这种关系必然是受物理材料规律支配的; 并且, 已有的大量研究表明: 建立一个精确、统一的解析方程来描述这种关系极为困难; 再者, 通过各类颗粒材料加载试验, 我们可以得到反映本构关系的大量应力?应变数据. 这些因素构成了发展基于深度学习框架的数据驱动材料本构关系的前提.

一般而言, 在准静态变形情况下, 材料内部一点的应力张量σ_ij和应变张量ε_mn可以用6个独立的分量来表示, 即

$${{{{boldsymbol{sigma}}}} _{ij}} = left( {begin{array}{*{20}{c}} {{sigma _{11}}}&{{sigma _{12}}}&{{sigma _{13}}} {{sigma _{21}}}&{{sigma _{22}}}&{{sigma _{23}}} {{sigma _{31}}}&{{sigma _{32}}}&{{sigma _{33}}} end{array}} ight),;{{{{boldsymbol{varepsilon}}}} _{mn}} = left( {begin{array}{*{20}{c}} {{{{varepsilon}} _{11}}}&{{varepsilon _{12}}}&{{varepsilon _{13}}} {{varepsilon _{21}}}&{{varepsilon _{22}}}&{{varepsilon _{23}}} {{varepsilon _{31}}}&{{varepsilon _{32}}}&{{varepsilon _{33}}} end{array}} ight)$$

(1)

材料的本构模型可以表示为

$$ {{{{boldsymbol{sigma}}}} }_{ij}={{f}}left({{{{boldsymbol{varepsilon}}}} }_{mn} ight) $$

(2)

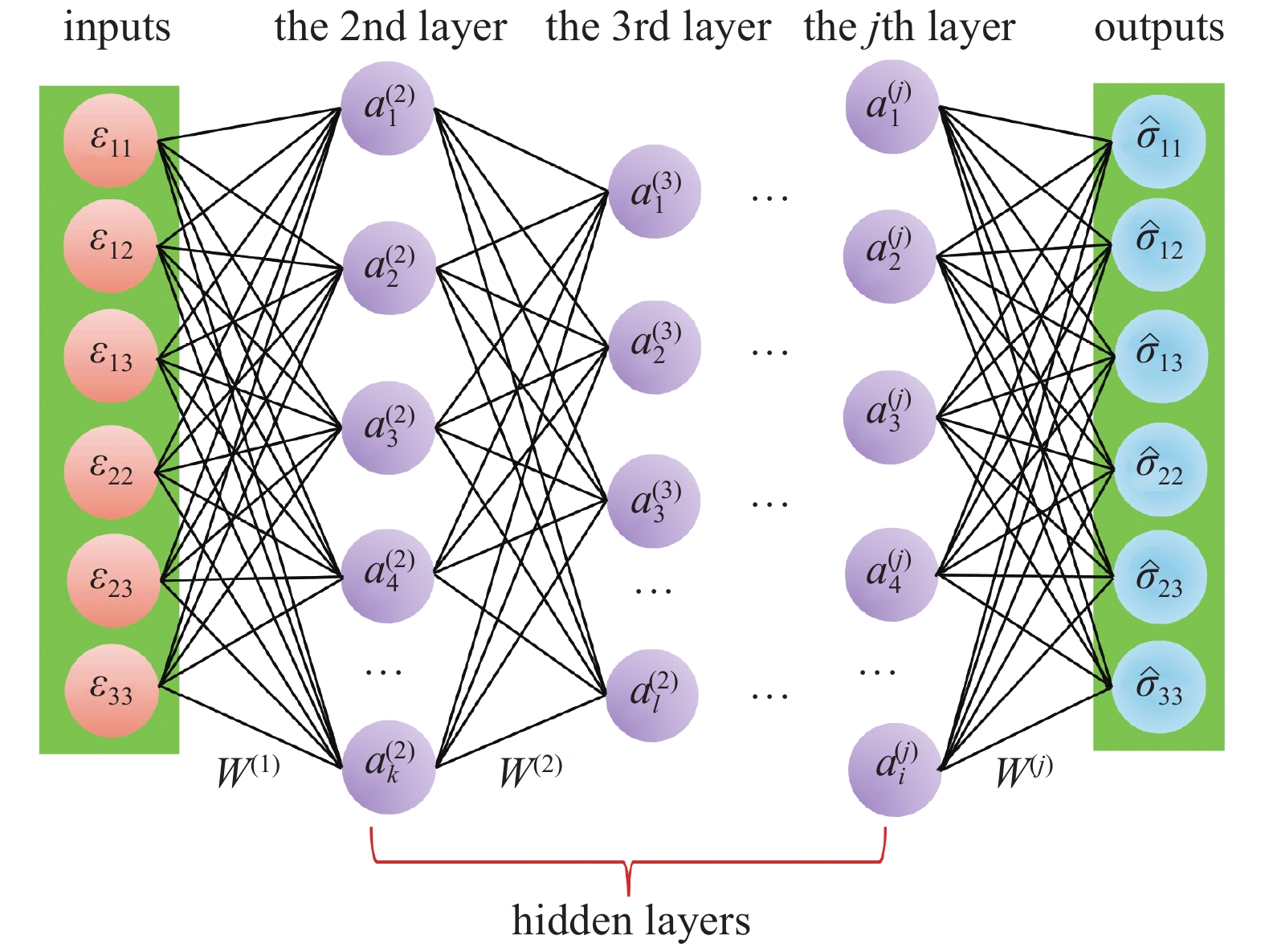
如图1所示, 基于深度学习的本构模型即是利用神经网络来建立材料应力和应变之间的映射关系. 通常输入参数为应变张量, 输出参数为应力张量, 中间隐藏层的激活函数可按如下方式计算

$${a}_{i}^{left(j ight)}={f}_{j}left(sumlimits_{k=1}^{d}{w}_{ki}^{(j-1)}{a}_{k}^{(j-1)}+{b}^{(j-1)} ight),;;jgeqslant 2$$

(3)

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-221-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
基于深度学习的本构模型示意图



Figure
1.
Diagram of deep learning-based constitutive models



下载:
全尺寸图片
幻灯片


其中, $ {a}_{i}^{left(j
ight)} $表示在第j层网络中第i个神经元的激活函数值; f_j表示第j层神经网络中的激活函数; d表示第(j?1)层网络中的神经元数量; $ {w}_{ki}^{(j-1)} $表示连接第(j?1)层上的第k个神经元与第j层网络上的第i个神经元之间的权重系数(weights); b^(j?1)为第(j?1)层网络的偏置系数(biases).

假设第j层为最后一个隐藏层, 第(j + 1)层为输出层, 那么应力的预测值${overset{frown} {{{boldsymbol{sigma}} }}}({{W}},{{b}})$可按照如下公式计算

$${overset{frown} {boldsymbol{sigma }}}({{W}},{{b}}) = {f_{j + 1}}left(sumlimits_{k = 1}^e {w_{ki}^{(j)}} a_k^{(j)} + {b^{(j)}} ight),;;j geqslant { m{2}}$$

(4)

其中, e为最后一个隐藏层的单元数量, W和b分别为神经网络的权重和偏置系数.

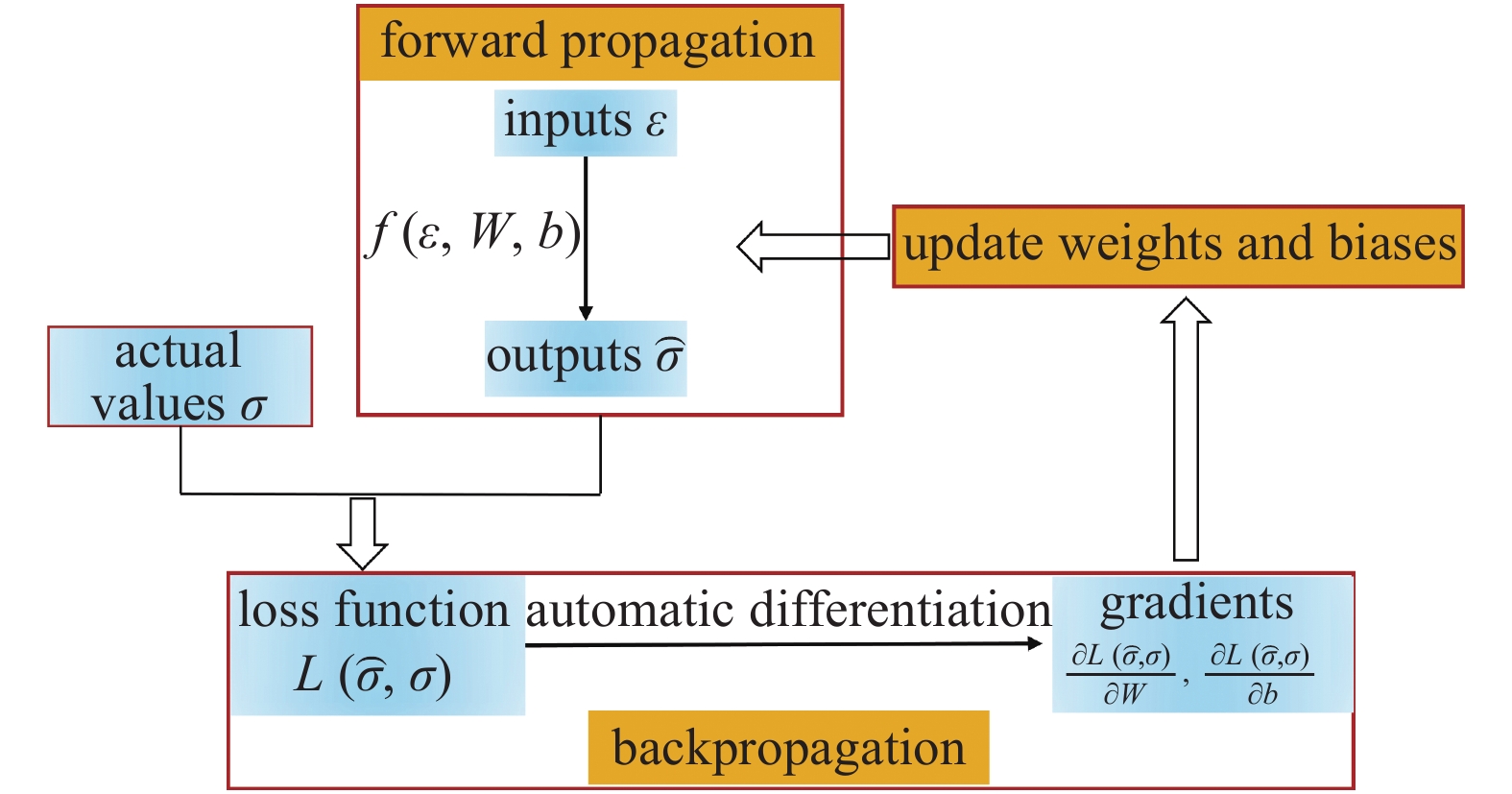
在一个确定的神经网络架构下寻找描述对应映射关系的网络权重和偏置的过程称为训练或者学习. 如图2所示, 一个神经网络的训练过程主要包括前向传播、反向传播和迭代更新网络参数(权重和偏置). 在训练前, 网络参数通常是随机初始化的, 此时通过前向传播计算得到的预测值必然是偏离实际值的. 这个预测值和实际值的差别通常用损失函数L来衡量. 训练一个可靠的预测模型的过程可以转化为一个以最小化损失函数L为目标的优化问题, 即

$$ left{ {left. {{{W}},{{b}}} ight}} ight. = arg min L({overset{frown} {boldsymbol{sigma }}}({{W}},{{b}}),{boldsymbol{sigma }}) $$

(5)

其中, argmin是指使得目标函数取最小值时的自变量值.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-221-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
人工神经网络的训练过程



Figure
2.
Basic procedures of training artificial neural networks



下载:
全尺寸图片
幻灯片


常规神经网络一般通过基于一阶梯度的优化算法, 如自适应矩估计算法(Adam)等来不断迭代, 从而找到使得L达到极小值时的网络参数. 现代神经网络中, 这些梯度信息都使用反向传播(BP)算法通过自动微分和链式法则计算得到. 对于一个已经训练好的模型, 也即网络中的权重和偏置参数能很好地描述映射关系时, 我们可以通过向前传播, 计算得到较为可靠的应力预测值.

1.2
材料本构模型的时序本质与深度学习模型的选用

颗粒材料应力响应具有明显的应变历史依赖和应变路径依赖特征, 一个能反映复杂应力?应变路径条件下的材料本构响应模型, 必须具备“记忆”应力或者应变历史的能力^[21], 因此本构模型本质上是一种时序模型或者过程模型. 在当前深度学习模型中, LSTM和GRU等循环神经网络(RNN)模型主要适用于包含时间序列的预测问题. 由于几种RNN模型预测能力近似, 同等网络规模条件下, GRU相比LSTM需要更少的训练参数, 因此本文主要采用GRU作为基本的深度学习模型来训练材料的本构行为.

2.
基于Vogit均质化假设的颗粒材料小应变应力?应变关系

本文尝试引入颗粒物质力学理论来指导深度学习, 以期降低深度学习在训练阶段对数据量的需求, 提高模型在预测阶段的泛化能力. 对于颗粒材料而言, 目前主要有两种唯象本构模型: 连续模型和细观力学模型. 基于连续假设的弹塑性模型采用屈服面来描述材料的塑性, 借助流动法则来描述塑性的发展. 细观力学模型虽然不再需要假想的屈服面, 但仍需要通过预测细观组构的演化来描述应力?应变关系. 不管是基于连续假设还是细观力学的唯象模型, 在预测材料随外部应变引起的应力响应时, 常常需要使用一些从试验数据中拟合得来的参数(如硬化参数等)来描述主应力?主应变关系. 为避免使用此类拟合参数, 在准静态加载条件下, 本研究将时序的应力?应变过程简化成单个时刻的应力?应变响应来考虑, 即小应变条件下的颗粒材料应力?应变关系.

散粒体在小变形情况下, 颗粒体系内的弹性势能$U$可按照如下方式计算

$$U = sumlimits_{k = 1}^{{N_c}} {left( {int_{ m{0}}^{Delta u_{ m{n}}^k} {{F_{ m{n}}}{ m{d}}} {delta _{ m{n}}} + int_{ m{0}}^{Delta u_{ m{s}}^k} {{F_{ m{s}}}{ m{d}}} {delta _{ m{s}}}} ight)} $$

(6)

式中, $Delta u_{
m{n}}^k$和$Delta u_{
m{s}}^k$分别表示接触k的法向和切向相对接触位移; F_n和F_s分别是法向和切向的接触力; dδ_n和dδ_s分别是法向和切向的无限小变形; N_c是颗粒体系内所有参与传递接触力的接触数量.

当颗粒接触为线性弹性接触时, 储存在接触k内的弹性势能U^k为

$${U^k} = frac{1}{{ m{2}}}left( {{k_{ m{n}}}Delta u_{ m{n}}^kDelta u_{ m{n}}^k + {k_{ m{s}}}Delta u_{ m{s}}^kDelta u_{ m{s}}^k} ight)$$

(7)

式中, k_n和k_s为颗粒之间的法向和切向刚度.

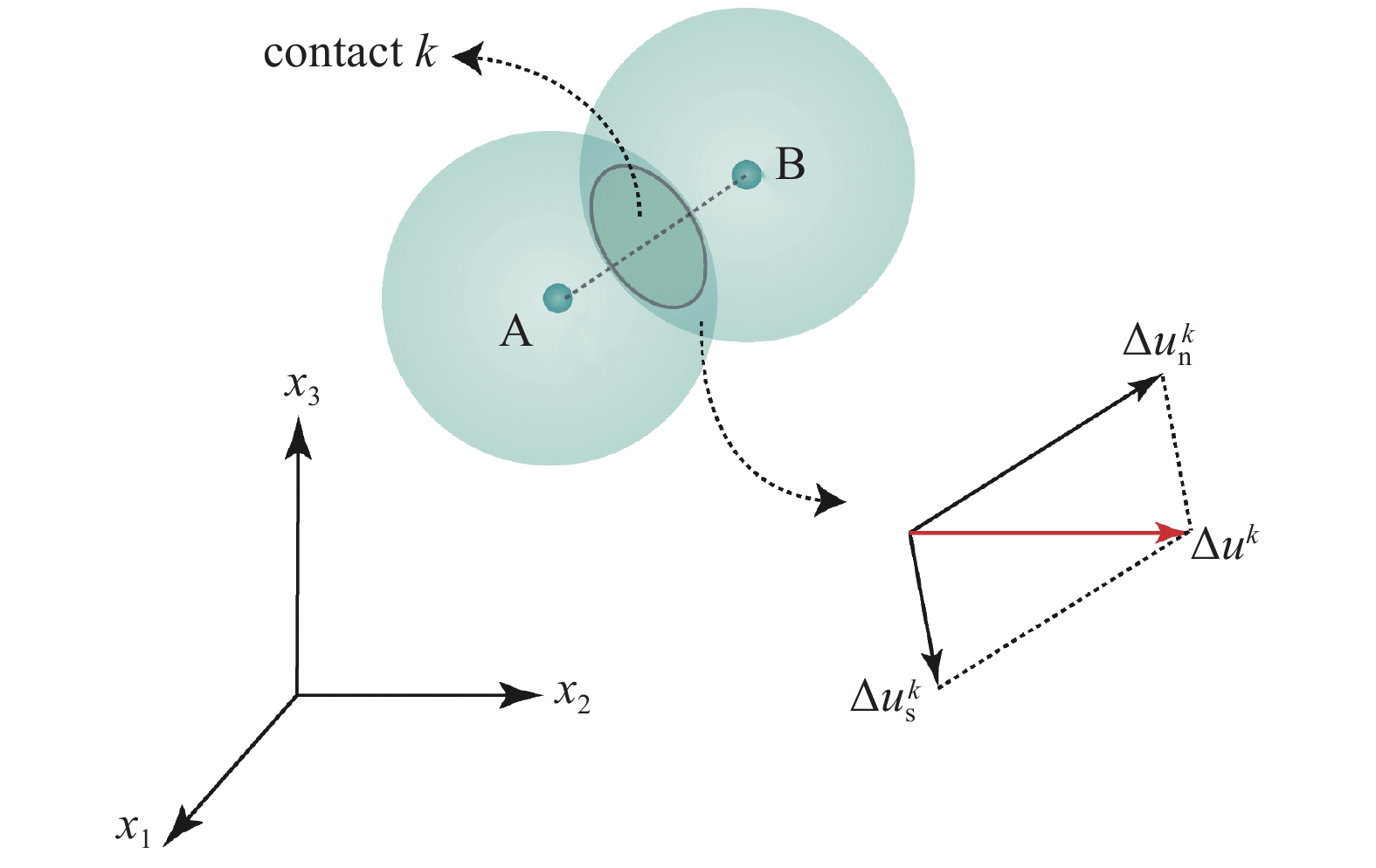
如图3所示, 通过将颗粒位移等效为相应连续体内对应点处的位移, 则颗粒相对位移$Delta {{u}}_i^k$与对应连续体内的局部应变${{varepsilon }}_{ij}^k$(颗粒A与B之间的等效应变)可表示为如下关系



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-221-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
颗粒接触与接触位移



Figure
3.
A contact between particles and contact displacements



下载:
全尺寸图片
幻灯片

$$Delta {{u}}_i^k = {{varepsilon}} _{ij}^kleft(x_j^{left( B ight)} - x_j^{left( A ight)} ight) = {{varepsilon}} _{ij}^k{L^k}{xi _j}^k$$

(8)

式中, $x_j^{left( A
ight)}$和$x_j^{left( B
ight)}$分别为颗粒A和B沿j方向的坐标, ${L^k}$为接触k的长度(颗粒A和B的中心距离); ${xi _j}^k$是接触k的方向向量在j方向的分量. 法向和切向相对位移$Delta u_{
m{n}}^k$和$Delta u_{
m{s}}^k$可表示为

$$Delta u_{ m{n}}^k = Delta u_i^kxi _{_i}^k = {{varepsilon}} _{ij}^k(x_j^{left( B ight)} - x_j^{left( A ight)}){xi _i}^k ={{ varepsilon}} _{ij}^k{L^k}{xi _i}^k{xi _j^k};;;,$$

(9)

$$Delta u_{ m{s}}^k = Delta u_i^k - Delta u_{ m{n}}^k = {{varepsilon}} _{mn}^k{L^k}{xi _n^k} -{{ varepsilon}} _{ij}^k{L^k}{xi _i}^k{xi _j}^k{xi _m^k},,,,,,$$

(10)

将式(9)和式(10)代入式(7), 可得

$$begin{split} U =& sumlimits_k^{N_{ m{c}}} {{U^k} = } frac{1}{{ m{2}}}sumlimits_{k = 1}^{{N_{ m{c}}}} {{k_{ m{n}}}{{varepsilon}} _{ij}^k{L^k}xi _i^kxi _j^k{{varepsilon}} _{mn}^k{L^k}xi _m^kxi _{ m{n}}^k} + frac{1}{{ m{2}}}cdot &sumlimits_{k = 1}^{{N_{ m{c}}}} {{k_{ m{s}}}({{varepsilon}} _{kl}^k{L^k}{xi _l}^k - {{varepsilon}} _{ij}^k{L^k}{xi _i}^kxi _j^kxi _k^k)({{varepsilon}} _{km}^k{L^k}xi _m^k - {{varepsilon}} _{mn}^k{L^k}xi _m^kxi _{ m{n}}^kxi _k^k)} end{split} $$

(11)

根据弹性力学理论, 连续体的应力张量可通过应变能密度u对应变张量求取偏导得到, 即

$${{{sigma}} _{ij}} = frac{{partial u}}{{partial {{{varepsilon}} _{ij}}}}$$

(12)

假设颗粒试样内的变形是统计均匀的(Vogit’s假设), 即在对应连续体内任意位置处的整体应变${{varepsilon}} _{ij}$等于材料中沿着颗粒接触方向的局部应变${{varepsilon}} _{ij}^k$

$${{{varepsilon}} _{ij}}{ m{ = }}{{varepsilon}} _{ij}^k$$

(13)

基于式(13), 假设散粒体和对应连续体在小应变情况下的弹性势能相等, 则式(12)可表示为

$$begin{split}{{{sigma}} _{ij}} =& frac{1}{V}sumlimits_{k = 1}^{{N_{ m{c}}}} {frac{{partial {U^k}}}{{partial {{varepsilon}} _{ij}^k}} = frac{1}{V}sumlimits_k^{{N_{ m{c}}}} {left[ {{k_n}{{varepsilon}} _{ij}^k{L^k}xi _i^kxi _j^k{{varepsilon}} _{mn}^k{L^k}xi _m^kxi _n^k + } ight.} } &left.{k_s}({{varepsilon}} _{ik}^k{L^k}xi _k^kxi _j^k - {{varepsilon}} _{mn}^kxi _i^kxi _j^kxi _m^kxi _n^k) ight]end{split}$$

(14)

其中, V为颗粒试样的体积.

将应力张量对应变张量求偏导, 可得到对应的弹性刚度矩阵为

$$begin{split}& {C_{ijmn}} =frac{{partial {{{sigma}} _{ij}}}}{{partial {{{varepsilon}} _{mn}}}} = frac{{partial {{{sigma}} _{ij}}}}{{partial {{varepsilon}} _{mn}^k}} = frac{1}{V}cdot&quad sumlimits_{k = 1}^{{N_{ m{c}}}} {left[ {{k_n}{{left( {{L^k}} ight)}^2}xi _i^kxi _j^kxi _m^kxi _n^k + {k_s}{{left( {{L^k}} ight)}^2}({delta _{in}}xi _j^kxi _m^k - xi _i^kxi _j^kxi _m^kxi _n^k)} ight]} = &quad frac{{({k_n} - {k_s})}}{V}sumlimits_{k = 1}^{{N_c}} {{{left( {{L^k}} ight)}^2}xi _i^kxi _j^kxi _m^kxi _n^k} + frac{{{k_s}}}{V}sumlimits_{k = 1}^{{N_{ m{c}}}} {{{left( {{L^k}} ight)}^2}{delta _{in}}xi _j^kxi _m^k} end{split} $$

(15)

式中, δ_in为克罗内克函数, 当i = n时, δ_in = 1; 当i ≠ n时, δ_in = 0. 若令

$${a_{ijmn}} = frac{1}{V}sumlimits_{k = 1}^{{N_c}} {{{left( {{L^k}} ight)}^2}xi _i^kxi _j^kxi _m^kxi _n^k},;{b_{ijmn}} = frac{1}{V}sumlimits_{k = 1}^{{N_{ m{c}}}} {{{left( {{L^k}} ight)}^2}{delta _{in}}xi _j^kxi _m^k} $$

(16)

则式(15)变成

$${C_{ijmn}} = ({k_{ m{n}}} - {k_{ m{s}}}){a_{ijmn}} + {k_{ m{s}}}{b_{ijmn}}$$

(17)

式(17)表明C_ijmn由颗粒间的法向接触刚度k_n、切向刚度k_s以及两个单位体积内的组构张量a_ijmn和b_ijmn构成. 在颗粒试样承受外界荷载作用时, 假设颗粒未发生破碎或其他材料劣化, 则k_n和k_s保持不变; 随着试样在宏观上发生不可恢复的塑性变形(微观上表现为颗粒间发生相互滑移)时, 组构张量a_ijmn和b_ijmn随之不断演化.

小应变情况下的颗粒材料的宏观应力?应变关系可表示为

$$ {Delta }{{{sigma}} }_{ij}={C}_{ijmn}{Delta }{{{varepsilon}} }_{mn} $$

(18)

当切应力和切应变为0时, 3个主应力主应变的增量关系展开后为

$$left( begin{array}{l} Delta {sigma _{11}} Delta {sigma _{22}} Delta {sigma _{33}} end{array} ight) = left( {begin{array}{*{20}{c}} {{C_{1111}}}&{{C_{1122}}}&{{C_{1133}}} {{C_{2211}}}&{{C_{2222}}}&{{C_{2233}}} {{C_{3311}}}&{{C_{3322}}}&{{C_{3333}}} end{array}} ight)left( begin{array}{l} Delta {varepsilon _{11}} Delta {varepsilon _{22}} Delta {varepsilon _{33}} end{array} ight)$$

(19)

其中, C₁₁₂₂ = C₂₂₁₁, C₁₁₃₃ = C₃₃₁₁, C₂₂₃₃ = C₃₃₂₂. 因而弹性刚度矩阵中共有6个独立分量描述主应力与主应变的关系. 对于准静态加载而言, 式(19)的关系在试样加载过程中总是成立, 但随着颗粒材料组构的不断演化, 弹性刚度矩阵C_ijmn中各个分量的值也会随之变化. 基于细观力学的唯象模型通常需要借助流动法则和硬化函数等来拟合得到试样内部组构的演化过程, 本文中, 这些微观结构的演化过程则直接由深度学习来预测得到.

3.
力学知识指导下的深度学习策略

由于颗粒材料内部描述细观结构的组构张量属于内变量, 在有限元等连续介质方法中计算应力?应变关系时, 此类内变量不能直接作为输入. 本文尝试引入有向图理论, 将微观结构的演化过程包含在应力?应变关系的描述中.

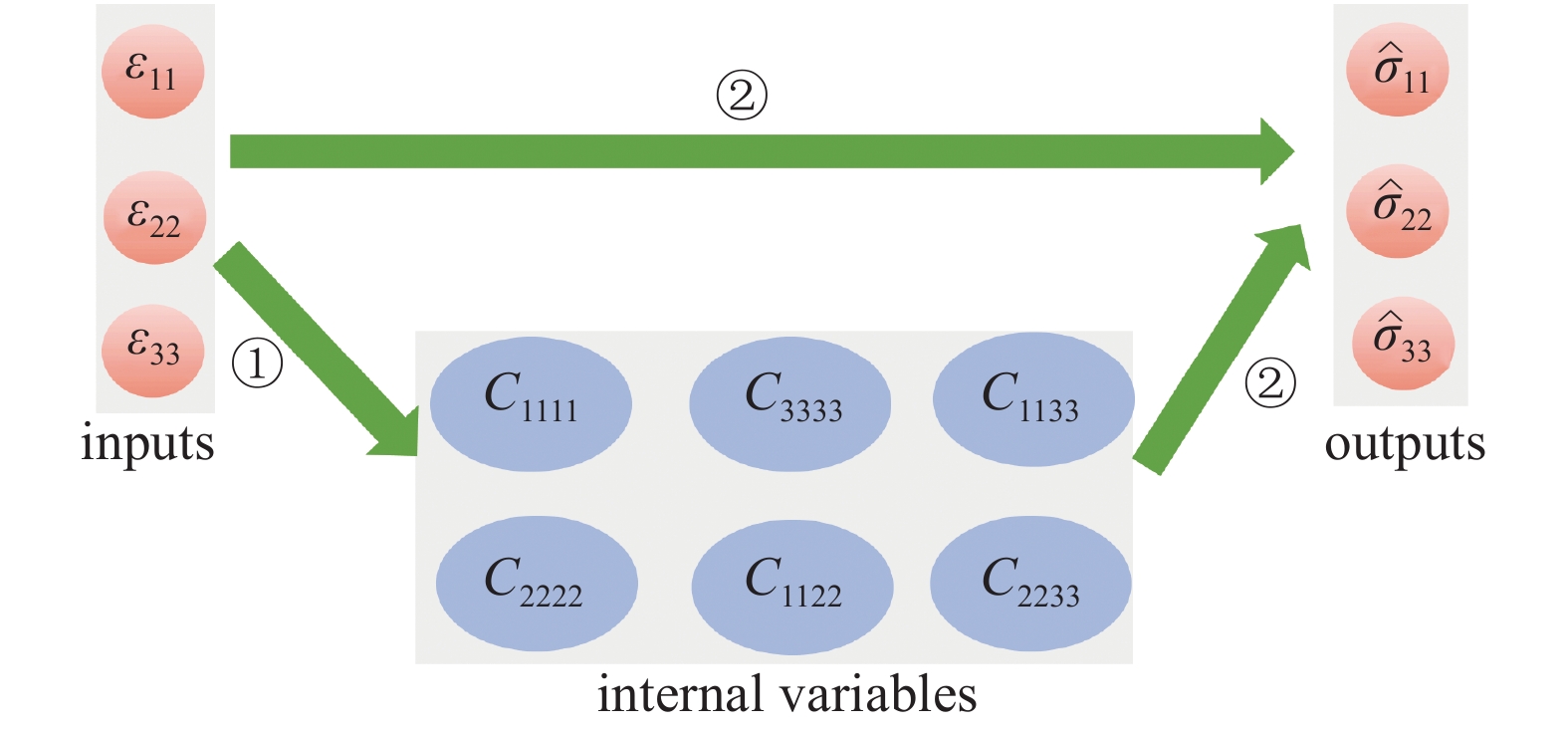
有向图是图论中用于描述物与物之间联系的一种方法, 主要由结点和含有方向的边(连接两个结点)构成. 结点表示某一个物理量或者对象, 边线表示两个物理量之间存在某种联系并且这种联系是从源结点(尾部)指向目标结点(头部)的. 根据有向图理论和小应变条件下得到的颗粒材料应力?应变关系, 本文设计的本构关系训练策略如图4所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-221-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
基于有向图包含组构演化的本构训练方式



Figure
4.
A directed graph-based constitutive training approach incorporating fabric evolution



下载:
全尺寸图片
幻灯片


图4中, 初始结点为主应变, 作为输入参数; 目标结点为主应力, 作为输出参数; 中间节点为6个相互独立的弹性刚度张量分量. 每条边之间的映射关系通过深度神经网络来描述. 将该有向图展开后, 可用两条子神经网络来描述整个有向图结构:

(1)子网络1:

[ε₁₁, ε₂₂, ε₃₃→C₁₁₁₁, C₂₂₂₂, C₃₃₃₃, C₁₁₂₂, C₁₁₃₃, C₂₂₃₃];

(2)子网络2:

[ε₁₁, ε₂₂, ε₃₃, C₁₁₁₁, C₂₂₂₂, C₃₃₃₃, C₁₁₂₂, C₁₁₃₃, C₂₂₃₃→${{overset{frown} {sigma}} _{11}},{{overset{frown} {sigma}} _{22}},{{overset{frown} {sigma}} _{33}}$].

注意到[ε₁₁, ε₂₂, ε₃₃→${{overset{frown} {sigma}} _{11}},{{overset{frown} {sigma}} _{22}},{{overset{frown} {sigma}} _{33}}$]由于未包含微观结构信息, 在本文框架下不作为一个单独的网络进行训练; 当子网络2中弹性刚度矩阵的几个分量对最终的应力响应没有贡献时, 子网络2将自动退化成上述映射关系.

在网络学习阶段, 两条子网络单独训练; 在使用阶段, 两条子网络合并成一条完整的信息流: 子网络1的输出连同3个主应变序列一起作为子网络2的输入, 共同预测材料的应力响应. 因此, 基于有向图的神经网络模型虽然充分利用了颗粒材料内部的微观结构演化信息, 但在使用过程中并不违背本构模型仅仅将主应变和主应力作为最终输入和输出信息的基本原则.

4.
数据准备与深度学习模型的实施

4.1
基于离散元的数值三轴试验与模拟工况

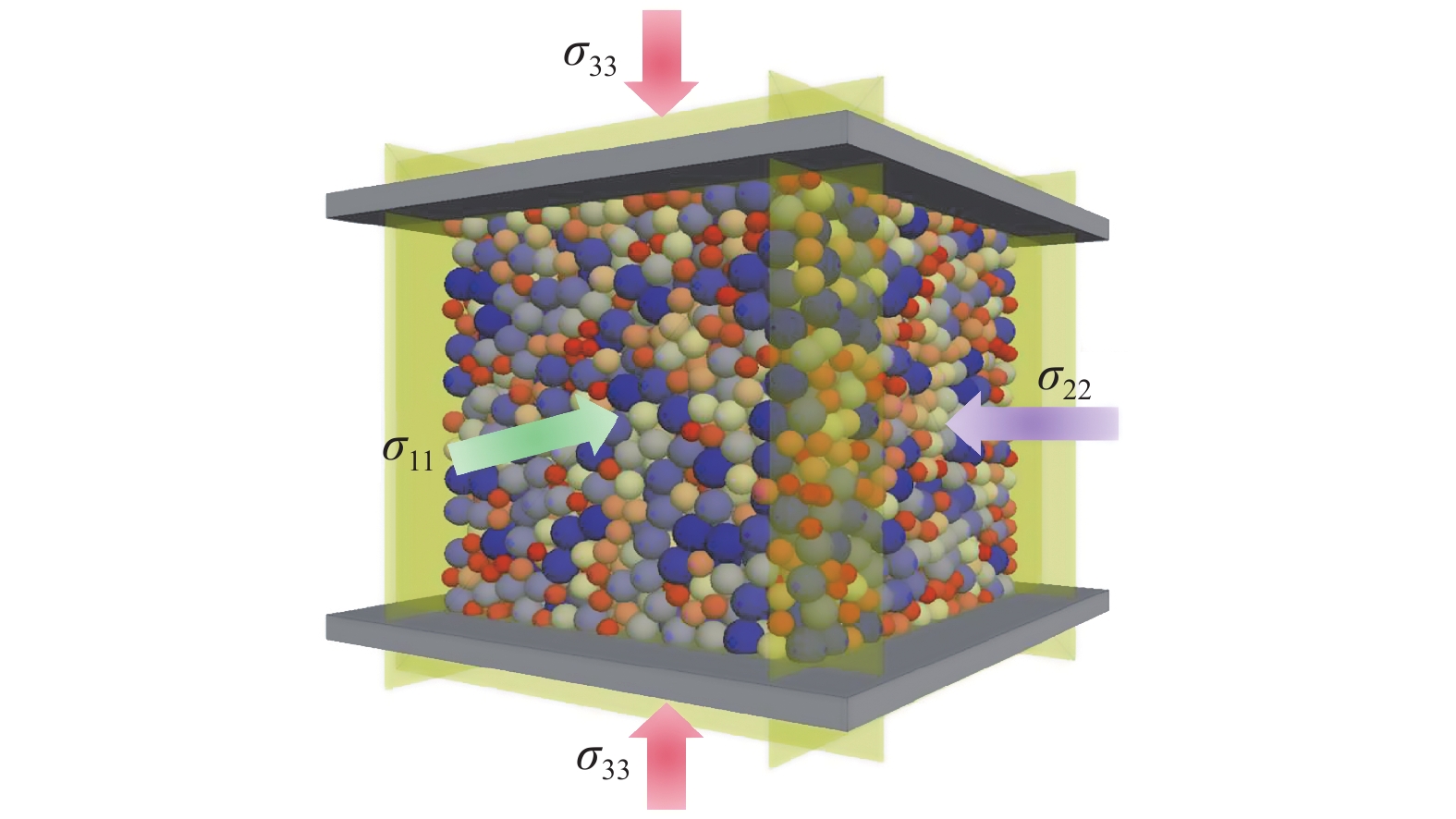
细观尺度的离散元仿真已经被证明能够有效模拟颗粒材料的本构行为^[22], 并且在层级多尺度计算模型中, 离散元模拟直接代替了传统的唯象本构关系进行有限元计算^[23]. 本文采用离散元模拟三轴实验来产生颗粒材料的应力?应变数据, 用于深度学习训练. 如图5所示是本文采用的数值三轴试样, 每个试样共包含4037个颗粒, 半径为2 ~ 4 mm均匀分布; 颗粒之间采用线性接触模型, 法向和切向接触刚度分别为10⁵ N/m和5 × 10⁴ N/m; 颗粒密度为2600 kg/m³, 局部阻尼系数为0.5. 为生成一个较密实的均匀试样, 在指定空间内生成颗粒后, 采用一个较小的制样颗粒摩擦系数(如 0.05), 使用伺服方法通过移动试样的6个边界来施加三向等压压力, 直到试样稳定地达到200 kPa的目标围压值, 再将制样阶段的接触摩擦系数改成实际样本摩擦系数0.5.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-221-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
离散元三轴试验模型



Figure
5.
Triaxial compression models via discrete element modelling



下载:
全尺寸图片
幻灯片


本文主要考虑了3类典型的三轴试验工况, 具体包括:

(1)包含应力?应变加卸载循环的常规三轴压缩试验291组;

(2)平均有效应力p恒定的真三轴加卸载试验122组($p = {sigma _{11}} + {sigma _{22}} + {sigma _{33}}$, ${sigma _{11}} = {sigma _{22}}$);

(3)主应力系数b恒定的真三轴压缩试验20组($b = dfrac{{{sigma _{22}} - {sigma _{11}}}}{{{sigma _{33}} - {sigma _{11}}}}$, σ₁₁=常数).

所有工况的最大轴向应变为12%, 在每组加卸载工况中, 卸载应变和再加载应变的取值各不相同, 在等b真三轴加载中, b以0.05的间隔在(0,1]之间取值. 在440组所有三轴试验中, 288组用于训练, 72组用于验证(validation), 剩下的80组用于测试(test). 注意验证不同于测试, 验证组用于神经网络模型在训练过程中调整超参数组合, 而测试集则仅用于测试目的, 测试数据在模型训练过程中从未接触到神经网络, 这样的设计可避免在测试神经网络模型时发生数据泄露的可能性, 从而保证神经网络测试结果的可靠性.

4.2
深度学习模型实施过程

在构建深度学习模型之前, 离散元模型中计算得出的数据需要预处理. 一方面, 现实问题中的输入变量往往具有不同的数据大小、单位以及分布特征, 而差异较大的原始输入数据会降低训练效率, 阻碍神经网络在训练过程中的收敛. 因此, 原始数据需要通过标准化将其缩放到平均值为0、标准差为1的分布空间, 这将有利于降低训练过程中网络陷入局部最优的可能性. 另一方面, 循环神经网络模型的输入数据需要满足某些特定特征: 所有的输入数据必须是三维矩阵的形式, 其中第一维表示样本, 一段应力?应变响应的序列数据即是一个样本; 第二维是时间步(time steps), 也称移动窗口的长度, 这是指循环神经网络在给出下一个预测输出时需要依据在此之前的输入变量的数量, 若时间步取20, 则在预测当前应力时, 需要输入当前应变值以及在此之前的19个应变值; 第三维则是数据特征, 比如3个主应变分量可当作3个数据特征.

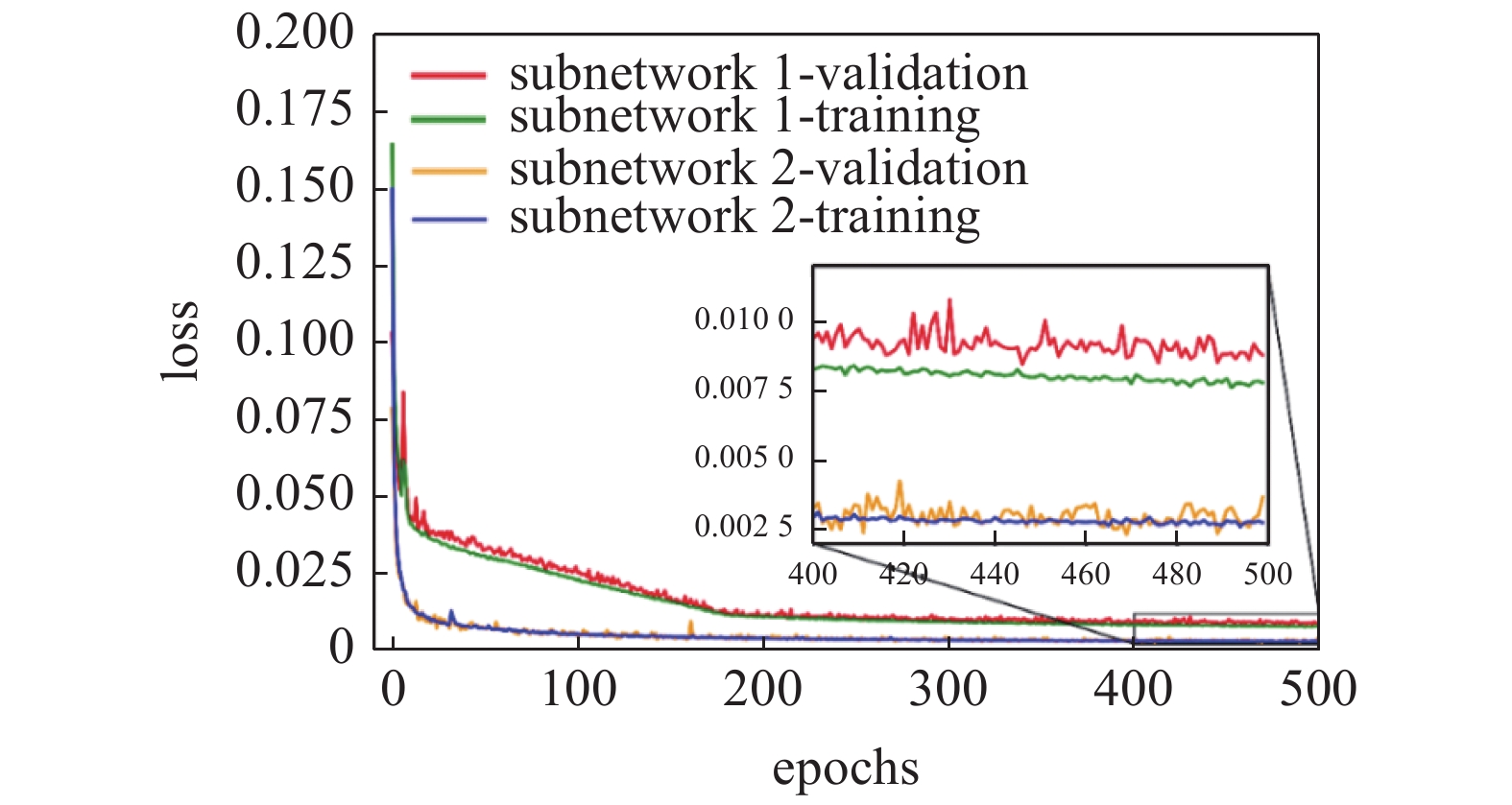
本文的深度学习模型通过Tensorflow和keras来构建和训练. 神经网络的大小(层数和神经元数量)决定了神经网络所能达到的上限表示能力、网络训练过程中学习速率等超参数则决定了模型能在当前数据集下将其预测能力发挥到何种水平. 本文采用的网络结构和超参数组合通过试错法得到: 两个子网络除了输入层和输出层以外, 还包括两个含有120个神经元的GRU隐藏层和20个神经元的全连接隐藏层. 全连接层采用Sigmoid激活函数, 输出层采用linear激活函数. 移动窗口的长度为40, 采用Adam优化器训练神经网络; 学习速率为0.01, 批量数据的尺寸(batch size)为128. 损失函数为预测值与实际值的平均绝对误差函数(MAE). 模型在训练了500个epochs后基本达到收敛状态, 两个神经网络在训练集和验证集上的预测表现分别如图6中的学习曲线所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-221-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
学习曲线



Figure
6.
Learning curves



下载:
全尺寸图片
幻灯片


需要说明的是, 选择40的移动窗口长度并不意味着不关注每条应力–应变曲线上前39步应变引起的应力值, 整个序列中的应力响应都应考虑进去. 实践中为了确保总能得到长度为40的应变序列, 对于前40组应力值, 我们通过在第一个应变值前面不断充填零值, 使得应变序列的长度总为选定的移动窗口长度. 这样的措施确保了整个应力序列都能够得到预测, 实践表明具有较好的预测效果. 此外, 充零的方式还具有较合理的物理意义, 即在荷载作用之前, 试样并不产生应变响应.

4.3
深度学习模型的评价指标

预测模型的好坏通过量化预测值与实际值的平均差异得到. 将平均绝对误差函数作为损失函数是评价模型预测能力的一种有效方式, 但此种误差评价指标往往与训练对象的值有关, 且缺乏对预测能力的直观体现. 本文除了采用平均绝对误差函数外, 还采用另外一种评分的方式来对模型进行评价. 该方法首先需要计算得到第j条应力?应变曲线上第i个点的平方误差损失SSE_ij

$$ SS{E}_{ij}=left({overline{y}}_{ij}^{{ m{True}}}-{overline{y}}_{ij}^{{ m{Prediction}}} ight)^{2} $$

(20)

式中, $bar y_{ij}^{{
m{True}}}$和$bar y_{ij}^{{
m{Prediction}}}$分别指在第j条应力?应变曲线上第i个数据点标准化后的实际值和预测值. 在得到第j条应力?应变预测曲线上所有的SSE_ij后, 可按照如下方式对该应力?应变曲线计算一个累积分布函数F_j

$${F_j}(SS{E_{ij}}) = frac{r}{{{N^j}}},;r = 1,2,cdots,{N^j}$$

(21)

式中, N_j为第j条应力?应变曲线上的样本点数目, 将曲线上所有点的SSE_ij按照升序排列, 可以为每条曲线计算一个对应的得分

$${A_{{ m{score}}}} = max left{frac{{lg [max ({varepsilon _{{ m{P}}% }},{varepsilon _{{ m{crit}}}})]}}{{lg ({varepsilon _{{ m{crit}}}})}},0 ight}$$

(22)

式中, ε_P%是累计分布函数上对应P%时的SSE值, 这个值被用来作为一个代表值来评价整条应力?应变曲线上的预测得分; 当预测应力?应变序列中ε_P%对应的SSE小于ε_crit时, 可认为预测足够准确, 得分为1. 在本文中, P%取90%, ε_crit为0.001.

以上介绍了单条应力?应变预测曲线的打分标准, 在评价每个神经网络模型的预测能力时, 一个更合理的指标是判断该模型在测试集上所有样本的平均预测表现, 即使用已经训练好的模型, 得到对所有测试样本上的平均MAE值或者平均得分.

5.
预测结果

5.1
总体预测表现

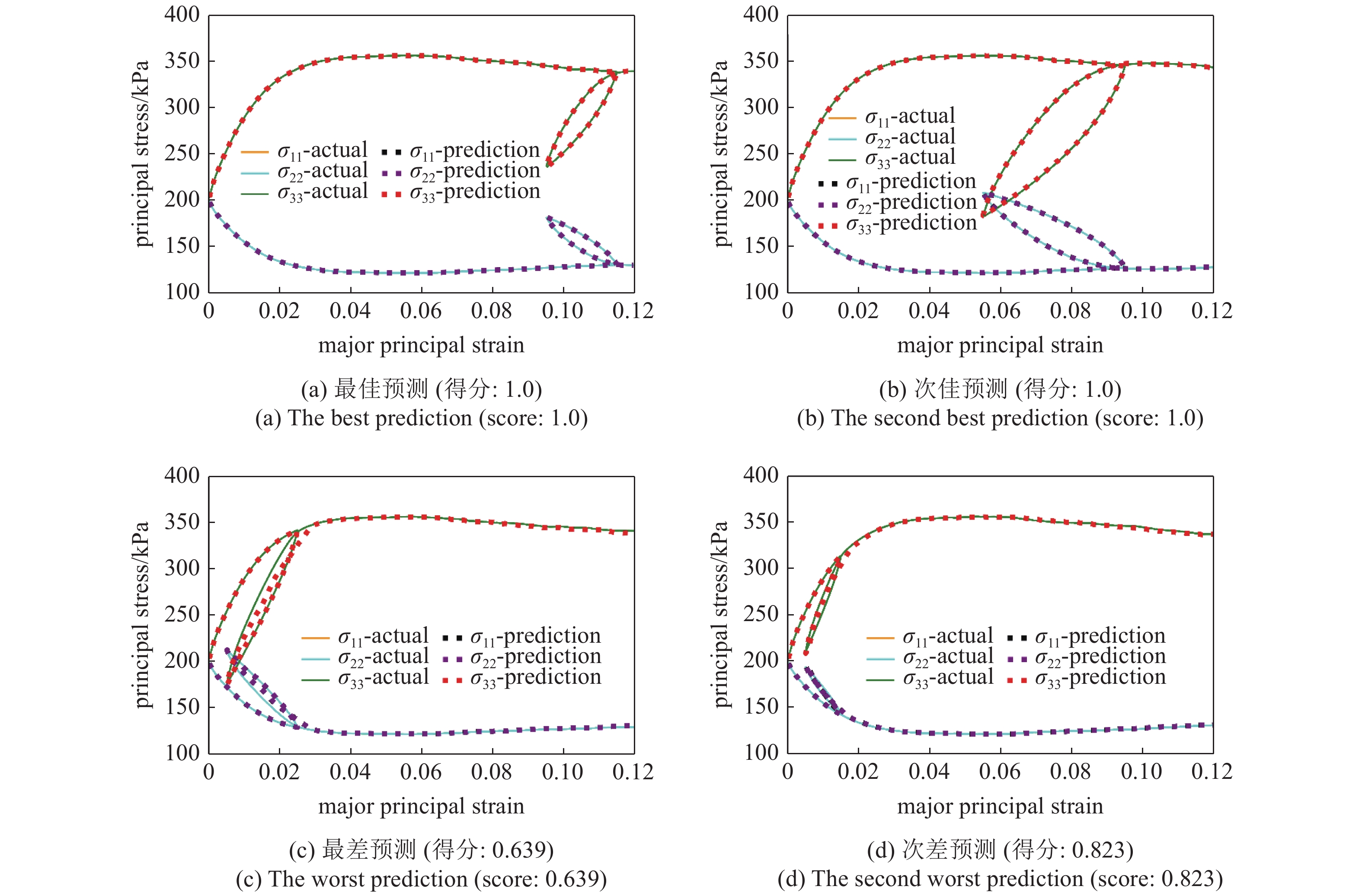
在80组测试样本中, 该深度学习模型在测试集上的平均MAE值为0.013; 平均得分为0.986; 87.5%的测试样本(70组)获得了满分, 其中最差的预测得分为0.639, 对应MAE值为0.051; 次差的一组预测得分为0.823, 对应MAE值为0.031; 在70组满分预测中, 最低的MAE值为0.004 2和0.004 5. 为直观体现模型的预测能力, 两组最好和最差的预测情况如图7所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-221-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
两组最佳与最差预测



Figure
7.
Examples of the two best and worst predictions



下载:
全尺寸图片
幻灯片


在得分最低的两组预测中, 尽管在加卸载处的应力?应变预测值与实际值存在差别, 但总体的应力响应趋势已经被神经网络模型捕捉到. 在损失函数MAE最低的两组预测中, 深度学习模型则几乎重现了实际的应力?应变响应.

5.2
内插与外推预测表现

根据已有数据以及模型预测未知区域的目标对象时, 若预测点在已有数据范围内通常称为内插预测; 若数据点完全在已有数据范围之外, 则为外插预测. 本文所用的训练数据集仅在常规三轴和等p真三轴中包含了一次应力?应变加卸载循环, 在等b真三轴压缩工况中仅包含单调加载工况. 图8分别给出了在测试集内的常规三轴和等p真三轴一次加卸载, 以及等b真三轴加载工况中的几个代表性内插预测.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-221-8.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8" />



图
8
几组代表性内插预测



Figure
8.
Some representative interpolation predictions



下载:
全尺寸图片
幻灯片


注意到在常规三轴加载工况下, 由于水平围压在加载过程中保持稳定, σ₂₂和σ₃₃均保持不变; 在平均有效应力p恒定的真三轴加载工况中, σ₂₂和σ₃₃保持了相同的变化趋势; 在中主应力系数b恒定的真三轴加载工况中, σ₃₃维持大小不变. 经过训练的神经网络模型均准确预测到了这些趋势.

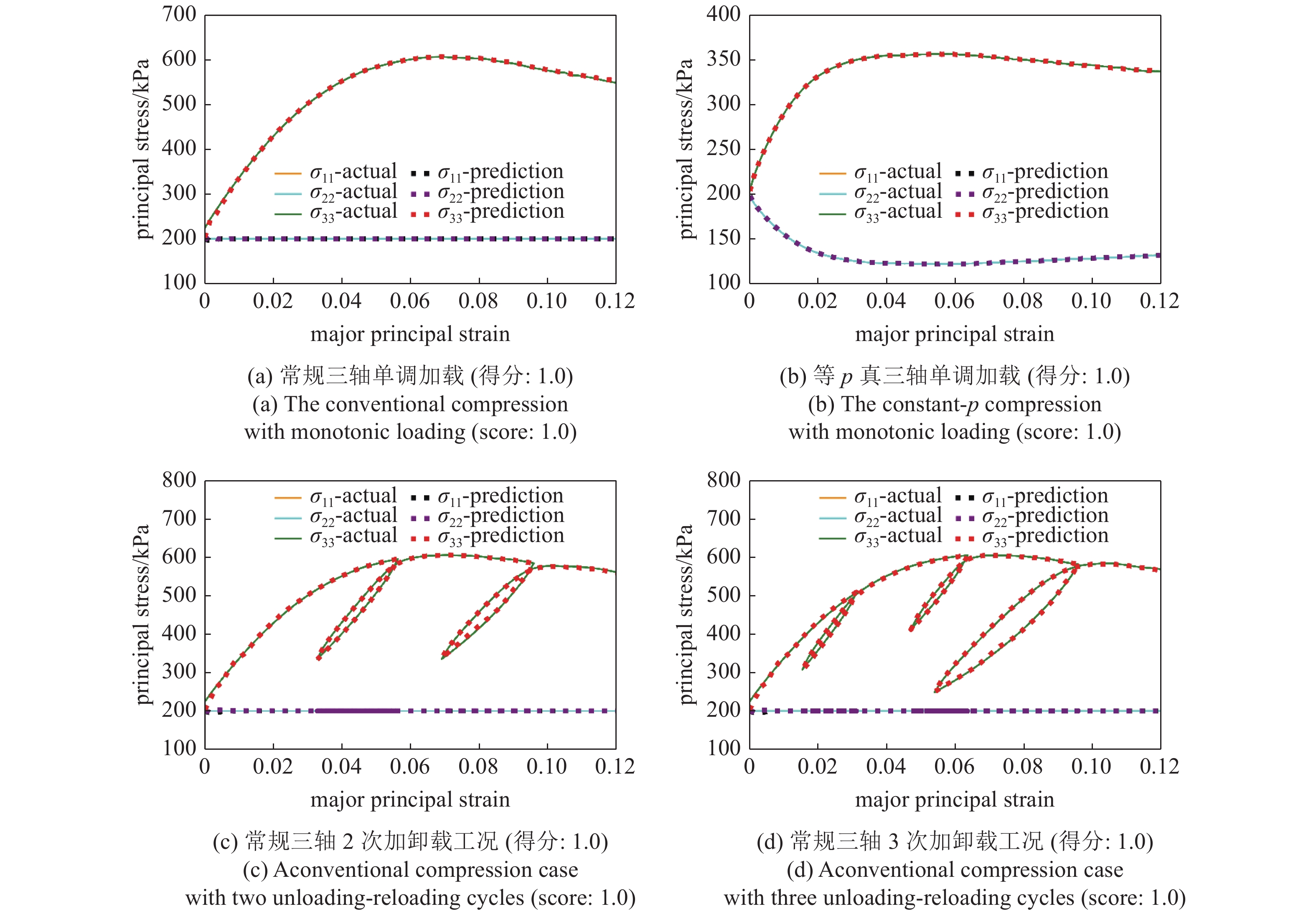
本研究在测试数据集中准备了常规三轴和等p真三轴单调加载工况, 也准备了6组包含2次及以上加卸载循环的常规三轴加载工况. 这些工况完全在模型训练过程中所用的训练集和测试集范围之外, 因此被用来测试神经网络的外推预测能力. 8组测试样本中除了一组预测得分为0.98以外, 其余预测都得到了满分. 几组代表性预测工况如图9所示, 结果表明深度学习模型能准确地适应单调加载和多次加卸载的外推工况.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-221-9.jpg'"
class="figure_img
figure_type2 ccc " id="Figure9" />



图
9
几种代表性外推预测



Figure
9.
Some representative extrapolation predictions



下载:
全尺寸图片
幻灯片

6.
讨论

颗粒材料的多次加卸载等复杂工况本质上都体现为细观结构的往复演化. 在材料参数不发生较大变化的情况下, 预测试样应力?应变响应的关键在于预测试样组构的演化. 由于采用了基于时序的循环神经网络模型, 在预测当前应力值时, 包含了足够长的应变历史信息来推断当前的组构演化和应力响应, 因此深度学习模型能有效区分加载和卸载, 做出准确的应力预测. 另外, 尽管包含多次加卸载的工况未曾直接出现在模型训练过程中, 但是类似的细观组构演化过程可能已经被训练数据所覆盖, 这也是深度学习模型对多次加卸载工况具备较好外推能力的原因. 外推预测结果表明当训练集中包含丰富的一次加卸载样本时, 模型将具有一定的两次或三次等加卸载工况的外推预测能力, 这在实践中能有效降低准备训练样本的数据规模.

相比于颗粒材料室内三轴试验, 基于离散元的虚拟三轴试验所需成本更低, 效率更高, 且方便模拟各类加载工况. 采用基于离散元的虚拟三轴试验产生颗粒材料应力?应变数据主要包含两个方面的意义: (1) 离散元方法已经表明具备定性再现颗粒材料基本响应特征的能力^[24], 通过低成本的离散元模拟, 可为探索数据驱动本构模型提供经验. (2) 高质量的离散元模拟本身有能力对实际颗粒材料的宏观力学响应做出定量预测. 在离散元的参数得到合理标定^[25-26], 使用更加真实合理的接触模型, 并考虑复杂形状因素的离散元模拟中^[27-28], 实际颗粒材料的本构行为能很好的被离散元所捕捉到, 此时基于离散元数据基本能代表真实材料数据^{[22, 29-30]}.

本文的理论推导主要基于线弹性接触模型, 由于从线弹性接触到非线性弹性接触的映射关系并不复杂, 深度神经网络完全有能力捕捉到这个映射关系的转变. 因此本文提出的深度学习框架也适用于预测非线性弹性接触模型的应力?应变响应. 此外, 若需严格地发展基于非线性弹性接触模型的深度学习策略, 可在本文提出的训练框架下, 参考文献[25]中推导的基于非线性弹性接触模型的颗粒材料应力?应变关系进行深度学习训练.

数据驱动本构模型相比于传统基于唯象假设的解析模型有几个突出优点: (1)可以根据新数据的补充而不断改进和优化, 而唯象模型在参数标定好以后, 成为一个封闭的体系, 无法充分利用工程活动中产生的海量数据资源; (2)复杂的唯象模型往往需要标定多达十多个, 甚至数十个自由参数, 并且有些模型在有限元中实施较为复杂; 然而数据驱动的本构模型不论考虑何种复杂的荷载条件, 在有限元等连续方法中实施时均能够做到标准化和模块化.

数据驱动模型和理论驱动模型具有不同的优点和缺点, 数据驱动本构模型并不能替代理论本构模型, 两种研究范式是相互补充和促进的. 一个典型的例子是, 尽管离散元模拟可以得到代表性试样中的剪应力分量, 在室内试验条件下我们一般仅能测到试样中的3个主应力和主应变分量; 深度学习模型在主应力和主应变数据集下也只能训练得到主应力与主应变空间的映射关系. 一个完整的本构模型需要进一步将主应力与主应变空间的应力关系变换到一般应力?应变空间当中. 由于颗粒材料在加载过程中主应力和主应变增量方向存在非共轴特征^[31], 因此纯粹的坐标变换方法将不可避免存在误差, 考虑颗粒材料主应力和主应变关系的非共轴特性是唯象模型和数据模型共同的挑战^[32].

7.
结论

本文结合小应变应力?应变理论关系和深度神经网络模型, 通过有向图发展了一种基于深度循环神经网络的颗粒材料应力?应变数据驱动模型训练方法. 通过常规三轴加卸载、等p真三轴加卸载和等b真三轴加载等多轴加载工况对模型进行训练和测试. 结果表明使用的深度神经网络模型能有效预测训练和验证过程从未见过的测试数据, 在仅含有常规三轴和等p真三轴一次加卸载循环的训练集中, 深度学习模型有足够的泛化能力预测到包含单调加载和多个加卸载循环的应力响应, 具有良好的内插和外推预测能力. 结果表明通过结合先验的应力?应变解析范式和经验的数据驱动范式, 可以发展出适应多种加载工况的颗粒材料主应力?主应变预测模型.