删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

面内变刚度薄板弯曲问题的挠度?弯矩耦合神经网络方法

本站小编 Free考研考试/2022-01-01


引言


面内功能梯度材料薄板结构在土木工程、海洋工程等领域应用广泛, 该结构由功能梯度材料所组成(functionally graded material, FGM), 其材料特性随着空间位置的变化而表现为梯度性的变化[1]. 在现有研究中, 于天崇等[2]研究了面内变刚度薄板在特定边界下弯曲问题的Levy解. 朱竑祯等[3]研究了周边固支圆形面内变刚度薄板轴对称弯曲问题的级数解答. 何建璋等[4]研究了面内变刚度矩形薄板自由振动问题的辛弹性解. 以上的理论解答仅针对特定的功能梯度函数及特定边界才成立, 一般的情况下难以得出理论解答, 而在数值解法上仍以有限元为主. Santare和Lambros[5]发展了一种针对材料属性为指数分布的梯度有限元求解格式. Kim和Paulino[6]研究了梯度单元以及分层单元在不同荷载下的计算性能. 黄立新等[7]基于分层法思想分析了功能梯度材料的平面应力问题. 田云德和秦世伦[8]采用分层法研究了功能梯度厚板的热应力问题. 对于面内变刚度功能梯度薄板, 采用分层法, 薄板求解域采用有限元网格划分, 每个单元的材料参数为常数, 而其材料参数则根据功能梯度函数由单元内特定点进行计算. 有限元网格划分越密其计算结果越精确, 而在实际计算中, 越精细的网格会导致总体刚度矩阵规模巨大, 需要耗费大量的计算机内存. 无论采用何种数值方法, 其最终目的均是求得面内变刚度薄板弯曲控制偏微分方程的近似解答, 为进一步丰富该类研究, 本文拟结合深度学习技术并发展求解该类问题的新解法.

在早期就有研究[9-10]将人工神经网络作为一类偏微分方程的求解器用于求解偏微分方程, 但由于其对计算机计算能力的要求过高以及优化算法中存在的问题, 这一解法在当时并未得到很好的发展. 而如今, 自深度学习在计算机视觉、语音文字识别取得成功的应用后, 深度学习技术也在各个学科领域加速发展. 在力学领域, Weinan和Yu[11]提出深度Ritz法, 该方法采用变分求解形式对偏微分方程进行求解. Raissi等[12]提出了用于求解高阶非线性偏微分方程的物理驱动的神经网络(physics-informed neural networks, PINNs). Sirignano和Spiliopoulos[13]则提出求解高阶微分方程的深度伽辽金法(deep galerkin method, DGM). Samaniego等[14]建立了深度能量法并将其应用于求解弹性、超弹性等力学问题. 瞿同明等[15]基于深度学习技术, 研究了细观力学中的颗粒本构关系. 谢晨月等[16]发展了一种模拟湍流大涡的神经网络方法. 刘宇翔等[17]基于卷积神经网络研究了无网格方法中影响域的优化问题. 郭宏伟和庄晓莹[18]采用深度配点法以及深度能量法求解了薄板弯曲问题. 陈豪龙和柳占立[19]基于数据驱动的神经网络模型求解了热传导反问题.

在上述研究中, 神经网络解法[11-14]并不像有限元解法一样可以轻松施加边界条件, 早期的研究采取根据边界条件构造满足偏微分方程特解试函数的形式来处理边界条件, 但采用该方法会使得简支边、自由边试函数的表达式变得复杂, 导致程序的实现较为复杂. 近期的研究则采用罚函数的方法将边界处的误差纳入神经网络的训练误差中, 从而将原问题转换为无约束优化问题, 在实际计算中, 也会存在着由于边界误差项难以收敛而影响求解精度的情况[20].

同时由于弯曲刚度函数是面内坐标的连续函数, 面内变刚度薄板弯曲问题的控制方程为一包含了弯曲刚度导数项的复杂4阶偏微分方程, 在实际计算中采用DGM和PINN等方法对其求解时, 会存在由于弯曲刚度偏导数在域内不收敛而导致网络拟合不佳的问题.

基于上述原因, 本文针对薄板弯曲问题求解的特点, 结合前面所述的两种边界处理方案, 建立了一种针对面内变刚度薄板弯曲问题的非全连接前馈神经网络模型, 该模型包含挠度网络与弯矩网络: 挠度网络用于预测薄板的挠度, 弯矩网络用于预测薄板的弯矩, 进而将问题转换为求解4个二阶偏微分方程组. 在边界条件的处理上, 本文仍采用罚函数方法, 不同之处在于本文模型的输出为挠度、弯矩, 因而可根据位移边界条件对挠度网络构造试函数, 根据广义应力边界条件对弯矩网络构造试函数, 这使得本文模型对于常见的边界条件的施加更为简便, 进而减小边界误差项带来的影响, 同时计算效率也得到提高. 本文采用Pytorch深度学习框架编写求解程序, 选取不同边界条件的面内变刚度薄板算例, 在Ubuntu Kylin操作系统上进行计算, 计算机的CPU配置为Intel(R) Core(TM) i7-8700 CPU @ 3.20GHz, 8GB内存, 并将计算所得结果与理论解、有限元解进行对比分析, 以验证本文方法的有效性.


1.
面内变刚度薄板弯曲理论


本文研究变厚度薄板或弹性模量参数在面内变化的薄板的弹性小变形弯曲, 设薄板的厚度函数为$ h(x,y), $材料的泊松比 $nu $为常数, 弹性模量函数为$ E(x,y) $ .

根据Kirchhoff板理论基本假定, 几何方程为







$$ left. {begin{array}{*{20}{l}} {{varepsilon _x} = - zdfrac{{{partial ^2}w(x,y)}}{{partial {x^2}}}} {{varepsilon _y} = - zdfrac{{{partial ^2}w(x,y)}}{{partial {y^2}}}} {{gamma _{xy}} = - zdfrac{{{partial ^2}w(x,y)}}{{partial xpartial y}}} end{array}}
ight} $$
(1)

物理方程为







$$ left. {begin{array}{*{20}{l}} {{sigma _x} = dfrac{{E(x,y)}}{{1 - {nu ^2}}}({varepsilon _x} + nu {varepsilon _y})} {{sigma _y} = dfrac{{E(x,y)}}{{1 - {nu ^2}}}({varepsilon _y} + nu {varepsilon _x})} {{tau _{xy}} = dfrac{{E(x,y)}}{{2(1 + nu )}}{gamma _{xy}}} end{array}}
ight} $$
(2)

平衡方程为







$$ frac{{{partial ^2}{M_x}}}{{partial {x^2}}} + 2frac{{{partial ^2}{M_{xy}}}}{{partial xpartial y}} + frac{{{partial ^2}{M_y}}}{{partial {y^2}}} + q = 0 $$
(3)

广义应力?应变关系为







$$ begin{split}&{M}_{x}={displaystyle {int }_{-h/2}^{h/2}frac{E}{1-{nu }^{2}}}left({epsilon }_{x}+nu {epsilon }_{y}
ight)z text{d}z=&qquad -frac{E(x,y)h{(x,y)}^{3}}{12left(1-{nu }^{2}
ight)}left[frac{{partial }^{2}w(x,y)}{partial {x}^{2}}+nu frac{{partial }^{2}w(x,y)}{partial {y}^{2}}
ight]end{split} $$
(4)

记弯曲刚度函数为







$$ D(x,y) = frac{{Eleft( {x,y}
ight)h{{left( {x,y}
ight)}^3}}}{{12left( {1 - {nu ^2}}
ight)}} $$
(5)

则







$$ {M_x} = - D(x,y)left[ {frac{{{partial ^2}w(x,y)}}{{partial {x^2}}} + nu frac{{{partial ^2}w(x,y)}}{{partial {y^2}}}}
ight] $$
(6)

同理







$$ {M_y} = - D(x,y)left[ {frac{{{partial ^2}w(x,y)}}{{partial {y^2}}} + nu frac{{{partial ^2}w(x,y)}}{{partial {x^2}}}}
ight] $$
(7)







$$ {M_{xy}} = int_{ - h/2}^{h/2} {{tau _{xy}}} z{
m{d}}z = - (1 - nu )D(x,y)frac{{{partial ^2}w(x,y)}}{{partial xpartial y}} $$
(8)

对于固支边界条件${varGamma _1}$







$$ {left( {w,frac{{partial w}}{{partial n}}}
ight)_s} = 0 $$
(9)

对于简支边界条件${varGamma _2}$







$$ {left( {w,{M_n}}
ight)_s} = 0 $$
(10)

对于自由边界条件${varGamma _3}$







$$ left( {{M_n},F_{{{s}}n}^t}
ight) = 0 $$
(11)

其中$n$表示边界的外法线方向, $s$表示边界的切线方向.

将式(4) ~ 式(6)代入平衡方程(3)即可得面内变刚度薄板弯曲偏微分控制方程







$$ begin{split}& {nabla ^2}left( {D{nabla ^2}w}
ight) - (1 - nu )left( {frac{{{partial ^2}D}}{{partial {y^2}}}frac{{{partial ^2}w}}{{partial {x^2}}}}
ight. - 2frac{{{partial ^2}D}}{{partial xpartial y}}frac{{{partial ^2}w}}{{partial xpartial y}} + & qquad left. {frac{{{partial ^2}D}}{{partial {x^2}}}frac{{{partial ^2}w}}{{partial {y^2}}}}
ight) + q = 0 end{split} $$
(12)

式中${nabla ^2} = dfrac{{{partial ^2}}}{{partial {x^2}}} + dfrac{{{partial ^2}}}{{partial {y^2}}}$为Laplace算子.


2.
神经网络模型



2.1
神经网络模型的构建


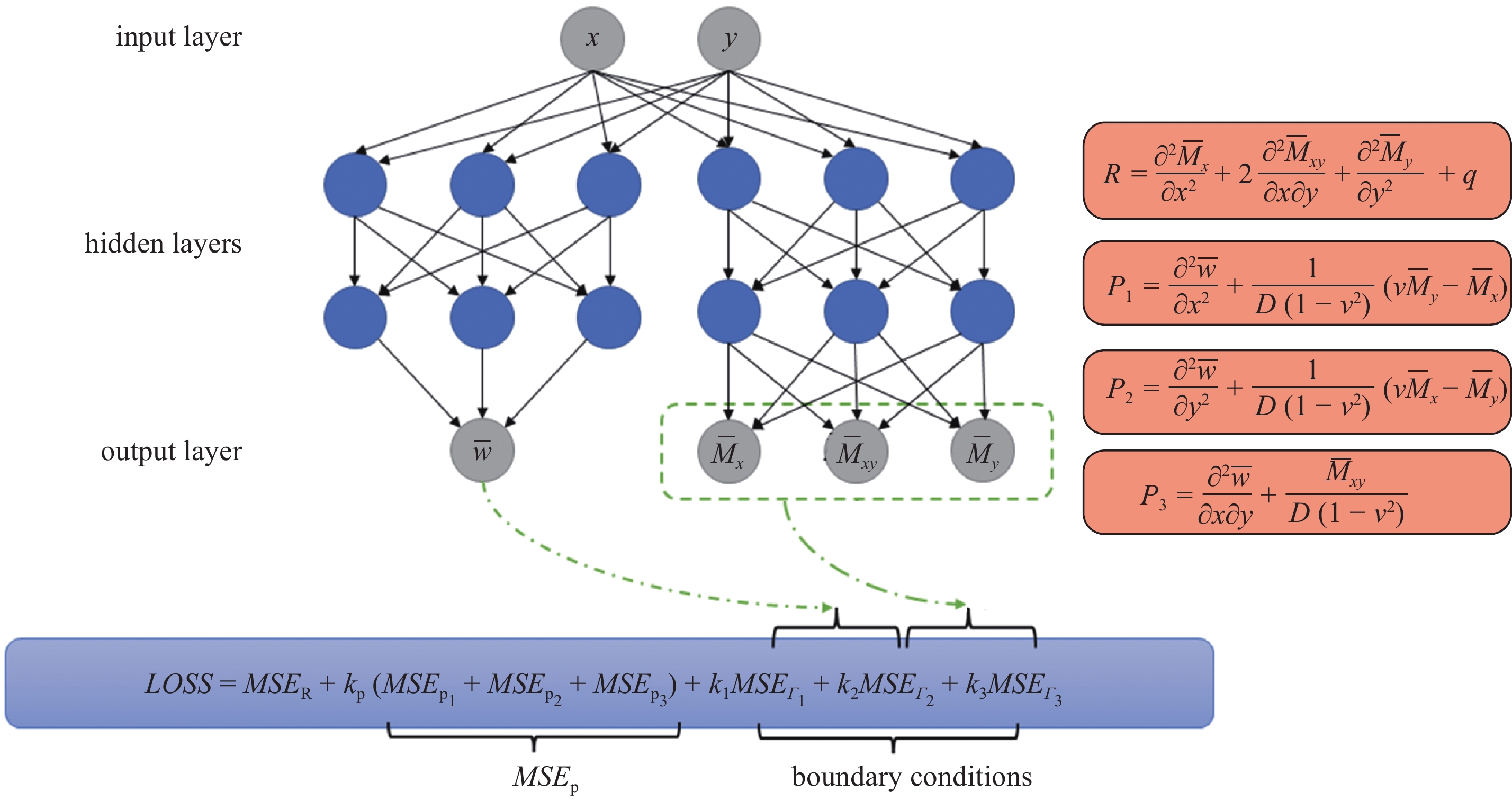
本文方法并非直接设计网络来求解方程(12), 而是采用两个神经网络模型来进行求解, 如图1所示, 将待求解的4阶偏微分控制方程转换为求解4个二阶偏微分方程组, 该解法本质上仍属于强形式的求解方案. 如果仅以挠度作为预测解, 在试函数的构造上对于不同形状的求解域以及简支、自由边界条件的构造会出现困难. 本文采用挠度网络预测薄板挠度$bar wleft( {x,y;{{{{boldsymbol{theta}} }}_{
m{w}}}}
ight)$, 弯矩网络预测薄板弯矩, $bar Mleft( {x,y;{{{{boldsymbol{theta}} }}_{
m{m}}}}
ight) = $$ left{ {{{bar M}_x}left( {x,y;{{{{boldsymbol{theta}} }}_{
m{m}}}}
ight),{{bar M}_{xy}}left( {x,y;{{{{boldsymbol{theta }}}}_{
m{m}}}}
ight),{{bar M}_y}left( {x,y;{{{{boldsymbol{theta}} }}_{
m{m}}}}
ight)}
ight}$, 这样的做法可以使得位移边界条件由挠度网络施加, 广义应力边界条件由弯矩网络施加.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure1" />



图
1
本文神经网络模型示意图



Figure
1.
The schematic diagram of neural network model in this paper



下载:
全尺寸图片
幻灯片



2.2
误差函数


根据广义应力?应变关系式(6) ~ 式(8)可求得挠度二阶偏导的弯矩表达式







$$ frac{{{partial ^2}w}}{{partial {x^2}}} = frac{1}{{Dleft( {1 - {nu ^2}}
ight)}}left( {nu {M_y} - {M_x}}
ight) $$
(13)







$$ frac{{{partial ^2}w}}{{partial {y^2}}} = frac{1}{{Dleft( {1 - {nu ^2}}
ight)}}left( {nu {M_x} - {M_y}}
ight) $$
(14)







$$ frac{{{partial ^2}w}}{{partial xpartial y}} = - frac{{{M_{xy}}}}{{D(1 - nu )}} $$
(15)

误差函数的构造是神经网络训练的核心, 由于本文方法引入两个网络进行计算, 故在训练中需要考虑两者之间的耦合误差. 若采用无约束优化方案, 本文误差函数主要根据挠度与弯矩网络在边界处的误差、弯矩网络在力平衡方程(3)中的误差、预测的挠度与弯矩通过式(13) ~ 式(15)建立的耦合误差来构造.

采用均方误差(mean square error, MSE)来衡量神经网络的拟合误差, 记挠度网络与弯矩网络的内部参数分别为$ {boldsymbol{theta }}_{{
m{w}}} $, ${boldsymbol{theta }}_{
m{m}}$, 本文模型的误差函数可构造为







$$ begin{split} Cleft( {{{{{boldsymbol{theta}} }}_{
m{w}}},{{{{boldsymbol{theta}} }}_{
m{m}}}}
ight) = & MS{E_{text{R}}} + {k_{
m{P}}}MS{E_{
m{P}}} + &{k_1}MS{E_{{varGamma _1}}} + {k_2}MS{E_{{varGamma _2}}} + {k_3}MS{E_{{varGamma _3}}} end{split} $$
(16)

如果采用构造试函数的形式使得边界误差强制满足, 则误差函数无需计算边界误差







$$ Cleft( {{{{{boldsymbol{theta}} }}_w},{{{{boldsymbol{theta}} }}_{
m{m}}}}
ight) = MS{E_{text{R}}} + {k_{
m{P}}}MS{E_{
m{P}}} $$
(17)

其中







$$ begin{split} MS{E_{
m{R}}} =& frac{1}{{{N_varOmega }}}sumlimits_{i = 1}^{{N_varOmega }} {left| {frac{{{partial ^2}{{bar M}_x}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight)}}{{partial {x^2}}}}
ight. + 2frac{{{partial ^2}{{bar M}_{xy}}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight)}}{{partial xpartial y}}} + & {left. {frac{{{partial ^2}{{bar M}_y}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight)}}{{partial {y^2}}} + q}
ight|^2} end{split} $$
(18)







$$ MS{E_{{varGamma _1}}} = frac{1}{{{N_{{varGamma _1}}}}}sumlimits_{i = 1}^{{N_{{varGamma _1}}}} {left[{{{left| {bar wleft( {{{boldsymbol{x}}_{{varGamma _1}}};{{boldsymbol{theta }}_{
m{w}}}}
ight)}
ight|}^2} + left. {{{left| {frac{{partial bar wleft( {{{boldsymbol{x}}_{{varGamma _1}}};{{boldsymbol{theta }}_{
m{w}}}}
ight)}}{{partial n}}}
ight|}^2}}
ight]}
ight.} ;;;;;;$$
(19)







$$ MS{E_{{varGamma _2}}} = frac{1}{{{N_{{varGamma _2}}}}}sumlimits_{i = 1}^{{N_{{varGamma _2}}}} {left[ {{{left| {bar wleft( {{{boldsymbol{x}}_{{varGamma _2}}};{{boldsymbol{theta }}_{
m{w}}}}
ight)}
ight|}^2} + left| {{{left. {{{bar M}_n}left( {{{boldsymbol{x}}_{{varGamma _2}}};{{boldsymbol{theta }}_{
m{m}}}}
ight) - {{tilde M}_n}}
ight|}^2}}
ight.}
ight]} $$
(20)







$$ begin{split} MS{E_{{varGamma _3}}} = &frac{1}{{{N_{{varGamma _3}}}}}sumlimits_{i = 1}^{{N_{{varGamma _3}}}} {Biggl[{23} {{{left| {left. {{{bar M}_n}left( {{{boldsymbol{x}}_{{varGamma _3}}};{{boldsymbol{theta }}_{
m{m}}}}
ight) - {{tilde M}_n}}
ight|}
ight.}^2}} } hfill + & {{{left| {frac{{partial {{bar M}_{ns}}left( {{{boldsymbol{x}}_{{varGamma _3}}};{{boldsymbol{theta }}_{
m{m}}}}
ight)}}{{partial s}} + {Q_n}left( {{{boldsymbol{x}}_{{varGamma _3}}};{{boldsymbol{theta }}_{
m{m}}}}
ight)}
ight|}^2}} Biggl]{23} hfill end{split};;;;;; ;;;;;;;;;;;;;;;;;;$$
(21)







$$ MS{E_{
m{P}}} = MS{E_{{
m{P}}1}} + MS{E_{{
m{P}}2}} + MS{E_{{
m{P}}3}};;;;;;;;;;;;;;;;;;;;;;;;;;; $$
(22)

其中, 向量${boldsymbol{x}} = left( {x,y}
ight)$表示神经网络的输入; n和s分别为边界的法线、切线方向; $varOmega $表示求解域; $ {{varGamma }_1} $, $ {{varGamma }_{2}} $, $ {{varGamma }_3} $分别为固支、简支、自由边界, $partial varOmega = {varGamma _1} cup {varGamma _2} cup {varGamma _3}$; $ {tilde M_n} $为施加于边界处的弯矩, ${M_n}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight)$, ${{{Q}}_n}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight)$分别为根据弯矩网络输出求得的弯矩、剪力; ${k_{
m{p}}}$为网络耦合系数, 取值范围为1 ~ 1000, 该系数的选取会影响挠度网络与弯矩网络之间的耦合效果; ${k_1}$, ${k_2}$, ${k_3}$为边界处的罚系数, 取值范围为1 ~ 10 000.

式(22)中







$$ begin{split} MS{E_{{
m{P}}1}} =& frac{1}{{{N_varOmega }}}sumlimits_{i = 1}^{{N_varOmega }} {left| {frac{{{partial ^2}bar wleft( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{w}}}}
ight)}}{{partial {x^2}}}}
ight.} hfill & {left. { - frac{1}{{Dleft( {1 - {nu ^2}}
ight)}}left[ {nu {{bar M}_y}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight) - {{bar M}_x}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight)}
ight]}
ight|^2} hfill end{split} $$
(23)







$$ begin{split} MS{E_{{
m{P}}2}} = &frac{1}{{{N_varOmega }}}sumlimits_{i = 1}^{{N_varOmega }} {left| {frac{{{partial ^2}bar wleft( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{w}}}}
ight)}}{{partial {y^2}}}}
ight.} hfill &{left.{- frac{1}{{Dleft( {1 - {nu ^2}}
ight)}}left[ {nu {{bar M}_x}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight) - {{bar M}_y}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight) }
ight]}
ight|^2} hfill end{split} $$
(24)







$$ MS{E_{{
m{P}}3}} = frac{1}{{{N_varOmega }}}sumlimits_{i = 1}^{{N_varOmega }} {{{left| {frac{{{partial ^2}bar wleft( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{w}}}}
ight)}}{{partial xpartial y}} + frac{{{{bar M}_{xy}}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight)}}{{D(1 - nu )}}}
ight|}^2}} $$
(25)

本文的误差函数表达式中包含挠度、弯矩对自变量的二阶偏导数项, 对于这些偏导项, 一方面可以利用神经网络的输出构造差分求解格式来近似求解, 但采用该方案需要较大的计算量才能得到精确的计算结果; 另一方面, 基于计算图的自动微分技术(automatic differentiation, AD)可以高效地处理神经网络对输入变量求导过程, 当前的深度学习框架如Tensoflow, Pytorch, MindsSpore等均支持自动微分. 本文基于Pytorch提供的自动微分接口实现对上述偏导项及误差函数梯度的计算.

在实际计算中, 也可灵活采用混合边界误差的形式进行求解, 如对于部分简单的边界条件构造特解, 而对于复杂的边界采用相应的无约束优化方案. 建立本文的误差函数后, 在每个训练批次(epoch)中均需计算其梯度并结合误差反向传播算法更新网络的内部参数, 关于该过程, Tang和Yang[21]对其进行了详细的讨论.


2.3
学习率选取方案


学习率的选取可直接影响神经网络的训练, 目前神经网络学习率的选取仍带有一定的经验性, 但总体而言, 在训练初期选取较大的学习率可以加快误差收敛速度, 在训练后期, 此时神经网络模型已经学习到相应的特征, 此时往往需要降低学习率, 以便对神经网络内部参数进行微调, 使得误差波动幅度不至于过大. 经过本文的实践, 本文学习率选取方案如下







$$ {alpha _t} = left{ {begin{array}{*{20}{l}} 1times{{{10}^{ - 3}},}&{t leqslant 5000} {5 times {{10}^{ - 4}},}&{5000 < t leqslant 10;000} 1times{{{10}^{ - 4}},}&{10;000 < t leqslant 20;000} {5 times {{10}^{ - 5}},}&{20;000 < t leqslant 30;000} 1times{{{10}^{ - 5}},}&{30;000 < t leqslant 40;000} {5 times {{10}^{ - 6}},}&{40;000 < t leqslant 45;000} 1times{{{10}^{ - 6}},}&{45;000 < t} end{array}}
ight. $$
(26)

其中, $t$为训练次数.


2.4
算法流程


算法1. 本文算法

输入: 学习率$alpha $; 最大迭代次数$N$; 训练误差下限?; 数据点生成参数${N_varOmega }$, ${N_{{varGamma _1}}}$, ${N_{{varGamma _2}}}$, ${N_{{varGamma _3}}}$

输出: 挠度网络; 弯矩网络

　　初始化神经网络模型及其内部参数${{{{boldsymbol{theta}} }}_{
m{w}}},{{{{boldsymbol{theta}} }}_{
m{m}}}$, 训练误差$C$

　　1, $t$=0 (initialization)

　　2 while ($C$ > = ?) and ($t$ < $N$) do

　　{

(1)在求解域中随机生成数据点坐标$left( {{x_{
m{d}}},{y_{
m{d}}}}
ight) in varOmega$, $left( {{x_{
m{b}}},{y_{
m{b}}}}
ight) in$ $partial varOmega$

(2)将数据点坐标作为参数输入神经网络模型, 通过前向传播算法, 求得$bar wleft( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{w}}}}
ight)$, ${bar M_x}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight)$, ${bar M_{xy}}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight)$, ${bar M_y}left( {{boldsymbol{x}};{{boldsymbol{theta }}_{
m{m}}}}
ight)$

(3)通过式(16)计算误差函数$C$

(4)计算误差函数$C$关于神经网络参数${{{{boldsymbol{theta }}}}_{
m{w}}},{{{{boldsymbol{theta}} }}_{
m{m}}}$的梯度, 结合Adam优化算法更新${{{{boldsymbol{theta}} }}_{
m{w}}},{{{{boldsymbol{theta}} }}_{
m{m}}}$

(5) $ t leftarrow t + 1 $

/}

算法中, 本文的数据点的默认生成参数为${N_varOmega }$=500, ${N_{{varGamma _1}}}$=${N_{{varGamma _2}}}$=${N_{{varGamma _3}}}$=100, 实际算例分析时会进行相应的调整; 在网络模型初始化中, 采用Xavier均匀分布[22]对参数${{{{boldsymbol{theta}} }}_{
m{w}}},{{{{boldsymbol{theta}} }}_{
m{m}}}$初始化.


3.
算例



3.1
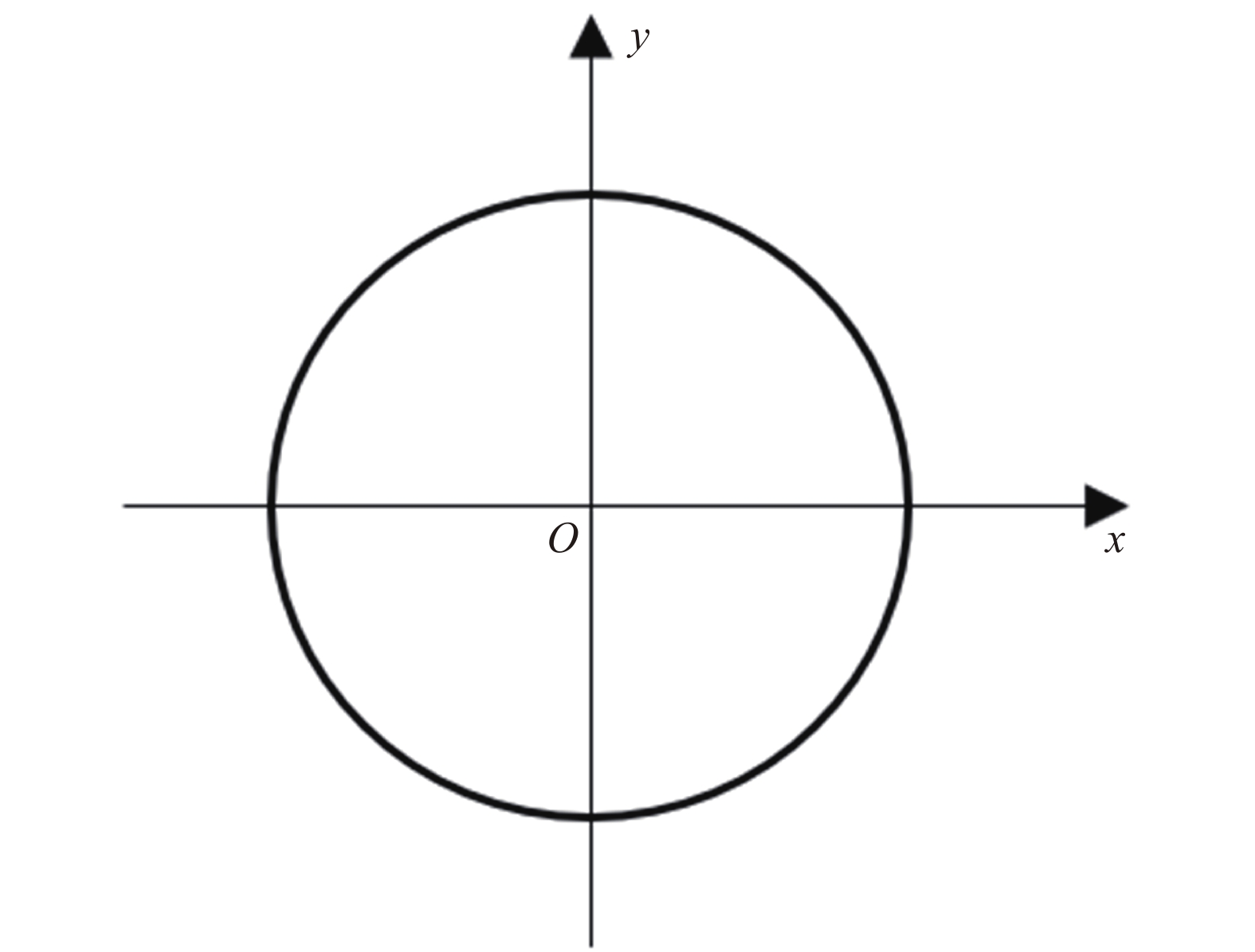
双向面内变刚度圆形薄板轴对称弯曲


图2所示受横向均布荷载$q(x,y) = - {q_0}$作用的周边固支圆形薄板, 其半径R, $nu = 0.3$, 弯曲刚度函数沿半径变化$D(
ho ) = {D_0}{{text{e}}^{ - m
ho /a}}$, 其中$
ho = sqrt {{x^2} + {y^2}} $, $m$为梯度系数, ${q_0}$, ${D_0}$为常数. 该问题存在理论解[14].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
圆形面内变刚度薄板



Figure
2.
Circular thin plate with in-plane stiffness gradient



下载:
全尺寸图片
幻灯片


本文选取梯度参数m分别为0, 0.5, 1, 2的情况进行计算. 本算例在计算过程中仅需要施加位移边界条件, 设$wleft( {x,y;{{{{boldsymbol{theta}} }}_{
m{w}}}}
ight)$为挠度网络的输出, 考虑到本算例边界条件较为简单, 构造挠度试函数为${w^*} = wleft( {x,y;{{{{boldsymbol{theta}} }}_{
m{w}}}}
ight) $$ {left( {{x^2} + {y^2} - {R^2}}
ight)^2}$.

本算例的挠度模型以及弯矩模型均采用具有6层隐藏层, 每层隐藏层具备30个神经元的网络结构(记为6 × 30), 采用${x^2}$作为激活函数, ${k_{
m{p}}} = 100$, ${N_varOmega } = 640$; 采用Adam优化算法, 对各个工况所采用的学习率方案均一致. 本文算例在不同的梯度下上述基本参数不变, 仅更改梯度系数. 为更加详细地显示误差函数的变化情况, 如无特殊说明, 本文均取误差的十进制对数作为等效误差并绘制相应的训练误差曲线.

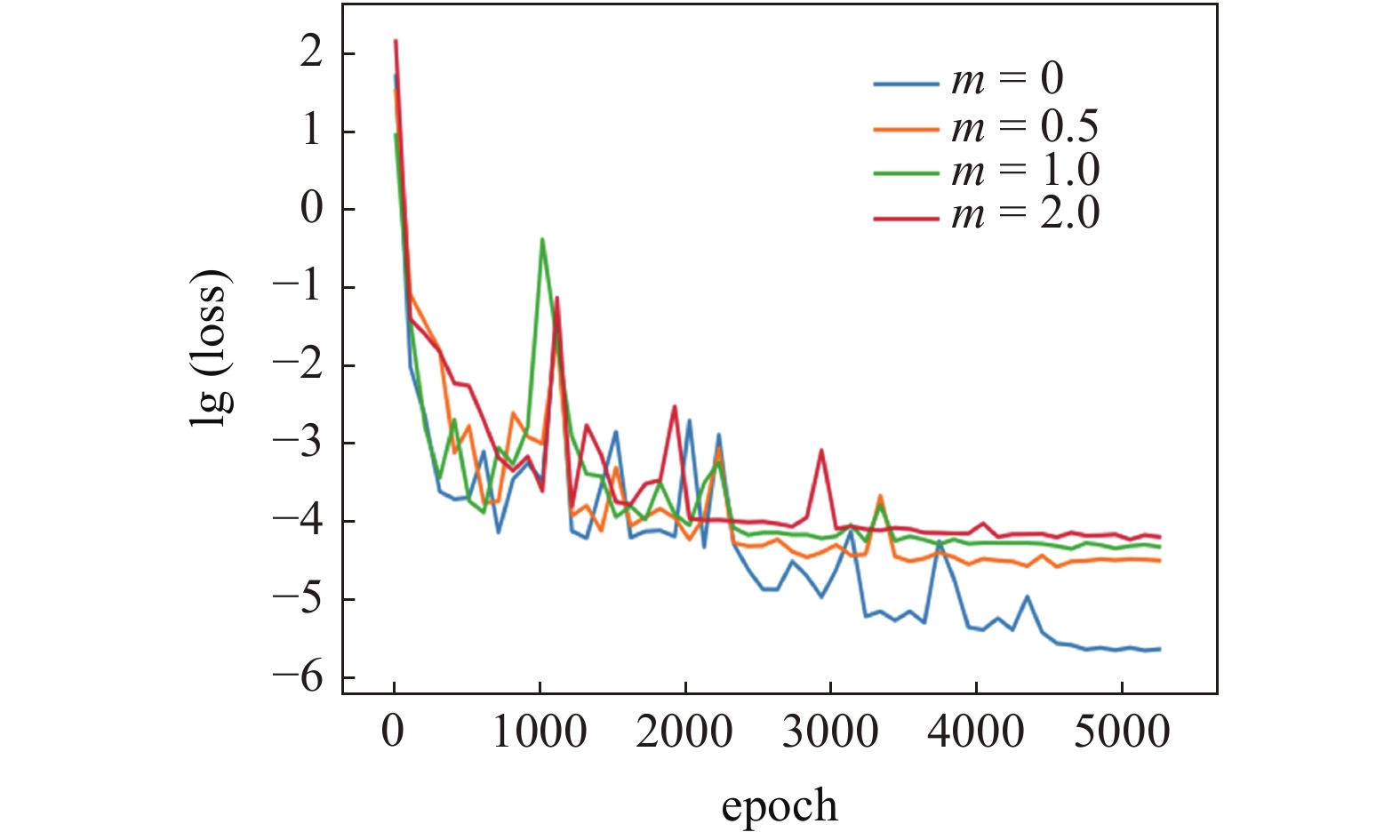
每个梯度参数下神经网络模型的计算误差如图3所示, 由此可见, m = 0时为刚度恒定的薄板, 此时误差函数收敛较快, 相比其他工况其误差最终的收敛值最小; 随着梯度系数的增大, 训练误差最终的收敛值出现增大的趋势.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
神经网络训练误差曲线



Figure
3.
The convergence curve of neural network training error



下载:
全尺寸图片
幻灯片


采用无量纲计算公式$bar w = dfrac{{{{10}^2}{D_0}}}{{{q_0}{R^4}}}{w^*}$, $bar M = dfrac{{10{M^*}{D_0}}}{{{q_0}{R^2}}}$将计算所得结果无量纲化, 其中${w^*}$和${M^*}$为实际计算所得的挠度、弯矩. 由图3和图4可以看出本文方法计算的结果与理论解答吻合. 由表1的挠度计算结果可见, 本文方法在挠度的求解上达到了相当高的精度, 本算例也选取各个梯度参数下薄板部分点的弯矩${bar M_x}$进行对比分析, 结果如表2所示, 理论解答中弯矩在原点处不存在解答, 故选取离原点较近的点(0.02, 0)求得相应的理论解, 由于本文采用了两个网络模型进行计算, 本文解中, ${bar M_{x1}}$为弯矩网络直接输出的结果, ${bar M_{x2}}$为根据挠度网络由式(4)求得, 两者相对理论解的误差分别为相对误差1、相对误差2. 可以发现当梯度系数m = 0时, 此时薄板为刚度恒定的薄板, ${bar M_{x1}}$和${bar M_{x2}}$均取得较高的精度, 而随着梯度系数的增大, 弯矩网络在靠近原点处所求得的弯矩与理论解的误差也随之增大, 在点(0.02, 0)处, 工况m = 2时${bar M_{x1}}$误差最大, 为4.086%, 而挠度网络计算的结果并未出现较大的差别, 这说明梯度系数的增大会导致本文模型的挠度与弯矩耦合误差在靠近原点处增大, 这也解释了图2所示不同梯度下神经网络误差收敛程度不同的原因, 但这并不影响挠度模型的求解精度.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
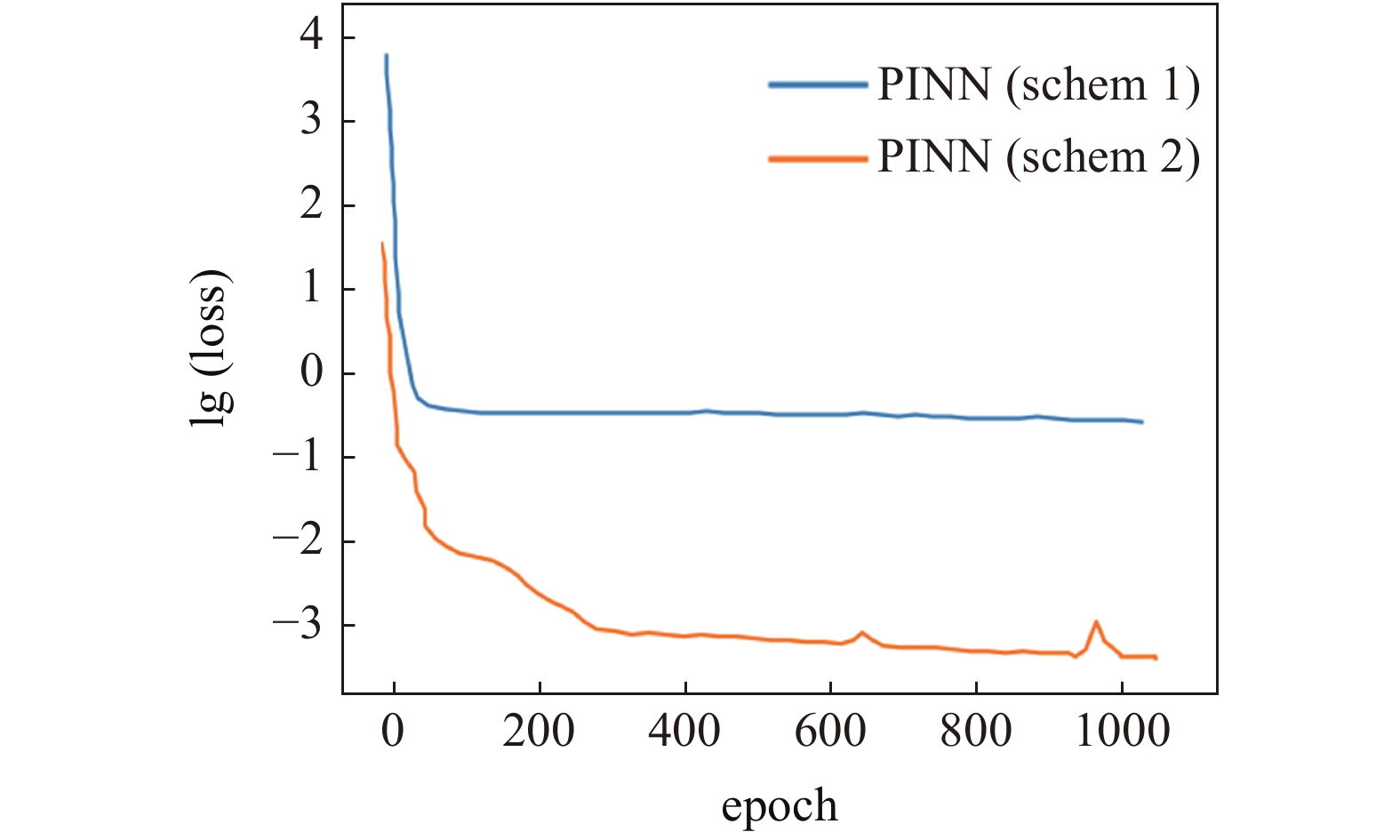
PINN求解圆形面内变刚度薄板弯曲问题的训练误差收敛曲线(m = 2)



Figure
4.
Training error convergence curve of PINN (m = 2)



下载:
全尺寸图片
幻灯片





表
1
本文方法计算$bar w$与理论解对比(无量纲)



Table
1.
Comparison of dimensionless $bar w$ calculated by neural network method and the theoretical solution



table_type1 ">
m(x, y)$ bar {w} $TheoryRelative error/%
0(0.0, 0)?1.5625?1.56250
(0.4, 0)?1.1024?1.1025?0.009
(0.8, 0)?0.2025?0.20250
1(0.0, 0)?0.8420?0.84180.024
(0.4, 0)?0.5517?0.5525?0.145
(0.8, 0)?0.0877?0.08770
2(0.0, 0)?0.4520?0.4522?0.044
(0.4, 0)?0.2725?0.27250
(0.8, 0)?0.0374?0.03730.267
注: 本文误差计算公式为$e = dfrac{{u - {u^*}}}{u} times 100% $, $u$为本文方法计算结果, ${u^*}$为理论解 (Note: The relative error in this paper is calculated by $e = dfrac{ {u - {u^*} } }{u} times $$ 100%$, where $u$ is the calculation results of this paper, ${u^*}$ is the theoretical solution)





下载:
导出CSV
|显示表格






表
2
本文方法计算${bar M_x}$与理论解对比(无量纲)



Table
2.
Comparison of dimensionless ${bar M_x}$ calculated by neural network method and the theoretical solution



table_type2 ">
m(x, y)${bar M_{x1}}$${bar M_{x2}}$TheoryRelative error 1/%Relative error 2/%
0(0.02, 0)?0.8122?0.8118?0.81170.0620.020
(0.4, 0)?0.4828?0.4824?0.48250.071?0.027
(0.8, 0)0.50770.50750.50750.037?0.004
(1.0, 0)1.25121.24991.25000.094?0.008
1(0.02, 0)?0.6027?0.5910?0.58532.8850.956
(0.4, 0)?0.3064?0.3076?0.3103?1.278?0.886
(0.8, 0)0.62640.62490.6282?0.287?0.524
(1.0, 0)1.35361.36341.35250.0770.797
2(0.02, 0)?0.4335?0.4150?0.41584.086?0.192
(0.4, 0)?0.1652?0.1651?0.1695?2.599?2.684
(0.8, 0)0.72730.72680.7319?0.637?0.712
(1.0, 0)1.43441.45431.4409?0.4580.921





下载:
导出CSV
|显示表格



为了说明本文方法在求解面内变刚度薄板弯曲问题上的优点, 本算例也利用PINN来求解其四阶偏微分控制方程(12), 采用隐藏层层数为6, 每层隐藏层具有30个神经元的神经网络模型对工况m = 2进行求解, 激活函数为Tanh函数, 训练的数据点由求解域中随机生成, 数据点的产生有两种方案:

方案(1)为在整个求解域中随机生成训练数据点, 此时的数据点可在原点附近生成;

方案(2)为在求解域中随机生成的数据点但离原点较远. 此时两方案在训练过程中的误差收敛情况如图4所示, 可见采用相同的模型, 而生成的数据点不同则会导致模型的训练出现不同的结果, 虽然采用数据点生成方案(1)的模型训练也收敛, 但由于其误差此时收敛于一个较大的值, 得不到正确解. 经过本文分析, 这主要是由于本算例的弯曲刚度函数D的二阶导数在靠近原点区域出现“爆炸”式变化的原因, 即刚度函数的二阶偏导在原点处不收敛, 在靠近原点处$dfrac{{{partial ^2}D}}{{partial {x^2}}}$等的解答急剧增大, 这会导致PINN采用方案(1)训练时, 遇到靠近原点处的点, 计算所得域内误差突然增大, 进而导致误差训练难以收敛. PINN最初提出时并未考虑求解域内存在奇异点的情况, 对于该情况, 一般情况下可在生成的数据点中排除掉奇异点, 但对于本算例中奇异点处被施予荷载的情况, 如果不能很好地处理则会影响求解的精度. 对此, 本文认为可以弱化相应的偏微分控制方程再利用PINN求解, 也可参考本文思路, 结合神经网络解法的特点, 根据具体问题对原偏微分控制方程等效化处理. 本文方法在求解时并非直接从方程(12)入手, 而是通过求解一系列偏微分方程组来逼近真实解, 避开了对弯曲刚度函数求偏导数, 故其求解仅与域内的刚度值有关, 其适应性更强, 对薄板弯曲问题的求解更具“鲁棒性”.


3.2
单向面内变刚度方形薄板受非线性荷载作用


如图5所示边长为$a$的方形薄板, 厚度$h$, $nu = 0.3$, 1, 2, 3边固支, 4边简支, 其弯曲刚度函数为$D(x) = {D_0}{(x + 1)^m}$, ${D_0} = dfrac{{{E_0}h}}{{12left( {1 - {nu ^2}}
ight)}}$, ${E_0}$为常数, m为梯度系数, 受横向非线性荷载$q(x) = - {{text{e}}^{frac{x}{a}}}$作用, 利用本文方法求解m分别为0, 1, 2情况下的挠度、内力.

本算例选取6 × 30的挠度网络模型, 5 × 50的弯矩网络模型, 激活函数选择Tanh函数, ${k_{
m{p}}} = $100, ${N_varOmega } = 450$, 采用Adam优化算法. 训练误差曲线如图6所示. 设$wleft( {x,y;{{{{boldsymbol{theta}} }}_{
m{w}}}}
ight)$为挠度网络的输出, 弯矩网络的输出为$Mleft( {x,y;{{{{boldsymbol{theta}} }}_{
m{m}}}}
ight) = left{ {{M_x},{M_{xy}},{M_y}}
ight}$, 考虑本算例的位移及广义应力边界条件, 挠度及弯矩试函数构造为






$$ left. begin{array}{l} {w^*} = wleft( {x,y;{{boldsymbol{theta }}_{
m{w}}}}
ight){left[left(sqrt 3 ax + y - a
ight)left( - sqrt 3 ax + y - a
ight)
ight]^2} hfill left{ {{M_x}^*,{M_{xy}}^*,{M_y}^*}
ight} = left{ {{M_x}(x - 1),{M_{xy}},{M_y}}
ight} hfill end{array}
ight} $$

如果将本算例的应力边界条件也通过挠度网络进行构造, 则挠度表达式将复杂许多.



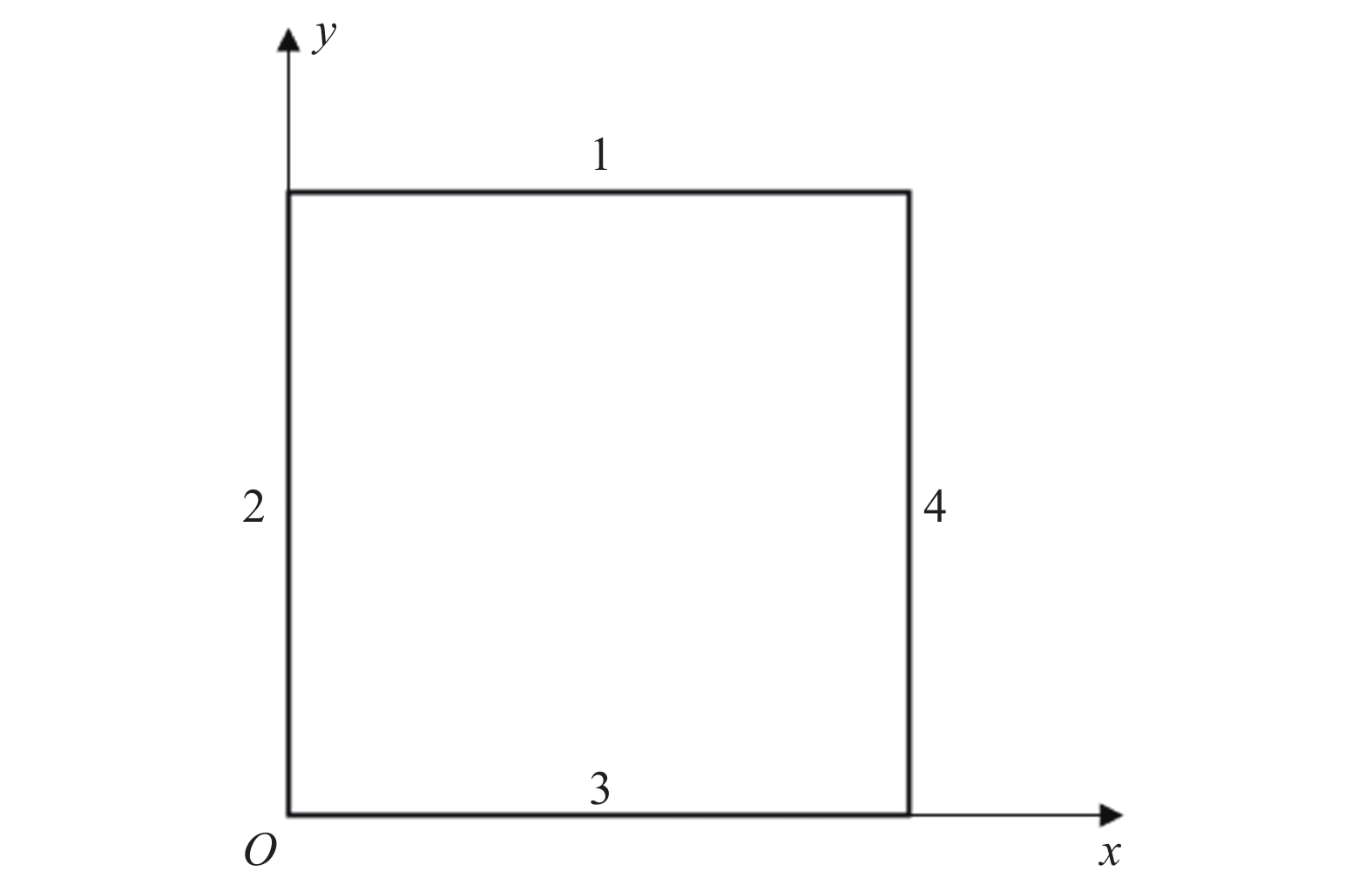onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
方形面内变刚度薄板



Figure
5.
Thin square plates with in-plane stiffness gradient



下载:
全尺寸图片
幻灯片




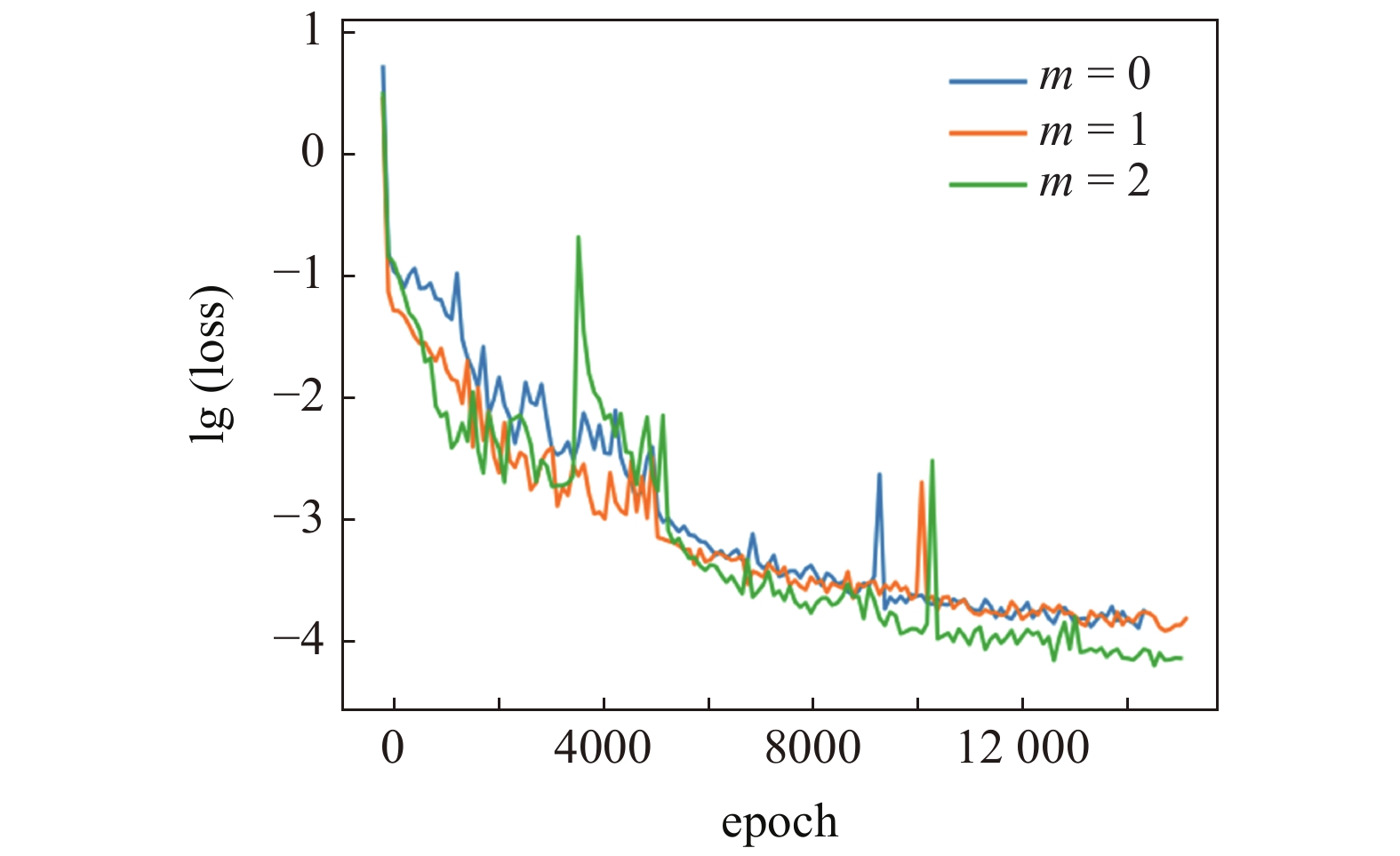onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
神经网络训练误差曲线



Figure
6.
Neural network training error-curve



下载:
全尺寸图片
幻灯片


将本算例的计算结果与有限元解答对比, 有限元计算中每个单元的弯曲刚度根据单元的形心坐标计算, 采用50$ times $50的矩形薄板非协调单元来对求解域进行离散, 离散方案通过小片测试, 对本文的3种工况该网格离散方案均收敛. 将本文与有限元计算结果的无量纲挠度、弯矩进行对比分析, 无量纲计算公式为$ overline{W}=dfrac{{10}^{2}{D}_{0}}{{q}_{0}{a}^{4}} {w}^{*} $, $bar M = dfrac{{100{M^*}{D_0}}}{{{q_0}{a^2}}}$, ${w^*}$和${M^*}$为实际计算所得的挠度、弯矩值.

由挠度计算图7可知, 在挠度的求解上, 本文解法与有限元解法一致. 由图8的弯矩对比图可发现, 本文弯矩解与有限元解答基本吻合, 而当梯度系数m = 2时, 虽然本文解与有限元解在部分点上弯矩的相对误差增大, 但整体上解答吻合.



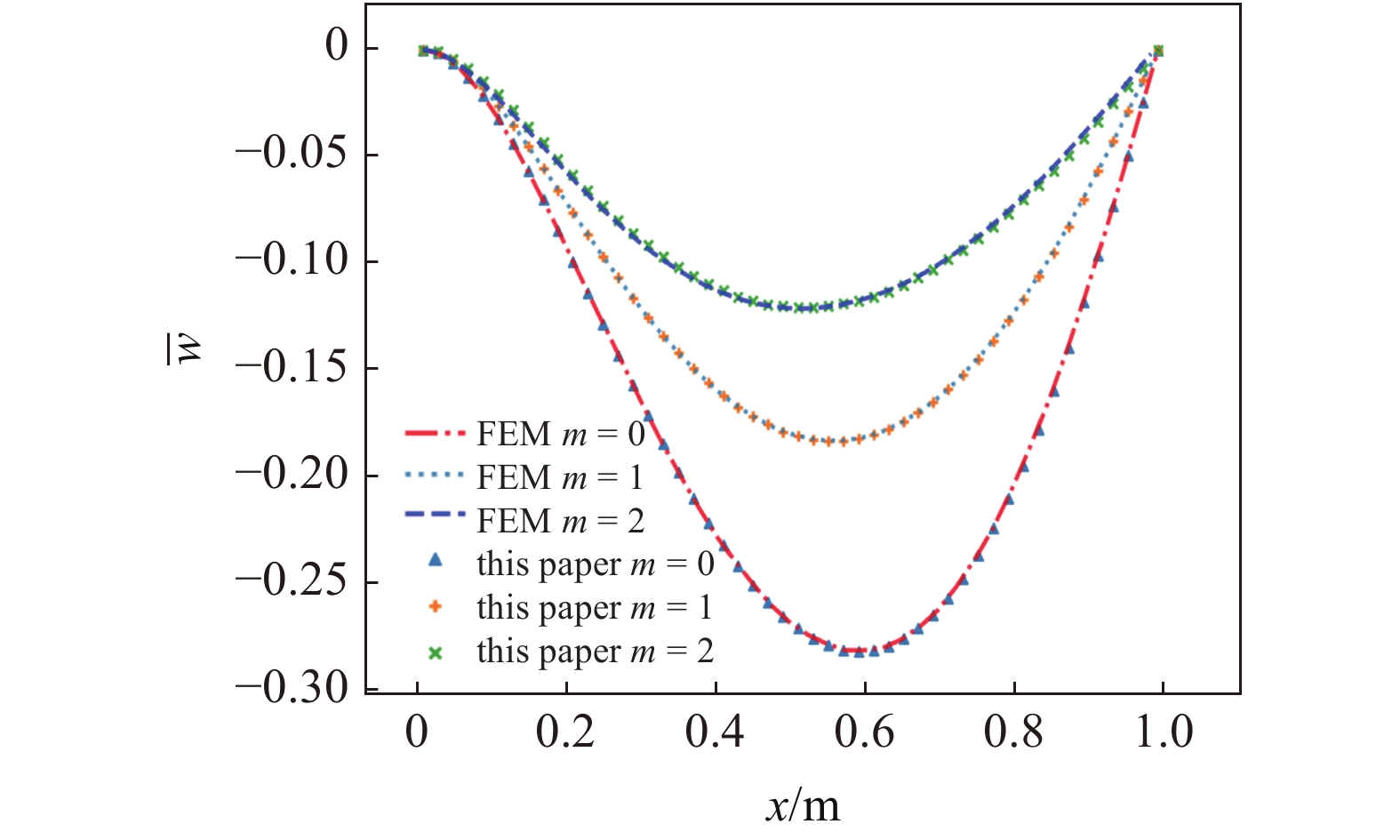onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
不同梯度参数下本文挠度计算结果与有限元对比(y = 0.5 m)



Figure
7.
Comparison of dimensionless deflection calculation results in this paper with FEM when different gradient parameters (y = 0.5 m)



下载:
全尺寸图片
幻灯片




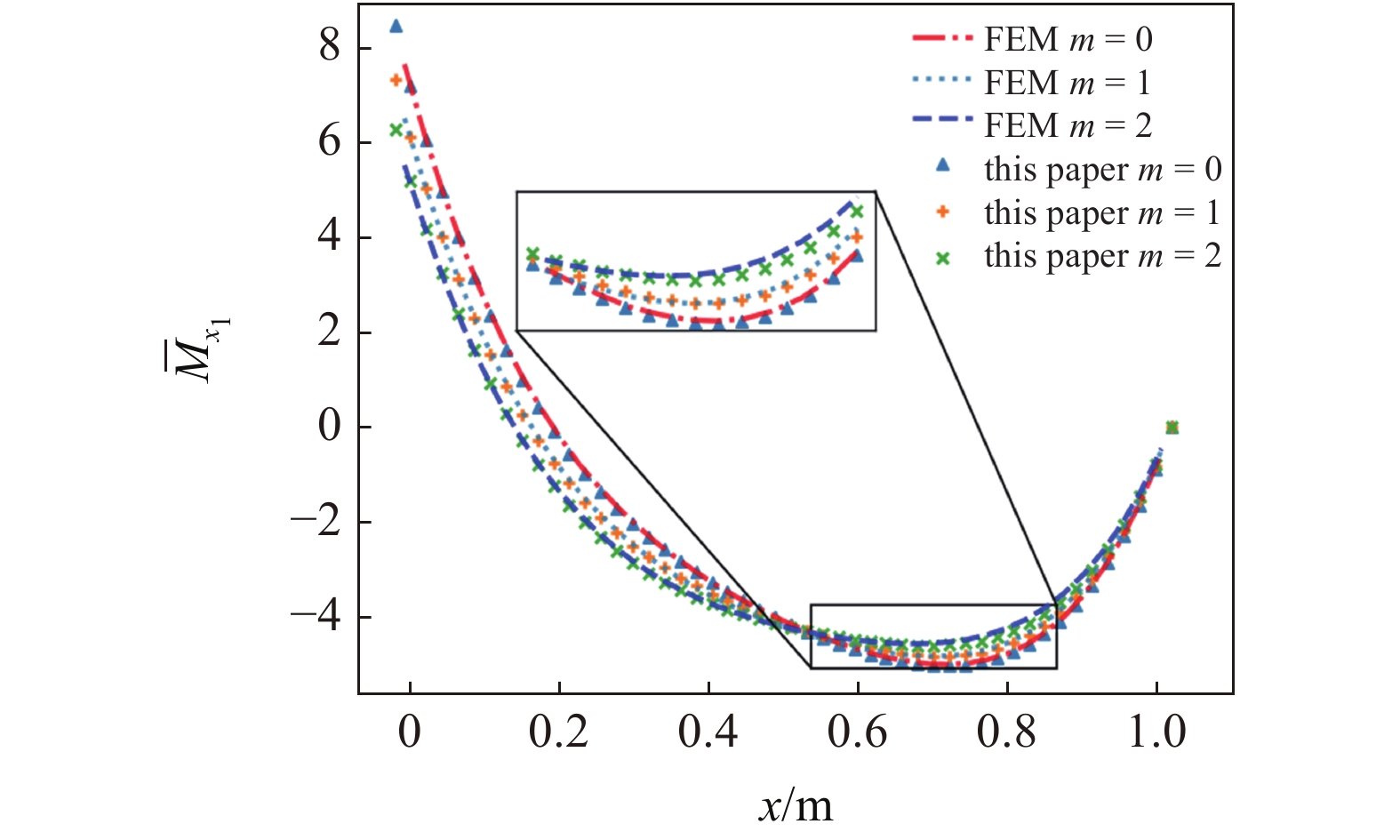onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
不同梯度参数下本文弯矩$ {overline{M}}_{x1} $计算结果与有限元对比(y = 0.5 m)



Figure
8.
Comparison of dimensionless bending moment $ {overline{M}}_{x1} $ calculation results of this paper with FEM when different gradient parameters (y = 0.5 m)



下载:
全尺寸图片
幻灯片



3.3
三角形面内变刚度薄板受线性分布荷载作用


工程中地下掩体结构有时可看作三角形薄板结构. 如图9所示, 厚度为$h$的等边三角形面内变刚度薄板两斜边固支, 水平边作自由边考虑, 弯曲刚度函数为$D(y) = {D_0}left[ {1 + msin left( {dfrac{{text{π}} }{a}y}
ight)}
ight]$, 其中${D_0} = dfrac{{{E_0}h}}{{12left( {1 - {nu ^2}}
ight)}}$, ${E_0}$为常数, $nu = $0.3. 其受线性分布横向荷载 $q(y) = $$ - dfrac{{{q_0}y}}{a}$, 计算m = 0, 0.2, 0.5时薄板的挠度、弯矩.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
三角形面内变刚度薄板



Figure
9.
Thin triangular plate with in-plane stiffness gradient



下载:
全尺寸图片
幻灯片


本算例的挠度网络与弯矩网络分别采用隐藏层层数为6和5, 每层分别具备30和50个神经元的神经网络结构进行计算, 两个模型均采用${x^2}$作为激活函数, 采用Adam优化算法, ${k_{
m{p}}} = 100$, ${N_varOmega } = 560$, ${N_{{varGamma _3}}} = 50$.

本算例的挠度、弯矩试函数为






$$ {begin{array}{*{20}{l}} {{w^*} = wleft( {x,y;{{{{boldsymbol{theta}} }}_{
m{w}}}}
ight){{left[left(sqrt 3 ax + y - a
ight)left( - sqrt 3 ax + y - a
ight)
ight]}^2}} left{ {{M_x}^*,{M_{xy}}^*,{M_y}^*}
ight} = hfill qquad left{ {{M_x}left( {x,y;{{{{boldsymbol{theta}} }}_{
m{m}}}}
ight),{M_{xy}}left( {x,y;{{boldsymbol{theta }}_{
m{m}}}}
ight)y,{M_y}left( {x,y;{{boldsymbol{theta }}_{
m{m}}}}
ight)y}
ight} hfill end{array}} $$

此时自由边的应力边界条件并未精确满足, 故在误差函数中引入自由边的剪力误差项






$$ MS{E_{{varGamma _3}}} = frac{1}{{{N_{{varGamma _3}}}}}sumlimits_{i = 1}^{{N_{{varGamma _3}}}} {{{left| {frac{{partial {M_y}left( {x,y;{{boldsymbol{theta}} _{
m{m}}}}
ight)}}{{partial y}} + frac{{partial {M_{xy}}left( {x,y;{{boldsymbol{theta}} _{
m{m}}}}
ight)}}{{partial x}}}
ight|}^2}} $$

根据式(16), 误差函数为






$$ Cleft( {{{boldsymbol{theta }}_w},{{boldsymbol{theta }}_{{m}}}}
ight) = MS{E_varOmega } + {k_{
m{p}}}MS{E_{
m{p}}} + {k_3}MS{E_{{varGamma _3}}} $$

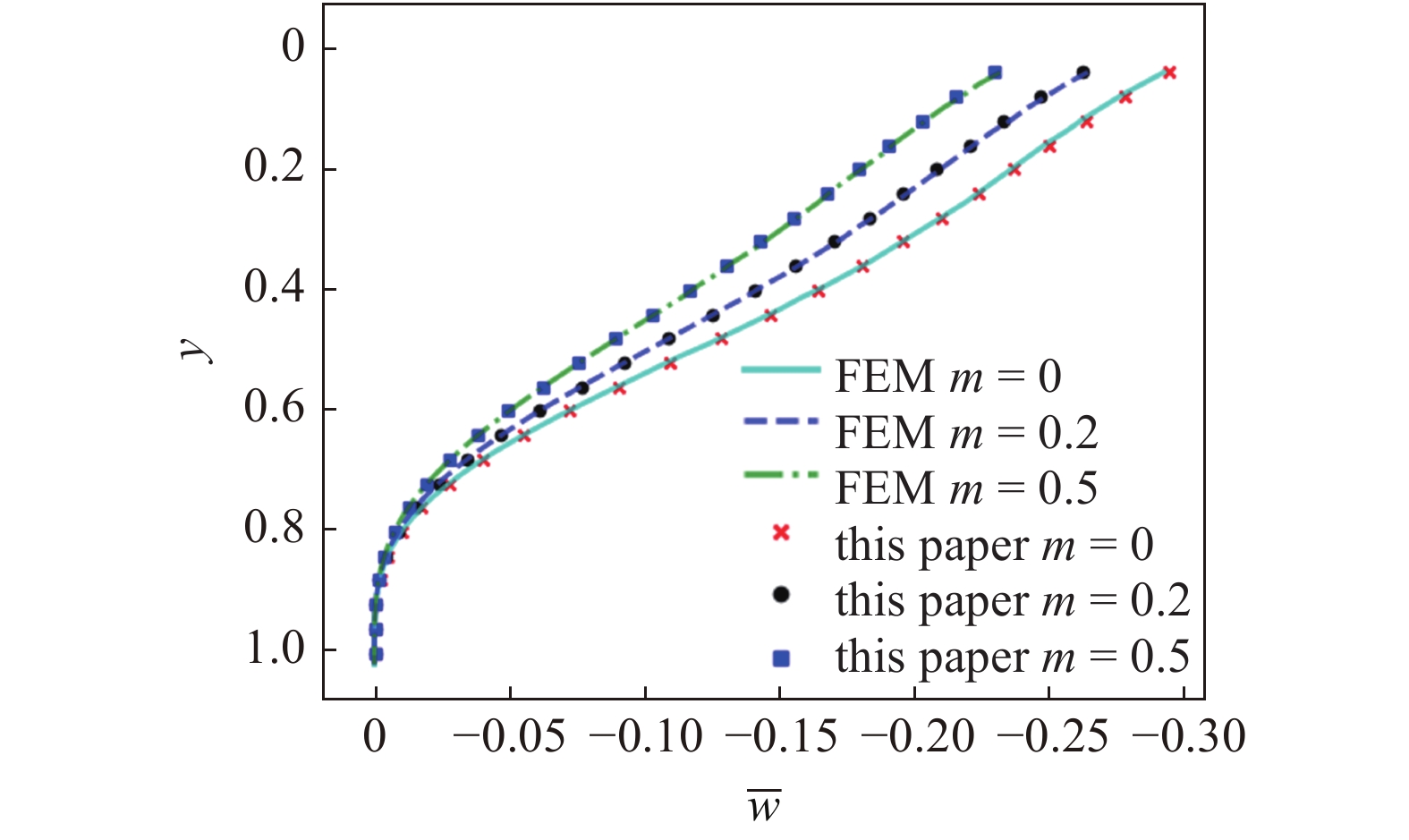
神经网络训练收敛后, 采用无量纲计算公式$bar w = dfrac{{{{10}^3}{D_0}}}{{{q_0}{a^4}}}w$, $bar M = dfrac{{{{10}^2}M{D_0}}}{{{q_0}{a^2}}}$, 将挠度网络及弯矩网络的输出无量纲化后与有限元计算结果对比, 有限元采用DKT薄板单元进行求解, 有限元计算收敛时单元总数为3032, 对比结果如图10 ~ 图12所示. 可以看出, 本文方法求解结果与有限元计算结果一致, 同时由于对挠度、弯矩输出进行了构造, 使得大部分边界条件严格满足, 也可看出弯矩在边界与边界交接处的收敛情况良好, 在一定程度上, 本文方法可避免由于边界处误差难以收敛而带来的影响.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
三角形面内变刚度薄板沿轴线x = 0上的挠度$ bar {w} $分布



Figure
10.
Dimensionless deflection variation of thin triangular plate with in-plane stiffness gradient along axis x = 0



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-11.jpg'"
class="figure_img
figure_type2 ccc " id="Figure11" />



图
11
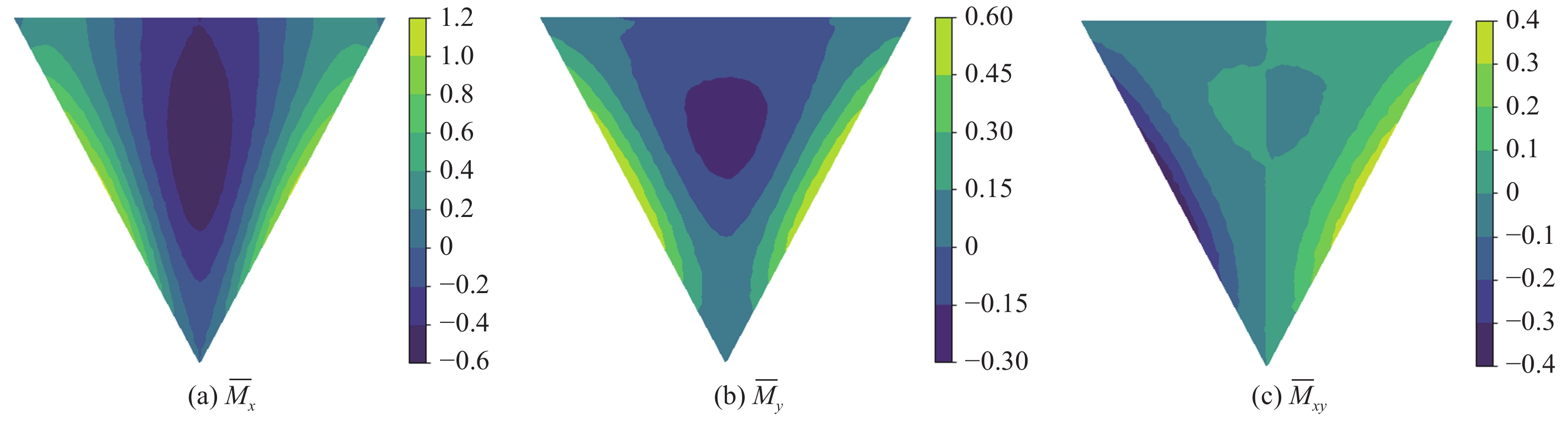
m = 0.2时三角形面内变刚度薄板弯矩的有限元计算结果



Figure
11.
Finite element calculation of bending moment of thin plate with triangular in-plane variable stiffness (m = 0.2)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-12.jpg'"
class="figure_img
figure_type2 ccc " id="Figure12" />



图
12
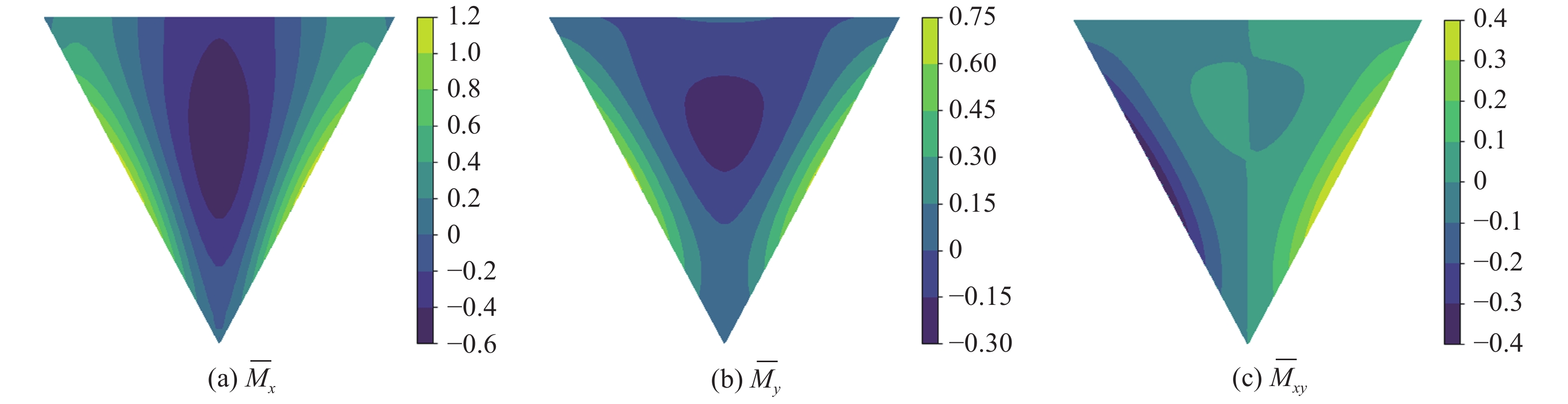
m = 0.2时三角形面内变刚度薄板弯矩的本文计算结果



Figure
12.
Neural network method calculation of bending moment of thin plate with triangular in-plane variable stiffness (m = 0.2)



下载:
全尺寸图片
幻灯片



4.
本文方法计算效率及其有限元对比分析


以$T$表示算例各个工况下的平均用时, ${T^prime }$表示各个工况下误差函数的构建及其梯度计算的平均耗时, 本文各算例求解时迭代所需的数据点数及所需的平均时间、内存如表3所示, 可看出本文误差函数的构建及其梯度的求解占据了神经网络训练总时长的70%左右.

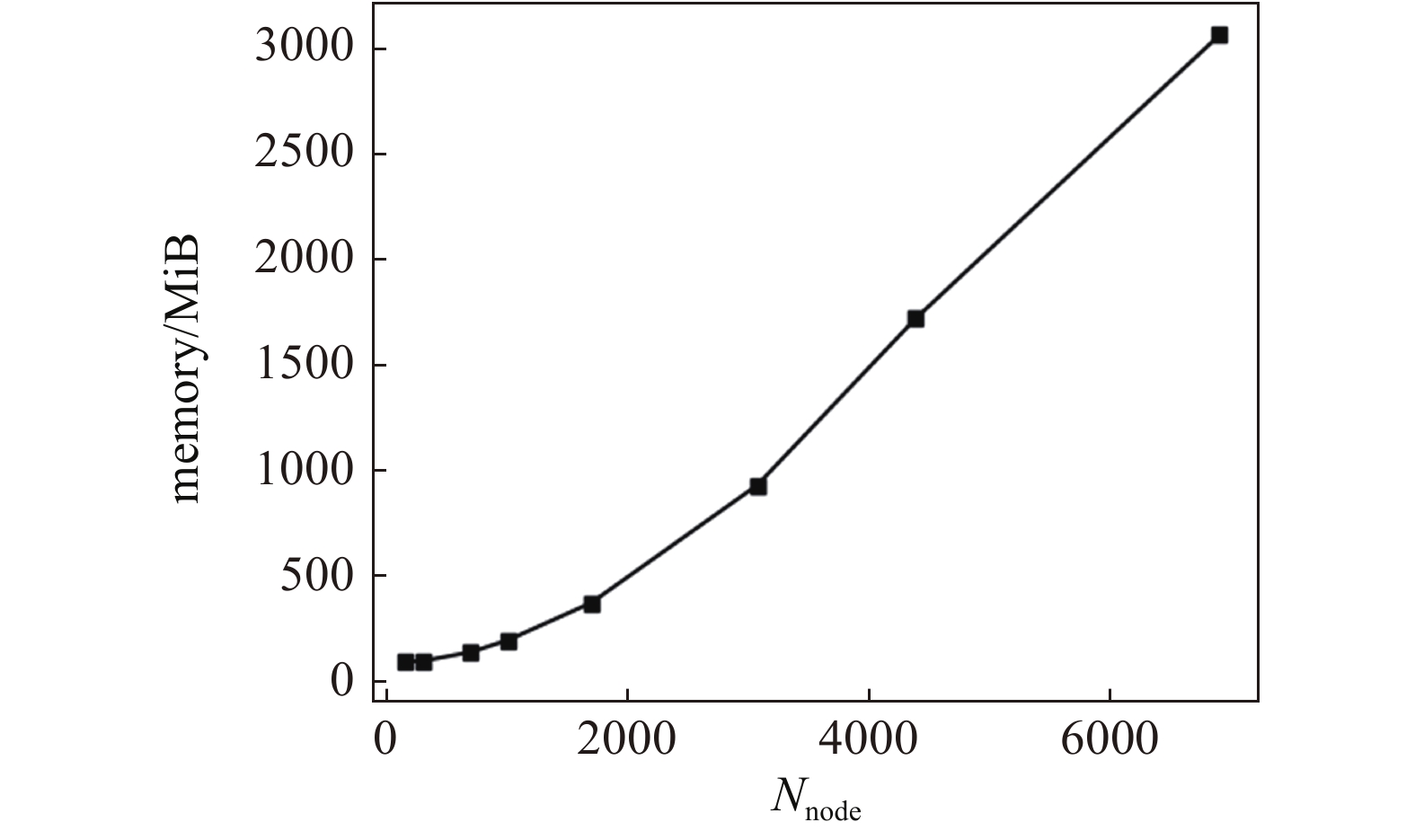
本文的有限元求解程序采用python语言进行编写, 选用每个节点有3个自由度的薄板弯曲单元计算, 刚度矩阵以 compressed sparse column (CSC)格式的稀疏矩阵存储, 利用科学计算库scipy中的线性求解器求解刚度方程. 根据有限元解答的最小挠度判断有限元解答是否收敛, 算例2和算例3中各个工况下有限元计算收敛时的节点数目如表4所示, 本文有限元计算所需的节点数与计算所需内存的关系如图13所示.




表
3
本文各算例求解所需的数据点数、内存、时间



Table
3.
The number of training data points, computational memory and computing time of numerical examples in this paper



table_type2 ">
Numerical exampleNumber of data pointsComputational memory/MiB$T(s)$${T^prime }(s)$${T^prime }(s)/T(s)$/%
1560121.3551.99374.6667.8
2450139.4673.81475.2270.5
3610169.3646.14479.8174.3





下载:
导出CSV
|显示表格






表
4
算例2、算例3的有限元求解收敛所需节点数目



Table
4.
The number of nodes needed for the convergence of the finite element solution of numerical example 2 and 3



table_type1 ">
Numerical examplemNumber of nodes
20441
1841
21681
30305
0.21331
0.51604





下载:
导出CSV
|显示表格




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
有限元计算所需内存与节点数的关系(薄板单元)



Figure
13.
The relationship between the number of nodes and the memory needed in finite element calculation using thin plate bending element



下载:
全尺寸图片
幻灯片


可以发现有限元解答收敛时所需的节点(网格)数目随着梯度系数的增大而增大, 节点数与所需内存并非呈现线性关系, 节点数的增多会导致所需计算内存的急剧增大, 而神经网络方法在梯度系数增大时, 在单次迭代时仍可以较少的数据点进行迭代, 这使得本文方法在求解时所需内存较小. 在时间上, 以算例3中梯度系数m = 0.5为例, 此时有限元求解收敛时, 所需内存为291.5 MiB, 刚度方程从组装到求解用时1.798 s, 可以看出本文解法的求解速度明显慢于有限元, 一方面是由于本文方法求解的是强形式的偏微分控制方程, 与求解弱形式的方程相比, 往往需要更多的迭代次数, 另一方面, 神经网络方法是一类以数据为驱动的解法, 在求解过程中需要往复迭代, 而对于本文研究的线性问题, 有限元仅需求解一次刚度方程.


5.
网络耦合系数$ {k}_{{
m{p}}} $、隐藏层层数与神经元个数、激活函数对网络收敛性的影响分析



5.1
网络耦合系数${k_{
m{p}}}$


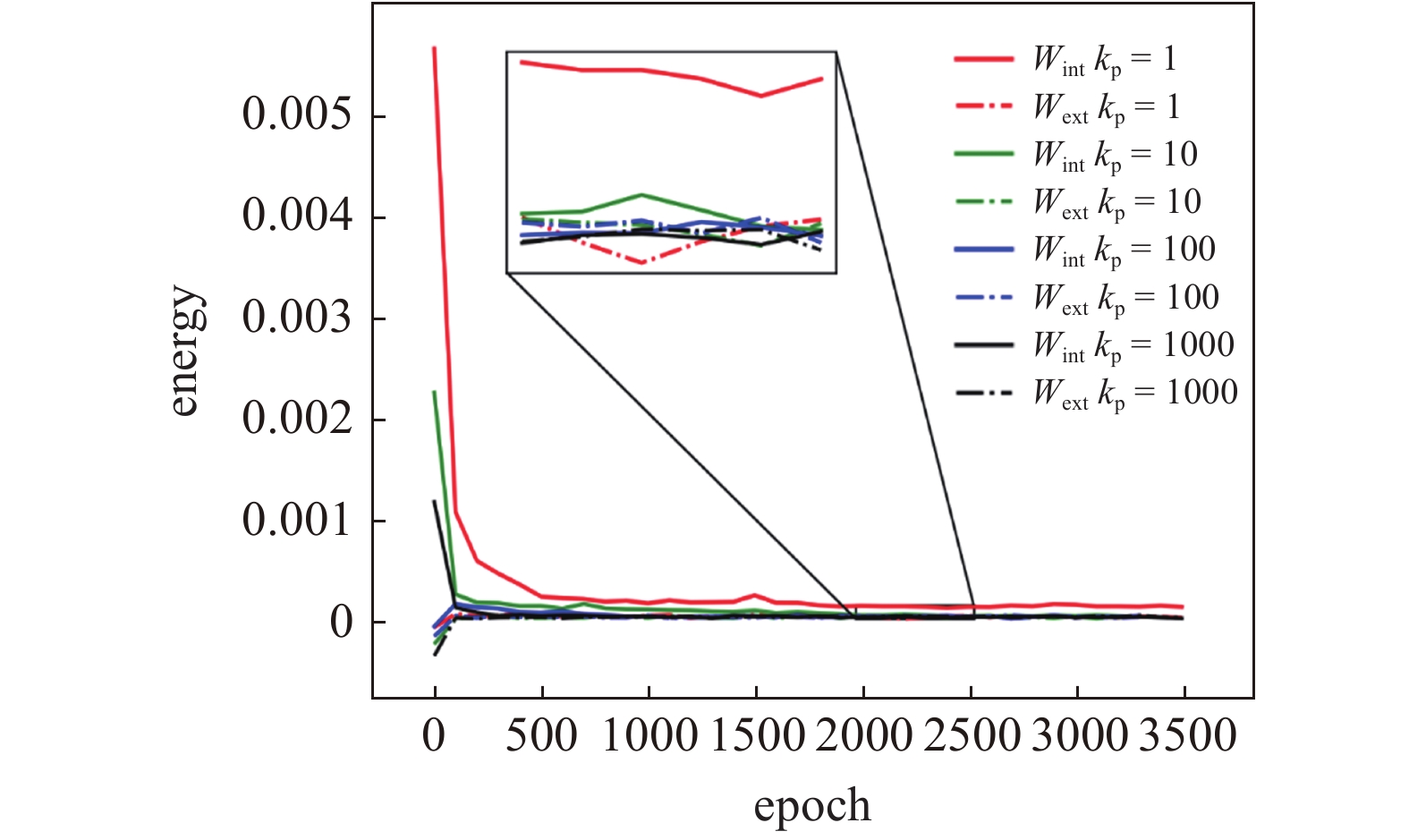
本文模型由于引入两个神经网络模型对面内变刚度薄板弯曲问题进行计算, 与采用单网络的神经网络方法相比, 在训练过程中需考虑网络之间的耦合误差, 本文引入网络耦合系数$ {k}_{{
m{p}}} $以加强网络之间的耦合, ${k_{
m{p}}}$的取值过小会导致网络耦合不佳, 过大则可能会导致训练不收敛, 因此需要对${k}_{{
m{p}}}$的取值进行讨论, 选取${k_{
m{p}}}$=1, 10, 100, 1000四种情况对算例2进行计算分析(梯度系数m = 2), 以网络训练时薄板的变形能、外力功变化情况衡量不同${k_{
m{p}}}$下本文模型的训练效果.

薄板变形能计算公式为







$$ {W_{{
m{int}}}} = frac{1}{2}int_varOmega {{{boldsymbol{k}}^{
m{T}}}} {boldsymbol{M}}{text{d}}varOmega = frac{1}{2}int_varOmega {{{boldsymbol{k}}^{
m{T}}}} {boldsymbol{Dk}}{text{d}}varOmega $$
(27)

其中







$$ {boldsymbol{D}} = D(x,y)left[ {begin{array}{*{20}{c}} 1&v&0 v&1&0 0&0&{(1 - v)/2} end{array}}
ight] $$
(28)







$$ {boldsymbol{k}} = left{ {begin{array}{*{20}{c}} {{k_x}} {{k_y}} {{k_{xy}}} end{array}}
ight} = - left{ {begin{array}{*{20}{c}} {dfrac{{{partial ^2}w}}{{partial {x^2}}}} {dfrac{{{partial ^2}w}}{{partial {y^2}}}} {2dfrac{{{partial ^2}w}}{{partial xpartial y}}} end{array}}
ight} $$
(29)

$ {boldsymbol{k}} $为根据弯矩网络的输出由式(8)和式(9)计算所得.

外力所作实功为







$$ {W}_{text{ext }}=frac{1}{2}{displaystyle {int }_{varOmega }q}w text{d}varOmega $$
(30)

其则根据挠度网络的输出值计算.

采用高斯积分, 由上述公式计算神经网络训练时薄板的变形能、应变能的变化情况, 根据挠度网络输出计算外力实功${W_{{
m{ext}}}}$, 根据弯矩网络输出计算薄板变形能${W_{{
m{int}}}}$. 当神经网络解答收敛时, 根据能量原理, 其外力实功应与变形能相等. 此时各工况下的变形能与外力实功在神经网络训练过程中的变化情况如图14所示. 可以看出, 随着训练的进行, 外力实功与薄板的变形能逐渐收敛, 在各个工况下, 变形能的收敛速度相比于外力功要慢, 进而说明挠度网络收敛速度较快. 当${k_{
m{p}}}$=1时, 此时薄板变形能与外力功收敛时, 两者相差较大; 而随着${k}_{{
m{p}}}$的增大, 神经网络计算的变形能收敛加快, 此时当变形能与外力功收敛时, 两者之间的差别减小, 而当${k_{
m{p}}}$=1000时, 其对训练的影响与${k_{
m{p}}}$=100时差别不大, 在实际计算中, 该系数不能过大, 过大会导致神经网络学习不到正确的特征, 进而导致训练不收敛.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
神经网络训练时不同${k_{
m{p}}}$下薄板变形能与外力功的变化情况



Figure
14.
Changes in the deformation energy and the external force work during the training process with different ${k_{
m{p}}}$



下载:
全尺寸图片
幻灯片



5.2
隐藏层层数与神经元个数


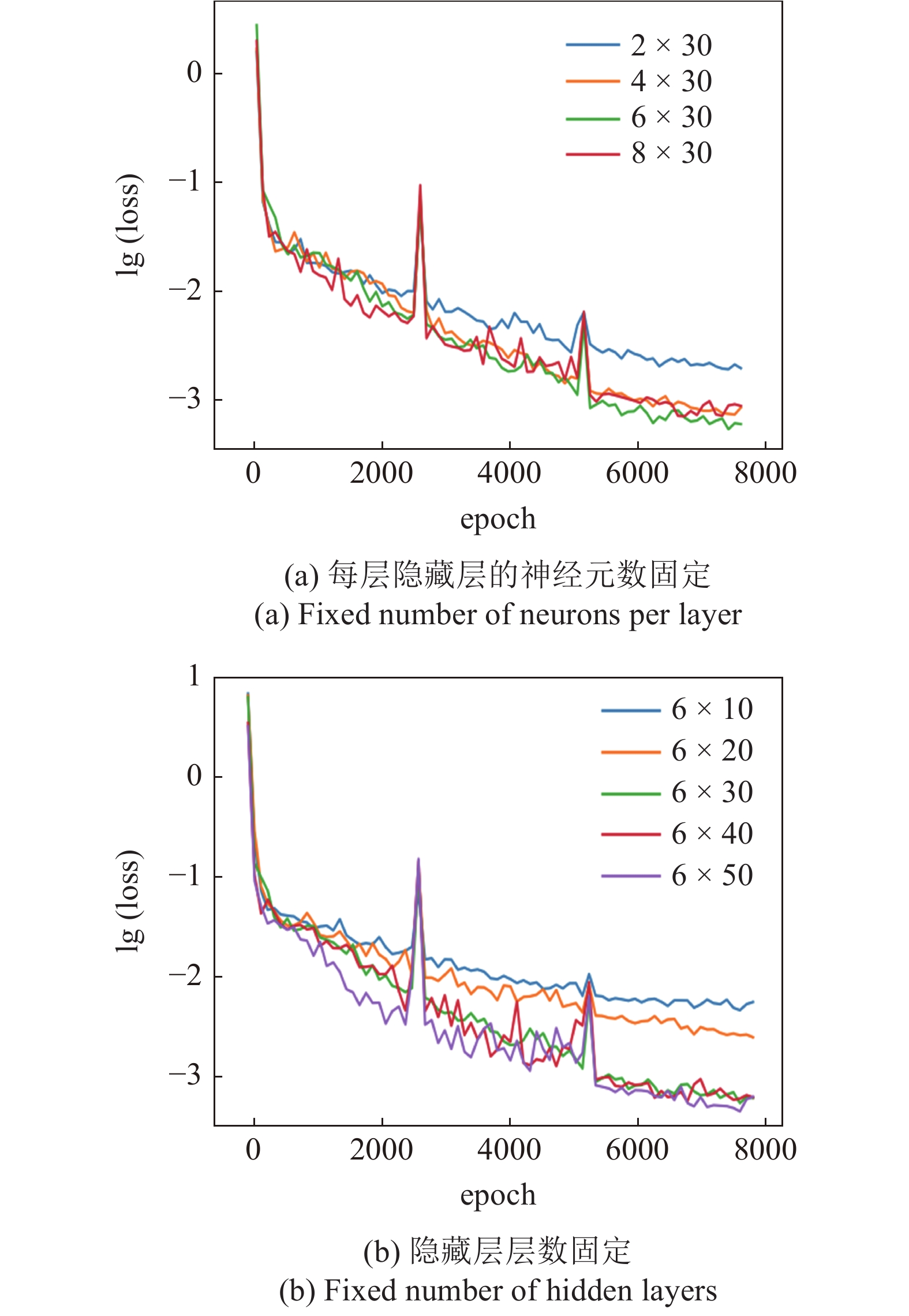
隐藏层层数与每层的神经元个数的选取均会影响到神经网络的训练效率, 不失一般性, 在其他计算参数不变的情况下, 本节选取算例2中m = 2的情况分别讨论隐藏层层数、神经元个数的改变对计算过程中误差函数收敛情况的影响, 计算结果如图15所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />



图
15
隐藏层数、每层神经元个数对计算误差的收敛影响对比



Figure
15.
Comparison of the effects of different number of hidden layers and neurons on the convergence of loss function



下载:
全尺寸图片
幻灯片


可以发现, 在一定程度内误差函数的收敛速度随着网络层数、隐藏层每层神经元数的增大而加快, 当两者都增大到一定程度时, 此时误差的收敛速度会趋向于一个“饱和”状态. 适当地增加层数或神经元的个数有利于误差函数的收敛, 目前在利用神经网络方法求解偏微分方程的研究中, 在两者的选取上仍带有一定的经验性. 结合上述的计算结果, 考虑到计算机硬件能力的限制, 本文算例的隐藏层层数在4 ~ 6层间选取, 每层神经元数目在30 ~ 50之间选取.


5.3
激活函数


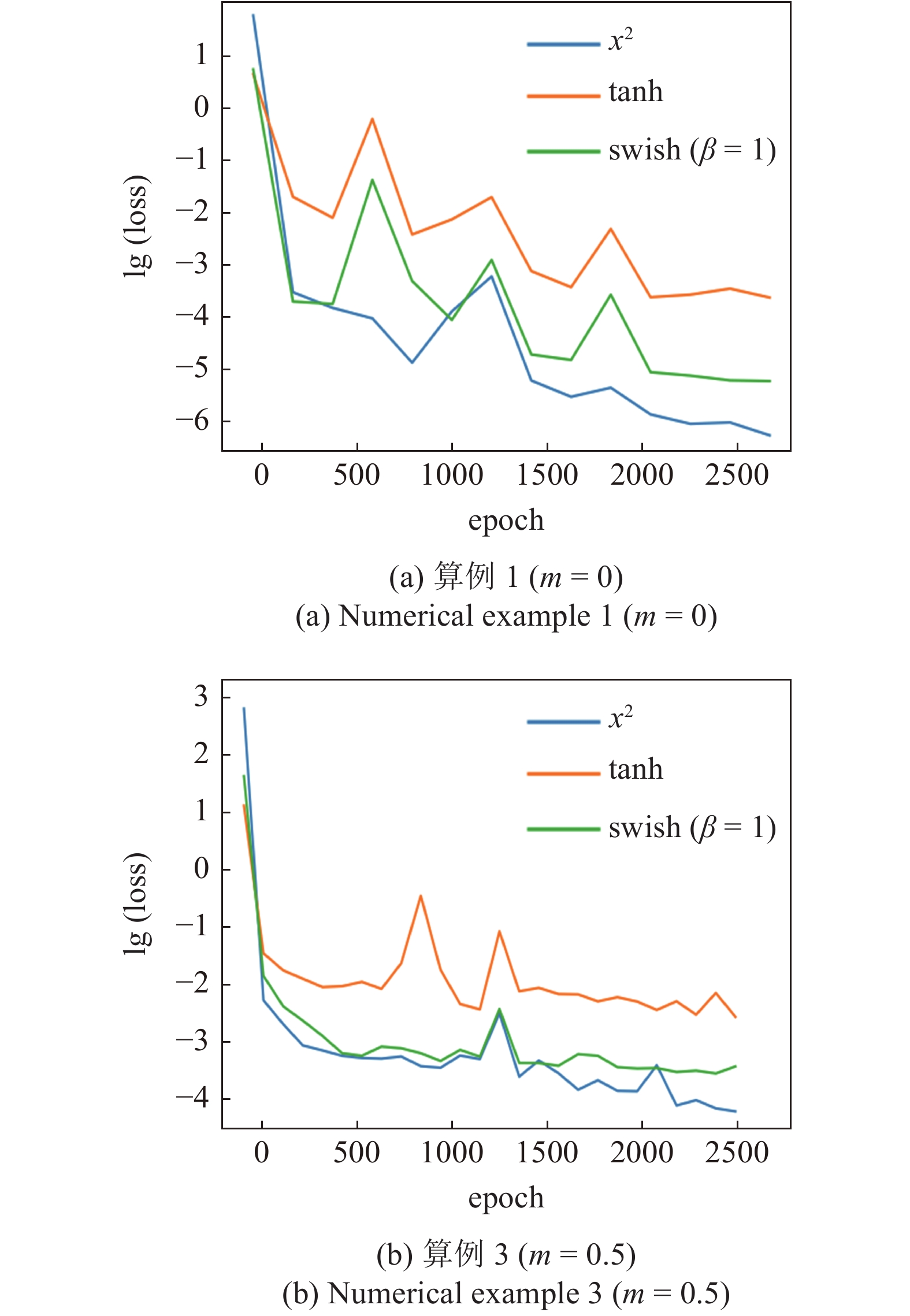
在神经网络的训练过程中, 有多种非线性激活函数可以选择, 非线性的激活函数是使神经网络具备拟合非线性函数能力的重要原因, 常用的激活函数有Tanh, ReLU, Sigmoid, Swish函数等. 为讨论激活函数对神经网络训练的影响, 其余计算参数不变, 本节选取${x^2}$作为激活函数并与Tanh, Swish函数进行对比分析, 对算例1、算例3进行计算, 训练过程中的误差走向如图16所示. 在误差函数的收敛速度上, ${x^2}$优于Tanh, Swish函数, 同时由于其函数形式较为简单, 在自动微分计算中其所需计算量较小. 本文经验表明, 在薄板弯曲问题的求解上, 采用多项式函数${x^2}$作为激活函数可加快神经网络的收敛.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-273-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />



图
16
不同的激活函数对计算误差的收敛影响对比



Figure
16.
Comparison of the effects of different activation functions on the convergence of loss function



下载:
全尺寸图片
幻灯片



6.
结论与展望


本文基于深度学习技术与强形式的求解方案建立了一种直角坐标下求解面内变刚度薄板弯曲问题的神经网络方法, 通过几个算例分析, 得出以下结论:

(1)本文解答与理论解、有限元解吻合, 证明了本文方法在求解面内变刚度薄板弯曲问题上的正确性, 本文的神经网络模型不需要对弯曲刚度函数求偏导, 其适应性更强, 同时在薄板的位移边界条件、应力边界条件的施加上较为方便.

(2)本文方法属于强形式的数值解法, 其计算所得结果具备连续性与可导性. 理论上, 本文方法可以求解弹性模量以及厚度在面内连续变化的薄板弯曲问题. 弯矩网络的求解受到梯度系数的影响, 在梯度变化较大处弯矩网络的求解精度受到一定的影响, 但对挠度网络的求解精度影响不大.

(3)由于神经网络方法为迭代类解法, 本文方法在薄板线性弯曲问题求解上的收敛速度较有限元慢, 但其计算所需内存较小. 通过本文的模型结构可看出, 神经网络方法具备相当大的灵活性, 根据这一特点, 可进一步发展求解面内变刚度功能梯度薄板非线性弯曲问题的神经网络方法, 神经网络方法在非线性问题的求解中具备潜在优势.

(4)本文模型仍存在优化空间: 一方面在本文模型的训练过程中, 误差函数及其梯度的计算在整个训练过程中占据大部分的时间, 可以考虑优化误差函数的构建过程, 如引入有限元中形函数的思想对算法进行优化; 另一方面为了使得挠度、弯矩网络具备较强的表达能力, 本文模型采用了两个具有独立参数的网络进行计算, 这导致了本文模型的训练参数较多, 为此后续优化中可将本文的两个网络合并为一个网络(2个输入, 4个输出), 对网络结构进行改良, 以减少训练参数.

相关话题/计算 网络 数据 方案 图片
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 一种新的玻尔兹曼方程可计算模型构造与分析
    引言近年来,随着对临近空间战略意义认识的加深,各航空航天大国发展了众多临近空间飞行器.为满足长航时、大载荷、高超声速巡航等需求,这类临近空间飞行器通常整体尺寸较大,各部件间差异显著,飞行过程会出现多物理多场耦合、多流区共存的多尺度复杂流动现象,传统的数值模拟方法如基于宏观连续介质假设的纳维?斯托克斯 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 数据驱动印度洋海域全局动力学研究
    引言海洋系统天然受到多种环境因素(风速、温度、海水含盐量等)、人类活动和天体运动等不确定扰动的影响,导致其洋流运动复杂而多样[1-2].然而,一些观测和研究发现,其内部蕴含着能够对洋流的运动方向和趋势起限制和导向作用的复杂动力结构和特征,影响甚至主导了表面漂浮物的流动形式和演化路径.例如,经志友等[ ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 页岩凝析气藏相平衡的快速准确计算方法
    引言随着以煤炭、石油和木柴为代表的传统能源消耗带来的巨量的空气污染日益引起全社会的关注,天然气作为一种相对较为清洁的能源得到了广泛的重视[1].近年来在非常规油气藏勘探和开发技术上的迅猛发展,使得具有巨大潜在储量但一直得不到有效开发的以页岩气为代表的非常规油气资源成为了投资热点和研究焦点[2].中国 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 循环神经网络在智能天平研究中的应用
    引言随着航空航天技术的不断发展,高超声速技术受到各个航空航天大国的广泛关注和深入研究,其科学问题具有重要的战略意义[1].对于高超声速飞行器气动外形布局设计和优化问题,高精度气动力测量试验起到决定性作用.激波风洞测力试验可以为高温真实气体效应的研究提供可靠的数据,同时为我国高超声速飞行器研究提供关键 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于Darcy-Stokes耦合模型的多孔介质颗粒悬浮液等效黏性系数计算
    引言颗粒悬浮液广泛存在于自然界及工程应用领域,其黏性特征对悬浮液的流动行为有着重要的影响[1-4].早在1905年,Einstein[5]就研究了低浓度条件下球形固体颗粒对流体黏性的影响,给出了悬浮液等效黏度系数计算的一个强有力的理论框架,并得到了低浓度球形颗粒悬浮液的著名的Einstein黏性公式 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于神经网络的差分方程快速求解方法
    引言近年来,人工神经网络(artificial?neural?networks,ANN),尤其是深度神经网络(deep?neural?networks,DNN)因其在处理和预测高维复杂系统方面的优异能力而被广泛应用于自然语言处理[1]、计算机视觉[2]与图像处理[3]等领域.此外,深度神经网络凭借其 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • DVC中内部散斑质量评价及计算体素点的优化选择
    引言数字体图像相关方法(digitalvolumecorrelation,DVC)是二维数字图像相关方法(two-dimensionaldigitalimagecorrelation,2DDIC)在三维体图像上的拓展.通过比较体成像设备获取的被测试样变形前后数字体图像,该方法可测量物体内部三维全场变 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于人工神经网络的声子晶体逆向设计
    引言声子晶体是一种新型人工周期性复合材料,具有独特的禁带特性,即声波或弹性波在声子晶体中传播时,由于受到周期性结构中波的散射或局部共振的作用,在某些频段范围即带隙内无法传播[1-4].该特性使得声子晶体在工程减振降噪领域具有巨大的应用潜力.声子晶体的拓扑结构和组分材料的属性决定了其带隙特性.因此,根 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于数据驱动的流场控制方程的稀疏识别1)
    江昊,王伯福,卢志明,2)上海大学,力学与工程科学学院,上海市应用数学和力学研究所,上海200072DATA-DRIVENSPARSEIDENTIFICATIONOFGOVERNINGEQUATIONSFORFLUIDDYNAMICS1)JiangHao,WangBofu,LuZhiming,2)S ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于组合神经网络的雷诺平均湍流模型 多次修正方法1)
    张珍*,&,叶舒然*,&,岳杰顺*,&,王一伟,*,&,2),黄晨光*,&,***中国科学院力学研究所流固耦合系统力学重点实验室,北京100190&中国科学院大学工程科学学院,北京100049**中国科学 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.