引 言
海洋系统天然受到多种环境因素(风速、温度、海水含盐量等)、人类活动和天体运动等不确定扰动的影响, 导致其洋流运动复杂而多样[1-2]. 然而, 一些观测和研究发现, 其内部蕴含着能够对洋流的运动方向和趋势起限制和导向作用的复杂动力结构和特征, 影响甚至主导了表面漂浮物的流动形式和演化路径. 例如, 经志友等[3-4]观测发现南海内部存在自循环环流结构, 以及跨海域间的贯穿流结构. 这种暗藏结构在动力学上表现为对周围流动体的吸引或排斥性效应, 并能够引起流场的涡漩, 进而可能导致表面漂浮物在某些水域的长期或短期聚集. Serra等[5]验证了海洋表面暂态吸引性的存在, 并展示了这种内在特征结构在海洋救援中的积极作用. 由此, 需全面系统地揭示这类系统复杂的内在结构状态和特性, 这是深入认识并利用海洋规律的关键.
海洋作为典型的强非线性随机系统, 对其洋流动态演化和动力结构特性的研究, 主要从数值模拟和解析分析两方面开展. 前者大多以水动力经典方程(如: Langevin方程、Fokker?Planck方程、Navier?Stokes方法和对流扩散方程等)为基础[6-7], 能利用数值算法针对复杂情况开展模拟, 但通常计算难度较大. 而传统对简化模型的解析分析简单高效, 但仅能从机理上研究特定条件下的局部定性行为(如海洋吸引结构的存在条件[8]和概率跃迁机理[9]), 却无法准确地描述耦合因素的影响和实际特征, 且计算结果依赖于模型简化的合理性和准确性. 遥感大数据的支撑大大提高了解析法的预测精度, 使其在工程应用上具有更广阔的应用前景[10-12]. 如薛红娟和顾耀林[13]通过对数据模型的拓扑分析, 研究了海洋涡旋的动力学特征及其形貌. 此外, 一些研究将数据的互相关信息[14]、主元分量[15]、嵌入维数[16]等作为刻画海洋系统动力特征的重要指标, 并结合实验浮漂轨迹及其统计分布[17], 利用贝叶斯估计[18]、机器学习[19]等数据驱动方法, 开海洋展表面漂浮物定位和轨迹预测. 海洋系统的内在动力结构十分复杂且主导着其动力学响应和趋势, 但现有的方法大多将数据看作是离散的轨迹信息, 仅反映了时间序列的非线性关系或数据的概率特征, 缺乏对系统动态演化行为与内在结构属性间联系的深入研究, 亟待进一步以数据为基础从全局动力学角度揭示其内在特征及其影响机理.
本文将数据驱动广义胞映射方法应用于海洋动力学的分析中, 通过建立浮漂运动状态间的映射关系, 形成表征海洋洋流运动特征的一步转移概率矩阵, 着重分析印度洋洋流的长期和短期全局动力结构和演化路径, 以期为该区域的研究海洋运动规律和污染物扩散、优化船舶航线、实施海洋救援等提供指导和依据, 也致力于推动胞映射方法在工程领域的应用和发展.
1.
数据来源和分析方法
1.1
数据来源
文中以实际测量数据为研究基础, 重点关注于印度洋附近海域(东经15° ~ 120°, 南纬60° ~ 北纬30°)洋流的全局动态特征及其引发的响应规律. 数据来源于美国国家海洋与大气管理局过去30年(1979—2019年)实施的全球漂流计划项目(Global Drifter Program). 该项目在全球海洋表面共部署了超过2.4万个电子浮漂, 并通过卫星每6小时监测浮漂器的状态数据. 目前, 初始部署在印度洋附近海域的浮漂数目有3680个, 而与该区域直接相关的浮漂则达到5006个, 如图1所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-218-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
印度洋海域部署的浮漂位置(黑色“*”)和运动轨迹(彩色实线)
Figure
1.
The initial locations and trajectories of drifters deployed in the Indian Ocean
下载: 全尺寸图片
幻灯片
通过对采集的时域数据预处理后, 数据结构可表示为如下形式
$$left.begin{split} &{boldsymbol{Data}} = left( {{{boldsymbol{Y}}^1},{{boldsymbol{Y}}^2}, cdots,{{boldsymbol{Y}}^{{N_{ m{d}}}}}} ight) & {{boldsymbol{Y}}^r} = left( {{boldsymbol{x}}_1^r,;{boldsymbol{x}}_2^r, cdots,{boldsymbol{x}}_{{N_{ m{r}}}}^r} ight),;;;;;;;r = 1,2, cdots,{N_{ m{d}}} end{split} ight}$$  | (1) |
式中,
1.2
数据驱动模型和分析方法
胞映射方法是开展复杂系统全局动力学分析的有效手段[20-24]. 该方法的基本思想是将连续的D维状态空间RD离散为一个在给定尺度下的胞状态空间, 且覆盖感兴趣区域的每个胞通过Nc个整数连续编号. 通过识别数据中所携带的动力学信息(如周期、主维数等), 并将其转变为离散空间中各胞之间的有向映射. 此时, 随机扰动下原动力系统的概率演化可通过胞空间中Markov过程描述[25]
$${boldsymbol{p}}(k + 1) = {boldsymbol{P}}(k){boldsymbol{p}}(k)$$  | (2) |
式中, p(k)为第k步下胞的概率向量, 其分量pi(k)则代表在该步映射下第i个胞的状态概率. P(k)表示动力系统的一步转移概率矩阵, 其元素Pij表示从第j个胞到第i个像胞的转移概率, 可通过如下公式计算
$$left.begin{split} &{P_{ij}} = int_{} {p(left. {{boldsymbol{x}},t} ight|{{boldsymbol{x}}_j},{t_0}){ m{d}}{boldsymbol{x}}} = int_{{C_i}} {p(left. {{boldsymbol{x}},tau } ight|{{boldsymbol{x}}_j},0){ m{d}}{boldsymbol{x}}} = &qquadsumlimits_{s = 1}^{{S_{ij}}} {p(left. {{boldsymbol{x}},tau } ight|{{boldsymbol{x}}_j},0)} & {p_i}(k) = int_{{C_i}}^{} {p({boldsymbol{x}},ktau ){ m{d}}{boldsymbol{x}}} end{split} ight}$$  | (3) |
式中, τ = t ? t0表示一个映射步长, Ci为在空间中RD第i个胞所在的区域, p(x, τ | xj, 0)表示从第j个胞映射到像胞的一步转移概率向量.
在数据驱动胞映射方法中[26], 通过选择一个给定的时间间隔(映射步长τ)对浮漂轨迹重新采样, 以此实现映射过程, 进而从数据中获得转移概率矩阵的近似估计. 从式(1)中, 第r个浮漂映射采样点可表示为
$$begin{split} {{boldsymbol{S}}^r}{ m{ = }}&left( {{boldsymbol{x}}_1^r,;{boldsymbol{x}}_{1 + n}^r, cdots,{boldsymbol{x}}_{1 + (i - 1)n}^r, cdots } ight);;;;;; & i = 1,2, cdots,{N_{ m{m}}},;;;;;r = 1,2, cdots,{N_{ m{d}}}end{split}$$  | (4) |
式中,
m{m}}}=mathrm{f}mathrm{l}mathrm{o}mathrm{o}mathrm{r}left(dfrac{{N}_{{
m{r}}}-1}{n}+1
ight)$
$$ begin{split} &{boldsymbol{x}}_{1 + in}^r = tilde P({boldsymbol{x}}_{1 + (i - 1)n}^r); &qquadi = 1,2, cdots,{N_{ m{m}}},;;;;;r = 1,2, cdots,{N_{ m{d}}}end{split} $$  | (5) |
式中,
ight)$
在式(5)的基础上, 通过确定所有浮漂的轨迹点
$${Z_{k + 1}} = tilde C({Z_k}),;;;;k = 1,2, cdots,{N_{ m{m}}}cdot {N_{ m{d}}}$$  | (6) |
此时, 数据驱动的转移概率Pij可以通过在胞空间中数值统计从j个胞到第i个胞的样本概率
真实海洋环境中, 海洋表面的洋流演化和变迁与当地海域季节性的气候变化、大洋环流等因素密切相关[27-29], 例如, 在北半球冬季, 当季风向西南吹时, 海洋表面洋流从印尼群岛附近向阿拉伯海方向向西流动. 在北半球夏季, 随着季风向东北方向的变化, 海洋环流逆转, 向东流从索马里延伸到孟加拉湾. 因此可见, 转移概率矩阵P将会受到海洋季节改变的影响, 从而表现为P与时间直接相关, 即式(2)为非自治Markov过程. 在本文中, 按照四季变化规律将一年分为1—3月(TJM), 4—6月(TAJ), 7—9月(TJS)以及10—12月(TOD) 4个时间区间刻画印度洋区域洋流的典型变化模式. 此时, 在这些时间区间内, 系统的状态演化可形成4个相应的分段季度转移概率矩阵: PJM, PAJ, PJS 和 POD.
根据胞映射方法, 映射步长τ的选取应反映系统动力学的演化特征. 海洋系统中, 拉格朗日不相关时间(lagrangian decorrelation time)可用于刻画海洋表面非均匀流体的扩散程度[30-31]. 本文选取该时间T = 3 d作为一步映射步长τ, 以此构建对应不同区间的一步映射矩阵Ps1, Ps2, Ps3和Ps4. 同时, 考虑每月均为31 d, 每季度为3个月, 此时季度一步转移概率矩阵可通过对式(2)的左乘, 表示为
$$left.begin{split} &{{boldsymbol{P}}_{{ m{JM}}}} = {boldsymbol{P}}_{{ m{s}}1}^{31},;;;{{boldsymbol{P}}_{{ m{AJ}}}} = {boldsymbol{P}}_{{ m{s}}2}^{31},;;;; & {{boldsymbol{P}}_{{ m{JS}}}} = {boldsymbol{P}}_{{ m{s}}3}^{31},;;;;{{boldsymbol{P}}_{{ m{OD}}}} = {boldsymbol{P}}_{{ m{s}}4}^{31} end{split} ight}$$  | (7) |
此时, 年度一步转移概率矩阵Py可进一步表示为
$${{boldsymbol{P}}_{ m{y}}} = {{boldsymbol{P}}_{{ m{OD}}}} cdot {{boldsymbol{P}}_{{ m{JS}}}} cdot {{boldsymbol{P}}_{{ m{AJ}}}} cdot {{boldsymbol{P}}_{{ m{JM}}}} = {boldsymbol{P}}_{{ m{s}}{ m{4}}}^{31} cdot {boldsymbol{P}}_{{ m{s}}{ m{3}}}^{31} cdot {boldsymbol{P}}_{{ m{s}}{ m{2}}}^{31} cdot {boldsymbol{P}}_{{ m{s}}{ m{1}}}^{31} $$  | (8) |
为了从有限数据中获得转移概率的精确估计, 每个胞中应包含尽量多的样本轨迹, 并确定对应的像胞, 形成广义胞映射. 根据图论理论, Pij > 0代表了从第j个结点到第i个结点的一条有向边, 由此转移概率矩阵实际上构成了一组以映射关系表征的有向图. 利用深度优先搜索方法对该有向图中强连通分量的搜索和挖掘, 可获得表征系统吸引性的涡旋结构及其影响区域等全局动力学特征[26], 其中涡旋中心通过映射自循环胞刻画, 而涡旋区域则由可达涡旋中心的胞构成. 需要说明的是, 根据大偏差理论[32], 海洋系统中的强随机扰动特征使得所有样本响应在足够长的演化时间下以概率1离开所在区域而遍历所有可能空间. 因此, 本文通过拓扑分析得到的涡旋结构具有动态特性, 其概念和性质与传统意义下的稳态自循环集合不完全一致, 在海洋系统中表征在一定时间区间内对周围轨道(样本)的导向和吸引, 并通过分布概率密度来描述样本的聚集程度.
2.
印度洋海域全局动力学分析
由于不确定因素的影响, 海洋系统的长期和短期动力结构具有明显的区别和联系. 长期动力结构表征了系统的稳态分布趋势和总体特征, 而短期动力结构则关注于在足够短的时间区间内系统的瞬态运动特征和内在的影响机制, 其行为更加复杂且受到噪声影响较大. 下文将从这两个方面分别开展研究.
2.1
长期动力结构
海洋表面漂浮物在较长时间后的位置分布和动力学状态与该区域洋流的长期全局动力学结构密切相关. 本文中选取印度洋海域R = {15° < x < 120°; ? 60° < y < 30°}为待分析区域, 在该区域内共划分Nc = 60 × 50 = 3000个离散胞. 此时, 在1979—2016年期间共有4241个浮漂形成4450139个有效轨迹点, 且每个胞中平均约包含1483.38个映射样本用于构造上述具有Nc × Nc维度的转移概率矩阵Psi (i = 1, 2, 3, 4), 进而从式(8)中形成年度一步转移概率矩阵. 通过上述方法对该矩阵拓扑分析, 形成表征印度洋海域全局吸引性的不变集结构(如图2). 图2中红色离散点为给定分辨率下胞尺度刻画的涡旋中心结构, 点的位置由具有稳态自循环拓扑特征的胞集合的中心坐标确定. 蓝色区域则表示经过年度转移概率Py演化后, 在95%置信概率下系统响应在该涡旋中心的聚集区域(约为南纬20° ~ 40°, 东经40° ~ 96°范围内). 这表明从来看, 海洋表面洋流将长期大概率地聚集在马达加斯加以东海面, 这些特征与文献[33-34]中的结果一致.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-218-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
印度洋长期海域涡旋结构和涡旋区
Figure
2.
Long-term vortex structure and its regions of influence in the Indian Ocean
下载: 全尺寸图片
幻灯片
图3显示了由式(2)获得的该系统随机响应概率分布及演化特征. 图3中可见, 在该区域内系统的影响由初始的均匀分布开始演化并逐渐远离赤道附近向西南方向运动, 最终经历1年的演化时间后, 大部分概率动态地聚集在南纬20° ~ 40°范围内, 特别是在上述涡旋区范围内分布概率达到最大, 而在南纬40°以南和赤道附近的概率较低. 同时, 在海洋与陆地交界面附近也表现较高的响应概率, 这主要是由于海岸线附近地貌特征和人类活动导致了浮漂运动的“黏滞效应”.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-218-3.jpg'" class="figure_img
figure_type2 ccc " id="Figure3" />
图
3
印度洋海域洋流流动概率分布及动态演化: (a) 演化时间T = 3个月; (b) 演化时间T = 6个月; (c) 演化时间T = 9个月; (d) 演化时间T = 12个月
Figure
3.
Probabilities and evolution of ocean currents in the region of the Indian Ocean: (a) evolving time T = 3 mon; (b) evolving time T = 6 mon; (c) evolving time T = 9 mon; (d) evolving time T = 12 mon
下载: 全尺寸图片
幻灯片
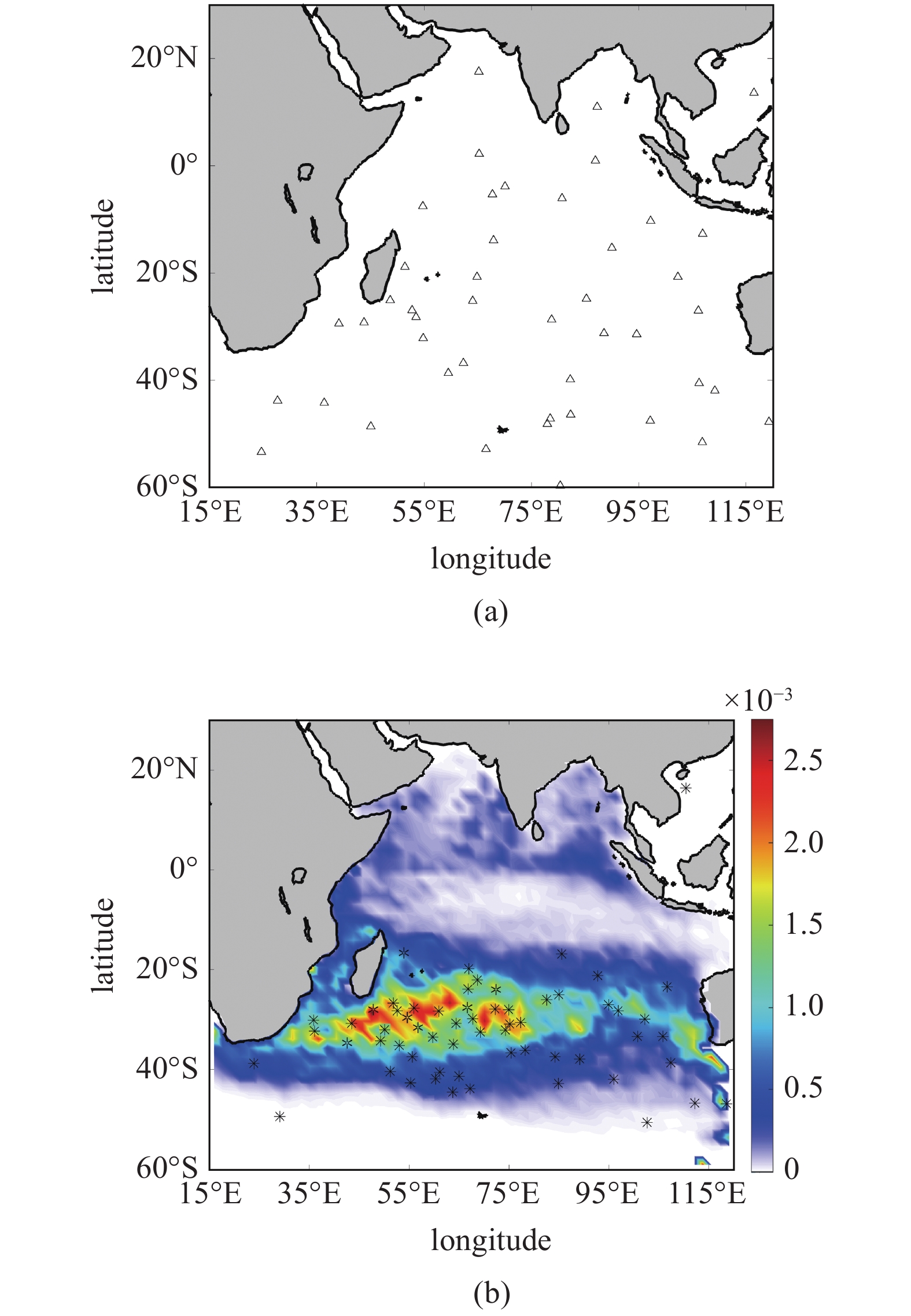
为了验证所提方法和结果的有效性, 本文提取2017—2019年在印度洋海域的浮漂样本作为检验数据, 其中2017年1月在该区域共新投入45个有效浮漂(图4(a)中“△”表示), 且总体成均匀分布. 以此为初始状态, 图4(b)中彩色区域显示了本文预测的2019年1月浮漂响应概率分布, “*”则表示浮漂真实状态. 图中可见, 虽然近海“黏滞效应”限制3个样本的自由漂移, 但仍有39个浮漂(约占86.7%)处于图2所示的涡旋区周围, 且主要集中在预测概率较高的核心区域(南纬23° ~ 37°, 东经40° ~ 75°范围), 这表明了所提出的数据驱动胞映射方法在海洋洋流预测方面的有效性.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-218-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
2017—2019年浮漂的位置分布: (a) 2017年1月浮漂位置(“△”); (b) 2019年1月浮漂状态(“*”)与预测结果对比
Figure
4.
Distributions of drifters during 2017?2019: (a) states of drifters in January, 2017; (b) Comparison of real states and predicted results in January, 2019
下载: 全尺寸图片
幻灯片
2.2
短期动力结构
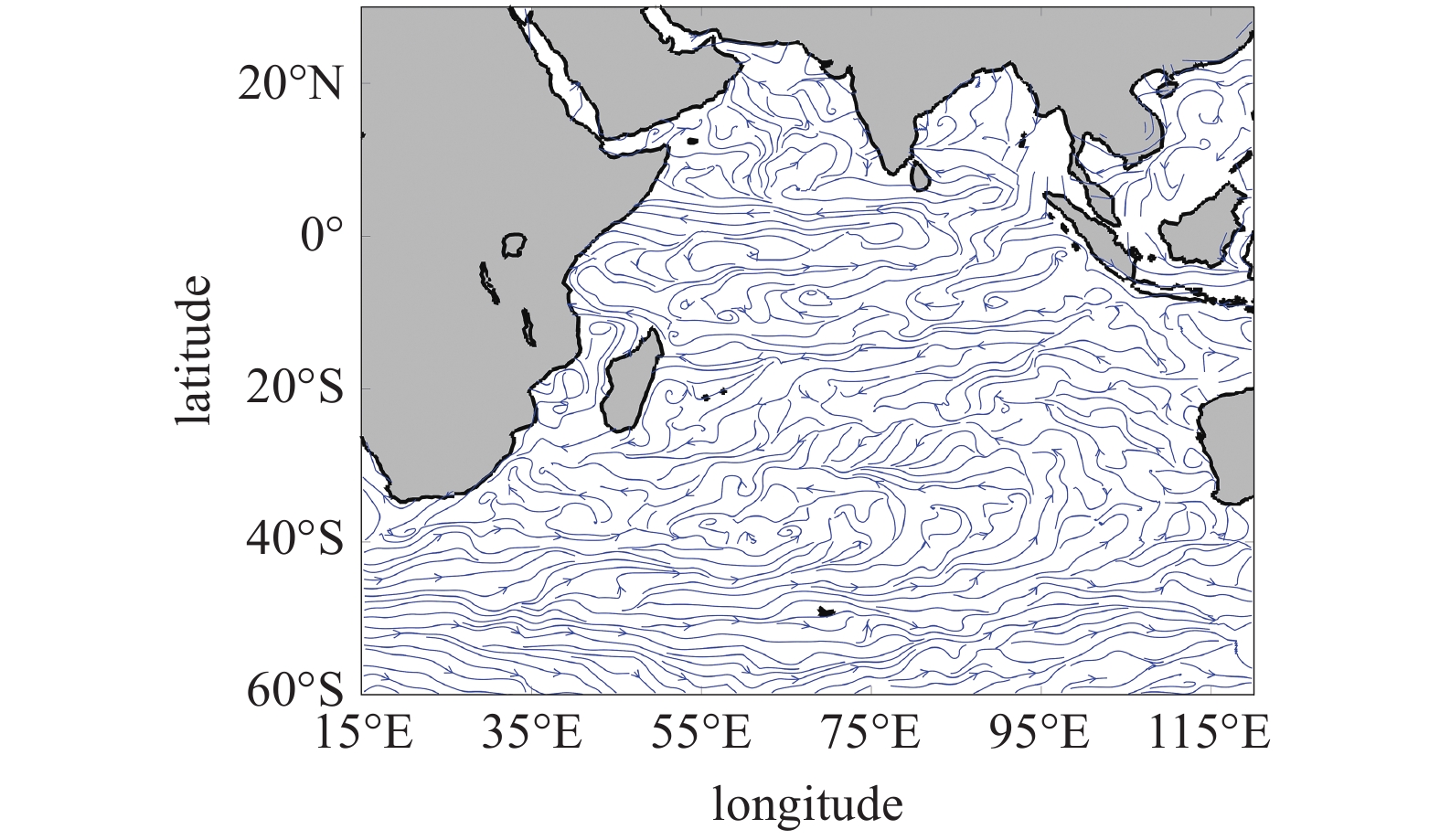
海洋短期动力结构能够揭示该区域漂浮物在经历短暂动态演化后的运动状态和趋势, 在海洋搜索和救援领域具有重要的实用价值. 本节将以2014年3月8日MH370航班失事(雷达消失)事件为时间节点, 研究此后1周内(3月8日—14日)该海域表面洋流的短期动力学特征. 分析时, 提取1979—2013年在此时间窗口内的所有历史数据, 形成以3 d为映射步长的一步短期瞬态转移概率矩阵Pt, 该矩阵表征系统在历史平均意义下的响应转移概率和趋势. 同时, 利用胞单元中浮漂的平均速度信息形成该海域60 × 50分辨率的平均流场图(如图5). 为了避免小样本容量导致Pt的统计误差, 文中借鉴插值胞映射方法的思想[35], 利用胞单元中已有样本的映射信息, 生成一个映射周期内新的短时估计样本, 并将流线的切线方向作为基本误差准则. 具体插值格式如下
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-218-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
印度洋海域平均流场图
Figure
5.
Average stream field of Indian Ocean
下载: 全尺寸图片
幻灯片
$${x_i}(T) = sumlimits_{j = 1}^2 {{a_{ij}}{x_j}(0) + } sumlimits_{j = 1}^2 {{b_{ij}}{x_j}{{(0)}^2} + } {c_i},;;i = 1,2$$  | (9) |
式中,
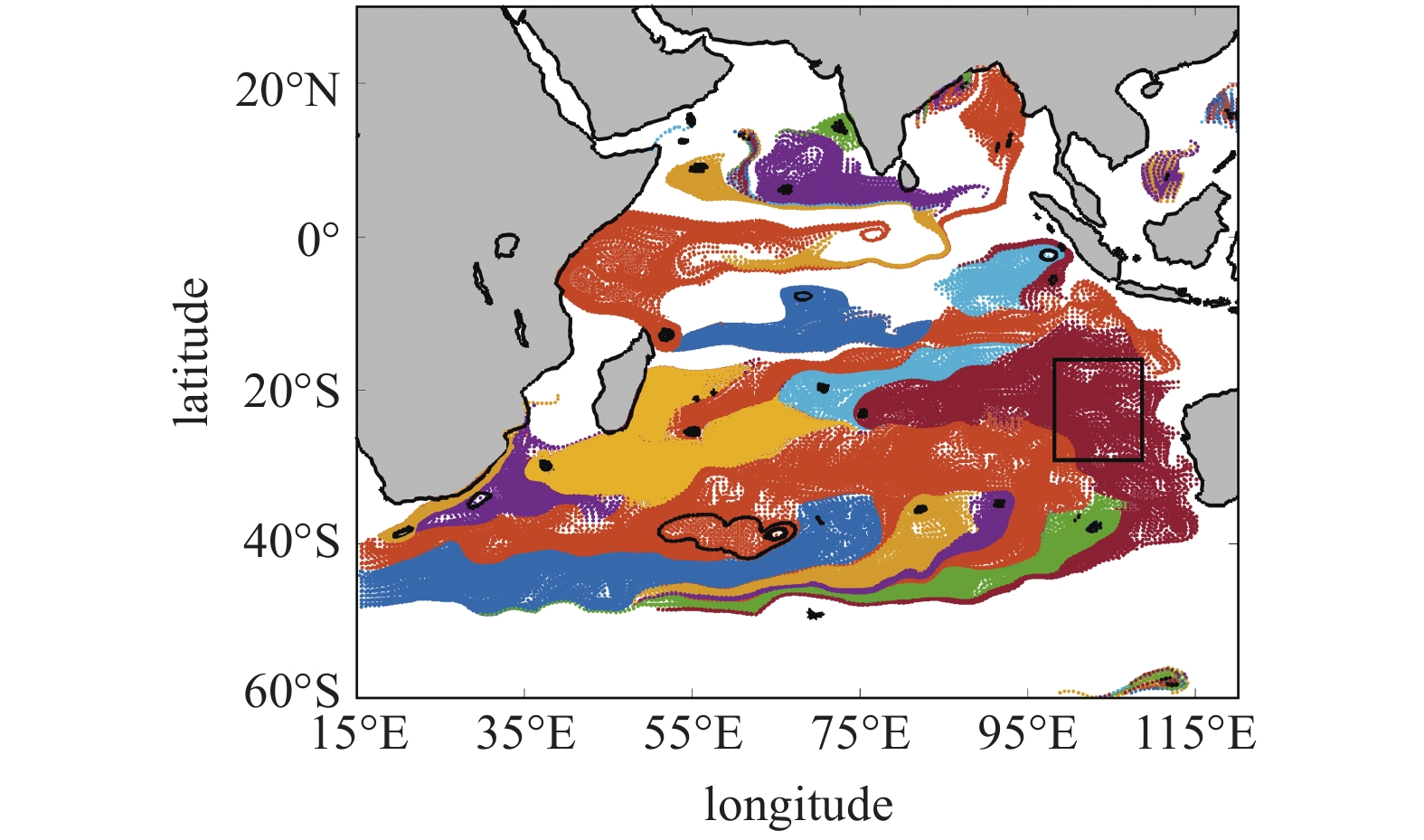
通过对扩充样本集的瞬态一步转移概率矩阵Pt拓扑分析, 得到印度洋海域具有吸引性的短期涡旋中心结构及其涡旋区域(如图6). 图6中黑色点代表短期涡旋中心, 表征了该区域洋流运动形成的瞬态聚集性和平均流动趋势, 彩色区域为各短期涡旋中心所主导的涡旋中心区域. 由图6可见, 在此时间窗口中, 赤道附近以北海域的洋流由西向东逐渐向远离赤道方向流动, 而南侧海域则受赤道逆流的影响较大, 沿逆时针远离赤道方向环流, 并且分别在纬度 ± 10°附近短暂聚集(短期涡旋中心). 在南印度洋海域, 由于南半球西风漂流影响, 南纬50°附近的表面洋流由西向东流动, 并受短期涡旋中心影响向北运动聚集在南纬40°附近海域, 其中在东经50° ~ 66°形成典型的环流效应(环状涡旋). 在南回归线附近, 受西澳大利亚寒流和南赤道暖流影响, 形成了在印度洋中部海域的吸引结构, 并使得海洋表面洋流由东向西流动. 上述这些特征构成了南印度洋在该季节的逆时针环流特点. Dong和Qin[15]指出, MH370在该时间窗口中最可能的坠海地点为南纬17° ~ 33°, 东经100° ~ 105° 范围内(图6黑色矩形框内), 位于图6中红色涡旋区, 并受该区域的短期涡旋中心影响将在后续的一周时间内总体向西运动, 这些特征与国际太平洋研究中心(International Pacific Research Center, IPRC)在该海域的相关研究结果一致[36].
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-218-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
2014年3月8日—14日印度洋海域短期涡旋中心(黑色点)和涡旋域(彩色区域)
Figure
6.
Short-term vortex cores and their regions of influence in the Indian Ocean on March 8 to 14, 2014
下载: 全尺寸图片
幻灯片
为了进一步证实短期涡旋结构对海洋表面洋流路径的影响, 图7提取了典型短期涡旋中心(黑色点)附近代表性浮漂的真实轨迹(彩色实线). 图7中能清楚地看出浮漂样本的轨迹演化规律受到附近短期涡旋中心的主导作用, 从而在短时间范围内有靠近该结构的趋势. 但也必须指出, 由历史数据获得的海洋全局结构仅反映了系统在时间窗口内的典型动力学特征和平均响应行为, 而海洋工况的随机性和突发性特点, 使得浮漂轨迹表现为明显的多样性和不确定性, 因而仍有一些样本在短期内所受吸引效应并不显著. 同时, 这些内在全局结构的位置和形式也是不断发展和变化的, 进而将导致漂浮物的进一步演化和聚集.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-218-7.jpg'" class="figure_img
figure_type2 ccc " id="Figure7" />
图
7
2014年3月8日—14日不同涡旋中心周围的浮漂样本轨迹
Figure
7.
Trajectories of samples near typical vortexes on March 8 to 14, 2014
下载: 全尺寸图片
幻灯片
3.
结 论
本文应用数据驱动的广义胞映射方法, 研究了印度洋海域表面洋流运动的长期和短期动力特征以及演化过程, 得到以下结论:
(1)提出的基于胞空间映射的数据驱动模型能够揭示不同周期尺度(天、季节或年度)下海洋系统的内在动态结构. 通过对比在不同时间跨度下的预测结果和工程实际, 从概率分布和响应趋势两方面验证了所提方法和结果的有效性和正确性.
(2)从长期动态特征来看, 印度洋海域在南纬20° ~ 40°, 东经40° ~ 96°附近范围内形成明显的大范围稳定的涡旋区域. 该结构主导了洋流流动趋势, 并导致大部分表面漂浮物动态聚集在该区域, 而在南纬40°以南和赤道附近则较为稀疏.
(3)从短期演化来看, 该区域在2014年3月8日—14日期间共存多个具有短期吸引性的涡旋结构, 它们在此期间促使洋流在南纬50°附近由西向东运动, 而在南回归线附近则导致了相反的流动方向, 这些特征构成了南印度洋在该季节的逆时针环流特点.
