引言
智慧城市[1-2]旨在利用互联网、物联网等通讯技术和传感技术构建万物互联的城市, 使得城市管理更加有序和高效. 智慧交通是智慧城市的重要组成之一. 构建智慧交通需要布置大量传感器和网络通讯设备, 传统的供能方式主要是电池和有线传输, 但存在污染环境、寿命短、成本高、不易维护等问题. 道路交通系统中蕴藏着丰富的能量, 这些能量以不同形式分布在环境中[3]. 如果将这些能量有效收集并转换为电能, 就能为传感器实现绿色可持续的供能.
道路能量收集包括道路太阳能收集技术[4]、道路热能收集技术[5]、道路机械能收集技术[6]等. 道路太阳能收集技术主要采用光伏板收集光能[7-9], 但光伏板安装在路面受环境影响较大, 成本高, 且结构可靠性差[10]. 道路热能收集利用道路的温差发电[11-12], 但这种方式发电效率低, 依赖道路内部结构的温度梯度[13], 受环境影响大, 成本高, 且与之相关的长期性能研究少[14]. 道路机械能收集技术主要是将车辆行驶时产生的机械能俘获并通过不同转换机制转换为电能, 因受环境影响较小, 能量来源广, 发电功率较高, 近年来受到越来越多的关注.
道路机械能量通过压电和电磁等技术进行能量转换[15]. 压电技术一般用于收集车辆在路面行驶时诱发的地面振动[16-17]与应力. 为了提高压电元件的输出功率, 研究人员设计出不同结构将外部激励放大, 如钹式结构[18]、多层式结构[19]、桥式结构[20]等. Wang等[21]提出了一种瓦片状的压电换能器, 当激励频率为10 Hz, 载荷为500 N时, 换能器的总功率为0.59 mW. Cao等[22]为了探究应用于路面的压电换能器输出规律, 建立了压电换能器的加载过程和输出模型, 结果表明一个压电换能器在0.7 MPa的载荷下能够输出0.058 J能量. Moure等[23]对钹式压电换能器在沥青道路上的俘能性能进行了评估, 每个换能器在重型车载荷下能达到16 μW的功率. 通过压电换能器收集道路能量对地面的损伤小, 可以很好地与地面结合, 但是其性能受材料、几何设计、以及载荷等因素的影响[24], 发电功率数量级多在mW及以下. 车辆经过减速带时会损失大量能量, 研究者通过液压系统和机械系统等[25]将车辆的冲击能量进行收集与转换, 以此驱动电磁发电机发电. Wang等[26]提出了一种基于机械运动整流机制的减速带道路能量收集装置, 该装置通过齿轮齿条传动, 能够将不规则的车辆脉冲激励转换成发电机的持续单向旋转, 显著提高了输出功率. Zhang等[27]提出了一种液压传动的高电压道路动能收集装置, 通过线性交流发电机发电, 原型机实验在车速为40 km/h时能够达到194 V的峰值电压, 55.2 V的平均电压. Gholikhani等[28]提出了一种齿条传动的减速带能量收集装置, 通过实验评估了装置的发电性能, 并探究了载荷大小和加载、卸载时间对装置输出性能的影响. Qi等[29]提出了一种基于摩擦滑板的道路能量收集装置, 该滑板由半金属摩擦材料制成, 能够在车辆行驶时通过摩擦吸收车辆动能, 传动模块能够将滑板的水平往复滑动转换为发电机输入轴的单向旋转, 该收集装置的输出电压可达29 V, 能量效率为57%. Azam等[30]设计了一种基于移动减速带的道路机械能收集装置, 原型机在120 mm/s, 载荷为150 N时可以达到11.99 W的峰值功率和20.75 V的峰值电压.
尽管国内外已经有许多道路能量收集的研究, 但针对道路能量收集装置的可靠性设计却较少, 而且输出功率也不够高, 距离应用还存在一定距离. 针对现有道路能量收集装置输出功率较低和可靠性差等缺点, 本文提出了一种全封闭高鲁棒性磁力耦合道路能量收集装置. 通过磁力耦合在减速带和能量采集装置之间实现无接触能量传递, 可以减缓冲击从而提高装置的鲁棒性; 无接触磁力传递使得装置容易全密封置于道路之下, 能够适应恶劣工作环境. 为了提高输出功率, 通过升频齿轮机构、棘轮机构将车辆滚压激励转换为高速单向旋转, 并且通过换向齿轮机构能够继续收集复位弹性势能. 利用能量法建立了该装置的机电耦合动力学模型, 进行了理论和数值仿真分析. 仿真探究了关键设计参数对系统的影响.
1.
设计
如图1(a)所示, 若干个全密封高鲁棒性磁力耦合道路能量收集装置密封安装在道路减速带下, 车辆行驶经过减速带时激励装置, 产生电能供给周围的用电设备或者进行存储. 如图1(c)所示, 能量收集装置包括磁铁、升降板、复位弹簧、齿条、传动齿轮组、棘爪盘、棘轮、磁铁盘和线圈等. 减速带底部和升降板对应位置都安装了磁铁, 两磁铁极性互斥. 减速带与升降板下方都设置有复位弹簧.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-374-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
全密封高鲁棒性磁力耦合道路能量收集装置. (a)应用场景, (b)车辆行驶过程, (c)结构简图及传动
Figure
1.
Fully sealed high robust magnetic coupling road energy harvesting device. (a) Application scenario, (b) vehicle running process, (c) structure and transmission
下载: 全尺寸图片
幻灯片
如图1(a)和图1(c)所示, 装置工作过程如下: 车辆经过时下压减速带, 升降板在磁铁排斥力作用下带动齿条向下运动. 齿轮组加增频率和改变方向后, 下方的棘爪盘与棘轮啮合, 带动磁铁盘转动, 造成线圈内的磁通量变化发电, 上方的棘爪盘滑过棘轮, 不影响磁铁盘转动; 当车辆驶离减速带时, 减速带在磁力和减速带复位弹簧作用下复位, 同时升降板在复位弹簧作用下带动齿条向上运动, 此时上方的棘爪盘棘爪与棘轮啮合, 带动磁铁盘转动, 下方的棘爪盘滑过棘轮. 通过齿轮组和棘轮机构将齿条上行和下行的运动转化为磁铁盘的快速单向旋转, 起到了升频和同向的作用, 提高了机电转换效率.
2.
工作原理与力学建模
基于全密封高鲁棒性车路能量收集装置的动力学模型以及传动原理简化如图2所示.
图2(a)为能量收集装置的动力学模型, 定义运动位移向下为正方向, y1和y2分别为减速带与升降板的位移, k1和k2分别为减速带复位弹簧以及升降板复位弹簧的刚度, 初始位置时两磁铁的中心面位置距离为d, 减速带距离地面为l, c1为减速带的等效阻尼, c2为升降板的等效阻尼, m1是减速带质量, m2是齿条(含升降板)质量. V2是齿条的速度, 升降板上的齿条在磁斥力的作用下向下运动, 带动下方啮合的传动机构.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-374-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
装置运作原理图
Figure
2.
Schematic diagram of device operation
下载: 全尺寸图片
幻灯片
图2(b)为能量收集装置的传动原理图. 齿条与升频齿轮啮合, 升频齿轮的大、小齿轮半径之比为
假设齿条所受磁力向下为正, Fmag为减速带与齿条间磁力, F为激励, 由图2 (a)有
$$ {m_1}{ddot y_1} + {c_1}{dot y_1} + {k_1}{y_1} = - {F_{{ m{mag}}}} + F $$  | (1) |
$$ {m_2}{ddot y_2} + {c_2}{dot y_2} + {k_2}{y_2} = {F_{{ m{mag}}}} $$  | (2) |
磁力公式为
$$ {F_{{ m{mag}}}}{text{ = }}frac{{3{M_1}{V_1}{M_2}{V_2}{mu _0}}}{{2{text{π}} {{(d - delta )}^4}}} $$  | (3) |
其中V1和V2是磁铁的体积, M1与M2是两个磁体的磁化矢量大小,
$$ {F_{{ m{mag}}}} = frac{{3{{B{r^2}}}{text{π}} {r^4}{h^2}}/{{{mu _0}}}}{{2{{left[ {d - left( {{y_1} - {y_2}} ight)} ight]}^4}}} $$  | (4) |
其中r是磁铁的半径, h是磁铁的高, y1是减速带的位移, y2是升降板的位移. 由图2(b)传动原理图, 棘爪盘线速度可表示为
$$ {V_3} = frac{{{r_2}}}{{{r_1}}}{dot y_2} $$  | (5) |
根据动量守恒定理, 磁铁盘与棘爪盘的速度关系式如下
$$ left( {{m_3} + {m_4}} ight){V'_4} = {m_3}{V_3} + {m_4}{V_4} $$  | (6) |
其中m3是棘爪盘的质量, m4为磁铁盘的质量, V3是棘爪盘的线速度, 当磁铁盘与棘爪盘啮合时, 磁铁盘的线速度为
$$ left. begin{array}{l} {{dot alpha }_{{ m{t}} + 1}} = dfrac{{{m_3}dfrac{{{r_2}}}{{{r_1}}}{{dot y}_2} + {m_4}{{dot alpha }_{ m{t}}}{r_{ m{m}}}}}{{left( {{m_3} + {m_4}} ight){r_{ m{m}}}}},;;{{dot alpha }_{ m{t}}} < dfrac{{{r_2}}}{{{r_1}}}{{dot y}_2} {{dot alpha }_{{ m{t}} + 1}} = - dfrac{{{m_3}dfrac{{{r_2}}}{{{r_1}}}{{dot y}_2} + {m_4}{{dot alpha }_{ m{t}}}{r_{ m{m}}}}}{{left( {{m_3} + {m_4}} ight){r_{ m{m}}}}},;;{{dot alpha }_{ m{t}}} > - dfrac{{{r_2}}}{{{r_1}}}{{dot y}_2} end{array} ight} $$  | (7) |
磁铁盘的转子动力学方程为
$$ Jddot alpha + cdot alpha + xi {I_{ m{e}}} = 0 $$  | (8) |
其中J是磁铁盘的转动惯量,
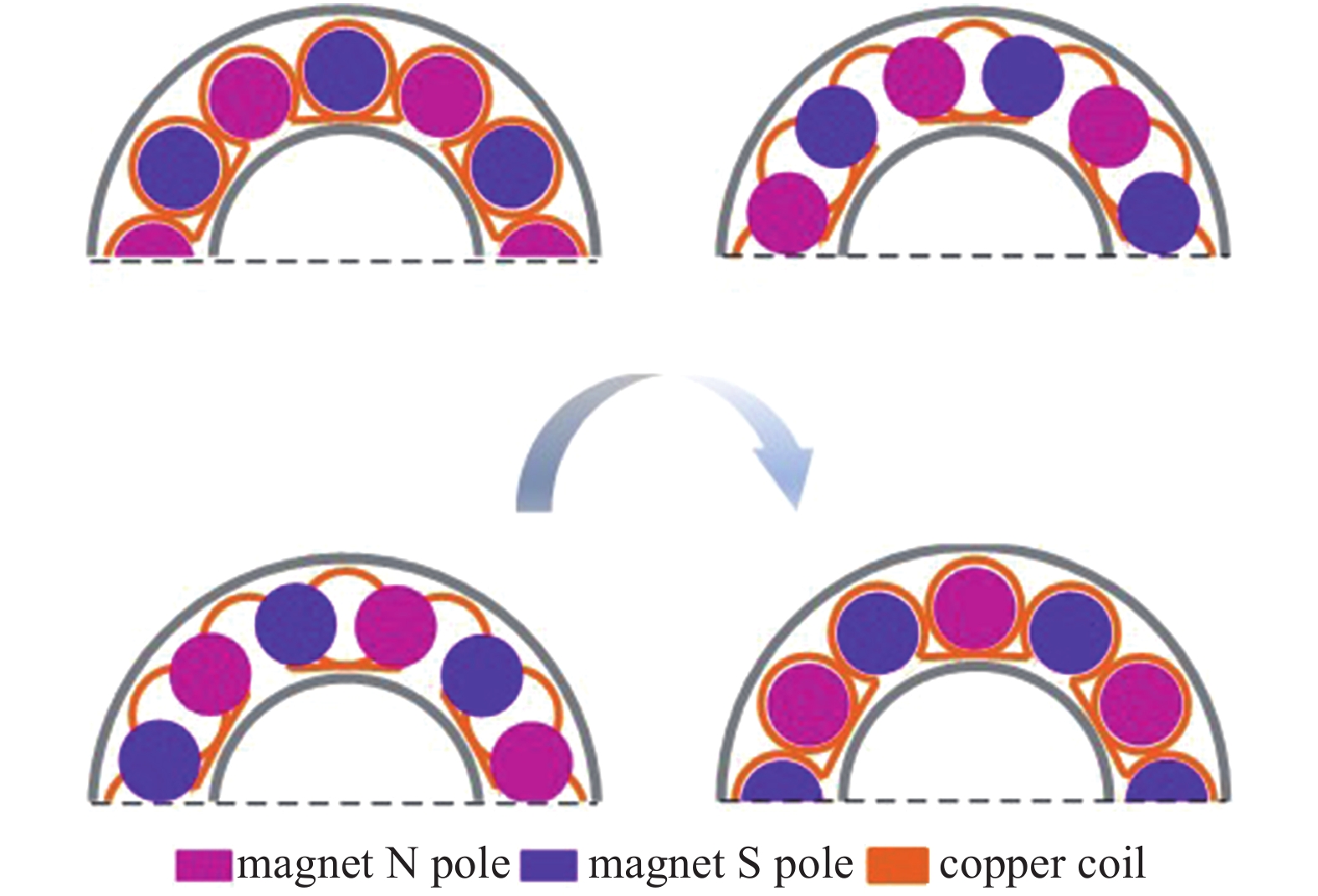
全密封高鲁棒性磁力耦合道路能量收集装置的机电转换原理图如图3所示, 磁铁盘转动时, 磁铁盘上的圆周阵列磁铁随之转动, 导致通过线圈的磁通量发生变化, 在电磁感应作用下产生电流. 由于圆周阵列中有12个磁铁, 相邻的磁铁磁极相反, 因而每转过30°, 磁通量方向就会反向, 所以电压频率为磁铁盘旋转频率的6倍.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-374-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
机电转换原理图
Figure
3.
Schematic diagram of electromechanical conversion
下载: 全尺寸图片
幻灯片
磁线圈中感应的电压可由法拉第定律确定
$$ {V_{ m{e}}} = - frac{{{ m{d}}psi }}{{{ m{d}}t}} = frac{{{ m{d}}psi }}{{{ m{d}}alpha }}frac{{{ m{d}}alpha }}{{{ m{d}}t}} = - frac{{{ m{d}}psi }}{{{ m{d}}alpha }}dot alpha $$  | (9) |
可设磁通量为
$$ L{dot I_{text{e}}} - 6kdot alpha sin (6alpha) + left( {{R_{{ m{coil}}}} + {R_{ m{e}}}} ight){I_{ m{e}}} = 0 $$  | (10) |
3.
性能分析
3.1
边界条件
当车轮驶离减速带后, 减速带和齿条应迅速复位, 以最大化能量输入. 齿条的复位弹簧的刚度k2必须提供足够的弹力, 从而带动齿条上行, 因此k2需满足边界条件
$$ {k_2} > frac{{{m_2}g + {F_{{ m{mag}}}}}}{{{x_2}}} $$  | (11) |
其中x2为升降板复位弹簧的最大压缩量. 对于减速带, 通常设置的磁铁斥力足够让其复位, 为了控制减速带离地面距离, 弹簧最大压缩量为x1, 则其下设置的减速带的复位弹簧刚度k1边界条件为
$$ {k_1} > frac{{{F_{{ m{mag}}}} - {m_1}g}}{{{x_1}}} $$  | (12) |
国内标准减速带最高为70 mm高, 假定减速带全高25 mm, 则减速带行程最大l = 45 mm, 以最大弹簧压缩量x1 = 45 mm, x2 = 25 mm, m1 = m2 = 2.5 kg计算, 可得升降板复位弹簧最小刚度k2 = 2.328 kN/m, 减速带复位弹簧的边界刚度182.2 N/m. 实际选用刚度时应考虑减速带和齿条的迅速复位, 选用的齿条复位弹簧刚度适当大于边界刚度. 减速带复位弹簧刚度可以设置得较大, 这样能够一定程度缓解车辆的冲击, 减少对减速带的损伤和提高驾驶员舒适度.
3.2
参数分析
为模拟车辆在不同速度下对减速带的冲击激励, 选用脉冲信号, S为减速带宽度, V为车速, 脉冲的脉宽T可表示为
$$ T{text{ = }}frac{S}{V} $$  | (13) |
根据减速带相关规格, 仿真中使用的减速带宽度均为0.35 m. 由式(13)可知, 脉冲的脉宽会随着车速增加而减小. 脉冲的峰值是根据车辆对装置的重力载荷(假设车重1 T)来近似的. 假设车辆经过减速带时的重力均匀分布在装置上, 将车轮对减速带的重力载荷近似为车重的一半, 则加载在装置上的脉冲信号峰值即为5 kN, 后续的仿真均为单次脉冲激励. 将机电耦合动力学方程在Matlab/Simulink进行数值求解, 仿真参数如表1所示.
表
1
仿真参数设置
Table
1.
Simulation parameter setting
table_type1 ">
| Parameter | Symbol | Value |
| excitation | F/kN | 5 |
| Mass of speed bump | m1/kg | 5 |
| mass of lifting plate | m2/kg | 5 |
| equivalent damping of speed bump | c1/(N·s·m?1) | 200 |
| equivalent damping of lifting plate | c2/(N·s·m?1) | 60 |
| equivalent damping of magnet plate | c3/(N·s·m?1) | 0.02 |
| resetting spring stiffness of speed bump | k1/(kN·m?1) | 3 |
| resetting spring stiffness of lifting plate | k2/(kN·m?1) | 3 |
| inductance coefficient | ζ | 0.05 |
| moment of inertia of magnet plate | J/(kg·m?2) | 0.0143 |
| electromagnetic load | R/Ω | 100 |
| electromagnetic equivalent coefficient | K | 0.045 |
下载: 导出CSV
|显示表格
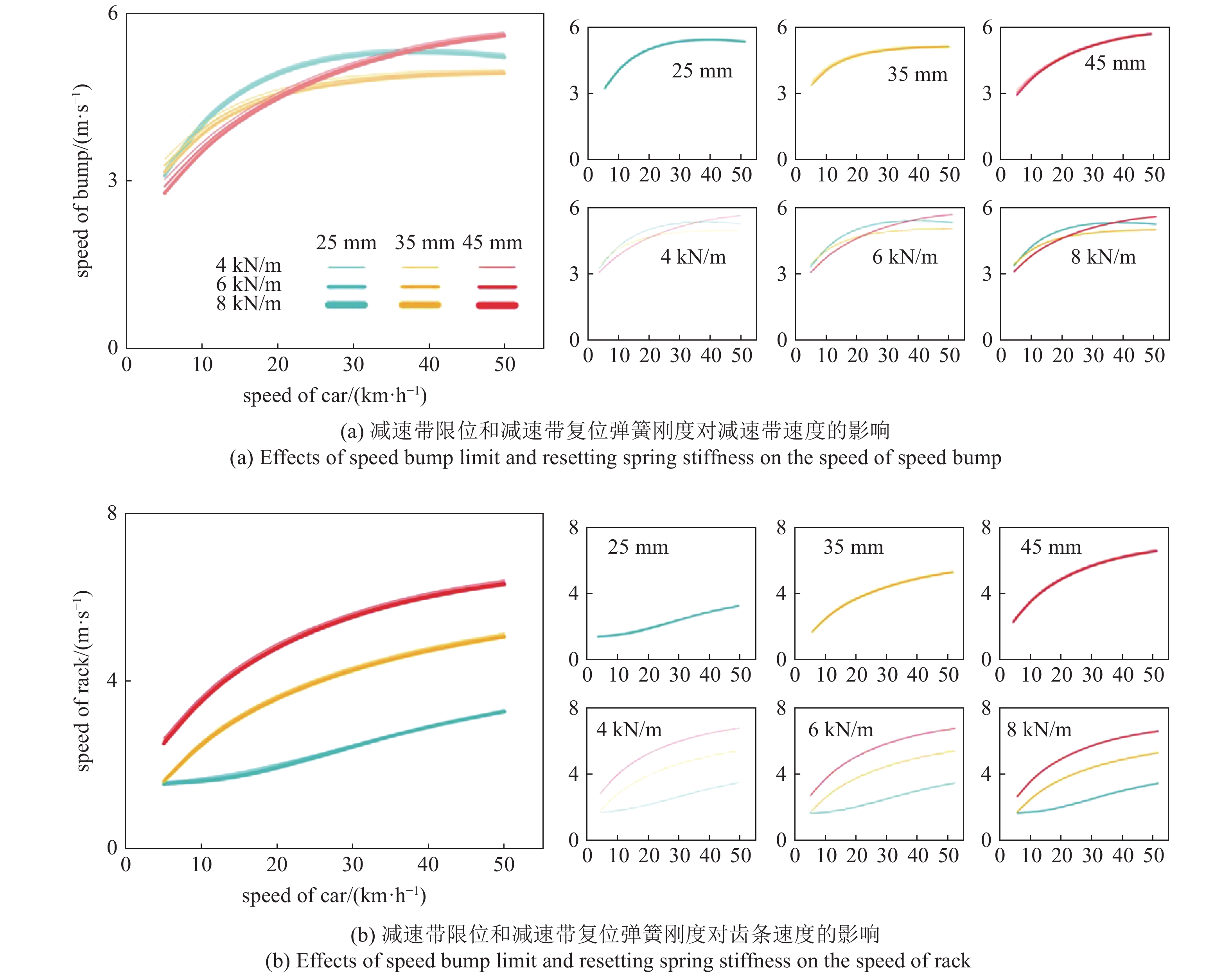
减速带作为承受输入激励的部件, 其速度响应值得探究. 考虑减速带的限位l和减速带复位弹簧的刚度k1对减速带和齿条速度的影响. 减速带限位l分别为25 mm, 35 mm和45 mm, 减速带复位弹簧刚度k1分别选取为4 kN/m, 6 kN/m和8 kN/m, 图4为两个参数的改变对减速带和齿条速度的影响. 可以发现减速带速度和齿条速度随车速增加而增加. 同一弹簧刚度下, 大限位更加有利于减速带的峰值速度响应, 因为限位的增加使得减速带有了更长的加速时间. 同一限位下, 刚度改变对速度响应的影响并不明显, 这是因为弹簧提供的弹力远小于车辆的冲击激励. 而小刚度下的减速带和齿条速度响应略好, 是因为小刚度提供的弹力小, 相同激励下减速带向下的加速度更大, 所以速度响应更好.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-374-4.jpg'" class="figure_img
figure_type2 ccc " id="Figure4" />
图
4
减速带限位和减速带复位弹簧刚度对齿条和减速带速度的影响
Figure
4.
Effects of speed bump limit and resetting spring stiffness on the speed of rack and speed bump
下载: 全尺寸图片
幻灯片
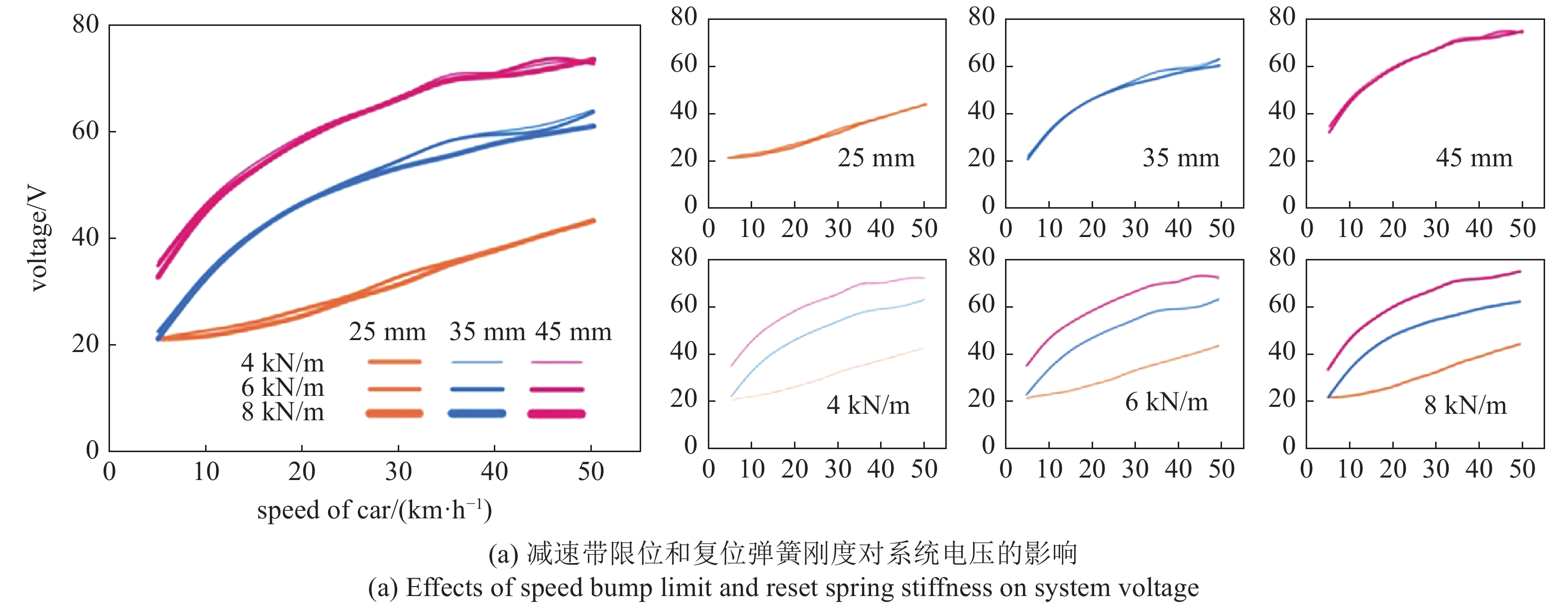
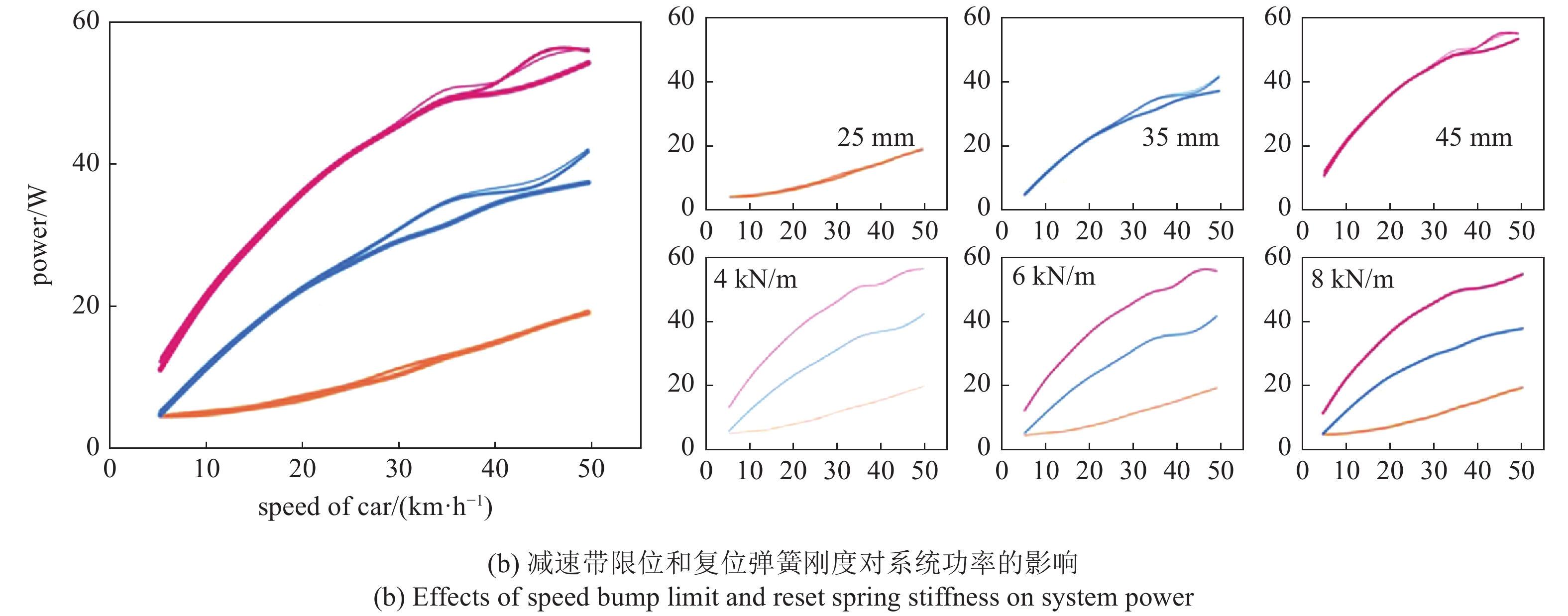
图5是减速带限位和减速带复位弹簧刚度对系统电压和功率的影响. 从图5可知系统的电压和功率输出都随车速增加而增加. 相同刚度下, 更大的限位明显有利于系统的电压和功率输出, 因为更大的限位下, 外界对系统输入的功更多. 同一限位下, 刚度变化对系统电学输出影响不明显.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-374-5-1.jpg'" class="figure_img
figure_type2 ccc " id="Figure5-1" />
5
减速带限位和复位弹簧刚度对系统电压和功率的影响
5.
Effects of speed bump limit and reset spring stiffness on system voltage and power
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-374-5.jpg'" class="figure_img
figure_type2 ccc " id="Figure5" />
图
5
减速带限位和复位弹簧刚度对系统电压和功率的影响(续)
Figure
5.
Effects of speed bump limit and reset spring stiffness on system voltage and power (continued)
下载: 全尺寸图片
幻灯片
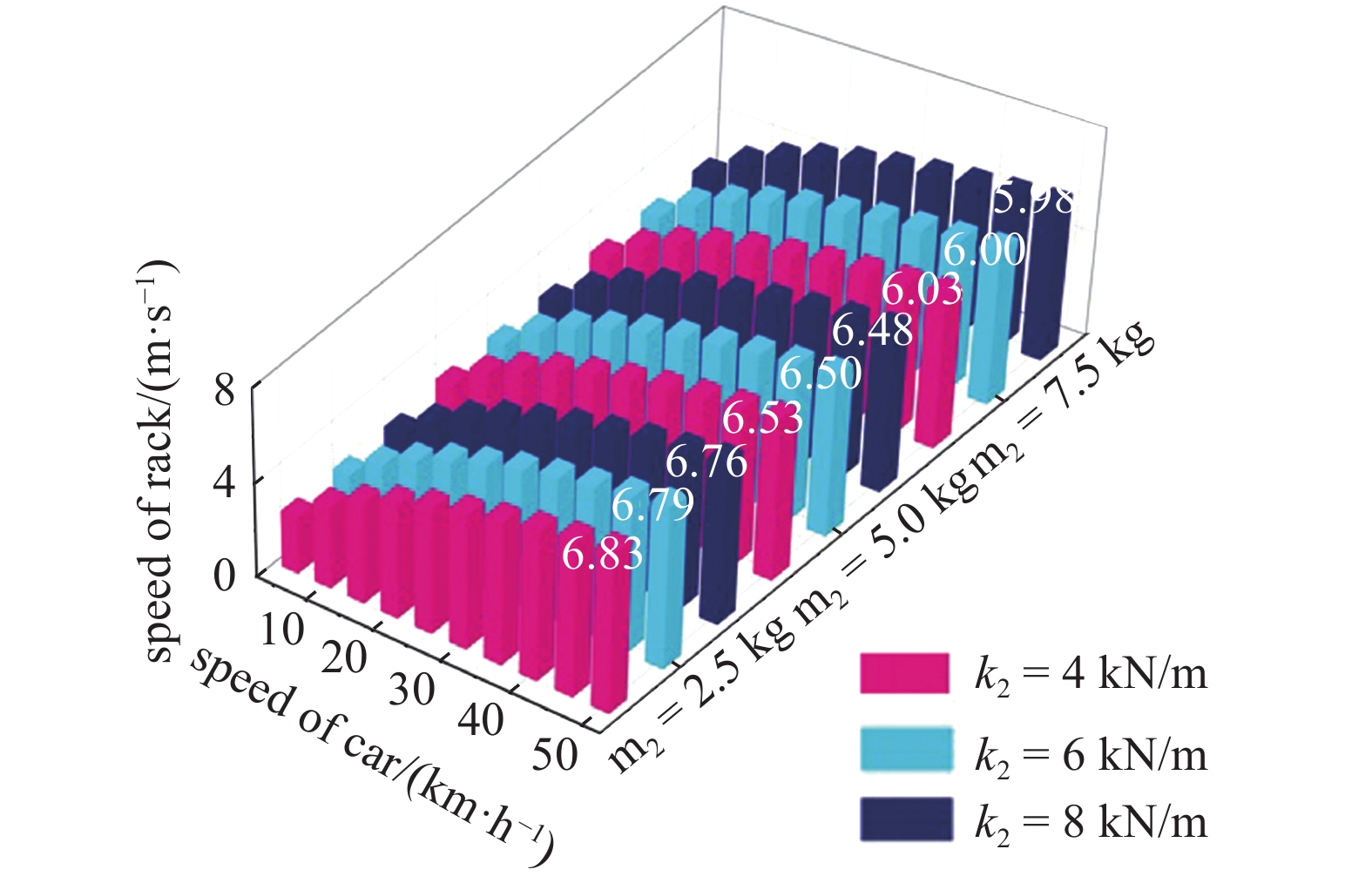
从式(5) ~ 式(9)可以看出, 系统的电压输出与齿条速度成正相关, 因此齿条的动力学特性对系统的电学输出有直接影响. 本文设计了9组仿真探究齿条的质量m2, 齿条复位弹簧刚度k2对齿条动力学特性的影响. 分别取m2质量为2.5 kg, 5 kg和7.5 kg, 齿条复位弹簧刚度k2为4 kN/m, 6 kN/m和8 kN/m进行仿真, 齿条结果如图6. 由图6可知, 随着车速的增加, 齿条质量和复位弹簧刚度参数的改变, 对齿条速度的影响很小. 相同质量时, 小刚度下的齿条速度略好于大刚度; 相同刚度时, 轻的齿条质量更有利于齿条的速度响应.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-374-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
齿条质量和齿条复位弹簧刚度对齿条速度影响
Figure
6.
Effects of rack mass and resetting spring stiffness on rack speed
下载: 全尺寸图片
幻灯片
根据图4 ~ 图6中的仿真参数变化对系统响应的影响, 可以得出结论: 较小的刚度更有利于装置的输出性能, 但复位弹簧刚度的选取需要考虑到齿条和减速带的及时复位和运动的平稳性, 因此选择的刚度大于边界刚度. 本文取减速带限位l = 45 mm、减速带复位弹簧刚度k1 = 4 kN/m、齿条质量m2 = 2.5 kg、齿条复位弹簧刚度k2 = 4 kN/m, 在上述参数下进行仿真, 观察系统的电学输出响应.
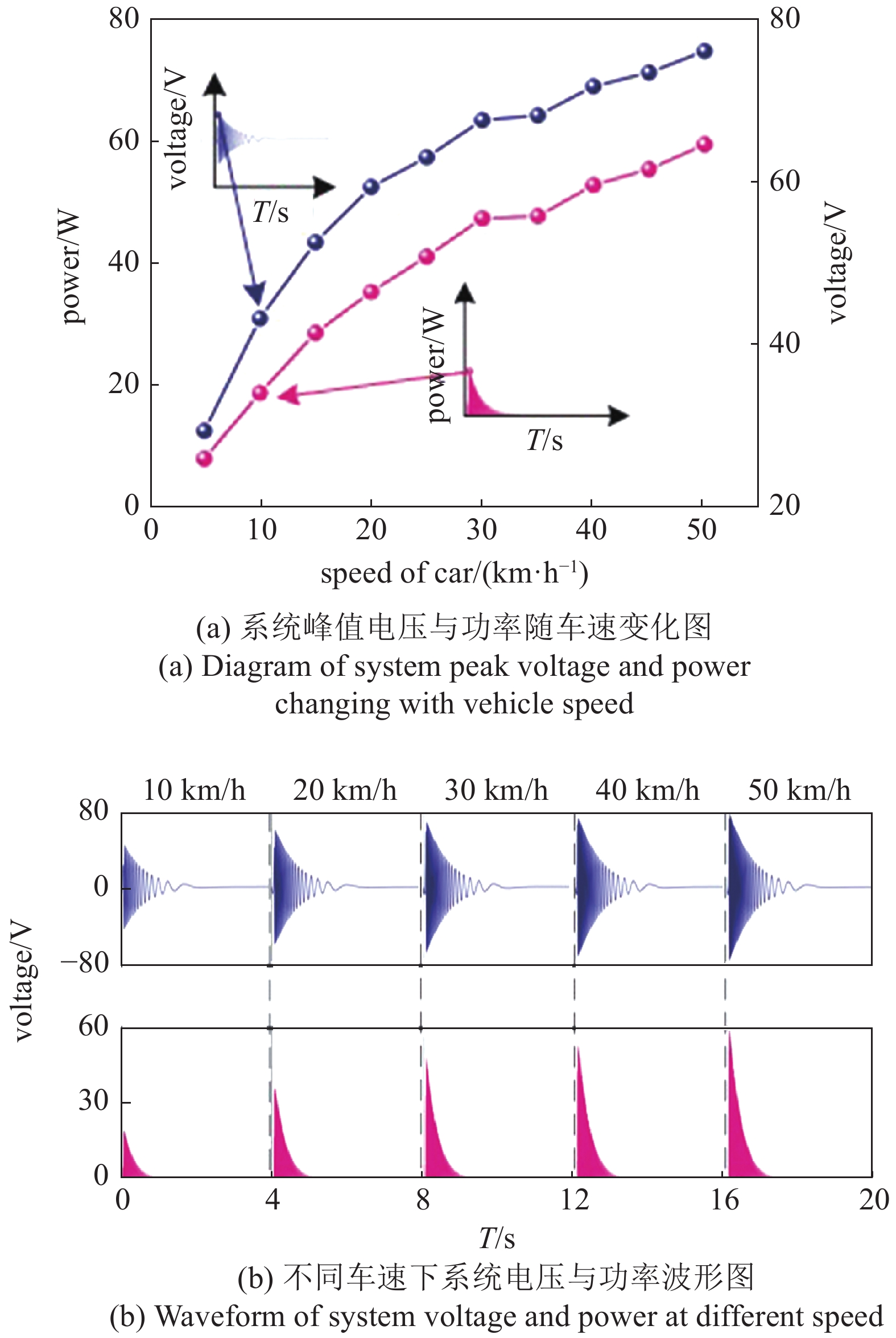
图7显示了系统在一组较好参数下的电学响应. 系统的峰值电压和最大瞬时功率随着车速增加而增加. 系统在50 km/h有最大输出电压峰值76.28 V, 最大瞬时功率59.94 W. 图7(b)为选取的5种不同车速下电压与功率的波形图. 可知电压峰值随着车速增加而增加的同时, 电压波形的频率增加, 持续时间延长.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-374-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
系统电学响应随车速变化
Figure
7.
Electrical response of the system varies with the speed
下载: 全尺寸图片
幻灯片
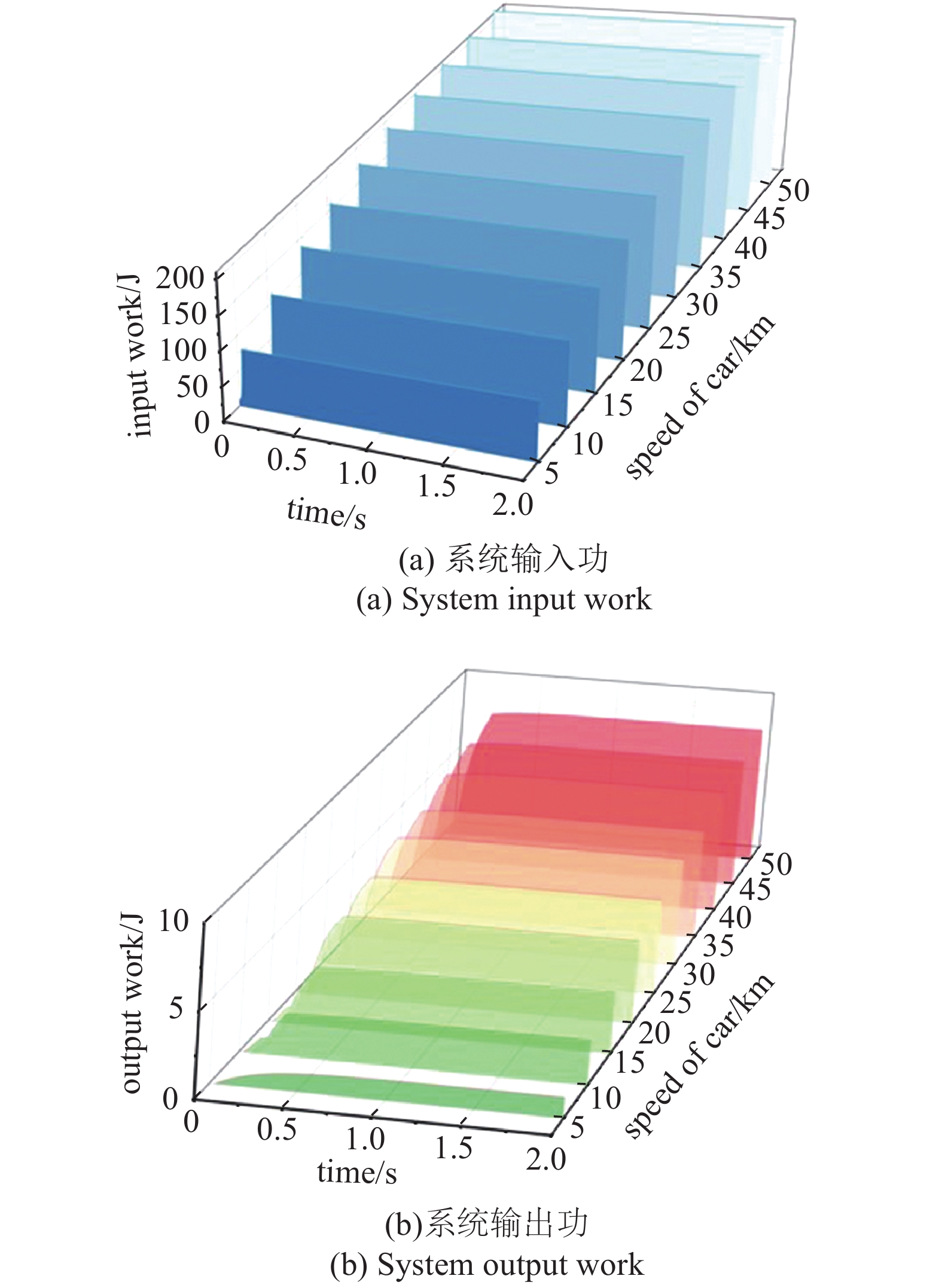
图8是优选参数下系统输入功和输出功随车速变化图. 从图8可知, 系统输入功和系统输出功随着车速增加而增加. 输入功在50 km/h有最大值208.8 J, 输出功在50 km/h有最大值8.3 J. 根据输入功与输出功可以计算出不同车速下装置的机电转化效率, 装置机电转化效率随着车速增加而增加, 在50 km/h时有最高机电转化效率3.99%.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-374-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
系统输入功输出功对比图
Figure
8.
Diagram of system input and output work comparison
下载: 全尺寸图片
幻灯片
4.
结论
本文提出了一种高鲁棒性磁力耦合道路能量收集装置. 通过引入非线性磁力传递车辆的冲击载荷, 使得装置具有良好的密封性和鲁棒性. 建立了磁力耦合道路能量收集装置的机电耦合动力学模型. 通过仿真探究了减速带复位弹簧刚度和减速带限位距离等关键参数对装置性能的影响. 总结以下几点结论:
(1)装置在高车速下具有更好的输出性能和更高的效率;
(2)为了提高装置的输出性能, 减速带的限位l应设置得尽量高, 但也应考虑行驶安全性和舒适性; 较小的复位弹簧刚度和更轻的齿条(含升降板)质量更有利于装置的电学输出;
(3)减速带限位l为45 mm、复位弹簧刚度k1为4 kN/m、齿条升降板质量为2.5 kg、复位弹簧刚度k2为4 kN/m, 在车速为50 km/h时, 单个装置有最大瞬时功率59.94 W, 最大输出电压峰值76.28 V;
高鲁棒性磁力耦合道路能量收集装置可以成为未来智慧交通系统的重要组成部分, 为交通环境微/小机电系统提供便捷、可持续的零碳电力.
