删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

带附加质量块的压电圆板能量采集器振动分析

本站小编 Free考研考试/2022-01-01


引言


近年来, 低功耗电子设备和无线传感器网络在民用和军事领域得到了广泛的应用[1-2]. 然而, 这些设备大多依靠电池作为电源, 到目前为止, 化学电池仍有许多问题待解决, 例如寿命短、体积大、对环境污染严重. 此外, 更换电池或为电池充电非常麻烦, 有时甚至不切实际, 例如人体内部的传感器[3-4]. 因此, 为了避免更换电池, 延长设备使用寿命, 用于自供电的能量采集技术得到广泛应用.

目前, 机械振动[5]由于不易受自然环境影响, 且储量丰富, 是当前最具吸引力的能源选择. 根据转换方法的不同, 机械能转化为电能的方法可分为压电[6]、电磁[7]和静电[8]转换. 压电能量采集技术因其强大的机电耦合效应、能量转换效率高和结构简单等优点, 成为最具有潜力的电池替代品. 因此, 在本研究中, 选择压电转换作为能量采集方法.

随着能量采集技术的发展, 悬臂梁结构受到普遍关注[9-12]. 与悬臂梁结构相比, 压电圆板因其轴对称结构和双向应变等优势吸引了研究者的关注[13-14]. 例如, 一些****研究了承受压力波动的压电圆板能量采集器的采集性能[15-17], 这些研究为参数优化提供了有用的设计工具. Yuan等[18]基于压电控制方程, 推导出压电鼓式换能器在弯曲模式下的解析解, 分析了换能器采集振动能量的性能. Kan等[19]利用Raleigh方法建立了不同边界的压电圆板的解析模型, 他们发现简支边界往往可以获得更高的机电耦合系数. Mohsen和Hamid[20]研究了随机激励下固支压电圆板能量采集器采集性能, 成功将功率密度提高到3.2 mW/m2.

遗憾的是, 上述文献中能量采集器的固有频率相较于低频环境来说较高, 导致了低发电效率. 为了克服这个问题, Chen等[21], Palosaari等[22]等发表了关于降低能量采集器固有频率的评论, 发现预应力对于降低固有频率和提高能量采集效率是必要的. 基于上述发现, 很多****对附加质量的圆板能量采集器进行了探究. 一些文献[23-27]借助于实验手段, 采用不同的设计来提高能量采集器的采集性能. Liu等[23-24]分别将平坦的粘合区域更改为弯曲的粘合区域, 将附加在中心的质量块更改为环形空心形状, 优化了压电圆板能量采集器的功率输出. Han等[25]发现, 有凹槽的压电圆板能量采集器相较于无凹槽的能量采集器, 输出功率明显增加. Solovyev和Duong[26]用ANSYS和ACELAN软件对压电双晶圆板能量采集器建模, 为设备的组装技术提供指导. 值得注意的是, 上述文献均是通过实验或仿真完成, 不能反映结构参数与能量采集器采集性能的关系. 因此, 封闭形式的解析解是描述和优化能量采集器的必要工具. Jiang和Hu[27]使用压电控制方程推导出中心带有刚性质量块的双晶压电圆板能量采集器的解析解, 结果表明调整参数可以提高能量采集器的采集性能. Yang等[28-29]基于板振动理论研究了附加质量的压电圆板的弯曲振动, 并通过仿真和实验进行验证.

影响压电圆板能量采集器的采集性能的参数有很多, 包括基板厚度、半径、质量块重量、压电片外径等. 然而关于压电片内径对能量采集器的采集性能的影响还鲜有报道. Xu等[30]通过实验发现了压电圆板能量采集器中的非均匀应变分布会降低输出功率. 因此, 他们减小压电片尺寸并在中心挖孔, 研究发现去除压电片的低电压输出部分能够提高采集效率. 与上述文献不同的是, 本文使用能量法和有限元仿真来研究考虑附加质量接触面积的压电圆板能量采集器的采集性能, 并探究了压电片内径对能量采集器采集性能的影响.

本文采用广义哈密顿原理, 推导出附加质量的压电圆板能量采集器的机电耦合方程, 用伽辽金法对方程近似离散, 通过离散方程得到输出电压、功率的闭合解. 最后基于闭合解探讨了负载阻抗、附加质量块、压电板的内、外径对压电能量采集器采集性能的影响, 并用有限元仿真对结果进行验证. 以期为工程对象提供参考数据.


1.
压电圆板能量采集器的理论模型



1.1
压电圆板能量采集器机电耦合方程


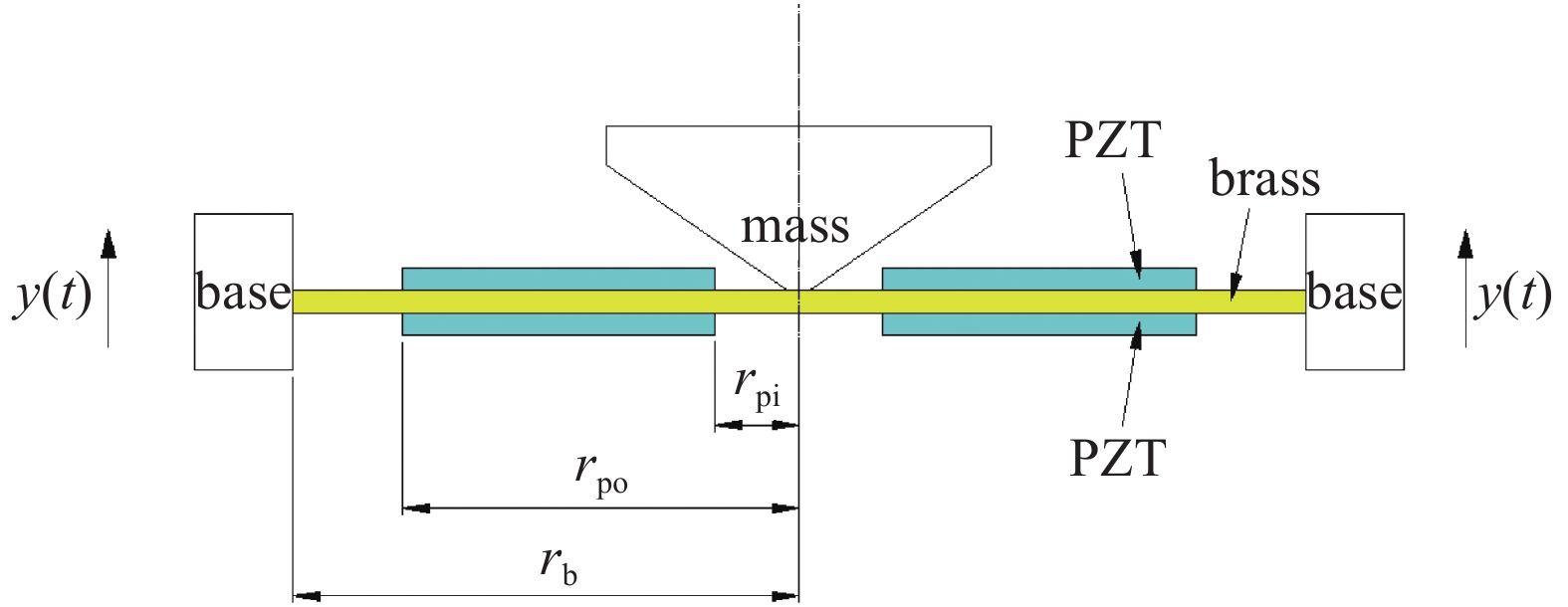
由质量块和压电复合板组成的能量采集器的剖视结构如图1所示. 复合板由两个串联的压电陶瓷片铺设在基板上组成, 其中基层的半径和厚度分别为rb和hb, 压电片内、外半径和厚度分别为rpi，rpo和hp. 压电复合板中心固定一个倒锥形质量块, 质量块尖端半径rm远小于复合板半径, 因此在理论建模中将质量块考虑为质点. 基板被固支在振动位移为y(t)基座上.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-441-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
附加质量块的圆板能量采集器的剖面图



Figure
1.
The cutaway view of the circular energy harvester considering proof mass



下载:
全尺寸图片
幻灯片


假设系统的挠度不足以引起非线性几何项, 考虑基础位移的位移矢量为







$$ {boldsymbol{U}} = - zfrac{{partial w}}{{partial r}}{boldsymbol{i}} + (w + y){boldsymbol{k}} $$
(1)

式中, i和k分别表示沿r和z轴的单位向量.

基于基尔霍夫薄板理论, 几何方程为







$$ left. begin{array}{l} {varepsilon _r} = - zdfrac{{{partial ^2}w}}{{partial {r^2}}} {varepsilon _theta } = - dfrac{z}{r}dfrac{{partial w}}{{partial r}} {varepsilon _{rtheta }} = 0 end{array}
ight} $$
(2)

遵循胡克定律, 基板的物理方程为[20]







$$ left. begin{array}{l} sigma _r^{left( {text{b}}
ight)} = dfrac{{{E_{text{b}}}}}{{1 - v_{text{b}}^2}}left( {{varepsilon _r} + {v_{text{b}}}{varepsilon _theta }}
ight) sigma _theta ^{left( {text{b}}
ight)} = dfrac{{{E_{text{b}}}}}{{1 - v_{text{b}}^2}}left( {{varepsilon _theta } + {v_{text{b}}}{varepsilon _r}}
ight) end{array}
ight} $$
(3)

式中, ($ sigma _r^{left( {text{b}}
ight)} $,$ sigma _theta ^{left( {text{b}}
ight)} $) 表示应力分量; ($ {varepsilon _r} $,$ {varepsilon _theta } $) 表示应变分量; vb，Eb分别是基板的泊松比和杨氏模量.

考虑压电材料的压电效应, 上压电陶瓷的物理方程[31]







$$ left. begin{array}{l} sigma _r^{left( {{text{p}}1}
ight)} = dfrac{ {{varepsilon _r} + {v_{text{p}}}{varepsilon _theta } - (1 + {v_{text{p}}}){d_{31}}{E_3}} }{{S_{11}^Eleft( {1 - v_{text{p}}^2}
ight)}} sigma _theta ^{left( {{text{p}}1}
ight)} = dfrac{ {{varepsilon _theta } + {v_{text{p}}}{varepsilon _r} - (1 + {v_{text{p}}}){d_{31}}{E_3}} }{{S_{11}^Eleft( {1 - v_{text{p}}^2}
ight)}} D_3^{left( {{text{p}}1}
ight)} = {d_{31}}left(sigma _r^{left( {{text{p}}1}
ight)} + sigma _theta ^{left( {{text{p}}1}
ight)}
ight) + varepsilon _{33}^T{E_3} end{array}
ight} $$
(4)

式中, ($ sigma _r^{left( {{text{p}}1}
ight)} $,$ sigma _theta ^{left( {{text{p}}1}
ight)} $) 表示上压电板的应力分量; $ D_3^{left( {{text{p}}1}
ight)} $是上压电板沿z方向的电位移; E3表示z方向的电场分量; d31, $ S_{11}^E $和vp分别表示压电材料的机电耦合系数、弹性柔度系数和泊松比; $ varepsilon _{33}^T $是压电材料在恒定应力下的介电系数.

下压电陶瓷的物理方程







$$ left. begin{array}{l} sigma _r^{left( {{text{p}}2}
ight)} = dfrac{ {{varepsilon _r} + {v_{text{p}}}{varepsilon _theta } + (1 + {v_{text{p}}}){d_{31}}{E_3}} }{{S_{11}^Eleft( {1 - v_{text{p}}^2}
ight)}} sigma _theta ^{left( {{text{p}}2}
ight)} = dfrac{ {{varepsilon _theta } + {v_{text{p}}}{varepsilon _r} + (1 + {v_{text{p}}}){d_{31}}{E_3}} }{{S_{11}^Eleft( {1 - v_{text{p}}^2}
ight)}} D_3^{left( {{text{p}}2}
ight)} = - {d_{31}}left(sigma _r^{left( {{text{p}}2}
ight)} + sigma _theta ^{left( {{text{p}}2}
ight)}
ight) + varepsilon _{33}^T{E_3} end{array}
ight} $$
(5)

式中, $ left(sigma _r^{left( {{text{p}}2}
ight)}
ight.$,$left. sigma _theta ^{left( {{text{p}}2}
ight)}
ight)$表示下压电板应力分量; $ D_3^{left( {{text{p}}2}
ight)} $是下压电板沿z方向的电位移.

z方向的电场强度与电压之间的关系[31]







$$ {E_3} = - frac{{v(t)}}{{2{h_{text{p}}}}} $$
(6)

式中, v(t)为上下压电板之间的电压.

压电圆板能量采集器的总动能表示为[32]







$$ begin{split} T =& frac{1}{2}{int_{{V^{left( {text{b}}
ight)}}} {{
ho _{text{b}}}[dot w(r,t) + dot y(t)]} ^2}{text{d}}V{text{ }} + & {text{ }} frac{1}{2}{int_{{V^{left( {{text{p}}1}
ight)}}} {{
ho _{text{p}}}[dot w(r,t) + dot y(t)]} ^2}{text{d}}V{text{ }}+ & {text{ }} frac{1}{2}{int_{{V^{left( {{text{p}}2}
ight)}}} {{
ho _{text{p}}}[dot w(r,t) + dot y(t)]} ^2}{text{d}}V + &frac{1}{2}{m_0}{left[ {dot w(0,t) + dot y(t)}
ight]^2} = & {text{ }} frac{1}{2}int_{{A_{text{b}}}} {left[ {m{text{ + }}{m_0}delta left( r
ight)}
ight]{{[dot w(r,t) + dot y(t)]}^2}} {text{d}}A end{split} $$
(7)

式中, m0是附加质量块的质量, m为压电复合板单位面积的质量, 表示为






$$ m = left{ begin{array}{l} {m_1} = {
ho _{text{b}}}{h_{text{b}}},;;;;;;;;;;;;;;;;;;;;;{text{ 0}} leqslant r leqslant {r_{{text{pi}}}} {m_2} = {
ho _{text{b}}}{h_{text{b}}} + 2{
ho _{text{p}}}{h_{text{p}}},;;;;;;;;;{r_{{text{pi}}}} leqslant r leqslant {r_{{text{po}}}} {m_3} = {
ho _{text{b}}}{h_{text{b}}},;;;;;;;;;;;;;;;;;;;;;{text{ }}{r_{{text{po}}}} leqslant r leqslant {r_{text{b}}} end{array}
ight. $$

式中, ρb和ρp分别表示基板和压电板的体积密度.

压电圆板能量采集器的总势能为[32]







$$ begin{split} U = &frac{1}{2}intlimits_{{V^{left( {text{b}}
ight)}}} {left( {sigma _r^{left( {text{b}}
ight)}{varepsilon _r} + sigma _theta ^{left( {text{b}}
ight)}{varepsilon _theta }}
ight)} {text{d}}V + & frac{1}{2}intlimits_{{V^{left( {{text{p}}1}
ight)}}} {left( {sigma _r^{left( {{text{p}}1}
ight)}{varepsilon _r} + sigma _theta ^{left( {{text{p}}1}
ight)}{varepsilon _theta }}
ight)} {text{d}}V + & {text{ }} frac{1}{2}intlimits_{{V^{left( {{text{p}}2}
ight)}}} {left( {sigma _r^{left( {{text{p2}}}
ight)}{varepsilon _r} + sigma _theta ^{left( {{text{p}}2}
ight)}{varepsilon _theta }}
ight)} {text{d}}V = & {text{ }} frac{1}{2}int_{{A_{text{b}}}} {{D_j}left[ {{{left( {frac{{{partial ^2}w}}{{partial {r^2}}}}
ight)}^2} + frac{{2{v_j}}}{r}frac{{partial w}}{{partial r}}frac{{{partial ^2}w}}{{partial {r^2}}} + {{left( {frac{1}{r}frac{{partial w}}{{partial r}}}
ight)}^2}}
ight]} {text{d}}A - & {text{ }} frac{1}{2}frac{{vleft( t
ight)left( {{h_{text{p}}} + {h_{text{b}}}}
ight){d_{31}}}}{{2S_{11}^{{E}}left( {1 - {v_{text{p}}}}
ight)}}int_{{A_{text{b}}}} {H(r)left( {frac{{{partial ^2}w}}{{partial {r^2}}} + frac{1}{r}frac{{partial w}}{{partial r}}}
ight)} {text{d}}A end{split} $$
(8)

式中, $ H(r) = Hleft( {r - {r_{{text{pi}}}}}
ight) - Hleft( {r - {r_{{text{po}}}}}
ight) $是Heaviside函数; Dj和vj分别是压电复合板的等效弯曲刚度和泊松比, 表示为






$$ {D_j} = left{ begin{array}{l} {D_1} = dfrac{{{E_{text{b}}}{I_{{text{b}}2}}}}{{ {1 - v_{text{b}}^2} }},{text{ 0}} leqslant r leqslant {r_{{text{pi}}}} {D_2} = dfrac{{{E_{text{b}}}{I_{{text{b}}2}}}}{{ {1 - v_{text{b}}^2} }} + dfrac{{{I_{{text{p}}2}}}}{{S_{11}^Eleft( {1 - v_{text{p}}^2}
ight)}},{text{ }}{r_{{text{pi}}}} leqslant r leqslant {r_{{text{po}}}}{text{ }} {D_3} = dfrac{{{E_{text{b}}}{I_{{text{b}}2}}}}{{ {1 - v_{text{b}}^2} }},{text{ }}{r_{{text{po}}}} leqslant r leqslant {r_{text{b}}}{text{ }} end{array}
ight. $$






$$ {v_j} = left{ begin{array}{l} {v_1} = {v_{text{b}}},{text{ 0}} leqslant r leqslant {r_{{text{pi}}}} {v_2} = dfrac{{dfrac{{{E_{text{b}}}{I_{{text{b}}2}}{v_{text{b}}}}}{{ {1 - v_{text{b}}^2} }} + dfrac{{{I_{{text{p}}2}}{v_{text{p}}}}}{{S_{11}^Eleft( {1 - v_{text{p}}^2}
ight)}}}}{{dfrac{{{E_{text{b}}}{I_{{text{b}}2}}}}{{ {1 - v_{text{b}}^2} }} + dfrac{{{I_{{text{p}}2}}}}{{S_{11}^Eleft( {1 - v_{text{p}}^2}
ight)}}}},{text{ }}{r_{{text{pi}}}} leqslant r leqslant {r_{{text{po}}}} {v_3} = {v_{text{b}}},{text{ }}{r_{{text{po}}}} leqslant r leqslant {r_{text{b}}}{text{ }} end{array}
ight. $$






$$ begin{split} 式中,;&{I_{{text{b2}}}} = displaystyleint_{ - frac{{{h_{text{b}}}}}{2}}^{frac{{{h_{text{b}}}}}{2}} {{z^2}{text{d}}z = } dfrac{{h_{text{b}}^3}}{{12}}&{I_{{text{p}}2}} = int_{frac{{{h_{text{b}}}}}{2}}^{frac{{{h_{text{b}}}}}{2} + {h_{text{p}}}} {{z^2}{text{d}}z + int_{ - left( {frac{{{h_{text{b}}}}}{2} + {h_{text{p}}}}
ight)}^{ - frac{{{h_{text{b}}}}}{2}} {{z^2}{text{d}}z} = }&qquad {frac{2}{3}left[ {{{left( {frac{{{h_{text{b}}}}}{2} + {h_{text{p}}}}
ight)}^3} - {{left( {frac{{{h_{text{b}}}}}{2}}
ight)}^3}}
ight]} end{split} quadquadqquadqquad$$

串联压电陶瓷片的总电能为[32]







$$ begin{split} {W_{{text{ie}}}} =& frac{1}{2}int_{{V^{left( {{text{p}}1}
ight)}}} {D_3^{left( {{text{p}}1}
ight)}{E_3}} {text{d}}V + {text{ }}frac{1}{2}int_{{V^{left( {{text{p2}}}
ight)}}} {D_3^{left( {{text{p2}}}
ight)}{E_3}} {text{d}}V{text{ = }} & {text{ }}frac{1}{2}int_{{A_{text{b}}}} {Hleft( r
ight)} Biggl{{18} {frac{{vleft( t
ight)left( {{h_{text{p}}} + {h_{text{b}}}}
ight){d_{31}}}}{{2S_{11}^Eleft( {1 - {v_{text{p}}}}
ight)}}left( {frac{{{partial ^2}w}}{{partial {r^2}}} + frac{1}{r}frac{{partial w}}{{partial r}}}
ight) + } & left. {frac{{{v^2}(t)}}{{2{h_{text{p}}}}}left[ {varepsilon _{33}^{text{T}} - frac{{2d_{31}^2}}{{S_{11}^{text{E}}left( {1 - {v_{text{p}}}}
ight)}}}
ight.}
ight]Biggl}{18}{text{d}}A end{split}$$
(9)

考虑内部电能的广义哈密顿原理为[31]







$$ int_{{t_1}}^{{t_2}} {left( {delta T - delta U + delta {W_{{text{ie}}}} + delta {W_{{text{nc}}}}}
ight)} {text{d}}t = 0 $$
(10)

式中, δT, δU, δWie和δWnc分别为动能、势能、电能和非保守能的变分. 在本研究中, 由于在动能中考虑了基础激励的影响, 机械阻尼在后续研究中引入, 因此非保守虚功为







$$ delta {W_{{text{nc}}}} = delta {W_{{text{nce}}}} = Q(t)delta v(t) $$
(11)

将式(7) ~ 式(9)和式(11)代入式(10), 忽略惯性矩和面内惯性, 机电耦合方程为







$$ begin{split}& D{nabla ^4}w + left[ {m + {m_0}delta left( r
ight)}
ight]ddot w - & qquad frac{{{d_{31}}left( {{h_{text{p}}} + {h_{text{b}}}}
ight)vleft( t
ight)}}{{2S_{11}^{text{E}}left( {1 - {v_{text{p}}}}
ight)}}left( {frac{{{delta _{text{F}}}}}{r} + frac{{partial {delta _{text{F}}}}}{{partial r}}}
ight) = - left[ {m + {m_0}delta left( r
ight)}
ight]ddot y end{split} $$
(12)







$$ begin{split}& displaystyleint_{{A_{text{p}}}} {left. {frac{{left( {{h_{text{p}}} + {h_{text{b}}}}
ight){d_{31}}{nabla ^2}w}}{{2S_{11}^Eleft( {1 - {v_{text{p}}}}
ight)}} + }
ight.} & left. {frac{{vleft( t
ight)}}{{2{h_{text{p}}}}}left[ {varepsilon _{33}^T - frac{{2d_{31}^2}}{{S_{11}^Eleft( {1 - {v_{text{p}}}}
ight)}}}
ight.}
ight]{text{d}}A + Q = 0 end{split} $$
(13)

式中, $ {delta _{text{F}}} = delta left( {r - {r_{{text{pi}}}}}
ight) - delta left( {r - {r_{{text{po}}}}}
ight) $为狄拉克函数.

对式(13)求关于时间的导数, 根据$ dot Q = dfrac{{vleft( t
ight)}}{{{R_{text{L}}}}} $, 得







$$ int_{{A_{text{p}}}} { {frac{{left( {{h_{text{p}}} + {h_{text{b}}}}
ight){d_{31}}{nabla ^2}dot w}}{{2S_{11}^Eleft( {1 - {v_{text{p}}}}
ight)}}}} {text{d}}A + {C_{text{p}}}dot vleft( t
ight) + frac{{vleft( t
ight)}}{{{R_{text{L}}}}} = 0 $$
(14)

式中, RL表示负载阻抗; 压电陶瓷的电容






$$ {C_{text{p}}} = dfrac{{{text{π}} left( {r_{{text{po}}}^2 - r_{{text{pi}}}^2}
ight)vleft( t
ight)}}{{2{h_{text{p}}}}}left[ {varepsilon _{33}^T - dfrac{{2d_{31}^2}}{{S_{11}^{text{E}}left( {1 - {v_{text{p}}}}
ight)}}}
ight]$$

将横向挠度假设为[33]







$$ wleft( {r,t}
ight) = sumlimits_{r = 1}^N {{phi _r}left( r
ight){q_r}left( t
ight)} $$
(15)

式中, $ {q_r}left( t
ight) $, $ {phi _r}left( r
ight) $分别表示r阶模态坐标和振型, 考虑到由压电片引起的几何变化, $ {phi _r}left( r
ight) $可表示为(具体过程见附录A)







$$ {phi _r}left( r
ight) = left{ begin{array}{l} {phi _{1r}}left( r
ight),{text{ 0}} leqslant r leqslant {r_{{text{pi}}}} {phi _{2r}}left( r
ight),{text{ }}{r_{{text{pi}}}} leqslant r leqslant {r_{{text{po}}}}{text{ }} {phi _{3r}}left( r
ight),{text{ }}{r_{{text{po}}}} leqslant r leqslant {r_{text{b}}}{text{ }} end{array}
ight. $$
(16)

将式(15)代入式(12)和式(14), 引入瑞利阻尼[31], 用伽辽金法对方程离散化得







$$ {boldsymbol{M}}ddot {boldsymbol{q}} + {boldsymbol{D}}dot {boldsymbol{q}} + {boldsymbol{Kq}} - {boldsymbol{theta}} vleft( t
ight) = - pddot yleft( t
ight) $$
(17)







$$ {{boldsymbol{eta}} ^{
m{T}}}dot {boldsymbol{q}} + {C_{text{p}}}dot vleft( t
ight) + frac{1}{{{R_{text{L}}}}}vleft( t
ight) = 0 $$
(18)

式中, M，D = μΜ+γK，K分别表示质量矩阵、阻尼矩阵和刚度矩阵, 其中μ和γ是比例系数[31]. θ和η分别代表反向耦合项和正向耦合项, 表示为






$$begin{split} {m_{ir}}{text{ = }}&intlimits_{{A_1}} {{m_1}{phi _{r1}}{phi _{i1}}{text{d}}A + } intlimits_{{A_2}} {{m_2}{phi _{r2}}{phi _{i2}}{text{d}}A + } & {intlimits_{{A_3}} {{m_3}{phi _{r3}}{phi _{i3}}{text{d}}A} + {m_0}{phi _{r1}}left( 0
ight){phi _{i1}}left( 0
ight){text{ = }}} & {{text{2}}{text{π}} left( {int_0^{{r_{{text{pi}}}}} {{m_1}{phi _{r1}}{phi _{i1}}r} {text{d}}r + int_{{r_{{text{pi}}}}}^{{r_{{text{po}}}}} {{m_2}{phi _{r2}}{phi _{i2}}r} {text{d}}r + }
ight.} & {left. {int_{{r_{{text{po}}}}}^{{r_{text{b}}}} {{m_3}{phi _{r3}}{phi _{i3}}r} {text{d}}r}
ight) + {m_0}{phi _{r1}}left( 0
ight){phi _{i1}}left( 0
ight)} {{text{ }}} end{split}$$






$$ begin{split} {k_{ir}} =& intlimits_{{A_1}} {{D_1}{nabla ^4}left( {{phi _{r1}}}
ight){phi _{i1}}{text{d}}A + intlimits_{{A_2}} {{D_2}{nabla ^4}left( {{phi _{r2}}}
ight){phi _{i2}}{text{d}}A} } {text{ }} + & {text{ }} intlimits_{{A_3}} {{D_3}{nabla ^4}left( {{phi _{r3}}}
ight){phi _{i3}}{text{d}}A{text{ = 2}}{text{π}} Biggl[{14} {int_0^{{r_{text {pi}}}} {{D_1}{nabla ^4}left( {{phi _{r1}}}
ight){phi _{i1}}r} {text{d}}r + } } & {int_{{r_{text {pi}}}}^{{r_{{text{po}}}}} {{D_2}{nabla ^4}left( {{phi _{r2}}}
ight){phi _{i2}}r} {text{d}}r + int_{{r_{{text{po}}}}}^{{r_{text{b}}}} {{D_3}{nabla ^4}left( {{phi _{r3}}}
ight){phi _{i3}}r} {text{d}}r} Biggl]{14}{text{ }}end{split}$$






$$ {theta _i} = frac{{{d_{31}}left( {{h_{text{p}}} + {h_{text{b}}}}
ight){text{π}} }}{{S_{11}^Eleft( {1 - {v_{text{p}}}}
ight)}}left( {{r_{{text{po}}}}frac{{{text{d}}{phi _{i2}}}}{{{text{d}}r}} {{r_{{text{po}}}}} - {r_{{text{pi}}}}frac{{{text{d}}{phi _{i2}}}}{{{text{d}}r}} {{r_{{text{pi}}}}} }
ight) $$






$$ begin{split} {p_i} &= intlimits_{{A_1}} {{m_1}{phi _{i1}}} {text{d}}A + intlimits_{{A_2}} {{m_2}{phi _{i2}}{text{d}}A} + intlimits_{{A_3}} {{m_3}{phi _{i3}}{text{d}}A} + {m_0}{phi _{i1}}left( 0
ight) = & {text{ 2}}{text{π}} Biggr( {int_0^{{r_{{text{pi}}}}} {{m_1}{phi _{i1}}r} {text{d}}r + int_{r_{{text{pi}}}}^{{r_{{text{po}}}}} {{m_2}{phi _{i2}}r{text{d}}r} + } & {int_{{r_{{text{po}}}}}^{{r_{text{b}}}} {{m_3}{phi _{i3}}r} {text{d}}r} Biggr) + {m_0}{phi _{i1}}left( 0
ight) end{split} $$






$$ begin{split} {eta _i} = &frac{{left( {{h_{text{p}}} + {h_{text{b}}}}
ight){d_{31}}}}{{2S_{11}^Eleft( {1 - {v_{text{p}}}}
ight)}}int_{{A_{text{p}}}} {left[ {phi _{i2}^{''}left( r
ight) + frac{1}{r}phi _{i2}'left( r
ight)}
ight]} {text{d}}A = &frac{{{text{π}} left( {{h_{text{p}}} + {h_{text{b}}}}
ight){d_{31}}}}{{S_{11}^Eleft( {1 - {v_{text{p}}}}
ight)}}int_{{r_{{text{pi}}}}}^{{r_{{text{po}}}}} {left[ {rphi _{i2}^{''}left( r
ight) + phi _{i2}'left( r
ight)}
ight]{text{d}}r} end{split}qquadqquad $$


1.2
电压和功率输出闭合解


假设$ddot yleft( t
ight) = a{{
m{e}}^{{
m{j}}omega t}}$, 外力矢量为







$$ {boldsymbol{f}} = - {boldsymbol{p}}ddot yleft( t
ight) = - {boldsymbol{p}}a{{
m{e}}^{{
m{j}}omega t}} $$
(19)

式中, a和ω分别表示基础激励的加速度幅值和频率.

基于线性机电假设, 广义坐标和输出电压可表示为







$$ left. begin{array}{l}{boldsymbol{q}}left( t
ight) = {boldsymbol{varTheta}} {{
m{e}}^{{
m{j}}omega t}}vleft( t
ight) = V{{
m{e}}^{{
m{j}}omega t}}end{array}
ight} $$
(20)

式中, ${boldsymbol{varTheta}}$, $ V $分别表示响应幅值和电压幅值.

将式(19)、式(20)代入式(17)、式(18), 得到能量采集器在短路(RL→0)和断路(RL→∞)状态下的固有频率、系统的响应幅值和电压幅值为







$$ left. begin{array}{l} left| { - {boldsymbol{M}}{omega ^2} + {boldsymbol{K}}}
ight| = 0{text{ }}left( {{R_{text{L}}} to 0}
ight) left| { - {boldsymbol{M}}{omega ^2} + {boldsymbol{K}} + dfrac{{{boldsymbol{theta}} {{boldsymbol{eta}} ^{text{T}}}}}{{{{{C}}_{text{p}}}}}}
ight| = 0{text{ }}left( {{R_{text{L}}} to infty }
ight) end{array}
ight} $$
(21)







$$ {boldsymbol{varTheta}} = {left( { - {boldsymbol{M}}{omega ^2} + {boldsymbol{D}}{
m{j}}omega + {boldsymbol{K}} + dfrac{{{boldsymbol{theta}} {{boldsymbol{eta}} ^{text{T}}}{
m{j}}omega }}{{{C_{text{P}}}{
m{j}}omega + {{{R_{text{L}}}^{ - 1}}}}}}
ight)^{ - 1}}left( { - {boldsymbol{p}}a}
ight) $$
(22)







$$ begin{split} &V = - dfrac{{{
m{j}}omega }}{{{C_{text{p}}}{
m{j}}omega + {{{R_{text{L}}^{-1}}}}}}{{boldsymbol{eta}} ^{text{T}}}.&;;;;;;;{left( { - {boldsymbol{M}}{omega ^2} + {boldsymbol{D}}{
m{j}}omega + {boldsymbol{K}} + dfrac{{{boldsymbol{theta}} {{boldsymbol{eta}} ^{text{T}}}{
m{j}}omega }}{{{C_{text{p}}}{
m{j}}omega + {{{R_{text{L}}^{ - 1}}}}}}}
ight)}left( { - {boldsymbol{p}}a}
ight) end{split}$$
(23)

功率幅值可以定义为







$$ P = frac{{{V^2}}}{{{R_{text{L}}}}} $$
(24)

求解$dfrac{{partial P}}{{partial {R_{text{L}}}}} = 0$, 得到最优负载







$$ {R_{text{L}}} = left({{{C_{text{p}}}{
m{j}}omega + dfrac{{{{boldsymbol{eta}} ^{
m{T}}}{boldsymbol{theta}} {
m{j}}omega }}{{ - {boldsymbol{M}}{omega ^2} + {boldsymbol{D}}{
m{j}}omega + {boldsymbol{K}}}}}}
ight)^{-1} $$
(25)


2.
结果与讨论


本节, 选择黄铜为基体结构, PZT-5H[31]为压电层来研究附加质量块的压电圆板能量采集器的采集性能. 压电圆板能量采集器的参数如表1所示.




表
1
圆板能量采集器的参数



Table
1.
The parameters of the circular energy harvester



table_type1 ">
ParameterUnitValue
Eb GPa 90
$ S_{11}^E $ m2/N 1.65 × 10?11
ρb kg/m3 8500
ρp kg/m3 7500
vb — 0.33
vp — 0.2897
d31 m/V ?2.74 × 10?10
$varepsilon _{33}^T$ F/m 3.021 × 10?8
hb mm 0.2
hp mm 0.2
rb mm 28
μ s?1 57.7715
γ s 7.7022 × 10?6





下载:
导出CSV
|显示表格



2.1
收敛性研究


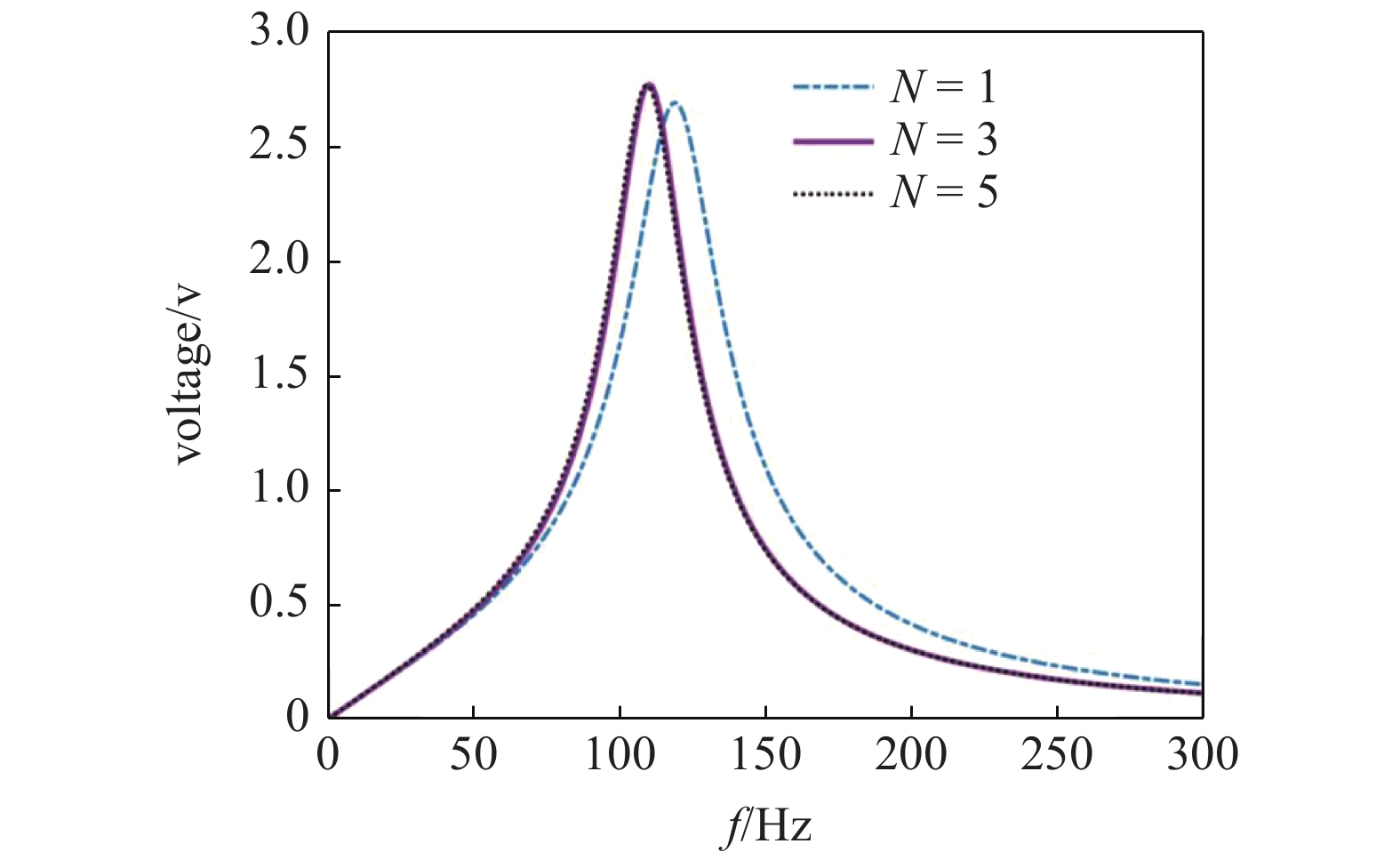
首先, 收敛性研究来确定准确预测出输出电压和功率的假设模态数量. 图2绘制了不同模态数量对应的电压频响图, 其他参数分别为rpi = 2 mm, rpo = 20 mm, RL = 25 kΩ, m0 = 74.3 g和a = 0.1g. 显然, 当N ≥ 3时, 结果趋于收敛, 因此选择N = 3进行数值分析.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-441-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
不同模态数下输出电压随基础激励频率变化



Figure
2.
The variation of the voltage output with base excitation frequency for different number of modes



下载:
全尺寸图片
幻灯片



2.2
有限元仿真和验证


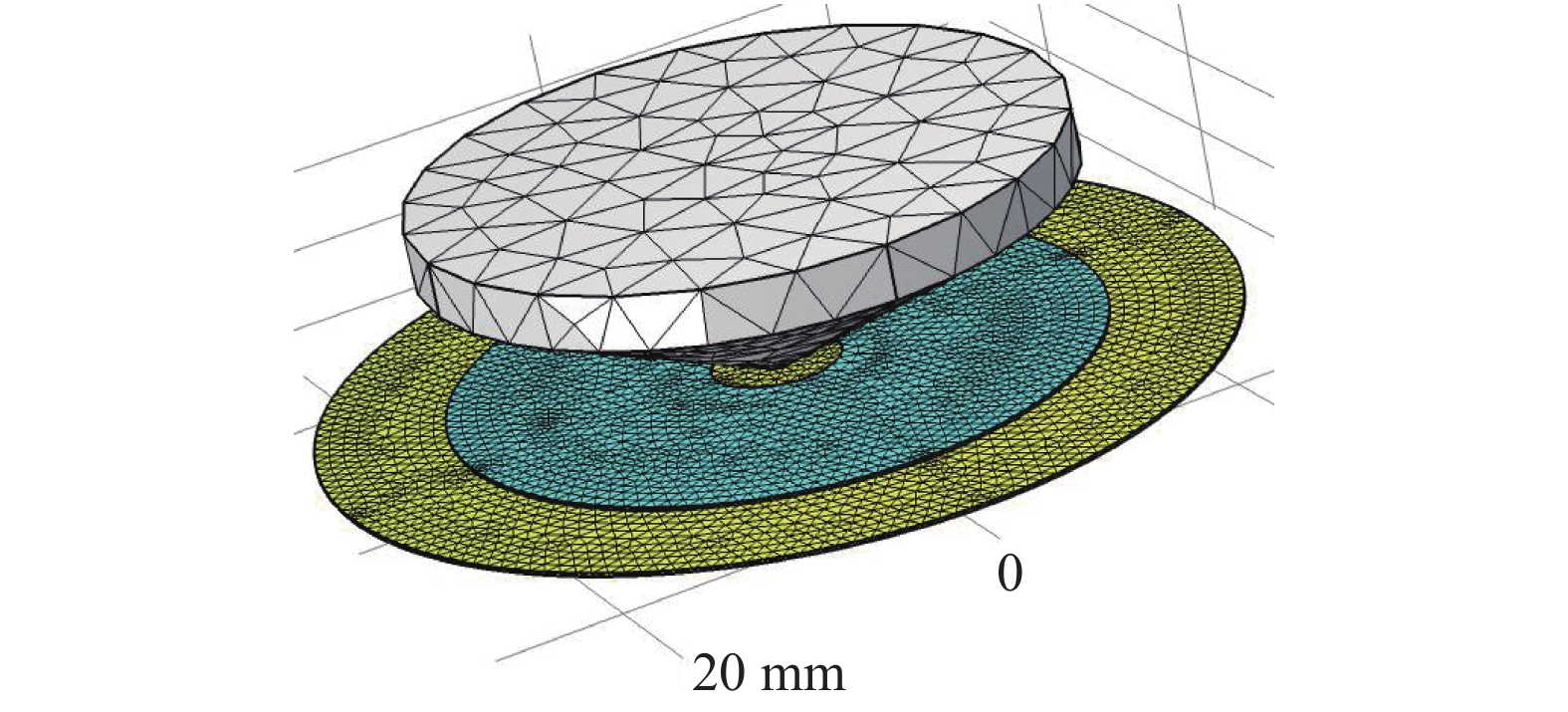
为验证理论推导的正确性, 采用有限元软件COMSOL建立了压电圆板能量采集器有限元分析模型, 如图3所示, 其中, 蓝色和黄色分别表示压电片和基体黄铜. 接下来, 使用压电和固体力学模块对压电圆板能量采集器进行模态分析, 稳态响应分析.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-441-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
压电圆板能量采集器的有限元模型



Figure
3.
Finite element model of the piezoelectric circular plate energy harvester



下载:
全尺寸图片
幻灯片


无附加质量时圆板能量采集器固有频率的解析计算与有限元计算结果对比, 如表2所示. 从表2中可以观察到最大相对误差为0.397%, 这说明了理论计算与有限元计算结果高度一致, 验证了理论推导的正确性. 表3总结了m0 = 74.3 g时圆板能量采集器固有频率的理论计算与有限元仿真结果, 同时有限元仿真中考虑了附加质量的接触半径, 定义χ = rm/rb (质量块与压电复合板的接触半径与基板半径比值). 分析可得, 当χ = 1/28时, 最大相对误差为1.141%, 当χ = 1/14时, 最大相对误差增大至5.87%. 表明相对误差随着质量块与复合板的接触半径的增加而增加. 产生误差的主要原因是在理论模型中, 将质量块考虑为中心质点, 而实际模型中, 质量块与复合板的接触半径会影响能量采集器的固有频率. 综上所述, 随着质量块与复合板接触半径的减小, 理论模型和有限元模型一致性增强.




表
2
m0 = 0时压电圆板能量采集器的固有频率理论值与仿真值比较



Table
2.
Comparison of natural frequency of circular energy harvester with m0 = 0 from theory and simulation



table_type2 ">
rpi/mmRL = 0 ΩRL = 10 kΩRL→∞
FEA/Hzmodel/Hz error/%FEA/Hzmodel/Hz error/%FEA/Hzmodel/Hz error/%
0 581.73 580.72 ?0.174 656.66 654.05 ?0.397 663.88 662.87 ?0.152
3 572.56 571.56 ?0.175 640.32 638.01 ?0.361 647.41 646.75 ?0.102
4 566.81 565.82 ?0.175 629.94 627.88 ?0.328 636.95 636.46 ?0.077
5 560.64 559.64 ?0.178 618.72 616.81 ?0.309 625.64 625.48 ?0.026





下载:
导出CSV
|显示表格






表
3
m0 = 74.3 g时压电圆板能量采集器的固有频率理论值与仿真比较



Table
3.
Comparison of natural frequency of circular energy harvester with m0 = 74.3 g from theory and simulation



table_type2 ">
rpi/mmRL = 0 ΩRL→∞
model/HzFEA (χ = 1/28)/Hzerror/%FEA (χ = 1/14)/Hzerror/%model/HzFEA (χ = 1/28)/Hzerror/%FEA (χ = 1/14)/Hzerror/%
0 109.81 110.23 ?0.383 113.6 ?3.33 125.61 126.88 ?1.003 130.89 ?4.04
3 97.89 97.73 0.164 102.02 ?4.05 108.72 108.27 0.411 113.96 ?4.60
4 92.85 92.03 0.893 96.81 ?4.09 101.54 100.42 1.116 106.55 ?4.70
5 87.57 86.58 1.141 91.66 ?4.46 94.04 93.26 0.835 99.56 ?5.87





下载:
导出CSV
|显示表格



2.3
参数对能量采集器采集性能的影响


附加质量块的压电圆板能量采集器的解析解是必不可少的, 它可以根据具体的要求快速设计采集器. 本节基于闭合解探讨负载阻抗、附加质量、压电板的内外径对能量采集器采集性能的影响, 并通过有限元仿真进行验证. 在有限元仿真中质量块与压电复合板的接触半径rm = 1 mm.

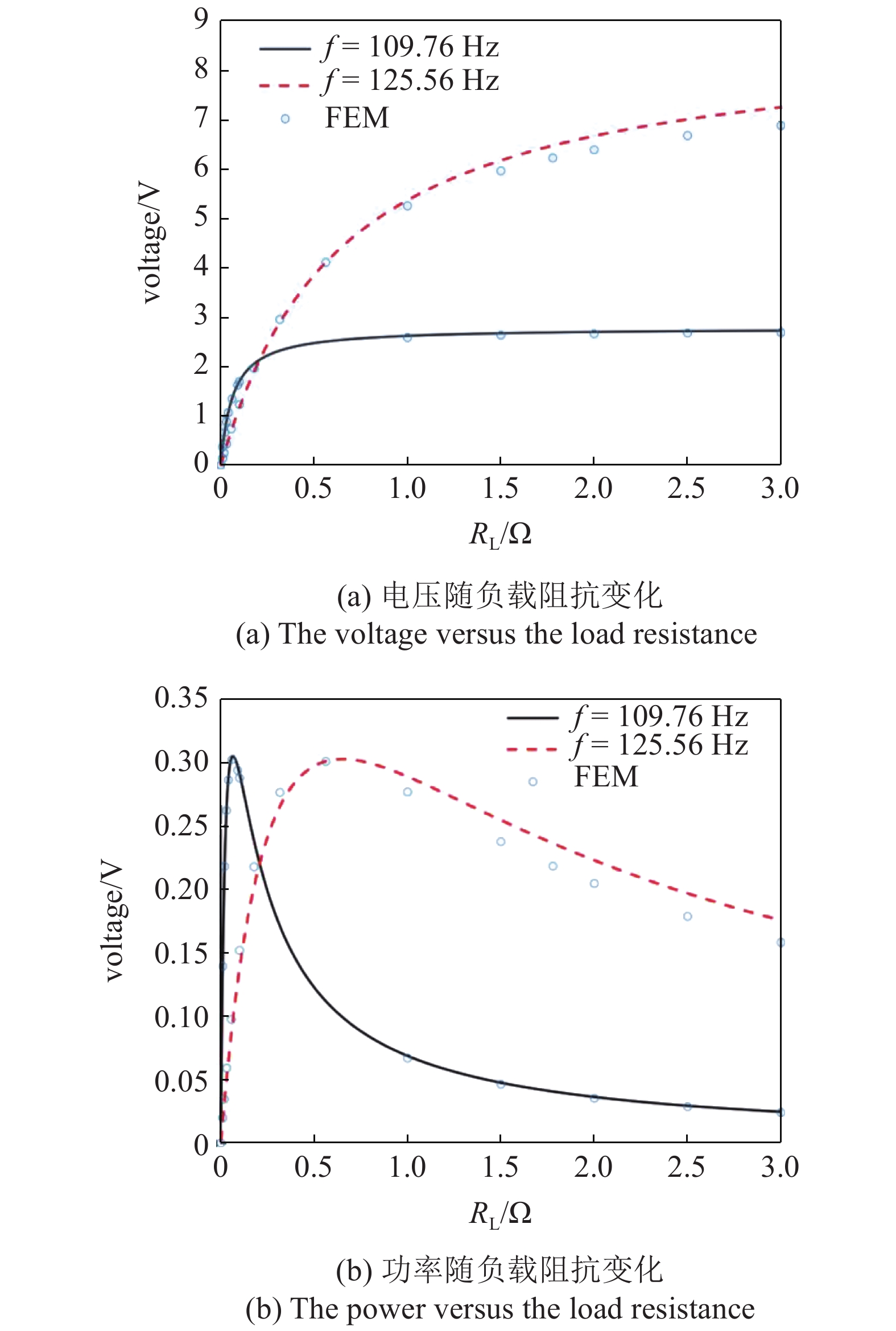
图4绘制了在短路和断路共振频率处激励时, 电压和功率随负载阻抗的变化, 其余参数分别为rpi = 0 mm, rpo = 20 mm, a = 0.1g, m0 = 74.3 g. 给出的结果表明理论解(线)与有限元解(空心点)高度一致. 分析可知, 给定基础激励频率, 电压随负载阻抗的增大而单调升高, 进而趋于稳定. 输出功率先增大再降低, 且不同基础激励频率下系统的最优阻抗也不同, 通过方程(25)得到最优阻抗. 从图4中还可以观察到, 负载阻抗较小时, 由于系统接近于短路, 因而短路共振频率激励下(f = 109.76 Hz) 的输出电压和功率相对较高. 随负载阻抗的增大, 曲线交于RL = 20.5 kΩ处, 此时电压和功率相等, 越过该点后, 由于负载阻抗较大, 系统接近开路状态, 断路共振频率激励下 (f = 125.56 Hz)的电压和功率较大.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-441-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
负载阻抗对输出电压和功率的影响



Figure
4.
The effect of the load resistance on the output voltage and power



下载:
全尺寸图片
幻灯片


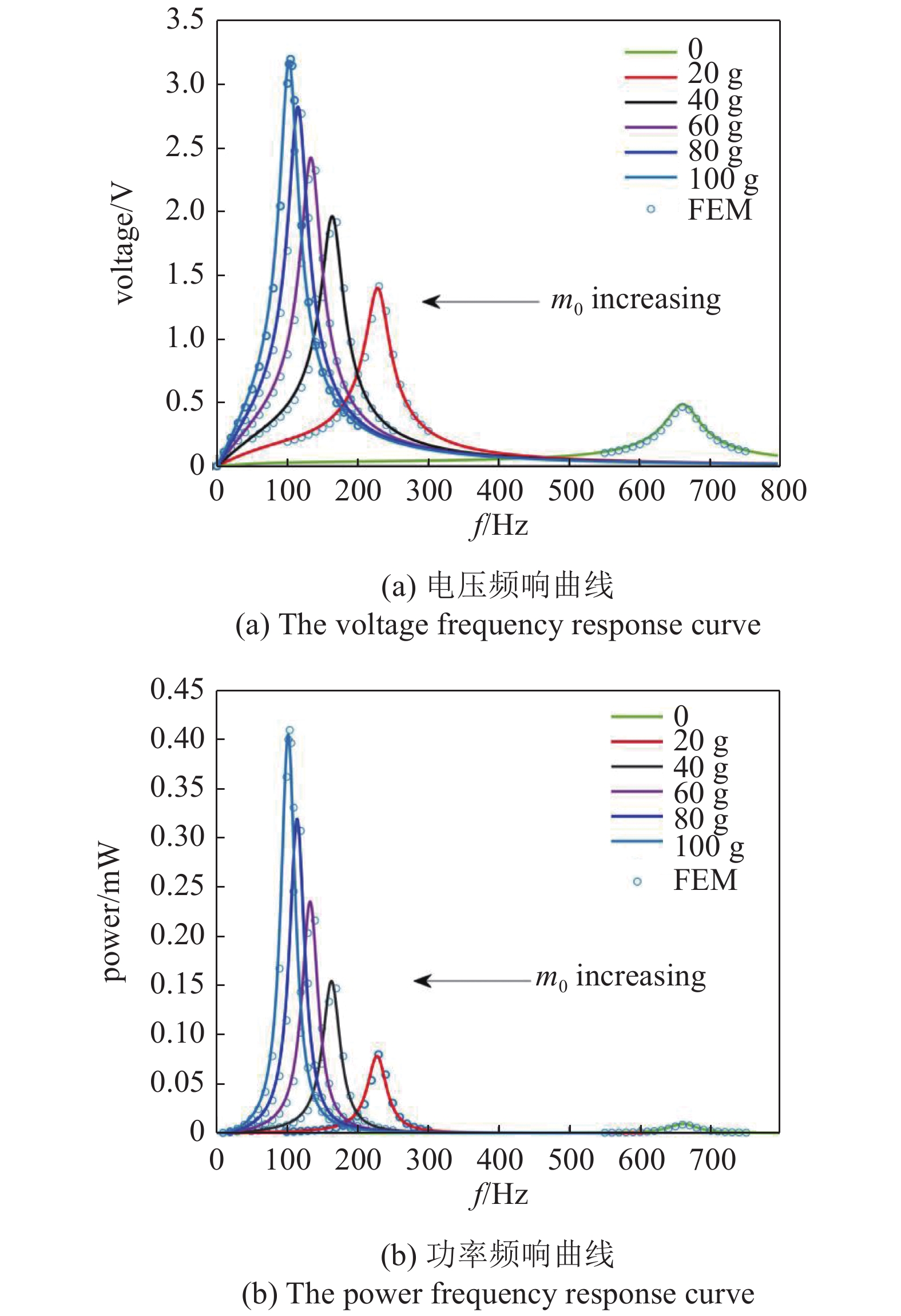
附加质量对压电能量采集器输出电压和功率的影响如图5所示, 其余参数分别为rpi = 0 mm, rpo = 20 mm, a = 0.1g, RL = 25 kΩ. 显然, 与无质量块相比, 附加20 g质量块的能量采集器固有频率从661.38 Hz降低到228.228 Hz, 输出电压和功率分别增长了187.74%和724.21%. 这表明质量荷载能够有效降低采集器的固有频率和增加其采集性能. 然而, 增加质量荷载对提高采集器的采集性能是有限制的, 具体而言, 附加40 g质量块的能量采集器输出电压和功率相较于20 g, 分别提升了40%和97%; 而附加60 g质量块的能量采集器的输出电压和功率相较于40 g, 分别提升了23%和52%. 显然随着质量块重量的提升, 电压和功率输出增长率降低. 且过重的质量块容易造成压电陶瓷板破裂.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-441-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
附加质量对能量采集器采集性能的影响



Figure
5.
The influence of the mass on the harvesting performance of the energy harvester



下载:
全尺寸图片
幻灯片


压电片外半径对固有频率、最大输出电压和功率的影响如图6所示, 定义λ = rpo/rb (压电片外半径与基板半径比值), 其余参数分别为rpi = 0, a = 0.1g, RL = 25 kΩ, m0 = 74.3 g. 图6(a)显示, 能量采集器的固有频率随外半径的增加而增大, 当λ大于0.928时, 固有频率斜率增大. 图6(b)和图6(c)描绘了最大输出电压和功率随λ的变化. 显然, 在λ$ in $(0.4, 0.58)区域内, 随λ的增加, 最大输出电压和功率增加; 在 λ$ in $(0.57, 0.9)的区域内, 最大输出电压和功率随着λ增大变化幅度较小; 在λ$ in $(0.9, 1)区域内, 随λ的增加, 最大输出电压和功率降低, 当λ = 1时, 最大输出电压和功率均为0. 也就是说, 完全覆盖压电层的固支圆板不能用作能量采集器, 在文献[15]中也发现了相同的现象. 综上所述, 给定压电片内径, 在λ$ in $(0.55, 0.62)区域内, 既可以降低能量采集器的固有频率, 又可以收获较高的输出电压和功率.



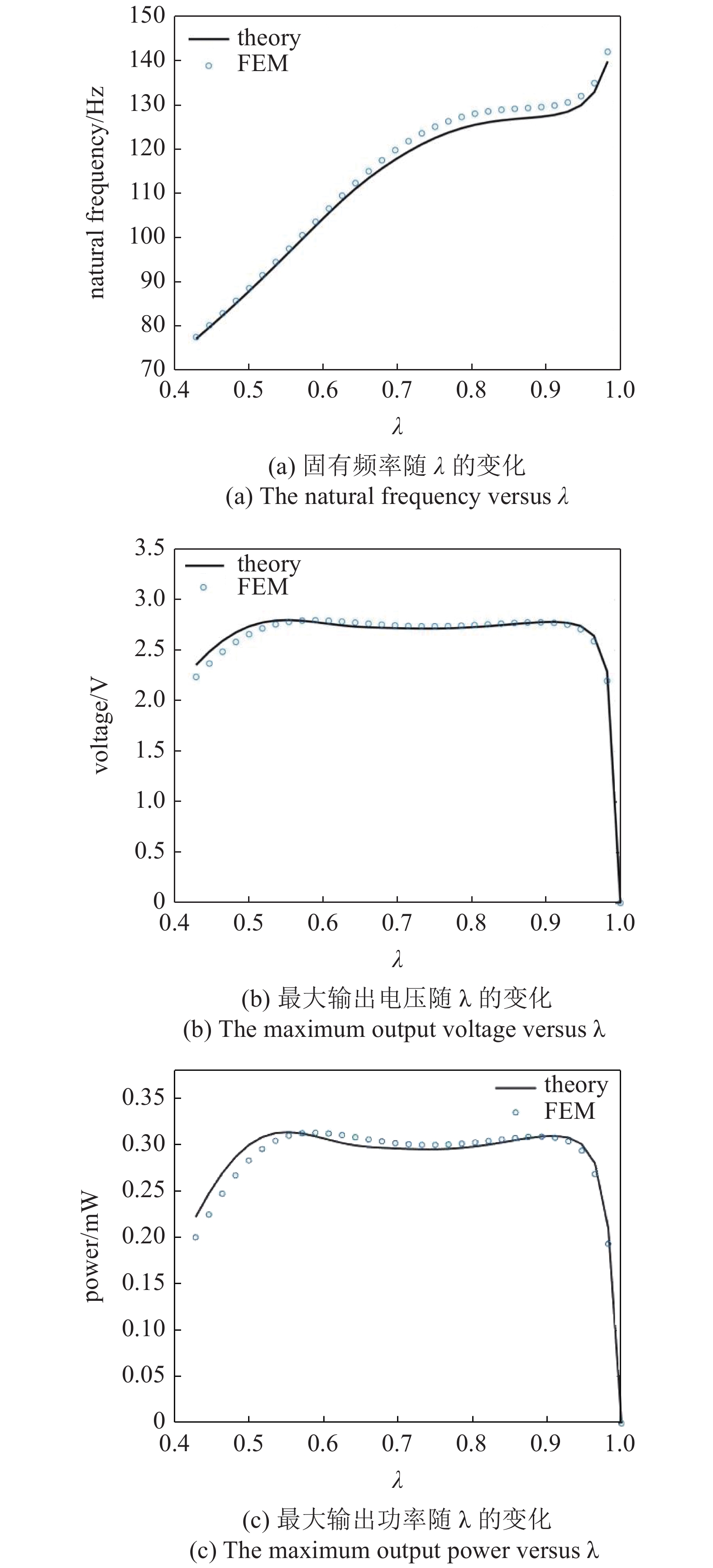onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-441-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
压电片外径对能量采集器的固有频率、最大输出电压和功率的影响



Figure
6.
The effect of the outer radius of the piezoelectric plate on the natural frequency, maximum output voltage and power of the energy harvester



下载:
全尺寸图片
幻灯片


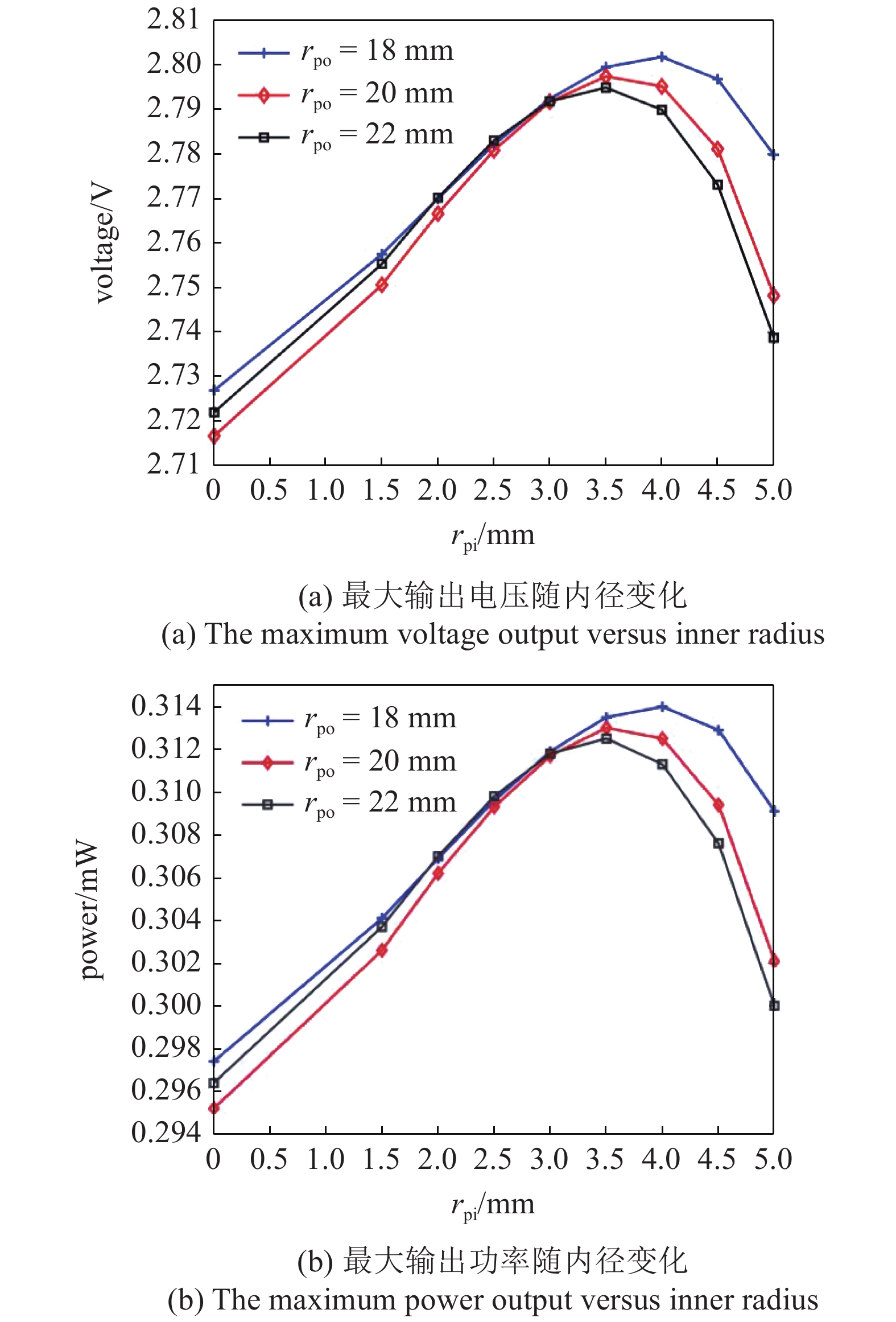
图7(a)和图7(b)绘制了不同的外半径下, 最大输出电压和功率随压电板内径的变化. 其余参数分别为m0 = 74.3 g, a = 0.1g, RL = 25 kΩ. 分析可得, 给定压电片外径, 随着内径的增大, 最大电压和功率的输出先增大再降低. 为了更具体地说明压电片内径对能量采集器性能的影响, 以外径为20 mm的压电圆板为例具体分析, 如图7(c)和图7(d)所示. 随着内径的增大, 共振频率降低, 最大输出功率和电压增加, 直至内径为3.5 mm, 此时, 共振频率为100.6 Hz, 输出功率和电压分别达到最大值0.313 mW和2.7974 V. 随着内径的进一步增大, 共振频率持续降低, 输出电压和功率开始下降. 因此, 相较于无孔的压电片, 内径位于2.5 ~ 4 mm范围内的压电片可以提高能量采集器的采集性能.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-441-7-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-441-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
压电片内半径对能量采集器采集性能的影响



Figure
7.
The effect of the inner radius of the piezoelectric plate on the harvesting performance of energy harvester



下载:
全尺寸图片
幻灯片



3.
结论


基于基尔霍夫薄板理论, 应用广义哈密顿原理建立了附加质量块的压电圆板能量采集器的理论模型. 采用数值分析和有限元仿真研究各参数对压电圆板能量采集器的采集性能的影响. 得到以下结论.

(1) 随着质量块与复合板接触半径的减小, 理论模型和有限元模型一致性增强.

(2) 能量采集器的输出电压、功率受负载阻抗、附加质量、压电片内外径等的综合影响. 随负载阻抗的增加, 能量采集器的输出电压增加, 直至趋于稳定, 输出功率先增加再降低. 不同基础激励频率下系统的最优阻抗也不同.

(3) 质量块的引入有效降低了能量采集器的固有频率, 提高了其采集性能. 与无质量块相比, 附加20g质量块的能量采集器固有频率降低了65%, 输出电压和功率分别增长了187.74%和724.21%.

(4) 压电片外径的增加会增大能量采集器的固有频率. 设置压电片内径为0, 在λ$ in $(0.55, 0.62)区域内, 能量采集器的采集性能相对较高.

(5) 相较于无孔的压电片, 压电片内径的合理选择不仅可以降低能量采集器的固有频率, 还可以提高其采集性能.

附录A$ ;$

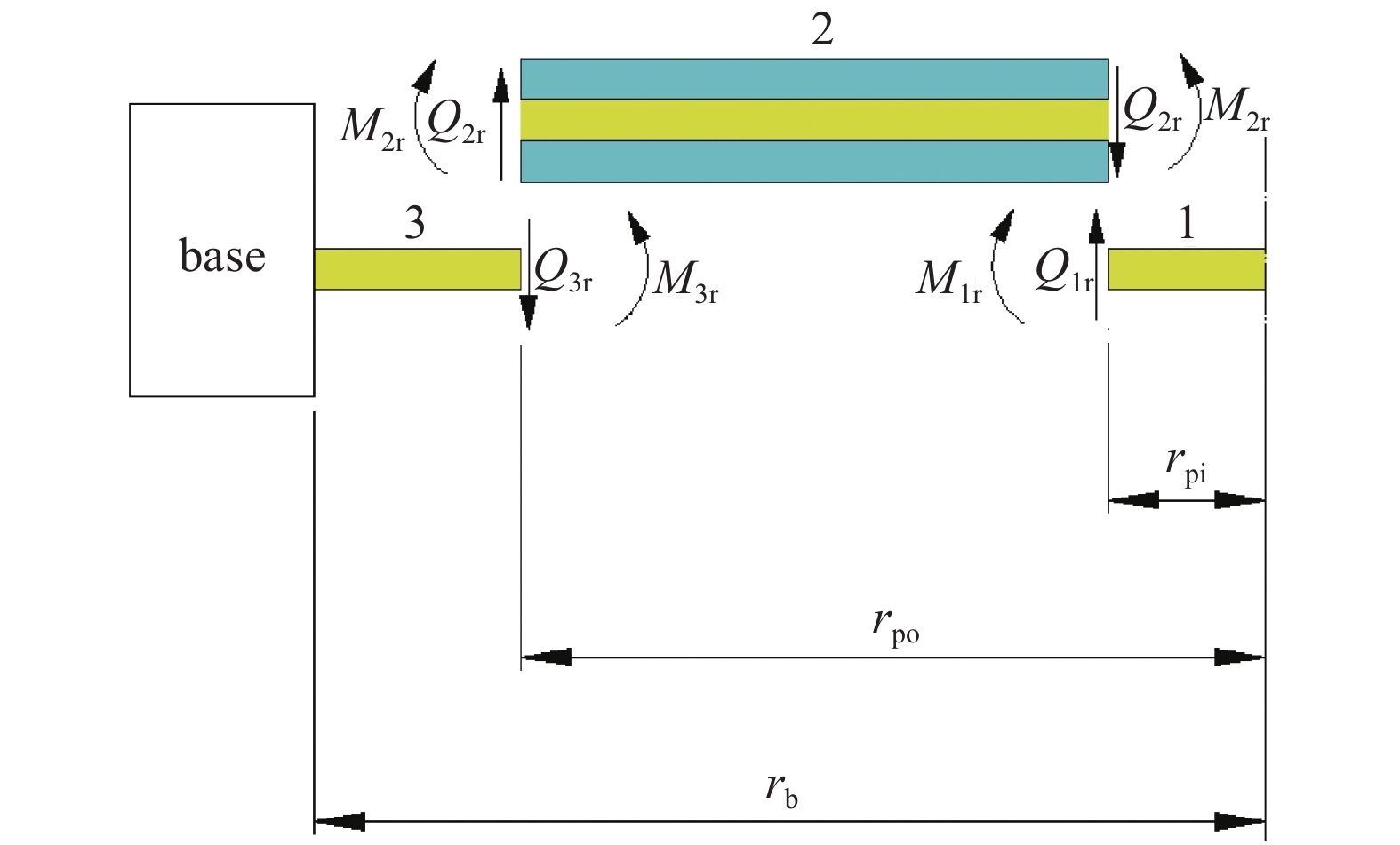
为得到压电复合板的振型, 将压电复合板分为3部分, 每部分的力学行为和边界条件如图A1所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-441-A1.jpg'"
class="figure_img
figure_type1 bbb " id="Suppl-FigureA1" />



A1
能量采集器3个截面受力分析



A1.
The force analysis of the three sections of the energy harvester



下载:
全尺寸图片
幻灯片


基于弹性板的弯曲振动理论, 假定$ {phi _r}left( r
ight) $为[34]






$$ left. begin{array}{l} {phi _{1r}}(r) ={A_1}{{
m{J}}_0}left( {{beta _1}r}
ight) + {C_1}{{
m{I}}_0}left( {{beta _1}r}
ight),qquad{text{ 0}} leqslant r leqslant {r_{{text{pi}}}} {phi _{2r}}(r) ={A_2}{{
m{J}}_0}left( {{beta _2}r}
ight) + {B_2}{{
m{Y}}_0}left( {{beta _2}r}
ight) + qquad {C_2}{{
m{I}}_0}left( {{beta _2}r}
ight) + {D_2}{{
m{K}}_0}left( {{beta _2}r}
ight),qquad{text{ }}{r_{{text{pi}}}} leqslant r leqslant {r_{{text{po}}}} {phi _{3r}}(r) = {A_3}{{
m{J}}_0}left( {{beta _3}r}
ight) + {B_3}{{
m{Y}}_0}left( {{beta _3}r}
ight) + {C_3}{{
m{I}}_0}left( {{beta _3}r}
ight) + qquad {D_3}{{
m{K}}_0}left( {{beta _3}r}
ight),qquad {text{ }}{r_{{text{po}}}} leqslant r leqslant {r_{text{b}}} end{array}
ight} tag{A1}$$

式中J0, Y0, K0和I0均为零阶贝塞尔函数.

$ omega = beta _1^2sqrt {dfrac{{{D_1}}}{{{m_1}}}} = beta _2^2sqrt {dfrac{{{D_2}}}{{{m_2}}}} = beta _3^2sqrt {dfrac{{{D_3}}}{{{m_3}}}} $, 系数Ai, Bi, Ci和Di可通过下列的边界条件确定.

r = rpi处的边界条件为






$$ left. {begin{array}{*{20}{l}}{phi _{1r}}{|_{{r_{{
m{pi}}}}}} = {phi _{2r}}{|_{{r_{{
m{pi}}}}}}dfrac{{{
m{d}}{phi _{1r}}}}{{{
m{d}}r}}{|_{{r_{{
m{pi}}}}}} = dfrac{{{
m{d}}{phi _{2r}}}}{{{
m{d}}r}}{|_{{r_{{
m{pi}}}}}}{M_{1r}}{|_{{r_{{
m{pi}}}}}} = {M_{2r}}{|_{{r_{{
m{pi}}}}}}{Q_{1r}}{|_{{r_{{
m{pi}}}}}} = {Q_{2r}}{|_{{r_{{
m{pi}}}}}}end{array}}
ight} tag{A2}$$

式中






$$ begin{array}{l} {M_{1r}} = - {D_1}left( {dfrac{{{partial ^2}{phi _{1r}}}}{{partial {r^2}}} + dfrac{{{v_1}}}{r}dfrac{{partial {phi _{1r}}}}{{partial r}}}
ight) {M_{2r}} = - {D_2}left( {dfrac{{{partial ^2}{phi _{2r}}}}{{partial {r^2}}} + dfrac{{{v_2}}}{r}dfrac{{partial {phi _{2r}}}}{{partial r}}}
ight) {Q_{1r}} = - {D_1}dfrac{partial }{{partial r}}left( {dfrac{{{partial ^2}{phi _{1r}}}}{{partial {r^2}}} + dfrac{1}{r}dfrac{{partial {phi _{1r}}}}{{partial r}}}
ight) {Q_{2r}} = - {D_2}dfrac{partial }{{partial r}}left( {dfrac{{{partial ^2}{phi _{2r}}}}{{partial {r^2}}} + dfrac{1}{r}dfrac{{partial {phi _{2r}}}}{{partial r}}}
ight) end{array} $$

r = rpo处的边界条件为






$$ left. begin{array}{l} {phi _{2r}}{|_{{r_{{text{po}}}}}} = {phi _{3r}}{|_{{r_{{text{po}}}}}}dfrac{{{text{d}}{phi _{2r}}}}{{{text{d}}r}}{|_{_{{r_{{text{po}}}}}}} = dfrac{{{text{d}}{phi _{3r}}}}{{{text{d}}r}}{|_{_{{r_{{text{po}}}}}}} {M_{2r}}{|_{{r_{{text{po}}}}}} = {M_{3r}}{|_{_{{r_{{text{po}}}}}}} {Q_{2r}}{|_{_{{r_{{text{po}}}}}}} = {Q_{3r}}{|_{_{{r_{{text{po}}}}}}} end{array}
ight} tag{A3}$$

式中






$$ begin{array}{l} {M_{3r}} = - {D_3}left( {dfrac{{{partial ^2}{phi _{3r}}}}{{partial {r^2}}} + dfrac{{{v_3}}}{r}dfrac{{partial {phi _{3r}}}}{{partial r}}}
ight) {Q_{3r}} = - {D_3}dfrac{partial }{{partial r}}left( {dfrac{{{partial ^2}{phi _{3r}}}}{{partial {r^2}}} + dfrac{1}{r}dfrac{{partial {phi _{3r}}}}{{partial r}}}
ight) end{array} $$

夹紧边r = rb处的边界条件为






$$ left. begin{array}{l} {phi _{3r}}{|_{{r_{text{b}}}}} = 0dfrac{{{text{d}}{phi _{3r}}}}{{{text{d}}r}}{|_{{r_{text{b}}}}} = 0 end{array}
ight} tag{A4}$$

相关话题/质量 电压 图片 基础 结构
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于压电振动能量俘获的弯曲结构损伤监测研究
    引言近年来,压电材料因其具有能实现电能和机械能互相转换的特性,在工程结构中日益受到重视[1-2],被广泛应用于结构的形状控制、振动和噪声控制、损伤检测等领域[3-4].从机械振动中提取能量的特性极大满足了传感器自给供电的经济需求与生态需求,因此压电材料广泛应用于俘能器中[5-6].到目前为止,最常用 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于人工神经网络的非结构网格尺度控制方法
    引言网格生成是计算流体力学(computationalfluiddynamics,CFD)数值计算的第一步,也是未来CFD六大重要研究领域之一[1-2].在现代CFD应用过程中,自动生成复杂构型的高质量网格(包括网格自适应)依然是一个重大挑战性问题.自动化程度和网格质量是网格生成过程中最重要的两个问 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • K<sub>0</sub>超固结结构性黏土的本构模型
    引言自然界存在的天然黏土通常是K0固结与结构性并存的状态[1-2],而K0固结又按照当前竖向应力是否大于先期固结压力而分为K0正常固结与K0超固结黏土.大量的室内试验以及现场测试表明,K0正常固结黏土由于初始固结为偏压固结,与等方向正常固结黏土相比,其在大主应力与先期固结压力一致的情况下,K0固结黏 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 隧道开挖影响下地层-基础体系的接触力学响应分析
    引言在地层条件软弱、周围建筑物繁多的城市环境中进行隧道的施工,不可避免需要穿越和邻近施工,隧道施工扰动将对既有建(构)筑物的力学状态产生较大影响,进而导致建筑物的沉降、变形,甚至发生破坏[1-3].在城市运行高可靠度的要求下,隧道施工引起既有结构的工程响应预测与安全控制问题受到众多专家****与工程 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 软材料粘接结构界面破坏研究综述
    引言因其特有的低模量和能量耗散等“软”的特性以及优异的“小激励大响应”等特征,多种多样的软材料,如水凝胶、介电弹性体以及聚甲基氧硅烷等被广泛应用在软机器人、生物医学和柔性电子等各个领域[1-4].近些年,软材料的力学行为已经成为学术界和工业界广泛关注的热点之一.在实际应用中,软材料一般需要粘附于某种 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于喷流拟序结构预测的SGS模型比较研究
    引言拟序结构普遍存在于湍流中[1–3],并影响湍流的发生、输运与耗散等过程,对湍流拟序结构的研究、对于理解湍流机理、分析流动相互作用有重要的意义.从大涡模拟来看,正确预测湍流拟序结构的关键就在于算法和亚网格尺度(sub-grid-scale,SGS)模型的准确性.在算法方面,传统的大涡模拟方法求解网 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 新型负刚度吸能结构力学特性分析
    引言在冲击载荷作用下,吸能材料的应用具有重要的工程意义.传统的减振吸能方法主要有两种:其一,利用材料的塑性变形实现能量吸收耗散[1],如汽车保险杠和轻型自行车头盔均是基于这一原理进行结构以及超材料设计,然而破坏性的塑性变形使得材料无法重复利用;其二,利用材料的黏弹特性[2-3],实现重复性的能量吸收 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • DVC中内部散斑质量评价及计算体素点的优化选择
    引言数字体图像相关方法(digitalvolumecorrelation,DVC)是二维数字图像相关方法(two-dimensionaldigitalimagecorrelation,2DDIC)在三维体图像上的拓展.通过比较体成像设备获取的被测试样变形前后数字体图像,该方法可测量物体内部三维全场变 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 一类新型仿生起竖结构设计及其动力学分析
    引言随着科学技术的不断发展,机器人的应用范围越来越广泛,应用场景也越来越多样化.为了进行灾后搜救、管道清理、未知区域探索等任务,机器人需要能在有限的工作空间和不规则的地形下移动并完成任务.于是,许多****以蚯蚓等蠕虫为仿生对象,设计了一系列仿蠕虫机器人[1-8].受到蚯蚓的运动来源于体节的轴向变形 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于人工弹簧模型的周期结构带隙计算方法研究1)
    冯青松*,杨舟*,郭文杰,*,2),陆建飞&,梁玉雄**华东交通大学铁路环境振动与噪声教育部工程研究中心,南昌330013&江苏大学土木工程与力学学院,江苏镇江212013RESEARCHONBANDGAPCALCULATIONMETHODOFPERIODICSTRU ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.