删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于压电振动能量俘获的弯曲结构损伤监测研究

本站小编 Free考研考试/2022-01-01


引 言


近年来, 压电材料因其具有能实现电能和机械能互相转换的特性, 在工程结构中日益受到重视[1-2], 被广泛应用于结构的形状控制、振动和噪声控制、损伤检测等领域[3-4]. 从机械振动中提取能量的特性极大满足了传感器自给供电的经济需求与生态需求, 因此压电材料广泛应用于俘能器中[5-6]. 到目前为止, 最常用的压电俘能器采用悬臂梁式, 通常是由一个结构层和压电材料(如压电陶瓷PZT、压电复合材料PVDF)层组成[7]. ****们对直梁压电振动能量俘获系统进行了大量且详细的研究. Erturk和Inman[8-9]在Euler-Bernoulli梁假设下, 研究了在基座横向运动时悬臂式压电俘能器横向振动的精确解析解. 另外考虑到常用的单自由度谐波激励对预测悬臂梁的运动可能会产生不准确的结果, 推导了修正因子以改进单自由度横向和纵向振动激励模型. Zhao等[10]应用格林函数法对悬臂式Timoshenko直梁压电俘能器进行了动力学分析, 得到了强迫振动的解析解, 探究了各类因素对电压响应的影响. Zhou和Lei[11]研究了非对称三稳态压电俘能器的非线性动力学特性, 以提高不同激励下的能量收集性能. Huang等[12] 对电阻?电感谐振电路非线性能量采集器的稳态响应机制进行了理论研究. Fang等[13]根据哈密顿原理提出了利用离心软化效果分析旋转冲击能量俘获的理论模型.

而曲梁形式的压电俘能器的优点在于可用于多方向振动能量收集[14], 在微型电子系统以及复杂边界的工程结构中应用广泛[15]. 王剑等[16]构建了空间压电曲梁单元形状控制模型并得到了结构的最优形状控制电压. 周勇等[17]提出了一种基于面内驱动的层合压电悬臂曲梁形式微位移驱动结构, 忽略方程中曲率半径的影响获得了该曲梁在外荷载作用下控制方程的解析解. 丁维高和谢进[18]利用哈密顿原理, 研究了在水平与数值方向简谐振动激励的作用下压电曲梁俘能器的机电耦合的解析解. Kathpalia等[19] 建立了采用智能陶瓷压电材料的弯曲式压电传感器的分析模型, 并获得了封闭式机电频率响应方程. Chen等[20]采用数值方法分析了具有弹性约束的功能梯度压电曲梁的自由振动特性和瞬时响应. Tabatabaei-Nejhad等[21]研究了嵌入压电层的层压曲梁的平面外振动特性, 考虑了扭转和弯曲变形造成的剪切变形和旋转惯性效应. 何燕丽和赵翔[22]利用格林函数法求解Prescott型曲梁俘能器强迫振动的响应.

曲梁结构如今广泛地应用于各种领域的工程结构中, 在外荷载激励下难免造成损伤产生裂纹, 从而严重影响材料结构的整体性能和使用寿命[23-24]. 对损伤曲梁的振动特性研究也一直是国内外研究的热点[24-27]. 为识别结构中的损伤发展了许多检测方法, 分别有超声波法、电涡流法、磁粉法和红外识别法[28], 以及基于结构振动特性的损伤识别法, 后者具有明显的非破坏性, 方便、快速、便宜的优点被广泛采用[28]. 另外, 还有基于压电效应的主动感应法对结构的健康监测和损伤检测方法. 孙威等[29]利用智能压电传感器对混凝土构件的裂缝损伤发展状况进行监测, 探索一种基于压电波动法的裂缝损伤监测方法. Hou等[30]将压电智能材料和压电陶瓷材料应用于传感器, 对地震力作用下的混凝土结构整体剪切应力进行监测研究. Markovic等[31]建立了使用压电智能传感器的主动监测系统和损坏检测的有效有限元模型, 对基于压电波动法的埋入式压电陶瓷混凝土梁损伤识别系统进行模拟分析. 由此, 本文提出可以采用逆方法, 即通过振动引起的压电俘能器的信号响应变化分析曲梁的振动问题, 从而对结构进行损伤监测.

目前已经有不少****对裂纹曲梁的振动问题和曲梁式压电俘能器进行了研究, 但是有关损伤曲梁式压电俘能器强迫振动问题的研究较少. 在上文已经阐述了裂纹存在给结构带来的负面影响, 因此对含裂纹损伤的曲梁压电俘能器的研究是有实际意义的. 本文不仅研究其强迫振动问题, 还采用逆方法, 即利用损伤曲梁振动时的俘能器电压响应变化, 提出了一种监测结构损伤的方法.

本文建立了含裂纹损伤的曲梁压电俘能器的力电耦合模型, 得到其强迫振动的解析解并基于压电俘能器的响应监测曲梁结构的损伤情况. 基于文献[22]中Prescott型曲梁压电俘能器的解析解, 引入局部刚度模型描述裂纹损伤截面的力学特性, 应用格林数法和传递矩阵法推导含多裂纹曲梁压电俘能器强迫振动下的解析解. 根据线性系统叠加原理, 对力电耦合系统解耦, 推导了该裂纹损伤模型的输出电压的解析式. 数值模拟了压电俘能器在曲梁结构处于振动状态下的响应信号, 提出了对结构进行损伤监测的方法, 以期为曲梁式压电俘能器的振动研究以及损伤结构的监测和优化设计提供理论参考.


1.
损伤曲梁压电俘能器的力电耦合模型


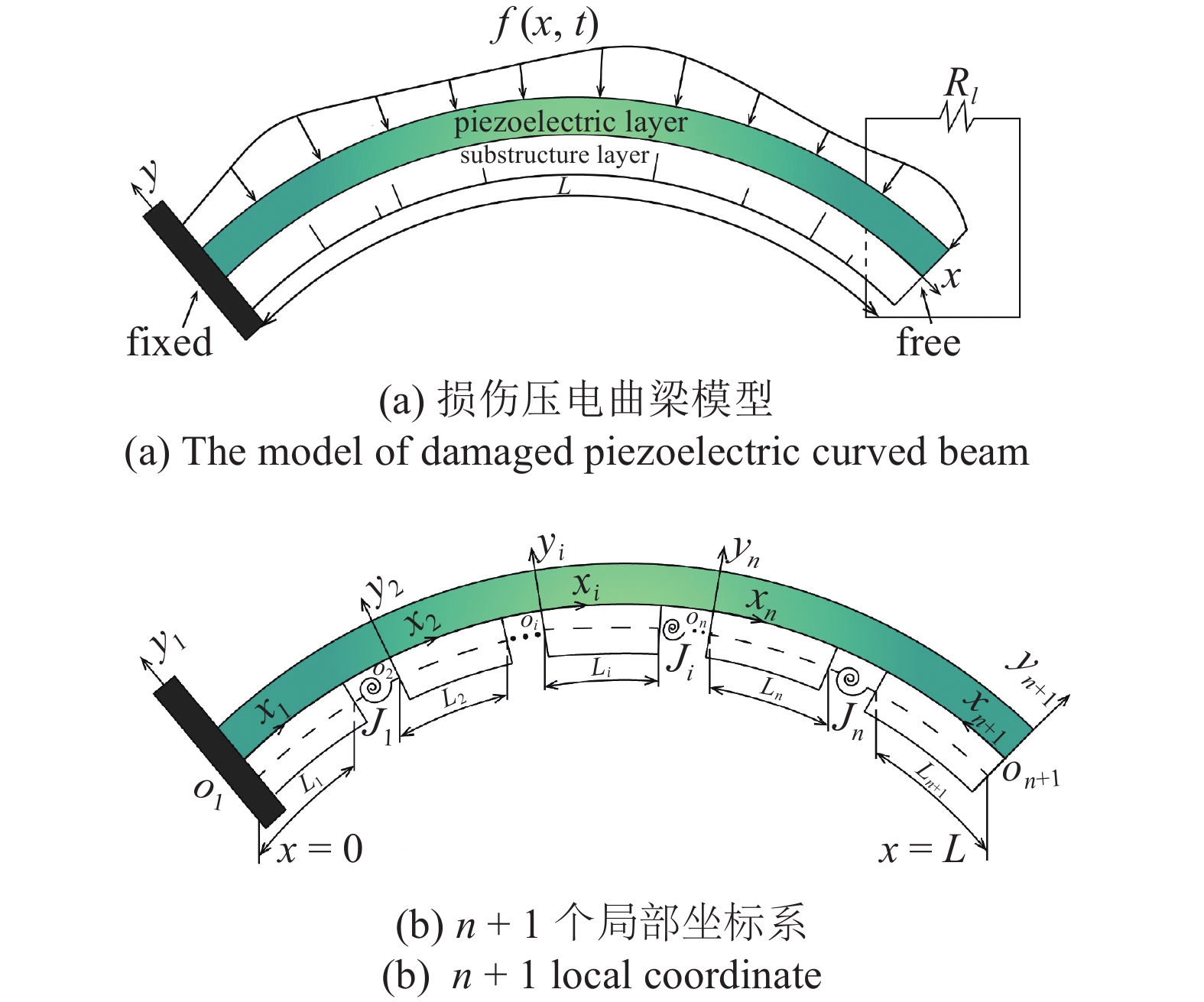
建立如图１所示的含裂纹损伤的悬臂式曲梁压电俘能器模型. 俘能器中的压电层材料比结构层材料的柔性好, 因此结构层上更容易产生裂纹. 如图1(a)所示, 该模型结构层上存在n个开口裂纹, 假设受到外力作用时, 裂纹截面处的局部刚度发生变化, 曲梁的挠度出现不连续性, 曲梁的未损伤部分没有受到影响[32]. 因此, 在裂纹损伤截面处建立局部柔度模型用来描述截面的力学特性, 将裂纹处视为一个刚度为${K_{eq}}$的等效无质量扭转弹簧, 该弹簧连接着相邻的两个完整部分, 可表示为



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-452-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
损伤曲梁压电俘能器模型



Figure
1.
The model of curved piezoelectric energy harvester with n cracks



下载:
全尺寸图片
幻灯片








$$ {K_{eq}} = frac{{EI}}{{{h_s}}}frac{1}{{{{overline C}_W}}} $$
(1)

式中$EI$为压电曲梁的有效刚度, ${h_s}$是结构层曲梁的高度, ${overline C_W}$局部柔度的无量纲常数, 在本模型中采用







$$ begin{split}& {overline C _W} = 5.346{{h'}^2}left( {1.86 - 3.95h' + 16.375{{h'}^2} - 37.226{{h'}^3} + }
ight. &quad 76.81{{h'}^4} - 126.9{{h'}^5}left. { + 172{{h'}^6} - 143.97{{h'}^7} + 66.56{{h'}^8}}
ight) end{split} $$
(2)

式中$ h' = {h_c}/{h_s} $是裂纹深度与曲梁高度的比值.

如图1(b)所示, 压电曲梁被n个裂纹分成n + 1段完整部分, 每段长度为${L_i}left( {i = 1,2,cdots,n{text{ + 1}}}
ight)$并且由一个等效无质量扭转弹簧连接. 为了得到裂纹压电曲梁的格林函数, 需要分别研究每段的变形情况. 因此, 建立$n + 1$个局部坐标系${o_i}{x_i}{y_i}left( {i = 1,2,cdots,n + 1}
ight)$[33]表示出出每段的格林函数后, 转换局部坐标为全局坐标即${x_1} = x$, ${x_i} = x - displaystylesumlimits_{i = 1}^k {{L_i}} ;left( {i = 2,3,cdots,n}
ight)$, ${x_{n + 1}} = L = x$, 即可得到压电曲梁的格林函数.

已知文献[22]中建立的Prescott曲梁模型, 没有考虑曲梁轴向力以及轴向惯性项, 仅考虑了曲梁的径向位移. 因此曲梁压电俘能器的振动控制方程是一个四阶偏微分方程, 引用文献[22]中的格林函数, 该格林函数是强迫振动下的压电曲梁径向位移$ Wleft( x
ight) $的解







$$left. begin{aligned}&{G_1}left( {x;{x_0}}
ight) = Hleft( {x - {x_0}}
ight){phi _{11}}left( {x - {x_0}}
ight) + {phi _2}left( x
ight){W_1}left( x
ight)+&qquadquad {phi _3}left( x
ight){W_{
m{1}}}^prime left( x
ight) + {phi _4}left( x
ight)W_1^{''}left( x
ight) + {phi _5}left( x
ight){W_1}^{prime prime prime }left( x
ight)&{G_2}left( {x;{x_0}}
ight) = bar VHleft( {x - {x_0}}
ight){phi _{12}}left( {x - {x_0}}
ight) + {phi _2}left( x
ight){W_2}left( x
ight)+&qquadquad {phi _3}left( x
ight){W_2}^prime left( x
ight) + {phi _4}left( x
ight)W_2^{''}left( 0
ight) + {phi _5}left( x
ight)W_2^{'''}left( 0
ight)&{G_3}left( {x;{x_0}}
ight) = bar VHleft( {x - {x_0}}
ight){phi _{13}}left( {x - {x_0}}
ight) + {phi _2}left( x
ight){W_3}left( x
ight)+&qquadquad {phi _3}left( x
ight){W_3}^prime left( x
ight) + {phi _4}left( x
ight)W_3^{''}left( 0
ight) + {phi _5}left( x
ight)W_3^{'''}left( 0
ight)n[-10pt]end{aligned}
ight}$$
(3)

式中${x_0}$表示单位力作用的位置, ${W'_i}$, ${W''_i}$, ${W'''_i}$是径向位移${W_i}left( {i = 1,2,3}
ight)$的各阶导数, $bar V$表示压电俘能器的电压. ${G_1}left( {x,{x_0}}
ight)$表示由外力引起的位移解, ${G_2}left( {x,{x_0}}
ight), $$ {G_3}left( {x,{x_0}}
ight)$是由电耦合效应引起的位移解, 且有







$$ left. begin{aligned} & {phi _{11}}left( x
ight) = sumlimits_{i = 1}^4 {{A_i}left( x
ight)left( {{b_1}s_i^2 - {b_2}}
ight)} & {phi _{12}}left( x
ight) = sumlimits_{i = 1}^4 {{A_i}left( x
ight)left( { - {b_3}{s_i}}
ight)} & {phi _{13}}left( x
ight) = sumlimits_{i = 1}^4 {{A_i}left( x
ight)left( {cs_i^{ - 1}}
ight)} & {phi _2}left( x
ight) = sumlimits_{i = 1}^4 {{A_i}left( x
ight)left( {s_i^3 + {a_1}{s_i}}
ight)} & {phi _3}left( x
ight) = sumlimits_{i = 1}^4 {{A_i}left( x
ight)left( {s_i^2 + {a_1}}
ight)} & {phi _4}left( x
ight) = sumlimits_{i = 1}^4 {{A_i}left( x
ight){s_i}} & {phi _5}left( x
ight) = sumlimits_{i = 1}^4 {{A_i}left( x
ight)} end{aligned}
ight}$$
(4)







$$ left. begin{aligned} & {A_1}left( x
ight) = frac{{{{
m{e}}^{{s_1}x}}}}{{left( {{s_1} - {s_2}}
ight)left( {{s_1} - {s_3}}
ight)left( {{s_1} - {s_4}}
ight)}} & {A_2}left( x
ight) = frac{{{{
m{e}}^{{s_2}x}}}}{{left( {{s_2} - {s_1}}
ight)left( {{s_2} - {s_3}}
ight)left( {{s_2} - {s_4}}
ight)}} & {A_3}left( x
ight) = frac{{{{
m{e}}^{{s_3}x}}}}{{left( {{s_3} - {s_1}}
ight)left( {{s_3} - {s_2}}
ight)left( {{s_3} - {s_4}}
ight)}} & {A_4}left( x
ight) = frac{{{{
m{e}}^{{s_4}x}}}}{{left( {{s_4} - {s_1}}
ight)left( {{s_4} - {s_2}}
ight)left( {{s_4} - {s_3}}
ight)}} end{aligned}
ight} $$
(5)

式(4)和式(5)中







$$ left. begin{aligned} & {a}_{1}=frac{1}{{R}^{2}} + frac{gamma {varOmega }^{2}}{EI} + frac{text{i}varOmega {c}_{1}-mu {varOmega }^{2}}{EA} & {a}_{2}=text{}frac{left(text{i}varOmega {c}_{1}-mu {varOmega }^{2}
ight)gamma {varOmega }^{2}}{EIEA} + frac{gamma {varOmega }^{2}}{EI{R}^{2}} & {b}_{1}=frac{1}{EA} & {b}_{2}=text{}frac{gamma {varOmega }^{2}}{EIEA} & {b}_{3}=text{}frac{{vartheta }_{2}}{EAR} + frac{{vartheta }_{1}}{EI} & c=text{}-frac{gamma {varOmega }^{2}{vartheta }_{2}}{EIEAR}end{aligned}
ight}$$
(6)

且${s_i}left( {i = 1,2,3,4}
ight)$是下列代数方程的根







$$ {s^4} + {a_1}{s^2} + {a_2} = left( {{s_1} - {s_1}}
ight)left( {{s_1} - {s_2}}
ight)left( {{s_1} - {s_3}}
ight)left( {{s_1} - {s_4}}
ight) $$
(7)

式(6)中, $R$是曲梁的半径, $mu $和$gamma $表示单位长度曲梁的质量和转动惯量, ${c_1}$表示阻尼系数, $A$表示截面面积. ${vartheta _1}$和${vartheta _2}$是力电耦合系数, 具体表达式见文献[22].

在本文的后续推导中需要用到轴向位移, 根据曲梁控制方程[22]可推出轴向位移$Vleft( x
ight)$







$$ begin{split}& Vleft( x
ight) = {d_1}W'''left( x
ight) + {d_2}W'left( x
ight) + {d_1}Fleft( x
ight) + & quad {d_3}bar Vleft[ {delta left( {x - {x_1}}
ight) - left( {x - {x_2}}
ight)}
ight] + {d_{text{4}}}bar Vleft[ {delta left( {x - {x_1}}
ight) - left( {x - {x_2}}
ight)}
ight] end{split} $$
(8)

式中







$$ left. begin{aligned}&{d}_{1}=frac{EIR}{gamma {varOmega }^{2}}&{d}_{2}=frac{text{i}{c}_{1}EIR}{gamma varOmega EA}-frac{mu EIR}{gamma EA}-frac{EI}{gamma {varOmega }^{2}R} + R&{d}_{3}={vartheta }_{1}&{d}_{4}=frac{{vartheta }_{2}EI}{EAR}end{aligned}
ight}$$
(9)

根据式(3) ~ 式(9)得到由外荷载引起的轴向位移的格林函数







$$ begin{split}& {V_1}left( {x;{x_0}}
ight) = Hleft( {x - {x_0}}
ight){{bar phi }_{11}}left( {x - {x_0}}
ight) + {{bar phi }_2}left( x
ight){W_1}left( x
ight) +&quad {{bar phi }_3}left( x
ight){W_{text{1}}}^prime left( x
ight) + {{bar phi }_4}left( x
ight){W_{text{1}}}^{prime prime }left( x
ight) + {{bar phi }_5}left( x
ight){W_1}^{prime prime prime }left( x
ight) end{split} $$
(10)

式中, ${bar phi _m} = left( {{d_1}s_i^{text{3}}{text{ + }}{d_2}{s_i}}
ight){phi _m};left( {m = 2,3,4,5,11}
ight)$. 因此, 局部坐标系下的格林函数为







$$ left. begin{aligned}& {W_{1i}}left( {{x_i};{x_{i0}}}
ight) = {{bar G}_{1i}}left( {{x_i};{x_{i0}}}
ight) =& qquadquad Hleft( {{x_i} - {x_{i0}}}
ight){phi _{11}}left( {{x_i} - {x_{i0}}}
ight) + {phi _2}left( {{x_i}}
ight){W_{1i}}left( x
ight) +& qquadquad {phi _3}left( {{x_i}}
ight){W_{{text{1i}}}}^prime left( x
ight) + {phi _4}left( {{x_i}}
ight){W_{{text{1i}}}}^{prime prime }left( x
ight) + {phi _5}left( {{x_i}}
ight){W_{1i}}^{prime prime prime }left( x
ight) & {V_{1i}}left( {{x_i};{x_{i0}}}
ight) = Hleft( {{x_i} - {x_{i0}}}
ight){{bar phi }_{11}}left( {{x_i} - {x_{i0}}}
ight) + {{bar phi }_2}left( {{x_i}}
ight){W_{1i}}left( x
ight)+ & qquadquad {{bar phi }_3}left( {{x_i}}
ight){W_{{text{1i}}}}^prime left( x
ight) + {{bar phi }_4}left( {{x_i}}
ight){W_{{text{1i}}}}^{prime prime }left( x
ight) + {{bar phi }_5}left( {{x_i}}
ight){W_{1i}}^{prime prime prime }left( x
ight) end{aligned}
ight} $$
(11)

式中, $ {W}_{1i}left(x
ight), {W}_{text{1i}}{}^{prime }left(x
ight), {W}_{text{1i}}{}^{prime text{}prime }left(x
ight), {W}_{1i}{}^{prime text{}prime text{}prime }left(x
ight) $是待解的未知常数. 为了求解系统中的4n + 4个未知常数, 在压电曲梁的裂纹截面处建立各状态矢量(横向位移、弯矩、剪力和转角位移)之间传递关系, 应用传递矩阵法求解局部格林函数.

在第$ ileft( {i = 1,2,cdots,n - 1}
ight) $个裂纹位置处和在第n个裂纹位置处各状态矢量的传递关系[34]如式(12)和式(13)所示, 曲梁的轴向位移、弯矩相等, 剪力大小相等但在第n处方向相反, 截面转角始终不连续







$$ left. begin{array}{l} {W_{1i}}left| {_{{x_i} = L_i^ - }}
ight. = {W_{1i + 1}}left| {_{{x_{i + 1}} = {0^ + }}}
ight. dfrac{{{partial ^2}{W_{1i}}}}{{partial x_i^2}} - dfrac{1}{R}dfrac{{partial {V_{1i}}}}{{partial {x_i}}}left| {_{{x_i} = L_i^ - }}
ight. = dfrac{{{partial ^2}{W_{1i + 1}}}}{{partial x_{i + 1}^2}} - dfrac{1}{R}dfrac{{partial {V_{1i + 1}}}}{{partial {x_{i + 1}}}}left| {_{{x_{i + 1}} = {0^ + }}}
ight. - left( {dfrac{{{partial ^3}{W_{1i}}}}{{partial x_i^3}} - dfrac{1}{R}dfrac{{{partial ^2}{V_{1i}}}}{{partial x_i^2}}}
ight){Big|_{{x_i} = L_i^ - }} = - left( {dfrac{{{partial ^3}{W_{1i + 1}}}}{{partial x_{i + 1}^3}} - }
ight.qquadleft. {dfrac{1}{R}dfrac{{{partial ^2}{V_{1i + 1}}}}{{partial x_{i + 1}^2}}}
ight){{{Big|}}_{{x_{i + 1}} = {0^{{{ + }}}}}}{theta _{1i}}{Big|_{{x_i} = L_i^ - }} = - {J_i}EIleft( {dfrac{{{partial ^2}{W_{1i + 1}}}}{{partial x_{i + 1}^2}} - }
ight.qquadleft. {dfrac{1}{R}dfrac{{partial {V_{1i + 1}}}}{{partial {x_{i + 1}}}}}
ight){{{Big|}}_{{x_{i + 1}} = {0^{{
m{ + }}}}}} + {theta _{i + 1}}{{{Big|}}_{{x_{i + 1}} = {0^{{
m{ + }}}}}}end{array}
ight} $$
(12)







$$ left. begin{gathered} {W_{1n}}left| {_{{x_n} = L_n^ - }}
ight. = {W_{1n + 1}}left| {_{{x_{n + 1}} = L_{n + 1}^ - }}
ight. hfill frac{{{partial ^2}{W_{1n}}}}{{partial x_n^2}} - frac{1}{R}frac{{partial {V_{1n}}}}{{partial {x_n}}}left| {_{{x_n} = L_n^ - }}
ight. = frac{{{partial ^2}{W_{1n + 1}}}}{{partial x_{n + 1}^2}} - frac{1}{R}frac{{partial {V_{1n + 1}}}}{{partial {x_{n + 1}}}}left| {_{{x_{n + 1}} = L_{n + 1}^ - }}
ight. hfill - left( {frac{{{partial ^3}{W_{1n}}}}{{partial x_n^3}} - frac{1}{R}frac{{{partial ^2}{V_{1n}}}}{{partial x_n^2}}}
ight){Big|_{{x_n} = L_n^ - }} = frac{{{partial ^3}{W_{1n + 1}}}}{{partial x_{n + 1}^3}} - hfill qquadqquadfrac{1}{R}frac{{{partial ^2}{V_{1n + 1}}}}{{partial x_{n + 1}^2}}{{{Big|}}_{{x_{n + 1}} = L_{n + 1}^ - }}{theta _{1n}}{{{Big|}}_{{x_n} = L_n^ - }} = - {J_n}left( {frac{{{partial ^2}{W_{1n + 1}}}}{{partial x_{n + 1}^2}} - }
ight. hfill left. {frac{1}{R}frac{{partial {V_{1n + 1}}}}{{partial {x_{n + 1}}}}}
ight){Big|_{{x_{n + 1}} = L_{n + 1}^ - }} - {theta _{1n + 1}}{Big|_{{x_{n + 1}} = L_{n + 1}^ - }}end{gathered}
ight} $$
(13)

式中, ${theta _{{text{1}}m}} = dfrac{{partial {W_{1m}}}}{{partial x}} + dfrac{1}{R}{V_{1m}}left( {m = 1,2,cdots,n}
ight)$表示截面转角; $ {J_i} $和$ {J_n} $表示第$ i $处和第n处的等效扭转弹簧的局部柔度, 是刚度$ {K_{eq}} $的倒数.

将局部格林函数式(11)带入传递关系式(12)和式(13)中可得到两个矩阵形式的传递方程






$$tag{14a} {{{boldsymbol{T}}}_{1i}}{{{boldsymbol{U}}}_i} = {{{boldsymbol{K}}}_i} + {{{boldsymbol{T}}}_{2i}}{{{boldsymbol{U}}}_{i + 1}} $$






$$tag{14b} {{{boldsymbol{T}}}_{1n}}{{{boldsymbol{U}}}_n} = {{{boldsymbol K}}_n} + {{{boldsymbol{T}}}_{2n}}{{{boldsymbol{U}}}_{n + 1}} $$

式中






$$begin{split}&{{{{boldsymbol{U}}}}_i} = {left[ {begin{array}{*{20}{c}} {{W_{1i}}left( x
ight)}&{{W_{{text{1i}}}}^prime left( x
ight)}&{{W_{{text{1i}}}}^{prime prime }left( x
ight)}&{{W_{1i}}^{prime prime prime }left( x
ight)} end{array}}
ight]^{
m{T}}} & {{{{boldsymbol{T}}}}_{1i}} = left[ {begin{array}{*{20}{c}} {{boldsymbol{varPhi}} left( {{L_i}}
ight)} {{{{boldsymbol{varphi}} '}}left( {{L_i}}
ight)} { - {{{boldsymbol{varphi}} ''}}left( {{L_i}}
ight)} {{{{boldsymbol{varphi}} }}left( {{L_i}}
ight)} end{array}}
ight] =end{split}$$







$$ begin{split} & qquad left[ {begin{array}{*{20}{c}} {{phi _2}left( {{L_i}}
ight)}&{{phi _3}left( {{L_i}}
ight)}&{{phi _4}left( {{L_i}}
ight)}&{{phi _5}left( {{L_i}}
ight)} {{{varphi '}_2}left( {{L_i}}
ight)}&{{{varphi '}_3}left( {{L_i}}
ight)}&{{{varphi '}_4}left( {{L_i}}
ight)}&{{{varphi '}_5}left( {{L_i}}
ight)} { - {{varphi ''}_2}left( {{L_i}}
ight)}&{ - {{varphi ''}_3}left( {{L_i}}
ight)}&{ - {{varphi ''}_4}left( {{L_i}}
ight)}&{ - {{varphi ''}_5}left( {{L_i}}
ight)} {{varphi _2}left( {{L_i}}
ight)}&{{varphi _3}left( {{L_i}}
ight)}&{{varphi _4}left( {{L_i}}
ight)}&{{varphi _5}left( {{L_i}}
ight)} end{array}}
ight] & {{{{boldsymbol{T}}}}_{2i}} = left[ {begin{array}{*{20}{c}} {{boldsymbol{varPhi }}left( 0
ight)} {{{{boldsymbol{varphi}} '}}left( 0
ight)} { - {{{boldsymbol{varphi}} ''}}left( 0
ight)} {{{bar {boldsymbol{psi}} }}left( 0
ight)} end{array}}
ight] = &qquad left[ {begin{array}{*{20}{c}} {{phi _2}left( 0
ight)}&{{phi _3}left( 0
ight)}&{{phi _4}left( 0
ight)}&{{phi _5}left( 0
ight)} {{{varphi '}_2}left( 0
ight)}&{{{varphi '}_3}left( 0
ight)}&{{{varphi '}_4}left( 0
ight)}&{{{varphi '}_5}left( 0
ight)} { - {{varphi ''}_2}left( 0
ight)}&{ - {{varphi ''}_3}left( 0
ight)}&{ - {{varphi ''}_4}left( 0
ight)}&{ - {{varphi ''}_5}left( 0
ight)} {{{bar psi }_{2i}}left( 0
ight)}&{{{bar psi }_{3i}}left( 0
ight)}&{{{bar psi }_{4i}}left( 0
ight)}&{{{bar psi }_{5i}}left( 0
ight)} end{array}}
ight] & {{boldsymbol K}_i} = Hleft( { - {x_{i0}}}
ight)left[ {begin{array}{*{20}{c}} {{phi _{11}}left( { - {x_{i0}}}
ight)} {{{varphi '}_{11}}left( { - {x_{i0}}}
ight)} { - {{varphi ''}_{11}}left( { - {x_{i0}}}
ight)} {{{bar psi }_{1i}}left( { - {x_{i0}}}
ight)} end{array}}
ight] - &qquad Hleft( {{L_i} - {x_{i0}}}
ight)left[ {begin{array}{*{20}{c}} {{phi _{11}}left( {{L_i} - {x_{i0}}}
ight)} {{{varphi '}_{11}}left( {{L_i} - {x_{i0}}}
ight)} { - {{varphi ''}_{11}}left( {{L_i} - {x_{i0}}}
ight)} {{varphi _{1i}}left( {{L_i} - {x_{i0}}}
ight)} end{array}}
ight] [-20pt]end{split}$$
(15)






$$ begin{split} & {{{{boldsymbol{U}}}}_n} = {left[ {begin{array}{*{20}{c}} {{W_{1n}}left( x
ight)}&{{W_{{text{1n}}}}^prime left( x
ight)}&{{W_{{text{1n}}}}^{prime prime }left( x
ight)}&{{W_{1n}}^{prime prime prime }left( x
ight)} end{array}}
ight]^{{{
m{T}}}}} & {{{{boldsymbol{T}}}}_{1n}} = left[ {begin{array}{*{20}{c}} {{{{boldsymbol{varPhi}} }}left( {{L_n}}
ight)} {{{{boldsymbol{varphi}} '}}left( {{L_n}}
ight)} { - {{{boldsymbol{varphi}} ''}}left( {{L_n}}
ight)} {{{{boldsymbol{varphi}} }}left( {{L_n}}
ight)} end{array}}
ight] = & qquadleft[ {begin{array}{*{20}{c}} {{phi _2}left( {{L_n}}
ight)}&{{phi _3}left( {{L_n}}
ight)}&{{phi _4}left( {{L_n}}
ight)}&{{phi _5}left( {{L_n}}
ight)} {{{varphi '}_{text{2}}}left( {{L_n}}
ight)}&{{{varphi '}_3}left( {{L_n}}
ight)}&{{{varphi '}_4}left( {{L_n}}
ight)}&{{{varphi '}_5}left( {{L_n}}
ight)} { - {{varphi ''}_2}left( {{L_n}}
ight)}&{ - {{varphi ''}_3}left( {{L_n}}
ight)}&{ - {{varphi ''}_4}left( {{L_n}}
ight)}&{ - {{varphi ''}_5}left( {{L_n}}
ight)} {{varphi _2}left( {{L_n}}
ight)}&{{varphi _3}left( {{L_n}}
ight)}&{{varphi _4}left( {{L_n}}
ight)}&{{varphi _5}left( {{L_n}}
ight)} end{array}}
ight] end{split} $$







$$ begin{split} & {{{{boldsymbol{T}}}}_{2n}} = left[ {begin{array}{*{20}{c}} {{{{boldsymbol{varPhi}} }}left( {{L_{n + 1}}}
ight)} {{{{boldsymbol{varphi}} '}}left( {{L_{n + 1}}}
ight)} {{{{boldsymbol{varphi}} ''}}left( {{L_{n + 1}}}
ight)} { - {{{boldsymbol{psi}} }}left( {{L_{n + 1}}}
ight)} end{array}}
ight] = & ;;left[ {begin{array}{*{20}{c}} {{phi _2}left( {{L_{n + 1}}}
ight)}&{{phi _3}left( {{L_{n + 1}}}
ight)}&{{phi _4}left( {{L_{n + 1}}}
ight)}&{{phi _5}left( {{L_{n + 1}}}
ight)} {{{varphi '}_{text{2}}}left( {{L_{n + 1}}}
ight)}&{{{varphi '}_3}left( {{L_{n + 1}}}
ight)}&{{{varphi '}_4}left( {{L_{n + 1}}}
ight)}&{{{varphi '}_5}left( {{L_{n + 1}}}
ight)} {{{varphi ''}_2}left( {{L_{n + 1}}}
ight)}&{{{varphi ''}_3}left( {{L_{n + 1}}}
ight)}&{{{varphi ''}_4}left( {{L_{n + 1}}}
ight)}&{{{varphi ''}_5}left( {{L_{n + 1}}}
ight)} { - {psi _{2n}}left( {{L_{n + 1}}}
ight)}&{ - {psi _{3n}}left( {{L_{n + 1}}}
ight)}&{ - {psi _{4n}}left( {{L_{n + 1}}}
ight)}&{ - {psi _{5n}}left( {{L_{n + 1}}}
ight)} end{array}}
ight] & {{{{boldsymbol{K}}}}_n} = Hleft( {{L_{n + 1}} - {x_{n + 10}}}
ight)left[ {begin{array}{*{20}{c}} {{phi _{11}}left( {{L_{n + 1}} - {x_{n + 10}}}
ight)} {{{varphi '}_{11}}left( {{L_{n + 1}} - {x_{n + 10}}}
ight)} {{{varphi ''}_{11}}left( {{L_{n + 1}} - {x_{n + 10}}}
ight)} { - {psi _{1n}}left( {{L_{n + 1}} - {x_{n + 10}}}
ight)} end{array}}
ight] - & qquad Hleft( {{L_n} - {x_{n0}}}
ight)left[ {begin{array}{*{20}{c}} {{phi _{11}}left( {{L_n} - {x_{n0}}}
ight)} {{{varphi '}_{11}}left( {{L_n} - {x_{n0}}}
ight)} { - {{varphi ''}_{11}}left( {{L_n} - {x_{n0}}}
ight)} {{varphi _{1n}}left( {{L_n} - {x_{n0}}}
ight)} end{array}}
ight][-15pt] end{split}$$
(16)

式中







$$ left. begin{aligned}&{phi }_{m}={{varphi }^{prime }}_{m}-frac{1}{R}{overline{varphi }}_{m}&{overline{psi }}_{mi}=-{J}_{i}EI{{phi }^{prime }}_{m} + {phi }_{m}& {psi }_{mn}={J}_{n}EI{{phi }^{prime }}_{m} + {phi }_{m}&left(m=1,2,{cdots},5;i=1,2,{cdots},n-1
ight)end{aligned}
ight} $$
(17)

根据传递方程式(14a)和式(14b)建立未知常数向量${{boldsymbol{U}}_1}$和${{boldsymbol{U}}_{n + 1}}$的关系







$$ begin{split}& {{boldsymbol{U}}_{n + 1}} = {left( {{{boldsymbol{T}}_{2n}}}
ight)^{ - 1}}{{boldsymbol{T}}_{1n}}left[ {prodlimits_{j = 1}^{n - 1} {{{left( {{{boldsymbol{T}}_{2n - j}}}
ight)}^{ - 1}}{{boldsymbol{T}}_{1n - j}}} }
ight]{{boldsymbol{U}}_1} - &quad {left( {{{boldsymbol{T}}_{2n}}}
ight)^{ - 1}}left[ {sumlimits_{k = 0}^{n - 2} {prodlimits_{l = 0}^k {{{boldsymbol{T}}_{1n - l}}{{left( {{{boldsymbol{T}}_{2n - l - 1}}}
ight)}^{ - 1}}{{boldsymbol{K}}_{n - k - 1}}} } }
ight] - {left( {{{boldsymbol{T}}_{2n}}}
ight)^{ - 1}}{{boldsymbol{K}}_n} end{split} $$
(18)

考虑到本文采用的是悬臂式压电俘能器, 已知悬臂梁的边界条件是







$$ left. begin{aligned}&{W}_{11}left(0
ight)=0&{{W}^{prime }}_{1text{1}}left(0
ight)=0& {{W}^{″}}_{1n + 1}left(L
ight)=0&{{W}^{?}}_{1n + 1}left(L
ight)=0end{aligned}
ight} $$
(19)

将边界条件(19)带入传递式(18)即可求解未知常数向量${{boldsymbol{U}}_1}$和${{boldsymbol{U}}_{n + 1}}$, 再通过式(14a)和式(14b)可以定义其余未知常数向量.

因此, 可以得到所有局部坐标系下的格林函数, 转换坐标后, 含n个裂纹的曲梁压电俘能器的格林函数为







$$ {G_{text{1}}}left( {x,{x_0}}
ight) = left{ begin{split} & {{bar G}_{11}}left( {{x_1};{x_{10}}}
ight),;x in left[ {text{0}}
ight.,left. {L_1^ - }
ight) hfill & {{bar G}_{1i}}left( {x - sumlimits_{i = 1}^k {{L_i}} ;{x_{i0}}}
ight),x in left( {{{left( {sumlimits_{i = 1}^{k - 1} {{L_i}} }
ight)}^ + },{{left( {sumlimits_{i = 1}^k {{L_i}} }
ight)}^ - }}
ight) hfill & {{bar G}_{1n + 1}}left( {L - x;{x_{n + 10}}}
ight),;x in left( {{{left( {sumlimits_{i = 1}^n {{L_i}} }
ight)}^ + },L}
ight] end{split}
ight. $$
(20)


2.
损伤力电耦合系统解耦


根据线性系统和格林函数的叠加原理, 建立裂纹曲梁的力学位移与电力学方程之间的解析关系, 含裂纹曲梁压电俘能器的位移$ Wleft( x
ight) $为







$$ begin{split}& Wleft( x
ight) = {W_1}left( x
ight) + {W_2}left( x
ight) + {W_3}left( x
ight) =&qquad int_0^L {Fleft( xi
ight)left[ {{{bar G}_1}left( {{x_1};{x_{10}}}
ight) + cdots + {{bar G}_i}left( {x - sumlimits_{i = 1}^k {{L_i}} ;{x_{i0}}}
ight) + }
ight.} &qquad left. {{{bar G}_{n + 1}}left( {L - x;{x_{n + 10}}}
ight)}
ight]xi {
m{d}}xi + &qquad int_0^L {{G_2}left( {x;xi }
ight)left[ {delta left( {xi - {x_1}}
ight) - delta left( {xi - {x_2}}
ight)}
ight]{
m{d}}xi } + &qquad int_0^L {{G_{text{3}}}left( {x;xi }
ight)left[ {Hleft( {xi - {x_1}}
ight) - Hleft( {xi - {x_2}}
ight)}
ight]{
m{d}}xi } [-12pt]end{split} $$
(21)

假设在基础加速度作用下压电曲梁上的外力$ fleft( {x,t}
ight) $是简谐力, 可将外力[35]写作







$$ Fleft( x
ight) = left( {mu {varOmega ^2} - {
m{i}}varOmega {c_1}}
ight){A_0} $$
(22)

式中, $ {A_0} $是指位移的振幅.

结合文献[22]中已知的输出电压和本文求解的多裂纹曲梁压电俘能器的格林函数解析式, 可以得到本模型的输出电压







$$ begin{split}& bar V = left( {mu {varOmega ^2} - {
m{i}}varOmega {c_1}}
ight){A_0}Bigg{ - int_{{x_1}}^{{x_2}} {Biggr[ {int_0^L {{{bar G}_1}left( {x;xi }
ight){
m{d}}xi } + cdots + } Biggr.} &quad {Biggr. {int_0^L {{{bar G}_i}left( {x - sumlimits_{i = 1}^k {{L_i}} ;xi }
ight){
m{d}}xi } + int_0^L {{{bar G}_{n + 1}}left( {L - x;xi }
ight){
m{d}}xi } } Biggr]^{prime prime }}{
m{d}}x +H{A_1} +&quad { H{A_2}} Bigg}Bigg/left{ {frac{{{
m{i}}varOmega {C_p}{R_l} + 1}}{{{
m{i}}beta {C_p}{R_l}}} + int_{{x_1}}^{{x_2}} {left[ {{{tilde G''}_2}left( {x;{x_2}}
ight) - {{tilde G''}_2}left( {x;{x_1}}
ight)}
ight]{
m{d}}x} }
ight. +&quad { H{A_3} + H{A_4} + H{A_5} + H{A_6}} Bigg} [-10pt] end{split} $$
(23)

式中






$$tag{24a} begin{split} & H{A_1} = left( {frac{{mu {varOmega ^2} - {
m{i}}varOmega {c_1}}}{{EA}} - frac{1}{{{R^2}}}}
ight)displaystyleint_{{x_1}}^{{x_2}} {Biggr[ {displaystyleint_0^L {{{bar G}_1}left( {x;xi }
ight){
m{d}}xi } + cdots + } Biggr.} &quad Biggr. {displaystyleint_0^L {{{bar G}_i}left( {x - sumlimits_{i = 1}^k {{L_i}} ;xi }
ight){
m{d}}xi } + displaystyleint_0^L {{{bar G}_{n + 1}}left( {L - x;xi }
ight){
m{d}}xi } } Biggr]{
m{d}}x end{split}$$






$$tag{24b}begin{split} & H{A_2} = - frac{{text{1}}}{{EA}}left( {{x_2} - {x_1}}
ight)& H{A_3} = frac{{{vartheta _2}}}{{EAR}}left( {{x_1} - {x_2}}
ight)end{split}$$






$$tag{24c} H{A_4} = - int_{{x_1}}^{{x_2}} {{{left[ {displaystyleint_0^L {{G_3}left( {x;xi }
ight){
m{d}}xi } }
ight]}^{prime prime }}{
m{d}}x} $$






$$tag{24d}H{A_5} = left( {frac{1}{{{R^2}}} + frac{{{
m{i}}varOmega {c_1} - mu {varOmega ^2}}}{{EA}}}
ight)int_{{x_1}}^{{x_2}} {left[ {{{tilde G''}_2}left( {x;{x_2}}
ight) - {{tilde G''}_2}left( {x;{x_1}}
ight)}
ight]{
m{d}}x} $$






$$tag{24e}H{A_6} = left( {frac{{mu {varOmega ^2} - {
m{i}}varOmega {c_1}}}{{EA}} - frac{1}{{{R^2}}}}
ight)int_{{x_1}}^{{x_2}} {int_0^L {{{tilde G''}_3}left( {x;xi }
ight){
m{d}}xi } {
m{d}}x}$$

因此, 压电俘能器的功率为






$$ P = {bar V^2}/{R_l} $$


3.
数值结果与讨论


本文探究了弧长$ L = 0.1;{text{m}} $, 宽$ b = 0.{text{0}}1;{text{m}} $受简谐激励的悬臂曲梁压电俘能器, 曲梁由上层的压电层和下层的结构层组合, 其厚度分别为0.005 m和0.005 m. 曲梁几何和材料参数、压电参数取值如表1所示. 其次, 从裂纹几何参数(裂纹深度和位置)对裂纹压电曲梁进行了模拟, 裂纹深度比$ h' $分别为0.02, 0.04和0.06, 用裂纹位置L1表示离固定端的距离. 在以下算例中, 没有考虑阻尼的影响. 为了方便起见, 引入阻尼效应的无量纲化







$$ {zeta _1} = frac{{{c_1}}}{{2mu {varOmega _0}}} $$
(26)

式中, $ {varOmega _0} = {{text{π}} ^2}sqrt {EI/
ho A} /{L^2} $是曲梁的一阶固有频率.




表
1
裂纹压电曲梁的几何参数和压电参数取值



Table
1.
Geometrical and electromechanical parameters of the cracked beam



table_type1 ">
ParametersValueParametersValue
radius, R/m 0.5 resistance load, $ {R_l}/Omega $ $ 1.0 times {10^6} $
electrode start distance
from the base, $ {x_1}/{text{m}} $		 0 electrode end distance from the base, $ {x_{text{2}}}/{text{m}} $ 0.1
Young’s modulus of substructure layer, $ {E_s}/{text{Pa}} $ $ 1.0 times {10^{11}} $ Young’s modulus of piezoelectric layer, $ {E_p}/{text{Pa}} $ $ 6.6 times {10^{10}} $
piezoelectric constant, ${d_{31} }/({text{m} } cdot { {text{V} }^{ { { - 1} } } } )$ ${{ - 1} }{text{.90} } times {10^{10} }$ permittivity ${varepsilon _{33} }/({text{nF} } cdot { {text{m} }^{ - 1} })$ 15.93





下载:
导出CSV
|显示表格



3.1
解的有效性验证


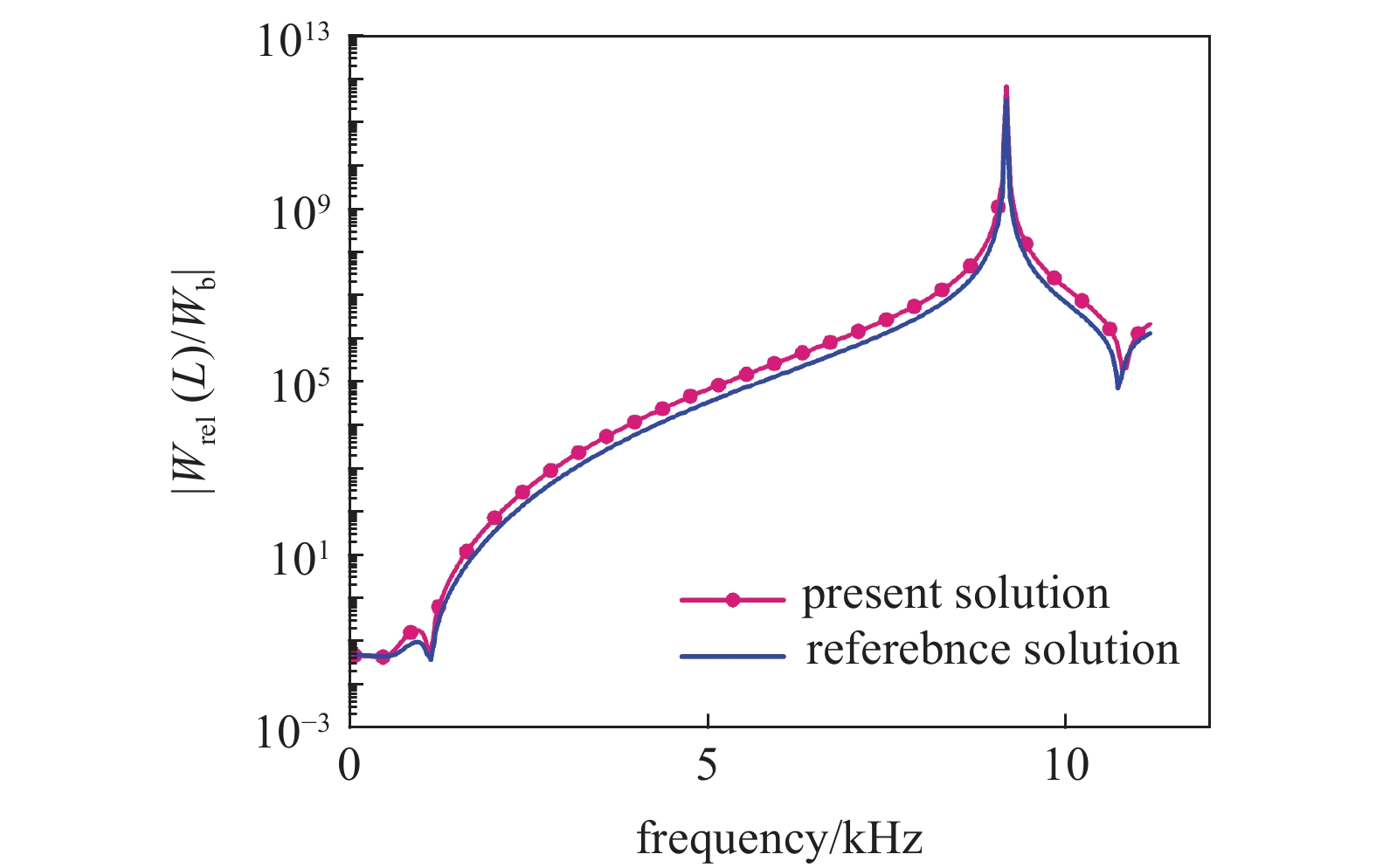
令裂纹深度为零, 含裂纹的曲梁可退化为完整曲梁模型. 利用这一点将含裂纹压电曲梁的解析解与文献[22]得到的完整压电曲梁模型的解作对比, 验证结果是否一致. 如图2所示, 本文的位移频率响应结果与文献中的结果基本吻合, 从而验证了本文解的有效性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-452-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
位移?频率响应的对比图



Figure
2.
The displacement for comparison of present solutions and the solutions from reference



下载:
全尺寸图片
幻灯片



3.2
裂纹损伤对压电俘能器电压?频率响应的影响


本节探究了压电俘能器电压响应在裂纹几何参数影响下的变化. 一方面为相关设计提供了理论依据, 另一方面介绍了如何通过电压响应的变化对结构进行损伤监测.

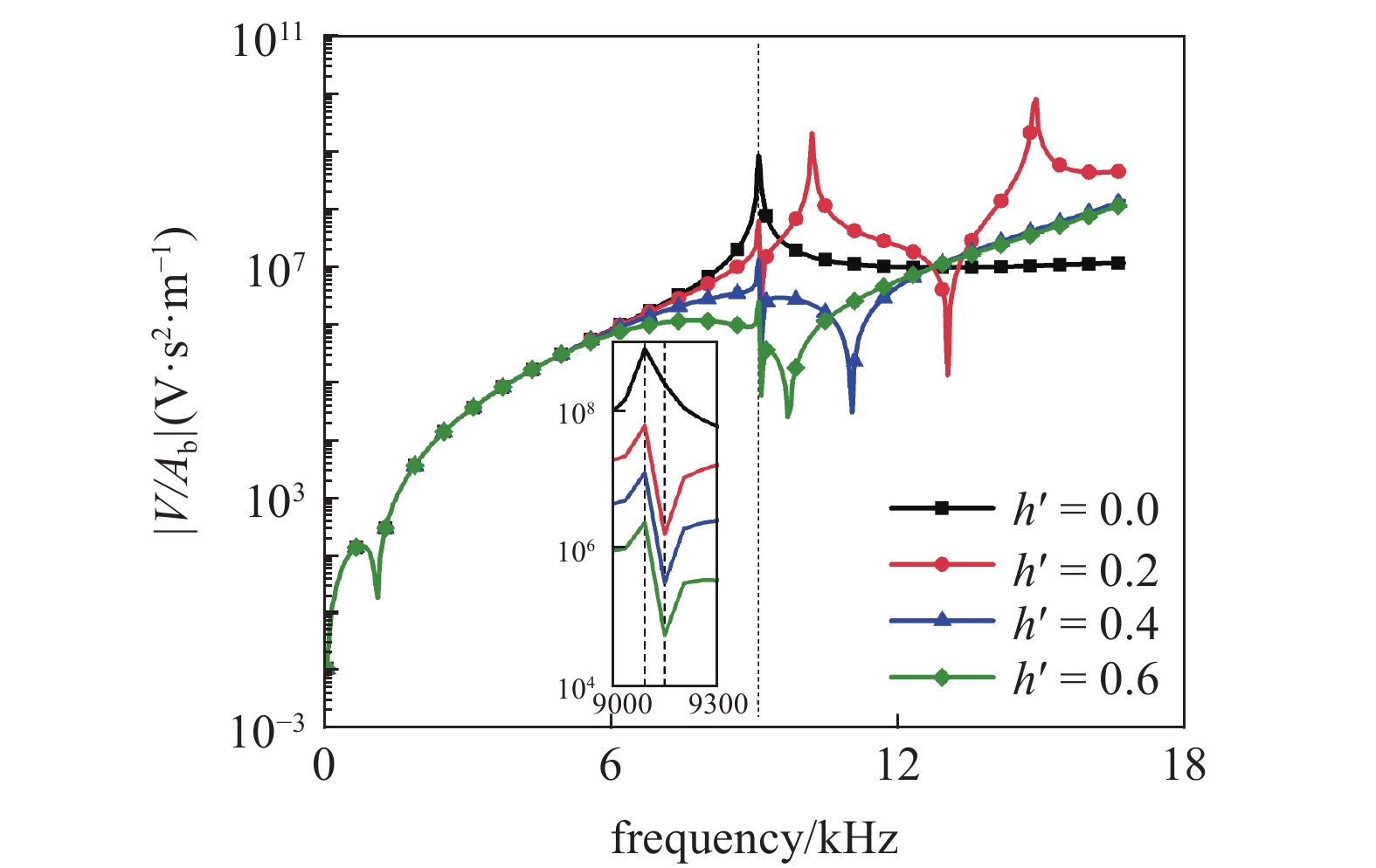
图3绘制了不同裂纹深度时压电俘能器的电压?频率响应图. 从图中可以看出, 频率在到5 kHz的时候, 各裂纹深度的电压响应之间有重叠部分. 当振动频率大于此重叠频率振动时, 损伤压电曲梁的响应效果与完整曲梁有了显著差异. 第一阶频率9088.6 Hz (虚线处)的峰值随着裂纹深度加深成比例的减小, 很快激励出二阶频率9144.4 Hz, 峰值的波动较小并且同样成比例减小深度加深至0.7左右后, 一阶频率甚至出现在9088.6 Hz之前, 且峰值极低. 特别说明, 此时的二阶频率9144.4 Hz时开路条件下压电曲梁的一阶频率值.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-452-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
不同裂纹深度的电压?频率响应(L1 = 0.06 m)



Figure
3.
The voltage frequency responses with different crack depths (L1 = 0.06 m)



下载:
全尺寸图片
幻灯片


对于浅裂纹($ 0 < h' < 0.2 $), 激励出正向峰值的三阶频率; 而在较深裂纹($ h' > 0.2 $)的情况下, 三阶频率的峰值远远小于浅裂纹时三阶频率的峰值, 且随着裂纹加深频率向一阶频率方向偏移. 因此, 在不同裂纹深度时, 压电曲梁的电压响应变化情况的趋势一致的.

裂纹损伤可能会出现在曲梁结构的任何位置, 由图3可知, 裂纹深度的深浅引起的电压?频率响应变化的差别较大. 因此在研究俘能器在裂纹位置变化下的电压响应时, 分别考虑了浅裂纹和深裂纹两种情况.

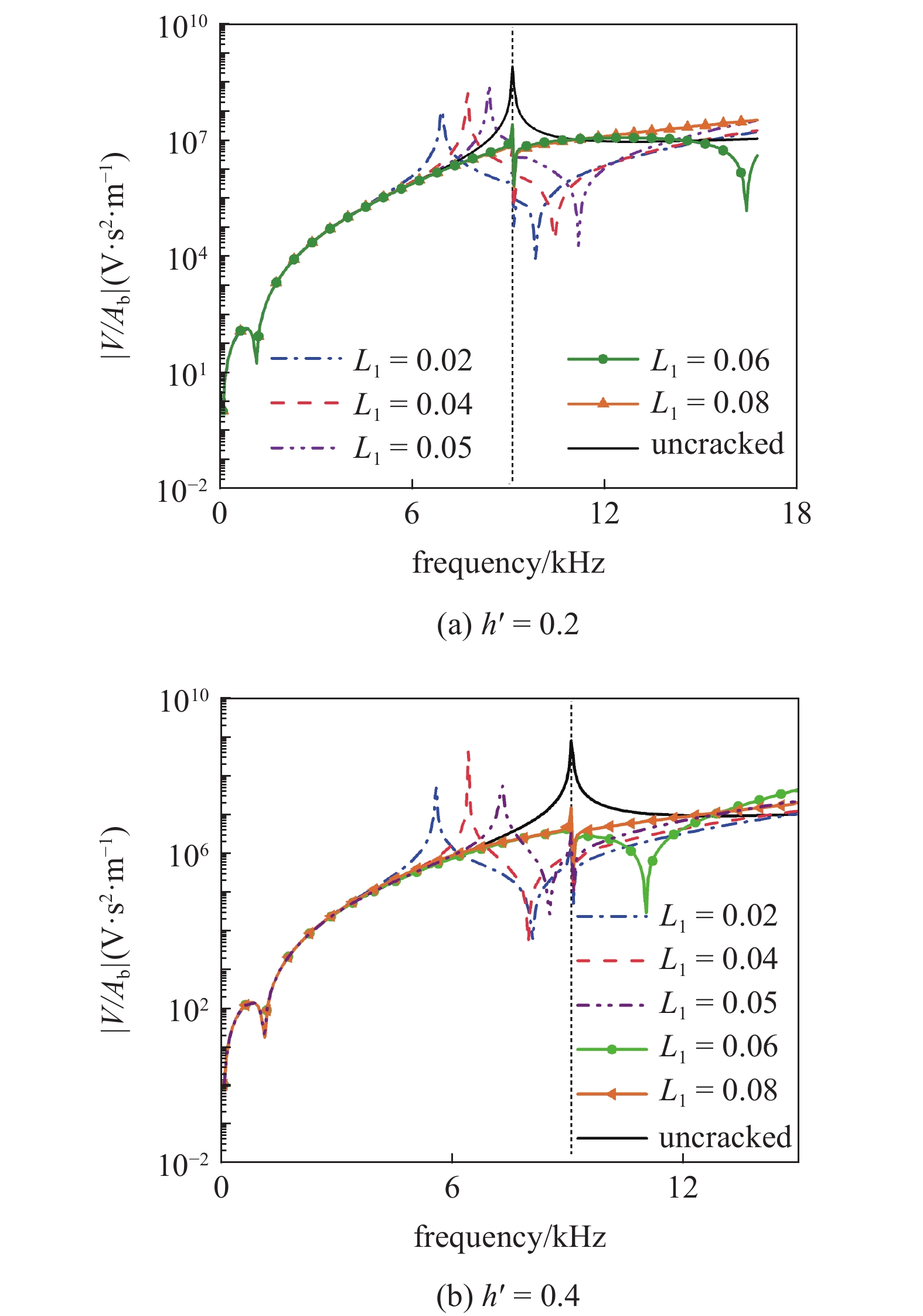
如图4所示, 随着裂纹位置不断从曲梁固定端靠近曲梁中部, 一阶固有频率逐渐增加. 但在图4(a)中, 一阶频率的峰值会不断增大, 二阶频率9088.6 Hz和三阶频率9144.4 Hz的峰值变大, 且四阶频率也向右偏移. 而在图4(b)中, 压电俘能器在9088.6 Hz前就被激励出了一阶和二阶频率, 且频率皆向右偏移. 当裂纹位置从曲梁中部不断靠近曲梁的自由端时, 一阶频率和二阶频率仍是9088.6 Hz和9144.4 Hz, 且峰值变大, 而三阶频率同样发生向右偏移.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-452-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
不同裂纹位置下的电压?频率响应



Figure
4.
The voltage frequency responses with different crack locations



下载:
全尺寸图片
幻灯片


总的来说, 不同裂纹深度和位置的损伤曲梁压电俘能器的电压响应的趋势是一致的, 不同的是被激励出的频率以及峰值.

因此想要检测结构的损伤情况, 就要根据结构振动响应引起的俘能器的电压响应变化. 一旦有裂纹出现, 健康曲梁的一阶频率就不再是损伤曲梁的一阶频率, 且随着裂纹加深该频率处峰值变小, 由此可以判断出出现损伤时裂纹的深度情况. 如若损伤曲梁被激励出的一阶频率小于健康曲梁的频率, 说明曲梁的固定端到中部这一段结构中出现了裂纹, 此时的裂纹深度也可以根据损伤曲梁是否在健康曲梁的一阶频率值前出现反向峰值的二阶频率. 相反, 如若损伤曲梁被激励出的一阶频率等于健康曲梁的一阶频率, 则损伤出现的范围在曲梁的中部至自由端. 至此, 本文提出的根据结构振动引起的压电俘能器信号响应变化监测结构损伤的逆方法得以验证.

从上述裂纹几何参数对压电俘能器电压响应的分析中可以看出, 在很多情况下固有频率都会发生偏移. 因此, 利用固有频率是否发生偏移这一条件仅能够监测结构中是否有损伤产生, 并不能准确检测出结构的损伤情况.


3.3
阻尼比对损伤压电曲梁电压?频率响应的影响


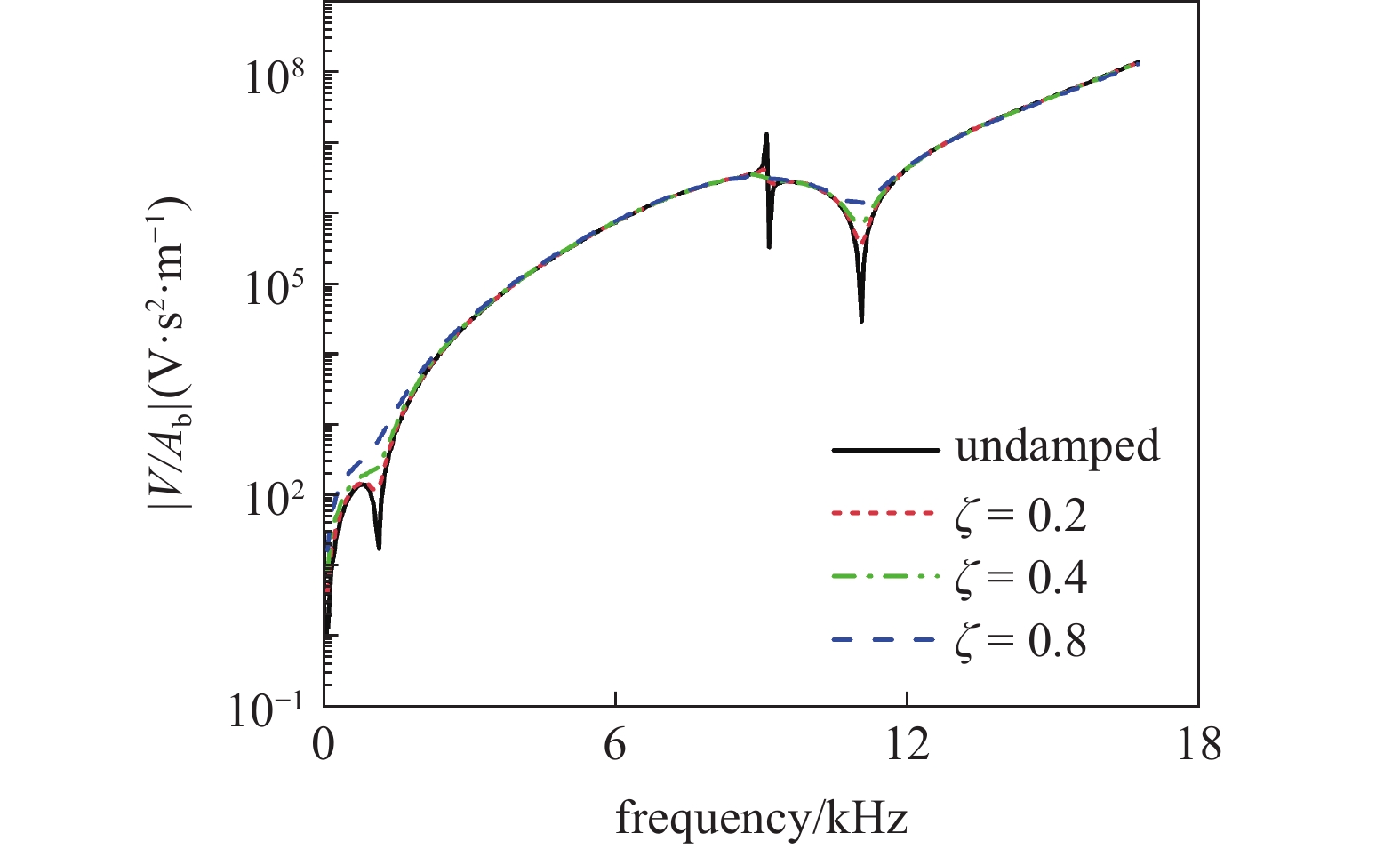
考虑到结构中阻尼的影响不可忽视, 研究了电压与阻尼之间的关系, 以预测在有阻尼的压电曲梁发生裂纹损伤时可能出现的情况. 从图5中可以看出随着阻尼增大, 电压响应如预期般减小. 在阻尼比取值到0.8时, 共振峰基本消失, 响应曲线趋于平缓. 并且几乎在所有情况下, 引入阻尼都会降低电压.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-452-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
不同阻尼比下的电压?频率响应(L1 = 0.04 m, h’ = 0.4)



Figure
5.
The voltage frequency responses with different damping coefficients ( L1 = 0.04 m , h’ = 0.4)



下载:
全尺寸图片
幻灯片



3.4
功率对损伤压电曲梁电压?频率响应的影响


图6绘制了不同裂纹深度下压电曲梁的输出功率的频率响应. 可以看出功率响应的变化情况与图3电压响应变化相同, 在一阶、二阶频率处的峰值也是成比例减小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-452-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
不同裂纹深度下的功率?频率响应(L1 = 0.06 m)



Figure
6.
The frequency responses of electric power with difference crack depth (L1 = 0.06 m)



下载:
全尺寸图片
幻灯片



4.
结 论


本文重点研究了裂纹损伤的曲梁压电俘能器的力电耦合强迫振动, 运用格林函数法推导出该振动问题的解析解. 在数值计算中, 通过与健康压电曲梁的文献解进行对比, 验证了解的有效性. 最后通过研究曲梁压电俘能器在裂纹几何参数影响下电压响应变化情况对结构进行损伤监测, 得出结论:

(1) 裂纹出现时, 损伤曲梁的电压响应在健康曲梁的一阶频率处成比例变小, 且随即被激励出二阶频率;

(2)通过对电压响应的监测可以确定的损伤裂纹的深度和在结构中出现的位置范围, 证明了逆方法的可行性;

(3)通过监测由振动响应引起的俘能器电压变化能准确地反映结构的健康状况.

相关话题/结构 电压 材料 文献 健康
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于人工神经网络的非结构网格尺度控制方法
    引言网格生成是计算流体力学(computationalfluiddynamics,CFD)数值计算的第一步,也是未来CFD六大重要研究领域之一[1-2].在现代CFD应用过程中,自动生成复杂构型的高质量网格(包括网格自适应)依然是一个重大挑战性问题.自动化程度和网格质量是网格生成过程中最重要的两个问 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于深度强化学习算法的颗粒材料应力?应变关系数据驱动模拟研究
    引言在研究泥沙、岩土、粉体等颗粒材料宏观力学行为时,通常在连续介质力学框架下建立其唯象本构模型,通过引入内变量来描述颗粒材料的路径相关、历史相关等特性[1-5].虽然基于连续假设的唯象本构模型在描述颗粒材料宏观力学特性时具备很好的工程适用能力,但是颗粒材料由于其自身的离散特性,具有摩擦性,剪胀性,压 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • K<sub>0</sub>超固结结构性黏土的本构模型
    引言自然界存在的天然黏土通常是K0固结与结构性并存的状态[1-2],而K0固结又按照当前竖向应力是否大于先期固结压力而分为K0正常固结与K0超固结黏土.大量的室内试验以及现场测试表明,K0正常固结黏土由于初始固结为偏压固结,与等方向正常固结黏土相比,其在大主应力与先期固结压力一致的情况下,K0固结黏 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于深度学习和细观力学的颗粒材料本构关系研究
    引言颗粒材料广泛存在于各类自然环境和工程活动中,人类几乎所有的基础设施都建造于岩土材料这类典型的颗粒材料上,理解和预测此类材料在外载作用下的力学响应具有重要的意义.岩土材料通常由粒径不一,形状各异的矿物颗粒以及颗粒之间的空隙组成.颗粒间的互相滑动会引起不可恢复的塑性变形,因而,颗粒材料在剪切作用下极 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 冲击载荷下颗粒材料临边界区域的波动行为及变形特征分析
    引言作为离散颗粒材料的土壤(或岩体),是日常生活中最常见的随机多孔介质,冲击载荷作用下材料的动力学响应对于工程实践和地质灾害防控有着重要的指导意义.注意到应力波的传播行为与介质性质密切相关,基于应力波的行为特征分析可提供一种非侵入式研究颗粒材料性质的途径.因此有非常多的****致力于研究冲击载荷作用 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 压电超构材料及其波动控制研究: 现状与展望
    引言超构材料或超材料(metamaterials)是将精心设计的基本单元通过一定的空间排列来实现普通材料所不具有的奇异或反常性能,如带隙、波导、负折射、负模量、负密度、超透镜、声学聚焦、声学隐身和拓扑态等[1-2],已成为一个多学科交叉的前沿研究领域.过去几十多年来陆续出现的左手材料[3]、光子晶体 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 软材料粘接结构界面破坏研究综述
    引言因其特有的低模量和能量耗散等“软”的特性以及优异的“小激励大响应”等特征,多种多样的软材料,如水凝胶、介电弹性体以及聚甲基氧硅烷等被广泛应用在软机器人、生物医学和柔性电子等各个领域[1-4].近些年,软材料的力学行为已经成为学术界和工业界广泛关注的热点之一.在实际应用中,软材料一般需要粘附于某种 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于喷流拟序结构预测的SGS模型比较研究
    引言拟序结构普遍存在于湍流中[1–3],并影响湍流的发生、输运与耗散等过程,对湍流拟序结构的研究、对于理解湍流机理、分析流动相互作用有重要的意义.从大涡模拟来看,正确预测湍流拟序结构的关键就在于算法和亚网格尺度(sub-grid-scale,SGS)模型的准确性.在算法方面,传统的大涡模拟方法求解网 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 新型负刚度吸能结构力学特性分析
    引言在冲击载荷作用下,吸能材料的应用具有重要的工程意义.传统的减振吸能方法主要有两种:其一,利用材料的塑性变形实现能量吸收耗散[1],如汽车保险杠和轻型自行车头盔均是基于这一原理进行结构以及超材料设计,然而破坏性的塑性变形使得材料无法重复利用;其二,利用材料的黏弹特性[2-3],实现重复性的能量吸收 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.