删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于人工神经网络的非结构网格尺度控制方法

本站小编 Free考研考试/2022-01-01


引 言


网格生成是计算流体力学(computational fluid dynamics, CFD)数值计算的第一步, 也是未来CFD六大重要研究领域之一[1-2]. 在现代CFD应用过程中, 自动生成复杂构型的高质量网格(包括网格自适应)依然是一个重大挑战性问题. 自动化程度和网格质量是网格生成过程中最重要的两个问题[3-4]. 据统计, 网格生成通常占据整个计算周期大约60%的人力时间, 高度自动化的网格生成方法无疑可以很大程度节约CFD计算周期内的人工成本.

网格空间尺度分布控制在网格生成中至关重要, 对于网格质量和流动求解精度影响较大. 通常希望在几何曲率大、流动梯度大等重点区域加密网格, 而在非重点区域则希望网格尽可能稀疏并均匀过渡.传统的非结构网格尺度控制方法主要有: 函数指定法、插值类方法、背景网格法和根据流场特征进行自适应等.

函数指定法适用于简单问题的全场网格尺度控制, 比如可以指定线性函数控制翼型的网格尺度分布; 或用于局部网格尺度控制, 比如可以指定几何级数或指数函数对局部网格进行加密[5].

采用背景网格法[6-9]进行网格尺度控制, 需要先用规则的矩形结构网格或采用较稀疏的非结构网格覆盖全计算域, 在计算域内分布一定的“点源”“线源”或者“面源”等局部网格分布控制参数, 将这些源视作离散的“热源”, 求解热传导方程(泊松方程), 得到的稳态解即为全计算域的尺度控制参数分布[6]. 或者根据局部几何特征(曲率、狭缝、窄边等信息)确定局部网格尺度, 再在背景网格上求解网格尺度满足的梯度限制方程, 将局部网格尺度光滑到全场, 得到背景网格上的网格尺度分布[7-9]. 在生成网格时, 根据控制空间中某点在矩形背景网格中所处的单元, 通过背景网格的尺度分布插值得到该点处的网格尺度.

除此之外, 还有一些****提出一些其他形式的背景网格法. 如Deister等[10]提出由最大最小尺度及最大曲率角对几何进行栅格化, 计算得到局部网格尺度, 并存储在自适应的背景笛卡尔网格上. Quadros等[11-12]提出采用几何体离散骨架的几何临近信息、特征尺寸、边界曲率来测量几何复杂度, 并根据几何复杂度生成点源, 根据点源确定网格尺度分布, 最终将网格尺度存储在叉树结构的笛卡尔背景网格上. Ruiz-Girones等[13]提出通过在背景网格上求解一种新的非线性方程来控制四边形网格尺度, 等等.

径向基函数(radial basis function, RBF)[14-15]可用于数据插值, 在已知边界上的网格尺度后, 可用RBF方法将边界网格尺度插值到内场, 采用贪婪算法还可以一定程度提高RBF插值的效率, 是一种简单高效的插值类尺度控制方法.

根据流动特征物理量的梯度量等判据进行网格自适应[16-17]也是控制网格尺度分布的一种有效方法, 能够根据流场变化控制网格疏密, 在梯度大的区域生成更密的网格, 能够更精细地捕捉流动特征, 具有更高的计算精度和适应性, 是来重要发展方向之一[18].

近年来, 基于人工神经网络的深度学习方法在工业社会甚至流体力学领域得到广泛研究和应用[19-21]. 大数据驱动的人工智能方法成为除理论分析、数值计算和实验技术以外一种新的研究范式, 为各个领域带来了新的研究思路和方法.

在网格生成领域, 经过多年的工程实践, 已经积累了大量各种类型的网格数据, 这些数据包含了网格生成规则及技术人员在网格生成方面的知识和经验, 是天然的机器学习训练样本. 通过机器学习对网格生成规则进行学习, 可以简化传统算法, 提高网格生成效率[22]. 而网格尺度分布的控制也需要技术人员根据对流动问题的分析和经验合理确定, 采用机器学习方法对网格尺度分布进行控制, 有望减少人工工作量和对人工经验的依赖.

本文从网格质量、效率、灵活性和自动化程度4个方面综合分析各类网格尺度控制方法的优缺点. 为了克服传统背景网格插值法效率低、自动化程度不高等方面的不足, 本文从效率和自动化程度角度提出两种网格尺度控制方法, 首先将RBF插值方法应用于网格尺度控制, 采用贪婪算法对RBF插值参考点序列进行精简, 实现高效的RBF网格尺度分布控制方法. 进一步将提出一种采用人工神经网络进行非结构网格尺度控制的方法, 通过引入相对壁面距离和相对网格尺度, 初步确定合理的神经网络输入输出参数, 建立人工神经网络训练模型, 采用商业软件生成二维圆柱和二维翼型非结构三角形网格作为训练样本, 通过训练和学习建立起相对壁面距离和相对网格尺度之间的映射关系, 进而实现不同密度的二维圆柱、不同二维翼型在不同远场大小情况下的网格尺度分布控制.


1.
基于背景网格法的尺度控制方法回顾


背景网格法可采用规则的笛卡尔直角结构网格、非规则的非结构网格或者自适应笛卡尔网格[9], 各种类型的背景网格各有优缺点, 由于规则结构网格求解和插值效率较高而得到广泛使用.

在背景网格上布置“点源”、“线源”或者“面源”等局部网格分布控制参数, 通过求解热传导方程, 得到稳态解即为全流场的尺度控制参数分布[5]. 该方法能够生成分布均匀的网格, 且能更灵活地考虑流动局部特征对网格分布的影响.


1.1
背景网格法


以二维问题为例, 网格尺度S满足如式(1)所示的稳态热传导方程(泊松方程), 以确保尺度源项的作用在物理空间内光滑分布.







$$frac{{{partial ^2}S}}{{partial {x^2}}} + frac{{{partial ^2}S}}{{partial {y^2}}} = G$$
(1)

式中G为源项, 定义如式(2)所示







$${G_{i,j}} = sumlimits_{n = 1}^N {{varPsi _n}} ({S_{i,j}}{J_n} - {I_n})$$
(2)

式中下标“i”, “j”代表背景网格节点, N为热源总数, ${varPsi _n}$为第n个源的强度因子, 函数In及Jn分别定义如下







$${I_n} = left{ begin{aligned} & {{{S_n}} / {r_n^2}},;;;;;;;;;;;;;;;;;;;;{
m{nodal; source}} & frac{1}{{left| {{l_n}}
ight|}}int_{{l_n}} {frac{{f(l)}}{{{r^2}(l)}}{
m{d}}l}, ;;;;;;{
m{line; source}} end{aligned}
ight.$$
(3)







$${J_n} = left{ begin{aligned} & 1/r_n^2,;;;;;;;;;;;;;;;;;;;;;{
m{nodal; source}} & frac{1}{{left| {{l_n}}
ight|}}int_{{l_n}} {frac{1}{{{r^2}(l)}}{
m{d}}l}, ;;;;{
m{line ;source}} end{aligned}
ight.$$
(4)

式中S和f为在各源处的尺度, r为背景网格节点到源的距离, |ln|为线源长度.

文献[5]还提出了考虑方向性的网格密度控制方法, 可以通过改变源的强度函数来实现, 具体可参考文献, 本文不再赘述.

因此, 采用背景网格法进行网格尺度控制的步骤为:

(1)在矩形背景网格上采用中心差分离散泊松方程;

(2)采用Gauss?Seidel超松弛迭代求解离散的泊松方程, 得到背景网格上的网格尺度分布;

(3)在网格生成过程中, 根据当地位置在背景网格中插值得到当地网格尺度, 用于控制网格生成过程.


1.2
背景网格法网格生成实例


本节采用二维圆柱、NACA0012翼型和30P30N多段翼型作为考核算例, 对背景网格法进行实例测试. 本文算例中采用的三角形网格生成算法为作者发展的基于ANN (artificial?neural?network)的阵面推进法[22], 该方法在传统阵面推进法的基础上, 通过引入ANN进行生成模式判断和新点预测, 减少了相交性判断次数, 网格生成效率提高30%, 其网格生成步骤可简要概括为:

(1)将几何边界离散成初始阵元;

(2)从最小阵面出发, 自动选择网格模板点, 人工神经网络根据网格模板判断生成模式并预测新点坐标;

(3)根据生成模式、新点坐标和局部网格尺度生成新网格单元;

(4)判断新单元是否合适, 合适则更新数据结构;

(5)回到步骤2, 直至所有面变成非活跃面, 整个计算域被网格填满.

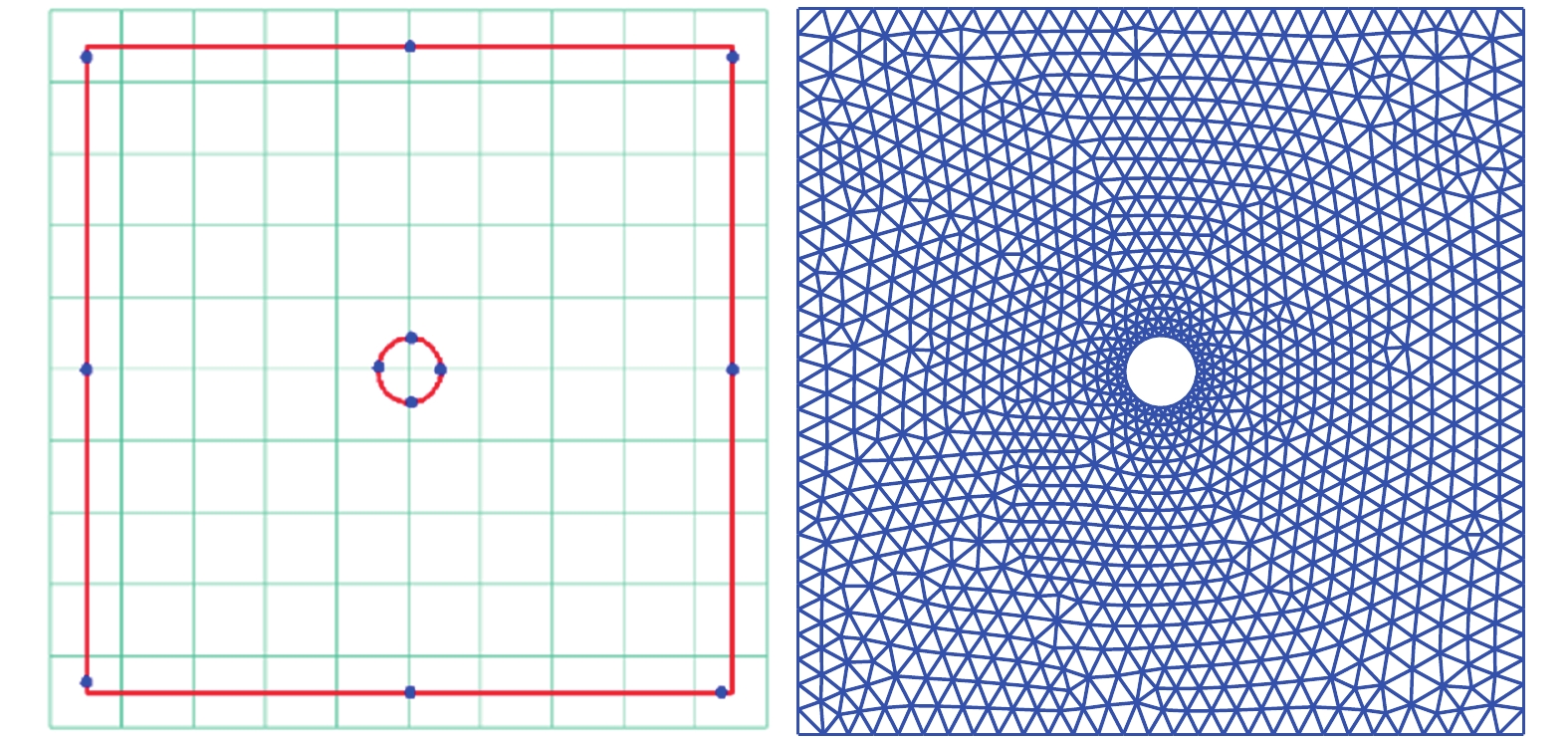
图1~图3给出了3个算例点源设置示意图和生成的网格, 图中蓝色圆点即为点源所在位置. 3个算例人工设置的点源数量分别为12, 24和44. 图中背景网格仅作为示意, 实际背景网格节点数量需要根据边界网格尺度进行调整, 以确保对网格尺度分布场的分辨率和插值精度. 比如对于在前后缘网格尺度较小的翼型, 背景网格必须足够密才可以有效反映出空间网格尺度的变化.

在本文三个算例中, 背景网格规模分别为51 × 51, 301 × 301和401 × 401. 由于是在背景网格上迭代求解泊松方程, 因此背景网格的网格数量直接决定了迭代求解的效率.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
圆柱算例点源设置及网格生成情况



Figure
1.
Nodal source settings and corresponding triangular mesh over a 2D cylinder



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
NACA0012算例点源设置及网格生成情况



Figure
2.
Nodal source settings and corresponding triangular mesh over NACA0012 airfoil



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
30P30N算例点源设置及网格生成情况



Figure
3.
Nodal source settings and corresponding triangular mesh over 30P30N airfoil



下载:
全尺寸图片
幻灯片


图中结果显示, 在人工设置合适的点源参数后, 可以在背景网格上得到恰当的网格尺度分布.

要说明的是本文暂未采用线源, 实际上线源可以看作按线段排列的具有一定强度分布的点源集合, 因此在处理本文的简单问题时, 只采用点源进行网格尺度的控制, 用以说明背景网格法的优缺点.


2.
基于RBF方法的尺度控制方法


径向基函数是一种常用的插值函数, 常用于网格变形的插值[14-15, 23-24], 如图4所示即为用NACA0012翼型的S型启动来模拟鱼的游动过程, 采用RBF插值方法将物面的变形插值到空间来生成动网格. RBF插值方法也可以用于网格尺度的插值控制, 在已知边界网格尺度的情况下, 求得插值系数矩阵, 可将边界尺度插值到整个计算域.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
RBF网格变形方法



Figure
4.
Mesh deformation controlled by RBF interpolation



下载:
全尺寸图片
幻灯片



2.1
基于贪婪算法的RBF插值方法


RBF插值方法是比较成熟的插值方法, 对于一个变量场, 如网格变形情况下的位移场, 或网格尺度控制情况下的网格密度场, 可以用RBF插值公式表示为







$$fleft( {boldsymbol{r}}
ight) = sumlimits_{i = 1}^N {{w_i}varphi left( {left| {{boldsymbol{r}} - {{boldsymbol{r}}_i}}
ight|}
ight)}$$
(5)

其中, N为参考点数目, $fleft( {boldsymbol{r}}
ight)$为某待求点的函数值(网格尺度), ${boldsymbol{r}}$为待求点的位置矢量, ${{boldsymbol{r}}_i}$为参考点的位置矢量, $varphi $为RBF基函数, $left| {{boldsymbol{r}} - {{boldsymbol{r}}_i}}
ight|$为参考点与待求点之间的欧氏距离. ${w_i}$为第i个参考点的权重系数.

以网格尺度分布控制为例, 权重系数满足







$$left( {begin{array}{*{20}{c}} {Sp_{1}} vdots {Sp_{N}} end{array}}
ight) = left( {begin{array}{*{20}{c}} {{varphi _{11}}}& cdots &{{varphi _{1N}}} vdots & ddots & vdots {{varphi _{N1}}}& cdots &{{varphi _{NN}}} end{array}}
ight)left( {begin{array}{*{20}{c}} {{w_1}} vdots {{w_N}} end{array}}
ight)$$
(6)

式中$Sp$为各个参考点的网格尺度, 参考点通常为边界点, 也即边界网格尺度. 基函数的类型包括全域型基函数和紧支型基函数, 具体可以参考文献[14-15, 23-24], 本文不再赘述.

权重系数的求解通常需要求解系数矩阵的逆, 在参考点数目较大时, 会导致求解效率较低, 因此可以引入贪婪算法对参考点进行精简.

基于贪婪算法的RBF方法的步骤可简要归纳为:

(1)初始参考点集为空集, 随机取一边界点作为初始参考点;

(2)根据参考点, 采用RBF插值计算其他边界点处的网格尺度;

(3)由于参考点数目太少, RBF插值得到的边界网格尺度与给定值存在一定误差, 找出误差最大的点;

(4)若误差最大的点不为已有参考点, 则将该点做为新参考点加入参考点序列, 否则重新任选一点加入参考点序列;

(5)重复步骤(2) ~ (4), 直到最大误差或者参考点数目满足要求, 确定最终参考点序列;

(6)根据最终参考点序列进行RBF插值, 得到空间所有位置的网格尺度分布.


2.2
RBF方法网格生成实例


本节仍然采用二维圆柱、NACA0012翼型和30P30N多段翼型作为考核算例, 对RBF方法进行实例测试. 算例中所采用的三角形网格生成算法仍为基于ANN的阵面推进法, 具体可参考文献[22].

RBF基函数取为Wendland’s C0, 紧支半径取为计算域范围大小的1/4. 网格尺度控制对尺度插值误差的要求不高, 本文以尺度的最大相对误差不超过5%为标准, 进行参考点序列精简, 表1给出了采用贪婪算法对参考点进行精简的结果, 结果显示对于翼型算例, 精简序列后参考点数量至少减少一半, RBF插值的耗时也减少了近一半, 在保证了插值效果的同时提高了插值效率.




表
1
RBF方法参考点的数目及插值耗时



Table
1.
Number of reference nodes and time consumption on interpolation



table_type1 ">
CaseNo. of Ref. nodesTime consumption/s
originalselectedoriginalselected
cylinder145121.070.16
NACA00123061422.171.44
30P30N3401622.391.81





下载:
导出CSV
|显示表格



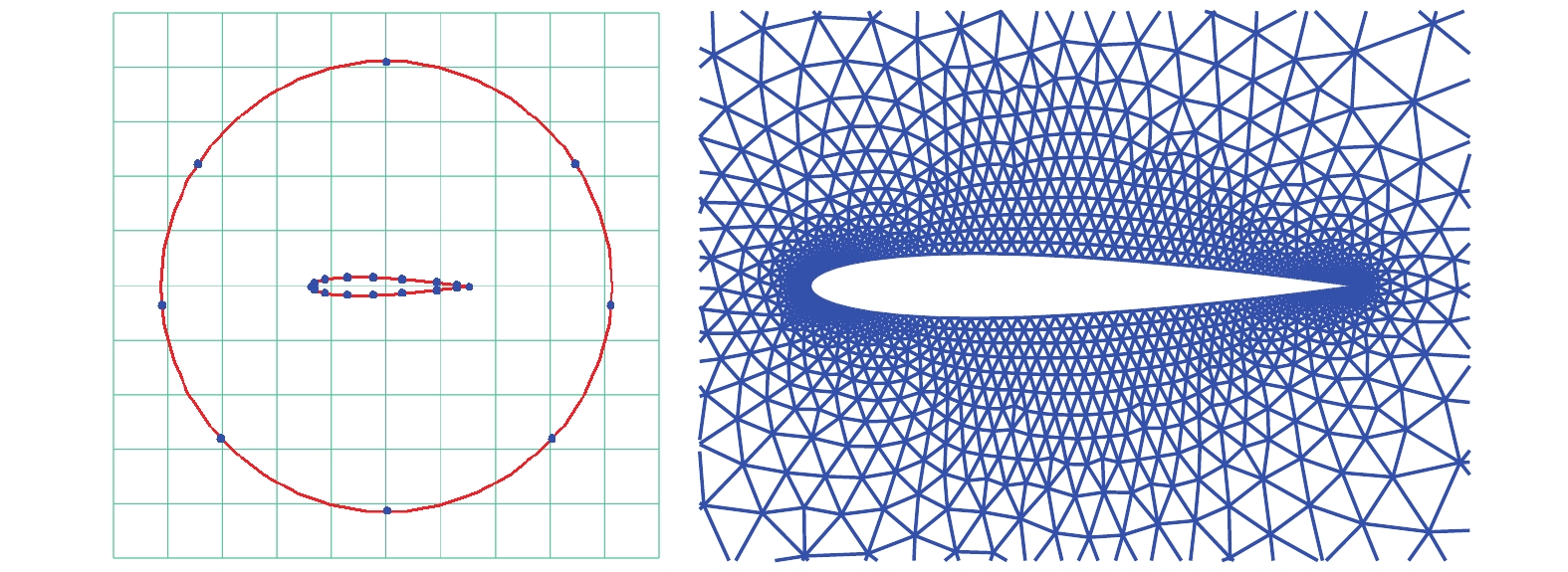
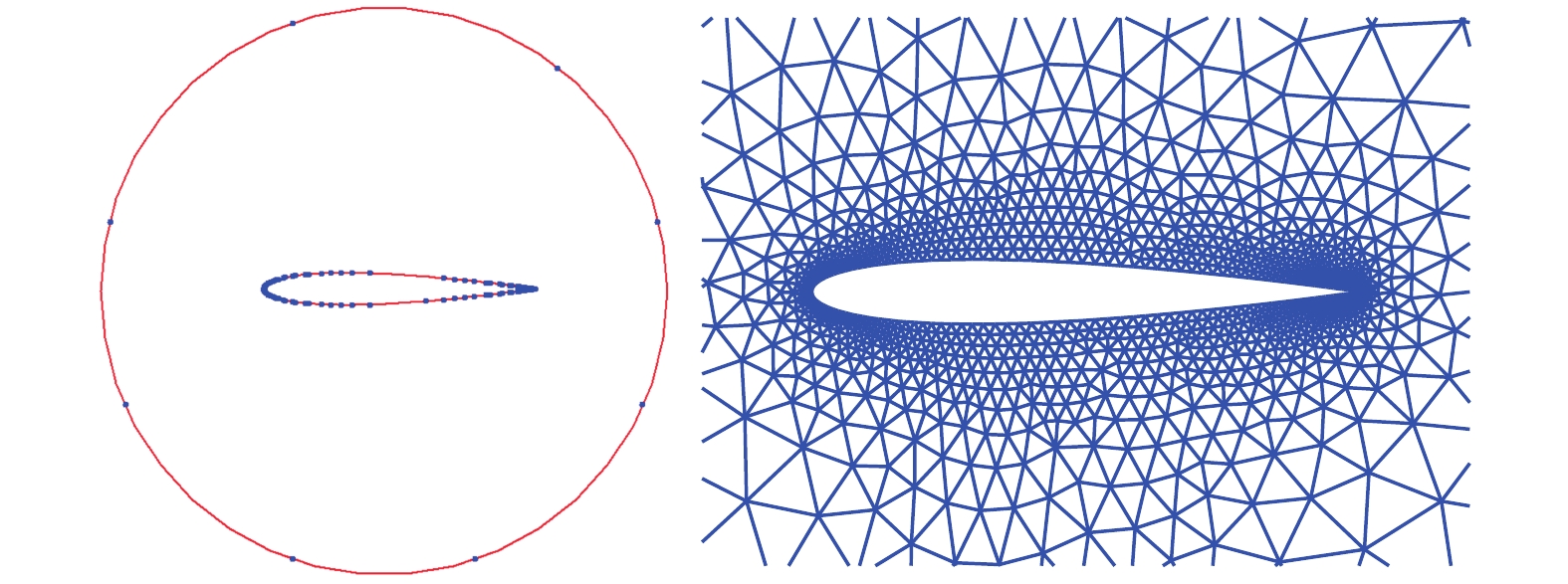
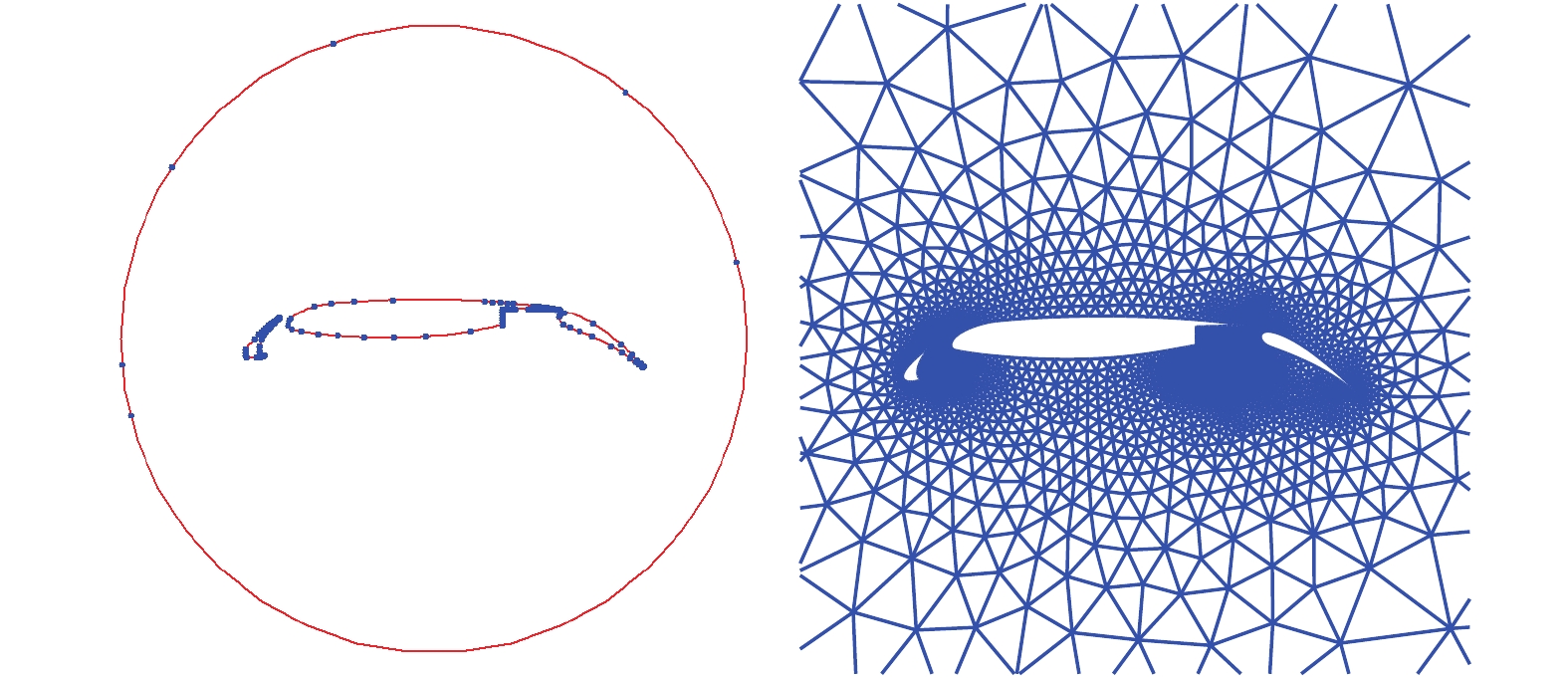
图5 ~ 图7给出了精简后的参考点的位置及根据精简参考点进行尺度控制生成的非结构网格. 结果显示RBF方法能够根据边界网格尺度插值得到空间的网格尺度, 插值得到的网格尺度分布过渡均匀. 由于初始参考点的选择是随机的, 参考点的分布具有一定的随机性, 但是均能够保证插值误差满足要求.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
圆柱算例精简后的参考点及网格生成情况



Figure
5.
Reference nodes corresponding triangular mesh over a 2D cylinder



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
NACA0012算例精简后的参考点及网格生成情况



Figure
6.
Reference nodes and corresponding triangular mesh over NACA0012 airfoil



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
30P30N算例精简后的参考点及网格生成情况



Figure
7.
Reference nodes and corresponding triangular mesh over 30P30N airfoil



下载:
全尺寸图片
幻灯片



3.
基于人工神经网络的尺度控制方法


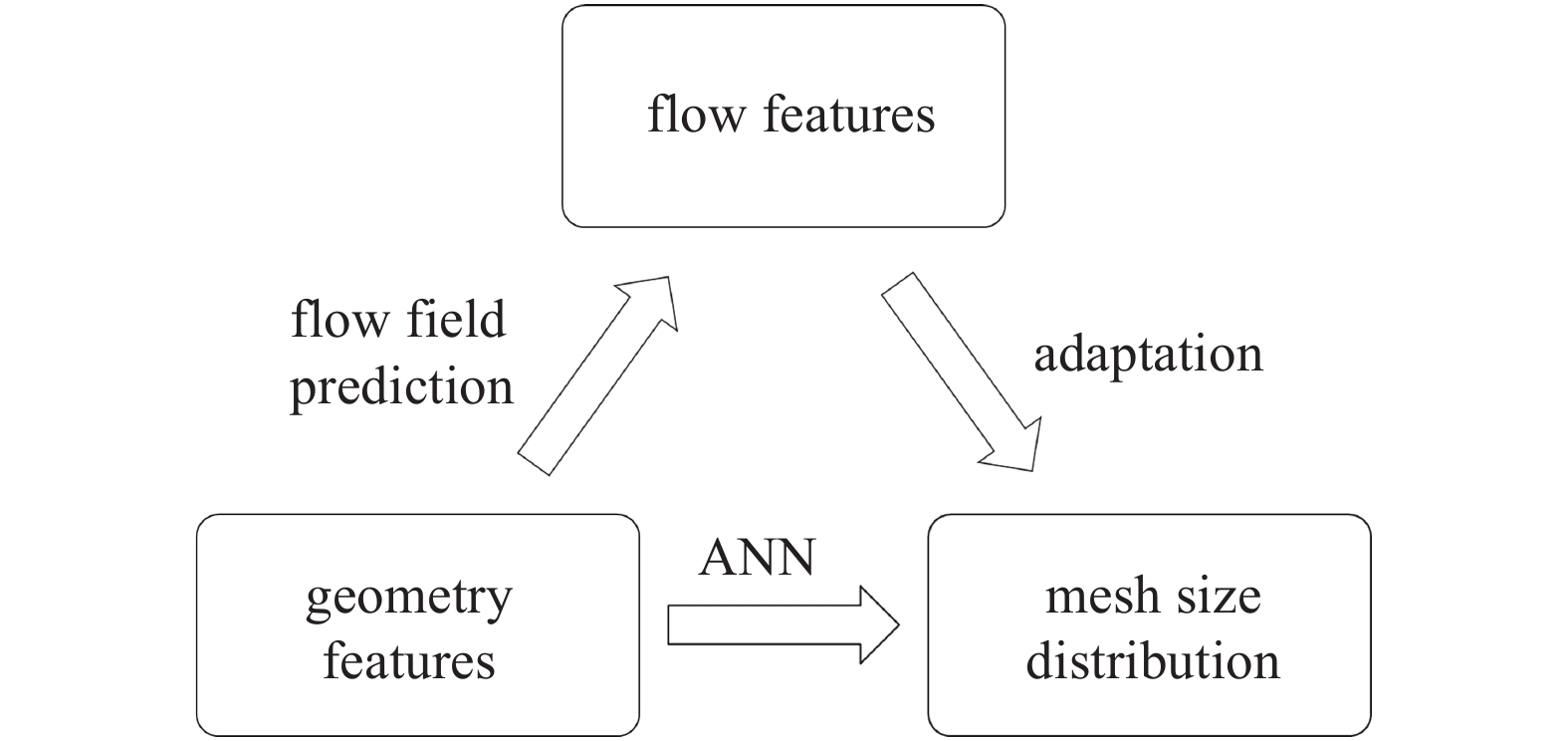
基于人工神经网络的深度学习具有较强的非线性拟合能力, 能够通过现有样本数据的训练识别出数据中隐含的非线性映射关系. 网格尺度分布实际上是一个关于几何特征、流场特征的非线性映射, 如图8所示, 几何特征(物面曲率、狭缝、细小结构等)可以直接影响网格尺度分布, 几何特征也可以决定流动特征(梯度量等), 从而间接决定网格分布. 不同几何外形的网格尺度分布不同, 同一几何外形在不同来流条件(流场特征)情况下, 网格尺度分布也不同.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
网格分布控制与几何特征和流场特征的关系



Figure
8.
Relationship between mesh size control, geometry, and flow features



下载:
全尺寸图片
幻灯片


流场特征与几何外形、来流条件和边界条件相关, 目前采用机器学习方法进行流场预测是一个热点研究问题[25-26]. 而根据流场特征确定网格分布则可以根据网格自适应的相关准则进行, 也可以采用机器学习的方法进行[27]. 本文初步考虑几何外形对网格分布的影响, 采用ANN建立几何特征与网格尺度分布之间的关系.


3.1
ANN输入输出参数


Chedid和Najiar等[28]曾尝试用ANN建立起网格密度与几何特征之间的关系, 如图9所示, 神经网络输入考虑了空间点${g_i}$到边界点的最小距离${delta _1}$, 次小距离${delta _2}$及其对应的夹角${a^*}$和${a^{**}}$及到夹角对应两边的投影距离${j_{1a}}$, ${j_{1b}}$, ${j_{2a}}$和${j_{2b}}$共8个输入参数, 输出该空间点处的网格密度, 定义为一定大小区域内节点的数量. 该方法能够较为全面地反映空间点与边界之间的几何关系(距离及投影距离), 以及空间点对应的边界处的几何特征(夹角、曲率), 但计算量较大不利于提高尺度控制效率, 同时由于无法网格局部加密控制, 失去了对网格尺度控制的灵活性, 因此优势并未得到发挥.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
文献[28]中神经网络的输入参数



Figure
9.
Input parameters for the artificial neural network in Ref. [28]



下载:
全尺寸图片
幻灯片


为提高效率, 本文初步选择最小壁面距离wdist作为输入参数, 网格尺度$Sp$作为输出参数. 为提高ANN的泛化性, 其输入输出参数通常需要进行归一化操作, 本文采用计算域的大小${L_{{
m{r_d}}}}$, 远场边界网格尺度${L_{{
m{r_f}}}}$和物面边界网格尺度${L_{{
m{r_w}}}}$对输入输出进行分别归一化.

同时, 由于从物面到远场, 网格尺度变化较大, 网格尺度相对值可能在103量级以上, 为尽量缩小输入输出的值域范围, 提高ANN训练效果, 本文对输入输出参数进行开根号. 此外, 在物面附近网格尺度变化快, 需要同时考虑物面参考值和远场参考值进行归一化, 具体输入输出参数形式如表2所示.




表
2
ANN输入输出模型



Table
2.
Parameter model for artificial neural network



table_type1 ">
Model
input${left( {dfrac{{wdist}}{{{L_{{
m{r_d}}}}}}}
ight)^{1/6}}$
output$left{ {begin{array}{*{20}{c} } { { {left[ {dfrac{ {S{ {p} } } }{ { { {left( { {L_{ {
m{r_w} } } } }
ight)}^{1/6} } } } + dfrac{ {S{ {p} } } }{ { {L_{ {
m{r_f} } } } } } }
ight]}^{1/6} }, ; wdist leqslant 0.25{L_{ {
m{r_d} } } } } { { {left[{dfrac{ {S{ {p} } } }{ { {L_{ {
m{r_f} } } } } } }
ight]}^{1/6} };;;;;;;;;;;;;;;;;{
m{ } }, ; wdist > 0.25{L_{ {
m{r_d} } } } } end{array} }
ight.$





下载:
导出CSV
|显示表格



3.2
训练方法及参数


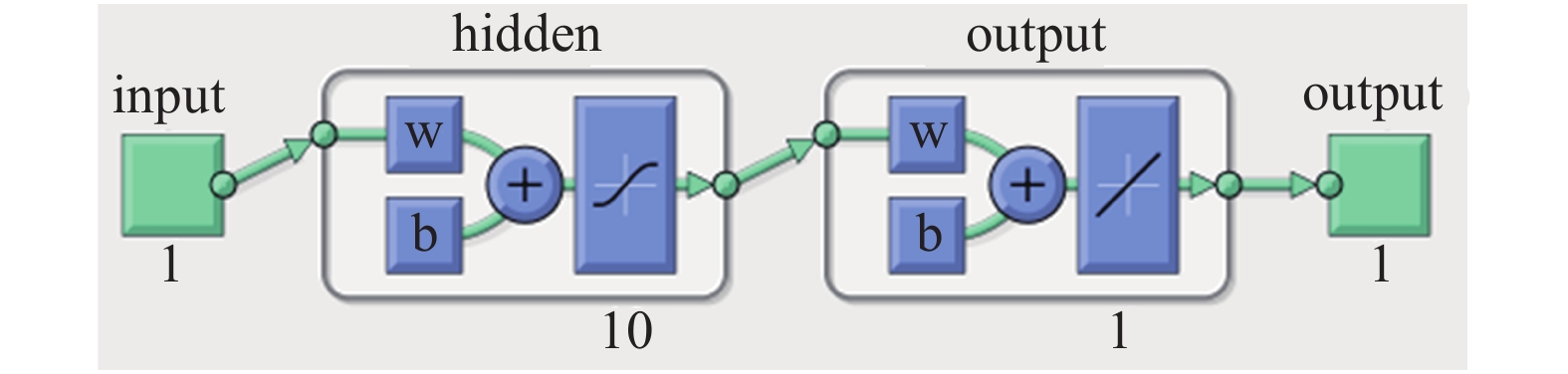
本文基于Matlab神经网络训练工具设计全连接的人工神经网络, 网络含有1个输入层, 1个隐藏层, 1个输出层. 输入层含有1个神经元, 输出层含有1个神经元, 隐藏层的神经元数量为10个, 激活函数采用Sigmoid函数, 损失函数为均方误差函数, 训练方法采用Levenberg?Marquardt反向传播方法, 该方法比常规的梯度下降反向传播算法训练效率更高, 具体可以参考文献[29]. 神经网络的结构如图10所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
基于Matlab的人工神经网络训练工具



Figure
10.
Artificial neural network training tool based on Matlab



下载:
全尺寸图片
幻灯片


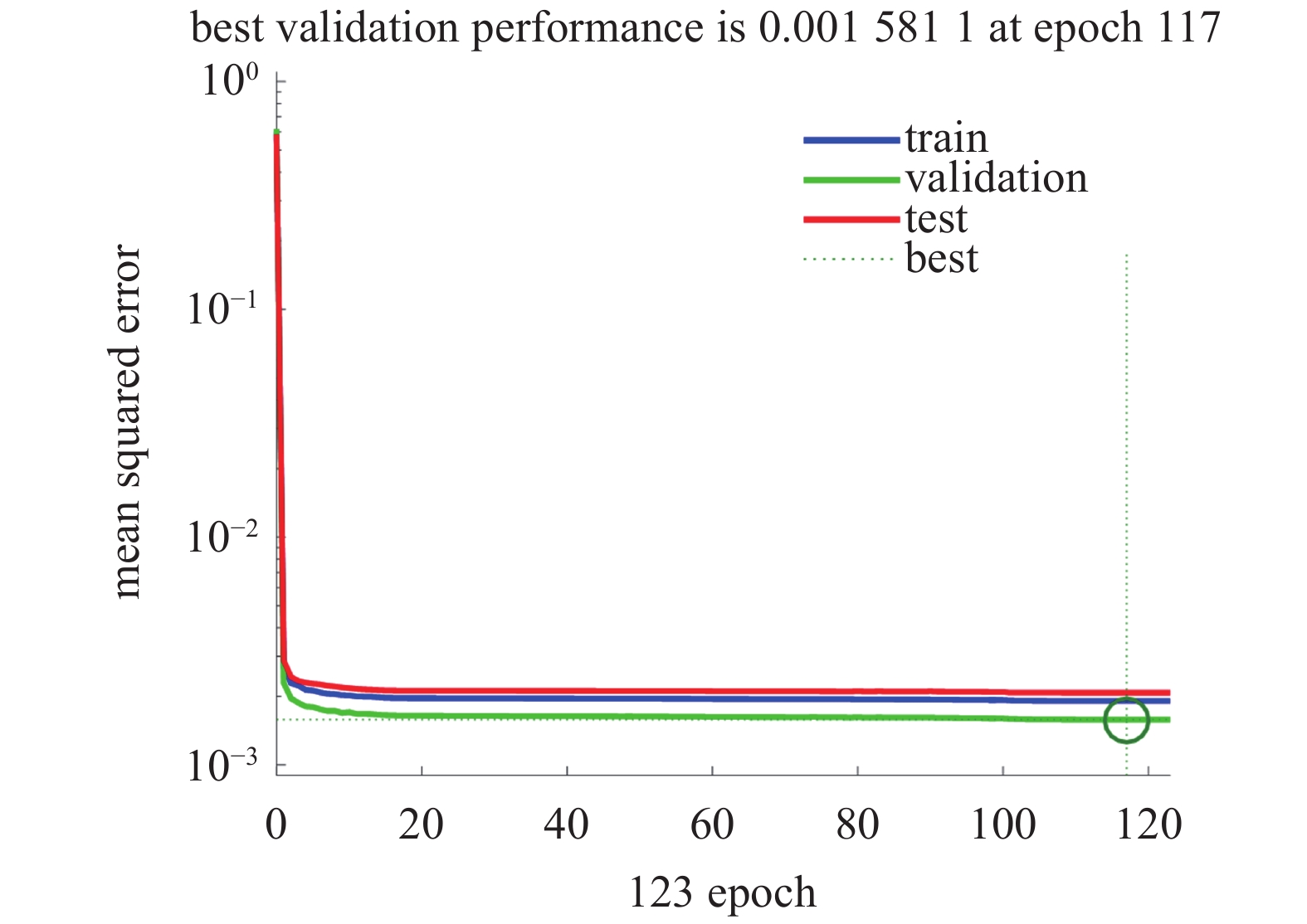
选择二维圆柱网格和NACA0012翼型网格作为训练样本, 如图11所示, 网格面个数分别为4295, 3950, 每个网格面对应一组样本数据点. 网格训练样本按70%, 15%和15%的比例随机划分为训练集、测试集和验证集, 图12给出了在翼型三角形网格训练集上的Loss值及在验证集上的预测精度收敛历程. 结果显示: 经过120次迭代后, Loss值及预测误差均下降到了0.00158左右.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
网格分布训练样本网格



Figure
11.
Sample grids for ANN training



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
训练Loss值和精度收敛历程



Figure
12.
Convergence of loss and accuracy on sample grids



下载:
全尺寸图片
幻灯片



3.3
ANN预测结果


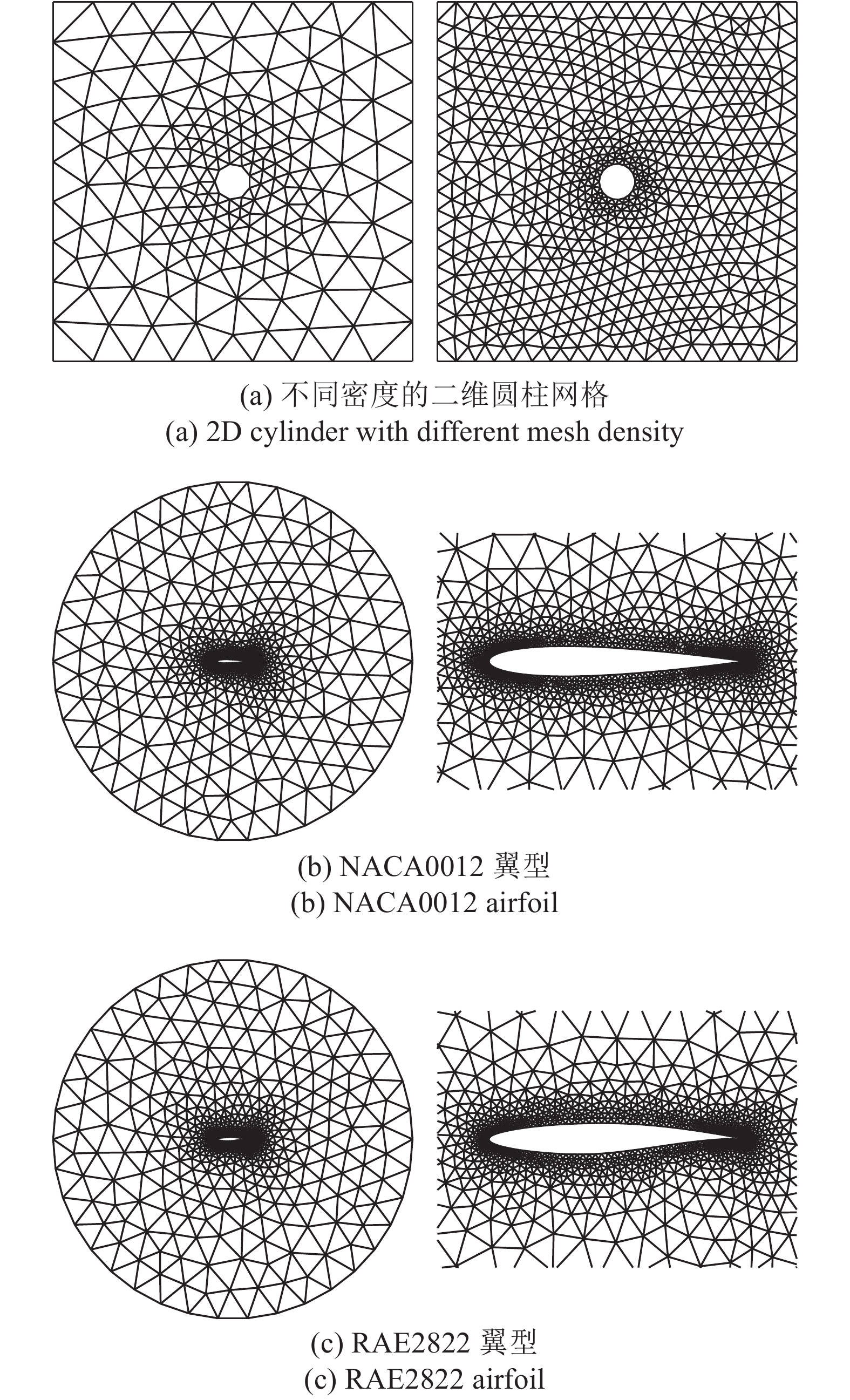
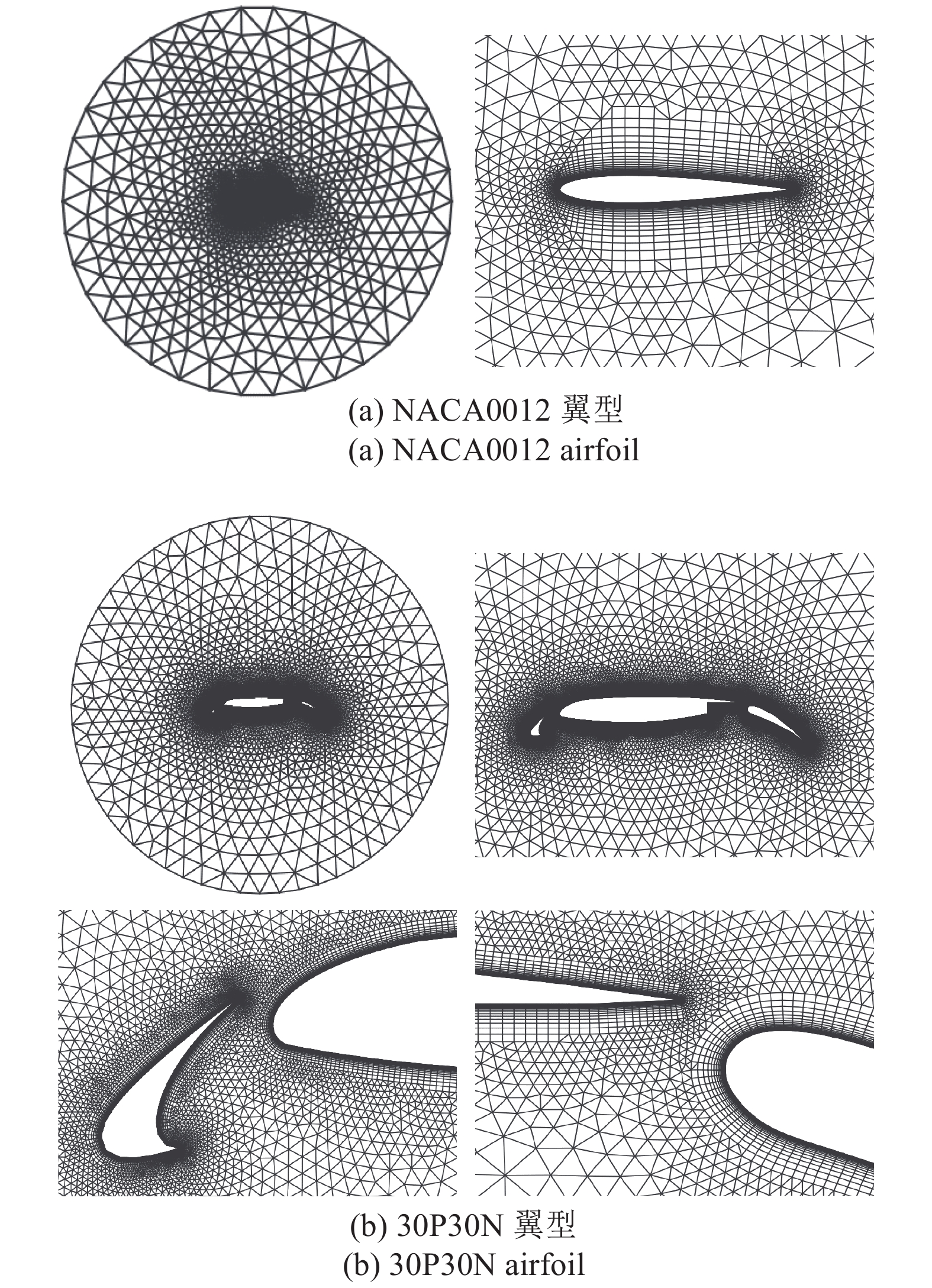
基于前述的ANN训练结果, 分别预测生成了不同密度的二维圆柱网格、NACA0012密网格、RAE2822翼型以及三段翼型, 在物面附近和远场均取得了较好的效果, 同时还能适应不同远场大小的情况, 如图13所示. 算例中所采用的三角形网格生成算法仍为基于ANN的阵面推进法, 具体可参考文献[22].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-13-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13-1" />



13
ANN模型各向同性网格预测结果



13.
Mesh size controlled by ANN model for isotropic triangular grids



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
ANN模型各向同性网格预测结果(续)



Figure
13.
Mesh size controlled by ANN model for isotropic triangular grids (continued)



下载:
全尺寸图片
幻灯片


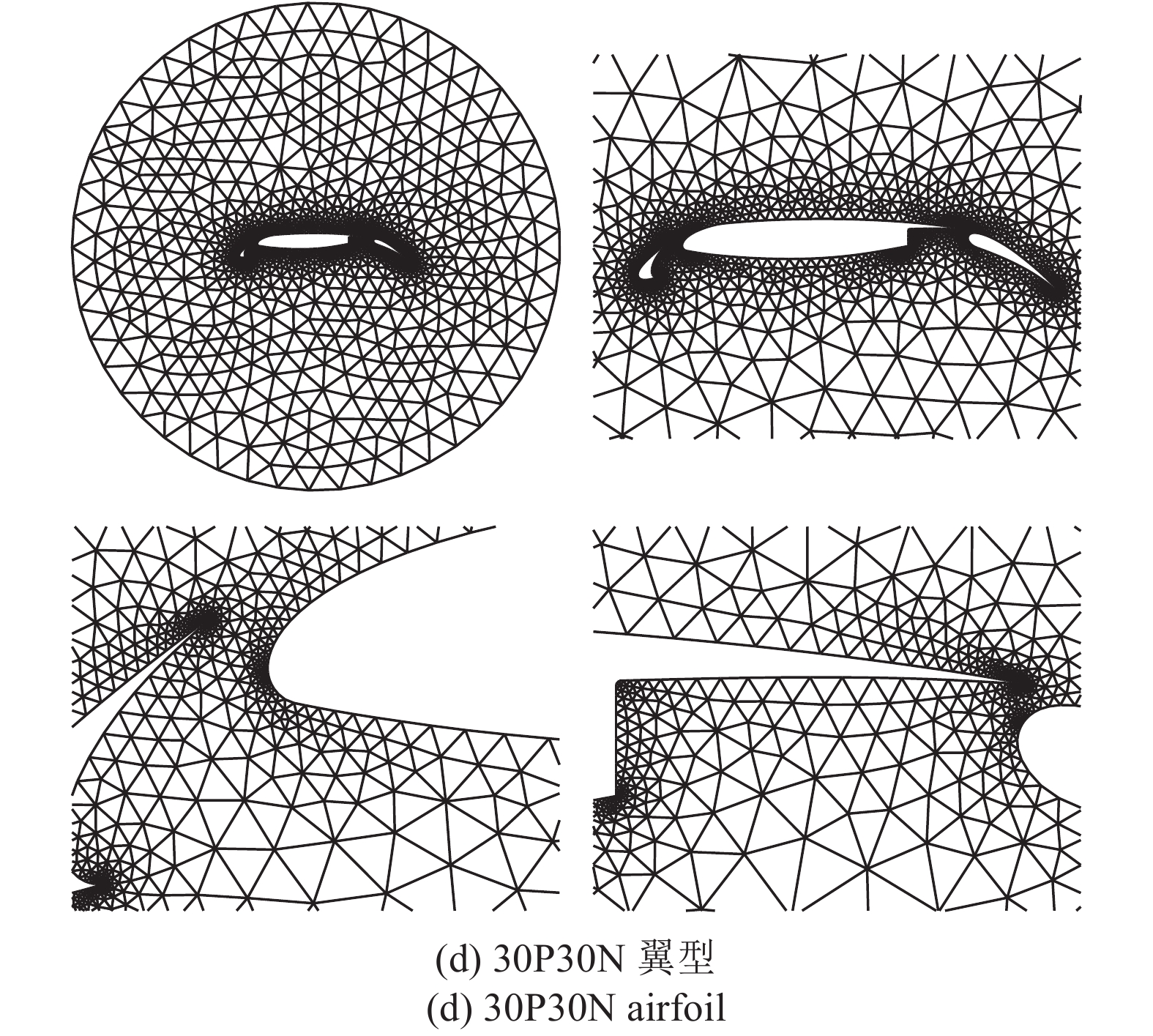
同时, 本文还将ANN应用于各向异性混合网格尺度控制, 各向异性四边形采用层推进逐层推进生成[30-32], 而各向同性三角形采用基于ANN的阵面推进生成[22]. 层推进的推进方向、多方向推进数量均采用ANN预测, 同时在凹角处考虑局部推进步长, 避免网格相交, 具体方法细节可以参考文献[30]. 为与各向同性网格尺度控制相一致, 本文将层推进生成的最后一层网格作为虚拟物面, 用于计算最小壁面距离, 作为ANN控制网格尺度的输入参数. 另外, 层推进的网格尺度控制仍然采用指定物面第一层网格高度和增长率的方式给定. 图14给出了NA0012翼型和30P30N三段翼型的生成结果. 由图中结果可见, 网格分布均匀合理, 网格质量满足要求, 说明本文发展的ANN方法可应用于各向异性混合网格的尺度控制.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-334-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
ANN模型各向异性混合网格预测结果



Figure
14.
Mesh size controlled by ANN model for anisotropic hybrid grids



下载:
全尺寸图片
幻灯片



4.
背景网格法、RBF方法与ANN方法的比较


本文分别采用3种方法生成了几个典型几何外形的非结构网格, 其网格生成质量、生成效率、尺度控制灵活性、自动化程度等情况存在一定差别, 本节对3种方法进行对比分析.

从网格质量的角度, 在网格尺度较小的部位, 如翼型前后缘、狭缝等, 背景网格法要求加密背景网格, 以分辨最小网格尺度, 而RBF方法和ANN方法不依赖于背景网格, 因此在尺度较小的部位得到的尺度分布控制效果比采用矩形背景网格要好.

从自动化程度和灵活性角度, 采用在背景网格上设置点源控制网格分布, 对分布的控制最为灵活, 能够根据几何特征和流场特征预先设置点源来改变网格分布. 而背景网格法需要人工设置点源, 本文算例中, 在远场和翼型附近人工设置数十个点源, 每个点源人为给定强度、位置等参数, 需要一定的经验, 自动化程度较低. 而RBF方法和ANN方法只需要给定离散的边界节点, 就可以得到空间网格尺度分布, 自动化程度相对较高, 但是灵活性较低.

从网格生成效率的角度, 背景网格法需要在笛卡尔网格上迭代求解泊松方程, 在背景网格很密时, 求解效率较低. 而RBF方法虽然需要求解矩阵的逆, 但在引入贪婪算法之后, 参考点数量减少, RBF方法的效率得到提高. ANN方法虽然需要求解最小壁面距离, 但壁面距离的值并不需要十分精确, 因此可以采用一些近似求法, 也可以达到更高的效率.

表3给出了3种方法在生成网格过程中尺度控制所耗费的时间, 由于每种方法生成的网格单元数存在一定差异, 因此表中也给出了网格单元数量.




表
3
3种方法控制网格尺度耗时对比



Table
3.
Efficiency comparison of the three methods



table_type1 ">
CaseBackground mesh method (s/cell)RBF method (s/cell)ANN method (s/cell)
cylinder0.60/28890.16/24270.44/2875
NACA00125.31/46801.44/48400.82/4390
30P30N14.77/61211.81/60501.03/4752





下载:
导出CSV
|显示表格



背景网格法耗时基本由背景网格的规模及点源的数量决定. 在本文三个算例中, 背景网格规模为51 × 51, 301 × 301和401 × 401, 点源的数量大致为20个, 因此在采用背景网格法时, 翼型算例耗时明显增加.

由表3中数据可见, 在背景网格数量较少时, 背景网格法的效率较高, 但是随着背景网格数量和点源数量的增加, 背景网格法效率明显下降. 相较于传统背景网格法, RBF方法和ANN方法的耗时明显减少, 耗时仅为背景网格法耗时的1/10 ~ 1/5, 网格尺度控制效率相应提高了5 ~ 10倍. 而且, 在外形相对复杂的情况下, ANN方法展现了更好的控制效率. 可以预见, 在三维复杂外形情况下, ANN的控制效果和效率会更高.


5.
总结与展望


本文提出了一种采用ANN进行网格尺度分布控制的方法, 初步确定了合理的神经网络输入输出参数, 基于Matlab建立人工神经网络模型, 采用商业软件生成二维圆柱和NACA0012翼型非结构三角形网格作为网格密度训练样本, 通过训练和学习建立起壁面距离和网格尺度的映射关系, 实现了不同密度的二维圆柱和不同二维翼型的网格尺度预测. 同时, 发展了基于RBF方法的网格尺度控制方法, 采用贪婪算法对插值参考点序列进行精简, 将RBF插值效率提高了一倍.

与传统背景网格法相比, 基于ANN方法和RBF方法的网格尺度预测效率提高5~10倍, 有助于进一步提高网格生成效率. 最后将基于ANN的网格尺度控制方法拓展应用于各向异性混合网格的尺度控制, 得到的网格质量满足要求, 证明了方法的实用性.

展望ANN方法在尺度分布控制领域的应用前景, 在以往的CFD研究和工程实践中, 已经积累了大量各种类型的网格, 其中包含了网格尺度分布信息. 对已有的网格数据按照几何外形进行分类, 训练得到可以处理不同类别几何外形的神经网络, 在需要对新的几何外形进行网格尺度控制时, 只需选择已经训练好的该类别的神经网络即可高效快速完成尺度控制. 进一步还可以考虑流场特征(来流条件), 对神经网络的适用范围进行细分, 使得其能够同时考虑几何外形和流场特征进行尺度控制.

可以进一步考虑物面几何曲率、局部特征尺寸(窄边、狭缝)等参数, 提高神经网络的泛化性, 同时研究通过神经网络进行流场预测, 并根据流场特征进行网格自适应.

相关话题/控制 网格 计算 图片 结构
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 水中开孔腔流激振荡控制实验研究
    引言空腔流激振荡是工程中常遇到的一类问题,它是指流体在流经开口结构时,边界层在开口前缘发生流动分离并形成不稳定的自由剪切层,在满足一定的流速和几何特征条件下,会引起剪切层发生稳定的自持振荡,产生很强的周期脉动压力,并通常引起高幅值纯音噪声辐射、附加阻力甚至是结构疲劳.以往对空腔流激振荡的研究主要集中 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑混凝土塑性耗散的CDM-XFEM裂缝计算方法
    引言混凝土结构是建筑、交通、水利等领域的重要基础材料,其可塑性高、耐久性好是受广泛应用的主要原因.但混凝土抗拉强度远低于抗压强度[1],结构在服役期间受外界载荷的影响容易产生裂缝[2],裂缝的出现不仅会降低结构刚度,还为外部侵蚀介质的侵入提供了快捷通道,从而加速内部钢筋锈蚀[3-4]、降低结构承载力 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • K<sub>0</sub>超固结结构性黏土的本构模型
    引言自然界存在的天然黏土通常是K0固结与结构性并存的状态[1-2],而K0固结又按照当前竖向应力是否大于先期固结压力而分为K0正常固结与K0超固结黏土.大量的室内试验以及现场测试表明,K0正常固结黏土由于初始固结为偏压固结,与等方向正常固结黏土相比,其在大主应力与先期固结压力一致的情况下,K0固结黏 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 倾斜吹吸控制下湍流边界层减阻的直接数值模拟
    引言湍流流动对流体质量、动量和能量的输运要远大于分子热运动产生的输运,湍流流动的控制(包括抑制和增强)是湍流研究领域的重要课题,如减阻控制等.湍流减阻控制研究能够在工程和国民经济领域发挥作用,如能够减少能量损失、减少环境污染、提高装置运行效率等.随着计算机水平的不断提高,数值模拟逐渐成为重要的湍流控 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 一种新的玻尔兹曼方程可计算模型构造与分析
    引言近年来,随着对临近空间战略意义认识的加深,各航空航天大国发展了众多临近空间飞行器.为满足长航时、大载荷、高超声速巡航等需求,这类临近空间飞行器通常整体尺寸较大,各部件间差异显著,飞行过程会出现多物理多场耦合、多流区共存的多尺度复杂流动现象,传统的数值模拟方法如基于宏观连续介质假设的纳维?斯托克斯 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 压电超构材料及其波动控制研究: 现状与展望
    引言超构材料或超材料(metamaterials)是将精心设计的基本单元通过一定的空间排列来实现普通材料所不具有的奇异或反常性能,如带隙、波导、负折射、负模量、负密度、超透镜、声学聚焦、声学隐身和拓扑态等[1-2],已成为一个多学科交叉的前沿研究领域.过去几十多年来陆续出现的左手材料[3]、光子晶体 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 页岩凝析气藏相平衡的快速准确计算方法
    引言随着以煤炭、石油和木柴为代表的传统能源消耗带来的巨量的空气污染日益引起全社会的关注,天然气作为一种相对较为清洁的能源得到了广泛的重视[1].近年来在非常规油气藏勘探和开发技术上的迅猛发展,使得具有巨大潜在储量但一直得不到有效开发的以页岩气为代表的非常规油气资源成为了投资热点和研究焦点[2].中国 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于T样条的变网格等几何薄板动力学分析
    引言随着柔性轻质结构在航天、汽车以及船舶工程等领域日益广泛的应用,柔性多体系统的动力学分析也愈加重要.然而,以线弹性小变形假设为基础的,将节点位移和转动作为坐标的传统有限单元不适合解决存在大位移、大变形的柔性多体系统的动力学问题.此外,对于传统结构有限元,将几何数据转换为有限元网格数据是困难且耗时的 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 软材料粘接结构界面破坏研究综述
    引言因其特有的低模量和能量耗散等“软”的特性以及优异的“小激励大响应”等特征,多种多样的软材料,如水凝胶、介电弹性体以及聚甲基氧硅烷等被广泛应用在软机器人、生物医学和柔性电子等各个领域[1-4].近些年,软材料的力学行为已经成为学术界和工业界广泛关注的热点之一.在实际应用中,软材料一般需要粘附于某种 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.