引 言
在研究泥沙、岩土、粉体等颗粒材料宏观力学行为时, 通常在连续介质力学框架下建立其唯象本构模型, 通过引入内变量来描述颗粒材料的路径相关、历史相关等特性[1-5]. 虽然基于连续假设的唯象本构模型在描述颗粒材料宏观力学特性时具备很好的工程适用能力, 但是颗粒材料由于其自身的离散特性, 具有摩擦性, 剪胀性, 压硬性, 各向异性, 荷载路径和历史相关性等典型特征, 并且在外载作用下还会呈现出应变局部化等复杂的演化机制, 连续模型要体现出颗粒材料精细的宏观特性就不得不引入繁杂的唯象假设和众多待标定的自由参数.
离散元方法[6](DEM)可跟踪并计算每个散体单元的运动信息及单元间的接触作用力, 在颗粒材料力学行为研究中得到了广泛的应用. 随着计算机硬件计算能力的提升, 以及颗粒几何特征的精准刻画[7-9]和高精度接触算法的提出[10-12], 使得离散元方法的应用领域和计算精度得到大幅提升. 然而离散元方法用于直接模拟较大空间尺度和时间尺度的工程问题仍需要巨大的计算成本. 为此, 人们提出了多尺度计算方法以提升颗粒材料问题的计算效率[13-14]. 在此框架中, 通常基于均匀化思想采用低尺度的离散元计算在宏观模拟中替代传统的唯象本构关系. 均匀化即从一定体积的颗粒聚集体内部颗粒间作用的微观物理量获得在该体积内连续性力学描述的过程[15]. 而均匀化的首要任务是创建代表性体积单元(RVE)[16], RVE是包含若干颗粒的颗粒聚集体, 是连接颗粒介质微结构尺度和宏观工程尺度的桥梁. 颗粒介质多尺度方法常采用DEM与FEM相结合的方式来实现, 即在FEM计算中提供施加给RVE的变形条件, RVE颗粒试样在变形条件下产生与应变对应的应力值, 随后将应力?应变关系或者切向刚度矩阵参数映射到FEM网格中高斯积分点上进行下一时步的求解[17-20]. 采用多尺度方法虽然避免了对颗粒介质全尺度的DEM求解, 但需要在FEM网格每个高斯积分点上构建单独的RVE[21-22], 并且需要在计算中维护与FEM网络中高斯点数量相当的RVE加载状态信息, 这又增加了计算机的存储与计算开销[19], 对于跨多个尺度的问题计算量会更大.
为此, 人们提出了“离线训练(offline training)、在线模拟(online prediction)”的计算策略[23-24]来提升计算效率. 相比于直接采用RVE模拟结果的“在线”计算来说, “离线”策略下的RVE模拟只产生用来训练“代理模型”的数据集[25-26], 即采用机器学习算法训练并获得RVE的应力?应变关系, 从而宏观尺度FEM的计算不再需要与细观尺度RVE的求解交替进行, 在FEM计算阶段直接读取RVE的应力?应变关系, 这就大大提高了计算效率[27].
可采用不同的神经网络模型对颗粒介质的本构关系进行训练与计算, 常用的基础模型有经典BP神经网络模型[28-29]和循环神经网络模型[30], 二者均可将应力、应变值分别作为输入、输出量进行训练. 循环神经网络中的长短期记忆网络(LSTM)和门控循环单元网络(GRU)具有记忆功能, 对于与加载路径和加载历史相关的颗粒材料而言, 在应力?应变关系建立方面表现出了较强的适用性和较高的拟合精度[26].
在常规循环神经网络模型基础之上, 也有一些****结合其他理论模型进一步研究了颗粒材料力学行为. Wang等[31-33]结合博弈论和强化学习模型研究了颗粒材料的界面位移与张力之间的力学行为以及本构关系. 瞿同明等[34]结合细观力学理论和循环神经网络模型训练了颗粒材料的应力?应变关系. Karapiperis等[35]在有限元中采用了基于离散元数据训练得到的循环神经网络本构模型. Qu等[36]基于坐标不变性原理讨论了从主应力?应变空间到一般应力?应变空间的数据驱动本构模型训练策略.
综上所述, 建立精度高、计算快的RVE应力?应变关系对于颗粒介质的多尺度模拟是至关重要的. 本文借助有向图方法和AlphaGo Zero深度强化学习算法, 在颗粒物质力学的研究基础之上, 试图建立一种自动寻找最优内变量间映射关系、完全依靠“数据驱动”的RVE力学行为建模方法.
1.
颗粒材料的本构关系
1.1
与颗粒材料应力?应变关系相关的重要内变量
离散元方法可有效地在细观尺度下模拟颗粒材料的宏观力学行为, 本文将基于球形离散单元法线性接触模型模拟颗粒材料的应力?应变关系. 从细观力学的角度, 颗粒材料的宏观应力?应变增量关系可表示为
$$ Delta {sigma _{ij}} = {C_{ijmn}}Delta {varepsilon _{mn}},;i,j,m,n = 1,2,3 $$  | (1) |
其中, 弹性刚度矩阵Cijmn在应变均质化的假设下可以表示为[37]
$$ begin{split}{C_{ijmn}} =& frac{{({k_{text{n}}} - {k_{text{s}}})}}{V}sumlimits_{k = 1}^{{N_{text{C}}}} {{{({L^k})}^2}xi _i^kxi _j^kxi _m^kxi _n^k} +& frac{{{k_{text{s}}}}}{V}sumlimits_{k = 1}^{{N_{text{C}}}} {{{({L^k})}^2}{delta _{in}}xi _j^kxi _m^k} end{split} $$  | (2) |
其中, kn和ks为颗粒之间的法向和切向接触刚度; V为颗粒试样的体积; δin为克罗内克函数; Lk为每个接触对内两个颗粒的中心距离;
$$ {a_{ijmn}} = frac{1}{V}sumlimits_{k = 1}^{{N_{text{C}}}} {{{({L^k})}^2}xi _i^kxi _j^kxi _m^kxi _n^k} $$  | (3) |
$$ {b_{ijmn}} = frac{1}{V}sumlimits_{k = 1}^{{N_{text{C}}}} {{{({L^k})}^2}{delta _{in}}xi _j^kxi _m^k} $$  | (4) |
则式(2)可表示为
$$ {C_{ijmn}} = ({k_{text{n}}} - {k_{text{s}}}){a_{ijmn}} + {k_{text{s}}}{b_{ijmn}} $$  | (5) |
弹性刚度矩阵Cijmn可由颗粒间的法向接触刚度kn和切向刚度ks, 以及单位体积内的细观结构张量表示. 当颗粒材料承受外载荷作用时, 颗粒间发生相对滑移, 导致组构张量在外载作用下会不断发生变化.
式(1)中, 当切应力和切应变为0时, 采用增量形式表示的主应力和主应变关系为
$$ left[ begin{array}{l}Delta {sigma _{11}} Delta {sigma _{22}} Delta {sigma _{33}} end{array} ight] = left[ {begin{array}{*{20}{c}}{{C_{1111}}}&{{C_{1122}}}&{{C_{1133}}} {{C_{2211}}}&{{C_{2222}}}&{{C_{2233}}} {{C_{3311}}}&{{C_{3322}}}&{{C_{3333}}} end{array}} ight]left[ {begin{array}{*{20}{c}}{Delta {varepsilon _{11}}} {Delta {varepsilon _{22}}} {Delta {varepsilon _{33}}} end{array}} ight] $$  | (6) |
其中, C1122 = C2211, C1133 = C3311, C2233 = C3322, 弹性刚度矩阵中共有6个独立分量表示主应力和主应变之间的关系.
除了上述推导所涉及的弹性刚度矩阵外, 颗粒物质力学研究表明颗粒材料的孔隙率? (对于单相颗粒材料, 孔隙率定义为一定体积内非颗粒组分所占据的体积分数)和组构参数对于其宏观力学行为具有重要的影响. 其中, 岩土材料作为一种典型颗粒材料, 现代土力学理论的一个突破性进步就在于将孔隙率等状态参数作为硬化法则的一部分, 将其考虑到岩土材料的本构关系研究中[38-39]. 近年来岩土本构研究领域另一个重要进步在于认识到颗粒材料的组构对于其本构行为的重要影响[40], 考虑组构参数的演化过程是近年来岩土本构理论的重要发展趋势[41-43]. 通常颗粒材料的细观组构有多种张量描述方式, 本文采用式(3)和式(4)中的4阶组构张量来共同描述颗粒材料的组构演化过程.
1.2
基于深度强化学习的本构研究思路
颗粒材料的本构研究从不同的视角发展了不同的理论模型和方法, 这些理论方法对问题本身的研究都取得了新的进展. 如何将这些来自不同视角的重要发现整合到一个统一的框架内是一个思路合理但是实践困难的挑战. 本文借助深度强化学习的思路, 将从颗粒物质力学研究中得到的弹性刚度矩阵(式(2), 用Cf表示), 孔隙率参数?和组构张量(式(3), 用Af表示)结合在一起, 试图在这些重要变量的数据样本基础上, 借助人工智能算法整合已有的知识资源, 发掘新的认识, 自动发现能描述颗粒材料应力应变行为的本构关系.
2.
本构关系的有向图表示
有向图来源于数学上的图论, 主要指采用节点来表示物理量, 采用边线来描述物理量之间相互关系的一种方法. 包含内变量的本构关系将通过有向图来表达[31], 有向图为信息从本构关系输入值开始, 流经内变量, 最终流向输出值的信息流动网络.
2.1
有向图网络
图1为以内变量和输入输出值构建的变量间信息流动的有向图, 图中的箭头代表了变量间的“源?目标”数据流动方向. 有向图中的变量称为节点, 变量间的链接称为边, 对于每个链接而言, 箭头指出的节点称为源节点, 箭头指向的节点称为目标节点, 整个有向图的输入称为根节点, 输出称为叶节点.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
有向图中的信息流动
Figure
1.
Information flow in a directed graph
下载: 全尺寸图片
幻灯片
一个有向图代表一种本构关系, 为保证本构关系中变量间信息流动的合理性, 有向图的构建需遵循以下规则:
(1)有向图中仅存在唯一的叶节点(该节点不作为其他任何节点的源节点, 仅作为目标节点);
(2)有向图中仅存在唯一的根节点(该节点不作为其他任何节点的目标节点, 仅作为源节点);
(3)有向图中可存在孤立节点, 该节点不参与到有向图的建立中, 即本构关系中不考虑该节点对应内变量对本构关系建立的贡献;
(4)有向图中不存在闭环信息流(即信息流从某一结点开始, 最后又流回该节点);
(5)如果某一节点链接到了根节点或叶节点, 那么此节点需包含在从根节点到叶节点的完整路径中.
2.2
信息流动路径
对于简单的有向图链接, 如图2(a)所示, 信息流动方向可直接表示为ε → ? → Af → Cf → σ, 而对于复杂的有向图链接, 如图2(b)所示, 需要建立合理的信息流动路径. 图2(b)中的信息流动路径需要从有向图输出变量σ开始以递归的方式向前寻找信息“源”, 每一节点只寻找直接指向该节点的“源”节点, 形成“一对一”或“多对一”的信息映射关系. 图2(b)中信息流动路径对可表示为: {ε → Cf}, {ε, Cf → Af}, {ε, Af → ?}及{ε, ?, Cf → σ}, 即信息从ε流入有向图后计算出Cf, 随后ε和Cf共同计算出Af, 接着由ε和Af共同计算出?, 最后由ε, ?, Cf共同计算出σ, 实现了ε到σ的信息流动. 将采用循环神经网络拟合出每对路径中变量间的映射关系, 用于后续“数据”本构模型的建立.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
有向图表示的两种本构关系
Figure
2.
Two constitutive laws represented by two directed graphs
下载: 全尺寸图片
幻灯片
2.3
本构模型打分
对有向图建立本构关系的预测精度进行打分, 以评估通过数据建立的本构关系对于训练数据的泛化能力. 通过比较信息流路径计算出的应力值与训练数据中应力值的均方误差(mean squared error, MSE), 评价强化学习算法中不同有向图代表的本构模型的优劣.
对于具有Ndata个数据样本的样本集, 每个样本的均方误差可表示为
$$ {{MS}}{{{E}}_i} = frac{1}{{{N_{text{f}}}}}sumlimits_{j = 1}^{{N_{text{f}}}} {{{left[ {{S_j}left( {Y_{ij}^{{text{data}}}} ight) - {S_j}left( {Y_{ij}^{{text{model}}}} ight)} ight]}^2}} $$  | (7) |
其中,
对集合{MSEi}内各均方误差值进行升序排序, 并取集合中第P%的MSE值(记为
$$ S = max left{ {frac{{lg left[ {max ({varepsilon _{P{text{%}} }},{varepsilon _{{text{crit}}}})} ight]}}{{lg {varepsilon _{{text{crit}}}}}}} ight} $$  | (8) |
式中
3.
AlphaGo Zero深度强化学习算法
本节将采用AlphaGo Zero中的强化学习算法建立基于有向图的本构关系. AlphaGo是Google DeepMind团队开发的一个基于深度神经网络的围棋人工智能程序. 2015年10月AlphaGo击败了欧洲冠军Fan Hui, 2016年3月击败韩国棋手Lee Sedol. 2017年10月, DeepMind公布了最新的AlphaGo Zero, 在与AlphaGo对战中取得了100∶0的战绩. 与AlphaGo不同的是, AlphaGo Zero未使用任何围棋领域的专业知识和人为干预, 训练数据全部来自于自我对弈(self-play), 算法方面, AlphaGo Zero只采用了一个神经网络, 将棋盘状态作为输入特征, 来指导蒙特卡洛树搜索(Monte Carlo tree search, MCTS)探索最优的落子动作.
本构模型建立过程中, 选定输入变量、输出变量和内变量后, 可以通过“穷举法”列出所有满足信息流动规则的有向图, 然后对每一种有向图打分, 得分最高者即为最优本构关系. 对于内变量较少的本构关系建立过程, 可考虑采用“穷举法”寻找出最优的本构关系, 但如果引入的内变量的数量较多, 采用直接寻找的方法将极大地增加计算成本, 因此建立一种能够自动寻找最优本构关系的算法是必要的. 本构关系建立过程与AlphaGo Zero实现过程类似, 同样可采用马尔可夫决策过程(Markov decision process, MDP)对有向图中变量链接关系进行选择, 以建立得分最高的有向图链接关系. 下面将给出采用AlphaGo Zero算法建立本构关系有向图的流程.
3.1
本构关系建立过程
本构关系建立过程可表述为马尔可夫决策过程, 本构关系的初始状态如图3(a)所示, 本构关系建立的过程就是智能体在初始状态下对有向图中的边进行激活, 并获得最大奖励的过程. 所有可能被激活的边称为“动作空间”, 并遵循有向图网络建立准则, 所有动作如图3(b)所示, 可描述为{ε → Af, ε → Cf, ε → ?, ε → σ, Af → Cf, Af → ?, Af → σ, Cf → Af, Cf → ?, Cf → σ, ? → Af, ? → Cf, ε → σ}. 马尔可夫决策过程中的“状态s”为动作空间中有向图边的激活状态; “动作a”为在当前状态下准备激活的有向图边; “奖励r”为根据本构关系打分情况确定的奖励值, 当打分高于给定的分值时取1, 否则取?1.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
MDP中的初始状态和可执行动作
Figure
3.
Initial state and all possible actions in MDP
下载: 全尺寸图片
幻灯片
在有向图当前状态st下, 智能体执行动作at (激活某一条有向边), 当前状态会转移到t + 1时间步的新状态st+1, 其中动作at选自于st状态下每一个有效动作概率的集合π(st), 同时智能体获得一个奖励rt+1, 该奖励值的获得是由于智能体在状态st下执行了动作at, 但是在实施过程中具体的奖励值rt只有在本构关系完全建立后才能获得. 当本构关系得分高于给定分值时, 本构建立过程中所有动作的奖励rt ≤ T = 1, 反之, rt ≤ T = ?1. 图4为由马尔可夫决策过程表示的一次完整的本构关系建立过程.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-4.jpg'" class="figure_img
figure_type2 ccc " id="Figure4" />
图
4
一次完整的有向图本构关系建立过程
Figure
4.
A complete modeling process of generating a constitutive relationship
下载: 全尺寸图片
幻灯片
3.2
自主学习[44]
在AlphaGo Zero算法中, 主要通过训练一个超参数为θ的策略/价值网络fθ来指导本构关系有向图建立过程中动作的选择. 策略/价值网络将有向图的链接状态作为输入, 输出一个向量p和标量v, 即(p, v) = fθ (s), p表示在当前状态下链接每一条有向边的概率, v表示在当前状态下本构关系获得最高分的概率.
策略/价值网络fθ通过自主学习来提升策略选择的能力, 使得有向图链接得分最高. 策略选择能力的提升通过MCTS算法来实现, 而在每一状态下蒙特卡洛树扩展过程中的动作概率则是通过策略/价值网络fθ进行计算, AlphaGo Zero实现的自主学习过程如图5所示. 自主学习过程中需运行多次MCTS算法使策略/价值网络fθ变得更强, 而MCTS算法的实施均采用更新后的策略/价值网络.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-5.jpg'" class="figure_img
figure_type2 ccc " id="Figure5" />
图
5
AlphaGo Zero实现的自主学习过程
Figure
5.
Self-play reinforcement learning in AlphaGo Zero
下载: 全尺寸图片
幻灯片
蒙特卡洛搜索树中的每个节点表示有向图的链接状态s, 搜索树中的每条边(s, a)表示在状态s下允许的动作a. 搜索树中每条边维持一个统计量集合{N(s, a), W(s, a), Q(s, a), P(s, a)}, 其中N(s, a)为在树搜索过程中节点被访问的次数, W(s, a)为总动作价值, Q(s, a)为平均动作价值, P(s, a)为选择边的先验概率.
(1)选择(select): 自主学习过程中从搜索树的根节点s0开始, 直至在时间步L遇到之前未被遍历的叶节点sL, 在t < L时间步内的动作选择则根据上置信边界
$$ U(s,a) = {c_{{text{puct}}}}P(s,a)frac{{sqrt {displaystylesumnolimits_b {N(s,b)} } }}{{1 + N(s,a)}} $$  | (9) |
其中, cpuct为MCTS算法中控制探索程度的常数, 在初始阶段倾向于选择具有较高先验概率的动作, 后续会逐步倾向于具有较高动作价值的动作; b的取值范围为状态s下所有可执行的动作.
(2)扩展和评价(expand and evaluate): 对叶节点扩展时, 叶节点状态下的每条边(sL, a)维持的统计量需初始化为{N(sL, a) = 0, W(sL, a) = 0, Q(sL, a) = 0, P(sL, a) = pa}, 同时动作概率p与状态价值v通过策略/价值网络fθ预测得到.
(3)回溯(backup): 对遍历过的边的统计量进行更新, 其中访问次数更新为N(st, at) = N(st, at) + 1, 动作价值更新为W(st, at) = W(st, at) + v, 及
(4)执行动作(play): 从根节点s0选择动作的概率与节点被访问次数相关, 可表示为
ight.} tau }}}} }}$
每一个时间步内, 在每个有向图当前状态s下, 每一次激活有向图边需进行若干次MCTS模拟, 最终MCTS给出最优的动作策略π. MCTS中策略π由
$$ l = sumlimits_t {{{({v_t} - {z_t})}^2}} + sumlimits_t {{{boldsymbol{pi }}_t}lg [{boldsymbol{p}}({s_t})]} $$  | (10) |
损失函数综合考虑了奖励值的均方误差和交叉熵损失.
表1为采用AlphaGo Zero强化学习算法建立应力?应变有向图的计算流程, 主要分为两个阶段: 策略/价值网络训练阶段和最优有向图生成阶段. 训练阶段共执行Niter次策略/价值网络的训练, 每次训练执行Ncollect次完整的有向图建立流程以收集所需的训练数据, 在链接每一条有向边时执行NMCTS次蒙特卡洛树搜索计算. 有向图生成阶段, 只需执行一次完整的有向图建立流程, 就可选定最终的应力?应变关系.
表
1
利用强化学习算法建立最优应力?应变关系有向图流程
Table
1.
Reinforcement learning of directed graph of the stress-strain relationship
table_type1 ">
| 定义: 有向图配置、状态、动作、模型得分、奖励、建模规则等 | |
| 1 | 随机初始化策略/价值网络fθ |
| 2 | 创建并初始化训练集Etrain |
| 3 | for i in [1, Niter]: |
| 4 | for j in [1, Ncollect]: |
| 5 | 初始化有向图链接状态 s, 初始化空的MCTS搜索树, 令探索系数τ = 1 |
| 6 | while True: |
| 7 | 依据建模规则进行NMCTS次蒙特卡罗树搜索获得 动作策略π(s, ?), 根据策略选择激活有向边a, 有向 图从当前状态s将转移到新状态$ s' $ |
| 8 | if $ s' $是最终状态 then |
| 9 | 计算应力?应变有向图得分, 并根据有向图得分计 算奖励值r |
| Break | |
| 10 | 将数据[s, a, π(s, ?), r]加入训练集Etrain |
| 11 | 利用Etrain训练策略/价值网络fθ |
| 12 | 探索系数设为τ = 0.01, 利用训练后的策略/价值网络 fθ 进行一次有向图建立过程, 获得最终的应力?应变有向图 |
| 13 | 计算完成 |
下载: 导出CSV
|显示表格
4.
建立“数据驱动”本构关系
4.1
数据制备
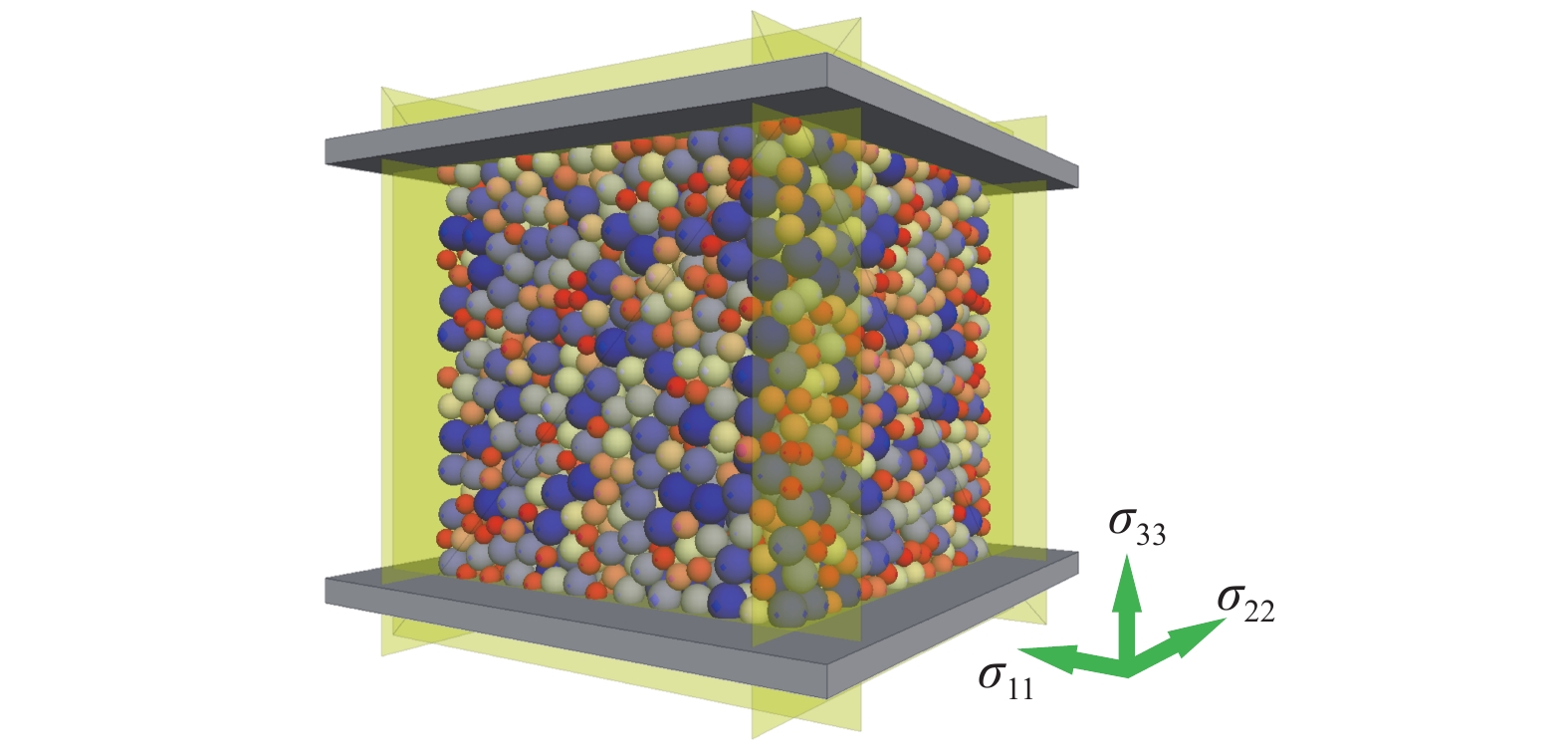
首先构建三轴数值试验来生成颗粒材料的应力?应变关系数据, 采用离散元方法建模的三轴试样如图6所示, 试样包含4037个球形颗粒, 颗粒半径在2 mm ~ 4 mm范围内服从均匀分布. 颗粒之间采用线弹性接触模型, 法向和切向接触刚度分别为1 × 105 N/m和5 × 104 N/m, 颗粒密度为2600 kg/m3, 局部阻尼系数为0.5. 虽然颗粒之间的接触作用是线弹性的, 但试样整体会由于细观组构的不断演化而发生复杂的塑性变形行为.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
三轴数值试样
Figure
6.
Numerical sample of triaxial test
下载: 全尺寸图片
幻灯片
试样制备时, 首先在一个较大空间内生成具有较小摩擦系数(0.05)的颗粒堆积体, 采用伺服方法给墙体边界施加速度直至试样稳定地达到目标压力值, 然后再将制样阶段的接触摩擦系数改成实际样本摩擦系数0.5. 这样有利于减小试样制备过程中的初始各向异性, 生成较为密实的均匀试样.
构造3种类型的3轴加载工况来生成数据, 分别为:
(1)包含加卸载循环的常规三轴试验;
(2)平均有效应力p不变的真三轴试验(等p加载:
(3)中主应力b不变的真三轴试验(等b加载:
4.2
训练变量间的映射关系
采用GRU (gated recurrent unit)循环神经网络对有向图内变量间的映射关系进行训练, 训练后的映射关系用于后续有向图本构关系的建立中. 有向图中共有5个变量, 包含1个输入变量ε, 一个输出变量σ, 和3个中间变量Af, Cf, ?. 5个变量间可形成36组基础映射关系, 映射关系遵循2.2节中的信息流动规则, 这36组基础映射关系最终可搭建出种类繁多的有向图链接关系. 以映射关系{ε, ? → Cf}为例, 应变值ε和孔隙率?将共同作为GRU网络的输入值, 弹性刚度矩阵Cf作为输出值, 训练时从440组应力?应变关系数据中随机选取340组作为训练集, 剩余100组作为测试集, 训练集中的34组作为验证集.
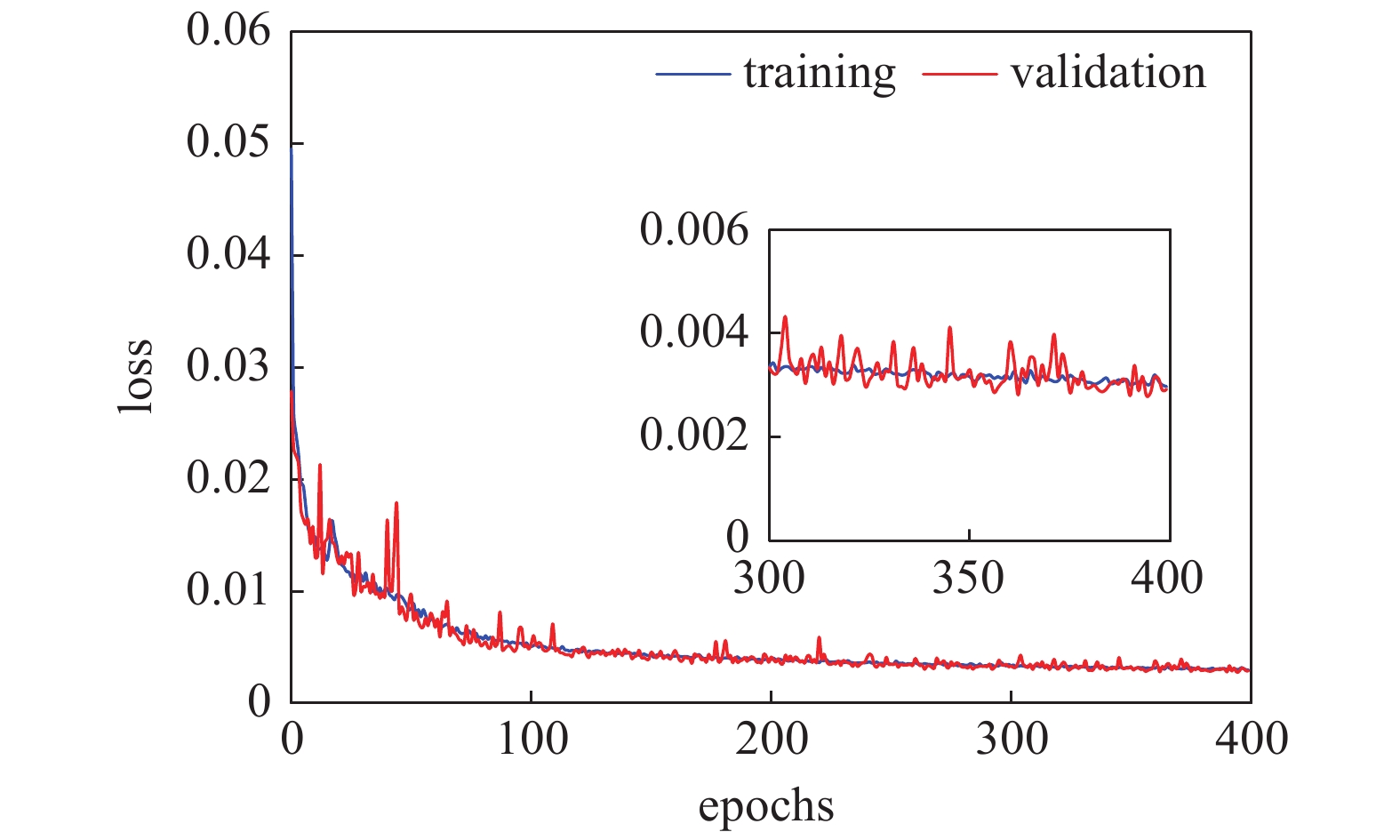
采用谷歌公司发布的基于TensorFlow深度学习库的Keras搭建了GRU循环神经网络模型. 本文选用的网络层结构和超参数为: 2个神经元数量为50的隐藏层, 输出层为采用linear激活函数的全连接层. 用于训练的输入和输出数据采用最小最大归一化处理, 并且输入变量包含当前和之前19个历史变量值, 训练中采用Adam优化算法, batch size取为256, 模型在训练400次(epochs)后收敛. 针对映射关系{ε, ? → Cf}, 训练过程中GRU模型在训练集和验证集上的性能表现如图7所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
训练集和验证集上GRU模型的训练性能
Figure
7.
Training performance of GRU architecture on training and validation data
下载: 全尺寸图片
幻灯片
同样地, 可对其余35组变量间映射关系训练出GRU神经网络模型. 值得注意的是, 并不是每一组映射关系均能获得图7所示的训练性能, 这主要取决于变量间是否存在内在的物理映射关系, 直接影响到不同有向图表征的本构模型得分的差异.
4.3
深度强化学习自动生成最佳“数据”本构关系
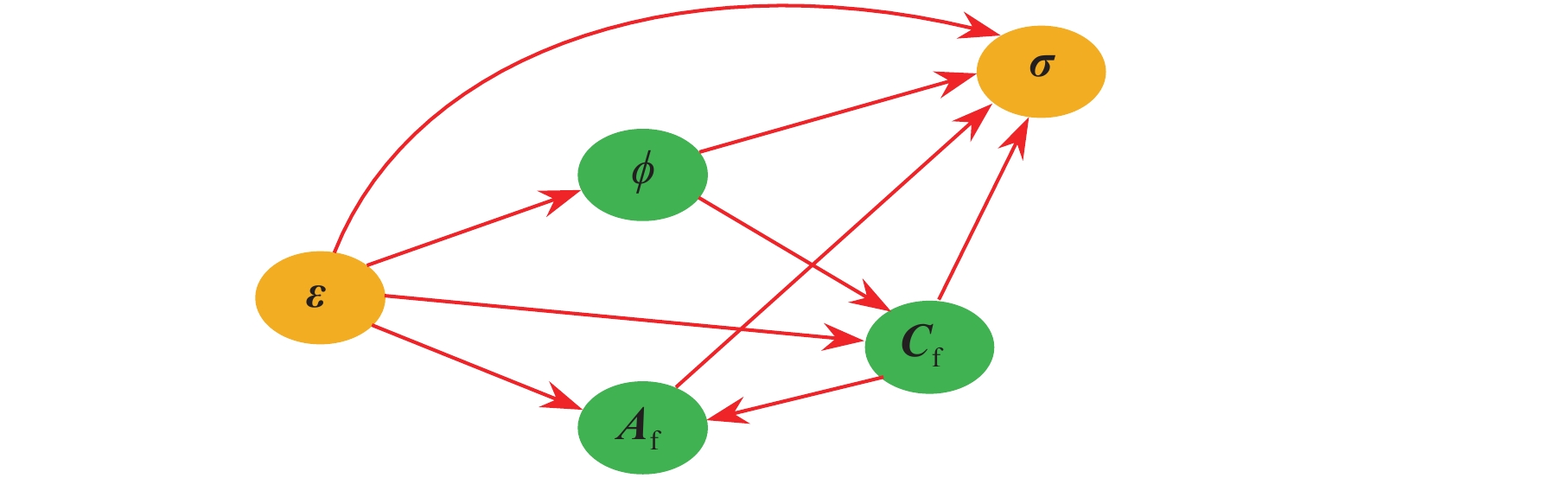
共执行Niter = 10次策略/价值网络的训练, 每次训练执行Ncollect = 20次完整的有向图建立过程以收集所需的训练数据, 在激活每一条有向边时执行NMCTS = 30次蒙特卡洛树搜索. 训练过程中探索系数τ = 1, 以探索未知的使本构得分较高的动作; 在利用训练好的策略/价值网络选择最终本构链接时τ = 0.01, 选择使本构得分较高的动作建立起最优的本构关系. 采用卷积神经网络训练策略/价值网络, 卷积神经网络的输入值为本构有向图的状态空间. 训练时随机改变策略/价值网络的初始超参数值以研究训练结果的收敛性, 计算结果表明最终建立的有向图链接是一致的. 生成的最优本构关系链接如图8所示, 该链接关系在所有测试数据上打分为0.720, 本构关系的信息流动路径为: {ε → ?; ε, ? → Cf; ε, Cf → Af; ε, Af, Cf, ? → σ}.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
采用强化学习算法建立的最优有向图
Figure
8.
Optimal directed graph of stress-strain laws learned by deep reinforcement learning
下载: 全尺寸图片
幻灯片
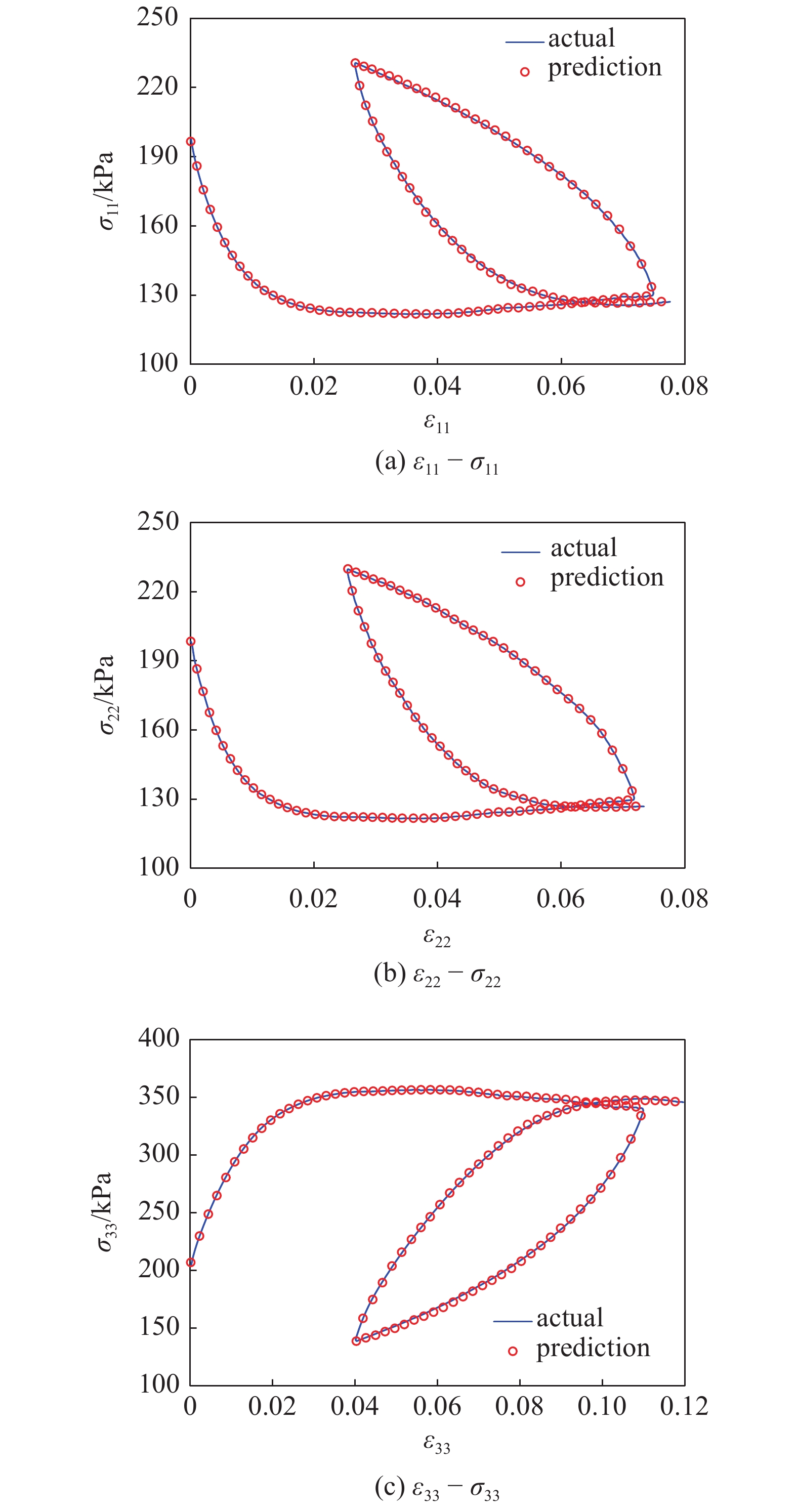
为验证“数据”本构模型的预测能力, 在测试集中任选一组ε-σ数据, ε作为输入值, 由映射关系ε → ?计算出?, 再由ε, ? → Cf计算出Cf, ε, Cf → Af计算出Af, 最后由ε, Af, Cf, ? → σ计算出最终的应力值σ. 针对等p加载、等b加载以及常规加载3种加载方式, 几组代表性工况下, 由“数据”本构模型预测的应力?应变关系与离散元计算结果的比较如图9 ~ 图11所示. 可以看出, 由强化学习算法生成的“数据”本构模型可很好地对测试集中的应力?应变关系及卸载、再加载过程进行预测.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
等p加载下“数据”本构模型预测比较
Figure
9.
Comparison between predictions and DEM simulation results for constant-p compression
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-11.jpg'" class="figure_img
figure_type1 bbb " id="Figure11" />
图
11
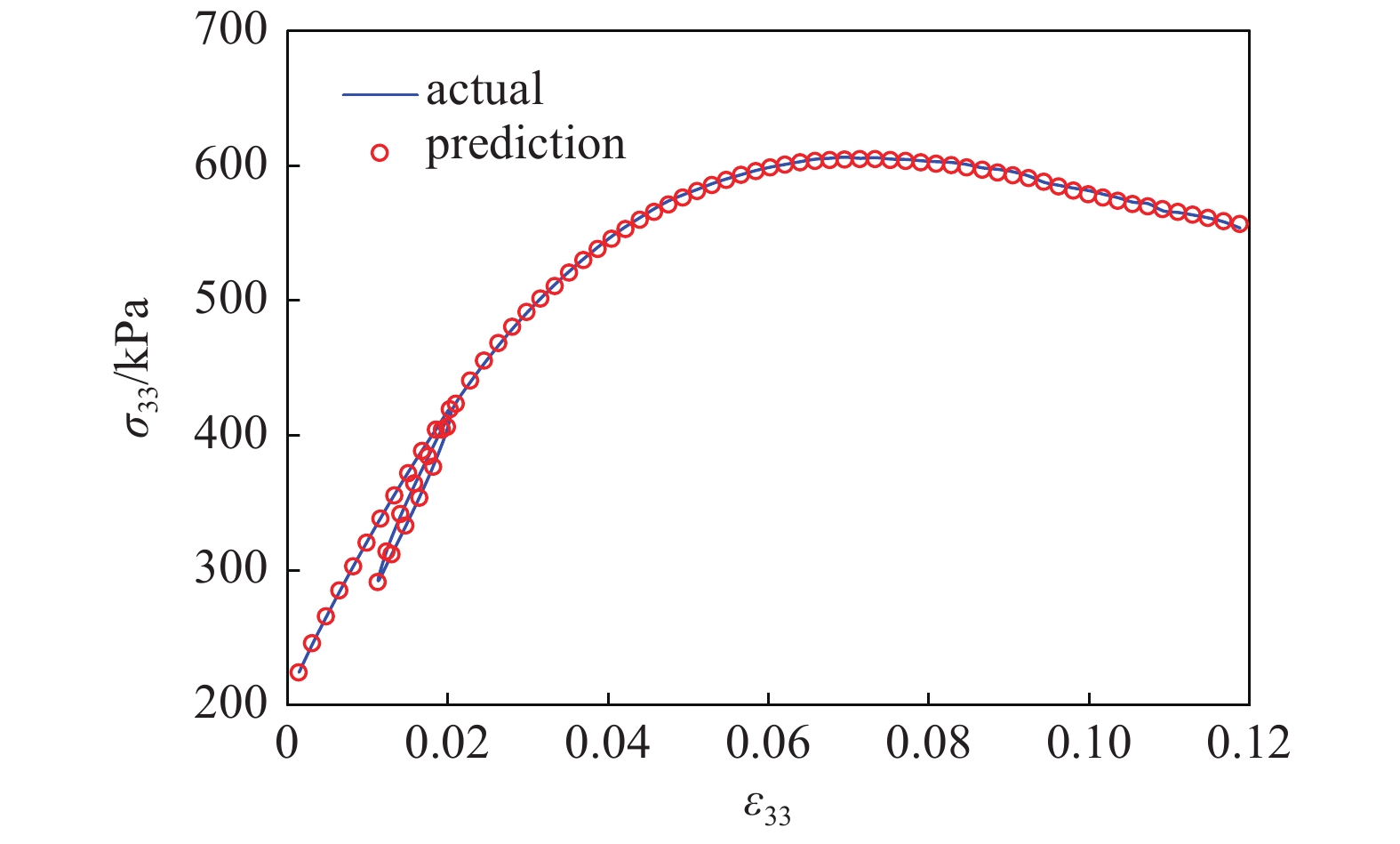
常规三轴加载下“数据”本构模型预测比较
Figure
11.
Comparison between predictions and DEM simulation results for conventional triaxial compression
下载: 全尺寸图片
幻灯片
需要指出的是, 图9(a) ~ 图9(c)分别是从3个主应力和主应变的角度展示训练模型对同一工况的预测表现. 颗粒材料的主应力分量与主应变分量间并不存在唯一的对应关系. 由于在等b加载工况下的最小主应力和常规三轴工况下的中主应力及最小主应力在加载过程中均保持初始围压不变, 因此图10和图11中仅分别展示了部分主应力与主应变的对比结果.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-10.jpg'" class="figure_img
figure_type1 bbb " id="Figure10" />
图
10
等b加载下“数据”本构模型预测比较
Figure
10.
Comparison between predictions and DEM simulation results for constant-b compression
下载: 全尺寸图片
幻灯片
在强化学习训练阶段发现ε, Cf, σ 3个变量参与的本构关系可获得最高0.702的打分, 对应的有向边链接关系为{ε → Cf; ε, Cf → σ}, 有向图如图12(a)所示. 该结果表明仅使用弹性刚度矩阵分量, 可在数据驱动模型中最为准确的描述颗粒材料的应力?应变关系.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-12.jpg'" class="figure_img
figure_type1 bbb " id="Figure12" />
图
12
ε, Cf, σ变量建立的有向图
Figure
12.
Generated directed graph based on ε, Cf and σ
下载: 全尺寸图片
幻灯片
4.4
信息流动路径的影响
基于有向图的深度强化学习算法不仅能从数据中自动寻找与颗粒材料本构行为联系最相关的物理量, 还能定量地描述相关物理量之间的信息流动路径, 并且这种定量描述方式对于数据驱动模型的预测能力也是极为关键的. 比如, 与4.3节中获得的最佳本构训练方式一样, 采用ε, Cf, σ 3个变量构建的链接关系{ε → Cf; Cf → σ}, 如图12(b)所示, 打分则为0.475.
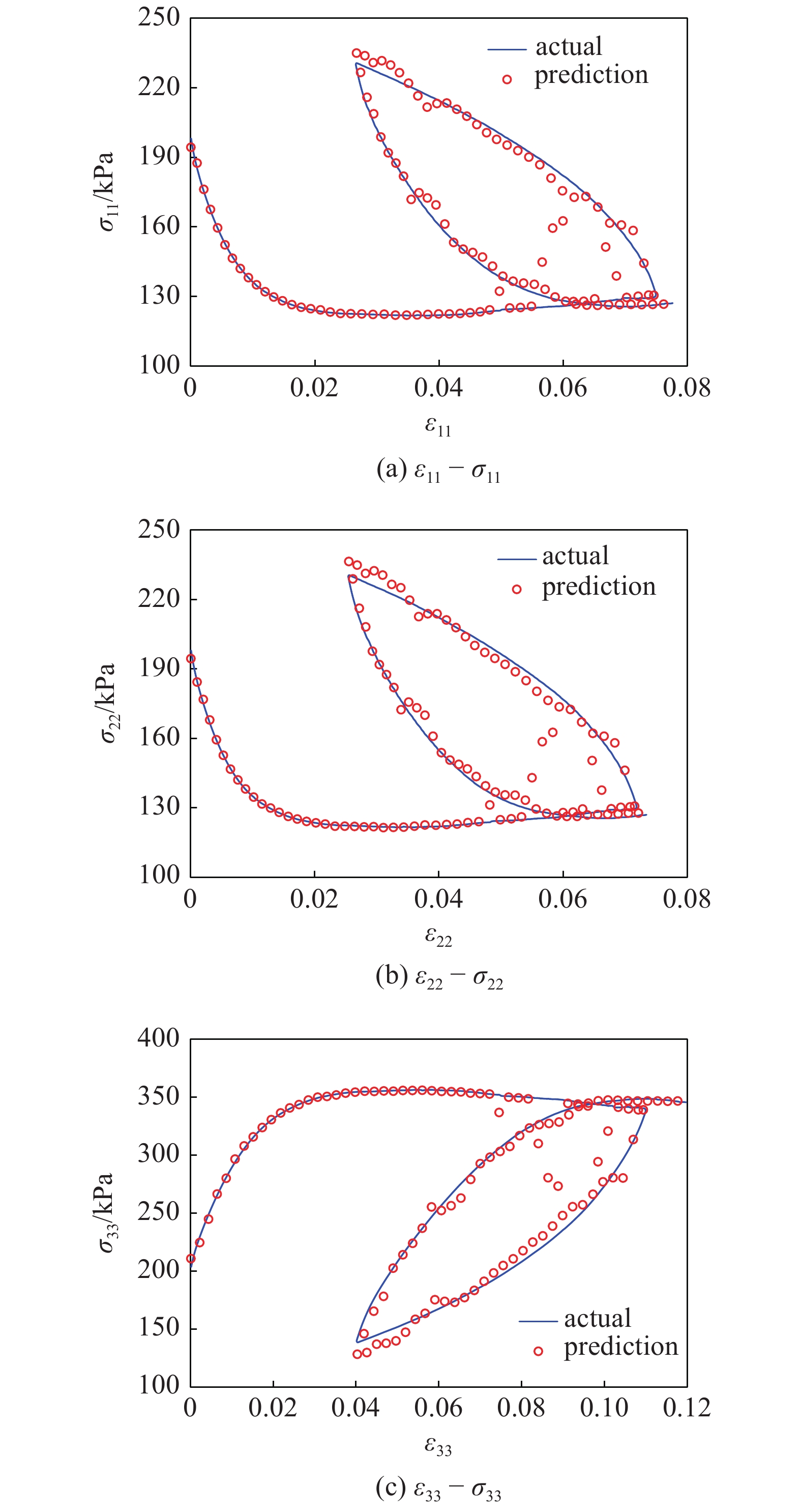
本构关系{ε → Cf; Cf → σ}的预测能力如图13所示. 从图中可以看出, 两个模型在加载段均表现出了较高的预测能力, 而在卸载、再加载阶段的预测能力表现不佳. 计算结果表明, 本构关系的建立虽然采用了相同的内变量, 但内变量间信息流动的路径不同会生成预测精度不同的本构模型. 将?与Af作为内变量时同样可以建立起不同打分的本构关系, 作为内变量时的打分分别为0.664 (信息流动路径: {ε → ?; ε, ? → σ})和0.453 (信息流动路径: {ε → ?; ? → σ}); Af作为内变量时的打分分别为0.657 (信息流动路径: {ε → Af; ε, Af → σ})和0.522 (信息流动路径: {ε → Af; Af → σ}). 以上结果表明, 虽采用了相同的内变量来构造本构关系, 但变量间不同的信息流动路径会形成精度不同的本构关系.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-312-13.jpg'" class="figure_img
figure_type1 bbb " id="Figure13" />
图
13
有向图链接{ε → Cf; Cf → σ}的预测精度
Figure
13.
Prediction performance of directed graph {ε → Cf; Cf → σ}
下载: 全尺寸图片
幻灯片
当直接将应变值ε和应力值σ链接成本构关系时, 本构模型打分为0.708, 得分高于图12(a)中的有向图. 这表明内变量的参与会降低部分本构模型的预测精度, 这是因为建模过程中激活的不同有向边使得数据流动路径发生了改变, 而改变后的数据流动路径需要用不同的变量间映射关系来表达. 由于变量间内在的物理关系, 并不能建立由GRU神经网络拟合的理想的映射关系, 这就导致了某些映射关系并不能很好地用来建立本构关系, 最终导致了本构模型预测精度降低. 因此, 为获得更高的打分需要多激活精度较高的变量间映射关系, 例如图8所示的信息流动路径.
5.
结论
本文以颗粒材料本构研究中所识别的重要相关内变量为基础, 采用有向图和深度强化学习算法来对代表性体积单元的力学行为进行建模. 一方面, 采用有向图来表征含有内变量的本构关系, 采用变量间的链接关系来模拟数据在内变量间的流动路径; 另一方面, 通过深度强化学习算法发掘数据之间的内在联系, 自主选择链接有向边, 能够使得有向图表征的本构关系具有最优的预测精度. 就计算结果讨论如下:
(1)本构关系建模过程完全由数据驱动, 即建模过程中不考虑内变量间是否存在理论层面的推演关系, 只按照离散元模拟的应力?应变关系数据建立本构模型.
(2)建模过程采用了由叶节点向前递归寻找源节点, 以及“一对一”、“多对一”的变量间信息流动规则, 对于不同的建模需求可遵循不同的信息流动约束条件. 此外, 对于本构模型优劣也可采用不同的打分标准, 例如, 采用同时兼顾得分最高和有向边数目最少的打分标准.
(3)本构关系的建立是基于常规、等p、等b 3种围压, 以及卸载后再加载的方式“激发”出的颗粒材料宏观力学行为, 除此之外, 还可增加新的加载方式, 产生新的训练数据进一步提升本构模型的预测精度.
(4)有向图与深度强化学习结合的方法, 将有可能整合来自多重视角的理论模型, 发展一个统一的、高质量的数据驱动本构模拟框架.
(5)借助深度强化学习算法在组合优化问题中的智能决策能力, 可以在海量数据基础上, 寻找与颗粒材料本构行为最为相关的重要物理量和信息流动方式, 这些发现将反过来提供新的信息, 从数据驱动角度整合和促进理论本构模型的发展.
