删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

动力吸振器复合非线性能量阱对线性镗杆系统的振动控制

本站小编 Free考研考试/2022-01-01


引 言


在机械零件中带孔零件占比为50% ~ 80%[1], 因此孔加工在金属切削加工中占有重要地位. 孔加工约占金属切削总量的33%[2], 而深孔加工是孔加工中的一个重要领域. 镗杆在深孔加工中应用广泛, 当镗杆的长度与直径比大于5时便容易发生颤振, 从而导致零件的加工质量大幅下降[3-5]. 因此, 对镗杆进行减振就显得尤为重要[6-8].

****们对镗杆的振动控制进行了深入研究, 主要采用阻尼减振和吸振技术抑制镗杆系统的振动. Mei等[9]提出了一种基于磁流变液控制镗杆颤振的方法. Li等[10]在镗杆内部增加变刚度动力吸振器来减振, 通过改变轴向压缩力调节吸振器的刚度来适应不同激励频率下的振动控制. Hayati等[11]通过一种内部摩擦阻尼结构, 在弯曲振动期间向镗杆施加额外的能量耗散, 以减小加工过程中的颤振. Yadav等[12]在细长镗杆内集成了调谐质量阻尼器, 以提高镗削过程的抗颤振性能. 基于约束层阻尼梁理论和有限元方法, Song等[13]提出了一种约束层阻尼镗杆专用镗刀的设计与优化方法. 侯学元等[14]将弹性质量块安装在不同的角度位置来改变镗杆的固有频率, 然后利用Ansys进行参数优化并利用Adams软件进行仿真. 刘强等[15]提出通过调整变质量吸振器的吸振块质量对减振镗杆的减振性能进行调节, 从而提高减振镗杆的减振性能. 孔天荣[16]提出了支撑刚度可控型的磁流变自抑振智能镗杆设计方案, 并对关键结构磁流变液抑振单元进行了参数优化. 赵勋等[17]开展了一种新材料镗杆在深孔加工的抗振性能研究. 谭骏等[18] 研究了一款内置阻尼减振器的减振镗杆. 张红卫和吴伏家[19]设计了一套在镗杆中装有减振装置及复合层叠结构的新型抗振镗杆.

非线性能量阱(nonlinear energy sink, NES)在振动抑制方面效果显著[20-21]. 非线性能量阱由较轻的附加质量, 强非线性刚度弹簧和阻尼元件组成, 可以将振动能量从主体结构单向传递至耗能元件. 非线性能量阱的定义是由Vakakis[22]在2001年提出的, 其非线性刚度可以通过将质量块与两根刚度相同且长度相等的线性弹簧相连接来实现, 这样两根线性弹簧所提供的恢复力与弹簧的伸长量可近似等效为3次刚度[23]. 研究发现[24-26], 非线性能量阱能够在较宽的频带范围内有效吸收主体结构的振动能量, 并利用阻尼元件将其耗散 , 具有更宽的减振频带和更高的鲁棒性. Etienne等[27] 在车刀上附加非线性能量阱吸振器, 以减少车削过程中的颤振. Ahmadabadi和Khadem[28]发现将非线性能量阱吸振器附接到钻柱的不同部件上可以有助于降低振幅. Giuseppe和Francesco[29]提出了一种用于减轻主体结构系统振动的调谐双稳态非线性能量阱, 并证实其对宽范围的脉冲振动具有很好的吸收效果. Ding和Chen[30]综述了非线性能量阱的发展及其重要的振动控制特性, 并强调了结构附加非线性能量阱后可能导致的复杂动力学行为. 时成龙等[31]对非线性能量阱在建筑结构等方面的减振应用进展进行了综述. 李晨等[32]提出了一种杠杆型并联非线性能量阱的吸振系统, 并基于谐波平衡法和伪弧长延伸法得到了系统的幅频响应曲线. 王国旭等[33]研究了简谐激励下双弹簧非线性能量阱的优化问题. 刘良坤等[34]对基底简谐激励下的非线性能量阱系统减振特性及其最优参数进行了研究.

本文通过将线性动力吸振器和非线性能量阱组合附加到镗杆内部, 基于线性镗杆模型研究复合式吸振器对镗杆在简谐激励下受迫振动的减振效果. 建立附加线性动力吸振器和非线性能量阱吸振器的线性镗杆系统模型, 然后基于平均法研究镗杆系统在简谐激励下受迫振动的近似解析解, 并利用数值解进行验证. 详细分析复合式动力吸振器的减振效果, 并对线性动力吸振器和非线性能量阱吸振器进行参数优化.


1.
系统模型


忽略镗杆模型中的非线性因素[35], 在附加线性动力吸振器的两自由度镗杆模型的基础上, 将非线性能量阱附加到镗杆内部用于吸振, 系统的物理模型如图1所示. 图1中m1是镗杆系统的等效质量, c1是镗杆系统的等效阻尼, k1是镗杆系统的等效线性刚度. m2, k2和c2分别是线性动力吸振器的质量、线性刚度和阻尼, m3, k3和c3分别是非线性能量阱的质量、非线性刚度和阻尼. x1, x2和x3分别表示质量块m1, m2以及m3的位移. 将包括切削力在内的组合外力简化为$Fcos( omega t)$, 其中F为激励幅值, $omega $为激励角频率.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
附加复合式吸振器的镗杆系统模型



Figure
1.
System model of boring bar with combined absorber



下载:
全尺寸图片
幻灯片


建立镗杆系统的动力学模型, 得到运动方程






$$ begin{gathered} {m_1}{{ddot x}_1} + {k_1}{x_1} + {c_1}{{dot x}_1} + {k_2}left( {{x_1} - {x_2}}
ight){text{ + }}{c_2}left( {{{dot x}_1} - {{dot x}_2}}
ight) hfill begin{array}{*{20}{c}} {} end{array}begin{array}{*{20}{c}} {} end{array}begin{array}{*{20}{c}} {} end{array} + {k_3}{left( {{x_1} - {x_3}}
ight)^3} + {c_3}left( {{{dot x}_1} - {{dot x}_3}}
ight) = Fcos (omega t )hfill end{gathered}tag{1a} $$






$$ {m_2}{ddot x_2} + {k_2}left( {{x_2} - {x_1}}
ight) + {c_2}left( {{{dot x}_2} - {{dot x}_1}}
ight) = 0 tag{1b}$$






$$ {m_3}{ddot x_3} + {k_3}{left( {{x_3} - {x_1}}
ight)^3} + {c_3}left( {{{dot x}_3} - {{dot x}_1}}
ight) = 0 tag{1c}$$

将相对位移表示为${x_{{text{r1}}}} = {x_1} - {x_2}$,${x_{{text{r2}}}} = {x_1} - {x_3}$, 代入式(1)中可以得到






$$ begin{gathered} {m_1}{{ddot x}_1} + {k_1}{x_1} + {c_1}{{dot x}_1} + {k_2}{x_{{text{r1}}}}{text{ + }} hfill begin{array}{*{20}{c}} {} end{array}begin{array}{*{20}{c}} {} end{array}{c_2}{{dot x}_{{text{r1}}}} + {k_3}x_{{text{r2}}}^3 + {c_3}{{dot x}_{{text{r}}2}} = Fcos( omega t) hfill end{gathered} tag{2a}$$






$$ {m_2}left( {{{ddot x}_{{text{r}}1}} - {{ddot x}_1}}
ight) + {k_2}{x_{{text{r1}}}} + {c_2}{dot x_{{text{r1}}}} = 0tag{2b} $$






$$ {m_3}left( {{{ddot x}_{{text{r2}}}} - {{ddot x}_1}}
ight) + {k_3}x_{{text{r}}2}^3 + {c_3}{dot x_{{text{r}}2}} = 0 tag{2c}$$

令$ omega _1^2 = {{{k_1}} mathord{left/ {vphantom {{{k_1}} {{m_1}}}}
ight. } {{m_1}}}, $ $ varepsilon {mu _1}{text{ = }}{{{c_1}} mathord{left/ {vphantom {{{c_1}} {{m_1}}}}
ight. } {{m_1}}}, $ $ varepsilon kappa {text{ = }}{{{k_2}} mathord{left/ {vphantom {{{k_2}} {{m_1}}}}
ight. } {{m_1}}}, $ $ omega _2^2{text{ = }}{{{k_2}} mathord{left/ {vphantom {{{k_2}} {{m_2}}}}
ight. } {{m_2}}}, $ $varepsilon {alpha _2}{text{ = }} {{{k_3}} mathord{left/ {vphantom {{{k_3}} {{m_{text{1}}}}}}
ight. } {{m_{text{1}}}}},$ $ varepsilon {alpha _3}{text{ = }}{{{k_3}} mathord{left/ {vphantom {{{k_3}} {{m_3}}}}
ight. } {{m_3}}}, $ $ varepsilon {eta _2}{text{ = }}{{{c_2}} mathord{left/ {vphantom {{{c_2}} {{m_1}}}}
ight. } {{m_1}}}, $ $ varepsilon {mu _{text{2}}}{text{ = }}{{{c_2}} mathord{left/ {vphantom {{{c_2}} {{m_2}}}}
ight. } {{m_2}}}, $ $varepsilon {eta _3}{text{ = }} {{{c_3}} mathord{left/ {vphantom {{{c_3}} {{m_1}}}}
ight. } {{m_1}}},$ $ varepsilon {mu _3}{text{ = }}{{{c_3}} mathord{left/ {vphantom {{{c_3}} {{m_3}}}}
ight. } {{m_3}}}, $ $ varepsilon f{text{ = }}{F mathord{left/ {vphantom {F {{m_1}}}}
ight. } {{m_1}}}, $$ {omega ^2} = omega _1^2 + varepsilon {sigma _1} ,$ ${omega ^2} = omega _2^2 + varepsilon {sigma _2}.$ 式(2)可以变换为






$$ begin{gathered} {{ddot x}_1} + {omega ^2}{x_1} = varepsilon left[ {fcos (omega t) - {mu _1}{{dot x}_1} - kappa {x_{{text{r1}}}}}
ight] {text{ + }}hfill begin{array}{*{20}{c}} {} end{array}begin{array}{*{20}{c}} {} end{array}begin{array}{*{20}{c}} {} end{array}varepsilon left( { - {eta _2}{{dot x}_{{text{r1}}}} - {alpha _2}x_{{text{r2}}}^3 - {eta _3}{{dot x}_{{text{r}}2}} + {sigma _1}{x_1}}
ight) hfill end{gathered} tag{3a}$$






$$ {ddot x_{{text{r}}1}} + {omega ^2}{x_{{text{r1}}}} = {ddot x_1} - varepsilon {mu _2}{dot x_{{text{r1}}}} + varepsilon {sigma _2}{x_{{text{r1}}}}tag{3b} $$






$$ {ddot x_{{text{r2}}}} + {omega ^2}{x_{{text{r}}2}} = {ddot x_1} + {omega ^2}{x_{{text{r}}2}} - varepsilon {alpha _3}x_{{text{r}}2}^3 - varepsilon {mu _3}{dot x_{{text{r}}2}}tag{3c} $$


2.
近似解析解


利用平均法研究镗杆系统的受迫振动, 设系统的周期解为






$$ {x_1} = {a_1}cos {psi _1} tag{4a}$$






$$ {dot x_1} = - {a_1}omega sin {psi _1} tag{4b}$$






$$ {x_{{text{r1}}}} = {a_2}cos {psi _2}tag{4c} $$






$$ {dot x_{{text{r1}}}} = - {a_2}omega sin {psi _2} tag{4d}$$






$$ {x_{{text{r2}}}} = {a_3}cos {psi _3}tag{4e} $$






$$ {dot x_{{text{r2}}}} = - {a_3}omega sin {psi _3}tag{4f} $$

其中, ${psi _1}{text{ = }}omega t{text{ + }}{theta _1}$, ${psi _2}{text{ = }}omega t{text{ + }}{theta _2}$, ${psi _3}{text{ = }}omega t{text{ + }}{theta _3}$.

对式(4)关于t求导, 得到






$$ {dot x_1} = {dot a_1}cos {psi _1} - {a_1}(omega + {dot theta _1})sin {psi _1} tag{5a}$$






$$ {ddot x_1} = - omega left[ {{{dot a}_1}sin {psi _1} + {a_1}(omega + {{dot theta }_1})cos {psi _1}}
ight]tag{5b} $$






$$ {dot x_{{text{r1}}}} = {dot a_2}cos {psi _2} - {a_2}(omega + {dot theta _2})sin {psi _2}tag{5c} $$






$$ {ddot x_{{text{r1}}}} = - omega left[ {{{dot a}_2}sin {psi _2} + {a_2}(omega + {{dot theta }_2})cos {psi _2}}
ight]tag{5d}$$






$$ {dot x_{{text{r2}}}} = {dot a_3}cos {psi _3} - {a_3}(omega + {dot theta _3})sin {psi _3} tag{5e}$$






$$ {ddot x_{{text{r2}}}} = - omega left[ {{{dot a}_3}sin {psi _3} + {a_3}(omega + {{dot theta }_3})cos {psi _3}}
ight]tag{5f} $$

根据式(3)~式(5)可以得到






$$ {dot a_1}cos {psi _1} - {a_1}{dot theta _1}sin {psi _1} = 0 tag{6a}$$






$$ {dot a_1}sin {psi _1} + {a_1}{dot theta _1}cos {psi _1} = frac{1}{omega }{P_1}tag{6b} $$






$$ {dot a_2}cos {psi _2} - {a_2}{dot theta _2}sin {psi _2} = 0tag{6c} $$






$$ {dot a_2}sin {psi _2} + {a_2}{dot theta _2}cos {psi _2} = frac{1}{omega }{P_2}tag{6d} $$






$$ {dot a_3}cos {psi _3} - {a_3}{dot theta _3}sin {psi _3} = 0tag{6e} $$






$$ {dot a_3}sin {psi _3} + {a_3}{dot theta _3}cos {psi _3} = frac{1}{omega }{P_3} tag{6f} $$

其中






$$ begin{split} {P_1}{text{ = }}&varepsilon left[ { - fcos left( {omega t}
ight) - {mu _1}omega {a_1}sin {psi _1} + kappa {a_2}cos {psi _2}}
ight]+ hfill & varepsilon left[ { - {eta _2}omega {a_2}sin {psi _2} + {alpha _2}{{left( {{a_3}cos {psi _3}}
ight)}^3}}
ight] +hfill & varepsilon left( { - {eta _3}omega {a_3}sin {psi _3} - {sigma _1}{a_1}cos {psi _1}}
ight) end{split} $$






$$ begin{split} {P_2}{text{ = }} &- varepsilon fcos left( {omega t}
ight) - varepsilon {mu _1}omega {a_1}sin {psi _1} + varepsilon {alpha _2}{left( {{a_3}cos {psi _3}}
ight)^3}+ hfill & varepsilon left( {kappa - {sigma _2}}
ight){a_2}cos {psi _2} - varepsilon left( {{eta _2} + {mu _2}}
ight)omega {a_2}sin {psi _2} - hfill & varepsilon {eta _3}omega {a_3}sin {psi _3} - varepsilon {sigma _1}{a_1}cos {psi _1} + {omega ^2}{a_1}cos {psi _1} end{split} $$






$$ begin{split} {P_3}{text{ = }}& - varepsilon fcos left( {omega t}
ight) - varepsilon {mu _1}omega {a_1}sin {psi _1} + varepsilon kappa {a_2}cos {psi _2}- hfill & {omega ^2}{a_3}cos {psi _3} + varepsilon left( {{alpha _2} + {alpha _3}}
ight){left( {{a_3}cos {psi _3}}
ight)^3} -hfill & varepsilon {eta _2}omega {a_2}sin {psi _2} - varepsilon left( {{eta _3} + {mu _3}}
ight)omega {a_3}sin {psi _3}- hfill & varepsilon {sigma _1}{a_1}cos {psi _1} + {omega ^2}{a_1}cos {psi _1} end{split} . $$

求解式(6), 可以得到






$$ {dot a_1} = frac{1}{omega }{P_1}sin {psi _1} tag{7a}$$






$$ {a_1}{dot theta _1} = frac{1}{omega }{P_1}cos {psi _1}tag{7b} $$






$$ {dot a_2} = frac{1}{omega }{P_2}sin {psi _2}tag{7c} $$






$$ {a_2}{dot theta _2} = frac{1}{omega }{P_2}cos {psi _2}tag{7d} $$






$$ {dot a_3} = frac{1}{omega }{P_3}sin {psi _3}tag{7e} $$






$$ {a_3}{dot theta _3} = frac{1}{omega }{P_3}cos {psi _3} tag{7f}$$

利用一个振动周期$T = {{2{text{π}} } mathord{left/ {vphantom {{2{text{π}} } omega }}
ight. } omega }$内的平均值来代替振幅和相位的慢变真值, 则式(7)可以改写为






$$ {dot a_1} = frac{1}{{Tomega }}int_0^T {{P_1}sin {psi _1}{text{d}}t}tag{8a} $$






$$ {a_1}{dot theta _1} = frac{1}{{Tomega }}int_0^T {{P_1}cos {psi _1}{text{d}}t} tag{8b}$$






$$ {dot a_2} = frac{1}{{Tomega }}int_0^T {{P_2}sin {psi _2}{text{d}}t}tag{8c} $$






$$ {a_2}{dot theta _2} = frac{1}{{Tomega }}int_0^T {{P_2}cos {psi _2}{text{d}}t} tag{8d}$$






$$ {dot a_3} = frac{1}{{Tomega }}int_0^T {{P_3}sin {psi _3}{text{d}}t} tag{8e}$$






$$ {a_3}{dot theta _3} = frac{1}{{Tomega }}int_0^T {{P_3}cos {psi _3}{text{d}}t} tag{8f}$$

对式(8)进行求解, 可以得到






$$ begin{split} {{dot a}_1}&{text{ = }} frac{1}{{2{text{π }}omega }}int_0^{2{text{π }}} {{P_1}sin {psi _1}{text{d}}{psi _1}} = hfill & - frac{{{a_1}varepsilon {mu _1}}}{2} - frac{{{a_2}varepsilon {eta _2}cos left( {{theta _1} - {theta _2}}
ight)}}{2} - frac{{{a_3}varepsilon {eta _3}cos left( {{theta _1} - {theta _3}}
ight)}}{2}- & frac{{varepsilon fsin {theta _1}}}{{2omega }} + frac{{varepsilon kappa {a_2}sin left( {{theta _1} - {theta _2}}
ight)}}{{2omega }} + frac{{3a_3^3varepsilon {alpha _2}sin left( {{theta _1} - {theta _3}}
ight)}}{{8omega }} hfill end{split} tag{9a}$$






$$ begin{split} {a_1}{{dot theta }_1}&{text{ = }}frac{1}{{2{text{π }}omega }}int_0^{2{text{π }}} {{P_1}cos {psi _1}{text{d}}{psi _1}} {text{ = }} hfill & - frac{{varepsilon fcos {theta _1}}}{{2omega }} + frac{{varepsilon kappa {a_2}cos left( {{theta _1} - {theta _2}}
ight)}}{{2omega }} + frac{{{a_3}varepsilon {eta _3}sin left( {{theta _1} - {theta _3}}
ight)}}{2}- hfill & frac{{{a_1}varepsilon {sigma _1}}}{{2omega }} + frac{{3a_3^3varepsilon {alpha _2}cos left( {{theta _1} - {theta _3}}
ight)}}{{8omega }} + frac{{{a_2}varepsilon {eta _2}sin left( {{theta _1} - {theta _2}}
ight)}}{2} hfill end{split}tag{9b} $$






$$ begin{split} {{dot a}_{text{2}}} =& frac{1}{{2{text{π }}omega }}int_0^{2{text{π }}} {{P_2}sin {psi _2}{text{d}}{psi _2}} {text{ = }} - frac{{{a_2}varepsilon left( {{mu _2} + {eta _2}}
ight)}}{2} - hfill & frac{{{a_1}varepsilon {mu _1}cos left( {{theta _1} - {theta _2}}
ight)}}{2} - frac{{{a_3}varepsilon {eta _3}cos left( {{theta _2} - {theta _3}}
ight)}}{2} + hfill & frac{{{a_1}varepsilon {sigma _1}}}{{2omega }}sin left( {{theta _1} - {theta _2}}
ight) - frac{{{a_1}omega sin left( {{theta _1} - {theta _2}}
ight)}}{2} - frac{{varepsilon fsin {theta _2}}}{{2omega }} +& frac{{3a_3^3varepsilon {alpha _2}sin left( {{theta _2} - {theta _3}}
ight)}}{{8omega }} hfill end{split}tag{9c} $$






$$ begin{split}& {a_2}{{dot theta }_2}{text{ = }}frac{1}{{2{text{π }}omega }}int_0^{2{text{π }}} {{P_2}cos {psi _2}{text{d}}{psi _2}} {text{ = }}frac{{{a_2}varepsilon left( {k - {sigma _2}}
ight)}}{{2omega }} hfill &quad- frac{{{a_1}varepsilon {sigma _1}cos left( {{theta _1} - {theta _2}}
ight)}}{{2omega }} - frac{{varepsilon fcos {theta _2}}}{{2omega }} + frac{{3a_3^3varepsilon {alpha _2}cos left( {{theta _2} - {theta _3}}
ight)}}{{8omega }} hfill & quad- frac{{{a_1}varepsilon {mu _1}sin left( {{theta _1} - {theta _2}}
ight)}}{2} + frac{{{a_1}omega cos left( {{theta _1} - {theta _2}}
ight)}}{2} & quad+ frac{{varepsilon {eta _3}{a_3}sin left( {{theta _2} - {theta _3}}
ight)}}{2} hfill end{split}tag{9d} $$






$$ begin{split}& {{dot a}_3}{text{ = }}frac{1}{{2{text{π }}omega }}int_0^{2{text{π }}} {{P_3}sin {psi _3}{text{d}}{psi _3}} = - frac{{{a_1}varepsilon {mu _1}cos left( {{theta _1} - {theta _3}}
ight)}}{2} hfill & quad- frac{{{a_3}varepsilon left( {{eta _3} + {mu _3}}
ight)}}{2} - frac{{{a_2}varepsilon {eta _2}cos left( {{theta _2} - {theta _3}}
ight)}}{2} + frac{{{a_1}varepsilon {sigma _1}sin left( {{theta _1} - {theta _3}}
ight)}}{{2omega }} hfill &quad- frac{{{a_1}omega sin left( {{theta _1} - {theta _3}}
ight)}}{2} - frac{{varepsilon kappa {a_2}sin left( {{theta _2} - {theta _3}}
ight)}}{{2omega }} - frac{{varepsilon fsin {theta _3}}}{{2omega }} hfill end{split} tag{9e}$$






$$ begin{split}& {a_3}{{dot theta }_3}{text{ = }}frac{1}{{2{text{π }}omega }}int_0^{2{text{π }}} {{P_3}cos {psi _3}{text{d}}{psi _3}} = frac{{3a_3^3varepsilon left( {{alpha _2} + {alpha _3}}
ight)}}{{8omega }} - frac{{{a_3}omega }}{2} hfill &quad + frac{{{a_1}left( {{omega ^2} - varepsilon {sigma _1}}
ight)cos left( {{theta _1} - {theta _3}}
ight)}}{{2omega }} + frac{{{a_2}varepsilon kappa cos left( {{theta _2} - {theta _3}}
ight)}}{{2omega }} hfill &quad - frac{{varepsilon fcos {theta _3}}}{{2omega }} - frac{{{a_1}varepsilon {mu _1}sin left( {{theta _1} - {theta _3}}
ight)}}{2} - frac{{{a_2}varepsilon {eta _2}sin left( {{theta _2} - {theta _3}}
ight)}}{2} hfill end{split} tag{9f}$$

为了确定系统稳态运动的定常解振幅${bar a_1}$, ${bar a_2}$和${bar a_3}$以及相位${bar theta _1}$, ${bar theta _2}$和${bar theta _3}$, 令式(9)中的$ {dot a_1} = 0 $, $ {dot theta _1} = 0 $, ${dot a_2} = 0$, $ {dot theta _2} = 0 $, ${dot a_3} = 0$, $ {dot theta _3} = 0 $, 并代入系统的原参数从而得到稳态运动方程






$$ begin{split} Fsin {{bar theta }_1} = & - {{bar a}_2}{c_2}omega cos left( {{{bar theta }_1} - {{bar theta }_2}}
ight) - {bar a_3}{c_3}omega cos left( {{{bar theta }_1} - {{bar theta }_3}}
ight) - hfill & {{bar a}_1}{c_1}omega + {k_2}{{bar a}_2}sin left( {{{bar theta }_1} - {{bar theta }_2}}
ight) + frac{{3bar a_3^3{k_3}sin left( {{{bar theta }_1} - {{bar theta }_3}}
ight)}}{4} hfill end{split}tag{10a} qquad$$






$$ begin{split} Fcos {{bar theta }_1} = & {{bar a}_1}{k_1} + {k_2}{{bar a}_2}cos left( {{{bar theta }_1} - {{bar theta }_2}}
ight) + frac{{3bar a_3^3{k_3}cos left( {{{bar theta }_1} - {{bar theta }_3}}
ight)}}{4} -hfill & {{bar a}_1}{m_1}{omega ^2} + {{bar a}_2}{c_2}omega sin left( {{{bar theta }_1} - {{bar theta }_2}}
ight) + {{bar a}_3}{c_3}omega sin left( {{{bar theta }_1} - {{bar theta }_3}}
ight) hfill end{split} tag{10b}$$






$$ begin{split} Fsin {{bar theta }_2} =& - {{bar a}_2}{c_2}omega - {{bar a}_1}{c_1}omega cos left( {{{bar theta }_1} - {{bar theta }_2}}
ight) - {{bar a}_1}{k_1}sin left( {{{bar theta }_1} - {{bar theta }_2}}
ight) -hfill & frac{{{{bar a}_2}{c_2}{m_1}omega }}{{{m_2}}} - {{bar a}_3}{c_3}omega cos left( {{{bar theta }_2} - {{bar theta }_3}}
ight) + frac{{3bar a_3^3{k_3}sin left( {{{bar theta }_2} - {{bar theta }_3}}
ight)}}{4} hfill end{split} tag{10c}$$






$$ begin{split} Fcos {{bar theta }_2} =& {{bar a}_2}{k_2} + frac{{{{bar a}_2}{k_2}{m_1}}}{{{m_2}}} + {{bar a}_1}{k_1}cos left( {{{bar theta }_1} - {{bar theta }_2}}
ight)+ hfill & frac{{3bar a_3^3{k_3}cos left( {{{bar theta }_2} - {{bar theta }_3}}
ight)}}{4} - {{bar a}_1}{c_1}omega sin left( {{{bar theta }_1} - {{bar theta }_2}}
ight)- hfill & {{bar a}_2}{m_1}{omega ^2} + {c_3}{{bar a}_3}omega sin left( {{{bar theta }_2} - {{bar theta }_3}}
ight) hfill end{split} tag{10d}qquadqquad$$






$$ begin{split} Fsin {{bar theta }_3} =& - {{bar a}_3}{c_3}omega - {{bar a}_1}{c_1}omega cos left( {{{bar theta }_1} - {{bar theta }_3}}
ight)- hfill & frac{{{{bar a}_3}{c_3}{m_1}omega }}{{{m_3}}} - {{bar a}_2}{c_2}omega cos left( {{{bar theta }_2} - {{bar theta }_3}}
ight) -hfill & {{bar a}_1}{k_1}sin left( {{{bar theta }_1} - {{bar theta }_3}}
ight) - {k_2}{bar a_2}sin left( {{{bar theta }_2} - {{bar theta }_3}}
ight) end{split}tag{10e} $$






$$ begin{split} Fcos {{bar theta }_3} = &frac{{3bar a_3^3{k_3}}}{4}left( {1 + frac{{{m_1}}}{{{m_3}}}}
ight) - {{bar a}_3}{m_1}{omega ^2}+ hfill & {{bar a}_1}{k_1}cos left( {{{bar theta }_1} - {{bar theta }_3}}
ight) + {{bar a}_2}{k_2}cos left( {{{bar theta }_2} - {{bar theta }_3}}
ight) -hfill & {{bar a}_1}{c_1}omega sin left( {{{bar theta }_1} - {{bar theta }_3}}
ight) - {{bar a}_2}{c_2}omega sin left( {{{bar theta }_2} - {{bar theta }_3}}
ight) end{split} tag{10f}$$


3.
数值解验证


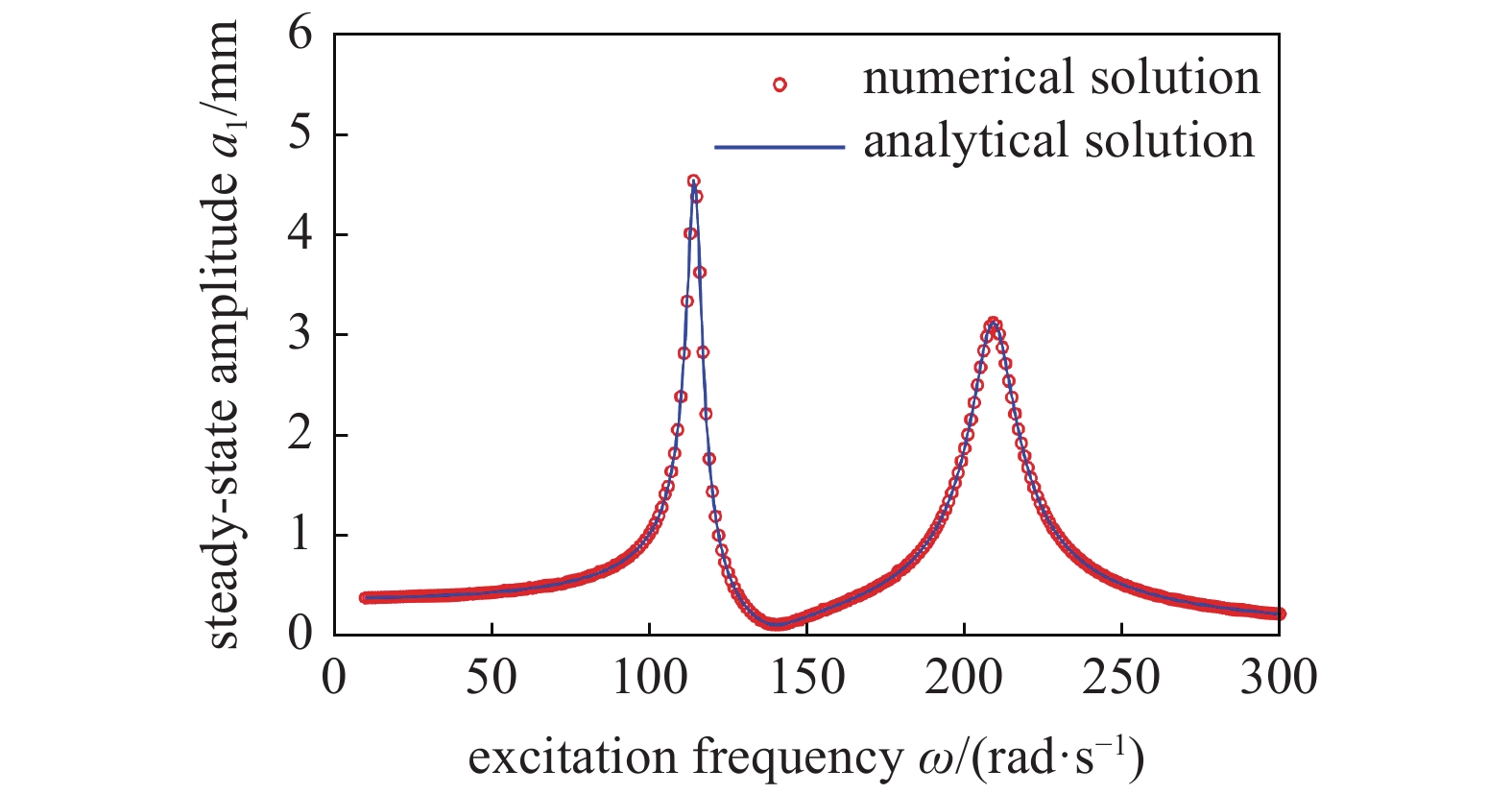
根据文献[36]选取镗杆的参数: m1=44 kg, k1=1.3 MN/m, c1=0.01 N·s/m, 以及线性动力吸振器的参数m2=18 kg, k2=350 kN/m, c2=207 N·s/m; 非线性能量阱的参数选择为: m3=4 kg, k3=130 kN/m3, c3=100 N·s/m; 外部激励幅值为F=500 N. 根据式(1), 利用龙格?库塔法可以得到线性镗杆的幅频响应曲线, 如图2所示. 根据式(10), 利用近似解析解也可以得到线性镗杆的幅频响应曲线. 从图2中可以看出, 近似解析解与数值解完全一致, 从而验证了近似解析解的正确性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
系统幅频响应曲线对比



Figure
2.
Comparison of amplitude-frequency response curves



下载:
全尺寸图片
幻灯片



4.
吸振器的振动控制效果



4.1
复合式吸振器的作用


为了更好地展示复合式动力吸振器的作用, 通过数值解得到线性镗杆无吸振器、单独附加线性动力吸振器(LDVA)和单独附加非线性能量阱(NES)时的稳态幅频响应曲线, 如图3所示. 同时, 利用近似解析解得到附加复合式动力吸振器时线性镗杆主系统的幅频响应曲线. 从图3中可以看出, 线性动力吸振器、非线性能量阱和复合式动力吸振器都可以降低镗杆系统的振动幅值, 其中复合式动力吸振器对镗杆的减振效果最好.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
附加不同吸振器的系统幅频响应曲线



Figure
3.
Amplitude-frequency curves for different absorbers



下载:
全尺寸图片
幻灯片



4.2
线性吸振器参数的影响


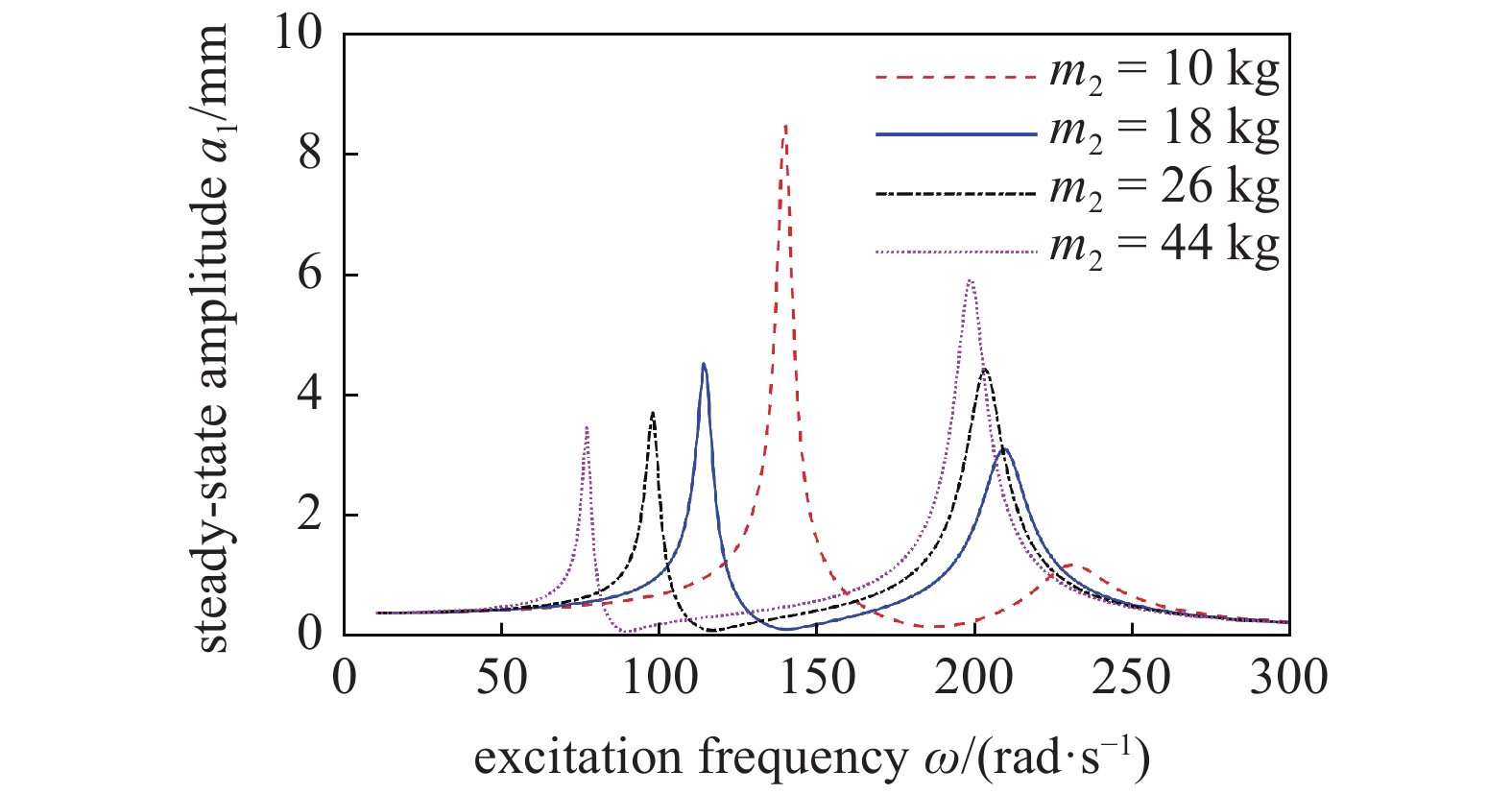
利用近似解析解分析线性动力吸振器参数对复合式动力吸振器减振效果的影响. 线性动力吸振器的质量m2分别为10 kg, 18 kg, 26 kg和44 kg, 其余参数保持不变, 可以得到附加复合式动力吸振器的镗杆主系统的幅频响应曲线, 如图4所示. 从图4中可以看出随着线性动力吸振器质量的逐渐增大, 第一共振峰值逐渐下降, 而第二共振峰值逐渐增大. 而且, 镗杆系统的共振频率也逐渐降低. 另外, 动力吸振器的质量越大, 内置式减振镗杆的制造难度就越大. 因此, 需要选择适中的动力吸振器质量, 使其具有合适的质量和满意的减振效果.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
不同m2的幅频响应曲线对比



Figure
4.
Amplitude-frequency curves of different m2



下载:
全尺寸图片
幻灯片


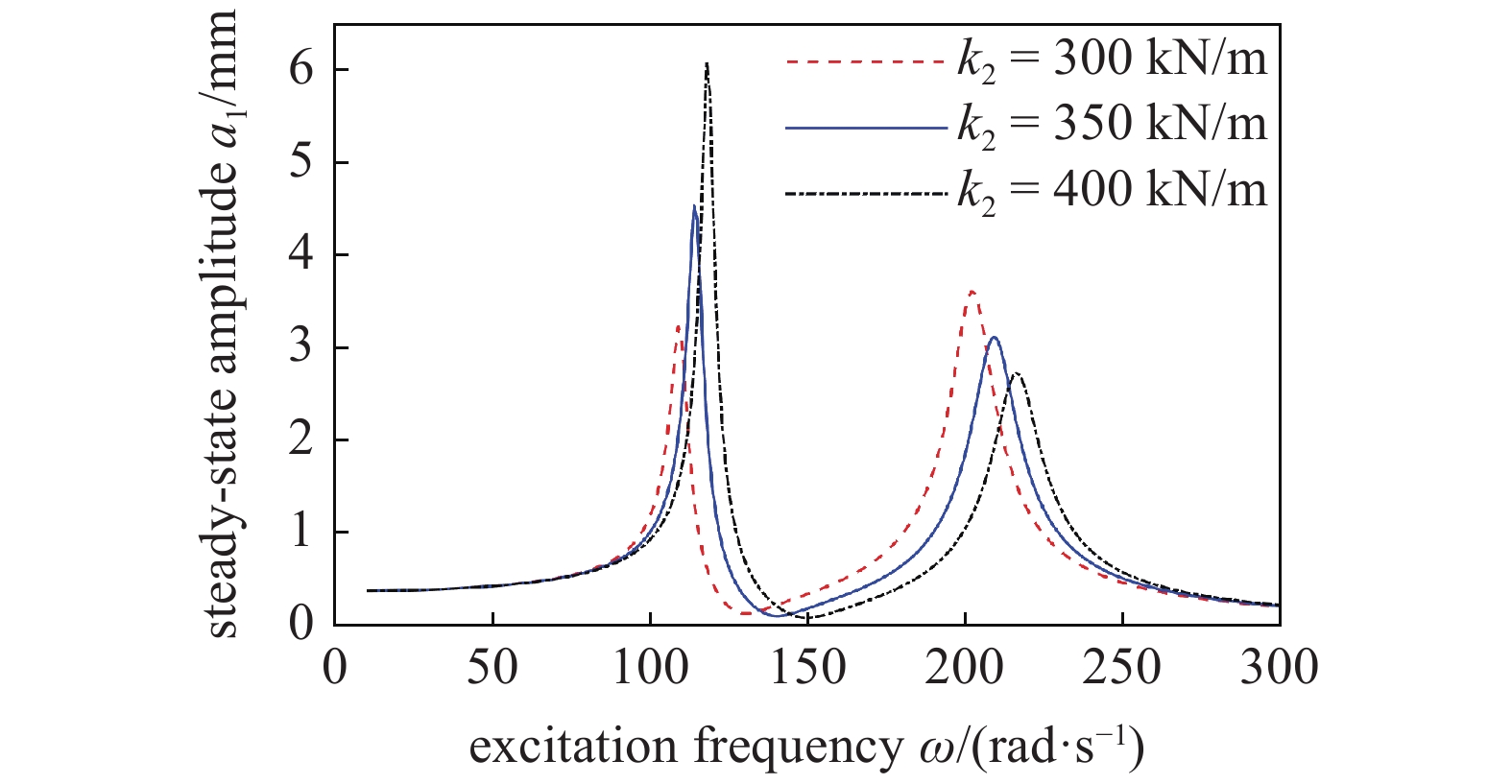
当线性动力吸振器的刚度k2分别为300 kN/m, 350 kN/m和400 kN/m时, 根据式(10)分别绘制镗杆主系统的幅频响应曲线, 如图5所示. 从图5中可以看出, 随着线性吸振器刚度的逐渐增大, 第一共振峰值逐渐增大, 而第二共振峰逐渐减小. 而且, 镗杆系统的共振频率也逐渐增大.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
不同k2的幅频响应曲线



Figure
5.
Amplitude-frequency curves of different k2



下载:
全尺寸图片
幻灯片


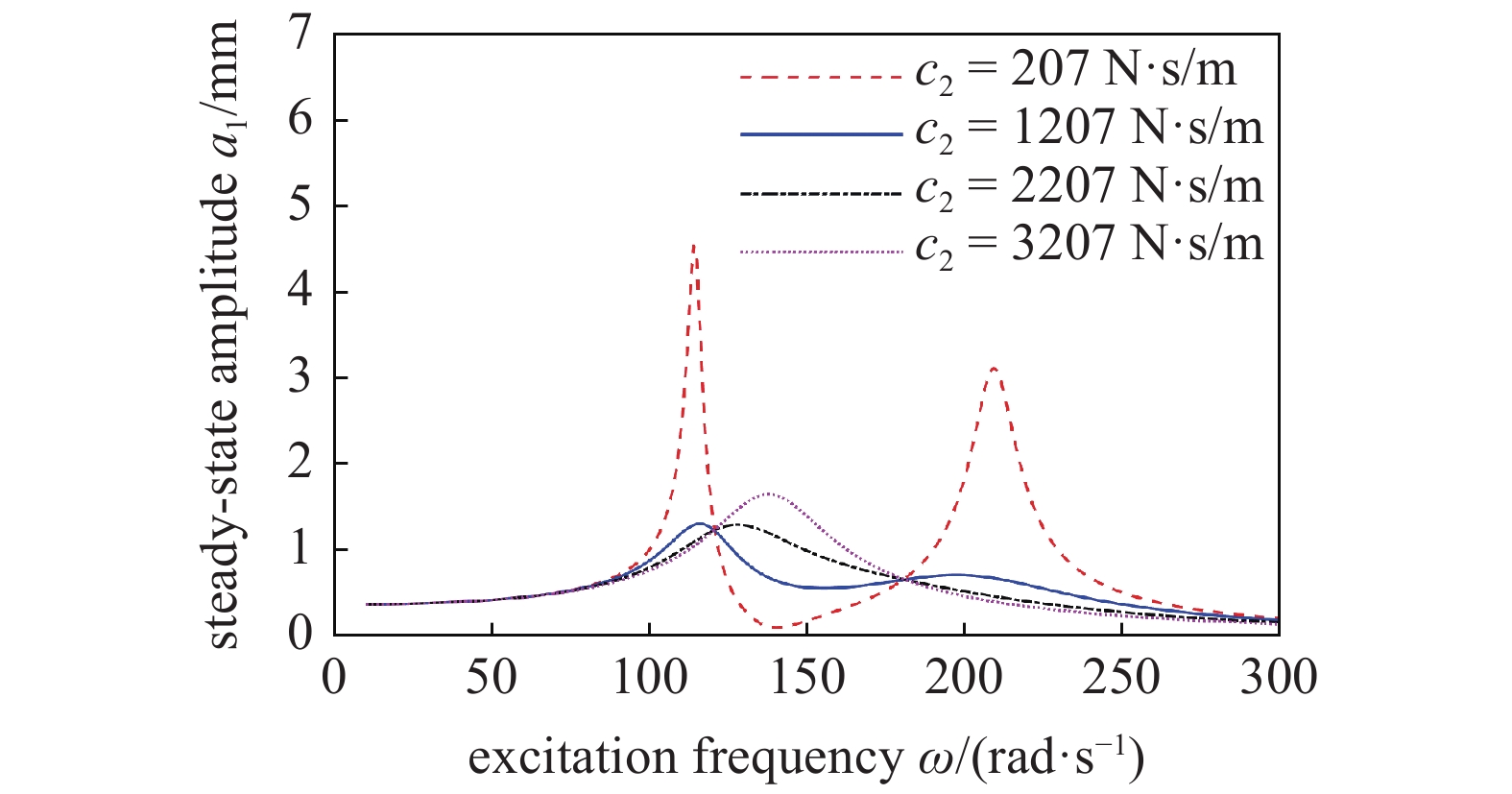
当线性动力吸振器的阻尼c2分别为207 N·s/m, 1207 N·s/m, 2207 N·s/m和3207 N·s/m时, 根据式(10)绘制镗杆主系统的幅频响应曲线, 如图6所示. 随着线性动力吸振器阻尼系数的增大, 第一共振峰先减小后增大, 第二共振峰先减小后消失. 因此, 通过选择合适的线性动力吸振器阻尼, 可以使线性镗杆系统只有一个共振峰. 另外, 需要注意的是当线性动力吸振器的阻尼变化时主系统的幅频响应曲线会近似的通过两个固定点.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
不同c2的幅频响应曲线



Figure
6.
Amplitude-frequency curves of different c2



下载:
全尺寸图片
幻灯片



4.3
非线性能量阱参数的影响


当非线性能量阱的质量m3分别为1 kg, 4 kg和18 kg时, 根据式(10)分别绘制镗杆主系统的幅频响应曲线, 如图7所示. 随着非线性能量阱质量的增大, 系统的两个共振峰值同时下降. 但是, 当非线性能量阱的质量增加到一定程度时, 其增加的减振程度会降低. 而且非线性能量阱质量越大, 也会增加内置式减振镗杆的制造难度.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
不同m3的幅频响应曲线



Figure
7.
Amplitude-frequency curves of different m3



下载:
全尺寸图片
幻灯片


当非线性能量阱阻尼c3分别为100 N·s/m, 300 N·s/m和1000 N·s/m时, 根据式(10)分别绘制镗杆主系统的幅频响应曲线, 如图8所示. 随着非线性能量阱阻尼的增大, 第一共振峰值先减小然后增大, 而第二共振峰值逐渐减小. 说明通过选择合适的非线性能量阱阻尼, 可以提高系统的减振效果.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
不同c3的幅频响应曲线



Figure
8.
Amplitude-frequency curves of different c3



下载:
全尺寸图片
幻灯片


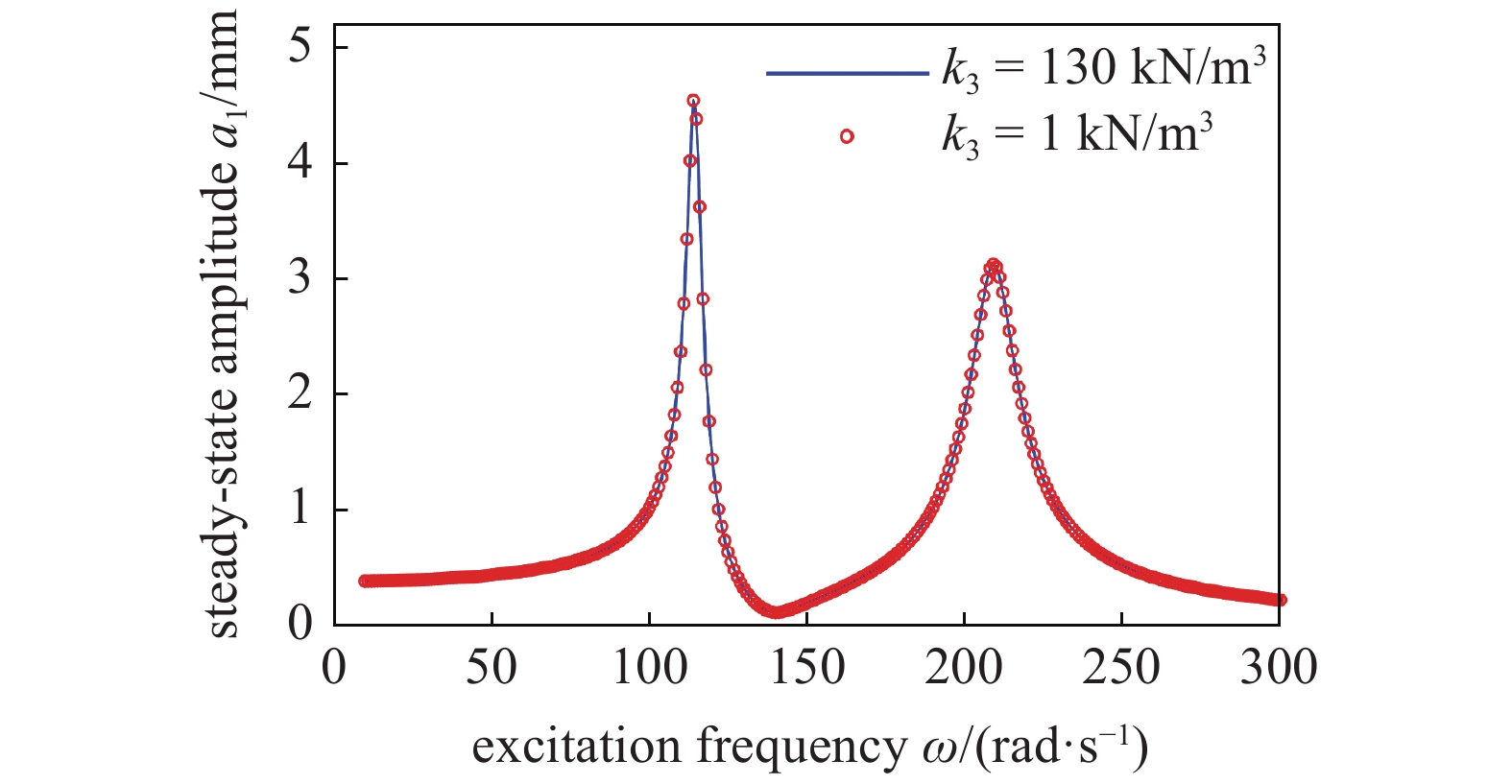
当非线性能量阱的非线性刚度k3分别为130 kN/m3和1 kN/m3时, 利用近似解析解得到镗杆主系统的幅频响应曲线, 如图9所示. 改变非线性能量阱的非线性刚度并不会改变镗杆主系统的抗振性能, 可以根据其他设计条件确定非线性刚度.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
不同k3的幅频响应曲线



Figure
9.
Amplitude-frequency curves of different k3



下载:
全尺寸图片
幻灯片



5.
参数优化



5.1
线性吸振器参数优化


首先对线性吸振器利用H∞优化方法进行参数优化, 也就是使用固定点理论, 当将共振幅值调整为相等的高度时使最大幅值响应最小化[37]. 文献[38]对含有阻尼的主系统附加的线性动力吸振器进行了H∞优化, 并得到了一阶近似解析表达式







$$ {zeta _1}{text{ = }}frac{{{c_1}}}{{2{m_1}{omega _1}}} $$
(11)







$$ gamma {text{ = }}frac{{{m_2}}}{{{m_1}}} $$
(12)







$$ A = sqrt {3left( {2 + gamma }
ight) - sqrt {gamma left( {2 + gamma }
ight)} } $$
(13)







$$ B = sqrt {3left( {2 + gamma }
ight) + sqrt {gamma left( {2 + gamma }
ight)} } $$
(14)







$$ C{text{ = }}sqrt {2left( {2{text{ + }}gamma }
ight)left( {9{text{ + }}4gamma }
ight)} $$
(15)







$$ {C_0} = 52 + 41gamma + 8{gamma ^2} $$
(16)







$$qquad begin{split} {C_1} = & - 1296 + 2124gamma + 6509{gamma ^2} + & 5024{gamma ^3} + 1616{gamma ^4} + 192{gamma ^5}end{split} $$
(17)







$$ qquadbegin{split} {C_2} = & 48;168 + 112;887gamma + 105;907{gamma ^2}+ & 49;664{gamma ^3} + 11;632{gamma ^4} + 1088{gamma ^5} end{split} $$
(18)







$$ quadbegin{split} v =& sqrt {frac{{{k_2}{m_1}}}{{{k_1}{m_2}}}} = frac{1}{{1{text{ + }}gamma }}-hfill & {zeta _1}frac{1}{{1{text{ + }}gamma }}sqrt {frac{1}{{2left( {1{text{ + }}gamma }
ight)}}left( {3 + 4gamma - frac{C}{{2 + gamma }}}
ight)} + hfill & zeta _1^2frac{{{C_0} - 4left( {5 + 2gamma }
ight)C}}{{4{{left( {1{text{ + }}gamma }
ight)}^2}left( {2 + gamma }
ight)left( {9 + 4gamma }
ight)}} end{split} $$
(19)







$$quad begin{split} {zeta _2} =& frac{{{c_2}}}{{2sqrt {{k_2}{m_2}} }} = sqrt {frac{{3gamma }}{{8left( {1{text{ + }}gamma }
ight)}}} {text{ + }} hfill & {zeta _1}frac{{60{text{ + }}63gamma {text{ + }}16{gamma ^2} - 2left( {3 + 2gamma }
ight)C}}{{8left( {1 + gamma }
ight)left( {2 + gamma }
ight)left( {9 + 4gamma }
ight)}} +hfill & zeta _1^2frac{{{C_1}left( {A + B}
ight)sqrt {2 + gamma } + {C_2}left( {A - B}
ight)sqrt gamma }}{{32left( {1 + gamma }
ight){{left( {2 + gamma }
ight)}^2}{{left( {9 + 4gamma }
ight)}^3}sqrt {2gamma left( {1 + gamma }
ight)} }} end{split} $$
(20)

对于给定镗杆主系统参数和线性动力吸振器的质量m2=18 kg, 代入式(11) ~ 式(20)可以得到最优调谐比$v{text{ = 0}}{text{.709;7}}$和最优阻尼比${zeta _2} = 0.33$. 因此, 可以得到优化以后的刚度和阻尼分别为: k2=267850 N/m和 c2=1449 N·s/m. 利用近似解析解分别绘制线性动力吸振器参数优化前后镗杆主系统的幅频响应曲线, 如图10所示. 可以看出, 通过优化线性动力吸振器的参数可以得到更好的振动控制效果, 而且优化后的两个共振峰值基本相等.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
线性动力吸振器优化前后系统的幅频响应



Figure
10.
Amplitude-frequency curves before and after optimization of LDVA



下载:
全尺寸图片
幻灯片



5.2
非线性能量阱参数优化


为了进一步提高复合式动力吸振器对线性镗杆受迫振动的减振效果, 对非线性能量阱的参数进行优化. 通过4.3节的分析可以发现, 对于给定质量的非线性能量阱, 只有阻尼需要优化. 在优化后的线性动力吸振器参数的基础上, 对非线性能量阱的阻尼进行优化. 当非线性能量阱的阻尼从0增加到2000 N·s/m时, 利用近似解析解可以得到m3=4 kg时对应的线性镗杆的最大共振峰值曲线, 如图11所示. 从图11中可以看出, 随着非线性能量阱阻尼的增大, 主系统的最大峰值先减小后增大. 也就是说, 当非线性能量阱的质量确定后, 存在一个最佳阻尼值可以使主系统的共振峰值最小, 最小峰值对应的阻尼为c3=150 N·s/m. 需要注意的是, 当非线性能量阱的阻尼从0增大到350 N·s/m时, 线性镗杆的最大共振峰值变化量仅约为0.01 mm.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
随c3变化的最大峰值



Figure
11.
Maximum peak value with c3



下载:
全尺寸图片
幻灯片


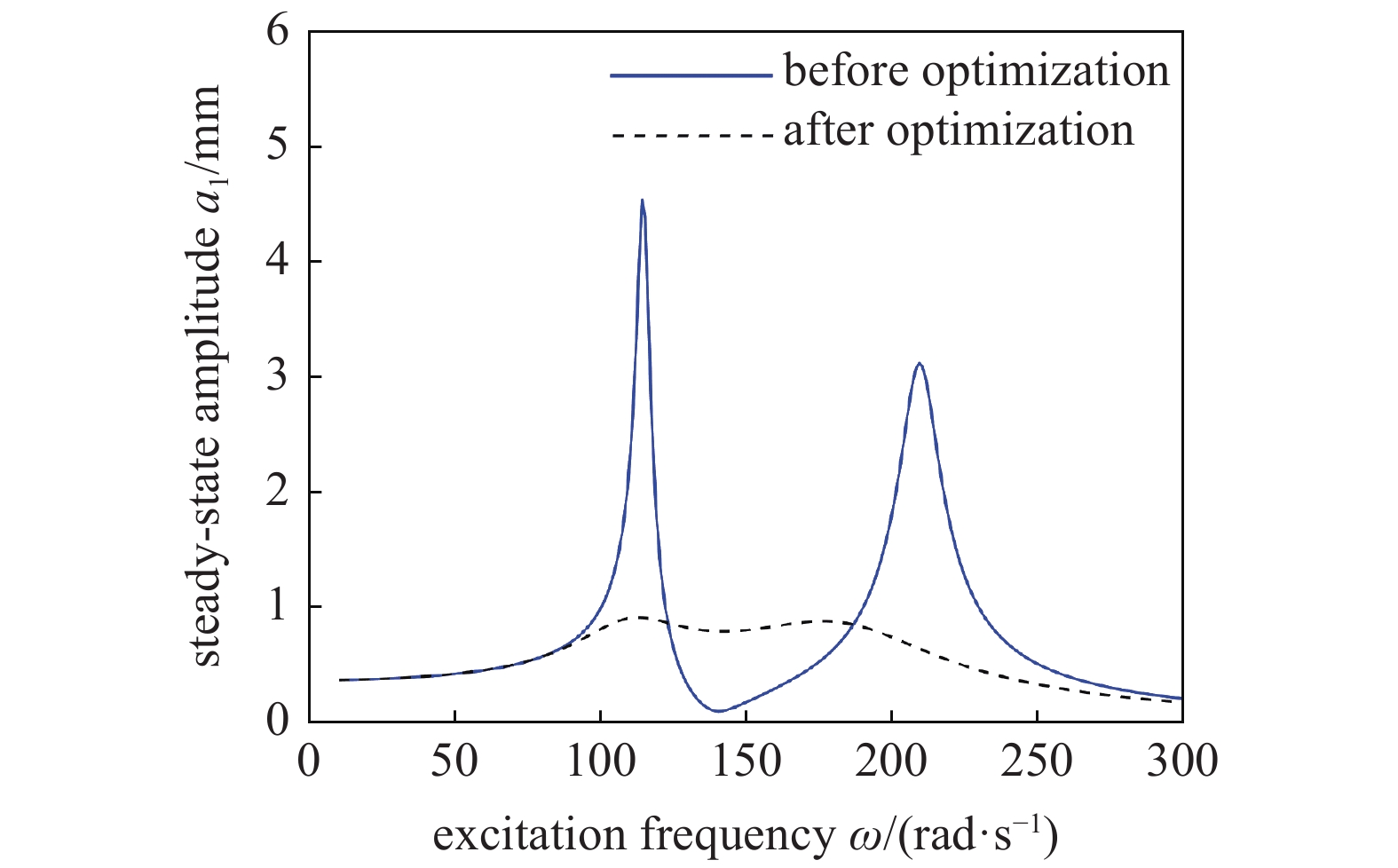
利用近似解析解绘制复合式动力吸振器参数优化前后镗杆主系统的幅频响应曲线, 如图12所示. 从图12中可以看出, 优化后的复合式动力吸振器能够很好地抑制线性镗杆的受迫振动幅值.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
复合式动力吸振器优化前后系统的幅频响应



Figure
12.
Amplitude-frequency curves before and after optimization of LDVA and NES



下载:
全尺寸图片
幻灯片


为了进一步说明附加非线性能量阱的作用, 利用数值解得到镗杆主系统单独附加优化后的线性动力吸振器时的幅频响应曲线, 如图13所示. 同时, 利用近似解析解将镗杆主系统附加优化后的复合式动力吸振器的幅频响应曲线也显示到图13中. 可以发现, 对于参数优化后的线性动力吸振器, 非线性能量阱仍然可以提高其振动抑制性能. 结合图3, 可以得出如下结论: 即使是由于刚度失效等原因导致线性动力吸振器的刚度降低后, 附加非线性能量阱仍然可以保证复合式动力吸振器达到一定的振动控制效果. 因此, 附加非线性能量阱可以提高振动控制系统的鲁棒性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-475-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
不同吸振器优化后系统的幅频响应



Figure
13.
Amplitude-frequency curves for different optimized absorbers



下载:
全尺寸图片
幻灯片



6.
结 论


本文利用平均法研究了附加线性动力吸振器和非线性能量阱吸振器的线性镗杆系统的受迫振动, 通过与数值解得到的线性镗杆幅频响应曲线进行对比, 验证了近似解析解的准确性. 通过比较线性镗杆单独附加线性动力吸振器、单独附加非线性能量阱吸振器和附加复合式动力吸振器时的幅频响应曲线, 证实了线性动力吸振器复合非线性能量阱吸振器可以更好地控制镗杆系统的受迫振动. 详细分析了复合式动力吸振器的参数对线性镗杆系统减振效果的影响, 发现适当增加非线性能量阱的质量可以获得较好的减振效果; 调整非线性能量阱的阻尼可以在一定程度上提高减振效果, 但调整非线性能量阱的非线性刚度并不能提高减振效果. 在分析复合式动力吸振器参数对振动控制影响规律的基础上, 对复合式动力吸振器的参数进行了优化. 分析结果表明, 参数优化后的复合式动力吸振器能更好地抑制线性镗杆的受迫振动幅值, 而且非线性能量阱可以提高线性动力吸振器的振动抑制效果和振动控制系统的鲁棒性. 本文的分析结果可以为内置式减振镗杆的设计提供理论基础, 也可以为其他系统的受迫振动控制提供参考.

相关话题/系统 动力 优化 质量 图片
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于离散单元法和人工神经网络的近壁颗粒动力学特征研究
    引言密集颗粒流及气粒两相流大量应用于食品和药物加工、石油化工和能源转化等行业.由于颗粒与颗粒之间及气体与颗粒之间存在强烈的非线性耗散作用,密集颗粒流及气粒流动中往往会出现复杂的非均匀多尺度流动现象[1-5].近年来,国内外诸多****致力于采用数值模拟方法来研究这种复杂流动,目前针对颗粒相的数值模拟 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 时间尺度上Lagrange系统的Hojman守恒量
    引言力学系统的对称性与守恒律密切相关.通过研究对称性而探索或发现复杂力学系统的守恒律,这是分析力学研究的一个重要方面[1-2].Lie对称性[3-9]、Noether对称性[10-20]和Mei对称性[21-28]是3种概念不同的对称性方法.利用对称性和守恒律,可以简化动力学问题甚至求解力学系统的精 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于能力评估的空间翻滚目标抓捕策略优化
    引言空间机器人在碎片清理、在轨维修、在轨装配等在轨服务(OOS)任务中发挥着重要的作用[1].与单机械臂相比,空间双臂机器人可以提供更大的负载能力和更好的稳定性[2].然而,双臂协调操作时末端执行器与目标接触形成闭链系统,闭链约束的引入会极大地限制双臂协调操作的工作空间.为了对翻滚目标的抓捕策略进行 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 多相流动的光滑粒子流体动力学方法研究综述
    引言多相流广泛存在于自然界和工业应用中.对多相流进行高精度和高效率的建模和模拟非常重要.然而,其中流动形态和界面跟踪的复杂性限制了基于网格的传统方法模拟多相流能力,尤其对于存在界面大变形、不连续性和多物理过程的多相流动.而无网格方法可以很好地处理网格方法遇到的上述问题.在过去几十年发展起来的无网格方 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 垂荡双气室振荡水柱波能装置水动力特性研究
    引言人类日益增长的能源需求不仅导致了不可再生能源如煤炭、石油、天然气临近枯竭,还加剧了全球环境的恶化.为了解决这一问题,人类开始寻找绿色可再生替代能源[1-2].全球海洋能最具有潜力,能源提取的选择范围最广,其中包括波浪、潮汐和洋流、海洋热能、盐度梯度、海洋生物能和海底地热能等[3-4].振荡水柱( ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑胎路多点接触的电动汽车?路面耦合系统振动分析
    引言近年来,轮毂电机驱动电动汽车,因传动效率高、便于实现智能控制等优点,得到了广泛关注[1-3],是未来电动汽车的发展方向.但独立驱动电动汽车的动力学与控制也面临诸多新问题,其一是簧下质量大,导致轮胎动载荷增加,轮胎与路面动力学相互作用更加突出.其二是电机激励进一步加剧车轮振动,影响轮胎的接地安全性 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 轮对系统的Hopf分岔研究
    引言近年来随着高速列车运行速度的提高,车辆系统的蛇行失稳问题越发突出,蛇形运动作为车辆系统的固有属性,严重影响着车辆系统的运行平稳性、乘坐舒适性和安全性[1],对车辆系统进行非线性动力学理论方面的研究,不仅可以从车辆动力学角度更加全面地了解蛇形运动,而且对车辆系统的设计与参数优化也具有非常重要的意义 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 数据驱动印度洋海域全局动力学研究
    引言海洋系统天然受到多种环境因素(风速、温度、海水含盐量等)、人类活动和天体运动等不确定扰动的影响,导致其洋流运动复杂而多样[1-2].然而,一些观测和研究发现,其内部蕴含着能够对洋流的运动方向和趋势起限制和导向作用的复杂动力结构和特征,影响甚至主导了表面漂浮物的流动形式和演化路径.例如,经志友等[ ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 挠性航天器太阳翼全局模态动力学建模与实验研究
    引言随着航天领域的发展,现代大型柔性航天器往往安装有诸如大型太阳翼等柔性结构,为了得到可持续的能源,其尺寸日益增大、结构重量越来越轻,太阳翼的弹性振动不可避免地与航天器主体平台的运动相互耦合,这种耦合效应随着太阳翼尺寸的增大显著增强.此时,单个太阳能帆板的模态(假设模态)并不能准确反映整个太阳翼在系 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于T样条的变网格等几何薄板动力学分析
    引言随着柔性轻质结构在航天、汽车以及船舶工程等领域日益广泛的应用,柔性多体系统的动力学分析也愈加重要.然而,以线弹性小变形假设为基础的,将节点位移和转动作为坐标的传统有限单元不适合解决存在大位移、大变形的柔性多体系统的动力学问题.此外,对于传统结构有限元,将几何数据转换为有限元网格数据是困难且耗时的 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.