删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于离散单元法和人工神经网络的近壁颗粒动力学特征研究

本站小编 Free考研考试/2022-01-01


引 言


密集颗粒流及气粒两相流大量应用于食品和药物加工、石油化工和能源转化等行业. 由于颗粒与颗粒之间及气体与颗粒之间存在强烈的非线性耗散作用, 密集颗粒流及气粒流动中往往会出现复杂的非均匀多尺度流动现象[1-5]. 近年来, 国内外诸多****致力于采用数值模拟方法来研究这种复杂流动, 目前针对颗粒相的数值模拟方法主要有离散单元法(DEM)和双流体方法(TFM). DEM相当于颗粒相的直接数值模拟, 计算准确性高, 但计算量大; 而TFM方法中颗粒相都被视为完全互穿的连续体, 由单独的质量、动量和能量守恒方程描述. 这种颗粒拟流体的连续性表示, 使得计算量不直接取决于颗粒数, 计算量相对较小. 但需要提供额外的颗粒相本构模型以及气体与颗粒相间作用模型, 而这些模型的可靠性将直接影响到TFM计算结果的准确性.

颗粒动力学理论[6-8](KTGF)被广泛用于推导颗粒相本构模型, 其中包含了描述颗粒与颗粒作用的本构模型和描述颗粒与固体壁面作用的壁面边界条件. 对于后者, 理论研究相对较少, 当前应用最广泛的是Johnson和Jackson边界条件[9], 它包含弹性恢复系数e和光滑因子? 两个输入参数, 分别用以描述颗粒与壁面碰撞时法向和切向上的速度变化. 光滑因子? 的直接实验测量是不可行的, 通常都是通过调整数值来拟合实验数据而获得, 这非常耗时且适用范围窄[10-11]. 为此, 一些****尝试使用颗粒物性和流动参数来建立光滑因子?的函数. Li和Benyahia[12]提出了一个适用于低摩擦系数下的光滑因子函数关联式, 其中光滑因子被拟合为壁面上颗粒法向恢复系数、摩擦系数和无因次滑移速度的函数. Jenkins[13]引入3个可测物性参数, 库伦摩擦系数μ、切向弹性恢复系数 $; beta $和法向弹性恢复系数e, 来共同描述微观颗粒与壁面的碰撞行为, 并通过假设近壁颗粒速度满足正态分布, 建立了小摩擦和大摩擦两种极限情况下的壁面边界条件. Schneiderbauer等[14]进一步推导了从小摩擦到大摩擦全域统一的边界条件表达式. Zhao等[15]和Yang等[16]考虑颗粒旋转运动, 建立了适用于粗糙颗粒的壁面边界条件, 并发现考虑颗粒旋转效应后, 模型预测与Louge[17]模拟结果的一致性要优于之前的模型. 由此可见, 可靠的壁面边界条件需要关联各种颗粒物性参数和更详尽的颗粒流动状态参数, 但由于壁面附近颗粒属性真实分布函数的缺乏以及三维碰撞过程数学积分求解的复杂, 想要通过理论精确推导出统一的壁面边界条件较为困难. 因而在前期研究中, 通常假设颗粒速度满足正态分布[12-16],并且忽略颗粒旋转效应[12-14]; 而考虑颗粒旋转效应时又会增加额外的旋转变量, 在TFM中需要求解附加的输运方程进行封闭[15-16]. 为此, 本文尝试在常规TFM中对近壁颗粒旋转变量进行局部代数型封闭, 从而避免在整个流场中求解旋转变量的输运方程.

近年来, 随着计算机技术不断提高, 使得机器学习等人工智能技术也快速发展, 其中作为机器学习研究热门之一的人工神经网络模型(ANN)已经发展得较为完善. 人工神经网络是对人脑组织和运行机制的某种抽象、简化和模拟, 根据已知的一系列训练集, 利用黑箱式学习方法的一种高效的数据处理和预测方法, 具有效率高、联想记忆、预测效果好等优点, 因此, 人工神经网络模型逐渐应用于不同学科的研究之中. 如胡洲等[18]采用神经网络建立非球形散体颗粒的休止角模型, 发现休止角随颗粒形状变量、摩擦因数的增加都呈现增大的趋势, 与现有研究结果一致; 闫盛楠等[19]采用人工神经网络模型, 对非球形颗粒气固曳力系数进行了预测及分析, 并将模拟结果同文献中的实验数据进行对比分析, 结果表明, 人工神经网络可用于非球形颗粒气固曳力系数的预测研究.

因此, 本文拟采用DEM方法对颗粒流进行直接模拟, 获得壁面附近颗粒微观运动数据和壁面与颗粒直接作用力; 在此基础上统计分析颗粒的宏观运动特征, 为颗粒动力学理论推导的基本假设提供参考, 并基于人工神经网络模型挖掘颗粒旋转运动变量与颗粒物性参数和平动运动变量之间的隐含关系. 旨在为常规TFM方法建立更加可靠的壁面边界条件寻求可行的方法和基础数据.


1.
数学模型


在DEM模拟中, 每个颗粒的运动受牛顿第二定律支配, 质量为$ {m_i} $的颗粒的平动和旋转运动可由下式描述[20]







$${m_i}frac{{{
m{d}}{{boldsymbol{v}}_i}}}{{{
m{d}}t}} = sumlimits_j {left( {{{boldsymbol{F}}_{n,ij}} + {{boldsymbol{F}}_{t,ij}}}
ight)} + {m_i}{boldsymbol{g}} $$
(1)







$${I_i}frac{{{
m{d}}{{boldsymbol{omega}} _i}}}{{{
m{d}}t}} = sumlimits_j {left( {{{boldsymbol{R}}_{c,ij}} times {{boldsymbol{F}}_{t,ij}} - {mu _r}{R^ * }left| {{{boldsymbol{F}}_{n,ij}}}
ight|frac{{{{boldsymbol{omega}} _{r,ij}}}}{{left| {{{boldsymbol{omega}} _{r,ij}}}
ight|}}}
ight)}$$
(2)

式中, $ {{boldsymbol{v}}_i} $, $ {{boldsymbol{omega }}_i} $和$ {I_i} $分别表示颗粒i的平动速度、旋转速度和惯性矩, $ {boldsymbol{g}} $为重力加速度. $ {{boldsymbol{F}}_{n,ij}} $和$ {{boldsymbol{F}}_{t,ij}} $分别表示颗粒j施加在颗粒i上的法向和切向接触力. $ {{boldsymbol{R}}_{c,ij}} $为从颗粒i的中心到颗粒i与颗粒j之间接触点的矢量. 式(2)中的最后一项为滚动摩擦引起的阻力扭矩. $ {mu _r} $为滚动摩擦系数, $ {R^ * } = {{{R_i}{R_j}} / {left( {{R_i} + {R_j}}
ight)}} $为等效半径, $ {{boldsymbol{omega}} _{r,ij}} = {{boldsymbol{omega}} _i} - {{boldsymbol{omega}} _j} $为相对角速度.

根据Hertz?Mindlin接触理论[21-22], 法向接触力可以由下式给出







$$begin{split}{boldsymbol{F}}_{n,ij}^{} = &frac{4}{3}{E^ * }sqrt {{R^ * }{delta _{n,ij}}} {delta _{n,ij}}{{boldsymbol{n}}_{ij}} - hfill sqrt {frac{5}{6}} frac{{2ln e}}{{sqrt {{{ln }^2}e + {{text{π}} ^2}} }}cdot&sqrt {2{m^ * }{E^ * }sqrt {{R^ * }{delta _{n,ij}}} } left( {{{boldsymbol{v}}_{n,ij}} cdot {{boldsymbol{n}}_{ij}}}
ight){{boldsymbol{n}}_{ij}}end{split}$$
(3)

式中, $ {{boldsymbol{n}}_{ij}} $是指从颗粒j的中心指向颗粒i的中心的单位矢量, $ {{boldsymbol{v}}_{n,ij}} $和$ {delta _{n,ij}} $分别为两个颗粒之间的法向相对速度矢量和接触重叠量, $ e $为弹性恢复系数; $ {m^ * }{{ = {m_i}{m_j}} / {left( {{m_i} + {m_j}}
ight)}} $为等效质量, ${E^ * } = {{E_i}{E_j}} / left[ left( {1 - nu _j^2}
ight){E_i}
ight.$$+ left. left( {1 - nu _i^2}
ight){E_j}
ight]$为等效杨氏模量, $ {nu _i} $和$ {nu _j} $为颗粒i和颗粒j的泊松比.

相应的切向接触力由下式给出







$$begin{split}{{boldsymbol{F}}_{t,ij}} =& 8{G^ * }sqrt {{R^ * }{delta _{n,ij}}} {{boldsymbol{delta}} _{t,ij}}{{boldsymbol{t}}_{ij}} - hfillsqrt {frac{5}{6}} frac{{2ln e}}{{sqrt {{{ln }^2}e + {{text{π}} ^2}} }} &sqrt {8{m^ * }{G^ * }sqrt {{R^ * }{delta _{n,ij}}} } left( {{{boldsymbol{v}}_{t,ij}} cdot {{boldsymbol{t}}_{ij}}}
ight){{boldsymbol{t}}_{ij}}end{split}$$
(4)

式中, $ {{boldsymbol{t}}_{ij}} $, $ {{boldsymbol{v}}_{t,ij}} $和$ {delta _{t,ij}} $分别表示两颗粒之间切向的单位矢量、相对速度矢量和重叠量, ${G^ * } = {{G_i}{G_j}} / left[ {left( {2 - {nu _j}}
ight){G_i} }
ight.$$+left. {left( {2 - {nu _i}}
ight){G_j}}
ight]$为等效剪切模量.

切向力的大小受到库仑摩擦定律的限制. 如果式(3)和式(4)计算结果满足以下条件







$$left| {{{boldsymbol{F}}_{t,ij}}}
ight| > mu left| {{{boldsymbol{F}}_{n,ij}}}
ight|$$
(5)

式中, $ mu $为摩擦系数, 则碰撞接触点上会发生滑动, 此时切向接触力按下式计算







$$ {{boldsymbol{F}}_{t,ij}} = mu left| {{{boldsymbol{F}}_{n,ij}}}
ight|{{boldsymbol{t}}_{ij}} $$
(6)


2.
模拟结果与讨论



2.1
模拟工况


在研究颗粒与壁面作用关系时, 可以选择相对简单的模拟对象, 如滚筒、斜槽[23]或者库埃特(Couette)流[17]. 本文以石油化工中常见的滚筒为模拟对象. 事实上, 已经有许多****对滚筒进行各种实验和模拟研究, 如顾丛汇等[24]通过实验和数值模拟研究丝状散体颗粒在滚筒内的停留时间; 胡陈枢等[25]采用DEM方法对滚筒内二元颗粒在不同转速下的运动进行模拟; 张立栋等[26]采用DEM方法研究滚筒内构件对二元颗粒体系运动混合的影响,并分析其增混机理. 但多数研究都是关注滚筒内部颗粒宏观运动特征, 然而颗粒和壁面作用通常至关重要[27-29], 对滚筒而言, 颗粒和壁面间的相互作用驱动着整个颗粒系统运动.

本文模拟的滚筒为Parker等[30]的实验装置. 为了最大限度的接近实验, 模拟采用与实验一致的全尺寸, 颗粒则简化为均一直径. 滚筒壁和颗粒材料均为有机玻璃, 相关结构和物性参数如表1所示. 模拟运行18 s, 时间步长为5.6 × 10?6 s, 为避免初始效应的影响, 用于统计的数据样本取自8 ~ 18 s.




表
1
模拟参数



Table
1.
Simulation parameters



table_type1 ">
ParametersValue
drum diameter, D/m 0.1
drum length, L/m 0.65
drum fill level/% 35
total number of particles 72000
particle diameter, d/m 0.003
particles density, ρ/(kg·m?3) 2500
Young modulus, E/(N·m?1) 1.0 × 107
Poisson ratio, $ nu $ 0.29
restitution coefficient, e 0.9
sliding friction coefficient, μ 0.7
rolling friction coefficient, μr 0.01





下载:
导出CSV
|显示表格



图1为瞬时颗粒分布, 其中颜色表示速度大小. 图中颗粒速度在轴向具有较好的相似性, 但在两端面附近表层颗粒速度略有增加. Zhang等[31]研究表明端壁摩擦对颗粒轴向扩散具有增强效应, 但其研究的滚筒长径比为1, 而本模拟的滚筒长径比为6.5, 因此端壁摩擦导致的轴向非均匀性较弱, 模拟结果在轴向上具有较好的对称性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-313-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure1" />



图
1
滚筒内的颗粒分布



Figure
1.
Particle distribution in the drum



下载:
全尺寸图片
幻灯片


图2为各转速下滚筒最低点偏右θ = 30°位置上颗粒切向速度模拟和实验结果对比图. 从图2(a)中可以看出, 摩擦系数取为0.7时得到的切向速度曲线与实验结果一致; 图2(b)中针对不同转速下也获得较好的预测结果, 特别是在近壁区域, 模拟预测与实验结果吻合较好. 通过DEM模拟获得接近物理实际的结果, 将保障后续数据统计分析结果的可靠性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-313-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
切向速度与实验数据的比较



Figure
2.
Comparison of the tangential velocity with experiment data



下载:
全尺寸图片
幻灯片


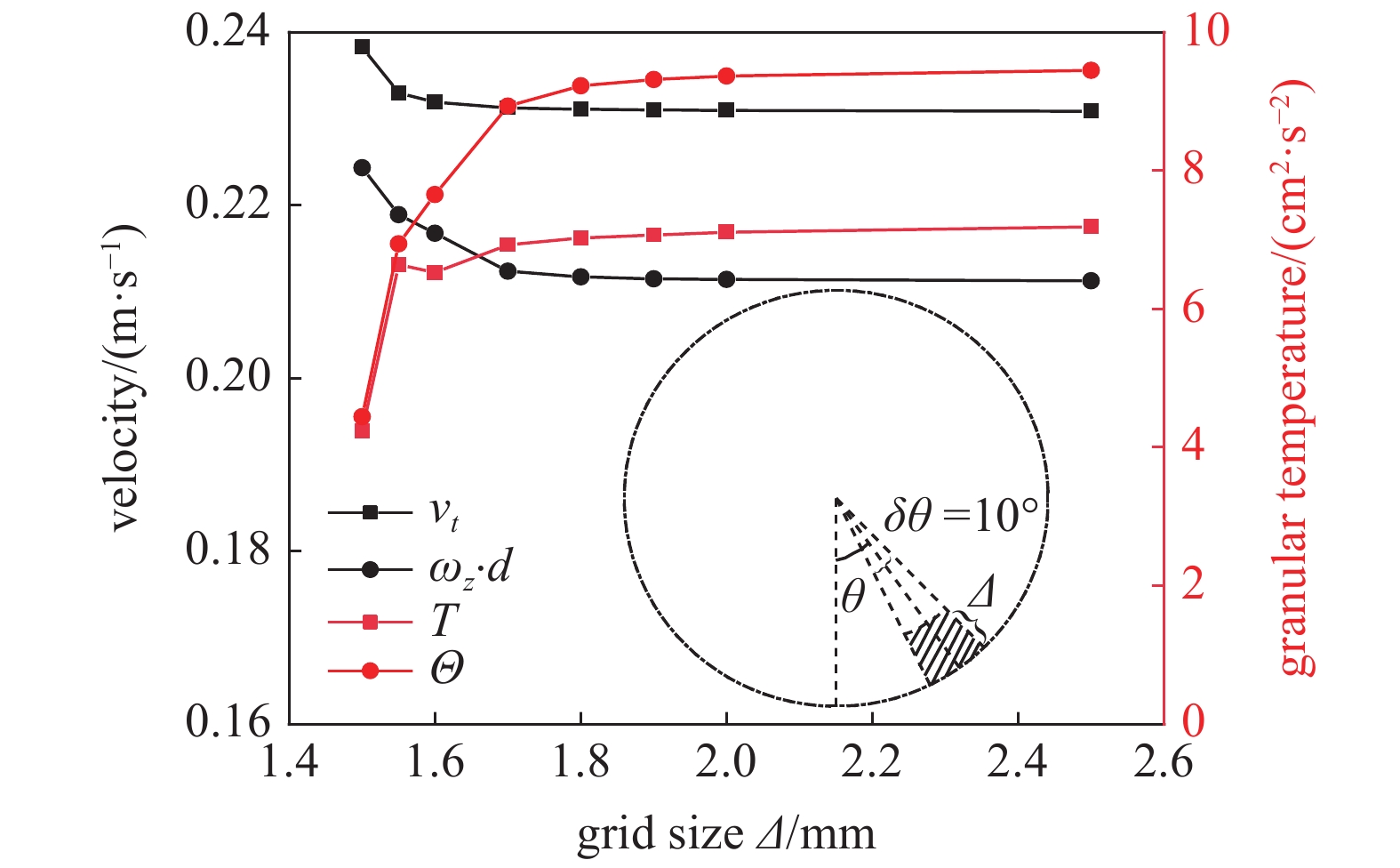
在统计近壁处颗粒信息时, 为保证结果的独立性, 选取贴壁网格应该尽量要小, 同时又要保证一定的颗粒数以减小统计误差. 考虑到颗粒在滚筒轴向的对称性, 贴壁网格在轴向取滚筒全长, 而在横截面上则如图3阴影区域所示, 由周向尺寸δθ和径向尺寸Δ共同确定. 其中径向尺寸Δ决定了统计颗粒靠近壁面的程度, 对近壁颗粒的统计特性更为重要. 图3显示了贴壁网格的径向尺寸Δ与平均颗粒变量(颗粒速度$ {v_t} $和$ {omega _z} $以及颗粒温度$ T $和$ varTheta $)的关系. 其中颗粒温度是颗粒速度脉动程度的度量, 颗粒平动温度和旋转温度的定义和统计公式如下所示



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-313-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
网格大小与平均颗粒变量的关系



Figure
3.
Relationship between mesh size and averaged particle variables



下载:
全尺寸图片
幻灯片








$$begin{split}T &= frac{1}{3}leftlangle {left( {{boldsymbol{v}} - bar {boldsymbol{v}}}
ight) cdot left( {{boldsymbol{v}} - bar {boldsymbol{v}}}
ight)}
ight
angle hfill &= frac{1}{{3N}}sumlimits_{i = 1}^N {left[ {{{left( {{v_{x,i}} - {{bar v}_x}}
ight)}^2} + {{left( {{v_{y,i}} - {{bar v}_y}}
ight)}^2} + {{left( {{v_{z,i}} - {{bar v}_z}}
ight)}^2}}
ight]}end{split}$$
(7)







$$begin{split}varTheta &= frac{I}{{3m}}leftlangle {left( {{boldsymbol{omega}} - bar {boldsymbol{omega}} }
ight) cdot left( {{boldsymbol{omega}} - bar {boldsymbol{omega}} }
ight)}
ight
angle hfill &{text{ }} = frac{I}{{3mN}}sumlimits_{i = 1}^N {left[ {{{left( {{omega _{x,i}} - {{bar omega }_x}}
ight)}^2} + {{left( {{omega _{y,i}} - {{bar omega }_y}}
ight)}^2} + {{left( {{omega _{y,i}} - {{bar omega }_z}}
ight)}^2}}
ight]}end{split}$$
(8)

式中, $ bar {boldsymbol{v}} $和 $ bar {boldsymbol{omega}} $分别是颗粒平动和旋转速度的平均值, 运算符$ leftlangle {}
ight
angle $表示系综平均, $ N $为贴壁网格内的颗粒样本总数. 从图3中可以看出, 当贴壁网格周向尺寸δθ = 10°, 径向尺寸Δ达到1.8 mm时平均颗粒速度和温度都趋于稳定, 因此选取贴壁网格大小δθ = 10°和Δ = 1.8 mm进行后续分析研究.


2.2
颗粒微观运动



2.2.1
平动速度分布

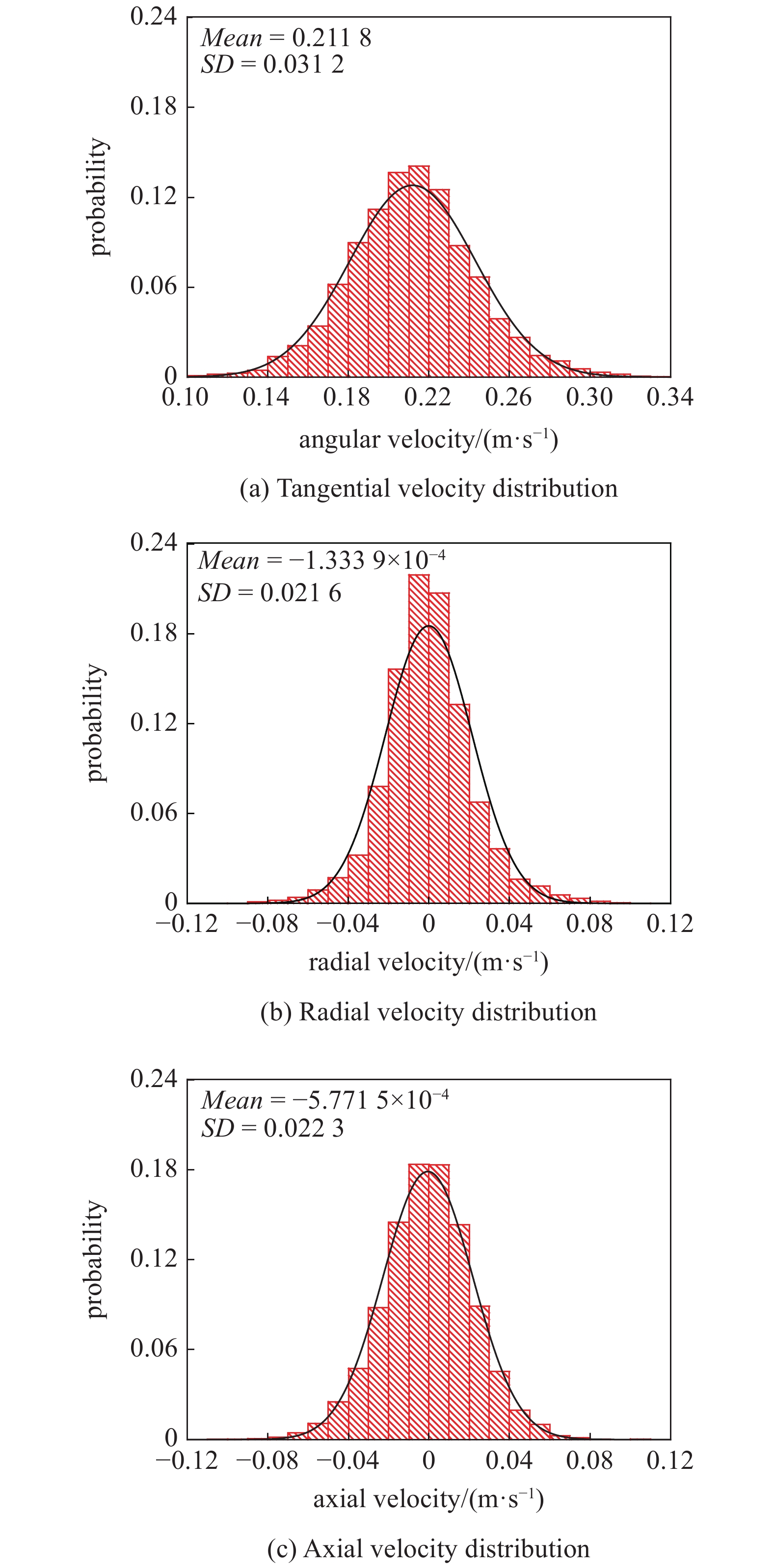
在欧拉方法中, 通常由颗粒动力学理论提供描述颗粒运动特性的本构关系. 颗粒动力学借鉴分子运动论, 假设颗粒运动速度近似满足正态分布, 颗粒壁面边界条件也是基于这样的假设[13]. 对颗粒运动信息进行统计分析, 发现近壁处颗粒的平动速度的确较好地符合正态分布, 如图4所示. 图中统计参数取自滚筒最低点偏右θ = 30°贴壁网格(网格见图3)内的颗粒. 由于受到壁面剪切作用, 切向的颗粒平动速度均值和标准差SD最大; 而在壁面阻碍和轴向对称性作用下, 径向和轴向的颗粒平动速度均值趋近零, 标准差SD也相对较小. 颗粒速度分布的标准差反映了颗粒速度脉动的强弱, 显然, 在壁面作用下颗粒速度脉动呈现出各向异性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-313-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
近壁颗粒平动速度分布



Figure
4.
Translational velocity distribution of near-wall particles



下载:
全尺寸图片
幻灯片


在研究壁面边界条件时, 摩擦系数对壁面颗粒运动具有显著影响[31]. 表2给出了不同摩擦系数下, 壁面附近颗粒平动速度分布的统计结果. 其中决定系数R2可以表征正态分布函数拟合的好坏, 取值范围为[0,1], 越接近1表明数据拟合地越好. 由表2可知, 4个摩擦系数下的决定系数均大于0.92, 表明颗粒平动速度都较好地符合正态分布; 此外, 不同摩擦系数下, 切向的标准差SD总是最大的, 表明颗粒平动速度脉动存在各向异性[32].




表
2
平动速度分布的标准差和决定系数



Table
2.
Standard deviation and determination coefficient of translational velocity distribution



table_type1 ">
μ0.30.50.70.9
SDt0.023770.030480.031220.02929
SDr0.013120.020870.021570.02168
SDz0.01890.020230.022330.02215
Rt20.935130.963930.988870.99515
Rr20.926830.931840.961790.97895
Rz20.985240.996930.995750.99548





下载:
导出CSV
|显示表格



随着摩擦系数的减小, 各个方向的标准差SD有减小的趋势; 当摩擦系数降为0.3时, 由于颗粒与壁面的摩擦作用减小, 颗粒受壁面剪切激发的程度也相对减弱, 颗粒速度脉动也因此减弱. 这在颗粒动力学理论中表现为颗粒从宏观运动中获得的能量减小, 从而导致颗粒温度下降. 此外, 摩擦系数减小后, 除轴向速度外, 切向和径向速度的决定系数也明显减小, 即正态分布假设的可靠性有所减弱; 这表明近壁颗粒速度分布的主要影响因素仍然是壁面的径向阻碍作用, 其次才是壁面切向的摩擦剪切作用. 因此, 在颗粒动力学理论中考虑颗粒与壁面作用时, 引入颗粒平动速度正态分布假设基本上是合理的, 但更精细的模型还应进一步考虑颗粒平动速度脉动的各向异性.


2.2.2
旋转速度分布

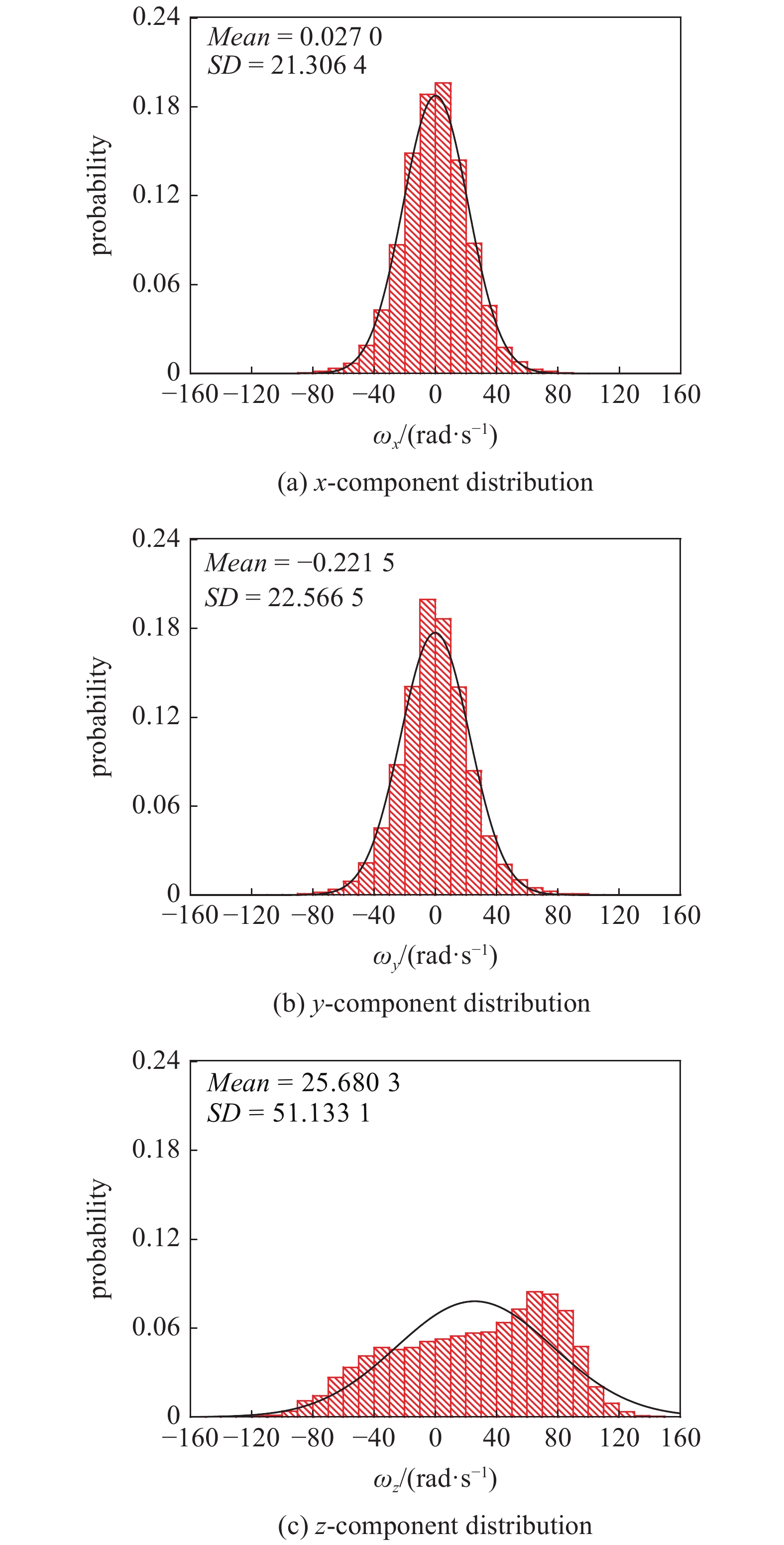
滚筒最低点偏右θ = 30°贴壁网格内颗粒旋转速度分布如图5所示, 其中$ {omega _x} $和$ {omega _y} $两个旋转速度可以通过坐标旋转得到切向和径向旋转速度, 因此它们的分布规律共同体现了切向和径向旋转速度分布特征. 由图5可知, x和y方向上旋转速度较好的满足正态分布, 且均值接近零、标准差SD也大小相当; 但轴向$ {omega _z} $均值和标准差都相对较大,并且离正态分布有较大的偏离. 因此, 在动力学理论中直接将颗粒旋转速度假设为正态分布, 将产生一定的误差. 根据Schneiderbauer等[14]研究, 颗粒在壁面上的旋转速度$ {omega _z} $主要由颗粒与壁面的平动滑移速度$ {V_{{text{slip}}}} = {bar v_t} - {v_{{text{wall}}}} $驱动, 如果颗粒速度满足正态分布, 则$ {omega _z} approx {{mu {V_{{text{slip}}}}} / d} $. 根据图4中的平动速度均值及滚筒转速可以计算出$ {omega _z} approx 30;{{{text{rad}}} / {text{s}}} $, 与模拟统计均值约25.7 rad/s相比误差明显.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-313-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
近壁颗粒旋转速度分布



Figure
5.
Rotational velocity distribution of near-wall particles



下载:
全尺寸图片
幻灯片


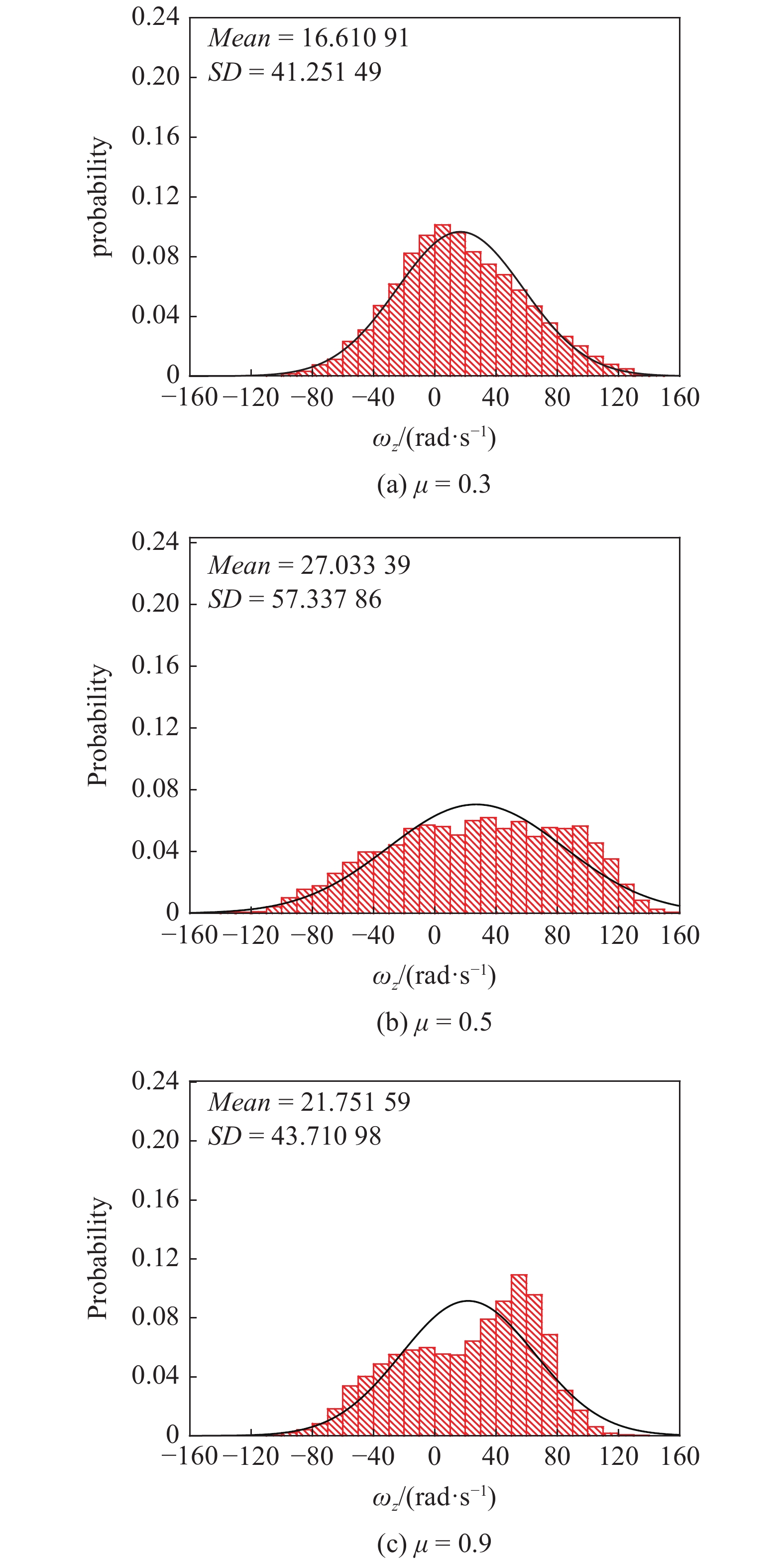
图6为摩擦系数为0.3, 0.5和0.9时, 颗粒轴向旋转速度分布. 结合图5(c),可以发现随着摩擦系数的提高, 颗粒轴向旋转速度$ {omega _z} $分布逐渐偏离正态分布; 在摩擦系数为0.9时, $ {omega _z} $分布明显趋近于双峰分布. 在Parker等[30]的实验分析中, 对Δ = 6 mm的贴壁网格也统计出双峰分布的结果, 并且双峰效应随着滚筒转速的增加而增强; 其解释为贴壁网格径向尺寸为6 mm至少包含两层直径为3 mm的颗粒, 不同层颗粒因受壁面剪切影响程度不同而具有各自不同的旋转特性, 从而导致在Δ = 6 mm的贴壁网格中出现双峰分布. 而本文贴壁网格Δ = 1.8 mm, 所统计颗粒都贴近壁面, 出现双峰分布的主要原因仍是剪切效应; 此时, 贴壁网格内的颗粒受到下层壁面和上层颗粒的两面剪切, 不同摩擦系数下两面剪切的影响程度不同, 当摩擦系数增大时, 两面剪切差异增加从而产生双峰结果.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-313-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
不同摩擦系数下的近壁颗粒轴向旋转速度分布



Figure
6.
Axial rotational velocity distribution of near-wall particles under different friction coefficients



下载:
全尺寸图片
幻灯片


表3为不同摩擦系数下的颗粒旋转速度统计分析结果. 从表3中可以看出, 摩擦系数为0.3时, 旋转速度分布的拟合决定系数接近1; 但随着摩擦系数增加, 轴向旋转速度分布的拟合决定系数明显减小, 摩擦系数在0.5, 0.7和0.9时, 拟合决定系数小于0.9, 表明其严重偏离正态分布, 这与图6旋转速度的直观分布是一致的. 同时, 不同摩擦系数下, 轴向旋转速度分布的标准差SD均明显大于其他两个方向, 表现出较强的各向异性. 总的来说, 切向和径向的旋转速度分布仍然较好的满足正态分布, 但轴向的旋转速度分布随着摩擦系数的增加越偏离正态分布. 因此, 与颗粒平动速度分布不同, 在动力学理论中将壁面附近颗粒旋转速度假设为正态分布需谨慎.




表
3
旋转速度分布的标准差和决定系数



Table
3.
Standard deviation and determination coefficient of rotational velocity distribution



table_type2 ">
μ0.30.50.70.9
SDX11.9036818.6548221.3064321.80627
SDY15.8622922.5867622.5665221.88801
SDZ41.2514957.3378651.1331343.71098
R2X0.986820.992910.995690.99535
R2Y0.990720.984690.985890.98491
R2Z0.977120.870480.767090.72841





下载:
导出CSV
|显示表格



2.3
无因次旋转温度


在颗粒动力学理论中, 颗粒温度将单个颗粒的微观小尺度脉动行为与大量颗粒所表现的宏观流动性质相关联, 出现在颗粒黏度、压力和扩散系数等参数的本构关系中. 实际颗粒碰撞过程中, 平动能量与旋转能量会相互转化, 因此颗粒平动温度与旋转温度应相互耦合. 颗粒与壁面作用时, 旋转温度的影响是不可忽略的[14], 但常规欧拉双流体模型中并未求解颗粒旋转温度, 为此需建立颗粒旋转温度的代数型封闭关联式. Jenkins和Zhang[33]曾将球形颗粒无因次旋转温度$ lambda = 2.5{varTheta / T} $关联为颗粒物性参数的函数; Zhao等[15]曾将λ关联为颗粒物性参数和无因次滑移速度的函数. 但这些封闭关联式, 主要是根据理论简化假设或简单数据拟合, 可能忽略了某些起作用的因素. 通过DEM模拟, 可以得到大量的近壁颗粒运动信息, 传统方法在处理这些数据时较为吃力; 而数据挖掘方法不仅能够处理大量数据, 同时能够探索数据之间的隐藏规律, 神经网络就是数据挖掘常用的一种方法. 因此本文将DEM模拟得到的颗粒运动信息包括颗粒速度和颗粒温度等作为神经网络的输入, 采用人工神经网络进行颗粒无因次旋转温度的预测学习, 尝试建立颗粒无因次旋转温度的封闭关联式.

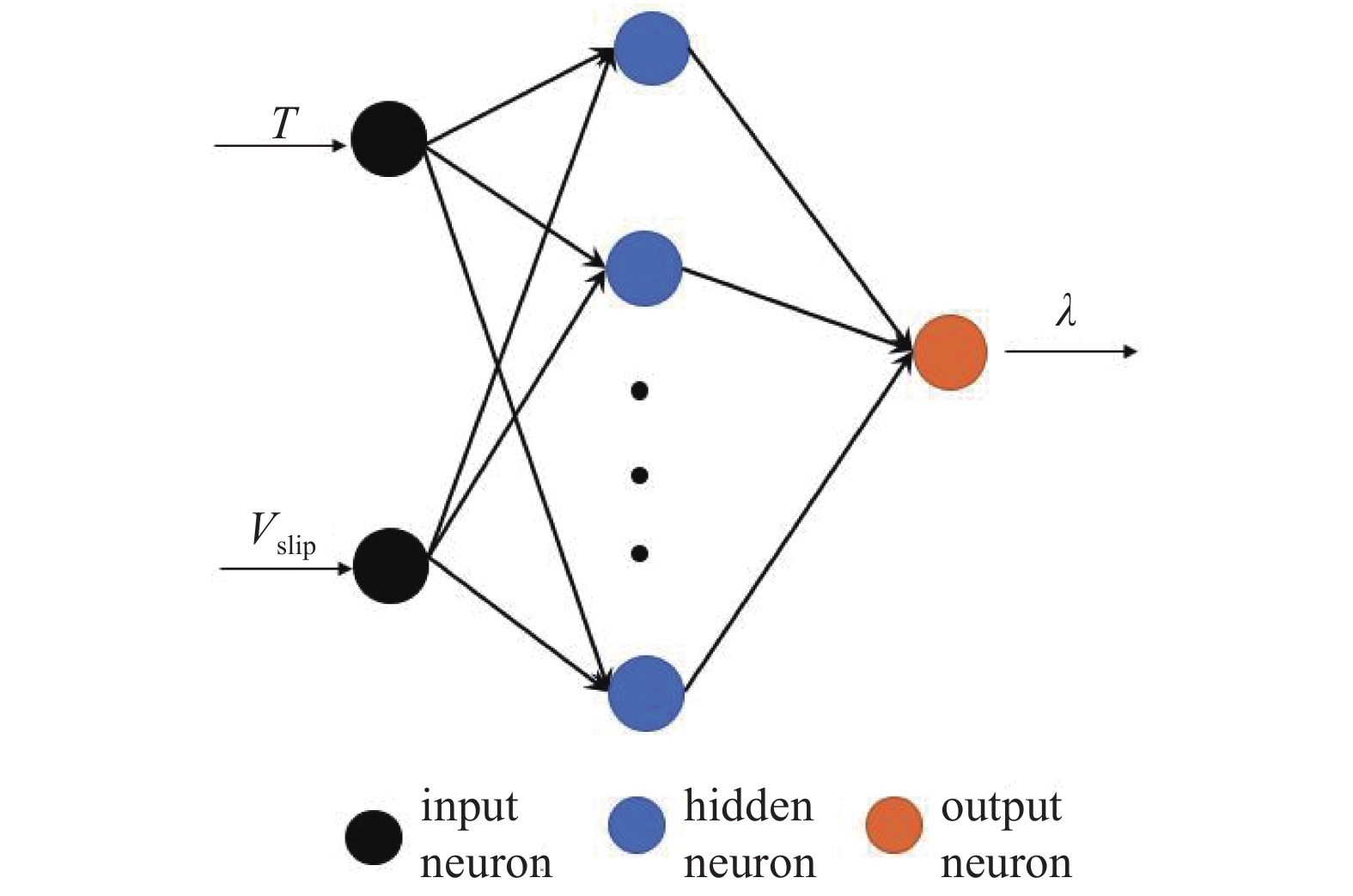
图7为本文采用的BP神经网络结构示意图. BP神经网络是一种多层的前馈神经网络, 其主要的特点是: 信号是前向传播的, 而误差是反向传播的, 传播过程主要分为两个阶段, 第一阶段是信号的前向传播, 从输入层经过隐含层, 最后到达输出层; 第二阶段是误差的反向传播, 从输出层到隐含层, 最后到输入层, 依次调节隐含层到输出层的权重和偏置, 输入层到隐含层的权重和偏置. 每层的神经元节点通过权值与偏置与下一层的节点相连接, 输入信号通过激活函数转换成输出结果, 最后网络输出如下



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-313-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
本文使用的神经网络结构



Figure
7.
Structure of neural network used in present work



下载:
全尺寸图片
幻灯片








$${y_p} = fleft( {sumlimits_{q = 1}^Q {{x_{pq}}{w_{pq}} + {b_p}} }
ight)$$
(9)

式中, $ {y_p} $为输出值, 对于隐含层下标$ p $为神经元序号, $ {x_{pq}} $则为第$ p $个神经元的$ q $个输入, $ {w_{pq}} $和$ {b_p} $为对应的权值和偏置, $ Q $为该层输入值总数. $ f $是对应层的激活函数, 本文隐含层使用Sigmoid函数, 输出层使用Linear函数.

当神经网络输出值与目标值$ hat y $不等时, 存在输出误差$ E $, 定义如下







$$ E = frac{1}{2}{left( {{y_p} - hat y}
ight)^2} $$
(10)

为了减小误差$ E $, BP神经网络使用梯度下降反向传播算法对输入与隐含层间以及隐含层与输出层间的权值和偏置进行调整.

本研究输入参数为平动温度$ T $和滑移速度$ {V_{{text{slip}}}} $, 预期输出值为无因次旋转温度$ lambda $. 为获取大范围滑移速度样本, 选取角度θ 为0°, 10°, 20°, 30°, 40°, 50°和60°的贴壁网格. 为加快收敛速度, 采用最大?最小标准化方法处理训练样本. 训练时, 以随机数对神经网络权值和偏置进行赋值, 然后根据误差$ E $反向传播对权值与偏置进行优化调整. 本文BP神经网络模型的具体细节见表4所示, 训练完的代数模型数学表达式如下






$$ begin{split} & {boldsymbol{lambda} } = {boldsymbol{W} }dfrac{1}{ {1 + { {
m{e} }^{ - ({W_x}x + {b_1})} } } } + {b_2} & {boldsymbol{x}} = left[ T ;; {{V_{{text{slip}}}}}
ight]&{{boldsymbol{b}}_1}{
m{ = [0}}{
m{.028;820;17,;0}}{
m{.028;820;17,;0}}{
m{.028;820;17, }}&qquad{
m{0}}{
m{.028;820;17,;0}}{
m{.028;820;17,;0}}{
m{.028;820;17, }}&qquad{
m{0}}{
m{.028;820;17,;0}}{
m{.028;820;17]}}&{{{b}}_2}{
m{ = 0}}{
m{.718;393;26}}&{{boldsymbol{W}}_x} = {[{W_1};;{W_2}]^{
m{T}}}&{boldsymbol{W}_1}{
m{ = [ - 0}}{
m{.522;647;14,; - 0}}{
m{.522;647;14,; - 0}}{
m{.522;647;14, }}&qquad{
m{ - 0}}{
m{.522;647;14,; - 0}}{
m{.522;647;14,; - 0}}{
m{.522;647;14, }}&qquad{
m{ - 0}}{
m{.522;647;14,; - 0}}{
m{.522;647;14]}}end{split}$$







$$ begin{split} &{boldsymbol{W}_2}{
m{ = [0}}{
m{.087;477;71,;0}}{
m{.087;477;71,;0}}{
m{.087;477;71, }}&qquad{
m{0}}{
m{.087;477;71,;0}}{
m{.087;477;71,;0}}{
m{.087;477;71, }}&qquad{
m{0}}{
m{.087;477;71,;0}}{
m{.087;477;71]}}&boldsymbol{W}{
m{ = [0}}{
m{.613;576;85,; 0}}{
m{.613;576;85,; 0}}{
m{.613;576;85,}}&qquad{
m{0}}{
m{.613;576;85,;0}}{
m{.613;576;85,;0}}{
m{.613;576;85, }}&qquad{
m{0}}{
m{.613;576;85,; 0}}{
m{.613;576;85}}{{
m{]}}^{
m{T}}}end{split}$$
(12)




表
4
人工神经网络模型的细节



Table
4.
Details of the artificial neural network model



table_type1 ">
No.ParticularsSpecifications
1network typeBP neural network
2activation functionsigmoid and linear
3error calculationMSE
4number of input layer unit2
5input parametersT, Vsilp
6number of output layer unit1
7output parametersλ
8number of hidden layer unit8
9learning rate0.0002
10training times600
11training set size2060
12test set size560





下载:
导出CSV
|显示表格



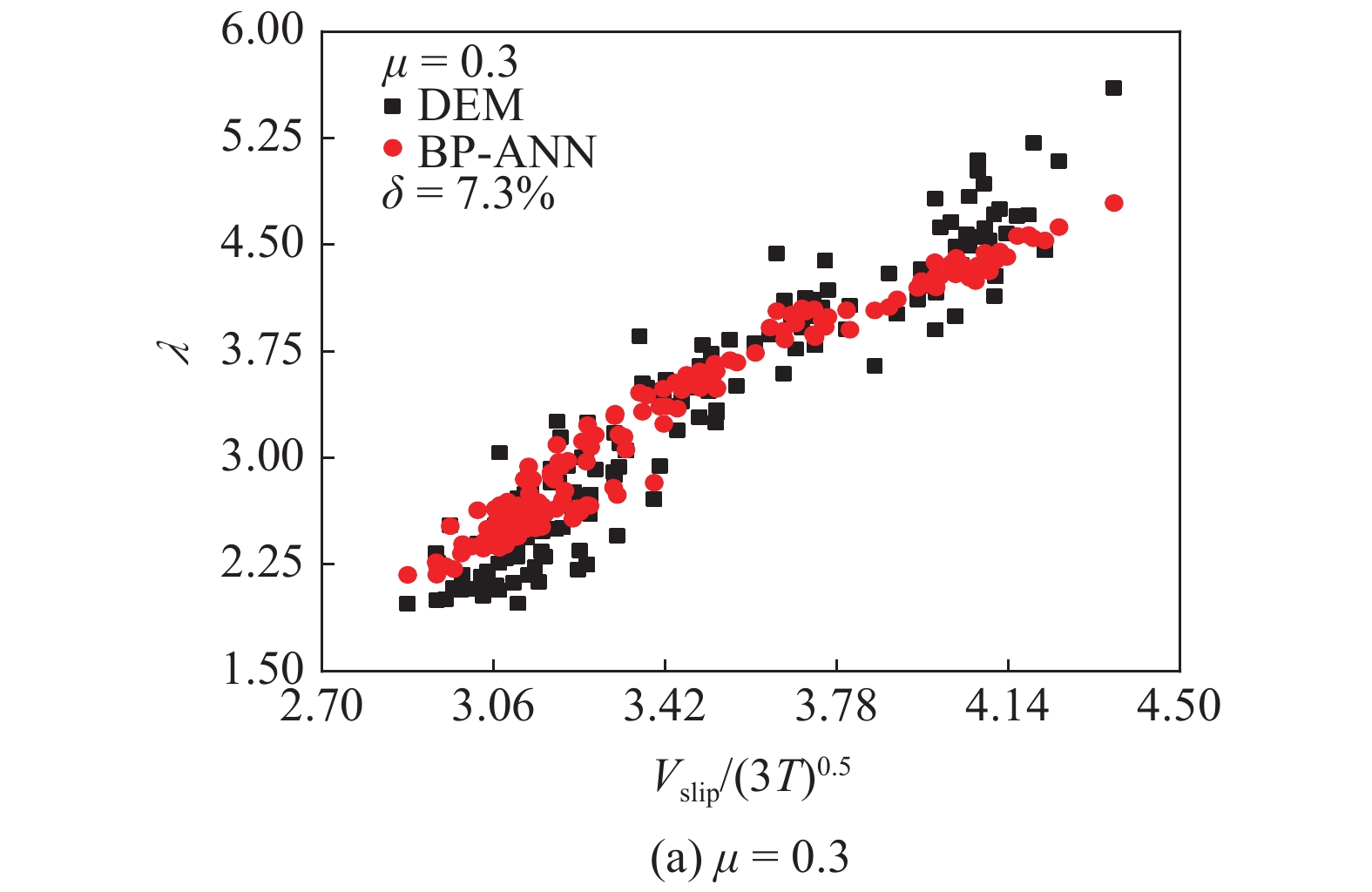
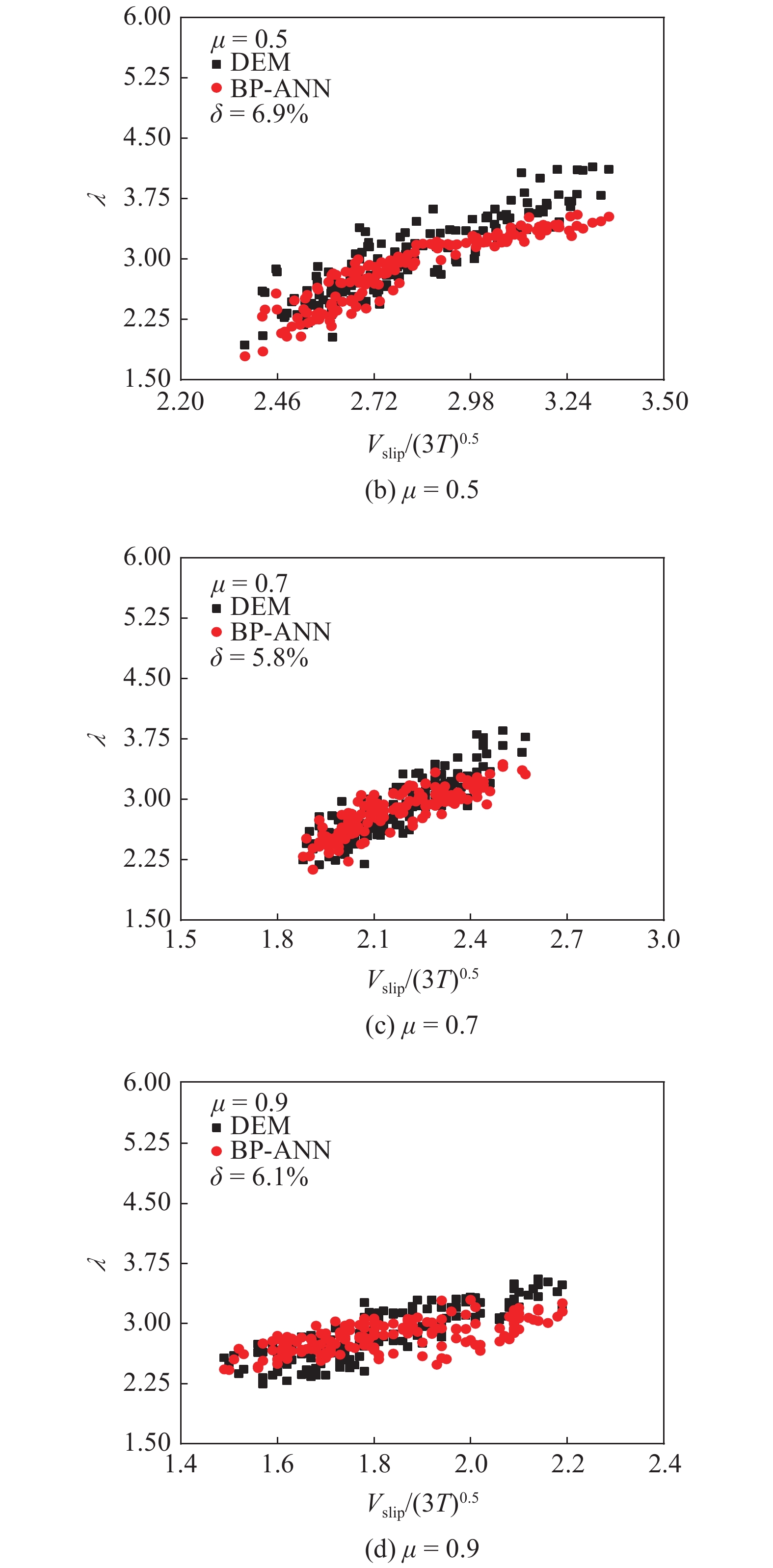
图8为模型预测结果与DEM统计结果的对比, 其中红色圆点为BP神经网络预测的无因次旋转温度λ, 黑色的正方形为DEM模拟结果, δ为统计的平均相对误差. 由图可见, 相同摩擦系数下, 无因次旋转温度随无因次滑移速度增大呈现出增长趋势; 且相同无因次滑移速度下, 随着摩擦系数的增加, 无因次旋转温度也表现为增长趋势. 此外, 即使样本数据点较为离散, BP神经网络预测结果的平均相对误差依然较小, 表明采用神经网络模型建立颗粒旋转温度的代数型封闭关联式是可行的.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-313-8-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8-1" />



8
无因次旋转温度的模型预测与DEM统计结果对比



8.
Comparison of predicted dimensionless rotational temperature with DEM results



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-313-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
无因次旋转温度的模型预测与DEM统计结果对比(续)



Figure
8.
Comparison of predicted dimensionless rotational temperature with DEM results (continued)



下载:
全尺寸图片
幻灯片



2.4
壁面处颗粒应力分析


欧拉双流体模型中, 颗粒壁面边界条件主要是通过壁面上颗粒相法向应力来关联切向应力. 因此, 通过DEM模拟并统计分析壁面所受颗粒的切向和法向应力, 可以为双流体模型中颗粒壁面边界条件的构建提供数据参考.

图9给出了不同摩擦系数下, 壁面上切向和法向应力比与颗粒无因次滑移速度之间的关系. 由图可知, 当摩擦系数为0.3和0.5时, 应力比随无因次滑移速度的增加而增大, 并趋近于摩擦系数值; 当摩擦系数增大到0.7和0.9时, 无因次滑移速度的增加到一定程度后不再增加, 应力比出现非单值型分布, 这和图中Louge[17]针对摩擦系数0.75和 ∞ 两种状态下给出的分布趋势是一致的. 本文统计结果和Louge的数据分布规律相同, 但数值上存在差异, 并随摩擦系数增加差异变大, 其原因可能在于Louge的模拟中壁面上镶嵌有半球体, 增大了颗粒与壁面的切向作用.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-313-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
不同摩擦系数下壁面切向与法向应力比



Figure
9.
Wall stress ratio under different friction



下载:
全尺寸图片
幻灯片


Johnson和Jackson壁面边界条件采用简单常数来描述应力比与无因次滑移速度的关系, 这与实际数据是不相符的, 只能作为一定范围内的近似或平均. Zhao等[34]对近壁颗粒平动和旋转速度采用各向同性的正态分布, 推导了应力比与滑移速度理论公式, 对比Johnson和Jackson壁面边界条件即可将光滑因子表示如下[15]







$$begin{split}phi = &mu frac{{1 + e}}{2}cot varPhi cdot hfill &left[ {frac{1}{{left( {lambda + 1}
ight){{cot }^2}varPhi + 1}} + frac{{arctan left( {sqrt {lambda + 1} cot varPhi }
ight)}}{{sqrt {lambda + 1} cot varPhi }}}
ight]end{split}$$
(11)

其中, $ cot varPhi = {{2left( {1 + beta }
ight)} / {left[ {7mu left( {1 + e}
ight)}
ight]}} $.

将神经网络模型预测的无因次旋转温度代入上述光滑因子, 再结合Johnson和Jackson壁面边界条件, 可以计算出壁面上应力比如图9中实线所示. 当摩擦系数为0.3时, 由表2和表3可知颗粒速度分布的确较好的符合正态分布, 因此公式预测结果与DEM统计结果相吻合; 但当摩擦系数提高后, 由于颗粒旋转速度偏离正态分布, 公式预测和DEM统计结果偏差增加.


3.
结 论


采用DEM方法数值模拟了滚筒内颗粒流动状况. 通过统计和ANN算法研究了壁面附近微观颗粒的运动特征, 得出了以下结论.

(1) 颗粒平动速度都基本符合正态分布, 小摩擦系数下颗粒旋转速度也满足正态分布, 但随着摩擦系数的提高, 壁面剪切产生的轴向旋转速度分布偏离正态分布; 同时颗粒平动和旋转速度脉动呈现较强的各向异性.

(2) 无因次旋转温度和无因次滑移速度存在一定的正相关, 并受摩擦系数的影响. 将滑移速度和颗粒平动温度作为输入, 采用人工神经网络构建颗粒旋转温度模型, 可以为常规欧拉双流体模型框架下考虑颗粒旋转温度提供代数型封闭.

(3) 壁面与颗粒作用的切向与法向应力比, 受无因次滑移速度和摩擦系数的影响, 摩擦系数增大后, 其理论关系的建立需要考虑更真实的颗粒速度分布, 如非正态分布、各向异性.

相关话题/统计 运动 数据 实验 颗粒
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • Gappy POD方法重构湍流数据的研究
    引言本征正交分解(properorthogonaldecomposition,POD)是一种统计分析、简化数据集的方法.对于一个函数系综,例如在实验中获得的数据,POD可以给出一组模态分解的基,具有很多应用中所需要的良好的性质.其中,最引人注目的就是最优性(optimality),即POD给出了采用 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于深度强化学习算法的颗粒材料应力?应变关系数据驱动模拟研究
    引言在研究泥沙、岩土、粉体等颗粒材料宏观力学行为时,通常在连续介质力学框架下建立其唯象本构模型,通过引入内变量来描述颗粒材料的路径相关、历史相关等特性[1-5].虽然基于连续假设的唯象本构模型在描述颗粒材料宏观力学特性时具备很好的工程适用能力,但是颗粒材料由于其自身的离散特性,具有摩擦性,剪胀性,压 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 亚毫米球体撞击液滴过程实验研究
    引言物体撞击液面广泛存在于自然界和工业过程,如昆虫水上行走、弹丸入水、湿法喷淋除尘、原料油催化裂化等[1-5].撞击过程包含液滴飞溅、空穴发展、毛细波传播、气体携带等复杂的流动现象[6-11].物体与气?液界面的相互作用对上述过程有重要影响,对物体撞击液面行为的研究能够为相关工业过程参数设计提供理论 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 均匀电场中气泡上升特性的实验研究
    引言强化传热技术在能源动力、石油工程、航空航天、化工等领域具有广泛的应用前景,而利用电场进行强化换热,能够有效减小换热器的体积和重量,提高能源利用效率[1-2].电场强化沸腾换热技术通过电场力控制气泡的生成、脱离、变形与运动[3-5],降低气泡脱离尺寸[6-7],加速气泡脱离频率[8],从而实现换热 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 水中开孔腔流激振荡控制实验研究
    引言空腔流激振荡是工程中常遇到的一类问题,它是指流体在流经开口结构时,边界层在开口前缘发生流动分离并形成不稳定的自由剪切层,在满足一定的流速和几何特征条件下,会引起剪切层发生稳定的自持振荡,产生很强的周期脉动压力,并通常引起高幅值纯音噪声辐射、附加阻力甚至是结构疲劳.以往对空腔流激振荡的研究主要集中 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 一种改进的颗粒移动床<i>μ</i>(<i>I</i>)拟流体模型及应用
    引言颗粒移动床在工业生产中具有很广泛的应用,如燃料热解气化[1],烟气除尘[2],高温散料余热回收等[3-4].颗粒移动床内的流动特性是工艺设计与优化运行的重要基础,尚待深入地揭示.现有的描述移动床颗粒流的研究方法有离散元方法(DEM)和连续性假设方法.离散元方法从单个颗粒出发研究每个颗粒与其他颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 倍频激励双转子振动同步机理与实验研究
    引言振动同步可以表征为运动系统根据内部子系统之间的耦合效应调整特征量的变化频率,并使子系统的位移、速度等变量具有一致性和统一性.近年来,由于同步在非线性耦合混沌系统[1-2]、复杂网络系统[3]、多轴控制系统[4-5]、振动筛系统[6-7]等工程技术中具有很高的应用价值和良好的应用前景,已成为国内外 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 椭球颗粒体系剪切过程中自由体积的分布与演化
    引言颗粒物质是由大量离散固体相互作用而形成的复杂体系,在自然界和工业界广泛存在.以水利和岩土工程中的堆石体为例,由于取材方便,且对地形、地质条件有较强的适应性,在堆石坝、路堤、机场高填方地基等工程建设中得到广泛应用.这些工程一旦出现问题和隐患,将会严重威胁人民生命财产安全,因此迫切需要深入研究颗粒材 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 冲击载荷下颗粒材料临边界区域的波动行为及变形特征分析
    引言作为离散颗粒材料的土壤(或岩体),是日常生活中最常见的随机多孔介质,冲击载荷作用下材料的动力学响应对于工程实践和地质灾害防控有着重要的指导意义.注意到应力波的传播行为与介质性质密切相关,基于应力波的行为特征分析可提供一种非侵入式研究颗粒材料性质的途径.因此有非常多的****致力于研究冲击载荷作用 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.