引 言

本征正交分解(proper orthogonal decomposition, POD)是一种统计分析、简化数据集的方法. 对于一个函数系综, 例如在实验中获得的数据, POD可以给出一组模态分解的基, 具有很多应用中所需要的良好的性质. 其中, 最引人注目的就是最优性(optimality), 即POD给出了采用有限模态来刻画一个无限维过程主要成分的最有效的方式.

POD方法由Lumley首次引入到湍流问题的背景中^[1]. 在大部分应用中, POD主要用来分析实验或计算数据以获取其中的主要模态^[2-5], 即拟序结构(coherent structures). 此外, 很多研究采用POD提供的基函数构成的低维子空间来对原始问题建立降维模型^[6-10].

Everson和Sirovich^[11]于1995年首次提出了采用POD来重构存在缺失的(gappy)数据的方法, 即gappy POD. 此后很多****针对不同的问题使用并发展了gappy POD 重构方法^[12-15]. Venturi和Karniadakis^[16]对于圆柱绕流的直接数值模拟数据进行了gappy POD重构研究. 通过引入适当修正, 他们提升了gappy POD的鲁棒性和精度. 同时, 研究了流场缺失率大小对gappy POD重构的影响, 并给出了相关解释. Gunes等^[17]对比了gappy POD和克里格(Kriging)插值对于非稳态圆柱绕流数据的重构效果, 发现当流场的时间分辨率不高或者空间缺失率较大时, 克里格插值比gappy POD重构更加有效.

在前人的工作中, 以下两个因素对gappy POD的影响均未被系统研究. 第一, 数据本身的复杂程度. 当雷诺数Re较低时, 流动处于层流状态, 此时描述流动的POD模态较少^[16-17]; 当Re很高时, 流动为复杂的湍流状态, 需要用来描述流动的POD模态往往很多. 给定流场的分辨率和破损区域, 流动的POD模态数量越多, 重构时所需要确定的未知系数就越多. 第二, 破损区域的几何形状. 很多关于gappy POD的研究考虑了不同缺失率(缺失面积)对重构效果的影响^[15-16], 但是其中的缺失区域均是随机生成的, 并没有对其几何形状的约束. 在破损区域面积相同时, 破损区域的几何形状不同会导致流场损失的相干信息不同, 从而可能会对gappy POD的重构效果产生影响.

在本文中, 选取旋转湍流流场来进行gappy POD重构的研究. 旋转湍流是一个具有丰富物理现象的湍流的典型范例. 其中, 通过外力输入的能量不仅导致了大尺度的气旋和反气旋结构, 也产生了小尺度的、间歇的、均匀各向同性的高度非高斯的扰动, 这使得旋转湍流表现为分布在不同空间尺度和时间尺度的混乱流动^[18-24]. 此外, 旋转湍流对于很多地球物理现象也有着重要的意义^[25-29].

本文通过旋转湍流场数据, 研究了不同流场复杂程度以及破损区域的面积大小和几何形状对gappy POD重构结果的影响. 通过更加严格地表述gappy POD重构过程, 其推导了gappy POD重构误差的公式, 并解释了它与流场复杂程度以及破损区域的关系. 本工作期待为gappy POD的应用和发展提供参考.

1.
POD理论与gappy POD重构

1.1
POD简介

为了在1.2节中系统、清楚地描述gappy POD重构过程, 本节简要介绍POD分解的过程. 在进行gappy POD重构之前, 需要由${N_c}$个已知的完整训练数据来求得POD模态.

对于第c个训练数据${u^c}left( boldsymbol{x}
ight)$, 可计算其在位置$boldsymbol{x}$处相对所有训练数据系综平均的偏移

$$ {phi ^c}left( boldsymbol{x} ight) = {u^c}left( boldsymbol{x} ight) - frac{1}{{{N_c}}}sumlimits_{c = 1}^{{N_c}} {{u^c}left( boldsymbol{x} ight)} $$

(1)

POD模态即为一组最优基$left{ {{psi _n}left( boldsymbol{x}
ight)}
ight}_{n = 1}^infty $, 使得如下平均误差

$$ varepsilon {text{ = }}leftlangle {{{left| {{phi ^c}left( boldsymbol{x} ight) - sumlimits_{n = 1}^{{N_n}} {a_n^c{psi _n}left( boldsymbol{x} ight)} } ight|}_2}} ight angle $$

(2)

对于任意的${N_n}$均取最小值. 这里${left| cdot
ight|_2}$代表L²范数, $leftlangle cdot
ight
angle $代表系综平均. $left{ {{psi _n}left( boldsymbol{x}
ight)}
ight}_{n = 1}^infty $可通过求解如下特征值问题获得

$$ int {boldsymbol{R}left( {boldsymbol{x},boldsymbol{y}} ight){psi _n}left( boldsymbol{y} ight){ m{d}}boldsymbol{y}} = {lambda _n}{psi _n}left( boldsymbol{x} ight) $$

(3)

$$left( {{psi _n},{psi _m}} ight) = int {{psi _n}left( boldsymbol{x} ight){psi _m}left( boldsymbol{x} ight){ m{d}}boldsymbol{x}} = {delta _{mn}}$$

(4)

其中相关矩阵

$$boldsymbol{R}left( {boldsymbol{x},boldsymbol{y}} ight) = leftlangle {{phi ^c}left( boldsymbol{x} ight){phi ^c}left( boldsymbol{y} ight)} ight angle = frac{1}{{{N_c}}}sumlimits_{c = 1}^{{N_c}} {{phi ^c}left( boldsymbol{x} ight){phi ^c}left( boldsymbol{y} ight)} $$

(5)

1.2
Gappy POD重构

本节介绍gappy POD的重构过程, 相比Everson和Sirovich^[11]中的描述, 这里进一步在数学上严格分析了不同因素对重构效果的影响, 包括数据复杂程度、采用的POD模态个数以及缺失区域.

假定考虑的流动数据最多可以由${N_{{
m{flow}}}}$个POD模态描述, 那么${N_{{
m{flow}}}}$的大小反映了流动的自由度或复杂程度. 当仅用前${N_{{
m{comp}}}}$个POD分量描述系统时, 对任意一个数据样本$phi left( boldsymbol{x}
ight)$, 有

$$ phi left( boldsymbol{x} ight) = sumlimits_{n = 1}^{{N_{{ m{comp}}}}} {{a_n}{psi _n}left( boldsymbol{x} ight)} + rleft( boldsymbol{x} ight) $$

(6)

式中的截断残差r取决于${N_{{
m{comp}}}}$, 为

$$rleft( boldsymbol{x} ight) = sumlimits_{n > {N_{{ m{comp}}}}}^{{N_{{ m{flow}}}}} {{a_n}{psi _n}left( boldsymbol{x} ight)} $$

(7)

一个存在部分缺失的样本可以被表示为

$$tilde phi left( boldsymbol{x} ight) = mleft( boldsymbol{x} ight)phi left( boldsymbol{x} ight)$$

(8)

其中在缺失的位置$ boldsymbol{x} $处有$m = 0$, 而在其他位置处有$m = 1$. 对于该样本, 有

$$tilde phi left( boldsymbol{x} ight) = sumlimits_{n = 1}^{{N_{{ m{comp}}}}} {{a_n}mleft( boldsymbol{x} ight){psi _n}left( boldsymbol{x} ight)} + tilde rleft( boldsymbol{x} ight)$$

(9)

$$tilde rleft( boldsymbol{x} ight) = sumlimits_{n > {N_{{ m{comp}}}}}^{{N_{{ m{flow}}}}} {{a_n}mleft( boldsymbol{x} ight){psi _n}left( boldsymbol{x} ight)} $$

(10)

Everson和Sirovich^[11]中通过最小二乘拟合, 即最小化如下误差

$$E = int_{boldsymbol{s}left[ {tilde phi } ight]} {{{left[ {tilde phi left( boldsymbol{x} ight) - sumlimits_{n = 1}^{{N_{{ m{comp}}}}} {{{tilde a}_n}{psi _n}left( boldsymbol{x} ight)} } ight]}^2}} { m{d}}boldsymbol{x}$$

(11)

得到$boldsymbol{a} = left{ {{a_n}}
ight}_{n = 1}^{{N_{{
m{comp}}}}}$的近似解$boldsymbol{tilde a} = left{ {{{tilde a}_n}}
ight}_{n = 1}^{{N_{{
m{comp}}}}}$. 其中, $boldsymbol{s}left[ {tilde phi }
ight]$为$ tilde phi $的支集, 即$m = 1$的所有位置$boldsymbol{x}$的集合.

由式(8) ~ 式(11)可知, 影响gappy POD重构过程的因素有: 数据自身的复杂程度${N_{{
m{flow}}}}$; 采用的POD模态个数${N_{{
m{comp}}}}$; 所有已知数据点的位置集合$boldsymbol{s}left[ {tilde phi }
ight]$. 集合$boldsymbol{s}left[ {tilde phi }
ight]$由数据自身的分辨率, 即完整数据的已知点的位置集合, 和缺失数据点的位置集合共同决定. 为了分析上述各个因素的影响, 下面重新表述gappy POD重构的过程.

将${N_{{
m{comp}}}}$个POD模态$ {psi _n}left( boldsymbol{x}
ight) $均作为列向量可以得到矩阵

$$ boldsymbol{X} = left[ {begin{array}{*{20}{c}}{{psi _1}left( boldsymbol{x} ight)}&{{psi _2}left( boldsymbol{x} ight)}& cdots &{{psi _{{N_{{ m{comp}}}}}}left( boldsymbol{x} ight)} end{array}} ight] $$

(12)

若上式中$ boldsymbol{x} $仅取为已知点的位置, 即$boldsymbol{x} in boldsymbol{s}left[ {tilde phi }
ight]$, 可得矩阵

$$ boldsymbol{tilde X} = {left[ {begin{array}{*{20}{c}}{{psi _1}left( boldsymbol{x} ight)}&{{psi _2}left( boldsymbol{x} ight)}& cdots &{{psi _{{N_{{ m{comp}}}}}}left( boldsymbol{x} ight)} end{array}} ight]_{boldsymbol{s}left[ {tilde phi } ight]}} $$

(13)

若$boldsymbol{s}left[ {tilde phi }
ight]$中共$ {N_{{
m{points}}}} $个点, 则$boldsymbol{tilde X}$为${N_{{
m{points}}}} times {N_{{
m{comp}}}}$的矩阵.

式(11)可写为如下线性方程系统的最小二乘拟合问题

$$boldsymbol{tilde Xtilde a} = tilde phi left( boldsymbol{x} ight)$$

(14)

该问题可通过$ boldsymbol{tilde X} $的伪逆求解如下. 对于$forall boldsymbol{tilde a} in {mathbb{R}^{{N_{{
m{comp}}}}}}$, 均有

$${left| {boldsymbol{tilde Xtilde a} - tilde phi } ight|_2} geqslant {left| {boldsymbol{tilde X}{{boldsymbol{tilde a}}_0} - tilde phi } ight|_2}$$

(15)

其中

$${boldsymbol{tilde a}_0}{ m{ = }}{boldsymbol{tilde X}^ + }tilde phi $$

(16)

式(15)中等号成立时当且仅当对任意向量$boldsymbol{w}$有

$$boldsymbol{tilde a}{ m{ = }}{boldsymbol{tilde X}^ + }tilde phi { m{ + }}left( {boldsymbol{I} - {{boldsymbol{tilde X}}^ + }boldsymbol{tilde X}} ight)boldsymbol{w}$$

(17)

当$left( {boldsymbol{I} - {{boldsymbol{tilde X}}^ + }boldsymbol{tilde X}}
ight)$为零矩阵时, $ boldsymbol{tilde X} $是列满秩的, 此时$ boldsymbol{tilde a} $存在唯一解${boldsymbol{tilde a}_0}$; 当$left( {boldsymbol{I} - {{boldsymbol{tilde X}}^ + }boldsymbol{tilde X}}
ight)$不是零矩阵时, 式(17)给出无穷多个解, 这里选取${boldsymbol{tilde a}_0}$作为$boldsymbol{a}$的近似解, 它在所有解中有着最小的L²范数.

上面的讨论中并未出现截断残差, 事实上, 式(9)可以写为

$$tilde phi left( boldsymbol{x} ight) = boldsymbol{tilde Xa} + tilde rleft( boldsymbol{x} ight)$$

(18)

因此

$${boldsymbol{tilde a}_0}{ m{ = }}{boldsymbol{tilde X}^ + }tilde phi { m{ = }}{boldsymbol{tilde X}^ + }boldsymbol{tilde Xa} + {boldsymbol{tilde X}^ + }tilde rleft( boldsymbol{x} ight)$$

(19)

此时POD系数$ boldsymbol{a} $的重构误差为

$$boldsymbol{e} = boldsymbol{a} - {boldsymbol{tilde a}_0} = left( {boldsymbol{I} - {{boldsymbol{tilde X}}^ + }boldsymbol{tilde X}} ight)boldsymbol{a} - {boldsymbol{tilde X}^ + }tilde rleft( boldsymbol{x} ight)$$

(20)

2.
旋转湍流流场重构

2.1
湍流数据简介和重构问题描述

本工作选用旋转湍流流场来进行gappy POD重构的研究. TURB-Rot是一个公开的旋转湍流数据集^[30], 包含105600张垂直于旋转方向的二维流场切片, 切片的分辨率为$64 times 64$, 所有切片均来自同一个三维旋转湍流的直接数值模拟. 由于数据集中的旋转湍流场高度二维化, 所有切片均可看作来自同一系综. 数值模拟中采用了周期边界条件, 因此可对二维流场切片进行如下傅里叶谱展开

$$boldsymbol{u}left( boldsymbol{x} ight) = sumlimits_{left| boldsymbol{k} ight| < {k_f}} {boldsymbol{hat u}left( boldsymbol{k} ight){ m{e}}^{{ m{i}}boldsymbol{k} cdot boldsymbol{x}}} $$

(21)

式中, $ boldsymbol{u} $为三维速度向量, $boldsymbol{hat u}left( boldsymbol{k}
ight)$为相应的傅里叶谱系数, $boldsymbol{x} = left( {{x_1},{x_2}}
ight)$代表空间位置, $boldsymbol{k} = left( {{k_1},{k_2}}
ight)$为谱空间中的波数. ${k_f}$是谱空间中的截断波数, 在TURB-Rot数据集中的值为32.

由于旋转流场的各向异性, gappy POD对$ boldsymbol{u} $的不同分量的重构效果并不相同. 不失一般性, 本文考虑速度模$u = {left| boldsymbol{u}
ight|_2}$的gappy POD重构. 在由速度$ boldsymbol{u} $计算速度模$u$时, 需要注意消除混淆误差^[31], 使得$u$可以写为

$$ uleft( boldsymbol{x} ight) = sumlimits_{left| boldsymbol{k} ight| < {k_f}} {hat uleft( boldsymbol{k} ight){ m{e}}^{{ m{i}}boldsymbol{k} cdot boldsymbol{x}}} $$

(22)

式中${k_f}$为32. 可以看到, ${k_f}$的大小确定了$u$所包含的傅里叶模态个数, 从而确定了流场的复杂程度. 因此可以通过仅保留$left| boldsymbol{k}
ight| < {k_f} = 8$的模态来获得一个低复杂度的流场数据. 值得指出的是, 对于现在所考虑的均匀湍流系统, 可以证明其傅里叶模态就是POD模态^[1].

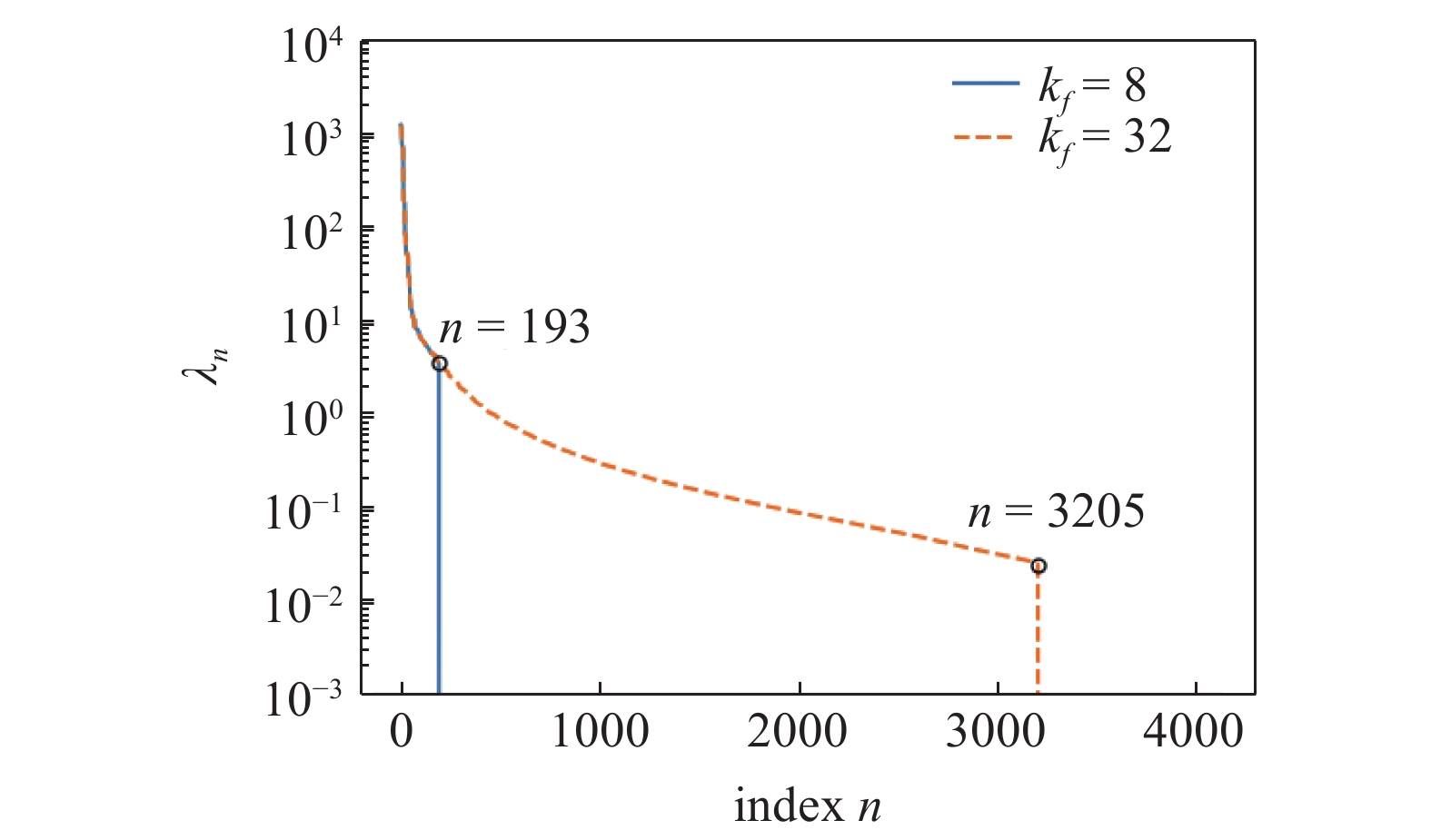
根据式(1) ~ 式(5), 选取N_c = 84480个速度模的二维切片(训练集), 可以得到${k_f} = 8$和${k_f} = 32$时POD模态的特征值曲线如图1所示. 图1表明对于${k_f} = 8$和${k_f} = 32$的数据分别有193和3205个特征值非零的POD模态, 这与相应的傅里叶模态数目相等.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-464-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
POD模态的特征值曲线



Figure
1.
Eigenvalues of the POD modes



下载:
全尺寸图片
幻灯片


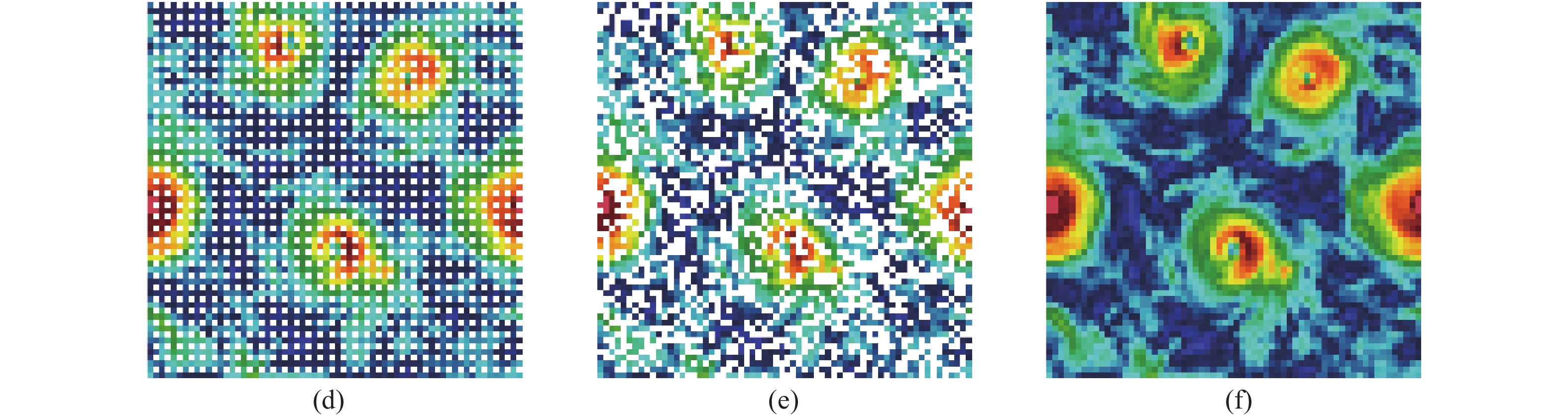
获得系统的POD模态后, 选取20480个非训练集的数据作为测试集, 来研究不同破损区域对gappy POD重构效果的影响. 图2(a) ~ 图2(e) 给出了拥有相同破损面积${A_{{
m{gap}}}} = 32 times 32$和不同几何的破损区域示意图. 其中, 图2(a) ~ 图2(d) 中的破损区域为均匀排布的方形区域, 但是不同图片中的方形边长和数量不同; 图2(e) 中的破损区域为随机分布的像素点. 真实的完整流场如图2(f)所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-464-2-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure2-1" />



2
(a)-(e) 破损面积相同但破损区域几何不同的部分缺失流场, (f) 真实的完整流场



2.
(a)-(e) Damaged flow fields with gaps of the same area but different geometries. (f) The complete flow field



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-464-2.jpg'"
class="figure_img
figure_type2 ccc " id="Figure2" />



图
2
(a)-(e) 破损面积相同但破损区域几何不同的部分缺失流场, (f) 真实的完整流场 (续)



Figure
2.
(a)-(e) Damaged flow fields with gaps of the same area but different geometries. (f) The complete flow field (continued)



下载:
全尺寸图片
幻灯片

2.2
湍流场复杂程度的影响

本节研究当分辨率相同时, 湍流场数据的复杂程度对gappy POD重构的影响. 下面以${N_{{
m{flow}}}}$代表湍流场数据的复杂程度, 即特征值非零的POD模态数目; 同时以${N_{{
m{comp}}}}$代表gappy POD重构采用的POD模态数目. 实际计算中往往会选取${N_{{
m{comp}}}} leqslant {N_{{
m{flow}}}}$, 以在获得一定重构精度的同时降低计算量. 下面对于复杂程度不同的数据, 考虑采用不同的${N_{{
m{comp}}}}$对gappy POD重构误差的影响.

对于2.1节中${k_f} = 8$和${k_f} = 32$的数据, 分别有${N_{{
m{flow}}}} = 193$和${N_{{
m{flow}}}} = 3205$. 为了定量描述重构效果, 选取N_c = 20480个测试数据, 它们与训练数据来自数值模拟中时间相关性很弱的不同时间段. 定义破损区域中的均方重构误差为

$$MS{E_{{ m{gap}}}} = dfrac{{dfrac{1}{{{N_c}}}displaystylesumlimits_{c = 1}^{{N_c}} {frac{1}{{{A_{{ m{gap}}}}}}} int_{{A_{{ m{gap}}}}} {{{left[ {u_{{ m{true}}}^cleft( boldsymbol{x} ight) - u_{{ m{pred}}}^cleft( boldsymbol{x} ight)} ight]}^2}{ m{d}}boldsymbol{x}} }}{{{E_u}}}$$

(23)

其中, $ u_{{
m{true}}}^c $和$ u_{{
m{pred}}}^c $分别代表第c个测试数据的真实值与重构值, 积分域仅为破损区域, ${A_{{
m{gap}}}}$为破损面积. 式中的因子$ {E_u} $由下式给出

$${E_u} = frac{1}{{{N_c}}}sumlimits_{c = 1}^{{N_c}} {frac{1}{A}} int_A {{{left[ {u_{{ m{true}}}^cleft( boldsymbol{x} ight) - {u_0}} ight]}^2}{ m{d}}boldsymbol{x}} $$

(24)

其中积分域为无破损的完整区域, $A$代表完整区域面积, $ {u_0} $为平均速度

$${u_0} = frac{1}{{{N_c}}}sumlimits_{c = 1}^{{N_c}} {frac{1}{A}} int_A {u_{{ m{true}}}^cleft( boldsymbol{x} ight){ m{d}}boldsymbol{x}} $$

(25)

对于一个位于流场中心的$8 times 8$的正方形破损(图2(a)), 图3对于${k_f} = 8$和${k_f} = 32$的数据给出了破损区域中的均方重构误差$MS{E_{{
m{gap}}}}$关于${{{N_{{
m{comp}}}}} mathord{left/{vphantom {{{N_{{
m{comp}}}}} {{N_{{
m{flow}}}}}}}
ight.} {{N_{{
m{flow}}}}}}$的变化曲线. 注意图中${N_{{
m{comp}}}}$的取值范围为$left[ {1,{N_{{
m{flow}}}} - 1}
ight]$.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-464-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
破损区域中的均方重构误差$ {
m{MS}}{{
m{E}}_{{
m{gap}}}} $关于${{{N_{{
m{comp}}}}} mathord{left/ {vphantom {{{N_{{
m{comp}}}}} {{N_{{
m{flow}}}}}}}
ight. } {{N_{{
m{flow}}}}}}$的变化曲线



Figure
3.
Normalized mean square error in the gap, $ {{MS}}{{{E}}_{{
m{gap}}}} $, as a function of ${{{N_{{
m{comp}}}}} mathord{left/ {vphantom {{{N_{{
m{comp}}}}} {{N_{{
m{flow}}}}}}}
ight. } {{N_{{
m{flow}}}}}}$



下载:
全尺寸图片
幻灯片


可以看出, 对于${k_f} = 8$的低复杂度的数据, 随着${{{N_{{
m{comp}}}}} mathord{left/{vphantom {{{N_{{
m{comp}}}}} {{N_{{
m{flow}}}}}}}
ight.} {{N_{{
m{flow}}}}}}$的增大, 重构误差逐渐降低并且收敛到一个很小的值($ < {10^{ - 3}}$). 因此对这种情况下的重构问题, 可以根据重构精度和计算量的要求来选取合适大小的${N_{{
m{comp}}}}$. 对于${k_f} = 32$的高复杂度的数据, 随着${{{N_{{
m{comp}}}}} mathord{left/{vphantom {{{N_{{
m{comp}}}}} {{N_{{
m{flow}}}}}}}
ight.} {{N_{{
m{flow}}}}}}$的增大, 重构误差先减小后增大, 并且在${{{N_{{
m{comp}}}}} mathord{left/{vphantom {{{N_{{
m{comp}}}}} {{N_{{
m{flow}}}}}}}
ight.} {{N_{{
m{flow}}}}}}$接近1时重构误差快速增大到非常大的值, 表明此时gappy POD无法进行有效的重构. 然而, 有趣的是, 当${N_{{
m{comp}}}} = {N_{{
m{flow}}}}$时, gappy POD在${k_f} = 8$和${k_f} = 32$的数据上的重构误差$ {{MS}}{{{E}}_{{
m{gap}}}} $均为一个非常小的值($ < {10^{ - 15}}$), 表明破损数据可以被完美地重构出来.

上述现象可以通过1.2节中的论述来解释. 对于两种复杂度不同的数据, 在给定的分辨率和破损下, 通过计算可知对任意${N_{{
m{comp}}}} in left[ {1,{N_{{
m{flow}}}}}
ight]$, $boldsymbol{tilde X}$是列满秩的, 即${boldsymbol{tilde X}^ + }boldsymbol{tilde X} = I$, 此时式(20)可以写为

$$boldsymbol{e} = boldsymbol{a} - {boldsymbol{tilde a}_0} = - {boldsymbol{tilde X}^ + }tilde rleft( boldsymbol{x} ight)$$

(26)

因此可得

$$left| boldsymbol{e} ight| simeq frac{{left| {tilde rleft( boldsymbol{x} ight)} ight|}}{{{sigma _{ m{min}}}}}$$

(27)

其中$ {sigma _{min }} $为$ boldsymbol{tilde X} $的最小奇异值. 式(27)表明重构误差的大小约为POD展开的截断误差大小$left| {tilde rleft( boldsymbol{x}
ight)}
ight|$除以矩阵$ boldsymbol{tilde X} $的最小特征值. 图4给出了$ {sigma _{min }} $随${{{N_{{
m{comp}}}}} mathord{left/{vphantom {{{N_{{
m{comp}}}}} {{N_{{
m{flow}}}}}}}
ight.} {{N_{{
m{flow}}}}}}$的变化曲线. 可以看到, 对于${k_f} = 8$的低复杂度的数据, $ {sigma _{min }} $的变化幅度不大, 始终位于$left[ {0.1,1}
ight]$区间内. 因此, 随着${{{N_{{
m{comp}}}}} mathord{left/{vphantom {{{N_{{
m{comp}}}}} {{N_{{
m{flow}}}}}}}
ight.} {{N_{{
m{flow}}}}}}$的增大, 截断误差$ left| {tilde rleft( boldsymbol{x}
ight)}
ight| $逐渐减小, 从而导致重构误差逐渐减小. 然而, 对于${k_f} = 32$的高复杂度的数据, 随着${{{N_{{
m{comp}}}}} mathord{left/{vphantom {{{N_{{
m{comp}}}}} {{N_{{
m{flow}}}}}}}
ight.} {{N_{{
m{flow}}}}}}$的增大, $ {sigma _{min }} $会迅速降低到非常小的值. 因此, 虽然截断误差$ left| {tilde rleft( boldsymbol{x}
ight)}
ight| $会逐渐减小, 但${1 mathord{left/{vphantom {1 {{sigma _{min }}}}}
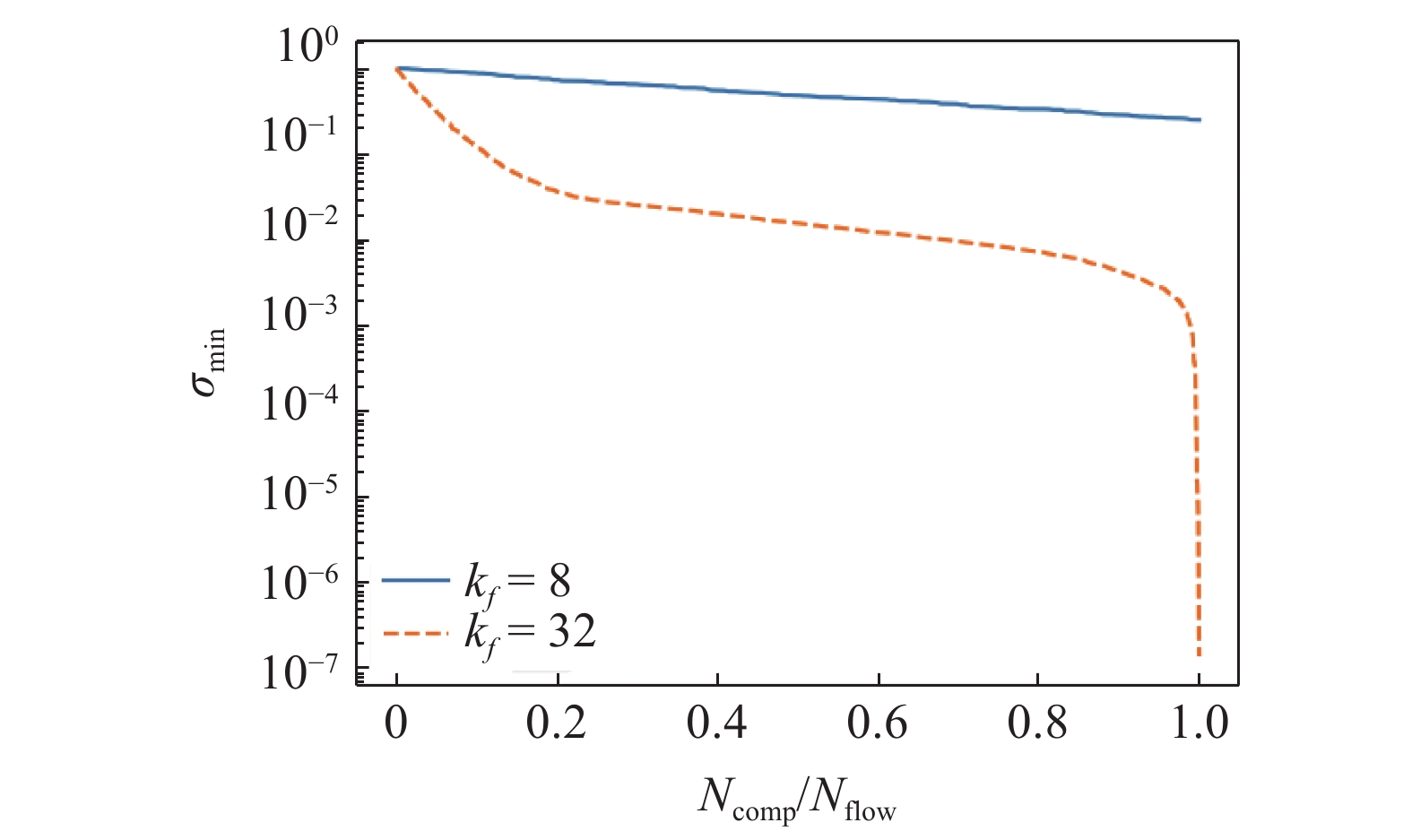
ight.} {{sigma _{min }}}}$的放大作用会导致重构误差迅速增大. 当${N_{{
m{comp}}}} = {N_{{
m{flow}}}}$时, 截断误差$ tilde rleft( boldsymbol{x}
ight) = bf{0} $, 此时重构误差$ boldsymbol{e} = boldsymbol{0} $.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-464-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
$boldsymbol{tilde X}$的最小奇异值$ {sigma _{min }} $关于${{N_{{
m{comp}}}}}$/$ {vphantom {{{N_{{
m{comp}}}}} {{N_{{
m{flow}}}}}}} {{N_{{
m{flow}}}}} $的变化曲线



Figure
4.
The minimum singular value of $ boldsymbol{tilde X} $, $ {sigma _{min }} $, as a function of ${{N_{{
m{comp}}}}}$/${ {vphantom {{{N_{{
m{comp}}}}} {{N_{{
m{flow}}}}}}} } {{N_{{
m{flow}}}}} $



下载:
全尺寸图片
幻灯片


本节讨论了湍流场的复杂程度对gappy POD重构的影响. 湍流场的复杂程度由对应的POD模态决定, 它们在已知点上的值构成了矩阵$ boldsymbol{tilde X} $(式(13)). 当破损区域使得$ boldsymbol{tilde X} $为列满秩时, 重构误差大小约等于流场POD展开的截断误差除以$ boldsymbol{tilde X} $的最小奇异值$ {sigma _{min }} $(式(27)). 当流场复杂度较低时, $ {sigma _{min }} $的值并不十分小, 重构误差主要由截断误差所影响, 可以根据对重构精度和计算量的要求采用较少的POD模态来进行重构. 当流场复杂度较高时, 由于截断误差会被极小的$ {sigma _{min }} $放大, 此时必须采用全部POD模态来进行有效的重构.

2.3
破损区域面积大小和几何形状的影响

本节研究破损区域大小和几何形状对gappy POD重构的影响. 考虑${k_f} = 32$的高复杂度的数据, 根据2.2节中的讨论, 始终选取${N_{{
m{comp}}}} = {N_{{
m{flow}}}}$来进行重构.

给定破损区域面积${A_{{
m{gap}}}}$, 定义破损尺寸(gap size)为$sqrt {{A_{{
m{gap}}}}} $. 对于图2(a) ~ 图2(e) 中所示的破损形状, 图5给出了破损区域中的均方重构误差$ {{MS}}{{{E}}_{{
m{gap}}}} $关于破损尺寸的变化曲线, 其中的误差棒代表重构误差在N_c = 20480个测试数据上的标准差. 可以看到, 对任何一个破损形状, 总是存在一个临界的破损尺寸, 使得破损小于等于该尺寸时重构误差很小, 而大于该尺寸时重构误差很大.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-464-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
对于不同几何形状的破损, 破损区域中的均方重构误差$ {{MS}}{{{E}}_{{
m{gap}}}} $关于破损尺寸的变化曲线



Figure
5.
Normalized mean square error in the gap, $ {{MS}}{{{E}}_{{
m{gap}}}} $, as a function of the gap size for different gap geometries



下载:
全尺寸图片
幻灯片


上述临界的破损尺寸可通过式(20)来解释. 由于${N_{{
m{comp}}}} = {N_{{
m{flow}}}}$, 截断误差$ tilde rleft( boldsymbol{x}
ight) = bf{0} $, 此时式(20)可以写为

$$boldsymbol{e} = boldsymbol{a} - {boldsymbol{tilde a}_0} = left( {boldsymbol{I} - {{boldsymbol{tilde X}}^ + }boldsymbol{tilde X}} ight)boldsymbol{a}$$

(28)

上式表明当$ boldsymbol{tilde X} $为列满秩, 即$rleft( {boldsymbol{tilde X}}
ight) = {N_{{
m{flow}}}}$时, 重构误差为零. 这里$rleft( {boldsymbol{tilde X}}
ight)$代表$ boldsymbol{tilde X} $的秩. 图6给出了对于不同几何形状的破损, ${N_{{
m{flow}}}} - rleft( {boldsymbol{tilde X}}
ight)$关于破损尺寸的变化曲线. 可以看到, ${N_{{
m{flow}}}} - rleft( {boldsymbol{tilde X}}
ight)$变为非零值时所对应的破损尺寸正好为图5中重构误差突变处的临界破损尺寸, 此时$ {boldsymbol{I} - {{boldsymbol{tilde X}}^ + }boldsymbol{tilde X}} $不再为零矩阵, 重构误差由式(28)给出.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-464-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
对于不同几何形状的破损, ${N_{{
m{flow}}}} - rleft( {boldsymbol{tilde X}}
ight)$关于破损尺寸的变化曲线



Figure
6.
${N_{{
m{flow}}}} - rleft( {boldsymbol{tilde X}}
ight)$ as a function of the gap size for different gap geometries



下载:
全尺寸图片
幻灯片


由图5和图6还可以看出, 对于不同的几何形状, 相应的临界破损尺寸也不同. 例如, 对于图2(a) 所示的一个方形的破损, 临界破损尺寸为12; 而对于图2(e) 所示的随机点破损, 临界破损尺寸为30. 这表明对于同样的破损尺寸, 当破损形状不同时, gappy POD的重构效果不同. 图7给出了破损尺寸为16时, 不同破损几何的重构结果图. 其中, 前3列分别为破损区域、重构结果和原始区域的示意图; 第4列为红色参考线上重构结果与真实结果的分布; 第5列显示了在固定的${x_1}$处的平均重构误差



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-464-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
相同破损面积, 不同破损几何的gappy POD重构结果(对应不同行). 第1列: 破损的流场; 第2列: 重构的流场; 第3列: 原始流场; 第4列: 第一列中红色参考线上重构结果(虚线)与真实结果(实线)的分布; 第5列: 平均重构误差(红色), $ {varDelta _u}left( {{x_1}}
ight) $, 及其在测试集上的平均(黑色), $ leftlangle {{varDelta _u}left( {{x_1}}
ight)}
ight
angle $. ${x_1}$和${x_2}$分别代表水平和竖直方向



Figure
7.
Gappy POD reconstruction results for the same gap area and different gap geometries (one for each row). 1st column: damaged image in input. 2nd column: image generated in output. 3rd column: ground truth. 4th column: generated (dashed) and ground truth (solid) profiles along the vertical line shown in the 1st column. 5th column: mean reconstruction error, $ {varDelta _u}left( {{x_1}}
ight) $, for each image (red line) and the average error, $ leftlangle {{varDelta _u}left( {{x_1}}
ight)}
ight
angle $, over the test images (black curve). Note that ${x_1}$ and ${x_2}$ denotes the horizontal and vertical directions, respectively



下载:
全尺寸图片
幻灯片

$${varDelta _u}left( {{x_1}} ight) = frac{1}{{{E_u}{L_{{ m{gap}}}}}}intlimits_{{L_{{ m{gap}}}}} {{{left[ {u_{{ m{true}}}^cleft( {{x_1},{x_2}} ight) - u_{{ m{pred}}}^cleft( {{x_1},{x_2}} ight)} ight]}^2}{ m{d}}{x_2}} $$

(29)

式中的积分区域为存在破损的${x_2}$位置, $ {L_{{
m{gap}}}} $为相应的破损长度. $ leftlangle {{varDelta _u}left( {{x_1}}
ight)}
ight
angle $代表$ {varDelta _u}left( {{x_1}}
ight) $在测试数据上的平均. 可以看到, 除了一个大的正方形破损, gappy POD对于其他几何形状的破损均可精确重构流场. 虽然破损区域的总面积相同, 相比于其他几何形状, 一个大的正方形破损会导致损失的信息具有更大的相关性, 因此导致gappy POD无法重构流场.

本节通过考虑${k_f} = 32$的高复杂度的湍流数据, 并选取${N_{{
m{comp}}}} = {N_{{
m{flow}}}}$, 研究了破损区域大小和几何形状对gappy POD重构的影响. 对于任何一种几何形状的破损, 都对应着一个保证重构成功的最大尺寸, 称为临界破损尺寸. 破损的几何形状影响着损失的信息具有的相关性, 从而影响着上述临界破损尺寸的大小.

3.
结 论

本文研究了gappy POD在湍流数据重构上的应用, 主要考虑了湍流场复杂程度以及破损区域的大小和几何形状的影响.

通过更严格地表述了gappy POD重构的过程, 本文指出重构误差由两部分构成. 第一部分来自流场POD展开的截断误差, 经由POD基函数在已知点上组成的矩阵的最小特征值放大. 当湍流场的复杂度较低时, 这一项随着采用的POD模态数目增大而减小, 因此实际应用中可根据精度和计算量要求合适选取POD模态数目. 然而, 当湍流场复杂度较高时, POD基函数在已知点上组成的矩阵的最小特征值非常小, 此时即使有很小的POD截断误差也会被极大地放大. 因此, 为了对高复杂度湍流场进行gappy POD重构, 必须采用其所有POD模态使得截断误差为零.

Gappy POD重构误差的第二部分来自POD基函数在已知点上组成的矩阵的非列满秩性, 它主要取决于破损区域的面积大小和几何形状. 对于固定几何形状的破损, 当破损区域增大时, 流场损失的信息逐渐增多, 使得上述矩阵逐渐变为非列满秩的, 从而使得重构失效. 而对于相同的破损面积, 当破损导致的损失信息包含的相关性越大(如一个大的方形破损), 上述矩阵越容易变为非列满秩的, 从而使得重构失效; 而当破损导致的损失信息包含的相关性不大时(如随机点组成的破损), 上述矩阵易于维持列满秩性质, 此时流场可以被精确重构.