引 言
空间机器人在碎片清理、在轨维修、在轨装配等在轨服务 (OOS) 任务中发挥着重要的作用[1]. 与单机械臂相比, 空间双臂机器人可以提供更大的负载能力和更好的稳定性[2]. 然而, 双臂协调操作时末端执行器与目标接触形成闭链系统, 闭链约束的引入会极大地限制双臂协调操作的工作空间. 为了对翻滚目标的抓捕策略进行优化, 有必要对空间双臂机器人的协调操作能力进行分析.
机械臂的操作能力包括全局操作能力和局部操作能力. 全局操作能力是指机械臂在工作空间或全局路径的操作能力, 局部操作能力是指机械臂在特定构型下的操作能力. 对于工作空间分析, 现有的研究方法主要包括解析法[3-4]、图解法[5]和数值法[6-9]. 解析法和图解法一般适用于3自由度以下和平面机械臂. 数值法主要是基于蒙特卡洛打靶法, 适用于高自由度机械臂. 然而, 传统的工作空间分析只能得到可达空间的边界, 不能描述可达空间内的姿态信息. 到达可达点的可行方向数量反映了机械臂的灵巧度, 是评价机械臂性能的一项重要指标. 为了定量描述机械臂的灵巧度, 需要生成同时包含位置信息和方向信息的工作空间. 通过将任务空间位置和姿态离散化, 可以采用逆向运动学[10-11]、正向运动学[12]和混合[13]方法生成包含方向信息的机械臂工作空间. 相比于单臂工作空间分析, 双臂协调操作时的工作空间分析更加复杂. 文献[14-17]中研究了双臂机器人的工作空间问题. 但是, 这些文献中对双臂协调操作的工作空间分析只是简单地求解单臂工作空间的交集, 忽略了目标的尺寸和闭链约束的影响. 对于局部操作能力分析问题, Yoshikawa[18]基于雅可比矩阵提出了操作椭球和可操作度 (manipulability measure) 的概念, 用于评估特定构型下机械臂的全方向操作能力, 也可表示构型的奇异性. 同时, 与雅可比矩阵相关的条件数[19]、最小奇异值[20]等指标也用于衡量机械臂构型的奇异性. 此外, Chui[21]和姚建初等[22]提出任务兼容度 (task compatibility) 的概念, 用于评估机械臂沿着某个方向的操作能力. 现有的局部操作能力分析主要是针对单机械臂, 对于空间双臂机器人协调操作的能力分析研究还较少. 空间双臂机器人协调操作能力的分析需要考虑基座与机械臂的耦合效应以及闭链约束的影响[23]. 本文提出了一种基于缩放因子法的任务兼容度指标计算方法, 可以提高任务兼容度的计算准确性. 在推导空间双臂机器人协调操作目标的运动学与动力学映射关系的基础上, 将任务兼容度的概念拓展到空间闭链系统中, 并结合协调工作空间分析双臂协调操作的全局操作能力.
执行抓捕任务时, 人类可以快速决策出如何抓捕目标以更好地执行任务. 人类的快速决策来源于对目标运动的估计和对自身能力的了解. 为了将人类的这种决策能力扩展到空间双臂机器人协调抓捕翻滚目标问题中, 本文基于空间双臂机器人协调操作能力分析开展对翻滚目标的抓捕策略研究. 为了实现对目标的捕获, 需要确定机器人抓捕目标时的抓捕点和抓捕构型. 针对抓捕点的确定, 现有研究主要集中在多指接触抓捕问题中[24], 而对末端固定抓捕的抓捕点确定问题研究较少. 对于空间双臂机器人抓捕构型的确定, 包括基座位姿和机械臂构型. 张博等[25]使用可操作度作为指标寻找空间机械臂的最优构型. Vosniakos和Matsas[26]和Yu等[27]采用优化方法寻找执行任务时机器人的最优基座位置. 然而, 工作空间的非线性使优化方法很容易陷入局部极小值. Sundaram等[28]采用能力图谱描述工作空间的全局操作能力, 并用于最优基座位置的选取. 能力图谱[29]是使用某一度量指标对工作空间所有可达位姿处的操作能力进行评估, 并采用热力图描述值的大小, 更直观地表示了全局操作能力的分布情况. 进一步, Vahrenkamp等[30]采用逆可达图确定移动机器人的最优基座位置. 执行任务时, 基座位置会极大地影响机械臂的构型, 进一步影响机械臂的操作能力. 然而, 上述研究对最优基座位置的选取主要是针对地面机器人和静态目标. 空间目标的翻滚运动使抓捕问题更加复杂, 然而, 现有文献中对空间双臂机器人协调抓捕翻滚目标的抓捕策略优化问题研究较少.
针对上述存在的问题, 本文的目标是在充分考虑空间双臂机器人的协调操作能力以及目标的翻滚特性下, 设计空间双臂机器人对翻滚目标的抓捕策略(抓捕点和抓捕构型), 以增强双臂运动的协调性和对翻滚目标的操作能力保证抓捕任务的成功.
1.
工作空间分析
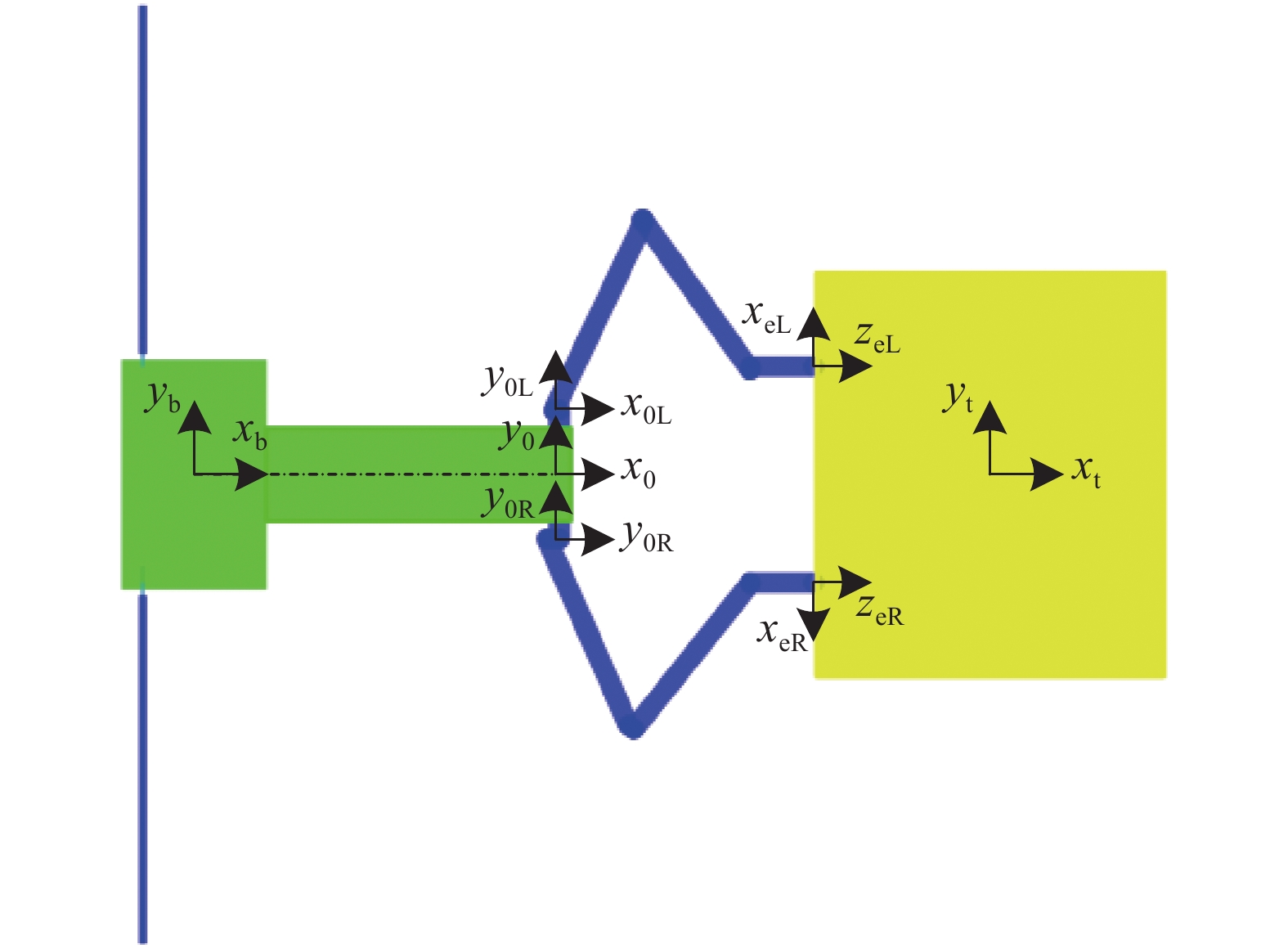
工作空间是衡量机械臂性能的一项重要运动学指标. 本节对空间双臂机器人协调操作目标(图1)的工作空间进行分析. 对任务空间位姿进行离散以表示位置和姿态信息. 在分析单臂工作空间的基础上, 建立闭链约束下的协调工作空间.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
工作空间参考坐标系
Figure
1.
Reference frames for workspace
下载: 全尺寸图片
幻灯片
1.1
任务空间离散化
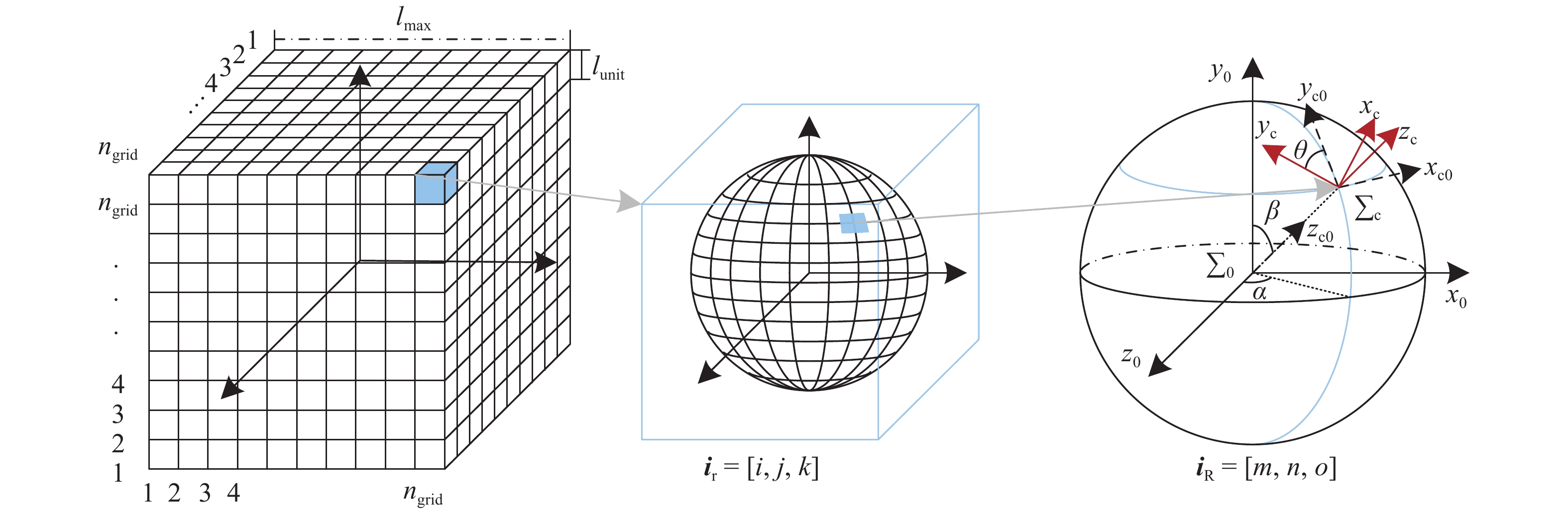
工作空间是机械臂关节空间到任务空间位姿映射的集合. 为了有效描述工作空间内的位姿信息, 本文使用离散的单元格和嵌入单元格的球对任务空间进行离散表示, 如图2所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-2.jpg'" class="figure_img
figure_type2 ccc " id="Figure2" />
图
2
任务空间位姿离散
Figure
2.
Task space’s pose discretization
下载: 全尺寸图片
幻灯片
首先, 以参考坐标系原点为中心, 使用边长为
ight. } {{l_{{text{unit}}}}}}}
ight)$
ight]$
$$ left. begin{split}& {{boldsymbol{r}} to {{boldsymbol{i}}_{text{r}}}:{{boldsymbol{i}}_{text{r}}} = {text{ceil}}left( {frac{{boldsymbol{r}}}{{{l_{{text{unit}}}}}}} ight) + frac{{{n_{{text{grid}}}}}}{2}} & {{{boldsymbol{i}}_{text{r}}} to {boldsymbol{r}}:{boldsymbol{r}} = left( {{{boldsymbol{i}}_{text{r}}} - frac{{{n_{{text{grid}}}}}}{2}} ight){l_{{text{unit}}}} - frac{{{l_{{text{unit}}}}}}{2}} end{split} ight}$$  | (1) |
接着, 采用嵌入单元格的球对任务空间姿态进行离散. 末端执行器或目标相对于参考坐标系的姿态可以使用角度
ight]$
$$ {boldsymbol{R}} = {text{Ro}}{{text{t}}_{{y}}}left( alpha ight){text{Ro}}{{text{t}}_{{x}}}left( {beta - {{ m{{text{π}}}} mathord{left/ {vphantom {{ m{{text{π}}}} 2}} ight. } 2}} ight){text{Ro}}{{text{t}}_{{z}}}left( theta ight) $$  | (2) |
其中,
ight)$
ight){
m{{text{π}}}}} mathord{left/ {vphantom {{left( {m - 1}
ight){
m{{text{π}}}}} {{n_alpha }}}}
ight. } {{n_alpha }}},;{beta _n} = {{left( {n - 1}
ight)2{
m{{text{π}}}}} mathord{left/ {vphantom {{left( {n - 1}
ight)2{
m{{text{π}}}}} {{n_beta }}}}
ight. } {{n_beta }}},;{theta _o} = left( {o - 1}
ight)$
m{{text{π}}}}} mathord{left/ {vphantom {{2{
m{{text{π}}}}} {{n_theta }}}}
ight. } {{n_theta }}} $
ight]$
ight) + 2}
ight]{n_theta }$
$$left. begin{split}& {{{boldsymbol{R}}_{text{a}}} to {{boldsymbol{i}}_{text{R}}}:{{boldsymbol{i}}_{text{R}}} = {text{round}}left( {{{boldsymbol{R}}_{text{a}}}frac{{left[ {{n_alpha },{n_beta },{n_theta }} ight]}}{{left[ {{ m{{text{π}}}},2{ m{{text{π}}}},2{ m{{text{π}}}}} ight]}}} ight) + {{1}}} & {{{boldsymbol{i}}_{text{R}}} to {{boldsymbol{R}}_{text{a}}}:{{boldsymbol{R}}_{text{a}}} = left( {{{boldsymbol{i}}_{text{R}}} - 1} ight)frac{{left[ {{ m{{text{π}}}},2{ m{{text{π}}}},2{ m{{text{π}}}}} ight]}}{{left[ {{n_alpha },{n_beta },{n_theta }} ight]}}} end{split} ight} $$  | (3) |
综上, 任务空间位姿
ight)$
ight)$
1.2
单臂工作空间
为了建立协调工作空间, 首先分析每个机械臂的工作空间. 机械臂的工作空间不仅与机械臂自身结构有关, 也与安装在航天器基座上的位置有关. 建立单臂工作空间的参考坐标系
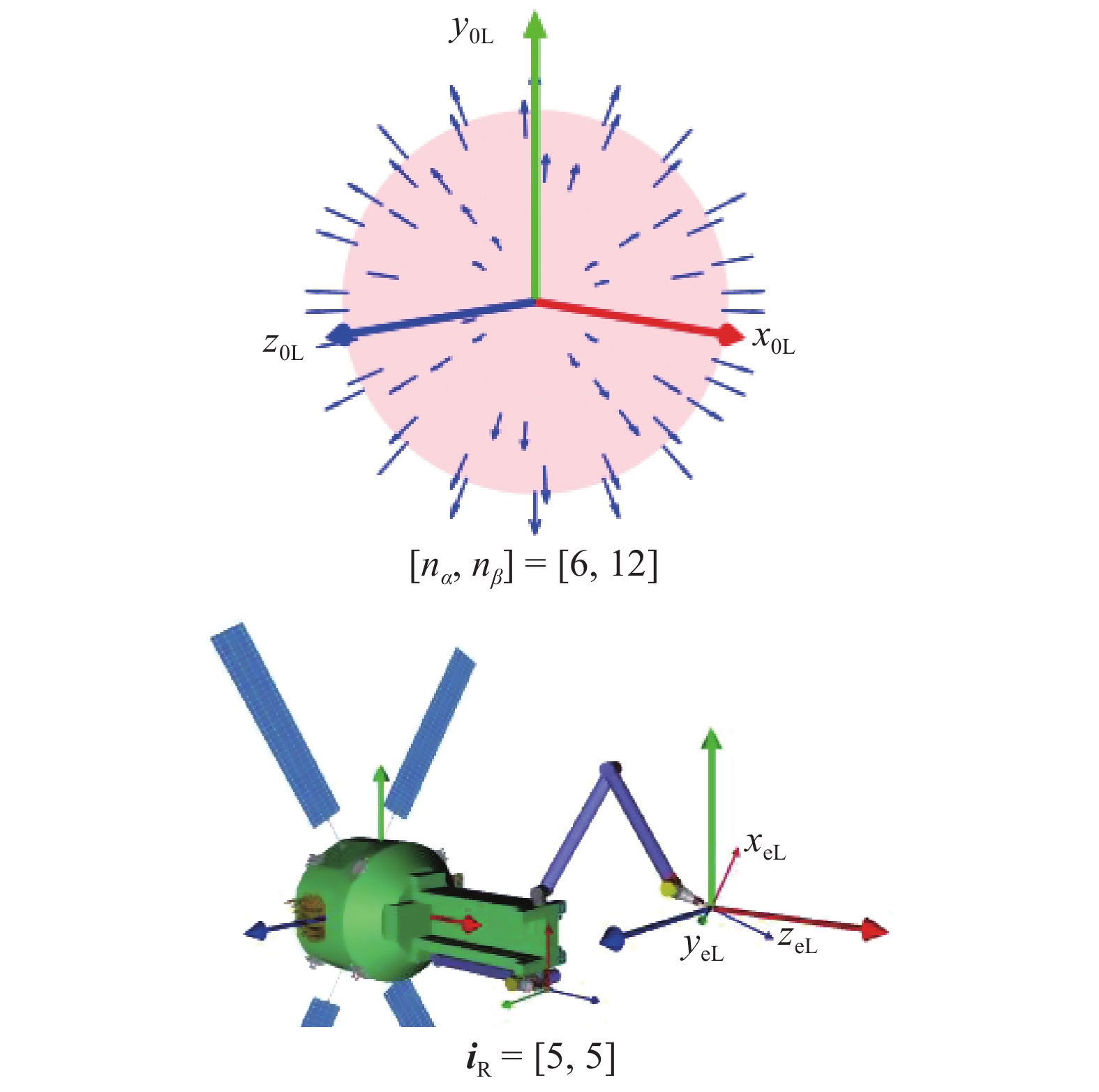
注意到, 如果机械臂末端关节可以自由旋转, 那么末端执行器能够以任意的方向沿着可行的z轴到达球心, 如图3所示. 为了便于查询和保存信息, 使用细胞数组
ight}$
ight]$
ight]$
ight)$
ight]$
ight} $
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
任务空间机械臂末端执行器位姿表示
Figure
3.
Pose of end-effector described in task space
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-4.jpg'" class="figure_img
figure_type2 ccc " id="Figure4" />
图
4
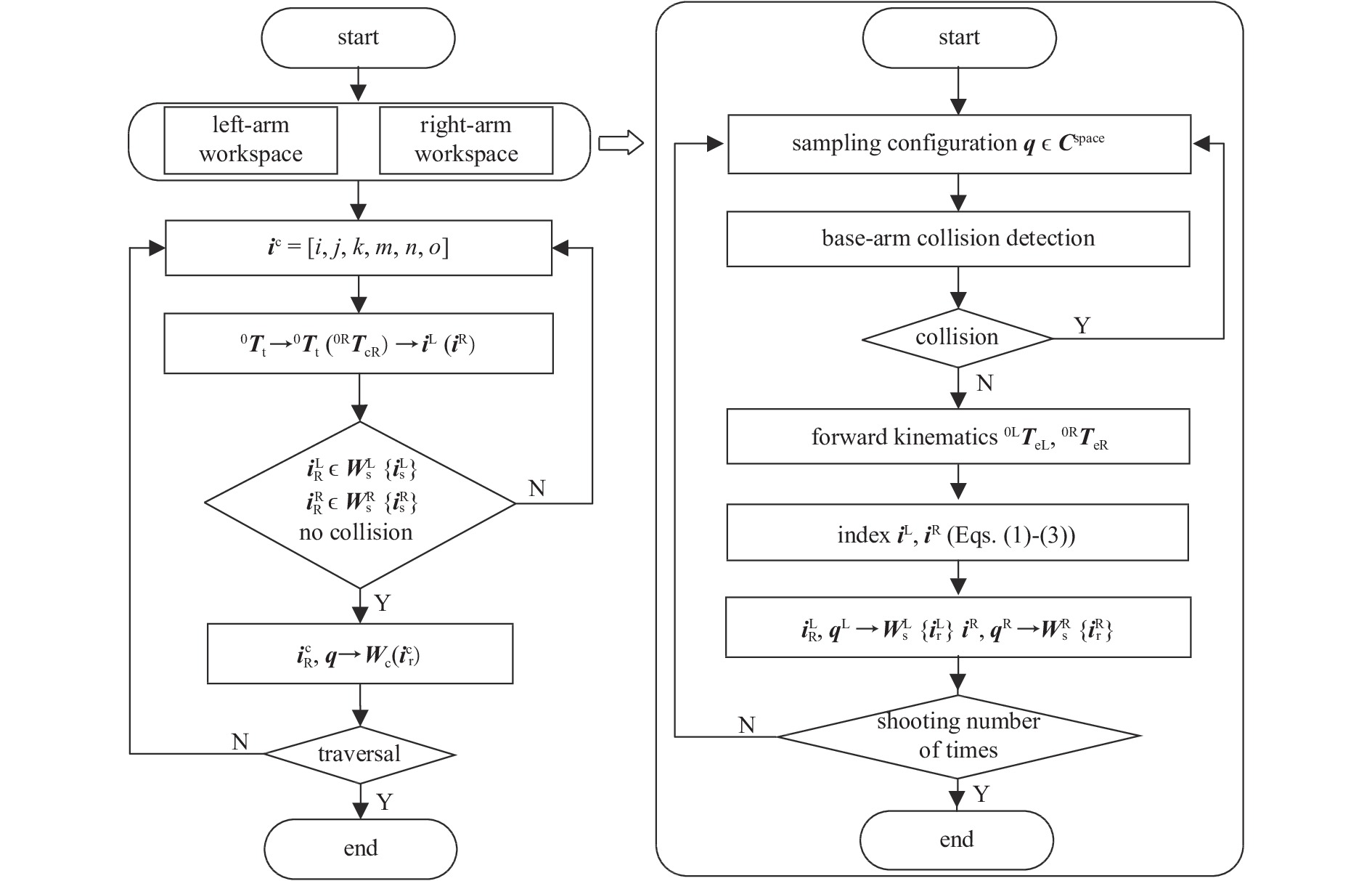
工作空间生成算法流程图
Figure
4.
Flow chart of workspace generation algorithm
下载: 全尺寸图片
幻灯片
1.3
协调工作空间
抓捕后的组合体系统包含闭运动学链, 位置级的闭链约束表示为
$$ left.begin{split}& {{}^{{text{0L}}}{{boldsymbol{T}}_{{text{eL}}}} = {}^{{text{0L}}}{{boldsymbol{T}}_0}{}^{text{0}}{{boldsymbol{T}}_{text{t}}}{}^{text{t}}{{boldsymbol{T}}_{{text{eL}}}}} & {{}^{{text{0R}}}{{boldsymbol{T}}_{{text{eR}}}} = {}^{{text{0R}}}{{boldsymbol{T}}_0}{}^{text{0}}{{boldsymbol{T}}_{text{t}}}{}^{text{t}}{{boldsymbol{T}}_{{text{eR}}}}} end{split} ight}$$  | (4) |
其中, 符号
ight),{text{t}}$
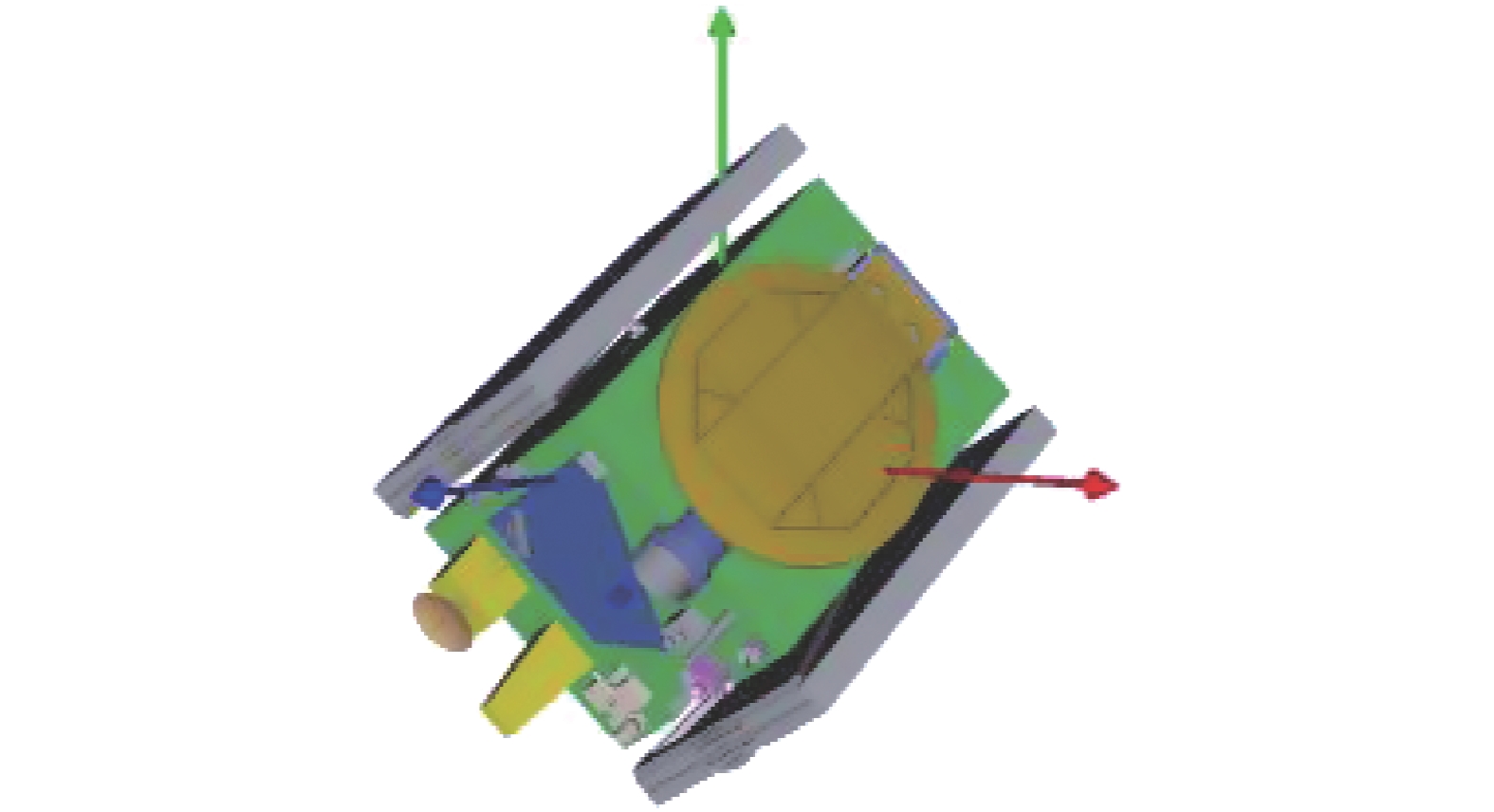
同样的, 使用细胞数组
ight}$
ight]$
ight}$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
任务空间目标位姿表示
Figure
5.
Pose of target described in task space
下载: 全尺寸图片
幻灯片
2.
任务兼容度
空间双臂机器人抓捕目标时末端执行器与目标接触形成闭链系统, 如图1所示. 为了快速地消除目标的翻滚运动, 双臂末端执行器在跟踪抓捕点运动的同时需要沿着翻滚反方向对目标施加力矩抑制目标的翻滚. 由于任务兼容度描述了机械臂在某一方向的操作能力, 可以用于评估双臂对目标翻滚运动的跟踪和消旋能力. 为了增加双臂对目标的消旋能力, 本文使用力任务兼容度作为空间双臂机器人最优抓捕构型的评估指标. 本节在分析运动学与动力学映射的基础上, 提出了一种新的缩放因子法可以更加准确地计算任务兼容度.
2.1
速度映射
空间双臂机器人的运动学方程为
$$ {dot{boldsymbol{x}}_{text{e}}} = {{boldsymbol{J}}_{text{b}}}{dot{boldsymbol{x}}_{text{b}}} + {{boldsymbol{J}}_{text{m}}}dot{boldsymbol{q}} $$  | (5) |
其中,
ight]^{text{T}}} in {mathbb{R}^{12}}$
ight]^{text{T}}} in {mathbb{R}^{2n}}$
假设抓捕前空间机器人系统动量为零, 目标初始动量为
$$ {{boldsymbol{H}}_{{text{bc}}}}{dot{boldsymbol{x}}_{text{b}}} + {{boldsymbol{H}}_{{text{mc}}}}dot{boldsymbol{q}} = {{boldsymbol{p}}_{text{0}}} $$  | (6) |
其中,
$$ {dot{boldsymbol{x}}_{text{e}}} = bar{boldsymbol{Jdot q}} + {{boldsymbol{J}}_{text{b}}}{boldsymbol{H}}_{{text{bc}}}^{ - 1}{{boldsymbol{p}}_0} $$  | (7) |
其中,
$$ {{boldsymbol{G}}^{text{T}}}{dot{boldsymbol{x}}_{text{t}}} = {dot{boldsymbol{x}}_{text{e}}} $$  | (8) |
其中,
$$ {boldsymbol{G}} = left[ {begin{array}{*{20}{c}} {boldsymbol{E}}&{bf{0}}&{boldsymbol{E}}&{bf{0}} {{{left( {{{boldsymbol{r}}_{text{L}}}} ight)}^ times }}&{boldsymbol{E}}&{{{left( {{{boldsymbol{r}}_{text{R}}}} ight)}^ times }}&{boldsymbol{E}} end{array}} ight] $$  |
其中,
ight)^ times } $
$$ dot{boldsymbol{q}} = {bar{boldsymbol{J}}_{text{v}}}{dot{boldsymbol{x}}_{text{t}}} + {{boldsymbol{delta }}_{text{v}}} $$  | (9) |
其中,
2.2
力映射
自由漂浮空间机器人系统的动力学方程为
$$ {boldsymbol{Hddot x}} + {boldsymbol{c}} = left[ {begin{array}{*{20}{c}} {bf{0}} {boldsymbol{tau }} end{array}} ight] - {{boldsymbol{J}}^{text{T}}}{{boldsymbol{F}}_{text{e}}} $$  | (10) |
其中,
ight]^{text{T}}}$
ight]^{text{T}}} in {mathbb{R}^{2n}} $
ight) times left( {6 + 2n}
ight)}}$
ight]$
$$ {boldsymbol{G}}{{boldsymbol{F}}_{text{e}}} = {{boldsymbol{F}}_{text{t}}} $$  | (11) |
因此, 抓捕后组合体中目标的动力学方程为
$$ {{boldsymbol{H}}_{text{t}}}{ddot{boldsymbol{x}}_{text{t}}} + {{boldsymbol{c}}_{text{t}}} = {boldsymbol{G}}{{boldsymbol{F}}_{text{e}}} $$  | (12) |
其中,
$$ {{boldsymbol{G}}^{text{T}}}{ddot{boldsymbol{x}}_{text{t}}} + {dot{boldsymbol{G}}^{text{T}}}{dot{boldsymbol{x}}_{text{t}}} = {boldsymbol{Jddot x}} + dot{boldsymbol{Jdot x}} $$  | (13) |
将式(10)和式(12)代入式(13)中, 可以得到
$$ {{boldsymbol{A}}_1}{{boldsymbol{F}}_{text{e}}} = {{boldsymbol{A}}_2}{boldsymbol{tau }} + {{boldsymbol{delta }}_1} $$  | (14) |
其中,
$$ {{boldsymbol{F}}_{text{t}}} = {boldsymbol{GA}}_1^{ - 1}{{boldsymbol{A}}_2}{boldsymbol{tau }} + {boldsymbol{GA}}_1^{ - 1}{{boldsymbol{delta }}_1} $$  | (15) |
因此, 关节空间与任务空间的力映射关系可以表示为
$$ {boldsymbol{tau }} = {bar{boldsymbol{J}}_{text{f}}}{{boldsymbol{F}}_{text{t}}} + {{boldsymbol{delta }}_{text{f}}} $$  | (16) |
其中
ight)^ + }$
ight)^ + }{boldsymbol{GA}}_1^{ - 1}{{boldsymbol{delta }}_1}$
2.3
任务兼容度
任务兼容度描述了机械臂沿着任务方向的操作能力. 与传统的使用操作椭球法计算相比[21], 本文采用缩放因子法可以更加准确的计算任务兼容度. 给定关节约束
ight| leqslant {boldsymbol{l}}_{text{v}}^{{text{max}}}$
ight| leqslant {boldsymbol{l}}_{text{f}}^{{text{max}}}$
ight)$
$$ - {boldsymbol{l}}_i^{max } leqslant {bar{boldsymbol{J}}_i}{{boldsymbol{u}}_i}{a_i} + {{boldsymbol{delta }}_i} leqslant {boldsymbol{l}}_i^{max },{text{ }}i = {{v,;f}} $$  | (17) |
将式(17)展 开为矩阵形式
$$ left[ {begin{array}{*{20}{c}} { - l_{i,1}^{max } leqslant {{left( {{{bar{boldsymbol{J}}}_i}{{boldsymbol{u}}_i}} ight)}_1}{a_i} + {delta _{i,1}} leqslant l_{i,1}^{max }} { - l_{i,2}^{max } leqslant {{left( {{{bar{boldsymbol{J}}}_i}{{boldsymbol{u}}_i}} ight)}_2}{a_i} + {delta _{i,2}} leqslant l_{i,2}^{max }} vdots { - l_{i,2n}^{max } leqslant {{left( {{{bar{boldsymbol{J}}}_i}{{boldsymbol{u}}_i}} ight)}_{2n}}{a_i} + {delta _{i,2n}} leqslant l_{i,2n}^{max }} end{array}} ight],{text{ }}i = {{v,;f}} $$  | (18) |
上述不等式约束可以通过式(19)计算
$$ left. {begin{array}{*{20}{c}} {dfrac{{ - l_{i,j}^{max } - {delta _{i,j}}}}{{{{left( {{{bar{boldsymbol{J}}}_i}{{boldsymbol{u}}_i}} ight)}_j}}} leqslant {a_i} leqslant dfrac{{l_{i,j}^{max } - {delta _{i,j}}}}{{{{left( {{{bar{boldsymbol{J}}}_i}{{boldsymbol{u}}_i}} ight)}_j}}}},&{{{left( {{{bar{boldsymbol{J}}}_i}{{boldsymbol{u}}_i}} ight)}_j} > 0} {{a_i} = + infty },;;;{{{left( {{{bar{boldsymbol{J}}}_i}{{boldsymbol{u}}_i}} ight)}_j} = 0,;;;{delta _{i,j}} leqslant l_{i,j}^{max }} {{a_i} = - infty },;;;{{{left( {{{bar{boldsymbol{J}}}_i}{{boldsymbol{u}}_i}} ight)}_j} = 0,;;;{delta _{i,j}} > l_{i,j}^{max }} {dfrac{{l_{i,j}^{max } - {delta _{i,j}}}}{{{{left( {{{bar{boldsymbol{J}}}_i}{{boldsymbol{u}}_i}} ight)}_j}}} leqslant {a_i} leqslant dfrac{{ - l_{i,j}^{max } - {delta _{i,j}}}}{{{{left( {{{bar{boldsymbol{J}}}_i}{{boldsymbol{u}}_i}} ight)}_j}}}},&{{{left( {{{bar{boldsymbol{J}}}_i}{{boldsymbol{u}}_i}} ight)}_j} < 0} end{array}} ight} $$  | (19) |
在关节速度或力矩约束下,
ight)$
$$ {a_i} = min left( {{a_{i,j}}} ight),{text{ }}j = 1,2, cdots ,2n $$  | (20) |
3.
抓捕策略
为了实现对目标的捕获, 需要首先确定机械臂对目标的抓捕点以及抓捕时空间机器人的抓捕构型(基座位姿和机械臂构型). 为了更好地执行抓捕任务, 抓捕点和抓捕构型需要根据任务需求选取合适的度量指标进行优化. 为了增加机械臂对目标操作的灵巧度以及快速地实现对翻滚目标的消旋, 本文使用全局操作灵巧度指标优化抓捕点, 使用考虑相机视角约束和末端速度跟踪约束的力任务兼容度指标选取最优抓捕构型.
3.1
抓捕点确定
首先, 利用协调工作空间分析空间双臂机器人协调操作目标的灵巧度. 双臂可以操作目标从多个方向到达同一个任务空间位置, 到达同一位置的可行方向数量反应了双臂协调操作目标的灵巧度. 基于协调工作空间, 到达单元格
$$ {boldsymbol{D}}left( {{boldsymbol{i}}_{text{r}}^{text{c}}} ight) = frac{{displaystylesum {{{boldsymbol{W}}_{text{c}}}left{ {{boldsymbol{i}}_{text{r}}^{text{c}}} ight}} }}{{left[ {{n_alpha }left( {{n_beta } - 2} ight) + 2} ight]{n_theta }}} $$  | (21) |
其中,
ight) = 0$
ight) = {{max left( {boldsymbol{D}}
ight)} mathord{left/ {vphantom {{max left( {boldsymbol{D}}
ight)} 2}}
ight. } 2}$
ight) = max left( {boldsymbol{D}}
ight)$
$$ {{boldsymbol{D}}_{text{c}}} = frac{{displaystylesum {boldsymbol{D}} }}{N} $$  | (22) |
其中,
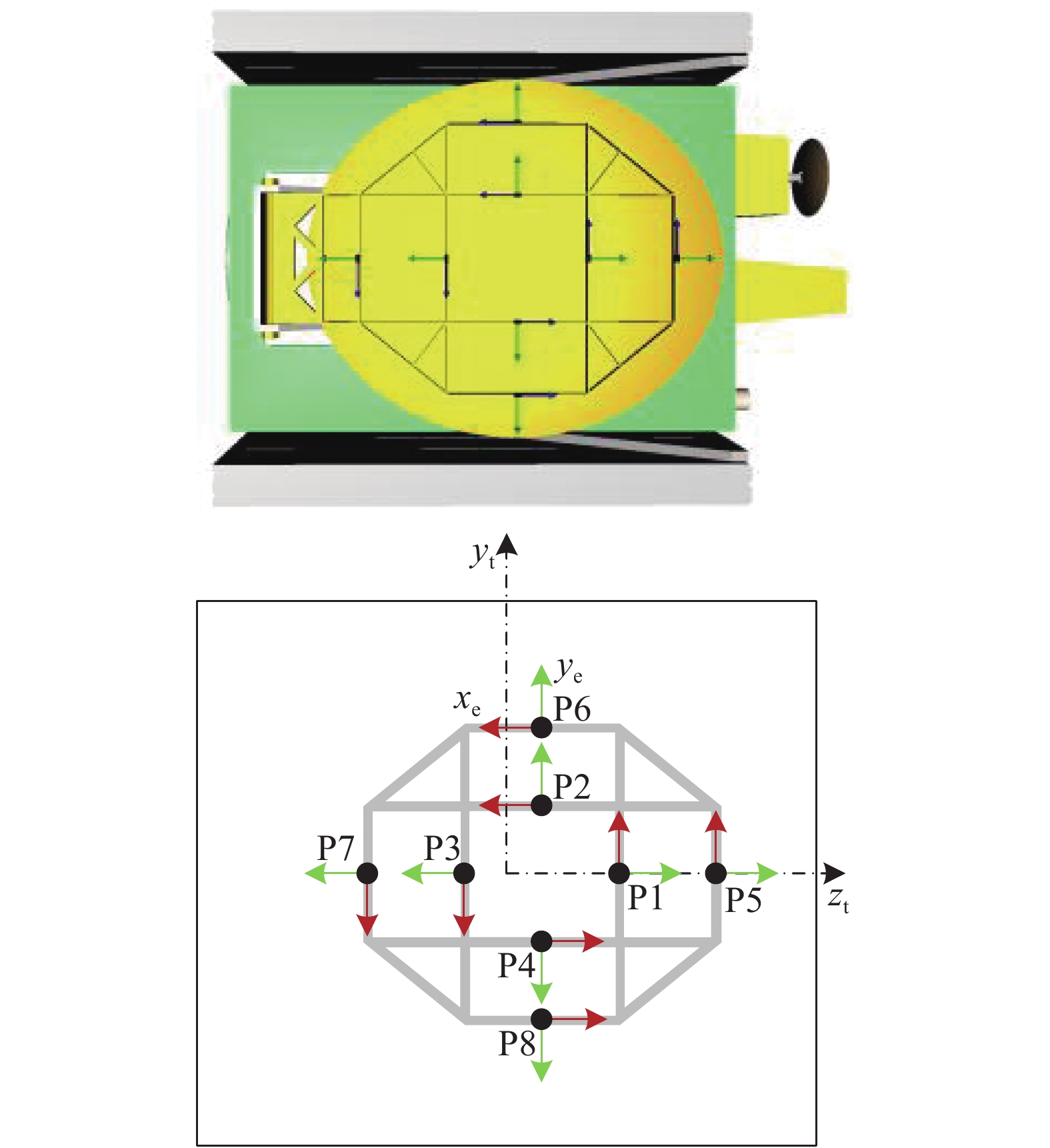
失效卫星上存在多个可行的抓捕机构, 如太阳帆板、对接环和通信天线等. 为了验证方法的有效性, 本文针对图6所示的失效卫星进行研究, 以通信天线上的加强筋为抓捕机构进行抓捕点的选取. 给定通信天线上8个可行的抓捕点, 可行抓捕点即为抓捕目标时末端执行器的位姿, 其相对于目标坐标系的关系在表1中给出. 考虑双臂以及抓捕点的对称性, 双臂协调抓捕目标时需要分析18对可行的抓捕点, 在表2中给出, 分别对应左臂和右臂的抓捕点. 通过分析每对抓捕点所对应的协调工作空间及灵巧度指标, 可以选出双臂协调操作目标的最优抓捕点对.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
目标上可行抓捕点
Figure
6.
Feasible grasping poses on target
下载: 全尺寸图片
幻灯片
表
1
可行抓捕点相对于目标坐标系位姿
Table
1.
Feasible grasping poses relative to target frame
table_type1 ">
| GP | Position/m | Attitude |
| P1 | [?1.22 0 0.58] | [0 0 1; 1 0 0; 0 1 0] |
| P2 | [?1.22 0.35 0.18] | [0 0 1; 0 1 0; ?1 0 0] |
| P3 | [?1.22 0 ?0.22] | [0 0 1; ?1 0 0; 0 ?1 0] |
| P4 | [?1.22 ?0.35 0.18] | [0 0 1; 0 ?1 0; 1 0 0] |
| P5 | [?1.22 0 1.08] | [0 0 1; 1 0 0; 0 1 0] |
| P6 | [?1.22 0.75 0.18] | [0 0 1; 0 1 0; ?1 0 0] |
| P7 | [?1.22 0 ?0.72] | [0 0 1; ?1 0 0; 0 ?1 0] |
| P8 | [?1.22 ?0.75 0.18] | [0 0 1; 0 ?1 0; 1 0 0] |
下载: 导出CSV
|显示表格
表
2
双臂末端执行器协调操作的可行抓捕点对
Table
2.
Feasible grasping point pairs for dual-arm end-effectors cooperative manipulation
table_type1 ">
| GP | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 |
| P1 | × | √ | √ | ? | √ | √ | √ | ? |
| P2 | ? | × | √ | √ | √ | √ | √ | √ |
| P3 | ? | ? | × | ? | √ | √ | √ | ? |
| P4 | ? | ? | ? | × | ? | ? | ? | ? |
| P5 | ? | ? | ? | ? | × | √ | √ | ? |
| P6 | ? | ? | ? | ? | ? | × | √ | √ |
| P7 | ? | ? | ? | ? | ? | ? | × | ? |
| P8 | ? | ? | ? | ? | ? | ? | ? | × |
下载: 导出CSV
|显示表格
3.2
抓捕构型确定
通过传感器观测目标可以得到目标的位姿以及目标的旋转角速度. 为了保证任务的安全, 抓捕目标后双臂末端执行器需要跟踪抓捕点运动的同时尽快地消除目标的翻滚运动. 沿着翻滚反方向的力任务兼容度反映了双臂施加在目标上的最大消旋力矩, 可以作为双臂消旋能力的评估指标. 因此, 本文选取力任务兼容度作为评估抓捕构型的性能指标. 抓捕构型优化问题描述如下
$$left. begin{split}& mathop {{text{max}}}limits_{{{boldsymbol{x}}_{text{b}}},{boldsymbol{q}}} ;;;;{a_{text{f}}}left( {{{boldsymbol{x}}_{text{b}}},{boldsymbol{q}}} ight) hfill & {text{s}}{text{.t}}{text{. }}fleft( {{{boldsymbol{x}}_{text{b}}},{boldsymbol{q}}} ight) = {{boldsymbol{x}}_{text{t}}} hfill & ;;;;;;;;;;{a_{text{v}}} geqslant left| {{{boldsymbol{omega }}_{text{t}}}} ight| hfill & {text{ g}}left( {{{boldsymbol{x}}_{text{b}}},{{boldsymbol{x}}_{text{t}}}} ight) leqslant {gamma _{max }} hfill end{split} ight}$$  | (23) |
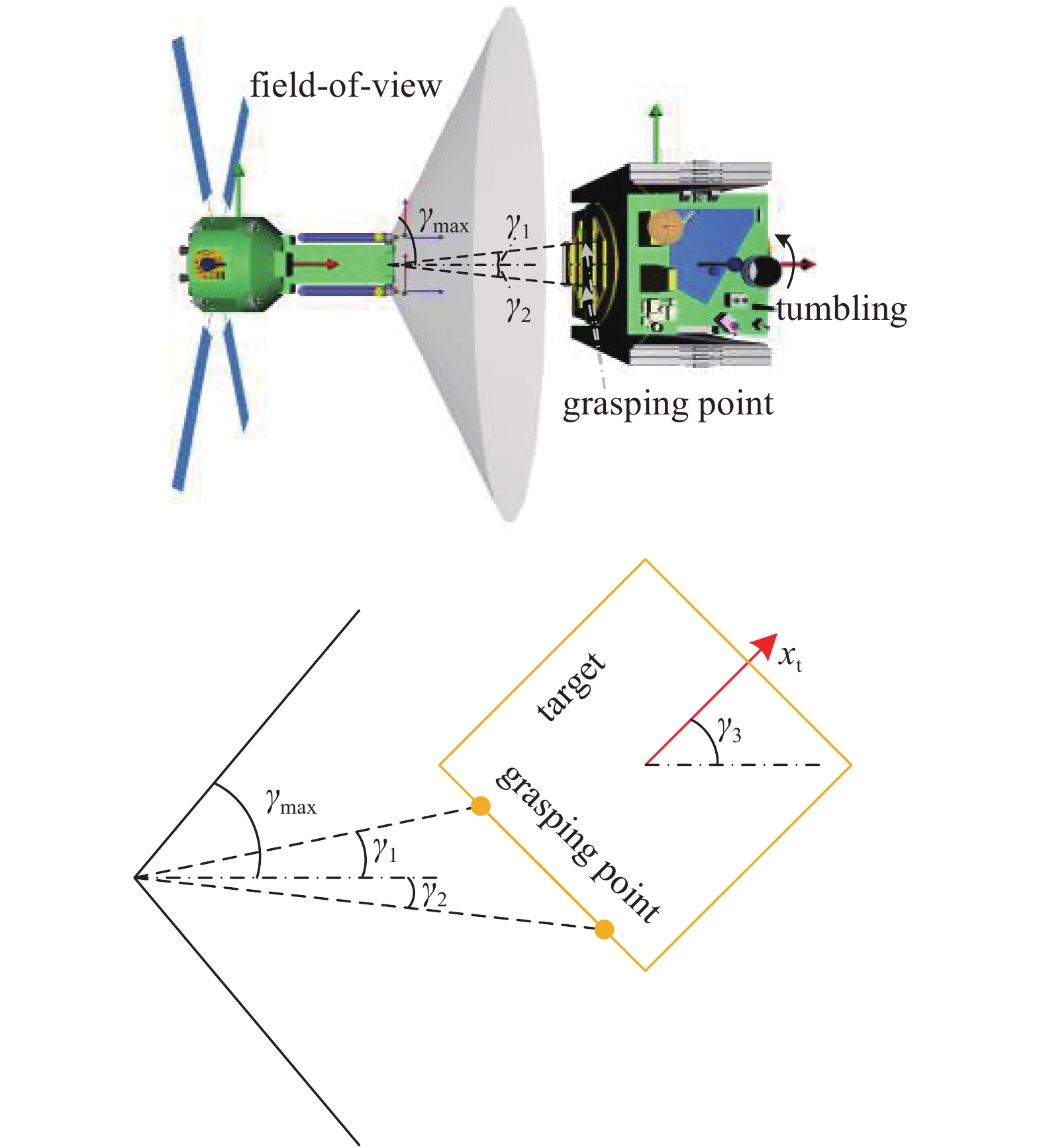
其中, 约束包括双臂协调操作目标时需要保持的闭链约束、双臂末端执行器对翻滚目标的运动跟踪约束(
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
相机视角约束
Figure
7.
Field of view constraint of camera
下载: 全尺寸图片
幻灯片
$$ left.begin{split}& mathop {{text{max}}}limits_{{{boldsymbol{i}}^{text{c}}}} ;;;;{{boldsymbol{M}}_{text{f}}}left( {{{boldsymbol{i}}^{text{c}}}} ight) hfill & {text{s}}{text{.t}}{text{. }}{{boldsymbol{M}}_{text{v}}}left( {{{boldsymbol{i}}^{text{c}}}} ight) geqslant left| {{{boldsymbol{omega }}_{text{t}}}} ight| hfill & ;;;;{gamma _i} leqslant {gamma _{max }},{text{ }}i = 1,2,3 hfill end{split} ight}$$  | (24) |
其中, 能力图谱中指标非零的索引值
$$ {}^{ m{I}}{boldsymbol{T}}_{text{b}}^* = {}^{ m{I}}{{boldsymbol{T}}_{text{t}}}{left( {{}^0{boldsymbol{T}}_{text{t}}^{text{*}}} ight)^{ - 1}}{left( {{}^{text{b}}{{boldsymbol{T}}_0}} ight)^{ - 1}} $$  | (25) |
其中,
ight)^{ - 1}}$
$$ {}^j{{boldsymbol{T}}_i} = left[ {begin{array}{*{20}{c}} {boldsymbol{R}}&{boldsymbol{r}} {bf{0}}&1 end{array}} ight] to {left( {{}^j{{boldsymbol{T}}_i}} ight)^{ - 1}} = left[ {begin{array}{*{20}{c}} {{{boldsymbol{R}}^{text{T}}}}&{ - {{boldsymbol{R}}^{text{T}}}{boldsymbol{r}}} {bf{0}}&1 end{array}} ight] $$  |
4.
仿真算例
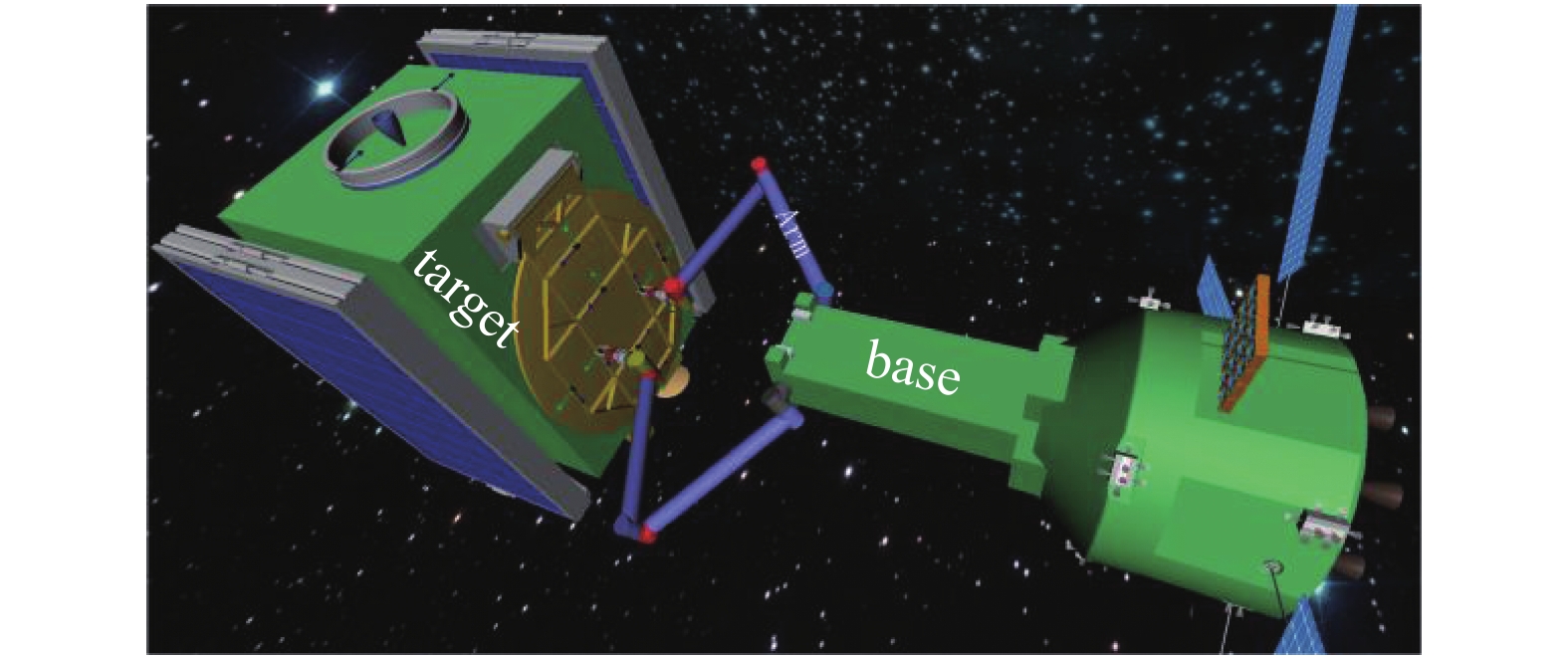
为了验证能力评估在抓捕决策问题中的有效性, 采用图8所示的7自由度空间双臂机器人和目标进行仿真验证. 系统的运动学和动力学参数如表3所示. 目标上的可行抓捕点见表1 ~ 表2. 机械臂关节角度约束为: 关节2为
m{{text{π}}}}} mathord{left/ {vphantom {{ - {
m{{text{π}}}}} {2,}}}
ight. } {2,}};{{
m{{text{π}}}} / 2}}
ight)$
m{{text{π}}}},{
m{{text{π}}}}}
ight)$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
空间双臂机器人抓捕目标
Figure
8.
Dual-arm space robot grasping a target
下载: 全尺寸图片
幻灯片
表
3
空间机器人系统的运动学和动力学参数
Table
3.
Kinematic and dynamic parameters of system
table_type1 ">
| Joint | $ a/{ m{m}}$ | $ alpha/(^ circ )$ | $ b/{ m{m}}$ | $ q/(^ circ )$ | $ {{m}}/{ m{kg}}$ | $ I_{{xx}}/({ m{kg}}cdot { m{m}}^2)$ | $ I_{{yy}}/ ({ m{kg}}cdot { m{m}}^2)$ | $ I_{{zz}}/ ({ m{kg}}cdot { m{m}}^2)$ |
| 0 | 2.52 | 0 | ±0.446 | 0 | 400 | 128 | 340 | 340 |
| 1 | 0 | $ mp $90 | 0 | $ q_1^j$ | 3 | 0.0041 | 0.0041 | 0.0096 |
| 2 | 0 | ?90 | 0.168 | $ q_2^j$ | 8 | 1.3824 | 0.0256 | 1.3824 |
| 3 | 0 | 90 | 1.450 | $ q_3^j$ | 2 | 0.0047 | 0.0064 | 0.0047 |
| 4 | 0 | 90 | 0.168 | $ q_4^j$ | 6 | 0.8712 | 0.0192 | 0.8712 |
| 5 | 0 | 90 | 1.290 | $ q_5^j$ | 2 | 0.0047 | 0.0064 | 0.0047 |
| 6 | 0 | ?90 | 0.168 | $ q_6^j$ | 2 | 0.0047 | 0.0047 | 0.0064 |
| 7 | 0 | 90 | 0.44 | $ q_7^j$ | 4 | 0.0645 | 0.0645 | 0.0128 |
| target | ? | ? | ? | ? | 100 | 50 | 50 | 50 |
下载: 导出CSV
|显示表格
机械臂展开的最大长度为3.3 m, 选取离散率
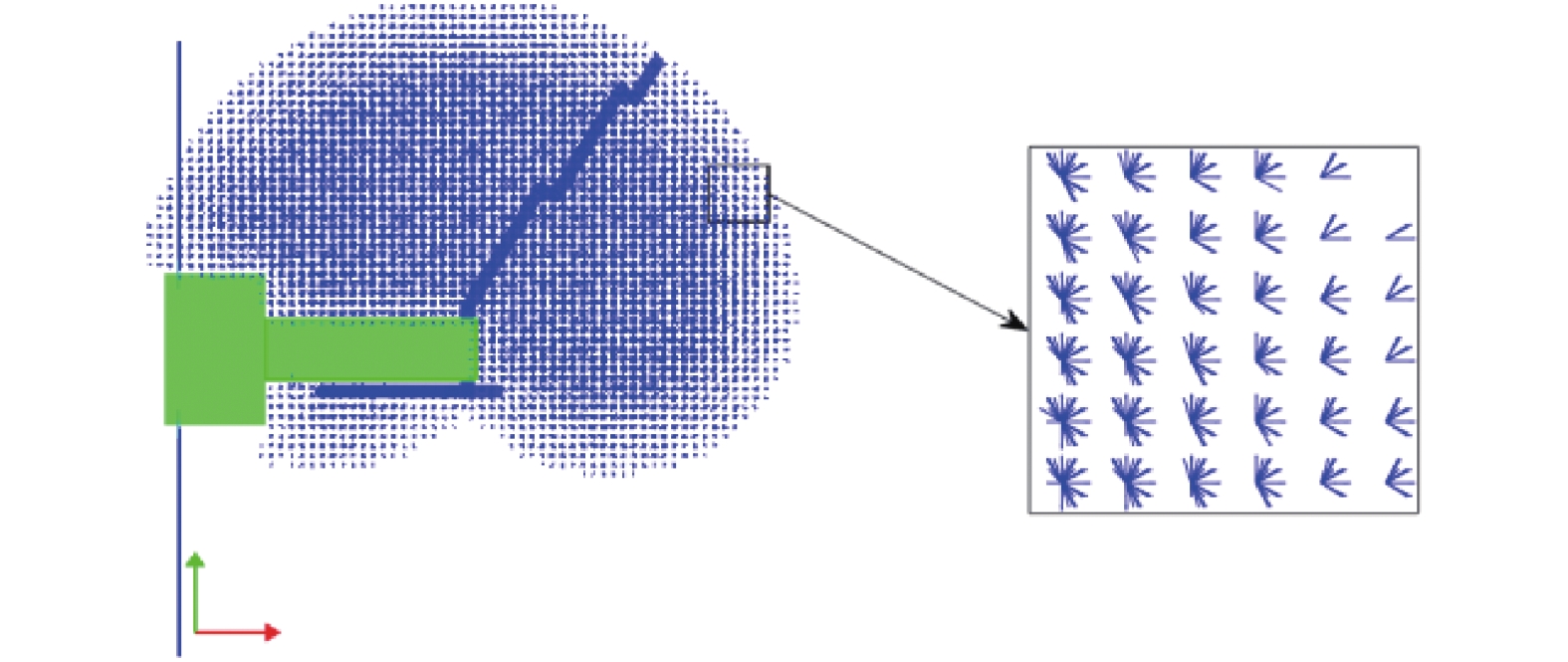onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
左臂工作空间
Figure
9.
Workspace of left-arm
下载: 全尺寸图片
幻灯片
机械臂操作目标到达的最远距离为5.2 m, 协调工作空间的离散率设置为
ight]$
ight]$
ight]$
ight]$
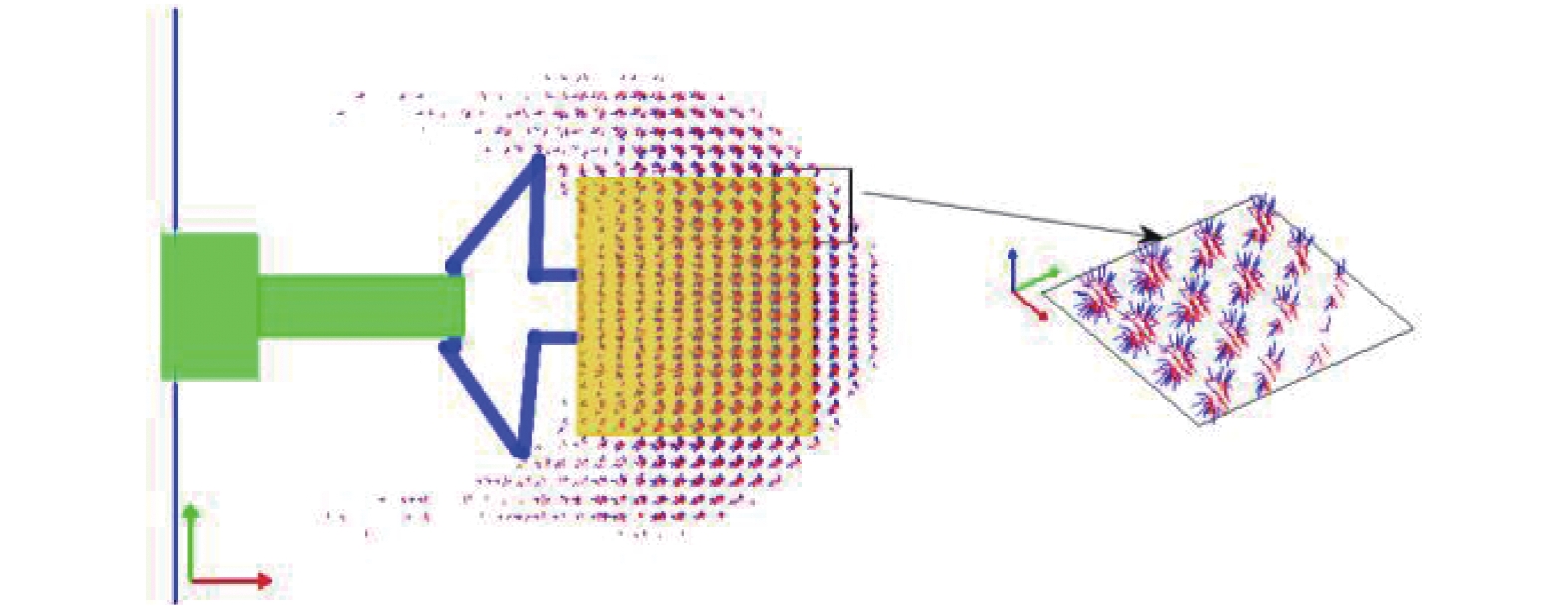onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-10.jpg'" class="figure_img
figure_type1 bbb " id="Figure10" />
图
10
协调工作空间(
ight] $
Figure
10.
Cooperative workspace(
ight] $
下载: 全尺寸图片
幻灯片
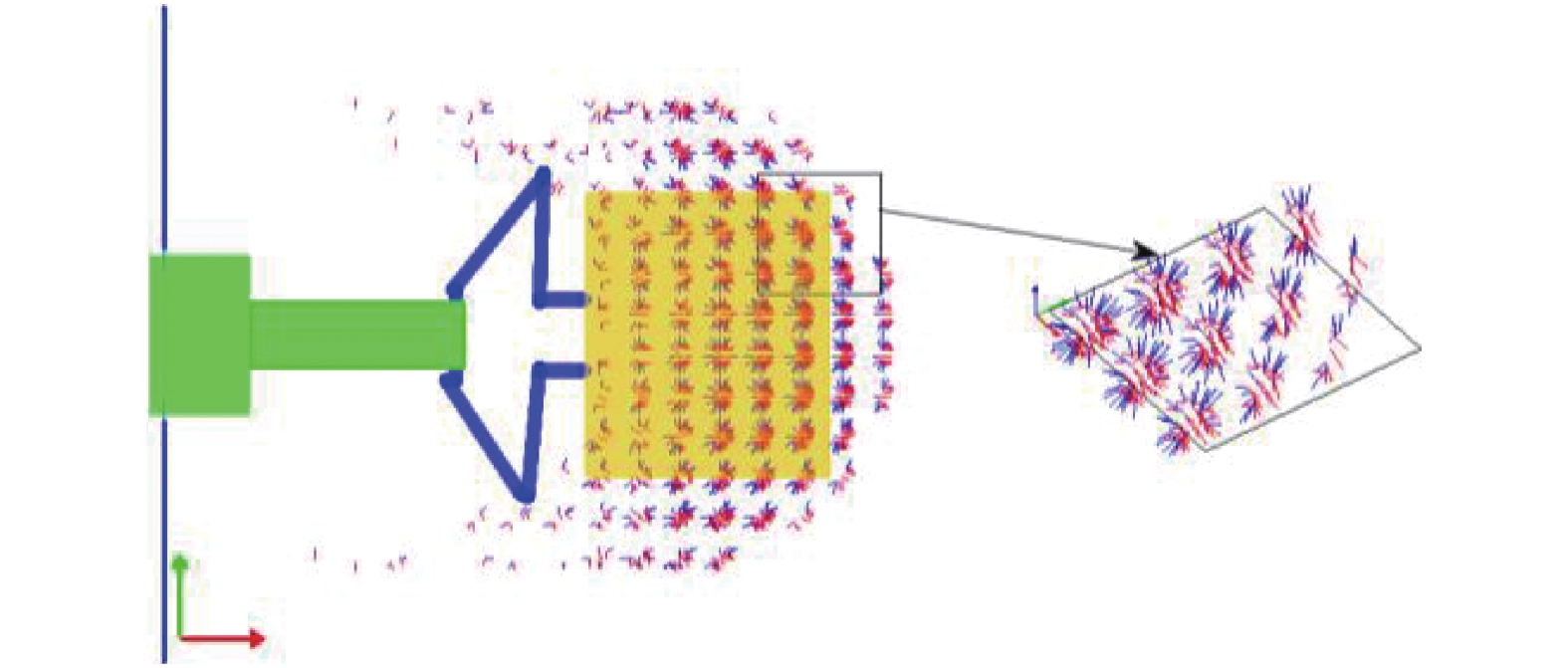onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-11.jpg'" class="figure_img
figure_type1 bbb " id="Figure11" />
图
11
协调工作空间(
ight] $
Figure
11.
Cooperative workspace (
ight]$
下载: 全尺寸图片
幻灯片
4.1
抓捕点优化
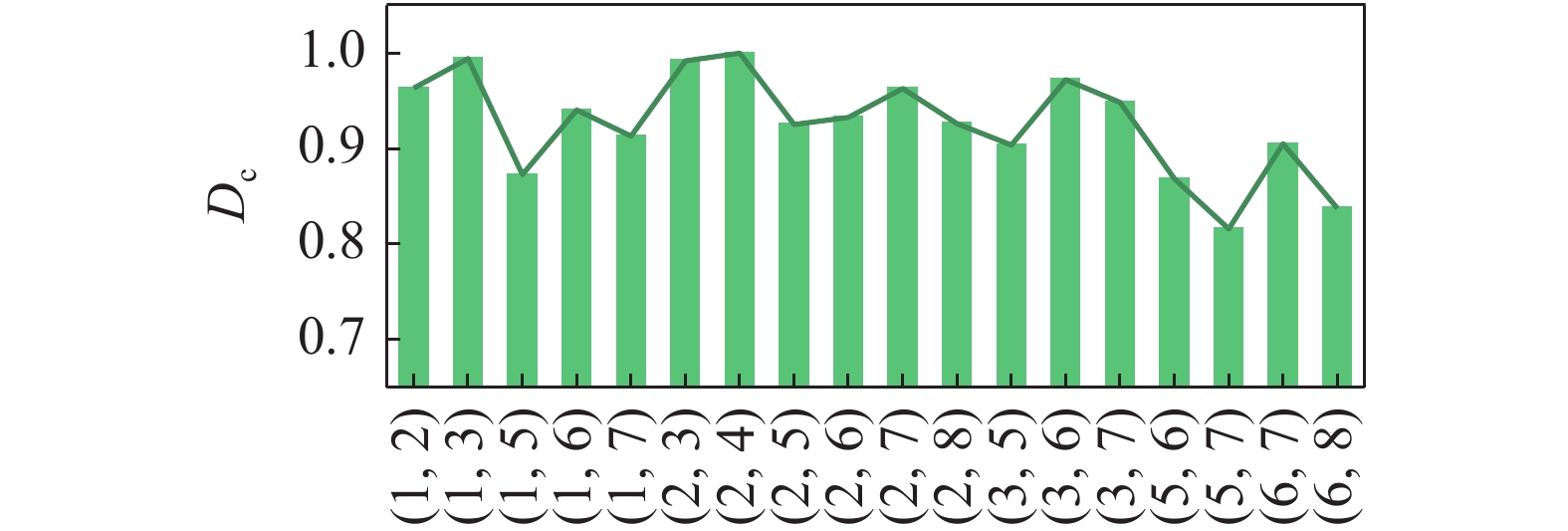
每个单元格内球上的可行方向数量反映了机械臂在对应位置的灵巧度. 空间双臂机器人末端执行器从不同的抓捕点抓捕目标时所对应的灵巧度是不同的. 而闭链约束的存在极大地限制了协调工作空间的灵巧度. 为了增加对目标操作的灵活性, 本文采用工作空间内平均灵巧度指标选取最优抓捕点. 首先, 计算18对抓捕点对应的协调工作空间. 当离散率选取为
ight]$
ight]$
ight]$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-12.jpg'" class="figure_img
figure_type1 bbb " id="Figure12" />
图
12
不同抓捕点的灵巧度
Figure
12.
Dexterity of different grasping points
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-13.jpg'" class="figure_img
figure_type1 bbb " id="Figure13" />
图
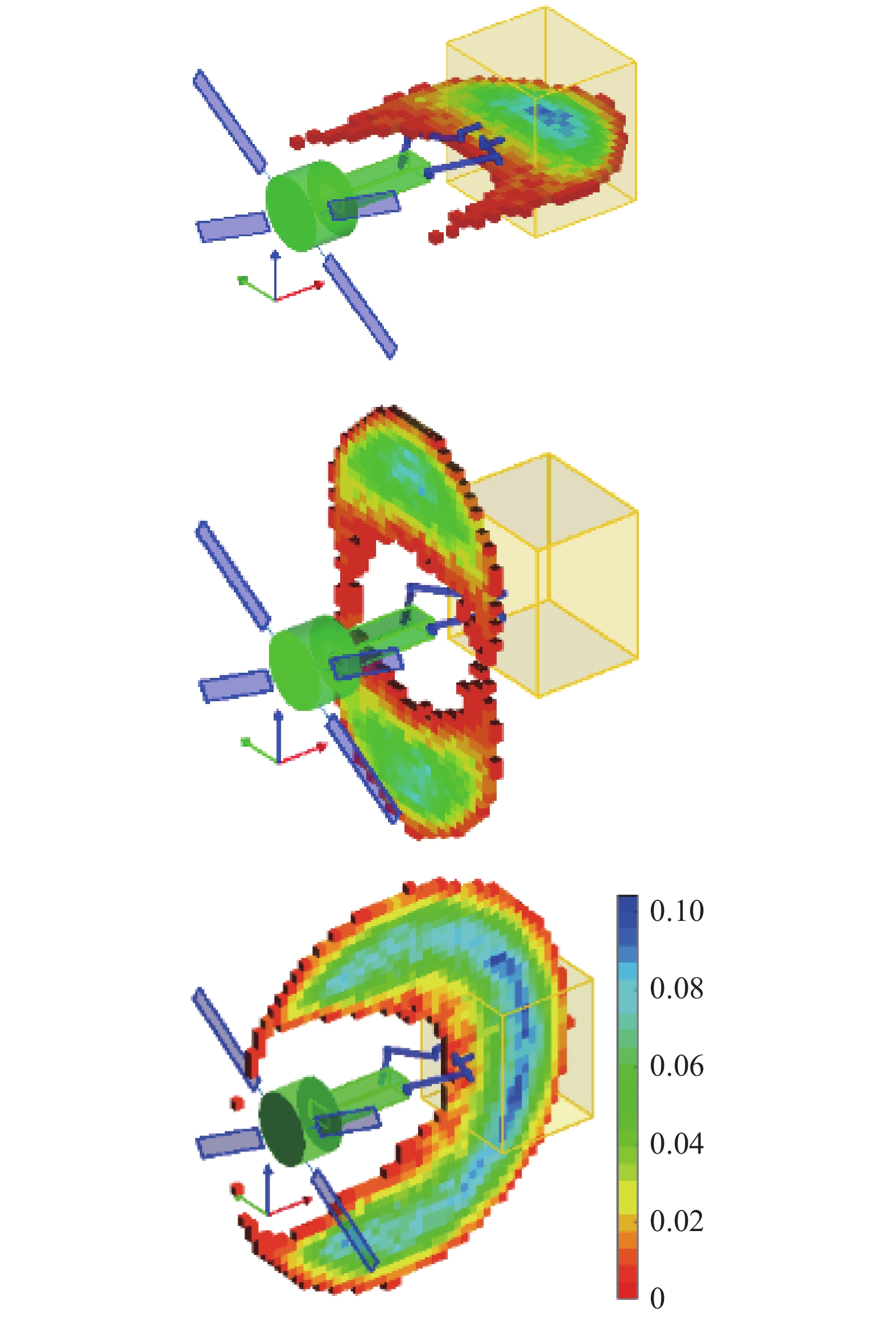
13
抓捕点为(P2, P4)的灵巧度能力图谱
Figure
13.
Dexterity capability map for grasping (P2, P4)
下载: 全尺寸图片
幻灯片
4.2
抓捕构型优化
假设翻滚目标绕
ight| leqslant {text{1}}{text{.047 2 rad/s}}$
ight| leqslant 1{text{0 N}}$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-14.jpg'" class="figure_img
figure_type1 bbb " id="Figure14" />
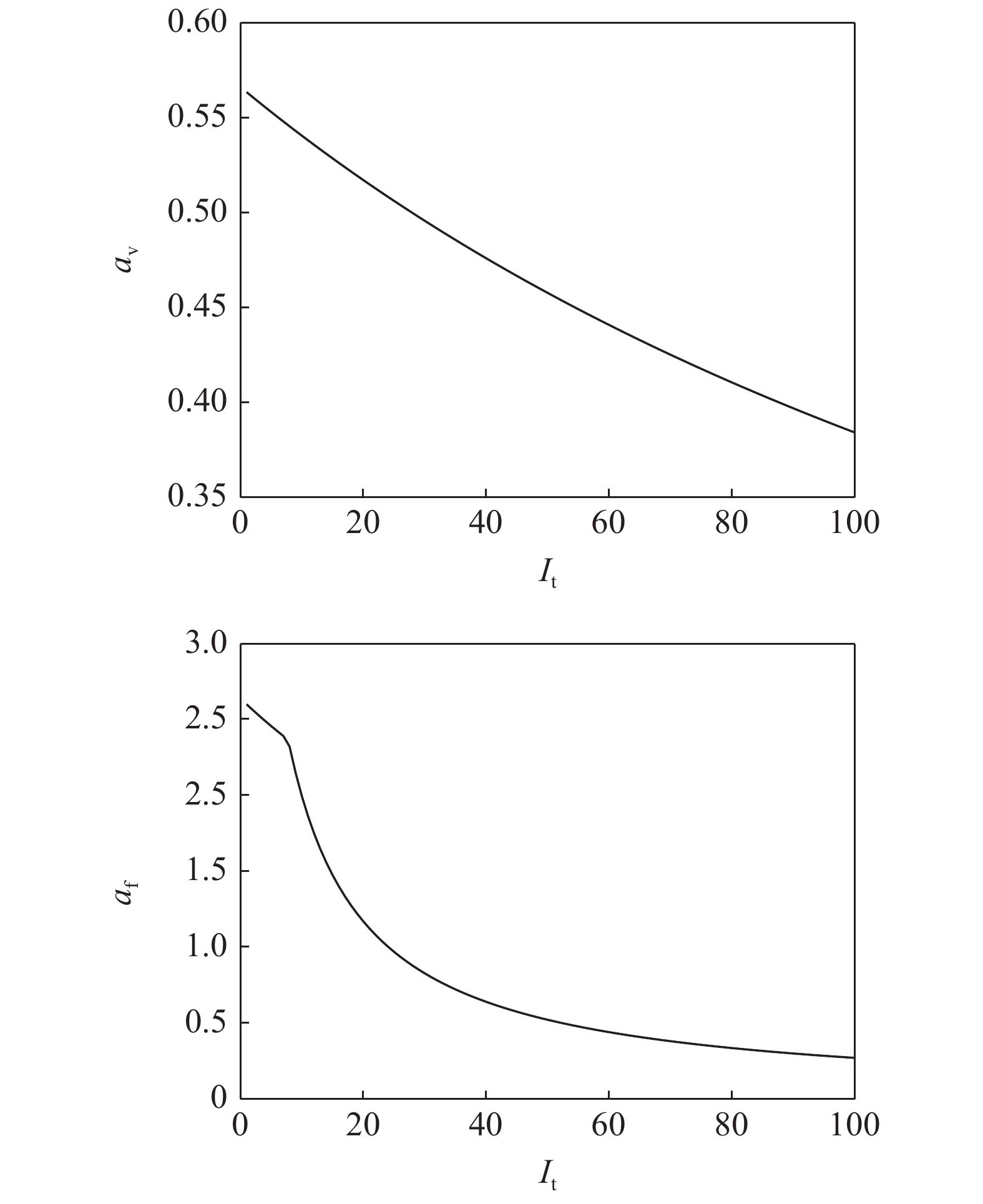
图
14
任务兼容度与目标惯量的关系
Figure
14.
The relationship between task compatibility and target inertia parameter
下载: 全尺寸图片
幻灯片
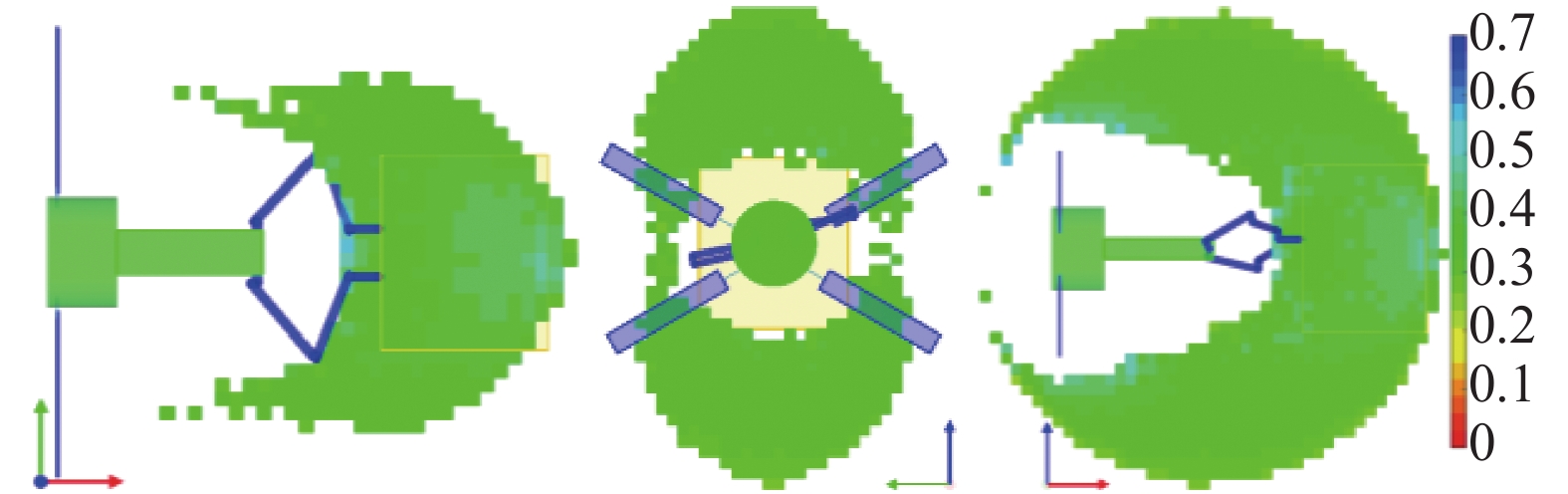
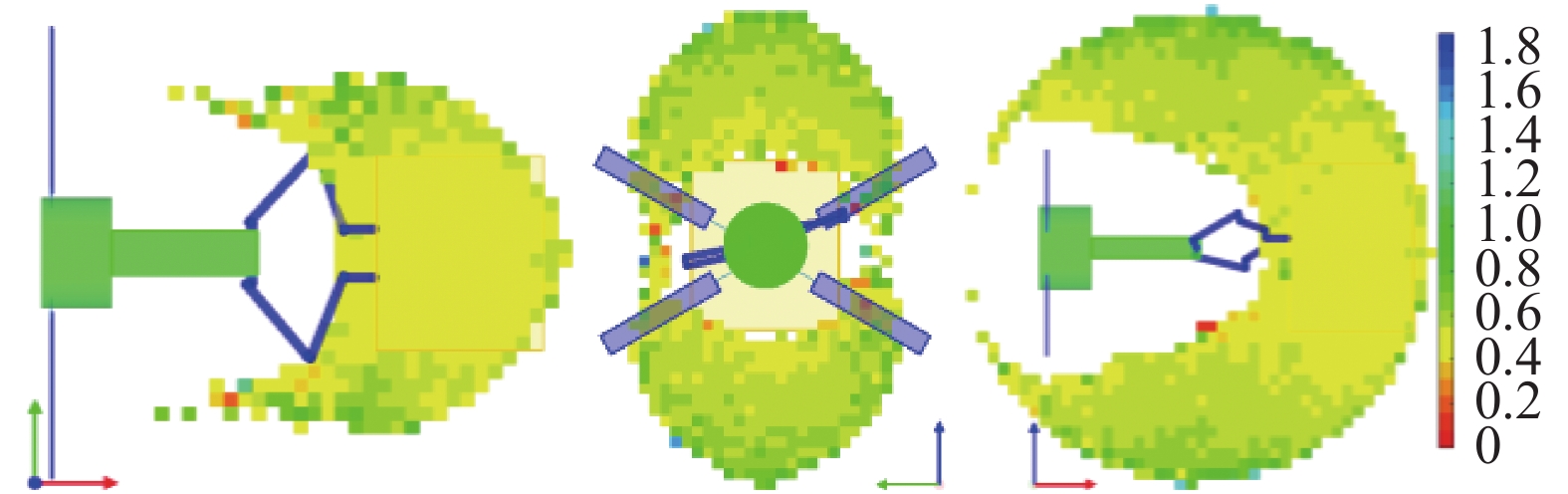
图15和图16分别给出了自由漂浮模式下目标惯量为
ight]}
ight)$
ight]$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-15.jpg'" class="figure_img
figure_type1 bbb " id="Figure15" />
图
15
速度任务兼容度能力图谱
Figure
15.
Capability map of velocity task compatibility
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-16.jpg'" class="figure_img
figure_type1 bbb " id="Figure16" />
图
16
力任务兼容度能力图谱
Figure
16.
Capability map of force task compatibility
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-17.jpg'" class="figure_img
figure_type1 bbb " id="Figure17" />
图
17
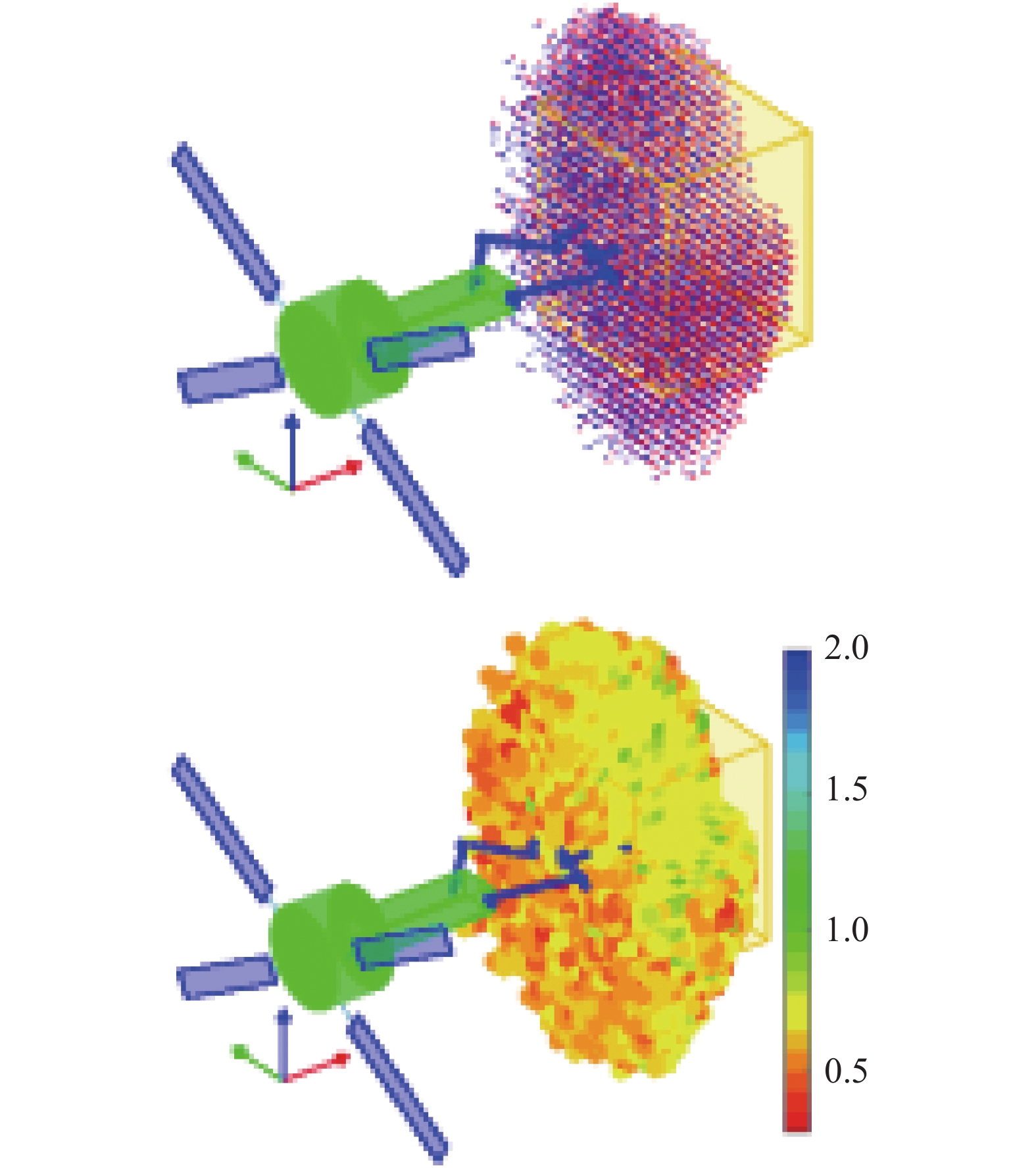
约束力任务兼容度能力图谱
Figure
17.
Capability map of force task compatibility under constraints
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-436-18.jpg'" class="figure_img
figure_type1 bbb " id="Figure18" />
图
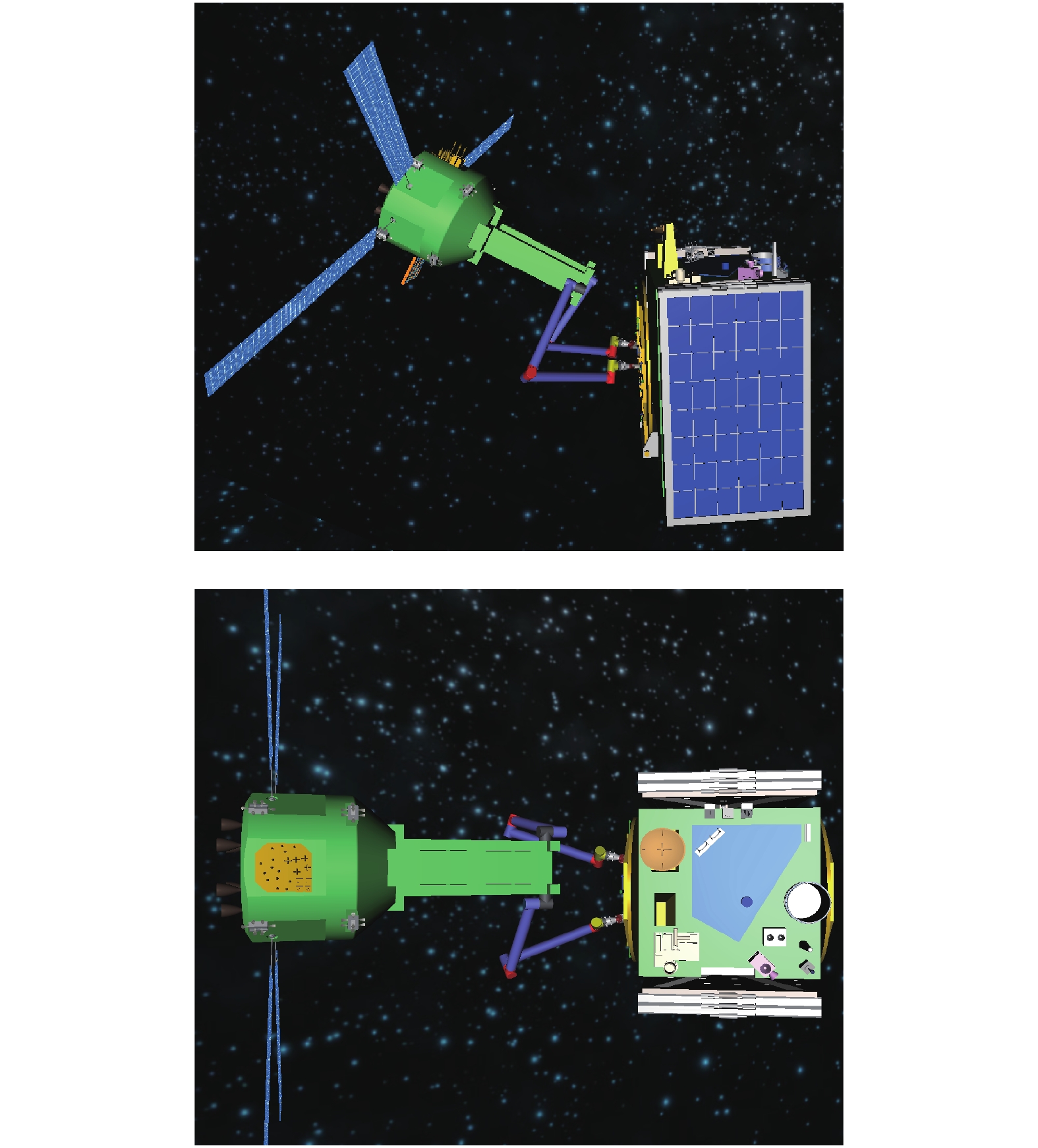
18
抓捕翻滚目标时的抓捕点和抓捕构型
Figure
18.
Grasping points and configuration for grasping tumbling target
下载: 全尺寸图片
幻灯片
5.
结 论
抓捕翻滚目标时, 抓捕点和抓捕构型会极大地影响空间机器人对目标的操作能力. 为了更好地实现对翻滚目标的捕获, 本文基于空间双臂机器人协调操作能力评估开展抓捕策略优化. 全局灵巧度指标被用于优化抓捕点的选取以增加双臂操作目标的灵巧性, 速度跟踪及相机视角约束下的力任务兼容度指标用于优化抓捕构型以增强对翻滚目标的消旋能力. 通过仿真给出了抓捕策略优化的结果, 证明了操作能力分析在抓捕决策问题中的有效性.
本文提出了一种有效的针对动态目标的抓捕策略优选方法. 但是未考虑目标参数不确定的情况, 在未来研究中需要进一步考虑目标动力学参数对抓捕策略的影响. 此外, 操作能力分析结果也可用于双臂协调操作任务的可行性评估、运动规划与控制等问题中以提高机器人系统运动的协调性.
