引 言

颗粒移动床在工业生产中具有很广泛的应用, 如燃料热解气化^[1], 烟气除尘^[2], 高温散料余热回收等^[3-4]. 颗粒移动床内的流动特性是工艺设计与优化运行的重要基础, 尚待深入地揭示.

现有的描述移动床颗粒流的研究方法有离散元方法(DEM)和连续性假设方法. 离散元方法从单个颗粒出发研究每个颗粒与其他颗粒作用的详细经历^[5], 模拟精度高, 近年来有很多****应用此方法对移动床内颗粒的流动情况进行研究, 包括移动床的几何构造和颗粒特性对颗粒出流量的影响^[6-8], 移动床壁面的应力分布^[9-10]以及移动床内颗粒绕管特性^[11]等. 但离散元方法的计算量庞大, 且对复杂形状的工业颗粒的表征尚待改进, 对实际大型工业移动床的模拟尚存在困难. 连续介质假设方法将移动床内的颗粒流视为拟流体, 在欧拉坐标下求解方程. 拟流体模型计算量小, 其关键是建立颗粒流的本构关系.

颗粒流一般认为有3种流动状态: 颗粒紧密堆积, 流动非常缓慢, 颗粒之间依靠摩擦相互作用的准静态状态^[12]; 颗粒非常稀疏, 颗粒之间以二元碰撞为主的快速流动状态^[13]; 以及处于二者之间, 摩擦和碰撞对颗粒流动均有影响的中间流动状态^[14-15]. 这3种流动状态也被称为颗粒固态, 颗粒气态和颗粒液态. 颗粒在不同流态中呈现不同的流动特性对于颗粒拟流体方法的发展是一大挑战, 颗粒固态时一般使用黏塑性理论描述, 颗粒气态时使用颗粒流动理学理论(KTGF)^[16], 对于颗粒液态, 还没有形成统一的理论去描述, 一般可以将准静态的黏塑性理论拓展到相对稀疏的颗粒流, 得到摩擦黏度模型, 或者通过修正颗粒动理学理论实现对颗粒液态的描述^[17-18]. 对于移动床内的密集颗粒流, 颗粒流存在几乎不流动的滞止区, 存在速度梯度很大的剪切区, 也存在流动较均匀的主流区, 不同结构的移动床内部可能存在2种或3种颗粒状态. 现有的普遍认为能用于描述这种密集颗粒流动的模型有Shaeffer模型^[19], S-S模型^[20], μ(I)模型^[21]等, 其中μ(I)模型基于黏塑性理论, 形式简单, 模型参数与颗粒物性关联直接, 近年来受到国内外****广泛重视 ^[22].

$mu left( I
ight)$模型将颗粒物料处理成黏塑性流体, 引入无量纲惯性数I来描述颗粒的流动状态与特性, 形式简单^[21]. 目前μ(I)模型在山体滑坡、泥石流、雪崩等颗粒坍塌的外流流动预测应用广泛^[23-25]. 近年来不断有研究者将μ(I)应用于不同结构的移动床流动模拟, Chauchat和Medale^[26]采用有限元的方法, 通过改进算法处理压力和黏度的强依赖关系, 并将改进后的模型应用于斜面颗粒流动和颗粒的圆柱绕流, 和理论以及实验的结果吻合较好; Tian等^[22]对移动床卸料过程进行模拟, 并将μ(I)模型与DEM模拟、Schasffer模型、S-S模型进行对比研究; Bartsch等^[27]将μ(I)模型应用于移动床热交换器, 对颗粒流在排管间的流动进行了模拟研究; Baumann等^[28]将μ(I)模型与传热模拟相结合研究移动床内颗粒流与管道的换热, 其重点在于研究传热, 对μ(I)模型和流动计算简化较大; Schneiderbauer等^[29]将动理学理论模型和μ(I)相结合, 应用于移动床和流化床颗粒流模拟; Staron等^[30]应用μ(I)模型模拟移动床卸料过程并和DEM方法进行对比.

在上述μ(I)模型的各种应用中, 一类是将颗粒流视为密度、颗粒体积分数不变的不可压缩单相μ(I)流体, 另一类则是联立气相控制方程, 考虑颗粒体积分数变化的多相流处理方法. 对于移动床内颗粒流动的模拟, 采用现有不可压缩单相μ(I)模型, 床内颗粒流密度和颗粒体积分数为不变的常数, 无法预报颗粒体积分数变化, 忽略了流动传热的关键局部细节, 误差较大^[25], 而若采用多相流模型, 又将绝大部分的计算量浪费在对颗粒力学作用可以忽略不计的气相方程求解上. μ(I)模型本质上是一种与局部流动状态密切相关的流变模型, 局部流动与局部压力、颗粒体积分数密切相关^[31]. 本文基于单相μ(I)模型, 补充局部颗粒体积分数与颗粒局部压力和局部似密度的关系式, 将移动床内密集颗粒处理成可压缩流体, 建立了单相可压缩流μ(I)模型, 对多个算例进行了计算, 并与实验结果进行了对比.

1.
基于改进μ(I)模型的数学模型

1.1
控制方程

对于多相流系统, 采用多相流方法颗粒相的控制方程的张量表示如下

$$frac{{partial {alpha _{ m{s}}}{ ho _{ m{s}}}}}{{partial t}} + frac{partial }{{partial {x_i}}}({alpha _{ m{s}}}{ ho _{ m{s}}}{u_i}) = 0$$

(1)

$$begin{split}& frac{partial }{{partial t}}({alpha _{ m{s}}}{ ho _{ m{s}}}{u_i}) + frac{partial }{{partial {x_i}}}({alpha _{ m{s}}}{ ho _{ m{s}}}{u_i}{u_j}) = & qquad- {alpha _{ m{s}}}frac{{partial p}}{{partial {x_i}}} - frac{{partial {p_{ m{s}}}}}{{partial {x_i}}} + frac{{partial {tau _{ij}}}}{{partial {x_i}}} + {alpha _{ m{s}}}{ ho _{ m{s}}}{f_i}end{split}$$

(2)

对于本文所研究的移动床, 没有外部强制流入的气流, 床内颗粒密集流动, 颗粒密度远大于气体密度, 空隙中的空气对颗粒的流动影响很小, 故气相压力p可忽略. 颗粒固相拟压力p_s, 一般认为由碰撞动力学压力和摩擦压力组成, 确定固相拟压力p_s是颗粒拟流体模拟的关键点与难点. 移动床内颗粒密集, 对于本文的研究对象, 假设摩擦压力p_f起主导作用, 只考虑摩擦压力的影响, 并采用Johnson和Jackson^[17](J & J)的公式描述摩擦压力

$${p_{ m{s}}} = {p_{ m{f}}} = F_{ m{r}}frac{{{{({alpha _{ m{s}}} - {alpha _{{ m{s,min}}}})}^n}}}{{{{({alpha _{{ m{s,max}}}} - {alpha _{ m{s}}})}^m}}}$$

(3)

对于移动床内密集颗粒流的计算, 一般常取n = 2, m = 5, F_r = 0.1α_s^[17], α_s,min和α_s,max分别代表颗粒最小和最大体积分数.

在多相流模型中, α_sρ_s是颗粒的堆积密度, 由于颗粒的体积分数α_s是变化的, 故颗粒的堆积密度也在不断变化. 在对于本文研究的移动床, 忽略气相对密度的影响, 直接将α_sρ_s视为拟流体密度

$$ ho = {alpha _{ m{s}}}{ ho _{ m{s}}}$$

(4)

由式(3)和式(4), 建立了颗粒流拟流体的密度ρ与颗粒体积分数α_s和颗粒拟压力p_s 关系式, 移动床内颗粒体积分数变化, 颗粒流密度及拟压力随之变化, 颗粒流动可表征为单相可压缩流动. 质量力只考虑重力, 控制方程为

$$frac{{partial ho }}{{partial t}} + frac{{partial ho {u_i}}}{{partial {x_i}}} = 0$$

(5)

$$frac{partial }{{partial t}}( ho {u_i}) + frac{partial }{{partial {x_i}}}( ho {u_i}{u_j}) = - frac{{partial {p_{ m{s}}}}}{{partial {x_i}}} + frac{{partial {tau _{ij}}}}{{partial {x_i}}} + ho {g_i}$$

(6)

1.2
本构关系

应用牛顿形式的张量表达描述移动床内摩擦应力和应变的关系

$${sigma _{ij}} = {p_{ m{s}}}{delta _{ij}} + {tau _{ij}} $$

(7)

右侧第一项为正应力, 在前文已有表述, 应用Johnson和Jackson^[17]的公式描述.

右侧第二项${tau _{ij}} $切应力. 在μ(I)中, 它被描述为摩擦系数和压力的乘积, 在本模型中, 体系的压力只考虑固相压p_s

$${tau _{ij}} = {{mu {p_{ m{s}}}{gamma _{ij}}} / {left| gamma ight|}}$$

(8)

其中, $ {gamma _{ij}} = dfrac{{partial {u_i}}}{{partial {x_j}}} + dfrac{{partial {u_j}}}{{partial {x_i}}} $, 为应变率张量; $left| gamma
ight| = {(0.5{gamma _{ij}}{gamma _{ij}})}^{0.5}$, 为应变率张量的第二不变量.

μ为拟流体的摩擦系数, 由μ(I)关系确定. 认为μ为无量纲惯性数I值函数

$$ mu (I) = {mu _{ m{s}}} + frac{{{mu _2} - {mu _{ m{s}}}}}{{{I_0}/I + 1}} $$

(9)

$$I = {{left| gamma ight|d} / {{{left( {{{{p_{ m{s}}}} / {{ ho _{ m{s}}}}}} ight)}}^{0.5}}}$$

(10)

惯性数表征是微观时间尺度和宏观时间尺度的比值. ${d / {{{({{{p_{
m{s}}}} / {{
ho _{
m{s}}}}})}}^{0.5}}}$为微观时间尺度, 它表示颗粒在压力p_s下落入大小为d中所需的时间, 表征微观重排的时间尺度. 宏观时间尺度1/γ表征宏观平均变形时间尺度. I较小, 一般认为对应准静态状态, I较大, 进入稠密惯性区, 颗粒之间主要作用为摩擦, I进一步增大, 则可能进入快速流动, 颗粒间相互作用以碰撞为主. 需说明的是, 对于本文所研究的移动床工况, 床内颗粒流动低速而密集, 假设颗粒压力主要是摩擦压力, 不考虑颗粒的碰撞作用.

1.3
壁面边界条件

黏性流体的无滑移的边界条件不能用于描述颗粒流在壁面处的运动, 根据Coulomb摩擦定律, 壁面最大静摩擦力为压力和壁面摩擦系数的乘积. 当壁面剪切力小于壁面最大静摩擦力时, 使用壁面剪切力; 当壁面剪切力大于壁面最大静摩擦力时, 使用最大静摩擦力. 为便于编程计算, 本文从Coulomb摩擦定律出发, 类比颗粒流内部μ(I)模型, 将壁面视作一个大颗粒, 颗粒在壁面所受剪切力为

$${tau _{{ m{w,sl}}}} = {{{p_{ m{s}}}{mu _{ m{w}}}(I){gamma _{ij}}} / {left| gamma ight|}}$$

(11)

将壁面摩擦系数μ_w和惯性数I相关联起来, 得到一个可小范围变化的壁面摩擦系数

$${mu _{ m{w}}}(I) = {mu _{{ m{w,s}}}} + frac{{{mu _{{ m{w}},2}} - {mu _{{ m{w}},{ m{s}}}}}}{{{I_{0,{ m{w}}}}/I + 1}}$$

(12)

1.4
参数正则化及计算方法

在μ(I)模型中, 由于拟流体压力和黏度高度耦合的复杂关系, 给数值求解带来了困难, 为保证数值求解的稳定性和收敛性, 近年来不少****采用参数正则化方法^[32-35]来解决此问题. 本文也对黏度和拟流体压力采用正则化技术.

将式(8)与式(9)之间引用黏度进行过渡

$$eta = {{mu (I){p_{ m{s}}}} / {left| gamma ight|}}$$

(13)

将式(9)代入式(13)并整理并进行正则化处理

$${eta}_{r;egu} = frac{{{mu _{ m{s}}}{p_{ m{s}}}}}{{left| gamma ight| + {lambda _{ m{r}}}}} + frac{{({mu _2} - {mu _{ m{s}}}){p_{ m{s}}}}}{{dfrac{{{I_0}}}{d}sqrt {dfrac{{{p_{ m{s}}}}}{{{ ho _{ m{s}}}}}} + left| gamma ight| + {lambda _{ m{r}}}}}$$

(14)

式中右端第一项决定颗粒流的屈服应力, 第二项表示非牛顿黏性的贡献, λ_r为远小于1的正则化参数, 本文计算中取λ_r = 1 × 10^?4.

对模型方程求解时, 必须保证黏度为正, 所以拟流体压力p_s需要始终为正值, 故同样对压力进行正则化处理

$${p_{{ m{regu}}}} = 0.5left({p_{ m{s}}} + sqrt {p_{ m{s}}^2 + lambda _p^2} ight)$$

(15)

上述模型与计算方法基于Fluent软件进行, 通过用户自定义函数编程改写黏度和密度以及边界条件对模型进行实现. 应用压力基求解器, 采用压力速度的耦合算法.

2.
3种典型散料在缩口料仓内的流动

采用上述改进的颗粒流单相可压缩流μ(I)模型及控制方程, 以表面光滑的球形玻璃珠、表面粗糙的球形刚玉球以及表面粗糙而形状不规则的粗沙为研究对象, 模拟研究了3种典型散料在薄层移动床缩口料仓内的出流流动过程.

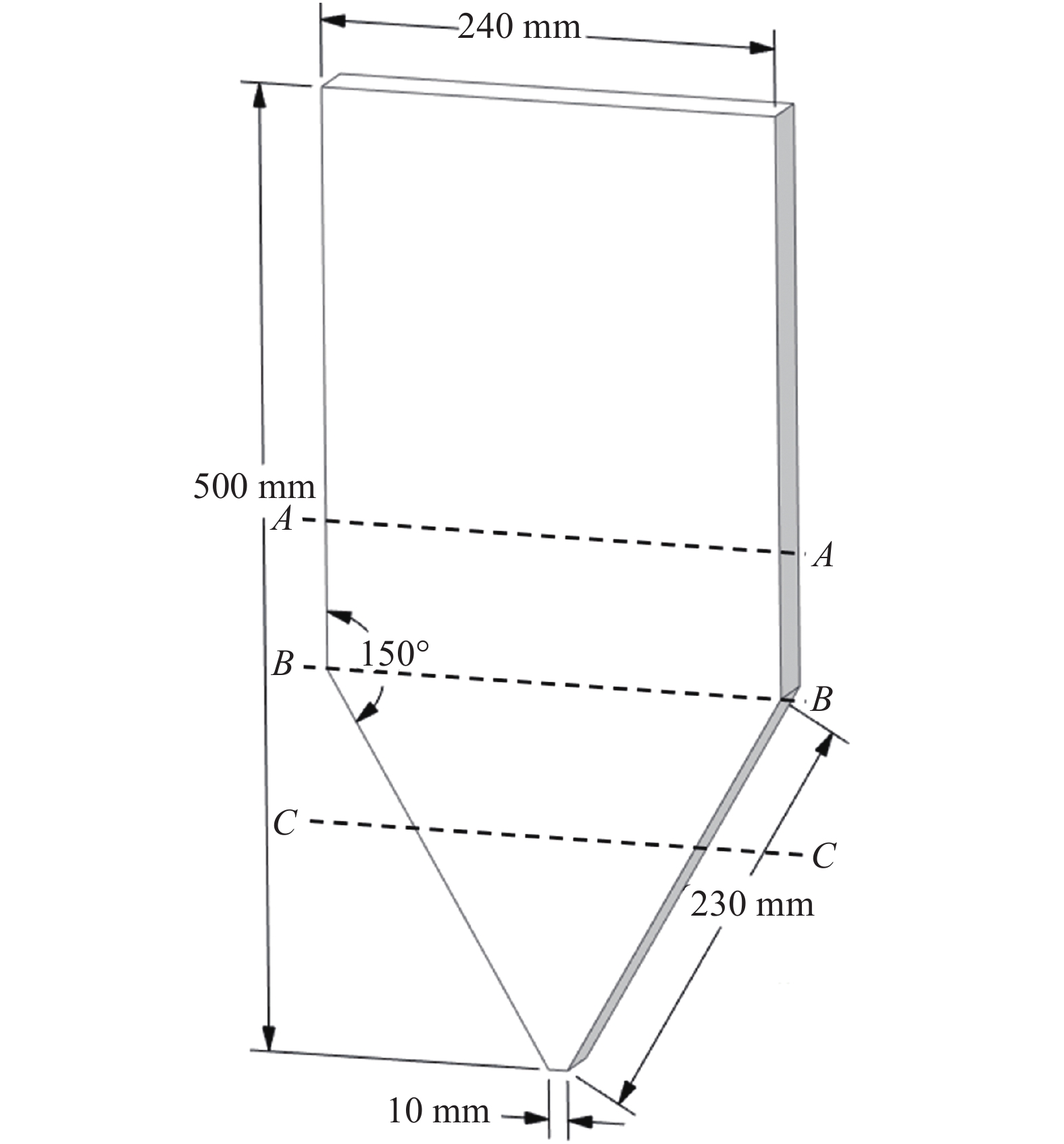
移动床缩口料仓结构如图1所示, 为便于实验测量, 料仓前后方向的厚度为30 mm, 整个料仓高500 mm, 宽240 mm, 上部为竖直段, 颗粒在重力作用下向下流动; 缩口段角度为60°, 缩口斜面长度为230 mm, 出口宽度为10 mm. 本课题组对不同散料在该装置内的流动特性进行了实验研究^[36], 采用PIV测量了玻璃珠、刚玉球和粗沙在料仓中速度. 本文针对实验工况进行了模型, 初始取床内颗粒体积分数为0.5, 出口根据实验测量采用速度出口, 上部采用压力入口条件, 对于本文的计算条件, 取入口固相压力为400 Pa. 计算中网格的划分采用非结构网格, 网格数约18万, 收敛条件为相对误差小于0.5%. 与采用多相流算法相比, 由于避免了气相流场和两相耦合计算, 计算时间大幅度减小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
料仓模型



Figure
1.
Sketch of the silo



下载:
全尺寸图片
幻灯片


需说明的是, 料仓前后方向的厚度如上文所述为30 mm, 一般实验研究认为这样的薄板结构可以忽略厚度方向的变化, 称此种料仓为近二维料仓, 模拟计算中则不能避免前后壁面的影响, 为三维计算, 厚度方向上的网格数为14个, 计算结果近前后壁面流速略低, 其他位置变化不大. 考虑到拟流体模拟中壁面效应的误差, 本文在后续分析和与实验对比中所取数据为取距前壁第2层网格计算结果.

$mu (I)$模型中计算参数与实际散料的实际物性密切相关, 本文所采用的参数具体如表1所示, 其中密度ρ_s、粒径d参考实验测量值取值, I₀和I_0,w根据文献[21]取为0.279. 另需说明的是, 对于本文研究的薄层移动床缩口料仓, 实验测量床内堆积状态下颗粒的体积分数在0.5左右, 为预报床内体积分数的变化, 本文在计算中取α_s,min和α_s,max分别为0.45和0.55. 对于$ mu (I) $模型中待确定的参数μ_s, μ₂, μ_w,s, μ_w,2, 基于实测物性, 初步确定各个参数的取值范围, 进行多组对比计算, 和PIV实验结果^[36]相对照, 最后确定了在改进的$mu (I)$拟流体模型中玻璃珠、刚玉球和粗沙的μ_s, μ₂, μ_w,s, μ_w,2参数, 具体如表1所示, 玻璃珠的内摩擦系数以及与壁面的摩擦系数最低, 刚玉球次之, 粗沙最大. 3种散料的$mu (I)$模型参数的取值规律与实测颗粒的堆积角、壁面堆积角^[36]的变化规律一致.




表
1
模拟参数



Table
1.
Simulation parameters



table_type1 ">

	Glass beads	Corundum beads	Coarse sand
μs	0.32	0.37	0.42
μ2	0.64	0.7	0.88
μw,s	0.22	0.27	0.37
μw,2	0.26	0.30	0.40
I0	0.279	0.279	0.279
I0,w	0.279	0.279	0.279
αs,max	0.55	0.55	0.55
αs,min	0.45	0.45	0.45
ρs/(kg·m?3)	2600	1800	2650
d/mm	3	2	1

下载:
导出CSV
|显示表格



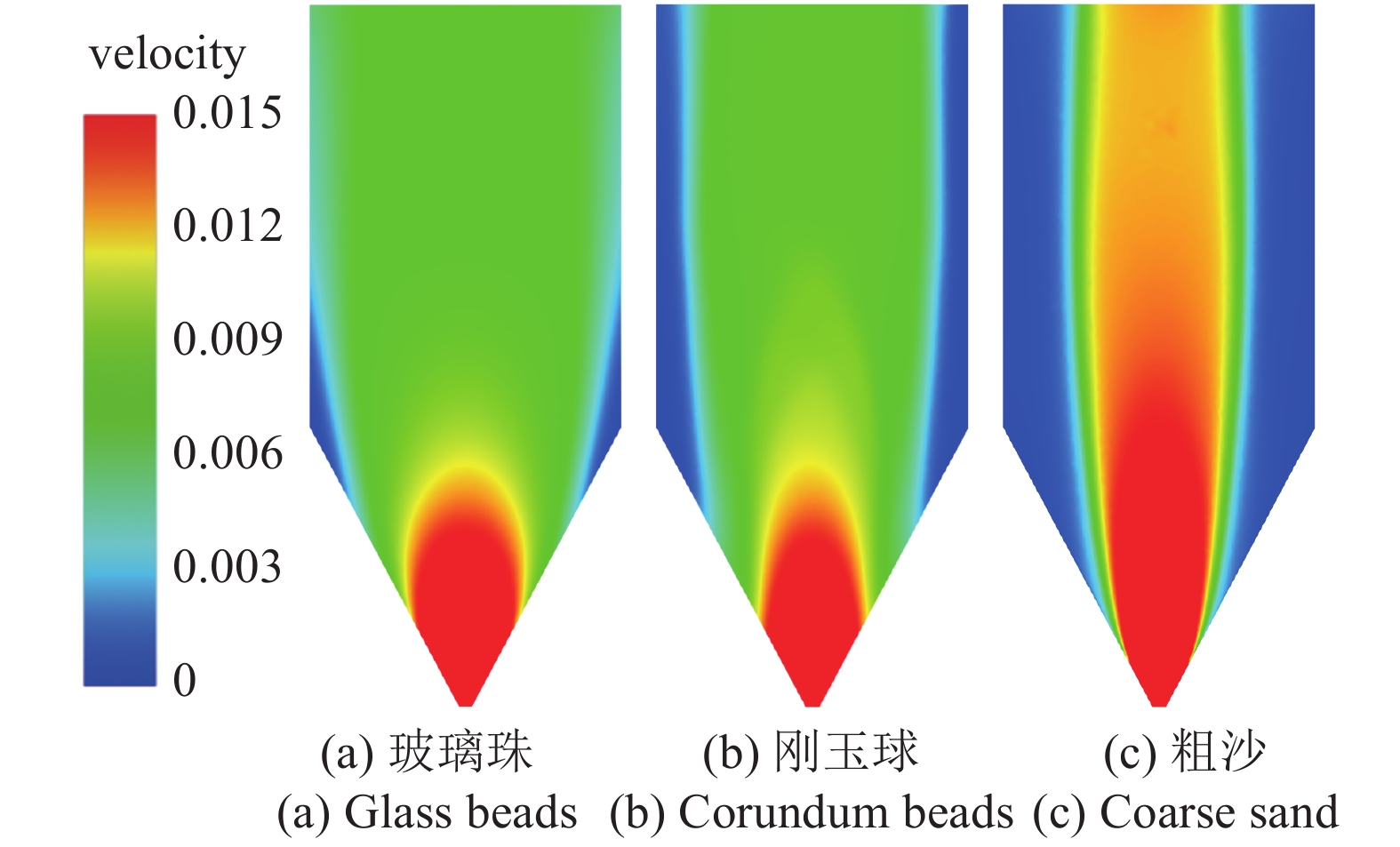
图2是计算所得3种散料的速度云图. 3种散料速度分布差异十分明显, 玻璃珠由于内部内摩擦系数以及与壁面的摩擦系数很小, 在料仓内整体流动最均匀, 只在拐角近壁处出现明显的低速区, 在其他区域玻璃珠都有较大流速. 由于出口位于料仓中心, 在水平方向上, 玻璃珠中心流速大, 两侧较低, 壁面处颗粒仍有较高流速; 在竖直方向上, 由于缩口和重力加速作用, 玻璃珠在中心处的流速不断增大, 出口处达到最大值. 刚玉球的内部内摩擦系数以及与壁面的摩擦系数都较玻璃珠大, 拐角附近以及竖直段两侧壁面处出现低速区, 流场的不均匀性增大. 粗沙流场的不均匀性较刚玉球进一步增大, 近侧壁有大范围的颗粒滞止区, 颗粒主要在中心流道内流动, 先进入料仓的两侧颗粒需在中心颗粒的高速剪切携带下进入中心流道才有可能流出料仓. 大量的研究表明, 不同颗粒在缩口料仓中的流型一般可分为整体流和漏斗流, 颗粒流动性越好就越趋向于整体流. 上述计算所得的流场分布中, 玻璃珠的流动属典型整体流, 粗沙则呈现明显的漏斗流特征. 这一结果也和文献[36]中3种散料的实验结果相一致. 图2的结果表明, 本文所采用的改进的μ(I)模型及计算方法能有效揭示不同物性散料在缩口料仓内的流动特性, 对整体流和漏斗流的流动特性都能较好表征.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
不同散料的的速度分布



Figure
2.
Velocity distribution of different granular materials



下载:
全尺寸图片
幻灯片


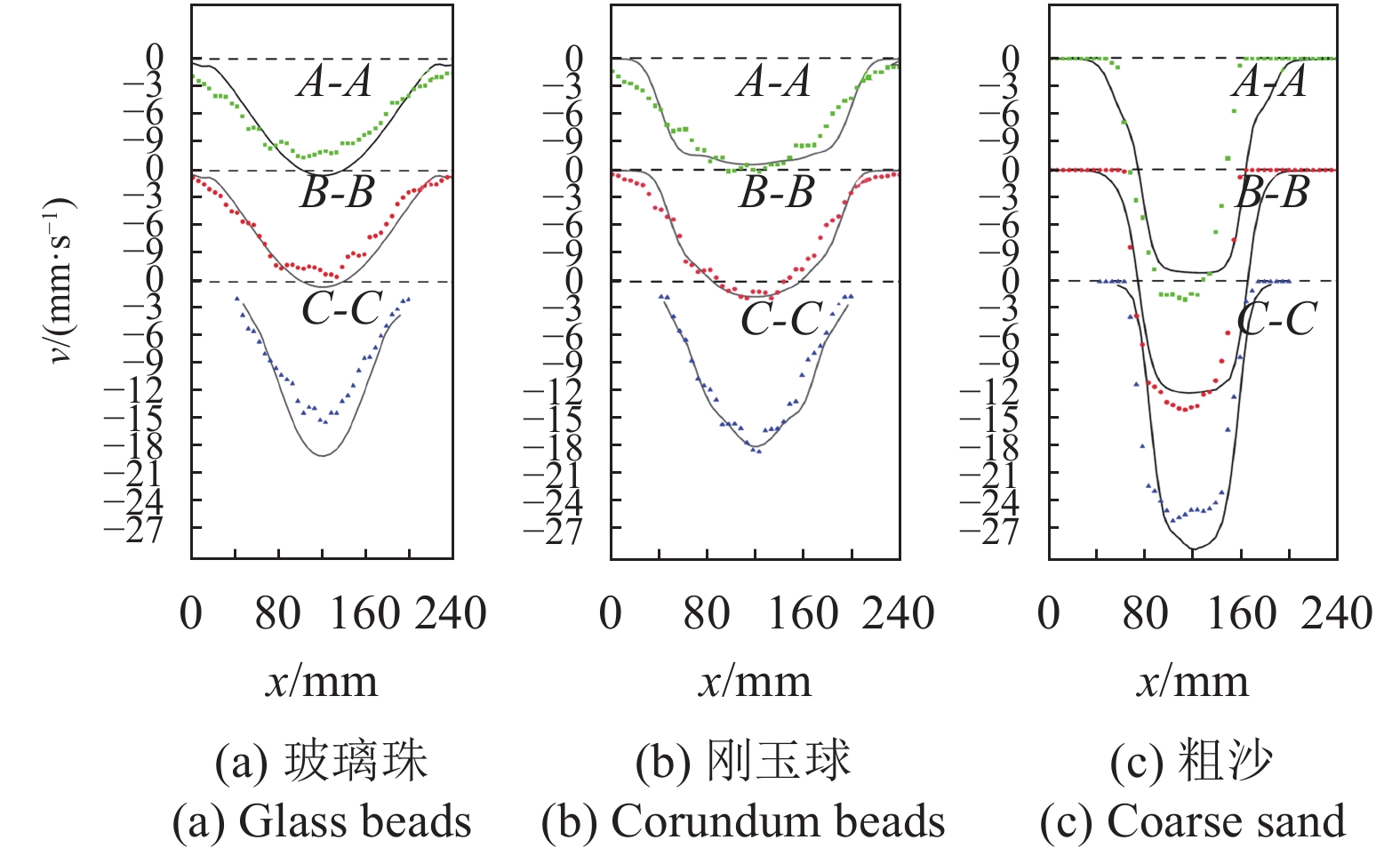
Dai等^[36]采用PIV测量了玻璃珠、刚玉球和粗沙在图1所示A-A, B-B, C-C 3个截面上的速度分布, 其中B-B截面为缩口开始位置, A-A和C-C分布位于其上、下100 mm. 图3所示为3个水平面上竖直方向上的速度模拟值与实验值的对比, 散点是文献中的实验数据, 实线是模拟结果. 各个截面上模拟结果与实验整体吻合较好, 但局部仍有一定误差, 如对于刚玉球, 上部竖直段近壁处模拟速度低于实验值, 粗砂中心流道的宽度低于实验值, 出口最大略高于实验值. 造成误差的原因一方面是由于实验本身有一定误差, 另一方面, 颗粒拟流体的假设也不可避免会牺牲局部流动细节的预报.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
速度实验值与模拟的对比



Figure
3.
Velocity comparison between the experiment and simulation



下载:
全尺寸图片
幻灯片


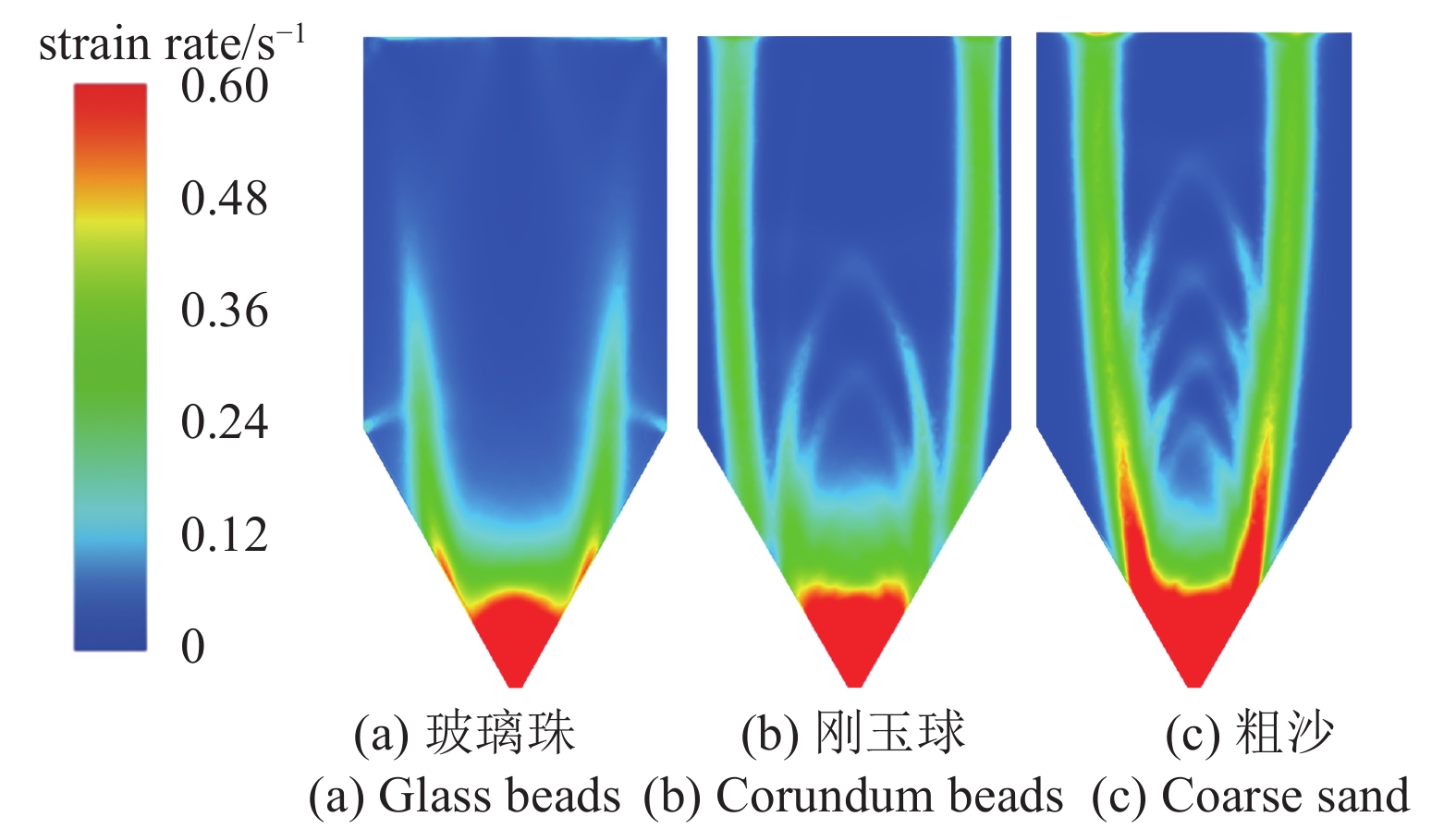
图4所示为3种散料的速度应变率云图, 从速度应变率的角度也明显体现3种散料内部相互作用的不同. 玻璃珠在料仓的上部竖直段趋于整体流, 颗粒之间的摩擦剪切作用较弱, 在料仓的上部竖直段部分基本没有高应变率剪切带存在, 下部缩口段受到拐角作用, 形成低速区, 产生局部的应变剪切带. 刚玉球和粗砂由于颗粒内摩擦系数以及颗粒与壁面的摩擦系数大, 近壁处颗粒滞流, 中心主流区流速高, 流场内产生明显的速度高应变率剪切带, 刚玉球的剪切带更窄且更靠近壁面. 高应变率的剪切带将刚玉球和粗砂在料仓上部竖直段内的流动分为颗粒低速区和颗粒主流区. 在底部缩口出流段, 3种散料都出现明显的高应变率区域, 这是由于料仓出口截面变小、颗粒流速变化大所引起的.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
不同散料的速度应变率分布



Figure
4.
Strain rate distribution of different granular materials



下载:
全尺寸图片
幻灯片


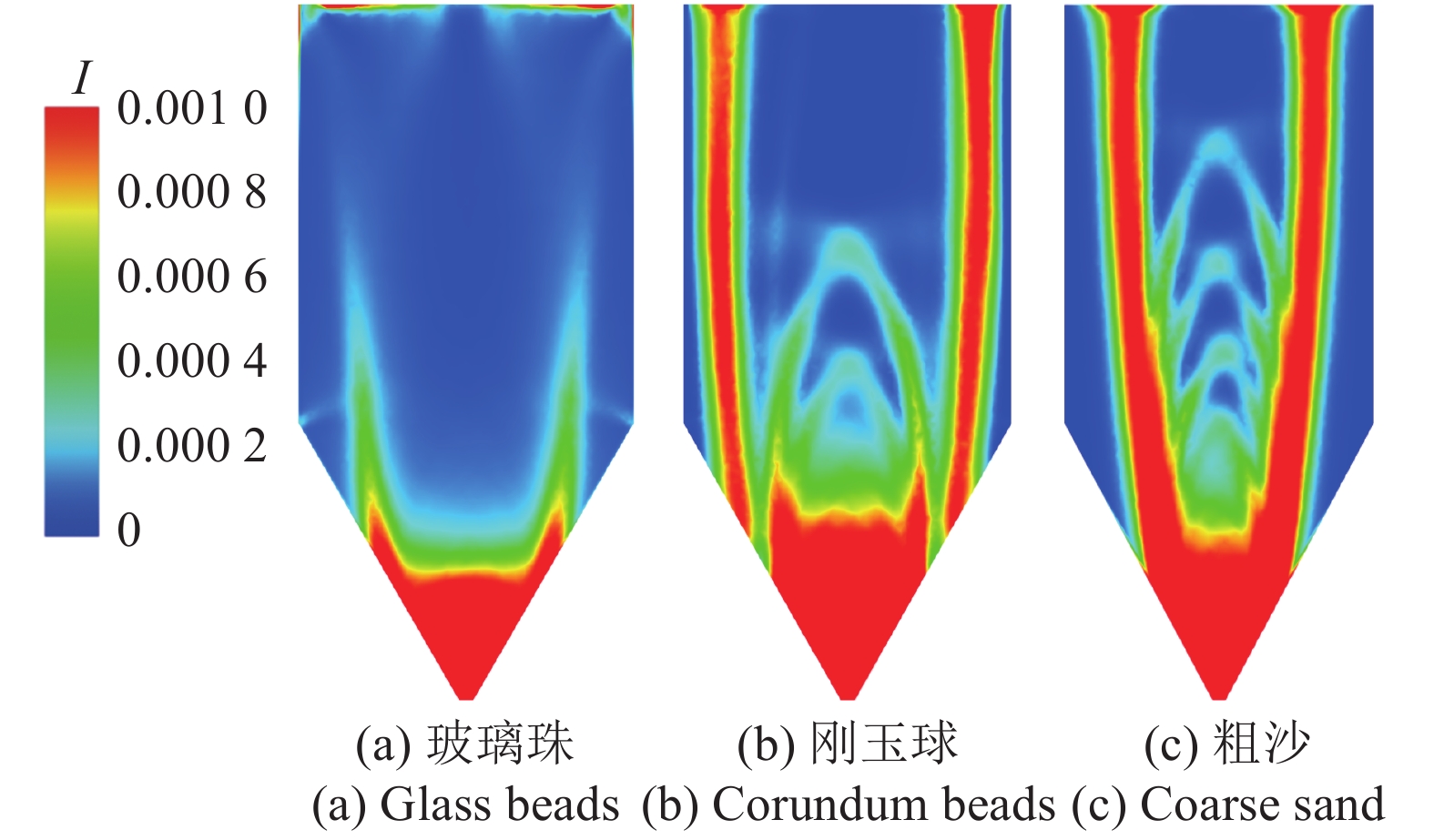
图5所示为3种散料的惯性数分布云图. 由式(10)可知局部惯性数主要取决于局部速度应变率, 因此不同散料的惯性数分布特点与速度应变率分布基本类似, 剪切应变高的地方惯性数大. 玻璃珠在料仓上部竖直段惯性数较小, 都在0.001以下, 刚玉球和粗砂则呈现两条高惯性数带状区域, 在高惯性数带状区域以及料仓出口附近颗粒流的惯性数I ≥ 0.001, 其他区域颗粒流的惯性数都小于0.001.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
不同散料的惯性数分布 (0 ~ 0.001)



Figure
5.
Inertial number distribution of different granular materials (0 ~ 0.001)



下载:
全尺寸图片
幻灯片


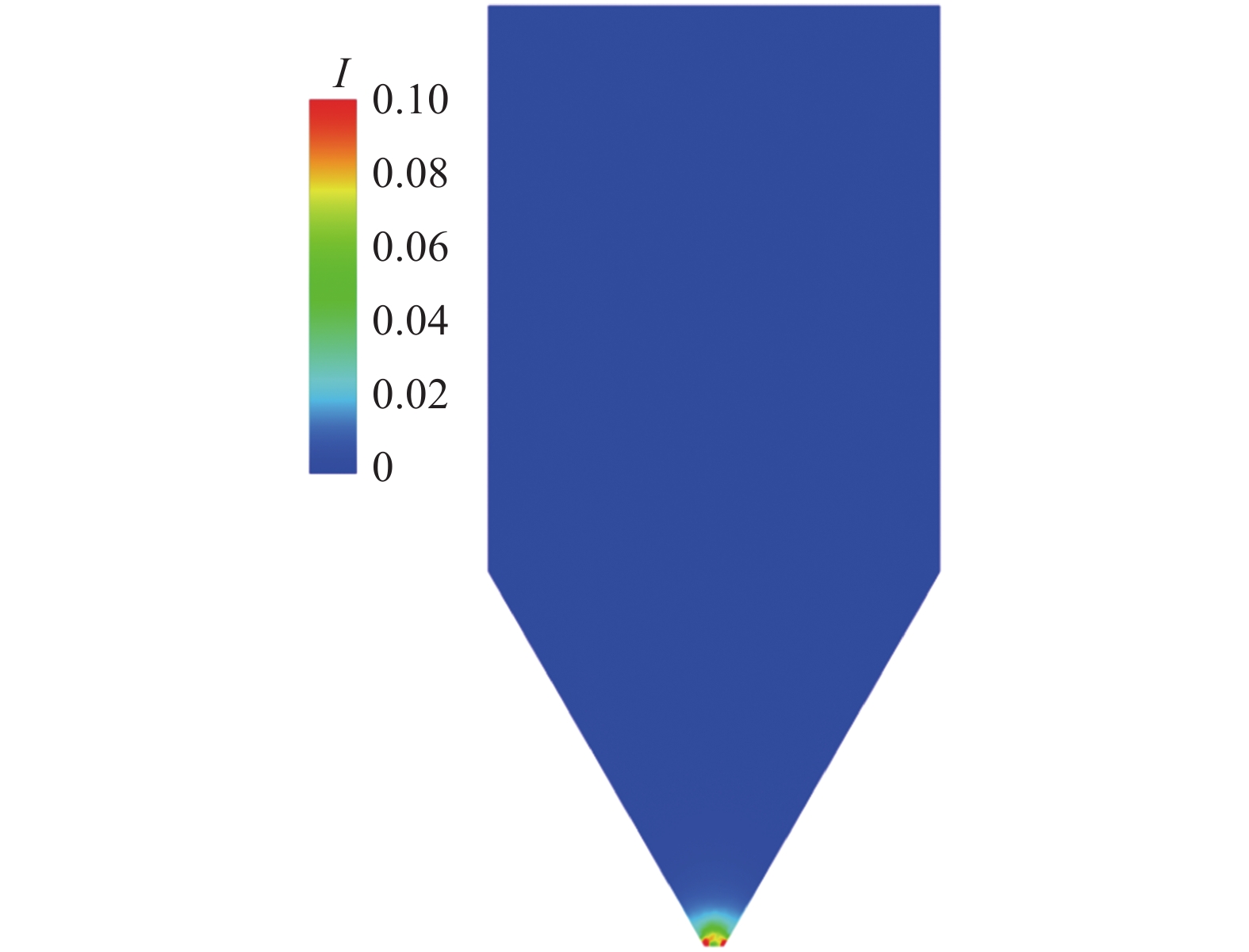
玻璃珠、刚玉球和粗沙在缩口料仓内流动的惯性数范围分别是10^?7 ~ 0.23, 10^?7 ~ 0.5和10^?7 ~ 0.33. 由于变化范围大且大部分都在0.001以下, 图5的惯性数云图的显示范围为0 ~ 0.001, 图6所示为玻璃珠惯性数显示范围为0 ~ 0.1的分布云图, 刚玉球和粗沙的云图与玻璃珠基本相同. 对于本文所计算的薄层移动床缩口料仓内的出流流动, 仅出口很小范围内颗粒流的惯性数大于0.1. 有关颗粒流分区的定量划分, 现有文献尚无统一的标准^[13-15], 对于恢复系数较大的颗粒, 文献[14]认为惯性数小于0.001时为准静态流动, 在0.001到0.1之间是稠密惯性区, 大于0.1是快速区, 若按此划分, 图5中红色区域大部分为稠密惯性流动区域, 图6中出口的红色小部分区域为快速区, 对于此区域本文的模型忽略颗粒碰撞造成的计算误差可能较大, 但如图6所示, 此部分占比极小, 本模型对绝大部分区域的模拟是适用的.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
玻璃珠惯性数分布(0 ~ 0.1)



Figure
6.
Inertial number distribution of glass beads (0 ~ 0.1)



下载:
全尺寸图片
幻灯片


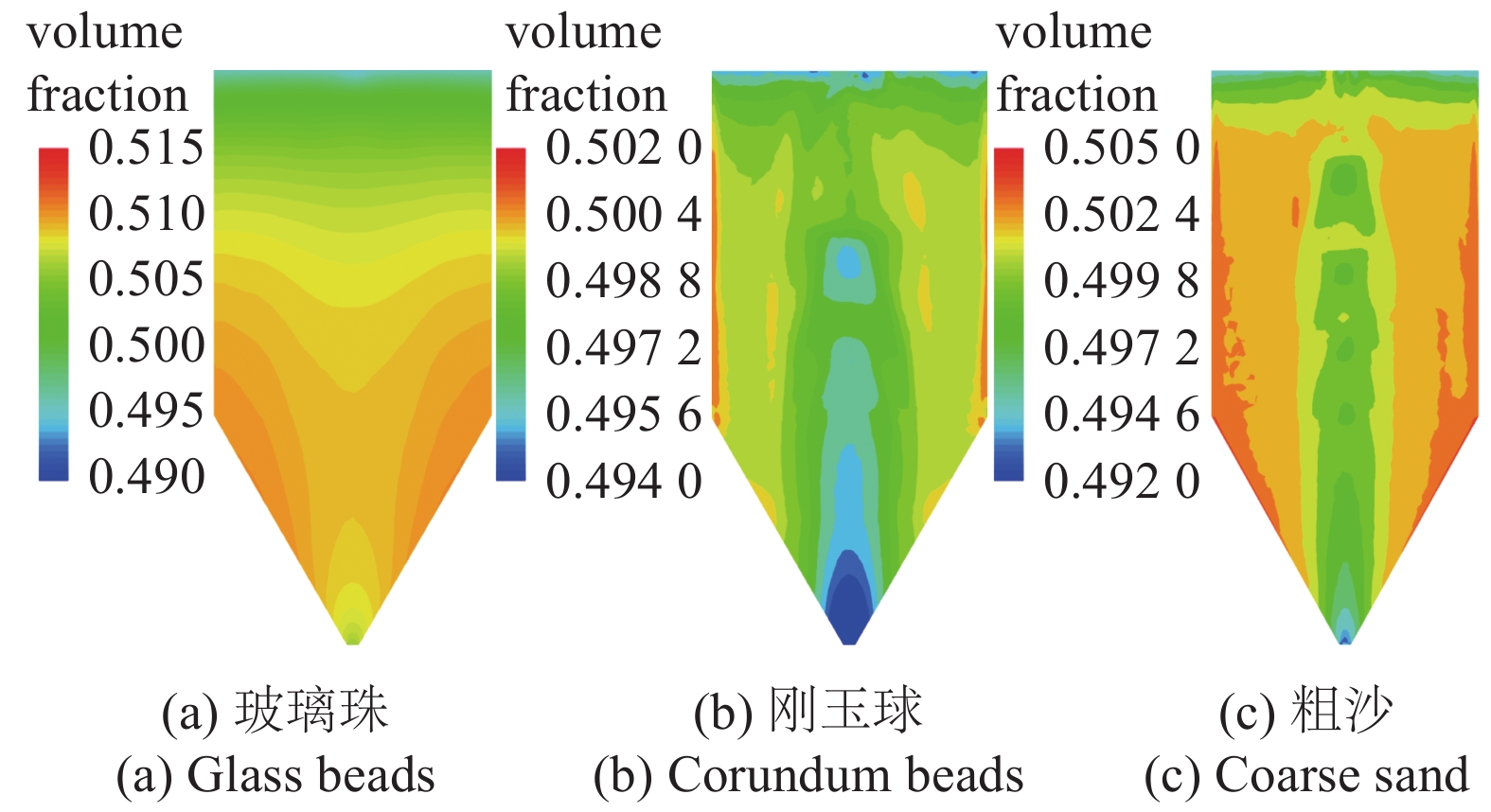
改进的μ(I)拟流体模型的优点在于可以对移动床内颗粒的体积分数进行预报. 图7所示为计算所得3种物料的体积分数在料仓中的分布. 玻璃的体积分数在床内变化较小, 变化范围分别是0.495 ~ 0.508, 上部竖直段水平方向上变化较小, 下部流动通道变窄, 颗粒体积分数变化增大, 拐角低速区颗粒流速低、体积分数最大, 到出口段, 由于颗粒在重力作用下快速流出, 颗粒体积分数达到最小值. 玻璃珠在下部缩口段水平方向上变化相对平缓, 竖直方向上逐渐变小, 出口处迅速降为最小值, 这一趋势是合理的, 与文献[37]定性相符. 刚玉球和粗沙由于存在近壁低速区和流速较大主流区, 当流速较大时, 颗粒的堆积也必然较为松散, 所以主流区的体积分数较低, 滞流低速区体积分数则相对较大, 计算域内刚玉球局部颗粒体积分数最大达0.510, 粗沙更可高达0.515, 到出口处刚玉球和粗沙局部颗粒体积分数最小达0.490. 这可以从力链的角度来理解, 在料仓的滞流低速区, 颗粒之间相互作用主要通过力链传播, 最后会汇聚到壁面, 壁面会承受很大一部分颗粒的重力, 同时力链会使得壁面附近的颗粒群更为“压实”, 所以壁面附近的体积分数更大. 另外, 物料在出口处体积分数都为最小值, 这一趋势也是合理的.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
不同散料的体积分数分布



Figure
7.
Volume fraction distribution of different granular materials



下载:
全尺寸图片
幻灯片

3.
移动床颗粒绕管流动特性研究

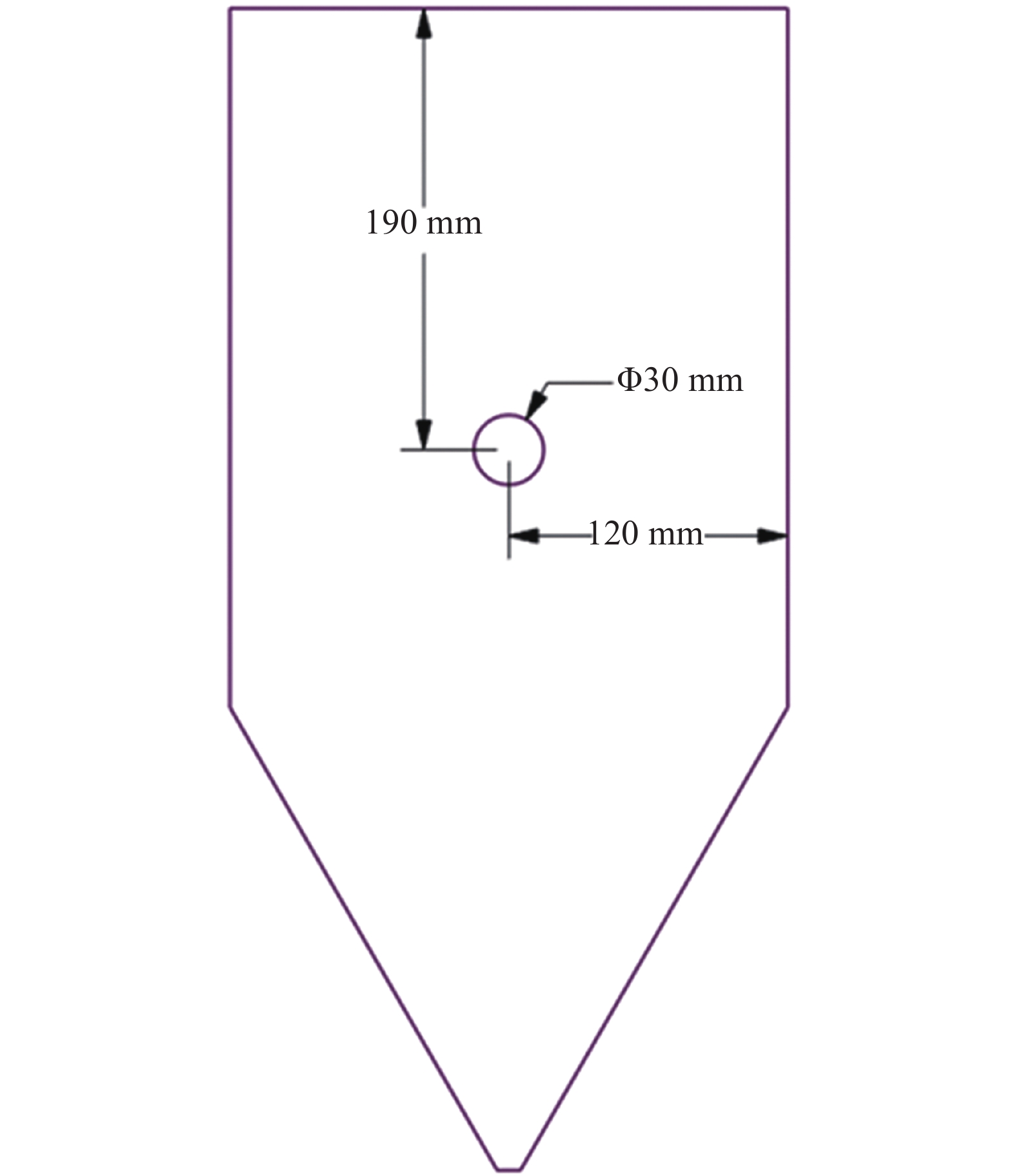
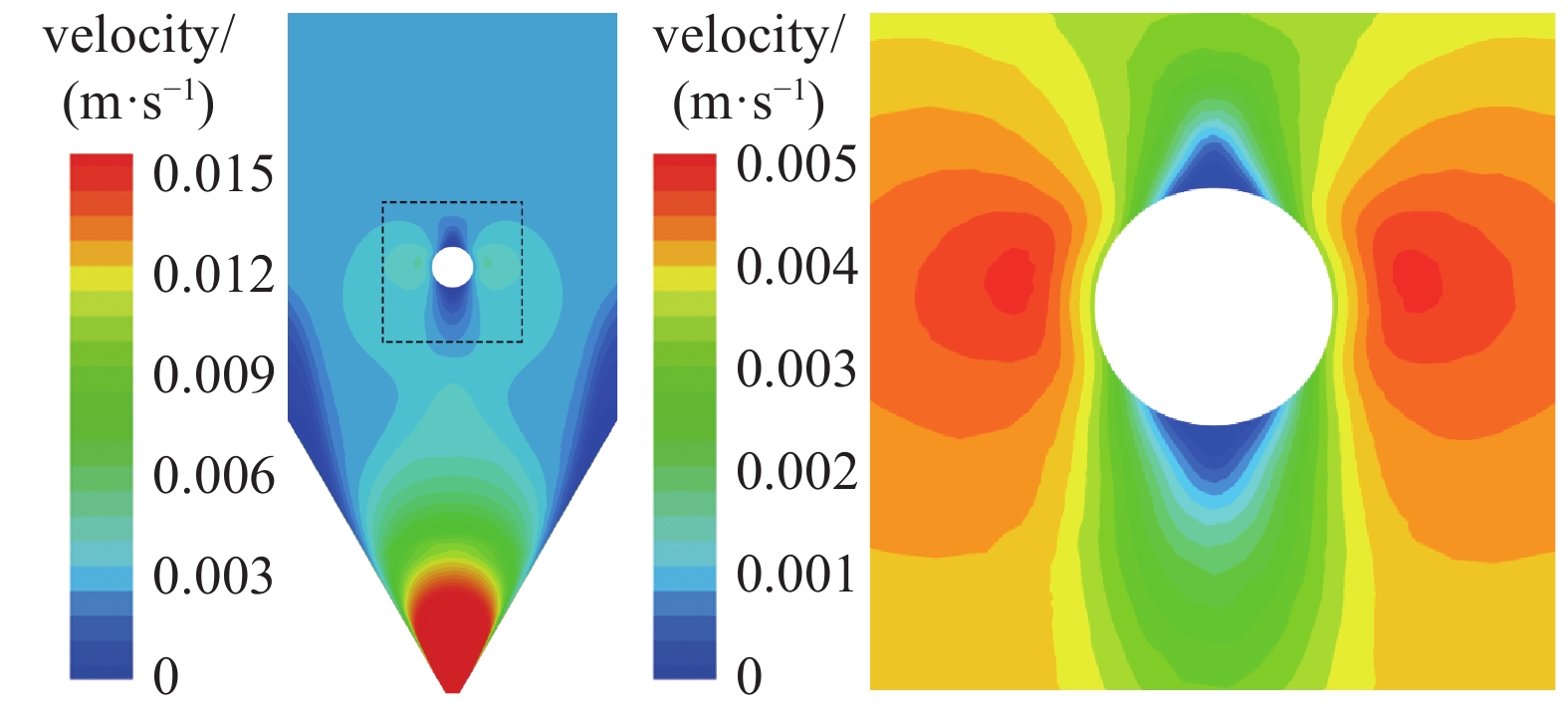
颗粒绕管移动床在工业领域应用广泛, 管道的布置对床内颗粒流动造成很大的影响, 本文首先对移动床单管绕流特性进行了模拟研究, 旨在分析改进的μ(I)拟流体模型对存在单管影响的情况下能否有效描述. 如图8所示, 管道直径30 mm, 管道中心位于料仓中心轴线上, 离上部入口距离为205 mm. 所研究的颗粒为玻璃珠, 选用的模拟参数如表1所示. 由于圆管的阻挡, 出口流速为低于上节出流工况, 计算中取为20 mm/s, 入口压力边界条件的设定方法与上节相同.

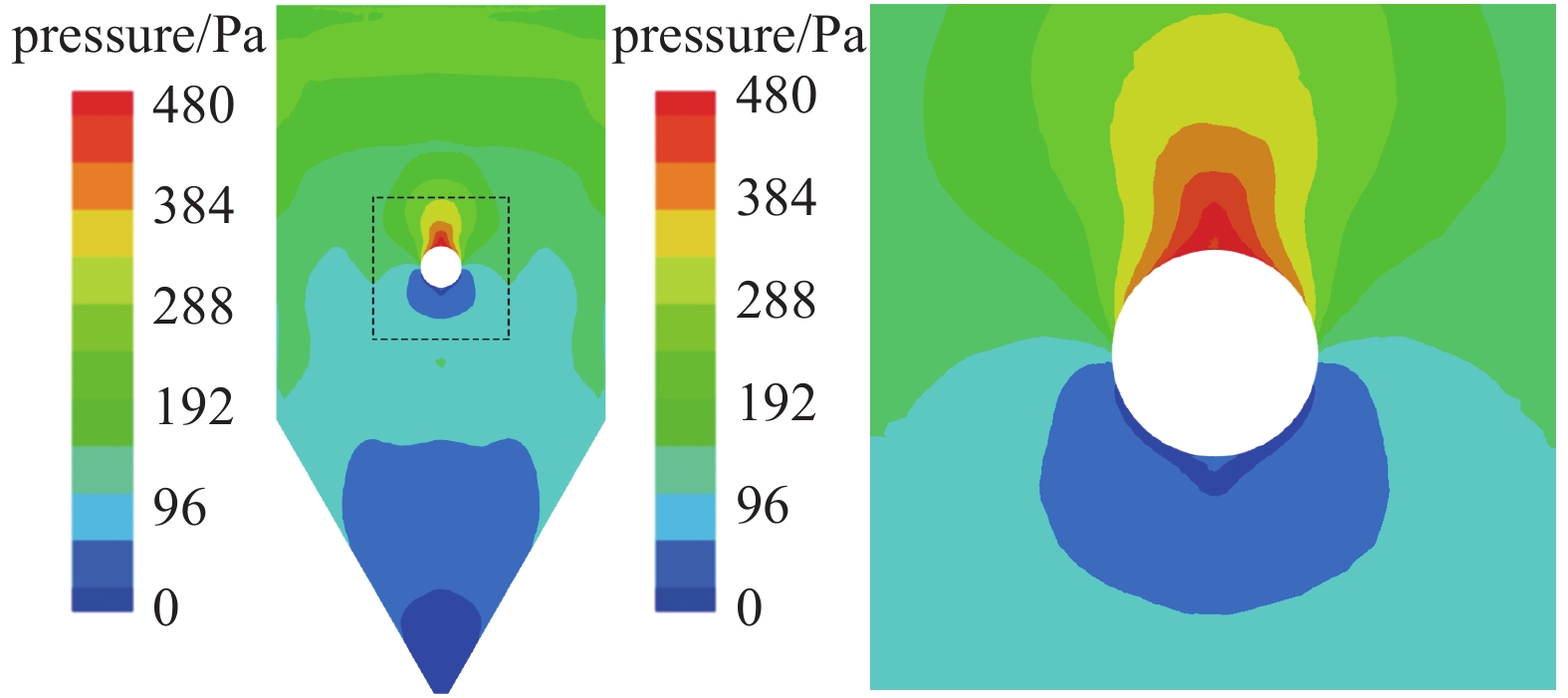
移动床单管绕流的速度和颗粒拟压力云图如图9和图10所示, 圆管位于管道中心, 对中心流动颗粒的流动起阻碍作用, 圆管上部竖直段速度分布均匀, 到管道上方速度变小, 压力增大, 管道正下方则速度小, 压力小, 管道两侧颗粒流速大. 与一般黏性流体不同, 除管正上方和正下方很小的区域, 近壁区域的颗粒流速不为零, 两侧颗粒以较大的速度流过圆管壁面, 管道下方也没有出现一般黏性流体的负压回流区域, 上述流动特性与文献[26]采用单相常密度μ(I)模型所得结果一致, 也与文献[36]实验观测相符, 说明采用本文的模拟与方法能有效预测颗粒流移动床单管绕流流动的特征.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
颗粒绕流流动模型



Figure
8.
Sketch of granular flow around a pipe



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
颗粒流绕管速度分布



Figure
9.
Velocity distribution of granular flow around a pipe



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
颗粒流绕管固相拟压力分布



Figure
10.
Particle pressure distribution of granular flow around a pipe



下载:
全尺寸图片
幻灯片


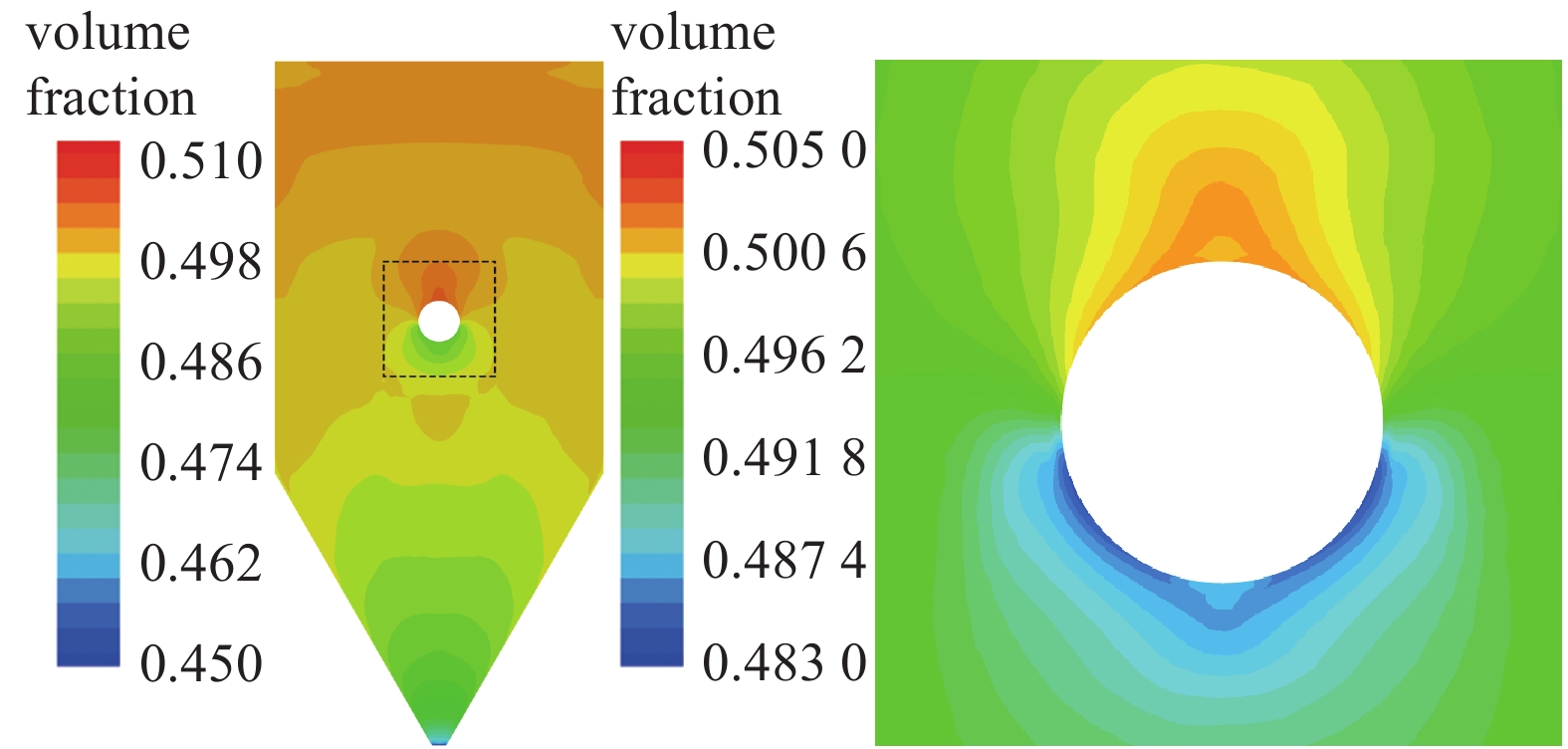
图11所示移动床单管绕流流场的体积分数分布, 单管上方由于颗粒流速低, 体积分数较大, 局部最大体积分数为0.510, 下方体积分数较小, 管下方低体积分数的区域与低固相压力的区域相一致, 正下方局部最小颗粒体积分数为0.463. 颗粒绕流经过单管后进入下部缩口段, 颗粒流速增加, 体积分数减小, 出口处局部颗粒体积分数最小为0.461.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
颗粒流绕管颗粒体积分数分布



Figure
11.
Particle volume fraction distribution of granular flow around a pipe



下载:
全尺寸图片
幻灯片


颗粒流绕管体积分数的变化近年来有不少研究报道, 部分实验还观测到了管下方的空隙区, 管下方空隙区的存在依颗粒材料和出口出流控制方式不同而变化, 但目前普遍认同颗粒在管下方体积分数减小, 本文的模型对管下方低体积分数这一现象能较好模拟. 但是, 拟流体模拟由于忽略单个颗粒的大小, 对于由于壁面效应引起的贴壁处颗粒体积分数变小无法精确预报.

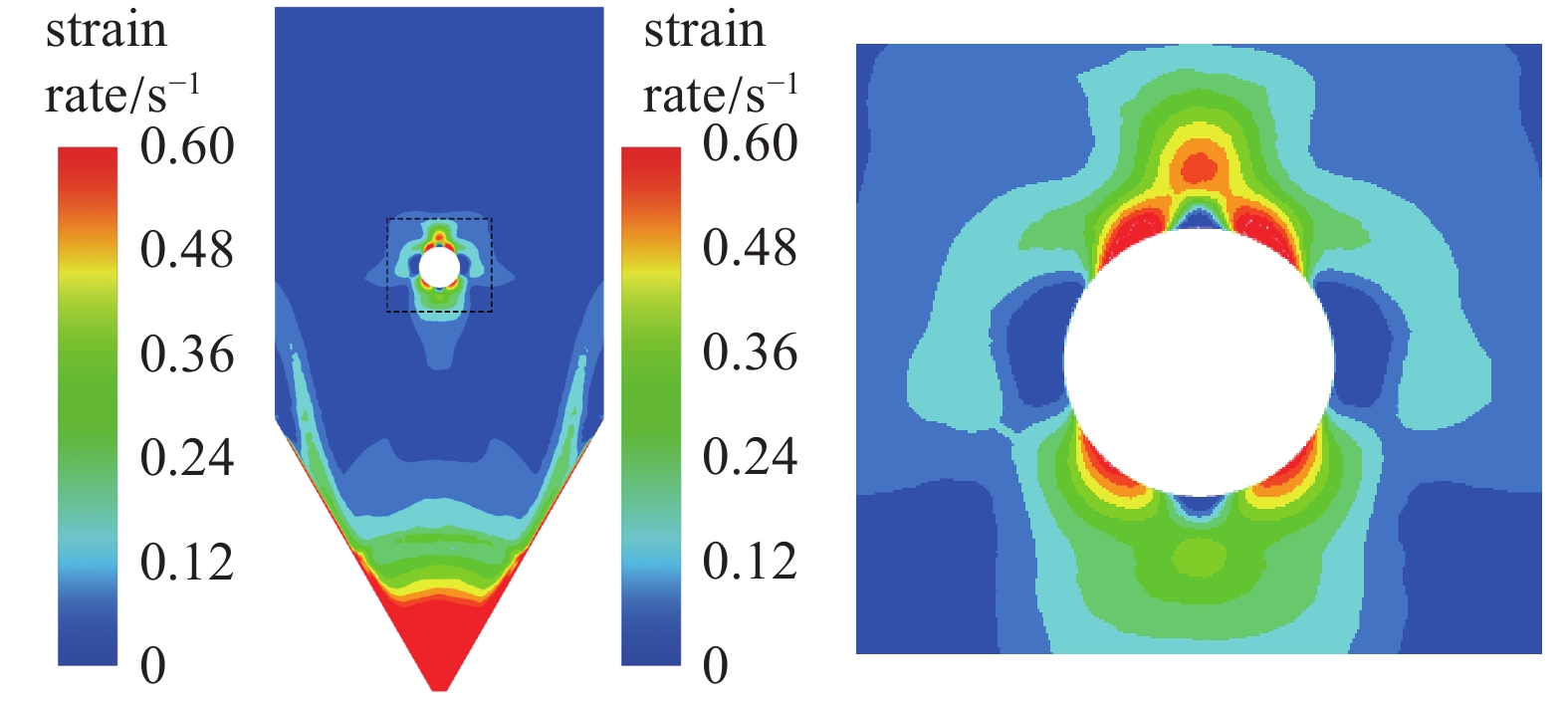
图12所示为颗粒流绕管速度应变率云图分布, 管道的附近存在复杂变化的速度变化. 管上部低速区外缘的颗粒受到主流区颗粒高速流动的影响, 出现高速度应变率区域, 圆管壁面对两侧颗粒的影响小, 两侧颗粒保持高速流动, 两侧对称出现两个低速度应变率区域, 这部分高速流动的颗粒又对管下部外缘区的颗粒造成剪切, 因此管下方两侧形成很小的两个高速度应变率区域, 但管道正下方的颗粒无法受到相邻颗粒的裹挟, 相应地出现一个小的速度应变率低值区域.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
颗粒流绕管速度应变率分布



Figure
12.
Strain rate distribution of granular flow around a pipe



下载:
全尺寸图片
幻灯片


颗粒流绕流经过管道后逐步回到低速度应变率水平, 相应的速度云图趋于均匀. 另外图12也表明了单管对周围流动的影响情况, 单管的存在使绕管两侧颗粒流速增大, 对下部缩口段拐角处低速颗粒的携带剪切作用增大, 使得拐角处的两道剪切带的位置更向壁面接近.

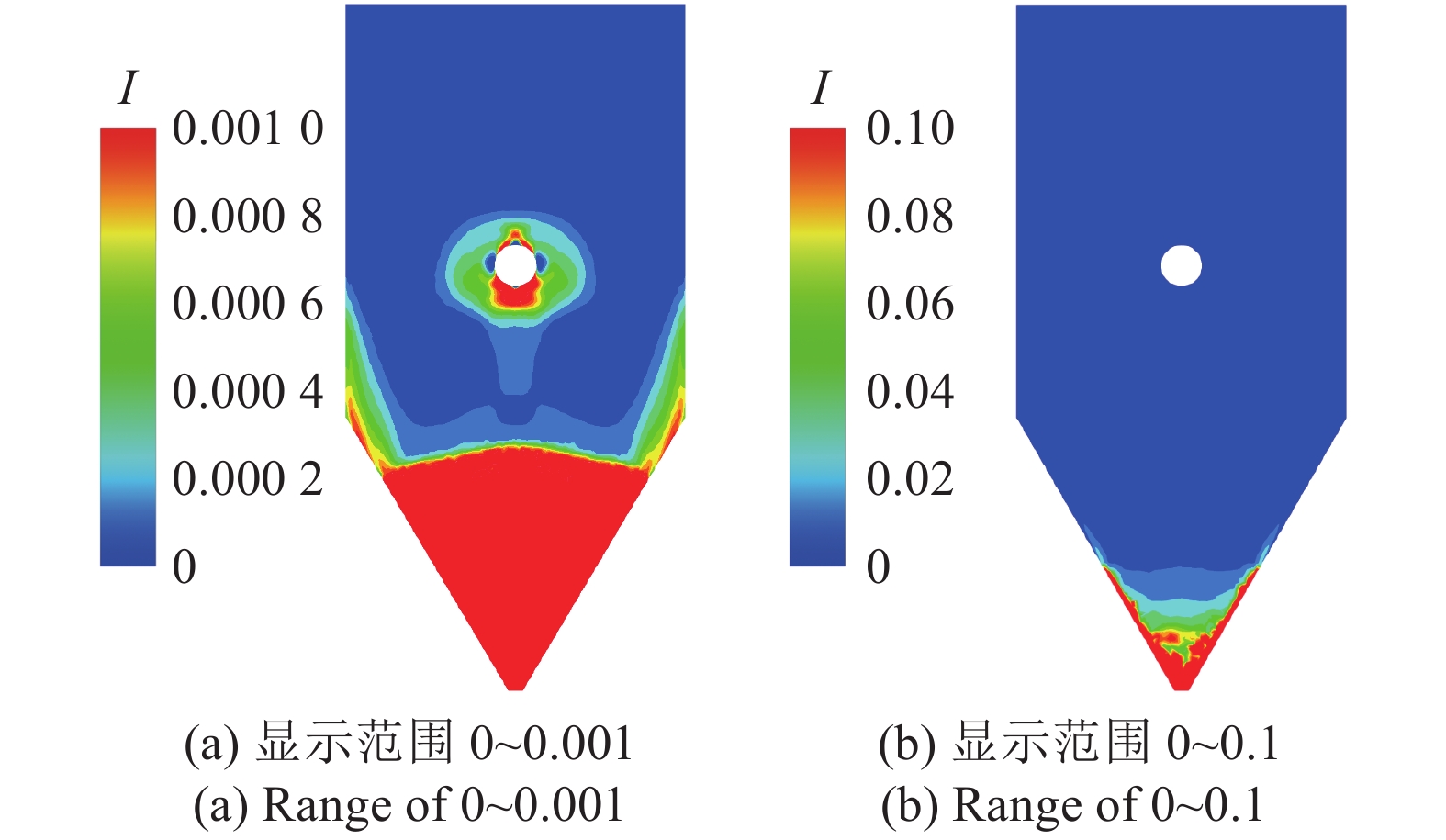
图13所示为移动床单管绕流流场的惯性数分布, 结合图13(a)显示范围为0 ~ 0.001和图13 (b)显示范围为0 ~ 0.1的惯性数分布云图, 按文献[14]的划分, 上部竖直段大部分区域颗粒处于准静态; 绕管附近局部区域和下部缩口段速度应变率增大, 颗粒摩擦作用增大, 大部分处于稠密惯性区; 出口处有很小区域内惯性数大于0.1, 处于颗粒快速流区. 虽然与图6相比, 惯性数大于0.1的区域变大, 但在全流场占比仍然很小, 本模型对绝大部分区域的模拟是适用的.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-320-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
颗粒流绕管惯性数分布



Figure
13.
Inertia number distribution of granular flow around a pipe



下载:
全尺寸图片
幻灯片

4.
结论

本文基于颗粒流单相μ(I)模型, 采用J & J摩擦压力公式, 补充局部颗粒体积分数与颗粒局部压力和局部颗粒流密度的关系式, 将移动床内密集颗粒处理成可压缩流体, 建立了颗粒流单相可压缩流μ(I)模型, 并建立了颗粒流?壁面摩擦条件, 在计算中对颗粒流黏度和压力进行正则化处理.

采用上述模型与算法对3种典型散料在移动床缩口料仓内的流动进行模拟, 与实验对比, 得到了玻璃珠、刚玉球和粗沙3种散料的μ(I)模型参数, 并对3种散料在料仓内的流动特性进行了分析, 得到了3种散料在料仓内的速度、应变率和体积分数等详细分布, 对于本文的计算工况, 玻璃珠、刚玉球和粗沙在缩口料仓内流动的颗粒体积分数的变化范围分别是0.495 ~ 0.508, 0.490 ~ 0.510和0.490 ~ 0.515, 绝大部分区域流动惯性数小于0.1, 计算结果对玻璃珠在料仓内的整体流和粗沙的漏斗流特性能较好预报, 模拟结果与实验测量结果定性符合较好.

进而对移动床颗粒单管绕流流动进行了模拟, 模拟结果详细揭示了绕管周围的颗粒速度、应变率和体积分数分布. 单管上方颗粒流速低、体积分数较大, 下方体积分数小, 计算结果合理, 与文献中揭示的颗粒绕管流动特性相符.

上述计算结果表明, 对于本文所研究的没有外部强制气流、颗粒在薄层移动床内低速密集流动情况, 颗粒体积分数变化最大范围为0.461 ~ 0.510, 绝大部分区域流动惯性数小于0.1, 本文所提出的单相可压缩流μ(I)模型与算法是可行的, 计算量较颗粒离散元方法和多相流方法大幅度减小. 当然, 基于拟流体假设的方法对由于壁面效应所引起的局部颗粒体积分数变化的预测、固相压力模型、算法的收敛性等多方面还有待进一步发展.