删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

时间尺度上Lagrange系统的Hojman守恒量

本站小编 Free考研考试/2022-01-01


引 言


力学系统的对称性与守恒律密切相关. 通过研究对称性而探索或发现复杂力学系统的守恒律, 这是分析力学研究的一个重要方面[1-2]. Lie对称性[3-9]、Noether对称性[10-20]和Mei对称性[21-28]是3种概念不同的对称性方法. 利用对称性和守恒律, 可以简化动力学问题甚至求解力学系统的精确解, 从而更好地理解其动力学行为. 微分方程的Lie理论最早由Lutzky[29]引入力学系统, 所得守恒量是Noether型的. Hojman[30]由Lie对称性直接导出一类不属于Noether型的守恒量, 称之为Hojman守恒量[21]. Hilger[31]于1990年提出了测度链上的分析理论, 而时间尺度作为测度链的特殊情形备受关注[32-34]. 时间尺度分析不仅是连续分析和离散分析的统一, 而且是经典微积分对任意时间尺度的拓广. Bartosiewicz和Torres[35]首先开展时间尺度上Noether对称性的研究, 此后关于时间尺度上Noether定理及其证明的探讨至今仍方兴未艾[36-42]. 但是, 时间尺度上Lie对称性直到最近才有一些初步的研究且所得守恒量均为Noether型的[43-46]. 鉴于此, 本文将研究并给出由时间尺度上Lie对称性直接导出的非Noether型的新型守恒量.


1.
时间尺度微积分


为方便读者, 这里对时间尺度微积分做一简单介绍, 详见文献[32-33].

设${{mathbb{T}}}$是一个时间尺度, 即实数集${{mathbb{R}}}$的任意非空闭子集, 如实数集${{mathbb{R}}}$、整数集${mathbb{Z}}$、非负整数集${{mathbb{N}}_0}$或$left[ {1,3}
ight] cup {mathbb{N}}$. 前跳算子$sigma left( t
ight) = inf left{ {s in {{mathbb{T}}}:s > t}
ight}$和后跳算子$
ho left( t
ight) = sup left{ {s in {{mathbb{T}}}:s < t}
ight}$是关于时间尺度的两个重要的量. 若$sigma left( t
ight) = t$, 称点$t in {{mathbb{T}}}$右稠密, $sigma left( t
ight) > t$则右发散; 若$
ho left( t
ight) = t$, 称点$t in {{mathbb{T}}}$左稠密, $
ho left( t
ight) < t$则左发散. 相邻点的位置关系在时间尺度上可用向前或向后步差函数$mu left( t
ight) = sigma left( t
ight) - t$或$upsilon left( t
ight) = t -
ho left( t
ight)$描述.

由${{mathbb{T}}}$可定义集合${{{mathbb{T}}}^k}$和${{{mathbb{T}}}_k}$: 当$sup {{mathbb{T}}} < infty $时, ${{{mathbb{T}}}^k} = $$ {{mathbb{T}}}backslash left( {
ho left( {sup {{mathbb{T}}}}
ight),sup {{mathbb{T}}}}
ight]$, 而当$sup {{mathbb{T}}} = infty $时, ${{{mathbb{T}}}^k} = {{mathbb{T}}}$; 与之相对应, 当$inf {{mathbb{T}}} > - infty $时, ${{{mathbb{T}}}_k} = {{mathbb{T}}}backslash left[ {sup {{mathbb{T}}},sigma left( {sup {{mathbb{T}}}}
ight)}
ight)$, 而当时$inf {{mathbb{T}}} = - infty $, ${{{mathbb{T}}}_k} = {{mathbb{T}}}$.

定义函数$y:{{mathbb{T}}} to {{mathbb{R}}}$在点$t in {{{mathbb{T}}}^k}$的delta导数为: 任给$varepsilon > 0$, 如果存在 $delta > 0$, 使得 $left| yleft( {sigma left( t
ight)}
ight) - yleft( tau
ight) -
ight. $$ left. {y^Delta }left( t
ight)left( {sigma left( t
ight) - tau }
ight)
ight| leqslant varepsilon left| {sigma left( t
ight) - tau }
ight|$对所有的 $tau in U = ( t - delta , $$ t + delta ) cap {{mathbb{T}}}$成立. 记为$ {y^Delta }left( t
ight) $或$dfrac{Delta }{{Delta t}}yleft( t
ight)$. 类似地, 在$t in {{{mathbb{T}}}_k}$的nabla导数定义为: 任给$varepsilon > 0$, 如果存在$delta > 0$, 使得$ left| {yleft( {
ho left( t
ight)}
ight) - yleft( tau
ight) - {y^nabla }left( t
ight)left( {
ho left( t
ight) - tau }
ight)}
ight| leqslant varepsilon left| {
ho left( t
ight) - tau }
ight| $成立. 记为$ {y^nabla }left( t
ight) $或 $dfrac{nabla }{{nabla t}}yleft( t
ight)$.

如果函数$ y:{mathbb{T}} to {mathbb{R}} $在$ {mathbb{T}} $的右稠密点连续且在左稠密点的左极限存在, 则称$ yleft( t
ight) $是$ {text{rd}} $连续的. $ {mathbb{T}} $上所有$ {text{rd}} $连续的函数的集合记为$ C_{{text{rd}}}^0left( {mathbb{T}}
ight) $, 而$ {{mathbb{T}}^k} $上具有$ {text{rd}} $连续的delta导数的delta可微函数的集合记为$ C_{{text{rd}}}^{1,Delta }left( {mathbb{T}}
ight) $.

如果对所有的$t in {{{mathbb{T}}}^k}$, 有$ {Y^Delta }left( t
ight) = yleft( t
ight) $, 则称$ Y:{mathbb{T}} to {mathbb{R}} $为$ y:{mathbb{T}} to {mathbb{R}} $的一个原函数. 定义函数$ y $的delta不定积分为$ int {yleft( t
ight)Delta t = Yleft( t
ight) + C} $, delta定积分为$ int_a^b {yleft( t
ight)} Delta t = Yleft( b
ight) - Yleft( a
ight) $, 其中$ a,b in {mathbb{T}} $, $C$是任意常数.

Dubois-Reymond引理: 令$ y:left[ {a,b}
ight] to {{mathbb{R}}^n} $, $ y in C_{{text{rd}}}^0 $, 对于任意的$ eta in C_{{text{rd}}}^1 $且$ eta left( a
ight) = eta left( b
ight) = 0 $, 积分$ displaystyleint_a^b {{y^T}left( t
ight)} {eta ^Delta }left( t
ight)cdot $$ Delta t = 0$成立的充分必要条件是在$t in {left[ {a,b}
ight]^k}$上$yleft( t
ight) equiv C$.

链式法则: 设函数$g为;{{{mathbb{T}}}_1} times {{{mathbb{T}}}_2} times cdots times {{{mathbb{T}}}_n} to {{mathbb{R}}}$在点${t^0}$完全delta可微, 函数${vartheta _j},left( {j = 1,2, cdots ,n}
ight)$在点${zeta ^0}$的delta导数存在, 其中$t_j^0 = {vartheta _j}left( {{zeta ^0}}
ight)$, 则复合函数$Gleft( zeta
ight) = gleft( {{vartheta _1}left( zeta
ight),{vartheta _2}left( zeta
ight), cdots ,{vartheta _n}left( zeta
ight)}
ight)$在该点的delta导数${G^Delta }left( {{zeta ^0}}
ight)$存在, 且有






$$begin{array}{l} {G^Delta }left( {{zeta ^0}}
ight) = g_{{t_i}}^{{Delta _i}}left( {{t^0}}
ight)vartheta _i^Delta left( {{zeta ^0}}
ight)+quad g_{{t_{i - 1}}}^{{Delta _{i - 1}}}left[ {{vartheta _1}left( {{zeta ^0}}
ight),{vartheta _2}left( {{zeta ^0}}
ight), cdots ,{vartheta _{i - 1}}left( {{zeta ^0}}
ight),{sigma _i}left( {{vartheta _i}left( {{zeta ^0}}
ight)}
ight)},
ight. quad left. {{vartheta _{i + 1}}left( {{zeta ^0}}
ight), cdots ,{vartheta _n}left( {{zeta ^0}}
ight)}
ight]vartheta _{i - 1}^Delta left( {{zeta ^0}}
ight) + cdots+ quad g_{{t_1}}^{{Delta _1}}left[ {{vartheta _1}left( {{zeta ^0}}
ight),{sigma _2}left( {{vartheta _2}left( {{zeta ^0}}
ight)}
ight), cdots ,{sigma _i}left( {{vartheta _i}left( {{zeta ^0}}
ight)}
ight)},
ight. quad left. {{vartheta _{i + 1}}left( {{zeta ^0}}
ight), cdots ,{vartheta _n}left( {{zeta ^0}}
ight)}
ight]vartheta _1^Delta left( {{zeta ^0}}
ight)+ end{array}$$







$$ begin{array}{*{20}{l}}quad g_{{t_{i + 1}}}^{{Delta _{i + 1}}}left[ {{sigma _1}left( {{vartheta _1}left( {{zeta ^0}}
ight)}
ight),{sigma _2}left( {{vartheta _2}left( {{zeta ^0}}
ight)}
ight) cdots ,{sigma _i}left( {{vartheta _i}left( {{zeta ^0}}
ight)}
ight)},
ight. {quad left. {{vartheta _{i + 1}}left( {{zeta ^0}}
ight), cdots ,{vartheta _n}left( {{zeta ^0}}
ight)}
ight]vartheta _{i + 1}^Delta left( {{zeta ^0}}
ight) + cdots + }quad g_{{t_n}}^{{Delta _n}}left[ {{sigma _1}left( {{vartheta _1}left( {{zeta ^0}}
ight)}
ight),{sigma _2}left( {{vartheta _2}left( {{zeta ^0}}
ight)}
ight), cdots ,{sigma _{n - 1}}left( {{vartheta _{n - 1}}left( {{zeta ^0}}
ight)}
ight),}
ight.left. {quad {vartheta _n}left( {{zeta ^0}}
ight)}
ight]vartheta _n^Delta left( {{zeta ^0}}
ight)end{array}$$
(1)

其中







$$begin{array}{l} g_{{t_i}}^{{Delta _i}}left( t
ight){buildrel Delta over =} dfrac{{partial gleft( t
ight)}}{{{Delta _i}{t_i}}} = mathop {lim }limits_{begin{subarray}{l} {s_i} to {t_i} {s_i} ne {sigma _i}left( {{t_i}}
ight) end{subarray}} dfrac{begin{array}{l}gleft( {{t_1},t_2, cdots ,{t_{i - 1}},{sigma _i}left( {{t_i}}
ight),{t_{i + 1}}, cdots ,{t_n}}
ight) - gleft( {{t_1}, t_2,cdots ,{t_{i - 1}},{s_i},{t_{i + 1}}, cdots ,{t_n}}
ight)end{array}}{{{sigma _i}left( {{t_i}}
ight) - {s_i}}}end{array} $$
(2)

称为函数$gleft( t
ight)$在点$t$相对${t_i}$的delta偏导数.

混合delta偏导数次序交换定理: 如果$g_{{t_i}{t_j}}^{{Delta _i}{Delta _j}}left( t
ight)$和$g_{{t_j}{t_i}}^{{Delta _j}{Delta _i}}left( t
ight)$在点${t^0}$连续, 则$g_{{t_i}{t_j}}^{{Delta _i}{Delta _j}}left( t
ight) = g_{{t_j}{t_i}}^{{Delta _j}{Delta _i}}left( t
ight)$.

对于delta可微函数$yleft( t
ight)$和$zleft( t
ight)$, 在时间尺度上成立Leibniz公式







$$ begin{split}&{left( {yz}
ight)^Delta }left( t
ight) = {y^sigma }left( t
ight){z^Delta }left( t
ight) + {y^Delta }left( t
ight)zleft( t
ight) =&;;;;;;;; yleft( t
ight){z^Delta }left( t
ight) + {y^Delta }left( t
ight){z^sigma }left( t
ight)end{split} $$
(3)

以及分部积分公式







$$ begin{split} &int_a^b {yleft( t
ight)} {z^Delta }left( t
ight)Delta t = &qquadleft( {yz}
ight)left( b
ight) - left( {yz}
ight)left( a
ight) - int_a^b {{y^Delta }left( t
ight){z^sigma }left( t
ight)Delta t}end{split} $$
(4)


2.
时间尺度上运动微分方程


时间尺度上Lagrange方程为[28]







$$ frac{nabla }{{nabla t}}frac{{partial L}}{{partial q_s^Delta }} - {sigma ^nabla }left( t
ight)frac{{partial L}}{{partial {q_s}}} = 0, ;{s = 1,2, cdots ,n} $$
(5)

其中$ Lleft( {{q_s},q_s^Delta ,t}
ight):{{{mathbb{R}}}^n} times {{{mathbb{R}}}^n} times {{{mathbb{T}}}^k} to {{mathbb{R}}} $是时间尺度上Lagrange函数, ${q_s}left( t
ight)$是时间尺度上广义坐标, $q_s^Delta left( t
ight)$是广义速度. 假设这些函数都是$C_{{text{rd}}}^1$函数.

假设系统非奇异, 即$D = det left( {dfrac{{{partial ^2}L}}{{partial q_s^Delta {Delta _{n + k}}q_k^Delta }}}
ight) ne 0$, 则由方程(5)可解得所有广义加速度, 简记为







$$ q_s^{Delta Delta } = {alpha _s}left( {{q_k},q_k^Delta ,t}
ight), ;{s = 1,2, cdots ,n} $$
(6)


3.
时间尺度上Lagrange系统的两个重要关系式


本节推导时间尺度上Lagrange系统的两个重要关系式, 它们是推导时间尺度上Hojman守恒量的基础.

设函数$ {varOmega _s} = {varOmega _s}left( {{q_k},q_k^Delta ,t}
ight) $是delta可微的, 将$ {varOmega _s} $按方程(6)对$t$求delta导数, 有







$$ frac{{bar Delta }}{{Delta t}}{varOmega _s} = frac{{partial {varOmega _s}}}{{{Delta _k}{q_k}}}q_k^Delta + frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}{alpha _k} + frac{{partial {varOmega _s}}}{{{Delta _{2n + 1}}t}}qquadqquad $$
(7)







$$ begin{split}& frac{{bar Delta }}{{Delta t}}frac{{bar Delta }}{{Delta t}}{varOmega _s} = {left( {frac{{partial {varOmega _s}}}{{{Delta _k}{q_k}}}}
ight)^sigma }{alpha _k} + frac{{bar Delta }}{{Delta t}}frac{{partial {varOmega _s}}}{{{Delta _k}{q_k}}}q_k^Delta +& qquad {left( {frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}}
ight)^sigma }left( {frac{{partial {alpha _k}}}{{{Delta _j}{q_j}}}q_j^Delta + frac{{partial {alpha _k}}}{{{Delta _{n + j}}q_j^Delta }}{alpha _j} + frac{{partial {alpha _k}}}{{{Delta _{2n + 1}}t}}}
ight) + & qquad frac{{bar Delta }}{{Delta t}}frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}{alpha _k} + frac{{{partial ^2}{varOmega _s}}}{{{Delta _{2n + 1}}t{Delta _k}{q_k}}}q_k^Delta+ & qquad frac{{{partial ^2}{varOmega _s}}}{{{Delta _{2n + 1}}t{Delta _{n + k}}q_k^Delta }}{alpha _k} + frac{{{partial ^2}{varOmega _s}}}{{{Delta _{2n + 1}}t{Delta _{2n + 1}}t}}end{split} $$
(8)

其中$dfrac{{bar Delta }}{{Delta t}}left( *
ight)$表示$left( *
ight)$按方程(6)对时间$t$的delta导数, 即有







$$ frac{{bar Delta }}{{Delta t}}left( *
ight) = frac{partial }{{{Delta _k}{q_k}}}left( *
ight)q_k^Delta + frac{partial }{{{Delta _{n + k}}q_k^Delta }}left( *
ight){alpha _k} + frac{partial }{{{Delta _{2n + 1}}t}}left( *
ight) $$
(9)

而符号$dfrac{{partial {varOmega _s}}}{{{Delta _k}{q_k}}}$, $dfrac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}$和$dfrac{{partial {varOmega _s}}}{{{Delta _{2n + 1}}t}}$表示按照链式法则(1)函数${varOmega _s}left( {{q_1},q_2, cdots ,{q_n},q_1^Delta , q_2^Delta,cdots ,q_n^Delta ,t}
ight)$分别对${q_k}$, $q_k^Delta $和时间$t$的delta偏导数, 即有







$$ dfrac{{partial {varOmega _s}}}{{{Delta _k}{q_k}}} buildrel Delta over = dfrac{partial }{{{Delta _k}{q_k}}}{varOmega _s}left( {q_1^sigma , q_2^sigma,cdots ,q_{k - 1}^sigma ,{q_k}, cdots ,{q_n},q_1^Delta ,q_2^Delta , cdots ,q_n^Delta ,t}
ight)quadquad $$
(10)







$$ begin{array}{l}dfrac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}buildrel Delta over = dfrac{partial }{{{Delta _{n + k}}q_k^Delta }}{varOmega _s}left( q_1^sigma , q_2^sigma ,cdots ,q_n^sigma ,q_1^{Delta sigma }, q_2^{Delta sigma },cdots ,
ight. quad left. q_{k - 1}^{Delta sigma },q_k^Delta , cdots ,q_n^Delta ,t
ight) end{array}$$
(11)







$$ dfrac{{partial {varOmega _s}}}{{{Delta _{2n + 1}}t}} buildrel Delta over = dfrac{partial }{{{Delta _{2n + 1}}t}}{varOmega _s}left( {q_1^sigma , q_2^sigma , cdots ,q_n^sigma ,q_1^{Delta sigma },q_2^{Delta sigma }, cdots ,q_n^{Delta sigma },t}
ight) quadquadquadquadquad$$
(12)

再将式(7)两端分别对${q_s}$和$q_s^Delta $求普通偏导数和delta偏导数, 有







$$ begin{split}&dfrac{partial }{{partial {q_s}}}dfrac{{bar Delta }}{{Delta t}}{varOmega _s} = dfrac{{{partial ^2}{varOmega _s}}}{{{Delta _k}{q_k}partial {q_s}}}q_k^Delta + dfrac{{{partial ^2}{varOmega _s}}}{{{Delta _{n + k}}q_k^Delta partial {q_s}}}{alpha _k}+&qquad dfrac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}dfrac{{partial {alpha _k}}}{{partial {q_s}}} + dfrac{{{partial ^2}{varOmega _s}}}{{{Delta _{2n + 1}}tpartial {q_s}}} end{split}$$
(13)







$$begin{split}& frac{partial }{{{Delta _s}{q_s}}}frac{{bar Delta }}{{Delta t}}{varOmega _s} = frac{{{partial ^2}{varOmega _s}}}{{{Delta _k}{q_k}{Delta _s}{q_s}}}q_k^Delta + {left( {frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}}
ight)^sigma }frac{{partial {alpha _k}}}{{{Delta _s}{q_s}}}+ &qquad frac{{{partial ^2}{varOmega _s}}}{{{Delta _{n + k}}q_k^Delta {Delta _s}{q_s}}}{alpha _k} + frac{{{partial ^2}{varOmega _s}}}{{{Delta _{2n + 1}}t{Delta _s}{q_s}}} end{split}$$
(14)







$$ begin{split}& frac{partial }{{partial q_s^Delta }}frac{{bar Delta }}{{Delta t}}{varOmega _s} = frac{{{partial ^2}{varOmega _s}}}{{{Delta _k}{q_k}partial q_s^Delta }}q_k^Delta + frac{{partial {varOmega _s}}}{{{Delta _s}{q_s}}} + &qquad frac{{{partial ^2}{varOmega _s}}}{{{Delta _{n + k}}q_k^Delta partial q_s^Delta }}{alpha _k} + frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}frac{{partial {alpha _k}}}{{partial q_s^Delta }} + frac{{{partial ^2}{varOmega _s}}}{{{Delta _{2n + 1}}tpartial q_s^Delta }}end{split} $$
(15)







$$begin{split}& frac{partial }{{{Delta _{n + k}}q_k^Delta }}frac{{bar Delta }}{{Delta t}}{varOmega _s} = {left( {frac{{partial {varOmega _s}}}{{{Delta _k}{q_k}}}}
ight)^sigma } + frac{{{partial ^2}{varOmega _s}}}{{{Delta _j}{q_j}{Delta _{n + k}}q_k^Delta }}q_j^Delta+ &qquad {left( {frac{{partial {varOmega _s}}}{{{Delta _{n + j}}q_j^Delta }}}
ight)^sigma }frac{{partial {alpha _j}}}{{{Delta _{n + k}}q_k^Delta }} + frac{{{partial ^2}{varOmega _s}}}{{{Delta _{n + j}}q_j^Delta {Delta _{n + k}}q_k^Delta }}{alpha _j} + &qquad frac{{{partial ^2}{varOmega _s}}}{{{Delta _{2n + 1}}t{Delta _{n + k}}q_k^Delta }}end{split} $$
(16)

将式(8)两端对$q_s^Delta $求普通偏导数, 有







$$begin{split}& frac{partial }{{partial q_s^Delta }}frac{{bar Delta }}{{Delta t}}frac{{bar Delta }}{{Delta t}}{varOmega _s} = frac{partial }{{partial q_s^Delta }}{left( {frac{{partial {varOmega _s}}}{{{Delta _k}{q_k}}}}
ight)^sigma }{alpha _k} + {left( {frac{{partial {varOmega _s}}}{{{Delta _k}{q_k}}}}
ight)^sigma }frac{{partial {alpha _k}}}{{partial q_s^Delta }} +&qquad frac{{bar Delta }}{{Delta t}}frac{{partial {varOmega _s}}}{{{Delta _s}{q_s}}} + frac{partial }{{partial q_s^Delta }}left( {frac{{bar Delta }}{{Delta t}}frac{{partial {varOmega _s}}}{{{Delta _k}{q_k}}}}
ight)q_k^Delta + frac{partial }{{partial q_s^Delta }}{left( {frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}}
ight)^sigma }cdot &qquad left( {frac{{partial {alpha _k}}}{{{Delta _j}{q_j}}}q_j^Delta + frac{{partial {alpha _k}}}{{{Delta _{n + j}}q_j^Delta }}{alpha _j} + frac{{partial {alpha _k}}}{{{Delta _{2n + 1}}t}}}
ight) + &qquad {left( {frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}}
ight)^sigma }left( {frac{{{partial ^2}{alpha _k}}}{{{Delta _j}{q_j}partial q_s^Delta }}q_j^Delta + frac{{partial {alpha _k}}}{{{Delta _s}{q_s}}}}
ight. + &qquad left. { frac{{{partial ^2}{alpha _k}}}{{{Delta _{n + j}}q_j^Delta partial q_s^Delta }}{alpha _j} + frac{{partial {alpha _k}}}{{{Delta _{n + j}}q_j^Delta }}frac{{partial {alpha _j}}}{{partial q_s^Delta }} + frac{{{partial ^2}{alpha _k}}}{{{Delta _{2n + 1}}tpartial q_s^Delta }}}
ight) + &qquad frac{partial }{{partial q_s^Delta }}left( {frac{{bar Delta }}{{Delta t}}frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}}
ight){alpha _k} + frac{{bar Delta }}{{Delta t}}frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}frac{{partial {alpha _k}}}{{partial q_s^Delta }} + &qquad frac{{{partial ^3}{varOmega _s}}}{{{Delta _{2n + 1}}t{Delta _k}{q_k}partial q_s^Delta }}q_k^Delta + frac{{{partial ^2}{varOmega _s}}}{{{Delta _{2n + 1}}t{Delta _s}{q_s}}} + &qquad frac{{{partial ^3}{varOmega _s}}}{{{Delta _{2n + 1}}t{Delta _{n + k}}q_k^Delta partial q_s^Delta }}{alpha _k} + frac{{{partial ^2}{varOmega _s}}}{{{Delta _{2n + 1}}t{Delta _{n + k}}q_k^Delta }}frac{{partial {alpha _k}}}{{partial q_s^Delta }} + &qquadfrac{{{partial ^3}{varOmega _s}}}{{{Delta _{2n + 1}}{t^2}partial q_s^Delta }} [-5pt]end{split}$$
(17)

将$dfrac{{partial {varOmega _s}}}{{partial {q_s}}}$对时间$t$求delta导数, 得到







$$ frac{{bar Delta }}{{Delta t}}frac{{partial {varOmega _s}}}{{partial {q_s}}} = frac{{{partial ^2}{varOmega _s}}}{{partial {q_s}{Delta _k}{q_k}}}q_k^Delta + frac{{{partial ^2}{varOmega _s}}}{{partial {q_s}{Delta _{n + k}}q_k^Delta }}{alpha _k} + frac{{{partial ^2}{varOmega _s}}}{{partial {q_s}{Delta _{2n + 1}}t}} $$
(18)

比较式(13)和式(18), 假设${varOmega _s}$对变量${q_s}$和$q_s^Delta $求delta偏导数和普通偏导数的次序可交换, 得到







$$ frac{{bar Delta }}{{Delta t}}frac{{partial {varOmega _s}}}{{partial {q_s}}} = frac{partial }{{partial {q_s}}}frac{{bar Delta }}{{Delta t}}{varOmega _s} - frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}frac{{partial {alpha _k}}}{{partial {q_s}}} $$
(19)

再将式(15)对时间$t$求delta导数, 得到







$$ begin{split} &frac{{bar Delta }}{{Delta t}}frac{partial }{{partial q_s^Delta }}frac{{bar Delta }}{{Delta t}}{varOmega _s} = {left( {frac{{{partial ^2}{varOmega _s}}}{{{Delta _k}{q_k}partial q_s^Delta }}}
ight)^sigma }{alpha _k} + frac{{bar Delta }}{{Delta t}}frac{{{partial ^2}{varOmega _s}}}{{{Delta _k}{q_k}partial q_s^Delta }}q_k^Delta +&qquad frac{{bar Delta }}{{Delta t}}frac{{partial {varOmega _s}}}{{{Delta _s}{q_s}}} + frac{{bar Delta }}{{Delta t}}frac{{{partial ^2}{varOmega _s}}}{{{Delta _{n + k}}q_k^Delta partial q_s^Delta }}{alpha _k} + &qquad {left( {frac{{{partial ^2}{varOmega _s}}}{{{Delta _{n + k}}q_k^Delta partial q_s^Delta }}}
ight)^sigma }left( {frac{{partial {alpha _k}}}{{{Delta _j}{q_j}}}q_j^Delta + frac{{partial {alpha _k}}}{{{Delta _{n + j}}q_j^Delta }}{alpha _j} + frac{{partial {alpha _k}}}{{{Delta _{2n + 1}}t}}}
ight)+ &qquad {left( {frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}}
ight)^sigma }left( frac{{{partial ^2}{alpha _k}}}{{partial q_s^Delta {Delta _j}{q_j}}}q_j^Delta + frac{{{partial ^2}{alpha _k}}}{{partial q_s^Delta {Delta _{n + j}}q_j^Delta }}{alpha _j} +
ight. &qquad left. frac{{{partial ^2}{alpha _k}}}{{partial q_s^Delta {Delta _{2n + 1}}t}}
ight) + frac{{bar Delta }}{{Delta t}}frac{{{partial ^2}{varOmega _s}}}{{{Delta _{2n + 1}}tpartial q_s^Delta }} + frac{{bar Delta }}{{Delta t}}frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}frac{{partial {alpha _k}}}{{partial q_s^Delta }} end{split}$$
(20)

类似地, 比较式(17)和式(20), 并假设函数${varOmega _s}$和${alpha _s}$对变量${q_s}$和$q_s^Delta $求delta偏导数以及普通偏导数的次序可交换, 有







$$begin{split}& frac{{bar Delta }}{{Delta t}}frac{partial }{{partial q_s^Delta }}frac{{bar Delta }}{{Delta t}}{varOmega _s} = frac{partial }{{partial q_s^Delta }}frac{{bar Delta }}{{Delta t}}frac{{bar Delta }}{{Delta t}}{varOmega _s} - frac{partial }{{{Delta _s}{q_s}}}frac{{bar Delta }}{{Delta t}}{varOmega _s}- &qquad left[ {frac{partial }{{partial q_s^Delta }}{{left( {frac{{partial {varOmega _s}}}{{{Delta _k}{q_k}}}}
ight)}^sigma } - {{left( {frac{{{partial ^2}{varOmega _s}}}{{{Delta _k}{q_k}partial q_s^Delta }}}
ight)}^sigma }}
ight]{alpha _k} - &qquad frac{partial }{{{Delta _{n + k}}q_k^Delta }}frac{{bar Delta }}{{Delta t}}{varOmega _s}frac{{partial {alpha _k}}}{{partial q_s^Delta }}- &qquad left[ {frac{partial }{{partial q_s^Delta }}{{left( {frac{{partial {varOmega _s}}}{{{Delta _{n + k}}q_k^Delta }}}
ight)}^sigma } - {{left( {frac{{{partial ^2}{varOmega _s}}}{{{Delta _{n + k}}q_k^Delta partial q_s^Delta }}}
ight)}^sigma }}
ight]frac{{bar Delta }}{{Delta t}}{alpha _k} end{split}$$
(21)

式(19)和式(21)是时间尺度上Lagrange系统导数运算的两个重要关系式.


4.
时间尺度上Lie对称性


在时间尺度上引进无限小变换







$$ {t^*} = t , ;q_s^*left( {{t^*}}
ight) = {q_s}left( t
ight) + varepsilon {xi _s}left( {{q_k},q_k^Delta ,t}
ight) $$
(22)

式中$varepsilon $是无限小参数, $ {xi _s} $是变换的生成元, ${kern 1pt} s,k = $$ 1,2, cdots ,n$. 变换式(22)的无限小生成元向量${X^{left( 0
ight)}}$及其一次拓展${X^{left( 1
ight)}}$和二次拓展${X^{left( 2
ight)}}$为[44]







$$left. begin{split} & {X^{left( 0
ight)}} = {xi _s}frac{partial }{{partial {q_s}}} & {X^{left( 1
ight)}} = {X^{left( 0
ight)}} + frac{{bar Delta }}{{Delta t}}{xi _s}frac{partial }{{partial q_s^Delta }} & {X^{left( 2
ight)}} = {X^{left( 1
ight)}} + frac{{bar Delta }}{{Delta t}}frac{{bar Delta }}{{Delta t}}{xi _s}frac{partial }{{partial q_s^{Delta Delta }}} end{split}
ight}$$
(23)

依据微分方程在单参数Lie变换群下的不变性, 可定义时间尺度上Lagrange系统的Lie对称性, 即

定义1. 对于时间尺度上Lagrange系统(5), 当且仅当







$$ {X^{left( 2
ight)}}left[ {q_s^{Delta Delta } - {alpha _s}left( {{q_k},q_k^Delta ,t}
ight)}
ight] = 0, ;{s = 1,2, cdots ,n} $$
(24)

则变换式(22)是Lie对称性的.

方程(24)可写为







$$ frac{{bar Delta }}{{Delta t}}frac{{bar Delta }}{{Delta t}}{xi _s} - {X^{left( 1
ight)}}left( {{alpha _s}}
ight) = 0 $$
(25)

或







$$ frac{{bar Delta }}{{Delta t}}frac{{bar Delta }}{{Delta t}}{xi _s} - {xi _k}frac{{partial {alpha _s}}}{{partial {q_k}}} - frac{{bar Delta }}{{Delta t}}{xi _k}frac{{partial {alpha _s}}}{{partial q_k^Delta }} = 0 $$
(26)

称方程(25)或式(26)为时间尺度上Lie对称性确定方程.


5.
时间尺度上Lie对称性定理


由Lie对称性可直接导出时间尺度上一类新守恒量, 即有:

定理1. 对于时间尺度上Lagrange系统(5), 如果变换式(22)是Lie对称性的, 并假设所有函数对其变量的混合delta偏导数连续, 且存在函数$psi = psi left( {{q_s}}
ight)$使得







$$ frac{{partial {alpha _s}}}{{partial q_s^Delta }} + frac{1}{psi }frac{{partial psi }}{{{Delta _s}{q_s}}}q_s^Delta = 0 $$
(27)

则该系统存在新的守恒量, 形如







$$ I = frac{1}{psi }frac{partial }{{partial {q_s}}}left( {psi {xi _s}}
ight) + frac{1}{psi }frac{partial }{{partial q_s^Delta }}left( {psi frac{{bar Delta }}{{Delta t}}{xi _s}}
ight) + varXi $$
(28)

其中







$$ begin{split}& varXi = int_{{t_1}}^t {Biggl{{18} {left( {dfrac{partial }{{{Delta _s}{q_s}}} - dfrac{partial }{{partial {q_s}}}}
ight)dfrac{{bar Delta }}{{Delta t}}{xi _s} + left( {dfrac{{partial {xi _s}}}{{{Delta _{n + k}}q_k^Delta }} - dfrac{{partial {xi _s}}}{{partial q_k^Delta }}}
ight)dfrac{{partial {alpha _k}}}{{partial {q_s}}}} } + &qquad left( {dfrac{partial }{{{Delta _{n + k}}q_k^Delta }} - dfrac{partial }{{partial q_k^Delta }}}
ight)dfrac{{bar Delta }}{{Delta t}}{xi _s}dfrac{{partial {alpha _k}}}{{partial q_s^Delta }} + &qquad left[ {dfrac{partial }{{partial q_s^Delta }}{{left( {dfrac{{partial {xi _s}}}{{{Delta _k}{q_k}}}}
ight)}^sigma } - {{left( {dfrac{{{partial ^2}{xi _s}}}{{{Delta _k}{q_k}partial q_s^Delta }}}
ight)}^sigma }}
ight]{alpha _k} + &qquad left[ {dfrac{partial }{{partial q_s^Delta }}{{left( {dfrac{{partial {xi _s}}}{{{Delta _{n + k}}q_k^Delta }}}
ight)}^sigma } - {{left( {dfrac{{{partial ^2}{xi _s}}}{{{Delta _{n + k}}q_k^Delta partial q_s^Delta }}}
ight)}^sigma }}
ight]dfrac{{bar Delta }}{{Delta t}}{alpha _k} + &qquad left[ {dfrac{1}{psi }dfrac{{partial psi }}{{{Delta _s}{q_s}}} - {{left( {dfrac{1}{psi }dfrac{{partial psi }}{{partial {q_s}}}}
ight)}^sigma }}
ight]dfrac{{bar Delta }}{{Delta t}}{xi _s} + &qquad { left[ {{X^{left( 1
ight)}}left( {dfrac{1}{psi }dfrac{{partial psi }}{{{Delta _s}{q_s}}}}
ight) - {xi _k}dfrac{partial }{{{Delta _s}{q_s}}}left( {dfrac{1}{psi }dfrac{{partial psi }}{{partial {q_k}}}}
ight)}
ight]q_s^Delta } Bigggr}{18}Delta tau end{split}$$
(29)

证明: 将式(28)按方程(6)对时间$t$求delta导数, 得







$$begin{split} &frac{{bar Delta }}{{Delta t}}I = frac{{bar Delta }}{{Delta t}}left[ {frac{1}{psi }frac{partial }{{partial {q_s}}}left( {psi {xi _s}}
ight) + frac{1}{psi }frac{partial }{{partial q_s^Delta }}left( {psi frac{{bar Delta }}{{Delta t}}{xi _s}}
ight)}
ight]+ &qquad left( {frac{partial }{{{Delta _s}{q_s}}} - frac{partial }{{partial {q_s}}}}
ight)frac{{bar Delta }}{{Delta t}}{xi _s} + left( {frac{{partial {xi _s}}}{{{Delta _{n + k}}q_k^Delta }} - frac{{partial {xi _s}}}{{partial q_k^Delta }}}
ight)frac{{partial {alpha _k}}}{{partial {q_s}}}+ &qquad left( {frac{partial }{{{Delta _{n + k}}q_k^Delta }} - frac{partial }{{partial q_k^Delta }}}
ight)frac{{bar Delta }}{{Delta t}}{xi _s}frac{{partial {alpha _k}}}{{partial q_s^Delta }}+ &qquad left[ {frac{partial }{{partial q_s^Delta }}{{left( {frac{{partial {xi _s}}}{{{Delta _k}{q_k}}}}
ight)}^sigma } - {{left( {frac{{{partial ^2}{xi _s}}}{{{Delta _k}{q_k}partial q_s^Delta }}}
ight)}^sigma }}
ight]{alpha _k} + &qquad left[ {frac{partial }{{partial q_s^Delta }}{{left( {frac{{partial {xi _s}}}{{{Delta _{n + k}}q_k^Delta }}}
ight)}^sigma } - {{left( {frac{{{partial ^2}{xi _s}}}{{{Delta _{n + k}}q_k^Delta partial q_s^Delta }}}
ight)}^sigma }}
ight]frac{{bar Delta }}{{Delta t}}{alpha _k} + &qquad left[ {frac{1}{psi }frac{{partial psi }}{{{Delta _s}{q_s}}} - {{left( {frac{1}{psi }frac{{partial psi }}{{partial {q_s}}}}
ight)}^sigma }}
ight]frac{{bar Delta }}{{Delta t}}{xi _s}+ &qquad left[ {{X^{left( 1
ight)}}left( {frac{1}{psi }frac{{partial psi }}{{{Delta _s}{q_s}}}}
ight) - {xi _k}frac{partial }{{{Delta _s}{q_s}}}left( {frac{1}{psi }frac{{partial psi }}{{partial {q_k}}}}
ight)}
ight]q_s^Deltaend{split} $$
(30)

根据假设, 所有函数对其变量的混合delta偏导数连续, 因此函数${xi _s}$和${alpha _s}$对变量${q_s}$和$q_s^Delta $求delta偏导数以及普通偏导数的次序可交换[33]. 利用关系式(19)和式(21), 有







$$ frac{{bar Delta }}{{Delta t}}frac{{partial {xi _s}}}{{partial {q_s}}} = frac{partial }{{partial {q_s}}}frac{{bar Delta }}{{Delta t}}{xi _s} - frac{{partial {xi _s}}}{{{Delta _{n + k}}q_k^Delta }}frac{{partial {alpha _k}}}{{partial {q_s}}} $$
(31)







$$begin{split}& frac{{bar Delta }}{{Delta t}}frac{partial }{{partial q_s^Delta }}frac{{bar Delta }}{{Delta t}}{xi _s} = frac{partial }{{partial q_s^Delta }}frac{{bar Delta }}{{Delta t}}frac{{bar Delta }}{{Delta t}}{xi _s} - frac{partial }{{{Delta _s}{q_s}}}frac{{bar Delta }}{{Delta t}}{xi _s}- &qquad left[ {frac{partial }{{partial q_s^Delta }}{{left( {frac{{partial {xi _s}}}{{{Delta _k}{q_k}}}}
ight)}^sigma } - {{left( {frac{{{partial ^2}{xi _s}}}{{{Delta _k}{q_k}partial q_s^Delta }}}
ight)}^sigma }}
ight]{alpha _k} - &qquad left[ {frac{partial }{{partial q_s^Delta }}{{left( {frac{{partial {xi _s}}}{{{Delta _{n + k}}q_k^Delta }}}
ight)}^sigma } - {{left( {frac{{{partial ^2}{xi _s}}}{{{Delta _{n + k}}q_k^Delta partial q_s^Delta }}}
ight)}^sigma }}
ight]frac{{bar Delta }}{{Delta t}}{alpha _k} - &qquad frac{partial }{{{Delta _{n + k}}q_k^Delta }}frac{{bar Delta {xi _s}}}{{Delta t}}frac{{partial {alpha _k}}}{{partial q_s^Delta }} end{split}$$
(32)

注意到$psi = psi left( {{q_s}}
ight)$, 因此有







$$ frac{Delta }{{Delta t}}left( {frac{1}{psi }frac{{partial psi }}{{partial {q_s}}}}
ight){xi _s} = frac{partial }{{{Delta _k}{q_k}}}left( {frac{1}{psi }frac{{partial psi }}{{partial {q_s}}}}
ight)q_k^Delta {xi _s} $$
(33)

将式(31) ~ 式(33)代入式(30), 得到







$$ begin{split} frac{{bar Delta }}{{Delta t}}I = frac{partial }{{partial q_s^Delta }}left( {frac{{bar Delta }}{{Delta t}}frac{{bar Delta }}{{Delta t}}{xi _s} - {X^{left( 1
ight)}}left( {{alpha _s}}
ight)}
ight) + {X^{left( 1
ight)}}left( {frac{{partial {alpha _s}}}{{partial q_s^Delta }} + frac{1}{psi }frac{{partial psi }}{{{Delta _s}{q_s}}}q_s^Delta }
ight)end{split} $$
(34)

将确定方程(25)和式(27)代入上式, 有







$$ frac{{bar Delta }}{{Delta t}}I = 0 $$
(35)

因此, 式(28)是该系统的守恒量. 证毕.

定理1可称为时间尺度上Lagrange系统的Lie对称性定理. 式(28)可称为时间尺度上Hojman守恒量, 它是由Lie对称性直接导致的.

对于任意时间尺度, 守恒量(28)中函数$varXi $一般不等于零. 函数$varXi $出现的原因在于任意时间尺度上delta偏导数不同于普通偏导数, 而当时间尺度${{mathbb{T}}} = {{mathbb{R}}}$时两者是一致的. 实际上, 若取${{mathbb{T}}} = {{mathbb{R}}}$, 则有







$$ left. begin{split}& frac{partial }{{{Delta _s}{q_s}}}frac{{bar Delta }}{{Delta t}}{xi _s} = frac{partial }{{partial {q_s}}}frac{{bar Delta }}{{Delta t}}{xi _s} & frac{partial }{{{Delta _{n + k}}q_k^Delta }}frac{{bar Delta }}{{Delta t}}{xi _s} =frac{partial }{{partial q_k^Delta }}frac{{bar Delta }}{{Delta t}}{xi _s} & frac{{partial {xi _s}}}{{{Delta _{n + k}}q_k^Delta }} = frac{{partial {xi _s}}}{{partial q_k^Delta }} & frac{partial }{{partial q_s^Delta }}{left( {frac{{partial {xi _s}}}{{{Delta _k}{q_k}}}}
ight)^sigma } ={left( {frac{{{partial ^2}{xi _s}}}{{{Delta _k}{q_k}partial q_s^Delta }}}
ight)^sigma } & frac{partial }{{partial q_s^Delta }}{left( {frac{{partial {xi _s}}}{{{Delta _{n + k}}q_k^Delta }}}
ight)^sigma } = {left( {frac{{{partial ^2}{xi _s}}}{{{Delta _{n + k}}q_k^Delta partial q_s^Delta }}}
ight)^sigma } & frac{1}{psi }frac{{partial psi }}{{{Delta _s}{q_s}}} = {left( {frac{1}{psi }frac{{partial psi }}{{partial {q_s}}}}
ight)^sigma } & {X^{left( 1
ight)}}left( {frac{1}{psi }frac{{partial psi }}{{{Delta _s}{q_s}}}}
ight) = {xi _k}frac{partial }{{{Delta _s}{q_s}}}left( {frac{1}{psi }frac{{partial psi }}{{partial {q_k}}}}
ight) end{split}
ight}$$
(36)

因此$varXi = 0$, 于是定理1退化为

定理2. 对于经典Lagrange系统, 如果无限小变换(22)是Lie对称性的, 且存在函数$psi = psi left( {{q_s}}
ight)$满足条件







$$ frac{{partial {alpha _s}}}{{partial {{dot q}_s}}} + frac{{{bar{text{d}}}}}{{{text{d}}t}}ln psi = 0 $$
(37)

则







$$ I = frac{1}{psi }frac{partial }{{partial {q_s}}}left( {psi {xi _s}}
ight) + frac{1}{psi }frac{partial }{{partial {{dot q}_s}}}left( {psi frac{{{bar{text{d}}}}}{{{text{d}}t}}{xi _s}}
ight) = {text{const}}. $$
(38)

是该系统的守恒量.

定理2与文献[30]的结果一致.


6.
算例


例. 设时间尺度为${{mathbb{T}}} = left{ {{2^m}:m in {{mathbb{N}}_0}}
ight}$, 研究两自由度Lagrange系统, 其Lagrange函数为







$$ L = frac{1}{2}left[ {{{left( {q_1^Delta }
ight)}^2} + {{left( {q_2^Delta }
ight)}^2}}
ight] - {q_2}t - {q_1} $$
(39)

试研究该系统的Lie对称性, 并求出对应的Hojman守恒量.

时间尺度上Lagrange方程(5)给出







$$ left. begin{array}{l}dfrac{nabla }{{nabla t}}q_1^Delta + {sigma ^nabla } = 0dfrac{nabla }{{nabla t}}q_2^Delta + {sigma ^nabla }t = 0end{array}
ight} $$
(40)

注意到, 对于时间尺度上任意函数$uleft( t
ight)$, 有关系







$$left. begin{split} & dfrac{nabla }{{nabla t}}{u^sigma }left( t
ight) = {sigma ^nabla }{u^Delta }left( t
ight) & {sigma ^nabla }{u^{Delta
ho Delta }}left( t
ight) = {u^{Delta Delta
ho }}left( t
ight) & {sigma ^{nabla sigma }}left( t
ight) = {sigma ^Delta }left( t
ight) end{split}
ight}$$
(41)

因此, 方程(40)可解出







$$left. begin{array}{l}q_1^{Delta Delta } = - {sigma ^Delta }left( t
ight) = {alpha _1}q_2^{Delta Delta } = - {sigma ^Delta }left( t
ight)sigma left( t
ight) = {alpha _2}end{array}
ight} $$
(42)

确定方程(25)给出







$$ left. begin{array}{l}dfrac{{bar Delta }}{{Delta t}}dfrac{{bar Delta }}{{Delta t}}{xi _1} = 0dfrac{{bar Delta }}{{Delta t}}dfrac{{bar Delta }}{{Delta t}}{xi _2} = 0end{array}
ight} $$
(43)

由于${{mathbb{T}}} = {2^{{{mathbb{N}}_0}}}$, 则$sigma left( t
ight) = 2t$, $mu left( t
ight) = t$, 因此方程(43)有如下解







$$ left. begin{array}{l}{xi _1} = left[ {{{left( {q_1^Delta }
ight)}^2} - 4{t^2}}
ight]left( {q_2^Delta + dfrac{4}{3}{t^2}}
ight){xi _2} = 1end{array}
ight} $$
(44)







$$ left. begin{array}{l}{xi _1} = 1{xi _2} = left( {{q_2} + dfrac{4}{{21}}{t^3}}
ight)left( {q_1^Delta + 2t}
ight)end{array}
ight} $$
(45)

与生成元式(44)和式(45)相应的变换是Lie对称的. 方程(27)给出







$$ frac{1}{psi }frac{{partial psi }}{{{Delta _1}{q_1}}}q_1^Delta + frac{1}{psi }frac{{partial psi }}{{{Delta _2}{q_2}}}q_2^Delta = 0 $$
(46)

方程(46)有解







$$ psi = 1 $$
(47)

根据定理1, 由式(44), 式(45)和式(47), 得到







$$ {I_1} = - frac{4}{t}left[ {{q_2}left( {2t}
ight) - {q_2}left( t
ight)}
ight] - frac{{16}}{3}{t^2} = {text{const}}. $$
(48)







$$ {I_2} = frac{2}{t}left[ {{q_1}left( {2t}
ight) - {q_1}left( t
ight)}
ight] + 4t = {text{const}}. $$
(49)

这是时间尺度上Lie对称性式(44)和式(45)导致的Hojman守恒量. 如果取初始条件为$ {q_1}left( 1
ight) = 1 $, $ {q_2}left( 1
ight) = 0 $, $ {q_1}left( 2
ight) = 2 $, $ {q_2}left( 2
ight) = 1 $, 在时间尺度为${{mathbb{T}}} = {2^{{{mathbb{N}}_0}}}$上计算运动轨迹$ {q_1},{q_2} $和守恒量$ {I_1},{I_2} $的值, 其结果如图1所示. 图1中具体的数据如表1所示.



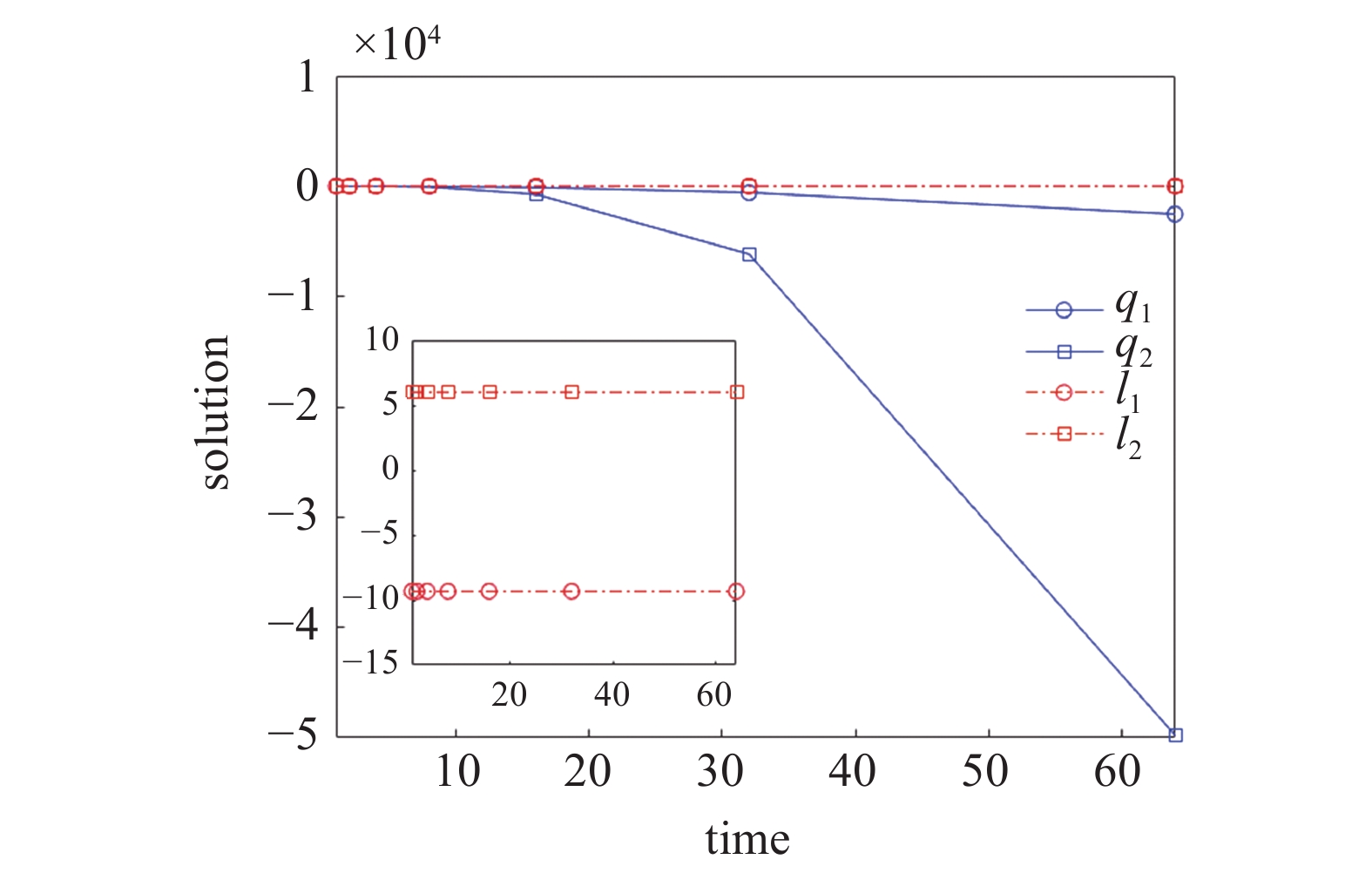onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-413-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
时间尺度$ {{mathbb{T}}} = {2^{{{mathbb{N}}_0}}} $上$ {q_1},{q_2},{I_1},{I_2} $的值



Figure
1.
Simulations of $ {q_1},{q_2},{I_1},{I_2} $ on the time scale $ {{mathbb{T}}} = {2^{{{mathbb{N}}_0}}} $



下载:
全尺寸图片
幻灯片





表
1
时间尺度$ {{mathbb{T}}} = {2^{{{mathbb{N}}_0}}} $上$ {q_1},{q_2},{I_1},{I_2} $的值



Table
1.
The values of $ {q_1},{q_2},{I_1},{I_2} $ on the time scale $ {{mathbb{T}}} = {2^{{{mathbb{N}}_0}}} $



table_type1 ">
$ {mathbb{T}}/{
m{s}} $		$ {q_1}/{
m{m}} $		$ {q_2}/{
m{m}} $		$ {I_1} $$ {I_2} $
110?9.336
221?9.336
40?5?9.336
8?20?81?9.336
16?124?745?9.336
32?588?6169?9.336
64?2540?49785?9.336





下载:
导出CSV
|显示表格



从图1和表1可以看出, 在时间尺度$ {{mathbb{T}}} = {2^{{{mathbb{N}}_0}}} $上, 由式(48)和式(49)所确定的$ {I_1} $, $ {I_2} $的值始终不变, 说明$ {I_1} $和$ {I_2} $确实是守恒量, 从而验证了定理1的正确性.

如取${{mathbb{T}}} = h{{mathbb{Z}}_ + }$, $h$为常数, 则$sigma left( t
ight) = t + h$, $mu left( t
ight) = h$, Lie对称性式(44)和式(45)成为







$$ left. begin{array}{l}{xi _1} = left[ {{{left( {q_1^Delta }
ight)}^2} - {t^2}}
ight]left( {q_2^Delta + dfrac{1}{2}{t^2} + dfrac{1}{2}ht}
ight){xi _2} = 1end{array}
ight}$$
(50)







$$left. begin{array}{l}{xi _1} = 1{xi _2} = left( {{q_2} + dfrac{1}{6}{t^3}}
ight)left( {q_1^Delta + t}
ight)end{array}
ight} $$
(51)

守恒量式(48)和式(49)成为







$$ {I_1} = - frac{2}{h}left[ {{q_2}left( {t + h}
ight) - {q_2}left( t
ight)}
ight] - tleft( {t + h}
ight) = {text{const}}. $$
(52)







$$ {I_2} = frac{2}{h}left[ {{q_1}left( {t + h}
ight) - {q_1}left( t
ight)}
ight] + 2t = {text{const}}. $$
(53)

仍取上述初始条件, 令$ h = 1 $, 在时间尺度为${{mathbb{T}}} = {{mathbb{Z}}_ + }$上计算运动轨迹$ {q_1} $, $ {q_2} $和守恒量$ {I_1} $, $ {I_2} $的值, 其结果和数据如图2和表2所示.



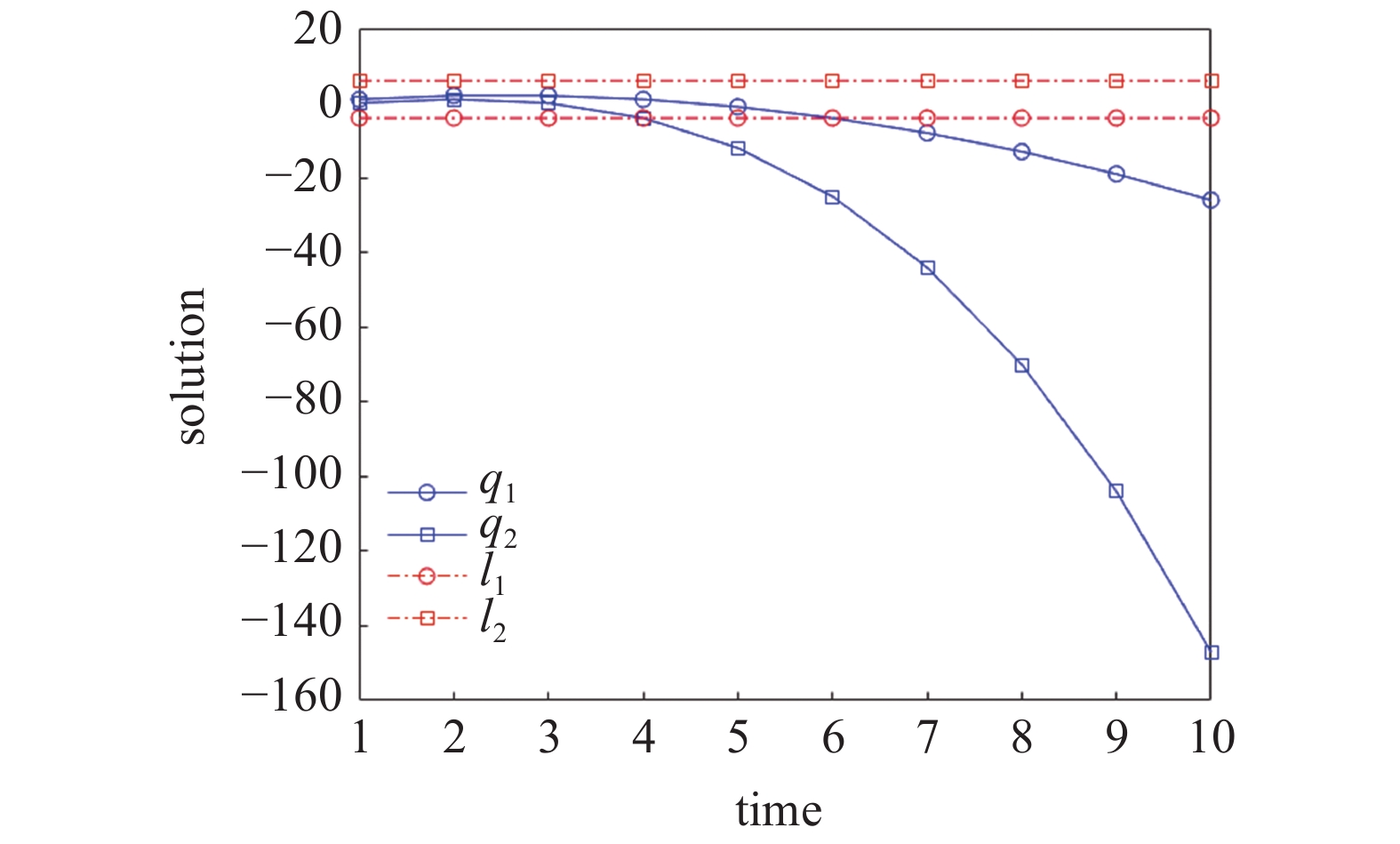onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-413-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
时间尺度${{mathbb{T}}} = {{mathbb{Z}}_ + }$上$ {q_1},{q_2},{I_1},{I_2} $的值



Figure
2.
Simulations of $ {q_1},{q_2},{I_1},{I_2} $ on the time scale ${{mathbb{T}}} = {{mathbb{Z}}_ + }$



下载:
全尺寸图片
幻灯片





表
2
时间尺度${{mathbb{T}}} = {{mathbb{Z}}_ + }$上$ {q_1},{q_2},{I_1},{I_2} $的值.



Table
2.
The values of $ {q_1},{q_2},{I_1},{I_2} $ on the time scale ${{mathbb{T}}} = {{mathbb{Z}}_ + }$



table_type1 ">
$ {mathbb{T}}/{
m{s}} $		$ {q_1} /{
m{m}}$		$ {q_2}/{
m{m}} $		$ {I_1} $$ {I_2} $
110?44
221?44
320?44
41?4?44
5?1?12?44
6?4?25?44
7?8?44?44
8?13?70?44
9?19?104?44
10?26?147?44





下载:
导出CSV
|显示表格



这里只取了$ t in left[ {1,10}
ight] $, 实际上随着时间的增加, 仍有$ {I_1} equiv - 4 $和$ {I_2} equiv 4 $. 由此可知式(52)和式(53)是守恒量, 再次验证了定理1的正确性.

若取${{mathbb{T}}} = {{mathbb{R}}}$, 则$sigma left( t
ight) = t$, $mu left( t
ight) = 0$, Lie对称性式(44)和式(45)成为







$$ left. begin{array}{l}{xi _1} = left( {dot q_1^2 - {t^2}}
ight)left( {{{dot q}_2} + dfrac{1}{2}{t^2}}
ight){xi _2} = 1end{array}
ight}$$
(54)







$$ left. begin{array}{l}{xi _1} = 1{xi _2} = left( {{q_2} + dfrac{1}{6}{t^3}}
ight)left( {{{dot q}_1} + t}
ight)end{array}
ight} $$
(55)

守恒量式(48)和式(49)成为







$$ {I_1} = - 2left( {{{dot q}_2} + frac{1}{2}{t^2}}
ight) = {text{const}}. $$
(56)







$$ {I_2} = 2left( {{{dot q}_1} + t}
ight) = {text{const}}. $$
(57)

这是经典情形的Hojman守恒量.


7.
结 论


本文将Lie对称性方法拓展到时间尺度上Lagrange系统, 给出了时间尺度上Hojman守恒量. 主要贡献在于: 一是利用时间尺度微积分的基本性质导出了时间尺度上Lagrange系统导数运算的两个重要关系式. 这是推导Hojman守恒量的基础; 二是由Lie对称性直接推导得到了时间尺度上Lagrange系统的Hojman类型的守恒量. 该守恒量不依赖于Lagrange函数的结构而仅取决于Lie对称性变换的生成元. 文中以时间尺度上两自由度系统为例, 给出了${{mathbb{T}}} = {2^{{{mathbb{N}}_0}}}$, ${{mathbb{T}}} = h{mathbb{Z}}$以及${{mathbb{T}}} = {{mathbb{R}}}$, 3种情形下的Hojman守恒量, 并通过数值模拟验证了结果的正确性. 当时间尺度取为实数集时, 本文结果退化为经典Lagrange系统的Hojman守恒量. 文章的方法和结果可进一步推广和应用, 如时间尺度上非完整系统, 时间尺度上Birkhoff系统等.

相关话题/系统 力学 尺度 运动 导数
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 多相流动的光滑粒子流体动力学方法研究综述
    引言多相流广泛存在于自然界和工业应用中.对多相流进行高精度和高效率的建模和模拟非常重要.然而,其中流动形态和界面跟踪的复杂性限制了基于网格的传统方法模拟多相流能力,尤其对于存在界面大变形、不连续性和多物理过程的多相流动.而无网格方法可以很好地处理网格方法遇到的上述问题.在过去几十年发展起来的无网格方 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于深度学习和细观力学的颗粒材料本构关系研究
    引言颗粒材料广泛存在于各类自然环境和工程活动中,人类几乎所有的基础设施都建造于岩土材料这类典型的颗粒材料上,理解和预测此类材料在外载作用下的力学响应具有重要的意义.岩土材料通常由粒径不一,形状各异的矿物颗粒以及颗粒之间的空隙组成.颗粒间的互相滑动会引起不可恢复的塑性变形,因而,颗粒材料在剪切作用下极 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于多介质、多尺度离散元方法的冰载荷数值冰水池
    引言近年来,中国在极地科学考察、北极商业航运、极地观光邮轮、冰区油气开发和新能源(风电、核电)等方面的发展,对极地船舶与海洋工程技术的研究提出了迫切的工程需求,其中工程结构冰载荷的合理确定是重要的核心内容[1].为确定船舶结构的冰载荷,芬兰于20世纪60年代最早开展了实船测量和反演,随后美国、加拿大 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑胎路多点接触的电动汽车?路面耦合系统振动分析
    引言近年来,轮毂电机驱动电动汽车,因传动效率高、便于实现智能控制等优点,得到了广泛关注[1-3],是未来电动汽车的发展方向.但独立驱动电动汽车的动力学与控制也面临诸多新问题,其一是簧下质量大,导致轮胎动载荷增加,轮胎与路面动力学相互作用更加突出.其二是电机激励进一步加剧车轮振动,影响轮胎的接地安全性 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 轮对系统的Hopf分岔研究
    引言近年来随着高速列车运行速度的提高,车辆系统的蛇行失稳问题越发突出,蛇形运动作为车辆系统的固有属性,严重影响着车辆系统的运行平稳性、乘坐舒适性和安全性[1],对车辆系统进行非线性动力学理论方面的研究,不仅可以从车辆动力学角度更加全面地了解蛇形运动,而且对车辆系统的设计与参数优化也具有非常重要的意义 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 数据驱动印度洋海域全局动力学研究
    引言海洋系统天然受到多种环境因素(风速、温度、海水含盐量等)、人类活动和天体运动等不确定扰动的影响,导致其洋流运动复杂而多样[1-2].然而,一些观测和研究发现,其内部蕴含着能够对洋流的运动方向和趋势起限制和导向作用的复杂动力结构和特征,影响甚至主导了表面漂浮物的流动形式和演化路径.例如,经志友等[ ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 非常规油气资源渗流力学进展专题序
    石油和天然气在我国经济发展中起到了积极支撑作用.随着经济发展的后石油时代到来,我国油气资源对外依存度已超出了能源安全的警戒线.为保障国家能源安全,我国对非常规油气资源的开发力度大幅增加.自1996年以来,我国在页岩油气、煤层气、致密油气以及天然气水合物等非常规油气资源勘探开发领域取得了显著进展.作为 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 含天然气水合物土微观力学特性研究进展
    引言天然气水合物(简称水合物)是由天然气分子与水分子在高压、低温环境下形成的非化学计量笼型结晶物质[1],广泛分布于全球近海大陆架及陆地永久冻土地带[2],资源储量巨大,被认为是21世纪最具潜力的替代能源之一[3].自20世纪开始,世界各国陆续成立了专门的水合物研究机构并开展了相关研究[4],在此基 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑热流固耦合作用的多孔介质孔隙尺度两相流动模拟
    引言经过多年的勘探与开发,我国浅层和中浅层的油气资源已经进入了较为成熟的开发阶段.伴随着勘探开发的深入,人们认识到在深层地层中同样孕育着丰富的可采能源,例如深层油气藏、地热资源等.深层能源储藏具有可观的挖潜能力,是未来助力我国增储上产的重要来源[1].深部地层内的流体流动同时受到了温度、压力及应力场 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.