引言
经过多年的勘探与开发, 我国浅层和中浅层的油气资源已经进入了较为成熟的开发阶段. 伴随着勘探开发的深入, 人们认识到在深层地层中同样孕育着丰富的可采能源, 例如深层油气藏、地热资源等. 深层能源储藏具有可观的挖潜能力, 是未来助力我国增储上产的重要来源[1].
深部地层内的流体流动同时受到了温度、压力及应力场的综合影响[2]. 伴随地层深度加深, 地层温度不断地升高. 不同地区的地温梯度不同, 一般处于20 ~ 30 °C/km, 部分异常区域可达40 ~ 80 °C/km. 当储层深度到达深层时, 地层温度可以达到100 °C以上. 综合考虑以上因素, 流体在岩石多孔介质内的流动受到了多物理场的综合影响[3]. 孔隙尺度下考虑两相流体[4]在热场、流场、应力场多场耦合作用下的流动模拟研究, 为解释油气资源在深部地层的运移规律提供了一种解决方案. 同时, 多场耦合的研究也有益于其他地下工程的研究, 如天然气水合物开采[5]、二氧化碳地质埋存工程[6]等.
最早提出流固耦合理论研究模型的是Terzaghi, 他提出了饱和多孔介质的有效应力公式和一维有效固结模型[7]. 李锡夔等[8-9]提出了一种混合有限元方法计算非饱和多孔介质中的热流固过程. 宋睿等[10-11]通过使用ANSYS和CFX求解热?流?固耦合模型, 结果表明随着岩石有效压力和温度的增加, 孔隙度和渗透率都会下降. Wu等[12]建立了具有周期性孔隙形态的分形理论模型, 用于模拟复杂多孔介质中的输运, 并基于分形模型, 进行了热?流?固耦合流动模拟. 邓佳等[13]通过考虑页岩储层的应力敏感特征, 分析了储层的应力敏感性对页岩气储层产量的影响. 王沫然和王梓岩等[14]采用了跨尺度混合模拟算法, 研究了深层页岩气藏的流固耦合问题. 樊冬艳等[15]研究了基于离散裂缝网络模型的干热岩储层热?流?固耦合问题, 结果表明出口端流量及温度会对流量产生影响. 孙致学等[16]将裂隙岩体视为离散裂隙网络和基质岩体的双重介质模型, 研究了基于热?流?固耦合模型的增强型地热系统的生产过程. 郭颖等[17]基于Biot方程、Darcy定律及Lord-Schulman准则研究了土壤在载荷作用下物理量的变化规律, 结果表明载荷对孔隙度和渗透率皆有明显影响.
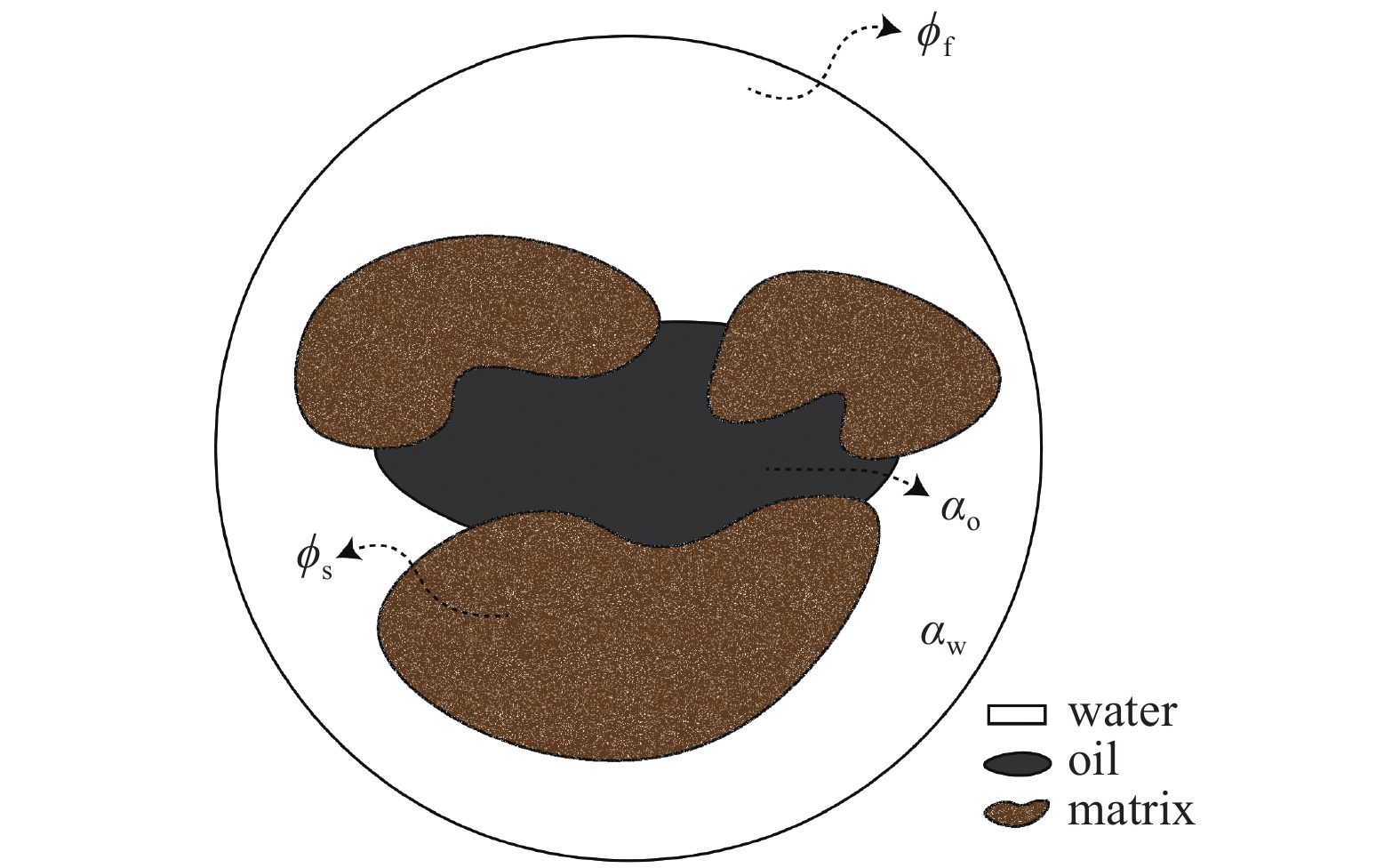
Darcy-Brinkman方法[18]被广泛地应用于多孔介质多尺度多场耦合流动模拟研究中, 如模拟酸岩反应过程[19]、流固耦合过程[20]等. 为了能够定量表征温度场、应力场及流场对发生在岩石多孔介质内的多相渗流的影响, 本研究使用了Darcy-Brinkman-Biot[21]耦合Duhamel-Neumann[22]热弹性应力准则的模型开展模拟工作. 采用体积平均方法(volume averaging method, VAM)[23]引入系列参数用以表征控制单元内的油相、水相及岩石固体颗粒的分布. 如图1所示, 模型中水相、油相、固体颗粒相在控制单元内共存, 水相与油相占据孔隙空间. 孔隙空间内的油水两相流动采用流体体积模型(volume of fluids, VOF)进行求解. 岩石固体颗粒由于流固耦合作用产生的弹性变形采用Biot弹性变形方程求解. 温度场的变化引起的热弹性应力则使用了Duhamel-Neumann热弹性应力准则进行求解, 从而实现了在孔隙尺度上的热流固耦合流动模拟.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-294-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
模型示意图
Figure
1.
Illustration of model
下载: 全尺寸图片
幻灯片
综上, 本工作采用Darcy-Brinkman-Biot方法, 耦合了Duhamel-Neumann热弹性应力准则, 推导了考虑热流固三场耦合作用下的多孔介质两相流动模拟模型, 研究了多场耦合作用对油水两相渗流的影响, 以期为油气田开发工程提供参考数据.
1.
数学模型
假设模型为饱和流体的多孔介质, 其中油相
$$ V = {V_{text{w}}} + {V_{text{o}}} + {V_{text{s}}} $$  | (1) |
其中, V为模型的总体积, m3;
油相与水相统称为流体相, 以相分数
$$ {phi _{text{f}}} = frac{{{V_{text{w}}} + {V_{text{o}}}}}{V} $$  | (2) |
$$ {phi _{text{s}}} = frac{{{V_{text{s}}}}}{V} $$  | (3) |
显然,
$$ {phi _{text{f}}} + {phi _{text{s}}} = 1 $$  | (4) |
通过
$$ {alpha _{text{w}}} = frac{{{V_{text{w}}}}}{{{V_{text{w}}} + {V_{text{o}}}}} $$  | (5) |
$$ {alpha _{text{o}}} = frac{{{V_{text{o}}}}}{{{V_{text{w}}} + {V_{text{o}}}}} $$  | (6) |
显然,
$$ {alpha _{text{w}}} + {alpha _{text{o}}} = 1 $$  | (7) |
因此, 通过图1中所定义的参数, 可以判断油相、水相及固体相在模型中的分布, 其判定标准为
$$ begin{array}{l}{phi }_{text{s}}=left{ begin{array}{l}1{, };;{ m{matrix}} text{0} {, };;{ m{water}}end{array} ight. {alpha }_{text{w}}=left{ begin{array}{l}0{, };;{ m{saturated ; oil}} (0,1) {, };;{ m{oil!-!water ; interface}} text{1} {, };;{ m{saturated ; water}}end{array} ight.end{array} $$  | (8) |
1.1
不可压缩两相流体控制方程
对于不可压缩、不可混溶的两相牛顿流体, 可以采用流体体积方法[24]描述多相流动过程. 采用Carrillo等[21]基于体积平均方法推广的流体体积方法公式来描述模型内的两相流动过程, 即
$$ frac{{partial {phi _{text{f}}}}}{{partial t}} + nabla cdot {{boldsymbol{U}}_{text{f}}} = 0 $$  | (9) |
$$ frac{{partial {phi _{text{f}}}{alpha _{text{w}}}}}{{partial t}} + nabla cdot ({alpha _{text{w}}}{{boldsymbol{U}}_{text{f}}}) + nabla cdot ({phi _{text{f}}}{alpha _{text{w}}}{alpha _{text{o}}}{{boldsymbol{U}}_{text{r}}}) = 0 $$  | (10) |
$$ begin{split} &frac{{partial {{ m{ ho }}_{text{f}}}{{boldsymbol{U}}_{text{f}}}}}{{partial t}} + nabla cdot left(frac{{partial {{ m{ ho }}_{text{f}}}}}{{{phi _{text{f}}}}}{{boldsymbol{U}}_{text{f}}}{{boldsymbol{U}}_{text{f}}} ight) = - {phi _{text{f}}}nabla p + {phi _{text{f}}}{{ m{ ho }}_{{ m{f}}} }{{boldsymbol{g}}} + nabla cdot {bar {boldsymbol{S}}} hfill +& qquad {{boldsymbol{D}}_{{text{w,s}}}} + {{boldsymbol{D}}_{{text{o,s}}}} + {{boldsymbol{D}}_{{text{s,w}}}} + {{boldsymbol{D}}_{{text{s,o}}}} + {{boldsymbol{D}}_{{text{w,o}}}} + {{boldsymbol{D}}_{{text{o,w}}}} hfill end{split} $$  | (11) |
式中, t为时间, s; Uf为流体流速, m/s; Ur为相对流速, m/s;
m{
ho }}_{text{f}}}$
$$ begin{split} frac{{partial {{ m{ ho }}_{text{f}}}{{boldsymbol{U}}_{text{f}}}}}{{partial t}} + nabla cdot left(frac{{partial {{ m{ ho }}_{text{f}}}}}{{{phi _{text{f}}}}}{{boldsymbol{U}}_{text{f}}}{{boldsymbol{U}}_{text{f}}} ight) =& - {phi _f}nabla p + {phi _{text{f}}}{{ m{ ho }}_{text{f}}}{{boldsymbol{g}}} + nabla cdot {bar {boldsymbol{S}}} hfill & - {phi _{text{f}}}{ m{mu }}{k^{ - 1}}({{boldsymbol{U}}_{text{f}}} - {{{bar {boldsymbol{U}}}}_{text{s}}}) + {phi _{text{f}}}{{boldsymbol{F}}_{text{c}}} hfill end{split} $$  | (12) |
式中,
m{mu }}{k^{ - 1}}({{boldsymbol{U}}_{text{f}}} - {{bar {boldsymbol{U}}}_{text{s}}}) $
m{mu }}$
m{Pa}} cdot {
m{s}} $
$$ {{boldsymbol{F}}_{text{c}}} = - frac{{ m{gamma }}}{{{phi _{text{f}}}}}nabla cdot ({boldsymbol{n}}{ _{{text{w,o}}}})nabla {alpha _{text{w}}} $$  | (13) |
式中,
1.2
线弹性固体变形控制方程
本研究采用的模型符合连续介质假设, 为了研究变形多孔介质对两相渗流过程的影响, 研究假设岩石骨架在弹性变形阶段为线弹性变形. 采用Carriillo和Bourg[25]体积平均方法推广的Biot变形方程
$$ frac{{partial {phi _{text{s}}}}}{{partial t}} + nabla cdot ({phi _{text{s}}}{bar {boldsymbol{U}}}_{text{s}}^{}) = 0 $$  | (14) |
$$ - nabla cdot {bar {boldsymbol{sigma}} } = {phi _{text{s}}}nabla cdot {{bar{boldsymbol{ tau}} }^{text{s}}} + {phi _{text{s}}}{{ m{ ho }}_{text{s}}}{{boldsymbol{g}}} + {{boldsymbol{B}}_{{text{s,w}}}} + {{boldsymbol{B}}_{{text{s,o}}}} $$  | (15) |
式中, Us为固体颗粒运动速度, m/s;
ho}} _{text{s}}}$
$$ {{boldsymbol{B}}_{{text{s,w}}}} + {{boldsymbol{B}}_{{text{s,o}}}} = {phi _{text{f}}}{ m{mu }}{k^{ - 1}}({{boldsymbol{U}}_{text{f}}} - {{bar {boldsymbol{U}}}_{ m{s}}}) $$  | (16) |
1.3
线性热弹性应力控制方程
在流固耦合的基础上, 进一步考虑岩石骨架在热场作用下产生的热弹性应力对两相流动过程的影响.
传热过程中的动能方程为
$$ frac{{partial }^{text{2}}({ m{ ho }}_{text{f}}{boldsymbol{U}}_{text{f}})}{partial {t}^{2}}-nabla cdot [{ m{mu }}nabla {boldsymbol{U}}_{text{f}}+{ m{mu }}{(nabla {boldsymbol{U}}_{text{f}})}^{text{T}}+{K}{{I}}{ m{tr}}(nabla {boldsymbol{U}}_{text{f}})]=0 $$  | (17) |
流体换热过程中的热传导方程为
$$ { ho _{text{f}}}cfrac{{partial T}}{{partial t}} = nabla cdot Knabla T $$  | (18) |
其中, c为比热容, J/(kg·K?1); T为温度, K; K为导热系数W/(m·K).
温度对骨架产生的热应力为
$$ {sigma _{text{t}}} = - { m{beta }}T $$  | (19) |
其中,
m{beta }}$
当岩石的温度发生改变时, 热应力作用于于岩石固体颗粒上, 发生形变. 在考虑流固耦合作用的基础上, 固体受到的应力可以分为两部分: 一部分是由于流固耦合作用发生的应力,
m{varepsilon }}}$
$$left. begin{array}{l} {sigma _x} = {sigma _{{ m{varepsilon}} x}} + {sigma _{{text{t}}x}} hfill {sigma _y} = {sigma _{{ m{varepsilon }}y}} + {sigma _{{text{t}}y}} hfill end{array} ight} $$  | (20) |
其中,
2.
模型与参数
2.1
模型参数
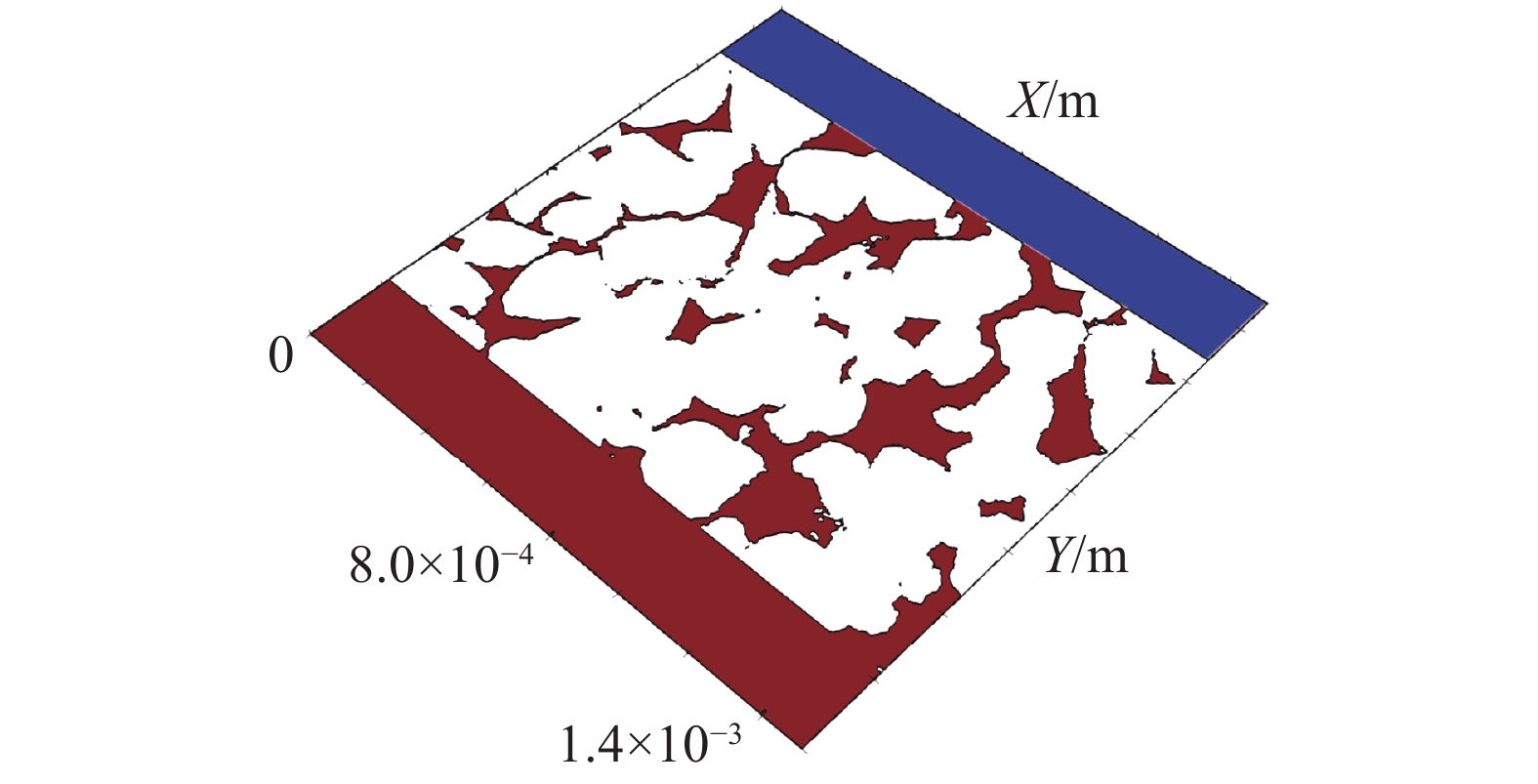
为了模拟油水两相在多孔介质内受热?流?固耦合作用下的流动过程, 采用二维Berea[26]砂岩岩心切片作为模拟模型, 开展流动模拟工作. 图2展示的是本研究所采用的岩心切片示意图, 切片体素大小为500×500, 分辨率为3.003 5 μm, 孔隙度
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-294-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
模型示意图
Figure
2.
Illustration of simulation model
下载: 全尺寸图片
幻灯片
模型模拟的过程为水相驱替油相的过程, 以速度边界条件作为控制条件, 在入口处以0.001 m/s的注入流速注入水相. 模型入口温度设置为350 K, 出口温度设置为300 K, 模型内部初始温度场设置为300 K. 模型网格采用六面体结构化网格, 网格数为10000个.
2.2
模拟参数
模型采用的模拟参数如表 1所示. 模型设置水相为润湿相, 其润湿角设置为45°. 流体物性参数假设在温度场的作用下为恒定值. 岩石的物理性质设置参考了砂岩实验的数据[27-28], 其中热扩散系数通过岩石密度、比热容及导热系数确定, 计算公式为
m{alpha }}_{text{t}}} = K/({{
m{
ho }}_{text{s}}}c)$
表
1
模拟参数设置
Table
1.
Simulation parameters
table_type1 ">
| Phase | Parameter | Value | |
| fluids | water | density$;{{ m{ ho }}_{text{w}}}$/(kg·m-3) | 1000 |
| viscosity$;{{ m{mu }}_{text{w}}}$/(Pa·s) | 0.001 | ||
| contact angle ${{ m{theta }}_{text{w}}}$/(°) | 45 | ||
| oil | density$;{{ m{ ho }}_{text{o}}}$/(kg·m-3) | 1000 | |
| viscosity $;{{ m{mu }}_{text{o}}}$/(Pa·s) | 0.001 | ||
| surface tension ${{ m{sigma }}_{{text{wo}}}}$/(N·m-1) | 0.077 | ||
| rock | density ${{ m{ ho }}_{text{s}}}$/(kg·m-3) | 2500 | |
| Poisson ratio $;{ m{nu }}$ | 0.3 | ||
| Young’s module E /(GPa) | 50 | ||
| specific heat capacity c /(J·K·kg-1) | 780 | ||
| thermal conductivity K/(W·m-1·K-1) | 2 | ||
| thermal diffusivity ${{ m{alpha }}_{text{t}}}$/K-1 | 1×10?6 | ||
下载: 导出CSV
|显示表格
2.3
模型求解
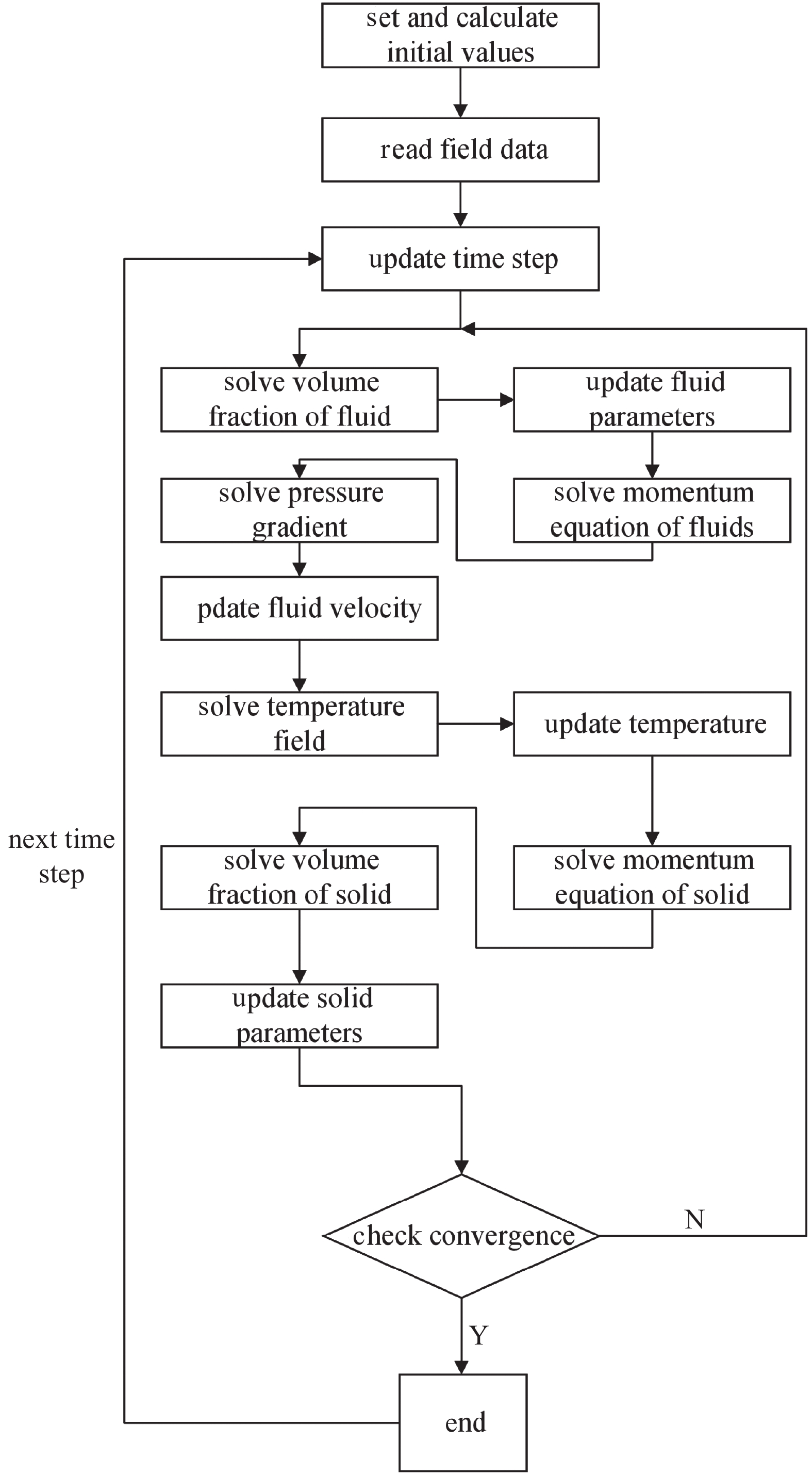
模型的求解流程如图3所示. 模型求解借助了著名的基于有限体积方法(finite volume method, FVM)的开源CFD软件OpenFOAM[29]完成. 在每个求解时间步内, 分别依次对流场、热场及固体场进行求解.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-294-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
模型求解过程示意图
Figure
3.
Illustration of solution algorithm
下载: 全尺寸图片
幻灯片
对于流体场的求解, 首先使用MULES (multidimensional universal limiter of explicit solution algorithm)算法对流体体积分数进行显式求解. MULES方法能够很好的保证流体体积分数的有界性, 从而减少计算越界的问题. 对于整个流体控制方程的求解采用了SIMPLE (semi-implicit method for pressure linked equations)算法. SIMPLE算法引入了压力修正方程, 使得流体速度场可以不断地进行修正, 从而使计算得到的速度满足控制方程收敛条件. 将计算得到的速度场传入温度场进行求解, 最后进行固体场的求解. 求解固体变形的算法采用了Jasak和Weller[30]在构建fsiFoam时所用的算法. 求解时间步长满足柯朗?弗里德里希斯?列维数(Courant-Friedrichs-Lewy number). 对于二维模型, CFL数计算公式为
$$ frac{{{{{U}}_x}Delta t}}{{Delta x}} + frac{{{{{U}}_y}Delta t}}{{Delta y}} leqslant { m{C}} $$  | (21) |
式中, Ux和Uy分别代表了速度在x, y方向上的分量, m/s;
3.
结果与讨论
3.1
模拟结果
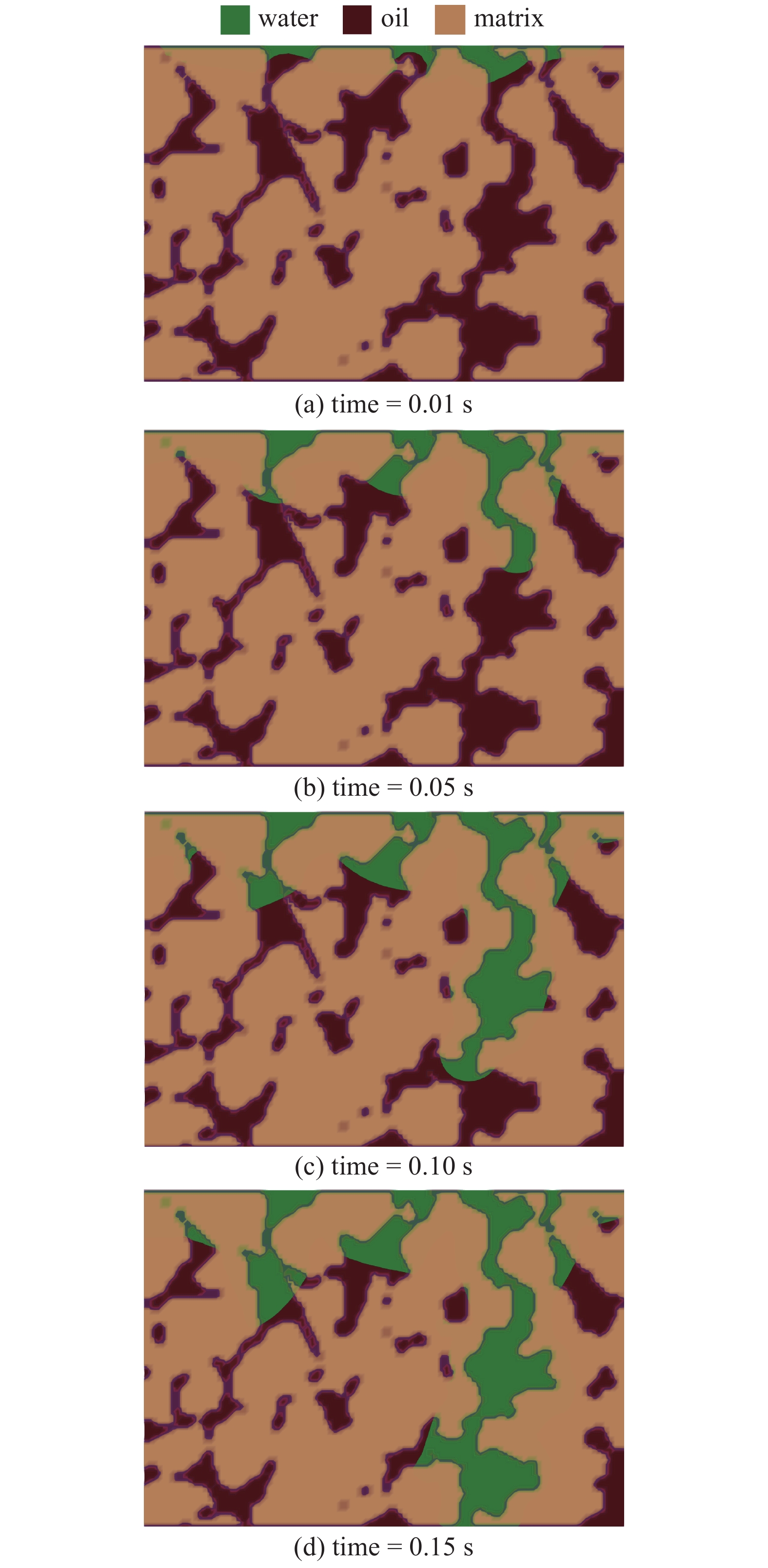
图4展示的是恒定流速0.001 m/s为注入流速, 水相润湿角设置为45°, 入口温度为350 K, 初始内部温度与出口温度为300 K的模型的模拟结果. 从图中可以看出, 水相在岩心切片的右侧形成了优势主力流动通道, 驱替前端在注入速度的作用下发生了润湿滞后. 随着驱替过程的进行, 水相不断地将油相驱替出岩心切片, 最终当水相到达出口时, 主力流动通道达到稳定状态, 模型内的两相饱和度趋于不变.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-294-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
不同模拟时刻的相分布
Figure
4.
Simulation results of phase distribution at different time steps
下载: 全尺寸图片
幻灯片
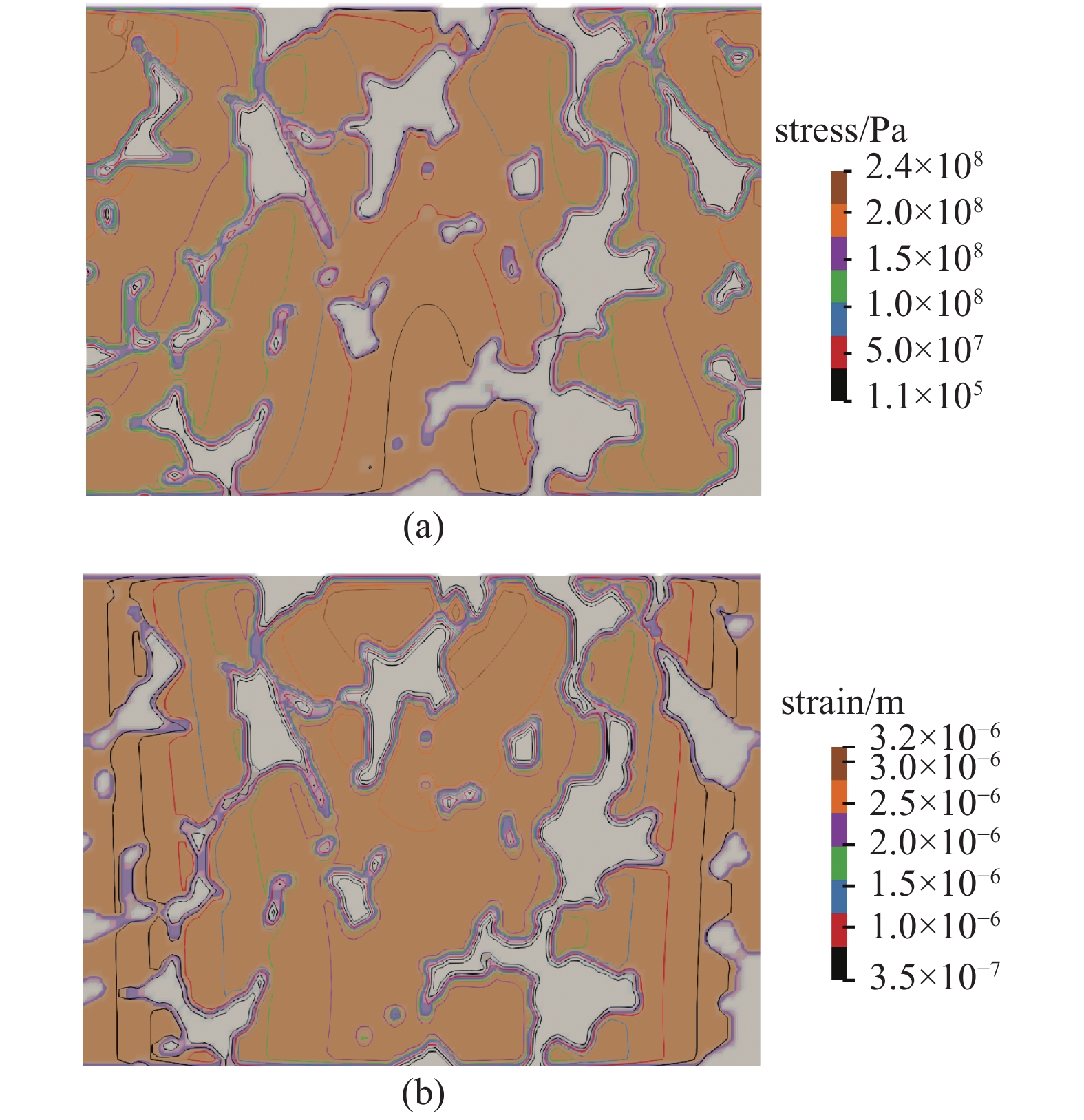
图5展示的是图4中的模型在0.15 s即两相饱和度达到稳定状态时的模型内的应力、应变分布状态. 两图中不同颜色的线段代表应力、应变数值大小的等值线分布. 从应力分布图中可以看出, 在驱替的进行过程中, 流体对于岩石骨架产生了挤压应力. 在流动通道的两侧, 岩石骨架由于受挤而产生了相应的压力梯度. 岩石骨架的应力主要由流固作用与热固作用产生, 流体挤压岩石产生了弹性应力, 温度的增加使得岩石产生了向外膨胀的热应力, 两者方向相反, 互相抵消一部分影响. 在本例中, 岩石的应力为受挤应力, 即流体对岩石骨架的影响大于温度对岩石骨架的影响. 从应变分布图中可以看出, 岩石的弹性应力使得岩石发生了弹性形变, 发生形变的数量级分布在0.1 ~ 1 μm之间.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-294-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
0.15 s时应力及应变模拟结果
Figure
5.
Simulation results of (a) stress and (b) strain profile at 0.15 s
下载: 全尺寸图片
幻灯片
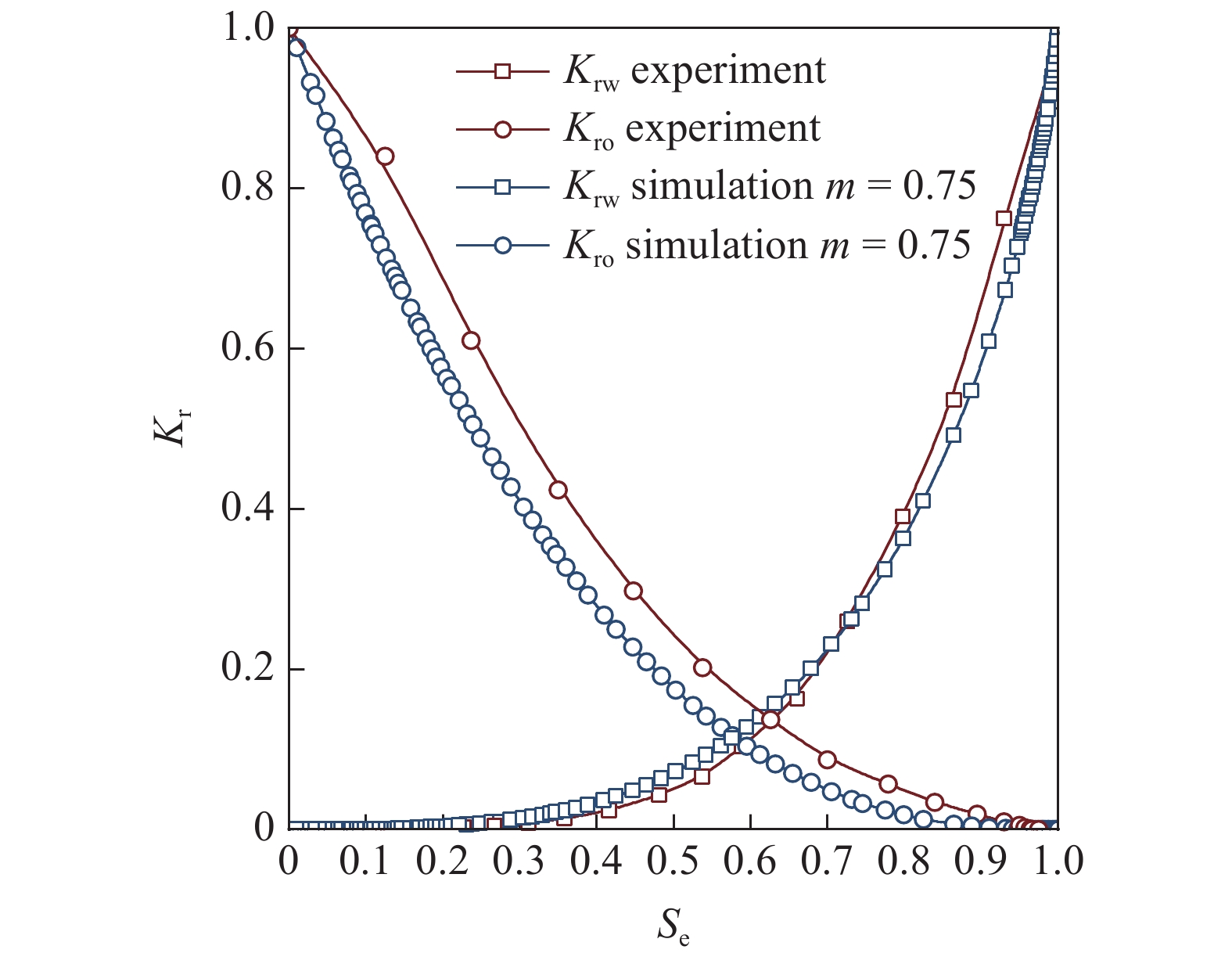
相对渗透率是反应两相流体在岩石多孔介质内相对流动能力的重要参数. 图6展示的是图4模型的归一化相渗曲线. 首先引入有效含水饱和度Se用以计算归一化相渗曲线, Se的计算公式如式(22)所示
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-294-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
归一化相渗曲线与实验结果对比
Figure
6.
Normalized relative permeability curve vs. experimental result
下载: 全尺寸图片
幻灯片
$$ {S_{text{e}}} = frac{{{S_{text{w}}} - {S_{{text{wc}}}}}}{{1 - {S_{{text{wc}}}} - {S_{{text{or}}}}}} $$  | (22) |
式中, Sw表示含水饱和度; Swc表示束缚水饱和度, 本例中, 由于模型初始状态为全部饱和油相, 因此Swc = 0; Sor表示残余油饱和度, 取驱替至油相饱和度不变时的饱和度.
相渗曲线的计算采用的是van Genuchten[31]模型, 计算公式如式(23)所示
$$left. begin{aligned} & {K_{{text{rw}}}} = sqrt {{S_{text{e}}}} {[1 - {(1 - {{S_{text{e}}}^{1/m}})^m}]^2} hfill & {K_{{text{ro}}}} = sqrt {1 - {S_{text{e}}}} {[{(1 - {S_{text{e}}})^{1/m}}]^{2m}} hfillend{aligned} ight} $$  | (23) |
式中, Krw与Kro分别代表水相与油相的相对渗透率; m为衡量流体润湿能力的参数, m数值越高代表流体的润湿性越好, 相对渗流能力越高.
图6展示模型归一化后的相渗曲线与Oak[32]的Berea砂岩实验结果的对比, 为了方便对比, 实验数据使用式(22)进行了归一化. 模型使用式(23)计算相渗曲线, 发现当m = 0.75时, 模拟结果与实验所获得的相渗曲线吻合较好. 模拟所获得的相渗曲线等渗点Se = 0.58, 实验获得的等渗点Se约等于0.62. 在低含水饱和度下, 水相对流动能力较小, 油相相对流动能力较大. 随着驱替过程的不断地进行, 水相的相对渗流能力不断增加, 油相的相对渗流能力快速下降. 在驱替过程达到末期时, 水相已经形成了优势流动通道, 相对渗流能力远大于油相, 油相基本不再流动.
对比实验结果, 模拟结果对油相的整体相对渗流能力的预测偏低, 对水相相对渗流能力的预测在等渗点的左侧偏高, 在等渗点的右侧偏低. 在实际岩心驱替的过程中, 在水湿岩心条件下, 水相在驱替早期含水饱和度较低的情况下, 会首先润湿壁面, 在壁面处形成润湿层, 从而造成了水相在贴近壁面处流动, 而油相占据孔隙中央区域流动的现象. 这样的现象便造成了在驱替实验的早期, 水相相对渗透率较低的情况. 随着驱替过程的进行, 水相逐渐填充了孔隙空间, 油相被驱替出岩心, 流动阻力逐渐减小, 使得水相相对渗透率大幅增加, 导致驱替阶段后期, 水相相对渗透率较高. 而在考虑了热流固耦合的综合影响下, 在驱替的早期, 由于固体发生了弹性形变(图5), 使得水相的流动通道变大, 因此相对渗流能力略有增加. 在达到等渗点后, 随着温度在流场内的传递, 岩石受热应力的影响, 形变大小减小, 水相流动通道减小, 使得相对渗流能力略有减小.
3.2
注入PV数的影响
注入PV数(pore volume number)指的是累计注入的流体体积占据孔隙空间的倍数. PV数是衡量流体注入能力及驱替阶段的重要参数. PV数越高, 代表越多的注入流体进入了岩心, 使得岩心内预先饱和的流体饱和度下降. 并且随着注入流体的不断增加, 注入流体在岩心内的分布面积变大.
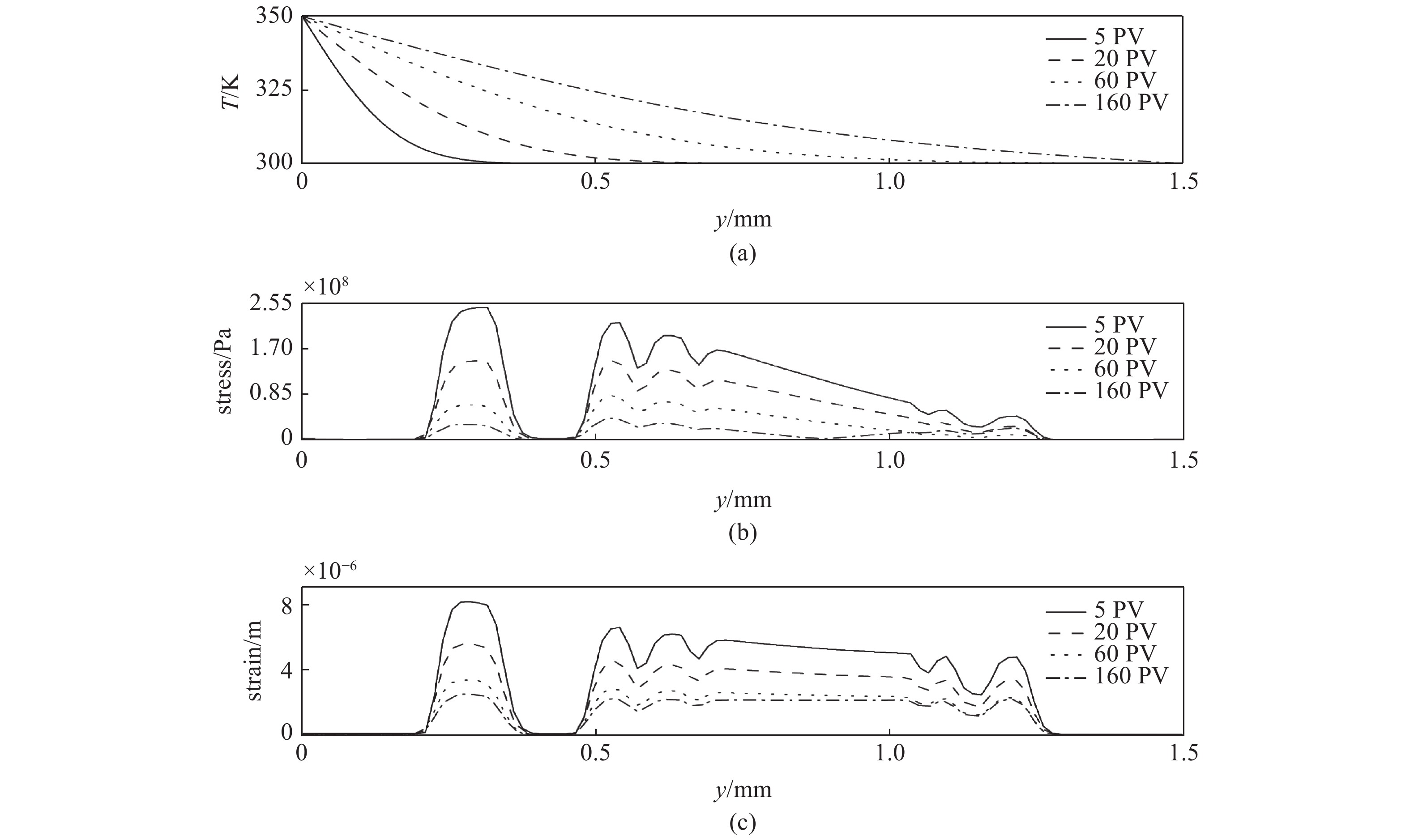
保持图4中的模拟条件不变, 图7展示的是PV数为5 ~ 160之间的模拟结果. 图7(a) ~ 图7(c)分别展示的是模型沿着驱替方向中心轴线的温度、应力及应变分布(图中应力、应变为零的部分为孔隙空间).
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-294-7.jpg'" class="figure_img
figure_type2 ccc " id="Figure7" />
图
7
不同注入PV数的模拟结果
Figure
7.
Simulation results under different PV numbers
下载: 全尺寸图片
幻灯片
从图7(a)可以看出, 随着注入PV数的不断增加, 热量不断地沿着驱替方向传播, 岩心固体不断地被加热. 如图7(b)所示, 随着PV数增加, 固体温度升高, 受到的热膨胀应力不断上升, 总应力不断下降, 并且沿着驱替方向, 总应力也在不断地下降. 根据式(19)和式(20), 热膨胀应力与固体所受的流体所施加的应力方向相反, 因此两者会相互抵消, 造成随着温度的上升, 而总应力下降的情况. 由于总应力随着PV数的增加而下降, 如图7(c)所示, 发生的弹性形变也在不断地下降, 与应力的变化呈现出相同的规律.
3.3
注入温差的影响
为了探究温度变化对两相流体在多孔介质内流动过程的影响, 本研究设置了五组模拟, 保持表 1中的参数设置不变, 分别设置入口温度为350 K, 400 K, 450 K, 500 K, 550 K开展模拟. 水相润湿角为45°, 入口端注入流速为0.001 m/s.
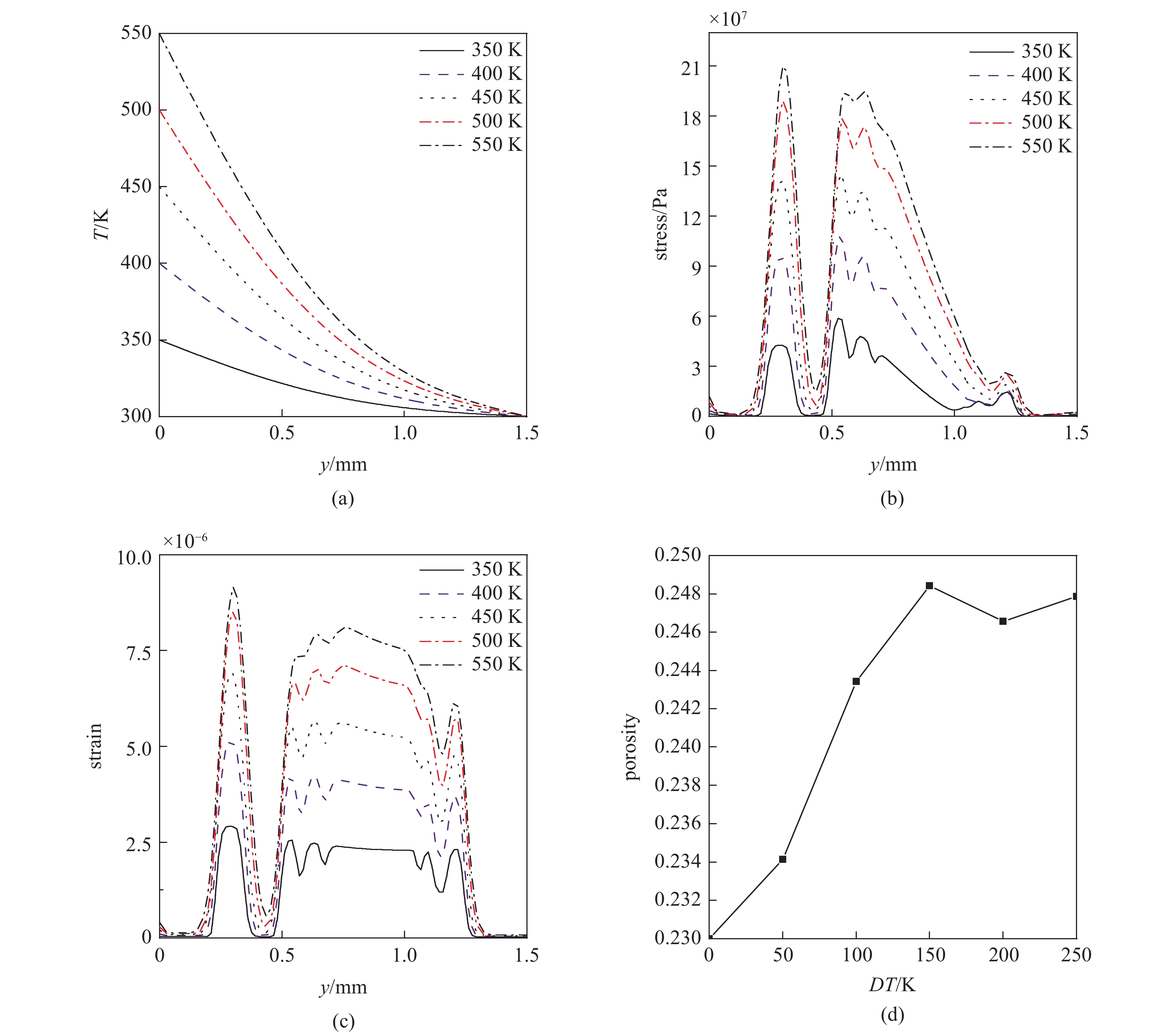
图8展示的是五组不同注入温差条件模型在100 PV的模拟结果, 五组模型中温度场沿着驱替方向中心轴线的分布情况如图8(a)所示; 图8(b)和图8(c)分别展示了应力、应变沿着驱替方向的分布情况; 图8(d)是孔隙度与注入温差的关系.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-294-8.jpg'" class="figure_img
figure_type2 ccc " id="Figure8" />
图
8
不同注入温度下的模拟结果
Figure
8.
Simulation results under different temperature difference
下载: 全尺寸图片
幻灯片
随着注入温差的不断增加, 模型内的温度梯度不断增加(如图8(a)所示). 此时, 热膨胀应力成为了造成岩石弹性变形的主导力. 如图8(b)和图8(c)所示, 随着温度的增加, 岩石固体所受的应力、应变随之增加. 与图7(b)和图7(c)相比, 当模型的注入温度达到400 K时, 热膨胀应力已经抵消了流体与骨架之间的流固耦合相应, 此时流体对骨架产生的应力已经不足以抵消热膨胀应力, 因此岩石的应力、应变随着温度的升高而增加. 同时, 对比图7(b)、图7(c)与图8(b)、图8(c)可以发现, 图7中原本孔隙占据的空间(应力、应变为零处)在图8中观察到了应力、应变的增加. 这是由于热膨胀应力导致了岩石固体发生向外扩张的形变(如图8(c), 当T > 400 K, 应变量在5 ~ 9 μm), 导致原本由孔隙占据的空间, 变成了固体占据的空间.
固体颗粒受热变形导致的直接结果便是岩心孔隙度的变化. 图8(d)展示的孔隙度随着岩心两端驱替温差的变化(孔隙度的计算方法如式(2)所示). 整体而言, 孔隙度随着温度的增加而增加, 当DT > 150 K(入口温度为450 K时), 孔隙度变化幅度不大. 从DT = 0 ~ 250 K, 孔隙度的变化幅度为8%. Sengun[33]认为温度与孔隙度的变化是正相关的关系, 在他的研究中观察到了当岩心从105 °C加热到600 °C后, 孔隙度增加的现象. Zhang等[34]也在实验中观察到了孔隙度随温度增加的现象.
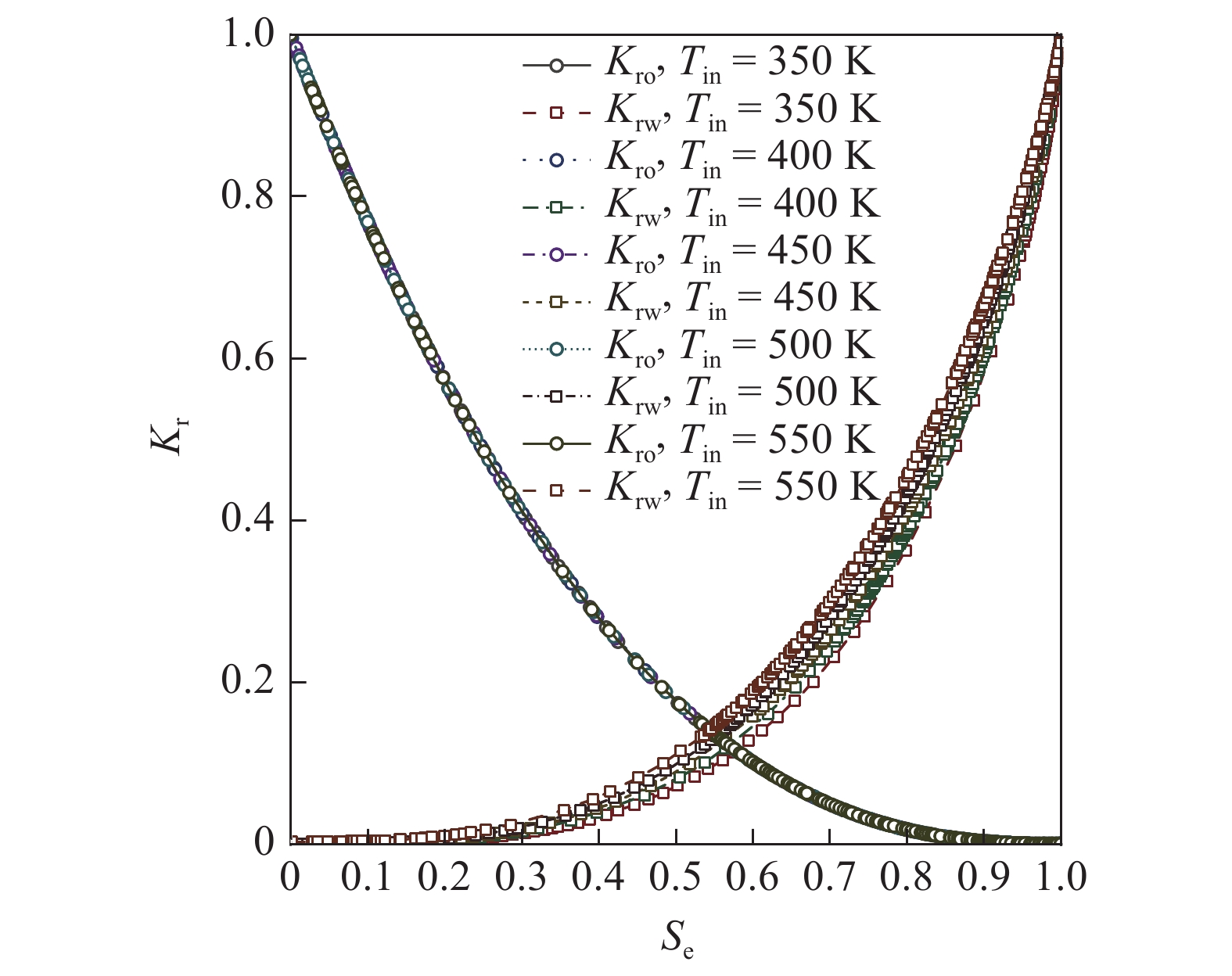
温度导致的微小孔隙结构变化改变了两相流体的相对渗流特征. 如图9所示, 温度的改变使得水相的相对渗流能力提高, 而油相的相对渗流能力几乎没有改变, 导致等渗点向原等渗点的左边移动[35-36].
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-294-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
不同注入温度下的归一化相渗曲线
Figure
9.
Normalized relative permeability curves at different injecting temperature
下载: 全尺寸图片
幻灯片
4.
结论
(1)基于Darcy-Brinkman-Biot的流固耦合数值方法, 使用了Duhamel-Neumann热弹性应力准则计算热应力, 实现了一个多孔介质内考虑热流固耦合作用的两相流动模型;
(2)热流固耦合的综合作用改变孔隙结构参数, 影响了两相流体在多孔介质内的渗流过程. 主要体现为孔隙的扩大提高了相对渗流能力, 孔隙的减小降低了相对渗流能力;
(3)在注入温度不变的情况下, 随着注入PV数的增加, 岩石所受热应力与流固耦合作用产生的应力达到平衡. 热应力与流固耦合作用产生的应力方向相反, 使得总应力比单独考虑流固耦合作用下的应力小;
(4)注入温度的增加使得模型孔隙度增加, 增加幅度为8%. 但当注入温差达到150 K后, 孔隙度不再有明显增加. 温度的增加改变了孔隙结构, 间接导致了两相渗流规律的变化, 使得水相的相对渗流能力随着温度的增加而增加, 等渗点左移.
