引 言
高性能能量俘获技术对状态监测传感器网络的可持续性供能具有重要意义, 能够弥补传统电池容量有限且需要及时更换的缺点. 这种技术广泛应用于汽车胎压监测[1-2]、机械设备运行故障监测[3-4]、人体健康状态监测[5-6]以及物联网环境信号监测[7]等场合. 非线性多稳态技术[8-10]是一种常见的能量俘获性能提升方法, 克服了传统线性系统俘能频带窄的问题. 该技术通过配置磁铁引入非线性磁力, 能够使系统的共振频率可调节, 进而拓宽俘能系统的响应频带.
近年来, 悬臂梁式多稳态压电俘能系统[11-13]有了很大的发展. Erturk等[14]基于Moon和Holmes[15]提出的磁耦合悬臂梁结构设计了一种悬臂梁式非线性双稳态压电能量俘获系统, 对比线性系统其电压和功率幅值分别提高了200%和800%, 同时有效频带也显著提高. 在此基础上, Zhou等[16-17]通过改变外部磁铁的旋转角度实现了三稳态能量俘获系统, 结果表明其相对于势阱较深的双稳态系统能够获得更宽的俘能频带和输出效率. 此外, Huang等[18]采用4块磁铁设计了五稳态的压电悬臂梁俘能系统, 并分析了系统的动力学特性. 为了研究多稳态系统中势阱对输出性能的影响机理, Cao等[19]揭示了较浅的势阱深度和较宽的势阱范围能提高系统在低频激励条件下的能量俘获性能. 虽然上述研究已经清晰地揭示了系统非线性特征与输出性能的关系, 但是多稳态系统非线性特征的正向设计方法尚未被探究. 由于混沌和分岔现象的存在, 多稳态系统对结构参数非常敏感, 比如磁铁配置、结构尺寸和空间位置等, 结构参数微小的改变都会对系统的非线性特征产生较大的影响. 因此, 为了进行结构优化和参数设计, 获取预期的非线性恢复力来提高俘能性能, 需要建立一种准确的非线性恢复力表征方法来定量描述结构参数与非线性恢复力关系. 由于非线性恢复力中非线性特征来源于磁力, 因而对多稳态系统中非线性磁力的准确建模成为了研究重点.
非线性磁力的表征方法主要包括有限元法、实验拟合法和理论建模法. Upadrashta和Yang[20]通过ANSYS非线性弹簧单元对系统的磁力进行建模, 进而模拟压电悬臂梁端部磁铁的非线性特性. 虽然有限元方法能够得到较高的准确度, 但是由于计算量大, 导致了对系统参数的数值优化不易. 实验拟合法是通过多项式来拟合实验测得的数据. Ferrari等[21]通过3阶多项式对系统非线性恢复力进行拟合, 研究了多稳态磁耦合能量俘获系统的特性, 理论分析了多项式系数以及弹性刚度系数对能量俘获系统势能函数的影响. 周生喜等[22]通过实验测量了双稳态和三稳态压电悬臂梁系统的非线性恢复力离散点, 并通过多项式拟合了非线性恢复力并获得了势能函数特性. Abdelmoula等[23]比较了3阶、5阶和7阶多项式拟合的非线性磁力, 研究表明3阶多项式会低估磁铁所受磁力和系统的固有频率, 而高阶多项式会更加准确. 然而, 虽然实验拟合的方法比较准确, 但是一旦系统的结构参数改变, 这种方法将失效, 且没有建立起结构参数与非线性磁力的联系.
理论建模法是通过结构参数直接建立模型来表征非线性磁力, 主要包括磁偶极子法、改进磁偶极子法以及磁化电流法. 磁偶极子法是由Yung等[24]在1998年提出, 将磁铁等效成位于磁铁几何中心的磁偶极子, 推导了两个磁偶极子间的磁力表达式. 由于这种方法表达式简单, 计算方便, 被广泛应用于俘能系统的非线性磁力计算[25-28]. 然而, 这种方法中只考虑了磁铁的体积, 忽略了磁铁的形状, 只能适用于小磁铁和大距离的场合. 在此基础上, Wang等[29-30]提出了一种改进磁偶极子法, 将磁铁等效为两个相对磁化表面上的磁偶极子, 位于磁化表面的几何中心, 并分析了三稳态压电悬臂梁系统的非线性磁力特征. 但是, 磁铁磁化表面面积的忽略会带来误差, 适用于磁化表面比较小的情况. 此外, 磁化电流法是将永久磁铁的磁化强度等效成电流, 然后运用毕奥萨伐尔定律求解等效电流在空间中产生的磁场强度, 进而求解永久磁铁之间的磁力[31]. Leng等[32]采用等效电流法分析了压电式磁耦合悬臂梁能量俘获系统的磁力特性, 并应用到三稳态系统的磁力建模, 但是将系统端部磁铁的等效电流集中在所在面的中心, 忽略了外部磁铁在端部磁铁表面产生的磁场强度分布情况.
为了克服以上建模方法的局限性, 提出一种多稳态系统非线性磁力的准确建模方法, 以更好地刻画多稳态俘能系统的输出性能. 本文基于磁荷理论以及磁铁间的空间相对位置推导了多稳态俘能系统的非线性磁力模型, 通过实验验证了不同结构参数下非线性磁力计算的准确性, 分析了不同系统结构参数对多稳态系统非线性特征和响应电压的影响, 并进行了参数分析与优化, 以期为多稳态系统的结构设计提供理论基础. 本文提出的多稳态俘能系统准确磁力建模方法具有更广泛的适用场合, 采用磁荷理论并未对磁力建模进行简化和忽略, 因而可以适用任意尺寸和空间位置的磁力计算.
1.
多稳态俘能系统的建模
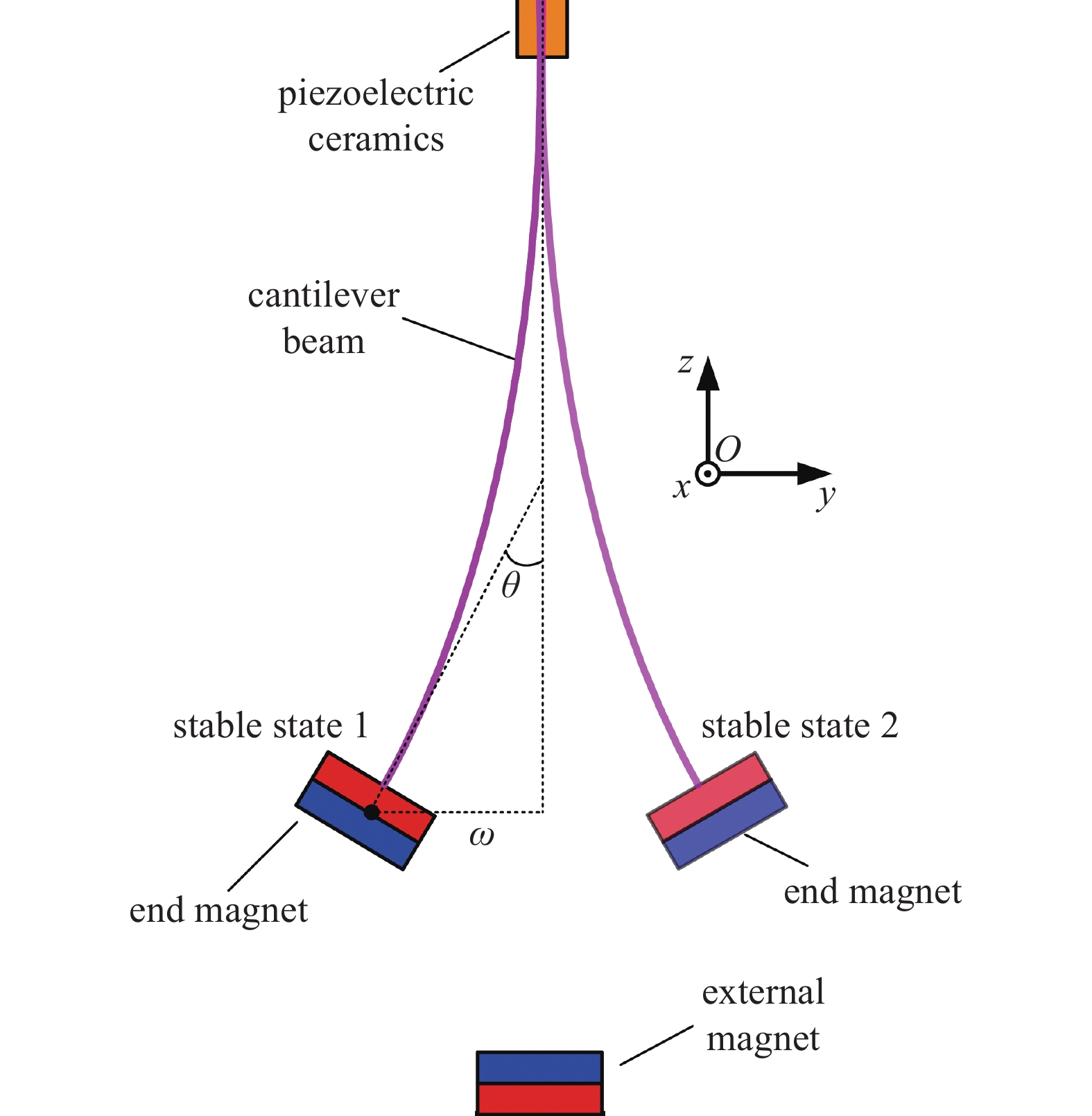
图1为常见的压电双稳态俘能结构, 包括压电片、悬臂梁、端部磁铁和外部磁铁. 其中, 端部磁铁与外部磁铁相对布置, 承受相斥的磁力, 使得系统存在两个稳态点. 若存在两块外部磁铁分布在两侧时, 系统则变为三稳态系统, 存在3个稳态点.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
压电双稳态俘能结构
Figure
1.
Piezoelectric bi-stable energy harvester
下载: 全尺寸图片
幻灯片
根据哈密顿原理和欧拉梁理论, 考虑悬臂梁的一阶模态, 压电多稳态系统的控制方程为[33-34]
$$ left. {begin{array}{*{20}{l}} {Mddot omega left( t ight) + Cdot omega left( t ight) + Komega left( t ight) + {F_m} - xi vleft( t ight) = Fleft( t ight)} {{C_p}dot vleft( t ight) + vleft( t ight){{left( {{R_l}} ight)}^{ - 1}} + xi dot omega left( t ight) = 0} end{array}} ight} $$  | (1) |
式中, M为系统的等效质量, C为系统的等效阻尼系数, K为系统的等效刚度, ξ为机电耦合系数, Cp为压电片的等效电容, Rl为外部电路负载, v(t)为压电陶瓷的响应电压, ω(t)为悬臂梁的横向位移, F(t)为外部激励, Fm为非线性磁力.
多稳态系统的非线性恢复力可以看作是悬臂梁弹力和磁力的和, 即
$$ {F_r} = Komega left( t ight) + {F_m} $$  | (2) |
在以往的研究中已经通过实验验证了在小范围内悬臂梁弹力可以看作是线性, 根据材料力学理论, 悬臂梁弹力的刚度可以表达为
$$ K = frac{{3EI}}{{{l^3}}} $$  | (3) |
式中, E为悬臂梁的弹性模量, I为悬臂梁截面的惯性矩, l为悬臂梁长度.
要求解非线性恢复力, 需要准确计算出多稳态系统中的非线性磁力Fm, 这里采用磁荷法推导多稳态系统的磁力表达式.
$$ nabla times {boldsymbol{E}} = {boldsymbol{0}} $$  | (4) |
$$ nabla cdot {boldsymbol{D}} = {{ ho }} $$  | (5) |
$$ nabla times {boldsymbol{H}} = {boldsymbol{j}} $$  | (6) |
$$ nabla cdot {boldsymbol{B}} = {{0}} $$  | (7) |
式(4)~式(7)是麦克斯韦方程组的微分形式, 其中式(4)和式(5)描述电场, 式(6)和式(7)描述磁场, E为电场强度, D为电位移, ρ为电荷密度, H为磁场强度, j为电流密度, B为磁通密度.
永久磁铁可以假设不存在电流密度, 则j = 0. 此时, 永久磁铁产生的磁场为无旋场, 式(6)可以改写为
$$ nabla times {{{boldsymbol H}}} = {boldsymbol{0}} $$  | (8) |
由于无旋场的积分与路径无关, 则可以通过定义磁标量势φm计算磁场强度
$$ {boldsymbol{H}} = {{ - }}nabla {varphi _m} $$  | (9) |
同样地, 通过在无旋场中定义两任意磁荷之间的磁势能进而可以计算磁力为
$$ {boldsymbol{F}} = - nabla W $$  | (10) |
因此, 要求解磁铁之间的磁力, 需要先计算出两磁铁之间的磁势能. 磁荷法通过将永久磁铁的磁化强度等效为分布在两个磁化表面相反极性的磁荷, 其磁荷密度的幅值等于磁铁磁化强度的幅值. 通过磁场库伦定律可以计算两磁荷密度之间的磁势能, 然后对整个磁铁表面的磁荷进行积分, 进而得到两磁铁之间的总势能.
对于如图2所示的双稳态系统磁铁空间位置, 端部磁铁和外部磁铁的磁化强度都为M, 沿x, y, z, 3个方向的尺寸分别为2a×2b×2c和2A×2B×2C, 其中磁化表面的尺寸分别是2a×2b和2A×2B. 端部磁铁和外部磁铁表面的磁荷密度分别定义为
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
双稳态系统磁铁空间位置
Figure
2.
Spatial position of magnets for bi-stable system
下载: 全尺寸图片
幻灯片
$$left. begin{split}& {sigma _1} = {mu _0}M hfill & {sigma _2} = - {mu _0}M hfill & {sigma _3} = - {mu _0}M hfill & {sigma _4} = {mu _0}M hfillend{split} ight} $$  | (11) |
式中, μ0为真空中的磁导率.
根据磁场库仑定律, 磁荷密度为σ1和σ3的磁铁表面之间的磁势能为
$$ {W_{1,3}} = int_{ - a}^a {{ m{d}}x} int_{ - b}^b {{ m{d}}y} int_{ - A}^A {{ m{d}}X} int_{ - B}^B {{ m{d}}Y} frac{{{sigma _1}{sigma _3}}}{{4{text{π}} {mu _0}r}} $$  | (12) |
式中, r为两磁荷之间的距离.
对所有磁化表面的磁势能进行求和, 得到端部磁铁和外部磁铁之间的总磁势能为
$$ W = {W_{1,3}} + {W_{1,4}} + {W_{2,3}} + {W_{2,4}} $$  | (13) |
对于两块相对旋转的方形磁铁, Charpentier和?Lemarquand[35]推导了完整的磁力计算表达式. 在此基础上, 要计算图2所示双稳态能量俘获系统所受磁力, 需要获取两磁铁之间的空间位置, 也就是两磁铁之间的相对距离和相对转角. 以悬臂梁处于y负半轴为例, 首先容易得到端部磁铁与外部磁铁沿逆时针方向的相对旋转角度为π?θ. 其次, 对于两磁铁之间的相对距离, 设定图示端部磁铁和外部磁铁的顶点分别为P1和P2, 根据坐标系和几何关系可得
$$ {{boldsymbol{P}}_1} = left[ {begin{array}{*{20}{c}} { - a};;{ - omega - sqrt {{a^2} + {c^2}} cos beta };;{{h_r} + sqrt {{a^2} + {c^2}} cos left( {dfrac{{text{π}} }{2} - beta } ight)} end{array}} ight] $$  | (14) |
$$ {{boldsymbol{P}}_2} = left[ {begin{array}{*{20}{c}} { - A}&{ - B}&{ - C} end{array}} ight] qquadqquadqquadqquadqquadqquadquad;;;$$  | (15) |
式中,
$$ left[ {begin{array}{*{20}{c}} {{x_{01}}}&{{y_{01}}}&{{z_{01}}} end{array}} ight] = {{boldsymbol{P}}_1} - {{boldsymbol{P}}_2} $$  | (16) |
基于上述系统参数以及磁铁间相对距离和转角, 进而能够计算两磁铁之间的磁力大小为
$$ begin{split}& {F_y}left( {{text{π}} - theta ,{x_{01}},{y_{01}},{z_{01}},A,B,C,a,b,c,M} ight) = hfill &quad {f_1}left( {{x_{01}},{x_{01}} + a,{y_{01}},{z_{01}},{text{π}} - theta ,0,0,b,c,M} ight) - hfill &quad {f_1}left( {{x_{01}} - A,{x_{01}} - A + a,{y_{01}},{z_{01}},{text{π}} - theta ,0,0,b,c,M} ight) + hfill &quad {f_1}left( {{x_{01}} - A,{x_{01}} - A + a,{y_{01}},{z_{01}},{text{π}} - theta ,B,0,b,c,M} ight) - hfill &quad {f_1}left( {{x_{01}},{x_{01}} + a,{y_{01}},{z_{01}},{text{π}} - theta ,B,0,b,c,M} ight) + hfill &quad {f_1}left( {{x_{01}} - A,{x_{01}} - A + a,{y_{01}},{z_{01}},{text{π}} - theta ,0,C,b,c,M} ight) - hfill &quad {f_1}left( {{x_{01}},{x_{01}} + a,{y_{01}},{z_{01}},{text{π}} - theta ,0,C,b,c,M} ight) + hfill &quad {f_1}left( {{x_{01}},{x_{01}} + a,{y_{01}},{z_{01}},{text{π}} - theta ,B,C,b,c,M} ight) - hfill &quad {f_1}left( {{x_{01}} - A,{x_{01}} - A + a,{y_{01}},{z_{01}},{text{π}} - theta ,B,C,b,c,M} ight) end{split} $$  | (17) |
式中
$$ begin{split}& {f_1}left( {v,w,{y_{01}},{z_{01}},{text{π}} - theta ,B,C,b,c,M} ight) = hfill &quad frac{{{M^2}}}{{4{text{π}} {mu _0}}} {{f_2}left( {v,w,{y_{01}},{z_{01}},{text{π}} - theta ,B,C,b,c} ight)} - hfill &quad {f_2}left( {v,w,{y_{01}},{z_{01}},{text{π}} - theta ,B,C,b,0} ight) end{split} $$  | (18) |
$$ begin{split}& {f_2}left( {v,w,{y_{01}},{z_{01}},{text{π}} - theta ,B,C,b,z'} ight) = hfill &quad {f_3}left( {w,{y_{01}},{z_{01}},{text{π}} - theta ,B,C,b,z'} ight) - hfill &quad {f_3}left( {v,{y_{01}},{z_{01}},{text{π}} - theta ,B,C,b,z'} ight) - hfill &quad {f_3}left( {w,{y_{01}},{z_{01}},{text{π}} - theta ,B,C,0,z'} ight) + hfill &quad {f_3}left( {v,{y_{01}},{z_{01}},{text{π}} - theta ,B,C,0,z'} ight) end{split} $$  | (19) |
$$ begin{split}& {f_3}left( {u,{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y',z'} ight) = hfill &quad u{f_6}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y'} ight)ln left( { - u + {f_4}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y',z'} ight)} ight) - hfill &quad u{f_6}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y'} ight) - {u^2}ln left( {{f_4}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y',z'} ight) + {f_6}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y'} ight)} ight) + hfill &quad u{f_5}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,z'} ight)arctan left( {frac{{ - f_5^2left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y'} ight) - {u^2} + u{f_4}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y',z'} ight)}}{{{f_5}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,z'} ight){f_6}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y'} ight)}}} ight) + hfill &quad frac{1}{2}u{text{π}} left| {{f_5}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,z'} ight)} ight|{text{sign}}left( {{f_6}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y'} ight)} ight) + hfill &quad frac{1}{2}{f_6}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y'} ight){f_4}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y',z'} ight) + hfill &quad frac{1}{2}left( {{u^2} + f_5^2left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y',z'} ight)} ight)ln left( {{f_4}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y',z'} ight) + {f_6}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y'} ight)} ight) end{split} $$  | (20) |
$$ begin{gathered} {f_4}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y',z'} ight) = hfill sqrt {{u^2} + f_5^2left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,z'} ight) + f_6^2left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y'} ight)} end{gathered} $$  | (21) |
$$ begin{split}& {f_5}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,z'} ight) = - {y_{01}}sin left( {{text{π}} - theta } ight) + hfill &quad {z_{01}}cos left( {{text{π}} - theta } ight) + bsin left( {{text{π}} - theta } ight) - c{ m{cos}}left( {{text{π}} - theta } ight) + z' end{split} $$  | (22) |
$$ begin{split}& {f_6}left( {{y_{01}},{z_{01}},{text{π}} - theta ,B,C,y'} ight) = {y_{01}}cos left( {{text{π}} - theta } ight) + hfill &quad {z_{01}}sin left( {{text{π}} - theta } ight) - Bcos left( {{text{π}} - theta } ight) - Csin left( {{text{π}} - theta } ight) + y' end{split} $$  | (23) |
式中, f1 ~ f6为中间函数, u, v, w, y'和z'为中间变量.
此外, 由于悬臂梁端部磁铁的位置随着位移变化而变化, 需要建立悬臂梁端部转角θ以及沿z方向长度随位移ω的变化关系, 因此有[36]
$$ {l_z} = frac{{12{l^3}}}{{{{text{π}} ^2}{omega ^2} + 12{l^2}}} $$  | (24) |
$$ theta = arcsin left[ {dfrac{{{text{π}} omegasin {dfrac{{{text{π}} {l_z}}}{{2l}}} }}{{2lleft( {1 - cos dfrac{{{text{π}} {l_z}}}{{2l}}} ight)}}} ight] $$  | (25) |
式中, lz为悬臂梁在位移为ω时沿z方向的长度, l为悬臂梁原始长度.因此, 悬臂梁沿z方向长度的变化为
$$ Delta l = l - {l_z} $$  | (26) |
对于三稳态系统而言, 非线性磁力的求解与双稳态系统类似, 需要分别计算两块外部磁铁对端部磁铁产生的磁力, 然后对磁力进行叠加得到总磁力.
2.
非线性磁力的实验验证
2.1
实验平台搭建
为了验证本方法计算多稳态俘能系统磁力的准确性, 搭建了图3所示非线性磁力测量实验平台, 包括测力计(force gauge model M5-2)、激光位移传感器(Panasonic HL-G105-A-C5)、外部磁铁、端部磁铁、悬臂梁和螺栓. 测力计直接连在外部磁铁上, 通过调节螺栓可以记录不同位置下端部磁铁所受的磁力, 同时激光位移传感器测量端部磁铁的位移. 悬臂梁端部磁铁的尺寸为10 mm × 10 mm × 4 mm, 外部磁铁的尺寸为10 mm × 10 mm × 10 mm. 磁铁的材料为N50, 磁化强度为1.46 T. 悬臂梁材料为不锈钢, 原始长度为120 mm.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
非线性磁力测量实验
Figure
3.
Experimental setup of nonlinear magnetic force
下载: 全尺寸图片
幻灯片
2.2
非线性磁力的验证结果
图4为双稳态系统的非线性磁力验证, 比较了实验测量(experiment)、本文方法(this model)、磁偶极子法(M1)、磁化电流法(M2)和改进磁偶极子法(M3)的磁力大小. 悬臂梁端部磁铁与外部磁铁的竖直距离h为17 mm. 可以看出, 本文方法与实验测量的磁力吻合较好, 而由于磁偶极子法、磁化电流法和改进磁偶极子法存在特定的适用场合, 其计算误差都比较大. 本文方法计算的磁力峰值为0.3758 N, 实验测量的磁力峰值为0.36 N, 误差为4.3%. 磁偶极子法计算的磁力峰值为0.4214 N, 误差为17.06%. 磁化电流法计算的磁力峰值为0.3193 N, 误差为11.29%. 改进磁偶极子法计算的磁力峰值为0.4955 N, 误差为37.60%. 此外, 当位移较大时, 磁偶极子法和改进磁偶极子法的误差会越来越小, 但是磁化电流法的误差一直保持较大.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
双稳态系统非线性磁力
Figure
4.
Nonlinear magnetic force in bi-stable system
下载: 全尺寸图片
幻灯片
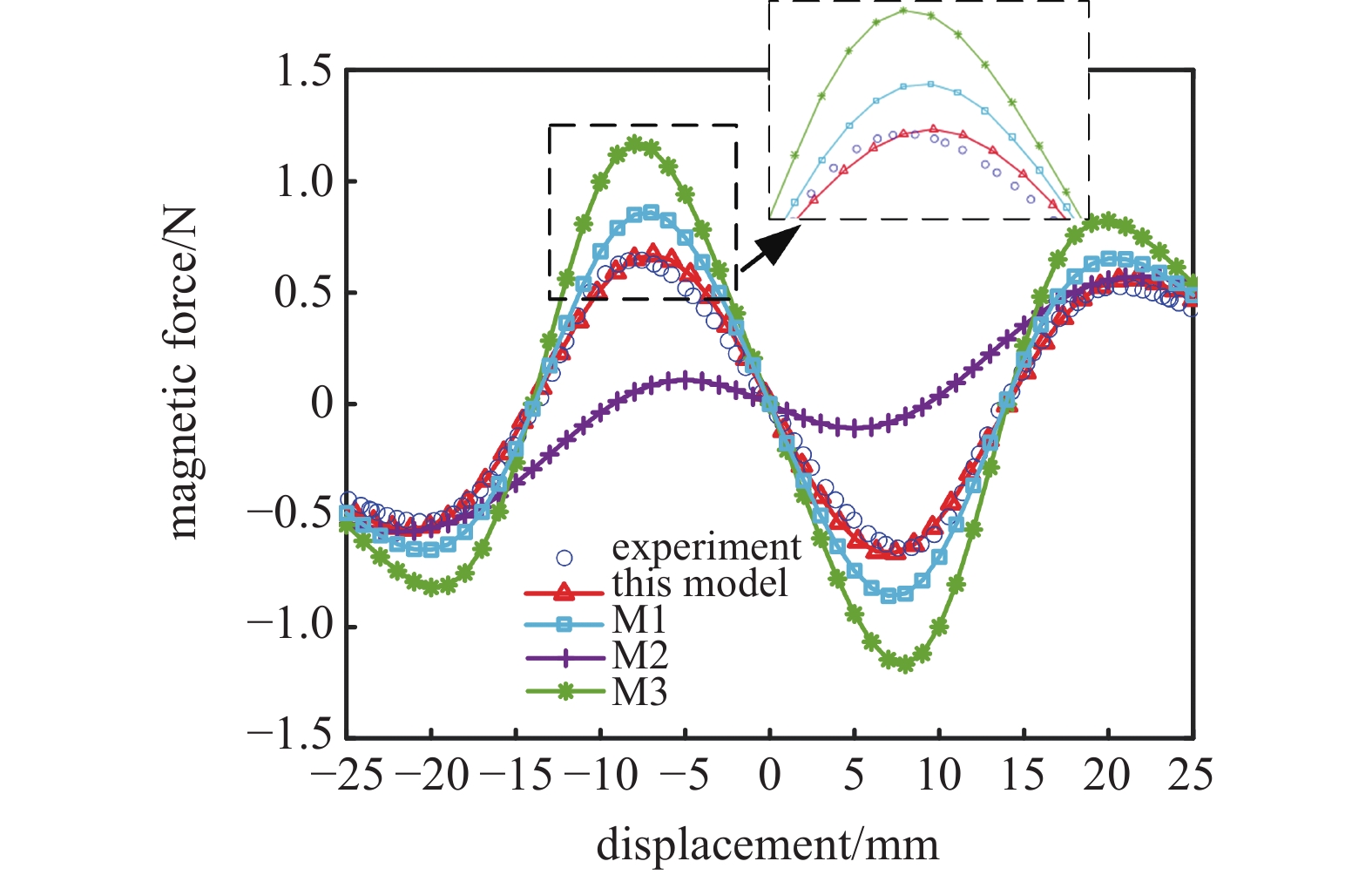
三稳态系统通常需要两块外部磁铁实现, 由于这里研究的是对称三稳态系统, 两块外部磁铁关于系统中心对称. 因此, 定义两外部磁铁之间的距离为2d, 则每块外部磁铁到系统中心的水平距离为d(沿y方向的距离). 图5为三稳态系统的非线性磁力验证, 比较了实验测量(experiment)、本文方法(this model)、磁偶极子法(M1)、磁化电流法(M2)和改进磁偶极子法(M3)计算的磁力大小. 悬臂梁端部磁铁与外部磁铁的竖直距离h为12 mm, 外部磁铁到系统中心的水平距离d为10 mm. 可以看出, 本文方法计算的磁力与实验测量结果最吻合. 本文方法计算的磁力峰值为0.6694 N, 实验测量的磁力峰值为0.6286 N, 误差为6.49%. 磁偶极子法计算的磁力峰值为0.8607 N, 误差为36.92%. 磁化电流法计算的磁力峰值为0.1027 N, 误差为83.66%. 改进磁偶极子法计算的磁力峰值为1.16778 N, 误差为85.77%.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
三稳态系统非线性磁力
Figure
5.
Nonlinear magnetic force in tri-stable system
下载: 全尺寸图片
幻灯片
综上所述, 通过本文方法计算得到的双稳态和三稳态系统磁力与实验测量结果比较吻合, 验证了本文方法的有效性.
3.
结构参数对非线性特征的影响
为了提高多稳态系统的俘能性能, 对系统进行参数优化具有重要的意义. 因此, 基于本文方法能够研究不同结构参数对系统势阱特性以及响应电压的影响, 并获取多稳态系统的最优输出性能. 双稳态结构和三稳态结构的系统等效质量M为1.7 g、等效阻尼系数C为2.4 mN·s/m、机电耦合系数ξ为?8.87 μN/V、压电片的等效电容Cp为8.3015 nF、外部负载R为10 MΩ. 激励为1~20 Hz的升频扫频信号, 幅值为0.3 g.
3.1
双稳态结构参数分析
3.1.1
竖直距离影响
图6为竖直距离h对双稳态系统势阱的影响, h从30 mm变化到40 mm. 可以看出, 当h为30 mm时, 系统为势阱较深的双稳态系统. 随着h逐渐增大到36 mm时, 两侧势阱变得越来越浅, 且势阱宽度越来越窄, 但始终都保持为双稳态系统. 然而, 当h增大到38 mm时, 系统由双稳态过渡成单稳态. 此后, 当h继续增大到40 mm时, 系统依然为单稳态系统, 且势阱宽度越来越窄. 由此可见, 双稳态系统的临界位置处于h从36~38 mm之间.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
竖直距离h对双稳态系统势阱的影响
Figure
6.
Influence of vertical distance h on bi-stable potential well
下载: 全尺寸图片
幻灯片
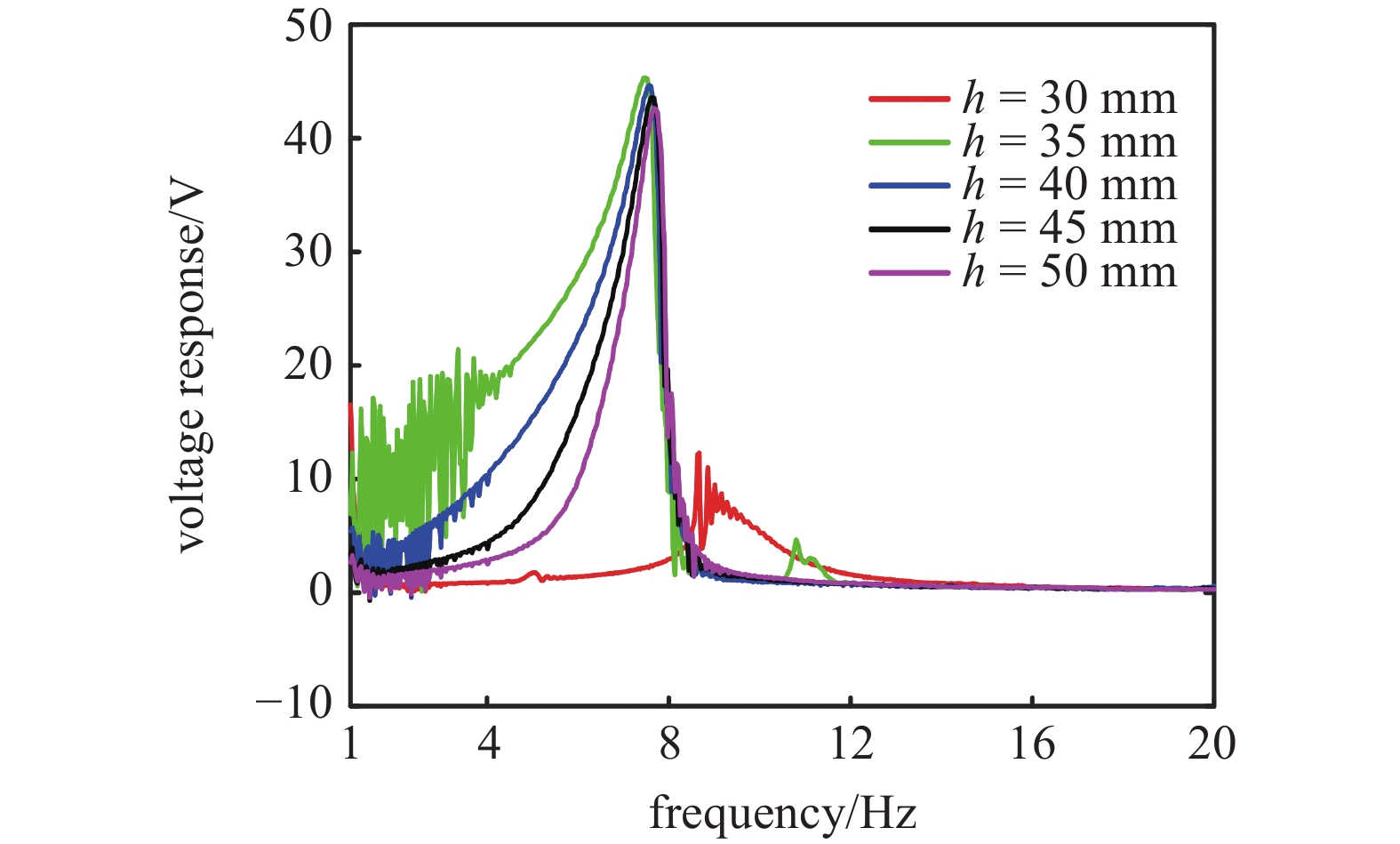
图7给出了竖直距离h对双稳态系统响应电压的影响, 选取h的变化范围为30~50 mm, 间隔为5 mm. 由图可知, 当h为30 mm时, 激励不足以使系统跨越势阱, 只产生位移较小的势阱内运动, 因而响应电压较小, 峰值仅为10 V左右. 当h增大为35 mm时, 响应电压的幅值达到最大为46 V左右, 且频带也最宽, 这是由于此时双稳态系统的势阱较浅. 当h从40 mm增大到50 mm的过程中, 单稳态系统势阱会逐渐变窄, 因而响应电压的幅值略有下降, 俘能频带明显变窄, 效率降低.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
竖直距离h对双稳态系统响应电压的影响
Figure
7.
Influence of vertical distance h on bi-stable voltage response
下载: 全尺寸图片
幻灯片
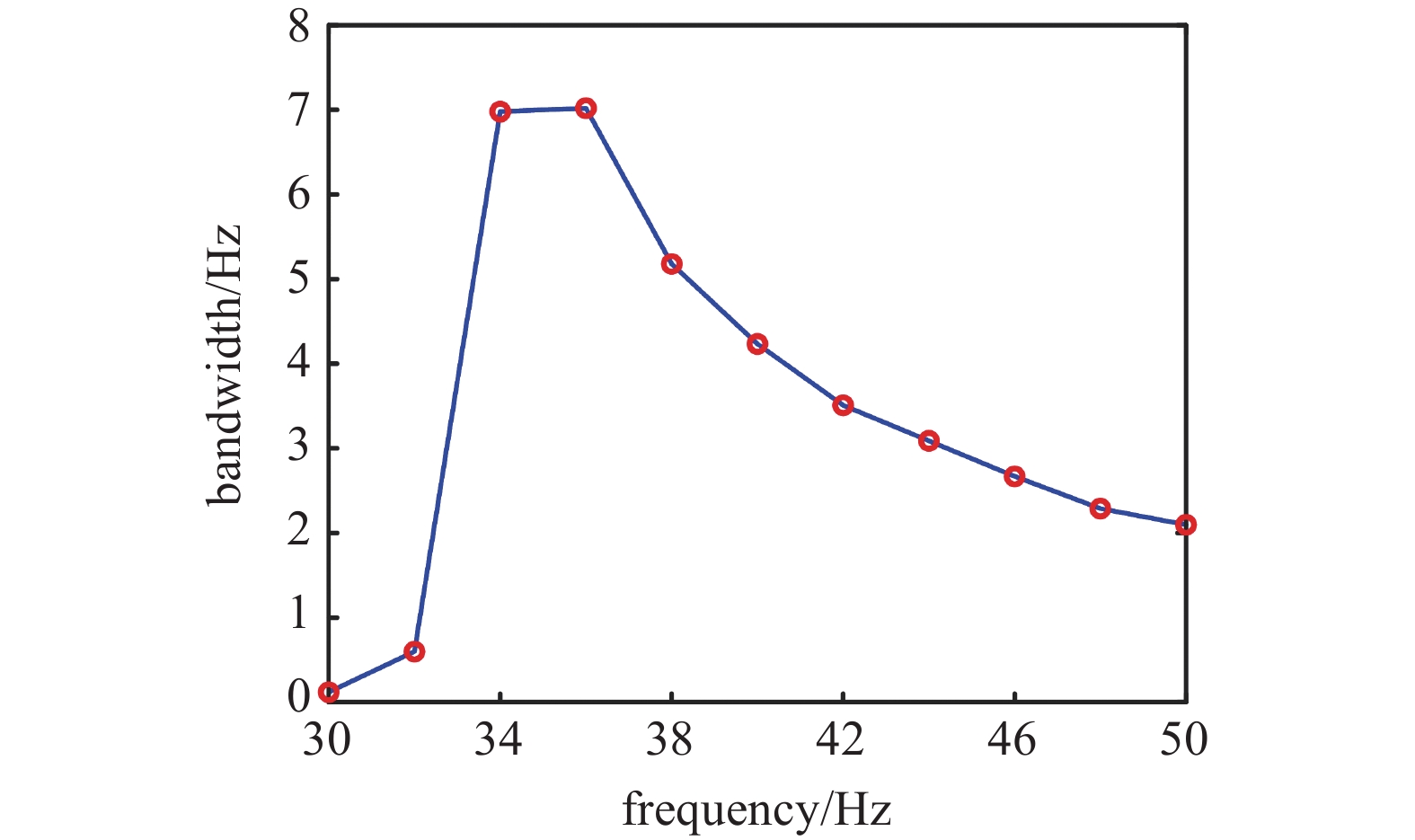
为了量化研究竖直距离h对响应电压频带宽度的影响, 设定响应电压10 V以上作为有效频带, 并得到了如图8所示的双稳态系统频带变化. 由图可知, 当竖直距离h从32 mm增大到34 mm时, 系统的带宽从0.6 Hz增加到6.98 Hz. 随着磁铁间竖直距离h的进一步增大, 系统的带宽逐渐减小. 当竖直距离h为50 mm时, 系统的带宽为2.098 Hz.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
竖直距离h对双稳态系统频带影响
Figure
8.
Influence of vertical distance h on bandwidth of bi-stable system
下载: 全尺寸图片
幻灯片
为了更好地研究系统的响应特性, 图9给出了不同竖直距离h的双稳态系统相轨迹图. 由图可知, 当竖直距离h为30 mm时, 系统主要为势阱内运动. 当竖直距离h为35 mm时, 系统主要为跨越势阱的大幅值运动. 当竖直距离h为40 mm时, 此时系统为单稳态系统, 系统也能产生幅值较大的运动.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
不同竖直距离h的双稳态系统相轨迹图
Figure
9.
Phase trajectory of bi-stable system under different vertical distance h
下载: 全尺寸图片
幻灯片
3.1.2
参数优化
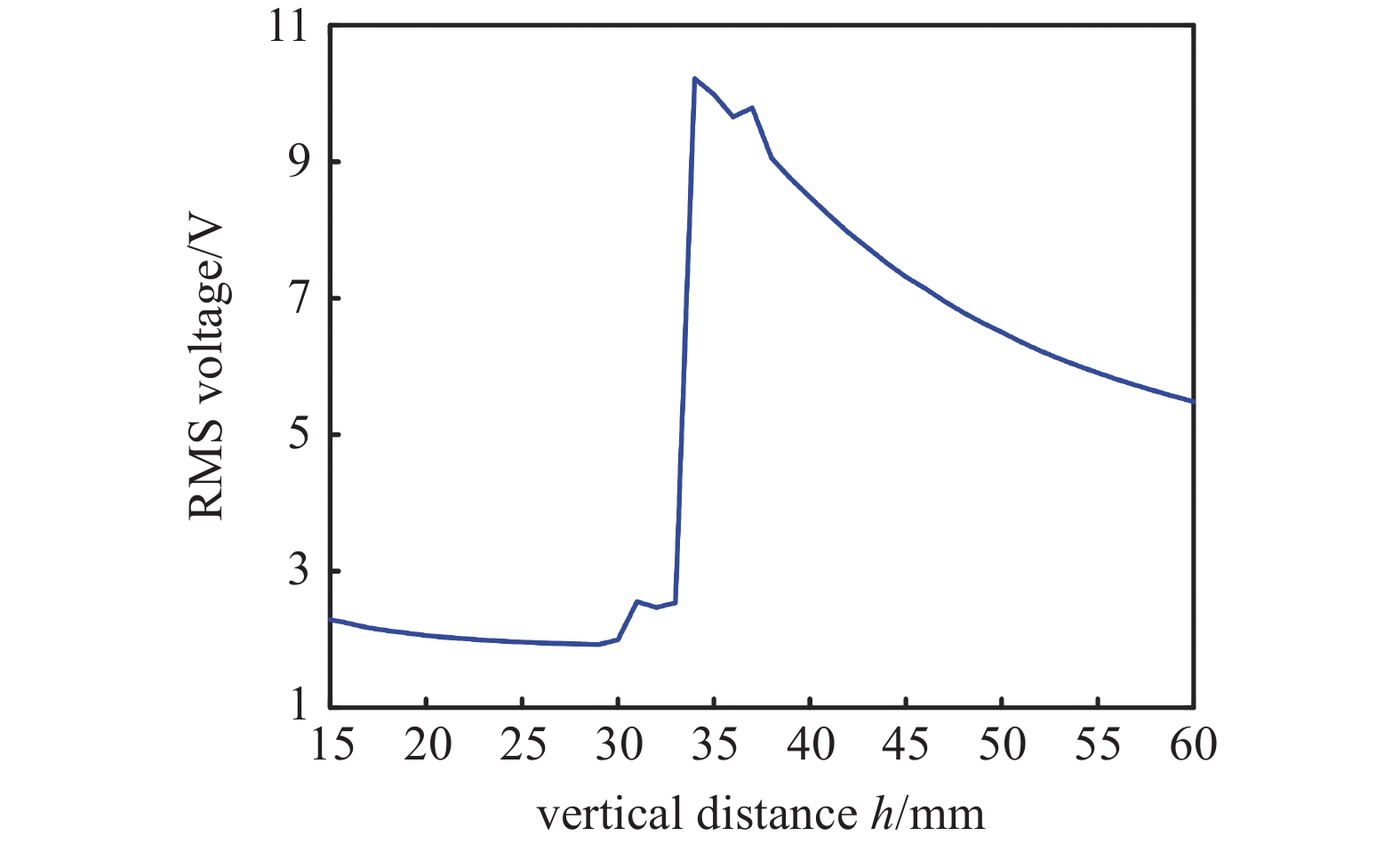
为了获取双稳态系统结构的最优参数, 对竖直距离h进行参数扫描得到了如图10所示均方电压的变化规律, h的变化范围为15~60 mm, 间隔为1 mm. 首先给定幅值为0.3 g的1~20 Hz扫频激励, 获取不同竖直距离h下的响应电压频响关系, 然后计算频域均方电压, 以此作为参数优化目标, 综合考虑了响应电压幅值和频带的影响. 由图可知, 当h从15 mm增大到33 mm时, 均方电压保持在较低的水平, 不超过3 V. 然而, 当h变化到34 mm时, 均方电压突然增大到10.22 V. 此后, 随着h的进一步增大, 均方电压逐渐降低, 但是也保持在较高的水平.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-10.jpg'" class="figure_img
figure_type1 bbb " id="Figure10" />
图
10
双稳态系统最优竖直距离h
Figure
10.
The optimal vertical distance h for bi-stable system
下载: 全尺寸图片
幻灯片
3.2
三稳态结构参数分析
3.2.1
竖直距离影响
图11为竖直距离h对三稳态系统势阱的影响, h从26 mm变化到36 mm. 可以看出, 当h为26 mm时, 三稳态系统的外侧势阱最深. 随着h增大到30 mm时, 势阱逐渐变浅, 且势阱宽度变窄, 但始终为三稳态系统. 然而, 当h增大到32 mm时, 系统由三稳态过渡为单稳态. 当h继续增大时, 系统依然为单稳态系统, 且势阱宽度越来越窄. 因此, 三稳态系统临界位置处于h从30~32 mm之间.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-11.jpg'" class="figure_img
figure_type1 bbb " id="Figure11" />
图
11
竖直距离h对三稳态系统势阱的影响
Figure
11.
Influence of vertical distance h on tri-stable potential well
下载: 全尺寸图片
幻灯片
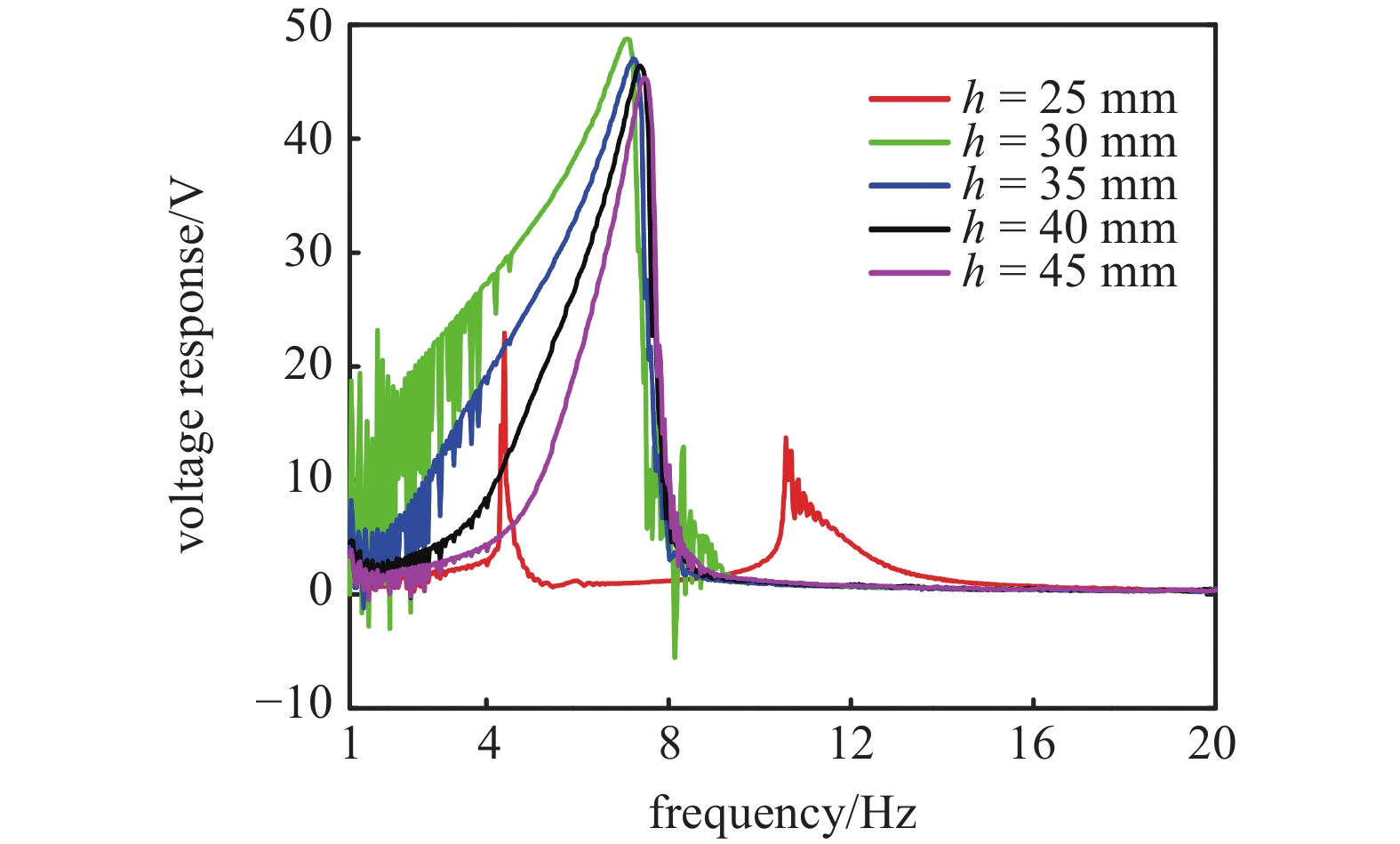
图12给出了竖直距离h对三稳态系统响应电压的影响, h的变化范围从25~45 mm, 间隔为5 mm. 可以看出, 当h为25mm时只产生位移较小的势阱内运动, 因而响应电压较小, 峰值仅为20 V左右, 这可能是由于三稳态势阱较深, 激励不足使系统产生跨越势阱运动. 当h增大为30 mm时, 响应电压的幅值达到最大为48 V左右, 且频带也最宽, 此时系统的势阱较浅, 容易产生跨越势阱运动. 当h从35 mm增大到45 mm时, 系统响应电压的幅值略有下降, 但是俘能频带明显变窄, 效率降低. 这是由于此过程中系统始终为单稳态, 且势阱的宽度会随着h的增大而变窄.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-12.jpg'" class="figure_img
figure_type1 bbb " id="Figure12" />
图
12
竖直距离h对三稳态系统响应电压的影响
Figure
12.
Influence of vertical distance h on tri-stable voltage response
下载: 全尺寸图片
幻灯片
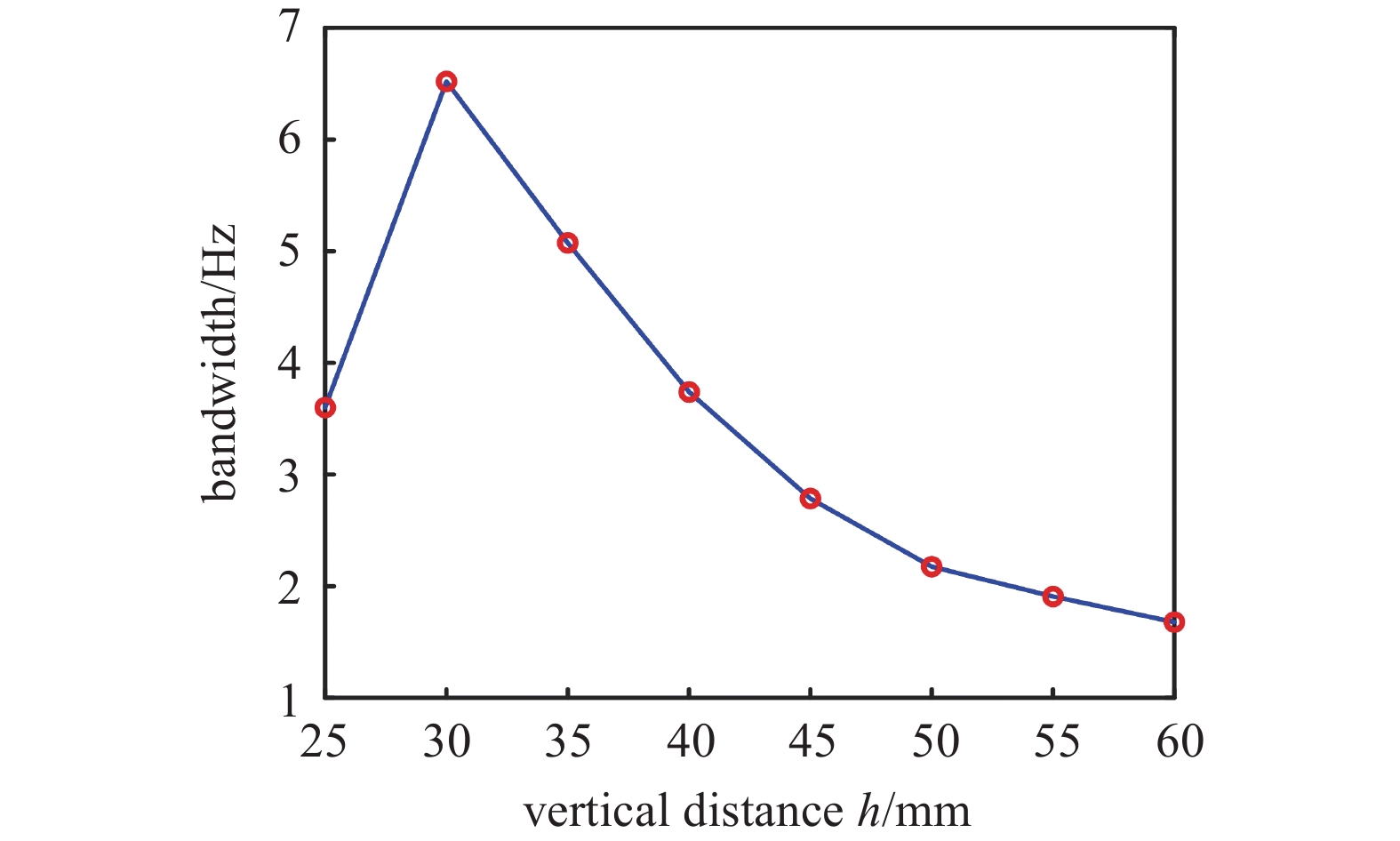
图13所示为竖直距离h对三稳态系统频带的影响, 设定响应电压10 V以上作为有效频带. 由图可知, 当竖直距离h从25 mm增大到30 mm时, 系统的带宽从3.6 Hz增加到6.52 Hz. 此后, 系统的带宽逐渐减小. 当竖直距离h为60 mm时, 系统的带宽为1.679 Hz.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-13.jpg'" class="figure_img
figure_type1 bbb " id="Figure13" />
图
13
竖直距离h对三稳态系统频带影响
Figure
13.
Influence of vertical distance h on bandwidth of tri-stable system
下载: 全尺寸图片
幻灯片
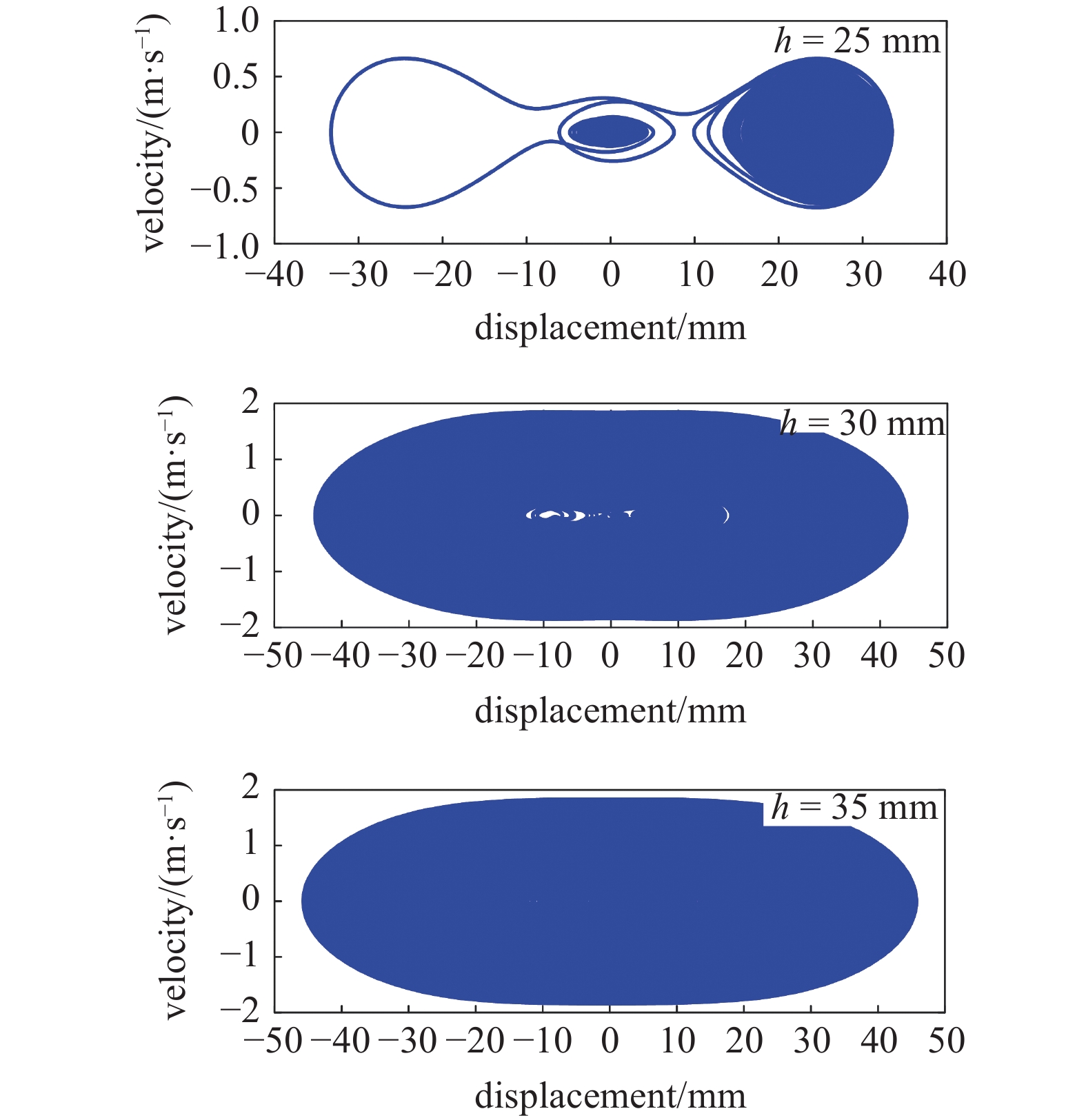
图14给出了不同竖直距离h的三稳态系统相轨迹图. 由图可知, 当竖直距离h为25 mm时, 系统的主要为幅值较小的势阱内运动. 当竖直距离h为30 mm时, 系统主要为跨越3个势阱的大幅值运动. 当竖直距离h为40 mm时, 此时单稳态系统也能产生幅值较大的运动.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-14.jpg'" class="figure_img
figure_type1 bbb " id="Figure14" />
图
14
不同竖直距离h的三稳态系统相轨迹图
Figure
14.
Phase trajectory of tri-stable system under different vertical distance h
下载: 全尺寸图片
幻灯片
3.2.2
水平距离影响
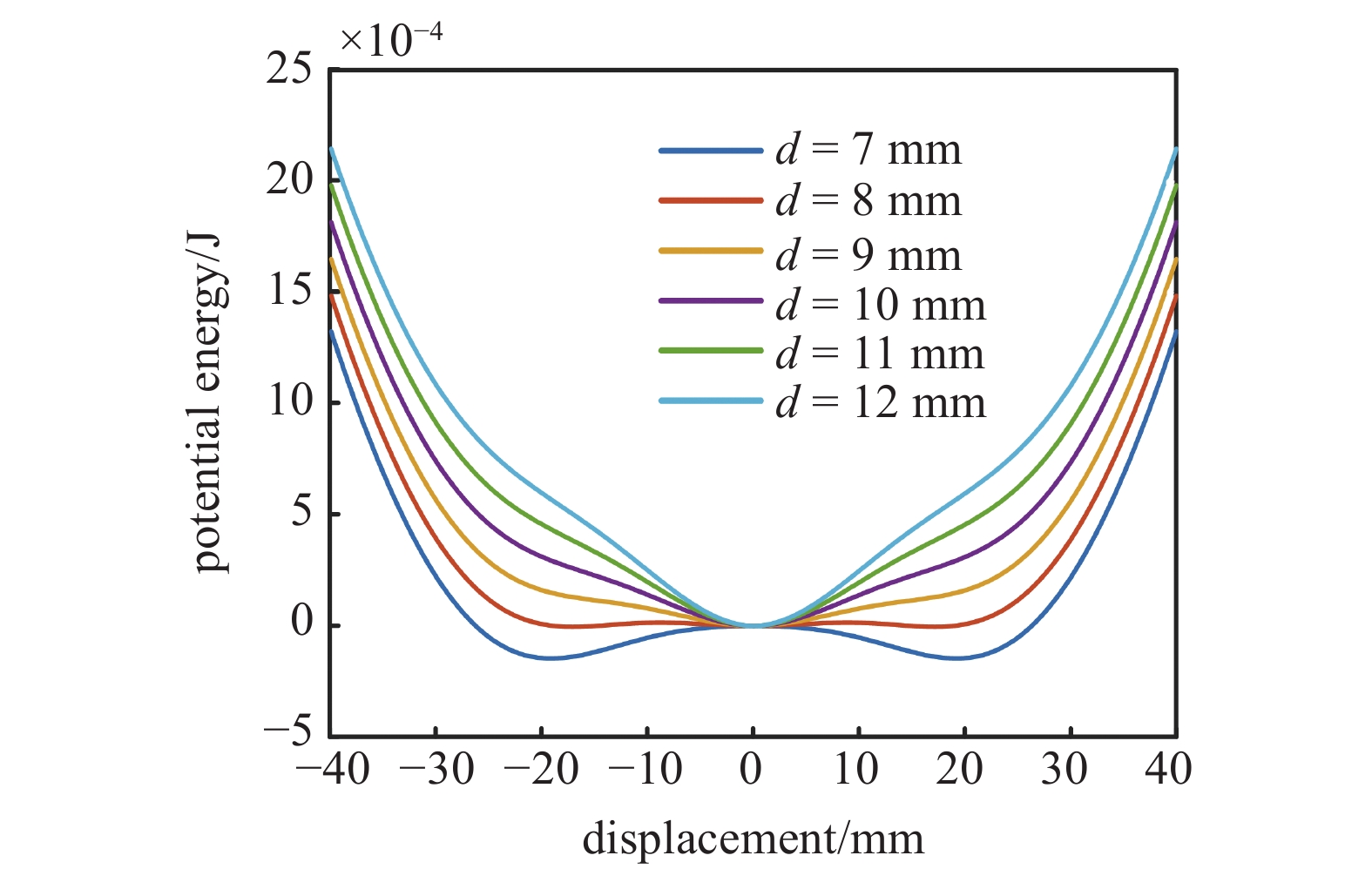
图15为水平距离d对三稳态系统势阱的影响, d从7 mm变化到12 mm. 可以看出, 当d从7 mm增加到8 mm时, 系统始终为三稳态, 内侧势阱较小, 外侧势阱逐渐变浅. 随着d增大到9 mm时, 系统变为单稳态. 当d继续增大时, 系统依然为单稳态系统, 且势阱宽度越来越窄. 因此, 三稳态系统的临界位置处于d从8~9 mm之间.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-15.jpg'" class="figure_img
figure_type1 bbb " id="Figure15" />
图
15
水平距离d对三稳态系统势阱的影响
Figure
15.
Influence of horizontal distance d on tri-stable potential well
下载: 全尺寸图片
幻灯片
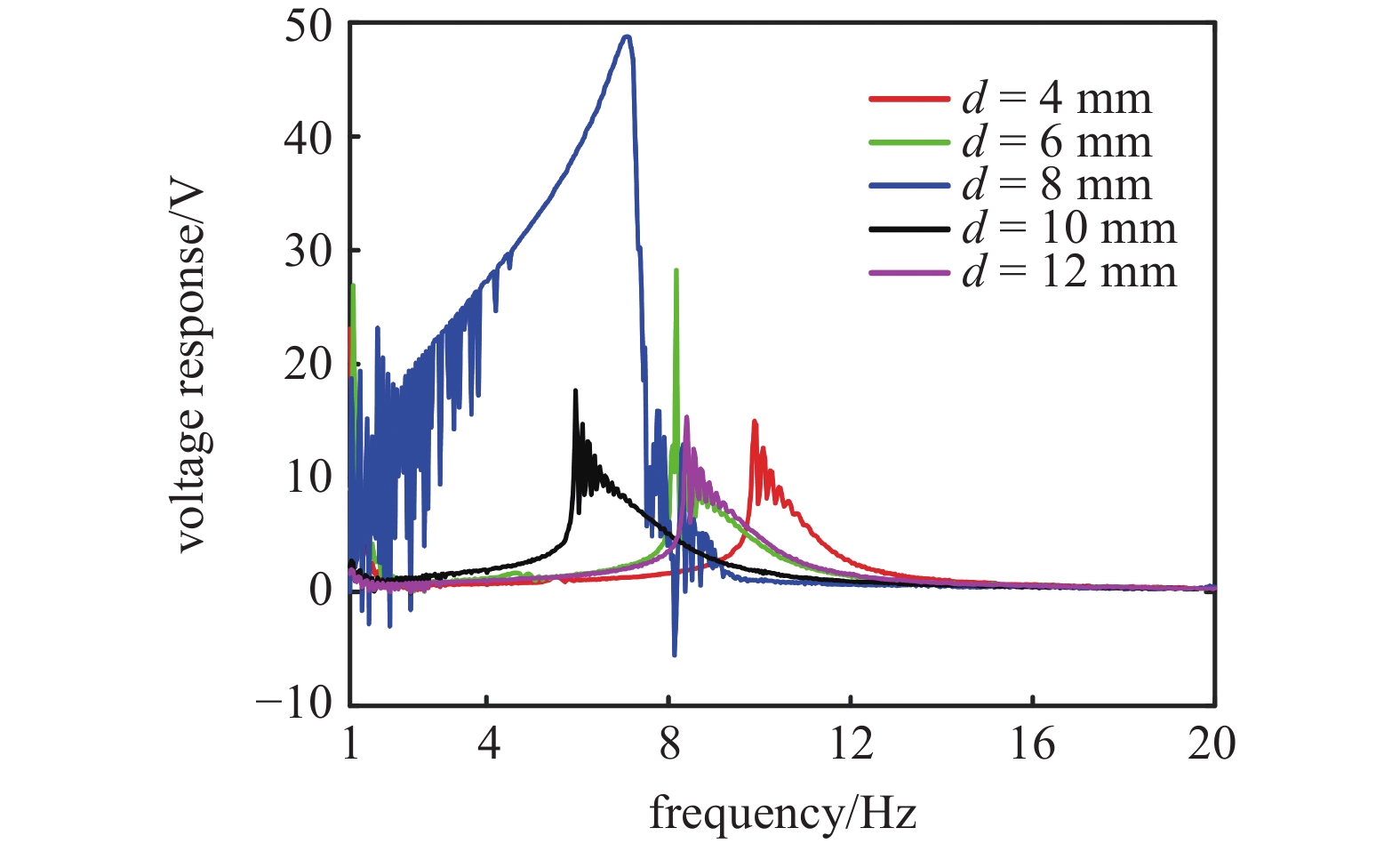
图16给出了水平距离d对三稳态系统响应电压的影响, d的变化范围从4~12 mm, 间隔为2 mm. 可以看出, 当d为4 mm和6 mm时, 系统的响应电压较小, 峰值仅为16 V和28 V左右, 且频带较窄. 这可能是此时三稳态系统的势阱较深, 难以产生跨势阱的运动. 当d增大为8 mm时, 响应电压的幅值达到最大为48 V左右, 且频带也最宽, 此时由于三稳态系统的势阱较浅, 容易产生跨越势阱运动. 当d继续从10 mm增大到12 mm时, 系统响应电压较低, 但是俘能频带明显变窄. 这是由于此过程中系统始终为单稳态, 且势阱的宽度会随着d的增大而变深且变窄.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-16.jpg'" class="figure_img
figure_type1 bbb " id="Figure16" />
图
16
水平距离d对三稳态系统响应电压的影响
Figure
16.
Influence of horizontal distance d on tri-stable voltage response
下载: 全尺寸图片
幻灯片
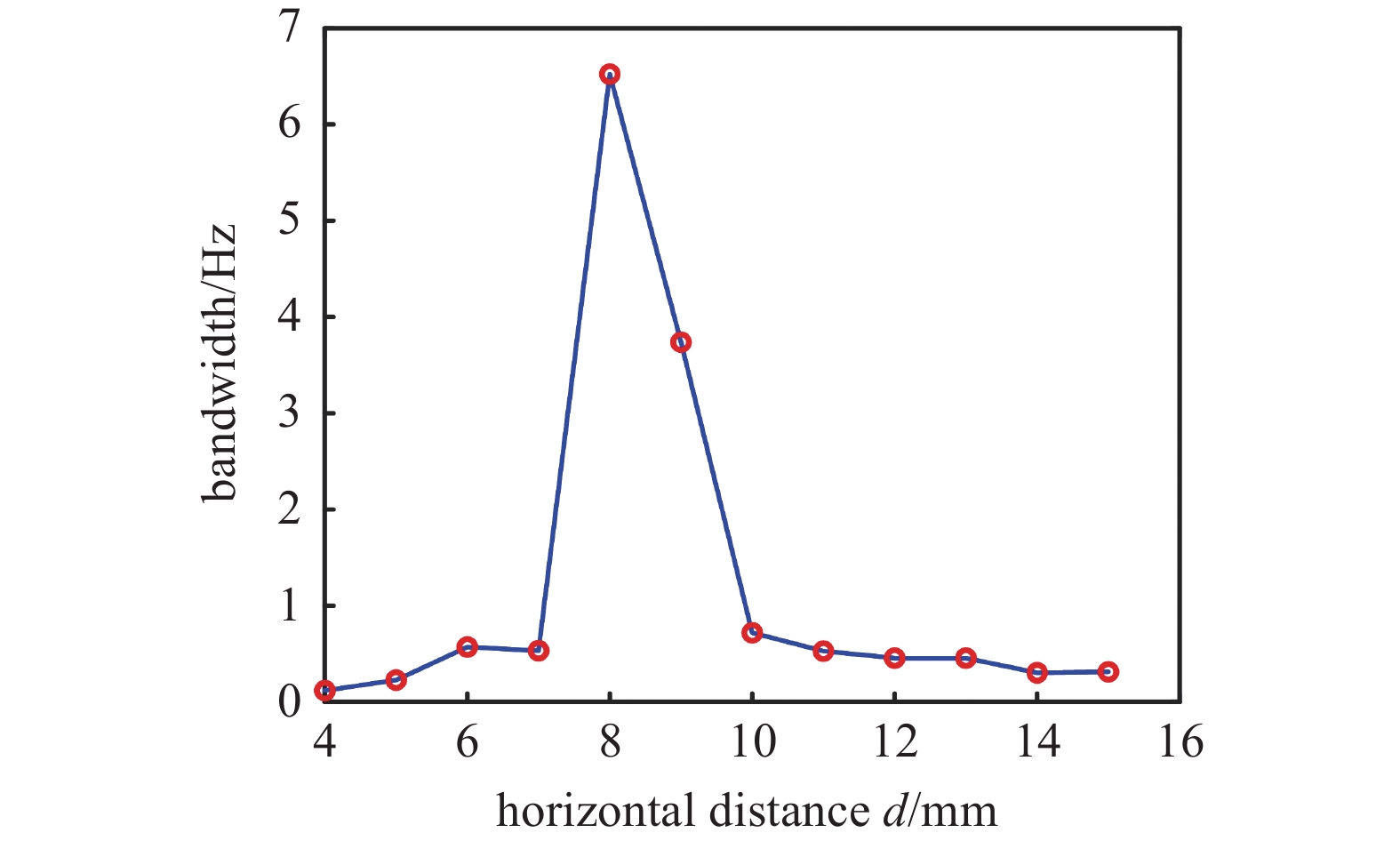
图17所示为水平距离d对三稳态系统频带的影响, 设定响应电压10 V以上作为有效频带. 由图可知, 当水平距离d从7 mm增大到8 mm时, 系统的带宽从0.534 Hz增加到6.524 Hz. 此后, 系统的带宽下降很快. 当水平距离d为10 mm时, 系统的带宽仅为0.72 Hz.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-17.jpg'" class="figure_img
figure_type1 bbb " id="Figure17" />
图
17
水平距离d对三稳态系统频带影响
Figure
17.
Influence of horizontal distance d on bandwidth of tri-stable system
下载: 全尺寸图片
幻灯片
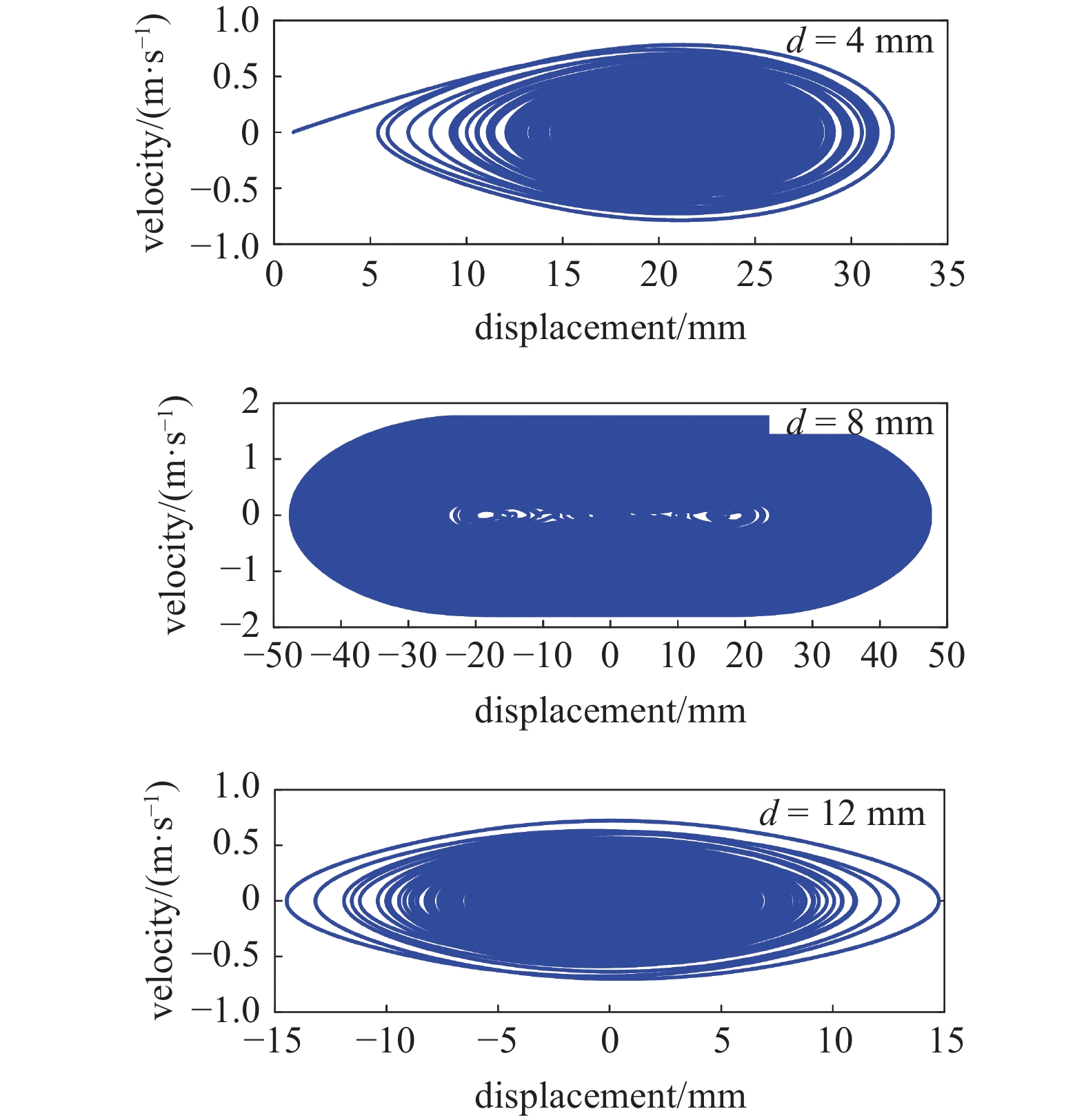
图18给出了不同水平距离d的三稳态系统相轨迹图. 由图可知, 当水平距离d为4 mm时, 系统为幅值较小的势阱内运动. 当水平距离d为8 mm时, 系统主要为跨越3个势阱的大幅值运动. 当水平距离d为12 mm时, 此时单稳态系统为幅值较小的运动.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-18.jpg'" class="figure_img
figure_type1 bbb " id="Figure18" />
图
18
不同水平距离d的三稳态系统相轨迹图
Figure
18.
Phase trajectory of tri-stable system under different horizontal distance d
下载: 全尺寸图片
幻灯片
3.2.3
参数优化
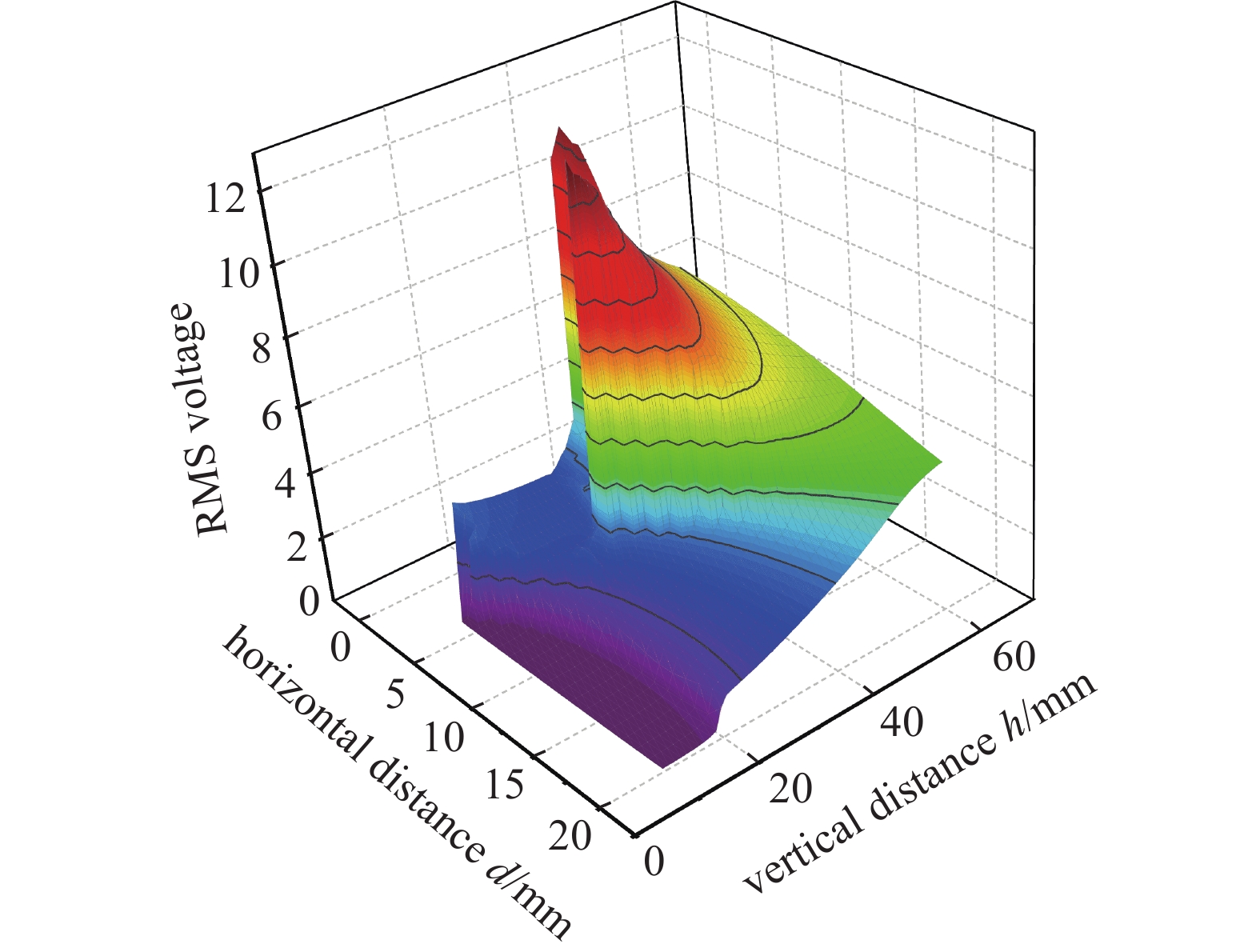
为了获取三稳态系统最优的结构参数, 对竖直距离h和水平距离d进行了参数扫描得到了图19所示均方电压的变化规律, h的变化范围为10~60 mm, d的变化范围为1~20 mm, 间隔都为1 mm. 由图可知, 随着h地增大, 均方电压刚开始增长比较缓慢, 但是当到达某个值后会出现突然地增加, 然后在呈现逐渐下降的趋势. 而当d增加时, 均方电压呈现较缓的上升趋势, 然后再逐渐下降. 此外, 当d为8 mm且h为28 mm时, 系统的最大均方电压为12.7 V.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-446-19.jpg'" class="figure_img
figure_type1 bbb " id="Figure19" />
图
19
三稳态系统参数优化
Figure
19.
Parameters optimization of tri-stable system
下载: 全尺寸图片
幻灯片
4.
结 论
针对多稳态系统结构设计与参数优化困难的问题, 提出了一种多稳态俘能系统的准确磁力建模方法. 通过计算多稳态系统中端部磁铁和外部磁铁的相对距离和相对转角推导了磁铁间的相对位置, 采用磁荷理论建立了系统的非线性磁力模型. 通过实验验证了本方法预测非线性磁力的准确性, 双稳态系统和三稳态系统的磁力峰值误差分别仅为4.3%和6.49%.
此外, 基于本方法探究了多稳态系统结构参数对系统势能和响应电压的影响机理, 找出了双稳态系统和三稳态系统的临界位置, 同时优化结构参数得到了最优输出性能. 首先, 对于双稳态系统, 随着竖直距离h增大, 双稳态会变为单稳态, 临界位置在h为36~38 mm之间, 且当h为34 mm时存在最大均方电压为10.22 V. 其次, 对于三稳态系统, 随着竖直距离h增大, 三稳态会变为单稳态, 临界位置在h为30~32 mm之间; 随着水平距离d增大, 三稳态会变为单稳态, 临界位置在d为8~9 mm之间. 当d为8 mm且h为28 mm时, 系统最大均方电压为12.7 V.
由于实际多稳态俘能系统往往具有确定的材料参数和外界激励, 基于提出的模型可以针对性地优化其结构参数. 首先基于本模型可以预测系统的非线性恢复力以及势阱, 然后通过求解系统非线性动力学方程得到响应电压的幅值和频带. 因此, 在给定激励谱条件下, 以响应电压幅值和带宽为优化目标, 可以优化竖直距离和水平距离等结构参数.
