引 言

能量的循环利用已经成为世界范围内具有重大意义的科学难题. 与此同时, 能量收集已经成为一种新兴的技术, 它可以将环境中冗余的能量转换为电能, 在微电子设备的自供能设计领域有着不可限量的应用前景, 受到国内外研究者的广泛关注^[1-3].

风能是一种常见的能源, 风力发电机是一种典型的能量转化装置, 可用于实现风能至电能转化. 但是风力发电机运行过程中会产生强烈的噪音, 并且对强风有较大的依赖性, 以上缺点限制其在人口密度较高地区的运行^[4]. 作为传统涡轮机的替代品, 流致振动能量收集装置也可将环境中的低速风能转化为电能, 按照流固耦合的作用机理可以分为抖振^[5-6]、涡激振动^[7-8]、驰振^[9-10]和尾流驰振^[11-12]. 由于实施方案的便利性, 近年来基于涡激振动与驰振的能量收集装置得到了广泛研究. 它们的结构设计都利用了流场和钝头体之间的不稳定的流固耦合作用. 涡激振动能量收集装置大都采用圆形截面的钝头体, 它只在特定的流速范围内产生较大位移, 然而当风速超过这一范围, 能量收集效果将会急剧地下降^[13-14]. 驰振能量收集装置的钝头体大都采用带有棱角的截面, 如矩形、三角形和D形等, 响应幅值随着风速的增加而增大. 然而驰振式能量收集装置只有在环境风速高于切入风速时才会有较好的能量收集效果, 在低风速下的能量收集特性还有待进一步提升^[15].

为了提高流致振动能量收集效果, 研究者提出了一系列方案, 包括钝头体优化^[16-17]、引入非线性^[18-25]以及多自由度的多模态阵列^[26-28]. 除此之外, 一些研究者开始聚焦于将涡激振动和驰振的优势结合起来, 提出了复合式流致振动能量收集装置^[29-31]. Sun 等^[32]提出了一种灯泡状的钝头体, 通过结合涡激振动和驰振的优势, 提升了能量收集效果. Qin 等^[33]使用十字梁将圆柱和两个长方体连接起来形成复合式钝头体, 充分发挥涡激振动和驰振在能量收集方面的优势, 拓宽了有效工作流速范围. Wang 等^[34]按照一定比例合成了矩形截面和圆截面的等长棱柱, 提出了一类复合式截面的钝头体, 开展了一系列的理论分析与实验验证. 研究结果表明他们所提出的装置能综合涡激振动和驰振的优势, 既能降低切入风速, 又能有效拓宽工作流速范围.

以往研究中, 尽管已经证明通过复合式钝头体可以提升能量收集效果, 但经典钝头体的宽度和厚度通常被认为是恒定的, 钝头体宽厚比因素没有进行深入的探讨. 本文考虑截面分别为矩形、三角形和D形的3种钝头体, 通过比较风速?电压曲线分析不同宽厚比时的能量收集效果, 探究了宽厚比对流致振动的影响机理. 为了深入研究流致振动能量收集装置中的钝头体宽厚比的几何尺寸效应, 本文开展了风洞实验和计算流体动力学仿真, 具体包括响应对比、参数分析以及内在力学机理解释, 以期为流致振动能量收集的动力学性能优化提供理论依据以及参考数据.

1.
模型描述

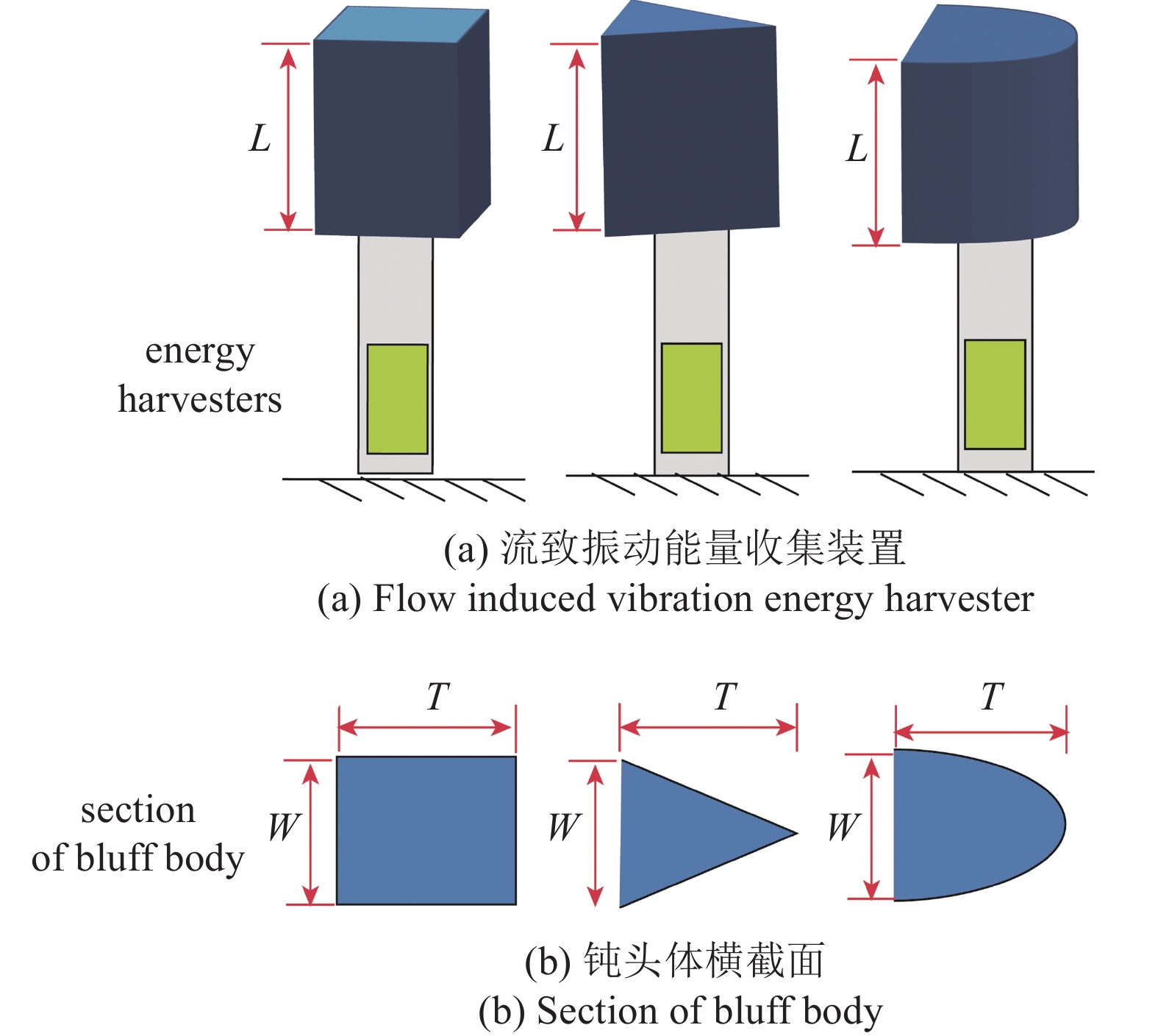
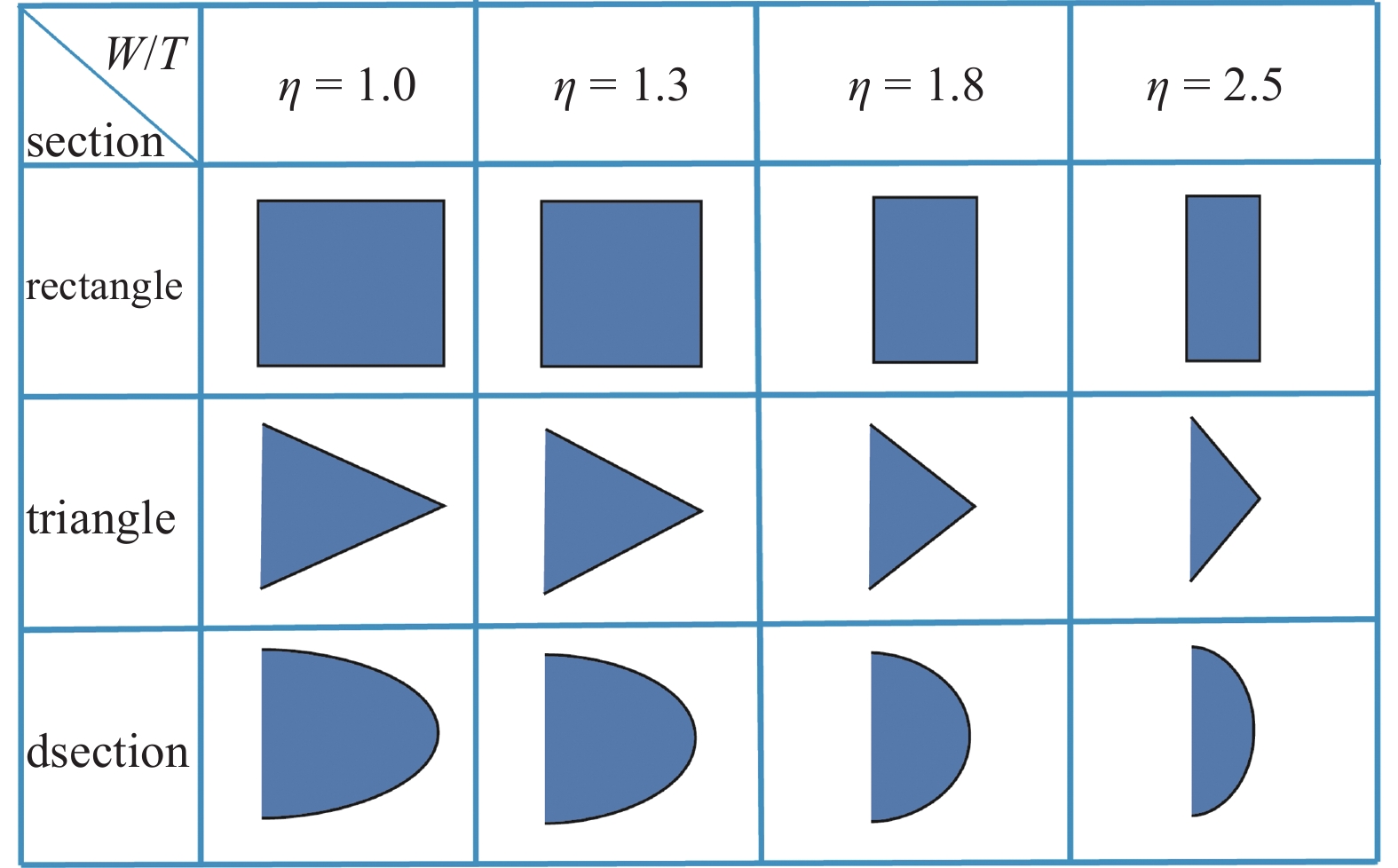
图1(a) 给出了三种截面钝头体的流致振动能量收集装置示意图. 三个能量收集装置均由悬臂式压电梁和钝头体连接而成. 三种钝头体截面分别为矩形、三角形和D形, 截面的分布会影响气动布局以及引起不同的气动特性. 如图1(b)所示, W和T分别为钝头体截面的宽度和厚度. L_b, W_b和h_b分别为压电悬臂梁的长度、宽度和厚度. 图2给出了宽厚比(η =W/T ) 分别为1, 1.3, 1.8和2.5时的钝头体截面形状. 当宽厚比为1时, 意味着钝头体的截面在横轴和纵轴的投影相等. 尽管改变钝头体的宽厚比虽然不影响钝头体迎风面的面积, 但是会影响作用在结构上的尾流轨迹以及气动力. 为了揭示钝头体几何尺寸效应对能量收集的影响规律, 得到有益于能量收集的宽厚比参数, 下面将开展全面的风洞测试实验研究.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
压电能量收集装置3D 效果示意图



Figure
1.
Schematic diagram of piezoelectric energy harvester with different bluff body



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
驰振能量收集实验测试中采用的3种钝头体类别以及宽厚比



Figure
2.
Three types of bluff body and width to thickness ratios used in flow-induced vibration energy harvesting tests



下载:
全尺寸图片
幻灯片

2.
实验平台搭建

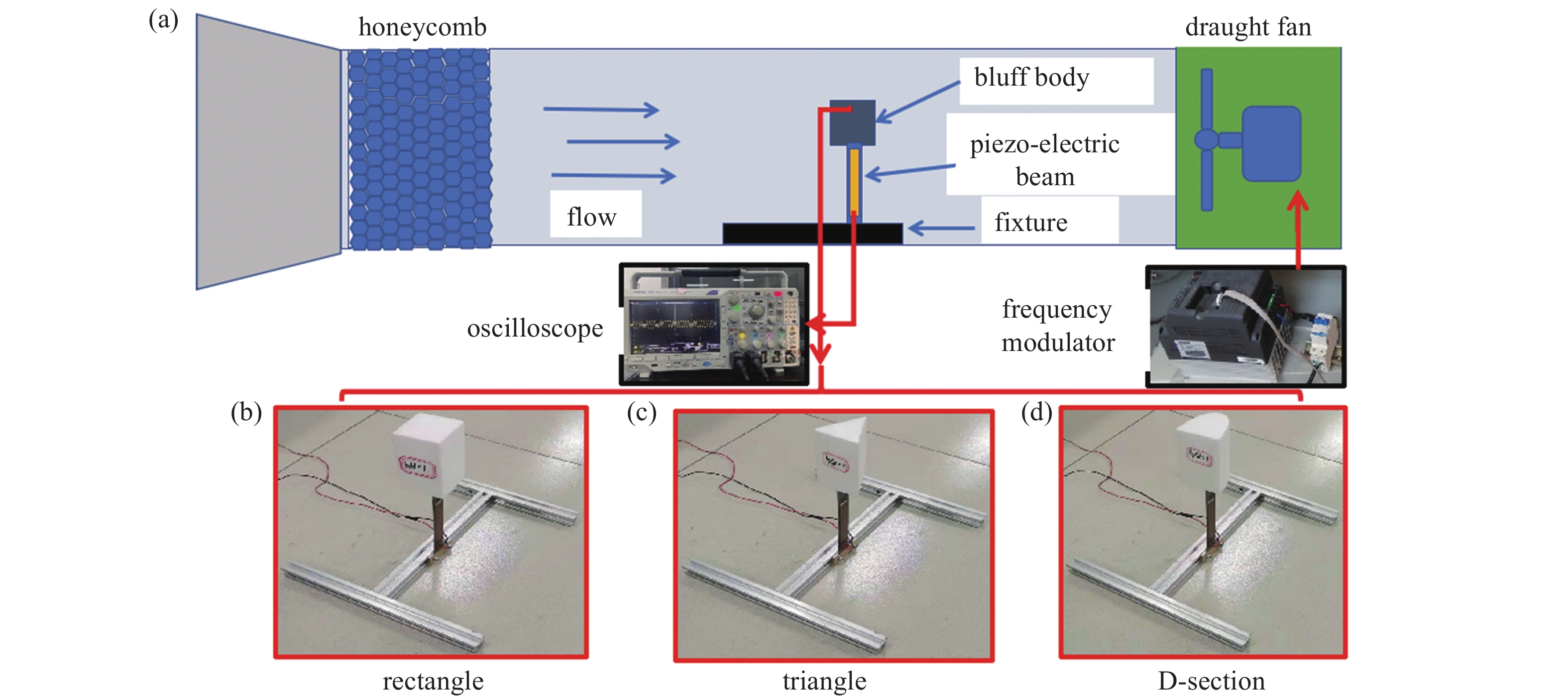
图3 给出了风洞实验装置平台以及宽厚比为1时3种钝头体情形下的流致振动能量收集装置实验试件. 如图所示, 3种钝头体的截面分别为矩形、三角形和D形. 本实验中, 钝头体、悬臂梁和压电片分别由硬度较高的泡沫、锰钢和MFC (MFC: macro fiber composite, M8514-P2, smart material corp)组成. 钝头体的长度 L = 80 mm, 宽度W = 49 mm. 悬臂梁的尺寸L_b × W_b × h_b = 124 mm× 20 mm × 1 mm. 实验测得MFC的尺寸为L_p × W_p × h_p = 85 mm× 14 mm × 0.5 mm, 电容为138 nF.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-3.jpg'"
class="figure_img
figure_type2 ccc " id="Figure3" />



图
3
(a)风洞实验平台搭建, (b)矩形钝头体, (c)三角形钝头体, (d) D形钝头体



Figure
3.
(a) The setup of wind tunnel test. (b) Bluff body with rectangle section. (c) Bluff body with triangle section. (d) Bluff body with D-shape section



下载:
全尺寸图片
幻灯片


风洞由直径为40 cm的亚克力管制作, 由收缩段、工作段和风机三个部分构成. 风机转动时, 环境风场将从收缩段进入到风洞. 收缩段和工作段之间安装有蜂窝器, 可将环境中紊乱的流场稳定为均匀来流. 风机的转速与风速的大小可以通过调频器控制, 两者呈现成正相关关系, U = 0.4f (其中U表示风速, f表示频率). 压电片产生的电压信号由数字示波器(Tektronix, MDO3040)记录. 在下列3种对比实验中, 示波器记录了40 s的稳态电压(共计10⁶个数据点), 随后计算了电压时间序列的均方根.

3.
实验结果讨论

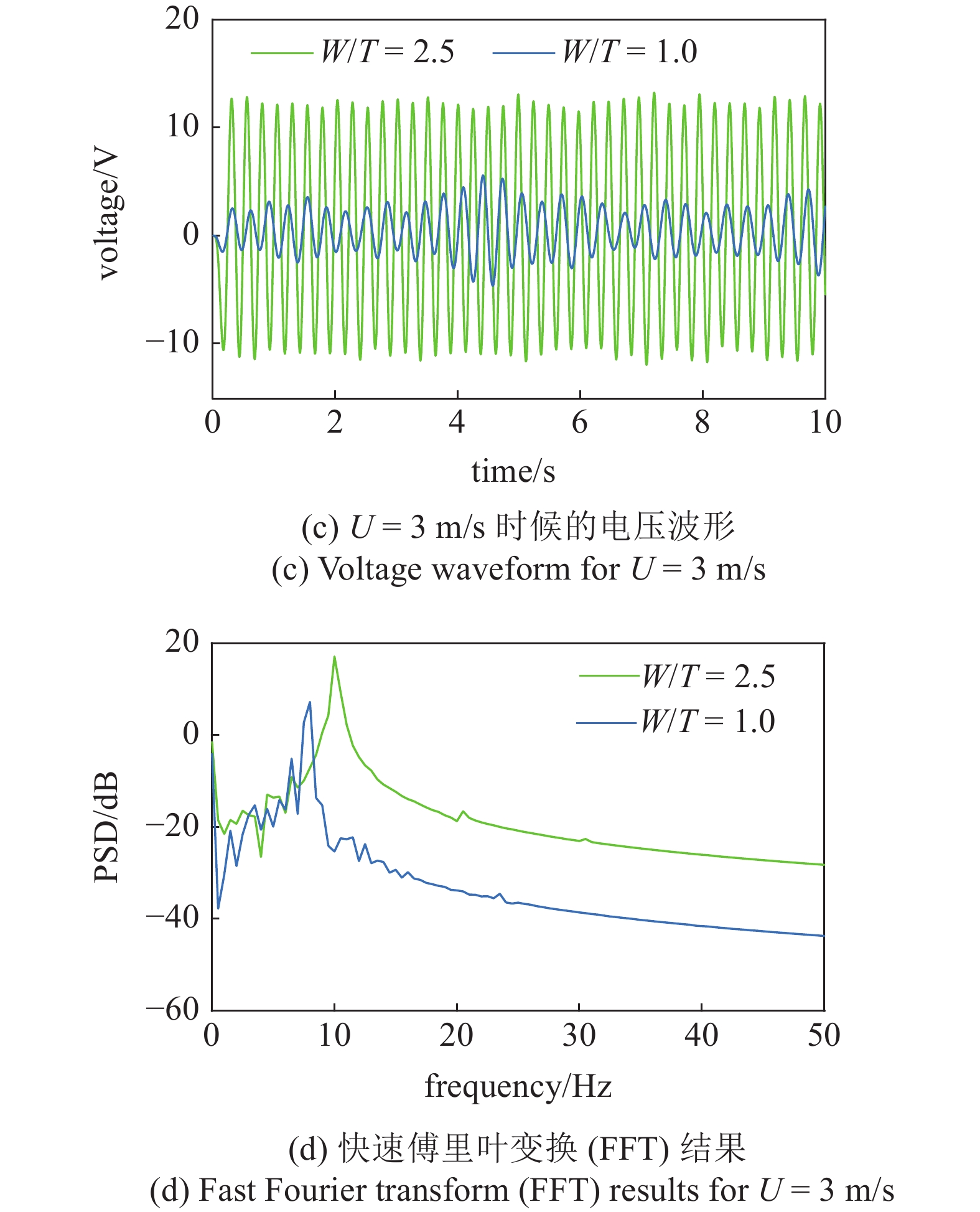
图4是截面为矩形状钝头体的风洞实验结果, 包括性能对比、参数研究和特定风速下的时程分析. 图4(a)和图4(b)给出了不同宽厚比的方形截面钝头体的位移和均方电压对比. 结果表明矩形截面在不同的宽厚比时都将会引起驰振响应, 宽厚比分别为W/T = 1, 1.3, 1.8, 2.5 时的切入风速都在U = 2.4 m/s 附近, 但是响应幅值将会随着宽厚比的增加而逐渐增大, 最大均方电压将达到20.86 V, 24.60 V, 27.57 V 和 30.04 V. 因此通过调整钝头体宽厚比可以显著改善低风速下的能量收集效果. 为了更好地展示流致振动力学响应, 图4(c)和图4(d)分别展示了U = 3 m/s时两种宽厚比 (W/T = 1和W/T = 2.5)时候的时域响应以及通过快速傅里叶变换(FFT)得到的频域响应. 可以看出在U = 3 m/s时, 宽厚比为W/T = 2.5时的响应幅值明显大于W/T = 1时的响应. 从频谱图中可以看出当宽厚比从1增加至2.5, 振动响应频率会从8.5 Hz增加至10 Hz, 并且响应幅值表现出良好的周期特性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-4-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
钝头体截面为正方形时的风洞测试结果



Figure
4.
Wind tunnel test results for a energy harvester with rectangular section bluff body



下载:
全尺寸图片
幻灯片


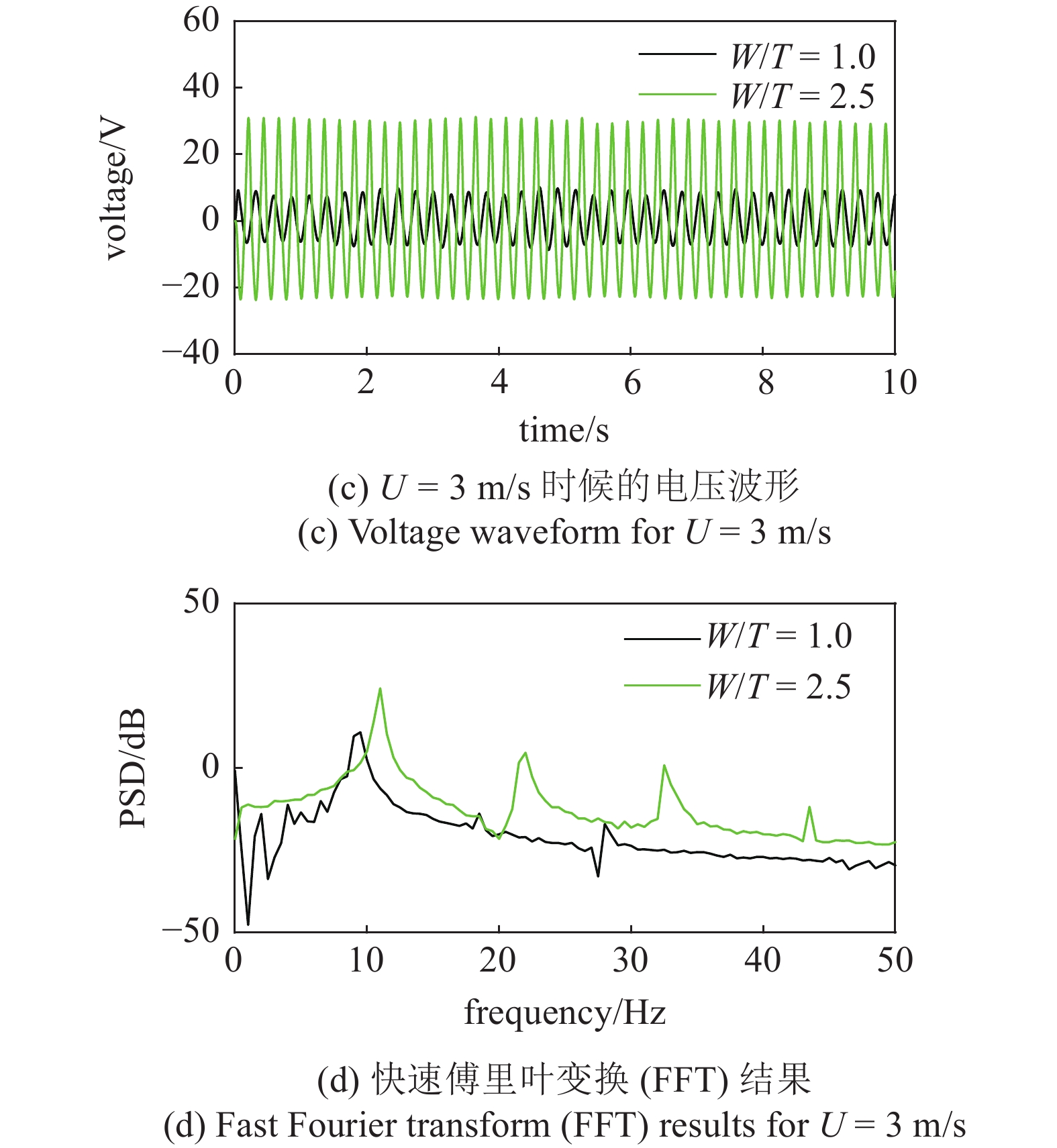
图5 给出了钝头体截面为三角形时的风洞测试结果, 包括风速参数的影响分析以及特定风速的时域响应和频域响应. 图5(a)给出了W/T分别为1和2.5时候在不同风速下的位移结果, 可以看出系统在两种宽厚比时表现出两种截然不同的流固耦合振动特性. 当W/T=1时, 系统表现出驰振响应特性, 切入风速为2.6 m/s; 当W/T增大至2.5时, 系统表现涡激振动(VIV)响应特性, 在风速范围U=2.4 m/s~3.6 m/s内明显高于W/T=1时的响应幅度.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-5-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
钝头体截面为三角形时的风洞测试结果



Figure
5.
Wind tunnel test results for a energy harvester with rectangular section bluff body



下载:
全尺寸图片
幻灯片


为了全面了解宽厚比对能量收集效果的影响规律, 图5(b)给出了W/T分别为1, 1.3, 1.8和2.5时流致振动能量收集装置的输出电压. 从风速?电压结果可以看出三角形截面钝头体与矩形截面钝头体对系统响应的影响随宽厚比的变化规律具有明显的差别: 随着宽厚比的增加, 系统的响应呈现“驰振”→“驰振 + 涡激振动”→“涡激振动”响应特性变化趋势. 由于涡激振动响应的出现, 系统在较低流速范围内响应开始优于单独基于驰振的能量收集系统. 图5(c)和图5(d)展示了风速为U = 3 m/s 时两种宽厚比情形 (W/T = 1和W/T = 2.5)的时域响应以及频域响应. 从频谱图中可以看出两种振动响应都表现出良好的周期特性, 并且随着W/T的增加, 钝头体结构体积与质量都会减小, 导致振动响应频率会升高.

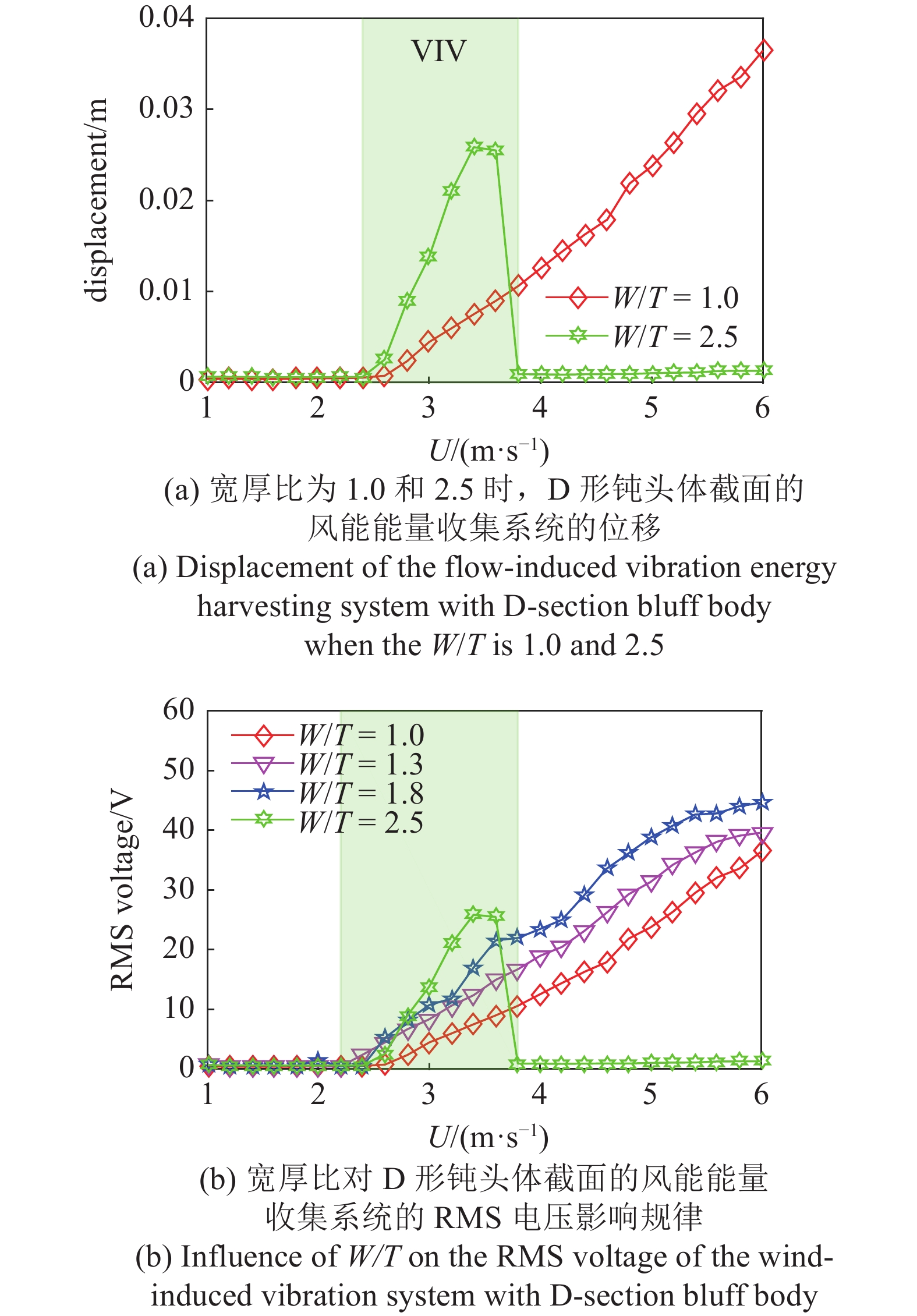
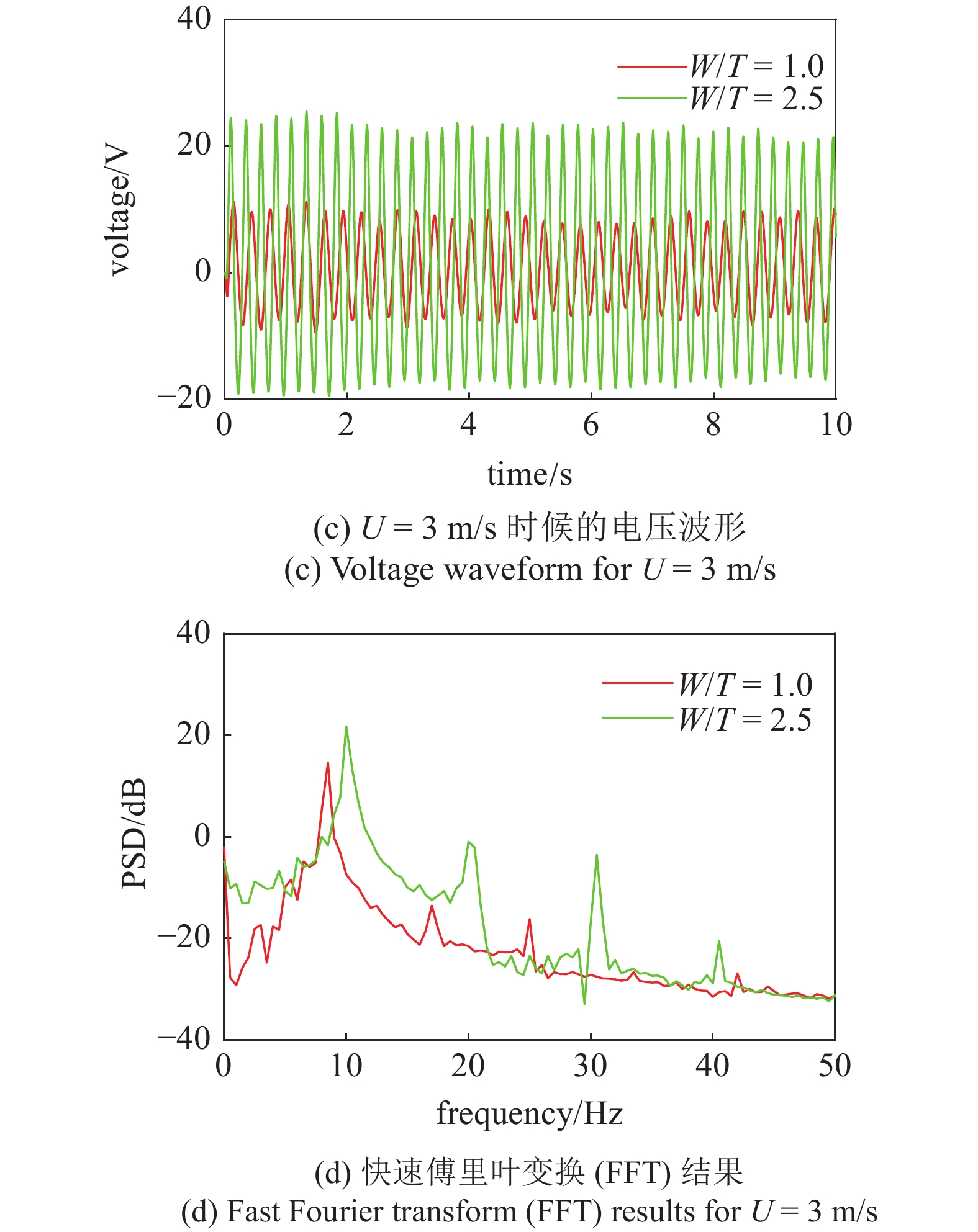
图6给出了钝头体截面为D形时的风洞测试结果, 包括风速参数的影响分析以及特定风速的时域响应和频域响应. 如图6(a)所示, W/T为1时与W/T为2.5时展现出两种完全不同的流致振动响应. D形钝头体的W/T为1时, 系统响应展现出驰振动力学特性; 当W/T增加至2.5, 在风速范围U = 2.4 m/s~3.8 m/s内展现出涡激振动动力学特性. 图6(b)给出了宽W/T分别为1, 1.3, 1.8和2.5时, 流致振动能量收集装置在不同风速下的输出电压. 可以看出, 除了W/T为2.5外, 其他情形的钝头体在U=1 m/s~6 m/s风速范围内只呈现出驰振动力学响应, 各个风速时电压幅值与宽厚比呈现正相关关系. 在VIV区域范围内, W/T为2.5的钝头体内响应优于宽厚比分别为1, 1.3和1.8的输出电压; 而在U>3.6 m/s的高风速范围内, 它由于受到锁频范围的限制, 性能不如驰振能量收集系统. 图6(c)和图6(d)给出了风速为3 m/s 时宽W/T = 1与W/T = 2.5时的时域响应以及频域响应. 当W/T = 1时, 振动响应展现出频率为8.5 Hz的单倍周期特性; 而当W/T分别为2.5时, 振动响应仍然呈现周期特性, 但耦合频率增加为10 Hz.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-6-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
钝头体截面为D形时的风洞测试结果



Figure
6.
Wind tunnel test results for a energy harvester with D-section bluff body



下载:
全尺寸图片
幻灯片

4.
基于计算流体力学模拟

为了进一步验证上述能量收集结果的发生机理, 探究钝头体宽厚比对流致振动能量收集效果的影响规律, 本节通过COMSOL软件中计算流体动力学模块开展了一系列的计算流体力学(compu-tational fluid dynamic, CFD)模拟. 模拟的风速设置为U = 3 m/s, 计算流场的范围为 120 cm × 60 cm, 共划分了13448个网格.

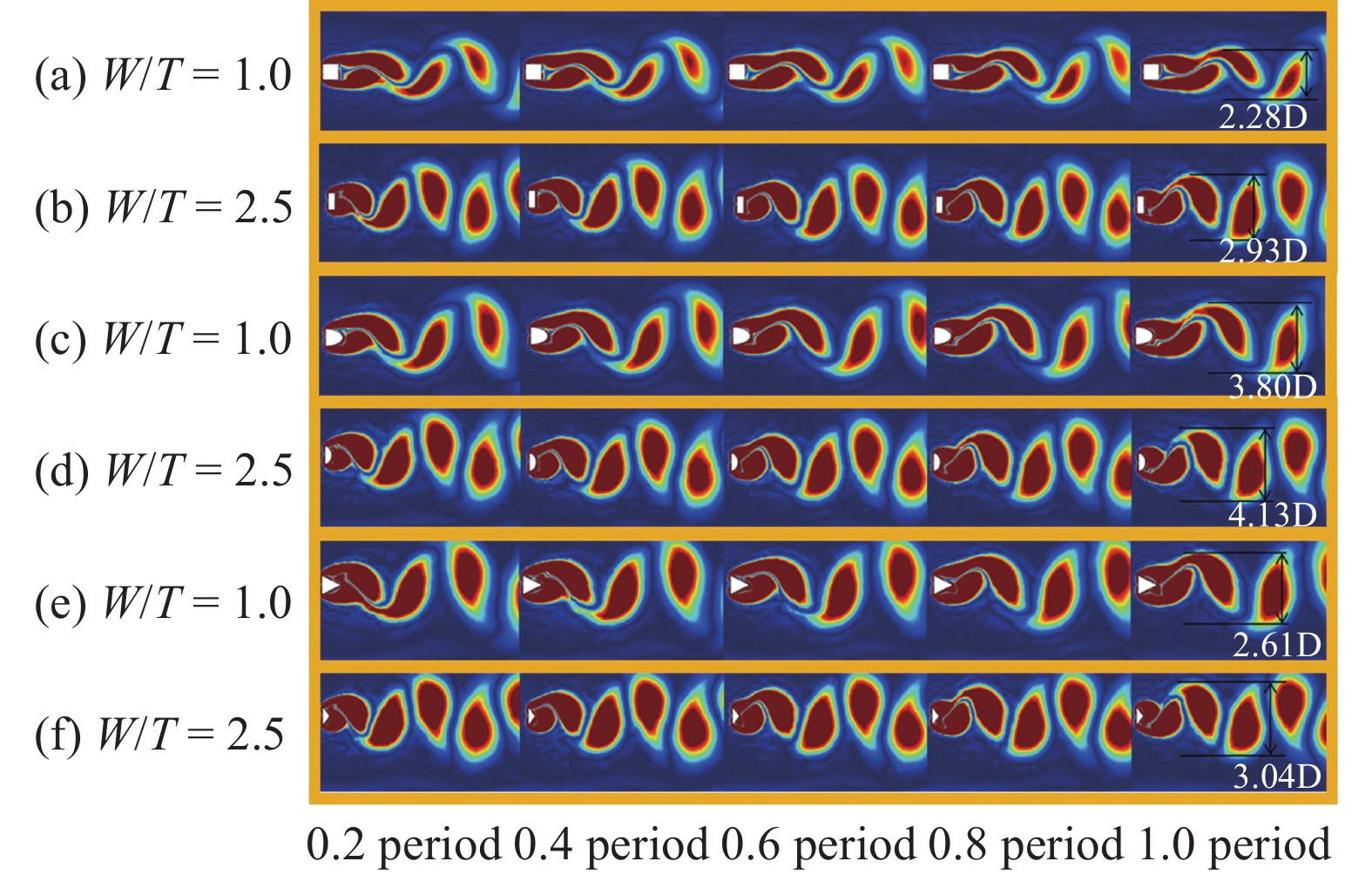
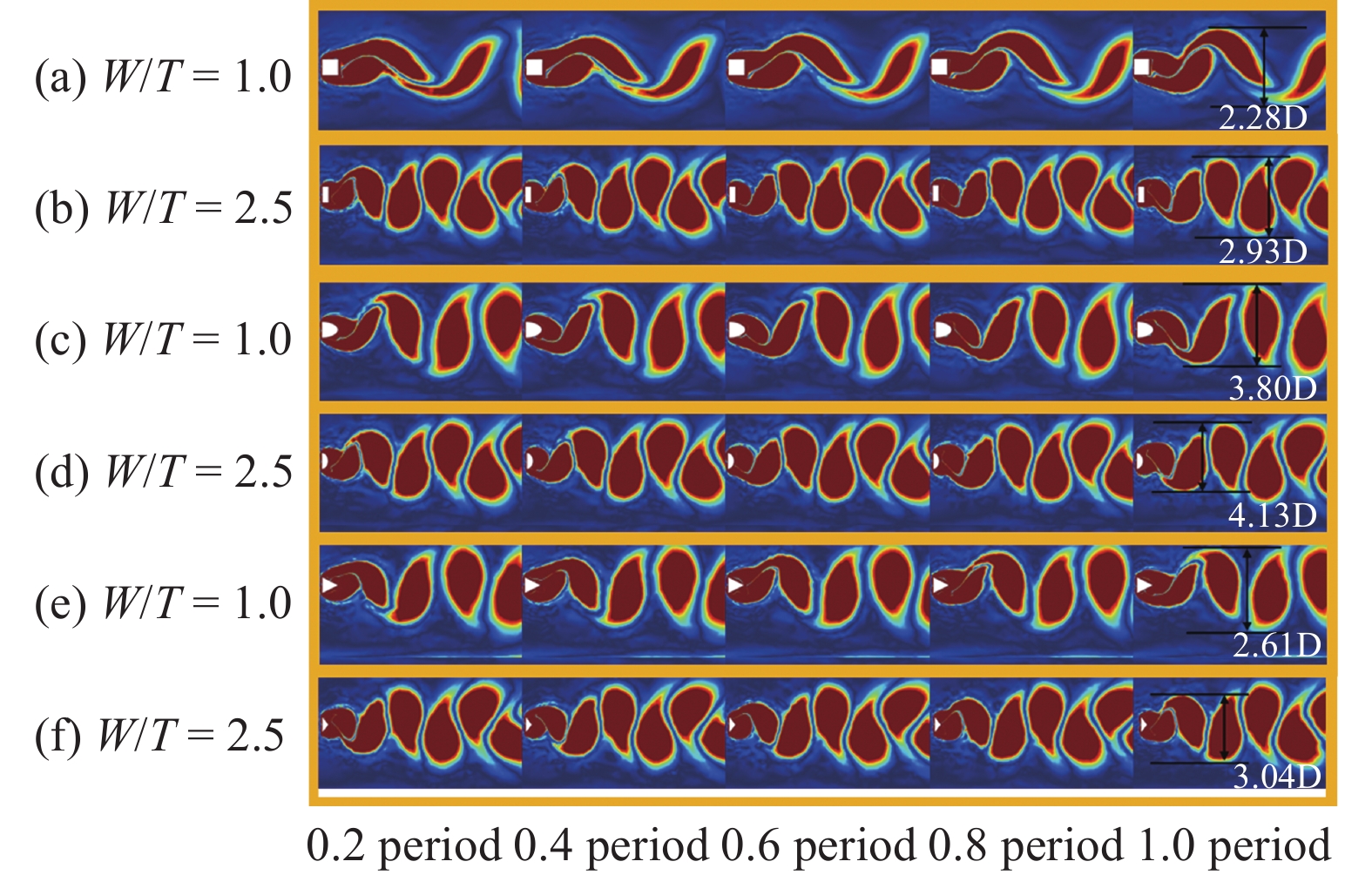
图7和图8分别给出了 U = 3 m/s 和 U = 6 m/s 时CFD 模拟结果. 为了定量描述涡街力的强弱, 表1比较分析了尾流涡街的宽度对能量收集效果的影响规律. 首先定义尾流涡街的宽度Wv, 它表示在5D (D为钝头体迎风面的宽度)尾流涡街的范围之内, 包含区域内所有独立的涡街的最大距离. 当Wv较大时, 意味着气动不稳定性引发的尾流涡街更加剧烈, 最终会诱发压电梁产生更加强劲的振动响应, 得到更高的能量收集转化效率. 通过对比图7(a)和图7(b)可知, 增加宽厚比可以在尾流处产生更加剧烈的涡. W/T = 2.5时尾流处的涡个体相比W/T = 1时候更大, 因此它产生的涡街力更加强劲. 可以看出当W/T = 1时, 截面为矩形、三角形和D形的钝头体所产生的尾流涡街的宽度Wv分别为2.28D, 3.80D 和2.61D, 而当W/T增大至2.5时, 尾流涡街的宽度分别为2.93D, 4.13D和3.04D, 同比增加了28.51%, 8.56%和17%. 因此, 增加宽厚比可以改善流致振动能量收集结构的气动特性, 提高低流速区域的风能收集效果.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
U = 3 m/s 时CFD 模拟. (a) W/T = 1时的矩形钝头体; (b) W/T = 2.5矩形钝头体; (c) W/T = 1时的D形钝头体; (d) W/T = 2.5的D形钝头体; (e) W/T = 1的三角形钝头体; (f) W/T = 2.5的三角形钝头体



Figure
7.
CFD simulation for U = 3 m/s. (a) The rectangular bluff body at W/T = 1; (b) The rectangular bluff body at W/T = 2.5; (c) The D-shape bluff body at W/T = 1; (d) The D-shape bluff body at W/T = 2.5; (e) The triangular bluff body at W/T = 1; (f) The triangular bluff body with W/T = 2.5



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
U = 6 m/s 时CFD 模拟. (a) W/T = 1时的矩形钝头体; (b) W/T = 2.5矩形钝头体; (c) W/T = 1时的D形钝头体; (d) W/T = 2.5的D形钝头体; (e) W/T = 1的三角形钝头体; (f) W/T = 2.5的三角形钝头体



Figure
8.
CFD simulation for U = 6 m/s. (a) The rectangular bluff body at W/T = 1; (b) The rectangular bluff body at W/T = 2.5; (c) The D-shape bluff body at W/T = 1; (d) The D-shape bluff body at W/T = 2.5; (e) The triangular bluff body at W/T = 1; (f) The triangular bluff body with W/T = 2.5



下载:
全尺寸图片
幻灯片





表
1
不同风速和不同钝头体截面的涡街宽度



Table
1.
The widths of vortex street (Wv) of different wind speeds and different sections of bluff body



table_type1 ">

Section		U = 3 m/s	U = 6 m/s
rectangle	W/T = 1	2.28 D	4.32 D
	W/T = 2.5	2.93 D	4.75 D
D-shape	W/T = 1	2.61 D	4.62 D
	W/T = 2.5	3.04 D	3.78 D
triangle	W/T = 1	3.80 D	4.94 D
	W/T = 2.5	4.13 D	3.56 D

下载:
导出CSV
|显示表格



通过对比图8(a)和图8(b)可知, 当风速增至U = 6 m/s时, 对于矩形截面增加宽厚比可以在尾流处产生更加剧烈的涡街. 当W/T = 1时, 矩形截面的钝头体所产生的尾流涡街的宽度Wv为4.32D, 而当W/T增加至2.5时, Wv 增加至4.75D. 由图8(c)~图8(f)可知, 当钝头体截面分别为D形或者三角形时, W/T = 1所产生的尾流涡街的宽度Wv分别为4.62D和4.94D, 而当W/T增加至2.5时, 尾流涡街的宽度分别减小至3.78D 和3.56D, 同比降低了18%和27%. 因此, 在较大风速区域, 增加宽厚比可以改善由矩形截面引起的驰振能量收集结构的气动特性; 而对于D形截面和三角形截面, 增加宽厚比将减弱尾流处涡街的剧烈程度, 降低低流速区域的风能收集效果.

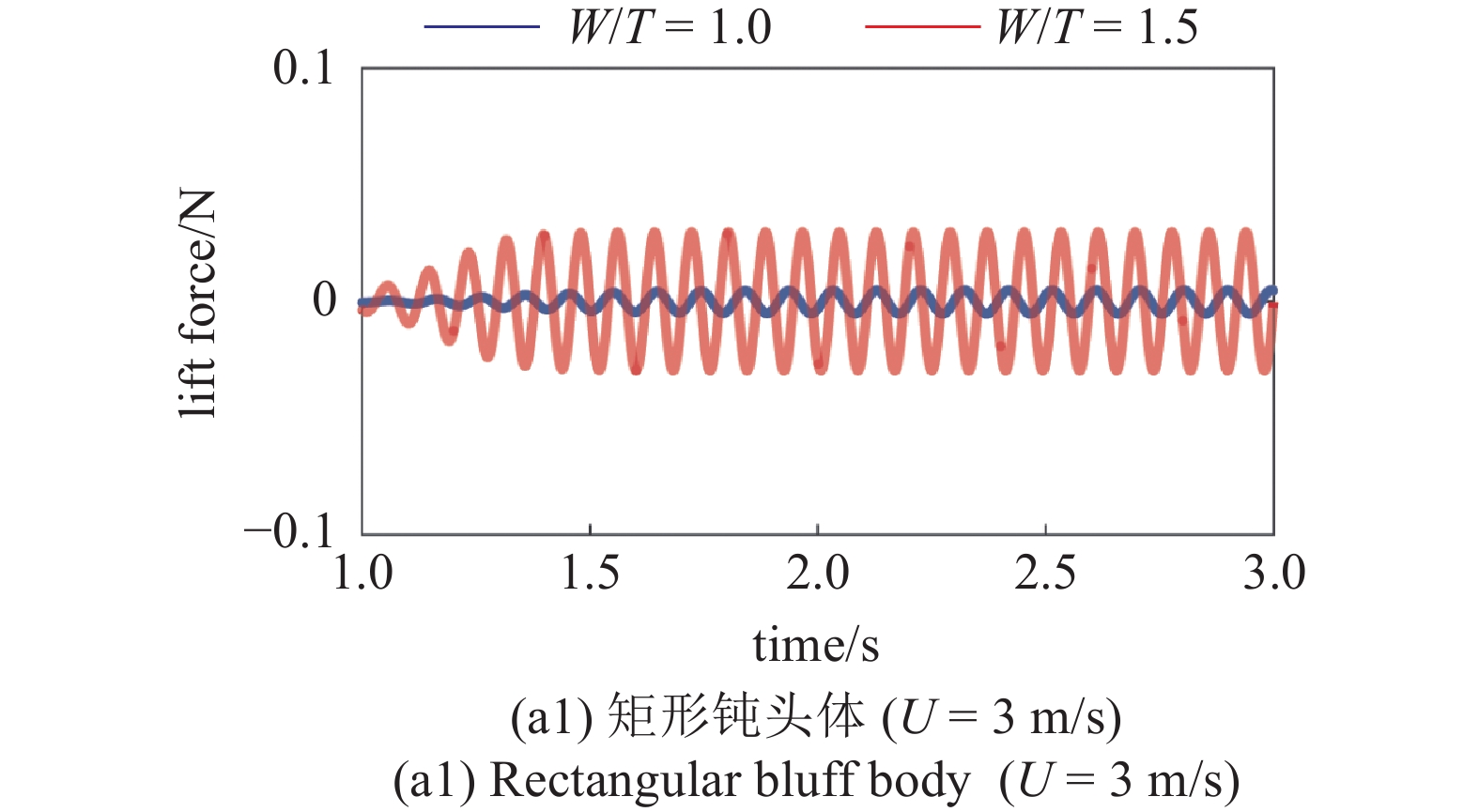
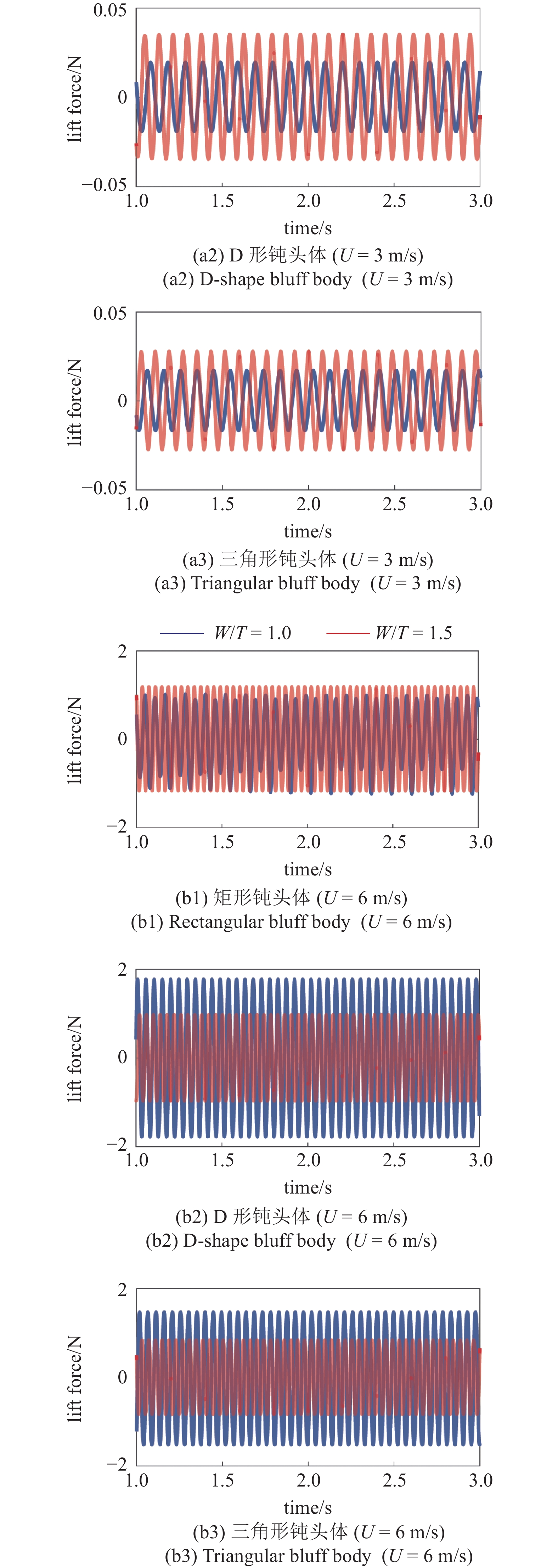
为了进一步验证涡街宽度与升力的关联性, 图9给出了U = 3 m/s和U = 6 m/s 时的升力计算结果. 当风速为U = 3 m/s时, 3种截面的钝头体在W/T = 2.5时的升力明显高于W/T = 1的情形. 当风速增大至U = 6 m/s, 矩形截面的钝头体在W/T = 2.5时的升力比W/T = 1时高, 而D形截面和三角形截面在W/T = 1时的升力比W/T = 2.5时高. 由此可知, 钝头体宽厚比对升力的影响规律与对涡街宽度的影响规律一致. 随着宽厚比增加, 在低流速区域流致振动钝头体会产生更加强劲的升力, 显著提高能量收集效果.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-9-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/11//lxxb2021-438-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
U = 3 m/s和U = 6 m/s 时的不同钝头体的升力计算结果



Figure
9.
Lift force for U = 3 m/s and U = 6 m/s



下载:
全尺寸图片
幻灯片

5.
结 论

本文针对3种钝头体开展风洞实验研究, 探究了钝头体宽厚比对流致振动能量收集效果的影响规律. 结果表明钝头体宽厚比显著影响流致振动的动力学特性与能量收集效果. 当钝头体截面为矩形时, 不同宽厚比的钝头体都将使系统呈现出驰振动力学响应, 增大宽厚比可以显著提高电压输出峰值; 当钝头体截面为三角形, 增加宽厚比将改变流致振动特性, 系统的响应呈现“驰振”→“驰振 + 涡激振动”→“涡激振动”响应特性变化趋势. 由于宽厚比增加引起涡激振动响应的出现, 系统在较低流速范围内的响应高于仅仅基于驰振的能量收集系统. 当钝头体截面为D形时候, 系统的响应呈现出类似于三角形钝头体的结果, 即展现出“驰振”→“涡激振动”响应特性变化趋势, 提高了低风速时候能量收集效果. 相关实验结果可以通过计算流体动力学模拟结果给予揭示. CFD模拟结果表明, 随着宽厚比增加, 流致振动能量收集结构的气动特性得到改善, 钝头体会产生更加强劲的涡街与升力, 显著提高低流速区域能量收集效果.