临近空间是火箭的通过区、临近空间飞行器的飞行区域,是返回式卫星、无控再入目标、危险小行星陨落等的必经区。这一区域的大气环境直接影响临近空间飞行器的设计、技术验证和作战使用[4-6]。例如:临近空间温度直接影响飞行器的仪器性能和材料温度疲劳损伤;臭氧具有很强的腐蚀性;中子辐射能引起单粒子效应等;密度、风场对临近空间飞行器的姿态和位置产生影响[7-9]。而且临近空间大气环境复杂多变,地域、时域变化强,在时间和空间上存在多种尺度的变化。这是由于临近空间存在复杂的动力-辐射和光化学过程。临近空间同时受到上下层的影响[10],例如:热层的氧原子吸收紫外辐射等过程可以激发大气潮汐波;地形和锋面、对流等非地形激发的重力波能够穿过对流层向上传播,耗散或者破碎释放动量通亮对临近空间环境产生作用[11-12]。因此,对临近空间大气环境的研究有助于临近空间飞行器的安全[13]。
临近空间大气风场是飞行器飞行过程中一个重要的环境因素[14]。最大风切变在飞行器的姿态控制系统设计、制导精度分析和载荷分析中,起到尤为重要的作用。分析临近空间大气风切变的特性,研究其对飞行器的影响对精确飞行有重要的参考价值。
目前而言,地面风和对流层区域的风切变特性,及对火箭的影响研究已经比较成熟。在实际工作中,酒泉、西昌和太原卫星发射中心已根据地面风和对流层风场数据研制出风场分析结果,并应用于相应的运载火箭设计中。但对临近空间的风场特性研究仍然比较缺乏。临近空间大气风场随时间、高度和经纬度的变化与地面风和对流层有明显的区别,有必要针对临近空间大气风场的时空分布特点、风切变特性进行研究,以及对飞行器的影响进行分析。
本文利用MERRA(the Modern Era Retrospective-analysis for Research and Applications)再分析资料2009—2013年共5年的风场数据,建立临近空间20~78 km的风切变设计模型,以酒泉(39.1°N,98.5°E)上空为例,给出最多风向、99%概率的最大风速、平均条件风、最小条件风、最大风切变和综合矢量风分析结果;并且评估了临近空间风切变对飞行器的影响,计算出风场对低动态飞行器(马赫数为3)和高动态飞行器(马赫数为5和8)产生的风攻角。
1 数据和分析方法 1.1 MERRA再分析资料 MERRA数据是由美国国家航空航天局(National Aeronautics and Space Administration, NASA)戈达德航天飞行中心(Goddard Space Flight Center, GSFC)下属的全球建模和同化办公室(Global Modeling and Assimilation Office, GMAO)发布的再分析气象资料。该数据也是NASA戈达德地球观测系统(Goddard Earth Observation Systems, GEOS)的资料同化系统(Data Assimilation Systems,DAS)版本5.2所生成的产品。MERRA是NASA为卫星时代提供的再分析资料, 其卫星资料包含的多种探测数据,有地基和卫星数据,例如MODIS、SSM/I、ERS-1、GEOS和AIRS,其主要致力于天气和气候时间尺度与水循环相关领域。MERRA数据覆盖时间是从1979年至今。MERRA的时间分辨率为6 h,水平分辨率是1.9° (纬度)×2.5°(经度),垂直范围从地面到78 km,共72层。MERRA再分析资料的详细描述见文献[15]。本文数据选取2009—2013年共5年数据。
1.2 分析方法 分析方法中采用赵人濂等高空风场统计分析方法[16],作为中华人民共和国航空航天工业部航天工业标准《地地导弹、运载火箭风场设计规范》,该方法适用于大子样、大尺度高空风数据的统计分析,不适用于小尺度阵风,涉及风场分布的各类飞行器设计可参照使用。
飞行器在飞行时,将在不同的高度遇到不同出现概率的最大风干扰,包括风切变和最小风。在设计中,选取对飞行器飞行影响最大的高度(称为参考高度),给出一定出现概率下的最大风速,那么在其他各高度上出现的风切变称为“条件切变”,由此切变造成的各高度的风速称为“条件风速”。这些风速沿高度分布就构成了综合矢量风剖面。这里的参考高度,一般只选取风速较大的区域,因为只有这些高度的风才是构成最危险条件设计的因素。风场设计中采用最危险条件设计,主要表现在概率设计上。这种风速既能反映实测风场,又不能在一次实测中完全重复;既能保证最危险条件设计,又不能无限保守约束条件。
本文首先采用三倍标准偏差去除异常值,插值计算酒泉上空20~78 km的纬向风和经向风,因为MERRA再分析资料的网格为规则网格,所以采用双线性插值方法可以确保精度。其次,分别计算最多风向、99%概率最大风速、平均条件风、最小条件风和最大风切变,进而给出综合矢量风。最后,分析临近空间风切变特性对飞行器的影响。
1) 最多风向
风场在某段时间存在大致确定的方向,此时风向满足二维正态分布。在极坐标系下,将风速从0~∞积分二维正态分布式后,得到风向α的概率密度分布:
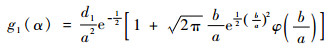 | (1) |
式中:
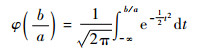 | (2) |
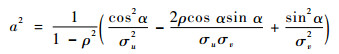 | (3) |
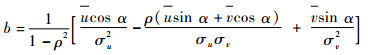 | (4) |
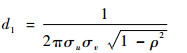 | (5) |
其中:u和σu分别为纬向风ui的数学期望和标准偏差;v和σv分别为经向风vi的数学期望和标准偏差;ρ为纬向风和经向风的相关系数;α为数学角度,与气象角度θ的关系为
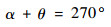 |
其中:气象角度的正北为0°,角度顺时针旋转。对风向进行统计,得到概率密度最大的最多风向θ*。
2) 给定风向时风速的条件分布
在给定方向α0时,利用条件分布,在极坐标系中确定风速。此时,在已知风向α0时,风速ω的分布条件为
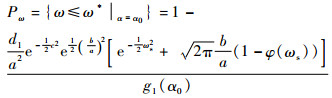 | (6) |
式中:
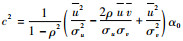
3) 条件风切变的统计特征量
风切变是2个高度上的风速差:
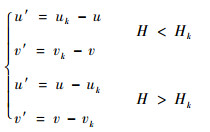 | (7) |
式中:Hk为参考高度;uk和vk分别为Hk高度的纬向风和经向风;H为其他高度;u和v分别为H高度的纬向风和经向风。
条件风切变是指在参考高度出现最大风条件下的条件切变。条件风切变的数学期望为
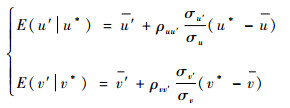 | (8) |
标准偏差为
 | (9) |
式中:u*和v*分别为最大风速下的纬向分量和经向分量; u′、v′、u′、v′、σu′、σv′分别为纬向风切变、经向风切变及其相对应的数学期望和标准偏差;ρuu′、ρvv′为风速与切变间的相关系数。由计算可知,σ(u′|u*)≈σ(v′|v*),而且ρvv′很小,所以切边(实为条件切变)为二维圆分布,条件风标准偏差为
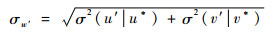 | (10) |
4) 条件风的统计特征量
在参考高度Hk上出现最大风条件下,其他高度H上的风都是由风切边而得来的,称为条件风。条件风的数学期望:
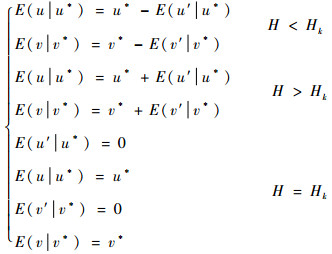 | (11) |
条件风概率圆的方程为
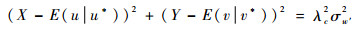 | (12) |
式中:X和Y分别为条件风风速的纬向分量和经向分量;

5) 综合矢量图剖面
对应于一个参考高度上确定的最大风速,可在其他高度做出无数的条件风圆。这些圆的集合可构成表示风特性的空间图形,它是以参考高度最大风为定点的上下2个对顶锥(见文献[16]图 1)。锥体上任一点沿高度的轨迹,从理论上都是风的空间分布。借助最多风向这个条件,利用最多风向构成一个高度平面,切取对顶锥,可得到2条交线,考虑最大切变,可得到靠近高度轴的交线,称为最小条件风。
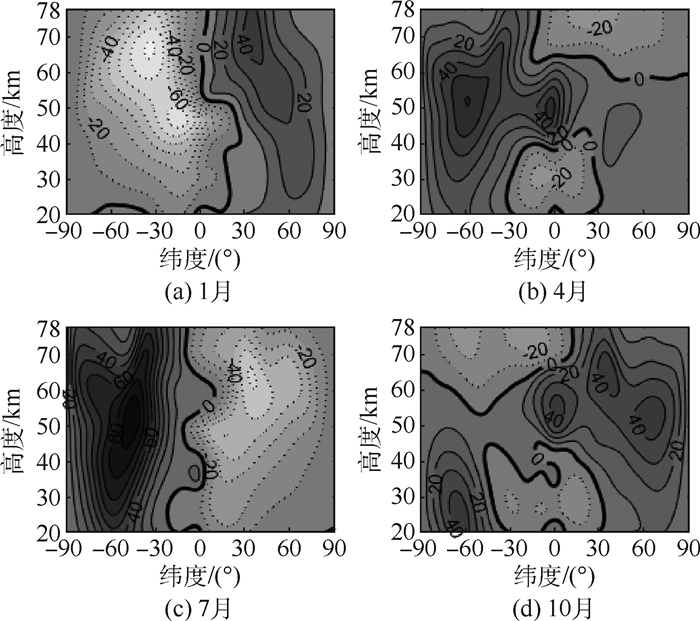 |
| 图 1 MERRA再分析资料纬圈平均纬向风分布 Fig. 1 Zonal mean zonal wind distribution from MERRA reanalysis data |
| 图选项 |
最多风向平面方程为
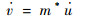 | (13) |
式中:m*为经向风分量
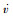
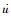
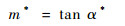 | (14) |
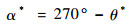 | (15) |
最多风向平面与对顶锥的交点坐标为
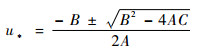 | (16) |
 | (17) |
式中:u*和v*分别为最小条件风的纬向分量和经向分量。
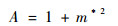 | (18) |
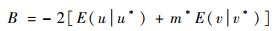 | (19) |
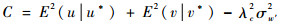 | (20) |
由于考虑最大风切变,因而取2个根中最小值(绝对值),这样最小条件风W*为
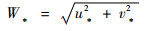 | (21) |
2 临近空间风切变特性分析 2.1 临近空间风场气候特征 利用MERRA再分析资料2009—2013年共5年的数据,分析临近空间20~78 km纬圈平均纬向风在1、4、7、10月份的气候态纬度-高度分布特征,分别代表冬、春、夏、秋的特点,结果如图 1所示。在1月份,北半球纬向风以西风为主,在35°N上空71 km高度有极大值约46 m/s,南半球纬向风以东风为主,在35°S上空67 km高度有极大值约82 m/s。在7月份,纬圈平均纬向风分布特征与1月份基本相反,北半球纬向风以东风为主,在35°N上空64 km高度有极大值约61 m/s,南半球纬向风以西风为主,在46°S上空51 km高度有极大值约96 m/s。对于4、10月份,大气纬向风为夏季和冬季之间过渡的特征。
图 2给出了临近空间20~78 km纬圈平均经向风在1、4、7、10月份的气候态纬度-高度分布特征。在1月份,经向风在60 km以上南北半球都以南风为主,60 km以下中低纬度(约40°S~40°N附近区域)以南风为主,其他纬度以北风为主;经向风范围为-4~13 m/s,经向风极大值出现在中间层。在7月份,纬圈平均经向风风向与1月份特征基本相反。对于4、10月份,大气经向风也是夏季和冬季之间过渡的特征。临近空间经向风明显弱于纬向风。
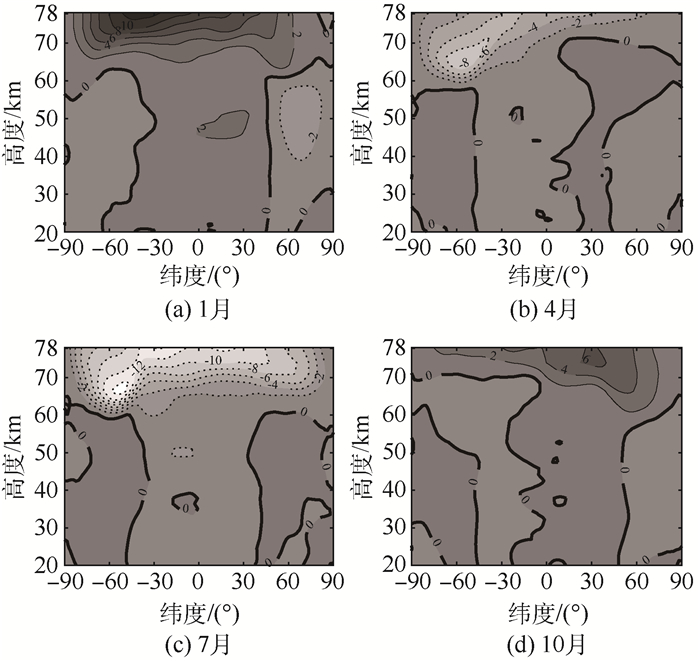 |
| 图 2 MERRA再分析资料纬圈平均经向风分布 Fig. 2 Zonal mean meridional wind distribution from MERRA reanalysis data |
| 图选项 |
综上所述,临近空间大气风场存在明显的季节变化特征。对风切变的特性分析需要风向属于正态分布,因此本文对不同月份进行计算和分析。
2.2 临近空间20~78 km风切变特性 酒泉卫星发射中心(39.1°N,98.5°E)是中国科学卫星、技术试验卫星和运载火箭的发射试验基地之一,是中国最早建立的运载火箭发射试验基地。本文选取酒泉为例,开展其上空临近空间风切变特性分析。
风向在某时间内具有大致确定的风向。在每个参考高度上的最多风向下找到一定出现概率的最大风速,这就需要首先确定最多风向,然后在这一风向下确定最大风速。图 3给出1、4、7、10月份的各个风向概率密度随高度的分布,0°为北风、90°为东风、180°为南风、270°为西风。从图中可以看出:1月份,风向概率密度在大部分高度极大值出现在270°附近,最多风以西风为主;在35~55 km高度存在双峰,在90°(东风)和270°(西风)附近有极大值。4月份,20~50 km以西风为最多风向,50~78 km高度的最多风向为东风。7月份,风向概率密度在所有高度在90°附近有极大值,最多风向出现在东风方向附近。10月份,风向概率密度在270°附近最大,最多风向为西风。
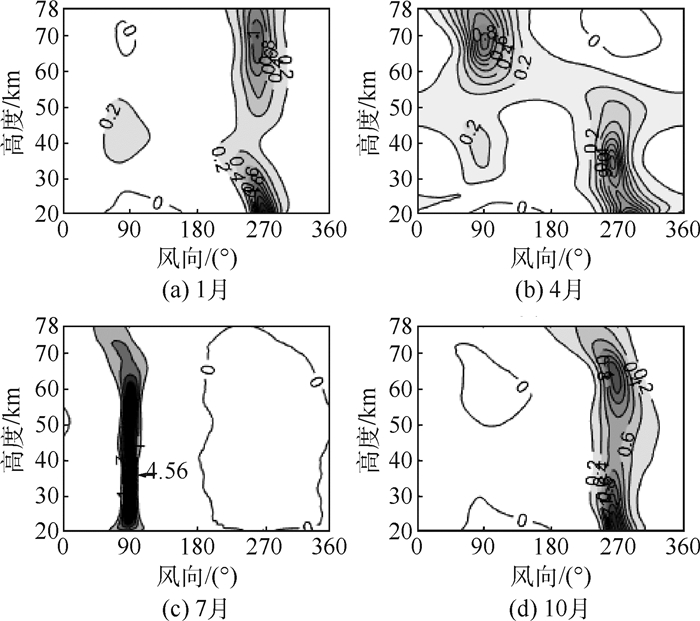 |
| 图 3 酒泉上空风向概率密度分布 Fig. 3 Probability density distribution of wind direction over Jiuquan |
| 图选项 |
在给定最多风向后,可利用条件分布计算每个参考高度的最大风速。图 4给出1、4、7、10月份的99%概率最大风速随高度的变化。图中最大的特点是1月份最大风速比其他月份强。1月份最大风速基本随高度增加,在40 km高度附近出现凹陷的区域与图 3(a)在该高度附近有东西风交替相对应。7月份最大风速在20~64 km基本呈增大趋势,在65~73 km略微减小,之后又增大。10月份变化趋势与7月份相似,但两者的风向正好相反,前者是西风,后者是东风。4月份最大风速在20~35 km递增,在35~50 km递减,之后又缓慢增加。
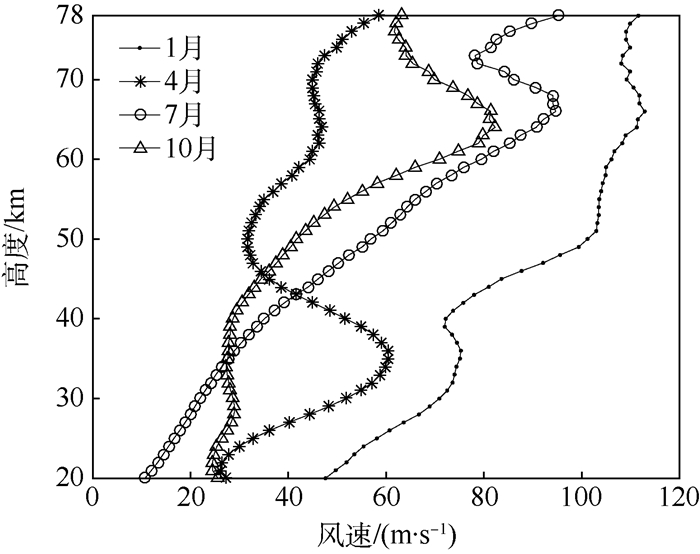 |
| 图 4 酒泉上空99%概率最大风速 Fig. 4 Maximum wind speed over Jiuquan with 99% probability |
| 图选项 |
对于每个参考高度,连接条件风圆的圆心可以得到平均条件风。考虑最大风切变,计算最小条件风。平均条件风可供精度分析使用,最小条件风可供姿态控制系统设计和载荷计算使用。从图 1中看出风速的极大值一般出现在50~70 km,以60 km为参考高度。图 5给出了以60 km为参考高度的平均条件风和最小条件风。图 5中2条廓线的交点就是60 km的99%概率最大风速。某高度的最大风速与此最小条件风的差就是60 km最大风速引起的最大风切变,见图 6。某高度的最大风切变在一定范围内随着与参考高度60 km的距离逐渐增大,但到超过一定距离有基本保持不变。例如,4、7和10月份最大风切变影响范围约为±10 km,1月份可能达到±20 km,这可能与1月份的最大风速较强有关。
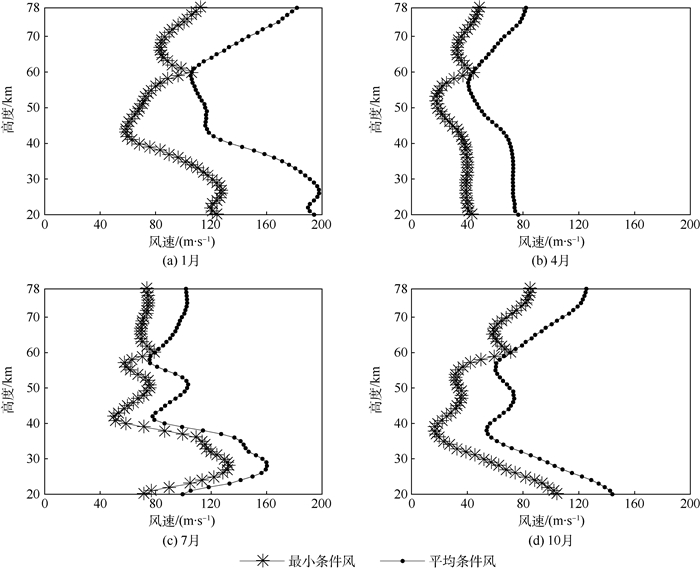 |
| 图 5 酒泉上空60 km最大风速引起的最小条件风和平均条件风 Fig. 5 Minimum and mean conditional wind caused by maximum wind speed at 60 km over Jiuquan |
| 图选项 |
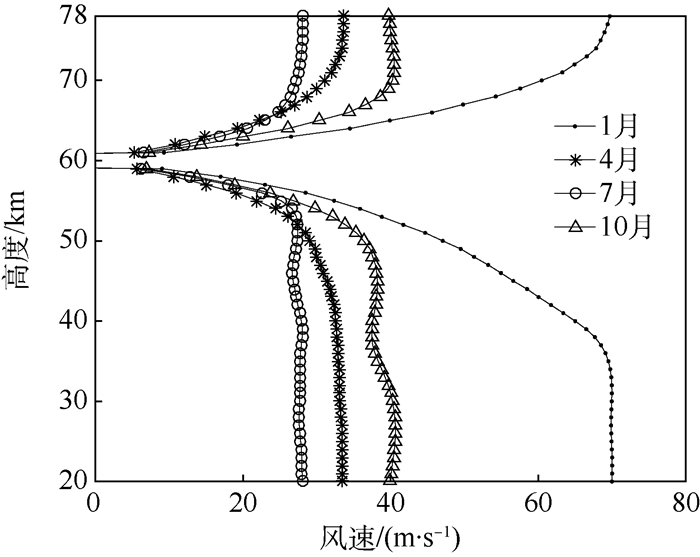 |
| 图 6 酒泉上空60 km 99%概率最大风速引起的最大风切变 Fig. 6 Maximum wind shear caused by maximum wind speed at 60 km over Jiuquan with 99% probability |
| 图选项 |
综合矢量风剖面是以各个高度一定出现的最大风为包络,不同高度各具特点的最小条件风综合出来的一个剖面图。本文研究高度为临近空间20~78 km,风场随高度变化显著。选取30、40、50、60和70 km为参考高度,给出99%概率最大风的综合矢量风剖面图,见图 7。考虑最大风速引起的风切变影响有一定范围,图中只给出参考高度的±10 km高度范围的最小条件风。
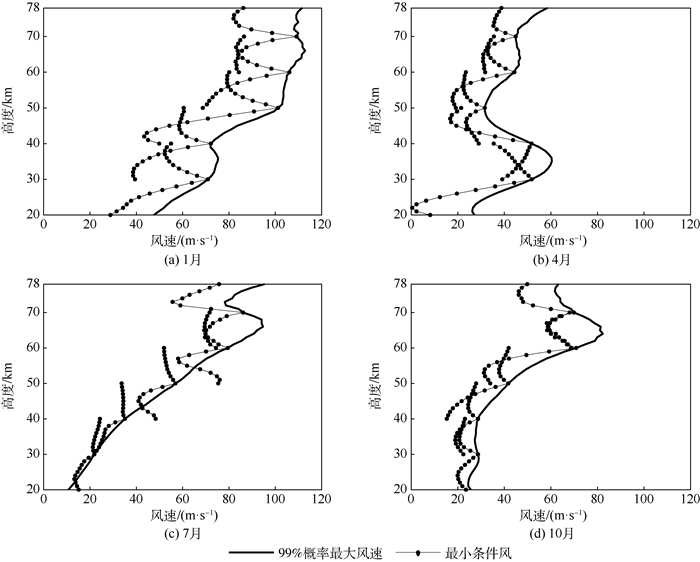 |
| 图 7 酒泉上空综合矢量风剖面图 Fig. 7 Synthetical wind vector profile over Jiuquan |
| 图选项 |
3 风切变对飞行器影响 风切变对飞行器的影响主要是在风作用下产生风攻角[15]。计算式为
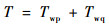 | (22) |
 | (23) |
 | (24) |
式中:T为风攻角;Wp为最小条件风;Wq为条件风切变;V为飞行器飞行速度;Twp和Twq分别为最小条件风Wp和条件风切变Wq引起的风攻角。
根据速度的不同,飞行器通常可分为低动态和高动态2类:低动态飞行器飞行速度一般不超过马赫数3,高动态飞行器马赫数大于5,通过采用特殊的动力装置,可实现超声速和高超声速飞行[17-18]。假设低动态飞行器马赫数为3和高动态马赫数为5和8,图 8给出了风攻角随高度和季节的变化。其中最小条件风和条件风切变分别来自于参考高度对-5km高度风场的影响,例如50 km风攻角来自于55 km参考高度99%概率最大风速引起的50 km最大风切变。1月和10月的风攻角随高度基本逐渐增加:1月份飞行器(马赫数为3、5、8)风攻角最小值在20 km处为3.3°、2.0°和1.3°,最大值在69 km处为8.5°、5.1°和3.2°;7月份飞行器(马赫数为3、5、8)风攻角最小值在20 km处为1.1°、0.6°和0.4°,最大值在69 km处为8.5°、5.1°和3.2°。飞行器马赫数越高,飞行速度越快,风攻角越小。相同马赫数飞行器在1月份的风攻角最大。火箭需要的最大风概率取95%,针对火箭的风攻角会比以上结果小8%~27%。
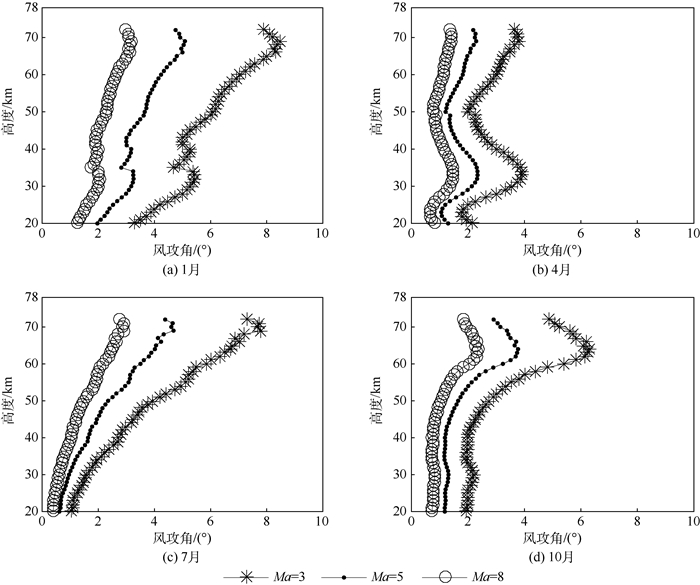 |
| 图 8 风攻角分布 Fig. 8 Wind attack angle distribution |
| 图选项 |
4 结论 本文利用MERRA再分析资料2009—2013年5年的风场数据开展了临近空间的20~78 km的风切变统计分析研究, 得出:
1) 临近空间纬向风和经向风存在显著的季节变化。1月份北半球纬向风以西风为主,南半球纬向风以东风为主;经向风在60 km以上以南风为主,60 km以下中纬度和低纬度以南风为主,其他纬度以北风为主。在7月份,纬圈平均纬向风和经向风风向与1月份特征基本相反。4、10月份大气风场主要为夏季和冬季之间过渡的特征。
2) 以酒泉(39.1°N,98.5°E)为例开展临近空间风切变特性分析:最多风向在1、10月份以西风为主,7月份以东风为主,4月份在50 km以下为西风,以上为东风。1月的99%概率最大风速最大。参考高度的最大风速能够引起风切变,但最小风切变在距离参考高度一定范围逐渐增大,然后基本不变。根据各个参考高度的最大风和最小风切变可给出了综合矢量风。
3) 临近空间99%概率最大风引起的风切变对飞行器产生的风攻角显著,以参考高度对-5 km为例,风切变对飞行器(马赫数为3、5、8)产生风攻角在69 km处最大可达8.5°、5.1°和3.2°。
4) 本文将风切变分析方法可应用于临近空间风场研究,充分考虑风的时间、空间变化,研究临近空间风场对飞行器的影响。另外,该研究可以应用到其他地区上空临近空间的风场分析。本项工作可为飞行器在临近空间飞行的姿态控制系统设计、制导精度分析和载荷分析计算等多方面工作提供了一定的参考。
致谢 感谢NASA Goddard Space Flight Center的GMAO (Global Modeling and Assimilation Office)工作组提供MERRA再分析资料。
参考文献
| [1] | 肖存英, 胡雄, 杨钧烽, 等. 临近空间38°N大气密度特性及建模技术[J]. 北京航空航天大学学报, 2017, 43(9): 1757-1765. XIAO C Y, HU X, YANG J F, et al. Characteristics of atmospheric density at 38°N in near space and its modeling technique[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(9): 1757-1765. (in Chinese) |
| [2] | 刘强, 武哲, 祝明, 等. 平流层气球热动力学仿真[J]. 北京航空航天大学学报, 2013, 39(12): 1578-1583. LIU Q, WU Z, ZHU M, et al. Thermal-dynamic simulation of stratospheric balloon[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(12): 1578-1583. (in Chinese) |
| [3] | 阎啸, 唐博, 张天虹, 等. 临近空间飞行器信息系统一体化载荷平台[J]. 航空学报, 2016, 37(S1): 127-132. YAN X, TANG B, ZHANG T H, et al. Payload platform of near space vehicle information system[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(S1): 127-132. (in Chinese) |
| [4] | 陈闽慷, 杜涛, 胡雄, 等. 北半球高空大气参数波动对临近空间飞行热环境的影响[J]. 科学通报, 2017, 62(13): 1402-1409. CHEN M K, DU T, HU X, et al. Effect of atmosphere parameter oscillation at high altitude in the northern hemisphere for near space hypersonic flight aerothermodynamic prediction[J]. Chinese Science Bulletin, 2017, 62(13): 1402-1409. (in Chinese) |
| [5] | 孙磊, 廉璞, 常晓飞, 等. 临近空间大气环境建模及其对飞行器影响[J]. 指挥控制与仿真, 2016, 38(5): 107-111. SUN L, LIAN P, CHANG X F, et al. Near space atmosphere modeling and its effect on the aircraft command control & simulation[J]. Command Control & Simulation, 2016, 38(5): 107-111. DOI:10.3969/j.issn.1673-3819.2016.05.023 (in Chinese) |
| [6] | MARTYUSHEY S G, SHEREMET M A. Conjugate natural convection combined with surface thermal radiation in an air filled cavity with internal heat source[J]. International Journal of Thermal Sciences, 2014, 76(2): 51-67. |
| [7] | 童靖宇, 向树红. 临近空间环境及环境试验[J]. 装备环境工程, 2012, 9(3): 1-4. TONG J Y, XIANG S H. Near space environment and environment tests[J]. Equipment Environmental Engineering, 2012, 9(3): 1-4. DOI:10.3969/j.issn.1672-9242.2012.03.001 (in Chinese) |
| [8] | 陈凤贵, 陈光明, 刘克华. 临近空间环境及其影响分析[J]. 装备环境工程, 2013, 10(4): 71-75. CHEN F G, CHEN G M, LIU K H. Analysis of near space environment and its effect[J]. Equipment Environmental Engineering, 2013, 10(4): 71-75. (in Chinese) |
| [9] | 蔡明辉, 张振龙, 封国强, 等. 临近空间中子环境及其对电子设备的影响研究[J]. 装备环境工程, 2007, 4(5): 23-29. CAI M H, ZHANG Z L, FENG G Q, et al. Study of near space neutron environment and its effects to electronic device[J]. Equipment Environmental Engineering, 2007, 4(5): 23-29. DOI:10.3969/j.issn.1672-9242.2007.05.007 (in Chinese) |
| [10] | SMITH A K. Global dynamics of the MLT[J]. Surveys in Geophysics, 2012, 33(6): 1177-1230. DOI:10.1007/s10712-012-9196-9 |
| [11] | 杨钧烽, 肖存英, 胡雄, 等. 中国廊坊(39.4°N, 116.7°E)中间层和低热层潮汐的季节变化[J]. 地球物理学进展, 2017, 32(4): 1501-1509. YANG J F, XIAO C Y, HU X, et al. Seasonal variations of wind tides in mesosphere and lower thermosphere over Langfang, China (39.4°N, 116.7°E)[J]. Progress in Geophysics, 2017, 32(4): 1501-1509. (in Chinese) |
| [12] | 郭文杰, 胡雄, 闫召爱, 等. 利用瑞利激光雷达观测北京地区上平流层地形重力波活动[J]. 地球物理学报, 2015, 58(10): 3481-3486. GUO W J, HU X, YAN Z A, et al. Terrain-generated gravity waves in the upper stratosphere detected by Rayleigh lidar[J]. Chinese Journal of Geophysics, 2015, 58(10): 3481-3486. DOI:10.6038/cjg20151004 (in Chinese) |
| [13] | HALE N, LAMOTTE N, GARNER T.Operational experience with hypersonic flight of the space shuttle[C]//AIAA/AAAF 11th International Space Planes and Hypersonic Systems and Technologies Conference.Reston: AIAA, 2002: 17_5259. https://arc.aiaa.org/doi/abs/10.2514/6.2002-5259 |
| [14] | 郭建国, 周军. 临近空间低动态飞行器控制研究综述[J]. 航空学报, 2014, 35(2): 320-331. GUO J G, ZHOU J. Review of the control of low dynamic vehicles in near space[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 320-331. (in Chinese) |
| [15] | RIENECKER M M, SUAREZ M J, GELARO R, et al. MERRA:NASA's modern-era retrospective analysis for research and applications[J]. Journal of Climate, 2011, 24(14): 3624-3648. DOI:10.1175/JCLI-D-11-00015.1 |
| [16] | 赵人濂, 陈振官, 付维贤. 风切变与运载火箭设计[J]. 宇航学报, 1998, 19(2): 105-108. ZHAO R L, CHEN Z G, FU W X. Wind shear and rocket design[J]. Journal of Astronautics, 1998, 19(2): 105-108. (in Chinese) |
| [17] | 李锋, 叶川, 李广佳, 等. 临近空间太阳能飞行器横航向稳定性[J]. 航空学报, 2016, 37(4): 1148-1158. LI F, YE C, LI G J, et al. Lateral-directional stability of near-space solar-powered aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(4): 1148-1158. (in Chinese) |
| [18] | 刘海东, 包为民, 李惠峰, 等. 高超声速飞行器全局有限时间姿态控制方法[J]. 北京航空航天大学学报, 2016, 42(9): 1864-1873. LIU H D, BAO W M, LI H F, et al. Attitude control method within finite time globally for hypersonic vehicles[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(9): 1864-1873. (in Chinese) |
