针对卫星时序数据的挖掘方法有很多,包括异变过程多类型特征分析、异变过程及特征变化规律获取[2-3]、多参数关联知识挖掘、状态关联知识挖掘[4-5]、状态异常形态挖掘[6-7]、异常和故障模式挖掘[8-9]、多诱因复合状态异变检测[10-11]、故障诊断等。这些方法在执行过程中涵盖了数据预处理、表示、分割、相似性度量、分类、聚类等多种算法。采取有效措施优化这些算法,缩短运行时间对于提高系统性能至关重要。
在更短时间内处理更多数据,一直是计算机科学追求的目标之一。该目标有多种实现策略,包括粗粒度的分布式计算及节点级较细粒度的并行计算。本文仅讨论用Python语言处理航天大数据的节点级并行与优化策略,并不涉及分布式计算。本文工作能够提高航天大数据挖掘效率,有利于提高卫星运行状态实时监控效能,对于保障卫星长期稳定在轨运行具有重要意义。
1 程序并行与优化方法 单个计算节点上的并行计算包括CPU+GPU等4种典型架构[12]。本文用到的主要方法有基于多核CPU的并行计算、基于CPU+GPU的异构计算、串行算法优化与向量化等。
Python语言存在全局解释锁(Global Interpreter Lock,GIL)问题,故在多核CPU上采用多进程而不是多线程进行并行计算。使用Python的multiprocessing并行库,可以并行开启多个进程,没有数量限制。每个进程都运作各自的GIL。
GPU(Graphics Processing Unit)以单指令多线程流(SIMT)方式运行,其显著特点有[13]:更高的内存带宽;更多的计算单元;更具性价比优势。GPU在浮点运算及并行计算性能方面可优于CPU达数十倍乃至上百倍。因此,基于GPU的并行计算已经成为很多领域应用中的主流,如天文观测[14]、航空计算[15]、气象预报[16]、水文模拟[17]、军事仿真[18]、生物研究[19]等。另外还有一大部分应用采用CPU+GPU异构平台。
除了硬件加速,对串行算法本身进行向量化改进也是一种广泛采用的代码优化方法。在不使用GPU的情况下,这种方法也能大幅提升矩阵或向量运算速度。
卫星数据是一种典型的时序大数据,其基本优化思路是:分析数据挖掘过程中各种算法的性能瓶颈,找出耗时大、时间复杂度、具有逻辑或数据独立性、可并行化的部分,在多核CPU或GPU上执行;对于耗时小或不可并行部分则仍在CPU上串行执行[20],并结合向量化等方法做进一步优化,以获得最优效果。
2 异变过程多类型特征分析 时序数据分析一般是在训练样本上找出数据统计特性和发展规律性,构建时序数据模型,然后进行样本外预测。同理,在卫星时序数据挖掘中,一些方法是为了挖掘频繁出现的模式,期望发现某种规律,异常数据被作为噪声忽略;而另外一些方法则更重视异常数据背后可能隐藏的重要信息,如挖掘异常检测、故障预测等模式在卫星应用中有很高价值。
如图 1所示,异变过程多类型特征(Multiple Feature of Anomaly Process,MFAP)分析是一个典型的卫星时序数据挖掘过程,包括了数据预处理、特征提取、机器学习算法等基本步骤。本文以该过程为代表,针对其中求周期、提特征、聚类等3个关键步骤,讨论其并行与优化方法。本文方法完全可以推广到其他类似过程。
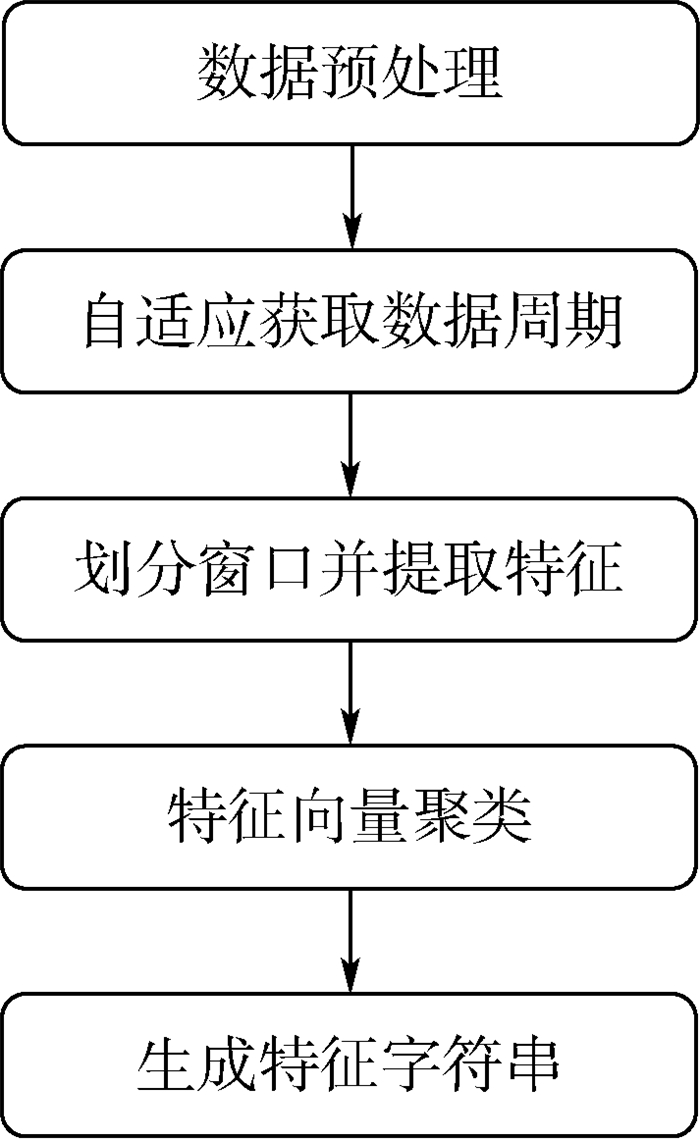 |
| 图 1 异变过程多类型特征分析流程 Fig. 1 MFAP analysis flowchart |
| 图选项 |
3 自适应获取周期优化 3.1 自适应获取周期算法 对于明显周期性变化的数据,其最小正周期是一个非常重要的信息。在数据挖掘过程中,数据周期可以人为设定,但是人为指定法缺乏适应能力。一旦卫星参数发生变化,难以及时响应到正确周期,这不但增加了系统维护负担,而且增加了设定错误的风险。而自适应获取周期算法根据数据序列自动识别出该参数的最小完整周期,不必人工逐一测算。若直接对原始数据用傅里叶变换求周期容易受到噪声干扰,因此本文首先求取数据窗口的相关性,然后在相关性(相似度)序列的基础上再求周期。算法步骤如下:
步骤1 ?设置观察向量长度为L,选择从第1条数据开始的L条数据作为基准向量v0。
步骤2 ?从起点依次往后移动kΔt,生成一系列等长度的偏移向量vk,k=1, 2, …,直到向量的长度小于L。
步骤3 ?计算基准向量v0与偏移向量vk间的相似度(内积),得到相似度列表。
步骤4 ?利用傅里叶变换获取相似度列表的周期。
步骤5 ?根据数据量、最大能量的频率、采样间隔Δt及傅里叶变换公式,得到原始数据周期。
3.2 串行算法优化与向量化
3.2.1 偏移向量的局部更新 自适应获取周期算法的步骤2生成了一系列滑动窗口。一般滑动窗口都有重叠,即滑动偏移量通常小于划分窗口大小。其实,每次窗口偏移后并不需要更新窗口内的所有元素(见图 2),只需向前次偏移向量中添加δ个新元素,再舍弃δ个旧元素即可。其中δ为偏移量大小。这称为局部更新。显然元素重叠部分占比越高,计算性能提升越明显。
 |
| 图 2 偏移向量局部更新示意图 Fig. 2 Partial update diagram of offset vector |
| 图选项 |
3.2.2 numpy向量化 Python的numpy包提供了经过优化的向量运算库。自行编写循环逐点计算的效率要远远低于使用numpy包向量化运算的效率。所以在程序中应当尽量消除循环,而使用Python的numpy相应向量化方法,同时更新向量中的多个元素,从而提高窗口向量整体的更新速度。在自适应获取周期算法的步骤3中,向量间内积也应用向量化计算方法numpy.dot实现。
3.2.3 计算相似度序列的改进 根据局部更新思想,计算相似度列表的方法也可进行优化。窗口重叠部分数据不需要重复计算,只需计算一次。也就是说,在自适应获取周期算法的步骤3中无需每次偏移后都在全部维度上重新计算偏移向量与基准向量的点积,而只需在前一次偏移时先记录好点积结果,后一次偏移时加上更新部分的元素点积,同时减去舍弃部分的元素点积。这样便省去了重复计算重叠部分数据点积的开销。算法复杂度由此大为降低,并且窗口重叠部分占比越高性能提升越大。
3.2.4 实验结果 本文中的所有实验均采用以下平台。GPU:Tesla K40c(2880 cores);CPU:Xeon(R) CPU 2.30 GHz×20;Memory:15.6 GB;Disk:5.9 TB;OS:ubuntu 16.04.3 desktop x64;Python:v3.5;Cuda:v8.0。
表 1对比了自适应获取周期算法的串行代码在改进优化前后的运行时间,其中数据大小是经过预处理之后数据序列所含数据点的个数。可以看出,当窗口偏移量相同时,数据量越大,加速比越高。
表 1 自适应获取周期算法串行代码优化前后耗时对比 Table 1 Comparison of adaptive cycle achieving algorithm's time consumption before and after serial optimization
| 数据大小 | 优化前耗时/s | 优化后耗时/s | 加速比 |
| 221 280 | 25.150 8 | 1.625 6 | 15.5 |
| 490 440 | 127.252 5 | 2.181 4 | 58.3 |
| 1 028 760 | 562.171 5 | 2.592 3 | 216.9 |
| 2 105 400 | 2 306.469 6 | 3.755 2 | 614.2 |
| 6 094 920 | 19 213.119 3 | 6.079 7 | 3 160.2 |
| 12 238 320 | 78 204.042 6 | 16.800 1 | 4 655.0 |
表选项
3.3 基于多核CPU的多窗口向量相似度获取
3.3.1 优化方法 观察窗口依次平移并获取偏移向量,目的都是为了计算每个偏移向量与基准向量间的相似度,再汇总为相似度列表并据此算出周期。这在原始串行程序中体现为一个高次循环内反复调用偏移向量获取函数及相似度计算函数的过程,是影响周期获取快慢的主要因素,应做重点优化。
优化后的程序流程如图 3所示。通过使用Python的multiprocessing库实现并行获取多窗口向量相似度。进程池中的任务分批执行,每一批可同时执行cores个任务,从而能够在整体上加快相似度列表的获取速度。不过需注意,由于这种方法忽略了依次获取窗口向量时的前后依赖关系,所以不能使用3.2.1节局部更新的优化方法,而应多个进程同时读取含有重叠部分的初始向量。
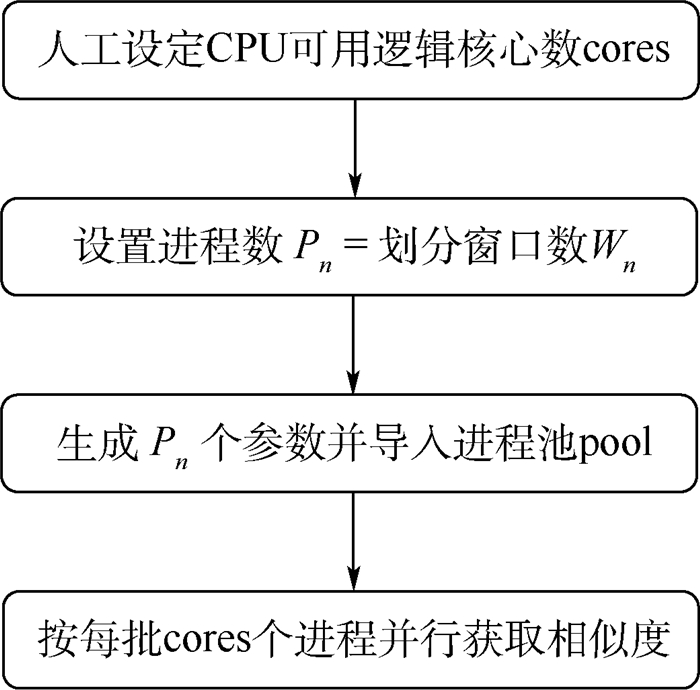 |
| 图 3 基于多核CPU并行的相似度列表获取流程 Fig. 3 Acquisition flowchart of similarity list based on multi-core CPU parallelization |
| 图选项 |
3.3.2 实验结果 针对同一数据用例,实验中设置了不同偏移量δ(决定了计算量),考察征用不同数目CPU核心完成并行计算的耗时, 结果如图 4所示。
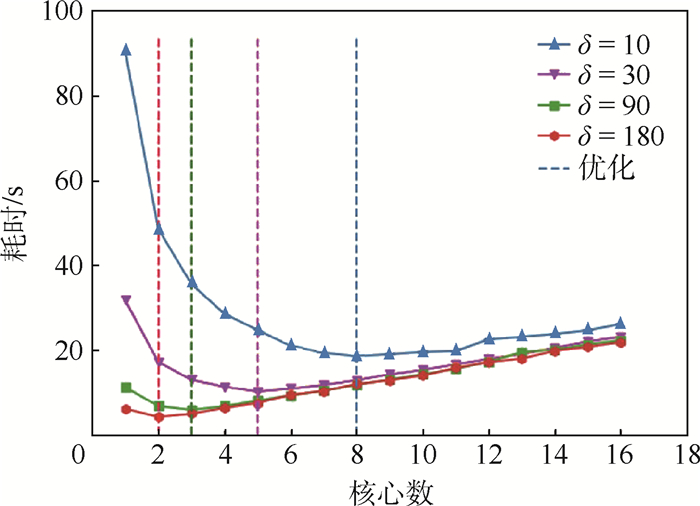 |
| 图 4 多窗口向量相似度获取耗时 Fig. 4 Time consumption of similarity acquisition of multiple window vectors |
| 图选项 |
表 2对比了多核CPU并行的最优耗时与串行代码优化后的耗时。可以看到,并行优化的效果并非总是优于串行优化,而与偏移量δ有关。
表 2 不同方法优化前后耗时结果对比 Table 2 Comparison of time consuming results before and after different optimization methods
| 偏移量δ | 耗时/s | ||
| 无优化 | 串行优化 | 并行最优 | |
| 10 | 95.285 1 | 33.591 8 | 18.403 6 |
| 30 | 58.576 9 | 11.697 2 | 10.048 8 |
| 90 | 19.269 7 | 4.038 3 | 5.716 7 |
| 180 | 9.632 6 | 1.975 2 | 4.020 8 |
表选项
原因在于Python以多进程方式实现多核CPU并行计算过程,其最大限制是非内存共享,即创建几个函数进程就要复制并传入几份相同的参数,这会消耗大量内存和时间。故应根据实际计算量设置合理进程数,使得程序并行化后“节省的计算时间超过复制数据时间”,才能得到更优的结果。经测试,最优条件为“活动核心数最少且每个核心的利用率接近满载”,亦即进程内计算量与进程间通信量的比值越高越好。因此在该实验中看到,偏移量值越小时生成的向量越多,实际计算量越高,此时用CPU多核并行效果更好,否则有可能不如串行优化。
3.4 基于GPU的单一窗口向量相似度计算
3.4.1 优化方法 两向量(基准向量与偏移向量)间的相似度计算属于数值密集型计算,特别是向量长度很大时,串行计算点积的时间就会很长。本文利用PyCuda将Cuda代码直接嵌入Python程序中,实现基于GPU的多线程并行,从而大幅缩短计算耗时。设备端代码流程如图 5所示。
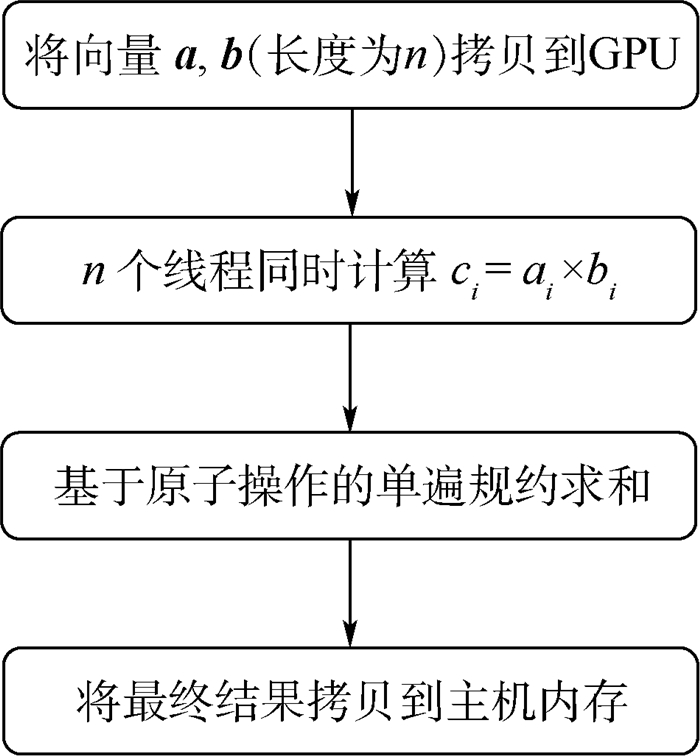 |
| 图 5 基于GPU并行的相似度计算流程 Fig. 5 Flowchart of similarity calculation based onGPU parallelization |
| 图选项 |
求和中使用原子操作和共享内存的组合可以避免内核二次调用。如果硬件支持操作符⊕的原子操作,那么就可以简单地使用单遍规约操作。如对于加法操作,只需调用atomicAdd()将块中部分结果加到全局内存中即可。如果硬件不支持,则采取两遍规约,启动两次GPU内核。这主要是针对Cuda线程块无法同步问题的解决方法。实际上,其异步执行效率并不低。
3.4.2 实验结果 实验中选取不同长度的向量作为数据用例,并分别采用CPU(包含pure python及numpy两种模式)和GPU计算两向量间的相似度,耗时结果如图 6所示。
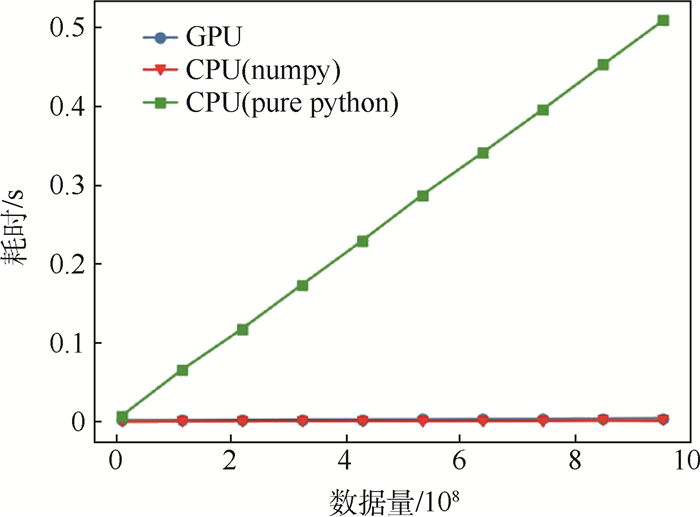 |
| 图 6 单一窗口向量相似度计算耗时 Fig. 6 Time consumption of single window vector similarity calculation |
| 图选项 |
对于相似度计算来说,经过向量化的代码在多核CPU上的执行时间与经过Cuda并行的代码在GPU上的执行时间不相上下。不过该结果也并非一成不变,而与主机和设备端的硬件性能、数据量、计算复杂度等因素均有关,实际中应根据具体情况选择最优策略。
4 特征向量提取与计算优化 4.1 特征向量提取与计算方法 分析时序数据特征时,一般要把数据划分成连续观察窗口。对于周期数据,窗口大小一般为周期的整倍数。而对于非周期数据,则需要人工指定窗口大小,如128。如果窗口中数据不完整,有缺失,则可以采用删除策略,直接删除该段窗口,如数据盲区前后的数据,以及最后一个不完整的窗口等。
窗口划分完之后,需要获取每个观察窗口的多种不同特征,主要包括统计特征、傅里叶特征、PCA特征和小波特征等。通过提取观察窗口的多类型特征,可以从不同角度获取数据特征信息,更有利于发现隐藏在数据中的规律或者模式。
4.2 基于多核CPU的多窗口向量特征提取
4.2.1 优化方法 4.1节所述多种特征可以各自构成单一特征向量,也可以经过组合之后构成合成特征向量。各种特征的计算过程相互独立,互不依赖,完全可以并行执行,而不必串行循环。即可以用cores个进程同时获取多个窗口的特征,实现较大粒度并行,其中cores为CPU核心数。
本文利用Python的multiprocessing库将4.1节串行程序替换为多核CPU并行程序。与图 3中计算多个向量间相似度过程不同,不用人工设定每批执行的进程数,直接自动获取CPU最大逻辑核心数作为最优进程数即可。因为点积运算相对简单,CPU会很快完成计算过程。如果进程数过多,单个进程的数据量偏少,就有可能造成在进程间切换,复制传递数据的消耗反而大于计算数据的消耗。但是在特征提取过程中,傅里叶变换、小波变换、PCA计算等复杂度比较高,故无需担心进程数设置过大导致单个CPU核心负载过低的问题。
4.2.2 实验结果 实验中选取2种不同长度的划分窗口,针对不同大小的测试用例分别开展单进程和多进程运算,耗时结果如图 7所示。
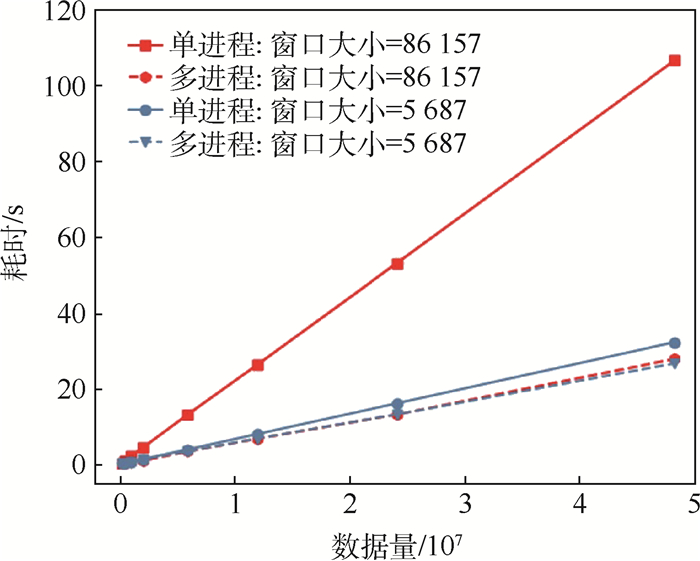 |
| 图 7 不同大小窗口的特征提取耗时 Fig. 7 Time consumption of feature extraction from different sizes of window |
| 图选项 |
可以看出,在CPU未满载的情况下,对大窗口数据用多进程提取特征的加速比高于多进程对小窗口数据的加速比。因为当数据量较大时,每个CPU核心的利用率较高。算法花在CPU计算上的时间会远远多于花在进程切换和复制数据的时间。当窗口较小时,更多时间被浪费在进程切换和复制数据上,所以导致多进程加速比减小。
4.3 基于GPU的单一窗口向量特征计算
4.3.1 优化方法 通过傅里叶变换提取频谱特征是处理时序数据的常见操作。4.2节利用多进程在多核CPU上实现较大粒度的任务级并行。在单个进程内,还可以利用GPU多线程实现较小粒度的线程级并行,进一步提升并行性能。
尽管Python的numpy库中已经提供了向量化的numpy.fft快速傅里叶变换函数,底层用C语言实现,其运算效率并不低,但是采用基于GPU的多线程并行还能带来更高的加速比。
需要注意的是,3.4节简单的计算是在Python中嵌入Cuda代码来使用GPU,而此处则通过调用Cuda库中已有的cufftExec方法来使用GPU。此时需要编写基于Cuda语句的.cu文件,导入cufft.h头文件,调用cufftExec方法计算傅里叶变换,然后将Cuda文件编译为动态链接库.so文件,再用Python的ctypes实现调用。另外.so文件应采用混合编译,才能正常调用相关库。
调用过程为:主机端先将原始程序运行过程中待处理的Python类型向量转换为C类型,再将主机内存中的C类型数据拷贝至设备端(GPU)全局内存中。设备端读取全局内存中的数据后开始核心傅里叶变换计算,并将结果保存在全局内存中。之后再将C类型结果数据从设备端拷贝回主机端,并转换成Python类型。这个过程中应特别注意Python与C类型数据间相互转换的效率问题。
4.3.2 实验结果 本实验对比了针对不同长度窗口数据,在CPU上运行numpy.fft获得傅里叶变换结果和在GPU上运行cufftExec方法获得傅里叶变换结果的运行时间。耗时结果和加速比如图 8所示。其中,基于CPU的numpy.fft方法中调用一次fft所花费时间记为该方法的核心耗时。基于GPU的cufftExec方法中将不考虑数据类型转换与数据拷贝过程的fft计算过程耗时记为核心耗时。算法整个完成时间记为总耗时。可以看出,数据量越大,GPU加速效果越明显。
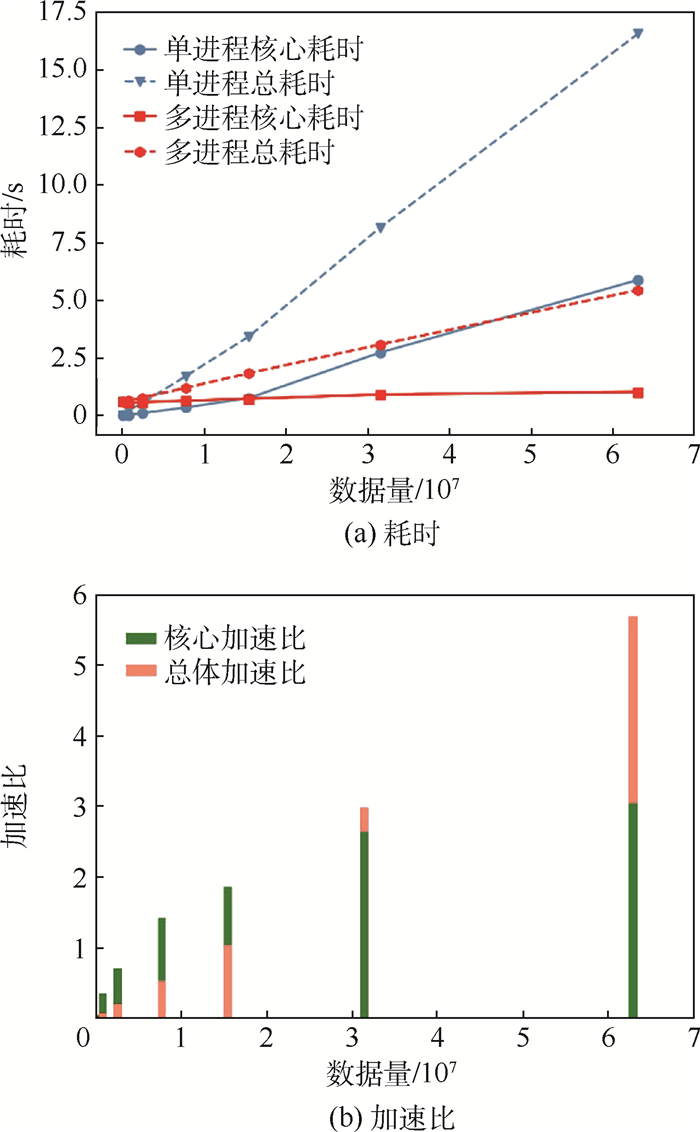 |
| 图 8 不同方法优化后的特征计算效率 Fig. 8 Characteristic calculation efficiency after optimization by different methods |
| 图选项 |
5 聚类过程优化 5.1 TK-Means聚类算法 聚类是一种非常重要的数据挖掘方法,特别是对于时序大数据,绝大部分数据都没有人工标签,无法使用分类方法,而只能用聚类进行初步挖掘。
传统的K-means聚类算法需要人工指定簇的数目,但是对于实际数据,最优簇数往往很难事先确定。在TK-Means聚类算法中,簇的数不是一个固定值,而是一个范围[min, max]。TK-Means聚类算法首先根据随机初始阈值t得到初次聚类结果。如果初次聚类结果的簇数目不在控制范围内,则调整阈值t,重新进行初次聚类。若初次聚类结果的簇数目满足要求,执行正常的K-Means聚类过程,直到聚类结果稳定。
TK-Means聚类算法步骤如下:
步骤1 ?初次聚类。
步骤2 ?如果初次聚类得到的簇数目在[min, max]范围中,则执行步骤3;否则调整阈值t并重复执行步骤1。
步骤3 ?对聚类结果进行调整,迭代次数递增。
步骤4 ?判断聚类结果是否稳定。如果聚类结果不稳定,且迭代次数小于最大迭代阈值,则重复执行步骤3;否则,聚类结束。
本文通过TK-Means聚类算法分别对第4节各特征向量进行聚类,并将得到的聚类结果表示成特征字符。对于聚类结果中点个数最多的簇,用a特征表示,即该簇中所有观察窗口都是a特征。该特征的支持度,也就是该簇的支持度,定义为簇中窗口数目与该数据所有窗口数目之比。
5.2 基于GPU的特征向量聚类
5.2.1 优化方法 通常的并行K-Means聚类算法只针对“计算所有点到簇心间距离”进行并行,而本文将算法迭代过程所有步骤都进行了并行优化,并综合运用GPU中的共享内存、常量内存、二维线程等措施优化提升并行聚类过程时间性能。本文实现的并行聚类算法步骤如下:
步骤1 ?初始化每个样本的簇标签。
步骤2 ?迭代过程:①统计每一簇的样本和;②统计每一簇的样本个数;③计算每一簇的中心:样本和/样本个数;④计算每个样本与每个簇中心的欧氏距离;⑤根据欧氏距离更新样本的簇标签。
上述过程从流程上看似乎与串行K-Means聚类算法没有区别,但实际上其迭代过程是在GPU中并行完成的。本文以310 000个样本(维度为10)聚成80类为例。在GPU中各个函数分解方式如下:
1) 初始化样本簇标签函数。由于只执行一次,且计算量非常小,故不作为优化的重点。线程块维度:256;线程格维度:(310 000+256-1)/256=1 211。每个线程负责初始化一个样本的簇标签。
2) 统计每一簇的样本和函数。如果每个簇的样本都放在连续空间,那么此函数可使用类似规约求和的方式实现,且效率很高。但是此处每个簇是分散的,所以换一种方式。线程块维度:(16, 16);线程格维度:((10+16-1)/16, (310 000+16-1)/16)=(1, 19 375)。每个线程负责一个样本中的一个数据。此处要使用原子操作,因为多个线程可能同时写一个聚类中心的数据。也可以按下列方式划分线程块和线程格。线程块维度:256;线程格维度:(310 000+256-1)/256=1 211。每个线程负责更新一个样本,但是此时的效率通常不如之前高。
3) 统计每一簇的样本个数函数。与初始化簇函数类似,计算量很少,每个负责处理一个样本的计数,只有一个原子操作的加法,所以依旧采用一维的线程方式。线程块维度:256;线程格维度:(310 000+256-1)/256=1 211。由于会有310 000个线程写80个位置,所以会存在许多冲突,此处对其进行优化,开辟线程数变为:线程块维度:1 024;线程格维度:(310 000+1 024-1)/1 024=303。与此同时,在每个块内申请80个整数大小的共享内存,先在块内进行统计,再写到全局内存,而不是像第一种方式那样,直接写全局内存,这样能避免很多冲突,获得更高加速比。
4) 计算每一簇的聚类中心函数。此函数用于对每个样本求和之后取平均操作,计算量极其少,不是优化的重点,开辟二维线程块。线程块维度:(16, 16);线程格维度:((10+16-1)/16, (80+16-1)/16)=(1, 5)。每个线程负责更新簇中心中的一个数。
5) 计算每个样本与每个簇中心的欧氏距离函数。优化重点,因K-Means聚类算法绝大部分计算量都集中在求每个样本与每个簇中心的欧氏距离,故此处也开辟二维线程块。线程块维度:(16, 16);线程格维度:(80+16-1)/16, (310 000+16-1)/16)=(5, 19 375)。每个线程负责计算一个样本与一个簇中心的欧氏距离。
因函数计算过程中簇中心是不变的,可以考虑使用常量内存将内存访问合并,进而隐藏内存访问延迟,在一定程度上提高读取效率,以此加快对簇中心的访问速度。
因此函数计算方式与矩阵乘法类似,可以考虑使用共享内存,每个线程块的任务是计算16个样本与16个簇中心的距离,将16个样本与16个簇中心的数据存到共享内存中。
实验中发现使用共享内存的计算时间远远小于未使用共享内存的计算时间。但是使用常量内存的计算时间却不一定比不使用常量内存的时间还长,而根据簇心数据大小和设备硬件具体分析才行。不仅要看GPU最大可用常量内存,还要看每个SM可供常量内存使用的高速缓存是多大。
6) 样本簇标签更新函数。用于寻找每个样本最近的簇中心,将当前样本划归到该簇,可以开辟一维线程。线程块维度:256;线程格维度:(310 000+256-1)/256=1 211。每个线程用于查找当前样本对应的与簇心间的最短距离(共80个)。因为求最小值与规约类似,而上述方式的每个样本却是完全串行的方式,所以对其进行优化,开辟二维线程。线程块维度:(16,16);线程格维度:((1, (3 100+16-1)/16)=(1, 19 375)。每个线程块用于计算16个样本的最小距离,也就是说用16个线程来完成原先1个线程的工作。最后,将规约后剩余2个元素的较小值作为最短距离。
5.2.2 实验结果 实验中选取含有不同样本数目的用例,分别用原始串行程序和经过并行与优化后的程序进行聚类,得到两者的耗时及加速比,如图 9所示。可以看到,在保证系统可用资源充足的情况下,聚类样本数越大,并行化之后的加速比越高。
 |
| 图 9 并行优化前后的聚类效率 Fig. 9 Clustering efficiency before and after parallel optimization |
| 图选项 |
5.3 基于Cuda的自适应聚类
5.3.1 优化方法 TK-Means聚类算法的自适应聚类依赖于距离阈值的调整,虽然可以采取二分法加快阈值收敛的过程,但却不能被有效的并行化。
实验中根据“簇大则分裂簇小则合并”的思想,提出一种K值自适应调整算法,将K值估计问题转化为单个簇中的样本数估计问题,从而能够在Cuda并行聚类程序中实现簇数的自适应调整。算法流程如图 10所示。
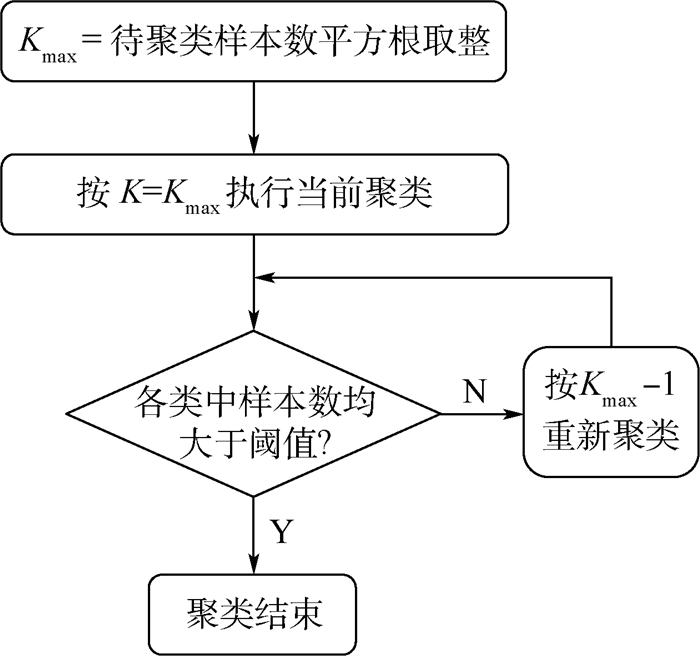 |
| 图 10 Cuda自适应聚类流程 Fig. 10 Cuda adaptive clustering flowchart |
| 图选项 |
分裂与合并过程为:设定一个簇中最小样本数作为参考阈值,当前聚类迭代至最后一次时会将样本个数小于该值的簇样本单列,不参与之后的簇号更新,并可根据这些簇的有无或多少判定最大簇数是设置大了还是小了,根据设大了则合并设小了则分裂的原则,调整K值后开始下一次聚类。Cuda自适应聚类算法则将上述过程简化为只合并不分裂,即K从双向收敛改为由最大值向最小值收敛。
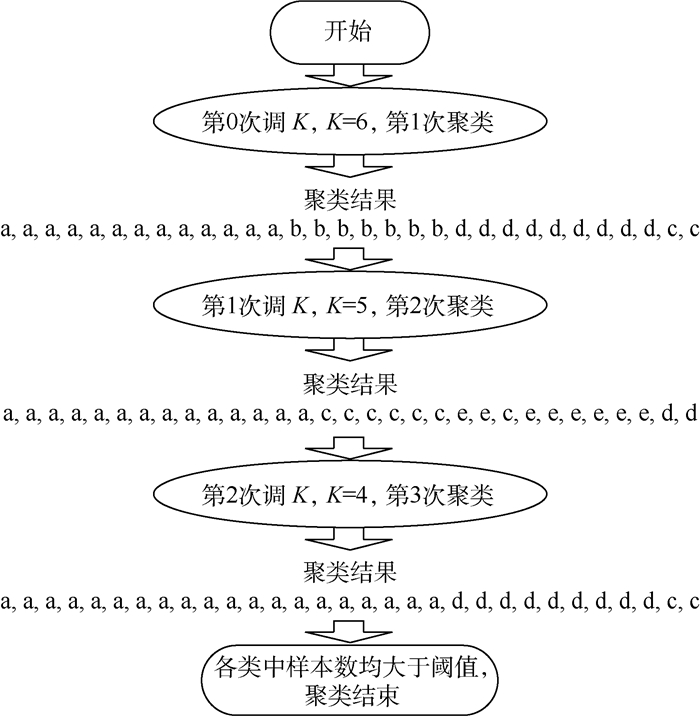
5.3.2 实验结果 实验中选取的数据用例包含31个样本,由5.1节的算法可知,最大聚类数Kmax应设为6。此外,将最小聚类数设为3,类中的最少样本数设为2,每次调K后重新聚类时的最大迭代次数设为100。图 11示例了改进后的Cuda聚类程序执行过程和结果。
 |
| 图 11 Cuda自适应聚类过程示例 Fig. 11 An example of Cuda adaptive clustering process |
| 图选项 |
在示例中,自适应聚类过程的初始K值等于6,经过2次调整后变为4,最终的聚类结果中含有3个类,其中含有最小样本个数的类为[2,2],此时若K再调整为3,簇会进一步合并,那么所有簇中的样本数都将超过参考阈值2,这与题设不符,故K调整至4便结束。由此可见,自适应聚类中的整个调整过程完全符合预期。
6 结束语 卫星智能化应用的不断拓展对卫星数据挖掘效率提出了更高要求。针对常规数据挖掘代码进行并行优化改进具有重要意义。本文以异变过程多类型特征分析过程为典型代表,针对窗口划分与向量相似度计算、特征提取、傅里叶变换、聚类等常见数据挖掘操作,提出了多种优化策略,大幅提高了算法执行效率。综合使用多种优化策略说明对卫星时序数据挖掘过程进行并行优化改进是一个复杂的过程,需要全面考虑多个算法运算效率的影响。本文方法和思路有较好的通用性,可应用于各种时序数据挖掘过程。当然,本文方法也并非完美无瑕,在CPU多进程+GPU多线程混合并行方面,以及基于Cuda流的多任务并行等方面,还有进一步改进空间。
参考文献
| [1] | CASELLA G, FIENBERG S, OLKIN I. Time series analysis and its applications:With R examples[J]. Publications of the American Statistical Association, 2006, 97(458): 656-657. |
| [2] | LI H, YANG L, GUO C. Improved piecewise vector quantized approximation based on normalized time subsequences[J]. Measurement, 2013, 46(9): 3429-3439. DOI:10.1016/j.measurement.2013.05.012 |
| [3] | WANG J, LI H, HUANG J, et al. Association rules mining based analysis of consequential alarm sequences in chemical processes[J]. Journal of Loss Prevention in the Process Industries, 2016, 41: 178-185. DOI:10.1016/j.jlp.2016.03.022 |
| [4] | LI H. Distance measure with improved lower bound for multivariate time series[J]. Physica A:Statistical Mechanics and Its Applications, 2017, 468: 622-637. DOI:10.1016/j.physa.2016.10.062 |
| [5] | MATTIOLI G, ANABLE J, VROTSOU K. Car dependent practices:Findings from a sequence pattern mining study of UK time use data[J]. Transportation Research Part A:Policy and Practice, 2016, 89: 56-72. DOI:10.1016/j.tra.2016.04.010 |
| [6] | DENG W, WANG G, XU J. Piecewise two-dimensional normal cloud representation for time-series data mining[J]. Information Sciences, 2016, 374(C): 32-50. |
| [7] | GUAN X, SUN G, YI X, et al. A novel data association algorithm for unequal length fluctuant sequence[J]. Procedia Engineering, 2015, 99: 1190-1202. DOI:10.1016/j.proeng.2014.12.648 |
| [8] | SUN Z Y, TSAI M C, TSAI H P.Mining uncertain sequence data on hadoop platform[C]//Pacific-Asia Conference on Know-ledge Discovery and Data Mining.Berlin: Springer, 2014: 204-215. |
| [9] | LAM H T, MORCHEN F, FRADKIN D, et al. Mining compressing sequential patterns[J]. Statistical Analysis and Data Mining, 2014, 7(1): 34-52. DOI:10.1002/sam.11192 |
| [10] | GONG X Y, FONG S, WONG R K, et al. Discovering sub-pa-tterns from time series using a normalized cross-match algorithm[J]. The Journal of Supercomputing, 2016, 72(10): 1-18. |
| [11] | JEYABHARATHI J, SHANTHI D. An efficient mining for app-roximate frequent items in protein sequence database[J]. Journal of Emerging Technologies in Web Intelligence, 2014, 6(3): 324-330. |
| [12] | 巨涛, 朱正东, 董小社. 异构众核系统及其编程模型与性能优化技术研究综述[J]. 电子学报, 2015, 43(1): 111-119. JU T, ZHU Z D, DONG X S. The feature, programming model and performance optimization strategy of heterogeneous many-core systems:A review[J]. Acta Electronica Sinica, 2015, 43(1): 111-119. DOI:10.3969/j.issn.0372-2112.2015.01.018 (in Chinese) |
| [13] | 戴春娥, 陈维斌, 傅顺开, 等. 通过GPU加速数据挖掘的研究进展和实践[J]. 计算机工程与应用, 2015, 51(16): 109-116. DAI C E, CHEN W B, FU S K, et al. Research progress and practice of accelerating data mining based on GPU[J]. Computer Engineering and Applications, 2015, 51(16): 109-116. DOI:10.3778/j.issn.1002-8331.1411-0027 (in Chinese) |
| [14] | CAVUOTI S, GAROFALO M, BRESCIA M, et al. Astrophysical data mining with GPU.A case study:Genetic classification of globular clusters[J]. New Astronomy, 2014, 26(1): 12-22. |
| [15] | 顾文恺. 基于GPU的脉冲压缩并行化研究[J]. 航空计算技术, 2017, 47(2): 121-124. GU W K. Study on parallel pulse compression based on GPU[J]. Aeronautical Computing Technology, 2017, 47(2): 121-124. DOI:10.3969/j.issn.1671-654X.2017.02.030 (in Chinese) |
| [16] | SCHALKWIJK J, JONKER H J J, SIEBESMA A P, et al. Weather forecasting using GPU-based large-eddy simulations[J]. Bulletin of the American Meteorological Society, 2015, 96(5): 715-723. DOI:10.1175/BAMS-D-14-00114.1 |
| [17] | VACONDIO R, MIGNOSA P, PAGANI S. 3D SPH numerical simulation of the wave generated by the vajont rockslide[J]. Advances in Water Resources, 2013, 59(11): 146-156. |
| [18] | 黄曦, 陈伟, 张建奇. 基于GPU的实时红外场景仿真系统研究[J]. 航空兵器, 2015(6): 49-54. HUANG X, CHEN W, ZHANG J Q. Study on real-time infrared scene simulation system based on GPU[J]. Aviation Weapon, 2015(6): 49-54. DOI:10.3969/j.issn.1673-5048.2015.06.012 (in Chinese) |
| [19] | SU X, WANG X, JING G, et al. GPU-Meta-Storms:Computing the structure similarities among massive amount of microbial community samples using GPU[J]. Bioinformatics, 2014, 30(7): 1031-1033. DOI:10.1093/bioinformatics/btt736 |
| [20] | 刘志文. 并行算法设计与性能优化[M]. 北京: 机械工业出版社, 2015: 162. LIU Z W. Parallel computing and performance optimization[M]. Beijing: China Machine Press, 2015: 162. (in Chinese) |
