充液成形工艺中,薄壁件大多处于双向拉伸应力状态[13],与单向拉伸相比,板材胀形试验更加符合充液成形工艺特点。由于非均匀变形存在,单向拉伸很难识别材料本身硬化或软化性能,并影响本构模型的外插能力。相比之下,板材胀形试验几乎不受颈缩的影响,且能获得较单向拉伸大得多的均匀变形应变。基于此,笔者认为采用热态胀形试验获取材料应力-应变曲线对研究板材充液热成形工艺具有十分重要的意义[14]。为了在试验中获取更为准确的应力-应变曲线,很有必要对试验中的胀形顶点进行应力状态分析,选取适当的顶点厚度解析模型,进而进行胀形流动应力计算[11, 15-16]。
1 流动应力计算理论分析 1.1 胀形件球形度评估 胀形过程中的流动应力计算需要采用合理的理论假设。双向等拉获得的胀形零件不是绝对的球形,在理论计算中,为简化运算,大多数研究者采用了胀形零件是球形的理论假设。因此,在采用球形假设之前,应该对胀形件球形度进行评估,转换到平面情况下[17],即为圆度评估问题。
Gutscher等[18]通过研究黏性介质压力(Viscous Pressure Bulging,VPB)胀形过程,指出材料强度系数K值、材料强度指数n值、厚向异性指数ξ值对胀形几何参数(如厚度分布及顶点曲率半径)影响很小,说明胀形几何形状不因材料的不同而发生很大改变,换言之,材料胀形轮廓形状是稳定的。选用铝合金7075-O材料数据,以直径80 mm的胀形零件为例,采用有限元软件MSC.Marc模拟胀形过程,提取轮廓边界上的节点,导出轮廓节点的二维坐标值(见图 1),将各坐标值进行5次多项式拟合和圆形最小二乘法拟合,则有
 | (1) |
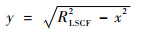 | (2) |
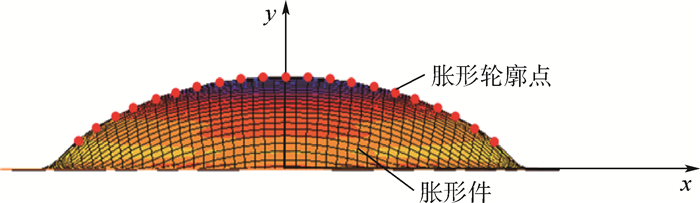 |
| 图 1 有限元胀形模型及轮廓点示意图 Fig. 1 Schematic of finite element bulging model and point of bulging profile |
| 图选项 |
式中:A0、A1、A2、A3、A4、A5为拟合参数;x为距离顶点中心点的水平向坐标;RLSCF为最小二乘法拟合的圆半径。抛物线拟合得到的曲线精度高,与胀形轮廓符合程度好,可反映胀形件的真实轮廓。对最小二乘圆拟合(Least Square Circle Fit,LSCF),Pratt[19]方法精度高且对于非线性圆弧数据的拟合适应性强。本文应用Pratt[19]方法进行最小二乘圆弧拟合,进而比较不同高径比(h/a)下前者曲率半径与后者圆形半径。
不同高径比(h/a)下胀形轮廓形状如图 2所示。高径比从小至大范围内,采用最小二乘法拟合的5次多项式所得的曲线全部通过胀形轮廓点,重合程度高,残差方量级为10-13~10-3。采用最小二乘圆拟合的圆心及半径,计算得到的圆形曲线不能与胀形件轮廓点完全重合,过小的高径比(h/a < 0.18)及过大的高径比(h/a>0.68)情况下,两者误差均较大。图 2中,h/a=0.061及h/a=0.696时,两者出现明显偏差,在0.061 < h/a < 0.696范围内,符合程度较好。采用式(3)计算式(1)沿x轴(见图 1)的任意点曲率半径:
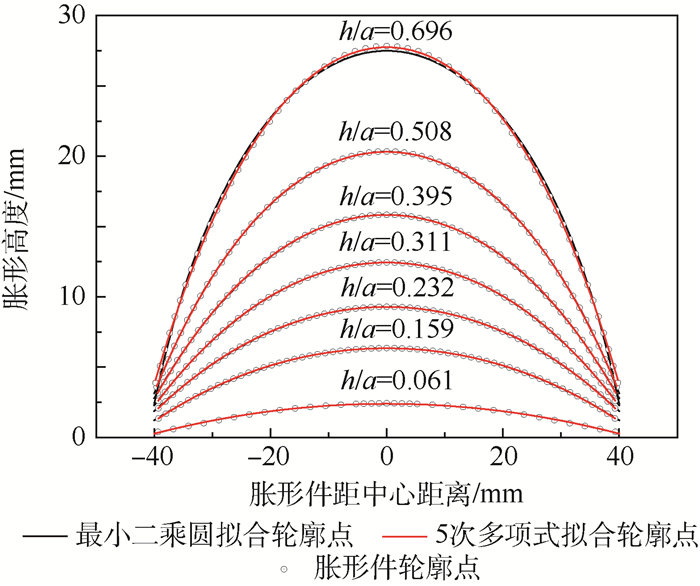 |
| 图 2 有限元胀形件轮廓点及5次多项式拟合、最小二乘圆拟合的轮廓形状比较 Fig. 2 Profile comparison of finite element bulging data points, five-order polynomial fitting and LSCF fitting |
| 图选项 |
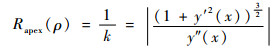 | (3) |
式中:Rapex(ρ)为曲率半径;k为曲率;y′和y″分别为式(1)的1阶和2阶导数。
h/a=0.27、0.6、0.64的曲率半径曲线如图 3所示。从图 3中可知,在h/a=0.27时,顶点曲率半径最大,越往边缘其值越小,与拟合得到的最小二乘圆半径有一个交点且远离顶点。在h/a=0.6时,靠近顶点的曲率半径趋于平缓且很接近最小二乘圆半径,边缘处曲率半径急剧增大,整个胀形轮廓曲率半径与最小二乘圆半径重合点有2处。通过对其他h/a进行比较,存在类似规律:h/a较小时(h/a < 0.18),顶点曲率半径大于最小二乘圆半径,边缘曲率半径小于最小二乘圆半径;随着h/a增大,顶点曲率半径减小且越来越接近最小二乘圆半径,边缘曲率半径偏离最小二乘圆半径严重;h/a过大时(h/a>0.68),顶点曲率半径小于最小二乘圆半径,边缘曲率半径偏离最小二乘圆半径更加严重。总体而言,在h/a中间范围内(0.18 < h/a≤0.68),胀形轮廓与球形有2处重合;而在h/a两端范围内(即h/a < 0.18、h/a>0.68),只有1处重合,表明不存在胀形轮廓任意曲率半径与球形处处重合的情况,即胀形轮廓远非球形。
 |
| 图 3 胀形轮廓沿x轴任意点曲率半径 Fig. 3 Arbitrary points radius of curvature of bulging profile along x axis |
| 图选项 |
应用式(3)计算式(1)中沿x轴的任意点曲率半径,图 4表示胀形轮廓曲率半径与最小二乘圆半径第1个重合点分布情况,图 5表示胀形顶点曲率半径与最小二乘圆半径沿高径比分布情况。可知,顶点曲率半径在特定范围内非常接近最小二乘圆半径。故在此特定范围内,可近似地用计算出的最小二乘圆半径代替胀形轮廓曲率半径。将顶点曲率半径与最小二乘圆半径进行比较,两者之间的圆形度误差为
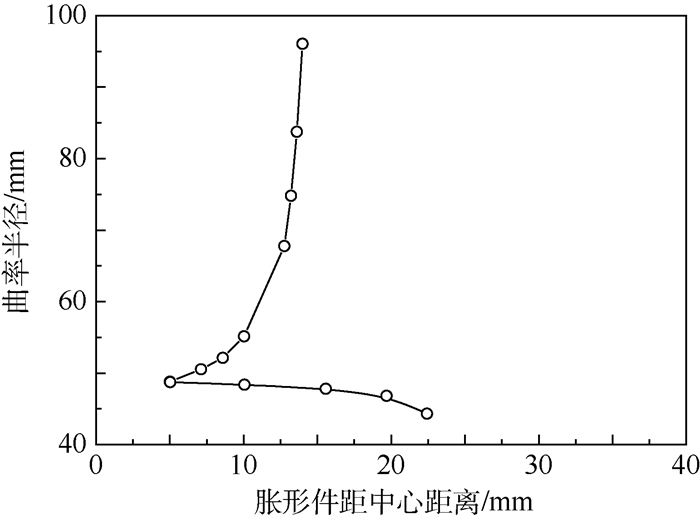 |
| 图 4 胀形轮廓曲率半径与最小二乘圆半径第1个重合点分布 Fig. 4 Distribution of the first coincidence point between radius of curvature of bulging profile and LSCF radius |
| 图选项 |
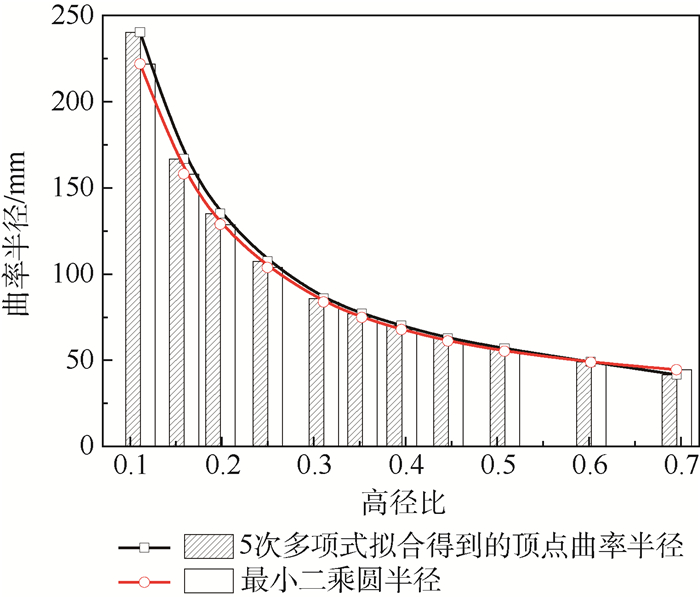 |
| 图 5 胀形顶点曲率半径与最小二乘圆半径沿高径比分布 Fig. 5 Distribution of radius of curvature of bulging vertex and LSCF radius along ratio of height to radius |
| 图选项 |
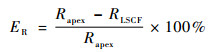 | (4) |
式中:ER为圆形度误差。
圆形度误差计算结果如图 6所示。h/a较小时(h/a < 0.18),两者误差比较大。随着h/a增大,两者误差逐渐减小,在h/a=0.6时达到最小值0.375%;而当h/a>0.6时,误差又急剧增大。从而可知,胀形顶点圆形度误差(不超过)5%时对应的高径比分布范围为0.18 < h/a≤0.68,误差(不超过)3%时对应的高径比分布范围为0.26≤h/a≤0.66。即在高径比分布范围0.18 < h/a≤0.68内,顶点曲率半径非常接近最小二乘圆半径,在此范围外,两者之间的圆形度误差较大。
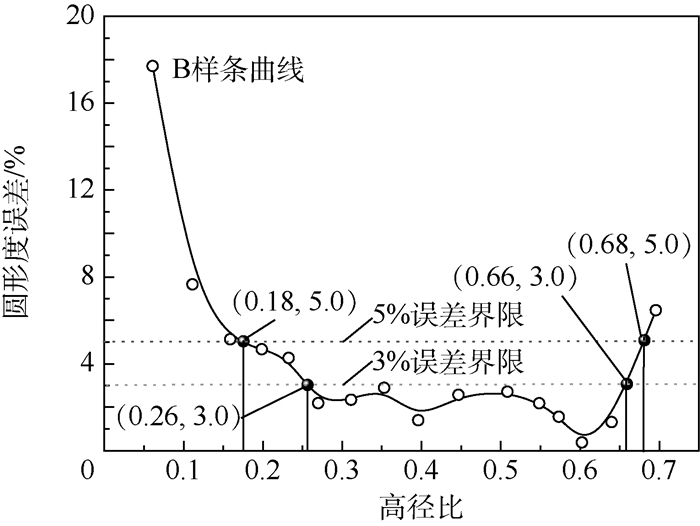 |
| 图 6 胀形顶点曲率半径与最小二乘圆半径圆形度误差沿高径比分布 Fig. 6 Roundness error distribution of radius of curvature of bulging vertex and LSCF radius along ratio of height to radius |
| 图选项 |
1.2 胀形应力应变状态分析 胀形顶点为双向等拉应力应变状态[20],对胀形顶点微元受力分析可知:
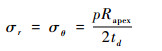 | (5) |
式中:p为胀形压力,MPa;td为胀形顶点厚度。
可知,胀形顶点的应力状态为
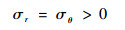 | (6) |
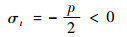 | (7) |
将式(6)、式(7)代入Mises等效应力公式,则有
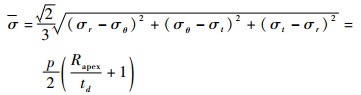 | (8) |
胀形顶点应变状态为
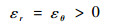 | (9) |
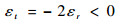 | (10) |
将式(9)、式(10)代入Mises等效应变公式,则有
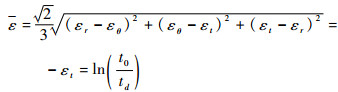 | (11) |
从式(8)、式(11)中可知,通过试验获取胀形压力p、曲率半径Rapex及顶点厚度td,便可计算出等效应力及等效应变。
2 胀形试验 2.1 试验材料 胀形试验所用材料为美铝公司(Alcoa)生产的7075-O铝合金,厚度为1 mm。该材料为Al-Zn-Mg-Cu系高强铝合金,主要用于某机型机身及机翼整体壁板制造,具有韧性较高、耐应力耐腐蚀较好等特点,其化学成分如表 1所示[16, 21]。
表 1 7075-O铝合金化学成分[16, 21] Table 1 Chemical composition of 7075-O aluminium alloy[16, 21]
| 成分 | Zn | Mg | Cu | Mn | Cr | Fe | Si | Ti | 其他 | Al |
| 含量/% | 5.1 | 2.1 | 1.2 | 0.3 | 0.18 | 0.5 | 0.4 | 0.2 | 0.2 | 余量 |
表选项
2.2 试验条件 胀形试验在专用的胀形试验机上进行[16]。根据需要,试验过程中通过压力率?(单位时间内压力的增量,MPa/s)控制实现整个胀形过程[16, 21]。选用(不超过)5%的胀形顶点圆形度误差,直径为80 mm的胀形零件,胀形高度范围为7.2~27.2 mm。在压力率?为0.005 MPa/s、温度为210℃时,进行指定胀形高度为10、12、16、20、22 mm的胀形试验。采用三坐标测量仪Century977(测量精度为0.03 μm,探针球头直径为1 mm)对不同指定胀形高度胀形件轮廓线轧制方向(0°)及垂直方向(90°)进行测量,每个方向各测21个点,从中间顶点向外,每个方向顶点两侧各测10个点,测量示意图如图 7所示。
 |
| 图 7 三坐标测量仪测量示意图 Fig. 7 Schematic of three coordinate measuring machine |
| 图选项 |
2.3 试验结果 根据2.2节所述试验条件,不同胀形高度胀形件如图 8所示。将所测数据点代入式(2)进行最小二乘圆拟合,并将结果与有限元(采用有限元软件MSC.Marc模拟胀形过程,结合Pratt[19]方法)最小二乘圆半径对比,所得结果如表 2及图 9所示。再将得到的最小二乘圆半径作为式(8)、式(11)中Rapex的试验数据,便可计算得到等效应力和等效应变。
 |
| 图 8 不同胀形高度胀形件 Fig. 8 Bulging parts with different bulging heights |
| 图选项 |
表 2 不同胀形高度时试验测量数据和有限元拟合数据胀形件轮廓最小二乘圆半径对比 Table 2 Comparison of LSCF radius of bulging parts profile based on experimental measurment data and finite element fitting data with different bulging heights
| mm | ||||||
| 胀形高度 | 轧制方向 | 垂直方向 | 有限元拟合最小二乘圆半径 | |||
| 圆心(y, z) | 最小二乘圆半径 | 圆心(x, z) | 最小二乘圆半径 | |||
| 10 | (-94.73, -159.32) | 107.16 | (108.77, -160.12) | 107.95 | 103.77 | |
| 12 | (-91.72, -133.30) | 84.18 | (113.19, -133.25) | 84.13 | 83.75 | |
| 16 | (-97.33, -114.89) | 68.79 | (117.74, -114.77) | 68.66 | 67.79 | |
| 20 | (-91.99, -94.10) | 53.70 | (117.51, -94.30) | 53.90 | 55.15 | |
| 22 | (-92.85, -91.94) | 52.35 | (120.50, -91.92) | 52.32 | 52.14 | |
表选项
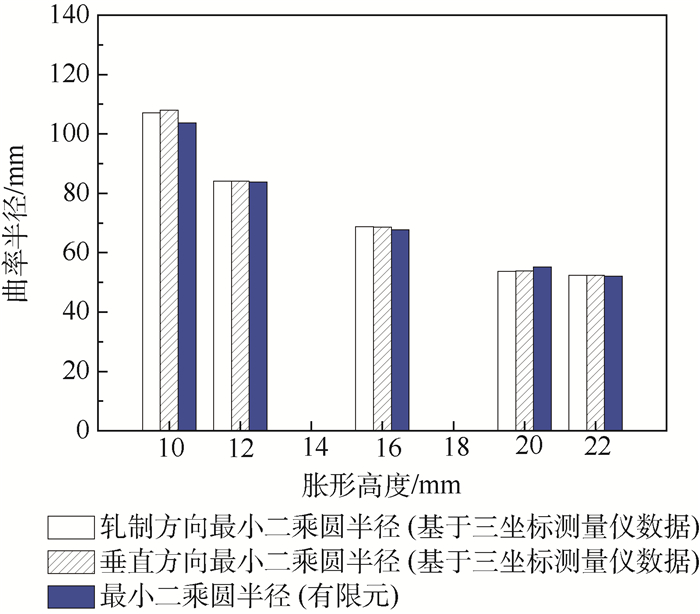 |
| 图 9 试验测量数据和有限元拟合数据胀形件轮廓最小二乘圆半径比较 Fig. 9 Comparison of LSCF radius of bulging parts profile based on experimental measurment data and finite element fitting data |
| 图选项 |
对比结果可知,除了胀形高度为10 mm时,基于试验测量数据拟合的最小二乘圆半径与基于有限元数据拟合的最小二乘圆半径有较明显误差外(该误差可接受,因为此时的高径比h/a=0.25,胀形顶点圆形度误差为3.87%,小于5%;且h/a在0.18 < h/a≤0.68范围内),胀形高度为12、16、20、22 mm时,两者结果符合程度很好。证明在一定范围内,顶点曲率半径非常接近最小二乘圆半径,可近似地用计算出的圆形曲率半径代替胀形轮廓顶点曲率半径。同时可知,温度为210℃时,方向异性(轧制方向、垂直方向)对7075-O铝合金胀形件曲率半径影响很小。
3 流动应力计算 3.1 胀形流动应力典型计算模型比较 采用超声波测厚仪测量胀形件顶点厚度,结合不同胀形高度胀形件的实测厚度,可计算出真实应力及真实应变。计算顶点曲率半径Rapex的典型解析表达式(Hill、Panknin等)及计算顶点厚度td的典型解析模型(Hill、Kruglov等)如表 3所示。
表 3 不同顶点曲率半径及顶点厚度解析模型 Table 3 Analytical model for different vertex radius of curvature and vertex thickness
| 顶点曲率半径 | 顶点厚度 | |||
| 模型 | 表达式 | 模型 | 表达式 | |
| Hill | 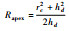 | Jovane |  | |
| Panknin | 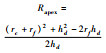 | Hill | 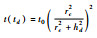 | |
| Kruglov | 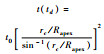 | |||
| 注:rc—胀形半径; hd—胀形高度; rf—胀形圆角半径; t(td)—顶点厚度; t0—板材初始厚度。 | ||||
表选项
对于胀形顶点曲率半径Rapex及顶点厚度td,可通过胀形直径Dc(Dc=2rc)、胀形高度hd两个参数表示。
各模型比较结果如图 10所示,Hill顶点曲率半径模型预测值小于试验值,Panknin顶点曲率半径模型预测值大于试验值,而2种模型预测值的平均值与试验值最接近。
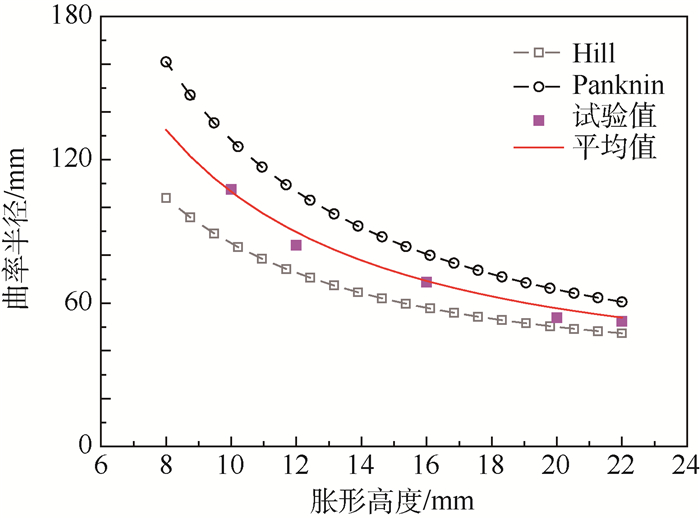 |
| 图 10 顶点曲率半径计算模型与试验数据对比 Fig. 10 Comparison of calculation model of vertex radius of curvature and experimental data |
| 图选项 |
图 11为顶点厚度计算模型与试验数据对比结果。可知,理论模型及试验值均显示随胀形高度增大顶点厚度减薄迅速。Jovane模型与Hill模型依赖于胀形高度,而Kruglov模型中含有顶点曲率半径信息,可采用表 3中Hill曲率半径模型或Panknin曲率半径模型,还可采用此2种模型的平均值,则Kruglov厚度模型可标注为Kruglov-Hill、Kruglov-Panknin或Kruglov-ave以示区别。可以看到,Hill厚度模型预测的顶点厚度偏小严重,Jovane、Kruglov-Panknin、Kruglov-ave厚度模型预测值较试验值偏大,Kruglov-Hill厚度模型预测值最接近试验值。
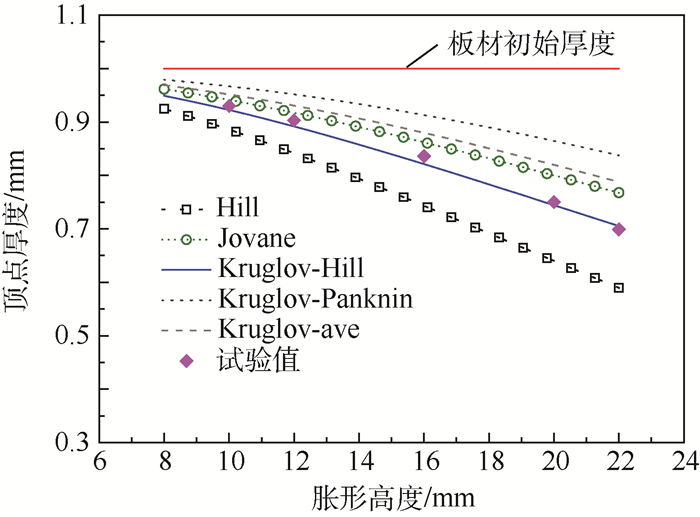 |
| 图 11 顶点厚度计算模型与试验数据对比 Fig. 11 Comparison of calculation model for vertex thickness and experimental data |
| 图选项 |
3.2 胀形试验流动应力计算过程 将基于试验数据得到的顶点曲率半径Rapex、胀形高度hd、胀形压力p、顶点厚度td代入式(8)、式(11),可得到基于试验数据的应力及应变数据点。对压力率0.005 MPa/s及210℃下胀形高度-压力曲线进行多项式拟合,结合表 3中的不同曲率半径、顶点厚度解析模型,可得到不同的应力-应变曲线。可以看到,方式1(Hill顶点曲率半径模型-Hill顶点厚度模型)及方式2(Hill顶点曲率半径模型-Kruglov-Hill顶点厚度模型)2种组合模型获得的应力曲线低于基于试验数据得到的应力曲线,方式3(Panknin顶点曲率半径模型-Kruglov-Hill顶点厚度模型)组合模型获得的应力曲线则高于试验值。在图 10中获得最佳顶点曲率半径的模型组合方式为Hill及Panknin顶点曲率半径模型的平均值,在图 11中获得最佳顶点厚度模型的组合方式为Kruglov-Hill,两者组合起来(方式4)能够预测得到最佳应力值,如图 12所示。
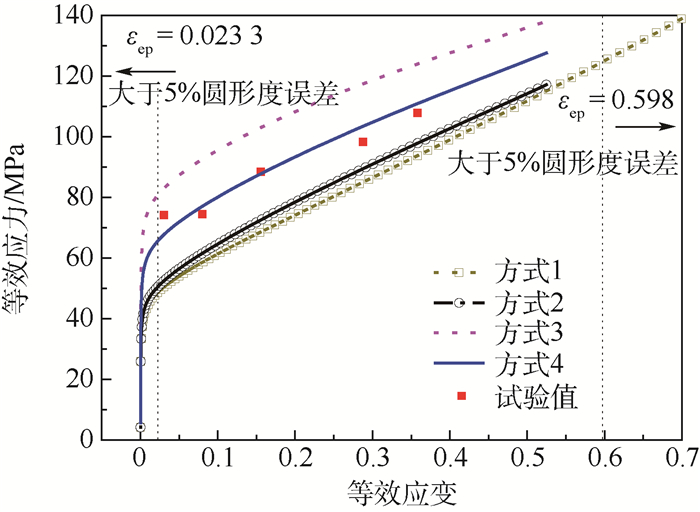 |
| 图 12 不同模型确定的应力-应变曲线对比 Fig. 12 Comparison of stress-strain curves determined by different models |
| 图选项 |
根据需要,选取100、80、60 mm 3种胀形直径(Dc=2rc),在压力率为0.005 MPa/s时进行胀形试验。在常温下采用不同胀形直径获得的胀形高度-压力曲线如图 13所示。单向拉伸获得的7075-O铝合金强度极限为270~280 MPa,而常温下采用胀形直径80 mm模具进行胀形所得的该材料强度极限在268 MPa(见图 14,其中拟合函数为y=A+BεC,A、B、C为拟合参数,ε为等效应变),可见两者符合较好,说明采用胀形直径为80 mm的模具进行胀形试验具有合理性。
 |
| 图 13 常温下不同胀形直径的胀形高度-压力曲线 Fig. 13 Bulging height-pressure curves obtained with different bugling diameters at room temperature |
| 图选项 |
 |
| 图 14 常温下不同胀形直径获得的应力-应变曲线(?=0.005 MPa/s) Fig. 14 Stress-strain curves obtained with different bulging diameters at room temperature(?=0.005 MPa/s) |
| 图选项 |
因这些经典模型均基于板材胀形轮廓为球形的理论假设,故图 12得到的应力-应变曲线并不是在全范围内有效。如前所述,圆形度误差控制在5%范围内,对应的胀形高度范围为7.2~27.2 mm,相应的有限元模拟得到的顶点厚度范围为0.98~0.56 mm,由式(8)、式(11)可知,其对应应变范围为0.023 3~0.598(见图 12)。将试验中的胀形高度-压力曲线进行5次多项式拟合,结果如表 4所示。
表 4 胀形高度-压力曲线5次多项式拟合 Table 4 Five-order polynomial fitting of bulging height-pressure curves
| 温度 | 压力率/(MPa·s-1) | 5次多项式拟合 | |||||
| A0 | A1 | A2 | A3 | A4 | A5 | ||
| 常温 | 0.05 | 0.003 | -0.011 | 0.068 | -0.005 | 1.94×10-4 | -3.19×10-6 |
| 0.005 | -0.022 | -0.014 | 0.061 | -0.004 | 8.73×10-5 | -7.88×10-7 | |
| 160℃ | 0.05 | -0.044 | 0.092 | 0.029 | -0.003 | 1.08×10-4 | -2.05×10-6 |
| 0.005 | 0.013 | -0.027 | 0.034 | -0.002 | 4.92×10-5 | -5.29×10-7 | |
| 210℃ | 0.05 | 0.001 | 0.080 | 0.018 | -0.001 | 6.23×10-5 | -1.09×10-6 |
| 0.005 | -0.038 | 0.116 | 0.002 | 6.23×10-5 | -9.21×10-6 | 1.52×10-7 | |
| 280℃ | 0.05 | -0.015 | 0.065 | 0.011 | -9.99×10-4 | 4.69×10-5 | -8.76×10-7 |
| 0.005 | -0.013 | 0.046 | 0.006 | -4.22×10-4 | 1.55×10-5 | -2.25×10-7 | |
表选项
采用Hill顶点曲率半径模型及Panknin顶点曲率半径模型的平均值+Kruglov-Hill顶点厚度模型的组合方式,结合表 4中胀形高度-压力曲线拟合结果,在应变范围0.023 3~0.598内,计算得到应力-应变曲线如图 15所示。可知,采用胀形试验获得的应力-应变曲线,即使在高温下也无明显的下降阶段,即在失稳前能够获得较大的均匀变形。压力率为0.05 MPa/s时,板材胀形速度大,获得的胀形高度低,进而得到的等效应变较小;相反,压力率为0.005 MPa/s时,即小变形速度下能够获得较大的等效应变。从而可知,压力率可影响其应力-应变曲线。
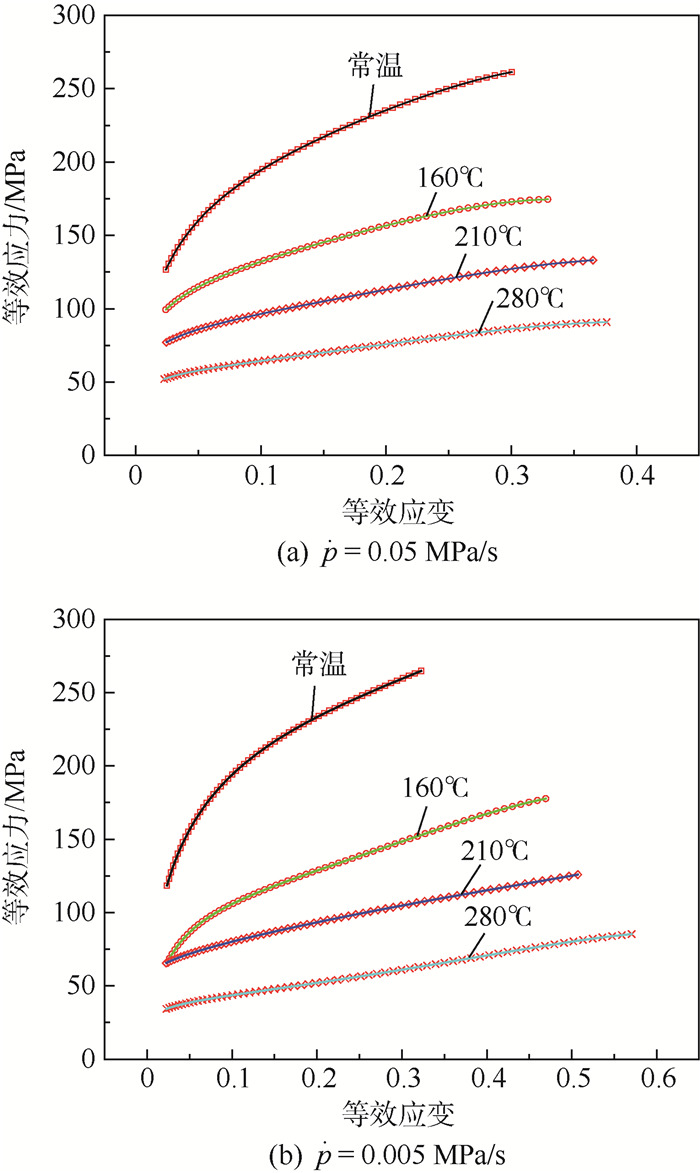 |
| 图 15 不同温度及压力率下应力-应变曲线 Fig. 15 Stress-strain curves with different temperatures and pressure rates |
| 图选项 |
4 结论 1) 本文在2种压力率(0.05、0.005 MPa/s)条件下进行了不同胀形高度及胀形直径的胀形试验,得到了不同胀形高度胀形件及胀形高度-压力曲线。
2) 在高径比0.18 < h/a≤0.68范围内,胀形顶点曲率半径与最小二乘圆半径之间的圆形度误差为(不超过)5%,顶点曲率半径非常接近最小二乘圆半径,此时最小二乘圆半径可近似代替胀形顶点曲率半径。
3) 基于三坐标测量仪测得的胀形件外形轮廓数据,拟合出了最小二乘圆半径;采用厚度仪测得的顶点厚度,结合胀形高度-压力曲线,计算得到了基于试验数据的5个应力应变数据点。
4) 对已有曲率半径及厚度理论模型进行比较,发现Hill和Panknin顶点曲率半径模型的平均值及Kruglov-Hill顶点厚度模型最符合试验数据。
5) 在210℃时,方向异性(轧制方向、垂直方向)对铝合金7075-O胀形件曲率半径的影响很小;同时,压力率可影响其应力-应变曲线。
参考文献
| [1] | SELLARS C M, MCTEGART W J. On the mechanism of hot deformation[J]. Acta Metallurgica, 1966, 14(9): 1136-1138. DOI:10.1016/0001-6160(66)90207-0 |
| [2] | HOULSBY G T, PUZRIN A M. Principles of hyperplasticity[M]. London: Springer-Verlag, 2006: 19-28. |
| [3] | KOC M, BILLUR E, CORA O N. An experimental study on the comparative assessment of hydraulic bulge test analysis methods[J]. Materials and Design, 2011, 32(1): 272-281. DOI:10.1016/j.matdes.2010.05.057 |
| [4] | LANG L H, CAI G S, LIU K N, et al. Investigation on the effect of through thickness normal stress on forming limit at elevated temperature by using modified M-K model[J]. International Journal of Material Forming, 2015, 8(2): 211-228. DOI:10.1007/s12289-014-1161-3 |
| [5] | NURCHESHMEH M, GREEN D E. Influence of out-of-plane compression stress on limit strains in sheet metals[J]. International Journal of Material Forming, 2012, 5(3): 213-226. DOI:10.1007/s12289-011-1044-9 |
| [6] | LANG L H, LIU B S, LI T, et al. Experimental investigation on hydromechanical deep drawing of aluminum alloy with heated media[J]. Steel Research International, 2012, 83(3): 230-237. DOI:10.1002/srin.v83.3 |
| [7] | 马高山.5A90铝锂合金板材热成形有限元模拟与试验研究[D].北京: 北京航空航天大学, 2008: 37-46. MA G S.FEM simulation and experimental research on hot forming of 5A90 Al-Li alloy sheet[D].Beijing: Beihang University, 2008: 37-46(in Chinese). |
| [8] | LIU B S, LANG L H, ZENG Y S, et al. Forming characteristic of sheet hydroforming under the influence of through-thickness normal stress[J]. Journal of Materials Processing Technology, 2012, 212(9): 1875-1884. DOI:10.1016/j.jmatprotec.2012.03.021 |
| [9] | HOFFMANNER A L.Development of workability testing techniques: F33615-67-C-1466[R].Cleveland: Interim Report on Air Force Contract, 1967. |
| [10] | GROCHE P, HUBER R, DOERR J, et al. Hydromechanical deep-drawing of aluminium-alloys at elevated temperatures[J]. CIRP Annals, 2002, 51(1): 215-218. DOI:10.1016/S0007-8506(07)61502-9 |
| [11] | KAYA S, ALTAN T, GROCHE P, et al. Determination of the flow stress of magnesium Az31-O sheet at elevated temperatures using the hydraulic bulge test[J]. International Journal of Machine Tools and Manufacture, 2008, 48(5): 550-557. DOI:10.1016/j.ijmachtools.2007.06.011 |
| [12] | MAHABUNPHACHAI S, KOC M. Investigations on forming of aluminum 5052 and 6061 sheet alloys at warm temperatures[J]. Materials and Design, 2010, 31(5): 2422-2434. DOI:10.1016/j.matdes.2009.11.053 |
| [13] | LANG L H, WANG Z R, KANG D C, et al. Hydroforming highlights:Sheet hydroforming and tube hydroforming[J]. Journal of Materials Processing Technology, 2004, 151(1-3): 165-177. DOI:10.1016/j.jmatprotec.2004.04.032 |
| [14] | SIEGERT K, JAGER S, VULCAN M. Pneumatic bulging of magnesium AZ 31 sheet metals at elevated temperatures[J]. CIRP Annals, 2003, 52(1): 241-244. DOI:10.1016/S0007-8506(07)60575-7 |
| [15] | STRANO M, ALTAN T. An inverse energy approach to determine the flow stress of tubular materials for hydroforming applications[J]. Journal of Materials Processing Technology, 2004, 146(1): 92-96. DOI:10.1016/j.jmatprotec.2003.07.016 |
| [16] | 刘宝胜.板材充液热成形机理及关键技术研究[D].北京: 北京航空航天大学, 2012: 95-105. LIU B S.Research on forming mechanism and key technologies of warm sheet hydroforming[D].Beijing: Beihang University, 2012: 95-105(in Chinese). |
| [17] | GOTOH M, CHUNG T, IWATA N. Effect of out-of-plane stress on the forming limit strain of sheet metals[J]. JSME International Journal Series A:Mechanics and Material Engineering, 1995, 38(1): 123-132. DOI:10.1299/jsmea1993.38.1_123 |
| [18] | GUTSCHER G, WU H C, NGAILE G. Determination of flow stress for sheet metal forming using the viscous pressure bulge (VPB) test[J]. Journal of Materials Processing Technology, 2004, 146(1): 1-7. DOI:10.1016/S0924-0136(03)00838-0 |
| [19] | PRATT V. Direct least-squares fitting of algebraic surfaces[J]. Computer Graphics, 1987, 21(4): 145-152. DOI:10.1145/37402 |
| [20] | PEIRS J, VERLEYSEN P, VAN PAEPEGEM W, et al. Determining the stress-strain behaviour at large strains from high strain rate tensile and shear experiments[J]. International Journal of Impact Engineering, 2011, 38(5): 406-415. DOI:10.1016/j.ijimpeng.2011.01.004 |
| [21] | LANG L H, DU P M, LIU B S, et al. Pressure rate controlled unified constitutive equations based on microstructure evolution for warm hydroforming[J]. Journal of Alloys and Compounds, 2013, 574: 41-48. DOI:10.1016/j.jallcom.2013.03.134 |
