近年来,3D视觉的研究与应用正呈现迅猛发展的态势,这是由于低成本的3D感知硬件的可用性增长所驱动的。如Microsoft公司于2010年发布了Kinect,利用了结构光技术快速重建3D场景。Occipital于2015年使用相同的原理,提供可连接的3D传感器。然而这类传感器的使用会有明显限制,主动光由于发散等物理条件约束,干扰后续算法如中心位置提取等处理[1]。最重要的是,这样会丢失图像的精细化结构,比如高纹理区、物体边缘和明光照射环境等。此外,对于高速运行的物体进行重建,面阵芯片的分辨率较低且采样速率较低,无法满足场景需求。TOF(Time of Flight)相机同样采用主动光探测方式,但其目的不是照明,而是利用入射光信号与反射光信号的变化来进行距离测量[2]。因此在室外等环境中,TOF比结构光技术应用更加广泛。同时,TOF的深度测量受物体表面灰度特征影响较小,测量准确度相对较高。但是,TOF相机分辨率较低,无法重建精细物体结构。
与TOF相机获得深度数据的方法不同,双目立体视觉三维重建可以恢复高纹理区更精细化的结构,且在高速检测中易获得较高分辨率图像[3]。但是双目立体匹配算法对场景要求较高,弱纹理区会产生很多误匹配,非前向平行平面易重建为阶梯状,边缘发生膨胀。因此,在有些应用场景中,双目立体系统获取的深度信息较不可靠。
目前,铁路等交通运输行业对零件等缺损检测,愈加依赖于三维信息。而市场上的3D产品很少能满足铁路货车车底三维重建精度和速度的要求。以运行速度为120 km/h的车底应用场景为例,基于TOF的深度相机拍摄速度目前可以达到5 000帧/s,即深度信息的精度仅可以达到5 mm。对于车底大型部件的细节和螺纹等小型部件的轮廓,会造成深度信息缺失。而对双目系统而言,车底的图像环境简单,缺少纹理,极易造成立体算法的误匹配,导致错误的深度信息。
综合上述TOF相机和双目立体匹配算法等技术的优缺点,可以建立一个多相机融合系统。包括TOF相机(低分辨率)、双目立体相机(高分辨率),实现3D与2D协同成像,在拍摄高质量火车2D图像的同时,输出与2D图像高度匹配的高精度3D图像。利用数据融合策略,既提升了3D图像的分辨率,也改善了重建精度。
基于双目与TOF系统具有互补的特性,科研人员开展了许多将两系统结合的研究工作。一些研究的重点放在TOF系统与单相机系统的结合上。文献[4]提出了基于双边滤波器的方法,利用彩色图像信息对于TOF上采样进行引导。文献[5]利用边缘保护的方法对TOF数据进行插值处理。但是TOF与双目系统的结合会得到更准确的视差结果,因为2个系统都可以得到各自的深度图。文献[6]根据贝叶斯理论提出了基于后验概率的马尔可夫随机场模型,并利用置信传播的方法进行优化求解,然而此类全局性算法计算复杂度较大。文献[7]将TOF深度数据转化为代价约束双目立体匹配算法,并未考虑TOF数据无效情况对双目立体匹配算法的干扰,且融合效果很大程度依赖于双目立体匹配算法。文献[8]采用局部算法将TOF系统与双目系统置信度聚合,但是默认两系统的权重值相等。本文根据两系统的优缺点,针对不同区域对其测量结果进行权重赋值,以得到最优效果。
1 双目立体匹配算法 1.1 算法原理 双目系统由2个相机从不同的位置对同一目标进行拍摄,通过内外参标定、畸变校正[9]和立体校正[10],输出标准前向平行图像,保证匹配点对的像素纵坐标Y相同,如图 1所示。然后通经过立体匹配算法实现图像的稠密匹配,即可计算得到视差值。在得到视差值后根据三角测量原理可以计算得出物体的深度信息,进而得到3D点云数据。
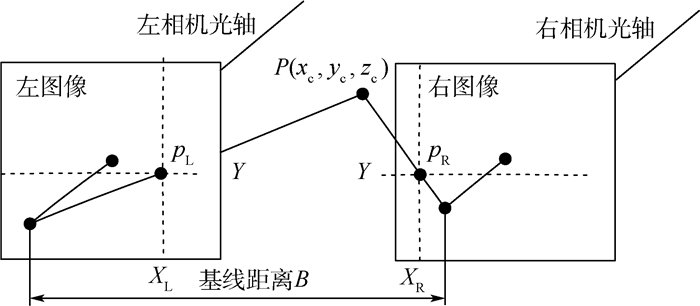 |
| 图 1 双目系统示意图 Fig. 1 Schematic diagram of stereo vision system |
| 图选项 |
根据图 1,对空间点P在左右图像上的对应像点pL和pR具有相同的Y坐标。设CL和CR分别为左、右相机的光心,光心之间的距离为B,相机焦距为f。
设P点在左相机坐标系下的坐标为(xL, yL, zL),在左、右图像上像点对应横坐标为XL和XR,则视差d可表示为
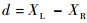 | (1) |
根据三角原理,点P在相机坐标系下的三维坐标为
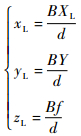 | (2) |
因此,当基线距离B、相机焦距f通过标定得到后,若左相机图像上的一点能够在右相机图像上找到对应的匹配点,即得到视差d,继而确定出该点在做相机坐标系下的三维坐标[9]。
1.2 局部匹配算法 一套完整的双目立体匹配系统主要包括:图像采集、相机标定与畸变矫正、立体匹配和三维重建。其中立体匹配是整个双目立体视觉中的核心部分,一般分为全局和局部2种算法。全局匹配算法通过构建匹配代价函数,不断迭代优化求解全局最优解,其精度比局部匹配算法高,但计算复杂度高、耗时长。而局部匹配算法计算复杂度低、实时性好,精度也可达到一定要求,因此得到广泛的应用。为保证系统的实时性能,本文采用局部匹配算法。
局部匹配算法一般包括代价计算、代价聚合、视差计算和视差优化4个部分[11]。基于生物视觉上的观察,以人眼立体匹配为参考给出“由粗到细”(coarse-to-fine)的策略进行立体匹配。
1.2.1 代价计算 常用的匹配代价主要有灰度绝对差和、平方差和、Census转换等。
绝对差和:
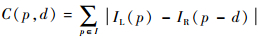 | (3) |
平方差和:
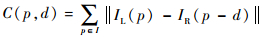 | (4) |
Census转换:
 | (5) |
式中:C(p, d)为左图像p处像素在视差d下的初始匹配代价;IL和IR分别为左、右图像上对应位置的像素大小;wp为像素p的邻域窗口;

1.2.2 代价聚合 通过对比基于ST(Segment-Tree)、EF (Edge-aware Filter)、BF(Bilateral Filter)、GF(Guided Filter)、NL(Non-Local)和Box等聚合算法的视差结果,以Middlebury数据库中图像Teddy为例,如图 2所示。对比图中Teddy熊与周围背景的视差细节可以发现,ST、EF、BF和Box聚合算法的结果图中存在大量噪点,而GF聚合算法在前景与背景的深度不连续区域存在很多误匹配。综合考虑算法复杂度和算法效率等因素,最终确定双目聚合算法采取NL。
 |
| 图 2 不同代价聚合算法的视差图对比 Fig. 2 Comparison of disparity maps generated by different cost aggregation algorithms |
| 图选项 |
1.2.3 视差计算 局部算法在视差计算中一般采用胜者为王(Winner-Takes-All,WTA)的计算策略。在匹配代价聚集之后能够得到一系列待定的视差值与对应的匹配代价, WTA是在这些视差值中,选择匹配代价最小的视差值作为视差计算的结果[3]。
1.2.4 视差优化 视差计算所得的初步视差图存在许多误匹配与无效视差。由于双目图像中存在许多由遮挡、视场角不同等原因所带来的匹配难点,并非所有像素点都在双目图像中可以得到匹配像素[4]。对于只在单幅图像中可见的区域,并不能由双目立体匹配算法进行重建,并且之前处理中会存在一些误匹配的区域。因此,在视差计算之后还需要一个优化求精的过程。
1) 左右视差不一致性检测
在得到初始视差图像后,首先对左、右图像的视差图像进行不一致性检验[3]。
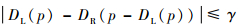 | (6) |
式中:DL和DR分别为左图像和右图像的视差;γ为检测阈值,通常取γ=2。当左图像上一点的视差与右图像对应点视差相差较大时,认为该点视差为异常值。
2) 空洞填充
经过上述步骤后,标记出不可信的点。这些点在视差图中产生大量的无效空洞,需要用周围的有效值进行填充。
定位所有的无效点,对每个无效点遍历如下操作:①分别向左、向右搜索,直到发现左边或者右边第1个有效视差的点,停止搜索;②若①中同时找到左、右第1个有效视差,则选取其中最小的一个赋值给当前点;若只发现其中的一个,则直接将其赋值给当前点。
由于离有效点近的无效点赋值的可信度远高于远离有效点的无效点,因此,执行完以上过程,并不能输出准确的视差图。尤其是一些空洞比较大的区域,赋值后视差的不可信程度急剧增加。故还需要把2D图像作为引导图像,参与滤波修补。
2 TOF系统置信度 TOF相机的测量原理:首先,通过连续发射经过调制的特定频率的光脉冲到被观测物体上;然后,接收从物体反射回去的光脉冲,通过探测光脉冲飞行的往返时间来计算被测物体离相机的距离,同时记录光线强度信息[12]。
如文献[1]中所述,TOF的置信度测量受很多因素的影响,如被测物体表面反射率,测量距离,以及对深度不连续处周围的像素测量,因此很难实现对每个像素位置的置信度测量。但是在后续的融合算法中,需要对每个像素位置给出准确的置信度值。因此,本文利用了TOF相机的辐射特性来定义每个像素处的置信度,包括接收信号的振幅和强度。
TOF接收到返回信号的振幅和强度取决于很多因素,其中最重要的是表面反射特性,以及与相机的距离2个方面。虽然也可以直接使用距离定义置信度,但是使用振幅和强度定义置信度考虑了除距离外的其他信息。接收到的振幅对测量的精度影响很大,振幅越大,信噪比越高,因此,测量精度越高。根据文献[1, 13],TOF相机测得深度值的噪声分布符合高斯标准差:
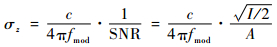 | (7) |
式中:fmod为TOF信号的频率;SNR为信噪比;A为振幅;I为强度;c为光速。双目系统获得的初始信息是视差值,因此,需要将TOF的深度值转换为视差值。同理,TOF系统的置信度也需要转化为与视差值的关系。对于测得的深度值z,设其标准差为σz,根据式(2),对应的视差标准差σd计算式为
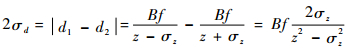 | (8) |
化简为
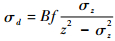 | (9) |
为了利用视差值的标准差构造TOF系统置信度rT,经过多次试验后,定义2个阈值σmin和σmax。其中σmin为接收到的景深最近处最亮像素的标准差;σmax为接收到的景深最远处最暗像素的标准差。当测得该处视差值标准差小于σmin时,认为该点完全稳定,即置信度为1;当标准差大于σmax时,认为该点不可靠,即置信度为0;标准差处于2个阈值之间时,设置信度范围为(0, 1),具体如下:
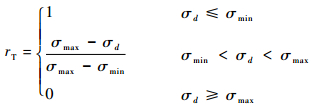 | (10) |
3 融合算法 根据双目立体数据和TOF相机3D数据的特性,采用如下方案生成最终的高分辨率和高精度3D点云数据。分别获取双目系统和TOF系统的视差数据,根据2个系统的优缺点分配不同的权重,融合视差数据,输出点云文件。方案的整体流程如图 3所示。
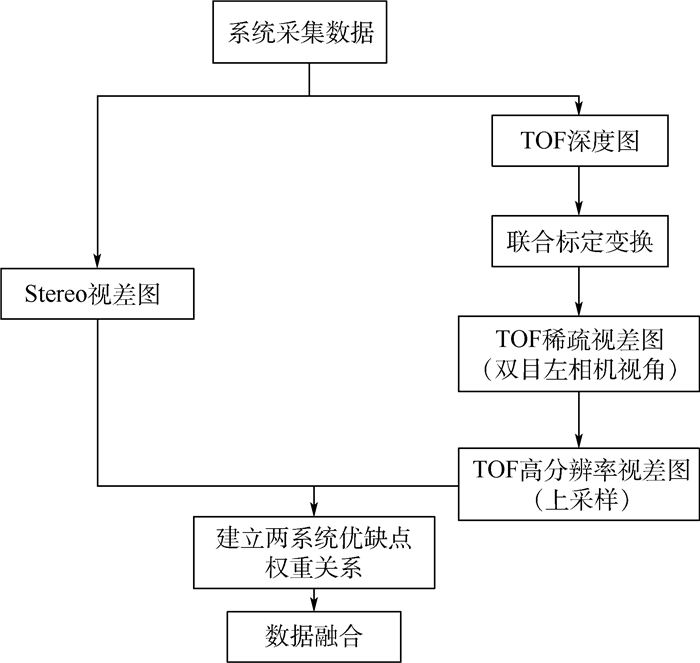 |
| 图 3 TOF与双目系统数据融合示意图 Fig. 3 Schematic diagram of data fusion of TOF and stereo vision system |
| 图选项 |
多系统间数据融合的核心技术主要有以下3个方面:
1) 数据角度的统一,即从不同相机视角获得的数据通过联合标定,转换到左相机视角下。
2) TOF深度图上采样,生成高分辨率、稠密视差[14]。根据2个系统的数据,逐个像素点进行融合,因此,必须通过一定的插值算法,将低分辨率图像转化为高分辨率图。
3) 融合策略[15]。假设dT和dS分别为TOF系统和双目系统的视差,最终生成的视差为d,则有如下关系:
 | (11) |
式中:wT为TOF系统求得的视差值权重; wS为双目系统求得的视差值权重。
3.1 TOF系统高分辨率视差图 TOF相机获取的深度图分辨率较低,因此在TOF深度图和双目匹配得到的视差图融合前,首先对TOF深度图进行稀疏式上采样,步骤如下:
步骤1?将TOF相机产生的点云通过联合标定的变换矩阵[R, T]映射到左相机的相机坐标系[5],R为旋转矩阵,T为平移矢量。即将TOF相机的中点的三维坐标XTi(i=1, 2, …, N)变换到以左相机为参考的双目系统的三维点XLi(i=1, 2, …, N)。
步骤2?将双目系统的三维点XLi,通过左相机的内参矩阵投影到左相机图像坐标系中,从而形成点阵xLj(j=1, 2, …, n)。这里相机将空间3D点投影变换为平面2D点,因此,必然存在部分点被遮挡,导致成像点数目与空间点数目不同。
步骤3?根据双目系统中左相机坐标系下的深度z与视差d的关系,可以将TOF得到的深度图转换为与该双目系统对应的视差图。
这样实现将TOF相机视差图的分辨率提升到与左相机一样的水平,如图 4所示。然而此时TOF的视差图仍为稀疏,还需要对缺失的数据进行填充[16-18]。
 |
| 图 4 TOF系统高分辨率视差图 Fig. 4 Disparity map of TOF system with high resolution |
| 图选项 |
根据稀疏的已知视差,在视差空间拟合出平滑的视差曲面,即可根据此视差曲面进行上采样对未知视差进行填充。显然二次曲面在一些复杂较扭曲场景下不能满足需求,而曲面方程的幂次越高,计算复杂度越大。因此,为了保证拟合的视差曲面最大程度上接近真实场景,此处采用二元三次方程对视差曲面进行拟合[19]:
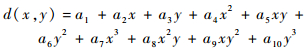 | (12) |
式中:d(x, y)表示一个三维视差曲面;a1, a2, …, a10为系数;x和y为像素坐标。
经过以上步骤,便可得到左相机视角下的高分辨率TOF相机视差图。
3.2 双目系统与TOF系统数据融合 数据融合的目的是通过不同权重将2个系统对应的视差值融合在一起,以得到高分辨率、高稠密的视差图。具体的融合权重确定方法如下:
1) 弱纹理区域
对双目图像进行梯度提取,可以确定弱纹理区域,在此部分的融合视差全部取TOF相机获得的视差值,即wS=0,wT=1。
2) 非弱纹理区域
首先计算双目系统视差图的置信度rS:
 | (13) |
式中:Cp1st和Cp2nd分别为双目中求得的最小和次小代价。此外,为避免Cp2nd为0,设常参数Tc>0。
此外,对TOF数据上采样后得到的视差图不可避免地会出现无效视差,针对上采样后的TOF视差图,将像素分为2类TOF数据有效区域Tvalid以及无效区域Tinvalid,p为图像上的像素。双目系统视差权重分配如下:
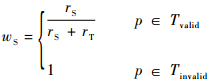 | (14) |
式中:rT为式(10)定义的TOF系统置信度;rS为式(13)定义的双目系统置信度。即当TOF像素视差有效时,采取两系统视差加权结果;否则采用双目视差结果。
确定双目权重后,相应的TOF系统权重也可确定:
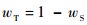 | (15) |
最后,即可根据式(11)的融合策略进行两系统视差结果的融合。
4 实验结果与分析 首先,搭造出模拟火车车底的环境拍摄图像,进行联合标定,建立TOF系统与双目系统之间的坐标关系。然后,对TOF图像进行深度转视差以及上采样处理,对双目图像进行畸变矫正,立体匹配。图 5展示了样图处理结果。
 |
| 图 5 样图处理结果示例 Fig. 5 Examples of processing results |
| 图选项 |
根据图 5可以直观地看出,TOF系统直接得到的视差图比双目系统得到的视差图结果更精确,但是分辨率较低。经过数据融合之后,得到的视差图在分辨率方面比TOF结果较好,精度比双目系统较好。由图 5(b)和(c)可知,TOF系统测量结果基本没有将左侧背景深度有效测量出,而双目系统测量结果对于物体细节的深度测量表现不好。经过融合后,对两系统各自不同测量缺陷都有效减小。
但图 5示例只能定性地分析系统性能,为了可以定量分析系统的精度,本文利用Middlebury数据集进行定量评测。
TOF系统得到视差图精度高,但分辨率低。首先,将Middlebury数据集的4组数据的视差图同时沿横、纵轴方放大4倍[20],对其进行高斯滤波;再利用本文方法采样得到高分辨率视差图,与双目立体匹配算法的视差图结果进行融合。以Teddy为例,具体结果如图 6所示。
 |
| 图 6 Teddy处理结果示例 Fig. 6 Examples of Teddy processing results |
| 图选项 |
从图 6直观上看,Teddy图像的数据融合后的视差图误匹配区域较双目系统减少。此外,数据集处理结果的定量分析如表 1所示。
表 1 双目立体匹配和融合算法结果分析 Table 1 Analysis of stereo vision and fusion algorithm results
| % | ||
| 图像 | 双目立体匹配算法误匹配率 | 融合算法误匹配率 |
| Teddy | 13.34 | 6.34 |
| Cones | 8.56 | 4.63 |
| Tsukuba | 6.52 | 2.39 |
| Venus | 4.79 | 1.43 |
表选项
5 结论 1) 针对TOF系统,考虑到系统精度与接收到信号振幅的关系,确定了TOF系统的置信度与振幅的关系式;针对双目系统,分为弱纹理区与非弱纹理区,并根据聚合代价的全局最小值与次小值,确定其置信度;即本文提出的融合算法将两系统的优点有效结合。
2) 根据标准数据集的实验结果,不同系统的视差融合之后的精度,比双目立体匹配算法的视差图精度提高了一倍以上,尤其平面区域更加平滑,且分辨率也较TOF系统高。
参考文献
| [1] | ZANUTTIGH P, MARIN G, DAL MUTTO C D, et al. Time-of-flight and structured light depth cameras:Technology and applications[M].Berlin: Springer, 2016: 23-25. |
| [2] | HANSARD M, LEE S, CHOI O, et al. Time-of-flight cameras:Principles, methods and applications[M].Berlin: Springer, 2013: 50-53. |
| [3] | TIPPETTS B, LEE D J, LILLYWHITE K, et al. Review of stereo vision algorithms and their suitability for resource-limited systems[J].Journal of Real-Time Image Processing, 2016, 11(1): 5–25.DOI:10.1007/s11554-012-0313-2 |
| [4] | YANG Q, AHUJA N, YANG R, et al. Fusion of median and bilateral filtering for range image up-sampling[J].IEEE Transactions on Image Processing, 2013, 22(12): 4841–4852.DOI:10.1109/TIP.2013.2278917 |
| [5] | GARRO V, MUTTO C D, ZANUTTIGH P, et al. A novel interpolation scheme for range data with side information[C]//Proceedings of the 2009 Conference on Visual Media Production. Piscataway, NJ: IEEE Press, 2009: 52-60. |
| [6] | ZHU J, WANG L, GAO J, et al. Spatial-temporal fusion for high accuracy depth maps using dynamic mrfs[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(5): 899–909.DOI:10.1109/TPAMI.2009.68 |
| [7] | VINEET G, JAN C, RADU H. High-resolution depth maps based on ToF-stereo fusion[C]//Proceedings of IEEE Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 2012: 4742-4749. |
| [8] | MUTTO C D, ZANUTTIGH P, MATTOCCIA S, et al. Locally consistent ToF and stereo data fusion[C]//Proceedings of the 12th International Conference on Computer Vision-Volume Part I. Berlin: Springer, 2012: 598-607. |
| [9] | FUSIELLO A, TRUCCO E, VERRI A. A compact algorithm for rectification of stereo pairs[J].Machine Vision and Applications, 2000, 12(1): 16–22.DOI:10.1007/s001380050120 |
| [10] | KAHLMANN T, INGENSAND H. Calibration and development for increased accuracy of 3D range imaging cameras[J].Journal of Applied Geodesy, 2008, 2(1): 1–11.DOI:10.1515/JAG.2008.001 |
| [11] | SCHARSTEIN D, SZELISKI R. A taxonomy and evaluation of dense twoframe stereo correspondence algorithms[J].International Journal of Computer Vision, 2002, 47(1-3): 7–42. |
| [12] | PIATTI D, RINAUDO F. SR-4000 and Camcube 3.0 time of flight (ToF) cameras:Tests and comparison[J].Remote Sensing, 2012, 4(4): 1069–1089.DOI:10.3390/rs4041069 |
| [13] | MUTTO C D, ZANUTTIGH P, CORTELAZZO G. Probabilistic ToF and stereo data fusion based on mixed pixels measurement models[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(11): 2260–2272.DOI:10.1109/TPAMI.2015.2408361 |
| [14] | DOLSON J, BAEK J, PLAGEMANN C, et al. Up-sampling range data in dynamic environments[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE Press, 2010: 1141-1148. |
| [15] | HU X, MORDOHAI P. A quantitative evaluation of confidence measures for stereo vision[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2121–2133.DOI:10.1109/TPAMI.2012.46 |
| [16] | GUDMUNDSSON S, AANAES H, LARSEN R. Fusion of stereo vision and time of flight imaging for improved 3D estimation[J].International Journal Intelligent System Technologies and Applications, 2008, 5(3): 425–433. |
| [17] | EVANGELIDIS G, HANSARD M, HORAUD R. Fusion of range and stereo data for high-resolution scene-modeling[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(11): 2178–2192.DOI:10.1109/TPAMI.2015.2400465 |
| [18] | NAIR R, LENZEN F, MEISTER S, et al. High accuracy ToF and stereo sensor fusion at interactive rates[C]//Proceedings of European Conference on Computer Vision Workshops. Berlin: Springer, 2012: 7584. |
| [19] | 刘娇丽, 李素梅, 李永达, 等. 基于TOF与立体匹配相融合的高分辨率深度获取[J].信息技术, 2016(12): 190–193. LIU J L, LI S M, LI Y D, et al. High-resolution depth maps based on TOF-stereo fusion[J].Information Technology, 2016(12): 190–193.(in Chinese) |
| [20] | 张康. 基于图像深度感知中的立体匹配和深度增强算法研究[D]. 北京: 清华大学, 2015: 84-87. ZHANG K. Stereo matching and depth enhancement in image-based depth perception[D]. Beijing: Tsinghua University, 2015: 84-87(in Chinese). |
