因此,为减小支承不同心的影响,多支点支承的高速柔性转子可采取松动支承设计,即在支承结构中设计合理的间隙。但是,对于支承带有间隙的转子结构系统,转子振幅变化时,支承的约束作用会产生突变,使得转子系统支承刚度具有阶跃的非连续特征。而航空发动机主轴承工作环境极其恶劣,因此,松动支承引起的支承刚度非连续特征可能会使转子系统产生复杂的非线性响应,影响航空发动机转子系统的动力特性稳定。尤其对于高速柔性转子,由于该类转子系统质量、刚度分布极为不均,弯曲临界转速低,工作在超临界状态下,使得松动支承对高速柔性转子动力特性的不利影响更加突出[1]。而当转子支承系统的结构参数如松动支承的位置、松动间隙、不平衡量等设计合理时,转子系统非线性振动响应会受到抑制,所以多支点支承高速柔性转子采用松动支承设计时保持良好的动力特性,需对其非线性振动响应特征进行研究。
Wang[2]及Hussien[3]等采用龙格库塔法对非线性油膜力及非线性支承共同作用下的Jeffcott转子的振动响应特征及其稳定性进行数值求解,将仿真结果和线性转子系统振动响应对比发现,支承刚度改变时,在一定转速范围内转子可产生拟周期运动;Goldman和Muszynska[4-6]考虑了支承结构的刚度、阻尼及切向摩擦,其研究结果表明松动支承激励下转子存在同步及次同步振动成分,同时存在高次谐波振动成分,一定工作状态下混沌运动可能产生;Karpenko等[7-8]仅考虑了支承间隙及非连续支承刚度的影响,建立的多点法数值求解结果表明,当转子与带有间隙的支承之间产生频繁碰撞时,可产生混沌运动;Kim、Noah[9]和Ehrich[10-11]综合考虑了挤压油膜和支承间隙对转子振动响应的影响,分别通过数值仿真和实验证明了松动支承的间隙是导致带有支承松动的转子系统产生复杂的非线性振动响应特征的原因;Kim和Noah[12]采用谐波平衡法研究了带有间隙支承的转子结构系统的分岔特性及其稳定性,发现转子系统可通过Hopt分岔产生拟周期运动;Wiercigroch等[13-14]利用Jeffcott转子研究了支承松动转子系统通往混沌的途径,发现间隙支承的转子结构系统可通过切分岔、倍周期分叉的途径通往混沌。
综上,目前针对松动支承激励下转子结构系统非线性振动响应特征的研究,计算模型多采用简单的Jeffcott转子,且没有综合考虑非连续支承刚度、切向摩擦及挤压油膜的影响,因而不能直接用于指导多支点支承高速柔性转子的松动支承设计。本文参考上述工作,基于松动支承的力学特征,研究得到非连续支承刚度产生机理,分析松动支承对柔性转子系统动力特性的影响,进而综合考虑阶跃的非连续支承刚度及油膜力的影响,建立带有松动支承的多支点支承高速柔性转子系统动力学模型,仿真研究得到了转子的非线性振动响应特征。进而根据支承结构参数对多支点支承高速柔性转子系统动力学特性的影响,对支承位置和支承刚度进行优化,以减弱非连续支承刚度对转子动力特性的影响,进而根据转子振动响应幅值随转速的变化设计松动间隙,使工作转速区域远离混沌响应区域,并具有一定的安全裕度,保证高速柔性转子采用松动支承设计时具有稳健的动力特性,从而为多支点支承高速柔性转子系统动力特性设计提供理论方法。
1 松动支承激励的力学特征及动力学模型 1.1 松动支承激励的力学特征 如图 1所示(图中osi为各支点位置处转子轴线位置),工程中典型的松动支承设计是通过调整挤压油膜阻尼器(Squeeze Film Damper,SFD)的间隙,加大转子与支承之间的间隙,从而消除装配时支承不同心对转子的附加约束[1]。
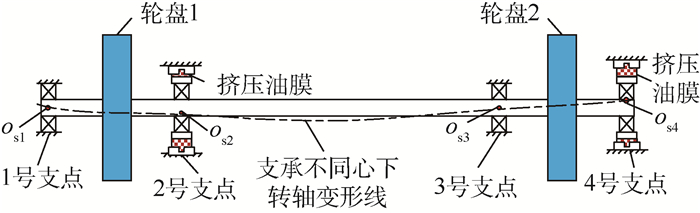 |
| 图 1 采用松动支承设计的多支点支承柔性转子模型 Fig. 1 Multi-supported flexible rotor model with bearing looseness design |
| 图选项 |
图 2(a)为带有挤压油膜阻尼器的支承结构物理模型。转子运动过程中,支承刚度主要由油膜压力产生的油膜刚度及刚性支承的支承刚度Ks串联而成,由于油膜压力不同,因而在不同位置处挤压油膜力在径向方向r和切向方向t分量有所差异,因而当转子振动位移与水平方向的夹角φ不同时,在水平和垂直方向分量也会随之改变。对于油膜间隙较大的挤压油膜阻尼器,转子作微幅振动油膜不受挤压时,支承不起约束作用。转子振幅增加,转子与油膜环内表面产生挤压油膜作用时,会产生油膜力,为转子提供油膜刚度,此时支承本身刚度与油膜刚度为串联关系,油膜刚度起主要支承作用,在油膜受挤压的扩张区内,靠近间隙小的一端阻力大,故而油压升高大,靠近间隙大的一端阻力小,油压升高小,从而会形成如图 2(a)所示的油压分布。同时,由于油膜力除受振幅影响外,运动速度及进动角度也会改变油膜力大小,从而在振幅一定时,根据转子运动轨迹的随机性,油膜力具有区间分布特征,如图 2(b)阴影所示。转子振幅继续增加与油膜环产生碰撞时,油膜会破裂,油膜刚度消失,此时支承本身刚度起主要支承作用。据此绘制支承支反力随振幅变化曲线,如图 2(b)所示,可以看出,松动支承可使转子支承刚度产生突变,从而支反力随振幅变化在油膜破裂点处导数不连续,具有非连续的力学特征,同时当转子与带间隙的支承之间产生频繁碰撞时,转子运动轨迹的随机性导致支承刚度具有区间分布特征,使转子系统具有非确定性特征。
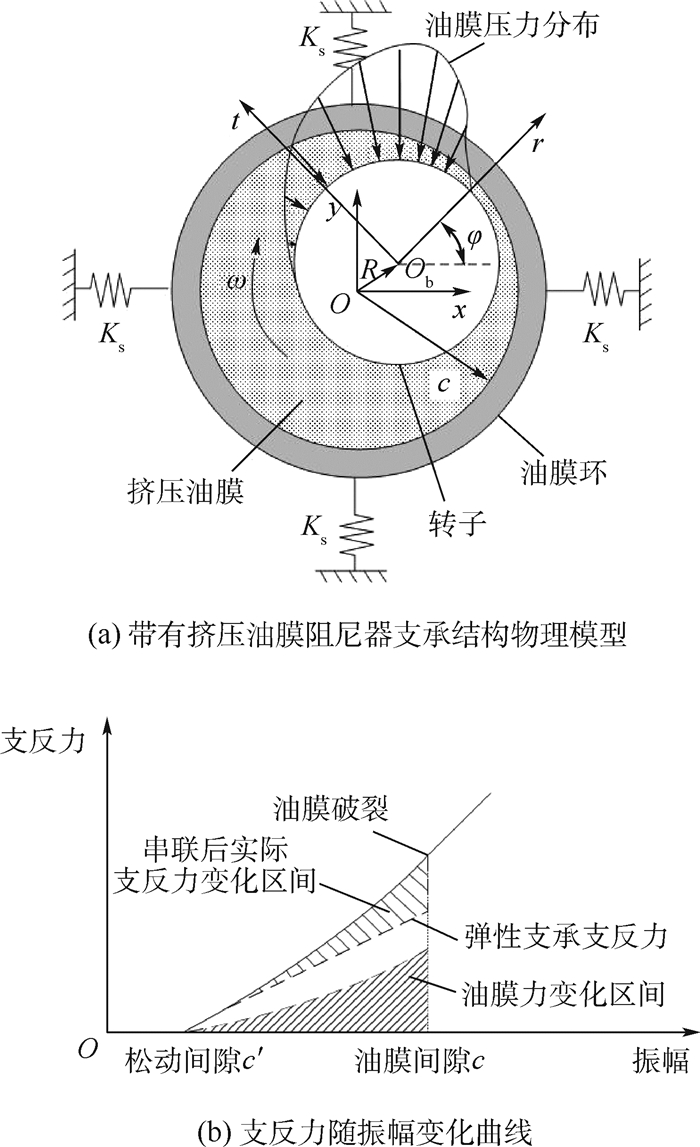 |
| 图 2 加大油膜间隙的挤压油膜阻尼器转子模型 Fig. 2 Model of SFD rotor system with increased oil film clearance |
| 图选项 |
支承刚度改变时,转子系统固有频率会随之改变,进而转子系统共振点会产生突变,使转子系统振动响应较为复杂。当转子动力特性对支承刚度敏感度较高时,支承松动可能会使转子产生混沌[1]。所以,高速柔性转子系统采用松动支承设计时,应对其支承方案及相应支承参数进行优化设计,以降低转子动力特性对支承刚度非连续变化的敏感度,使工作转速区域远离混沌响应区域并具有一定裕度,以保证转子动力特性稳定。
1.2 松动支承激励下多支点支承高速柔性转子系统的动力学模型 根据高速柔性转子多支点支承的特点以及松动支承的力学特征,建立如图 3所示多支点支承高速柔性转子系统力学模型。O1、O2为轮盘的几何中心,O1e、O2e为轮盘的质心,e1、e2为质心到形心距离,轮盘质量分别为m1、m2,轮盘处阻尼分别为Cd1、Cd2。Ksi和Csi分别为各支点的支承刚度和阻尼,c2、c3为油膜间隙,c′2、c′3为松动间隙。
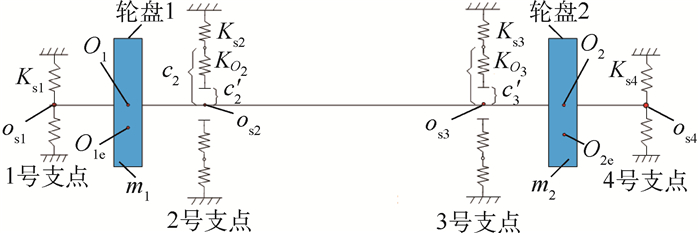 |
| 图 3 多支点支承高速柔性转子系统力学模型 Fig. 3 Mechanical model of multi-supported high-speed flexible rotor system |
| 图选项 |
忽略陀螺力矩和扭转振动的影响,转子系统横向振动的运动微分方程为
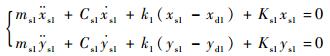 | (1a) |
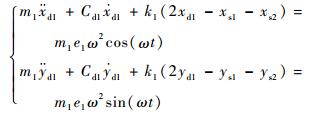 | (1b) |
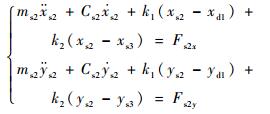 | (1c) |
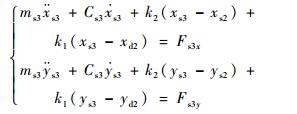 | (1d) |
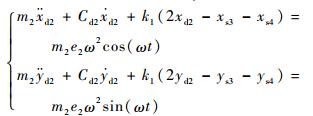 | (1e) |
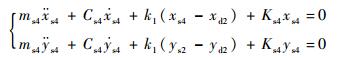 | (1f) |
式中:ω为转子同步进动角速度;msi为支承质量;ki为转子在轮盘i处的刚度;xsi、ysi为支承位置处转子振动位移分量;xdi、ydi为轮盘振动位移分量;Fsix、Fsiy为松动支承支反力;2、3号支点采用支承松动设计,支承刚度为Ks2、Ks3。支承的支反力随转子振幅变化具有非连续特征,其表达式为
 | (2) |
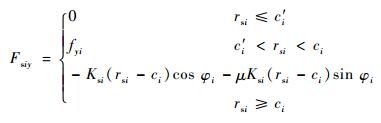 | (3) |
式中:fxi、fyi为油膜力;
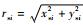
采用短轴承油膜理论,半油膜条件下油膜力的表达式为
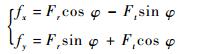 | (4) |
式中:
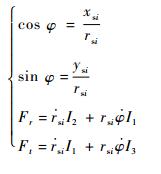 | (5) |
其中:I1、I2、I3为Sommerfeld系数[15-16]。
2 松动支承激励下的转子系统动力学特性分析 2.1 非线性振动响应特征 根据松动支承激励下多支点支承高速柔性转子系统力学模型和动力学模型,参考涡轴发动机动力涡轮转子结构,选取结构的各参数如表 1、表 2所示。
表 1 结构参数取值 Table 1 Values of structural parameters
| 参数 | 数值 |
| m1e1/(g·mm) | 10 |
| m2e2/(g·mm) | 10 |
| c′2/mm | 7×10-4 |
| c′4/mm | 4×10-4 |
| c2-c′2/mm | 2×10-4 |
| c4-c′4/mm | 2×10-4 |
| k1/(N·m-1) | 2×105 |
| k2/(N·m-1) | 1×104 |
表选项
表 2 挤压油膜阻尼器参数取值 Table 2 Values of SFD parameters
| 参数 | 滑油黏度/(Pa·s) | 轴向承载长度/mm | 轴承半径/mm |
| 数值 | 1×10-3 | 90 | 40 |
表选项
改变转子转速,仿真计算得到松动支承激励下高速柔性转子系统振动响应,如图 4~图 7所示。
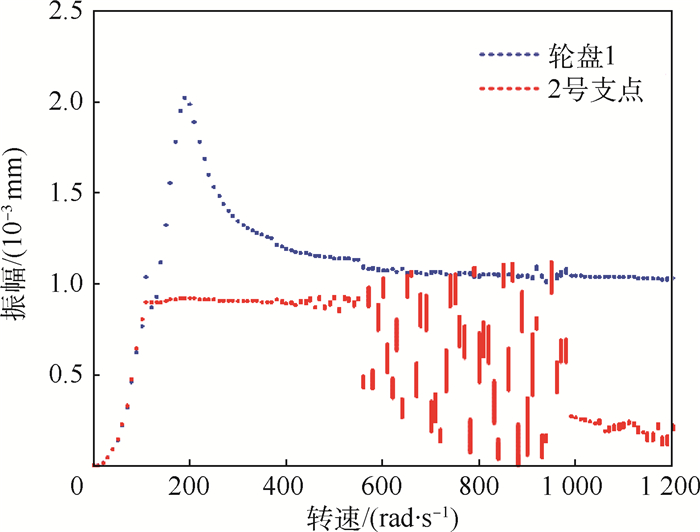 |
| 图 4 振幅随转速变化的分岔图 Fig. 4 Bifurcation diagram of vibration amplitude changing with rotational speed |
| 图选项 |
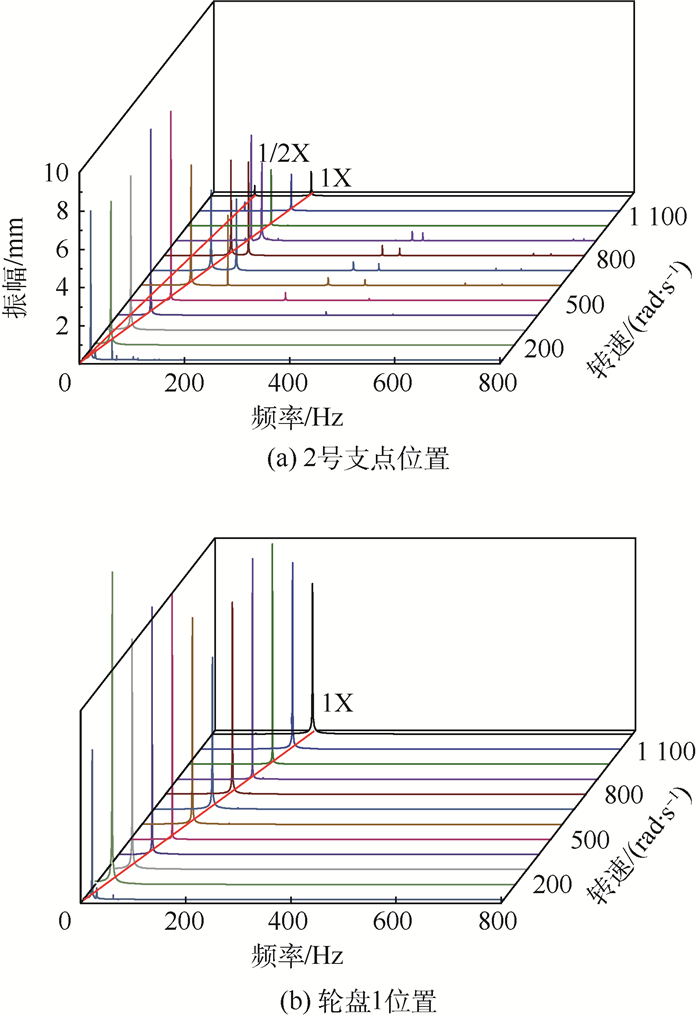 |
| 图 5 随转速变化的频域瀑布图 Fig. 5 Waterfall curve of frequency domain changing with rotational speed |
| 图选项 |
 |
| 图 6 2号支点位置转子的振动响应 Fig. 6 Vibration response of rotor at position of Support 2 |
| 图选项 |
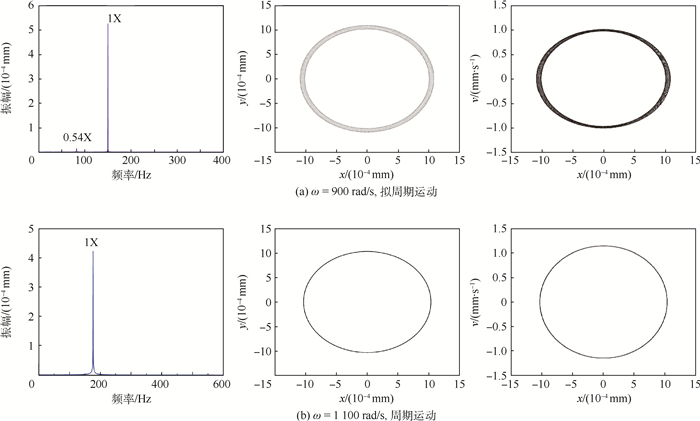 |
| 图 7 轮盘1位置转子的振动响应 Fig. 7 Vibration response of rotor at position of Disk1 |
| 图选项 |
从图 4、图 5可以看出,松动支承激励下的柔性转子,其振动响应具有如下特征:
1) 对于带有间隙的2号支点位置处的振动响应,在10~1200rad/s转速范围内,随转速增加,其运动形式依次为周期—拟周期—混沌—拟周期运动。
如图 4所示,当转速较低(ω < 100rad/s)时,由于转子振幅很小,松动支承几乎不起约束作用,轮盘1和2号支点振幅相同,此时转子处于两支点支承状态,为线性系统,频域响应仅为1倍频,转子做周期运动。
转子转速继续增加,向临界转速靠近,在不平衡力作用下,转子振幅增加使转子与松动支承之间的油膜受到挤压时,油膜的刚度和阻尼会抑制转子的振动,此时轮盘1和2号支点振幅出现差异,在非线性油膜力作用下,频域响应为1倍频和3倍频成分的叠加,转子产生拟周期运动。
转子转速继续增加,逐渐远离共振转速,不平衡激振力加大,当振幅下降至与松动支承之间产生频繁碰撞时,整个系统可看成2个系统的耦合:①固有非线性系统,即无不平衡激振作用下的松动支承转子系统;②不平衡激振力作用下的线性振动系统。其中,不平衡激振力可代表 2个系统的耦合程度[16]。当不平衡激振力很小时,线性系统的振动很弱,对应非线性系统的作用也很弱。系统的运动便可近似看成是2个独立运动的叠加,即整个系统的运动是围绕平衡点之一的线性振动。此时根据初始条件不同,系统会绕不同的平衡点运动,从而在相平面上形成不同的流域。由于不平衡激振很小,振动很弱,系统的振动才不会越出既定的流域而趋近于另一平衡点。
根据图 4和图 6(c)的相图所示,当转速增加至580rad/s左右时,受松动支承的影响,频域响应为1倍频、3倍频、5倍频及多种其他频率成分的叠加,运动形式为混沌运动。这是由于不平衡激振力增加,使得2个系统的相互影响增强到使振动可以超过初始流域的界限,从而可从初始的流域转到新的流域,将向其他平衡点靠近。同时,系统振幅也可能增大到超过新流域的界限而趋近于初始流域,此时系统会绕初始的平衡点运动。而系统在自发随机性的影响下会从一个流域进入另一个流域,系统在不同流域之间产生跳动而具有随机的特点,从而产生混沌运动[17-18]。
转速继续增加,不平衡激振力增大,使得线性系统的振动处于主导地位,振幅继续下降,在非线性油膜力作用下,转子运动状态为拟周期运动。
当不平衡激振力很大时,线性系统完全处于支配地位,松动支承引起的非线性影响极弱。此时,整个系统便按线性系统的运动方式运动,变为周期运动[16-17]。
2) 图 7为松动支承激励下轮盘的振动响应,运动形式主要为拟周期和周期运动。2号支点位置处存在混沌运动时,对应轮盘振动响应以转速1倍频为主,同时包含其他频率成分,呈拟周期运动;2号支点位置为拟周期和周期运动时,对应轮盘振动响应仅为1倍频,呈周期运动。
2.2 参数影响规律 为了研究松动间隙、非连续支承刚度、不平衡量大小及松动支承位置对转子响应的影响,以转子系统的加速过程为例,分析不同参数下的松动支承激励的转子系统响应分岔图。
2.2.1 松动支承位置影响 改变松动支承位置,将2号、4号支点处设计松动间隙,其物理模型如图 8所示。得到2号、3号支点位置处及轮盘2位置处转子振幅随转速变化的分岔图。根据图 9,改变轮盘2位置处松动支承的位置,对2号支点位置处转子的振动响应影响较小,混沌响应区域稍有偏移。如图 10所示,松动支承位置改变对轮盘2及其支承位置处振动响应影较大,4号支点采用松动支承设计时,轮盘2在共振点处的峰值略有降低。根据图 11可知,随转速增加,不平衡激振力增加使得转子与松动支承之间存在碰撞冲击时,松动支承位置处响应幅值对转速变化较敏感,因而在2号、3号支点位置设计松动间隙时,3号支点位置处转子响应幅值对转速变化较敏感。同时由于3号支点靠近转子质心,其振幅变化在非连续支承刚度影响下对转速变化敏感时,不利于转子动力特性稳定,因此,优先选择2号、4号支点采用松动支承设计。
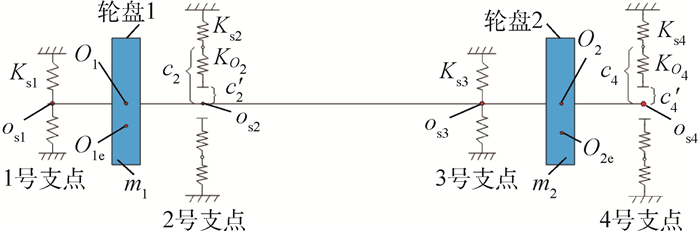 |
| 图 8 2号、4号支点采用松动支承设计的多支点支承柔性转子系统 Fig. 8 Multi-supported flexible rotor system with bearing clearance designed at Support 2 and Support 4 |
| 图选项 |
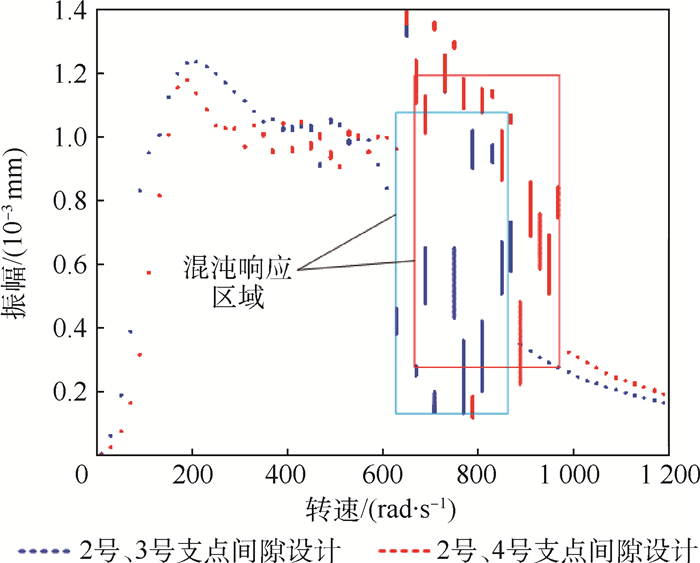 |
| 图 9 松动支承位置不同时2号支点振幅随转速变化的分岔图 Fig. 9 Bifurcation diagram of vibration amplitude of Support 2 changing with rotational speed when location of bearing looseness is different |
| 图选项 |
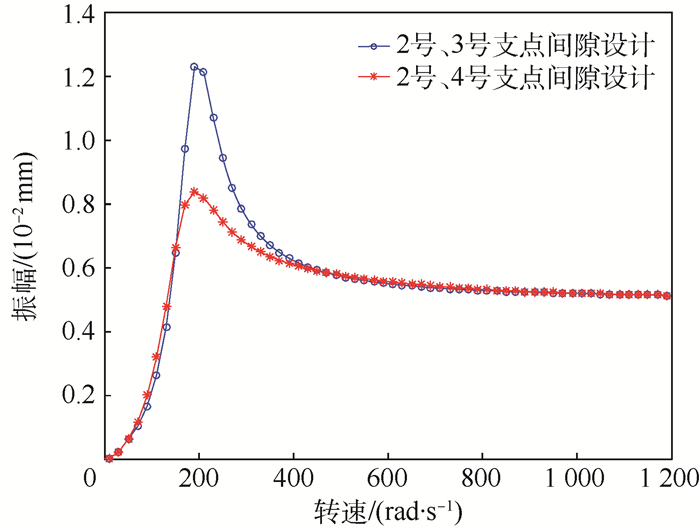 |
| 图 10 松动支承位置不同时轮盘2振幅随转速变化的分岔图 Fig. 10 Bifurcation diagram of vibration amplitude of Disk 2 changing with rotational speed when location of bearing looseness is different |
| 图选项 |
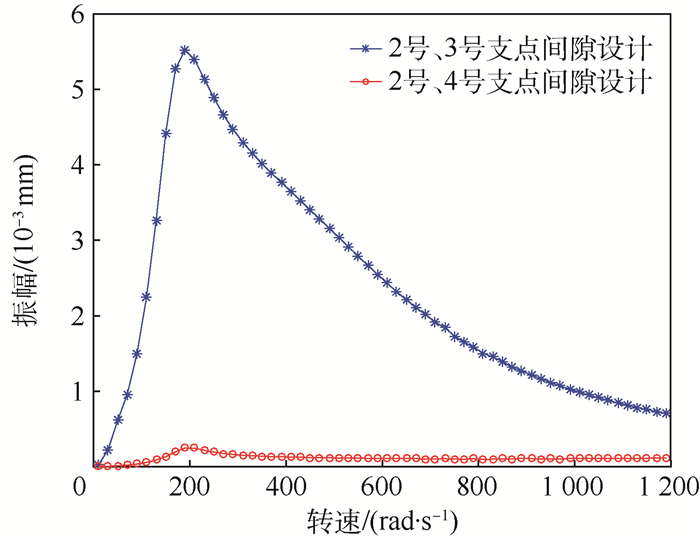 |
| 图 11 松动支承位置不同时3号支点振幅随转速变化的分岔图 Fig. 11 Bifurcation diagram of vibration amplitude of Support 3 changing with rotational speed when location of bearing looseness is different |
| 图选项 |
2.2.2 不平衡量影响 如表 3所示,改变轮盘1、2的不平衡量,得到轮盘1及2号支点位置处转子振幅随转速变化的分岔图,如图 12所示。可以看出,转子不平衡量增加时,混沌响应的转速区域向高转速区偏移。这是由于当松动支承处的间隙保持不变时,只有当振幅达到0.4×10-3~0.9×10-3mm时,2号支点位置处转子才会与支承发生频繁碰撞,从而产生混沌运动。由于转子不平衡量增加时,转子振幅随转速变化会整体增加,因此与不平衡量小的情况相比转子在更高的转速范围内,2号支点位置处转子的振幅才会减小至0.4×10-3~0.9×10-3mm,与支承产生频繁碰撞,从而产生混沌运动,且由于该振幅范围对应转速范围较宽,因此,对应混沌响应的转速范围较宽广。
表 3 轮盘不平衡量取值 Table 3 Unbalance value of disk
| 不平衡量 | m1e1/(g·mm) | m2e2/(g·mm) |
| 小不平衡量 | 10 | 10 |
| 大不平衡量 | 50 | 50 |
表选项
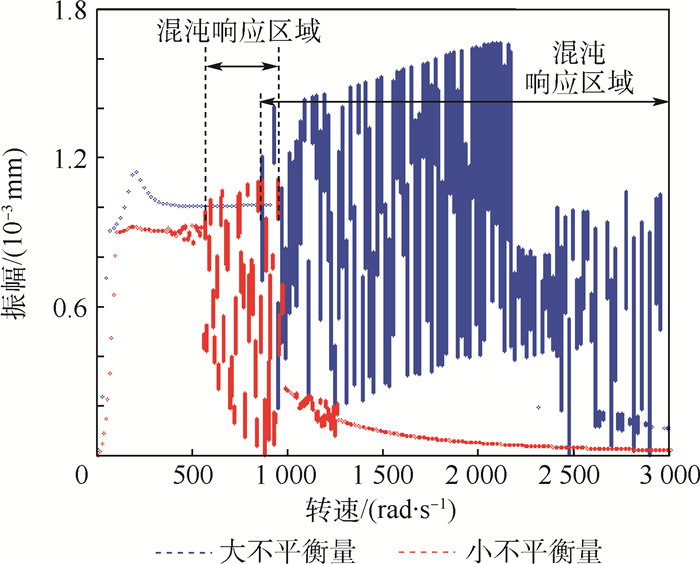 |
| 图 12 不平衡量不同时2号支点振幅随转速变化的分岔图 Fig. 12 Bifurcation diagram of vibration amplitude of Support 2 changing with rotational speed when unbalance value is different |
| 图选项 |
2.2.3 非连续支承刚度影响 如表 4所示,为研究支承刚度非连续的影响,改变松动支承位置处的支承刚度变化的区间范围,得到2号支点位置处转子振幅随转速变化的分岔图,如图 13所示。可以看出,松动支承位置处支承刚度变化范围增大时,混响应区域稍有扩大。
表 4 支承刚度变化区间 Table 4 Variation range of bearing stiffness
| 支承刚度变化范围 | Ks2/(N·m-1) | Ks3/(N·m-1) |
| 支承刚度变化范围小 | 0~1×105 | 0~1×105 |
| 支承刚度变化范围大 | 0~1×107 | 0~1×107 |
表选项
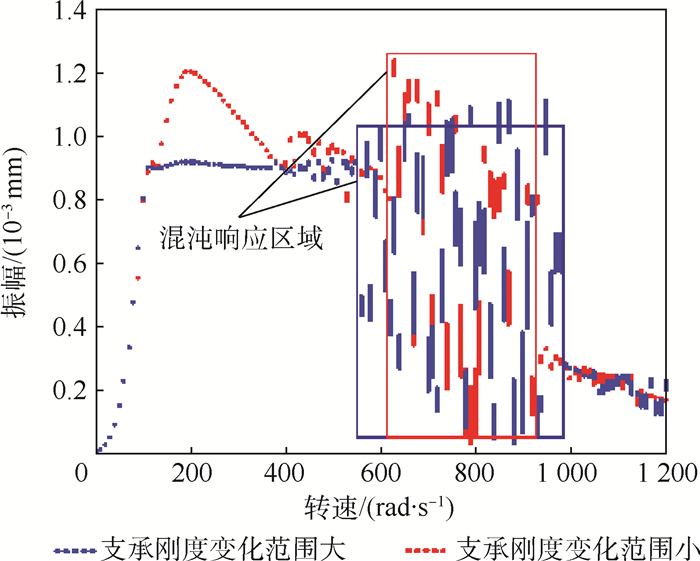 |
| 图 13 支承刚度不同时2号支点振幅随转速变化的分岔图 Fig. 13 Bifurcation diagram of vibration amplitude of Support 2 changing with rotational speed when bearing stiffness is different |
| 图选项 |
2.2.4 松动间隙影响 如表 5所示,改变松动支承位置处的间隙,得到2号支点位置处转子振幅随转速变化的分岔图,如图 14所示。可以看出,松动支承的间隙加大时,松动支承位置处转子振幅需增加至可与支承产生频繁碰撞才能引发混沌运动产生,所以产生混沌运动的转速区域向共振区域靠近,且混沌运动振幅随之增加。
表 5 松动间隙参数取值 Table 5 Parameter values of bearing clearance
| 松动间隙 | c′2/mm | c′4/mm | c2/mm | c4/mm |
| 小松动间隙 | 1.4×10-3 | 8×10-4 | 2×10-4 | 2×10-4 |
| 大松动间隙 | 7×10-3 | 4×10-3 | 2×10-3 | 2×10-3 |
表选项
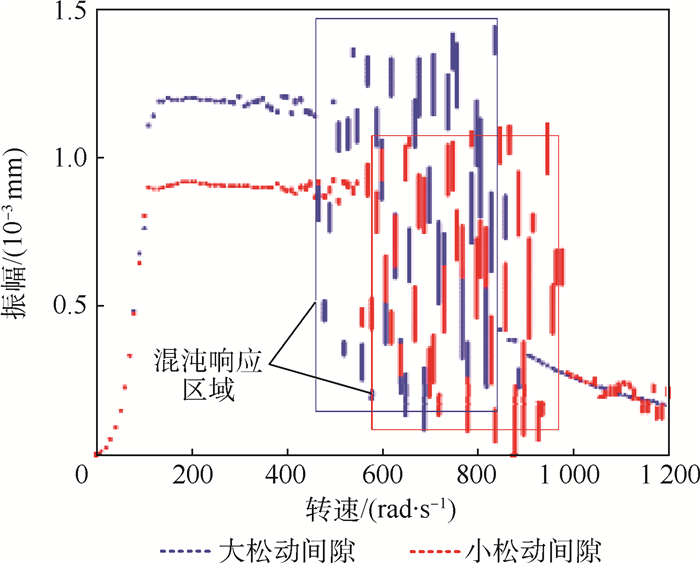 |
| 图 14 松动间隙不同时2号支点振幅随转速变化的分岔图 Fig. 14 Bifurcation diagram of vibration amplitude of Support 2 changing with rotational speed when bearing clearance is different |
| 图选项 |
3 结论 松动支承激励下多支点支承柔性转子的运动状态具有非线性特征,其非线性振动形式主要为拟周期和混沌运动:
1) 在一定不平衡量下,转子与松动支承之间产生频繁碰撞时,松动支承位置处转子的运动形式为混沌运动。对应轮盘处运动形式为拟周期运动。
2) 非线性油膜力作用下,松动支承位置处转子的运动形式为拟周期运动,对应轮盘处运动形式为周期运动。
参考文献
| [1] | 于欢, 马艳红, 肖森, 等. 高速柔性转子支承松动力学特征及动力特性[J].北京航空航天大学学报, 2017, 43(8): 1677–1683. YU H, MA Y H, XIAO S, et al. Mechanical and dynamic cha-racteristics of bearing with looseness on high-speed flexible rotor[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(8): 1677–1683.(in Chinese) |
| [2] | WANG R, GUO X, WANG Y. Nonlinear analysis of rotor system supported by oil lubricated bearings subjected to base movements[J].Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2016, 230(4): 167–172. |
| [3] | HUSSIEN M, AL-WEDYAN H, TAHAT M S, et al. The behaviour of the Jeffcott rotor under a vibrating base of fluid film bearing[J].Suranree Journal of Science and Technology, 2008, 15(3): 167–176. |
| [4] | GOLDMAN P, MUSZYNSKA A. Chaotic behavior of rotor-stator systems with rubs[J].Journal of Engineering for Gas Turbines and Power, 1994, 116(3): 692–701.DOI:10.1115/1.2906875 |
| [5] | GOLDMAN P, MUSZYNKA A. Dynamic effects in mechanical structures with gap and impacting:Order and chaos[J].Journal of Vibration and Acoustics, 1994, 116(4): 541–547.DOI:10.1115/1.2930461 |
| [6] | GOLDMAN P, MUSZYNKA A. Chaotic response of unbalanced rotor/bearing/stator systems with looseness or rubs[J].Chaos, Solitons & Fractals, 1995, 5(9): 1682–1704. |
| [7] | KARPENKO E V, WIERCIGROCH M, PAVLOVSKAIA E E, et al. Piecewise approximate analytical solutions for a Jeffcott rotor with a snubber ring[J].International Journal of Mechanical Sciences, 2002, 44(3): 475–488.DOI:10.1016/S0020-7403(01)00108-4 |
| [8] | KARPENKO E V, WIERCIGROCH M, CARTMELL M P. Re-gular and chaotic dynamics of a discontinuously nonlinear rotor system[J].Chaos, Solitons & Fractals, 2002, 13(6): 1231–1242. |
| [9] | KIM Y B, NOAH S T. Quasi-periodic response and stability analysis for a non-linear Jeffcott rotor[J].Journal of Sound and Vibration, 1996, 190(2): 239–253.DOI:10.1006/jsvi.1996.0059 |
| [10] | EHRICH F F. High order subharmonic response of high speed rotors in bearing clearance[J].Journal of Vibration and Acoustics, 1988, 110(1): 9–16.DOI:10.1115/1.3269488 |
| [11] | EHRICH F F. Subharmonic virbration of rotors in bearing clea-rance: ASME Paper No. 66-MD-1[R]. Ner York: ASME, 1966. |
| [12] | KIM Y B, NOAH S T. Bifurcation analysis for a modified Jeffcott rotor with bearing clearances[J].Nonlinear Dynamics, 1990, 1(3): 221–241.DOI:10.1007/BF01858295 |
| [13] | CHáVEZ J P, WIERCIGROCH M. Bifurcation analysis of periodic orbits of a non-smooth Jeffcott rotor model[J].Communications in Nonlinear Science & Numerical Simulation, 2013, 18(9): 2571–2580. |
| [14] | WIERCIGROCH M, DE KRAKER B. Applied nonlinear dynamics and chaos of mechanical systems with discontinuities[M].Singapore: World Scientific, 2000: 177-200. |
| [15] | INAYAT-HUSSAIN J I, KANKI H, MUREITHI N W. On the bifurcations of a rigid rotor response in squeeze-film dampers[J].Journal of Fluids & Structures, 2003, 17(3): 433–459. |
| [16] | INAYAT-HUSSAIN J I, KANKI H, MUREITHI N W. Stability and bifurcation of a rigid rotor in cavitated squeeze-film dam-pers without centering springs[J].Tribology International, 2001, 34(10): 689–702.DOI:10.1016/S0301-679X(01)00062-7 |
| [17] | 刘秉正, 彭建华. 非线性动力学[M].北京: 高等教育出版社, 2004: 132-135. LIU B Z, PNEG J H. Nonlinear dynamics[M].Beijing: Higher Education Press, 2004: 132-135.(in Chinese) |
| [18] | 赖志慧. 基于Duffing振子混沌和随机共振特性的微弱信号检测方法研究[D]. 天津: 天津大学, 2014. LAI Z H. Weak-signal detection based on the chaotic and stochastic-resonance characteristics of Duffing oscillator[D]. Tianjin: Tianjin University, 2014(in Chinese). |
