超流体陀螺是通过检测薄膜位移而实现角速度测量的,因此位移传感器的分辨率是影响超流体陀螺分辨率的重要因素。文献[8]通过改进测量电路,将位移传感器的输出噪声由3×10-5 m/Hz降低到了1×10-5 m/Hz,从而提高了超流体量子干涉陀螺的测量精度。文献[9]对超流体陀螺的热噪声进行了分析,验证了增加弱连接微孔数目可实现陀螺热噪声的抑制,然而受限于弱连接的加工技术,微孔数目不宜过多。文献[10]设计了多圈环绕结构,在一定程度上降低了陀螺噪声,但增加了加工难度和成本,且不能实现噪声的完全抑制。
此外,关于噪声抑制的滤波算法方面,由于非线性自适应滤波计算较复杂且硬件实现困难,因此实际中仍多采用线性自适应滤波[11]。考虑维纳滤波和卡尔曼滤波对先验知识的初始条件依赖较大[12],最小均方(LMS)算法对非平稳信号的适应性差[13],为此,本文在明晰陀螺相位波动噪声形成机理的基础上,结合陀螺角速度噪声与外界输入角速度互不相关的特性,提出了一种基于递推最小二乘(RLS)自适应滤波的陀螺相位波动噪声抵消系统。该方法结合陀螺混合角速度信息,基于RLS算法实现滤波参数调节,使得RLS自适应滤波器的输出与混合角速度中噪声部分相抵消,在对信号的适应性和收敛速率方面有很大优势。
1 超流体陀螺相位检测模型 超流体陀螺结构如图 1所示,该陀螺装置主要由热驱动部分、干涉环路和薄膜检测模块组成。
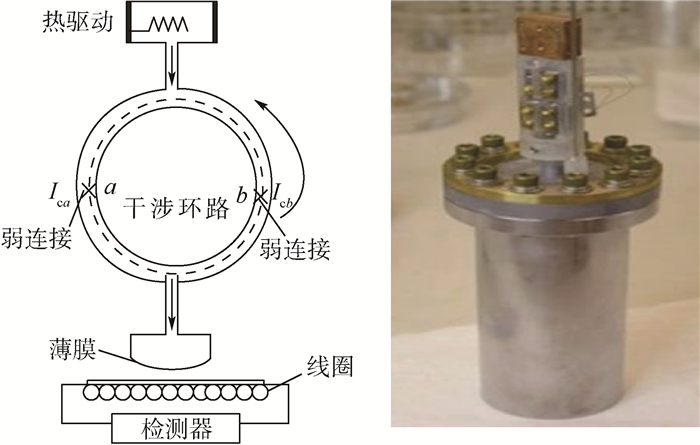 |
| 图 1 超流体陀螺示意图 Fig. 1 Schematic of superfluid gyroscope |
| 图选项 |
超流体陀螺工作时,启动热驱动装置使得超流体在环形干涉环路的双弱连接处发生约瑟夫森效应从而产生物质波,超流体流经单个微孔的物质波流量I0可表示为[14]
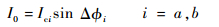 | (1) |
式中:Ica、Δ?a和Icb、Δ?b分别为流过弱连接a、b两端单个微孔的超流体临界流量和相位。
则环形腔内超流体的总物质波流量I为
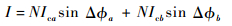 | (2) |
式中:N为单弱连接包含的微孔数目。
假设双弱连接加工完全一致,则流过弱连接a、b两端的临界流量大小一致,即Ica=Icb=Ic,由和差化积公式,得到总物质波流量为
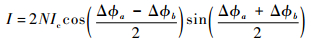 | (3) |
当存在外界角速度时,由于物质波Sagnac效应,超流体物质波流量幅值H将被调制为[15]
 | (4) |
式中:Δ?s为外界输入角速度引起的转动相位;A为陀螺的感应面积;m4为氦-4的原子质量;h为普朗克常数;ω为外界输入角速度;k4=h/m4为超流体量子环流量。
在超流体物质波流量的作用下,陀螺的薄膜位移发生变化,使用高精度的超导量子干涉仪作为薄膜位移的检测模块,将检测到的薄膜位移经快速傅里叶变化便可得到约瑟夫森频率下的位移幅值Xm。位移幅值Xm与流量幅值H满足[16]:
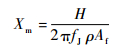 | (5) |
式中:fJ为约瑟夫森频率;ρ为总的流体密度;Af为柔性薄膜面积。
根据式(4),当陀螺检测较小的角速度时, 则由该角速度引起的转动相位也较小,此时超流体陀螺转动相位与薄膜幅值的关系可表示为
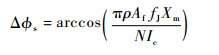 | (6) |
2 相位波动噪声分析及抑制 2.1 相位波动噪声分析 考虑超流体内部分子的热运动始终存在,超流体陀螺环路中的流体热能量为KBT/2,KB为玻尔兹曼常数,T为陀螺工作温度。热能量作用下,超流体流过弱连接的流体包含的动能为NρsD2?Δvs2/2,ρs为超流体密度,D为微孔孔径,Δvs为超流体流动速度,?为弱连接厚度。
超流体流动速度与弱连接两侧相位差Δ?满足[14]:
 | (7) |
式中:
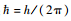
根据能量守恒关系可得,由热运动引起弱连接两侧的相位波动为
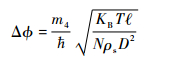 | (8) |
超流体陀螺的角速度检测原理是通过检测薄膜位移而间接得到外界输入角速度信息。由式(6)、式(8)易知,相位波动噪声的存在将直接影响陀螺的薄膜检测幅值。显然弱连接a、b在位置上相互独立,波动相位掺杂在转动相位中,由相位波动噪声引起的角速度噪声属于热噪声范畴[6]。结合式(4)、式(8),得到相位波动噪声引起的陀螺等效输入角速度噪声为
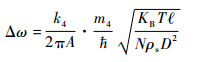 | (9) |
由式(9)易知,由相位波动噪声引起的陀螺角速度噪声与外界输入角速度无关,只与弱连接的结构和陀螺工作温度有关,通过设置合适的陀螺工作温度、弱连接厚度、微孔数目和孔径横截面积,可以在一定程度上实现陀螺相位波动噪声的抑制。
由于超流体在弱连接处发生约瑟夫森效应的前提为[4]
 | (10) |
式中:ξ4为与温度相关的关联长度,单位为nm,表示为[3]
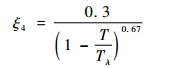 | (11) |
其中:Tλ为超流体的相变温度。
可见,微孔孔径的选取受到关联长度的限制,且陀螺的工作温度应结合弱连接微孔孔径而选取。考虑受限于弱连接的微制造加工技术和微孔的边缘效应,通常微孔的厚度在50~90 nm之间。结合式(9)、式(10)可知,在微孔数目和弱连接厚度固定时,设置
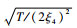
2.2 基于RLS算法的噪声自适应抵消系统设计 根据超流体陀螺工作原理,通过薄膜幅值信息可以求解出相位波动噪声影响下陀螺输出的混合噪声角速度信息。针对该角速度信息中相位波动噪声引起的角速度噪声与输入角速度互不相关的特性,设计的陀螺波动噪声自适应抵消系统如图 2所示。期望输入d(i)为陀螺薄膜解算出的有用角速度信息ω(i)和噪声δω(i)的混合角速度信息,u(i)为与δω(i)相关但与ω(i)不相关的参考噪声输入。
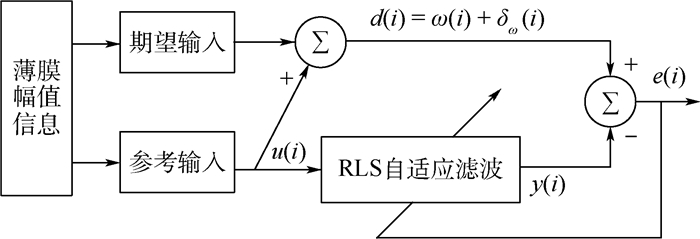 |
| 图 2 噪声自适应抵消系统示意图 Fig. 2 Schematic of noise adaptive cancellation system |
| 图选项 |
通过将薄膜幅值信息解算出的混合角速度信息作为噪声自适应抵消系统的期望输入,相位波动引起的角速度噪声作为RLS自适应滤波器的参考噪声输入, 经过参数调节使得RLS自适应滤波器的输出与混合角速度的噪声部分相抵消。其中,RLS自适应滤波器采用如图 3所示的横向滤波器结构。
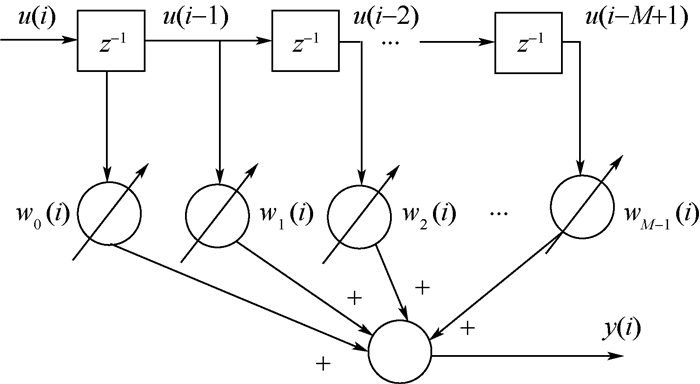 |
| 图 3 横向滤波器结构 Fig. 3 Structure of transversal filter |
| 图选项 |
RLS横向滤波器的输出为
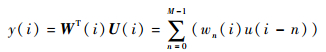 | (12) |
式中:U(i)=[u(i), u(i-1), …, u(i-M+1)]T为输入向量;W(i)=[w0(i), w1(i), …, wM-1(i)]T为权系数向量,i为时间序列,M为滤波器阶数。
则超流体陀螺噪声自适应抵消系统的实际输出为
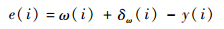 | (13) |
对式(13)平方得到
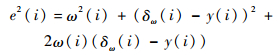 | (14) |
由式(9)可知,由相位波动噪声引起的陀螺角速度噪声与输入角速度不相关,即ω(i)与y(i)及δω(i)互不相关,则ω(i)与δω(i)-y(i)也不相关,对式(14)取数学期望得到
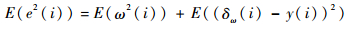 | (15) |
调节权系数使E((δω(i)-y(i))2)为0,E(e2(i))对应也为最小,此时超流体陀螺噪声自适应抵消系统的输出即为有用角速度信息。
采用RLS算法时,为使得系统期望输出和实际输出之间误差最小,取代价函数[17]为
 | (16) |
式中:λ为遗忘因子,其作用是使得离k时刻远的误差赋较小权重。
将误差代入代价函数,得到加权误差平方和的完整表达式为
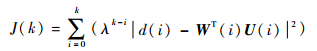 | (17) |
为使代价函数取得最小值,可通过对权向量求导,得到代价函数达到最小值时,存在如下关系:
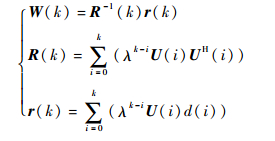 | (18) |
R(k)和r(k)可由递推关系得到
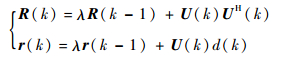 | (19) |
根据矩阵逆的引理,令P(k)=R-1(k),得到
 | (20) |
将式(19)、式(20)代入式(18),得权向量的更新方程为
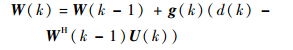 | (21) |
超流体陀螺噪声自适应抵消系统通过实时比较期望信息和RLS自适应滤波器输出信息的差值信息,自适应调整权向量W(k),同时更新P(k),并把RLS自适应滤波器的输出与期望输入信息相抵消,最终实现对陀螺角速度噪声的完全抑制。
3 仿真分析 为保证微孔发生约瑟夫森效应的一致性,通常设定工作温度在临界温度以下的10 mK以内。恒定的温度保持系统和高精度的温度控制系统是超流体陀螺稳定工作的前提,为了获得恒定的陀螺工作温度,通常将陀螺装置放置于体积远远大于超流体陀螺的液氦浴恒温系统中,通过高精度温度控制系统维持低温液氦浴系统在恒温环境。因此,陀螺启动后的工作温度也是恒定的,可不考虑其对陀螺标度因数的影响。超流体陀螺的主要参数如表 1所示,分析陀螺参数对陀螺角速度噪声的影响,在保证超流体在弱连接处发生约瑟夫森效应的基础上,仿真得到相位波动噪声引起的角速度噪声随工作温度和弱连接厚度的变化曲面如图 4所示。
表 1 超流体陀螺的主要参数 Table 1 Main parameters of superfluid gyroscope
| 参数 | 数值 |
| 柔性薄膜面积/cm2 | 0.5 |
| 微孔数目 | 4 225 |
| 超流体密度/(kg·m-3) | 3 |
| 陀螺的感应面积/cm2 | 10 |
| 临界流量/(kg·s-1) | 5.6×10-12 |
表选项
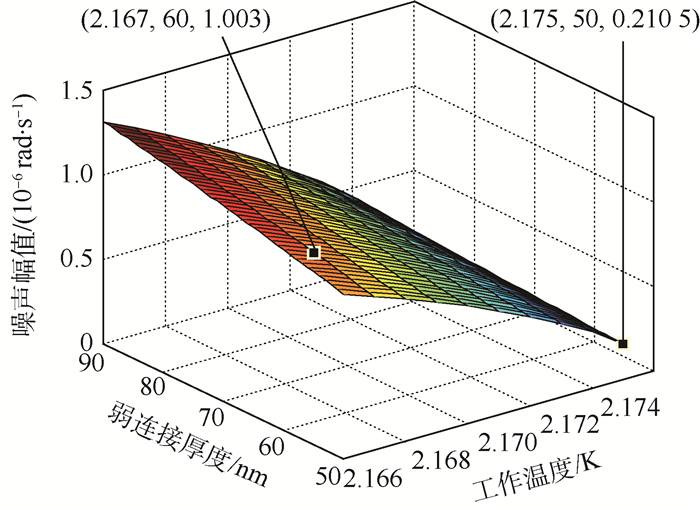 |
| 图 4 角速度噪声变化曲面 Fig. 4 Change surface of angular velocity noise |
| 图选项 |
由图 4的曲面走势可知,角速度噪声随着陀螺工作温度的升高而降低,陀螺的工作温度为2.175 K时,角速度噪声达到最小。在工作温度固定的情况下,陀螺的角速度噪声随着弱连接厚度的增加而增大。在陀螺工作参数范围内,取陀螺工作温度为2.175 K,弱连接厚度为50 nm时,角速度噪声幅值达到最小为0.210 5×10-6 rad/s。可见,通过合理设置陀螺相关参数,在一定程度上可实现陀螺角速度噪声的抑制。
分析图 4易知,一旦陀螺工作温度和弱连接厚度确定时,由相位波动噪声引起的等效角速度噪声也是确定的,该噪声幅值(标准偏差)在10-7~10-6 rad/s数量级。不失一般性,考虑陀螺角速度噪声标准偏差为1.003×10-6 rad/s的情况(对应陀螺参数为:工作温度为2.167 K,弱连接厚度为60 nm),相位波动噪声属于热噪声范畴,则其等效角速度噪声可表示为10-6 randn(1, i)。
超流体陀螺噪声自适应抵消系统的关键是要保证参考输入与被抵消噪声相关,而与有用信息无关。因此,选取参考输入u(i)与被抵消噪声δω(i)这2路噪声都来自于同一个噪声源,则可满足相关性要求,即参考输入噪声为u(i)=10-6·randn(1, i);此外,相位波动引起的角速度噪声是只与陀螺结构参数相关的独立随机变量,与外界输入角速度显然不相关。
为了验证所设计的超流体陀螺噪声自适应抵消系统的可行性和有效性,对超流体陀螺薄膜输出的混有噪声的正弦角速度信息进行研究。有用角速度设为2×10-6sin(0.03πi) rad/s,背景信息的时域和频域信息特性如图 5所示。图 5(a)为噪声源的时域特性,可见噪声源是在整个时域内呈均匀分布的白噪声;图 5(b)为混合噪声的角速度信息的频域特性,分析可知,背景信息在0.015 Hz频率处有一个幅度突变,其余频率处信息幅度都为均匀分布,突变点处的幅值在2×10-6 rad/s附近,说明背景信息中包含频率为0.015 Hz、幅值为2×10-6 rad/s的交流分量信息,此信息即有用角速度信息。
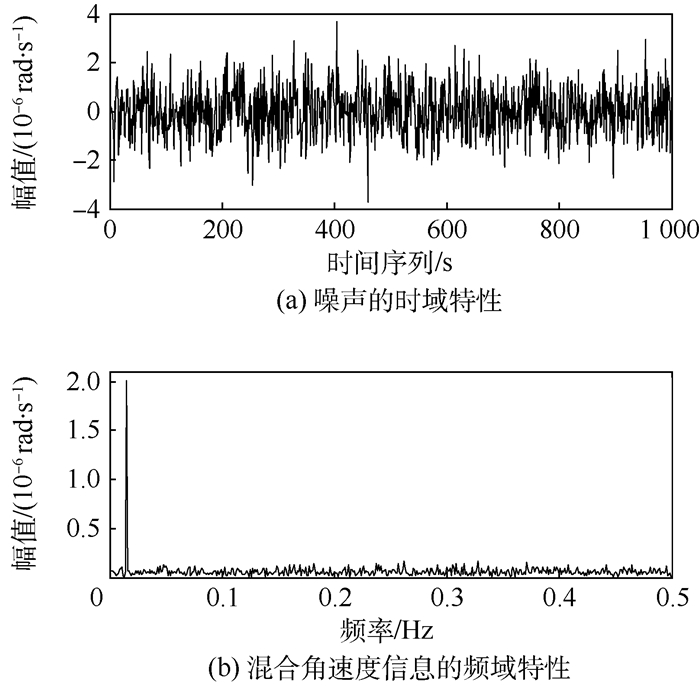 |
| 图 5 背景信息的时域和频域特性 Fig. 5 Time domain and frequency domain characteristics of background information |
| 图选项 |
考虑输入信噪比为3 dB的情况,设计滤波器阶数为3,遗忘因子为0.99,仿真得到基于RLS算法的噪声抵消效果如图 6所示。可知,经过约100次的迭代运算后,陀螺角速度噪声已基本被抵消掉,基于RLS算法的噪声自适应抵消系统能够有效抑制陀螺相位波动噪声引起的角速度噪声对测量角速度的污染。
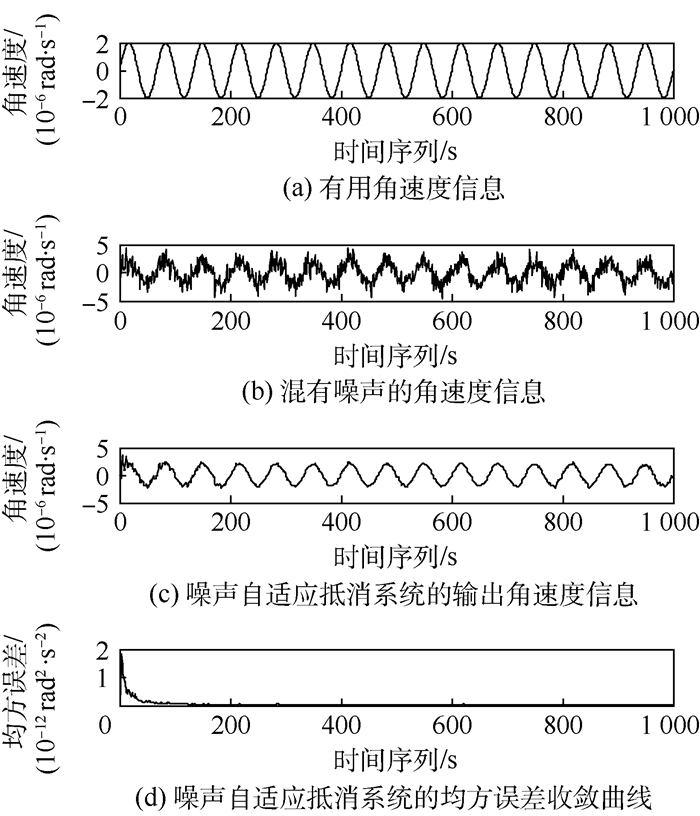 |
| 图 6 基于RLS算法的噪声抑制效果 Fig. 6 Noise suppression effect based on RLS algorithm |
| 图选项 |
固定滤波器阶数为3,图 7为采用RLS算法、LMS算法和归一化LMS(NLMS)算法调节滤波器参数时得到的噪声自适应抵消系统输出结果。对比分析可知,与RLS算法相比,其他2种算法初始时速度波动较大,且调整时间较长。基于RLS算法的噪声自适应抵消系统的输出角速度较为平滑且调整时间较短,可实现有用角速度信息的快速精确跟踪。
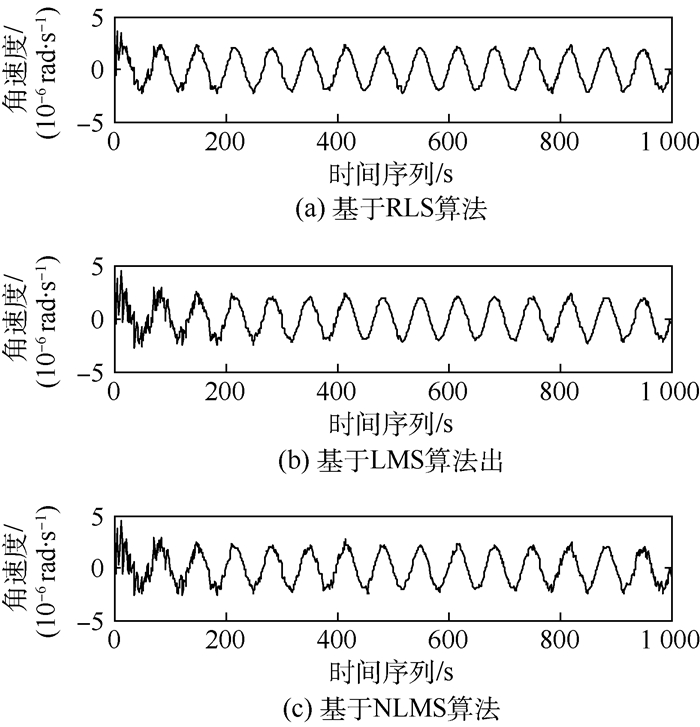 |
| 图 7 3种算法的噪声抑制效果 Fig. 7 Noise suppression effect of three algorithms |
| 图选项 |
为了直观分析不同算法对有用角速度跟踪的误差收敛情况,仿真得到采用RLS算法、LMS算法和NLMS算法时噪声自适应抵消系统的输出与有用角速度信息误差的平方变化情况,如图 8所示。可知,3种算法都能实现良好的噪声抑制效果,噪声自适应抵消系统的输出误差最终均能收敛,且RLS算法具有较快的收敛速度和较好的跟踪精度。
 |
| 图 8 3种算法的输出误差平方 Fig. 8 Square of output error of three algorithms |
| 图选项 |
表 2为使用3种算法时,有用角速度信息为2×10-6sin(0.03πi) rad/s、输入信噪比为3 dB时,得到的相关量化指标的对比。其中,输入信噪比是指输入有用信息的能量与噪声能量的比值,输出信噪比是指输出有用信息的能量和剩余噪声能量的比值。分析可知,3种算法作用下,系统最终的输出信噪比均远远大于输入信噪比3 dB,表明3种算法对噪声均具有较好的抑制能力,其中,RLS算法作用下输出信噪比最大为16.43 dB。
表 2 输入信噪比为3 dB时的相关量化指标 Table 2 Relevant quantitative indicators when input signal to noise ratio is 3 dB
| 算法 | 均方误差/(10-12rad2·s-2) | 输出信噪比/dB | 100次迭代运算耗时/s |
| RLS | 1 | 16.43 | 5.124 |
| LMS | 1 | 12.03 | 2.552 |
| NLMS | 1 | 12.39 | 3.414 |
表选项
考虑陀螺中可能存在其他白噪声增强效应的影响,将角速度噪声的强度增大4倍,有用角速度信息保持不变,对应信噪比变为-3 dB,滤波参数不变。考虑在强噪声背景条件下,基于3种不同算法的噪声自适应抵消系统输出与有用角速度信息的均方误差收敛曲线对比如图 9所示。可知,在强噪声背景下,基于RLS算法的噪声自适应抵消系统能够使均方误差快速收敛;而采用LMS算法和NLMS算法时,不仅收敛速度慢,且系统始终存在未被抵消的剩余误差,即无法精确地跟踪有用角速度信息。
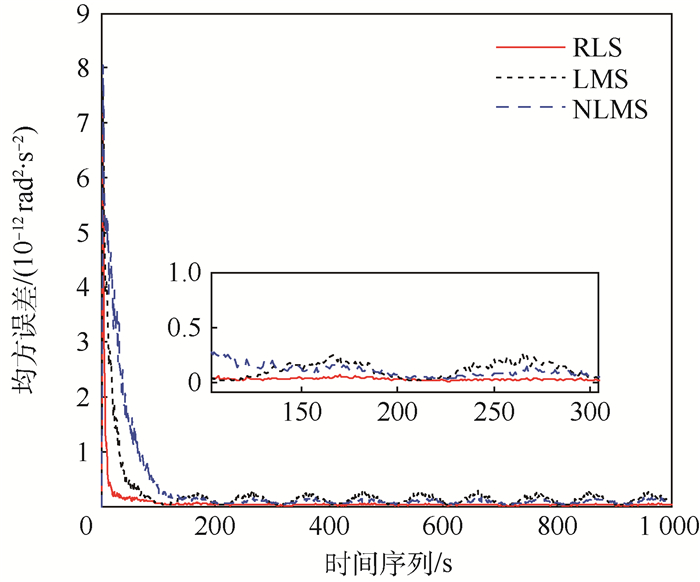 |
| 图 9 3种算法的均方误差 Fig. 9 Mean square error of three algorithms |
| 图选项 |
表 3为使用3种算法时,有用角速度信息为2×10-6sin(0.03πi) rad/s、输入信噪比为-3 dB时,得到的相关量化指标对比。对比表 2、表 3可知,随着均方误差的增大,采用LMS算法和NLMS算法对噪声的抑制能力较为有限,输出信噪比明显降低,而采用RLS算法仍能保持较大的输出信噪比。
表 3 输入信噪比为-3 dB时的相关量化指标 Table 3 Relevant quantitative indicators when input signal to noise ratio is -3 dB
| 算法 | 均方误差/(10-12rad2·s-2) | 输出信噪比/dB | 100次迭代运算耗时/s |
| RLS | 4 | 16.31 | 5.281 |
| LMS | 4 | 9.29 | 2.474 |
| NLMS | 4 | 9.48 | 3.282 |
表选项
进一步考虑大输入角速度、大噪声复杂情况对噪声自适应抵消系统的影响,角速度噪声的方差增大16倍,相应的增大输入角速度噪声幅值,使得信噪比为3 dB保持不变,得到大角速度、大噪声时,3种算法均方误差收敛曲线如图 10所示。可知,基于LMS算法的噪声自适应抵消系统受到大角速度、大噪声的影响,系统失稳而不能收敛,这是由于LMS滤波器受到了梯度噪声放大的影响。NLMS算法对LMS算法进行了归一化处理,规避了梯度噪声放大的影响。基于NLMS算法的噪声自适应抵消系统在初始时可实现较快的误差收敛,但系统最终仍存在未被抵消的剩余误差,导致均方误差曲线无法收敛为0。基于RLS算法的噪声自适应抵消系统在大角速度、大噪声的情况下,仍能实现快速稳定的收敛和角速度信息的精确跟踪。
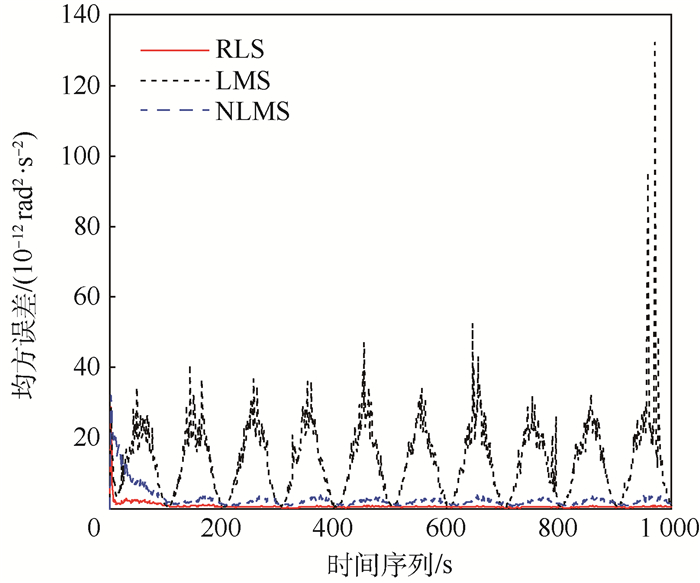 |
| 图 10 大角速度、大噪声时3种算法的均方误差 Fig. 10 Mean square error of three algorithmswhen angular velocity and noise are large |
| 图选项 |
表 4为使用3种算法时,有用角速度信息为8×10-6sin(0.03πi) rad/s、输入信噪比为3 dB时,得到的相关量化指标的对比。可知,在输入大幅值角速度信息、大噪声的复杂情况时,采用LMS算法对噪声的抑制能力极小,输出信噪比几乎接近输入信噪比3 dB。NLMS算法仍能保持较好的噪声抑制能力,这是由于NLMS算法归一化处理而规避了梯度噪声放大的影响。对比表 2~表 4中3种算法的输出信噪比变化情况可知,相比于其他2种算法,RLS算法作用下噪声自适应抵消系统的输出信噪比始终能维持在16 dB附近,表明RLS算法对噪声的抑制能力是最好的。
表 4 大角速度、大噪声时的相关量化指标 Table 4 Relevant quantitative indicators when angular velocity and noise are large
| 算法 | 均方误差/(10-12rad2·s-2) | 输入信噪比/dB | 输出信噪比/dB | 100次迭代运算耗时/s |
| RLS | 16 | 3 | 16.44 | 5.304 |
| LMS | 16 | 3 | 4.52 | 2.492 |
| NLMS | 16 | 3 | 10.48 | 3.293 |
表选项
综上所述,相比于其他2种算法,RLS算法在不同输入信噪比、均方误差情况下,均能有效抵消陀螺混合角速度信息中的噪声成分,且具有较快的均方误差收敛速度和较好的稳定性。然而通过分析表 2~表 4中3种算法在不同工况时的100次迭代运算耗时可知,相比于其他2种算法,RLS算法由于计算复杂度较高导致其计算时间是最长的。可见,为了实现RLS算法从离线处理走向实时系统应用,还需进一步研究如何降低RLS算法的计算复杂、计算时间长的问题。
4 结论 针对超流体陀螺相位波动噪声影响陀螺角速度检测精度的问题,本文开展了超流体陀螺噪声抑制的相关研究,得出以下结论:
1) 相位波动噪声引起的等效角速度噪声随着工作温度的升高而降低,随着弱连接厚度的增加而增大。在陀螺参数范围内,其噪声幅值为10-7~10-6 rad/s,通过合理设置陀螺相关参数,在一定程度上可以实现陀螺角速度噪声的抑制。
2) 在不同输入信噪比、均方误差情况下,基于RLS算法的噪声自适应抵消系统均能够有效消除陀螺混合角速度信息中的噪声成分,且具有较快的收敛速度和较好的稳定性。然而,相比于LMS算法和NLMS算法,RLS算法由于计算复杂度较高导致其计算时间是最长的。
参考文献
| [1] | DOLBIN A V. Physics of nanostructures at low temperatures[J].Low Temperature Physics, 2016, 42(2): 75.DOI:10.1063/1.4941964 |
| [2] | PACKARD R. Principles of superfluid helium gyroscopes[J].Physical Review B, 1992, 46(6): 3540–3549.DOI:10.1103/PhysRevB.46.3540 |
| [3] | SATO Y, ADITYA J, PACKARD R. Superfluid 4He quantum interference grating[J].Physical Review Letters, 2008, 101(8): 085302–1.DOI:10.1103/PhysRevLett.101.085302 |
| [4] | HOSKINSON E. Superfluid 4He weak links[D]. Berkeley: University of California, 2005: 45-58.http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.210.7628&rep=rep1&type=pdf |
| [5] | SATO Y. Sagnac-based rotation sensing with superfluid helium quantum interference devices[J].Comptes Rendus Physique, 2014, 15(10): 898–906.DOI:10.1016/j.crhy.2014.10.004 |
| [6] | GOLOVASHKIN A I, ZHERIKHINA L N, TSKHOVREBOV A M, et al. Ordinary SQUID interferometers and superfluid helium matter wave interferometers:The role of quantum fluctuations[J].Journal of Experimental and Theoretical Physics, 2010, 111(2): 332–339.DOI:10.1134/S1063776110080285 |
| [7] | SIMMOND R W, MARCHENKOV A, HOSKINSON E, et al. Quantum interference of superfluid 3He[J].Nature, 2001, 412(6842): 55–58.DOI:10.1038/35083518 |
| [8] | SATO Y, PACKARD R. DC superconducting quantum interference device based neodymium magnet displacement sensor for superfluid experiments[J].Review of Scientific Instruments, 2009, 80(5): 055102.DOI:10.1063/1.3129942 |
| [9] | CHUI T, HOLMES W, PENANEN K. Fluctuations of the phase difference across an array of Josephson junctions in superfluid 4He near the Lambda transition[J].Physical Review Letters, 2003, 90(8): 085301. |
| [10] | NARAYANA S, SATO Y. Superfluid quantum interference in multiple-turn reciprocal geometry[J].Physical Review Letters, 2011, 106(25): 255301.DOI:10.1103/PhysRevLett.106.255301 |
| [11] | MAO Y, DING F, ALSAEDI A, et al. Adaptive filtering parameter estimation algorithms for Hammerstein nonlinear systems[J].Signal Processing, 2016, 128: 417–425.DOI:10.1016/j.sigpro.2016.05.009 |
| [12] | DU G, ZHANG P. A markerless human-robot interface using particle filter and Kalman filter for dual robots[J].IEEE Transactions on Industrial Electronics, 2015, 62(4): 2257–2264.DOI:10.1109/TIE.2014.2362095 |
| [13] | AMIRYARAHMADI N, KROPP W, LARSSON K. Application of LMS algorithm to measure low-frequency transient forces from human walking[J].Acta Acustica United with Acustica, 2016, 102(1): 23–34.DOI:10.3813/AAA.918921 |
| [14] | SATO Y, ADITYA J, PACKARD R. Flux locking a superfluid interferometer[J].Applied Physics Letters, 2007, 91(7): 1–3. |
| [15] | SATO Y. Experiments using 4He weak link[D]. Berkeley: University of California, 2007: 51-58.http://gradworks.umi.com/33/06/3306328.html |
| [16] | PACKARD R. The role of the Josephson-Anderson equation in superfluid helium[J].Review of Modern Physics, 1998, 70(2): 641–651.DOI:10.1103/RevModPhys.70.641 |
| [17] | KOHLI A K, RAI A. Numeric variable forgetting factor RLS algorithm for second-order volterra filtering[J].Circuits, Systems, and Signal Processing, 2013, 32(1): 223–232.DOI:10.1007/s00034-012-9445-7 |
