目前，航空电子系统正飞速从联合架构(federated avionics)向综合模块航电(Integrate Modular Avionics，IMA)架构转换^[1]。IMA架构在一台共享的计算平台上部署拥有多个航电子系统功能的高集成度分区系统，即各个分系统共享软件(操作系统)和硬件资源。这种架构已经广泛应用在实际飞机航电系统中，例如波音777、空客A380等机型^[2]。
由于在IMA架构下，多个应用共享计算资源，因此一个应用的错误可能会影响到其他应用。为了提高系统可靠性和安全性，IMA系统软件必须提供应用之间的隔离机制^[3]。
ARINC 653^[4]是一个分区操作系统标准，其通过引入分区来提供应用在时间和空间上的隔离。在空间上，任何应用只能访问预先分配给它的物理内存，而不能访问分配给其他分区的物理内存；在时间上，任何应用只能在预先分配给它的时间窗口内执行，而不能占用其他应用的时间窗口。
ARINC 653调度策略包括2级。分区间采用时间片轮转调度算法。用户需定义在一个主时间帧内各个分区的调度表，操作系统以主时间帧为周期，根据调度表中为每个分区分配的时间窗口调度分区，应当注意分区没有优先级^[5]。分区内的实时任务可以选用固定优先级抢占调度算法。
由于时间分区的引入，传统的响应时间可调度性分析方法^[6]不再适用。目前，已经有很多文献基于传统的方法，对分区系统的可调度性进行了研究。文献[7]对分区进行了建模，提出了关键分区(critical partition)的概念，并给出了多时间窗口分区中任务可调度的充分条件。文献[8]给出了多时间窗口分区任务可调度的充分必要条件，但算法复杂度要高得多。除了理论计算，还可以通过建模工具进行可调度性分析。例如，文献[9]给出了一种基于时序Petri网的分析方法，不但可以分析可调度性，而且可以分析时序约束的满足性。文献[10]综述了分区系统的可调度性分析方法。
除了可调度性研究，分区时间窗口分配也是当前研究热点。文献[11]研究了当各个分区采用RM静态调度算法，且各个分区在主时间帧内只被分配一个时间窗口时，分区任务的最大利用率U与分区时间窗口和主时间帧的比值π_Ω(称为分区参数)之间的关系式，并以此来设计分区参数。文献[12]给出了当各个分区采用任意优先级调度算法时，分区参数的设计方法。这些方法的主要思想是将其他分区视为本分区的一个最高优先级的任务。
文献[13]将一个分区的周期调度抽象为服务，并引入处理器降速因子来模拟分区中的时间流逝，在此基础上提出了一种分区参数的设计方法。文献[14]研究了服务模型下任务可调度的充分条件。
上述文献提出的算法只为分区在主时间帧中分配一个时间窗口。事实上，为满足某些系统的可调度性，必须要在主时间帧内为某些分区分配多个时间窗口。目前还没有太多文献给出多时间窗口的分配算法。本文研究在单处理器平台下满足特定条件(和谐周期^[15]条件)的分区系统的多时间窗口分配算法。与已有算法相比，本文提出的算法能够为任何在理论上可调度的和谐周期分区系统生成可行的分区调度表，因此更具有实用性。
1 调度模型定义 本文研究分区系统的调度。在分区系统中，分区间采用时间片轮转的调度算法，而分区内部的任务采用可抢占的固定优先级调度算法。全局调度器周期地按照预先定义好的调度表调度分区占用计算资源。当分区被调度运行后，首先执行优先级最高的任务，并且就绪的高优先级任务可以抢占正在执行的低优先级任务。另外，规定分区中的所有任务都是周期任务。
定义1??系统S定义为分区P_k的集合，即S={P_k}。
定义2??分区P_k定义为周期任务τ的集合，即P_k={τ}。
定义3??周期任务τ定义为四元组，即τ=(p, d, e, pri)，p为任务的周期，d为任务的截止时间，e为任务的最坏执行时间，pri为任务的优先级。
值得注意的是，任务参数e是最坏执行时间。文献[16]从执行时间概率的角度提出了一种优化任务响应时间的分区调度算法。
定义4??工作实例J表示任务在某个特定周期内的实际执行。
在下文中，用τ.x表示元组τ中的分量x。另外，用时间片表示任务执行时间的单位，例如τ.e=1表示任务τ的一次执行需要1个时间片。规定任务τ的最坏执行时间τ.e是整数。
2 和谐周期分区系统及其可调度性 定义5(和谐周期^[15]任务集)??假设集合T是任务的集合，如果T中的任何任务τ∈T的截止时间τ.d和周期τ.p相等，并且对于任何τ_i, τ_j∈T，如果τ_i.p＜τ_j.p，则有τ_j.p是τ_i.p的倍数，那么称T是和谐周期任务集。
定义6(和谐周期分区系统)??假设系统S={P_k}，其所有分区P_k={τ}中的所有任务构成集合。如果ST是和谐周期任务集，则称系统S是和谐周期分区系统。
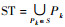
下面讨论和谐周期分区系统各个分区中任务的可调度性。假设和谐周期分区系统S={P_k}，其所有分区中的所有任务构成的任务集为。用集合period表示ST中所有任务的所有可能的周期的集合，即

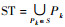
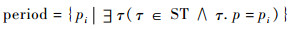period中的周期按照从小到大的顺序排序，其中p₁为最小周期，p_max为最大周期，p_i表示第i小的周期。
由于p_max是所有ST中所有任务的周期的最小公倍数，因此，可将主时间帧的长度设置为p_max^[8]。
定义7??集合A_ki表示分区P_k中所有周期小于等于p_i的任务的集合，即A_ki={τ∈P_k|τ.p≤p_i}。
定义8??集合B_ki形式化地定义为：B_ki={τ∈P_k|τ.p＞p_i∧?τ′(τ′∈A_ki∧τ′.pri＜τ.pri}, 即表示P_k中所有周期大于p_i且优先级高于A_ki中任务最低优先级的任务的集合。
引理1??对于任何分区P_k，周期p_i∈period以及l=0, 1, …, ，如果任务τ∈B_ki的周期τ.p满足lp_i mod τ.p≠0，即τ中没有任何工作实例在lp_i时刻释放，则任务τ∈B_ki的任何工作实例不在[lp_i, (l+1)p_i)间隔内执行。
证明??由于任务τ的周期大于p_i，所以在[lp_i, (l+1)p_i)间隔内最多只可能执行τ的一个工作实例J，并且J在lp_i之前释放，截止时间在lp_i时刻之后(见图 1)。假设J的释放时间为mτ.p，由于τ.p是p_i的整倍数，所以mτ.p一定可以写成l′p_i，l′＜l。由于在时间间隔[l′p_i, (l′+1)p_i)内，在l′p_i时刻释放的A_ki中的任务全部执行完成。而τ的任务的优先级比A_ki中任务的最低优先级高，因此，在l′p_i时刻释放的A_ki中的任务全部执行完成之前，工作实例J一定执行完成，即J在(l′+1)p_i时刻之前完成。由于(l′+1)p_i≤lp_i，所以J一定在[lp_i, (l+1)p_i)开始前完成，并且τ不会在(l+1)p_i时刻前产生新的工作实例。因此，τ不会有任何工作实例在区间[lp_i, (l+1)p_i)内执行。

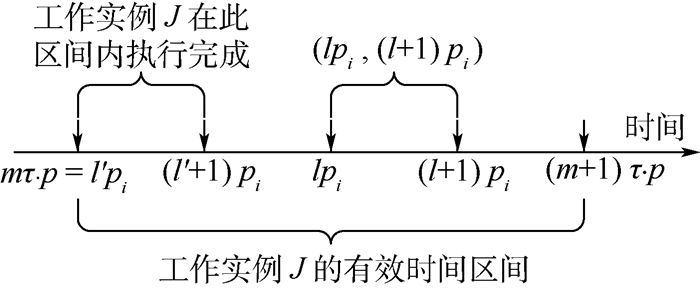图 1 引理1证明示意图 Fig. 1 Schematic for proving Lemma 1

图选项

现在考虑在满足可调度性的前提下，任何一个分区P_k在时间区间[lp_i, (l+1)p_i)内应当被分配到的时间片数。在该区间内，任何周期不大于p_i的任务τ∈A_ki，都会产生p_i/τ.p个工作实例，并且第1个工作实例的释放时刻为lp_i，最后1个工作实例的截止时刻为(l+1)p_i。因此，在该区间内分区P_k得到的时间片应满足这些工作实例的执行时间需求。其次，对于周期大于p_i的任务τ∈B_ki，如果其某个工作实例在时刻lp_i释放，由于其优先级高于A_ki中任务的最低优先级，那么，当A_ki中的任务产生的工作实例完成之前，此高优先级任务的实例一定被执行完成。因此，分区P_k在[lp_i, (l+1)p_i)间隔内得到的时间片还要满足在lp_i时刻释放的B_ki中任务的工作实例的执行时间需求。而对于B_ki中不在lp_i时刻释放的任务，根据引理1，它的任何工作实例一定不会在[lp_i, (l+1)p_i)间隔内执行，因此，无需考虑这些任务。
综上所述，可以得到如下定理。
定理1??如果系统S={P_k}是和谐周期分区系统，函数f(k, i, j)表示分区P_k在时间区间[i, j)内分配得到的时间片数量，则分区P_k中任务可调度的充分必要条件是对任何p_i∈period，对于任何l=0, 1, …, ，都有

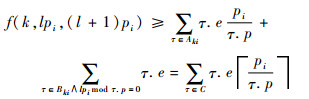(1)

式中：集合C={τ|τ∈A_ki∪B_ki∧lp_i mod τ.p=0}，即A_ki中所有任务，以及B_ki中所有在lp_i时刻有新的工作实例被释放的任务构成的集合。
证明??根据上述分析，定理1的必要性是显然的。下面用反证法证明其充分性。如果式(1)成立，假设某个以p_i为周期的任务τ的工作实例J超时，其中J的释放时间是lp_i，截止时间是(l+1)p_i，则一定有

(2)

式中：集合D为所有周期不比τ.p大、优先级比τ.pri高的任务的集合；集合E为所有周期比τ.p大、优先级比τ.pri高且有工作实例在lp_i时刻释放的任务构成的集合。显然有集合C包含D∪E∪{τ}，这样就有

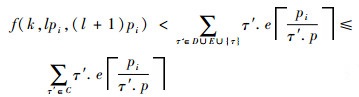(3)

这与条件相矛盾，假设不成立，即没有任何任务的任何工作实例超时。因此，分区是可调度的，原命题得证。
为了下文叙述方便，定义：

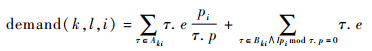(4)

即demand(k, l, i)表示为满足任务可调度性，在时间间隔[lp_i, (l+1)p_i)内分区P_k最少得到的时间片数。
3 时间窗口分配算法 时间窗口分配算法在实质上是将主时间帧中的时间片分配给各个分区。假设主时间帧的长度为F，即其中共有F个时间片。用数组distribute[0…F-1]表示时间片的分配情况：distribute[n]=k表示从n时刻开始的时间片被分配给分区P_k；distribute[n]=-1表示该时间片尚未被分配给任何分区。
算法distribute_operator在给定时间间隔[s, e)内为分区P_k分配指定数量的时间片。它从distribute数组中的s位置开始寻找空闲时间片(即语句distribute[i]=-1)，并将此空闲时间片分配给分区P_k(语句distribute[i]=k)。
输入：分区号k，时间间隔[s, e)和时间片数量m。
输出：是否分配成功标识。
begin
??for i from s to e-1
???if distribute[i] = -1 then
?????distribute[i]=k，m=m-1
?????if m=0 ???return success
???end if
??end for
??return failure
end
从定理1可以看出，为满足某个分区P_k中任务的可调度性，必须为它在任意的时间间隔[lp_i, (l+1)p_i), p_i∈period, l=0, 1, …, 内分配demand(k, l, i)个时间片以满足其中任务的执行时间需求。由于时间间隔[lp_i, (l+1)p_i)(i＞1)内包括p_i/p_i-1个长度为p_i-1的时间间隔，当这些长度为p_i-1的时间间隔内的时间需求都得到满足时，还需要为该分区在[lp_i, (l+1)p_i)间隔内分配的时间片数additionT为

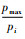
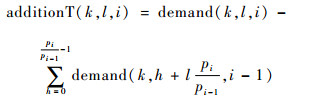(5)

而对于时间间隔[lp₁, (l+1)p₁)，分区在此间隔内必须至少得到demand(k, l, 1)个时间片。因此，可以考虑按照p₁, p₂, …, p_max的顺序，在[lp_i, (l+1)p_i)间隔内为各个分区分配满足要求的最少数量的时间片。具体的分配算法如算法Window_Distribute_algorithm所示。
输入：分区集{P_k}。
输出：分配成功或失败的标识。
begin
??for i from 1 to max
???for j from 0 to p_max/p_i-1
????for k from 1 to partitionNum
?????if i=1 then
??????m=demand(k, j, 1)
?????else
??????m=additionT(k, j, i)
?????end if
?????ret=distribute_operator(k, jp_i, (j+1)p_i, m)
?????if ret=failure then
?????return failure
????end for 3
???end for 2
??end for 1
??return success
end
当算法Window_Distribute_algorithm返回success后，数组distribute中即存储了时间片的分配方案，也就是时间窗口的分配方案。
如果在某次迭代中调用的distribute_operator返回失败，表明在此时间区间内无法为所有任务都分配满足式(1)的时间片数，也就表明此分区系统是不可调度的，因此算法返回失败。
下面讨论Window_Distribute_algorithm算法的时间复杂度。假设和谐周期分区系统S={P_k}共包括n个分区，每个分区最多有m个任务，并且所有任务的最大周期为p_max。首先，根据demand函数的定义，计算一次demand函数要遍历分区中的所有任务。因此，计算demand函数的时间复杂度是O(m)。而additionT(k, j, i)函数的计算涉及一次demand(k, j, i)的计算，以及p_i/p_i-1个demand(k, l, i-1)值的求和。如果上一次迭代计算得到的demand(k, l, i-1)保存在数组中，则由于p_i/p_i-1的最大值是所有任务的最大周期p_max，则additionT(k, j, i)的计算复杂度就是O(m+p_max)。根据最大周期p可得系统中最多可能有lb p种不同的周期，这意味着算法最外层循环最多迭代lb p次。易知，第2层和第3层循环最多执行p_max次和n次。因此，Window_Distribute_algorithm算法的时间复杂度是O((m+p_max)p_maxnlb p_max)。
4 案例分析 本节通过一个例子来演示第3节算法的执行过程。假设某IMA系统包括2个应用：液压应用和环控应用。这2个应用分别位于分区A和分区B。液压应用包括2个任务：健康管理任务task1和主控任务task2。环控应用只包括主控任务task3。task1、task2和task3的周期、最坏执行时间、截止时间和优先级如表 1所示。由于系统中所有任务的截止时间和周期相等，且任何大的任务周期是任何小的任务周期的倍数，因此，该系统是和谐周期分区系统。
由表 1可见，由于最大的任务周期是8，因此将主时间帧设置为8。现在需要将这8个时间片分配给A、B 2个分区。从表 1中可见，最小周期是2。根据算法，首先应在长度为2的时间间隔[0, 2)，[2, 4)，[4, 6)，[6, 8)内根据任务时间需求为这2个分区分配时间片。在分区A内，task2的周期为2。由于0时刻task2与比其优先级高的task1同时就绪，因此demand(A, 0, 1)=1+2/2×1=2。在剩余的3个长度为2的区间内，demand(A, l, 1)=0, l=1, 2, 3，即分区A应当在这3个区间内分别得到1个时间片。分区B中没有周期为2的任务，所以demand(B, l, 1)=0, l=0, 1, 2, 3，因此本轮不为分区B分配时间片。本轮分配完成后的结果如图 2所示。
表 1 用于案例分析的分区系统的任务参数 Table 1 Parameters of tasks of partitioning systems for case analysis

任务	分区	周期	截止时间	最坏执行时间	优先级
task1	A	8	8	1	H
task2	A	2	2	1	L
task3	B	4	4	1	H

表选项

图 2 第1轮分配结果 Fig. 2 Distribution results of the first iteration

图选项

然后应当在长度为4的时间区间[0, 4)，[4, 8)内为2个分区分配时间片。对于分区A，demand(A, 0, 2)=3，demand(A, 1, 2)=2，所以有additionT(A, 0, 2)= 3-2-1=0，additionT(A, 1, 2)=2-1-1=0，故在这2个区间内不为分区A分配额外时间片。在分区B中，task3的周期为4，可得demand(B, 0, 2) =demand(B, 1, 2)=1，而任何demand(B, 0, 1)都等于0，因此additionT(B, 0, 2)=additionT(B, 1, 2)=1-(0+0)=1，即需要在[0, 4)和[4, 8)区间内分别为分区B分配一个时间片。本轮迭代分配结果如图 3所示。

图 3 第2轮分配结果 Fig. 3 Distribution results of the second iteration

图选项

最后考虑长度为8的时间间隔。对于分区A，demand(A, 0, 3)=5，所以additionT(A, 0, 3)=5-3-2=0，因此，无需再为分区A分配额外的时间片；对于分区B，demand(B, 0, 3)=2，additionT(B, 0, 3)=2-1-1=0，即也无需为分区B分配额外时间片。图 3所示的分配结果即是最终的分配结果。根据分配结果生成的时间窗口布局如图 4所示。分区调度器可以通过此调度方案周期地调度分区，并且保证任何分区中的任何周期任务都不会超时。

图 4 主时间帧内分区时间窗口布局 Fig. 4 Layout of partition time windows in main time frame

图选项

从图 4可以看出，在一个主时间帧内将发生5次分区切换。而如果将从7时刻开始的空闲时间片分配给分区A，分区切换将只发生4次。因此，分区调度表中需要预先设置的条目至少是4条。根据此调度方案调度分区，各个分区中任务的工作实例的延迟情况如表 2所示。
表 2 任务的工作实例的响应时间 Table 2 Response time of jobs instances of tasks

任务	最大响应时间	最小响应时间	平均响应时间
task1	0	0	0
task2	1	0	0.25
task3	3	1	2

表选项






从表 2可见，task3的工作实例的响应时间较长。可以将在4时刻开始执行的task1的第2个实例和5时刻开始执行的task2的第2个实例的执行顺序交换，以降低task2的响应时间。这虽然增长了task1的响应时间，但却可以提高整个系统的性能。本文算法目前无法实现这样的优化。
5 与其他算法的比较 本节对本文算法和已有算法进行比较。引言已经提到，文献[11]给出了一种分区系统时间窗口分配算法，因此，本文主要与文献[11]中的算法进行比较。
文献[11]中的算法适合于分区内应用RM静态调度算法的分区系统。在这种算法下，每个分区在主时间帧内只被分配一个时间窗口，并且每个分区P_k在主时间帧内被分配的时间窗口长度占整个主时间帧长度的比例为

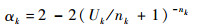(6)

式中：n_k为分区P_k中的任务总数；U_k为分区P_k中所有任务利用率的和，即

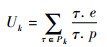(7)

如果某个分区系统中所有分区的时间窗口占比α_k之和小于1，此算法就可以成功为此分区系统生成调度表；相反，如果所有分区的α_k之和大于1，此算法就对此分区系统失效。
现在考虑如表 3所示的分区系统，此系统包括2个分区。其中，分区B中只包括一个周期为4的任务；分区A包括2个任务：周期为8的task1和周期为2的task2。根据RM静态调度算法，task2的优先级高于task1的优先级。
表 3 用于算法对比的分区系统的任务参数 Table 3 Parameters of tasks of partitioning systems for algorithms comparison

任务	分区	周期	截止时间	最坏执行时间	优先级
task1	A	8	8	1	L
task2	A	2	2	1	H
task3	B	4	4	1	H

表选项






对于此系统，如果应用文献[11]的算法，根据式(6)可得，α_A=0.839，α_B=0.4。由于α_A+α_B＞1，因此此算法失效。
而如果应用本文算法，将生成如图 5所示的调度表。

图 5 本文算法生成的调度表 Fig. 5 Schedule table of proposed algorithm

图选项

事实上，正如文献[11]已经指出的，当系统的总利用率大于50%后，本文算法的成功率将大幅下降。而本文算法只要保证系统在理论上可调度，就一定能够生成可行的调度表；并且文献[11]中的算法只适合于分区内部采用RM静态调度算法的系统，而本文算法适合于分区内部应用任何固定优先级调度算法的系统。当然，本文算法和文献[11]中算法相比，最大的局限是只适用于满足和谐周期条件的分区系统，对于不满足和谐周期条件的分区系统，本文算法不再适用。
6 结论 本文以IMA系统为背景，基于传统的响应时间分析方法，研究了满足和谐周期条件的分区系统中各个分区中任务可调度的充分必要条件，并以此为基础给出了一种分区时间窗口分配算法。对于任何和谐周期分区系统，如果该系统在理论上存在一种可行的调度方案，这种算法就一定能够生成一种可行的调度方案。反之，如果该算法返回失败，就表明该和谐周期分区系统在理论上是不可调度的。
然而本文算法也存在一些不足。最大的局限就是要求分区系统必须满足和谐周期条件。另外，还存在分区切换次数过多、任务响应时间过长等问题。
虽然存在上述问题，本文给出的算法依然可以用于实际工程中的分区调度表设计。后续的工作将集中在优化分区切换次数及任务响应时间上。

参考文献

[1]	WATKINS C B, WALTER R. Transitioning from federated avionics architectures to integrated modular avionics[C]//Digital Avionics Systems Conference, 2007. Piscataway, NJ: IEEE Press, 2007: 2. A. 1-1-2. A. 1-10.
[2]	周强, 熊华钢. 新一代民机航空电子互连技术发展[J].电光与控制, 2009, 16(4): 1–6. ZHOU Q, XIONG H G. Development of the new generation civil avionic interconnection technology[J].Electronics Optics & Control, 2009, 16(4): 1–6.(in Chinese)
[3]	沈玉龙, 崔西宁, 马建峰, 等. 综合化航空电子系统可信软件技术[J].航空学报, 2009, 30(5): 938–945. SHEN Y L, CUI X N, MA J F, et al. Trust software technology in integrated avionics systems[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(5): 938–945.(in Chinese)
[4]	ARINC. avionics application software standards interface: ARINC 653[S]. Annapolis: AEEC, 2003.
[5]	杨霞, 桑楠, 雷剑, 等. 嵌入式高可信架构中基于静态模型的调度研究[J].航空学报, 2009, 30(12): 2387–2394. YANG X, SANG N, LEI J, et al. Scheduling based on static model in trusted architecture for embedded systems[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(12): 2387–2394.DOI:10.3321/j.issn:1000-6893.2009.12.022(in Chinese)
[6]	LIU J W S. Real-time sytem[M].Upper Saddle River: Prentice Hall, 2003: 130-140.
[7]	MOK A K, FENG X, CHEN D. Resource partition for real-time systems[C]//7th IEEE Proceedings of Real-time Technology and Applications Symposium. Piscataway, NJ: IEEE Press, 2001: 75-84.
[8]	谭龙华, 杜承烈, 雷鑫. ARINC 653分区实时系统的可调度分析[J].航空学报, 2015, 36(11): 3698–3705. TAN L H, DU C L, LEI X. Schedulability analysis for ARINC 653 partitioned real-time systems[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(11): 3698–3705.(in Chinese)
[9]	CARNEVALI L, PINZUTI A, VICARIO E. Compositional verification for hierarchical scheduling of real-time systems[J].IEEE Transactions on Software Engineering, 2013, 39(5): 638–657.DOI:10.1109/TSE.2012.54
[10]	陈平, 魏峰, 李蜀瑜. ARINC 653调度算法研究[J].现代电子技术, 2015, 38(15): 29–32. CHEN P, WEI F, LI S Y. Study on ARINC 653 scheduling algorithm[J].Modern Electronics Technique, 2015, 38(15): 29–32.(in Chinese)
[11]	李昕颖, 顾健, 何锋, 等. 硬实时系统在强分区约束下的双层分区调度[J].计算机学报, 2010, 33(6): 1032–1039. LI X Y, GU J, HE F, et al. Two-level partition scheduling in hard real time system under strong partition constraints[J].Chinese Journal of Computers, 2010, 33(6): 1032–1039.(in Chinese)
[12]	周天然, 熊华钢. 航空电子系统混合实时任务的双层调度[J].航空学报, 2011, 32(6): 1067–1074. ZHOU T R, XIONG H G. Two-level hierarchical scheduling for hybrid real-time tasks in avionics systems[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(6): 1067–1074.(in Chinese)
[13]	LIPARI G, BINI E, NGUYEN C, et al. A methodology for designing hierarchical scheduling system[J].Journal of Embedded Computing-Real-time System, 2005, 1(2): 257–269.
[14]	WAN M, TIAN S. Research on schedulability of partition scheduling for IMA[C]//20114th International Symposium on Computational Intellingence and Design. Piscataway, NJ: IEEE Press, 2011, 2: 322-325.
[15]	NASRI M, FOHLER G. An efficient method for assigning harmonic periods to hard real-time tasks with period ranges[C]//201527th Euromicro Conference on Real-Time Systems. Piscataway, NJ: IEEE Press, 2015: 149-159.
[16]	桥乃强, 徐涛, 谷青范. ARINC 653分区调度算法的研究与改进[J].计算机工程, 2011, 37(20): 249–251. QIAO N Q, XU T, GU Q F. Research and improvement of ARINC 653 partition schedule algorithm[J].Computer Engineering, 2011, 37(20): 249–251.DOI:10.3969/j.issn.1000-3428.2011.20.085(in Chinese)