网络控制系统是一类利用网络构成闭环的自动控制系统^[1]。由于网络的介入，改变了自动控制系统点对点连接的传统模式，简化了系统的连接，降低了成本，便于维护与升级，因此在工业控制、航空航天、汽车、机器人等领域得到了广泛的应用。与此同时，由于网络带宽有限，分时复用等特征，改变了控制系统信息传输的方式，带来了网络诱导时延、数据包丢失、乱序、采样/传输间隔的波动等因素^[2]，这些因素不仅影响了系统性能，也违背了传统控制理论研究中确定性、同步性等假设前提，使得控制理论无法直接应用于网络控制系统，这给控制带来了新的挑战。近年来，网络控制系统受到了广泛的关注，已有许多理论方法被提出并应用于网络控制系统的建模、分析与设计中^[3-7]。
随着现代工业、通信技术的发展与渗透，工业控制与信息管理系统的融合，派生了许多大型复杂网络化工业控制系统。这些系统往往包含有多个子系统。子系统内部的各部件之间通过现场总线的网络连接构成闭环，而子系统之间通过某种工业控制网络与管理信息系统、监控系统等连接。同时，子系统之间除了信息的交互外，有时还存在物理上的耦合作用。这种具有分层结构的网络化控制系统在航空航天、汽车等领域也比较常见。针对上述分层网络化控制系统，此前网络控制系统研究中常见的集中控制模式在适用性、可实现性等方面均存在先天不足，而分布式控制模式更具有生命力，也更具有研究价值。
目前，关于分布式的控制多集中于多智能体系统，相关研究结果可参见文献[8-10]。由于多智能体的分布式控制研究多针对一阶或二阶积分模型描述的对象，因此相关结论无法直接应用于通常含有高阶动态特性的网络控制系统中。近年来，网络控制系统的分布式控制也得到了研究人员的关注。文献[11]分析了一阶、二阶积分模型网络系统的分布式控制协议，提出了一种分布式PI控制器。文献[12]为补偿网络诱导时延的影响，在本地反馈控制基础上，引入了远端控制，给出了增益控制器的设计方法, 但该控制器实质上仍是集中式控制。文献[13]针对一类具有多个相互作用子系统的网络控制系统，提出了分布式模型预测控制方法, 但没有考虑网络诱导时延等因素对系统的影响。文献[14]针对具有多个子系统的网络控制系统，分析了分布式事件触发控制策略的稳定性条件。文献[15]针对具有N个相互作用的线性时不变子系统的网络控制系统，设子系统信息采用基于事件的广播机制，给出了保证系统稳定的事件触发机制条件，并证明了引入模型预测控制可以扩大事件的最小间隔，降低网络负载。但文献[14-15]并未考虑网络诱导时延的影响，且未涉及控制器设计。文献[16]针对一类可用Takagi-Sugeno模糊模型描述的非线性大规模系统，考虑诱导时延的影响，构造了一种分布式静态输出反馈控制器，基于Lyapunov-Krasovskii函数法，给出了系统渐近稳定的条件, 但未考虑数据包丢失的影响。综上，针对具有分层结构、多个相互作用子系统的网络控制系统的研究结果尚不多见。
为此，本文研究一类分层网络控制系统的分布式控制，考虑由于网络诱导时延、数据包丢失以及资源限制，构建了基于本地反馈和部分子系统反馈信息的分布式控制律。本文的主要贡献在于：①提出了一种分层网络控制系统的分布式控制律，并给出了网络控制系统的模型，该模型可描述分布式网络诱导时延和数据包丢失对系统的影响；②基于Lyapunov-Krasovskii函数法，给出了系统渐近稳定和满足H_∞控制性能指标的充分条件，该条件依赖于时延的上界信息，具有较弱的保守性；③利用锥补线性化方法，给出了控制器设计的迭代求解方法。
1 问题描述 设分层网络控制系统的结构如图 1所示。图中，x_i(k)、分别为子系统i的状态及其在控制器节点处的镜像，k为采样次数，u_i(k)、分别为子系统i的控制输入及其在控制器节点的镜像，为传输到子系统i的其他子系统的状态，q为子系统序号，N_i为子系统i的邻域，包含了所有状态能传输到子系统i的子系统。

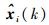
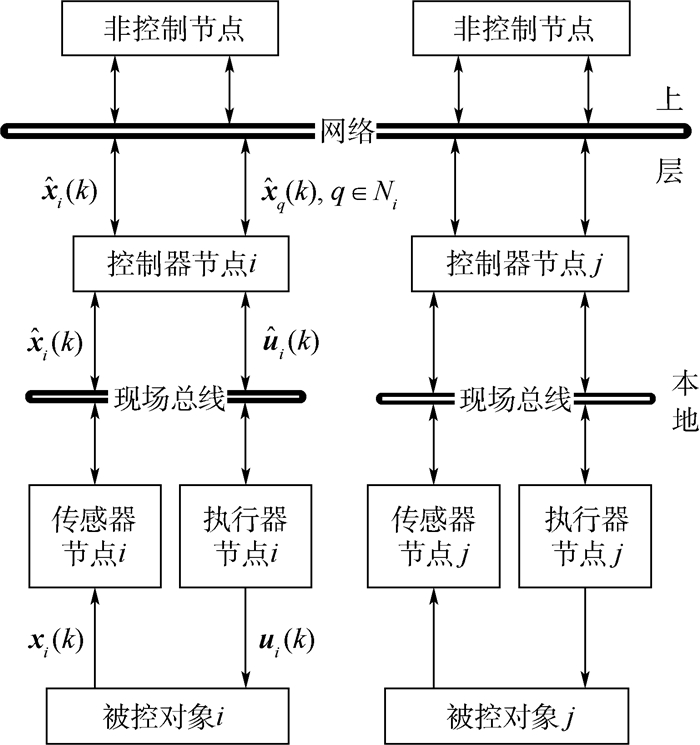图 1 分层网络控制系统结构 Fig. 1 Structure of hierarchical networked control system

图选项

如图 1所示，本地控制层包含了若干子系统，子系统通过现场总线或局域网构成闭环。上层除了控制器节点外，还有若干非控制节点，这些节点传输的信息包括了视频、音频、警告等，通常采用大数据包传输，是非周期性的信息。各子系统的控制器节点通过上层网络交换信息。
为便于描述问题，首先给出有关假设条件。
假设1 ?所有传感器节点和控制器节点均采用时间驱动，它们的采样和计算周期为T，T>0。
假设2 ?与控制系统相关的节点均采用单包传输，且数据包带有时间戳。
假设3 ?网络传输中存在网络诱导时延和丢包，且连续丢包次数存在上界。
考虑任一子系统可以描述为

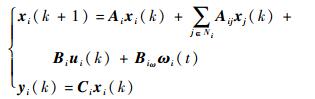(1)

式中：x_i(k)、x_j(k)∈Rⁿ，u_i(k)∈R^m，y_i(k)∈R^p分别为子系统i的状态、输入和输出；ω_i(k)∈R^r为外部扰动；A_i、A_ij、B_i、B_iω、C_i为适维系数矩阵，A_ij表征了子系统之间的相互耦合作用。(A_i, B_i)可控，(A_i, C_i)可观。
考虑网络的存在，子系统i自身的传感器、控制器和执行器通过现场总线连接构成闭环。由于现场总线多采用短帧结构，其导致的网络诱导时延往往小于采样周期，故忽略不计。上层网络多用如工业以太网等，虽具有较快的传输速率，但大数据包仍可能导致长时延(大于采样周期)，不可忽略。
此外，若数据包在传输过程中丢失，则控制器节点将采用上次接收到的数据计算控制量。因此，数据包丢失可等效为额外的网络诱导时延。因而，该时延是时变的。不失一般性，设由网络诱导时延和数据包丢失导致的等效时延存在上界d。
鉴于上述分析，采用如式(2)所示的分布式控制律。

(2)

式中：K_il、K_id∈R^m×n分别为本地控制增益与分布式控制增益；a_ij为信号增益; d_ij(k)为等效的网络诱导时延。
由式(1)和式(2)，子系统i可描述为

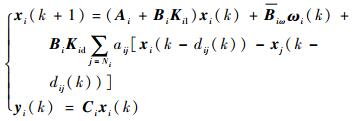(3)

令x(k)=[x₁^T(k), x₂^T(k), …, x_N^T(k)]^T，则有

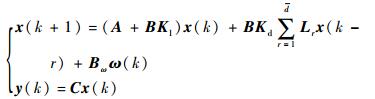(4)

式中：



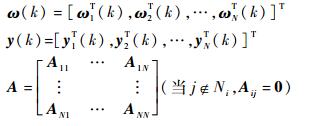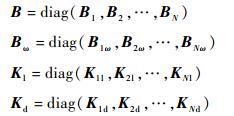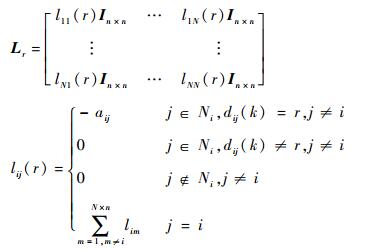显然，若时延d_ij(k)是时变的，则L_r也是时变的，因而式(4)是一个具有分布式时变时延的离散切换系统。值得指出的是，当时延上界已知时，该系统的切换模态是有限的。
综上，本文所研究的问题可描述为：对如式(4)所描述的网络控制系统，设计如式(2)所示的分布式控制律，使得系统满足如下要求：
1) 系统是渐近稳定的，即当ω(k)=0时，有

2) 系统具有H_∞扰动抑制水平γ，即当ω(k)∈L²[0, ∞)时，有

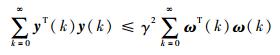2 主要结果 定理1 ?对于如式(4)所示的网络控制系统，已知ω(k)=0，网络诱导时延的上界为d，若存在对称正定阵Z₁、Z₂、P，使得矩阵不等式(5)成立，则系统(4)是渐近稳定的。

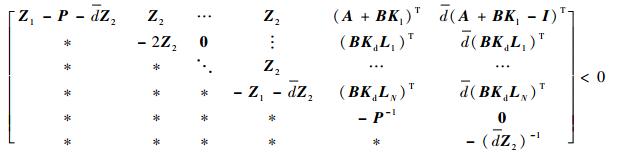(5)

式中：“*”表示对称部分。
证明?选取Lyapunov-Krasovskii泛函为

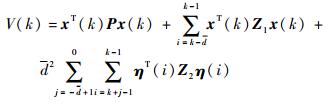(6)

式中：η(i)=x(i+1)－x(i)。
因此，


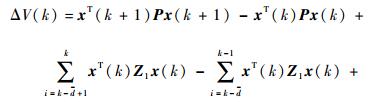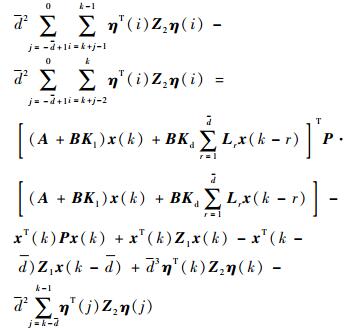由于

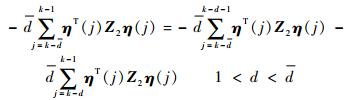由Jensen不等式，有

因而，有


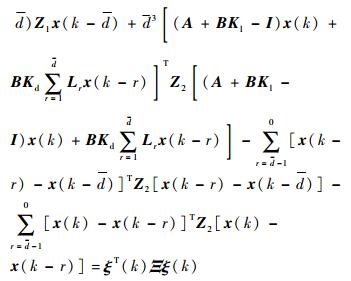式中：

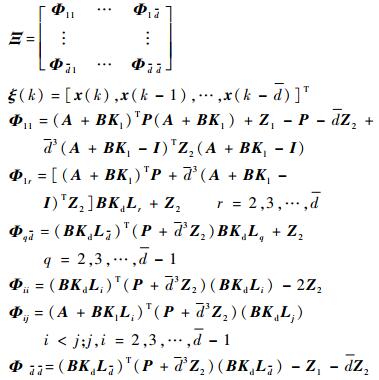由Schur补引理，可得：等价于式(5)。因此，若矩阵不等式(5)成立，则系统式(4)是渐近稳定的。证毕
定理1给出了系统渐近稳定的充分条件，利用类似方法，有定理2。
定理2 ?对于如式(4)所示的网络控制系统，已知网络诱导时延的上界为d，H_∞性能指标γ>0，若存在对称正定阵Z₁、Z₂、P，使得不等式(7)成立，

(7)

则系统式(4)是渐近稳定的，且满足给定的H_∞性能指标γ。
证明 ?选取Lyapunov-Krasovskii泛函如式(6)所示，则有

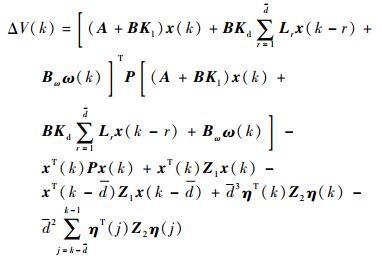类似的，利用Jensen不等式，有


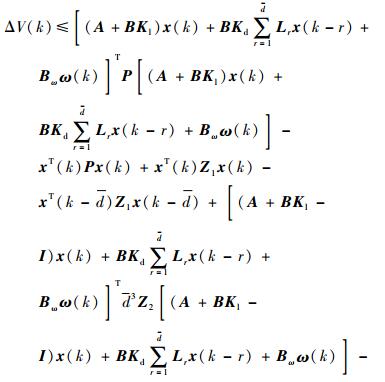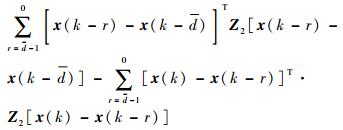令性能指标函数，显然，。
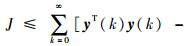
由Schur补引理，可知：当式(7)成立时，即。证毕
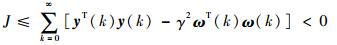
当利用定理1或2分析系统的H_∞控制系统性能指标是否能够达成时，可利用初等变换将式(5)或式(7)转化为LMI工具箱直接求解的形式，在此不再给出相应的推论。
注：由于网络诱导时延是时变的，实际上式(7)并不是一个矩阵不等式，而是矩阵不等式组，其中的不等式数量n₀≤2^r。
利用锥补线性化^{[1, 17]}方法，给出控制器设计的参数化方法。
优化问题1 ?对于如式(4)所示的网络控制系统，已知网络诱导时延的上界为d，H_∞性能指标γ>0，若存在对称正定阵Z₁、Z₂、P、S、T，使得如下优化问题有解：

使得式(8)~式(10)成立,

(8)

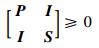(9)

(10)

则系统式(4)是渐近稳定的，且满足给定的H_∞性能指标γ。进一步，上述优化问题的解K_l^*、K_d^*即是所求的控制器增益。
由优化问题1，可给出如下迭代求解算法。
算法1
步骤1 ?利用LMI工具箱，求满足式(8)~式(10)的一组可行解：P⁰, Z₁⁰, Z₂⁰, K_l⁰, K_d⁰, S⁰, T⁰，并设迭代次数h=0。
步骤2 ?对于矩阵变量(P, Z₁, S, T)，求解如下问题：

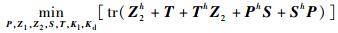使得式(8)~式(10)成立。
求得更新后的解P^h+1, Z₁^h+1, Z₂^h+1, S^h+1, T^h+1。
步骤3 ?将步骤2求得的解代入式(7)验算，若上述解是该矩阵不等式的可行解，则迭代结束。否则，转往步骤2，直到迭代次数达到上界。
3 数值仿真 考虑文献[3]中的网络化伺服系统，如图 2所示，含2个具有耦合作用的直流伺服电机，被控对象可以描述为

图 2 网络化伺服系统结构 Fig. 2 Structure of networked servo system

图选项

式中：



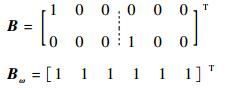考虑网络影响，采用如式(2)所示的分布式控制律，则系统可描述为式(4)。在本例中，式(2)部分参数说明如下：

设网络诱导时延和数据包丢失共同作用下的等效网络诱导时延上界d=3，H_∞性能指标γ=0.4。
根据实际传输情况，L₁、L₂、L₃的取值组合有：①Δ₁、Δ₄、Δ₄，②Δ₄、Δ₁、Δ₄，③Δ₄、Δ₄、Δ₁，④Δ₂、Δ₃、Δ₄，⑤Δ₂、Δ₄、Δ₃，⑥Δ₃、Δ₂、Δ₄，⑦Δ₃、Δ₄、Δ₂，⑧Δ₄、Δ₂、Δ₃，⑨Δ₄、Δ₃、Δ₂。因此，优化问题3中实际上由9组矩阵不等式组成。
利用算法1，求解可得

设系统的初始条件为x(0)=[2, 1, 2, 3, 2, 1]^T，网络诱导时延值如图 3所示(纵坐标为时延τ，横坐标t为时间)，此时系统的零输入状态响应曲线如图 4所示，x₁~x₆为x的分量，可以看到在外界扰动为ω(k)=0时，尽管存在时变的时延，系统仍能渐近稳定。进一步，通过验证发现，若利用所求得的K_l或K_d实施集中控制，在上述网络诱导时延的影响下，系统是不稳定的。

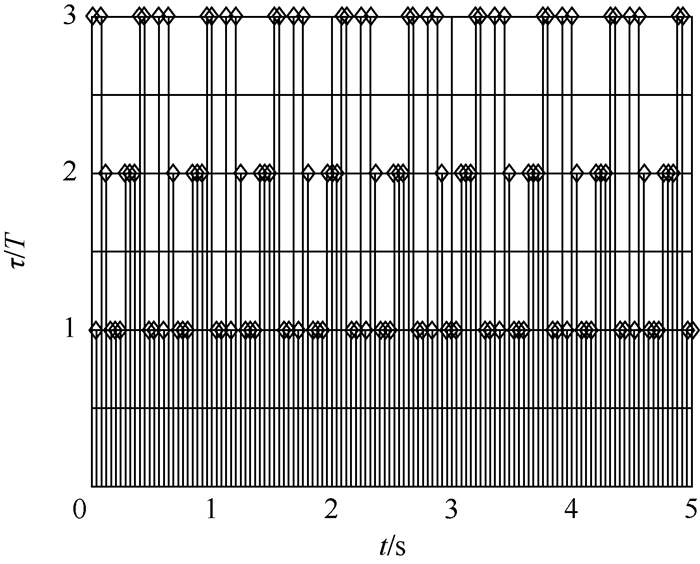图 3 网络诱导时延值 Fig. 3 Values of network induced delayes

图选项

图 4 系统状态响应曲线 Fig. 4 State response curves

图选项

当外部扰动其他时，系统在零初始条件下的输出响应曲线如图 5所示，y₁、y₂为y的分量。通过计算可得：γ=0.121 7 < 0.4，满足性能指标要求。

图 5 系统输出响应曲线 Fig. 5 Output response curves

图选项

4 结论 1) 针对一类具有分层结构的网络控制系统，针对部分子系统反馈信息无法获取的非理想网络状况，提出了一种分布式反馈控制律，并将该控制律作用下的闭环系统建模为一类离散切换系统。该模型蕴含了网络诱导时延、数据包丢失因素对于系统结构和参数的影响，可以较为全面的描述此类网络控制系统。
2) 构造了一种Lyapunov-Krasovskii泛函，基于Jensen不等式和Schur补引理，给出了系统渐近稳定且满足给定H_∞性能指标要求的充分条件。该条件包含了网络诱导时延和数据包丢失次数共同作用下等效时延的上界信息，具有较弱的保守性。
3) 利用锥补线性化方法，将控制器设计问题转化为一类优化问题，并给出了控制器设计的迭代求解算法。该算法可借助MATLAB LMI toolbox或YALMIP工具箱方便求解。

参考文献

[1]	ZHANG W.Stability analysis of networked control systems[D].Cleveland:Case Western Reserve University, 2001.
[2]	ZHANG L X, GAO H J, KYANAK O. Network-induced constraints in networked control systems-A survey[J].IEEE Transactions on Industrial Informatics, 2012, 9(1): 403–416.
[3]	XIA Y Q, LIU X P, LIU G P, et al. Stabilization analysis and implementation for MIMO NCS with time-varying delays[J].International Journal of Adaptive Control and Signal Process, 2011, 25(7): 639–652.DOI:10.1002/acs.v25.7
[4]	OKAJIMA H, SAWADA K, MATSUNAGA N, et al. Dynamic quantizer design for MIMO systems based on communication rate constraint[J].Electronics and Communications in Japan, 2013, 96(5): 28–36.DOI:10.1002/ecj.v96.5
[5]	GUAN Z H, ZHAN X S, FENG G. Optimal tracking performance of MIMO discrete-time systems with communication constraints[J].International Journal of Robust and Nonlinear Control, 2012, 22(13): 1429–1439.DOI:10.1002/rnc.v22.13
[6]	LI J N, ZHANG Q L, YU H B, et al. Real-time guaranteed cost control of MIMO networked control systems with packet disordering[J].Journal of Process Control, 2011, 21(6): 967–975.DOI:10.1016/j.jprocont.2010.10.011
[7]	DU D J, FEI M R, JIA T G. Modelling and stability analysis of MIMO networked control systems with multi-channel random packet losses[J].Transactions of the Institute of Measurement and Control, 2011, 35(1): 66–74.
[8]	YANG X, WANG J Z.Distributed robust H∞ consensus control of multi-agent systems with communication errors using dynamic output feedback protocol[J/OL].Mathematical Problems in Engineering, 2013:979087[2016-12-06].http://dx.doi.org/10.1155/2013/979087.
[9]	GAO Y P, MA J W, ZUO M, et al. Consensus of discrete-time second-order agents with time-varying topology and time-varying delays[J].Journal of the Franklin Institute, 2012, 349(8): 2598–2608.DOI:10.1016/j.jfranklin.2012.06.009
[10]	LI Z K, GUAN Z S, XIE L H, et al. Distributed robust control of linear multi-agent systems with parameter uncertainties[J].International Journal of Robust and Nonlinear Control, 2012, 85(8): 1039–1050.
[11]	ANDREASSON M, DIMAEOFONAS D V, SANDVERG H, et al. Distributed control of networked dynamical systems:Static feedback, integral action and consensus[J].IEEE Transactions on Automatic Control, 2014, 59(7): 1750–1764.DOI:10.1109/TAC.2014.2309281
[12]	HIRCHE S, MATIAKIS T, BUSS M. A distributed controller approach for delay-independent stability of networked control systems[J].Automatica, 2009, 45(8): 1828–1836.DOI:10.1016/j.automatica.2009.04.016
[13]	ZHENG Y, LI S L, QIU H. Networked coordination-based distributed model predictive control for large-scale system[J].IEEE Transaction on Control Systems Technology, 2013, 21(3): 991–998.DOI:10.1109/TCST.2012.2196280
[14]	LIU D, HAO F. Decentralized event-triggered control strategy in distributed networked systems with delays[J].International Journal of Control, Automation, and Systems, 2013, 11(1): 33–40.DOI:10.1007/s12555-012-0094-1
[15]	GUINALDO M, DIMAROGONAS D V, JOHANSSON K H, et al. Distributed event-based control strategies for interconnected linear systems[J].IET Control Theory and Applications, 2013, 7(6): 877–886.DOI:10.1049/iet-cta.2012.0525
[16]	LATRACH C, KCHAOU M, RACHI A, et al. Decentralized networked control system design using Takagi-Sugeno (TS) fuzzy approach[J].International Journal of Automation and Computing, 2015, 12(2): 125–133.DOI:10.1007/s11633-015-0879-9
[17]	GHAOUI L E, QUSTRY F, AITRAMI M. A cone complementarity linearization algorithm for static output-feedback and related problems[J].IEEE Transaction on Automatic Control, 1997, 42(8): 1171–1176.DOI:10.1109/9.618250