当前,国内外对于多无人机编队重构进行了广泛的研究。针对战场威胁环境条件与机载不同载荷的无人机编队重构问题,文献[9]设计了一种基于纳什议价的分布式模型预测控制(DMPC)方法,能够使编队无人机协同躲避各种威胁以完成战术战略任务,但是整个飞行过程不考虑无人机编队的通信距离。在考虑各种约束条件(终端状态、安全防撞距离、通信距离等)的前提下,文献[10]采用控制作用参数化与时间离散化方法将寻找连续控制输入和终端时刻的无人机编队重构时间最优问题近似为寻找最优常数参数几何和分段时间问题进行求解,但是并没有涵盖障碍环境。通过使用编队中无人机与障碍的视线角以及无人机之间的相对速度,文献[11]提出了一种基于微分几何的控制律以实现无人机编队的避障与重构,但是这种方法很可能会产生过多的输入控制量从而使得结果不是很理想。文献[12]提出了一种用于四旋翼无人机编队重构的控制律,以使无人机编队稳定快速实现各种编队构型的重构切换,但是没有涉及避障问题。文献[13]将监控容错机制引入无人机编队控制律以实现重构,但是存在与文献[12]同样的问题。
在考虑各种约束条件以及队形切换的情况下,针对无人机数学模型、编队模型及碰撞环境威胁约束,本文首先通过引入邻居集这一概念并结合分布式协同策略构建多无人机编队的重构代价函数,进而提出了改进量子粒子群优化(RQPSO)算法对其进行求解,并与采用粒子群优化(PSO)算法求解的结果进行了对比。仿真结果表明,本文算法能安全、有效地完成无人机编队自主重构,实现隐蔽突防。
1 预备知识 1.1 模型预测控制 模型预测控制(MPC)主要包括3个方面,即预测模型、滚动优化与反馈校正。预测模型是指通过被控对象的过去信息和未来输入状态预测未来输出状态;滚动优化是指通过在线改变具有固定形式的优化性能指标的时间区域以实现优化;反馈校正用于修正模型失配。由于MPC采用的是一种有限时域优化,而不是全局优化策略,因此其抗干扰性能与鲁棒性能都非常强[13-15]。
依据图 1所示,典型的MPC算法可以简单描述如下:
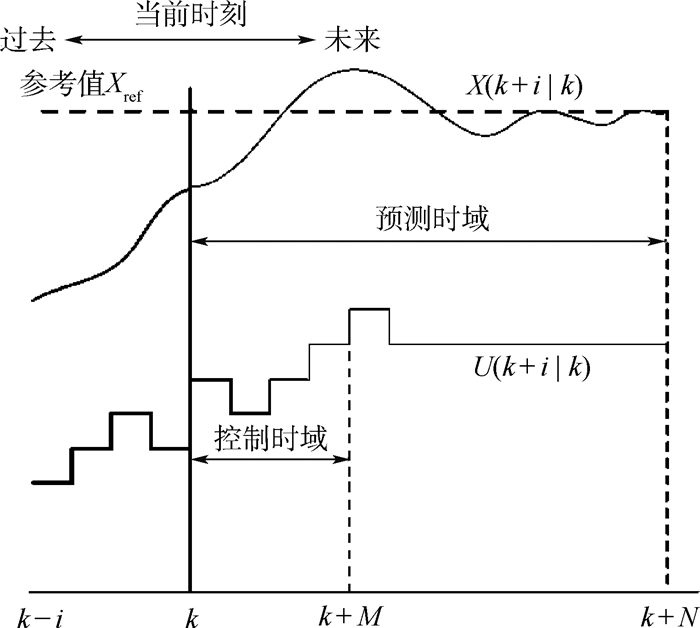 |
| 图 1 模型预测控制原理图 Fig. 1 Schematic of model predictive control |
| 图选项 |
1) k时刻系统状态x(k),使用系统过去的输入信息预测其未来的输出状态。
2) 选取某个性能指标进行在线优化计算,得到预测时域N内系统开环最优控制输入序列u*(k)=[u*(k∣k), u*(k+1∣k), …, u*(k+N-1∣k)]。
3) 取u*(k)的第1项u*(k∣k)作为k时刻的输入控制。
4) k+1时刻在新的时域上重复上述步骤。
1.2 量子粒子群优化算法 PSO算法自诞生以来就一直被用于求解各种复杂的优化问题[16-17],然而PSO算法本身具有搜索速度有限这一缺陷使得其不可能以概率1搜索全局最优解。科研人员经过研究发现,粒子在量子空间中具有聚集性的性质,通过将这一性质应用到PSO算法中就可以克服其存在的固有缺陷,这就是量子粒子群优化(QPSO)算法[18]。在QPSO算法中,可以通过波函数ψ(X, t)来对粒子的运动状态进行描述[19-20]:
 | (1) |
式中:Q为概率密度函数,其满足如下条件:
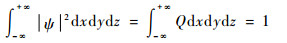 | (2) |
在量子空间中,粒子的运动能够满足如下方程:
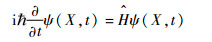 | (1) |
式中:?为普朗克常数;?为哈密顿算子,可以描述为如下形式:
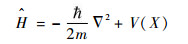 | (4) |
其中:m为粒子质量;V(X)为粒子所在的势能;
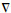
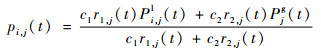 | (5) |
式中:r1, j和r2, j为[0,1]之间随机数;c1和c2分别为自身因子和全局因子。
QPSO算法中构建了平均最好位置这一概念,其定义为种群中所有粒子个体最好位置的平均值,即
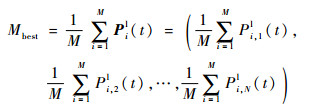 | (6) |
式中:M为种群规模。
QPSO算法的进化方程为
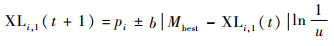 | (7) |
式中:u为[0,1]之间随机数;b为收缩-膨胀因子,一般,b取值为从1.0线性减小到0.5时,可以达到比较好的效果,即
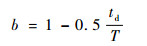 | (8) |
其中:T为最大迭代次数;td为当前迭代次数。与PSO算法相比,在QPSO算法中,对于聚集在Pg附近的粒子,由于吸引子pi点是在Pi, jl和Pjg之间,所以粒子以很大的概率在Pg附近出现[20-25]。
2 无人机编队重构模型 2.1 无人机运动模型 假设无人机编队中共有Nv架无人机,则无人机编队集合可表示为Vc={uvi|i=1, 2, …, Nv},无人机自身能够实现速度与滚转角的相互解耦,能够始终保持飞行高度不变,则无人机近似离散化后的质心运动模型可以描述为[26-27]
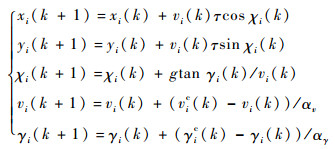 | (9) |
式中:xi、yi和vi分别为无人机的坐标和速度;χi和γi分别为无人机的航迹方位角和航迹倾斜角;vic和γic分别为速度指令和航迹倾斜角指令;αv和αγ分别为速度时间常数和航迹倾斜角时间常数;g为重力加速度;τ为采样周期。
取编队第i架无人机uvi在k时刻状态变量为: Xi(k)=[xi(k),yi(k),vi(k),χi(k),γi(k)]T,第i架无人机uvi在k时刻的控制变量为:Ui(k)=[vic(k),γic(k)]T,这样可将无人机速度vi运动方程简化为式(10),并可得到约束条件如式(11) 所示。
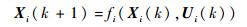 | (10) |
 | (11) |
通常存在一条已知参考轨迹以使无人机编队跟踪飞行,假设参考轨迹满足如下方程[28]:
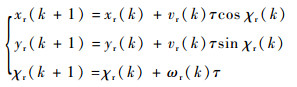 | (12) |
式中:xr、yr和χr分别为参考轨迹在地面坐标系的坐标和方位角;vr和ωr分别为参考轨迹的速度和角速度,vr与ωr满足分段连续且一直有界,满足如下约束方程:
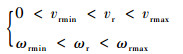 | (13) |
2.2 编队模型 多无人机编队控制策略主要包括以下3种:领航-跟随法、虚拟领航法以及行为控制法[29-30]。由于领航-跟随法具有误差传导等问题,而行为控制法具有数学模型不易建立等缺点,所以本文选用虚拟领航法。假设存在一无人机跟随轨迹的参考点,编队中的无人机能够提前或者通过无线通信实时获取参考点的轨迹,并且时刻保持与参考点的相对距离和角度,无人机之间不存在参考误差。轨迹参考点坐标系XrOrYr固连于参考点Or(见图 2),可以得到编队中所有无人机的期望位置:
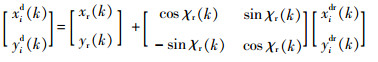 | (14) |
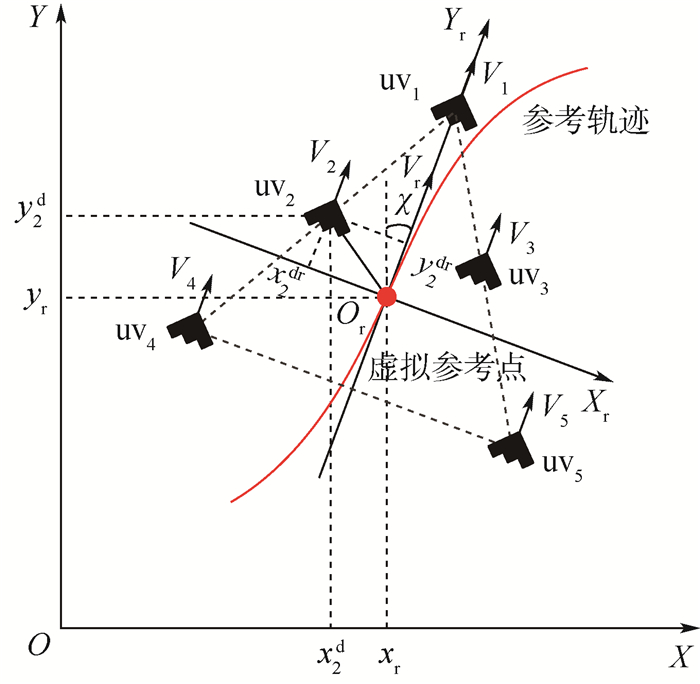 |
| 图 2 虚拟领航编队控制模型 Fig. 2 Virtual leader formation control model |
| 图选项 |
式中:xidr和yidr(k)分别为k时刻无人机uvi期望位置与虚拟轨迹参考点位置之间的相对距离。
3 编队重构问题描述 3.1 威胁描述 战争中敌方的重要目标一般处于各种保护之中,为了实施战略战术纵深打击,多无人机编队需要隐蔽突防敌方防御区域,到达指定区域才能完成这一任务。在突防的过程中,多无人机编队会面临多种威胁,本文考虑预警雷达、防空雷达、禁飞区(包括固定障碍物、固定威胁以及移动威胁)3种威胁,假设编队中的无人机都能够探测到敌方预警雷达和防空雷达,且无人机携带干扰设备,能够对预警雷达与防空雷达实施一定程度的干扰。
1) 预警雷达威胁
如图 3所示,假设预警雷达位置为(xewr, yewr),干扰设备位置为(xje, yje),干扰设备的有效干扰距离为Rewr,预警雷达最大探测半径为Rmax,当无人机对预警雷达进行干扰时,其探测半径R可以描述为[9, 31]
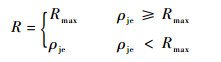 | (15) |
式中:
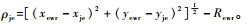
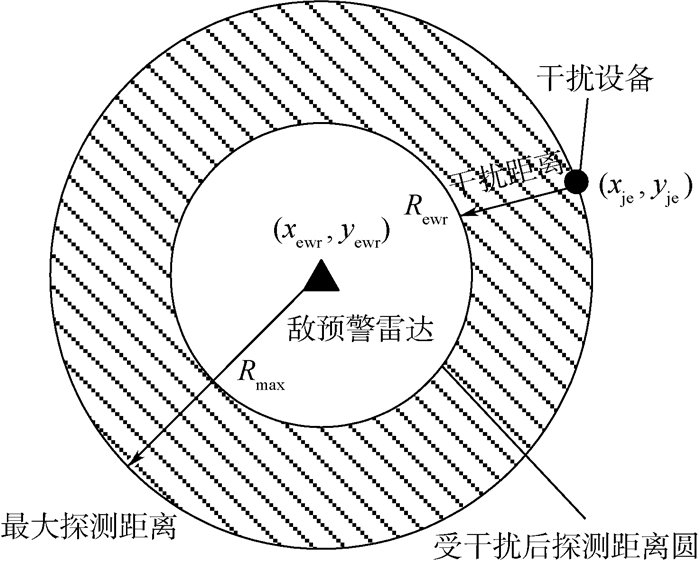 |
| 图 3 预警雷达与干扰示意图 Fig. 3 Schematic of early warning radar and interference |
| 图选项 |
2) 防空雷达威胁
如图 4所示,假设防空雷达位置为(xadr, yadr),干扰设备的位置为(xje, yje),无人机uvi位置为(xi, yi),干扰设备的有效干扰距离为Radr,防空雷达最大探测半径和最大探测角度分别为Rmax和β,则无人机处于安全区域的条件为[9, 31]
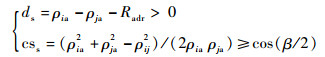 | (16) |
式中:
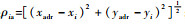
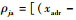
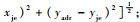
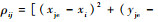
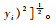
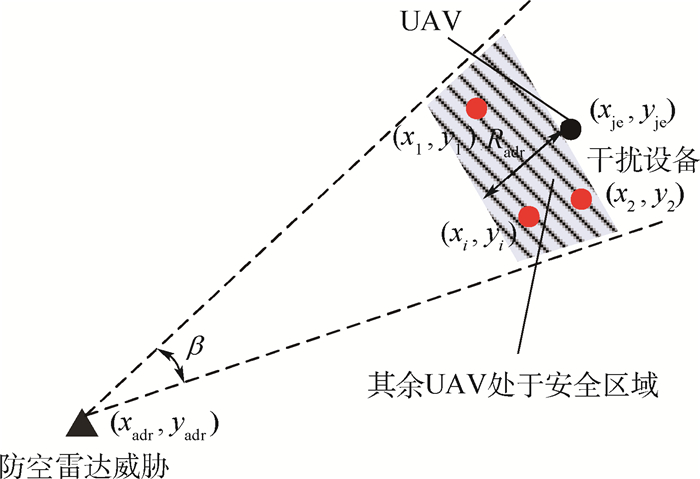 |
| 图 4 防空雷达与干扰示意图 Fig. 4 Schematic of air-defense radar and interference |
| 图选项 |
3) 禁飞区威胁
如图 5所示,多无人机编队一旦遇到禁飞区或者障碍物只能够绕行避开,为了简化问题,本文统一将上述不规则图形或者矩形的最小外接圆作为禁飞区或者障碍物来讨论。假设禁飞区最小外接圆圆心位置和半径分别为(xirc, yirc)和Rirc,则无人机编队处于安全区域的条件为
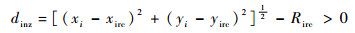 | (17) |
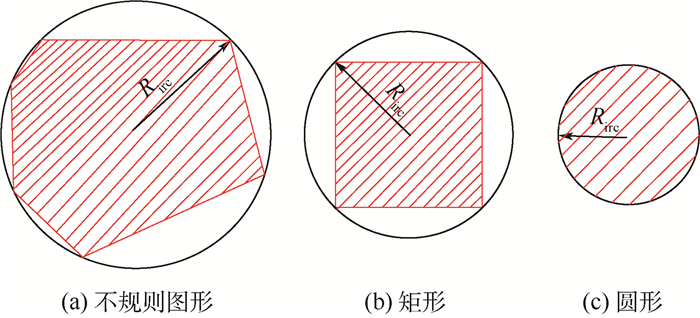 |
| 图 5 禁飞区或障碍威胁示意图 Fig. 5 Schematic of non-fly zone or obstacle threat |
| 图选项 |
3.2 编队无人机约束条件构造 一方面,由于无人机编队面临各种威胁(预警雷达威胁、防空雷达威胁、禁飞区或障碍威胁),只有躲避这些威胁,无人机编队实现隐蔽突防飞抵指定区域才能实施对敌方目标的有效打击;另一方面,在无人机编队执行战略战术任务的过程中,需要避免编队内部的碰撞以及保持正常的实时通信。针对上述情况,可以构造如下约束条件:
1) 预警雷达威胁约束
假设k时刻编队内无人机探测到Newr个敌预警雷达ewrj(j=1, 2, …, Newr),预警雷达的位置为(xewrj, yewrj),被干扰后的探测半径为Rj,根据图 3可知,编队内的无人机只有处于被干扰后预警雷达探测距离之外时才能保证其不被预警雷达发现,由此可以构造第i架无人机uvi面临第j个预警雷达的威胁约束条件为
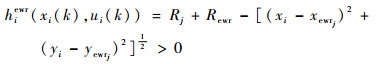 | (18) |
2) 防空雷达威胁约束
假设在k时刻编队内无人机探测到Nadr个敌防空雷达adrj(j=1, 2, …, Nadr),防空雷达的位置为(xadrj, yadrj),被干扰后的安全距离和安全角余弦分别为dsj和cssj,根据图 4可知,编队内的无人机只有处于安全区域内时才能保证其不被防空雷达发现,由此可以构造第i架无人机uvi面临第j个防空雷达的威胁约束条件为
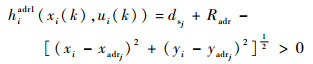 | (19) |
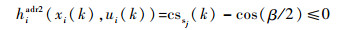 | (20) |
3) 禁飞区威胁约束
假设在k时刻编队内无人机探测到Nnfz个敌防空雷达nfzj(j=1, 2, …, Nnfz),禁飞区最小外接圆圆心的位置为(xircj, yircj),根据图 5可知,编队内的无人机只有不飞抵禁飞区时才能保证其安全飞行,由此可以构造第i架无人机uvi飞临第j个禁飞区的威胁约束条件为
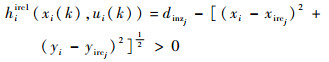 | (21) |
4) 无人机防碰撞约束
为了防止编队内无人机发生碰撞,无人机之间的距离一定要大于防撞安全距离Dsafe,由此可以构造k时刻uvi与uvj之间的防碰撞距离约束条件为
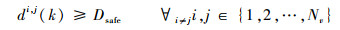 | (22) |
式中:
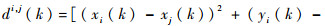
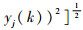
5) 无人机通信距离约束
多无人机编队执行任务期间需要接收各种指令及信息,如上层发送的改变任务指令或者编队无人机各自的状态信息等,所以无人机之间必须能够进行正常实时的通信,由于通信设备的通信距离有限,所以需要保证编队内无人机之间的距离小于通信保障距离Dcom,由此可以构造k时刻uvi与uvj之间的通信距离约束条件为
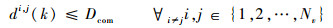 | (23) |
3.3 编队重构过程 在参照虚拟参考轨迹的情况下,编队中所有无人机在各自预定的相对位置飞行。当探测并定位出敌方预警雷达或者防空雷达威胁后,编队可以选择靠近威胁的某个无人机采用干扰,其余无人机进行队形调整,位于进行干扰无人机所产生的安全区域内,从而实现隐蔽突防。自动形成期望队形,根据威胁进行自动变换,以提高编队的安全性以及协同突防的有效性。
假设无人机编队可以对进行干扰任务的无人机自动分配,本文不进行研究。无人机编队能够根据环境威胁以及飞行过程中需要执行的任务进行构型自动选择。由于预警雷达和防空雷达系统2类威胁的作战能力和行为不同,因此针对这2类威胁应该选择不同的构型。
4 无人机编队重构控制问题的求解 4.1 邻居集定义 定义1 无人机uvi的邻居集定义为与其具有耦合约束关系的所有无人机的集合。如用κ(i)表示无人机uvi的邻居集,则无人机uvi与无人机uvj∈κ(i)存在耦合约束关系。另外,?(i)表示与无人机uvi存在紧约束的无人机集合。显然不是所有的耦合约束都是紧约束。
结合编队重构控制的特点以及MPC的预测特性,将邻居集内的无人机再进行分类,将在MPC预测时域内会违背最小间距约束的无人机视为紧约束邻居,在进行在线滚动优化时将紧约束邻居无人机的代价一起进行优化。这样做的好处是:不仅与邻居无人机进行了协同,而且避免了集中式优化问题中考虑邻居无人机内所有无人机的代价,降低了决策空间的维数,求解时间将缩短。如图 6所示,无人机uvi的邻居集内拥有j1、j2、j3、j4和j5 5架无人机,但只有j1和j2属于紧约束邻居(图 6中标红色),无人机uvi在进行轨迹优化时,将考虑这2架无人机的代价,可以看出这一集合是时变的,这里假设每个时刻所有无人机能得到一致的紧约束邻居集合。
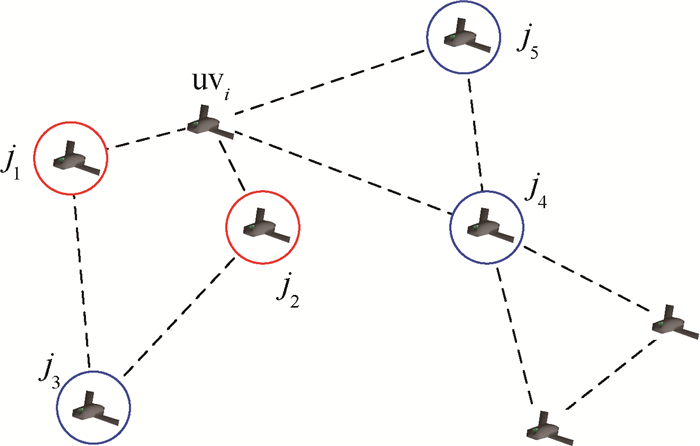 |
| 图 6 无人机uvi的紧约束邻居示意图 Fig. 6 Schematic of close constraint neighbor of UAV uvi |
| 图选项 |
4.2 基于分布式模型预测控制的协同策略 在传统的集中式编队队形重构控制方法中,重构控制器需要在线优化所有无人机的控制输入,计算量非常大,不具有扩展性[32]。
本文提出的分布式编队重构控制方法原理框图如图 7所示。无人机uvi和无人机uvj之间相互传递协同信息,并以某种性能指标最小为控制目标。常见的一种协同策略是重构完成时刻的协调,即相互协同确定重构完成时刻Tr,每个无人机的主要任务就是规划一条轨迹使得Tr时刻编队重构任务是可以保证完成的,并且还要保证自身的安全性。Tr是协调变量,每个无人机必须将其作为航迹生成的约束[7-9]。
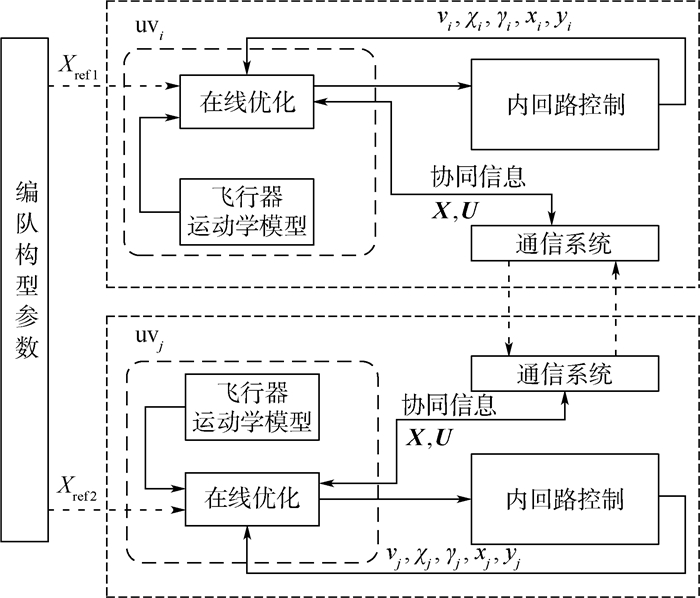 |
| 图 7 分布式协同编队构型重构原理框图 Fig. 7 Principle block diagram of distributed cooperating formation reconfiguration |
| 图选项 |
当耦合约束不是紧约束时,每个无人机“冻结”其他无人机的决策行为,然后求解自身的局部优化问题。当存在紧耦合约束时,每个无人机将考虑存在紧约束邻居无人机的局部代价以及编队总体代价,以在必要时需要牺牲自身性能来满足整体编队的性能指标。
当无人机uvi在无人机uvj之后求解优化问题时,对耦合约束进行修改,如果是紧约束,有
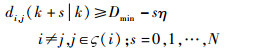 | (24) |
显然,当参数η>0时松弛了耦合约束,可能会使得局部性能变差,但对整个编队的代价有利。这样,无人机uvi在求解自身优化问题时也考虑到了其他无人机的性能指标,即对整个编队的性能指标也有利。
利用无人机之间耦合约束的稀疏特性,决策空间将明显减小,计算量不会太大,这种协同优化策略的优点在于:① 存在紧耦合约束时不“冻结”其他无人机的行为;② 缩小了决策空间,局部优化问题求解的复杂性大大降低。
图 8所示为3种不同在线优化形成的航迹。图 8(a)所示为非协同优化航迹,无人机uvi和无人机uvj均优化自身的局部代价,则很容易违背最小间距约束;图 8(b)所示为基于优先级的协调航迹,无人机uvj将无人机uvi视为移动的障碍物进行规避,但由于进行了非协同的规避机动,无人机uvj到达自身期望位置的时间较长,从而编队总体代价较大;图 8(c)所示为进行协同优化的航迹,无人机uvi和无人机uvj以编队总体代价为优化目标,无人机uvi牺牲自身局部代价获得了编队总体代价最优。
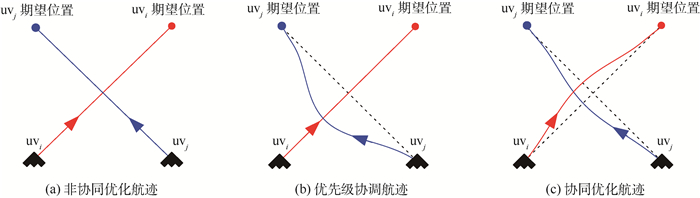 |
| 图 8 3种优化航迹示意图 Fig. 8 Schematic of three types of optimized trajectory |
| 图选项 |
编队重构分布式协同优化的步骤如下:
1) k时刻,无人机uvi优化的目标函数中增加紧约束邻居无人机的局部代价以及编队总体代价。
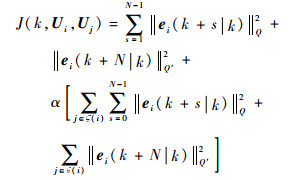 | (25) |
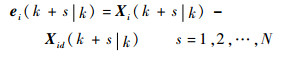 | (26) |
式中:α>0;
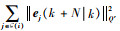
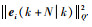
2) 根据预测时域对无人机最小间距约束进行单调性松弛(松弛因子为η)。
3) 优化求解得到Ui*和Uj∈?(i)*,实施Ui*的第1项Ui*(k∣k),并将预测状态向量Xi*发送给无人机uvj。
4) k+1时刻,再根据新的状态和新的邻居集j∈?(i)重复上面过程,得到k+1时刻的控制输入。
综上,可得无人机编队的整体重构优化模型为
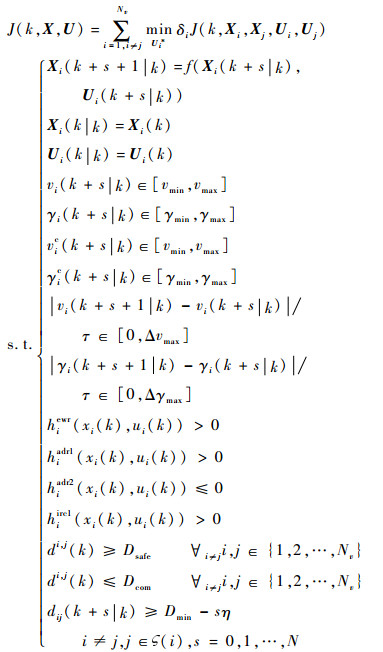 | (27) |
4.3 RQPSO-DMPC算法求解编队重构问题 2002年,Riget等[32-33]将多样性引导策略引入PSO算法中,提出吸引-排斥PSO算法。多样性的大小能够改变搜索模式(即是进行全局搜索还是进行局部搜索)。其中吸引对应的是收敛阶段,而排斥则对应的是发散阶段。
本文选用粒子与中心点之间的平均欧几里得距离表示多样性,分别将粒子当前位置组成的种群和个体最好位置组成的种群表示为
 | (28) |
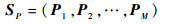 | (29) |
这样可以得到QPSO算法的多样性度量为
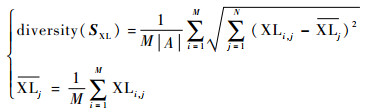 | (30) |
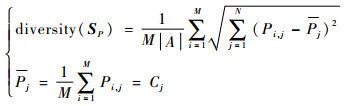 | (31) |
式中:∣A∣为种群搜索空间中粒子最大值与最小值之间的一种关系表示;N为求解问题的空间维数。
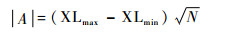 | (32) |
时间对于战场来说至关重要,然而在QPSO算法中,种群多样性将随着搜索时间而下降,因此当进入搜索后期时,粒子多样性降低,全局搜索能力也将随之大大减弱,为了有效避免早熟现象,在文献[21]的基础上,设置多样性的下限dlow,本文将多样性引导的QPSO算法应用于多无人机编队重构控制。
多样性控制的量子粒子群优化(DCQPSO)算法中,diversity(SXL)被用于引导算法搜索方向(即收敛方向还是发散方向)。一旦预先设定的下限dlow大于diversity(SXL),整个粒子群将由收敛状态进入到发散状态,此时多样性将会出现暂时性增加的情况,直到多样性diversity(SXL)再次大于dlow。
当diversity(SXL)或diversity(SP)降低到dlow以下时,进行如下变异操作:
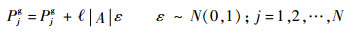 | (33) |
式中:Pjg为处于最好位置的粒子;ε为服从标准正态分布的随机数;
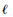
通过施加变异操作,可以使得Pi(t)与Mbest之间距离增加,从而增大diversity(SP)。与此同时,由于Pg(t)的变动导致Mbest改变,这样粒子当前位置与Mbest之间距离也会增大,势必引起粒子产生一定程度的发散,从而增大diversity(SXL)。因此可以通过增加2种多样性(diversity(SP)或者diversity(SXL))而进行变异,前一种方法称为DCQPSOP,后一种方法称为DCQPSOX。
除了对粒子群进行变异操作以增加种群多样性,本文还通过在群体全局最好位置Pg上施加选择操作以丰富种群的多样性,从而避免种群过早陷入局部最优解。即pi不再通过Pg(t)和Pil决定,而是由Pil和某个随机选择出的其他粒子的个体最好位置(其目标函数值要比Pil好)决定。在从粒子群中随机选择某个其他粒子Pkl(t)后,可以进行如下操作:
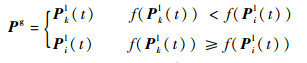 | (34) |
当选择出来的Pkl(t)的目标函数值好于Pil(t),则pi由Pkl(t)和Pil决定,否则Pi(t)仍由Pg(t)和Pil(t)决定。因此,通过上述选择操作选出Pg后,Pi(t)的坐标为
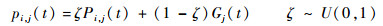 | (35) |
引入多样性与选择策略可以得到改进的QPSO算法,即RQPSO算法,其流程描述如下[34-35]:
步骤1 对粒子进行编码(见图 9),设置算法基本参数,随机初始化粒子群。
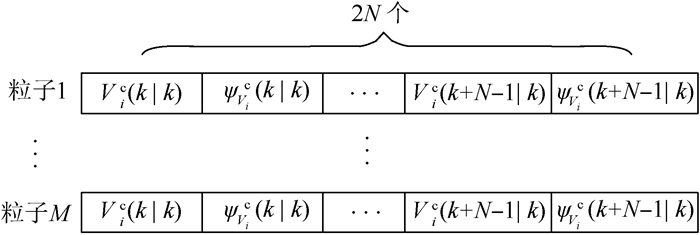 |
| 图 9 粒子编码 Fig. 9 Particle coding |
| 图选项 |
构建无人机编队重构问题与RQPSO算法粒子之间的映射关系,即粒子编码。本文采用的非线性模型中控制输入指令为速度和航向,每个时刻无人机uvi优化的变量维数并不一样,因为邻居集是时变的,所以粒子群的维数也是时变的。如图 9所示,如果无人机uvi只优化自身局部代价,粒子群的维数为M×2N,即M个粒子,每个粒子包含2N个变量。考虑紧耦合约束无人机后,无人机uvi在线优化的变量个数为2(n+1)N(n为?(i)内元素的个数),此时粒子群的维数为M×2(n+1)N。
步骤2 当迭代次数小于T时,执行以下步骤。
步骤3 计算粒子群的平均最好位置Mbest。
步骤4 计算粒子的当前适应值,并与前一次迭代的适应值比较,如果f(XLi(t+1)) < f(Pi(t)),则Pi(t+1)=XLi(t+1)。
步骤5 计算群体当前的全局最优位置Pg。
步骤6 将当前时刻全局最优位置与前一次迭代的全局最优位置进行比较,选择更优值作为群体的全局最优位置。
步骤7 对每一个粒子,选择点Pg。对粒子的每一维,根据式(35) 计算pi, j。
步骤8 根据式(7) 计算粒子的新的位置。
步骤9 计算粒子群的多样性diversity(SXL)(DCQPSOX)或diversity(SP)(DCQPSOP)。
步骤10 通过式(8) 计算收缩-扩张因子(收敛模式)。
步骤11 判断diversity(SXL)或diversity(SP),如果小于dlow,则进行变异操作(发散模式)。
步骤12 按照QPSO算法进化方程对种群中所有粒子进行位置更新。
步骤13 返回步骤2。
5 仿真与分析 为了验证本文所提算法的有效性,使用MATLAB编译环境进行仿真验证,分别选用PSO、RQPSO 2种算法对无人机编队重构控制进行仿真实验,粒子群规模都设置为20。对于PSO算法,c1=c2=2,w=0.5,T=800;对于RQPSO算法,b的值将随着算法的运行从1.0线性减小到0.5,dlow=0.000 4,
假设编队中的无人机之间不存在通信时延;无人机的速度、航向不受任何其他因素干扰影响。各无人机的初始运动以及参考轨迹参数如表 1和表 2所示,各无人机与参考轨迹相对距离如表 3所示,预警雷达、防空雷达、禁飞区坐标及作用距离如表 4所示。
表 1 无人机初始运动参数 Table 1 Initial kinematic parameters of UAVs
| 无人机 | (x, y)/km | v/(m·s-1) | χ/(°) |
| uv1 | (3.8, 8.2) | 152 | 90 |
| uv2 | (2.8, 7.7) | 152 | 90 |
| uv3 | (2.8, 8.7) | 152 | 90 |
| uv4 | (1.8, 7.2) | 152 | 90 |
| uv5 | (1.8, 9.2) | 152 | 90 |
表选项
表 2 参考轨迹参数 Table 2 Parameters of reference trajectory
| 参数 | 时间/s | 数值 |
| 初始位置 | 0 | (2.8, 8.2) km |
| 速度 | [0,200] | 152m/s |
| 航向 | [0,200] | 90° |
表选项
表 3 编队初始构型参数 Table 3 Parameters of Initial formation configuration
| 初始坐标 | 数值 |
| (x1rd,x1rd ) | (0,1/sin(π/3)) |
| (x2rd,x2rd ) | (0.5,0.5/sin(π/6)) |
| (x3rd,x3rd ) | (-0.5,0.5/sin(π/6)) |
| (x4rd,x4rd ) | (1,-0.5/cos (π/6)) |
| (x5rd,x5rd ) | (-1,-0.5/cos (π/6)) |
表选项
表 4 敌方威胁参数 Table 4 Parameters of enemy threat
| 参数 | 数值 |
| 预警雷达坐标/km | (30, 20) |
| 预警雷达作用距离/km | 20 |
| 防空雷达坐标/km | (32, 18) |
| 防空雷达作用距离/km | 12 |
| 防空雷达角度/(°) | 10 |
| 禁飞区1区间范围/km | [(12, 12), (18, 12), (18, 18), (12, 5)] |
| 禁飞区2区间范围/km | [(25, 25), (35, 25), (35, 5), (25, 5)] |
| 机间防碰撞距离/km | 0.5 |
| 最大通信距离/km | 2 |
表选项
仿真结果如图 10~图 15所示。
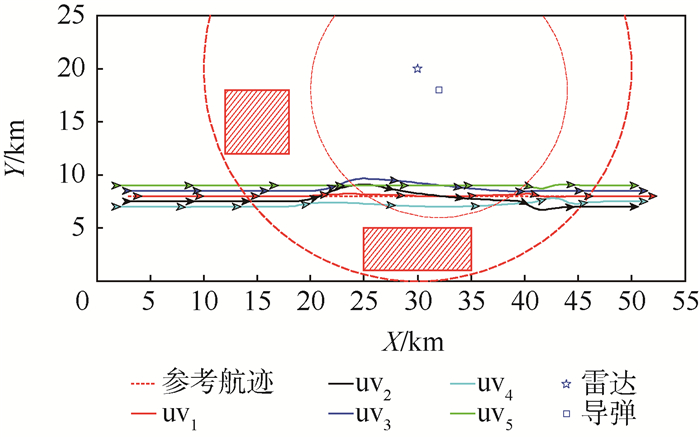 |
| 图 10 威胁环境下无人机编队自动构型变换轨迹 Fig. 10 Automatic configuration transforming flight trajectory of UAV formation in threatened environment |
| 图选项 |
 |
| 图 11 无人机uv1速度指令及响应曲线 Fig. 11 Velocity instruction and response curves of uv1 |
| 图选项 |
 |
| 图 12 无人机uv1航向角指令及响应曲线 Fig. 12 Course angle instruction and response curves of uv1 |
| 图选项 |
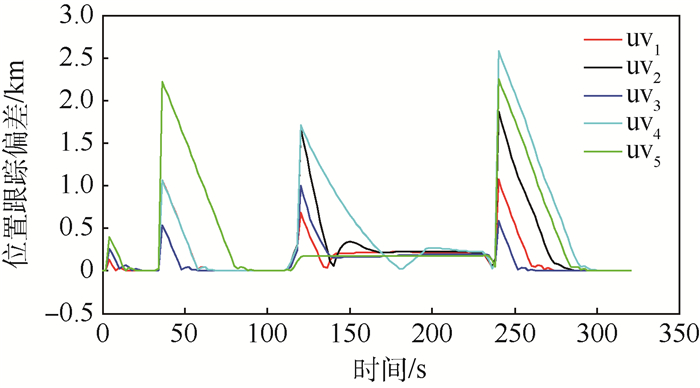 |
| 图 13 无人机期望位置跟踪偏差曲线 Fig. 13 Desired location tracking deviation curves of UAVs |
| 图选项 |
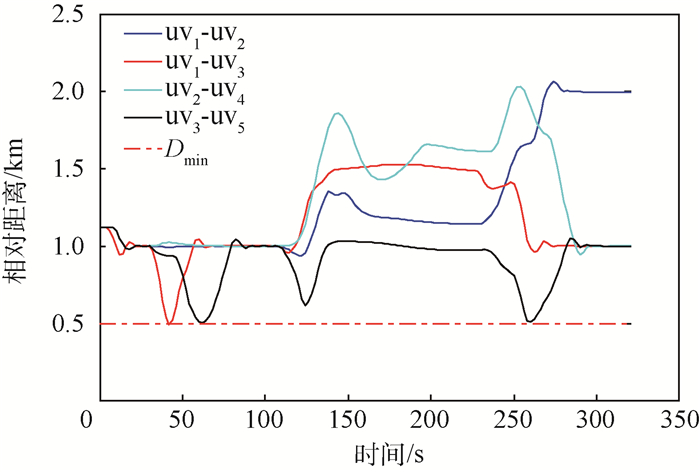 |
| 图 14 无人机之间相对距离 Fig. 14 Relative distance between UAVs |
| 图选项 |
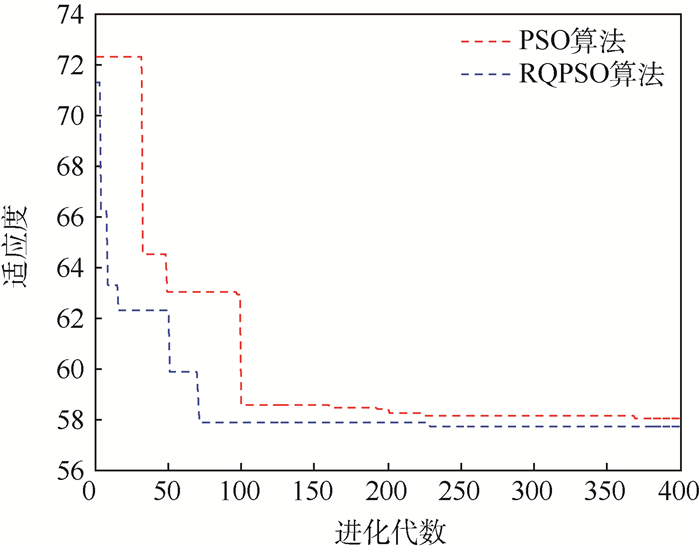 |
| 图 15 RQPSO算法与PSO算法收敛速度比较 Fig. 15 Comparison of convergence speed between RQPSO and PSO algorithms |
| 图选项 |
从图 10可以看出,无人机编队在整个飞行过程中基本没有偏离虚拟参考轨迹,当发现敌方搜索雷达,需要进行突防时,无人机编队中的uv5被选择对敌搜索雷达进行干扰,其余无人机能够以uv5与虚拟参考轨迹为参考自动进行编队构型重构,以实施安全突防;当发现敌方防空导弹跟踪雷达时,无人机编队中的uv3被选择对敌跟踪雷达进行干扰,此时编队中的uv3与uv5相互协作,同时还要参考虚拟参考轨迹以便选择出最佳干扰位置,其余无人机也自动进行编队构型重构,以实现安全突防;当整个编队突防成功后,需要根据此时的位置和期望的编队构型在此进行编队重构。从图 11和图 12可以看出,uv1的速度和航向控制输入满足控制约束。从图 14可以看出,无人机之间的相对距离也满足约束条件,从而验证了所设计的编队构型控制算法是有效的。图 15表明,RQPSO算法进行编队重构的效果要明显优于PSO算法。
6 结论 本文提出了一种基于RQPSO算法的多无人机编队重构控制算法,并验证了其有效性与安全性。
1) 相比传统的PSO算法,RQPSO算法的变异操作和选择操作使得整个算法的搜索能力更强大,且不易于陷入局部最优值,而使得到的解不是最优的。
2) 通过引入邻居集降低编队重构代价问题的复杂性,提高了优化求解的效率,更有利于对实时性要求高的多无人机编队自主重构。
3) 与以往的各种多无人机编队重构约束条件相比,本文考虑的约束条件更加全面具体,具有更多的现实意义。
参考文献
| [1] | 王祥科, 李迅, 郑志强. 多智能体系统编队控制相关问题研究综述[J].控制与决策, 2013, 28(11): 1601–1613. WANG X K, LI X, ZHENG Z Q. Survey of delvelopmrnts on multi-agent formation control related problems[J].Control and Decision, 2013, 28(11): 1601–1613.(in Chinese) |
| [2] | SCHIANO F, FRANCHI A, DAN Z, et al.A rigidity-based decentralized bearing formation controller for groups of quadrotor UAVs[C]//IEEE/RSJ International Conference on Intelligent Robots and System, 2016:1109-1118. |
| [3] | 陈宗基, 张汝麟, 张平, 等. 飞行器控制面临的机遇与挑战[J].自动化学报, 2013, 39(6): 703–710. CHEN Z J, ZHANG R L, ZHANG P, et al. Flight control:Challenges and opportunities[J].Acta Automatica Sinica, 2013, 39(6): 703–710.(in Chinese) |
| [4] | 段海滨, 刘森琪. 空中/地面机器人异构协同技术研究:现状和展望[J].中国科学:技术科学, 2010, 40(9): 1029–1036. DUAN H B, LIU S Q. Unmanned air/ground vehicles heterogeneous cooperative techniques:Current status and prospects[J].Scientia Sinica Technologica, 2010, 40(9): 1029–1036.(in Chinese) |
| [5] | 朱华勇, 牛轶峰, 沈林成, 等. 无人机系统自主控制技术研究现状与发展趋势[J].国防科技大学学报, 2010, 32(3): 115–120. ZHU H Y, NIU Y F, SHEN L C, et al. State of the art and trends of autonomous control of UAV systems[J].Journal of National University of Defense Technology, 2010, 32(3): 115–120.(in Chinese) |
| [6] | BRUST M R, STRIMBU B M.A networked swarm model for UAV deployment in the assessment of forest environments[C]//2015 IEEE 10th International Conference on Intelligent Sensors, Sensor Networks and Information Processing, 2015. |
| [7] | 吕明海, 魏瑞轩, 许卓凡. 基于改进微分进化的无人机编队重构安全控制[J].电光与控制, 2014, 21(9): 65–70. LU M H, WEI R X, XU Z F. Safety control for UAV formation reconfiguration based on modified differential evolution[J].Electronics Optics & Control, 2014, 21(9): 65–70.(in Chinese) |
| [8] | 吴清坡, 周绍磊, 周超. 基于粒子群优化的无人飞行器编队分布式协同构型重构控制[C]//2012导航、制导与控制会议, 2012. WU Q P, ZHOU S L, ZHOU C.Distributed cooperative configuration control for UAV based on particle swarm optimization[C]//5th International Congress of Navigation, Guidance and Control, 2012(in Chinese). |
| [9] | 茹常剑, 魏瑞轩, 戴静, 等. 基于纳什议价的无人机编队自主重构控制方法[J].自动化学报, 2013, 39(8): 1349–1360. RU C J, WEI R X, DAI J, et al. Autonomous reconfiguration control method for UAV's formation based on Nash bargin[J].Acta Automatica Sinica, 2013, 39(8): 1349–1360.(in Chinese) |
| [10] | 熊伟, 陈宗基, 周锐. 运用混合遗传算法的多机编队重构优化方法[J].航空学报, 2008, 29(Supl): S209–S214. XIONG W, CHEN Z J, ZHOU R. Optimization of multiple flight vehicle formation reconfiguration using hybrid genetic algorithm[J].Acta Aeronautica et Astronautica Sinica, 2008, 29(Supl): S209–S214.(in Chinese) |
| [11] | SEO J, KIM Y, TSOURDOS A, et al.Multiple UAV formation reconfiguration with collision avoidance guidance via different geometry concept[C]//28th International Congress of the Aeronautical Sciences, 2016. |
| [12] | FERNáNDEZ-CABALLERO A, BELMONTE L M, MORALES R, et al. Generalized proportional integral control for an unmanned quadrotor system[J].International Journal of Advanced Robotic Systems, 2015, 12(1): 1–7.DOI:10.5772/59888 |
| [13] | MAYNE D Q, RAWLINGS J B, RAO C V, et al. Constrained model predictive control:Stability and optimality[J].Automatica, 2000, 36(6): 789–814.DOI:10.1016/S0005-1098(99)00214-9 |
| [14] | PENI T, VANEK B, SZABO Z, et al.Supervisory fault tolerant control of the GTM UAV using LPV methods[C]//IEEE Control and Fault-Tolerant Systems.Piscataway, NJ:IEEE Press, 2013:655-660. |
| [15] | 席裕庚, 李德伟, 林殊. 模型预测控制——现状与挑战[J].自动化学报, 2013, 39(3): 222–236. XI Y G, LI D W, LIN S. Model predictive control:Status and challenges[J].Acta Automatica Sinica, 2013, 39(3): 222–236.(in Chinese) |
| [16] | 黄海滨, 马广富, 庄宇飞, 等. 基于协同进化粒子群和Pareto最优解的卫星编队队形重构方法[J].航空学报, 2011, 32(11): 2073–2082. HUANG H B, MA G F, ZHUANG Y F, et al. Satellite formation reconfiguration using co-evolutionary particle swarm optimization and Pareto optimal solution[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(11): 2073–2082.(in Chinese) |
| [17] | 金久才, 张杰, 官晟, 等. 自推进粒子群的空间同步平行编队控制[J].控制理论与应用, 2011, 28(4): 587–590. JIN J C, ZHANG J, GUAN S, et al. Control for spatial synchronized parallel formation of self-propelled particles[J].Control Theory & Applications, 2011, 28(4): 587–590.(in Chinese) |
| [18] | 李盼池, 王海英, 宋考平, 等. 量子势阱粒子群优化算法的改进研究[J].物理学报, 2012, 61(6): 060302-1–060302-6. LI P C, WANG H Y, SONG K P, et al. Research on the improvement of quantum potential well-based particle swarm optimization algorithm[J].Acta Physica Sinica, 2012, 61(6): 060302-1–060302-6.(in Chinese) |
| [19] | 刘朝华, 张英杰, 章兢, 等. 基于免疫双态微粒群的混沌系统自抗扰控制[J].物理学报, 2011, 60(1): 019501-1–019501-9. LIU C H, ZHANG Y J, ZHANG J, et al. Active disturbance rejection control of a chaotic system based on immune binary-state particle swarm optimization algorithm[J].Acta Physica Sinica, 2011, 60(1): 019501-1–019501-9.(in Chinese) |
| [20] | 张宏立, 宋莉莉. 基于量子粒子群算法的混沌系统参数辨识[J].物理学报, 2013, 62(19): 190508-1–190508-6. ZHANG H L, SONG L L. Parameter identification in chaotic systems by means of quantum particle swarm optimization[J].Acta Physica Sinica, 2013, 62(19): 190508-1–190508-6.DOI:10.7498/aps.62.190508(in Chinese) |
| [21] | 孙俊. 量子行为粒子群优化算法研究[D]. 无锡: 江南大学, 2009. SUN J.Particle swarm optimization with particles having quantum behavior[D].Wuxi:Southern Yangtze University, 2009(in Chinese). |
| [22] | 方伟, 孙俊, 谢振平, 等. 量子粒子群优化算法的收敛性分析及控制参数研究[J].物理学报, 2010, 59(6): 3686–3692. FANG W, SUN J, XIE Z P, et al. Convergence analysis of quantum-behaved particle swarm optimization algorithm and study on its control parameter[J].Acta Physica Sinica, 2010, 59(6): 3686–3692.DOI:10.7498/aps.59.3686(in Chinese) |
| [23] | 施展, 陈庆伟. 基于改进的多目标量子行为粒子群优化算法的多无人机协同任务分配[J].南京理工大学学报, 2012, 36(6): 945–951. SHI Z, CHEN Q W. Cooperative task allocation for multiple UAVs based on improved multi-objective quantum-behaved particle swarm optimization algorithm[J].Journal of Nanjing University of Science and Technology, 2012, 36(6): 945–951.(in Chinese) |
| [24] | 施展, 陈庆伟. 基于量子行为特性粒子群和自适应网格的多目标优化算法[J].信息与控制, 2011, 40(2): 214–220. SHI Z, CHEN Q W. Multi-objective optimization algorithm based on quantum-behaved particle swarm and adaptive grid[J].Information and Control, 2011, 40(2): 214–220.(in Chinese) |
| [25] | 吴祥兴, 陈忠. 混沌学导论[M].上海: 上海科学技术文献出版社, 1997. WU X X, CHEN Z. Introduction to chaos theory[M].Shanghai: Shanghai Scientific and Technical Literature Press, 1997.(in Chinese) |
| [26] | REN W. Trajectory tracking control for a mininature fixed-wing unmanned air vehicle[J].International Journal of Systems Science, 2007, 38(4): 361–368.DOI:10.1080/00207720601170586 |
| [27] | 叶水跟. 某型无人机空中阶段控制律设计与仿真[D]. 成都: 电子科技大学, 2011. YE S G.Design and simulation of the control law for a certain UAV in the air phase[D].Chengdu:University of Electronic Science and Technology, 2011(in Chinese). |
| [28] | REN W. On contrained nonliear tracking control of a small fixed-wing UAV[J].Journal of Intelligent and Robotic Systems, 2007, 48(4): 525–537.DOI:10.1007/s10846-006-9123-8 |
| [29] | REN W, BEARD R W.Distributed consensus in multi-vehicle cooperative control:Theory and applications[M].WU X F, translated.Beijing:Electronic Industry Press, 2014(in Chinese). |
| [30] | 周绍磊, 康宇航, 万兵, 等. 多无人机协同编队控制的研究现状与发展前景[J].飞航导弹, 2016(1): 78–82. ZHOU S L, KANG Y H, WAN B, et al. Research status and development prospect of cooperative control for multiple UAVs[J].Aerodynamic Missile Jounal, 2016(1): 78–82.(in Chinese) |
| [31] | 周超, 王亚峰, 周绍磊, 等. 输入状态稳定的鲁棒预测控制[J].控制与决策, 2013, 28(7): 58–62. ZHOU C, WANG Y F, ZHOU S L, et al. Robust model predictive control with input-to-state stability[J].Control and Decision, 2013, 28(7): 58–62.(in Chinese) |
| [32] | TRODDEN P, RICHARDS A.Multi-vehicle cooperative search using distributed model predictive control[C]//Proceedings of the AIAA Conference on Guidance, Navigation and Control.Reston:AIAA, 2008:1-11. |
| [33] | RIGET J, VESTERSTROEM J.A diversity-guided particle swarm optimizer -The ARPSO:2002-02[R].EVALife Technical Report, 2002. |
| [34] | 董娜, 陈增强, 孙青林, 等. 基于粒子群优化的有约束模型预测控制器[J].控制理论与应用, 2009, 26(9): 965–969. DONG N, CHEN Z Q, SUN Q L, et al. Particle-swarm optimization algorithm for model predictive control with constrains[J].Control Theory & Applications, 2009, 26(9): 965–969.(in Chinese) |
| [35] | 张雷, 王道波, 高宇辉, 等. 基于粒子群优化的无人战斗机编队任务协调方法研究[J].系统工程与电子技术, 2009, 31(2): 439–442. ZHANG L, WANG D B, GAO Y H, et al. Study on uninhabited combat air vehicle formation tasks scheduling method based on particle swarm optimization algorithm[J].Systems Engineering and Electronics, 2009, 31(2): 439–442.(in Chinese) |
