但是在变形机构为飞行系统提供额外自由度的同时,会对飞行器的稳定性和操纵性产生很大影响。变体过程会使飞行器的展长、弦长、质心和转动惯量等固有结构参数发生变化,从而加剧了飞行器建模的复杂性[4]。同时,气动特性的不规则变化与附加的干扰力矩对飞行控制系统的控制性能提出了更高的要求。如何在不同的气动外形转换时避免飞行器出现剧烈的姿态变化,而导致航迹精度差、飞行品质不佳甚或失稳等问题成为当前研究领域亟待解决的关键。
目前,针对变体飞行器线性变参数(Linear Parameter Varying,LPV)模型的稳定性分析与控制器设计已较为成熟。文献[5]利用拟合出的气动参数函数建立了纵向LPV模型,并采用增益调度的控制方法设计了全局稳定控制器。文献[6-10]将切换系统与变体LPV模型相结合,设计了连续且平滑的切换型控制器。文献[11-12]针对折叠翼飞行器的LPV模型,设计内外环鲁棒自整定控制器,以保证翼型变化过程中的稳定性。文献[13]基于速度线性化的LPV建模,设计了鲁棒H∞状态反馈控制器。然而,现有针对变体LPV模型的研究存在以下局限:为了应用多胞型LPV系统的设计方法,使得后期控制器设计摆脱无穷多的限制条件,LPV模型的系数矩阵等必须写成仿射参数依赖形式,如
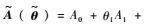
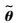
本文以一种翼展可变飞行器的非仿射参数依赖LPV模型为研究对象,将非仿射结构经数学变换后变为等价线性分式表示(Linear Fractional Representation,LFR)系统[14-16],并给出此系统的状态反馈H∞控制器设计方法。本文的创新点在于:① 以LFR模型设计控制器,研究非仿射参数依赖LPV变体飞行器模型控制方法;② 推导出一种可直接应用于控制器设计的二次稳定性线性矩阵不等式(Linear Matrix Inequality,LMI)条件,并进行了详细数学证明。
1 变体飞行器的LFR建模 对于现有的多种变体方式[17-18],本文以轻型飞机Navion L-17[5, 8, 19]作为本体进行变翼展的研究。翼展变形方式是左右机翼对称的沿翼展方向水平伸缩,从而快速地影响到飞机的总体气动力和气动力矩,其可达到的最大翼展是本体翼展的2倍,如图 1所示。定义翼展变形率ξ=Δb/b,Δb为翼展变形量, b为本体翼展,可知ξ∈[0, 1]。本文只考虑飞行器纵向运动, 选取飞行器在高度h=1 524 m,以马赫数Ma=0.1做水平无侧滑匀速平飞时的运动过程为待研究的目标。
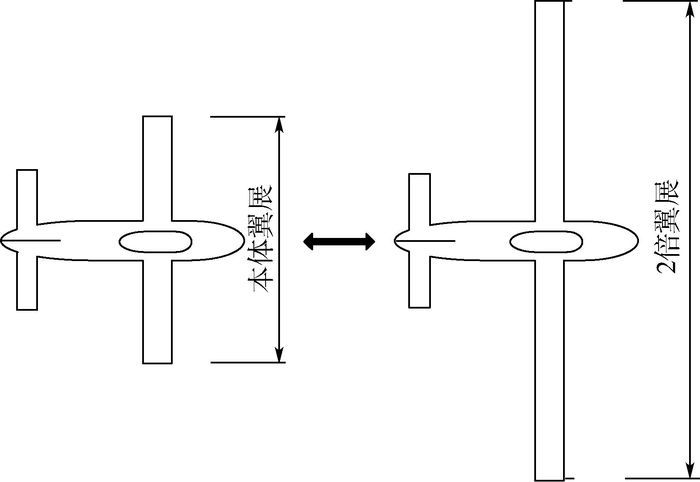 |
| 图 1 变体形态示意图 Fig. 1 Schematic of morphing configuration |
| 图选项 |
1.1 变体模型描述 在气流坐标系中,建立此变体飞行器纵向运动的非线性模型:
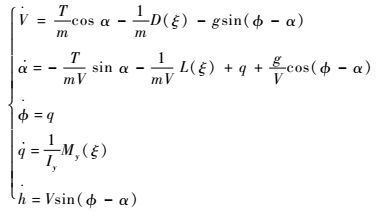 | (1) |
式中:V和h分别为飞行速度和高度;φ和q分别为俯仰角和俯仰角速度;α为迎角;m和Iy分别为飞行器的质量和绕y轴的转动惯量;g为重力加速度;推力T=Tδtδt,Tδt为推力系数,δt为油门开度;L为升力;D为阻力;My为纵向俯仰力矩。
升力L、阻力D、俯仰力矩My分别为
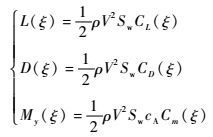 | (2) |
式中:Sw为机翼面积;cA为平均气动弦长;ρ为大气密度;CL为升力系数;CD为阻力系数;Cm为俯仰力矩系数。
各气动系数与迎角α、升降舵偏角δe关系的近似表达式为
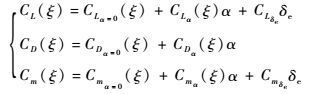 | (3) |
式中:CLδe和Cmδe分别为升降舵引起的升力系数和俯仰力矩系数;α∈[0°, 10°];δe∈[-40°, 40°]。通过Datcom软件计算不同翼展变形率ξ下的气动参数,利用MATLAB分析、拟合相关数据,得到各气动系数及零迎角时的气动系数分别是ξ的函数[5]。
 | (4) |
式中:各气动系数的单位为1/(°)。
可见,机翼伸缩能直接改变飞行器的气动参数,从而影响整体的气动性能,这正是变形对于飞行器的本质作用[19]。
1.2 LFR建模 考虑到平衡点的迎角都很小,根据Jacobian线性化方法可构建出变体飞行器纵向运动LPV模型。为了更精确地描述变体过程中系统变换模型,平衡点选取为ξ=0, 0.1, 0.2, …, 1.0。此变体飞行器的LPV模型可表示为H∞控制的标准形式[20]:
 | (5) |
式中:z=[eV??eh]T为被控量,分别为速度与高度相对于指令的偏差;x=[ΔV??Δα ??Δφ??Δq ??Δh??IV??Ih]T为状态变量,IV=∫eVdt,Ih=∫ehdt;u=[δe?? δt]T为升降舵控制量和油门控制量;w为外部输入干扰,主要为式(1) 中3个动力学方程中的不确定性部分和干扰,包括由变体运动引起的惯性附加力、附加力矩、空气动力的不确定性、建模误差及其他不确定性和干扰;Aξ(ξ)、B1(ξ)、B2(ξ)、C1(ξ)、D11(ξ)和D12(ξ)为系数矩阵。
不局限于系数矩阵的参数依赖仿射形式,从而更精确地拟合其中的各个离散平衡点,得到LPV系数矩阵为
 |
选取A(ξ)矩阵中最具代表性的2个元素A11与A21进行高次系数拟合,并与常规的一次系数拟合作对比可知,高次拟合能够使得到的LPV模型更准确地描述原非线性方程的动态特性,如图 2所示,进而为后续的控制器设计提供了有力基础。
对于状态方程式(5),于A(ξ)不是仿射参数依赖形式,不能采用传统基于多胞体方法[21]对其进行H∞控制器设计。在此采用LFR转换方法[14],将原本的LPV系统转化为线性时不变(Linear Time-Invariant,LTI)系统,并且构建虚拟的输入输出项将包含原时变参数的对角矩阵作为此LTI系统的反馈回路,如图 3所示。
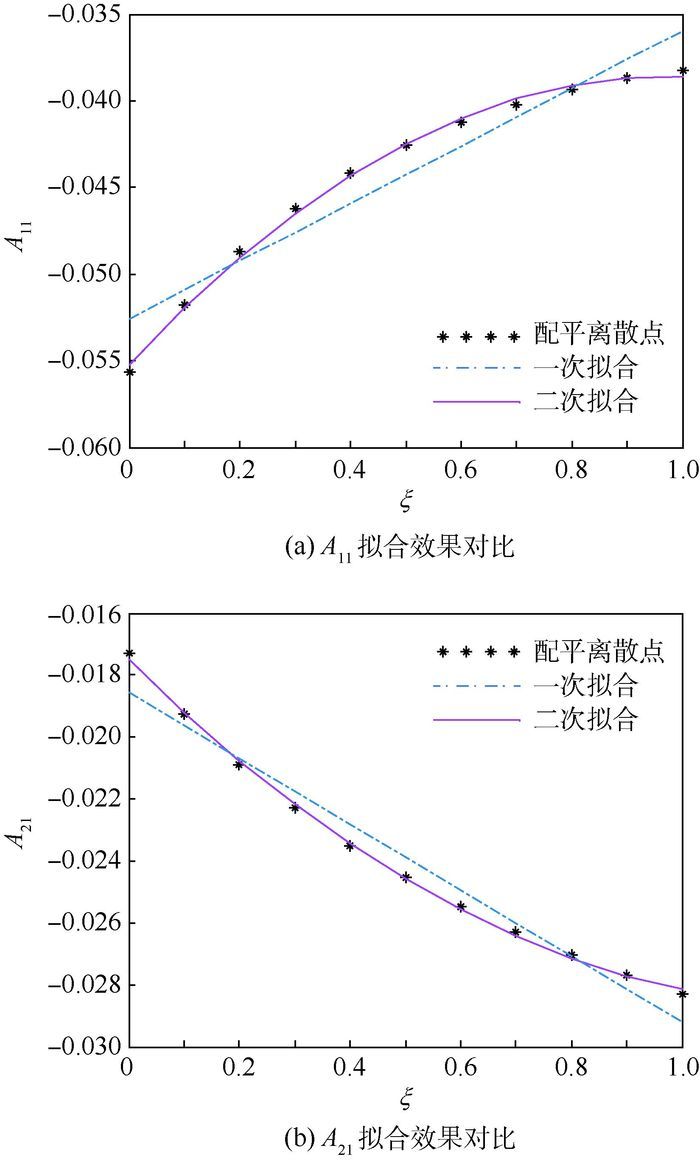 |
| 图 2 系数矩阵拟合对比 Fig. 2 Comparison of coefficient matrix fitting |
| 图选项 |
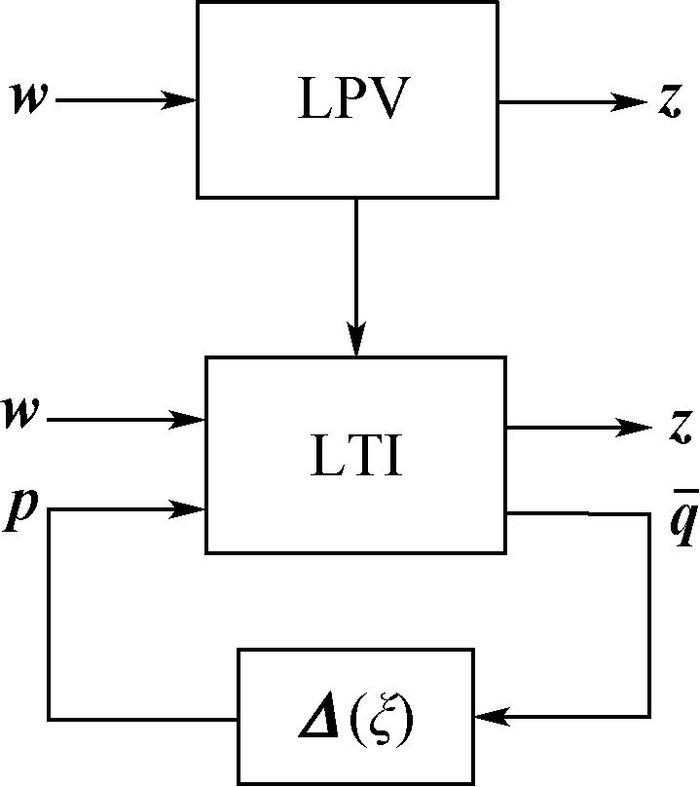 |
| 图 3 系统等效图 Fig. 3 Equivalent systems |
| 图选项 |
对于状态方程式(5),由于其时变系数矩阵中的所有元素都为ξ的实函数,故有
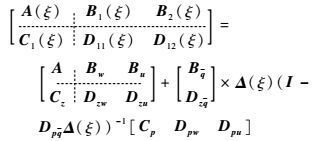 | (6) |
式中:
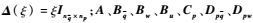
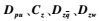
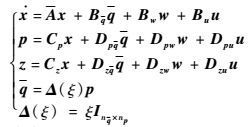 | (7) |
式中:
 |
至此,式(7) 以一种特殊的LTI形式完整地描述了此变体飞行器在变体过程中的动态模型,可以基于此形式设计H∞控制器。
2 LFR的状态反馈H∞控制器设计 2.1 LFR模型的H∞控制LMI条件 考虑如下形式的LPV系统模型:
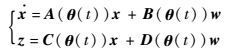 | (8) |
式中:时变参数向量θ(t)=[θ1(t), θ2(t), …, θm(t)]T∈Rm,并且θ(t)在由2m个顶点组成多胞型Θ中取值。
当式(8) 中系数矩阵为θ(t)的有理实数形式时,其可以等效地表示为LFR形式[16]:
 | (9) |
假定对于所有的θ(t)∈Θ,有det(I-DpqΔ(θ))≠0。同时定义Δ=Δ(θ),θ(t)∈Θ。由于Θ是多胞型结构,使得Δ也是多胞型。Δi(i=1, 2, …,m)表示Δ的顶点。定义矩阵
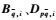
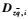
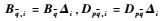
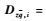
定理1??设常数γ>0,LFR系统式(9) 是二次稳定的,且从w至z的传递函数Tzw(s)满足||Tzw(s)||∞<γ(即系统的诱导L2增益小于γ),当且仅当存在实矩阵P=PT>0和实矩阵M=MT满足下述LMI约束条件:
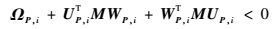 | (10) |
式中:
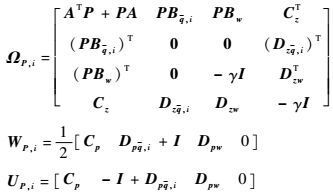 |
证明??此定理证明与文献[16]中的定理1证明相似,只是将其中的H、G与J取为
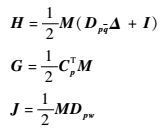 |
证毕
然而,应用此定理设计状态反馈控制器会导致未知矩阵相乘的情况出现,从而使MATLAB中的LMI工具箱无法直接使用。鉴于这种情况,给出以下推论。
推论1??设常数γ>0,LFR系统式(9) 是二次稳定的,且从w至z的传递函数Tzw(s)满足||Tzw(s)||∞<γ,当且仅当存在实矩阵Q=QT>0和实矩阵M=MT满足下述LMI约束条件:
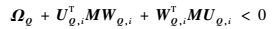 | (11) |
式中:
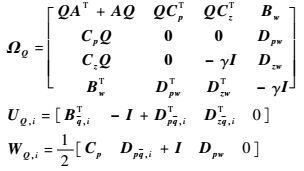 |
下面给出此推论的详细证明,其在文献[16]中没有给出。
证明??根据界实定理[21],系统式(8) 是二次稳定的,且其诱导L2增益小于γ,当且仅当存在实矩阵P=PT>0满足下述LMI约束:
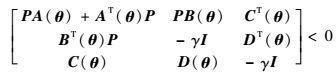 | (12) |
用对角矩阵diag(P-1, I, I)分别左乘和右乘式(12),并记Q=P-1得
 | (13) |
根据Schur补定理可知,式(13) 等价于
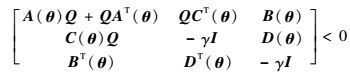 | (14) |
根据式(14) 推得系统式(8) 的对偶系统式(15) 满足界实定理:
 | (15) |
 | (16) |
 | (17) |
由式(16) 和式(17) 可推得等式(18):
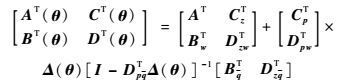 | (18) |
根据式(18) 可以写出对偶系统式(15) 的等价LFR形式为
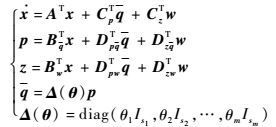 | (19) |
系统式(15) 等价形式的系统式(19) 满足二次H∞性能,应用定理1即可得到推论。
证毕
2.2 状态反馈H∞控制器设计 考虑系统
 | (20) |
假设系统状态是可以测量的,将u=Kx代入式(20) 中得到式(8) 的形式,直接应用推论1可得式(11) 中各项为
 |
则控制器增益矩阵为K=RQ-1,其中R为LMI式(11) 中待求的矩阵变量。
3 仿真分析与验证 为验证本文基于LFR模型所设计的H∞控制器的有效性,对式(1) 所示的翼展可变飞行器非线性模型进行仿真。变体飞行器的基本参数及大气参数与文献[5]一致。根据推论1,利用MATLAB中的LMI工具箱对已知的LFR模型式(7) 设计静态的状态反馈控制器,设计过程依照2.2节内容。为了避免状态反馈矩阵中的元素数值过大引起控制器饱和,取γ=10。最终得到如下控制器增益矩阵:
 |
将控制器引入变体飞行器原始非线性模型式(1) 中,利用MATLAB仿真目标运动过程。令变体飞行器从第5 s开始变形, 并在10 s内从本体翼展匀速伸长至2倍翼展。飞行器在变体过程中还会受到外加干扰力与力矩的作用。在非线性模型式(1) 中的力与力矩方程中引入高斯白噪声信号,模拟随机力矩与力对飞行器变体过程中控制性能的影响,以此验证该控制器在干扰作用下的稳定性以及对干扰的抑制作用。这些干扰的幅值分别为翼展未变化前的配平状态下静态阻力最大值的6%、静态升力最大值的0.72%和变体过程中最大俯仰力矩的2.4%。
仿真结果如图 4所示。可以看出,在变形过程中,所设计的控制器在外部存在干扰的情况下依然能很好地使飞行器在高度和速度上保持稳定。为了保持变体过程中的平衡,升降舵偏角随迎角的减小而逐渐减小,同时油门大小由于所受阻力的减小也成减小趋势。由于在状态变量中引入了高度和速度的误差积分项,在15 s变体结束进入新的平衡态后,飞行器与之前状态的高度和速度一致,无静差存在。
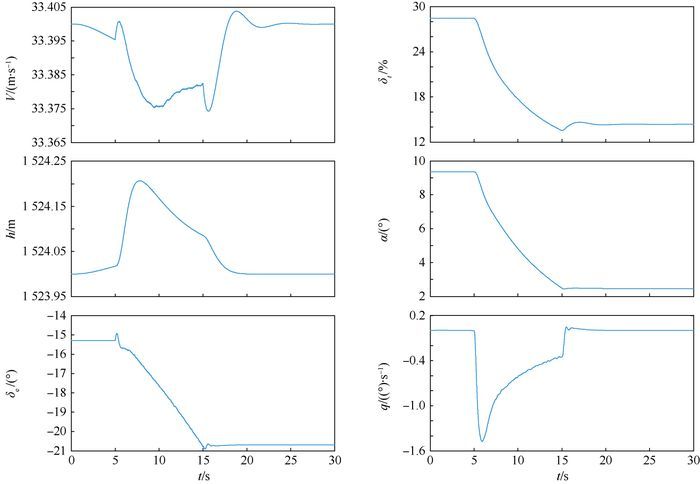 |
| 图 4 控制效果图 Fig. 4 Effectiveness of controller |
| 图选项 |
4 结论 1) 在Jacobian线性化基础上,利用多个平衡点推导出变体过程中的精确LPV模型,所得的LPV模型中系数矩阵是非仿射参数依赖的。
2) 采用LFR转换方法将系统转化为特殊形式下的等价LTI模型,原时变参数作为对角矩阵存在于此LTI系统的反馈回路中。针对此LFR模型,设计了一种可直接应用的二次稳定性LMI条件,从而推导出基于状态反馈形式的H∞控制器设计方法。
3) 非线性仿真结果表明,运用所设计的控制器,当翼展变化时,变体飞行器状态稳定,在外部存在干扰力与干扰力矩情况下,控制性能良好。
4) 本文所研究的基于LFR转化的LPV控制方法可以广泛地应用到有理实数形式的LPV系统中,如飞行器的大包线LPV控制、高超声速飞行器和涡轮风扇发动机等。并且对于仿射参数依赖和非仿射参数依赖的LPV系统,此设计过程基本一致,具有普遍的适用性。
参考文献
| [1] | BONNEMA K L, STEPHEN B S.AFTI/F-111 mission adaptive wing flight research program[C]//4th Flight Test Conference, 2006:155-161. |
| [2] | PENDLETON E W, BESSETTE D, FIELD P B, et al. Active aeroelastic wing flight research program:Technical program and model analytical development[J].Journal of Aircraft, 2000, 37(4): 554–561.DOI:10.2514/2.2654 |
| [3] | KUDVA J N. Overview of the DARPA smart wing project[J].Journal of Intelligent Material Systems & Structures, 2004, 15(4): 261–267. |
| [4] | 杨贯通, 唐胜景, 赵林东, 等. 变后掠变展长飞行器动力学建模与动态响应分析[J].兵工学报, 2014, 35(1): 102–107. YANG G T, TANG S J, ZHAO L D, et al. Dynamic modeling and response of a morphing UAV with variable sweep and variable span[J].Acta Armamentarii, 2014, 35(1): 102–107.(in Chinese) |
| [5] | 殷明, 陆宇平, 何真. 变体飞行器LPV建模与鲁棒增益调度控制[J].南京航空航天大学学报, 2013, 45(2): 202–208. YIN M, LU Y P, HE Z. LPV modeling and robust gain scheduling control of morphing aircraft[J].Journal of Nanjing University of Aeronautics and Astronautics, 2013, 45(2): 202–208.(in Chinese) |
| [6] | JIANG W L, DONG C Y, WANG Q. A systematic method of smooth switching LPV controllers design for a morphing aircraft[J].Chinese Journal of Aeronautics, 2015, 28(6): 1640–1649.DOI:10.1016/j.cja.2015.10.005 |
| [7] | 李玮, 王青, 董朝阳. 一类非理想切换系统的H∞控制器设计[J].北京航空航天大学学报, 2014, 40(10): 1405–1410. LI W, WANG Q, DONG C Y. H∞ controller design for a class of nonideal switched systems[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(10): 1405–1410.(in Chinese) |
| [8] | 江未来, 董朝阳, 王通, 等. 变体飞行器连续平滑切换LPV控制[J].系统工程与电子技术, 2015, 37(6): 1347–1353. JIANG W L, DONG C Y, WANG T, et al. Continuous smooth switching LPV control for morphing aircraft[J].Systems Engineering & Electronics, 2015, 37(6): 1347–1353.DOI:10.3969/j.issn.1001-506X.2015.06.19(in Chinese) |
| [9] | 王通, 王青, 江未来, 等. 基于切换多胞模型的变体飞行器增益调参控制[J].北京航空航天大学学报, 2014, 40(1): 75–79. WANG T, WANG Q, JIANG W L, et al. Gain schedule control of morphing vehicle based on switched polytopic system[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(1): 75–79.(in Chinese) |
| [10] | 何墉, 章卫国, 王敏文, 等. 基于多目标控制的变体飞行器切换线性变参数控制器[J].控制理论与应用, 2015, 32(11): 1518–1525. HE Y, ZHANG W G, WANG M W, et al. Switching linear-parameter-varying controller for morphing aircraft based on multi-objective[J].Control Theory & Applications, 2015, 32(11): 1518–1525.(in Chinese) |
| [11] | YUE T, WANG L, AI J. Gain self-scheduled H∞ control for morphing aircraft in the wing transition process based on an LPV model[J].Chinese Journal of Aeronautics, 2013, 26(4): 909–917.DOI:10.1016/j.cja.2013.06.004 |
| [12] | BALDELLI D H, LEE D H, PE?A R S S, et al. Modeling and control of an aeroelastic morphing vehicle[J].Journal of Guidance, Control, and Dynamics, 2008, 31(6): 1687–1699.DOI:10.2514/1.35445 |
| [13] | 王青, 王通, 后德龙, 等. 基于速度线性化的变体飞行器鲁棒LPV控制[J].系统工程与电子技术, 2014, 36(6): 1130–1136. WANG Q, WANG T, HOU D L, et al. Robust LPV control for morphing vehicles via velocity-based linearization[J].Systems Engineering & Electronics, 2014, 36(6): 1130–1136.DOI:10.3969/j.issn.1001-506X.2014.06.18(in Chinese) |
| [14] | HECKER S, VARGA A, MAGNI J F. Enhanced LFR-toolbox for MATLAB[J].Aerospace Science and Technology, 2005, 9(2): 173–180.DOI:10.1016/j.ast.2004.12.001 |
| [15] | WANG F, BALAKRISHNAN V. Improved stability analysis and gain-scheduled controller synthesis for parameter-dependent systems[J].IEEE Transactions on Automatic Control, 2002, 47(5): 720–734.DOI:10.1109/TAC.2002.1000267 |
| [16] | PREMPAIN E, POSTLETHWAITE I. Brief paper:L2 and H2 performance analysis and gain-scheduling synthesis for parameter-dependent systems[J].Automatica, 2008, 44(8): 2081–2089.DOI:10.1016/j.automatica.2007.12.008 |
| [17] | YUE T, WANG L, AI J. Longitudinal linear parameter varying modeling and simulation of morphing aircraft[J].Journal of Aircraft, 2013, 50(6): 1673–1681.DOI:10.2514/1.C031316 |
| [18] | 张杰, 吴森堂. 一种变体飞行器的动力学建模与动态特性分析[J].北京航空航天大学学报, 2015, 41(1): 58–64. ZHANG J, WU S T. Dynamic modeling for a morphing aircraft and dynamic characteristics analysis[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(1): 58–64.(in Chinese) |
| [19] | 殷明, 陆宇平, 何真, 等. 变体飞行器变形辅助机动的建模与滑模控制[J].系统工程与电子技术, 2015, 37(1): 128–134. YIN M, LU Y P, HE Z, et al. Modeling and sliding mode control of morphing aircraft for morphing-aided maneuver[J].Systems Engineering & Electronics, 2015, 37(1): 128–134.(in Chinese) |
| [20] | 贾英民. 鲁棒H∞控制[M].北京: 科学出版社, 2007. JIA Y M. Robust H∞ control[M].Beijing: Science Press, 2007.(in Chinese) |
| [21] | APKARIAN P, GAHINET P. A convex characterization of gain-scheduled H∞ controllers[J].IEEE Transactions on Automatic Control, 1995, 40(5): 853–864.DOI:10.1109/9.384219 |
