电磁线圈用于航天器相对运动控制首先由麻省理工学院空间实验室的Kong和Miller等提出[3-4]。Elias[6]针对2颗电磁航天器的相对运动利用Kane方法建立了非线性动力学模型,并提出固定自由偶极子的磁矩求解方法。Ahsun等[5, 7]和Elias[6]分别采用自适应控制方法和人工势函数法研究了电磁卫星编队的构型控制,并将两者的控制结果进行了比较。苏建敏和董云峰[8]在Ahsun研究的基础上将人工势函数法和C-W方程结合研究了电磁航天器编队的构型重构控制,并建立非线性方程组求解磁矩,但是该磁矩求解方法不能根据编队卫星的差异进行磁矩分配。徐增文等[9]针对双电磁航天器编队的构型维持问题设计了自适应控制律,并给出了基于能量均衡原则进行双星磁矩分配的磁矩解析表达式。邵龙飞等[10]研究了电磁航天器编队的绳系动力学模型与运动规划方法,提出通过序列控制实现多颗电磁航天器的编队构型控制。但目前电磁航天器编队控制研究基本上都采取主从式的控制策略,并未考虑成员卫星之间的信息交互,导致编队的协同能力较差,而且在求解磁矩时没有充分考虑各成员卫星的差异。为了增强电磁航天器编队的协同性,有必要引入信息一致性理论描述卫星间的信息拓扑关系,并且结合电磁航天器编队特殊的飞行原理和受力特点,分析相应的协同控制方法。
在基于一致性理论研究卫星编队的协同控制方面,毕鹏等[14]考虑了通信拓扑变换的情况,基于C-W方程给出了卫星编队非线性协同控制律。马广富和梅杰[15]基于非线性相对运动动力学方程,考虑了卫星质量的不确定性,提出了能够有效补偿卫星质量不确定性的自适应协同控制律。张保群等[13]综合考虑了存在通信时延、拓扑结构切换、质量不确定和外部扰动等情况下的编队卫星协同控制问题,分别设计了鲁棒位置和姿态协同控制器。郑重和宋申民[16]基于势函数法考虑了卫星质量的不确定性,对无期望轨迹和有期望轨迹2种情况研究了编队卫星避免碰撞的自适应协同控制。Su和Dong[17]通过模仿鱼群的运动规则研究了分布式电磁卫星集群的协同控制,但是该方法只适用于无期望轨迹的情况。由于电磁航天器编队卫星所受到的电磁力真实值通常不能精确计算,并且大多数空间任务对卫星的相对位置是有要求的,所以电磁航天器编队在一般情况下的位置跟踪协同控制不能采取以上的方法。
本文重点研究了多个电磁航天器编队飞行的相对位置协同控制问题。首先,对电磁航天器编队协同控制问题进行建模,分析了电磁航天器编队飞行的基本原理,考虑电磁力模型的不确定性,建立了相对运动动力学模型。然后,采用自适应方法和一致性理论针对电磁航天器编队设计了自适应协同控制器。进一步结合工程实际情况,将磁矩求解问题转化为优化问题,给出了一种考虑成员卫星差异的磁矩求解方法。最后,通过数值仿真验证了控制方法和磁矩求解方法的有效性。
1 电磁航天器编队控制问题描述 1.1 电磁航天器编队基本原理 电磁航天器编队中各成员卫星上都安装有3个正交的超导线圈,利用线圈通电后产生的电磁力可以实现电磁航天器编队构型的建立、保持或重构。对由n颗成员卫星组成的电磁航天器编队,规定其编号依次为0~n-1。忽略地球磁场对电磁航天器编队的作用力,则整个编队所受到的电磁力合力为0[7],即如果第i颗卫星所受到的电磁力为fmi,则有
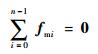 | (1) |
为了实现电磁航天器编队的控制,可以采用毕奥-萨伐尔定律对电流微元进行积分精确计算2个卫星间的电磁力和电磁力矩,但在实际工程中由于计算过于复杂往往采用近似的远场模型[11]。当2个圆形线圈之间的距离大于半径的8倍时,每个线圈可以假设为偶极子,其大小方向用磁矩μ描述,计算公式为
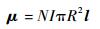 | (2) |
式中:N为线圈匝数;I为线圈电流大小;R为线圈半径;l为磁偶极子的方向,与电流方向符合右手定则。
第i颗卫星的磁矩μi为3个正交方向线圈磁矩之和,由远场偶极子模型可计算卫星i对卫星j的电磁力和电磁力矩分别为
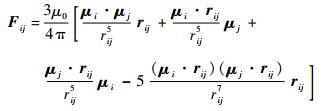 | (3) |
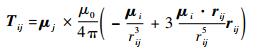 | (4) |
式中:μ0为真空磁导率;μj为第j颗卫星的磁矩;rij为卫星i到卫星j的距离;rij为位置矢量,由卫星i指向卫星j,并且电磁力矩通常作为干扰力矩需要被其他姿态控制执行机构抵消。远场偶极子模型只是近似的电磁力计算模型,相对于电磁力真实值存在一定偏差[7]。
1.2 相对运动动力学模型 选取卫星0为参考卫星,定义OXYZ为参考卫星的轨道坐标系,记为Fo,其原点O位于参考卫星的质心,X轴沿参考卫星运动方向,Z轴由参考卫星质心指向地心,Y轴方向由右手定则确定。在惯性坐标系下第i颗卫星的位置矢量为ri,大小为ri。则第i(i=1, 2, …, n-1) 颗卫星相对参考卫星的动力学方程为[18]
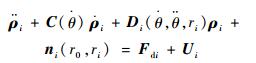 | (5) |
式中:
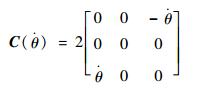 | (6) |
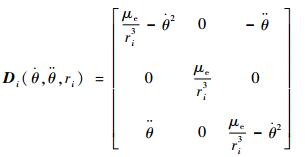 | (7) |
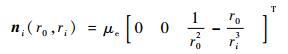 | (8) |
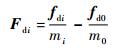 | (9) |
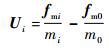 | (10) |
式中:r0为参考星在惯性坐标系下位置的大小;ρi为第i颗卫星在参考卫星轨道坐标系的相对位置;θ为参考卫星的真近角;μe为地球引力常数;Fdi和Ui分别为相对摄动加速度和相对控制加速度;mi和fdi分别为第i颗卫星的质量和受到的空间摄动力。
需要说明的是,本文与相对运动有关的变量下标i均为从1~n-1,其他情况如描述各个卫星的磁矩、质量等参数,下标i均为从0~n-1。
以上相对运动动力学方程对参考卫星的轨道没有限制条件,可以精确地描述n颗电磁航天器间的相对运动。在进行电磁航天器编队的控制时需要计算出Ui,然后求出fmi,求解时联立式(1) 和式(10) 可得n阶线性方程组,该方程组具有唯一解。由于电磁力计算采用的模型是远场近似模型,计算出的电磁力与真实值存在不确定偏差。假定偶极子模型计算出的电磁力为

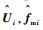
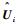
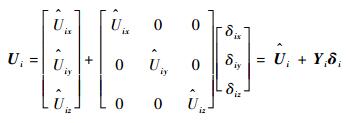 | (11) |
式中:
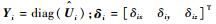
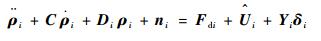 | (12) |
1.3 图论 采用加权无向图描述电磁航天器编队各成员卫星间的信息交互。一个加权无向图G=(V, E, A)由节点集V={0, 1, …, n-1},边集E?V×V和加权邻接矩阵A=[aij]∈Rn×n组成[13-15]。节点i(i=0, 1, …, n-1) 代表第i颗卫星,边(i, j)∈E代表卫星i与卫星j有通信,加权邻接矩阵A表示整个编队的通信拓扑结构和通信性能[13]。无向图中,如果节点i和节点j有信息传递,则有(i, j)∈E且(j, i)∈E。如果i≠j且(i, j)∈E,则aij=aji>0,否则aij=0。通常认为卫星自身没有通信,即aii=0。如果无向图任意两节点都有通信,则称该无向图是连通的[13]。
2 自适应协同控制器设计 为实现电磁航天器编队的协同控制,即要求卫星i相对参考卫星0跟踪期望相对位置ρid和期望相对速度vid的同时电磁编队整体也能暂态保持一定的编队构型。卫星i的位置跟踪误差和速度跟踪误差分别为
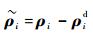 | (13) |
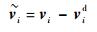 | (14) |
式中:
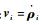
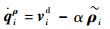 | (15) |
其中:α>0为正常数,采用滑模变结构控制律,则卫星i的切换函数为
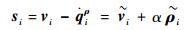 | (16) |
由式(12) 和式(16) 得
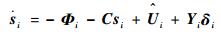 | (17) |
式中:
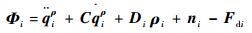 | (18) |
1.2节对电磁力模型的不确定性进行了分析,此外卫星在进行信息交互时,由于传输距离和传输设备的限制,传输过程不可避免地存在时间延迟,假定延迟时间为常值并记为τij。借鉴文献[13-16]基于一致性理论的协同控制算法,对电磁航天器编队设计相应的位置跟踪协同控制器为
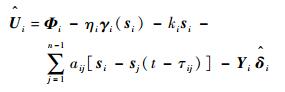 | (19) |
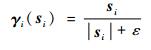 | (20) |
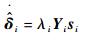 | (21) |
式中:ηi、ki和λi均为正常数;ε为很小的正数;
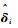
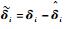
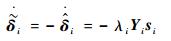 | (22) |
控制律式(19) 共有5项,其中前3项为位置与速度跟踪项,采用趋近律为指数趋近律的滑模变结构控制;第4项为协同控制项,用于实现位置跟踪时暂态构型的保持;最后一项为相对控制加速度补偿项。
电磁航天器的线圈会产生电磁干扰力矩,由式(4) 可知电磁力矩大小和相对位置有关,而传统的滑模控制存在抖振现象,如果位置控制的结果存在较大误差或抖振现象,会严重影响卫星的姿态控制,所以第2项主要是为了削弱抖振,提高控制精度。从协同控制项可看出,为了实现编队的协同,成员卫星需要通过通信获得其他卫星的位置跟踪误差和速度跟踪误差,从而使各卫星的相对状态趋于一致,并且还可注意到,电磁航天器编队中参考卫星0和其他卫星有无通信并不影响编队的协同,这是因为式(1) 充当了参考卫星和其他卫星之间的信息交换。
定理??对动力学方程式(12) 描述的电磁航天器编队,采用控制律式(19)~式(21),有以下结论成立:对?i, j,有
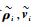
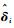
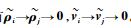
证明??选取Lyapunov函数为
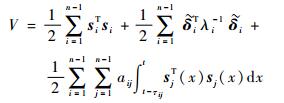 | (23) |
对时间求导得
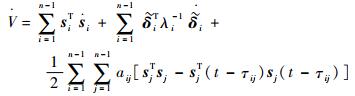 | (24) |
结合式(17) 和式(19) 有
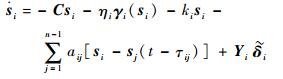 | (25) |
注意到C是反对称阵,且aij=aji,则有
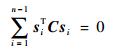 | (26) |
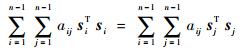 | (27) |
将式(22) 和式(25) 代入式(24),可得
 | (28) |
根据如下不等式:
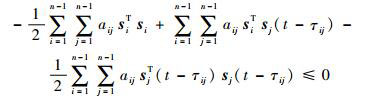 | (29) |
可得
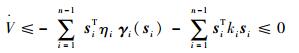 | (30) |
因为V>0且
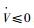
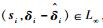
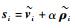
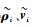
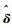
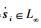
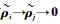
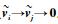
证毕
3 考虑卫星差异的磁矩求解 在电磁航天器编队的控制中通常需要根据已知的电磁力反解控制磁矩。为了求解磁矩,在轨道坐标系Fo下由式(3) 求解每颗卫星受到的电磁力可得非线性方程组:
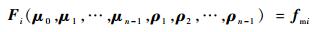 | (31) |
注意到有式(1) 的限制,导致该非线性方程组有效的方程只有3(n-1) 个,但未知量μi共有3n个,所以该方程组具有无穷多解[8]。在利用超导线圈进行编队控制时,工程上往往有很多约束,例如为了节省能量磁矩要求尽量小,为了使控制过程容易实现磁矩改变量也要尽量小,为了减轻姿态控制的压力电磁干扰力矩也要尽量小,所以引入目标函数
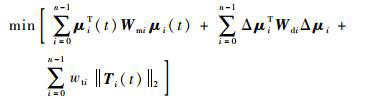 | (32) |
式中:Wmi与Wdi为权重矩阵;Δμi为卫星i磁矩相对上一时刻的改变量;wti为电磁力矩加权系数;||Ti(t)||2为卫星i受到的电磁干扰力矩大小,由于在量级上远小于磁矩,需要通过权重wti增加比重。
对于n颗成员卫星组成的编队,如果卫星的功能、组成或尺寸存在不同,则电磁线圈产生磁矩的能力或卫星姿态控制的能力会存在差异,为了实现资源的高效利用,就需要根据卫星的差异进行磁矩的分配。在计算磁矩时,可以根据卫星能力的差异设定磁矩分配目标,通过对卫星设置不同的加权系数使式(32) 在设定的分配目标处有最优解,另外也可以根据对不同能力的重视程度整体调整3个部分各自所占的比重。在式(31) 的约束下,对目标函数式(32) 进行寻优,可以得到一组控制效果较好的磁矩。对此类优化问题,一般可采用数值方法迭代求解,具体可采用“MATLAB”的“fmincon”函数。
4 数值仿真 4.1 仿真工况设定 为验证控制律的有效性,对4颗卫星组成的电磁航天器编队进行仿真。初始时刻4颗卫星位于半径为5 m的空间圆上,组成正四边形编队,卫星0的轨道根数为(7 000 km, 0.09, π/4, π/6, π/3, 0)。现要求编队尽量维持正四边形构型的前提下重构到不同平面的另一个半径为10 m的空间圆上。初始时刻4颗卫星的位置和速度由相对于中心的轨迹决定:
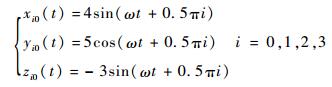 | (33) |
式中:ω为卫星0的轨道角速度。目标构型4颗卫星相对中心的轨迹为
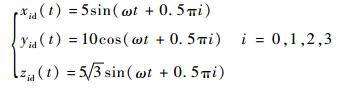 | (34) |
卫星质量均为100 kg,卫星0线圈半径为0.8 m,其他卫星线圈半径均为0.5 m,4颗卫星线圈的匝数和材料均相同,由式(2) 可知卫星0每个方向上的最大磁矩为其他卫星的2.56倍,选择与文献[8]相同的材料,则4颗卫星单个方向上的最大磁矩分别为81 250×(2.56, 1, 1, 1) A·m2。
计算摄动干扰时主要计算地球J2项摄动力,其具体形式及参数见文献[20]。因卫星0与其他卫星有无通信不影响编队的协同控制,所以只考虑卫星1、卫星2和卫星3的通信拓扑结构为三角环形拓扑结构,通信时延为3 s。
考虑到卫星的磁矩有最大值的限制,自适应控制律的参数设置为:||fmi||∞≤1 N,α=0.01,ηi=0.000 01,ε=0.000 01,ki=0.01,λi=0.1,
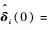
由于卫星0的电磁线圈具有更强的产生磁矩的能力,磁矩求解的目标是在小于最大磁矩的前提下,让卫星0的磁矩平均值大约为其他卫星的2.56倍,所以设置磁矩求解的有关参数为:Wm0=0.07I3×3,Wmi=0.31I3×3(i=1, 2, 3;I3×3为单位矩阵),Wdi=0.1I3×3,wti=103。
4.2 仿真结果 图 1给出了4颗卫星相对运动的三维立体图,可以看出4颗卫星均达到了期望的编队构型。图 2和图 3为卫星1、卫星2和卫星3相对卫星0的位置跟踪误差曲线和速度跟踪误差曲线,从图中可看出位置跟踪误差和速度跟踪误差一致收敛到零,并且位置跟踪稳态误差在10-3量级,而速度跟踪稳态误差在10-5量级。仿真结果表明,所设计的自适应协同控制律实现了对期望轨迹的准确跟踪,并且位置和速度收敛具有一定的同步性。
 |
| 图 1 编队卫星相对运动轨迹 Fig. 1 Relative motion trajectories of formation satellites |
| 图选项 |
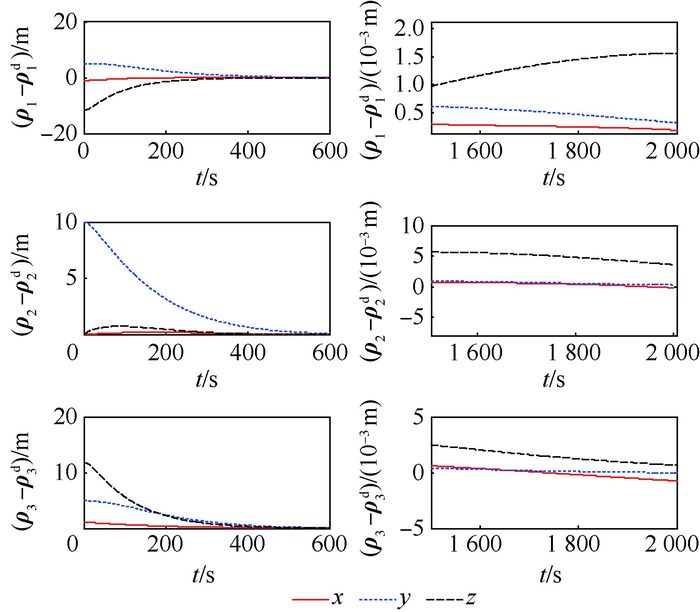 |
| 图 2 相对位置跟踪误差曲线(ηi>0) Fig. 2 Curves of relative position tracking errors (ηi > 0) |
| 图选项 |
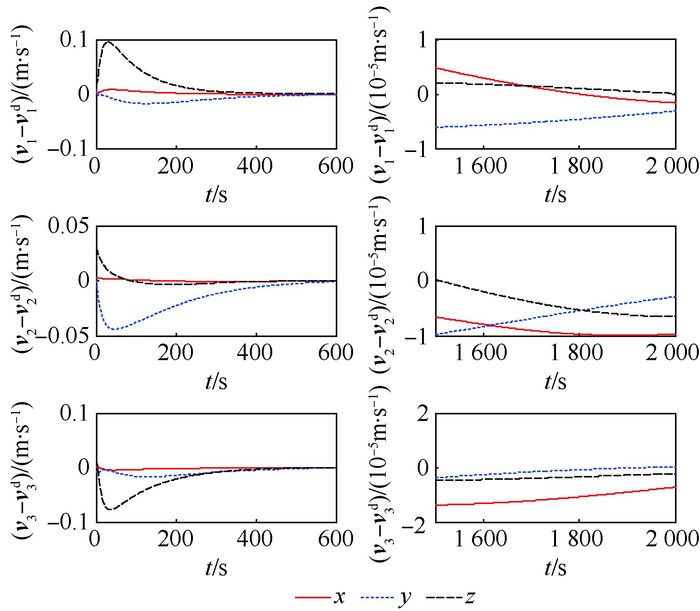 |
| 图 3 相对速度跟踪误差曲线 Fig. 3 Curves of relative velocity tracking errors |
| 图选项 |
图 4为4颗卫星的电磁控制力曲线。图 4中稳态时刻的电磁力不为零,主要由控制律式(19) 的第1项前馈补偿项和最后一项电磁力不确定补偿项引起。
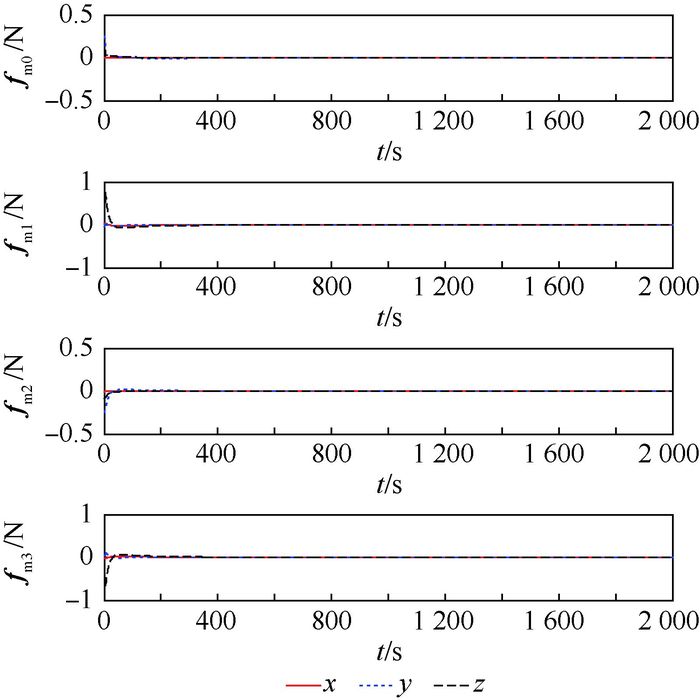 |
| 图 4 电磁控制力曲线 Fig. 4 Curves of electromagnetic control force |
| 图选项 |
图 5为4颗卫星所需的控制磁矩曲线。从图 5可看出,4颗卫星的磁矩均在最大磁矩的范围内,并且卫星0的磁矩大约为其他卫星的2倍,4颗卫星根据产生磁矩能力的不同实现了磁矩的合理分配。
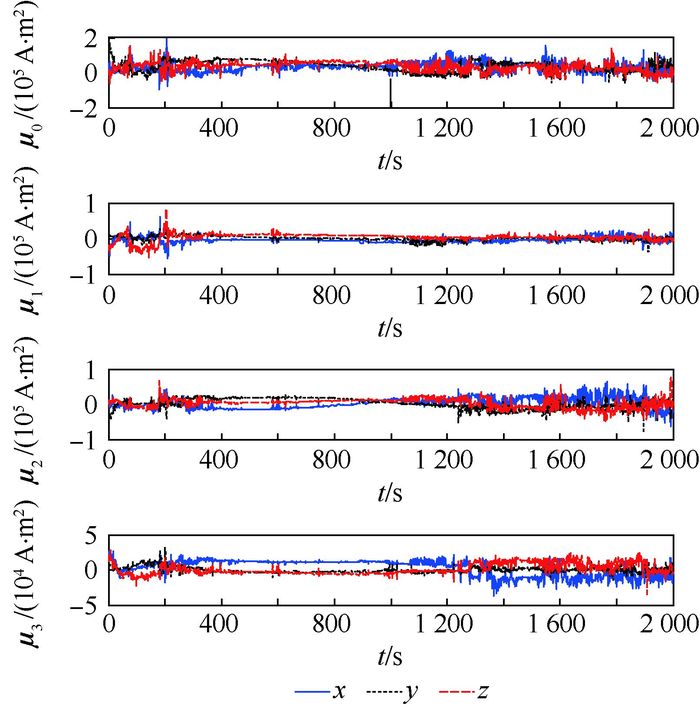 |
| 图 5 控制磁矩曲线 Fig. 5 Curves of control magnetic moments |
| 图选项 |
图 6为电磁力不确定性修正系数估计值变化曲线。从图 6可看出修正系数大小为10-4量级并且有界,这与第2节中证明的
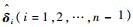
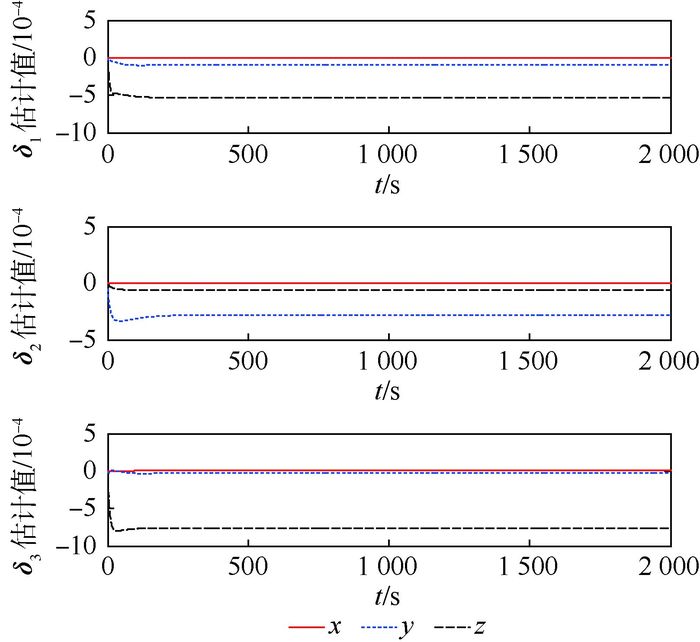 |
| 图 6 修正系数变化曲线 Fig. 6 Curves of adjustment coefficients |
| 图选项 |
为了说明本文所设计的控制律具有较高的控制精度,令式(19) 中ηi=0,可得位置跟踪误差曲线如图 7所示,可看出稳态误差较大。实际上增大ki也可提高精度,但会显著增加电磁力使磁矩超过最大值,而ηi对电磁力影响很小,可见式(19) 中第2项主要在稳态时刻起作用提高控制精度。
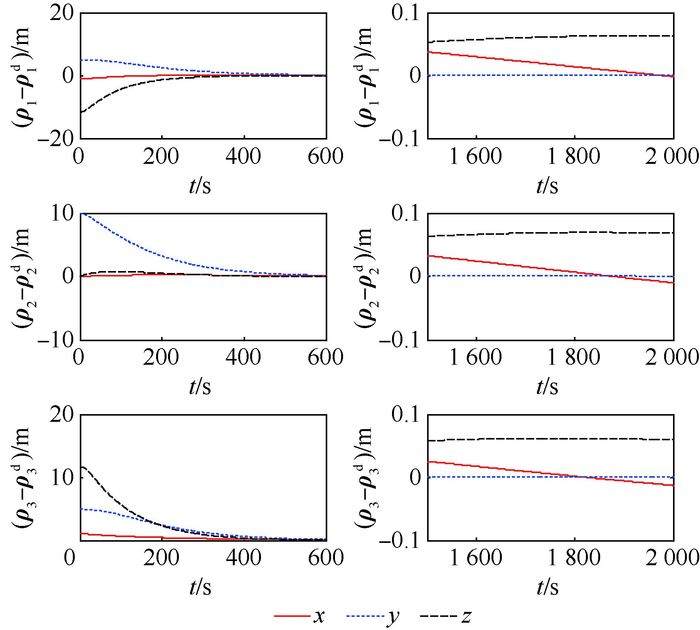 |
| 图 7 相对位置跟踪误差曲线(ηi=0) Fig. 7 Curves of relative position tracking errors (ηi=0) |
| 图选项 |
4.3 与人工势函数法的比较 人工势函数法是一种分布式控制方法,特点是可以在避免碰撞的前提下实现对期望轨迹的有效跟踪[8],但是避免碰撞也可以通过选择合理的标称轨迹来实现[7]。为了分析本文协同控制方法的有效性,在同样工况下利用人工势函数法进行仿真,并引入编队暂态构型维持误差σ作为评价指标,其计算公式为[21]
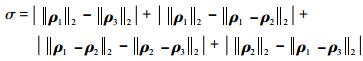 | (35) |
其中σ值越小,表明构型重构过程中暂态维持构型的能力越强,编队的协同性越强[21],同时计算σ平均值的倒数用来直观地表征暂态构型维持能力。当控制律式(19) 中不含协同项时,成员卫星间没有信息交互,是主从式编队控制。图 8为无协同项、有协同项和采用人工势函数法3种情况下的编队暂态构型维持误差曲线图。图中0.71, 1.52和4.17为σ平均值的倒数。从图 8可看出,初始阶段有协同项时反而暂态构型维持误差最大,这是由通信延迟造成的。经过多次仿真发现,当通信时延减少时,有协同项情况下的暂态构型维持误差可逐渐减小,可见通信时延对编队的协同控制造成了一定影响。但从整体来看,有协同控制项时电磁航天器编队的协同性获得了明显提高,相比人工势函数法,暂态构型维持能力提高了4.9倍,与无协同项的主从式控制相比,稳态时刻的暂态构型维持能力也提高了近1倍。人工势函数法稳态时刻的暂态构型维持误差较大,且变化周期大约为1/4轨道周期,这是由于人工势函数法有避免碰撞项的存在且采用的是近似的C-W方程[18]。
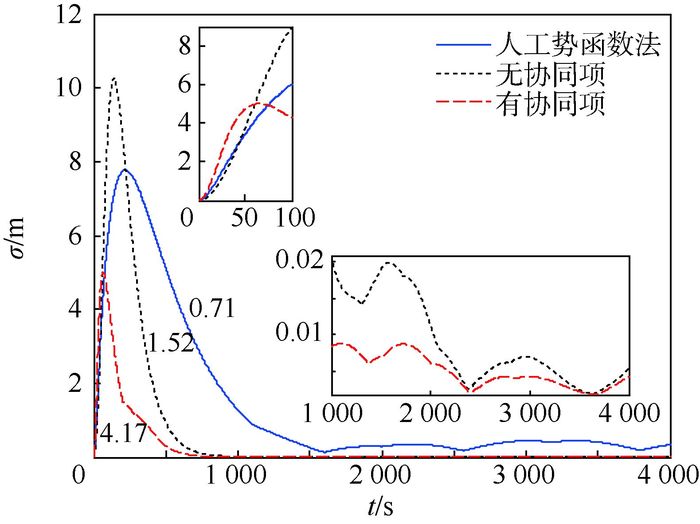 |
| 图 8 编队暂态构型维持误差曲线 Fig. 8 Curves of formation instantaneous configuration position keeping error |
| 图选项 |
通过仿真说明了本文所设计的自适应协同控制器在实现电磁航天器编队对期望轨迹准确跟踪的同时能更好地保持编队构型的不变性。进一步仿真发现,协同控制项也可提高电磁编队的稳态跟踪精度,这是由于编队成员之间有信息交互能使控制精度更高。
5 结论 本文基于一致性理论提出了电磁航天器编队的协同控制方法,可得出以下结论:
1) 针对n颗电磁航天器编队飞行的协同控制问题,在考虑了电磁力计算模型不确定性和成员卫星信息交互的情况下给出的自适应协同控制器可以有效地实现电磁航天器编队的协同控制。该控制器不仅具有较高的位置跟踪精度,而且相比其他主从式控制方法,可使编队的协同性获得明显提高。
2) 给出的磁矩求解方法,充分考虑了成员卫星的差异性和工程应用的限制,能够根据卫星的能力实现磁矩的合理分配,为电磁航天器编队资源的高效利用提供了一种有效途径。
本文所提出的电磁航天器编队自适应协同控制方法可有助于航天器利用电磁力完成空间干涉仪、合成孔径雷达以及交会对接等协同性要求较高的空间任务,并且在一定程度上通过提高编队的协同性也可减小电磁编队成员卫星间碰撞的概率。
参考文献
| [1] | 张博, 罗建军, 袁建平. 一种基于信息一致性的卫星编队协同控制策略[J].航空学报, 2010, 31(5): 1004–1013. ZHANG B, LUO J J, YUAN J P. A satellite formation cooperative control strategy based on information consensus[J].Acta Aeronautica et Astronautic Sinica, 2010, 31(5): 1004–1013.(in Chinese) |
| [2] | 王龙, 杨乐平, 许军校. 电磁编队飞行与电磁交会对接关键技术及进展[J].装备指挥技术学院学报, 2009, 20(1): 74–78. WANG L, YANG L P, XU J X. The key technology and development of electromagnetic formation flight and electromagnetic rendezvous docking[J].Journal of Academy of Equipment Command & Technology, 2009, 20(1): 74–78.(in Chinese) |
| [3] | KONG E M C, KWON D W, SCHWEIGHART S A, et al. Electromagnetic formation flight for multisatellite arrays[J].Journal of Spacecraft and Rockets, 2004, 41(4): 659–666.DOI:10.2514/1.2172 |
| [4] | MILLER D W, SEDWICK R J.Electromagnetic formation flight phase I report[R].Boston:Massachusetts Institute of Technology, 2003. |
| [5] | AHSUN U, MILLER D W, RAMIREZ J L. Control of electromagnetic satellite formations in near-earth orbits[J].Journal of Guidence, Control and Dynamics, 2010, 33(6): 1883–1891.DOI:10.2514/1.47637 |
| [6] | ELIAS L M.Dynamics of multi-body space interferometers including reaction wheel gyroscopic stiffening effects:Structurally connected and electromagnetic formation flying architectures[D].Boston:Massachusetts Institute of Technology, 2004. |
| [7] | AHSUN U.Dynamics and control of electromagnetic satellite formations[D].Boston:Massachusetts Institute of Technology, 2007. |
| [8] | 苏建敏, 董云峰. 利用人工势函数法的卫星电磁编队控制[J].北京航空航天大学学报, 2012, 38(2): 213–217. SU J M, DONG Y F. Artificial potential function method for satellite electromagnetic formation control[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2): 213–217.(in Chinese) |
| [9] | 徐增文, 师鹏, 赵育善. 双电磁航天器编队构型保持自适应控制[J].北京航空航天大学学报, 2015, 41(12): 2302–2308. XU Z W, SHI P, ZHAO Y S. Adaptive control for two-spacecraft electromagnetic formation keeping[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(12): 2302–2308.(in Chinese) |
| [10] | 邵龙飞, 师鹏, 赵育善. 电磁航天器编队动力学建模与运动规划方法[J].北京航空航天大学学报, 2015, 41(4): 737–743. SHAO L F, SHI P, ZHAO Y S. Dynamics modeling and motion programming for electromagnetic formation flight[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(4): 737–743.(in Chinese) |
| [11] | SCHWEIGHART S A.Electromagnetic formation flight dipole solution planning[D].Boston:Massachusetts Institute of Technology, 2005. |
| [12] | 黄涣, 杨乐平, 朱彦伟, 等. 双星电磁编队的动力学平衡态稳定性与控制[J].国防科技大学学报, 2013, 35(3): 12–17. HUANG H, YANG L P, ZHU Y W, et al. Stability and control of dunamics equilibrium for two-spacecraft electromagnetic formation[J].Journal of National University of Defense Technology, 2013, 35(3): 12–17.(in Chinese) |
| [13] | 张保群, 宋申民, 陈兴林. 带时延和拓扑切换的编队卫星鲁棒协同控制[J].宇航学报, 2012, 33(7): 910–919. ZHANG B Q, SONG S M, CHEN X L. Robust coordinated control for formation flying satellites with time delays and switching topologies[J].Journal of Astronautics, 2012, 33(7): 910–919.(in Chinese) |
| [14] | 毕鹏, 罗建军, 张博. 一种基于一致性理论的航天器编队飞行协同控制方法[J].宇航学报, 2010, 31(1): 70–74. BI P, LUO J J, ZHANG B. Cooperate control algorithm for spacecraft formation flying based on consensus theory[J].Journal of Astronautics, 2010, 31(1): 70–74.(in Chinese) |
| [15] | 马广富, 梅杰. 多星系统相对轨道的自适应协同控制[J].控制理论与应用, 2011, 28(6): 781–787. MA G F, MEI J. Adaptive cooperative control for relative orbits of multi-satellite systems[J].Control Theory & Applications, 2011, 28(6): 781–787.(in Chinese) |
| [16] | 郑重, 宋申民. 考虑避免碰撞的编队卫星自适应协同控制[J].航空学报, 2013, 34(8): 1934–1943. ZHENG Z, SONG S M. Adaptive coordination control of satellites within formation considering collision avoidance[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1934–1943.(in Chinese) |
| [17] | SU J M, DONG Y F. Gathering the fractionated electromagnetic satellites cluster by simulating fish school[J].Aircraft Engineering and Aerospace Technology, 2012, 84(2): 115–119.DOI:10.1108/00022661211207938 |
| [18] | KRISTIANSEN R, NICKLASSON P J, GRAVDAHL J T.Formation modelling and 6DOF spacecraft coordination control[C]//Proceedings of the 2007 American Control Conference.Piscataway, NJ:IEEE Press, 2007:4690-4696. |
| [19] | KRSTIC M, KANELLAKOPOULOS I, KOKOTOVIC P. Nonlinear and adaptive control design[M].New York: John Wiley & Sons, Inc., 1995: 490-491. |
| [20] | 章仁伟. 卫星轨道姿态动力学与控制[M].北京: 北京航空航天大学出版社, 1998: 50-51. ZHANG R W. Orbit and attitude dynamics and control of satellite[M].Beijing: Beihang University Press, 1998: 50-51.(in Chinese) |
| [21] | ZHANG B Q, SONG S M. Decentralized coordinated control for multiple spacecraft formation maneuver[J].Acta Astronautica, 2012, 74: 79–97.DOI:10.1016/j.actaastro.2011.12.017 |
