上述方法均基于Lyapunov稳定性理论。在此基础上,文献[10-11]考虑系统无源性的特点,从能量角度出发设计姿态控制律,但无源性本身只能保证系统不存在干扰时的稳定性,而航天器在轨运动会受到空间中干扰力矩的作用,同时自身的转动惯量存在非对角元素等不确定性[2, 7, 12],从而使得基于无源性设计的控制律难以直接应用。
由Ortega等[13-14]提出的互连和阻尼分配无源控制(Interconnection and Damping Assignment Passivity-Based Control, IDA-PBC)方法结合了端口受控哈密顿(Port-Controlled Hamiltonian, PCH)系统和无源特性。由于具有物理意义直观和全局收敛特性等优点,IDA-PBC方法在机械系统[15]、电机系统[16]、船舶定位系统[17]、功率变换系统[18]等领域得到了广泛应用,是目前控制理论领域的研究热点[19-21],但IDA-PBC方法在航天器姿态领域的应用还比较少见。
IDA-PBC方法的基本思想是:将控制系统模型表示为PCH系统形式,利用PCH的互连结构矩阵和阻尼矩阵揭示出系统的内部能量交换和耗散关系,通过求解一组偏微分方程来使得闭环系统具有期望能量平衡关系的控制输入。与基于Lyapunov理论的设计方法相比,IDA-PBC方法的物理含义更加直观,与期望闭环系统对应的哈密顿函数可直接作为稳定性分析的Lyapunov函数,在这一点上两者是等同的;与单独基于无源性的控制方法相比,IDA-PBC通过设计阻尼矩阵,利用耗散能量的方式保证系统存在干扰时的输入-状态稳定性[22],这一点是前者难以做到的。航天器的姿态运动属于一类运动系统,本质上也遵循能量的物理定律,因此控制律设计同样可从能量的角度进行。
本文将IDA-PBC方法引入航天器的姿态控制,一方面,在IDA-PBC的框架下,将姿态控制模型表示为PCH形式,通过增加与姿态误差积分有关的状态来保证闭环系统的输入-状态稳定性;另一方面,考虑到执行器具有动态特性[23-24],利用反步法对控制指令进行补偿设计,结合指令滤波技术[25]避免了虚拟控制量高阶导数的计算,并从理论上证明了闭环系统一致最终有界。仿真结果表明,在不考虑执行器动态特性时,本文所提方法实现了存在干扰时的航天器姿态控制系统的输入-状态稳定性;在考虑执行器动态特性时,本文所提方法依旧能够保证姿态误差的收敛性,且控制性能要优于单独基于无源性的控制方法。
1 姿态控制模型建立 以四元数表示时,航天器的姿态运动方程可写为[3]
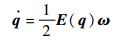 | (1) |
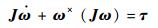 | (2) |
式中:q=[q0, q1, q2, q3]T为表示姿态的四元数;E为由q组成的4×3矩阵;ω=[ωx, ωy, ωz]T为体坐标系下的角速度;J为只包含对角元素的转动惯量阵;ω×为ω组成的反对称阵;τ=τF+τd为作用在航天器上的力矩,τF为执行器产生的控制力矩,τd为由转动惯量阵非对角元素、外部干扰等引起的等效干扰力矩[3, 7]。
E(q)的具体组成为
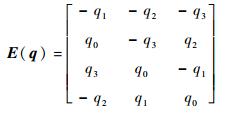 | (3) |
ω×的具体组成为
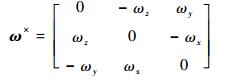 | (4) |
取状态变量x=[x1T, x2T]T,x1=Jω,x2=q,哈密顿函数取为H(x)=x1TJ-1x1/2,则式(1) 和式(2) 可写为如下PCH形式:
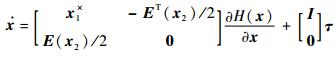 | (5) |
式中:x1×为x1组成的反对称阵;I和0分别为适当维数的单位矩阵和零矩阵。
控制的目的是使系统式(5) 在平衡点x0=[x1, 0T, x2, 0T]T处稳定,x1, 0=[0, 0, 0]T,x2, 0为目标姿态四元数。
给出如下合理假设。
假设1?τd是连续有界的,即存在未知常数Δd>0,使得║τd║≤Δd。
进一步,在推导控制器之前,给出以下定义和引理。
定义1[26]?对于系统
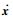
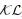
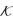
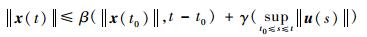 |
那么系统是输入-状态稳定的。
引理1[26]?对于系统
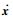
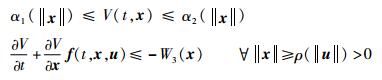 |
式中:α1和α2为
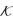
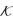
假设1、定义1和引理1中的范数可以是任何一种范数,在本文后续的分析中统一取为2-范数,即范数的表示符号为║·║2。
2 IDA-PBC姿态控制器设计 由于干扰力矩τd的存在,在利用IDA-PBC设计控制器时,将τF拆分成两部分,即τF=τFr+τFi,τFr为调节控制器,保证在τd为零时系统的渐近稳定;τFi为积分控制器,保证存在干扰时系统的输入-状态稳定性。
2.1 调节控制器设计 在τFr作用下,定义期望的闭环系统如下:
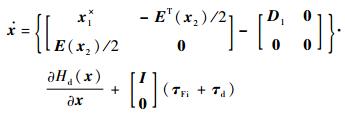 | (6) |
式中:D1为选取的正定矩阵,表示注入的阻尼项;Hd(x)为期望的哈密顿函数。为保证系统在τd为零时渐近稳定,Hd(x)应在x0处取极小值。选取Hd(x)=[x1TJ-1x1+(x2-x2, 0)TM(x2-x2, 0)]/2,M为正定矩阵,则匹配方程为
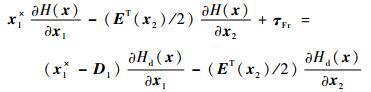 | (7) |
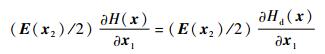 | (8) |
对于所选择的Hd(x),式(8) 恒成立,由式(7) 可解得
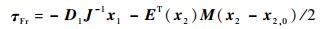 | (9) |
当τd为零时,取τFi为零,系统式(6) 的Lyapunov函数为V1=Hd(x),则有
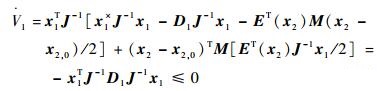 | (10) |
根据LaSalle不变原理,由
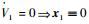
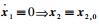
由上面的设计可以看出,由于只在角速度上增加了阻尼项,因此当干扰不为零时系统渐近稳定的结论不再成立。
2.2 积分控制器设计 在获得τFr的表达式后,进一步考虑干扰力矩τd的作用来设计τFi,并在系统式(6) 的基础上增加与姿态误差积分有关的状态。
取误差状态变量为e=[e1T, e2T, e3T]T,e2=x2-x2, 0,e1和e3为待设计的误差状态,其表达式在后面给出,期望的闭环系统为
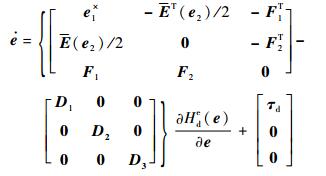 | (11) |
式中:E(e2)=E(e2+x2, 0)=E(x2);F1和F2为待设计的适当维数矩阵;D2和D3为选取的对称正定矩阵;Hde(e)=(e1TJ-1e1+e2TMe2+e3TNe3)/2为期望的哈密顿函数,N为正定矩阵,Hde(e)在原点处取极小值。
由e2=x2-x2, 0,结合式(11) 可得
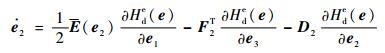 | (12) |
由式(6) 可得
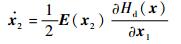 | (13) |
结合式(12) 和式(13) 可得
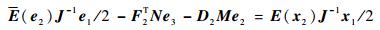 | (14) |
考虑到ET(e2)E(e2)=ET(x2)E(x2)=I,取F2=ET(e2),则由式(14) 可得
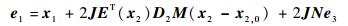 | (15) |
进一步,由式(11) 可得
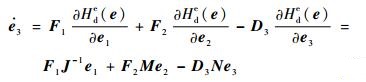 | (16) |
将式(15) 代入式(16) 并取F1=D3/2,可得
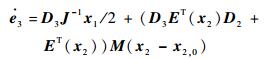 | (17) |
因此有
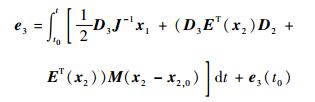 | (18) |
式中:e3(t0)为e3的初值。
对式(15) 求导可得
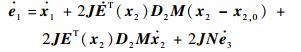 | (19) |
由式(11) 有
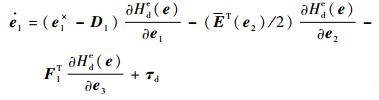 | (20) |
此外,由式(6) 有
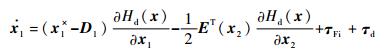 | (21) |
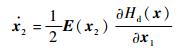 | (22) |
将式(17)、式(21) 和式(22) 代入式(19),可得
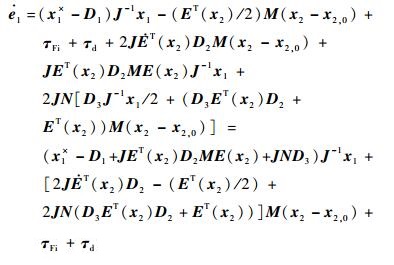 | (23) |
由式(20) 和式(23) 可得
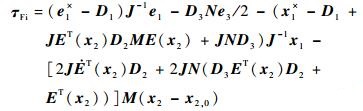 | (24) |
2.3 稳定性分析 对所设计的控制器τFr和τFi,有如下定理。
定理1?在τF=τFr+τFi作用下,闭环系统式(11) 是输入-状态稳定的;进一步,定义误差变量
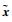
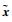
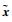
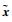
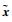
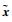
证明?根据2.1节和2.2节中的分析,e1和e3的表达式分别为式(15) 和式(18),e2=x2-x2, 0,则在τF=τFr+τFi作用下,e系统的状态方程为
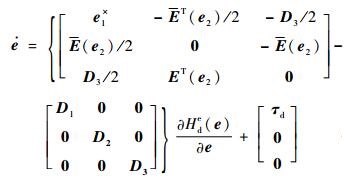 | (25) |
取Lyapunov函数为Ve=(e1TJ-1e1+e2TMe2+e3TNe3)/2,则有
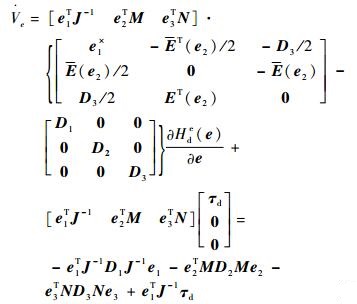 | (26) |
令λmin(·)和λmax(·)分别表示矩阵的最小和最大特征值,并设λ1m=λmin(D1),则有
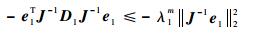 | (27) |
根据Young不等式[26],有
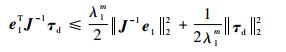 | (28) |
由式(27) 和式(28) 可得
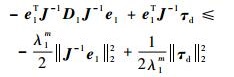 | (29) |
设λ2m=λmin(MD2M),λ3m=λmin(ND3N),则有
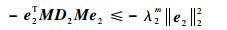 | (30) |
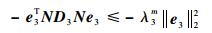 | (31) |
由于║J-1e1║22=║e1T(J-1)2e1║2≥λ4m║e1║22,λ4m=λmin[(J-1)2],因此
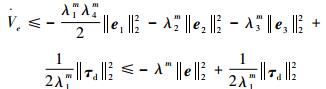 | (32) |
式中:λm=min{λ1mλ4m/2, λ2m, λ3m}。则对?e,τd和0<θ<1,当║e║2≥
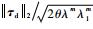
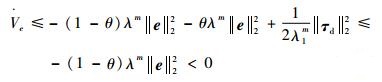 | (33) |
由于Ve正定且径向无界,根据引理1,系统式(11) 是输入-状态稳定的,即存在
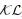
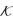
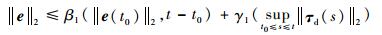 | (34) |
下面进一步证明在τF=τFr+τFi作用下
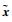
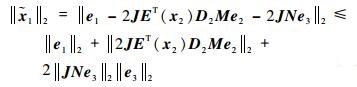 | (35) |
由式(3) 中E(x2)的具体组成可得
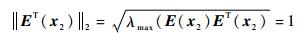 |
因此有
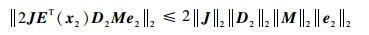 | (36) |
定义σ=max{1, 2║J║2║D2║2║M║2, 2║JN║2},则由式(35) 和式(36) 可得
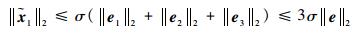 | (37) |
进一步,有
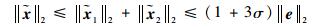 | (38) |
结合式(34) 和式(38) 可得
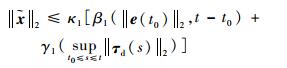 | (39) |
式中:κ1=1+3σ。
在式(18) 中,取e3(t0)=0,则有
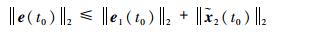 | (40) |
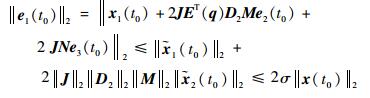 | (41) |
结合式(40) 和式(41) 可得
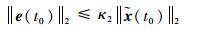 | (42) |
式中:κ2=1+2σ。
根据
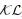
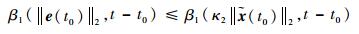 | (43) |
进一步,定义
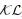
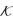
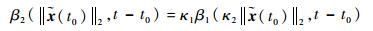 | (44) |
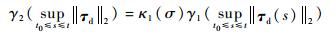 | (45) |
结合式(39)、式(43)~式(45) 可得
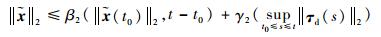 | (46) |
从而由定义1可知在τF=τFr+τFi作用下,
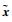
由定理1的证明过程可以看出,由e系统的稳定性可推出
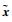
3 考虑执行器动态特性的控制设计 航天器的姿态控制是通过喷管、动量轮等执行器实现的,当执行器的运动并不是足够快时,忽略执行器的动态特性可能会降低姿态控制的性能,甚至使得系统不稳定[23-24]。本节在考虑执行器动态特性的前提下,重新设计控制指令。
设航天器的执行器具有如下二阶动态特性[23]:
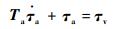 | (47) |
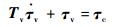 | (48) |
式中:τa为航天器实际产生的力矩;τv为中间变量;τc为控制器解算的指令力矩;Ta和Tv为正定矩阵,其对角元素和执行器时间常数有关。
取状态变量x4=τa,x5=
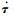
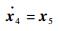 | (49) |
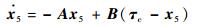 | (50) |
式中:A=(TaTv)-1(Ta+Tv);B=(TaTv)-1。
由式(9) 和式(24) 可获得使系统式(11) 输入-状态稳定所需要的控制力矩τF,由于执行器的二阶动态特性,为使得实际产生的力矩能够达到τF,需要进一步根据执行器的动态特性对指令力矩τc进行设计。
取误差变量η4=x4-τF,则有
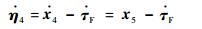 | (51) |
将x5看作虚拟控制输入,设计x5的指令为x5d=
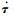
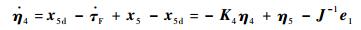 | (52) |
设计指令力矩τc为
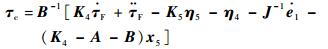 | (53) |
式中:K5为正定矩阵。
对式(53) 所设计的指令力矩,有以下定理。
定理2?对于系统式(11),当执行器具有式(47) 和式(48) 的二阶动态特性时,在指令力矩输入式(53) 作用下,闭环系统是输入-状态稳定的。
证明?采用式(53) 中的指令力矩作为输入时,整个(e, η4, η5)系统的动态方程为
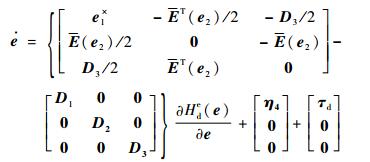 | (54) |
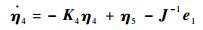 | (55) |
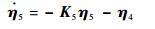 | (56) |
对于系统式(54)~式(56),取Lyapunov函数为V2=Ve+(η4Tη4+η5Tη5)/2,则有
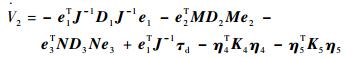 | (57) |
设λ5m=λmin(K4),λ6m=λmin(K5),则有
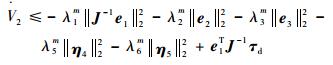 | (58) |
类似于定理1中的分析,有
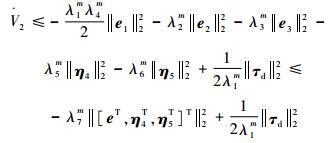 | (59) |
式中:λ7m=min{λ1mλ4m/2, λ2m, λ3m, λ5m, λ6m}。则对?[eT, η4T, η5T]T,τd和0<θ<1,当║[eT, η4T, η5T]T║2≥
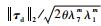
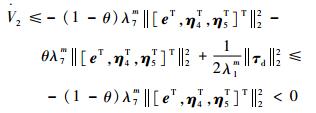 | (60) |
由于V2正定且径向无界,根据引理1,系统式(54)~式(56) 是输入-状态稳定的。证毕
由定理2可知,采用式(53) 设计指令力矩时,可以保证系统的输入-状态稳定性,但是需要计算τF的一阶和二阶导数,这会造成指令力矩表达式上的繁琐;同时τF导数中的高频分量可能会激发执行器的未建模动态特性[23];此外,τF表达式中包含误差项导数
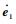
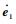
为此,进一步考虑对τF进行如下形式的指令滤波[25]:
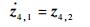 | (61) |
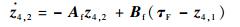 | (62) |
式中:z4, 1和z4, 2为滤波器状态;Af和Bf为滤波器参数,具体表达式为
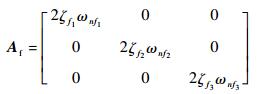 | (63) |
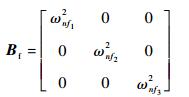 | (64) |
式中:ζfi(i=1, 2, 3)>0为阻尼比;ωnfi(i=1, 2, 3)>0为自然频率。
滤波器式(61) 和式(62) 的初始状态满足z4, 1(t0)=τF(t0),z4, 2(t0)=[0, 0, 0]T。
取误差变量η4=x4-z4, 1,则有
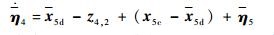 | (65) |
式中:x5d为虚拟控制指令,设计为x5d=-K4η4+z4, 2-J-1e1;η5=x5-x5c;x5c为x5d通过指令滤波器后的状态,即令z5, 1=x5c,z5, 2=
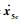
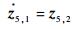 | (66) |
 | (67) |
式中:z5, 1(t0)=x5d(t0);z5, 2(t0)=[0, 0, 0]T。
设计指令力矩τc为
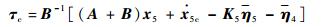 | (68) |
对式(68) 所设计的指令力矩,有以下定理。
定理3?对于系统式(11),当执行器具有式(47) 和式(48) 的二阶动态特性时,在指令力矩输入式(68) 作用下,闭环系统是一致最终有界的,且最终的上界可以通过控制参数进行调节。
证明?采用式(68) 中的指令力矩作为输入时,整个(e, η4, η5)系统的动态方程为
 | (69) |
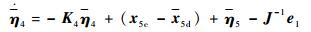 | (70) |
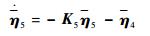 | (71) |
根据指令滤波器的性质[25],║z4, 1-τF║2和║x5c-x5d║2始终有界,且对给定的ζfi(i=1, 2, 3)>0,T>0,ε1>0和ε2>0,存在ωnfi(i=1, 2, 3)>0,使得当t>T时有
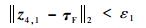 | (72) |
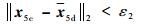 | (73) |
选取Lyapunov函数为
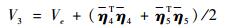 |
则有
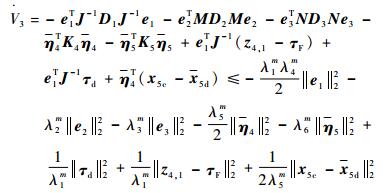 | (74) |
由假设1,║τd║2有界,结合║z4, 1-τF║2和║x5c-x5d║2的有界性可知,当0≤t≤T时V3有界,从而║e║2有界,e=[eT, η4T, η5T]T;当t>T时,由式(74) 有
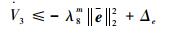 | (75) |
式中:λ8m=min{λ1mλ4m/2, λ2m, λ3m, λ5m/2, λ6m};Δe=Δd/λ1m+ε1/λ1m+ε2/(2λ5m)。
又由于α3║e║22≤V3≤α4║e║22,α3=min{λmin(J-1), λmin(M), λmin(N), 1/2},α4=max{λmax(J-1), λmax(M), λmax(N), 1/2},因此,系统式(67)、式(71) 和式(72) 一致最终有界,且当t>T时有
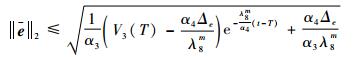 | (76) |
由式(76) 可知,通过选择合适的矩阵D1、D2、D3和K4,可使得λ8m足够大,从而使得║e║2的上界足够小,即保证姿态控制误差足够小。证毕
注1?在第3节的指令力矩设计过程中使用了2个指令滤波器,作用分别是对τF的导数和虚拟控制量x5d的导数进行近似。指令滤波器本质上是一个二阶线性系统,目的是使输出尽可能好地跟踪输入,从系统阶跃响应的角度看,指令滤波器的参数,即阻尼比ζfi(i=1, 2, 3)>0和自然频率ωnfi(i=1, 2, 3)>0的选取需要在超调量、调节时间、稳态误差等指标之间取一个折中。阻尼比通常可取为0.707[27-29],即工程上认为的最佳阻尼比。
注2?从能量的角度看,Lyapunov函数可以看作是系统的广义能量,M、N 2个矩阵的最小特征值越大,则表示系统的能量越大,而稳定本质上是需要衰减系统的能量到极小值,因此需要的控制增益越大;D1、D2、D3 3个矩阵的最小特征值越大,表示期望衰减系统能量的速率越大,则需要的控制增益也越大。因此,M、N 2个矩阵决定了系统能量的大小,D1、D2、D3 3个矩阵决定了能量衰减的速率。
注3?指令力矩τc包含了K4和K52个增益矩阵,K4决定了虚拟控制指令x5d的大小,而第2个滤波器的输出z5, 1需要跟踪x5d,因此K4的最小特征值越大,则滤波器跟踪的难度也越大,需要的自然频率也越大;K5包含在反步法最后一步设计的误差项中,与τc线性相关。结合注1和注2来看,控制器增益和滤波器参数需要根据系统响应综合选取。
4 仿真验证 为验证本文控制器设计的效果,分别在不考虑和考虑执行器动态特性的前提下进行2组对比仿真。采用文献[10]中的模型和控制目标参数,并以文献[10]作为参照,在考虑干扰力矩的前提下对航天器姿态进行控制。
按照偏航—俯仰—滚转的旋转顺序,航天器初始姿态为:滚转角15°,俯仰角30°,偏航角-30°,对应的四元数为[0.812 5, 0.237 5, 0.159 2, -0.508 1]T,初始角速度为[0.002, -0.002, 0.002]Trad/s;目标姿态为:滚转角-15°,俯仰角0°,偏航角0°,对应的四元数为[0.991 4, -0.130 5, 0, 0]T。
航天器的转动惯量阵为J=diag{14, 13.5, 0.75}kg·m2,干扰力矩设为
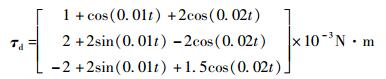 |
4.1 不考虑执行器动态特性 不考虑执行器的动态特性,希望系统能量衰减部分没有振荡,即阻尼矩阵的特征值虚部为0,因此阻尼矩阵取为对角阵形式,设计阻尼阵为D1=0.5I,D2=0.5I,D3=0.2I,同时希望系统的能量组成尽量减少状态之间的耦合,则M和N也设计为对角阵形式,取M=0.2I,N=0.3I。采用控制力矩为τF=τFr+τFi,τFr和τFi表达式分别为式(9) 和式(24),仿真时间设为300 s,得到仿真结果如图 1~图 3所示。
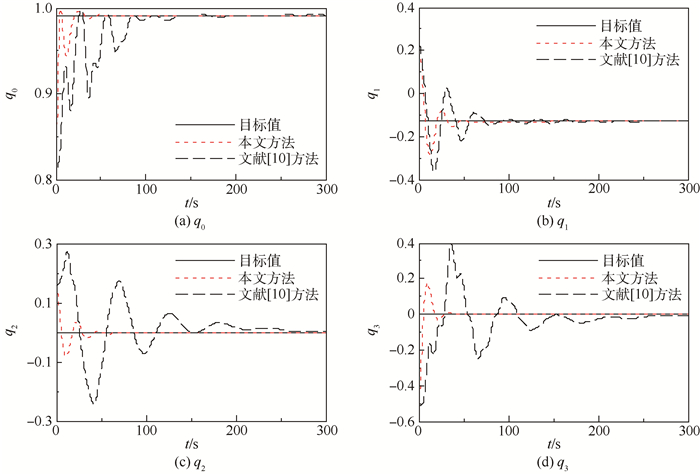 |
| 图 1 四元数变化曲线(不考虑执行器动态特性) Fig. 1 Variation curves of quaternion (without consideration of actuator dynamics) |
| 图选项 |
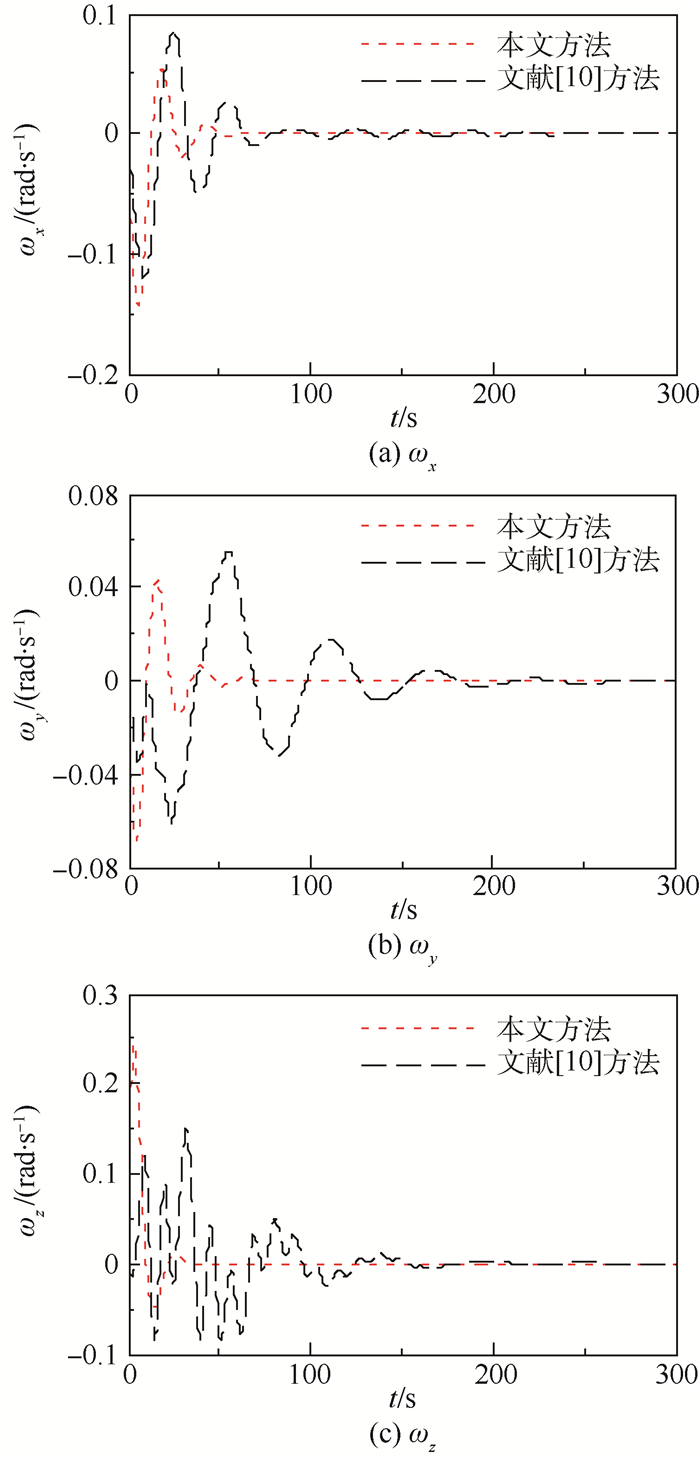 |
| 图 2 角速度变化曲线(不考虑执行器动态特性) Fig. 2 Variation curves of angular rate(without consideration of actuator dynamics) |
| 图选项 |
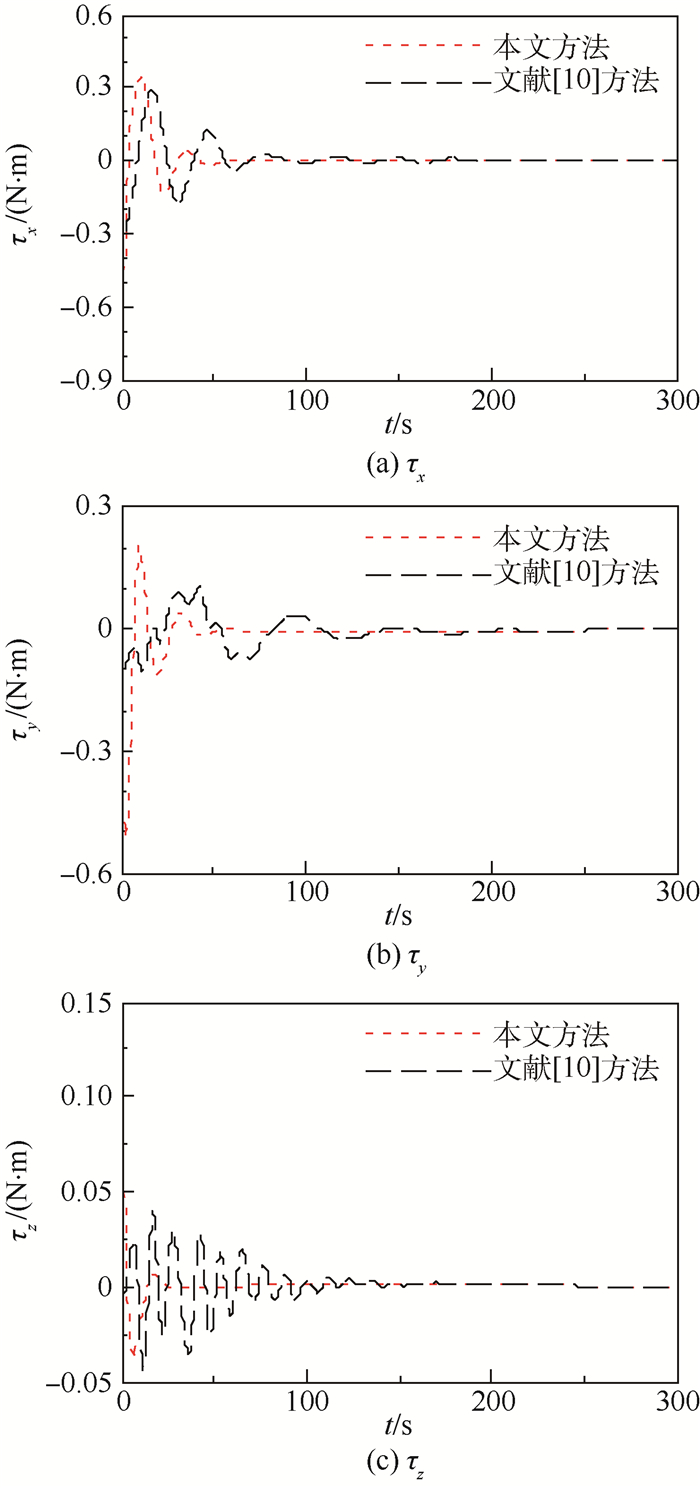 |
| 图 3 姿态控制力矩变化曲线(不考虑执行器动态特性) Fig. 3 Variation curves of attitude control torque(without consideration of actuator dynamics) |
| 图选项 |
图 1给出了姿态四元数的变化曲线。从四元数变化曲线上看,2种方法均能克服干扰力矩,但与文献[10]方法相比,本文方法能够使得航天器的姿态更快地收敛到目标值。
图 2给出了3个方向的角速度变化曲线。从对比曲线可以看出,本文方法能够使得航天器的角速度更快地收敛到原点。
图 3给出了3个方向的姿态控制力矩的变化曲线。从变化曲线可以看出,2种方法所需的控制力矩量级相差不大。因此,综合前面四元数和角速度的变化曲线来看,本文方法的控制性能要好于文献[10]方法。
4.2 考虑执行器动态特性 进一步考虑执行器的动态特性,根据文献[23],设定Ta=5I,Tv=3I;D1、D2、D3、M和N的取值与4.1节中相同;指令滤波器参数中,ζfi=0.707,ωnfi=5,i=1, 2, 3;希望尽量减少控制器3个通道的耦合,因此K4和K5也设计为对角阵形式,取K4=2I,K5=3I。采用指令力矩为式(68),仿真时间设为100 s,得到仿真结果如图 4和图 5所示。
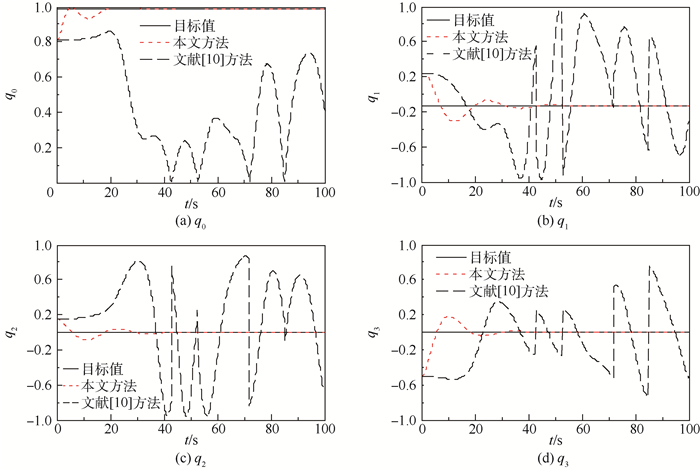 |
| 图 4 四元数变化曲线(考虑执行器动态特性) Fig. 4 Variation curves of quaternion(with consideration of actuator dynamics) |
| 图选项 |
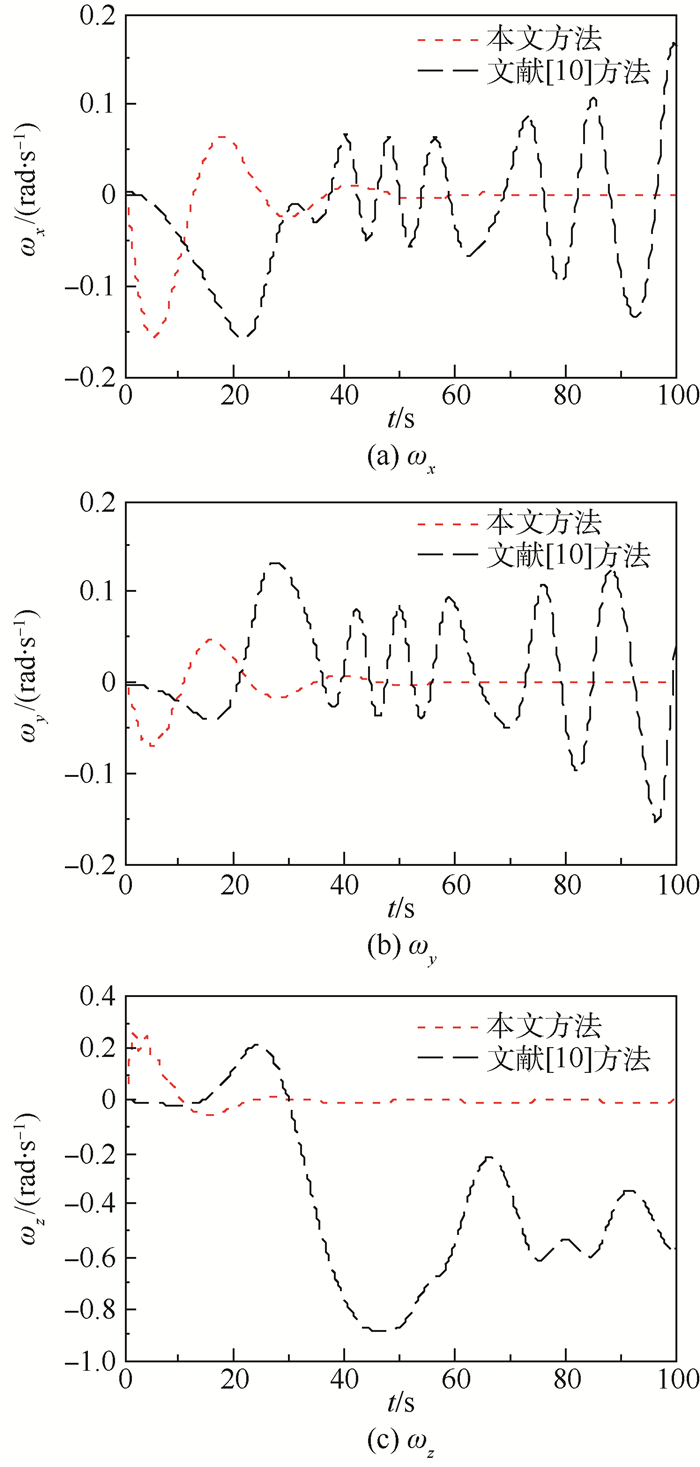 |
| 图 5 角速度变化曲线(考虑执行器动态特性) Fig. 5 Variation curves of angular rate(with consideration of actuator dynamics) |
| 图选项 |
从图 4中四元数变化曲线和图 5中角速度变化曲线可以看出,文献[10]方法由于未考虑执行器的动态特性,使得姿态出现不稳定的情况,无法收敛到目标值,而在本文方法的控制作用下,姿态能够收敛到目标值,且角速度收敛于原点。
综合4.1节和4.2节中的仿真结果来看,本文方法比单独基于无源性的控制方法具有更好的控制性能。
5 结论 1) IDA-PBC方法通过耗散能量来保证系统的稳定性,通过增加与姿态误差积分有关的状态,实现了闭环系统的输入-状态稳定性,期望的哈密顿函数可直接作为Lyapunov函数进行稳定性分析。
2) 考虑执行器动态特性时,结合反步法和指令滤波技术对控制指令进行补偿设计,可以保证闭环系统一致最终有界,且最终的上界对控制器增益和指令滤波器的阻尼及自然频率选取提出了要求。
3) 仿真结果表明,闭环系统能够实现对最终目标姿态的良好跟踪,且控制性能好于单独基于无源性的控制方法,验证了本文所提方法的有效性。
参考文献
| [1] | LEE T. Global exponential attitude tracking controls on SO3[J].IEEE Transactions on Automatic Control, 2015, 60(10): 2837–2842.DOI:10.1109/TAC.2015.2407452 |
| [2] | DE ANGELIS E L, GIULIETTI F, DE RUITER A H J, et al. Spacecraft attitude control using magnetic and mechanical actuation[J].Journal of Guidance, Control, and Dynamics, 2016, 39(3): 564–573.DOI:10.2514/1.G000957 |
| [3] | RODRIQUEZ-VAZQUEZ A L, MARTIN-PRATS M A, BERNELLI-ZAZZERA F. Spacecraft magnetic attitude control using approximating sequence Riccati equations[J].IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 3374–3385.DOI:10.1109/TAES.2015.130478 |
| [4] | ALI I, RADICE G, KIM J. Backstepping control design with actuator torque bound for spacecraft attitude maneuver[J].Journal of Guidance, Control, and Dynamics, 2010, 33(1): 254–259.DOI:10.2514/1.45541 |
| [5] | ZHANG H, FANG J. Robust backstepping control for agile satellite using double-gimbal variable-speed control moment gyroscope[J].Journal of Guidance, Control, and Dynamics, 2013, 36(5): 1356–1363.DOI:10.2514/1.59327 |
| [6] | ZHU Z, XIA Y Q, FU M Y. Adaptive sliding mode control for attitude stabilization with actuator saturation[J].IEEE Transactions on Industrial Electronics, 2011, 58(10): 4898–4907.DOI:10.1109/TIE.2011.2107719 |
| [7] | LU K F, XIA Y Q, ZHU Z, et al. Sliding mode attitude tracking of rigid spacecraft with disturbances[J].Journal of the Franklin Institute, 2012, 349(2): 413–440.DOI:10.1016/j.jfranklin.2011.07.019 |
| [8] | WANG X K, YU C B. Unit dual quaternion-based feedback linearization tracking problem for attitude and position dynamics[J].Systems & Control Letters, 2013, 62(3): 225–233. |
| [9] | BAJODAH A H. Asymptotic generalised dynamic inversion attitude control[J].IET Control Theory & Applications, 2010, 4(5): 827–840. |
| [10] | FORBES J R. Passivity-based attitude control on the special orthogonal group of rigid-body rotations[J].Journal of Guidance, Control, and Dynamics, 2013, 36(6): 1596–1605.DOI:10.2514/1.59270 |
| [11] | WANG H L, XIE Y C. Passivity based attitude control of rigid bodies[J].Asian Journal of Control, 2014, 16(3): 802–817.DOI:10.1002/asjc.2014.16.issue-3 |
| [12] | PARK Y. Robust and optimal attitude control of spacecraft with disturbances[J].International Journal of Systems Science, 2015, 46(7): 1222–1233.DOI:10.1080/00207721.2013.815824 |
| [13] | ORTEGA R, VAN DER SCHAFT A, MASCHKE B, et al. Interconnection and damping assignment passivity-based control of port-controlled Hamiltonian systems[J].Automatica, 2002, 38(4): 585–596.DOI:10.1016/S0005-1098(01)00278-3 |
| [14] | JELTSEMA D, ORTEGA R, SCHERPEN J M A. An energy-balancing perspective of interconnection and damping assignment control of nonlinear systems[J].Automatica, 2004, 40(9): 1643–1646.DOI:10.1016/j.automatica.2004.04.007 |
| [15] | ACOSTA J A, ORTEGA R, ASTOLFI A, et al. Interconnection and damping assignment passivity-based control of mechanical systems with underactuation degree one[J].IEEE Transactions on Automatic Control, 2005, 50(12): 1936–1955.DOI:10.1109/TAC.2005.860292 |
| [16] | BATLLE C, DòRIA-CEREZO A, ESPINOSA-PEREZ G, et al. Simultaneous interconnection and damping assignment passivity-based control:The induction machine case study[J].International Journal of Control, 2009, 82(2): 241–255.DOI:10.1080/00207170802050817 |
| [17] | DONAIRE A, PETER T. Dynamic positioning of marine craft using a port-Hamiltonian framework[J].Automatica, 2012, 48(5): 851–856.DOI:10.1016/j.automatica.2012.02.022 |
| [18] | ZENG J W, ZHANG Z, QIAO W. An interconnection and damping assignment passivity-based controller for a DC-DC boost converter with a constant power load[J].IEEE Transactions on Industry Applications, 2014, 50(4): 2314–2322.DOI:10.1109/TIA.2013.2290872 |
| [19] | CRASTA N, ORTEGA R, PILLAI H K. On the matching equations of energy shaping controllers for mechanical systems[J].International Journal of Control, 2015, 88(9): 1757–1765.DOI:10.1080/00207179.2015.1016453 |
| [20] | AOKI T, YAMASHITA Y, TSUBAKINO D. Vibration suppression for mass-spring-damper systems with a tuned mass damper using interconnection and damping assignment passivity-based control[J].International Journal of Robust and Nonlinear Control, 2016, 26(2): 235–251.DOI:10.1002/rnc.3307 |
| [21] | NUNNA K, SASSANO M, ASTOLFI A. Constructive interconnection and damping assignment for port-controlled Hamiltonian systems[J].IEEE Transactions on Automatic Control, 2015, 60(9): 2350–2361.DOI:10.1109/TAC.2015.2400663 |
| [22] | ROMERO J G, DONAIRE A, ORTEGA R. Robust energy shaping control of mechanical systems[J].Systems & Control Letters, 2013, 62(9): 770–780. |
| [23] | KRISTIANSEN R, HAGEN D. Modelling of actuator dynamics for spacecraft attitude control[J].Journal of Guidance, Control, and Dynamics, 2009, 32(3): 1022–1025.DOI:10.2514/1.42574 |
| [24] | HU Q L, XIAO B, WANG D W, et al. Attitude control of spacecraft with actuator uncertainty[J].Journal of Guidance, Control, and Dynamics, 2013, 36(6): 1771–1776.DOI:10.2514/1.58624 |
| [25] | DONG W, FARRELL J A, POLYCARPOU M M, et al. Command filtered adaptive backstepping[J].IEEE Transactions on Control Systems Technology, 2012, 20(3): 566–580.DOI:10.1109/TCST.2011.2121907 |
| [26] | KHALIL H K. 非线性系统[M]. 朱义胜, 董辉, 李作洲, 等译. 3版. 北京: 电子工业出版社, 2011: 96-118. KHALIL H K.Nonlinear systems[M].ZHU Y S, DONG H, LI Z Z, et al, translated.3rd ed.Beijing:Publishing House of Electronics Industry, 2011:96-118(in Chinese). |
| [27] | ZOU Y, ZHENG Z. A robust adaptive RBFNN augmenting backstepping control approach for a model-scaled helicopter[J].IEEE Transactions on Control Systems Technology, 2015, 23(6): 2344–2352.DOI:10.1109/TCST.2015.2396851 |
| [28] | SUN L, ZUO Z. Nonlinear adaptive trajectory tracking control for a quad-rotor with parametric uncertainty[J].Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2015, 229(9): 1709–1721.DOI:10.1177/0954410014558692 |
| [29] | ZHU B, WANG Q, HUO W. Longitudinal-lateral velocity control design and implementation for a model-scaled unmanned helicopter[J].Nonlinear Dynamics, 2014, 76(2): 1579–1589.DOI:10.1007/s11071-013-1230-z |
