相比在地面使用的固定基座机械臂,空间机器人的特点是机械臂安装在一个可在空间中运动的平台(航天器)上,且整个系统处在微重力环境下。微重力环境使得机械臂不需要支撑其重量,而可动的平台则为系统带来了复杂的运动学、动力学耦合,这一耦合是空间机器人运动学、动力学的一个特点。平台对机械臂的扰动使得机械臂的轨迹跟踪出现误差;机械臂对平台的扰动则可能使其上搭载的天线、太阳能帆板等装置不能正常工作,同时很可能引起姿态控制系统燃料的消耗增加,降低空间机器人使用寿命。
为了降低机械臂与平台间的相互扰动,Vafa[3]和Torres[4]等提出扰动图和增强扰动图,在机械臂关节空间中计算出各点处扰动最大和最小的运动方向,指导设计对平台扰动较小的轨迹。Yoshida[5]和Nenchev[6]等利用冗余机械臂的冗余自由度规划对平台无扰动的轨迹。最近,Peck等[7-8]在Osuka等[9]提出的力矩单元机械臂(torque-unit manipulator)概念的基础上,使用Hokamoto[10]提出的控制力矩陀螺(Control Moment Gyroscopes,CMGs)驱动力矩单元机械臂以降低机械臂运动对平台姿态的扰动。这一方法的基本原理在于使用CMGs代替关节电机作为执行机构,使得各臂杆、平台不受到执行机构的反作用力矩,从而减小机械臂与平台间的相互扰动。Carpenter和Peck[11]研究了这一系统中平台受机械臂扰动的情况,指出使用CMGs减小了机械臂对平台的扰动,并在文献[12-13]中讨论了其能量最优控制问题。Brown等[14-15]则讨论了这一系统的设计方法和能量学问题。贾英宏[16]和赵楠[17]等将这一概念扩展至使用球铰链和任意构型CMGs的空间机器人系统,并对其设计了运动控制器。
但是,上述使用CMGs驱动空间机器人的研究仅考虑了CMGs的力矩输出特性,并没有考虑CMGs的角动量容量,这可能导致CMGs在驱动机械臂运动的过程中出现角动量饱和。各臂杆CMGs的容量决定了系统的运动能力,是性能的上限。当某些臂杆上的CMGs饱和而其他臂杆上的CMGs未饱和时,尽管未饱和的CMGs仍具有控制能力,但是由于饱和的CMGs已不能输出力矩,此时机械臂不能完成预定控制任务,这会使得系统的运动能力大为降低。从理论上分析,当机械臂存在冗余自由度时,可以通过机械臂的空转尽量平均地使用各臂CMGs的角动量,从而减少某些臂杆先行饱和的可能性,充分地发挥系统的性能。基于这一思想,本文提出一种利用逆动力学和加速度分解技术的控制方法,同时达到工作空间轨迹跟踪和各臂CMGs角动量平衡使用的目标,在保证系统完成任务的同时避免某些CMGs角动量先行饱和。
1 系统描述 CMGs驱动的空间机器人系统的示意图如图 1所示,系统由空间平台和一部串联机械臂构成。为突出主要问题,这里采用文献[11]的假设条件,即假设空间平台在惯性空间中的位置、姿态固定;在实际中,这意味着对平台的位置、姿态进行主动控制并且较好地补偿了机械臂运动造成的干扰。机械臂与平台间使用旋转铰链连接,机械臂各臂杆间也采用同样的连接方式,每个铰链提供一个旋转自由度。铰链数目多于任务变量数时,机械臂系统为冗余系统。在每节机械臂上安装有一对Ⅴ构型的CMGs,其结构如图 2所示。Ⅴ构型CMGs中2个CMG的框架轴平行,均垂直于所在机械臂的旋转轴,通过同步机构使这2个CMG的框架角?始终相同,使得Ⅴ构型CMGs的总角动量始终沿机械臂旋转铰链的转轴方向。
 |
| 图 2 Ⅴ构型控制力矩陀螺示意图 Fig. 2 Schematic diagram of CMGs in scissored-pair configuration |
| 图选项 |
用B0表示平台,机械臂各臂杆由平台向外依次用B1, B2, …, Bn表示,其中n为机械臂臂杆数目,也是系统的自由度数。
一般地,机械臂系统在三维空间中运动,为描述其运动,在各旋转铰处引入一对直角参考系,如图 1所示(仅以第4节臂杆为例)。其中:qj为Fj相对Fjref沿转轴旋转的角度,Fjref固连于Bj的内接臂杆Bj-1上,Fj固连Bj上;这2个参考系的原点重合,在旋转轴上;某个同名轴(x/y/z)始终重合,沿旋转铰链转轴方向。臂杆Bj在Bj-1上的安装参数可以用参考系Fjref相对参考系Fj-1的安装位置lj, ref和由Fj-1到Fjref的坐标转换矩阵Aref(j), j-1完全描述。
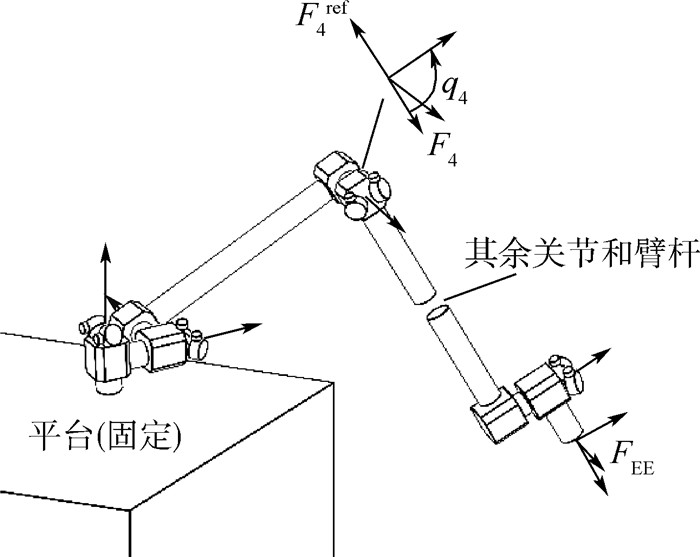 |
| 图 1 控制力矩陀螺驱动的冗余机械臂示意图 Fig. 1 Schematic diagram of redundant manipulator with CMGs for joint actuation |
| 图选项 |
最后一节机械臂Bn上安装有末端作用器,为了描述其位置、指向,在其上固连一个直角参考系FEE,这一参考系的原点在惯性空间中的位置和参考系相对惯性空间的指向一般是机械臂工作空间控制中的被控量。
2 运动学与动力学 取系统的广义位移为q=[q1 q2 … qn]T,广义速度为
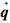
当机械臂使用关节电机的力矩进行控制时,其动力学模型为[18]
 | (1) |
式中:M为与构型相关的广义质量矩阵;
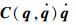
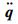
由于空间机器人的机械臂处于失重环境,式(1) 中没有考虑重力的影响。另外,为了突出空间机械臂的主要控制问题,在本文中不考虑机械臂关节摩擦、间隙的影响。
使用文献[19]中的Kane方法,可以导出使用Ⅴ构型CMGs时系统的动力学方程。当不考虑CMGs框架运动带来的惯量变化,并且以每组Ⅴ构型CMGs角动量的变化率为系统输入时,系统的动力学方程如下:
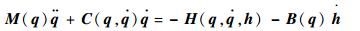 | (2) |
方程式(2) 左侧项与方程式(1) 中左侧项相同,而右侧项则反映了用CMGs作执行机构时系统的特点。其中
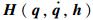
方程式(2) 左侧项(即方程式(1) 左侧项)的结构已经得到了较多研究,在数学仿真和控制算法中,可以使用文献[20]中的方法编写计算式(2) 左侧各项的通用程序。下面仅介绍式(2) 右侧项公式。右侧项实际上是CMGs对机械臂作用力对应的广义主动力,其表达式可以从CMGs对机械臂的作用力和刚体上力系的广义主动力的公式推导得到。若不考虑CMGs框架运动带来的惯量变化,CMGs对机械臂的作用为一力偶,力偶的大小与方向由CMGs角动量相对惯性空间的变化率得到。
因CMGs为Ⅴ构型,安装于Bj的一组CMGs的总角动量沿转轴方向,其在Fj系内的投影为
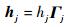 | (3) |
式中:Γj为转轴方向单位矢量的投影,仅对应转轴的分量为1;hj为Bj上Ⅴ构型CMGs的总角动量。CMGs作用于Bj的力偶为
 | (4) |
式中:ωj为Fj的角速度列阵,ωj×为ωj的叉乘反对称阵。ωj可由各关节角速度的贡献之和得到
 | (5) |
式中:Aj, i为Fi系到Fj系的坐标转换矩阵。
系统的广义主动力可写为[19]
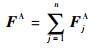 | (6) |
式中:FjA为各刚体臂杆上作用的主动力系对系统广义主动力的贡献。依文献[20]和式(5) 可定义参考系Fj的偏角速度矩阵pωj为
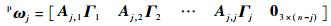 | (7) |
在主动力为力偶时,有[19]
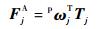 | (8) |
将式(4) 代入式(8) 得到Bj上Ⅴ构型CMGs对系统广义主动力的贡献为
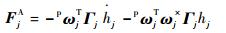 | (9) |
将式(9) 代入式(6) 得到Ⅴ构型CMGs驱动机械臂系统的广义主动力为
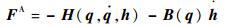 | (10) |
式中:
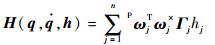 | (11) |
 | (12) |
式(5)、式(7)、式(11)、式(12) 就给出了式(2) 右端项全部表达式。
3 角动量平衡控制器设计 为减少某些臂杆CMGs先行饱和的可能性,充分利用CMGs的控制能力,本节针对冗余机械臂,提出一种角动量平衡控制器设计方法。该方法在使末端作用器跟踪工作空间轨迹的同时尽可能均衡地使用各臂的角动量,从而达到减小CMGs角动量饱和可能性的目的。
机械臂的工作空间变量与关节变量可以通过一个非线性映射相联系:
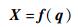 | (13) |
式中:X为工作空间变量,也称为任务变量,一般由末端作用器的位置、姿态坐标组成。
式(13) 的一次、两次求导表达了机械臂的微分运动学关系:
 | (14) |
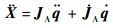 | (15) |
式中:
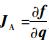
在轨迹预先给定的条件下,机械臂的工作空间控制目标可以陈述为,给定工作空间期望轨迹Xd、

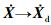
对式(2)、式(13) 表示的系统,可以将控制分为2个层次进行。首先以工作空间指令加速度


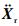
第1个层次中待控制的系统为n个二阶积分器:
 | (16) |
可以使用如下控制律进行控制[18]:
 | (17) |
式中:

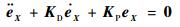 | (18) |
因KD、KP为对角元素为正的对角阵,有eX→0、
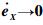
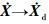
在上述控制中使用了工作空间变量及其速度的反馈X、
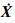
第2个层次中待控制的系统为式(2) 和式(15),最直接的控制方法是利用冗余机械臂的加速度分解方法和逆动力学,其控制律如下:
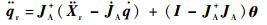 | (19) |
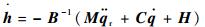 | (20) |
式中:
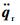
式(17)、式(19)、式(20) 完成了对CMGs驱动的冗余机械臂的轨迹跟踪控制,而θ的任意性可以在保证轨迹跟踪的同时使得系统满足特定的性能要求。如前所述,为了充分使用各臂角动量容量,增加可执行的工作空间轨迹,可利用θ的选取设计空转运动,以在轨迹跟踪过程中尽量平衡地使用各臂的角动量。
类似文献[21]对飞轮转速平衡指标的定义,定义角动量平衡指标如下:
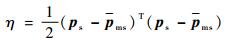 | (21) |
式中:
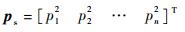 | (22) |
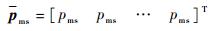 | (23) |
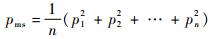 | (24) |
归一化角动量pj定义为
 | (25) |
式中:hjmax>0,为第j节臂杆上Ⅴ构型CMGs的角动量容量。可见pj的大小表示使用的角动量占角动量容量的比例,pj的正负代表使用角动量的方向。当pj=±1时,第j节臂杆上的Ⅴ构型CMGs角动量饱和。由pj构成列阵p:
 | (26) |
由式(21) 可知η≥0,当且仅当p12=p22=…=pn2,即角动量大小完全平衡时,η=0。指标函数中使用pj2而不使用pj的原因是角动量平衡仅指其大小平衡,与其方向无关。
为了利用空转,使η尽量减小,对式(21) 求时间导数得
 | (27) |
式中:d[]表示列阵元素构成的对角矩阵;

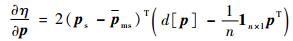 | (28) |
 | (29) |
式中:1n×1表示n行1列的全1矩阵。
将式(19)、式(20) 代入式(27) 得到η的变化规律为
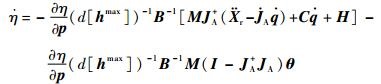 | (30) |
式中:第1项代表使用伪逆解对工作空间加速度进行分解时,角动量平衡指标η的变化规律,这一项与空转运动无关;而第2项可在一定程度上人为设计,从而达到角动量平衡,即使η尽量小的目的。根据文献[22],(I-JA+JA)是幂等的,因此至少是正半定矩阵,为了使η在机械臂运动过程中尽量减小,选择θ如下:
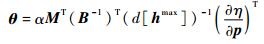 | (31) |
其中:α>0,为可调整的参数。根据式(31) 的设计,式(30) 变为
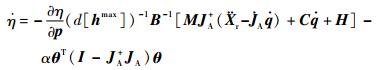 | (32) |
式中:第2项不大于零,从而使得η尽量减小。
式(17)、式(19)、式(20) 和式(31) 为CMGs驱动机械臂角动量平衡控制器的最终形式。在机械臂不奇异时,这一控制器可以对机械臂末端作用器进行轨迹跟踪控制;同时,空转项使得指标η尽量向零靠近,使得各臂的角动量使用更加平衡,减少了单组CMGs饱和的可能性,增强了机械臂执行任务的能力。
4 数值仿真与分析 本节通过数值仿真验证角动量平衡控制器设计的有效性。仿真中选用的模型为一平面机械臂,由3节臂杆通过旋转铰链连接而成,每节臂杆长1 m,如图 3所示,每节机械臂上安装有一对Ⅴ构型的CMGs。
 |
| 图 3 数值仿真中使用的机器人 Fig. 3 Robot used in numerical simulation |
| 图选项 |
各坐标系按第1节中的规定进行安置,Fjref与Fj-1的指向相同,FEE在第3节机械臂末端,与F3的指向相同,图 3中带上、下标的x、y表示对应上、下标坐标系的x、y轴,各旋转铰链绕z轴旋转(z轴指向纸面外),安装参数如表 1所示, 各臂杆的惯性参数如表 2所示, 各臂杆上Ⅴ形构型CMGs的角动量容量如表 3所示。
表 1 安装参数 Table 1 Installation parameters
| 臂杆编号 | 安装位置/m | 安装方向 |
| 1 | [0 0 0]T | 单位阵 |
| 2 | [1 0 0]T | 单位阵 |
| 3 | [1 0 0]T | 单位阵 |
表选项
表 2 惯性参数 Table 2 Inertial parameters
| 臂杆编号 | 质量/kg | 静矩/(kg·m) | 惯量/(kg·m2) |
| 1 | 25 | [12.5 0 0]T | [0.0313 8.349 8.349] |
| 2 | 25 | [12.5 0 0]T | [0.0313 8.349 8.349] |
| 3 | 25 | [12.5 0 0]T | [0.0313 8.349 8.349] |
表选项
表 3 角动量容量 Table 3 Angular momentum capacities
| 臂杆编号 | 角动量容量/(N·m·s) |
| 1 | 5 |
| 2 | 5 |
| 3 | 5 |
表选项
仿真中选择的平面机械臂具有3个自由度。假设对末端作用器姿态的要求可以通过在第3节臂杆上附加一组长度可以忽略的臂杆实现,则这3节较长的臂杆只要使末端作用器的位置跟踪给定轨迹,就可以完成对末端作用器的工作空间控制。需要控制的工作空间位置是二维的,而机械臂具有3个自由度,因此对于这一任务,这一三自由度机械臂是冗余的。
在机械臂的运行过程中,最常见的工作空间轨迹是直线,在仿真中取末端作用器的轨迹为
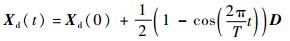 | (33) |
式中:Xd(0) 为轨迹初值;T为完成运动的时间;D为运动的距离。
取系统初值q(0)=[11.5° 34.5° 80°]T,
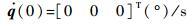
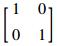

为说明角动量平衡控制器的控制效果,首先取α=0进行仿真,这时角动量平衡项不起作用,运动控制是加速度层面的伪逆控制,在仿真中考虑了CMGs饱和带来的影响。机械臂的运动过程如图 4(a)所示,可见机械臂的末端作用器在运动后期不能够有效地跟踪给定轨迹。末端作用器跟踪误差如图 5(a)所示,跟踪误差变化率如图 6(a)所示。其中
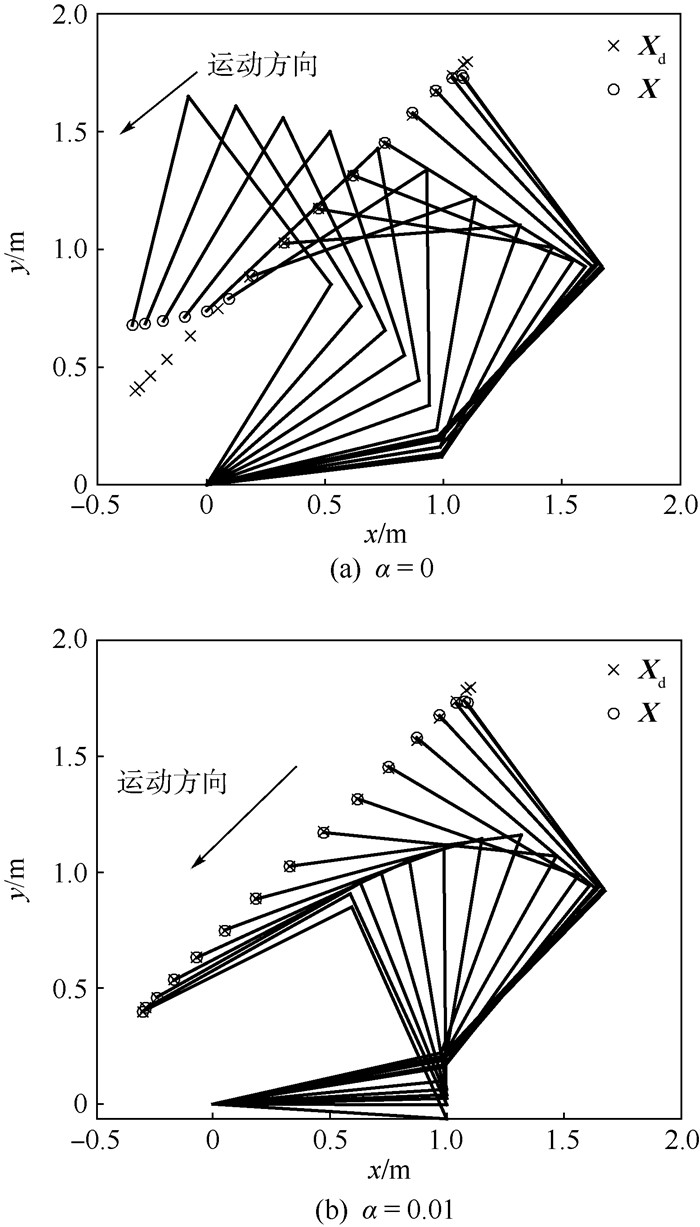 |
| 图 4 机械臂运动过程 Fig. 4 Manipulator motion |
| 图选项 |
 |
| 图 5 末端作用器跟踪误差 Fig. 5 End-effector tracking error |
| 图选项 |
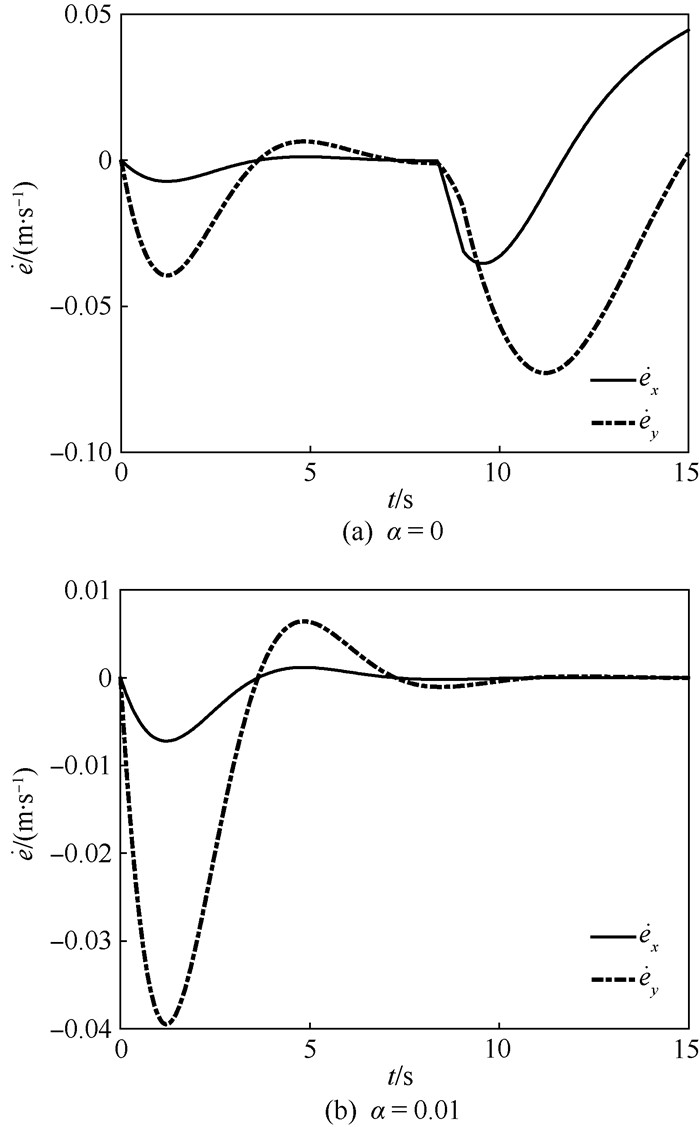 |
| 图 6 末端作用器跟踪误差变化率 Fig. 6 Change rate of end-effector tracking error |
| 图选项 |
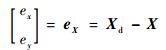 | (34) |
可见误差在收敛到较小的值后开始发散,这主要是由于2个臂杆的CMGs先行饱和引起的。如图 7(a)所示,臂杆1与臂杆2上的CMGs在运动后期进入饱和,而臂杆3上的CMGs仅使用了其角动量容量的一小部分,角动量平衡指标如图 8中的实线所示。这时,以角动量容量而言,系统仍有未使用的能力,而由于臂杆1和臂杆2上CMGs角动量的饱和,系统已经不能准确地跟踪末端作用器的轨迹。
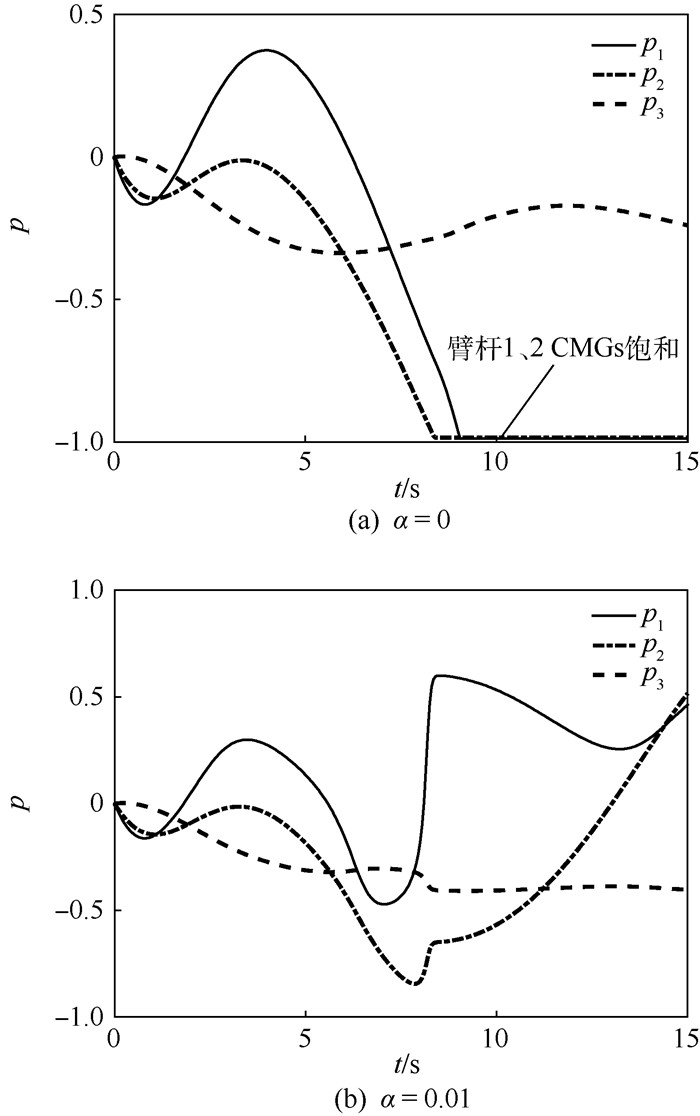 |
| 图 7 归一化角动量 Fig. 7 Normalized angular momentum |
| 图选项 |
 |
| 图 8 角动量平衡指标 Fig. 8 Angular momentum equalization index |
| 图选项 |
启用角动量平衡项,取α=0.01,得到机械臂的运动过程如图 4(b)所示,可见此时末端作用器能够精确地跟踪给定轨迹。末端作用器跟踪误差如图 5(b)所示,跟踪误差变化率如图 6(b)所示。各组CMGs的归一化角动量如图 7(b)所示,对比图 7(a)可以发现,在运动的后期,使用角动量平衡项时,臂杆3的CMGs的归一化角动量开始增加;而不使用角动量平衡项时,臂杆3的CMGs的归一化角动量仍在原有范围内振荡。这正反映了角动量平衡控制器的作用,将未使用的角动量通过机械臂空转进行分配,减小某些臂杆上的CMGs先行饱和的可能性,使得机械臂的能力得到最大程度的使用。角动量平衡指标如图 8中点划线所示,对比α=0的情况,可以发现在运动后期,由于角动量平衡项的作用,平衡指标被有效地控制,说明了控制方法的有效性。
最后,对第1节中所作的“空间平台在惯性空间中的位置、姿态固定”的假设进行简单地讨论。在实际的空间机器人系统中,空间平台的位置、姿态并不是固定的,而是受控制系统的控制,在一定范围内变化。对于机械臂系统的动力学而言,这意味着其相对非惯性系进行运动,因此将受到惯性力的影响,使得机械臂受到惯性力带来的附加干扰力矩。若平台质量/惯量越大,这一影响越小;反之,这一影响则越大。实际操作中,考虑到载荷的质量/惯量可能较大,因而平台质量/惯量相对会减小,因此,考虑平台位置、姿态运动时的角动量平衡控制是值得进一步研究与分析的。
5 结论 1) 针对Ⅴ构型CMGs驱动的冗余空间机器人,利用加速度分解方法和逆动力学方法提出了一种角动量平衡控制器,可在保证机械臂跟踪工作空间轨迹的同时,利用机械臂的空转运动尽量使各臂杆CMGs角动量平衡,从而有效减小CMGs角动量饱和的可能性,充分利用CMGs的控制能力。
2) 基于平面三自由度冗余空间机械臂的数值仿真结果验证了所设计的控制器的有效性。
为了突出主要问题,本文没有考虑空间平台位置、姿态运动造成的影响,对这一影响的研究与分析将是今后的主要方向之一。
参考文献
| [1] | FLORES-ABAD A, MA O, PHAM K, et al. A review of space robotics technologies for on-orbit servicing[J].Progress in Aerospace Sciences, 2014, 68: 1–26.DOI:10.1016/j.paerosci.2014.03.002 |
| [2] | XU W, LIANG B, XU Y. Survey of modeling, planning, and ground verification of space robotic systems[J].Acta Astronautica, 2011, 68(11): 1629–1649. |
| [3] | VAFA Z. On the dynamics of space manipulators using the virtual manipulator, with applications to path planning[J].The Journal of the Astronautical Sciences, 1990, 38(4): 441–472. |
| [4] | TORRES M A, DUBOWSKY S. Minimizing spacecraft attitude disturbances in space manipulator systems[J].Journal of Guidance, Control, and Dynamics, 1992, 15(4): 1010–1017.DOI:10.2514/3.20936 |
| [5] | YOSHIDA K, HASHIZUME K, ABIKO S.Zero reaction maneuver:Flight validation with ETS-Ⅶ space robot and extension to kinematically redundant arm[C]//IEEE International Conference on Robotics and Automation, 2001 ICRA.Piscataway, NJ:IEEE Press, 2001, 1:441-446. |
| [6] | NENCHEV D N. Reaction null space of a multibody system with applications in robotics[J].Mechanical Sciences, 2013, 4(1): 97–112.DOI:10.5194/ms-4-97-2013 |
| [7] | PECK M, PALUSZEK M, THOMAS S, et al.Control-moment gyroscopes for joint actuation:A new paradigm in space robotics[C]//1st Space Exploration Conference:Continuing the Voyage of Discovery, American Institute of Aeronautics and Astronautics Inc.Reston:AIAA, 2005, 1:204-233. |
| [8] | PECK M A.Low-power, high-agility space robotics[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston:AIAA, 2005:1-12. |
| [9] | OSUKA K, YOSHIDA K, ONO T.New design concept of space manipulator:A proposal of torque-unit manipulator[C]//Proceedings of the 33rd IEEE Conference on Decision and Control.Piscataway, NJ:IEEE Press, 1994, 2:1823-1825. |
| [10] | HOKAMOTO S. Torque unit manipulator driven by control moment gyros[J].Advances in the Astronautical Sciences, 1997, 96: 865–876. |
| [11] | CARPENTER M D, PECK M A. Reducing base reactions with gyroscopic actuation of space-robotic systems[J].IEEE Transactions on Robotics, 2009, 25(6): 1262–1270.DOI:10.1109/TRO.2009.2032953 |
| [12] | CARPENTER M D, PECK M A.Minimum-power robotic maneuvering using control-moment gyroscopes[C]//AIAA Guidance, Navigation, and Control Conference 2007.Reston:AIAA, 2007:210-222. |
| [13] | CARPENTER M D, PECK M A.Power-optimal steering of a space robotic system driven by control-moment gyroscopes[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston:AIAA, 2008. |
| [14] | BROWN D.Control moment gyros as space-robotics actuators[C]//AIAA Guidance, Navigation and Control Conference and Exhibit.Reston:AIAA, 2008. |
| [15] | BROWN D, PECK M. Energetics of control moment gyroscopes as joint actuators[J].Journal of Guidance, Control, and Dynamics, 2009, 32(6): 1871–1883.DOI:10.2514/1.42313 |
| [16] | 贾英宏, 赵楠, 徐世杰. 控制力矩陀螺驱动的空间机器人轨迹跟踪控制[J].北京航空航天大学学报, 2014, 41(3): 285–291. JIA Y H, ZHAO N, XU S J. Trajectory tracking control of space robot actuated by control moment gyroscopes[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 41(3): 285–291.(in Chinese) |
| [17] | 赵楠, 贾英宏, 徐世杰. 无反作用力矩空间机器人轨迹跟踪控制[J].中国空间科学技术, 2014, 34(2): 13–21. ZHAO N, JIA Y H, XU S J. Trajectory tracking control of a reactionless space robot[J].Chinese Space Science and Technology, 2014, 34(2): 13–21.(in Chinese) |
| [18] | SICILIANO B, SCIAVICCO L, VILLANI L, et al. Robotics:Modelling, planning and control[M].Berlin: Springer Science & Business Media, 2010: 305. |
| [19] | KANE T R, LEVINSON D A. Dynamics, theory and applications[M].New York: McGraw Hill, 1985: 106. |
| [20] | 胡权, 贾英宏, 徐世杰. 多体系统动力学Kane方法的改进[J].力学学报, 2011, 43(5): 968–972. HU Q, JIA Y H, XU S J. An improved Kane's method for multibody dynamics[J].Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(5): 968–972.DOI:10.6052/0459-1879-2011-5-lxxb2010-856(in Chinese) |
| [21] | JIA Y H, XU S J. Spacecraft attitude tracking and energy storage using flywheels[J].Chinese Journal of Aeronautics, 2005, 18(1): 1–7.DOI:10.1016/S1000-9361(11)60274-4 |
| [22] | YOSHIKAWA T. Analysis and control of robot manipulators with redundancy[C]//Robotics Research:The First International Symposium.Cambridge, MA:MIT Press, 1984:735-747. |
