目前，全自动着舰是舰载机着舰回收的重要方式之一，由舰载空中管制雷达指挥飞机飞向进舰下滑道入口，导引雷达测得舰载飞机的实际位置和速度，反馈至舰载计算机，与理想下滑航迹比较，产生误差信号，计算得到舰载机航迹指令，导引飞机沿理想航迹下滑，直至安全着舰。
现役的全自动着舰系统(ACLS)最主要的导引方式是雷达导引，由于它相对于人工助降和菲涅尔光学透镜导引等方式，精度较高，而更精确的卫星导引还在试验之中，技术尚未成熟，故雷达导引仍是全自动着舰系统的主要导引方式。雷达在探测过程中，影响探测信号的因素有多种，即雷达探测误差有较多的种类。一切测量误差都会影响输入到舰载计算机中的误差信号，造成着舰指令的偏差，影响着舰控制的质量，因此必须装备高精度导引雷达，确保舰载机安全着舰^[1]。
美国现役精确进近着舰系统核心雷达装备型号为AN/SPN-46，该雷达为使用圆锥扫描技术的Ka波段脉冲跟踪雷达，飞机在进近着舰窗口被捕捉后，纵向采用距离(高度)及俯仰对飞机进行跟踪，直至着舰或复飞。现役舰载雷达在海战中面临的威胁和挑战越来越大：各类有源及无源干扰压制、反辐射制导弹药、目标隐身性能及低空突防能力等。多方面、高强度的威胁，要求雷达系统必须具备极高的测量精度和作业速度，以及强大的抗干扰性能，用于减少电磁干扰的各类电磁兼容性设计尤为重要^[2]。
除电磁干扰外，雷达系统、舰载计算机和飞控系统交联时，不可避免产生时间延迟，F/A-18A飞控系统时间延迟效应的范围已有公布，延迟效应主要影响飞机的负反馈控制，降低系统的稳定性。雷达系统本身具有一定的测量误差，包括零点漂移等系统误差和各类热噪声等随机误差，造成位置测量的偏移，影响着舰点和着舰成功率。分析以上3种主要干扰对着舰性能的影响，对于着舰系统与导引雷达的设计具有指导意义和极高的工程应用价值，促进雷达导引方式具备更高的精度和更快的响应速度。
本文以美国现役“尼米兹”级航空母舰和美国海军F/A-18A舰载战斗机为参考对象，建立了着舰导引阶段的全自动着舰控制系统模型。由于AN/SPN-46雷达数据尚未公开，本文仍采用AN/SPN-42雷达进行仿真分析，引入模拟的雷达引导信号误差，对飞机在常规环境中的引导下滑阶段进行了仿真分析，得到了与不同程度的误差相对应的着舰结果，以着舰成功率为指标，分析了雷达信号误差对着舰控制的影响。
1 舰载飞机模型特性 1.1 舰载机模型状态方程 进舰着舰过程中，F/A-18A的状态方程为

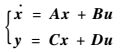(1)

式中：状态变量x、控制变量u和输出变量y分别为

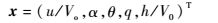(2)

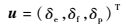(3)

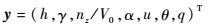(4)

其中：V₀为舰载机着舰速度；α为扰动迎角；θ为扰动俯仰角；q为扰动俯仰角速度；h为高度；u为扰动速度；δ_e、δ_f和δ_p为升降舵、襟翼和油门杆的偏转；γ和n_z为扰动航迹角和扰动纵向过载。
1.2 加入舰尾流扰动的增广模型 上述的飞机模型输入包括：升降舵输入、襟翼输入以及油门输入。本文在研究中，为了尽量与飞机实际着舰环境相一致，引入了舰尾流模型作为扰动，在Simulink仿真环境中，以突风迎角的形式来体现，作为飞机模型输入的第4部分。
根据状态变量、控制变量及输出变量的维数可知，飞机在未加入舰尾流时，模型的状态矩阵的维数分别为：A_5×5、B_5×3、C_7×5和D_7×3。由于舰尾流以突风迎角α_airwake的形式加入，则新的控制变量：

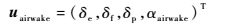(5)

相对应的矩阵B和矩阵D行数不变，各增加一列元素，即对应于状态变量中的突风迎角α的一列元素。新状态矩阵变为

(6)

2 全自动着舰系统 ACLS的结构和组成部分早在20世纪60年代即已确定下来，所不同的仅仅是系统设备、引导方式、传感器和惯导系统的改进等^[3]。飞行控制系统接收ACLS指令，控制飞机姿态及航迹，使飞机成功着舰，其结构层次主要分为4级。第1、2级反馈回路主要改善阻尼特性和控制飞行姿态，第3、4级控制高度等长周期变量。
ACLS的结构及组成部分包括：甲板运动补偿器(DMC)、指令计算机、自动驾驶仪、进场功率补偿系统(APCS)及舰载机的本体特性模型等^[4]，已有的控制律及控制方程较为成熟，每一部分的控制方程及相互关系如下。
2.1 自动驾驶仪 自动驾驶仪的反馈设计的主要目的是改善飞机的长、短周期飞行品质，设计步骤一般为从内环到外环。
典型的内环设计为俯仰角速度q的反馈，具体设计方法可参考相关的飞行品质准则规范。F/A-18A应用(高度变化率)指令系统，其内环结构包括：前向通道增益、比例积分控制、陷波滤波器、平尾作动器、飞机本体以及反馈回路中的滞后超前滤波器和增益等。其中，滞后超前滤波器用于补偿回路的相位滞后；比例积分可增加系统的响应速度并消除稳态误差；加入陷波滤波器避免伺服振动。
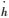
外环反馈回路参数一般比内环参数变化慢，如航迹角、高度等。目前的ACLS为了直接精确控制航迹，引入高度变化率及纵向过载反馈，构成负反馈回路。在进舰着舰下滑阶段，飞机的高度变化率由式(7) 计算^[4]：

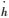
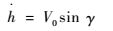(7)

由于飞机着舰过程中几乎保持定速下滑，因此控制高度变化率实际上就是直接控制航迹角，而不是通过俯仰角控制航迹角，这有利于保持恒定的下滑航迹。
2.2 进场功率补偿系统 为了保持航迹角与俯仰角的同步，则需引入进场功率补偿系统，通过油门控制速度和迎角恒定。反馈参数选择纵向过载和迎角。迎角决定飞机空速，纵向过载反映高度变化率的导数。
进场功率补偿系统的被控参数为速度和迎角，这是根据以往进行人工着舰的飞行员的实际操作经验来选择的。升降舵控制高度和姿态，油门控制速度，响应较快，控制效果好^[4]，故进场功率补偿系统采用了这种控制方法。
本文仿真中仅考虑纵向着舰误差，未考虑非线性因素，进场功率补偿系统控制律中的迎角反馈加入了积分环节，提高响应速度，消除误差^[4]。控制律如下:

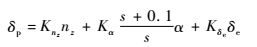(8)

式中：K_nz、K_α和K_δe分别为过载、迎角和升降舵反馈系数; 为比例和积分环节。
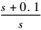
2.3 甲板运动补偿系统 考虑航空母舰在海上的实际运动，还需加入甲板运动补偿部分。将飞行甲板的上下起伏加入到高度指令中，即可使飞机跟踪甲板运动，从而准确着舰。考虑到滤除高频噪声，目前常用的甲板运动补偿器传递函数结构如下：

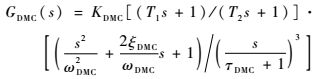(9)

式中:K_DMC为增益；T₁、T₂为超前网络的时间常数，超前网络用于相位补偿；是补偿滤波网络，可有效抑制高频噪声且满足网络的带宽要求, τ_DMC、ξ_DMC、ω_DMC分别为补偿器时间常数、补偿器阻尼和补偿器自然频率。
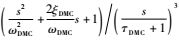
2.4 PIDD导引律 由于作动器近似为惯性环节，为了改善其滞后性，将传统PID传递函数与作动器传递函数相除，即得到PIDD导引律，结构如式(10)：

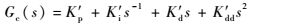(10)

式中：K′_p、K′_i、K′_d、K′_dd分别为比例增益、积分增益、微分增益及二次微分增益。
进一步的微分提供了额外的相角超前，改善了控制系统的相角滞后，提高了系统的控制精度。
3 雷达信号误差类型及特性 如引言中所述，雷达信号误差直接影响舰载计算机对于导引控制律的计算，进而影响舰载机着舰的准确性。在仿真计算前，首先讨论雷达信号误差的分类及量级。
3.1 测量数值类误差 此类误差包括：零点设置或零点抖动误差、刻度漂移、机内热噪声误差、采样测量误差、闪烁引起的距离误差、输出数据量化误差、各类校正误差、转动机械误差、天线指向误差、目标起伏误差等^[5]。
由于误差种类较多，为便于仿真计算，首先进行估算，确定数值量级范围。文献[6]中指出，测距误差可估算为飞机与雷达之间实际距离的1%，如采取最后25 s作为着舰最后阶段，飞机速度为69.96 m/s，航迹下滑角为-3.5°，下滑道入口高度为114 m，则舰面高度为19.1 m，可计算雷达与飞机最大高度差产生的误差值约为

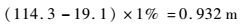(11)

取最大常值作为误差边界值，加入ACLS的高度反馈回路，模拟雷达的零点漂移、测距测角数值等误差，探究存在误差值时的着舰成功率。
3.2 时间延迟类误差 接收机回波延迟误差、大气折射延迟及其变化而产生的误差、多径效应延迟误差，非标准大气额外延迟误差、舰载计算机处理延迟误差、飞机传感器接收处理信号延迟误差等，都属于信号延迟误差。信号延迟主要使系统的相位发生滞后，降低系统的稳定裕度，使系统振荡、超调，最终甚至导致发散，无法准确跟踪航迹。由于电子器件本身因计算运行和惯性，具有一定的延迟；使用时间越长，延迟时间也会增加。
表 1为F/A-18舰载机全自动着舰系统各部分的时间延迟范围^[7]。上述误差以系统内延迟误差为主，因系统部件的异步动作、滤波器计算延迟以及数据机解码译码等而产生，故而将延迟时间累加，取最大值作边界，仿真计算信号延迟的影响。
表 1 F/A-18全自动着舰系统时间延迟^[7] Table 1 Delay time of F/A-18 ACLS^[7]

ms
ACLS延迟主要组成部分	延迟时间
舰载雷达计算机α-β滤波器计算延迟	10
信号传送异步延迟	[0, 50]
接收机译码时间	1
任务计算机异步延迟	[0, 50]
任务计算机计算延迟	[12, 50]
飞控系统异步延迟	[0, 50]
飞控系统前台计算时间	[6.25, 56.25]
飞控系统计算延迟	6.25(多数指令)

表选项






3.3 噪声杂波类误差 航空母舰舰载导引雷达必然处于复杂的电磁环境中，舰队其他舰船的信号，空中舰载机的雷达电子系统，航空母舰上的其他雷达航电系统，都会对导引信息造成不同程度的杂波影响；作战时，导引雷达还可能面对敌方的电磁干扰，振幅过大的干扰信号可导致雷达系统崩溃，无法工作。
雷达噪声信号以中高频和高频为主^[8]，通过文献[9]给出的参考信号幅值量级，设定正弦信号组合模拟雷达电子闪烁噪声和高频噪声，取一定的步长，改变信号幅值，仿真研究对着舰的影响。仿真中，将中高频的频率设为4 rad/s，高频信号频率设为10 rad/s，叠加后加入高度反馈回路中。
4 雷达信号误差仿真分析 误差对于着舰的影响，可通过着舰成功率来验证。根据下滑理想航迹的要求，下滑角为-3.5°，飞机重心高度约为2 m，舰面高度为19.1 m，结合以上条件，可以确定飞机在下滑道入口处一直到着舰啮合所需要的时间。对于算例飞机，进舰速度为69.96 m/s，可估计从下滑道入口到着舰啮合的飞行时间为

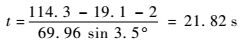(12)

根据飞机的空速和下滑角，可知飞机的水平速度分量，利用理想着舰点与第1根和第4根拦阻索的距离，可得着舰点的边界，即着舰安全区，进而计算出着舰成功的时间范围，本文在计算时，考虑工程实用性，采用着舰允许区作为边界，即理想着舰点前后12 m的范围^[10-11]；当加入各类误差进行分析时，超出了时间范围即为着舰失败，着舰成功率便可计算。
根据上述误差的分类及量级，用控制变量法，每次选择一种误差，以一定间隔设置误差值，加入系统，在系统中加入舰尾流扰动和相位变化的甲板起伏运动。本文在仿真时，每次只加入单一种类误差进行仿真。每次仿真改变甲板运动和舰尾流的相位，每个数据点进行400组仿真，计算着舰成功率，并且对3级和4级海况下的成功率进行对比^[12]。仿真过程及结果如下。
4.1 测量数值误差仿真 加入常值误差，在式(11) 中0.932 m基础上加以扩大，最终以[-2.5, 2.5] m作为仿真范围。相邻误差值之差首先设为0.5 m，进行仿真。由于初步结果在[-1.5, -1.0] m、[-1.0, -0.5] m、[0.5, 1.0] m及[1.0, 1.5] m区间内，计算结果变化率很大，故在以上区间内额外取值仿真，仿真过程中，加入舰尾流扰动、甲板起伏运动和雷达测量数值误差的影响，忽略其他影响因素。结果如表 2和图 1所示。
表 2 存在测量误差时的着舰成功率 Table 2 Carrier landing success rate withmeasuring error

测量误差/m	着舰成功率
	3级海况	4级海况
-2.5	0.000 0	0.000 0
-2.0	0.000 0	0.000 0
-1.5	0.000 0	0.000 0
-1.4	0.072 5	0.030 0
-1.2	0.177 5	0.077 5
-1.0	0.250 0	0.130 0
-0.9	0.305 0	0.237 5
-0.8	0.417 5	0.322 5
-0.7	0.502 5	0.430 0
-0.6	0.642 5	0.555 0
-0.5	0.792 5	0.655 0
0	0.937 5	0.772 5
0.5	0.822 5	0.717 5
0.6	0.677 5	0.652 5
0.7	0.605 0	0.525 0
0.8	0.445 0	0.402 5
0.9	0.395 0	0.347 5
1.0	0.337 5	0.257 5
1.2	0.250 0	0.185 0
1.4	0.145 0	0.075 0
1.5	0.112 5	0.032 5
2.0	0.000 0	0.000 0
2.5	0.000 0	0.000 0

表选项

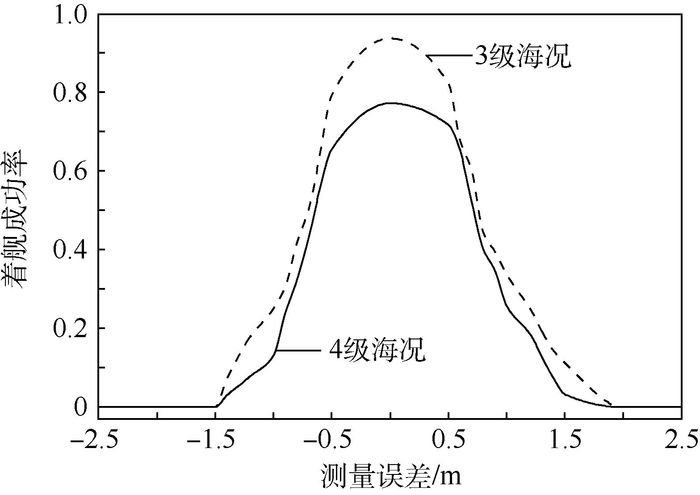图 1 着舰成功率与测量误差曲线 Fig. 1 Curves of carrier landing success rate versus measuring error

图选项

4.2 时间延迟误差仿真 采用在PIDD导引模块之后加入延迟环节的方法，模拟延迟误差。累加文献[7]中的延迟时间，并适度扩大，最终将延迟时间取值范围确定为[0, 1 000] ms，以100 ms作为相邻取值之差，仿真中加入舰尾流扰动、甲板起伏运动和雷达及计算机时间延迟的影响，忽略其他影响因素。仿真结果如表 3和图 2所示。
表 3 存在时间延迟误差时的着舰成功率 Table 3 Carrier landing success rate with time delay

延迟时间/ms	着舰成功率
	3级海况	4级海况
0	0.937 5	0.725 0
100	0.767 5	0.547 5
200	0.542 5	0.422 5
300	0.407 5	0.355 0
400	0.360 0	0.285 0
500	0.285 0	0.235 0
600	0.240 0	0.207 5
700	0.212 5	0.187 5
800	0.207 5	0.180 0
900	0.192 5	0.177 5
1 000	0.170 0	0.160 0

表选项

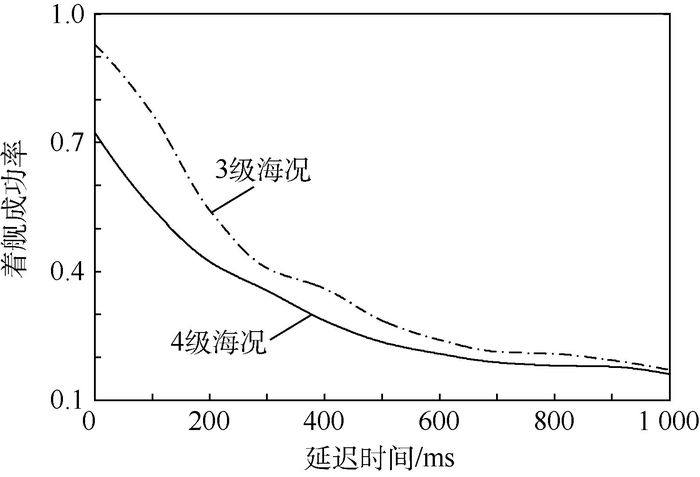图 2 着舰成功率与延迟时间曲线 Fig. 2 Curves of carrier landing success rate versus delay time

图选项

4.3 噪声杂波误差仿真 采用正弦信号叠加的方法，模拟雷达电子闪烁噪声和高频噪声，采用逐渐增加的噪声幅值，分别仿真计算，文献[9]中给出的幅值大小为2.5 m，此处加以扩大，设置仿真幅值的范围为[0, 10] m，以1 m为相邻幅值之差，在计算结果变化大的区间[7, 8] m里，额外取值仿真，仿真过程中，加入舰尾流扰动、甲板起伏运动和雷达杂波误差的影响，忽略其他影响因素。仿真结果如表 4和图 3所示。
表 4 存在噪声杂波误差时的着舰成功率 Table 4 Carrier landing success rate with noise error

噪声杂波幅值/m	着舰成功率
	3级海况	4级海况
0	0.940 0	0.727 5
1	0.902 5	0.705 0
2	0.792 5	0.687 5
3	0.687 5	0.657 5
4	0.605 0	0.582 5
5	0.557 5	0.537 5
6	0.500 0	0.482 5
7	0.467 5	0.422 5
7.3	0.387 5	0.357 5
7.6	0.305 0	0.305 0
7.8	0.270 0	0.270 0
8	0.235 0	0.235 0
9	0.175 0	0.175 0
10	0.022 5	0.022 5

表选项

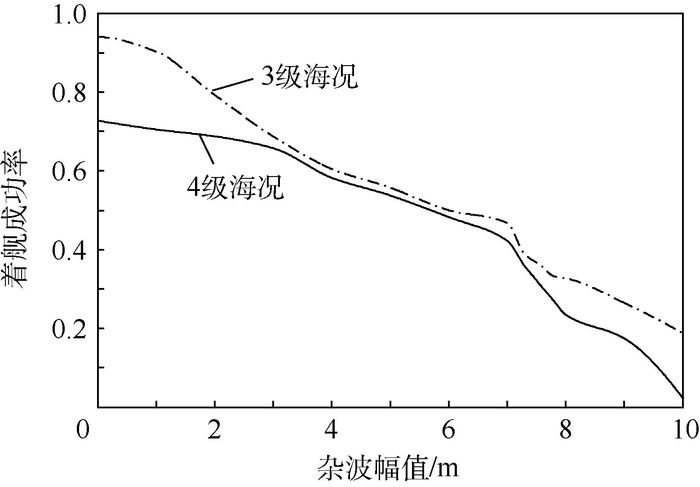图 3 着舰成功率与杂波幅值曲线 Fig. 3 Curves of carrier landing success rateversus noise amplitude

图选项

根据对3类雷达信号误差的仿真分析，可知着舰成功率随误差特征量的绝对值的增加而增加，随海况恶化而降低。当着舰成功率小于工程要求的阈值时，则必须启动紧急措施，使用备降方法保障安全；同时，及时监测并校正雷达系统误差，监测每一时刻的海况，减小其对着舰的影响。
5 结论 综上所述，通过对导引信息的3个主要精度影响因素分析，得出了雷达信号测量误差、雷达时间延迟和杂波信号对舰载飞机着舰的影响。以着舰成功率为量度，模拟仿真F/A-18A在中等海况，且舰船运动具有不同的相位时的着舰成功率，仿真过程中采用控制变量方法，每次加入测量误差、延迟误差和杂波误差中的一种，其他条件视为理想状况。
1) 同一种类误差存在下的着舰成功率，随误差绝对值增大而降低，呈单调变化规律。
2) 对于测量误差，在正负0.5 m幅值范围内，着舰成功率较高，变化不大；绝对值大于0.5 m时，成功率急剧下降，着舰落点迅速超出着舰允许区，成功率降低至0.7或更低；延迟误差随时间增加，递减速度逐渐减缓，3级海况时，100 ms以内的延迟值保证80%的着舰允许区落点；噪声杂波幅值在4~7 m时，经过混合滤波器反馈至舰载计算机的幅值与甲板运动波形幅值较为接近，2种海况的着舰成功率相差较小。
3) 相同种类和大小的误差存在下的着舰成功率，随海况升级而降低；4级海况难以保证80%以上的着舰允许区80%的落点数，表明海况超过3级时，需采用防范及备降措施。
本文在传统着舰控制系统基础上，通过加入幅值不同的3种典型雷达测量误差，定量分析着舰成功率在不同海况下的变化规律，并结合α-β滤波器及预处理混合滤波器，分析不同大小幅值误差的成功率的变化规律，且阐明不同变化规律的原因。仿真结果定量表明了误差及其数值对于着舰成功率的影响，便于工程人员根据着舰实际标准确定信号误差边界。该结果能够对着舰控制及设计提供支持与参考，对舰载机实际工程具有指导意义。

参考文献

[1]	徐产兴. 舰载机着舰引导雷达系统[J].现代舰船, 2003(4): 34–35. XU C X. Director radar system of carrier-based aircraft landing[J].Modern Ships and Warships, 2003(4): 34–35.(in Chinese)
[2]	戴征坚, 严科伟, 谭昕. 国外航母雷达的现状与发展[J].舰船电子工程, 2016, 36(5): 4–7. DAI Z J, YAN K W, TAN X. Development and status of foreign carrier radar[J].Ship Electronic Engineering, 2016, 36(5): 4–7.(in Chinese)
[3]	HUFF R W, KESSLER G K.Enhanced displays, flight controls and guidance systems for approach and landing:AD/A244 869[R].[S.l:s.n.], 1978.
[4]	彭兢. 舰载飞机进舰着舰的自动引导和控制研究[D]. 北京: 北京航空航天大学, 2001: 45-69. PENG J.Research on the automatic guide and control of carrier-based airplane approach and landing[D].Beijing:Beihang University, 2001:45-69(in Chinese).
[5]	郦能敬. 对空情报雷达的测量精度分析[J].雷达科学与技术, 2005, 3(1): 1–10. LI N J. Measurement accuracy analysis of air defense intelligence radar[J].Radar Science and Technology, 2005, 3(1): 1–10.(in Chinese)
[6]	倪树新. 航母载机着舰引导系统的体制研究[J].电光系统, 2000(2): 8–19. NI S X. Electronic and Research of pilot system of carrier-based aircraft landing[J].Electronic and Electro-optics System, 2000(2): 8–19.(in Chinese)
[7]	URNES J M, HESS R K. Development of the F/A-18A automatic carrier landing system[J].Journal of Guidance, Control, and Dynamics, 1985, 8(3): 289–295.DOI:10.2514/3.19978
[8]	杨一栋, 余俊雅. 舰载飞机着舰引导与控制[M].北京: 国防工业出版社, 2007: 149-152. YANG Y D, YU J Y. Direction and control of carrier-based aircraft landing[M].Beijing: National Defence Industry Press, 2007: 149-152.(in Chinese)
[9]	MOOK D J, SWANSON D A, ROEMER M J, et al. Improved noise rejection in automatic carrier landing systems[J].Journal of Guidance, Control, and Dynamics, 1992, 15(2): 509–519.DOI:10.2514/3.20864
[10]	ANDERSON M R.Inner and outer loop manual control of carrier aircraft landing:AIAA-1996-3877[R].Reston:AIAA, 1996.
[11]	RICHARDS R, CHRENKA J, THORDSEN M.Artificial intelligence techniques for pilot approach decision aid logic (PADAL) system:N68335-98-C-0027[R].[S.l:s.n.], 1998.
[12]	张永花. 舰载机着舰过程甲板运动建模及补偿技术研究[D]. 南京: 南京航空航天大学, 2012: 16-22. ZHANG Y H.Research of deck motion modeling and compensation technology during carrier-based aircraft landing[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2012:16-22(in Chinese).