随着现代航天技术的发展，航天器控制系统日趋复杂，各部件的可靠性、准确性要求越高，同时部件出现故障的可能性越大。如何避免航天任务的失败和经济损失，切实保障航天器的可靠性和安全性，提高航天器规避风险的能力成为控制系统的新的研究内容，并基于此提出了容错控制理论。
目前，按照设计方法的特点，容错控制一般分为主动容错控制和被动容错控制^[1-2]。主动容错控制是在故障发生后，根据所期望的特性重新设计一个控制系统，并至少能使整个系统达到稳定^[2]。被动容错控制采用固定的控制器来确保闭环系统对特定故障不敏感，保持系统的稳定^[2]。相比主动容错控制，被动容错控制由于不需要对系统故障进行检测或诊断，也不需要故障反应时间，因此结构简单、响应速度快且设计难度较低。目前国内外很多****都基于被动控制方法进行航天器的姿态容错控制研究。文献[3]应用神经网络智能控制结合滑模控制对挠性航天器存在部分失效时进行姿态容错控制；文献[4]采用自适应反步设计法设计容错控制，且该算法允许存在少量飞轮完全失效；文献[5]则设计了基于时滞控制 (TDC) 算法的时滞容错控制系统来控制刚性航天器的姿态，该算法相比PD算法控制性能更佳；文献[6]设计了不基于姿态角速度信息和故障信息的姿态容错算法；文献[7]利用鲁棒控制，通过在线求解线性矩阵不等式 (LMI) 确定状态反馈增益阵来控制航天器姿态，能够克服Riccati方程处理方法中存在的不足; 文献[8]提出一种基于PD学习型观测器的系统故障重构方法，不仅能够估计卫星姿态角速度和姿态角，而且能够快速精确重构卫星执行机构故障；文献[9]引入力矩分配矩阵，对各飞轮的力矩输出进行容错控制，使得航天器的姿态渐进稳定；文献[10]也通过设计状态观测器观测系统状态，并针对控制力矩陀螺可能出现的奇异性问题设计操纵律，从而实现航天器的姿态稳定。文献[11]进一步考虑了执行机构输出受限情况下，通过状态观测器观测故障信息实现对控制器的重构。
上述文献给出的控制方法虽然能够实现航天器的姿态容错控制，但是选用的被控对象和故障都是针对控制力矩进行建模。然而在实际工程应用中，当采用角动量交换装置作为姿态控制执行机构时，执行机构故障通常是转子转速输出故障，因此，上述理论成果在实际工程应用中有一定的局限性。此外，当采用控制力矩陀螺群为执行机构时，陀螺具有的奇异性问题以及陀螺横向矩阵时变的特点，也使得上述理论成果难以应用。考虑到控制力矩陀螺作为执行机构具有的优点，且目前针对控制力矩陀螺的被动容错控制研究较少，本文将针对单框架控制力矩陀螺 (SGCMGs) 的框架转速故障，基于滑模和自适应理论，设计一种不基于故障信息的鲁棒容错姿态控制方法，以提高航天器控制系统的可靠性和安全性。
1 SGCMGs框架转速故障下的航天器数学模型 带有n个SGCMGs的刚性航天器的动力学方程和运动学方程可以描述为^[12]

(1)

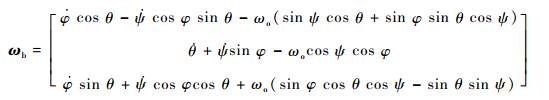(2)

式中：I_b为整个系统惯量矩阵，一般随着陀螺框架角变化，但因其变化率较小，因此本文中认为I_b为一个常值惯量矩阵；ω_b=[ω_x?ω_y?ω_z]^T为航天器绝对角速度在本体坐标系中的分量列阵；ω_b^×定义为

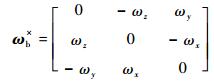(3)

I_ws为SGCMGs转子轴向转动惯量阵；Ω为转子转速向量；h₀为各个陀螺转子的标称角动量；为陀螺实际输出的框架转速向量；T_d为航天器受到的干扰力矩向量；φ、θ和ψ分别为航天器的滚动角、俯仰角和偏航角；ω_o为轨道系相对惯性系的转速；矩阵A_s=[s₁?s₂?…?s_n]、A_t=[t₁?t₂?…?t_n]分别为SGCMGs转子转速方向矩阵和横向矩阵，n为SGCMGs中陀螺的个数, A_s、A_t各分量可计算如下：

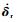
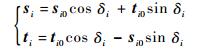(4)

其中：s_i0、t_i0为s_i、t_i的初始值，与陀螺安装构型有关；δ_i(i=1, 2, …, n) 为第i个陀螺的框架角。
动力学方程式 (1) 未考虑陀螺故障的情况。一般地，陀螺的故障分为加性故障和乘性故障^[13]，即陀螺在受到故障时，实际框架转速输出为

(5)

式中：为理论框架轮速；E=diag (e₁?e₂?…?e_n) 为乘性故障因子，0≤e_i≤1(i=1, 2, …, n) 为陀螺的失效因子，且：

f=[f₁?f₂?…?f_n]^T为加性故障对陀螺框架转速的影响，一般地，这种影响会使得陀螺框架转速变慢，因此f_i≤0且其绝对值较小。
对式 (1)，设J=I_b/h₀，h_c=A_sI_wsΩ/h₀，d=T_d/h₀，并令u= 作为控制系统的控制量，将式 (5) 代入式 (1) 得到

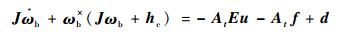(6)

对式 (2)，设x=[φ?θ?ψ]^T，且在姿态角为小角度情况下，忽略二阶及二阶以上小量，式 (2) 可近似改写为

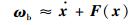(7)

式中：

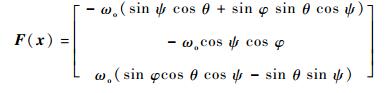(8)

基于上述描述，提出本文设计控制器的目标为：对以SGCMGs为执行机构的航天器，若执行机构存在部分故障 (0＜e_i≤1)，而加性故障和外界干扰对陀螺框架转速影响有限，设计合适的控制律对陀螺的理论框架转速进行控制，使得航天器的姿态角实现渐进稳定，即t→∞时，φ, θ, ψ→0且。
2 容错控制律设计 2.1 基础准备 基于航天器在轨运行的工程实际，本文作出如下假设。
假设1?航天器运行过程中受到的干扰力矩有界，即║d║≤T_d, T_d为║d║的上界; 且加性故障对陀螺框架转速的影响有限，║A_t f║≤T_f, T_f为║A_t f║的上界。其中约定║·║表示矩阵或向量的2-范数^[14]，若用到其他的范数形式再做具体声明；T_d和T_f为未知常数；综合假设1可以得到

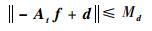(9)

式中：M_d为未知常数。
假设2?航天器转动惯量矩阵为正定对称矩阵，亦即J对称且正定。
假设3?本文不考虑陀螺完全失效的情况，即假设存在未知常数e₀满足：

(10)

基于上述假设，采用滑模控制方法设计控制器。
选取滑模面为

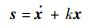(11)

式中：k＞0, 为定常数。若能设计合适的控制律u能使得所选状态能在设计的滑模面 (11) 上滑动，则当t→∞时，x→0，→0。
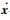
定义下列参数：η1－e₀∈0, 1，ξ1/e₀。
引理1?针对有n个陀螺的作为执行机构的航天器，有如下不等式成立：

(12)

式中：I为单位矩阵。
证明?对A_t=[t₁?t₂?…?t_n]，结合式 (4)，有结论。
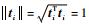
设s=[s₁?s₂?s₃]^T，因此

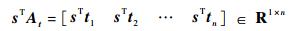(13)

由2-范数的性质：s^Tt_i≤║s^T║║t_i║=║s^T║(i=1, 2, …, n)，因此有

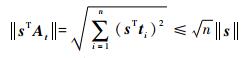(14)

另一方面，设u=[u₁?u₂?…?u_n]^T。

(15)

所以

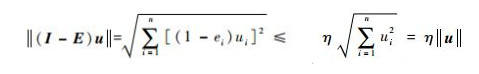(16)

结合式 (14) 和式 (16) 可以证明不等式 (12) 成立。
2.2 控制律设计及稳定性证明 基于假设1~假设3，可以得到如下定理。
定理1?对于以SGCMGs为执行机构的航天器，当存在外部干扰力矩及执行机构部分故障时，其动力学和运动学方程分别为式 (6) 和式 (2)，在未知故障及干扰信息的情况下，可以通过设计如下容错控制律实现航天器的姿态渐进稳定：

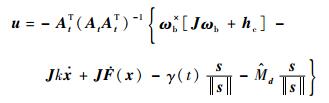(17)

上述控制律中各参数的取值和意义如下：
：表示式 (9) 中M_d的估计值，取自适应控制律为

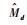
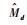
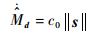(18)

γ(t)：引入的一个参数，取

(19)

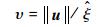(20)

(21)

其中:c₀、c₁、ε₀为一个正常数。
证明?取Lyapunov函数为

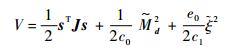其中:=M_d－ ; =ξ－。为了方便表示，记ΔE=I-E。
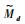
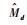
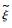
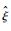
对上述Lyapunov函数求导：

(22)

利用2-范数的性质和=ξ－、=M_d－ ，并结合引理1进一步得到

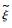
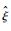
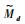
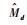
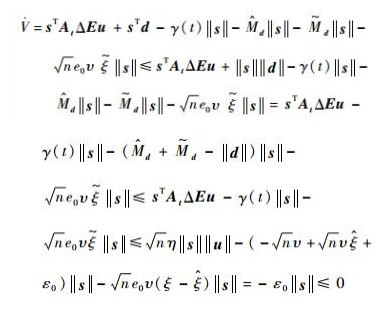(23)

式 (23) 表明，函数V至少不会单调递增，因此可得，其中sup (·) 表示上确界，即有界，因此，，从而存在且有界，根据Barbalat引理，有，从而有x→0，→0。
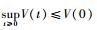
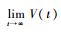
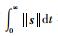
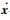
2.3 控制律的改进 控制律式 (17)~式 (21) 存在如下2个问题。
1) 抖振问题：由于滑模控制具有控制的不连续性，因此存在抖振现象。按照滑模控制理论，本文采用s/(║s║+τ) 近似代替符号函数s/║s║，其中τ为一个较小的正数，本文选取为τ=0.01。
2) 奇异性问题：当各陀螺输出力矩共面 (或共线) 时，其法线 (或法向平面) 方向无法输出力矩，此时A_t不满秩，控制律式 (17) 无法求解。可通过定义某一函数来测量奇异度的大小，本文选用函数^[15]：

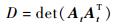(24)

作为奇异度测量函数，其中det (·) 表示方阵的行列式；D=0表示框架构型奇异，且D越大，表明越远离奇异状态。
按照陀螺广义鲁棒伪逆操纵律^[16]的设计思路，设计最终控制律如下：

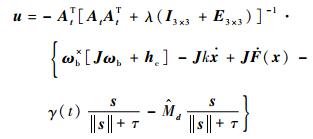(25)

式中：λ为一个较小的正数；I_3×3为三阶单位矩阵；E_3×3为对角阵，形式为

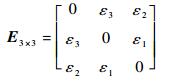其中：ε_i=0.01(0.5πt+φ_j)，j=1, 2, 3，φ_j=π(j－1)/2；τ=0.01。其余参数由式 (18)~式 (21) 给出。
3 数学仿真 3.1 金字塔构型 本文以某航天器为例进行数学仿真，航天器参数如下。
航天器转动惯量矩阵为

选用金字塔构型的SGCMGs，其中陀螺的标称角动量h₀=200 N·m·s，陀螺个数n=4；初始姿态角为：φ(0)=1.5°, θ(0)=1.5°, ψ(0)=1.5°；ω_b的初始值为ω_b(0)=[0?0?0]^T, 轨道飞行高度为26 600 km，环境干扰力矩综合考虑地球引力摄动、太阳光压力矩、太阳辐射压力扰动等，采用文献[17]给定的外干扰形式：

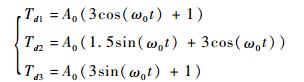其中：A₀为干扰力矩幅值，取A₀=1.5×10^-5 N·m，ω₀为轨道角速度，由飞行高度决定，横向矩阵A_t表达式^[18]为

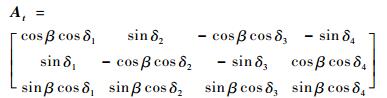(26)

式中：β=53.1°。
在陀螺无故障工作时，调节控制器参数，以实现较好的姿态控制性能，选用如下控制器参数：k=2, c₀=0.5, ε₀=0.5, c₁=10, λ=0.001。
2个自适应参数的初值选取如下。
(0)： (0) 未知，在本例中直接设定为0。
(0)：由于一般认为在仿真开始时，系统不存在故障，因此，选取(0)=1。
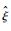
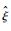
另外，利用PID控制器进行数值仿真与本文提出的容错控制律进行对比。为了更好地比较效果，本文选择设计的PID控制参数保证无故障情况下，2种控制器对该模型具有相似的控制性能，因此选择PID控制参数如表 1所示, 其中：K_ii、K_pi、K_di分别为PID控制积分、比例及微分控制参数，i=1, 2, 3。
表 1 PID控制参数 Table 1 Parameters of PID control

参数	滚转通道				俯仰通道				偏航通道
	Ki1	Kp1	Kd1		Ki2	Kp2	Kd2		Ki3	Kp3	Kd3
数值	0.1	300	3 000		0.1	500	9 000		0.1	500	9 000

表选项






下面针对不同的故障模式进行仿真。
Case 1?常值乘性故障+常值加性故障。

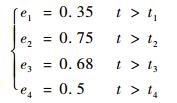(27)

式中：t₁=150 s；t₂=180 s；t₃=200 s；t₄=240 s。
图 1表明，无故障情况下，航天器在滑模控制或PID控制下，都能在50 s内实现姿态的稳定，且控制性能基本接近。图 1和图 2表明，在150 s故障发生之后，PID控制下的姿态角和姿态角速度开始发散，而滑模控制仍能够使得姿态角及姿态角速度稳定，这表明控制律式 (25) 对该常值故障具有较强的鲁棒性。图 3表明，故障发生后，框架构型逐渐靠近奇异状态，但不会达到奇异状态，这证明了本文采用广义鲁棒伪逆操纵率的合理性。

图 1 Case1故障模式下姿态角响应 Fig. 1 Attitude angle response under Case 1 fault mode

图选项

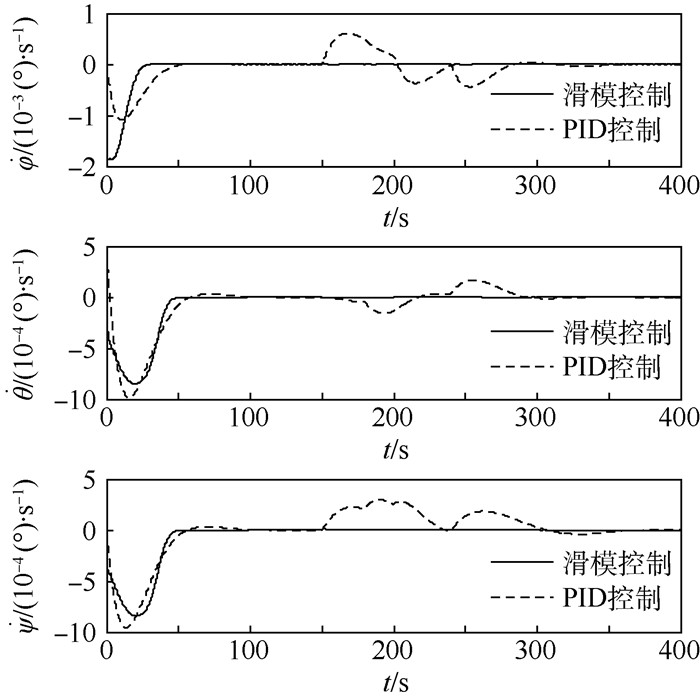图 2 Case 1故障模式下姿态角速度响应曲线 Fig. 2 Attitude angular velocity response under Case 1 fault mode

图选项

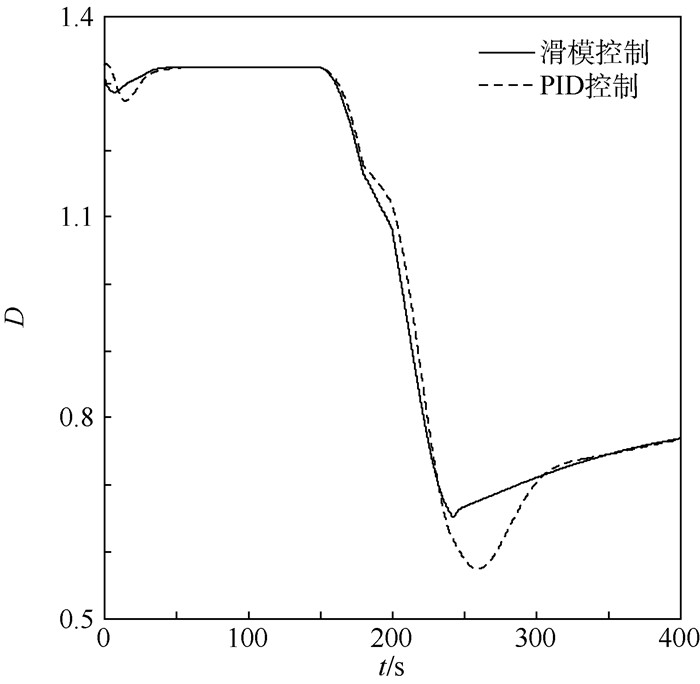图 3 Case 1故障模式下奇异度测量 Fig. 3 Singularity measurement under Case 1 fault mode

图选项

Case 2?时变随机型乘性故障+常值加性故障。

(28)

式中：rand (·) 表示幅值为1的随机函数。
图 4和图 5表明，当航天器执行机构受到的故障为时变随机型乘性故障，PID控制下的航天器姿态在故障发生之后会逐渐偏离平衡状态，航天器失稳，而控制律式 (25) 能够使得航天器在故障发生前后姿态基本保持不变，同样表现出对这种时变随机乘性故障较强的鲁棒性。而图 3和图 6共同表明，无论发生哪种故障，无论PID控制或控制律式 (25)，故障发生时刻，陀螺的奇异值都会发生明显的改变，这代表了控制器对故障的反应会使得框架角迅速改变，因此奇异值也有一个快速变化，但始终没有奇异。

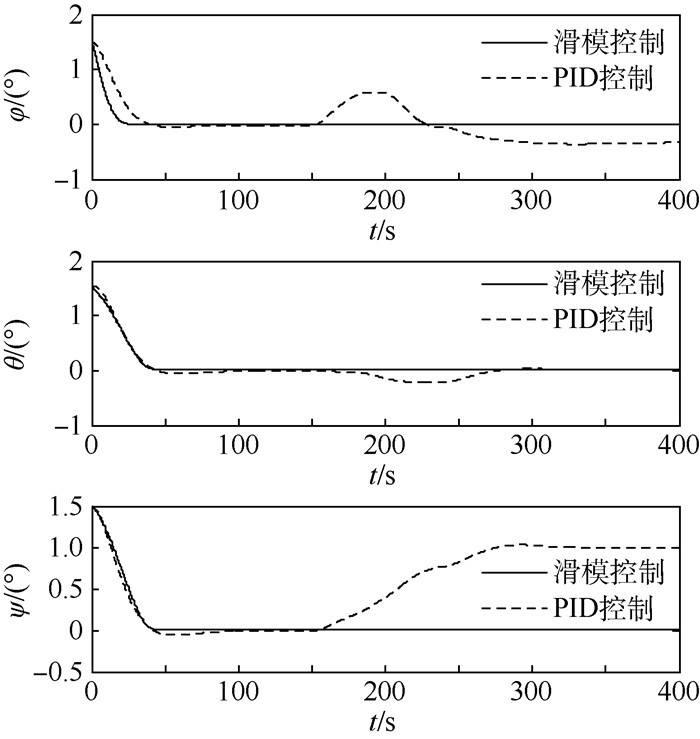图 4 Case 2故障模式下姿态角响应 Fig. 4 Attitude angle response under Case 2 fault mode

图选项

图 5 Case 2故障模式下姿态角速度响应曲线 Fig. 5 Attitude angular velocity response under Case 2 fault mode

图选项

图 6 Case 2故障模式下奇异度测量 Fig. 6 Singularity measurement under Case 2 fault mode

图选项

3.2 四棱锥构型 选用航天器参数、初始姿态角、轨道高度以及环境干扰力矩同3.1节。采用的陀螺构型为四棱锥构型，即陀螺个数为5，陀螺的标称角动量h₀=200 N·m·s。横向矩阵A_t为^[19]

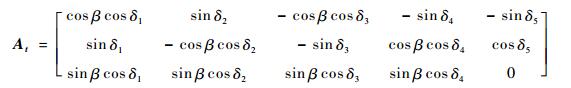(29)

式中：β=68.7°。
控制器参数设置为：k=2, c₀=0.5, ε₀=0.5, c₁=10，自适应控制参数积分初值同3.1节。
Case 3?假设存在陀螺在工作初期发生失效故障，故障参数为

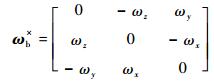(30)

式中：t₁=0 s；t₂=20 s；t₃=100 s；t₄=130 s；t₅=200 s。
图 7和图 8表明针对四棱锥构型的陀螺，即使存在陀螺完全失效故障且存在陀螺工作初期出现故障，本文设计控制律仍能保证航天器在50 s左右实现姿态稳定，这说明控制律式 (25) 对故障具有较好的鲁棒性。图 9的奇异值测量曲线虽然有波动，但是都为正值，这表明整个过程中，陀螺框架角运动不会到达奇异状态。

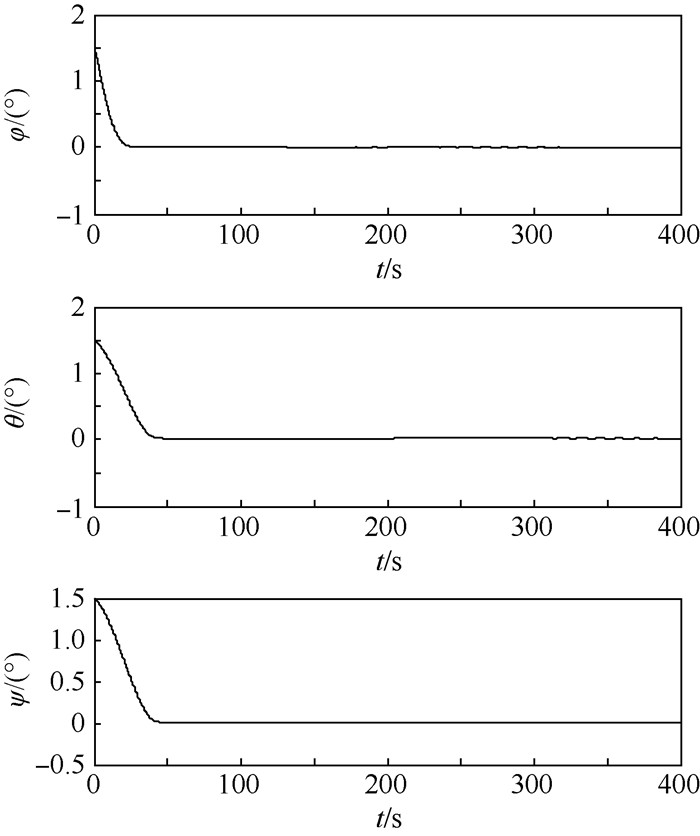图 7 Case 3故障模式下姿态角响应曲线 Fig. 7 Attitude angle response under Case 3 fault mode

图选项

图 8 Case 3故障模式下姿态角速度响应曲线 Fig. 8 Attitude angular velocity response under Case 3 fault mode

图选项

图 9 Case 3故障模式下奇异度测量 Fig. 9 Singularity measurement under Case 3 fault mode

图选项

4 结论 本文针对以SGCMGs为执行机构的航天器，在执行机构存在故障的情况下，设计了基于滑模控制理论的被动容错控制算法，并通过MATLAB/Simulink进行了数值仿真验证。该算法具有以下特点：
1) 通过自适应参数对陀螺故障信息及干扰进行实时估计，从而在未知故障和干扰先验信息时，能够对航天器的姿态进行稳定控制。
2) 该算法适用于任意构型SGCMGs的部分失效模式。
3) 该算法将陀螺框架转速直接作为控制量，更适用于工程实际。
4) 本文设计的滑模控制律虽然以SGCMGs为背景进行设计，但是由于陀螺的动力学特性与飞轮相似，本文设计控制器同样适用于以飞轮为执行机构的航天器容错控制。
为了进一步提高控制律的工程应用价值，如何修正控制器使得其能适用于陀螺框架转速受限的情况是下一步需要做的工作。

参考文献

[1]	葛建华, 孙优贤. 容错控制系统的分析与综合[M].杭州: 浙江大学出版社, 1994: 5-12. GE J H, SUN Y X. Analysis and synthesis of fault-tolerant control systems[M].Hangzhou: Zhejiang University Press, 1994: 5-12.(in Chinese)
[2]	姜斌, 冒泽慧, 杨浩, 等. 控制系统的故障诊断与故障调节[M].北京: 国防工业出版社, 2009: 1-6. JIANG B, MAO Z H, YANG H, et al. Fault diagnosis and fault accommodation for control systems[M].Beijing: National Defense Industry Press, 2009: 1-6.(in Chinese)
[3]	HU Q L, XIAO B, ZHANG Y M.Robust fault tolerant attitude stabilization control for flexible spacecraft under partial loss of actuator effectiveness[C]//2010 Conference on Control and Fault Tolerant Systems.Piscataway, NJ:IEEE Press, 2010:263-268.
[4]	JIANG Y, HU Q L, MA G F. Adaptive backstepping fault-tolerant control for flexible spacecraft with unknown bounded disturbances and actuator failures[J].ISA Transactions, 2010, 49(1): 57–69.DOI:10.1016/j.isatra.2009.08.003
[5]	JIN J, KO S, RYOO C K. Fault tolerant control for satellites with four reaction wheels[J].Control Engineering Practice, 2008, 16(10): 1250–1258.DOI:10.1016/j.conengprac.2008.02.001
[6]	XIAO B, HU Q L, ZHANG Y M, et al. Fault-tolerant tracking control of spacecraft with attitude-only measurement under actuator failures[J].Journal of Guidance, Control, and Dynamics, 2014, 37(3): 838–849.DOI:10.2514/1.61369
[7]	管宇. 卫星姿态控制系统的鲁棒容错控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2006: 30-46. GUAN Y.Research on fault diagnosis and fault-tolerant control of satellite attitude control system[D].Harbin:Harbin Institute of Technology, 2006:30-46(in Chinese).
[8]	贾庆贤, 张迎春, 陈雪芹, 等. 卫星姿态控制系统故障重构观测器设计[J].宇航学报, 2016, 37(4): 442–450. JIA Q X, ZHANG Y C, CHEN X Q, et al. Observer design for fault reconstruction in satellite attitude control system[J].Journal of Astronautics, 2016, 37(4): 442–450.(in Chinese)
[9]	CAI W C, LIAO X H, SONG D Y. Indirect robust adaptive fault-tolerant control for attitude tracking of spacecraft[J].Journal of Guidance, Control and Dynamics, 2008, 31(5): 1456–1463.DOI:10.2514/1.31158
[10]	JIN L, XU S J. Fault tolerant attitude control for small satellites using single gimbal control moment gyros and magnetic torquers[J].Journal of Aerospace Engineering, 2014, 28(3): 1–12.
[11]	ZHANG A H, HU Q L, ZHANG Y M. Observer-based attitude control for satellite under actuator fault[J].Journal of Guidance, Control, and Dynamics, 2015, 38(4): 806–811.DOI:10.2514/1.G000625
[12]	YAN R D, ZHONG W.Disturbance observer-based attitude control of spacecraft with single-gimbal control moment gyros[C]//Proceeding of the 11th World Congress on Intelligent Control and Automation.Piscataway, NJ:IEEE Press, 2014:3107-3111.
[13]	欧阳高翔, 倪茂林, 孙承启, 等. 航天器的故障建模于应用[J].航天控制, 2011, 29(5): 22–29. OUYANG G X, NI M L, SUN C Q, et al. The fault modeling and application to aerospace engineering[J].Aerospace Control, 2011, 29(5): 22–29.(in Chinese)
[14]	史荣昌, 魏丰. 矩阵分析[M].北京: 北京理工大学出版社, 2010: 168-187. SHI R C, WEI F. Matrix analysis[M].Beijing: Beijing Institute of Technology Press, 2010: 168-187.(in Chinese)
[15]	WIE B. Singularity analysis and visualization for single-gimbal control moment gyro systems[J].Journal of Guidance, Control, and Dynamics, 2004, 27(2): 271–282.DOI:10.2514/1.9167
[16]	WIE B. Singularity escape/avoidance steering logic for control moment gyro systems[J].Journal of Guidance, Control and Dynamics, 2005, 28(5): 948–958.DOI:10.2514/1.10136
[17]	张爱华, 霍星. 航天器执行机构姿态容错控制[M].北京: 科学出版社, 2015: 53-58. ZHANG A H, HUO X. Actuator attitude fault tolerant control for spacecraft[M].Beijing: Science Press, 2015: 53-58.(in Chinese)
[18]	李力文, 周军, 黄河, 等. 附加框架角速度的SGCMG操纵律设计[J].宇航学报, 2004, 35(1): 69–75. LI L W, ZHOU J, HUANG H, et al. Steering law design for SGCMG system based on appending gimbal rates[J].Journal of Astrenautics, 2004, 35(1): 69–75.(in Chinese)
[19]	张锦江. 单框架控制力矩陀螺系统的构型分析和对比研究[J].中国空间科学技术, 2003(3): 52–56. ZHANG J J. Research on configuration analysis and comparison of SGCMG system[J].Chinese Space Science and Technology, 2003(3): 52–56.(in Chinese)