自20世纪90年代以来，正交频分复用技术 (OFDM) 以其高频谱效率、均衡简单、可有效对抗多径衰落信道和适合高速宽带无线环境等特点成为国内外研究的热点，大规模集成电路的发展，近代移动通信综合化多媒体化的趋势，促使OFDM技术及其相关技术得到巨大的发展，如第四代移动通信系统LTE^[1]，具有中国自主知识产权的数字电视DTMB^[2]等系等均已获得成熟商业应用。
OFDM作为一种宽带通信系统，很容易受到干扰。在现代移动通信系统中，无论在民用还是军用领域，存在着各种各样的自然或人为干扰。其中窄带干扰 (NBI) 已经成为一种典型的破坏通信系统干扰类型，多音干扰 (单音干扰可看作多音干扰的一种) 则是NBI的一种最直接和常见的干扰形式^[3]，文献[3]的仿真表明，多音干扰对OFDM系统性能有很恶劣的影响。如何有效抑制多音干扰，对于OFDM系统来说变得尤为迫切。
文献[4-6]采用加窗法抑制NBI，如果单音干扰采样序列在快速傅里叶变换 (FFT) 的观察窗口内不满足其周期整数倍，则会造成频谱泄漏。余弦窗可有效减小频谱泄漏，而采用重叠加窗、反加窗法不但有效降低频谱泄漏并能最大程度减小因加窗带来的信噪比损失。文献[7]设计了接收端窄带干扰滤波器，在时域通过采用循环前缀块最小均方算法 (CP-BLMS) 构造一个时域窄带干扰滤波器从而进行干扰抑制。文献[8]提出一种OFDM系统的联合均衡与干扰抑制的算法，利用循环前缀 (CP) 的信息进行时域滤波器的设计以达到抗干扰和均衡的目的。文献[9]给出一种低秩线性最小均方误差 (LMMSE) 的窄带干扰抑制方案。考虑了所有子载波上的干扰频谱泄漏，是一种频域干扰信号的估计重构以及去除的方法，但需要预先获知窄带干扰信号的功率谱密度函数。文献[10]利用最大似然估计算法在频率域估计多音干扰参数，并将此干扰信息重构、消除。文献[11-13]研究了窄带干扰的检测以及检测门限的优化，当干扰位置被检测出后将对应谱线幅度置零。显然，此类干扰消除方法性能直接取决于干扰位置的检测性能，而多音干扰功率会泄漏在整个带宽，泄漏功率相对较小的位置不仅分布带宽广且很难被检测。
综上，接收端抗NBI干扰主要包括干扰抑制以及干扰消除2大类，抑制方法实现相对简单，但当干扰严重时，干扰抑制效果有限。文献[10]虽然提出了对多音干扰进行参数估计、重构和消除的方法，但当相邻单音干扰间隔较小且无法分辨时，干扰重构性能会受到很大影响。本文提出的方案通过提升频率分辨率以区分间隔较近的单音干扰，之后基于迭代过程逐一对单音干扰进行最大似然的参数估计、干扰重构和消除，且保证算法具有较低的运算复杂度。
1 系统模型 OFDM系统基带信号可表示为

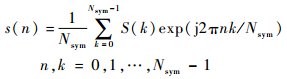(1)

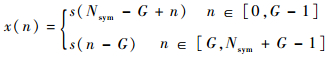(2)

式中：S(k) 为调制符号；N_sym为快速傅里叶逆变换 (IFFT) 点数；j=；x(n) 为添加CP后OFDM信号；G为CP长度。
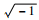
单音干扰可表示为^[14]

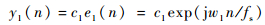(3)

式中：c₁=a₁exp (jφ₁), a₁为信号幅度，φ₁为初始相位；w₁=2πf₁, f₁为单音频率；f_s为采样频率。
多音干扰由多个单音干扰叠加而成^[3]：

(4)

式中：Q为单音干扰个数。
存在多音干扰时，去CP后的OFDM符号的频域接收表达式为

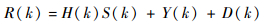(5)

式中：H(k) 为信道频域响应；Y(k)=FFT (y(n)) 为多音干扰频域信号；D(k)~N(0, σ_n²) 表示0均值功率为σ_n²的高斯白噪声 (AWGN)。
2 FFT-MLE单音参数估计 多音干扰是由若干单音干扰叠加而成，因此，单音干扰参数估计是多音干扰消除的基础。文献[10]采用了基于离散傅里叶变换 (DFT) 的最大似然单音干扰参数估计 (DFT-MLE) 方法重构单音，参数的估计过程如下：

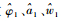
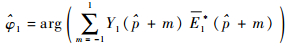(6)

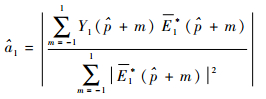(7)

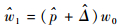(8)

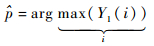(9)

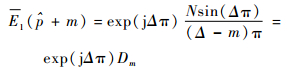(10)

(11)

式中：E₁(p+m) 为e₁(n) 经DFT变化后，在峰值点位置p及其附近m点位置上的值，需满足m?N；p=round (w₁/w₀), w₁=(p+Δ)w₀，w₀为单音信号DFT变化后的频域分辨率，Δ为频率分辨率w₀的小数倍。
可见，MLE估计方法基于DFT并利用单音频域功率峰值位置及其左右位置所对应的3个幅值完成参数估计。
显然，当DFT点数过大则会带来较大的实现复杂度。为了降低复杂度和增加运算速度，需要使用FFT运算代替DFT运算。本文推导了一种基于时域补零和FFT变化的最大似然单音参数估计方法FFT-MLE。
对e₁(k) 进行DFT变换^[14]:

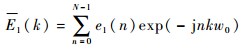(12)

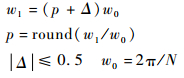(13)

令k=p+m，则有

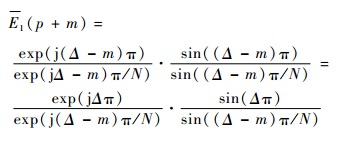(14)

当m?N，exp (j(Δ-m)π/N)≈1，sin (((Δ-m)π)/N)≈(Δ-m)π/N，则E₁(p+m) 可表示为式 (10)。
本文首先对e₁(n) 进行补零至N_FFT点, 得到新的序列e₁′(n)：

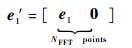(15)

进行FFT变化得到：

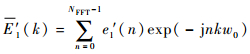(16)

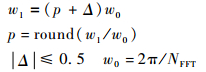(17)

令k=p+m，则

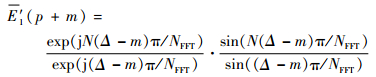(18)

当m?N_FFT，exp (j (Δ-m)π/N_FFT)≈1，sin ((Δ-m)π/N_FFT)≈(Δ-m)π/N_FFT，则有

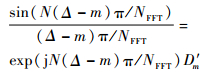(19)

对于FFT-MLE，的估计方法按式 (11) 不再适用，证明如下：
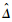
假设α=+1，对于DFT-MLE则有

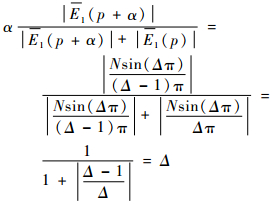(20)

对于FFT-MLE则有

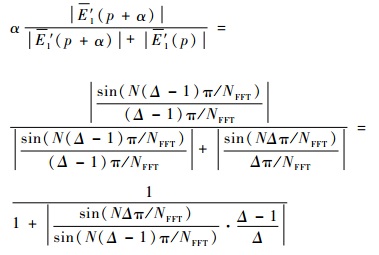(21)

其中: ，显然式 (21) 不等于Δ。
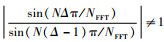
为了估计Δ，本文构造函数：

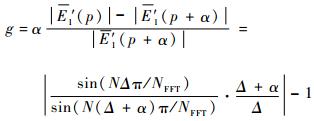(22)

对sin x进行泰勒展开：

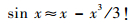(23)

则有

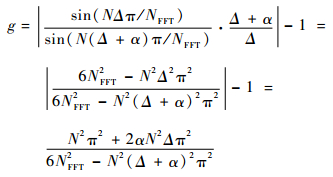(24)

由于N²(Δ+α)²π²与6N_FFT²相比较小，则式 (24) 可简化为

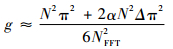(25)

于是得到：

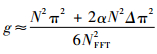(26)

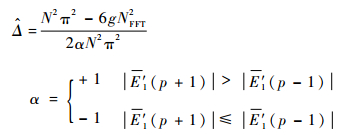(27)

在得到后，可根据式 (6)~式 (9) 求得、和，不同的是，需用E′₁(p+m) 代替E₁(p+m)，用Y′₁(+m) 代替Y₁(+m)，Y′₁为对单音干扰接收序列y₁(n) 进行补零至N_FFT点并进行FFT变化后的序列。
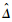
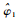
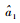
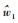
对于DFT-MLE，假设序列长度为2^N+1点，则DFT运算需要2^N+1²次复数乘法。对于FFT-MLE，补2^N+1-2^N-1个零后，做2^N+1点FFT运算共需要2^Nlb (2^{N + 1}) = 2^N(N + 1) 次复数乘法。前者运算量至少约为后者的倍。
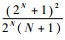
3 多音干扰消除方案 3.1 多音干扰识别 如果存在相隔较近的相邻单音干扰时，当频域分辨率不够，则单音参数会估计失效，举例如下：
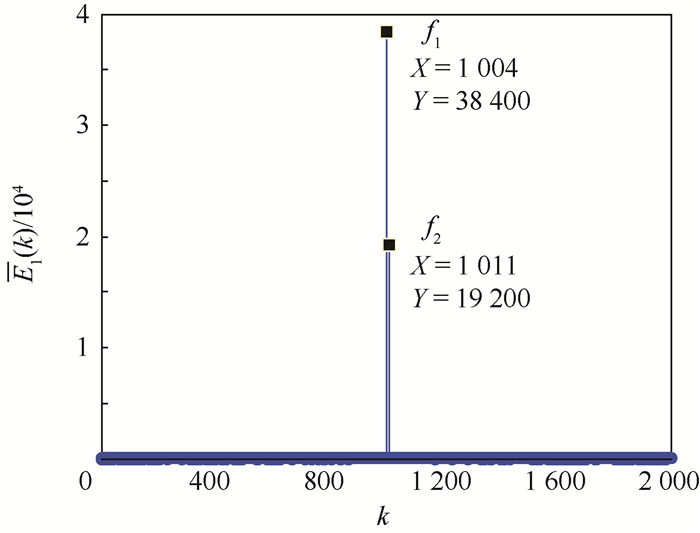
假设在增加采样点前频率分辨率f₀=2 000 Hz，2个单音干扰的频率分别为f₁=200.6 kHz和f₂=202 Hz，则对应的峰值分别为p₁=101，p₂=102，显然，如图 1(a)所示，对于单音干扰2来说，单音干扰1在p₂点仍有较大峰值，从而带来干扰而影响估计准确度。增加采样序列长度使得f₀′=200 Hz，则2个单音的间隔相应增大，见图 1(b)所示。

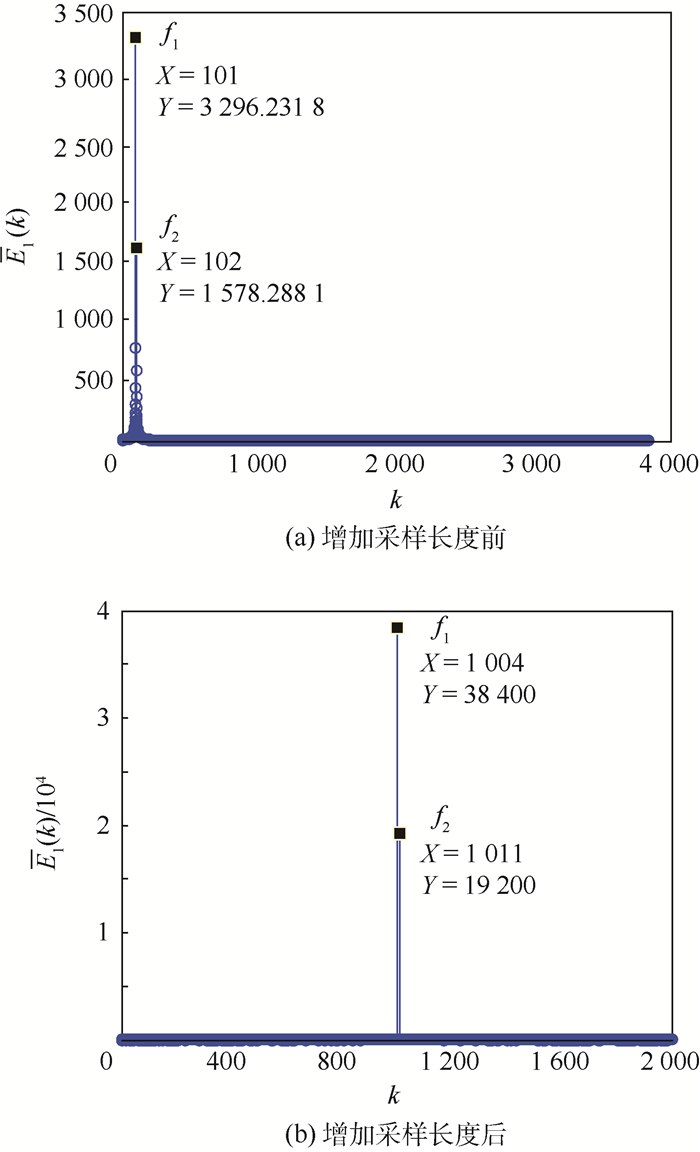图 1 增加采样长度前后多音干扰频域示意图 Fig. 1 Schematic diagram of multi-tone interference frequency domain before and after sampling length increase

图选项

根据DFT变化性质可知，基带采样速率为f_s，满足频率分辨率为f₀时的采样点数为N=f_s/f₀，假设存在2个相邻单音，频率分别为f₁和f₂，则单音1的峰值位置为p₁=round (f₁/f₀)，单音2的峰值位置为p₂=round (f₂/f₀)，当N增大即f₀变小时，2个相邻单音峰值位置间隔的谱线数p₁₂=p₂-p₁相应增大，从而使得容易分辨与识别。
当采样点数N足够大时，不仅得到更高的频率分辨率，而且相邻单音对目标单音带来的相对干扰足够小，使得目标单音的参数估计性能会足够好。分析如下:
假设存在2个相邻单音，单音1为预估计参数的目标单音，单音2为干扰。考虑单音2在单音1的频谱峰值位置处带来的干扰。
单音1在其主峰p₁处的有用信号功率为

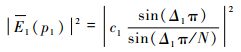(28)

式中：p₁=round (f₁/f₀)，f₁=(p₁+Δ₁)f₀，Δ₁为第1个单音频率相对于f₀的小数倍。
当N→∞时，Δ₁π/N足够小，所以有sin (Δ_{1, N}π/N)≈Δ₁π/N→0，且由于|sin (Δ₁π)|≤1，所以得到|E₁(p₁)|²→∞。
单音2在单音1主峰p₁处的干扰功率为

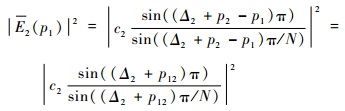(29)

式中：p₂=round (f₂/f₀)，f₂=(p₂+Δ₂)f₀；p₁₂=p₂-p₁为在采样点数为N时，2个单音在频域上峰值位置间隔的谱线数；Δ₂为第2个单音频率相对于f₀的小数倍。
考虑到存在：(Δ₂+Δp)π/N=Δ₂π/N+Δpπ/N，假设当采样点数N变为之前的k倍，p₁₂也相应变为之前的k倍，则当k足够大，(Δ₂+Δp)π/N→Δpπ/N。
所以当N→∞时，|E₂(p₁)|²不会超过某一常数η，即|E₂(p₁)|²≤η。
定义单音1在峰值p₁处的载干比 (CIR) 为

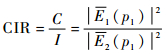(30)

可见，当N→∞即f₀→0时，CIR→∞。此时相邻单音对目标单音参数估计的相对干扰足够小。
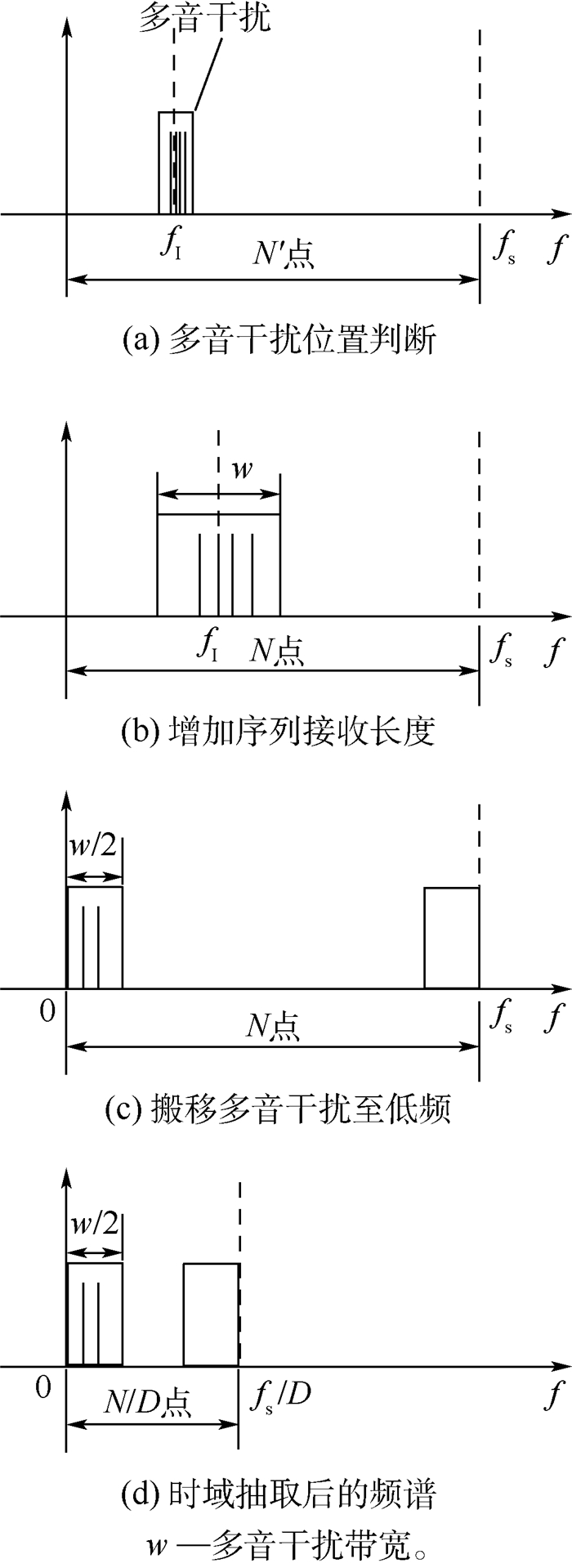
虽然增加序列采样长度N会带来足够高的频率分辨率并提升单音参数估计性能，但同时需要较大的存储空间。为了降低复杂度，本文采用ZoomFFT^[15]技术，先提取感兴趣的频带，再通过移频—低通滤波—降采样的步骤对局部频带分辨率进行放大并减少处理点数 (见图 2)。本文采用该技术进行干扰识别的具体步骤如下：

图 2 采用ZoomFFT技术的多音干扰识别示意图 Fig. 2 Schematic diagram of multi-tone interference identification using ZoomFFT

图选项

1) 判断多音干扰的中心频率f_I
先取N′点较短长度接收数据r₁′并进行FFT变化后得到R₁′，基带采样频率为f_s, 此时的频域分辨率为f₀=f_s/N′，N′为此步骤中FFT变换的点数。在频域设置信噪比门限T₁，采用门限法检测干扰簇位置p_I′。

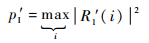(31)

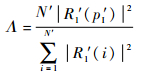(32)

式中：Λ为干扰峰值功率与信号平均功率的比值。
如果Λ>T₁，则认为存在多音干扰，其中心频率为f_I=p_I′ f_s/N′。
2) 增加序列接收长度至N点得到r₂，此时的频域分辨率为f₀=f_s/N。
3) 将多音干扰搬移至低频

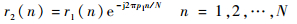(33)

此时，搬移后的频谱与原频谱关系为R₂(k)=R₁(k+p_I)，其中，p_I=round (p_I′N/N′)。
在降采样前，为抗混叠，在时域进行低通滤波，保留多音干扰所在频段。低通滤波器W通带带宽为B。

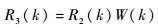(34)

式中：W(k) 为理想低通滤波器的频率响应。
4) 在时域进行D倍抽取

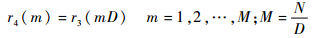(35)

r₄(m) 与原抽样前信号频谱关系为

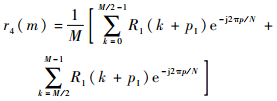(36)

r₄(m) 频域信号可表示为

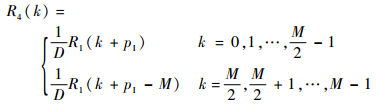(37)

D应满足

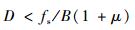(38)

式中：μ为低通滤波器滚降因子。
可见，此时通过ZoomFFT操作保留了多音干扰的谱线相位与幅度值，在达到相同频谱分辨率的前提下，储存序列长度减小为ZoomFFT前的1/D倍。
3.2 基于迭代的多音干扰消除方案 多音干扰消除方案包含3个模块，分别为多音干扰识别模块、多音干扰估计模块、多音干扰消除模块。方案框图如图 3所示。

图 3 多音干扰消除方案流程图 Fig. 3 Flowchart of multi-tone interference cancellation scheme

图选项

干扰消除方案步骤如下：
1) 利用第4.1节方案识别多音干扰并得到
ZoomFFT输出的M点时域序列r₄。
2) 基于迭代的多音干扰参数估计。
①?由于M往往不一定为2的幂次方，对r₄补零至N_FFT得到r₄′；对r₄′进行FFT变化得到R₄′，类似式 (29) 原理，通过判断频域样点值R₄′(i) 的相对功率值并设置信噪比门限T₂可找到第1个单音干扰的峰值位置p₁。
②?利用第3节提出的FFT-MLE算法对频域序列R₄′进行单音参数估计，得到第1个单音参数估计值: 。
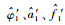
③?对第1个单音进行M点的时域重构：

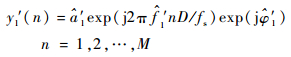(39)

④?将第1个单音从r₄中删除：r₄⁽¹⁾=r₄-y₁′, r₄^(q), q=1, 2, …, Q表示r₄经过第q次单音消除后的序列。
⑤?重复步骤①~步骤④，直至经过Q次单音干扰删除后，r₄^(Q)在第①步中不再检测到单音干扰存在。此时，得到多音干扰中所有Q个单音的参数估计：。
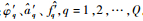
⑥?由于在干扰识别模块中进行了移频操作，需对频率进行还原：。储存所有单音干扰参数。
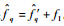
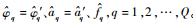
3) 多音干扰重构及消除。
①?根据第2) 步储存的各单音干扰参数，重构N点的时域多音干扰

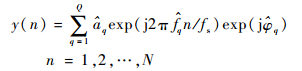(40)

②?对N点接收数据r₁进行干扰消除

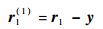(41)

③?此时式 (5) 中的多音干扰Y得以消除，之后进行去CP以及OFDM解调操作。
4 仿真结果与分析 4.1 FFT-MLE与DFT-MLE算法的性能对比 仿真分别给出频率、相位和幅度在高斯白噪环境下的归一化均方根误差统计：

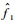
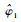
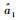
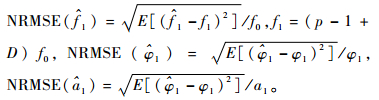设定单音信号功率归一化，仿真中定义信噪比：SNR=10 lg (1/σ_n²)。仿真参数如表 1所示。
表 1 单音参数估计仿真参数配置 Table 1 Simulation parameter configuration of single-tone parameter estimation

仿真条件	参数配置
采样率/MHz	7.56
采样点数N	595
FFT点数NFFT	3 780
单音参数配置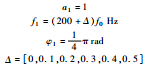
信道模型	AWGN信道

表选项






DFT-MLE参数估计性能如图 4所示, FFT-MLE参数估计性能如图 5所示。

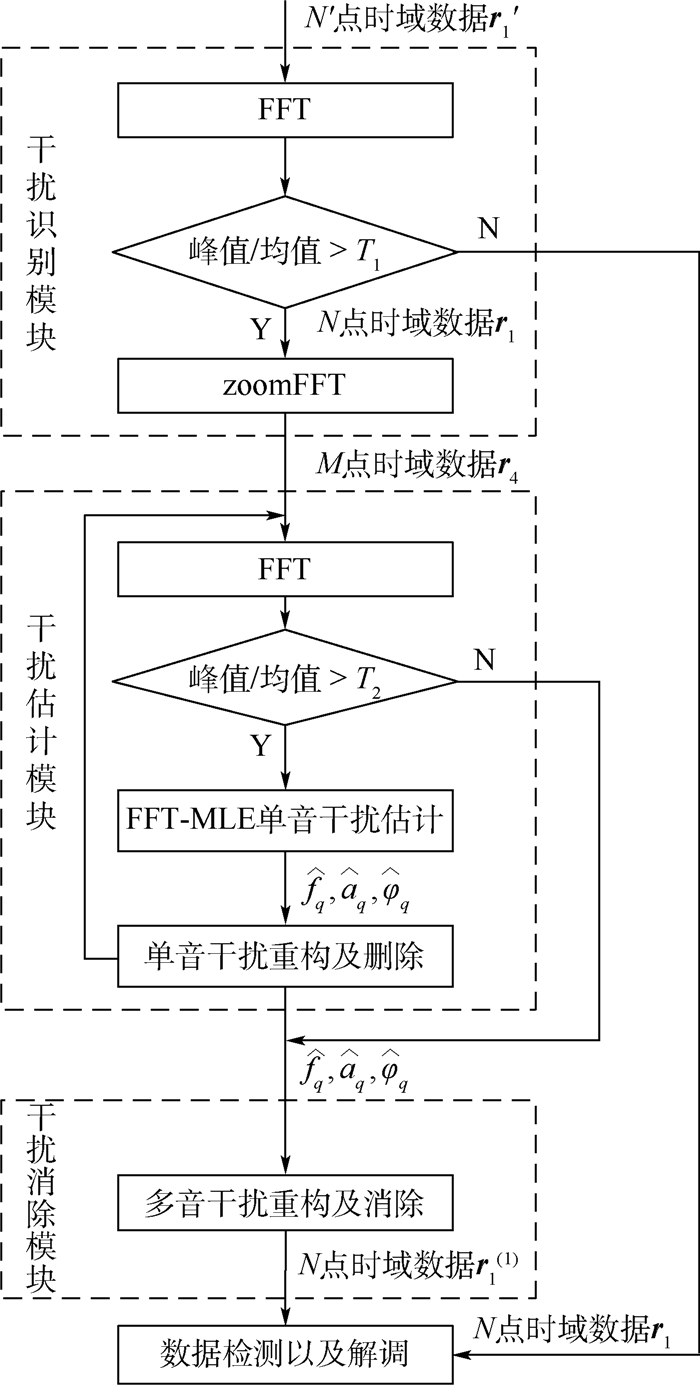图 4 DFT-MLE参数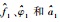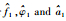估计性能 Fig. 4 Estimated performance of parameter based on DFT-MLE

图选项

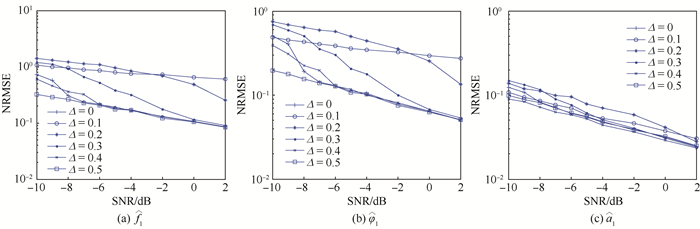图 5 FFT-MLE参数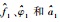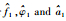估计性能 Fig. 5 Estimated performance of parameter based on FFT-MLE

图选项

由仿真结果图 4可见，对于DFT-MLE，性能随着小数倍频率Δ的变化而不同，在信噪比SNR=0时，的NRMSE区间约为0.1~0.6，的NRMSE区间约为0.06~0.30，的NRMSE区间约为0.025~0.030。由仿真结果图 5可见，对于FFT-MLE，在SNR=0时，的NRMSE约为0.1，的NRMSE约为0.06，的NRMSE约为0.025，Δ的变化对性能影响不大。这是因为，据式 (11) 可得到Δ与Y₁之间的关系，对于DFT-MLE，Y₁(+α) 随着不同Δ值的变化较大，对于FFT-MLE，变化则较小，所以有较好的鲁棒性, 见图 6。

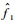
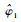
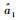
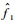
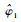
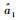
图 6 DFT-MLE和FFT-MLE Y1值相对Δ变化示意图 Fig. 6 Schematic diagram of value range of Y1 with different Δ based on DFT-MLE and FFT-MLE

图选项

可见，对于DFT-MLE，当Δ从0~0.5，Y₁() 幅值下降了约2 dB，Y₁(+1) 上升了约25 dB。而对于FFT-MLE，Y₁的值变化却很小。
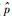
4.2 基于迭代的多音干扰消除方案性能 设定OFDM发送信号功率归一化，仿真中定义信干比：SIR=10 lg (1/a_q²)。
仿真中，将本方案与另外2种方案性能进行了对比，分别为文献[4]的汉明窗干扰抑制方案和文献[10]的基于迭代的干扰消除方案。假设信道信息H理想已知，采用迫零ZF检测。仿真参数如表 2所示。QPSK调制下采用抗干扰方案的误码率 (BER) 性能如图 7和图 8所示。
表 2 多音干扰消除方案仿真参数配置 Table 2 Simulation parameter configuration of multi-tone interference cancellation scheme

仿真条件	参数配置
采样率/MHz	7.56
OFDM符号点数	3 780
CP样点数	595
调制方式	QPSK
r′1长度N′	3 780
r1长度N	(3 780+595)×10=43 750
NFFT	8 192
降采样倍数D	10
低通滤波器L	带宽：B=1 MHz 滚降系数：μ=0.5 阶数：256
单音参数配置	aq=[a1, a2, a3, a4, a5](对应SIR中各设定值) fq=[200 400, 201 400, 202 400, 1 199 400, 1 200 400]Hz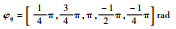
SIR	SIR1=[10,0,10,0,0] dB SIR2=[0,-10,0,-10,-10] dB SIR3=[-10, -20, -10, -20, -20] dB
信道模型	AWGN信道TU信道[16]

表选项

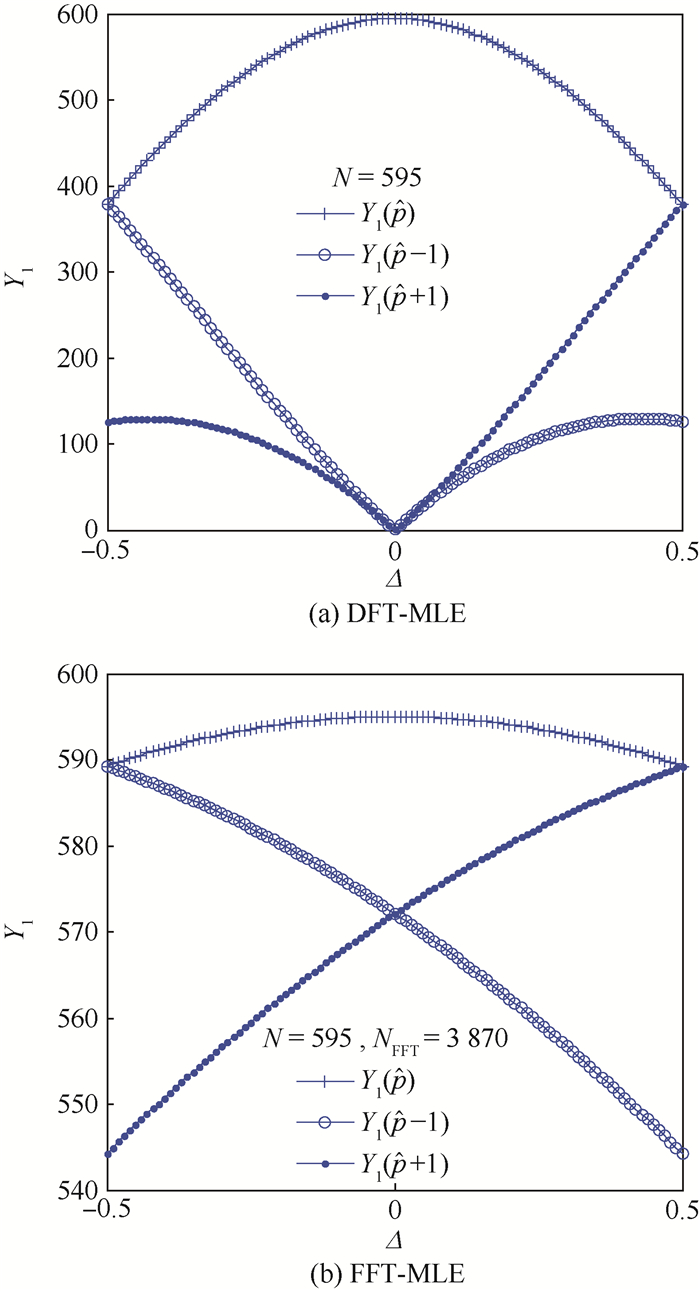图 7 AWGN信道下本文方案与其他2种文献方案性能对比 Fig. 7 Performance comparison between proposed scheme and two schemes in reference under AWGN channel

图选项

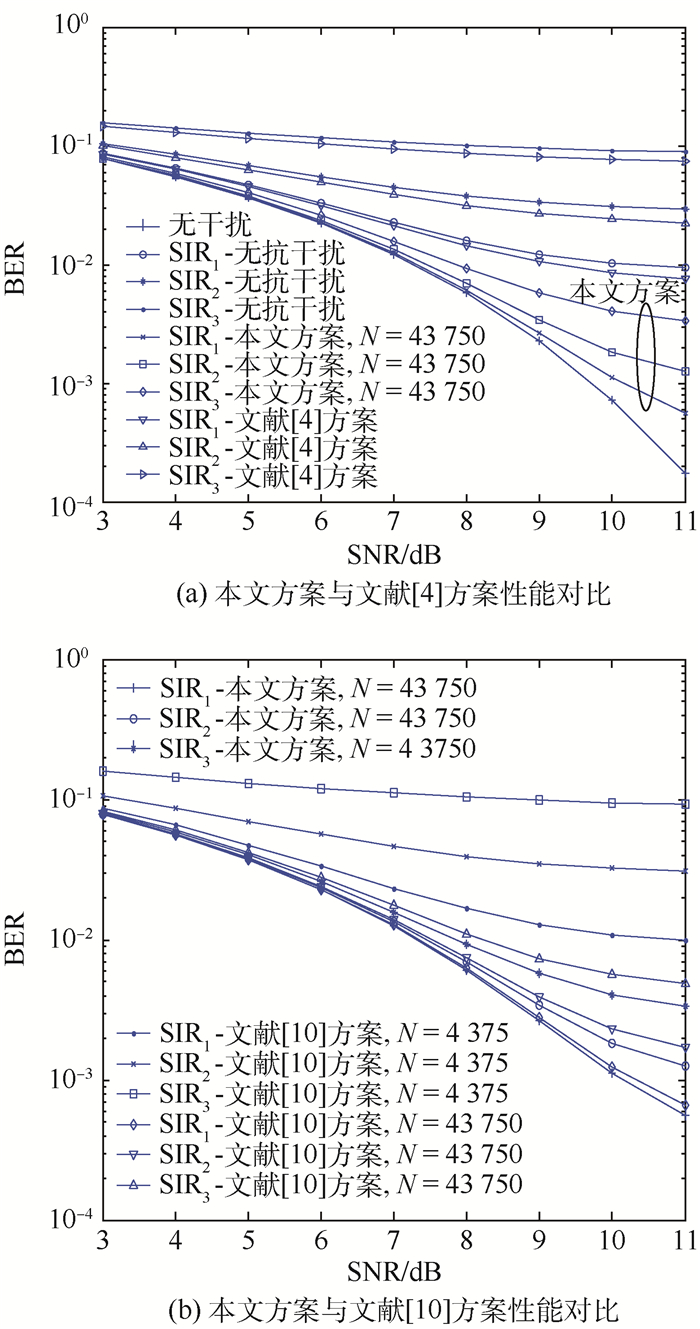图 8 TU信道下本文方案与其他2种文献方案性能对比 Fig. 8 Performance comparison between proposed scheme and two schemes in reference under TU channel

图选项

由仿真结果图 7和图 8可见，AWGN信道下，信干比设置为SIR₁，当BER=0.01，存在干扰时的性能与无干扰的理想性能相比恶化了约3 dB，采用汉明窗干扰抑制方案时性能恶化了约2 dB，采用本文方案，接收序列采样长度N=43 750，ZoomFFT后长度为M=4 375，即使BER=0.001时，性能恶化也只0.5 dB。SIR₂和SIR₃配置时，本文方案的性能改善也很明显。TU信道下，各SIR配置时，无抗干扰算法和汉明窗干扰抑制方案下的BER已无法下降，采用本文方案时，SIR₁配置，即使BER=0.001时，性能恶化也只3 dB。
对比本文方案与文献[10]方案的性能结果表明，当采样序列长度同为N=43 750时，文献[10]的性能要略差于本文方案，这是由于本文提出的FFT-MLE较DFT-MLE有更好的鲁棒性 (见4.1节)。同时，由于本方案采用了ZoomFFT技术，所以储存样点仅为4 375点。本方案相比不仅有更好的干扰消除性能并且有更低的处理复杂度。而当文献[10]方案储存样点降为N=4 375时，频谱分辨率降低，正如4.1节分析，采样长度减小导致干扰估计与消除性能发生较大恶化。
5 结论 本文提出一种基于迭代的多音干扰消除方案，包括多音干扰识别、多音参数估计和多音干扰消除3个模块，具有低运算复杂度的特点。
1) 在多音干扰识别模块中，通过增加采样序列长度以减小单音参数估计过程中的互干扰。为简化运算复杂度，采用ZoomFFT技术。
2) 在多音参数估计模块中，由于ZoomFFT的输出序列点数并不一定满足2的N次幂，因此给出一种基于FFT的最大似然参数估计方法FFT-MLE。相比经典DFT-MLE，不仅有更低的运算复杂度，且在不同的小数倍频率下其估计性能有更好的鲁棒性。
3) 最后的仿真结果表明，本文的多音干扰消除方案在OFDM系统中表现出较好的抗干扰性能。

参考文献

[1]	SESIA S, TOUFIK I, BAKER M. LTE——UMTS长期演进理论与实践[M]. 马霓, 邬钢, 张晓博, 等, 译. 北京: 人民邮电出版社, 2012: 84-101.SESIA S, TOUFIK I, BAKER M.LTE-The UMTS long term evolution:From theory to practice[M].MA N, WU G, ZHANG X B, et al, translated.Beijing:Posts & Telecom Press, 2012:84-101(in Chinese).
[2]	国家标准化管理委员会. 数字电视地面广播传输系统帧结构、信道编码和调制: GB 20600-2006[S]. 北京: 数字电视地面广播传输国家标准特别工作组, 2006: 7-26.Standardization Administration of China.Digital television terrestrial transmission system frame structure, channel encoding and modulation:GB 20600-2006[S].Beijing:Special Working Group of National Standard for Transmission of Digital Television Terrestrial Broadcasting, 2006:7-26(in Chinese).
[3]	熊李娜, 李涛, 梅林, 等. OFDM系统的抗窄带干扰性能分析[J].通信技术, 2011, 44(10): 25–29.XIONG L N, LI T, MEI L, et al. Performance of OFDM system under narrow-band interference[J].Communications Technology, 2011, 44(10): 25–29.(in Chinese)
[4]	邹宁, 徐松涛, 刘明园, 等. 一种重叠加窗频域抑制窄带干扰算法及研究[J].现代防御技术, 2010, 38(3): 120–126.ZOU N, XU S T, LIU M Y, et al. An overlap window-based frequency-domain narrow-band interference suppression algorithm and its analysis[J].Modern Defence Technology, 2010, 38(3): 120–126.(in Chinese)
[5]	孟东, 缪玲娟, 张希. 反加窗算法及其在扩频系统窄带干扰抑制中的应用[J].电子与信息学报, 2015, 37(10): 2349–2355.MENG D, MIAO L J, ZHANG X. Inverse windowing algorithm and its application to narrow-band interference suppression in direct sequence spectrum system[J].Journal of Electronics & Information Technology, 2015, 37(10): 2349–2355.(in Chinese)
[6]	SHEN W J, SUN H X, CHENG E, et al.Narrowband interference suppression in underwater acoustic OFDM system[C]//International Asia Conference on Informatics in Control, Automation and Robotics (CAR).Piscataway, NJ:IEEE Press, 2010:496-499.
[7]	ZHANG J, MENG J. Robust narrowband interference rejection for power-line communication systems using IS-OFDM[J].IEEE Transactions on Power Delivery, 2010, 25(2): 680–692.DOI:10.1109/TPWRD.2009.2036179
[8]	DARSENA D, GELLI G, PAURA L, et al. Joint equalization and interference suppression in OFDM systems[J].IET Electronics Letters, 2003, 39(11): 873–874.DOI:10.1049/el:20030542
[9]	NILSSON R, SJOBERG F, LEBLANC J P. Rank-reduced LMMSE canceller for narrowband interference suppression in OFDM-based systems[J].IEEE Transactions on Communications, 2003, 51(12): 2126–2140.DOI:10.1109/TCOMM.2003.820761
[10]	周军. 基于相干检测的迭代干扰抑制技术研究[D]. 成都: 电子科技大学, 2010.ZHOU J.Iterative interference suppression technology investigation based on coherent detection[D].Chengdu:University of Electronic Science and Technology of China, 2010(in Chinese).
[11]	付卫红, 宋长汉, 黄坤. 基于差分求门限的变换域窄带干扰抑制[J].电子与信息学报, 2013, 35(12): 2960–2965.FU W H, SONG C H, HUANG K. Narrow-band interference suppression in transform domain based on difference-cluster-threshold algorithm[J].Journal of Electronics & Information Technology, 2013, 35(12): 2960–2965.(in Chinese)
[12]	李艳红, 岳珍梅, 常宏韬, 等. SC-FDE UWB系统连续窄带干扰抑制[J].兰州理工大学学报, 2014, 40(2): 102–105.LI Y H, YUE Z M, CHANG H T, et al. Suppression of continuous narrow-band interference in SC-FDE UWB systems[J].Journal of Lanzhou University of Technology, 2014, 40(2): 102–105.(in Chinese)
[13]	张韬韬, 张文逸. 基于频域互相关的窄带干扰抑制方法[J].中国科学院大学学报, 2013, 30(5): 671–675.ZHANG T T, ZHANG W Y. Suppression of narrowband interference using frequency-domain cross-correlation[J].Journal of Graduate University of Chinese Academy of Sciences, 2013, 30(5): 671–675.(in Chinese)
[14]	MALCOLM D M. Fast nearly ML estimation of the parameters of real or complex single tones or resolved multiple tones[J].IEEE Transactions on Signal Processing, 1998, 46(1): 141–148.DOI:10.1109/78.651200
[15]	江波, 唐普英. 基于复调制的的ZoomFFT算法在局部频谱细化中的研究与实现[J].大众科技, 2010(7): 48–49.JIANG B, TANG P Y. Analysis and realization of complex modulation ZoomFFT for the study of zooming in the local spectrum[J].Public Science Technology, 2010(7): 48–49.(in Chinese)
[16]	3GPP.Multiple input multiple output (MIMO) simulators:TR25.996V7.0.0[R].Valbonne:3GPP, 2007:6.