数据驱动技术逐渐被证明为一种研究故障时间序列的有效方法^[1]，特别是对于飞机这种高可靠性需求的复杂系统。对于这种系统，人们很难从影响故障产生的众多要素入手对故障时间序列进行分析，原因是覆盖不全以及一些突发因素。因此，从历史故障数据出发，应用数学方法建立故障模型，发现其中的潜在规律并对未来做出预测，是目前故障时间序列的主要研究方法。
总的来说，故障时间序列分析覆盖众多领域和方法，如水利、软件工程等领域的人工神经网络方法^[2-3]，可靠性领域的奇异谱分析(Singular Spectrum Analysis，SSA)^[1]、支持向量回归机^[4]、人工神经网络^[5-7]等方法，道路交通领域的向量自回归移动平均(Autoregressive Integrated Moving Average，ARIMA)方法^[8-9]。这些方法都是以原始数据作为输入，大致可以划分为统计和人工智能2类，其中统计类又分为时域、频域2种视角。然而，在航空领域，故障时间序列预测的研究较为罕见，且研究对象也很局限，比如文献^[7]中提到的人工神经网络方法对波音737飞机轮胎故障时间序列建模和预测。
SSA^[10-11]是一种时域和频域相结合的非参数方法，可以用于处理非线性、非平稳性以及包含噪声的时间序列^[1]，能够有效提取时间序列中的主要成分，适用性广泛且操作灵活。文献^[1]应用SSA对柴油机涡轮增压器和汽车发动机2个故障时间序列^[4]进行了建模和预测，结果表明比其他方法更为有效。然而，该文献没有清晰地给出故障时间序列应用SSA方法的数学模型，也没有进一步分析模型参数的优选问题。文献^[12]提出了一种基于SSA和ARIMA的组合模型，并用该模型预测水库中长期年径流，实验结果表明,组合模型要优于单一模型。然而，该组合方法仅通过ARIMA方法对SSA分解出的各个成分建立预测模型，没有针对每个成分的特点应用不同的分析方法，也没有清晰地给出建立该组合模型的具体算法。
本文首先针对故障时间序列，定义了应用SSA方法进行建模和预测的数学模型，在此基础上，定义了参数优选目标函数及约束条件，提出了一种基于均方根误差(Root Mean Square Error，RMSE)的参数优选算法，进一步以SSA为基础，定义了一种更为广泛的组合模型，给出了模型组合算法。最后，应用这些方法对某航空公司波音737飞机的整机故障时间序列进行实验，其中模型组合实验引入了三次指数平滑(Holt-Winters)和ARIMA2种经典的时间序列分析方法，通过实验结果对比验证了SSA方法在故障时间序列分析中的有效性和优良性。
1 相关理论和技术 1.1 奇异谱分析 SSA是一种广义功率谱分析^[12]，其主要思想是提取时间序列中的有效成分进行建模和预测。SSA包括分解和重构2个过程，分解过程又分为嵌入和奇异值分解(Singular Value Decomposition，SVD)，重构过程又分为分组和对角平均^{[11, 13-14]}。

1.1.1 嵌 入 定义时间序列X_N=(x₁,x₂,…,x_N)，序列长度为N，设置窗口长度为L，L为整数且1<L<N/2，K=N-L+1，定义延迟向量X_i=(x_i,x_i+1,…,x_i+L-1)^T，X_N的轨迹矩阵为

(1)

轨迹矩阵是一个Hankel矩阵，其列向量和行向量均是原始序列X_N的子集，且对角平均后可还原为原始序列。

1.1.2 奇异值分解 对XX^T进行奇异值分解，得到L个降序排列的非负特征值λ₁,λ₂,…,λ_L，以及对应的正交特征向量U₁,U₂,…,U_L，令d为非零特征值的个数，则X可表示为如式(2)所示，其中λ_i为X的奇异值，{λ₁,λ₂,…,λ_d}为奇异谱，U_i通常由经验正交函数(Empirical Orthogonal Functions，EOF)表示，V_i为主成分(Principal Components，PC)，(λ_i,U_i,V_i)为X的第i个三重特征向量。

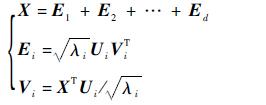(2)

1.1.3 分 组 截取式(2)中的前r个E_i近似X，并将其分为p组，设第I_j组内有j_m个矩阵，然后将每个组内的矩阵相加得到新的矩阵X_Ij，则轨迹矩阵X可以近似表示为

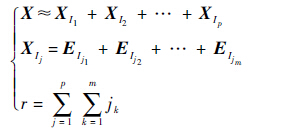(3)

式中:X_Ij的贡献率为。

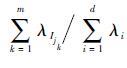
1.1.4 对角平均 对角平均是将矩阵还原为时间序列的方法。设X_Ij的元素为y_i,j，L^*=min(L,K)，K^*=max(L,K)，则X_Ij还原为对应的时间序列{g₀,g₁,…,g_N-1}可由式(4)得出：

(4)

应用对角平均对式(2)中的子矩阵E_i还原可以得到d个重构序列{RC₁,RC₂,…,RC_d}。

1.1.5 预 测 SSA的预测使用了线性递归公式(Linear Recurrent Formulae,LRF)，即用前L-1个数据点的线性组合作为当前数据点的预测值，如下：

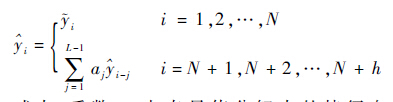(5)

式中：系数a_j由奇异值分解中的特征向量确定^[14]；k为预测点个数。
除了这种递归预测方法，文献^[15]中还提到一种向量预测方法，与递归预测方法相比具有更好的稳定性，但是需要消耗更多的计算资源。

1.1.6 参数选择 SSA的参数选择仅涉及嵌入和分组这2个步骤。在嵌入过程中，窗口长度L的选择主要依据2个原则：① 不能大于时间序列长度的一半；② 可以整除时间序列的已知周期。此外，较小的L有利于提取趋势成分，较大的L有利于分析周期成分^{[14, 16]}。在分组过程中，需要确定截取的子矩阵个数r和分组数p，以及子矩阵在每个分组内的分配。r主要根据奇异值的贡献率来确定，通过比较前r个子矩阵的贡献率之和同预先设定的阈值η(0.85~0.95)的大小，得到满足阈值的子矩阵个数；子矩阵的分组一般是综合考虑贡献率、谐波和噪声等因素，将子矩阵分为趋势组、周期组和噪声组，可以采用一些定量和统计的手段，如用特征向量、重构序列等的散点图来检测谐波成分等^[15]，用Kendal非参数检验的方法判断某个重构序列是否属于趋势成分^[17]，用加权相关系数来判断重构序列之间的可分性^[18]，根据周期图或者加权相关系数对重构序列自动分组^[19]等。
1.2 三次指数平滑 三次指数平滑是一种处理含有趋势性和周期性成分时间序列的方法^[20-22]，主要思想是用历史数据的不同特征来递推当前数据点。三次指数平滑模型分为加法和乘法2种类型。加法预测模型可以表示为

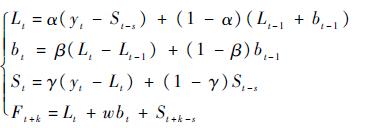(6)

式中:α、β和γ为平滑系数，取值均为0~1之间，靠近1说明预测模型更多依赖最近观测值，其值根据均方误差最小来确定；L_t、b_t和S_t分别为t时刻的水平、趋势的斜率和季节性成分，在实际使用中需依次计算初值；w为预测步长；F_t+k为t时刻的第k步预测值。
1.3 自回归移动平均 ARIMA是20世纪70年代Box和Jenkins^[23]提出的时间序列分析方法，其模型可以表示为ARIMA(b，c，q)，其中，b、c和q分别为自回归项数、差分次数和移动平均项数，当序列平稳即c=0时，对应的模型为

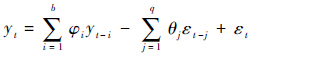(7)

式中:y_t－i表示为t－i时刻的观测值；ε_t－j表示为t－j时刻的随机项；φ_i和θ_j为对应的系数，可以通过参数估计确定^[24]。
当序列包含趋势性时，可通过c阶逐期差分转化为平稳序列。当序列既包含趋势性又包含季节性时，可以建立乘积季节ARIMA模型，记为SARIMA(b，c，q)(B，C，Q)^[s]，其中，B、C和Q分别为季节性的自回归项数、季节性差分次数和季节性移动平均项数，s为季节长度。文献^[25]给出了SARIMA模型的详细介绍。在实际建模中，b和q可以通过观测自相关函数(Auto Correlation Function，ACF)和偏自相关函数(Partial Auto Correlation Function，PACF)确定，也可以通过计算Akaike Information Criterion(AIC)或Bayesian Information Criterion(BIC)值取其最小来确定。另外，文献^[26]给出了ARIMA的自动建模方法。
1.4 故 障 率 设备故障率是可靠性分析的重要指标，通常故障率函数λ(t)可以用Weibull分布来表示^[27]，不同参数取值对应浴盆曲线的不同阶段。在实际应用中，复杂系统常使用平均故障率来描述指定时间内的故障率^[28]，即

(8)

式中：n_i为第i次使用周期中发生的故障数；t_i为第i次使用周期的工作时长；C_w为指定时期内的工作次数；MTBF为平均故障间隔时间。
1.5 度量指标 为了比较不同预测模型的优劣，本文采用RMSE作为模型的度量指标。RMSE与Mean Absolute Error(MAE)、Mean Absolute Percentage Error(MAPE)等其他度量准则相比对异常点更为敏感^[29]，RMSE的计算式为

(9)

式中:y_t和f_t分别为时间序列在t时刻的观测值和模型输出值；T为数据点的个数。
本文对训练集和测试集分别计算RMSE来评价模型的拟合精度和预测精度。
2 研究方法 根据故障时间序列的特点，在SSA方法的基础上，设计的分析框架如图 1所示，包括数据准备和模型计算2个步骤。下面重点介绍SSA模型、参数优选和组合模型3个核心模块。

图 1 故障时间序列分析框架 Fig. 1 Analysis framework of failure time

图选项

2.1 SSA模型 定义故障时间序列TFS以及划分的训练集TR和测试集TE如下：

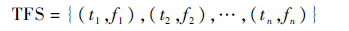(10)

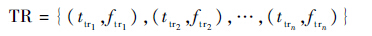(11)

(12)

满足的约束条件为

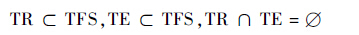(13)

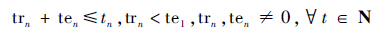(14)

式中：tr_n为训练集的大小，即样本容量；f_trn为tr_n时刻对应的故障数量。
以TR为输入，依据第1.1节，构建SSA模型的过程可以表示为

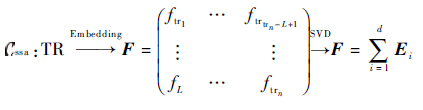(15)

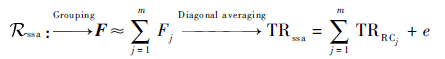(16)

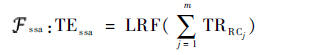(17)

式中：C_ssa、R_ssa和F_ssa分别表示SSA分解、重构和预测。通过 C_ssa和 R_ssa 2个步骤，TR序列被转换为一些主要成分序列(TR_RCj)之和，而无效部分(e)被滤除，然后这些主要成分被用来建立预测模型。
2.2 参数优选 在第2.1节的SSA模型中，除了样本容量tr_n外，还需要确定3个参数：窗口长度L、分组数p以及预测模型的类型F_ssa.type。这些参数一般通过第1.1.6 节描述的原则人工确定。但是，由于参数取值范围较广且参数组合数目较大，需要对参数组合进行优选。优选的依据是使得最终模型的预测精度(RMSE值)最小，目标函数可以表示为

(18)

约束条件为

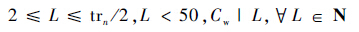(19)

(20)

(21)

式中:y_te为预测模型的输出值。根据第1.1.6节，L的最大值为样本容量的一半，p的最大值取经验值50。当L=1时不能进行奇异值分解，故L的最小值为2。由于SSA递归预测方法的限制，p的最大值不能等于L。具体优选流程由内到外依次包括单元计算(O_ssa.unit)、分组优化(O_ssa.groups)和窗口长度优化(O_ssa.window)3层，优化算法如算法1所示，其中，V_RMSE为RMSE值的计算函数。
算法1 SSA模型参数优选
输入：TFS,tr_n。
输出：不同个数预测点的最小RMSE值及其对应的SSA模型。
1. execute O_ssa.window(TFS,tr_n)
2. for all L:2,3,…,min(tr_n/2,50)
3. execute O_ssa.groups(TFS,tr_n,L)
4. for all p:1,2,…,min ((L-1),50)
5.execute O_ssa.unit(TFS,tr_n,L,p)
6. get TR and TE
7.s←O_ssa(TR,L)
8.r←R_ssa(s,p)
9f←F_ssa(s,p,te_n,F_ssa.type)
10.execute V_RMSE(f.output,TFS,tr_n)
11.return l_G←V_RMSE.output
12.end(for)
13.return l_L←min(list(l_G))
14.end(for)
15.return l←min(list(l_L))
2.3 组合模型 模型组合的核心思想是将故障时间序列应用SSA方法分解成不同成分，包括趋势、周期和残差等，对这些成分分别建立预测模型，然后再将结果合并。模型组合流程如图 2所示。

图 2 模型组合流程 Fig. 2 Process of model combination

图选项

分解过程采用了第2.1节中的 C_ssa和 R_ssa 2个步骤，整合结果如式(22)所示。建模过程选用Holt-Winters、ARIMA和SSA 3种模型。由于SSA分解的可加性，组合过程直接将每种成分的计算模型相加得到最终模型。式(23)和式(24)给出了组合模型(M_com)和组合预测模型(F_com)的表达式。

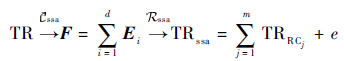(22)

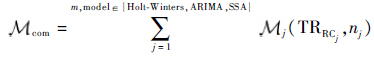(23)

(24)

在分解过程中，趋势成分的提取选用故障时间序列已知的周期(定义为A)作为窗口长度。在这种情况下，奇异值分解的第1个特征值一般占有较大的贡献率，并且可以重构为趋势成分。周期成分从故障时间序列去除趋势成分后的部分中进一步提取，剩余部分为残差。建立组合模型的算法如算法2所示，其中，D_ssa为SSA分解函数，n_j为第j个成分的样本容量。
算法2 建立组合模型
输入：TFS,n_d,n₁,n₂,…,n_m。
输出：组合模型的RMSE值以及模型参数。
1. execute D_ssa(TFS,n_d)
2.get TR_com and TE by TFS,n_d
3.s₁←C_ssa(TR_com,A)
4. r₁←R_ssa(s₁,list(1))
5. TR_RC1←r₁ $ F1
6. s₂←C_ssa(TR_com-TR_RC1,L_max)
7. get p by the features of s₂
8. r₂←R_ssa(s₂,p)
9. for each RC in r₂
10. TR_RCj←r₂$ F_j-1
11. end(for)
12.
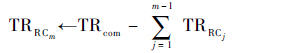
13.execute M_com,F_com,input:TR_RCj，n₁,n₂,…,n_m
14.for each TR_RCj
15. get M_l by the features of TR_RCj
16. execute M_j(TR_RCj,n_j),F_j(TR_RCj,n_j)
17. end(for)
18.
19. execute V_RMSE(F_com.output,TFS,M_com)
20.return M_com,F_com,V_RMSE
3 案例分析 实验原始数据来自某航空公司正在运营的2架波音737飞机的故障库。经过数据采集、整理和校验后，得到包含飞行小时数FH、飞行起落数FC、故障数FA、故障率FR和MTBF在内的5类按月统计的数据集，截取最近18年216个数据点作为实验数据。
图 3展示了2架飞机5类数据的散点图。可以看出，成正相关性的序列对有FH和FC，FA和FR；成负相关性的序列对有FR和MTBF；FH和FA无显著相关性。根据第1.4节，通过FH和FA可以计算出FR和MTBF，而FH以及FC可以通过飞行计划得到，预测的意义不大，故选择FA这个关键序列作为实验对象，并将最后一年的12个数据点作为测试集。

图 3 A、B飞机故障数据集散点图 Fig. 3 atter diagram of failure dataset for aircraft A and B

图选项

为了减少原始数据中的异常点(过大或过小值)对预测模型的不良影响，对FA序列进行预处理。本文采用一种简单的设置门限方法，即小于下限或者大于上限的数据点分别用下限值和上限值替换，本文实验分别以0.1倍和2倍均值为上下门限值。最终得到的FA序列如图 4所示。

图 4 A、B飞机预处理后的故障序列 Fig. 4 Failure series of aircraft A and B after preprocessing

图选项

3.1 基本模型实验 应用第2.1节的方法对A飞机的FA序列建立SSA模型。根据第1.1.6 节确定参数取值范围，本例选取该范围内的最大值，即样本容量为204，窗口长度为96，分组数为50。奇异值分解的结果如图 5和图 6所示，图 7为对应的重构序列。

图 5 FA序列的前50个奇异值 Fig. 5 First 50 singular values of FA series

图选项

图 6 FA序列前12个奇异值对应的特征向量 Fig. 6 First 12 singular values’ eigenvectors of FA series

图选项

图 7 FA序列前12个奇异值对应的重构序列 Fig. 7 First 12 singular values’ reconstructed series of FA series

图选项

可见，第1个奇异值贡献率较大(74.19%)，蕴含了一个增长的趋势成分。另外，第2个和第3个奇异值大小相近，特征向量图和重构序列图也表现出相似的曲线，并且从图 8中的特征对散点图中可以观察到较为明显的四边形，说明蕴含了4个月的周期成分，进一步计算周期估计值为4.098372。接下来重构分解结果，选择前50个奇异值对应的重构序列作为预测模型，模型的拟合结果和预测结果如图 9和图 10所示。

图 8 第2个和第3个奇异值对应的特征对 Fig. 8 Eigenvector pairs of 2nd and 3rd singular values

图选项

图 9 A飞机重构序列的拟合图 Fig. 9 Fitting chart of reconstructed series for aircraft A

图选项

图 10 A飞机2种预测方法的实验结果 Fig. 10 Experimental results of two forecast methods for aircraft A

图选项

为了进一步比较SSA模型的实际效果，本文分别选取180和204作为样本容量，对2架飞机的FA序列应用Holt-Winters、ARIMA和SSA 3种方法建立预测模型，模型参数和实验结果如表 1和表 2所示。
可以看出，样本容量为204的情况下，SSA向量预测模型12个月的预测精度最高(RMSE分别为2.2947和2.3619)；SSA模型的拟合优势明显，但是随着样本容量的增大而有所下降，这是因为随着样本容量的增大，对应的窗口长度增大，进而奇异值个数增加，分组数所占的比重减小，模型的贡献率减小，故拟合精度降低；SSA向量预测方法比递归预测方法的结果更平稳，整体精度较高，与第1.1.5 节的理论一致。
表 1 A飞机不同模型实验结果 Table 1 Experimental results of different models for aircraft A

Holt-Winters样本容量	α	β	γ	拟合RMSE	预测RMSE
					1	2	3	6	12
180a	0.0073	0.4348	0.2233	2.6059	0.1180	0.2874	2.5912	2.7752	2.4159
180m	0.0101	0.2824	0.3502	2.8859	0.9178	0.7694	2.6128	2.8313	2.5968
204a	0.0440	0.0728	0.2233	2.6172	0.0884	0.0687	2.2783	2.8825	2.5951
204m	0.0000	0.0000	0.6000	3.1987	1.7044	1.2054	2.8371	3.1791	3.0663
ARIMA样本容量	b	c	q	拟合RMSE	预测RMSE
					1	2	3	6	12
180	2	1	3	2.3169	1.4440	1.2108	2.7102	2.8438	2.5292
204	0	1	1	2.3644	1.4123	1.2243	2.7922	2.7590	2.3416
SSA样本容量	L	p	拟合RMSE	预测RMSE
				1	2	3	6	12
180r	84	list(1:50)	0.6600	3.7181	2.6824	2.4439	2.9820	3.2423
180v	84	list(1:50)	0.6600	2.3112	1.7406	2.2802	2.8875	2.8722
204r	96	list(1:50)	0.7696	2.4873	1.7811	1.8713	2.4372	2.6217
204v	96	list(1:50)	0.7696	2.5093	1.8427	2.1750	2.5000	2.2947
注：a和m分别表示Holt-Winters加法和乘法季节性模型；r和v分别表示SSA递归和向量预测模型。

表选项






表 2 B飞机不同模型实验结果 Table 2 Experimental results of different models for aircraft B

Holt-Winters样本容量	α	β	γ	拟合RMSE	预测RMSE
					1	2	3	6	12
180a	0.0447	0.0910	0.2737	3.0459	1.6212	3.5408	3.3524	2.5858	2.4386
180m	0.0000	0.0000	0.6193	3.7322	1.7157	4.5208	3.9449	3.1509	3.0339
204a	0.0105	0.2096	0.1910	2.9067	1.7486	3.6045	3.3526	2.6091	2.4742
204m	0.0000	0.0000	0.4384	3.2315	1.8368	4.2517	3.8066	2.9498	2.8160
ARIMA样本容量	b	c	q	拟合RMSE	预测RMSE
					1	2	3	6	12
180	2	1	3	2.6897	2.4327	3.1074	2.9356	2.5425	2.3812
204	0	1	1	2.5723	2.4483	3.1196	2.9428	2.5448	2.3746
SSA样本容量	L	p	拟合RMSE	预测RMSE
				1	2	3	6	12
180r	84	list(1:20)	1.6284	1.6903	1.2344	1.6472	3.4426	3.5343
180v	84	list(1:20)	1.6284	0.2107	2.4131	2.7029	2.3903	2.2043
204r	96	list(1:20)	1.7041	0.1117	0.7530	2.0155	3.4850	3.3469
204v	96	list(1:20)	1.7041	1.4923	2.5154	2.5599	2.3032	2.3619
注：a和m分别表示Holt-Winters加法和乘法季节性模型；r和v分别表示SSA递归和向量预测模型。

表选项






3.2 参数优选结果 以A飞机为例，应用第2.2节的方法对第3.1节中SSA模型参数进行优选。最大样本容量设为204，根据式(19)~式(21)可知，共有3825个参数组合，分3层计算最优参数：第1层，遍历窗口长度L的取值范围，本例为2~102共101个值，返回所有窗口长度的RMSE最小值及其对应的参数；第2层，对于每一个L，遍历分组数p的取值范围，本例分2种情况，当L>50时p∈[1，50]，当L≤50时p∈[1,L-1]，最后返回所有分组数的RMSE最小值及其对应的参数；第3层，对于每一个分组数p，建立SSA分解模型和2种预测模型，并计算RMSE。最后得到的结果如表 3所示。与表 1对比可知，优化后的模型精度明显提高。
表 3 A飞机SSA模型参数优选结果 Table 3 Parameter optimization results of SSA models for aircraft A

样本容量	优选参数组合(L,p,类型)						拟合RMSE	预测RMSE
		1	2	3	6	12		1	2	3	6	12
180	50,49,r	9,3,v	43,42,v	43,42,v	31,26,v	15,3,v	0.0437	0.0038	0.1385	0.6323	1.5738	2.0527
204	51,50,r	44,40,v	41,39,v	49,45,v	25,23,v	91,49,v	0.0944	0.0009	0.0451	0.5854	1.6240	2.0840

表选项






3.3 组合模型实验 以A飞机为例，根据第2.3节的方法建立组合模型。组合模型的类型众多，除了样本容量外，还与以下几个因素相关：分解模型的参数，包括窗口长度、分组数，根据第1.1.6 节，本例取L=12，第1个奇异值对应的重构序列作为趋势成分，其余为残差成分；每种成分所应用的预测模型及其模型参数，本例选择SSA(趋势)-ARIMA(残差)模型，其中参数选择取值范围内的最大值。组合过程为：首先将FA序列分解为趋势和残差2个子序列；然后分别建立趋势SSA模型和残差ARIMA模型，返回2个模型的拟合和预测序列；最后将拟合和预测序列相加，得到组合结果，并计算其RMSE。
表 4展示了趋势-残差二成分9种组合模型的14次实验结果。通过与表 1对比可以看出，组合模型的整体拟合和预测精度要高于单一模型，特别是当趋势成分选用SSA模型时，其预测精度较高；趋势和残差任何一个成分采用SSA方法，都会提高组合模型的拟合精度，当两者均为SSA方法时，其拟合精度高于第3.1节中的基本SSA方法。
表 4 残差二成分组合模型实验结果 Table 4 Experimental results of trend-residual two components combination model

预测模型		参数		拟合RMSE	预测RMSE
趋势	残差	趋势	残差		1	2	3	6	12
Holt-Wintersa	Holt-Wintersa	0.9519,0.5533,1	0.0032,1,0.2286	2.5001	0.2846	0.2020	2.4030	2.8151	2.5535
	ARIMA		ARIMA(1,0,2)(1,0,0)[12]	2.0250	0.8782	1.4507	3.0536	2.7995	2.3433
	SSAr		84,50	0.5444	3.1262	2.5566	2.6195	2.4319	2.8765
	SSAv		84,50	0.5444	2.3345	1.8197	2.3910	2.3591	2.6257
ARIMA	Holt-Wintersa	ARIMA(2,1,1)(2,0,2)[12]	0.0032,1,0.2286	2.4889	0.3187	0.2420	2.2304	3.0000	2.8746
	ARIMA		ARIMA(1,0,2)(1,0,0)[12]	1.9577	0.9122	1.3673	2.8652	2.9376	2.6282
	SSAr		84,50	0.5343	3.1602	2.6316	2.5683	2.5903	3.1310
	SSAv		84,50	0.5343	2.3685	1.8879	2.2930	2.5419	2.9058
SSAr	Holt-Wintersa	84,50	0.0032,1,0.2286	2.4884	0.2580	0.2087	2.5315	2.7176	2.4345
	ARIMA		ARIMA(1,0,2)(1,0,0)[12]	1.9589	0.8516	1.5196	3.1937	2.7400	2.2743
	SSAr		84,50	0.5344	3.0996	2.4989	2.6627	2.3523	2.8309
SSAv	Holt-Wintersa		0.0032,1,0.2286	2.4884	0.2678	0.2054	2.5193	2.7005	2.4041
	ARIMA		ARIMA(1,0,2)(1,0,0)[12]	1.9589	0.8614	1.5026	3.1773	2.7221	2.2442
	SSAv		84,50	0.5344	2.3177	1.7834	2.4656	2.2632	2.5669

表选项






3.4 讨 论
3.4.1 组合方法的优势 某种方法可能不适用于故障时间序列的建模和预测，但是很可能对序列分解出的某一成分有很好的建模和预测能力，这也是组合方法的优势。充分发挥每种时间序列分析方法的特性，比如SSA方法在残差预测中效果较好，ARIMA方法在趋势预测中效果更优。在进行飞机故障序列的建模时，可以构造多种预测模型，针对重点关注的内容，如短期预测能力、趋势提取能力和趋势预测能力等，选择有优势的模型进行分析，则会取得较好的效果。

3.4.2 预测结果中的分歧点 预测结果中存在一些与真实数据相悖的分歧点，这些数据点明显脱离实际水平，严重影响预测精度。如从图 10中可以看出，2013年9月份故障数的预测值与真实值形成了明显的反差：预测值为局部最小极值，真实值为局部最大极值。调整模型类型和参数后仍然得到相同的效果，这让笔者有理由认为该月的故障数据存在严重分歧。判明飞机故障序列中的分歧点有很大的应用价值，可以为故障诊断、整机可靠性分析等提供重要参考。分歧点出现的原因众多，飞机在一段时间内发生的故障数受任务强度、飞行环境和人为等多方面因素的影响，这些因素中都存在突发情况，如政策性的停飞、持续性的恶劣天气或者突发性的上级检查等。通过实地调研发现，2013年9月份该架飞机接受了上级的不定期检查，导致维护人员对飞机的检查力度加大，进而发现的故障增多。

3.4.3 样本容量对预测效果的影响 为了得到更优的组合模型，可以进一步调整模型参数。如预测趋势成分时选择的建模方法及样本容量，从图 11可以看出，以A飞机为例，不同方法和样本容量所得到的趋势预测结果差异很大，图中的黑线是全样本点进行SSA分解提取趋势后得到的曲线，有明显的增长趋势，这与单独对测试集进行简单线性回归的结果一致，而样本容量为204的Holt-Winters和ARIMA方法的预测结果呈现出下降的趋势，与实际不符。从图 11(Holt-Winters为季节性加法模型；SSA的窗口长度为84，分组数为50，递归预测模型)中可以观察到，2007年开始趋势成分有明显的转变点，且波动也出现比较稳定的规律，因此选取从2007年开始的72个数据点作为趋势模型的样本更为合理，实验结果也证明了这一点。

图 11 不同模型的趋势成分预测结果 Fig. 11 Trend component prediction results of different models

图选项

4 结 论 本文在应用SSA技术建立飞机故障时间序列分析模型的基础上，提出了参数优选和模型组合算法，经实验验证表明：
1) SSA方法的建模和预测性能与Holt-Winters和ARIMA相比更优，特别是拟合精度，在A飞机样本容量为204的情况下RMSE达到了0.7696。
2) 参数优选算法的效果显著，在A飞机样本容量为204的情况下，模型的拟合和预测RMSE达到了0.0944和2.0840。
3) 趋势-残差二成分组合模型的总体效果优于单一SSA方法。
4) 组合模型中趋势成分的预测结果对所选定的建模方法，特别是样本容量的大小较为敏感。
基于目前工作，后续还可以做进一步研究，如组合模型的参数优化过程、时间序列模型的扩展机制和自适应的数据预处理等内容。此外，对于故障时间序列分析，目前的研究方法是从历史数据出发逆向分析和预测，发现其内在规律。下一步可以从数据产生的领域知识入手，提取关键特征和要素，正向构建故障序列的分析模型。
致谢    
感谢任健老师在实验数据方面提供的大力支持，感谢陈勇博士在语言方面给予的帮助，感谢评阅论文的各位专家。
参考文献

[1]	ROCCO S C M. Singular spectrum analysis and forecasting of failure time series[J].Reliability Engineering & System Safety, 2013, 114(6): 126–136.
[2]	KUTY?OWSKA M. Neural network approach for failure rate prediction[J].Engineering Failure Analysis, 2015, 47(1): 41–48.
[3]	CAI K Y, CAI L, WANG W D, et al. On the neural network approach in software reliability modeling[J].Journal of Systems and Software, 2001, 58(1): 47–62.DOI:10.1016/S0164-1212(01)00027-9
[4]	MOURA M D, ZIO E, LINS I D, et al. Failure and reliability prediction by support vector machines regression of time series data[J].Reliability Engineering & System Safety, 2011, 96(11): 1527–1534.
[5]	FINK O, ZIO E, WEIDMANN U. Predicting component reliability and level of degradation with complex-valued neural networks[J].Reliability Engineering & System Safety, 2014, 121(1): 198–206.
[6]	XU K, XIE M, TANG L C, et al. Application of neural networks in forecasting engine systems reliability[J].Applied Soft Computing, 2003, 2(4): 255–268.DOI:10.1016/S1568-4946(02)00059-5
[7]	AL-GARNI A Z, JAMAL A. Artificial neural network application of modeling failure rate for Boeing 737 tires[J].Quality and Reliability Engineering International, 2011, 27(2): 209–219.DOI:10.1002/qre.v27.2
[8]	GARCíA F P, PEDREGAL D J, ROBERTS C. Time series methods applied to failure prediction and detection[J].Reliability Engineering & System Safety, 2010, 95(6): 698–703.
[9]	BARBA L, RODRíGUEZ N, MONTT C. Smoothing strategies combined with ARIMA and neural networks to improve the forecasting of traffic accidents[J].Scientific World Journal, 2014(1): 152375.
[10]	VATUTARD R, YIOU P, GHIL M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals[J].Physica D:Nonlinear Phenomena, 1992, 58(1-4): 95–126.DOI:10.1016/0167-2789(92)90103-T
[11]	ELSNER J B, TSONIS A A. Singular spectrum analysis-A new tool in time series analysis[M].New York: Plenum Press, 1996: 39-50.
[12]	ZHANG Q, WANG B D, HE B, et al. Singular spectrum analysis and ARIMA hybrid model for annual runoff forecasting[J].Water Resources Management, 2011, 25(11): 2683–2703.DOI:10.1007/s11269-011-9833-y
[13]	王解先, 连丽珍, 沈云中. 奇异谱分析在GPS站坐标监测序列分析中的应用[J].同济大学学报(自然科学版), 2013, 41(2): 282–288.WANG J X, LIAN L Z, SHEN Y Z. Application of singular spectrum analysis to GPS station coordinate monitoring series[J].Journal of Tongji University(Natural Science), 2013, 41(2): 282–288.(in Chinese)
[14]	ELSNER J B. Analysis of time series structure: SSA and related techniques[J].Journal of the American Statistical Association, 2002, 103(4): 1207–1208.
[15]	GOLYANDINA N, KOROBEYNIKOV A. Basic singular spectrum analysis and forecasting with R[J].Computational Statistics & Data Analysis, 2014, 71(s1): 934–954.
[16]	GOLYANDINA N. On the choice of parameters in singular spectrum analysis and related subspace-based methods[J].Statistics and Its Interface, 2010, 3(3): 259–279.DOI:10.4310/SII.2010.v3.n3.a2
[17]	HIPEL K W, MCLEOD A I. Time series modelling of water resources and environmental systems[M].Amsterdam: Elsevier, 1994: 893.
[18]	HASSANI H. Singular spectrum analysis:Methodology and comparison[J].Journal of Data Science, 2007, 5: 239–257.
[19]	ALEXANDROV T,GOLYANDINA N.Automatic extraction and forecast of time series cyclic components within the framework of SSA[C]//Proceedings of the 5th Workshop on Simulation,2005:45-50.http://www.gistatgroup.com/gus/autossa2.pdf
[20]	WINTERSP R.Forecasting sales by exponentially weighted moving averages[M]//FUNKE U H.Mathematical models in marking.New York:Springer,1976:384-386.
[21]	HOLT C C. Forecasting seasonals and trends by exponentially weighted moving averages[J].International Journal of Forecasting, 2004, 20(1): 5–10.DOI:10.1016/j.ijforecast.2003.09.015
[22]	CHATFIELD C. The Holt-Winters forecasting procedure[J].Journal of the Royal Statistical Society, 1978, 27(3): 264–279.
[23]	BOX G E P, JENKINS G M, REINSEL G C. Time series analysis:Forecasting and control (revised edition)[J].Journal of Marketing Research, 1976, 22(2): 199–201.
[24]	KUMAR U, JAIN V K. ARIMA forecasting of ambient air pollutants (O3, NO, NO2 and CO)[J].Stochastic Environmental Research and Risk Assessment, 2010, 24(5): 751–760.DOI:10.1007/s00477-009-0361-8
[25]	JEONG K, KOO C, HONG T. An estimation model for determining the annual energy cost budget in educational facilities using SARIMA (seasonal autoregressive integrated moving average) and ANN (artificial neural network)[J].Energy, 2014, 71(14): 71–79.
[26]	HYNDMAN R J, KHANDAKAR Y. Automatic time series forecasting: The forecast package for R[J].Journal of Statistical Software, 2008, 27(3): 1–22.
[27]	EBELING C E. An introduction to reliability and maintainability engineering[M].New York: McGraw-Hill, 1997.
[28]	SU C, JIN Q, FU Y. Correlation analysis for wind speed and failure rate of wind turbines using time series approach[J].Journal of Renewable and Sustainable Energy, 2012, 4(3): 1–13.
[29]	LI G, SHI J. On comparing three artificial neural networks for wind speed forecasting[J].Applied Energy, 2010, 87(7): 2313–2320.DOI:10.1016/j.apenergy.2009.12.013