目前,已经在多种类型的模型发动机实验中观察到了不稳定燃烧现象[2-5],然而实验研究中可测量数据有限,因此需要借助其他手段来对实验结果进行分析。采用线性[6]/非线性模型[7-8]分析观察不稳定燃烧现象时,往往对燃烧过程进行了大量简化,使得在处理气液两相燃烧过程中的复杂非线性问题时面临诸多困难。随着计算流体力学(Computational Fluid Dynamics,CFD)的发展,数值模拟成为分析不稳定燃烧现象的重要方法。近年来,国内外研究者采用数值仿真方法从燃烧室构型、工况参数变化及燃烧不稳定性激励源分析等方面对发动机内的燃烧不稳定性相关问题进行了大量研究[9-12],并取得了很多研究成果。由瑞利准则[13]易知,燃烧不稳定性的产生与燃烧释热波动和燃烧室内压力振荡耦合过程直接相关,而当前对于释热与压力振荡变化过程的分析相对较少。文献[14-16]在研究单喷嘴燃烧室内的纵向燃烧不稳定性时,分析了释热波动与压力之间的振荡波形及相位关系,但研究结果主要针对燃烧不稳定性完全激励起来之后二者之间的关系,而当前对燃烧不稳定性逐渐发展过程中二者之间的变化过程缺乏足够认识。
为此,本文基于课题组开发的气液两相燃烧程序,对自燃推进剂燃烧室内的燃烧过程进行了数值仿真,两相反应流的控制方程包括欧拉坐标系中的Navier-Stokes方程组和拉格朗日坐标系下描述喷雾运动规律的控制方程,气液两相之间的耦合通过控制方程中的源项来考虑,采用标准 k-ε 湍流模型来描述湍流对于流动和燃烧过程影响。通过与实验数据比较验证仿真结果正确性的基础上,对燃烧不稳定性发展过程中燃烧室内压力变化及压力分布特点、燃烧释热波动和压力振荡变化关系进行了分析。
1 数学模型及计算方法 1.1 气相控制方程 三维非定常的雷诺时均Navier-Stokes方程组可表示为如下守恒形式:
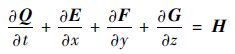 | (1) |
式中:Q为解向量;E、F和G为通量矢量项;H为各方程中源项。各量详细表达式见文献[17]。
假设燃气满足理想气体状态方程,计算如下:
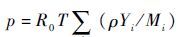 | (2) |
式中:R0为气体常数;p、T和 ρ 分别为燃气的压力、温度和密度;Mi和Yi分别为第i种组分的摩尔质量和质量分数。
1.2 液相控制方程 拉格朗日坐标系下任意液滴的运动方程通过式(3)计算:
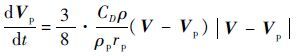 | (3) |
式中:CD为液滴阻力系数; ρp 和rp分别为液滴密度和半径;V和Vp分别为气相和液相速度矢量。
单个液滴蒸发过程中的质量和能量守恒方程如下:
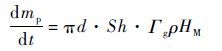 | (4) |
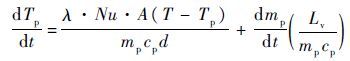 | (5) |
式中:mp、Tp、d、A、cp、 λ 和Lv分别为液滴的质量、温度、直径、液滴表面积、液滴比热、导热系数和汽化潜热; Γg 为混合物内蒸气的质量扩散率;HM为质量传递驱动力[18];Sh和Nu分别为Sherwood数和Nusselt数。
1.3 湍流燃烧模型 自燃推进剂为四氧化二氮和甲基肼(NTO/MMH),其化学反应过程通过一步总包反应进行模拟,其反应式如下:
 | (6) |
采用Arrenius-EBU模型来描述湍流燃烧化学反应过程,燃烧速率 ″ 计算如下:
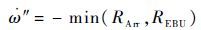 | (7) |
式中: RArr为化学反应速率,可通过总包化学反应动力学的Arrenius表达式确定; REBU为旋涡破碎速率,其为未燃气体微团在湍流作用下破碎成更小微团的速率。
1.4 数值方法 采用有限体积方法对控制方程组进行离散,对流相和扩散项分别采用2阶迎风格式和中心差分格式离散,时间项采用2阶向后差分格式离散,离散方程组采用压力隐式算子分裂(Pressure Implicit of Splitting Operator,PISO)算法进行求解。
2 物理模型及工况参数 数值模拟采用的燃烧室几何构型和工况参数来自于西安航天动力研究所的模型燃烧室实验,实验中通过布置在燃烧室壁面的脉动压力传感器采集燃烧室压力振荡数据,燃烧室几何构型示意图如图 1(a)所示,图中燃烧室直径D和长度L分别为62mm和145mm,喷注参数见表 1。液体推进剂进入燃烧室后通过直流互击式喷嘴进行雾化,氧化剂和燃料喷嘴直径分别为0.3mm和0.2mm,内/外环喷嘴数量分别为20组和40组,图 1(b)为喷注器面板上撞击点位置示意图,内/外环撞击点对应直径分别为20mm和40mm,距离喷注器面板距离分别约为4mm和3mm,另外燃料总流量的18%为冷却液,从喷注器面板靠近壁面处的20个冷却液膜喷孔进入燃烧室,喷孔直径0.2mm,射流与壁面角度约20°。仿真研究中,假设推进剂撞击雾化后混合均匀,利用撞击点后推进剂雾化形成的雾化锥角、粒径分布等参数来给定初始边界条件,内/外环喷嘴雾化锥角分别为72°和76°,推进剂液滴平均直径为60μm,液滴分布假设满足Rosin-Rammler函数,计算如下:
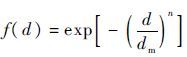 | (8) |
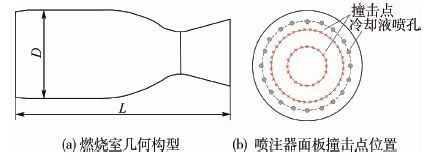 |
| 图 1 燃烧室及喷注器示意图 Fig. 1 Schematic diagram of combustor and injector |
| 图选项 |
表 1 燃烧室内喷注参数 Table 1 Injector parameters in combustor
| 喷注参数 | 数值 |
| 氧化剂流量/(kg·s-1) | 0.272 |
| 燃料流量/(kg·s-1) | 0.163 |
| 推进剂温度/K | 300 |
| 液滴平均直径/μm | 60 |
表选项
式中:f(d)为液滴直径大于d的液滴占整个液滴质量的质量分数;dm为液滴平均直径;n为液滴直径分布参数,n=5时液滴尺寸范围约为10~90μm。
为了减少计算时间,仿真初始时刻燃烧室内为温度2000K、压力0.9MPa的高温N2。
3 结果与讨论 3.1 仿真与实验结果比较 在表 1工况下,模型燃烧室在实验过程中出现了不稳定燃烧,实验中测得的燃烧室稳态压力约为0.9MPa,对该工况下的两相燃烧过程进行数值仿真,得到的燃烧室压力为1.03MPa,误差约为14%,仿真得到的室压偏高。图 2(a)给出了监控点处燃烧室内脉动压力p′的仿真结果,监控点距离喷注器面板和燃烧室中心分别为5mm和26mm;图 2(b)为脉动压力p′的实验结果,仿真与实验结果选取时间范围均为1ms。通过比较可以发现,仿真与实验结果压力振荡形态相似,压力随时间的变化产生了类似于激波形式的陡峭形态变化,表明此时振荡非常剧烈。另外,最大压力振荡范围均都达到了近3MPa,可见在压力脉动变化方面,仿真结果与实验结果吻合较好。由于压力振荡幅值远大于燃烧室平均室压,可见燃烧室内出现了不稳定燃烧。
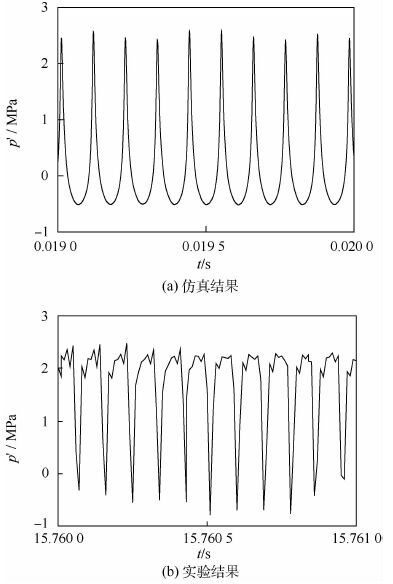 |
| 图 2 脉动压力随时间变化的仿真与实验结果 Fig. 2 Fluctuation pressure histories in simulation and experiment |
| 图选项 |
对仿真结果得到的压力数据进行频谱分析,结果如图 3所示。压力振荡主频为9200Hz,同时出现了振荡主频的一系列倍频,表明仿真中出现了高频不稳定燃烧。压力脉动的实验数据计算得到的压力振荡主频为11259Hz,另外,该模型燃烧室内燃气理论声速为1222m/s,通过理论计算可知该燃烧室的1阶切向频率为11552Hz,从频率特征角度可以判定此时燃烧室内发生的是1阶切向高频不稳定燃烧。实验与理论结果均大于仿真结果,存在差异的可能原因如下:燃烧室圆柱段切向声学特性与燃烧室半径及燃烧室内燃气平均声速(声速受控于燃气组分、温度分布)密切相关,由于数值模拟采用的燃烧室几何构型与真实发动机半径是一致的,故燃烧室喷注器附近燃气组分及温度等参数与真实情况可能存在一定差异。文献[19]采用多步化学反应,在0.9MPa、氧燃混合比1.65(四氧化二氮与甲基肼的质量比)条件下得到燃气平衡温度约2850K,该工况参数与实验条件非常接近(实验中室压0.9MPa,氧燃混合比约1.67),仿真中监控点所在横截面内燃气平均温度约为2700K,略低于化学平衡计算得到的燃气温度,温度偏低使得声速降低,这与仿真得到切向主频率偏小一致。另外,采用总包反应模拟推进剂的化学反应过程,忽略了燃烧过程中的其他小分子产物(如H、OH和NO等[19]),导致得到的燃气产物平均分子量偏大,该因素同样使得燃气内声速偏小。综上所述,由于仿真得到的燃气温度偏低且燃气平均分子量偏大使得燃烧室内声速偏低,故导致得到的切向主频低于实验结果。
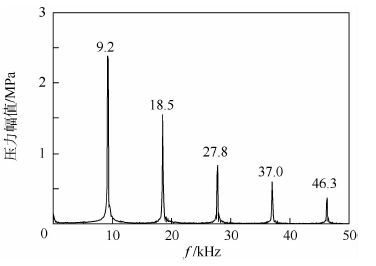 |
| 图 3 仿真所得压力数据的频谱分析 Fig. 3 Spectrum analysis of pressure data in simulation |
| 图选项 |
通过发动机室压、不稳定燃烧阶段脉动压力变化和压力振荡主频3个方面,对比了仿真结果与实验数据,表明该工况边界下得到的仿真结果较好地反映了模型发动机实验过程中出现的不稳定燃烧现象,可以用于进一步的分析。
3.2 压力振荡发展变化过程分析 图 4给出了仿真过程中监控点(监控点位置与第3.1节中一致)处脉动压力随时间变化曲线。依据压力振荡特点,可将该燃烧过程分为3个阶段:I时间段内(4~5ms),压力振荡范围约为0.11MPa,相对于燃烧室平均室压振幅小于10%,此时燃烧室内为稳定燃烧过程;II时间段内,压力振荡范围由0.11MPa逐渐增大到了0.7MPa,振幅由10%逐渐增加到了66%,且脉动压力围绕平均燃烧室压力做等幅振荡,该阶段内已经为不稳定燃烧;III时间段内,燃烧室内进入了剧烈不稳定燃烧阶段,压力振荡范围急剧增大直至达到极限饱和状态,压力波动表现为非等幅度振荡,振幅超过了平均室压的200%。
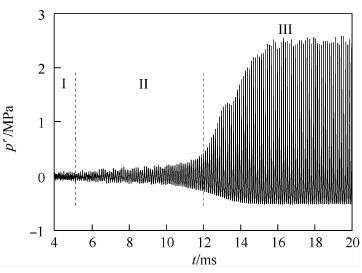 |
| 图 4 监控点处脉动压力随时间变化 Fig. 4 Fluctuation pressure history at monitor point |
| 图选项 |
在燃烧过程发展变化的3个典型时刻,燃烧室内横向压力分布如图 5所示(横向截面切片距离喷注器面板15mm)。图 5(a)为4ms时压力分布云图,该时刻压力分布无规律;而在10ms时(见图 5(b)),燃烧室内高低压区域呈典型的1阶切向压力分布形态,从压力分布形态也可以判断此时燃烧室内的不稳定燃烧为1阶切向不稳定燃烧;20ms时(见图 5(c)),压力仍呈现1阶切向压力分布形态,压力极高区域集中于很小范围内。
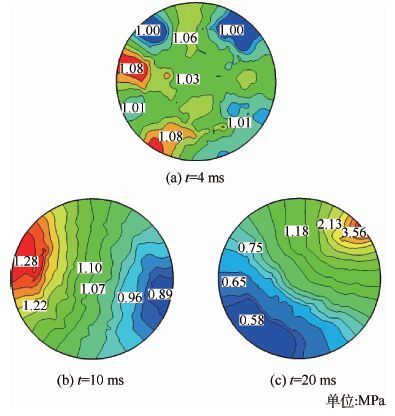 |
| 图 5 不同燃烧阶段燃烧室横向压力分布 Fig. 5 Transverse pressure distribution at different combustion stages in combustor |
| 图选项 |
3.3 燃烧释热与压力振荡耦合过程分析 为了分析燃烧不同阶段能量释放与压力振荡之间的耦合过程,对主要释热区域的相关参数进行了监控,监控点位于距离燃烧室中心20mm处外环撞击点下游5mm(雾化液滴蒸发、燃烧的主要区域)。
图 6给出了燃烧过程中不同阶段内监控点处能量释热q和压力p随时间的变化过程。图 7为释热和压力振荡数据的频谱分析结果,纵坐标幅值通过各变量振荡幅值极大值进行了无量纲处理。通过比较可以发现如下规律:①4~5ms内的稳定燃烧过程中,压力和能量释放过程均随时间无规律振荡,模型燃烧室内互击式喷嘴间雾化过程的相互影响及湍流的存在,使得推进剂在燃烧室内横向分布不均匀,从而造成了燃烧释热和压力的初始脉动,部分释热过程与压力振荡相位相同,使得压力振荡获得能量,由图 7(a)频谱特性可以发现,该时间段内压力振荡主要频率分别为9、20、25和30kHz,而燃烧释热振荡频率主要为1、4、8.5、9和30kHz,二者在10kHz和30kHz频率处实现了耦合。②在10~11ms时间内的不稳定燃烧过程中,压力振荡幅值约在35%左右,此时压力振荡具有显著周期性,图 7(b)给出了该时间段内释热和压力振荡频谱分析结果,压力振荡频率主要为9kHz,但能量释放过程仍表现为无规律波动,其频谱特性表明此时仍包含多个振荡主频。③剧烈不稳定燃烧阶段,通过比较图 6(c)、图 6(d)和图 7(c)、图 7(d)可以发现,在图中压力振幅快速增长(13~14ms)和振幅达到极限饱和状态阶段(20~21ms),燃烧释热与压力振荡在波形、振荡频率方面都是一致的,压力振荡相位略滞后于释热过程,该现象与文献[14-16]分析单喷嘴燃烧室内的纵向燃烧不稳定性时得到的结论一致,这也表明释热与压力振荡的完全耦合对于不同类型燃烧不稳定性都是需要满足的条件。正是由于释热与压力振荡在波形、相位的完全耦合,才使得压力在振荡过程中不断从燃烧释热过程中快速获得能量,表现为图 6(c)中压力、释热幅值相较于图 6(b)增长明显加快;另外,波形、相位的耦合使得大振幅压力振荡所需的巨大能量耗散得以补充,直至燃烧室内能量交换达到平衡,压力振荡达到极限振荡幅值。在压力振幅快速增大至极限幅值过程中,图 7(c)和图 7(d)中高阶模态相对幅值的增大表明,由于非线性效应影响,燃烧室内压力振荡基态能量不断向高阶模态传递。
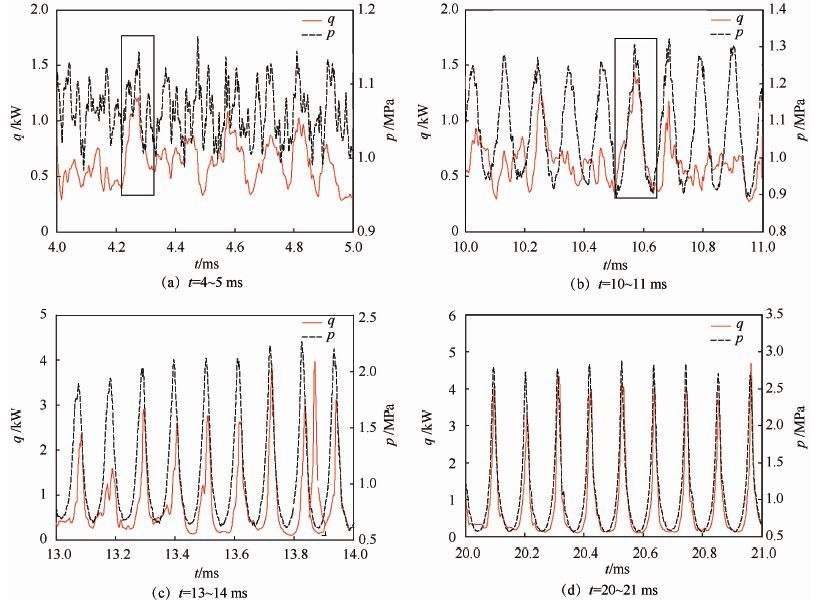 |
| 图 6 不同燃烧阶段释热与压力随时间变化曲线 Fig. 6 Heat release and pressure histories at different combustion stages |
| 图选项 |
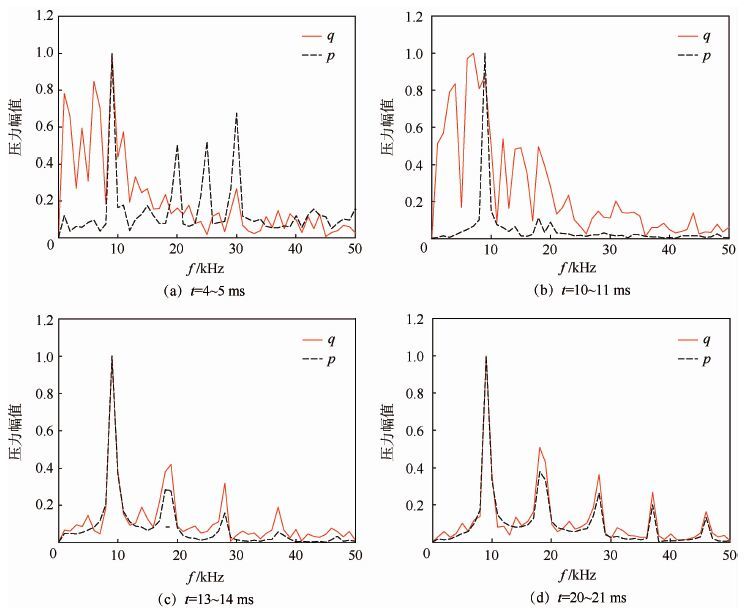 |
| 图 7 不同燃烧阶段释热与压力频谱分 Fig. 7 Spectrum analysis of heat release and pressure at different combustion stages |
| 图选项 |
另外,从图 6和图 7中还可以发现,压力首先达到周期性振荡,而释热过程由无规律波动到周期性振荡过程较为缓慢。释热过程与压力振荡没有完全耦合时,压力振荡仅从部分释热波动中获得能量,比较图 6(a)和图 6(b)中2个不同燃烧阶段,压力振荡波形发生了很大变化,而释热波动变化不大,图中利用矩形框分别标示出了一个典型的释热波动与压力振荡相位一致的区域,在图 6(b)中的矩形框内,释热波动峰值内仅包含一个压力振荡峰值,且二者相位一致,而在图 6(a)中矩形框内,释热波动区域内包含了多个压力振荡峰值,此时压力振荡获得的能量分散在多个频率的压力波中,从而使得在该时间段内压力振荡幅值较小,而图 6(b)中压力振荡获得能量主要用于维持和增强单一振荡频率波动,能量利用率更高。由于燃烧室本身阻尼特性对与燃烧室固有声学特征频率一致的压力振荡耗散性相对较弱,使得压力在振荡中频率特性逐渐与燃烧室固有声学频率一致,该频率压力波从释热中获得的能量除可以维持自身振荡外,仍有剩余能量用于进一步增强振荡强度,表现为该阶段内压力振荡幅值的不断升高,且振荡主频与燃烧室固有声学特性一致。切向压力振荡环境下,液滴蒸发特性[20]和燃烧室内产生的周向速度[21]与压力振荡频率和振幅幅值密切相关,这些因素变化进一步影响释热过程,使得释热波动频率逐渐与压力振荡频率一致,二者之间耦合逐渐加强直至实现完全耦合。
4 结 论 本文对自燃推进剂模型燃烧室内的两相燃烧过程进行了数值仿真,分析了不稳定燃烧不同发展阶段的特点,得到以下结论:
1) 自燃推进剂模型燃烧室数值仿真结果出现了1阶切向自激高频不稳定性燃烧,压力振荡表现出典型的非线性特征,其振荡主频为9200Hz并出现了其倍频,仿真结果与实验结果吻合较好。
2) 不稳定燃烧发展过程中,燃烧室内压力振荡幅值逐渐增大与释热和压力之间耦合性逐渐增强密切相关。
3) 燃烧释热是压力振荡直接能量来源,而压力振荡频率又受控于燃烧室固有声学特性,压力率先达到周期性振荡后,会对燃烧子过程产生影响从而进一步影响释热波动,使得无规律释热波动与压力振荡耦合逐渐增强,当二者振荡波形、频率和相位完全一致时,燃烧室内出现剧烈不稳定燃烧现象。
参考文献
| [1] | YANG V, ANDERSON W E. Liquid rocket engine combustion instability[M].Reston: AIAA, 1995: 1-2. |
| Click to display the text | |
| [2] | YU Y C, SISCO J C, ROSEN S. Spontaneous longitudinal combustion instability in a continuously variable resonance combustor[J]. Journal of Propulsion and Power,2012, 28(5): 876–887. |
| Click to display the text | |
| [3] | POMEROY B R,MORGAN C,ANDERSON W E.Response of a gas-centered swirl coaxial injector to transverse instabilities:AIAA-2011-5698[R].Reston:AIAA,2011. |
| Click to display the text | |
| [4] | MILLER K, SISCO J, NUGENT N, et al. Combustion instability with a single-element swirl injector[J]. Journal of Propulsion and Power,2007, 23(5): 1102–1112. |
| Click to display the text | |
| [5] | POMEROY B R,NUGENT N,ANDERSON W E.Measuring transverse combustion stability at full scale frequencies in a subscale combustor:AIAA-2010-7146[R].Reston:AIAA,2010. |
| Click to display the text | |
| [6] | PIERINGER J, SATTELMAYER T, FASSL F. Simulation of combustion instabilities in liquid rocket engines with acoustic perturbation equations[J]. Journal of Propulsion and Power,2009, 25(5): 1020–1031. |
| Click to display the text | |
| [7] | TYAGI M, CHAKRAVARTHY S R, SUJITH R I. Unsteady combustion response of a ducted non-premixed flame and acoustic coupling[J]. Combustion Theory and Modeling,2007, 11(2): 205–226. |
| Click to display the text | |
| [8] | RICHECOEUR F, DUCRUIX S, SCOUFLAIRE P, et al. Effect of temperature fluctuations on high frequency acoustic coupling[J]. Proceedings of the Combustion Institute,2009, 32(2): 1663–1670. |
| Click to display the text | |
| [9] | 尕永婧, 张会强, 王希麟. 推力室中压力剧烈振荡区域的燃烧特性分析[J]. 推进技术,2012, 33(5): 785–789.GA Y J, ZHANG H Q, WANG X L. Analysis of combustion characteristics in the region with violent pressure oscillations in thruster chamber[J]. Journal of Propulsion Technology,2012, 33(5): 785–789.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | ZHANG H Q, GA Y J, WANG B, et al. Analysis of combustion instability via constant volume combustion in a LOX/RP-1 bipropellant liquid rocket engine[J]. Science China Technological Sciences,2012, 55(4): 1066–1077. |
| Click to display the text | |
| [11] | SMITH R, XIA G, ANDERSON W, et al. Computational simulations of the effect of backstep height on nonpremixed combustion instability[J]. AIAA Journal,2010, 48(9): 1857–1868. |
| Click to display the text | |
| [12] | JONES W P, LYRA S, NAVARRO-MARTINEZ S. Numerical investigation of swirling kerosene spray flames using large eddy simulation[J]. Combustion and Flame,2012, 159(4): 1539–1561. |
| Click to display the text | |
| [13] | DUROX D, SCHULLER T, NOIRAY N, et al. Rayleigh criterion and acoustic energy balance in unconfined self-sustained oscillating flames[J]. Combustion and Flame,2009, 156(1): 106–119. |
| Click to display the text | |
| [14] | HUANG C,ANDERSON W E,HARVAZINSKI M E,et al.Analysis of self-excited combustion instabilities using decomposition techniques: AIAA-2013-1007[R].Reston:AIAA,2013. |
| Click to display the text | |
| [15] | HARVAZINSKI M E,XIA G,ANDERSON W E,et al.Analysis of self-excited combustion instability using a combination of two-and three-dimensional simulations:AIAA-2012-0782[R].Reston:AIAA,2012. |
| Click to display the text | |
| [16] | HARVAZINSKI M E,ANDERSON W E,MERKLE C L.Combustion instability diagnostics using the rayleigh index:AIAA-2011-5548[R].Reston:AIAA,2011. |
| Click to display the text | |
| [17] | 聂万胜. 液体火箭发动机燃烧动力学模型与数值计算[M].北京: 国防工业出版社, 2011: 46-49.NIE W S. Combustion kinetic models and numerical calculation in liquid rocket engine[M].Beijing: National Defence Industry Press, 2011: 46-49.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [18] | 辛娟娟, 周致富, 辛慧, 等. 单个液滴蒸发模型中不同质量传递公式的有效性分析[J]. 化工学报,2012, 63(6): 1704–1708.XIN J J, ZHOU Z F, XIN H, et al. Validation analysis of different mass transfer formula in single droplet evaporation model[J]. CIESC Journal,2012, 63(6): 1704–1708.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [19] | 巴延涛, 侯凌云, 毛晓芳, 等. 甲基肼/四氧化二氮反应化学动力学模型构建及分析[J]. 物理化学学报,2014, 30(6): 1042–1048.BA Y T, HOU L Y, MAO X F, et al. Construction and analysis of a chemical kinetic model for monomethylhydrazine/nitrogen tetroxide reactions[J]. Acta Physico-Chimica Sinica,2014, 30(6): 1042–1048.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [20] | HSIAO G C, MENG H, YANG V. Pressure-coupled vaporization response of n-pentane fuel droplet at subcritical and supercritical conditions[J]. Proceedings of the Combustion Institute,2011, 33(2): 1997–2003. |
| Click to display the text | |
| [21] | LUBARSKY E,HADJIPANAYIS M,SHCHERBIK D,et al.Control of tangential combustion instability by asymmetric baffle:AIAA-2008-955[R].Reston:AIAA,2008. |
| Click to display the text | |
