研究直升机旋翼的非定常气动特性,就是研究旋翼诱导速度场、非定常气动力以及旋翼纵横交叉耦合等课题。旋翼诱导速度场的模型与旋翼的气动力和力矩特性模型的准确性直接相关。直升机稳定飞行时,可使用动量理论粗略估算旋翼气动力,但当直升机做俯仰运动还是滚转运动或处于外部扰动状态时,旋翼的气动力以及诱导速度场均处于显著的动态变化之中,最后会影响桨叶载荷和旋翼挥舞动力学特性。因此,旋翼桨盘及附近的诱导速度的准确模拟是开展机动飞行时旋翼气动特性分析的关键[2]。目前,计算旋翼诱导流场的方法主要有3种:动态入流方法[3, 4]、自由尾迹方法[5, 6]、计算流体力学(CFD)方法[7, 8]。动态入流方法通过假设桨盘入流线性分布,诱导速度各分量用3个线性常微分方程描述,与旋翼气动力和力矩密切相关,可以确定任意时刻桨盘上任意点的诱导速度及应用于所有直升机飞行动力学模型。自由尾迹方法采用弹性桨叶模型,能较准确计算非定常/动态失速旋翼气动力,在实时飞行模拟中很少用此方法。另外,描述直升机运动的非线性微分方程(连续系统)与描述自由尾迹方法的差分方程(离散系统)相互嵌套,还没有一个成熟的、高效的、两者耦合的求解方法[9]。而CFD方法尽管发展较快,但是由于计算机水平和数值方法的限制,需要耗费数小时得到仅仅若干问题的解,显然不适用于实时分析。为此,根据不同的研究目的,国外许多****已经建立了准定常刚性桨叶模型[10, 11]、动态入流及非定常气动力模型[3, 12]以及非定常自由尾迹模型[13, 14],目前,这些模型已经被开发成飞行模拟器系统平台,由于保密因素,内部实现方法并未公布。在国内,南京航空航天大学对旋翼自由尾迹模型也进行了研究并取得了很多成果[9, 15, 16, 17, 18],但上述研究主要集中在动态响应和求解计算方法上,而对适用于实时飞行运动仿真的旋翼模型研究很少。北京航空航天大学结合直升机虚拟现实技术的发展需求,开展了非定常/动态失速气动力模型[19, 20, 21]研究,通过逆解技术[20]得到操纵输入和飞行姿态,应用涡流理论、动力入流理论和非定常翼型气动模型来数值模拟非定常的旋翼气动力,并给定输入条件通过商用软件测试某型直升机平飞跃升和紧急转弯等机动过程中的旋翼拉力响应曲线。
本文的目的是针对直升机机动飞行实时仿真的要求,采用小扰动理论建立了机动飞行状态下桨叶叶素气动载荷计算方法。算法集合桨叶剖面气动力非定常特性、动态入流模型及桨叶气弹变形特点。整个算法表示成状态空间格式以便使用统一的数值求解方法。最后,通过算例验证本文计算方法的有效性,为直升机旋翼非定常气动力的模拟提供了参考。
1 旋翼叶素气弹模型由于旋翼系统的复杂性,桨叶除了挥舞、摆振、变距运动以及各运动间的耦合外,桨叶也存在着弹性变形。前述非线性、非定常气动力模型虽考虑了桨叶气弹特性,建模较困难以及求解过程存在不稳定性。桨叶气动弹性系统受到随时间变化的外界周期性扰动力的作用,叶素位置也会产生扰动的变化。本文将桨叶叶素位置矢量进行线化处理,即根据“小扰动”假设,在桨叶某叶素位置进行动力学方程的干扰得出扰动矢量,通过变量分离法得出桨叶弹性变形方程,继而得出桨叶气动载荷。
1.1 模型概述旋翼叶素气弹模型方程包括旋翼惯性方程、旋翼入流和旋翼气动方程。经典的旋翼桨叶的弹性变形方程[22]为
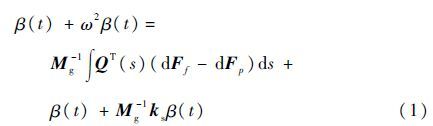
式中:ω为角速度;Mg为质量矩阵;ks为刚度矩阵;dFf和dFp分别为弹性桨叶2个叶素f和p的微元力;非线性力函数β(t)为旋翼桨叶的弹性变形,t为时间常数;QT(s)为模态矩阵转置,s为叶素长度,s∈[0,R],R为半径。此方程为一个二阶线性微分方程的对角表达式,与刚性挥舞运动方程形式一致,其表示方法可以等同考虑惯性模态和气动模态,而不必从工程角度考虑应当保留哪些项以及应当将其放在方程哪一边。ks是方程右侧相对于β的线性导数,可以通过数值微分计算:
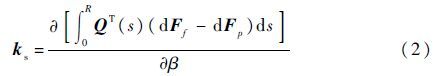
某一时刻t,在桨叶上任一点处取一叶素f,其位置矢量为Pf(s,t),质量为m(y)dy,分布的惯性张量为dI(y),该矢量沿桨叶基准线(BRL)从旋转中心指向桨叶上的某个点,BRL在伸长方向假设为无限刚度,在其他方向可以自由移动微小距离,叶素坐标系的xf位于BRL上,与BRL相切,指向桨毂; yf与弦线平行,指向前缘;zf方向按右手规则确定。角坐标Φx测量绕xf轴的角度,指向前缘下方为正,即桨距角;角坐标Φy测量绕局部yf轴的角度,即局部挥舞角,向下挥舞为正;角坐标Φz测量叶素摆振的角度,向后摆振为正,如图 1所示。
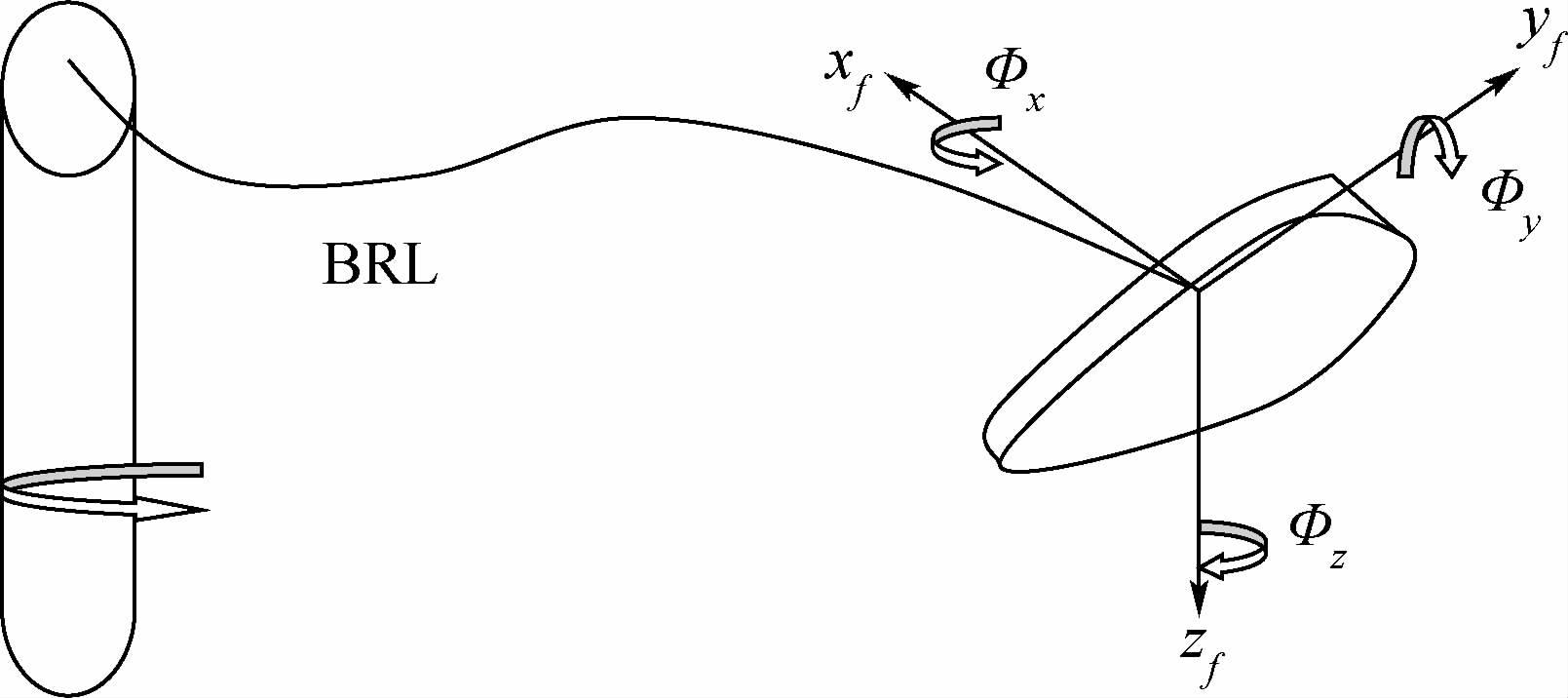 |
| 图 1 桨叶基准线和叶素坐标系 Fig. 1 Blade baseline and element coordinate |
| 图选项 |
将位置矢量
Pf(s,t)= [xf(s,t)yf(s,t)zf(s,t)Φx(s,t)Φy(s,t)Φz(s,t)]T
采用小扰动模型的标准模态法进行旋翼弹性分析,作为线性变形方程的完全非线性力函数放在方程右侧,而线性变形方程位于方程左侧。扰动从预定的位置矢量Pf(s,t)处开始测量,通过飞行员输入的桨距θ(t)=θ0+A1cos(Ωt)+B1sin(Ωt),其中:θ0为总距角;A1和B1分别为横向和纵向周期变距铰;Ω为旋翼相对于机身的旋转速度。预定的位置矢量改变为
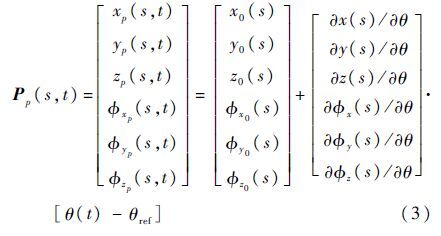
式中:第2个等号右侧第1项下标带0的矢量是空间的函数,第2项为BRL坐标相对于一个桨距θ(t)的偏导数,θref为桨距θ(t)的基准值,取零周期変距和悬停配平时的总距值。
设定dFf和dFp的分布载荷:
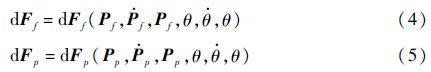
令扰动矢量:
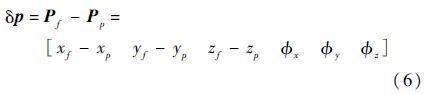
式(4)和式(5)的差值是惯性加速度、旋转刚度和其他气动载荷的函数:
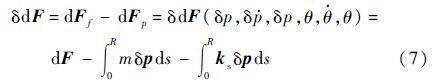
而

联立式(7)和式(8),得到
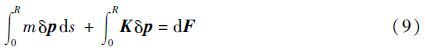
式中:K=ks+ke,ke为刚度矩阵,符合Maxwell互逆定理;m为叶素微段分布质量。合并式(9)和扰动载荷可得

使用变量分离法,将扰动位移、速度和加速度表示为
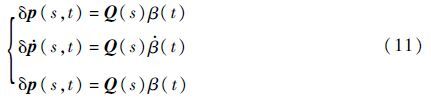
式中:将式(9)代入式(8),并将结果左乘QT(s),再沿桨叶积分得到式(1)。
1.2 弹性旋翼的惯性模型旋翼模型包括桨叶模型和桨毂模型、桨毂模型有线速度和角速度,这些矢量相对于桨毂坐标系求解,表达式是一个微分力形式,沿径向积分计算桨毂载荷。
在桨毂坐标系下产生的总加速度为
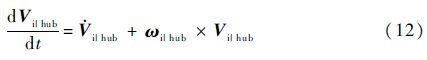
式中:Vi|hub和ωi|hub分别为线速度和角速度。桨毂的旋转角速度Ω=[0 0 -Ω]T,则旋翼坐标下旋翼的总角速度为
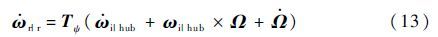
式中:TΨ为桨毂坐标系到旋转坐标系变换矩阵,Ψ为机身方位角。
桨叶位置矢量为
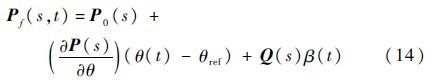
旋翼坐标系下叶素的速度和加速度分别为

所有微段叶素总加速度为
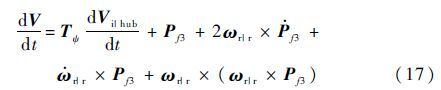
式中:Pf3为位置矢量的线性部分。
任意叶素在旋翼坐标系下的微分惯性载荷为

式中:Fi和Mi分别为惯性力和惯性力矩;Vb为微段叶素总速度;s=[0 0 s]。
1.3 诱导速度实践证明,Pitt和Peters[3]的一阶谐波动态入流模型通过微分方程组,将非定常入流和旋翼拉力及力矩联系起来,能有效地模拟机动飞行状态下旋翼的气动特性,它考虑了诱导速度在桨盘上的不均匀分布,以及随旋翼气动力变化的滞后效应,使旋翼气动载荷(拉力系数CT、滚转力矩系数Cl和俯仰力矩系数Cm)同旋翼的诱导速度的瞬态变化联系起来[3],适合于实时求解运动仿真旋翼的诱导速度。任意方位角Ψ下任意站位r/R的诱导速度[23]为
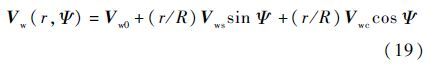
式中:Vw0为旋翼中心的诱导速度;Vwc为旋翼诱导速度的纵向分量;Vws为旋翼诱导速度的横向分量。诱导速度的动态性体现在诱导速度是滞后于瞬态载荷的,可以用一阶线性微分方程来表示[23]:
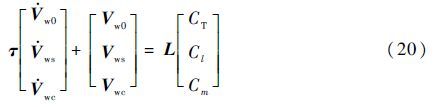
式中:τ和L分别为时间常数矩阵和静态增益矩阵。
1.4 弹性旋翼的气动载荷桨毂坐标系的直线和旋转气动速度分别为
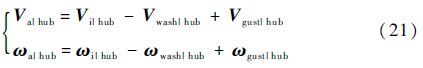
式中:Vwash|hub和ωwash|hub为直线和旋转诱导速度;Vgust|hub和ωgust|hub为直线和旋转突风速度,设置为0。
把直线速度加到弹性变形以及相对于桨毂的角运动产生的速度上:
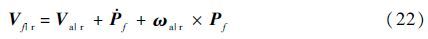
式中:Va|r和ωa|r为旋转坐标系下的线速度和角速度,即Va|r=TΨVa|hub,ωa|r=TΨ(ωa|hub+Ωz),Ωz为Ω的z轴分量。
叶素坐标系下的气动速度为
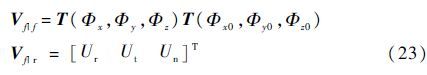
式中:T(Φx0,Φy0,Φz0)和T(Φx,Φy,Φz)分别为变换矩阵和小扰动旋转矩阵;Ur、Ut和Un分别为桨叶径向、切向和垂向速度。
考虑到偏航流的影响,叶素微段上的迎角和俯仰速率[24]分别为

式中:c为桨叶弦长;Φ和θG分别为滚转角和桨叶几何俯仰角;γ为偏航角。将迎角α和俯仰速率q代入Leishman-Beddoes非定常动态失速模型[12]:
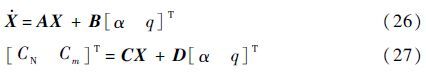
[CNCm]T=CX+D[αq]T(27) 式中:X为状态向量;CN为法向力系数;A、B、C和D为变换矩阵,C和D定义可参见文献[25]。
翼型升力和阻力系数为
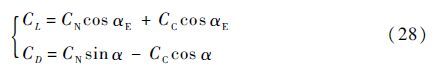
式中:CC为弦向力系数;αE为有效迎角。
桨叶坐标系下的微分气动载荷为
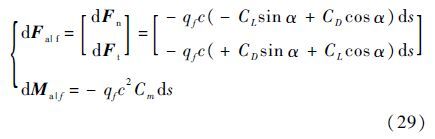
式中:qf=ρ(U2t+U2n)/2为动压,ρ为空气密度。
旋翼坐标系下的微分气动载荷为
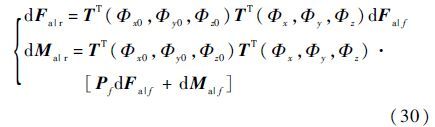
模态方程中完整的分布载荷为

2 挥舞动力学方程桨叶的挥舞运动与气动载荷关系密切,为了能准确计算旋翼非定常载荷,需要建立合适的桨叶挥舞动力学模型,根据在挥舞铰处根据力矩平衡的原理,计入桨叶的一阶刚性挥舞特性,忽略桨叶重量的影响,在单桨叶坐标系(IBC)中建立挥舞动力学方程[26]
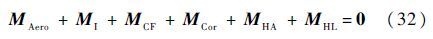
式中:MAero为桨叶的气动力矩;MI=-Iββ,Iβ为桨叶关于挥舞铰的惯性矩;MCF=-Ω2(Iβcos β+ebMβ)sin β为离心力矩,eb为挥舞铰偏置量,Mβ为质量静距;哥氏力矩MCor=2(Iβcos2β+eb cos β·Mβ)(phΩ cos Ψ-qhΩ sin Ψ),ph和qh分别为旋翼桨毂滚转和俯仰角速率;桨毂中心角加速度引起的力矩MHA=(Iβcos2β+ebcos β·Mβ)(p·h·sin Ψqhcos Ψ);由桨毂中心线加速度引起的附加力矩MHL=Mβ(cos β·ahz-sin β·ahxcos Ψ+sin β·ahysin Ψ),ahx、ahy和ahz分别为桨毂中心线加速度的3个分量。文献[26]给出关于挥舞角β的二阶微分解析式较为冗长,本文不再赘述。
3 旋翼配平模型配平就是飞行员通过旋翼操纵输入来改变机身欧拉角,使沿着机体坐标系每个轴的力和力矩之和达到平衡的过程[22]。因此,完整的仿真模型须包含旋翼配平模型。由于旋翼仿真模型是一个非线性时不变系统,本文在配平时,固定旋翼的轴倾角和前飞速度,通过调整旋翼操纵量z(总距角θ0和周期变距角A1、B1)来满足给定的状态量y(包括CT、桨盘侧倾角a1和后倒角b1)。旋翼配平方程可以表示为[18]

式中:y=[CT a1 b1]T;z=[θ0 A1 B1]T;雅克比矩阵J=∂y/∂z。
将上述的诱导速度模型、非定常气动模型、桨叶挥舞动力学模型、旋翼配平模型经桨毂坐标系转换到机身,采用常微分方程(ODE)解法程序要求的标准形式:

式中:x为力、力矩和状态量;u为操纵位移输入变量矩阵,u=[ucoll ulong ulat uped]T,ucoll 、ulong 、ulat 和uped分别为总距、纵向周期变距、横向周期变距和脚蹬的位移输出变量。旋翼系统模型如图 2所示。
 |
| 图 2 旋翼系统模型 Fig. 2 Rotor system model |
| 图选项 |
式(1)、式(20)和式(32)都是标准常微分方程,采用4阶Runge-Kutta时间积分法求解计算。输入初始化参数及操纵量,以时间步长(0.017 s)为单位,每一时间步长内更新诱导速度、叶素气动速度及加速度、旋翼气动载荷、挥舞角、角速度及角加速度经旋翼配平代入机身方程,求解机身线速度、角速度及欧拉角,判断计算的状态量与目标量是否一致,如一致进入下一时间步长进行迭代计算,如不一致结束系统程序。
4 偏航流效应由于桨叶在向前飞行时会遇到径向来流(即偏航流)的影响,在大纵横比的无限翼长的桨叶的压力分布可用前飞速度法向分量来表示[27]。本文采用小扰动原理建立的桨叶系统模型考虑了径向来流的影响。图 3模拟了大纵横比翼长上4个站位的偏航角γ随方位角Ψ变化关系图。由图可见,偏航角随方位角呈谐波变化,在0°(360°)最大,在210°最小;并且站位越大,偏航角越小。在低速飞行时(见图 3(a)),径向来流对旋翼气动性能影响不大,即偏航角峰值较小。这是因为径向流稳定在桨叶边界层使之失速延迟;在高速飞行时(见图 3(b)),径向来流对旋翼气动性能影响较大,即偏航角峰值较大,最大达到35°。这是由于在高速飞行时,较高的马赫数会引起较大扰动的桨叶非线性,导致了较大的径向来流非线性。
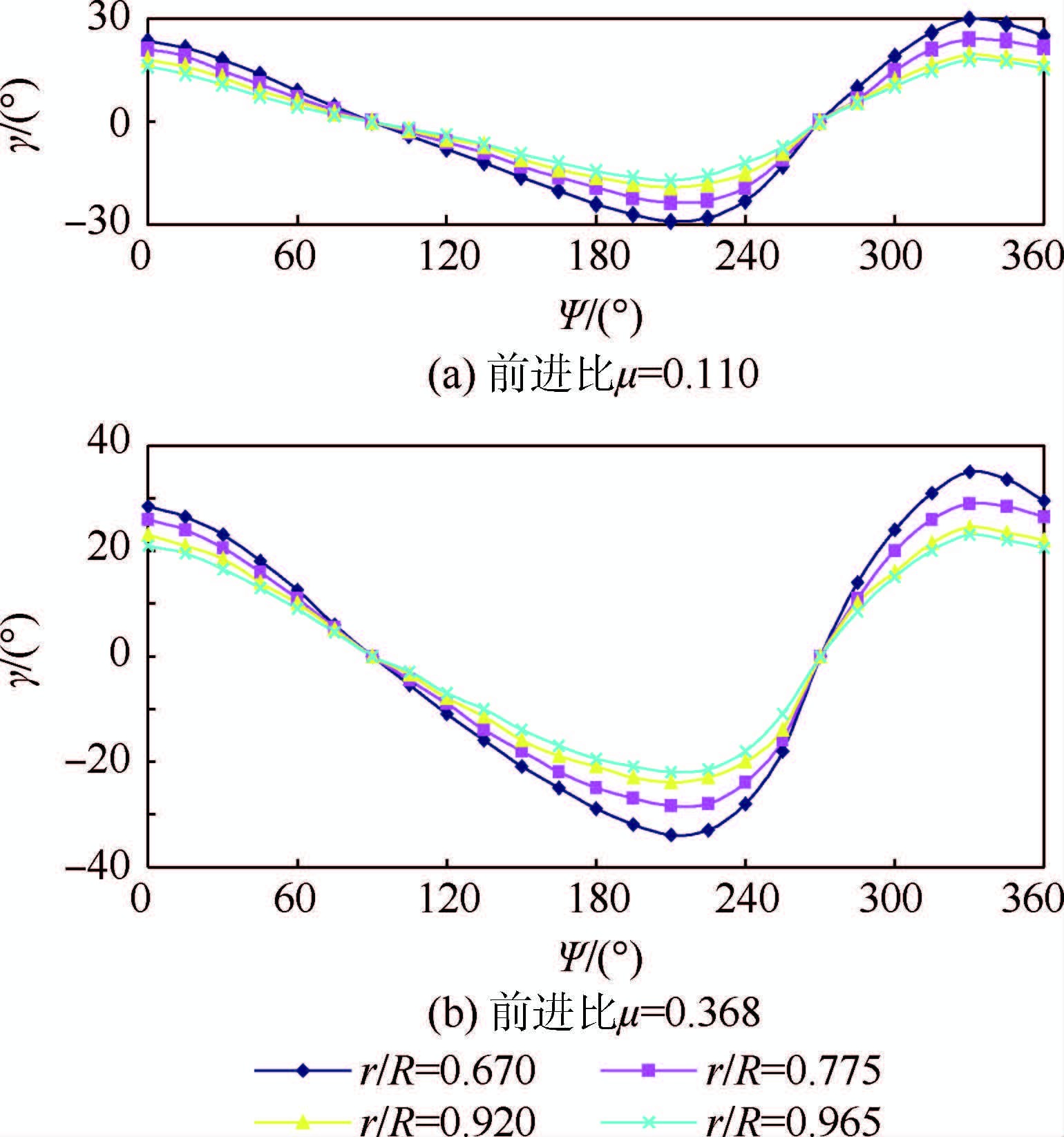 |
| 图 3 偏航角变化曲线 Fig. 3 Yaw angle changing curves |
| 图选项 |
5 算例验证与分析对于大扰动、大机动飞行,尤其是高速、大过载条件下的非定常机动飞行,外界干扰因素较多,由于缺乏公开的飞行测试数据,很难进行对比验证。本文以UH-60A直升机为例,桨盘实度σ=0.082 6,桨叶约-16°非线性扭曲,有关桨叶具体参数详见文献[12]。旋翼转速Ω=27 rad/s,每片桨叶沿展长方向分为9个叶素(r/R=0.225,0.400,0.550,0.675,0.775,0.865,0.920,0.965和0.990),在前进比μ分别为0.110(前飞速度为85 km/h,Cw/σ=0.078,Cw为重量系数)和0.368(前飞速度为287 km/h,Cw/σ=0.084)情况下,分别模拟旋翼流场、气动力和俯仰力矩。根据状态量和控制量,经过反复验证和比较,采取如下小扰动数值:桨叶两叶素位置的扰动量设为0.001,与控制变量相关的扰动量设为0.020,对于本文的高速前飞算例,经过检验发现上述小扰动设置误差稍大,但仍然适用。表 1给出了经过旋翼配平的直升机2种稳定飞行的旋翼操纵和旋翼轴倾斜角度(αs为纵向倾斜角,Φs为横向倾斜角)。与飞行试验数据[28]相比,本文模型计算值与试飞值基本一致。
表 1 旋翼操纵与旋翼轴倾角Table 1 Rotor controls and shaft angles
| 参数 | μ=0.110 | μ=0.368 | ||
| 本文计算 数据/(°) | 飞行试验 数据/(°) | 本文计算 数据/(°) | 飞行试验 数据/(°) | |
| θ0 | 8.69 | 7.75 | 13.86 | 13.21 |
| θ1c | 4.79 | 4.06 | 7.87 | 6.56 |
| θ1s | -1.84 | -2.08 | -7.95 | -9.07 |
| αs | -1.9 | -2.3 | 7.9 | 7.8 |
| Φs | -0.98 | -1.22 | 1.2 | 1.6 |
表选项
5.1 旋翼诱导速度分布图 4分别模拟了前进比为μ=0.110和μ=0.368条件下的旋翼诱导速度Vw分布。从图 4可知,桨盘平面上沿桨盘站位r/R和方位角Ψ诱导速度分布不均,随桨叶展长方向站位越大,诱导速度峰值越大;在第1象限和第4象限诱导速度峰值最大,与式(20)计算一致,并且前飞速度越大,诱导速度越大。
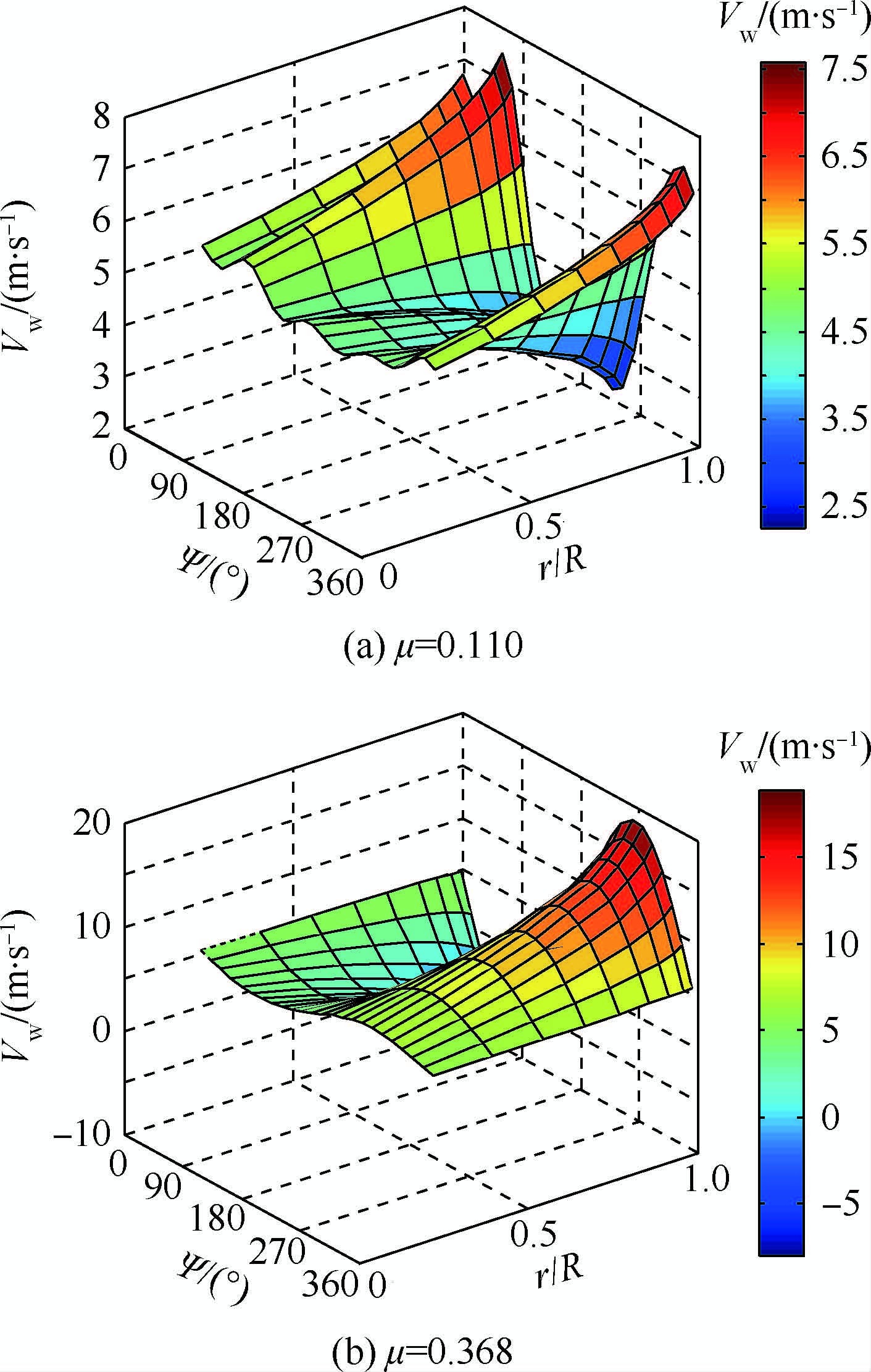 |
| 图 4 旋翼诱导速度分布图 Fig. 4 Rotor induced velocity graph |
| 图选项 |
5.2 气动力与力矩模拟图 5和图 6分别模拟了前进比为μ=0.110和μ=0.368条件下的桨叶气动力载荷。由图 5可见,低速飞行时,桨叶气动载荷计算结果与试验飞行数据吻合较好;高速飞行时,桨叶气动载荷与试验飞行数据相比产生了气动载荷的相位偏移。产生误差的原因可能是未计入桨叶尾涡流场的自诱导和偏航流效应(见图 3)。图 7和图 8分别模拟了前进比为μ=0.110和μ=0.368条件下的桨叶俯仰力矩。低速飞行时(见图 7),俯仰力矩预测趋势与试验数据一致。高速飞行时(见图 8),俯仰力矩预测趋势与试验数据基本吻合,这可能是由桨叶大速度前飞时遇到较大扰动非线性气流以及旋翼-机体自身产生耦合效应而导致的。
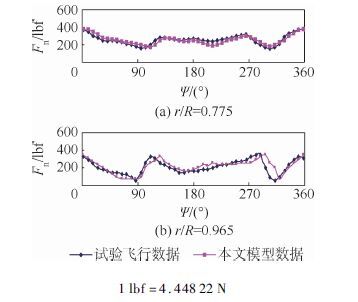 |
| 图 5 法向力比较(μ=0.110) Fig. 5 Normal force comparison (μ=0.110) |
| 图选项 |
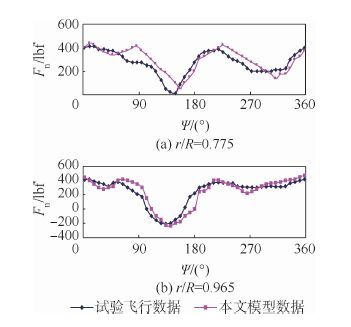 |
| 图 6 法向力比较(μ=0.368) Fig. 6 Normal force comparison (μ=0.368) |
| 图选项 |
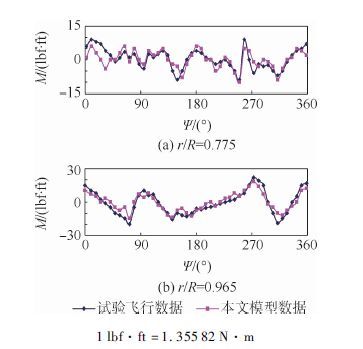 |
| 图 7 俯仰力矩比较(μ=0.110) Fig. 7 Pitching moment comparison (μ=0.110) |
| 图选项 |
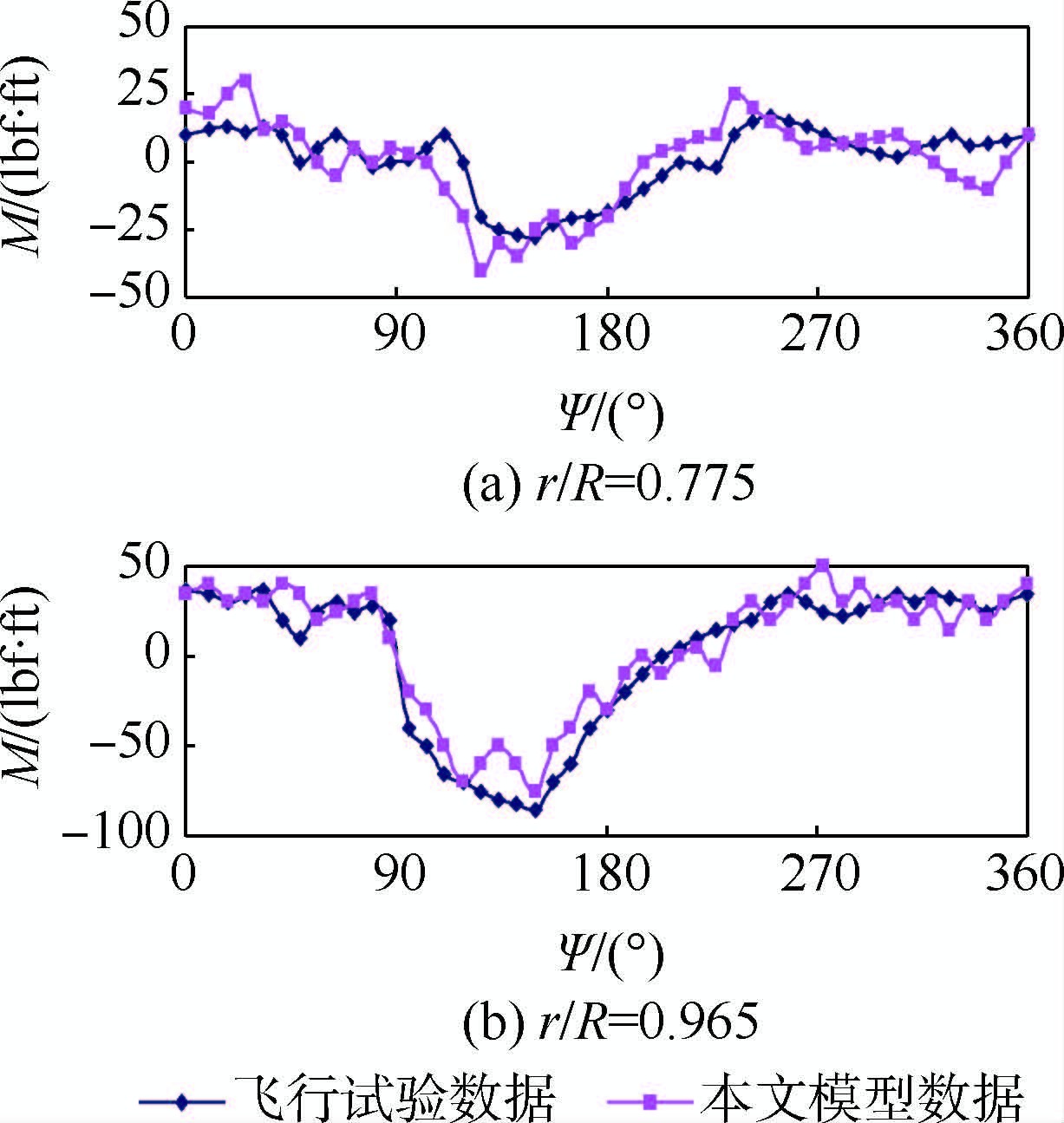 |
| 图 8 俯仰力矩比较(μ=0.368) Fig. 8 Pitching moment comparison (μ=0.368) |
| 图选项 |
根据本文建立的旋翼系统模型,在VC平台上编制了部分代码,在装有Intel(R) Xeon(R) CPU E5-1607的Del工作站上完成旋翼系统的模拟,桨叶载荷计算周期为26.8 ms。通过操纵游戏杆实现了直升机实时模拟,仿真画面如图 9所示。
 |
| 图 9 机动飞行仿真画面 Fig. 9 Scene of maneuver flight simulation |
| 图选项 |
6 结 论本文采用小扰动理论方法计算了桨叶气动载荷并建立了一个适于直升机实时飞行仿真的旋翼系统模型。集成Pitt和Peters的一阶谐波动态入流模型和Leishman-Beddoes非定常动态失速模型的基础上,模拟了桨叶的偏航流效应、诱导速度场以及气动载荷。
1) 采用小扰动原理建立的桨叶系统模型考虑了偏航流效应。低速飞行时,偏航流对旋翼气动性能影响较小;高速飞行时,偏航流对旋翼气动性能影响较大,即偏航角峰值较大,最大达到35°。
2) 建立的旋翼系统模型能够准确预测了UH-60A直升机在低速和高速2种飞行条件下的旋翼诱导速度场,既能较好地反映出随桨盘平面不均匀分布变化,又能体现出随相位变化的规律以及随旋翼气动力变化的滞后效应,能够满足实时飞行仿真的要求。
3) 本文计算的桨叶叶素气动载荷分布趋势与飞行试验数据吻合,既能较好地反映载荷的幅值变化,又能体现出相位变化的规律,其计算精度能够满足旋翼设计的要求,计算速度满足实时飞行模拟。
4) 高速飞行时,由于前行桨叶遇到较大扰动非线性气流以及尾涡流场畸变效应,使得桨叶气动载荷变化剧烈并在方位角90°/270°附近产生了相位偏移,俯仰力矩存在较大非线性扰动性。
参考文献
| [1] | 栗英杰. 直升机飞行模拟器关键技术研究[D].长春:吉林大学,2012:1-2. LI Y J.Research on key technologies of helicopter flight simulator[D].Changchun:Jilin University,2012:1-2(in Chinese). |
| Cited By in Cnki (6) | |
| [2] | 王芳. 机动飞行状态下的旋翼入流和响应分析[D].南京:南京航空航天大学,2007:4-5. WANG F.Investigation on the inflow and aerodynamic response of rotors in maneuvering flight[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2007:4-5(in Chinese). |
| Cited By in Cnki (1) | |
| [3] | PITT D M,PETERS D A.Theoretical prediction of dynamic inflow derivatives[J].Vertica,1981,5(1):21-34. |
| [4] | PETERS D A,BOYD D D,HE C J.Finite-state induced-flow model for rotors in hover and forward flight[J].Journal of the American Helicopter Society,1989,34(4):5-17. |
| Click to display the text | |
| [5] | KELLER J D. An investigation of helicopter dynamic coupling using an analytical model[J].Journal of the American Helicopter Society,1996,41(4):322-330. |
| Click to display the text | |
| [6] | ZHAO J G. Dynamic wake distortion model for helicopter maneuvering flight[D].Atlanta,Georgia:Georgia Institute of Technology,2005:35-36. |
| Click to display the text | |
| [7] | DUMONT A,LE PAPE A,PETER J.Aerodynamic shape optimization of hovering rotors using a discrete adjoint of the reynolds-averaged navier-stokes equations[J].Journal of the American Helicopter Society,2011,56(3):256-258. |
| Click to display the text | |
| [8] | 徐广,王博,徐国华.基于CFD的直升机旋翼流场及气动力计算[J].南京航空航天大学学报,2011,43(3):369-374. XU G,WANG B,XU G H.Computation on flow field and aerodynamic load of helicopter rotors based on CFD[J].Journal of Nanjing University of Aeronautics & Astronautics,2011,43(3):369-374(in Chinese). |
| Cited By in Cnki (1) | |
| [9] | 李攀. 旋翼非定常自由尾迹及高置信度直升机飞行力学建模研究[D].南京:南京航空航天大学,2010:6-7. LI P.Rotor unsteady free-vortex wake model and investigation on high-fidelity modeling of helicopter flight dynamics[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010:6-7(in Chinese). |
| Cited By in Cnki (8) | |
| [10] | CURTISS H C. Stability and control modeling[J].Vertica,1988,12(4):381-394. |
| [11] | TISCHLER M B. System identification requirements for high-bandwidth rotorcraft flight control system design[J].Journal of Guidance,Control,Dynamics,1990,13(5):835-841. |
| Click to display the text | |
| [12] | HOWLETT J J. UH-60 black hawk engineering simulation program:Volume I-mathematical model:NASA CR-166309[R].Reston:AIAA,1981:27-58. |
| [13] | BHAGWAT M J.Mathematical modeling of the transient dynamics of helicopter rotor wakes using a time-accurate free-vortex methods[D].College Park,Maryland:University of Maryland,2001:97-121. |
| [14] | RIBERA M. Helicopter flight dynamics simulation with with a time-accurate free-vortex wake model[D].College Park,Mary-land:University of Maryland,2007:104-150. |
| [15] | 赵景根,徐国华,招启军.基于自由尾迹分析的直升机旋翼下洗流场计算方法[J].兵工学报,2006,27(1):63-68. ZHAO J G,XU G H,ZHAO Q J.A calculating method of helicopter rotor downwash flowfield based on free wake analysis[J].Acta Armamentarii,2006,27(1):63-68(in Chinese). |
| Cited By in Cnki (6) | |
| [16] | LI P,CHEN R L.Rotor unsteady aerodynamics model using an efficient free-vortex method[J].Aircraft Engineering and Aerospace Technology,2012,84(5):311-320. |
| Click to display the text | |
| [17] | 刘勇,邵松,朱清华,等.基于时间精确自由尾迹方法的旋翼非定常气动特性分析[J].航空学报,2012,33(4):607-616. LIU Y,SHAO S,ZHU Q H,et al.Analysis of rotor unsteady aerodynamic characteristics based on time accurate free wake formulation[J].Acta Aeronautica et Astronautica Sinica,2012,33(4):607-616(in Chinese). |
| Cited By in Cnki (2) | |
| [18] | 吕维梁,史勇杰,魏鹏,等.旋翼非定常气动载荷及瞬态气动响应计算[J].南京航空航天大学学报,2013,45(1):21-27. LV W L,SHI Y J,WEI P,et al.Computation of rotor unsteady aerodynamic loads and transient aerodynamic response[J].Journal of Nanjing University of Aeronautics & Astronautics,2013,45(1):21-27(in Chinese). |
| Cited By in Cnki (7) | |
| [19] | 曹义华. 直升机机动飞行旋翼的气动力模拟[J].航空学报,1999,20(1):39-42. CAO Y H.Modeling the aerodynamic forces of a maneuvering helicopter rotor[J].Acta Aeronautica et Astronautica Sinica,1999,20(1):39-42(in Chinese). |
| Cited By in Cnki (8) | |
| [20] | CAO Y H. A new inverse solution technique for studying helicopter maneuvering flight[J].Journal of the American Helicopter society,2000,45(1):43-53. |
| Click to display the text | |
| [21] | 苏媛,曹栋,曹义华.计及大迎角失速的直升机旋翼的气动力模拟[J].北京航空航天大学学报,2010,36(2):168-171. SU Y,CAO D,CAO Y H.Simulation of helicopter rotor aerody-namic force in conditions of high angle of attack and dynamic stall[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(2):168-171(in Chinese). |
| Cited By in Cnki (3) | |
| [22] | DREIER M E. Introduction to helicopter and tiltrotor flight simulation[M].Reston:AIAA,2007:190-194. |
| [23] | HOUSEN S S,BROWN R E.Rotor-wake modeling for simulation of helicopter flight mechanics in autorotation[J].Journal of Aircraft,2003,40(5):938-945. |
| Click to display the text | |
| [24] | LI P,CHEN R L.A mathematical model for helicopter comprehensive analysis[J].Chinese Journal of Aeronautics,2010,23(3):320-326. |
| Click to display the text | |
| [25] | Leishman J G,Crouse G L.State-space model for unsteady airfoil behavior and dynamic stall:AIAA-1989-1219[R].Reston:AIAA,1989:36-38. |
| [26] | 徐进. 直升机大机动飞行中旋翼非定常空气动力研究[D].南京:南京航空航天大学,2007:47-48. XU J.Unsteady aerodynamics investigation for the isolated rotor in large amplitude maneuvering flight[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2007:47-48(in Chinese). |
| Cited By in Cnki (5) | |
| [27] | PURSER P E,SPEARMAN M L.Wind-tunnel tests at low speed of swept and yawed wings having various plan forms:NACA Technical Note 2445[R].Reston:NACA,1951:86-87. |
| [28] | SITARAMAN J. CFD based unsteady aerodynamic modeling for rotor aeroelastic analysis[D].Maryland:University of Maryland,2003:119,152. |
