以“并行设计”为主要特征的可靠性定量设计包括可靠性定量模型建模与分析、可靠性与性能综合优化等多方面内容。前者为后者提供定量设计模型和可靠性分析结果,后者利用前者计算当前设计点的性能输出和可靠度,据以搜索最优设计点。
可靠性定量设计的本质是参数设计,主要手段是可靠性与性能综合优化,RBMDO和RBDO是典型代表。随着故障机理(Physics of Failure,PoF)研究逐步深入,可靠性定量设计进一步将PoF对可靠性与性能这类系统级指标的影响纳入研究视野,把传统上时间无关的综合优化拓展到时变的综合优化,得到产品寿命周期内设计变量的最优取值[10]。例如Wang等[11]提出以时变运动学可靠性和时变结构可靠性为约束的时变RBDO方法,以起落架为对象,以磨损为关键失效机理构建多学科可靠性模型,以最小化总重量的均值和方差为目标进行了综合优化。张义民[12]阐述了机械产品常见的动态和渐变特性(如振动和磨损)给机械可靠性设计带来的新需求和发展。
实现可靠性定量设计、开展可靠性与性能综合优化的基础是可靠性定量模型的建模工作,例如优化中使用的代理模型即从该模型提取。与RBMDO和RBDO侧重综合优化不同,IDRP除了变量参数设计外,还包括系统构型设计和单元强化设计,后者实质上处理了可靠性定量模型的建模问题。曾声奎等[3, 13]提出了IDRP的技术框架,给出了基于故障模式影响分析、波动模式影响分析及故障机理分析进行IDRP模型建模的方法,提出了基于Logistic变换建立性能可靠度与关键设计参数函数关系的响应面方法,建立了参数优化模型和容差优化模型及优化流程,并利用舵机案例进行了验证。陈云霞等[14, 15]探索了IDRP仿真建模和分析的方法,并以某导弹飞控系统为例进行了验证。
可靠性定量模型建模是以功能性能模型为基础,引入由故障模式影响分析、波动模式影响分析及故障机理分析得到的故障率模型、参数波动模型、环境扰动模型、故障机理模型,借助仿真工具,得到仿真形式的可靠性定量模型。可靠性定量模型建模活动本质上反映了设计人员对产品故障模式、波动因素和故障机理等故障规律的既有知识。这些知识主要决定可靠性定量模型的结构,而知识固有的有限性和不完整性必然会给模型带来误差,也会给设计变量、模型常参数和退化特征量等与性能波动和退化相关的模型输入参数的量化带来不确定性。另一方面,可靠性活动产生了丰富的数据,这些数据通常多用于数据融合的可靠性评估,以确定寿命分布参数的不确定性。因此,借鉴可靠性评估的数据融合思想,将知识与数据相融合,量化可靠性定量模型的模型误差和输入参数不确定性,能够为克服可靠性定量模型建模活动中由知识有限性和不完整性带来的不足提供有效手段。
贝叶斯方法是可靠性评估中常用的数据融合方法,而Kennedy和O’hagan[16]利用贝叶斯方法处理模型误差量化和未知参数估计的做法,事实上拓展了贝叶斯方法解决模型和数据相融合这个问题的潜力。但文献[16]仅以高斯过程为研究对象,与复杂的可靠性定量模型相去甚远。另外,文献[16]并未考虑数据的特点,而故障统计数据具有鲜明的多样性,例如来自多个数据来源(如试验数据、维修数据、使用数据等),或者体现为多种数据类型(如成败型数据、寿命数据、性能波动数据、性能退化数据等)。本文将针对可靠性定量模型建模的需求和故障统计数据的特点,提出与之相适应的方法。此外,相比频率方法,贝叶斯方法更适用于小样本情景。这与可获得的故障统计数据通常有限的特点相吻合,因此本文借鉴文献[16]的做法,采用贝叶斯方法实现故障规律知识与故障统计数据的融合。
针对可靠性定量设计中,基于知识建立可靠性定量模型的现有方式存在由设计人员知识的不完整性带来模型误差和输入参数不确定性的不足,本文提出知识与数据融合的可靠性定量模型建模方法。以下首先论述知识与数据融合的可靠性定量模型建模活动并建立相应框架;接着阐述基于贝叶斯理论的知识和数据融合原理;然后提出基于贝叶斯理论融合知识与数据的通用方法,并分别针对性能波动数据和性能退化数据2种常见数据类型的特点进一步详细讨论各自适用的贝叶斯融合方法;最后通过机载轴向柱塞泵的案例验证前述方法的可行性和有效性。
1 知识与数据融合的可靠性定量模型建模开展可靠性定量设计的基础是建立可靠性定量模型。一般意义上,定量模型包括输入、输出和二者量化关系3个元素。建立定量模型主要是指建立输入输出的量化关系。对于可靠性定量模型而言,就是要建立设计变量、模型常参数和退化特征量等模型输入与性能指标、可靠度等输出的量化关系。
在可靠性定量模型建模中,构建输入输出量化关系的依据来自设计人员对产品对象的任务要求、环境剖面、功能需求、性能指标和故障规律等方面的认识。这些认知体现为功能模型、性能模型、故障机理模型、故障率模型、环境扰动模型和参数波动模型等形式的知识。由于产品对象多学科耦合、软硬故障并存,所以需要将这些模型集成起来才能刻画产品性能波动、退化等故障特征。多学科仿真工具及其交互为实现上述模型集成提供了有效手段。因此,构建可靠性定量模型中输入输出的量化关系,是利用仿真工具集成可靠性、性能等多学科模型,得到可靠性与性能综合集成的一体化仿真模型。
由于产品设计阶段设计人员对产品的故障规律尚缺乏把握,相关知识主要来自相似产品、相似材料和历史数据等渠道,知识的有限性和不完整性势必制约上述一体化仿真模型对产品对象的刻画能力,带来模型误差。因此,需要在可靠性定量模型中引入模型误差,从而得到完整的输入输出量化关系。
模型输入是可靠性定量模型中与量化关系相辅相成的另一重要元素。可靠性定量模型的输入参数包括设计变量、模型常参数和退化特征量等。这些输入参数具有不确定性,其量化主要依赖公差设计、相似材料、仿真计算或专家经验等手段。事实上,这些不确定性量化依据本质上也基于设计人员的相关知识,自然也受限于知识的有限性和不完整性。此外,模型误差也包含自身的参数,也需量化其不确定性。
为克服上述知识有限性和不完整性给可靠性定量模型建模带来的制约,本文通过融合知识和数据的方式,利用数据更新设计变量、模型常参数、退化特征量以及模型误差参数等的不确定性,确定模型误差,完成可靠性定量模型建模。
由于设计变量、模型常参数、退化特征量及模型误差参数都是模型输入,为消除与之无关的特征,可以利用近似技术把引入模型误差的一体化仿真模型简化为相应的代理模型。此时,知识与数据的融合就转化为代理模型(提取自刻画故障规律知识的可靠性与性能一体化仿真模型)与统计数据的融合。利用贝叶斯理论,就可以更新设计变量、模型常参数、退化特征量等输入参数以及模型误差参数的不确定性。进一步地,利用更新的输入参数不确定性,可以得到更新的代理模型,与更新的输入参数不确定性,以及更新的模型误差及其不确定性,共同组成可靠性定量模型,完成可靠性定量模型建模工作。
综上所述,知识与数据融合的可靠性定量建模涵盖以下几方面:
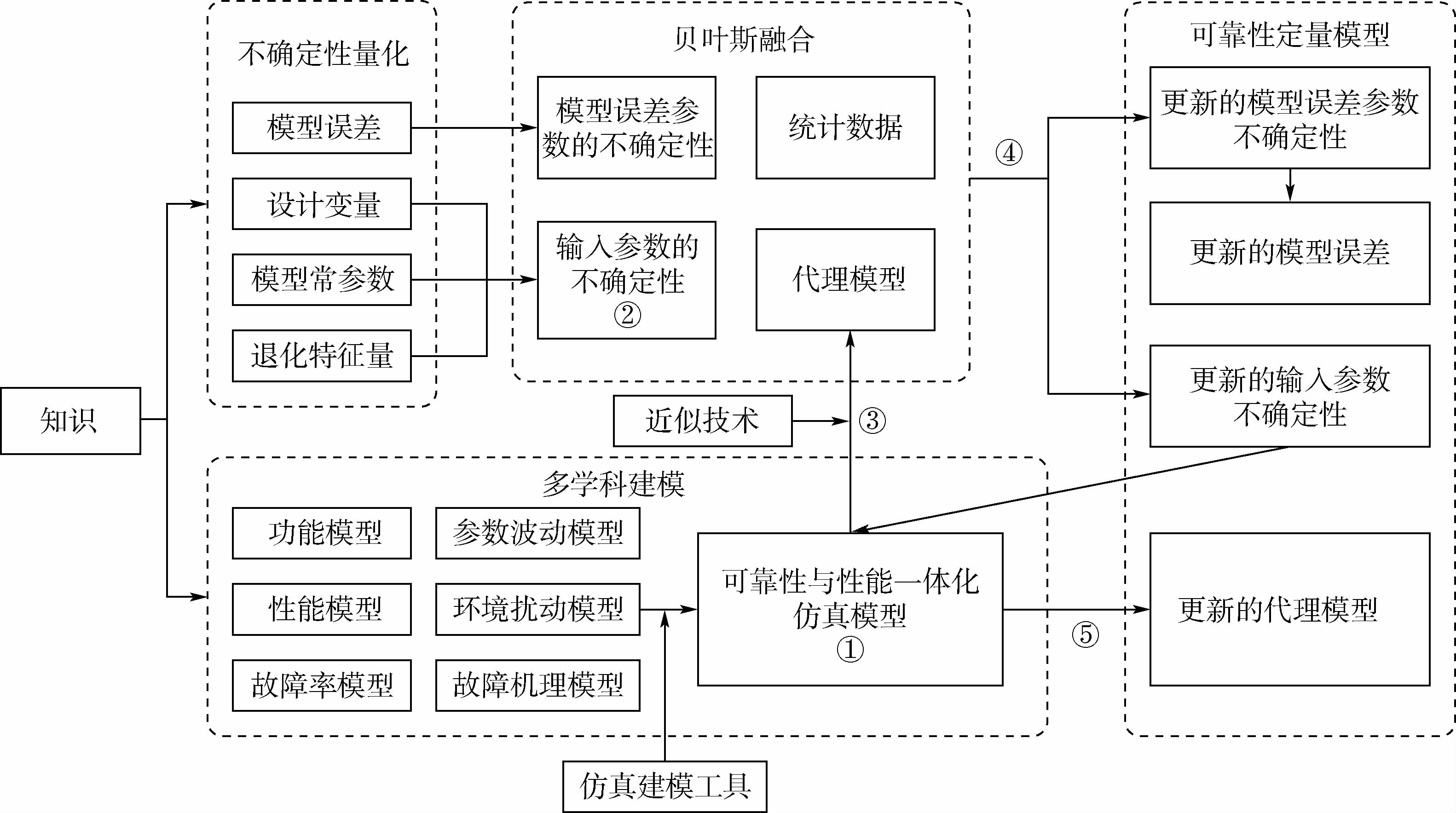
1) 可靠性定量模型建模框架包括(如图 1所示):
 |
| 图 1 知识与数据融合的可靠性定量模型建模框架Fig. 1 Modeling framework of quantitative reliability model based on integration of knowledge and data |
| 图选项 |
① 建立可靠性与性能一体化仿真模型。
② 量化模型输入参数的不确定性。
③ 通过①提取代理模型。
④ 基于贝叶斯理论融合数据、代理模型,更新模型输入参数和模型误差参数的不确定性。
⑤ 利用④,采用近似技术,得到更新后的可靠性与性能一体化仿真模型的代理模型。
2) 上述模型间的关系如下:
① “可靠性与性能一体化仿真模型”是建立“可靠性定量模型”、开展贝叶斯融合的基础。
② 贝叶斯融合所需的“代理模型”由“可靠性与性能一体化仿真模型”提取得到。
③ 完成贝叶斯融合后,“可靠性与性能一体化仿真模型”得到更新,从而得到“更新的代理模型”。
④ “更新的代理模型”和更新的模型误差一起组成“可靠性定量模型”。
3) 可靠性定量模型建模的成果包括更新的输入参数不确定性、代理模型和模型误差。
2 基于贝叶斯理论的知识与数据融合原理从图 1所示知识与数据融合的可靠性定量模型建模框架可以看出,知识和数据分处不同层次。其中,处于输入输出量化关系层次的包括:①反映设计人员对产品的功能性能、故障规律等知识的可靠性与性能综合集成仿真模型,及其代理模型;②表征知识有限性和不完整性的模型误差。处于输入层次的包括:①设计变量、模型常参数和退化特征量等输入参数及其不确定性;②模型误差参数及其不确定性。而统计数据处于输出层次。因此,知识和数据的融合是定量模型三因素——量化关系、输入与输出的整体融合。而数据融合的可靠性评估中,待融合的数据均处于输出层次(如寿命和性能),融合成果也只是更新输出分布中参数的不确定性。由此可见,知识和数据的融合与单纯的数据融合截然不同。
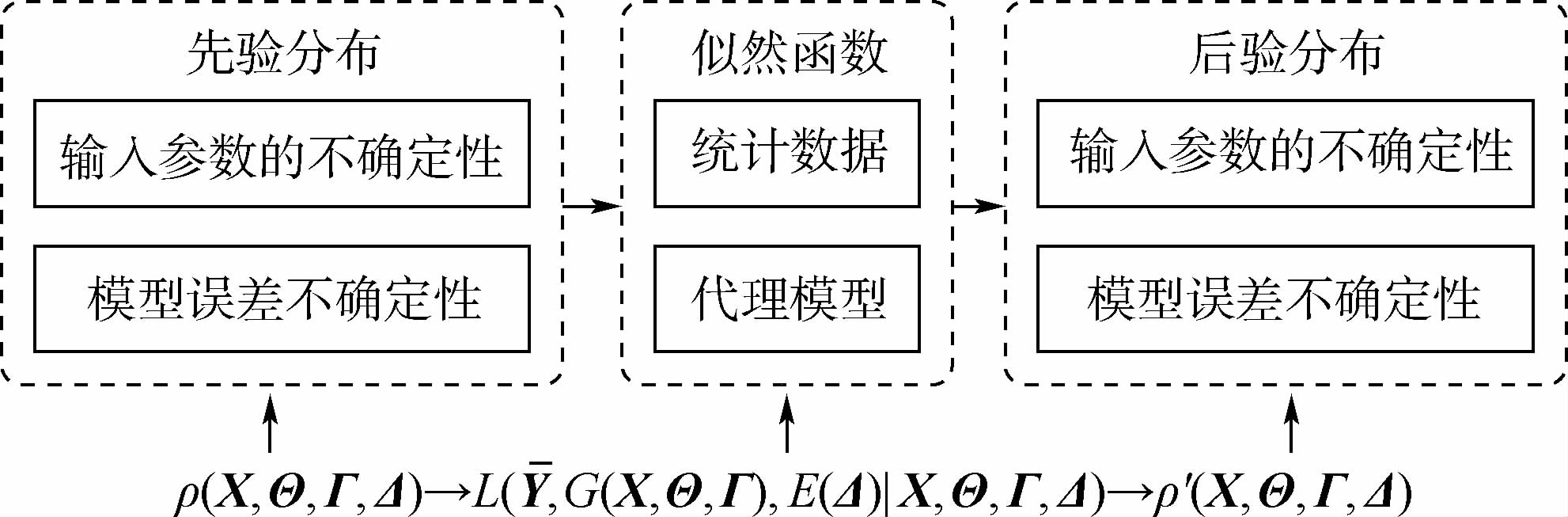
可靠性定量模型建模的贝叶斯融合环节主要目的就是用来完成知识与数据的融合,实现更新设计变量、模型常参数、退化特征量等输入参数以及模型误差参数的不确定性的目的。利用贝叶斯理论,实现知识与数据融合的原理如图 2所示。其中:Y为产品性能指标Y的样机试验数据且不考虑测量误差;G(X,Θ,Γ)为可靠性与性能一体化仿真模型的代理模型,X为设计变量,Θ为模型常参数,Γ为退化特征参数;E(Δ)为模型误差,Δ为其参数;ρ(X,Θ,Γ,Δ)为设计变量、模型常参数、退化特征量及模型误差参数的先验分布(不确定性);L(Y,G(X,Θ,Γ),E(Δ)X,Θ,Γ,Δ)为形式化表达代表故障规律等知识的代理模型和统计数据融合的贝叶斯似然函数;ρ′(X,Θ,Γ,Δ)为经贝叶斯融合得到的输入参数和模型误差参数的后验分布(更新的不确定性)。
 |
| 图 2 知识与数据的贝叶斯融合原理Fig. 2 Principle of Bayesian integration of knowledge and data |
| 图选项 |
3 知识与数据融合的贝叶斯方法在第2节阐述知识与数据的贝叶斯融合原理基础上,本节进一步具体给出知识与数据融合的贝叶斯方法。
假设产品共有n个不相关的性能指标,从简洁且不失一般性的角度出发,本节以图 2所示的单个性能指标Y为例,给出基于贝叶斯理论融合知识与数据的通用方法。
由于融合知识与数据的目的是更新设计变量、模型常参数和退化特征量等输入参数以及模型误差参数的不确定性,故可以采用近似方法排除其他无关因素,将复杂的仿真模型简化为这些参数与模型输出(如性能指标)的代理模型。形式上,图 2所示基于贝叶斯理论融合知识与数据的通用方法可以表示为(各符号遵循图 2说明的含义)

贝叶斯融合的关键是似然函数的形式。本节将式(1)的似然函数进一步表达为范数形式:
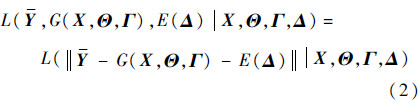
范数定义不同,式(2)的具体形式也不同。本文根据最小二乘原理,定义其为高斯范数(也可选择其他形式),则有
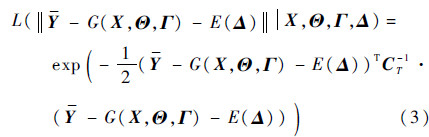
式中:CT为协方差矩阵。
在知识与数据的贝叶斯融合(式(1))中,似然函数包括3个组成部分:试验数据和代理模型、模型误差。代理模型通过可靠性与性能一体化仿真模型得到,体现了设计人员对产品故障规律的知识,是相对不变的。模型误差反映了设计人员知识的有限性和不完整性,一般也会给出相对不变的形式。而统计数据具有多样性,例如来自多个数据来源(如试验数据、维修数据、使用数据等),或者体现为多种数据类型(如成败型数据和寿命数据、性能波动数据和性能退化数据等)。因此,根据数据特点不同,贝叶斯融合中的似然函数形式也会发生相应变化。以下针对2种典型的数据类型,给出对应的似然函数形式。
3.1 性能波动数据的情形产品设计需要将工作环境纳入考察范围,而振动、温变等环境扰动通常会造成产品性能输出发生波动。此外,由于产品设计周期紧凑,所以试验时间往往有限,而有限时间内产品性能退化并不明显。因此,可以认为有限时间内通过环境扰动测得的性能试验数据是性能波动数据。性能波动数据的主要特点之一是数据间相互无关。
假设有限时间内记录下受试产品性能指标Y的一组性能波动数据(yi,i=1,2,…,k),则
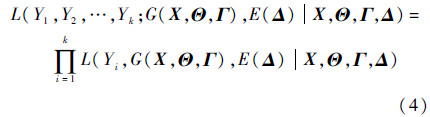
式中:{Yi,i=1,2,…,k}表示记录下的性能波动是随机变量。
如果有l台产品参加测试,得到的性能波动数据记为(yij,i=1,2,…,k,j=1,2,…,l),似然函数相应变为
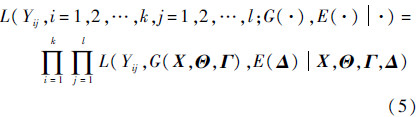
通过将式(5)代入式(1),可以得到设计变量X、常参数Θ、退化特征量Γ和模型误差参数Δ等输入参数的后验分布,达到量化模型误差、更新输入参数不确定性的目的。需要注意的是,由于有限时间内受试产品性能退化并不明显,因此,融合性能波动数据更新退化特征量的不确定性存在一定局限。
3.2 性能退化数据的情形性能退化数据是另一种常见的数据类型。与波动数据不同的是,相继时刻的退化数据存在关联关系。因此,融合性能退化数据时,式(4)中的似然函数有新的形式。
考虑到试验条件的限制,收集到的性能退化数据可能是来自单台产品的一条退化轨迹,也可能是来自多台产品的多条退化轨迹。在不同情形下,似然函数的形式还存在一定差异。以下分别论述。
1) 单一退化轨迹的情况
假设在k个时刻记录下受试产品性能指标Y的一组退化轨迹{yi,i=1,2,…,k}。由于后一时刻退化量yi受前一时刻退化量yi-1影响,也即
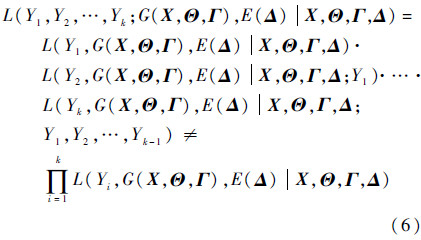
式中:{Yi,i=1,2,…,k}表示ti时刻的退化量是随机变量。可见融合性能退化数据得到的似然函数形式与融合性能波动数据得到的似然函数形式截然不同。将式(6)代入式(1),则有
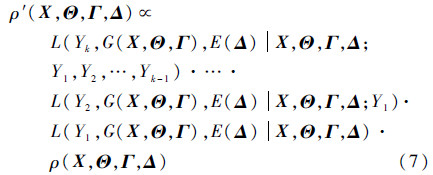
事实上,令ρ0(X,Θ,Γ,Δ)=ρ(X,Θ,Γ,Δ),从而有
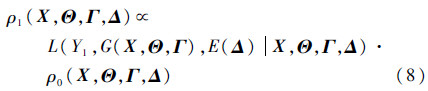
相应的
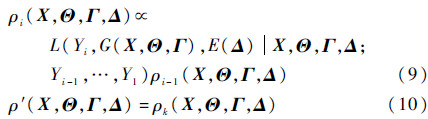
经如上k次迭代后,就完成了所有k个退化数据也就是整个退化轨迹的融合,得到模型误差参数和输入参数的后验分布,完成了量化模型误差、更新输入参数不确定性的任务。
2) 多条退化轨迹的情况
假设l个相互独立的产品受试,k个时刻共记录下l条退化轨迹{yij,i=1,2,…,k,j=1,2,…,l}且各条轨迹相互独立,那么式(4)中的似然函数可以表达为
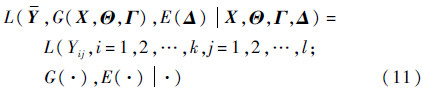
式(11)还可以进一步表达为
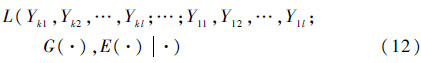
或
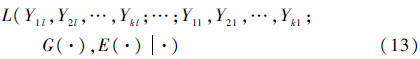
需要指出的是,式(12)和式(13)的2种分组形式代表了2种不同的融合思路。对式(12)和式(13)而言,分别有
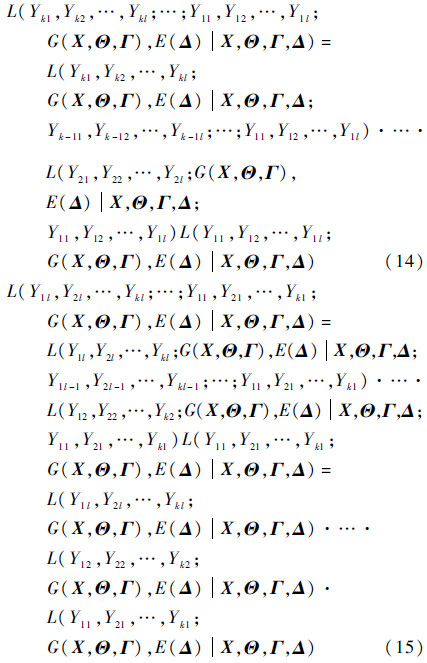
进一步分析式(12)和式(14)代表的融合思路可以发现,尽管式(14)右侧的各个分量鲜明地表示出同一时刻不同产品的性能数据是相互独立的波动数据,但难以给出相继2个时刻的2组波动数据间的关联关系。因此,采取式(12)和式(14)代表的融合思路并不恰当。而式(13)和式(15)代表的融合思路是逐一融合各条退化轨迹。由于各个产品相互独立,式(15)的变换是恰当的。从而有
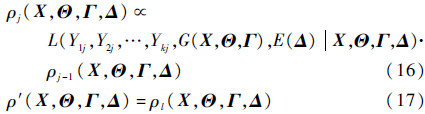
通过采用上述融合多条退化轨迹的方法,得到模型误差参数和输入参数的后验分布,完成了量化模型误差、更新输入参数不确定性的任务。
4 案例验证本文选取航空液压系统的动力元件柱塞泵作为案例验证对象。柱塞泵利用发动机带动,通过柱塞腔容积变化完成吸、排液压油动作,并在舵机控制下推动液压作动机构,偏转舵面,控制飞行姿态。可见,柱塞泵的可靠性对整个液压乃至飞控系统的可靠性起决定性作用。根据泵内柱塞分布,柱塞泵可分为轴向柱塞泵和径向柱塞泵,轴向柱塞泵又包括直轴式轴向柱塞泵和斜盘式轴向柱塞泵。轴向柱塞泵结构简单、体积小、容积效率高、传输功率大,适应液压机械大流量、高速高压化发展趋势,得到广泛应用[17]。本节研究的某型轴向柱塞泵结构如图 3所示。
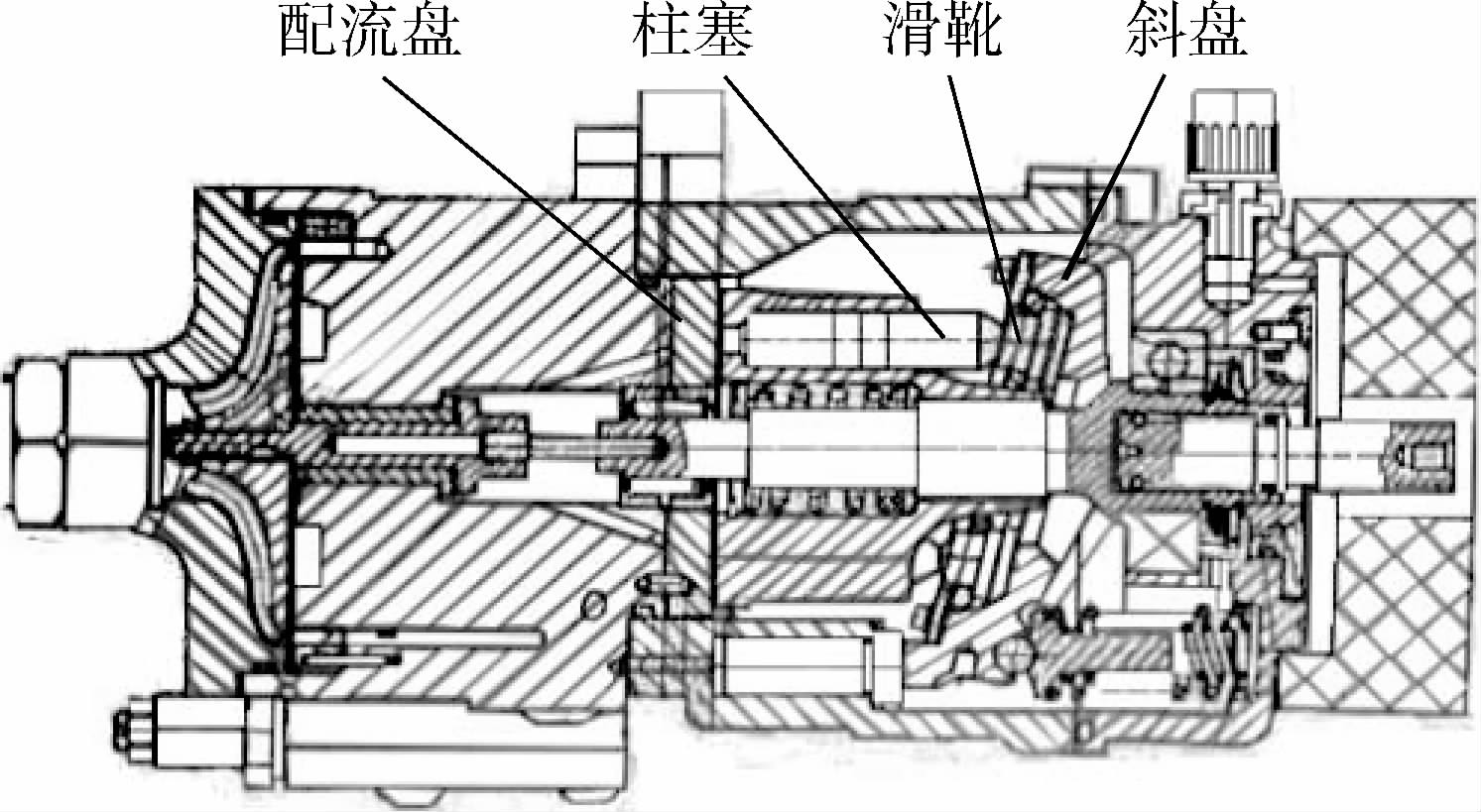 |
| 图 3 某型轴向柱塞泵结构Fig. 3 Structure of an axial piston pump |
| 图选项 |
轴向柱塞泵的主要技术参数包括压力、转速、排量、流量、功率和效率等。由于柱塞泵的主要功能是通过吸、排液压油,为液压系统提供动力,因此本文主要考察流量这个指标。输出流量衰减或称退化会造成柱塞泵因性能不达标而报废。造成流量退化的主要原因是泵工作过程中液压油泄漏量增大。导致泄漏加大的主要故障机理是润滑条件下的磨损,主要磨损部位包括滑靴副、柱塞副和配流副。其中,滑靴副和配流副磨损造成的泄漏占总泄漏的绝大部分[18]。因此,本文主要考察滑靴副和配流副这2个摩擦副。滑靴副的结构如图 4 所示,磨损模型采用文献[19]提出的润滑条
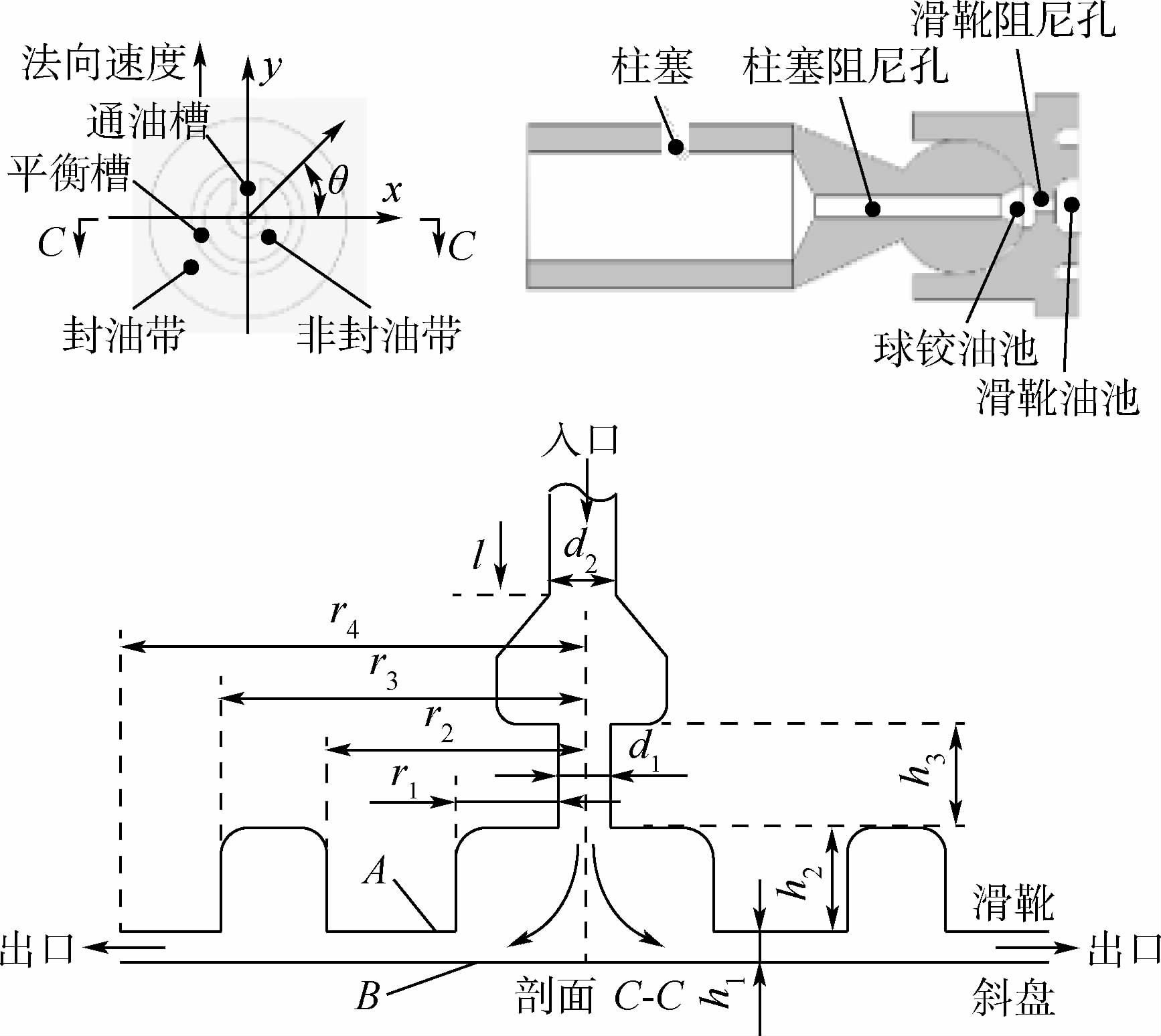 |
| 图 4 滑靴副几何结构Fig. 4 Geometric structure of slipper-swash plate |
| 图选项 |
件下二体磨粒磨损模型,建立的仿真模型如图 5所示。配流副的结构如图 6所示,磨损模型采用文献[20]提出的三体磨粒磨损模型,建立的仿真模型如图 7所示。柱塞泵泄漏量的仿真模型依据文献[21]方法建立。
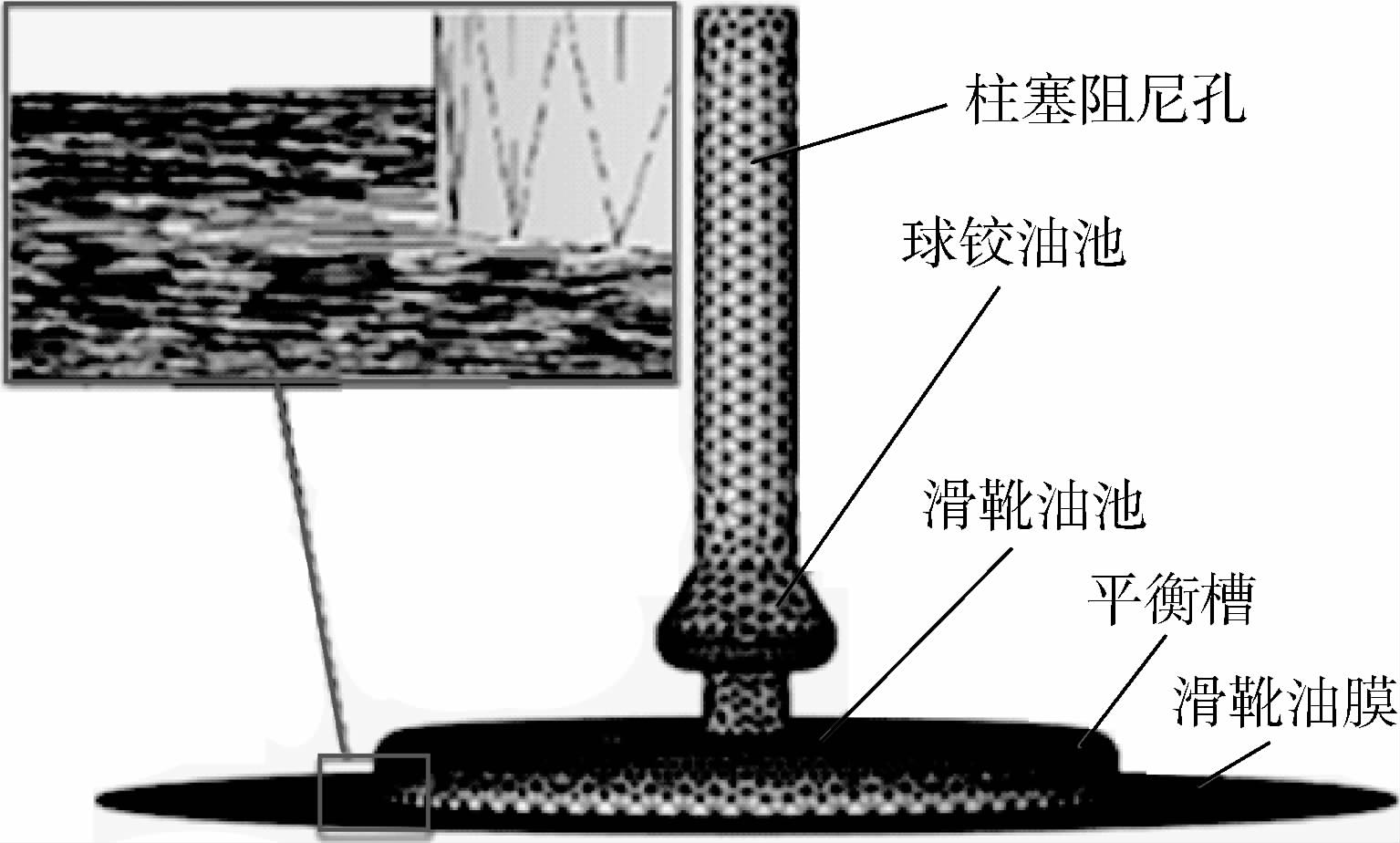 |
| 图 5 滑靴副仿真模型Fig. 5 Simulation model of slipper-swash plate |
| 图选项 |
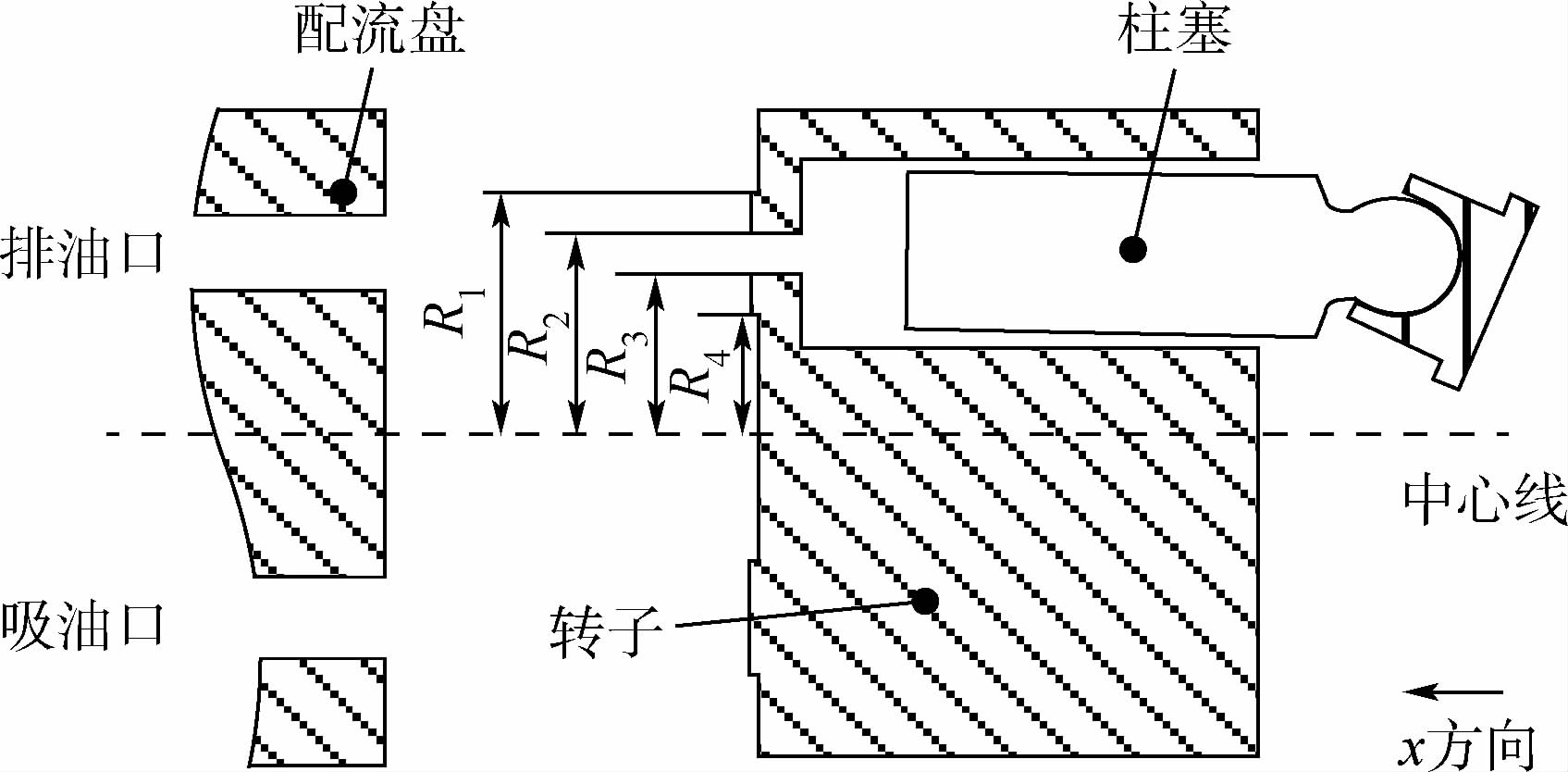 |
| 图 6 配流副几何结构Fig. 6 Geometric structure of barrel-port plate |
| 图选项 |
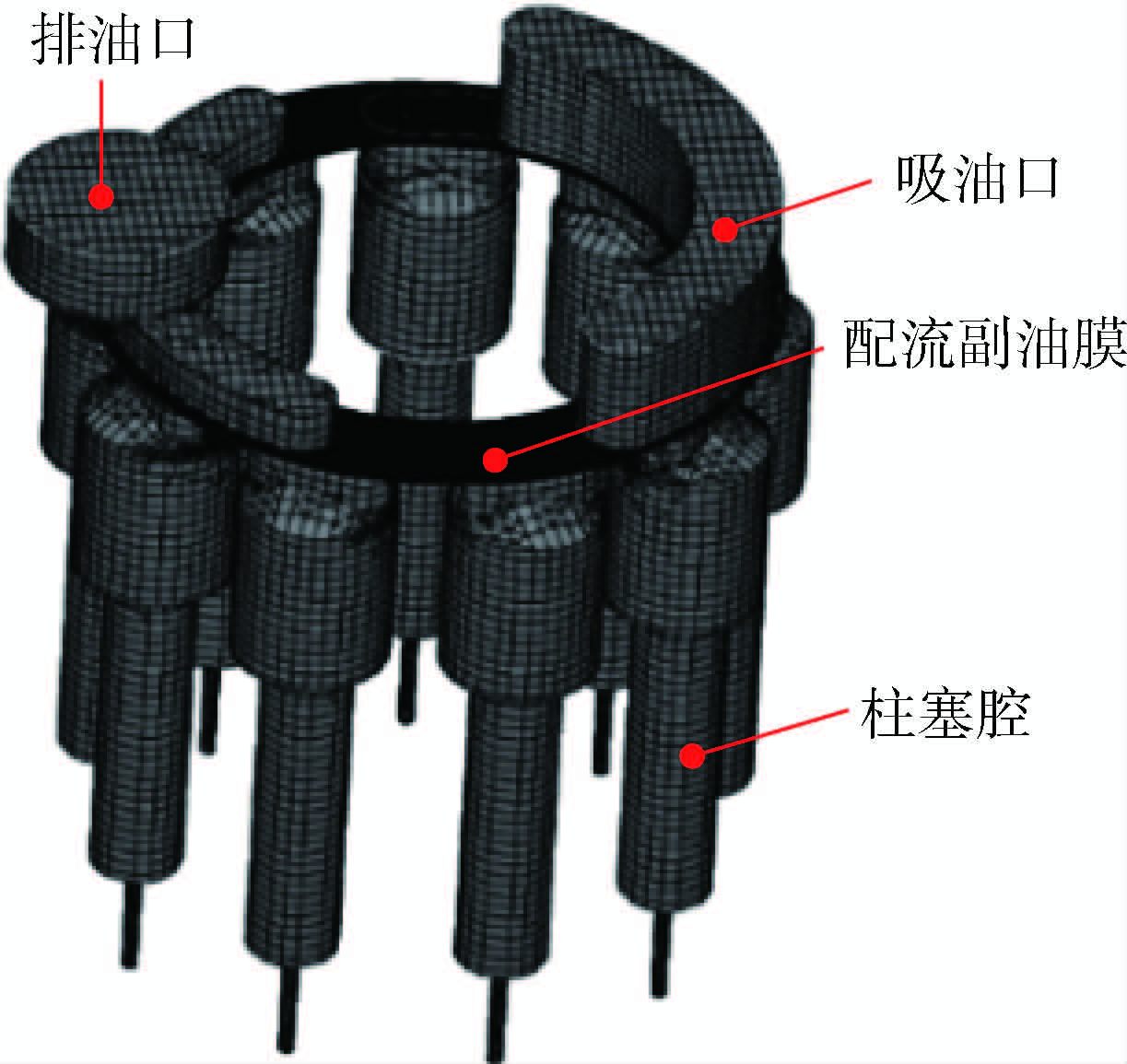 |
| 图 7 配流副仿真模型Fig. 7 Simulation model of barrel-port plate |
| 图选项 |
滑靴副和配流副的主要结构尺寸参数如表 1和表 2所示。尺寸参数的不确定性主要来自加工公差,本文依据航空工业标准确定其不确定性范围及分布[22]。摩擦副间隙是指液压油形成的油膜,起润滑作用,其大小由摩擦副工作时压紧力和分离力间的力平衡确定。表中间隙值的不确定性由设计人员通过仿真计算给出。摩擦副发生润滑磨损,是由于柱塞泵工作时打破了摩擦副的力平衡导致。本文假设两摩擦副的磨损速率为常数,由仿真计算给出,相应的不确定性由设计人员确定并在表 1和表 2列出。随着磨损累计,间隙持续加大,液压油泄漏量出现退化态势。柱塞泵泄漏数据取自中航工业金城南京机电液压工程研究中心轴向柱塞泵综合试验平台(见图 8)开展的轴向柱塞泵磨损特性试验,共2 700 h(见表 3)。
表 1 滑靴副尺寸参数、退化特征量及其不确定性Table 1 Dimensions, degradation parameters and associated uncertainties of slipper-swash plate
| 参数 | 不确定性分布/mm |
| 柱塞阻尼孔直径 d 2 | N(1.2,0.035) |
| 柱塞阻尼孔长度 l | N(9.0,0.04) |
| 封油带内径 r 3 | N(4.4,0.04) |
| 封油带外径 r 4 | N(7.7,0.05) |
| 滑靴副间隙 h h | N(0.006 6,0.001) |
| 滑靴副磨损速率 r h | U(0.000 08,0.000 12) |
表选项
表 2 配流副尺寸参数、退化特征量及其不确定性Table 2 Dimensions, degradation parameters and associated uncertainties of barrel-port plate
| 参数 | 不确定性分布/mm |
| 外封油带半径 R 1 | N(27.10,0.07) |
| 排油窗外半径 R 2 | N(25.70,0.07) |
| 排油窗内半径 R 3 | N(20.10,0.07) |
| 内封油带半径 R 4 | N(18.65,0.07) |
| 配流副间隙 h p | N(0.009,0.001) |
| 配流副磨损速率 r p | U(0.000 1,0.000 15) |
表选项
 |
| 图 8 柱塞泵试验平台Fig. 8 Test bench of piston pump |
| 图选项 |
表 3 性能试验测得的泄漏量退化量Table 3 Degradation of leakages of performance testing
| 时刻 | 泄漏量/(L·min -1) |
| 0 | 0.79 |
| 140 | 1.12 |
| 420 | 1.28 |
| 700 | 1.20 |
| 980 | 1.13 |
| 1 260 | 1.25 |
| 1 540 | 1.36 |
| 1 820 | 1.45 |
| 2 100 | 1.59 |
| 2 380 | 1.69 |
| 2 700 | 1.78 |
表选项
考虑到柱塞泵泄漏量随时间退化的特点,本文采用截断形式的时变混沌多项式(Time-Dependent generalized Polynomial Chaos,TDgPC)构建泄漏量仿真模型的代理模型[23]。滑靴副泄漏量的TDgPC如下:
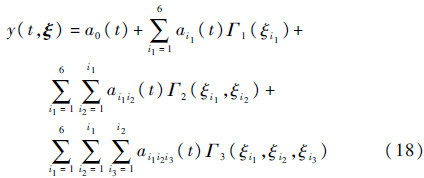
式中:t为时间;ξ=(d2,l,r3,r4,hh,rh)为表 1中的参数,考虑到参数分布形式不同,在此通过变量变换将rh统一为与其他参数一致的正态分布形式;Γi(·)为与正态分布对应的TDgPC基函数[24];ai.(t)为TDgPC的时变系数。相应的,配流副泄漏量的TDgPC如下:

式中:ξ′=(R1,R2,R3,R4,hp,rp)为表 2中的参数,基函数形式不变。
本文采用文献[11]提及的移动最小二乘法求取TDgPC的时变系数,图 9(a)和图 9(b)分别展示了式(18)和式(19)的前2个系数的时变特征。
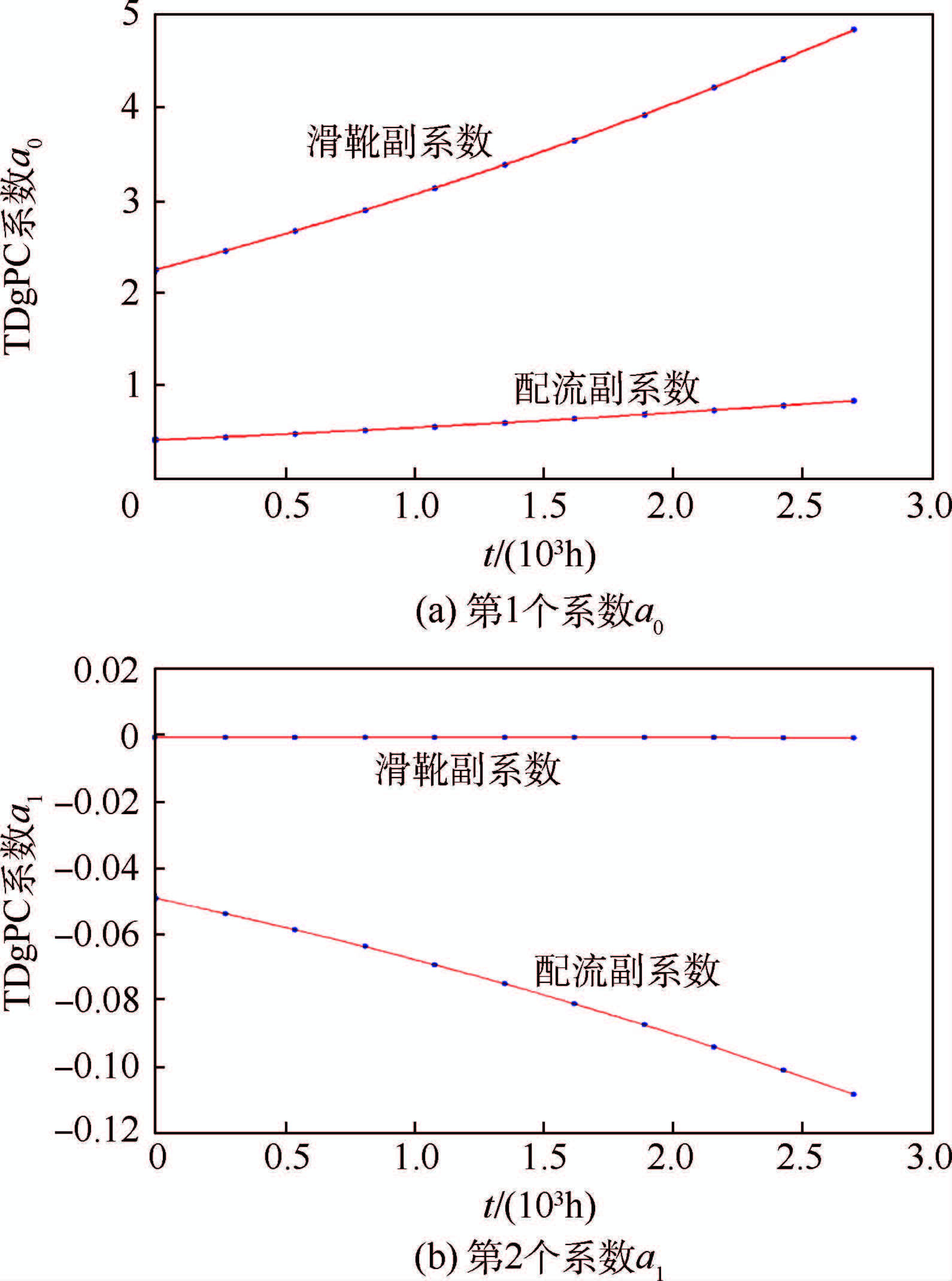 |
| 图 9 摩擦副泄漏量TDgPC系数的时变特征Fig. 9 Time-varying characteristics of TDgPC coefficients for friction pair leakage |
| 图选项 |
利用第3节提出的退化数据贝叶斯融合方法,摩擦副间隙等设计变量和磨损速率的不确定性都得到更新,如表 4和表 5所示。
表 4 滑靴副尺寸参数、退化特征量的后验分布概要统计量Table 4 Summary statistics of posterior distribution of dimensions and degradation parameters of slipper-swash plate
| 参数 | 均值 | 标准差 | 5%分位点 | 中值 | 95%分位点 |
| d 2/mm | 1.275 | 0.014 43 | 1.252 | 1.275 | 1.298 |
| l/mm | 9.045 | 0.008 651 | 9.031 | 9.045 | 9.058 |
| r 3/mm | 4.49 | 0.017 32 | 4.463 | 4.49 | 4.517 |
| r 4/mm | 7.812 | 0.021 67 | 7.779 | 7.812 | 7.846 |
| h h/μm | 6.218 | 0.941 | 4.641 | 6.234 | 7.744 |
| r h/μm | 0.10 | 0.012 | 0.082 | 0.10 | 0.12 |
表选项
表 5 配流副尺寸参数、退化特征量的后验分布概要统计量Table 5 Summary statistics of posterior distribution of dimensions and degradation parameters of barrel-port plate
| 参数 | 均值 | 标准差 | 5%分位点 | 中值 | 95%分位点 |
| R 1/mm | 27.26 | 0.030 48 | 27.21 | 27.26 | 27.31 |
| R 2/mm | 25.86 | 0.030 49 | 25.81 | 25.86 | 25.91 |
| R 3/mm | 20.26 | 0.030 51 | 20.21 | 20.26 | 20.31 |
| R 4/mm | 18.81 | 0.030 5 | 18.76 | 18.81 | 18.86 |
| h p/μm | 8.618 | 0.941 | 7.041 | 8.634 | 10.14 |
| r p/μm | 0.125 | 0.014 | 0.103 | 0.125 | 0.148 |
表选项
图 10和图 11进一步展示了利用OpenBUGS绘制的摩擦副间隙和磨损速率的后验分布。本文根据文献[25]的建议,绘制后验分布时舍弃前1 000个抽样点。
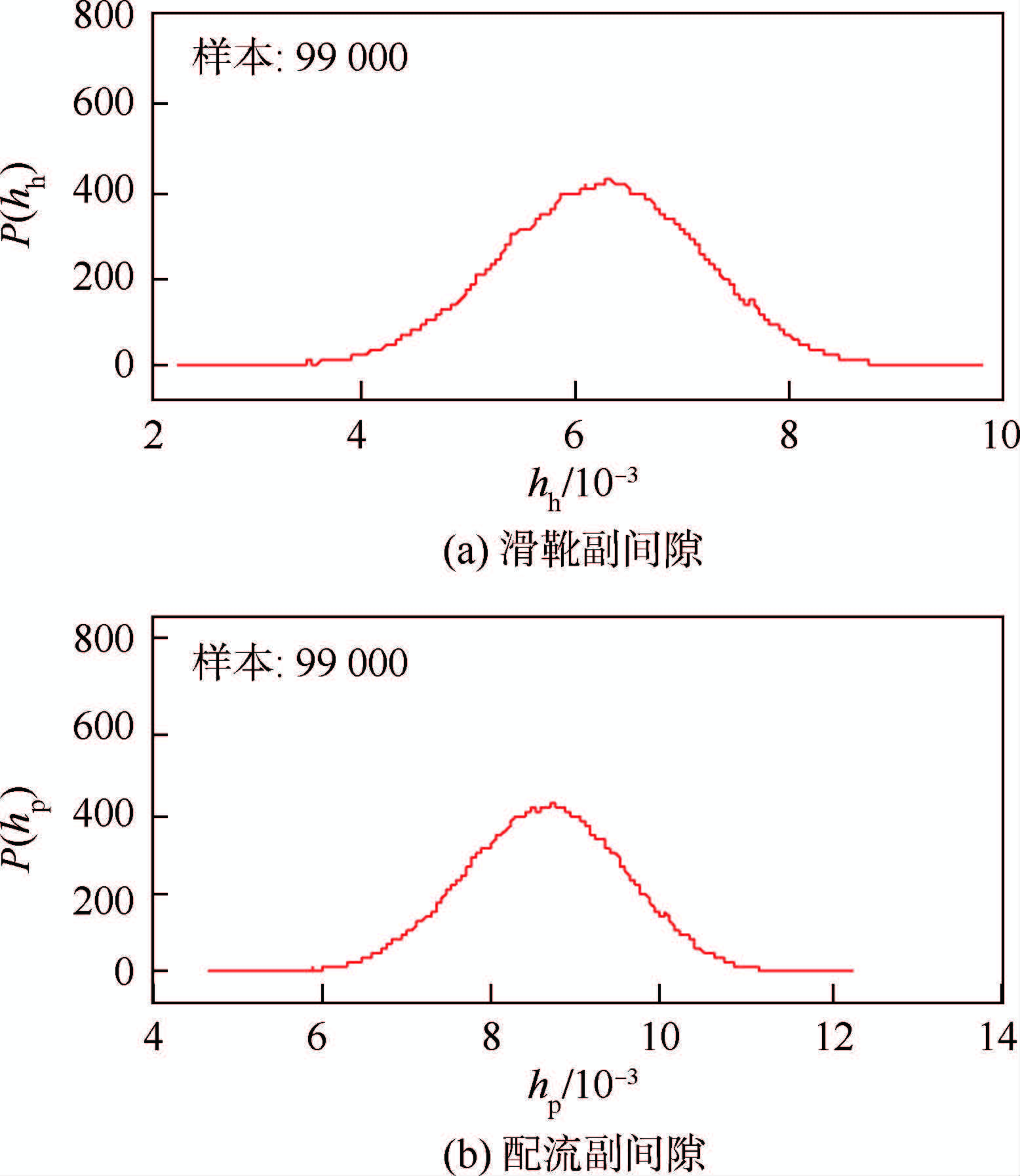 |
| 图 10 滑靴副间隙和配流副间隙的后验分布Fig. 10 Posterior distribution of clearances of slipper-swash plate and barrel-port plate |
| 图选项 |
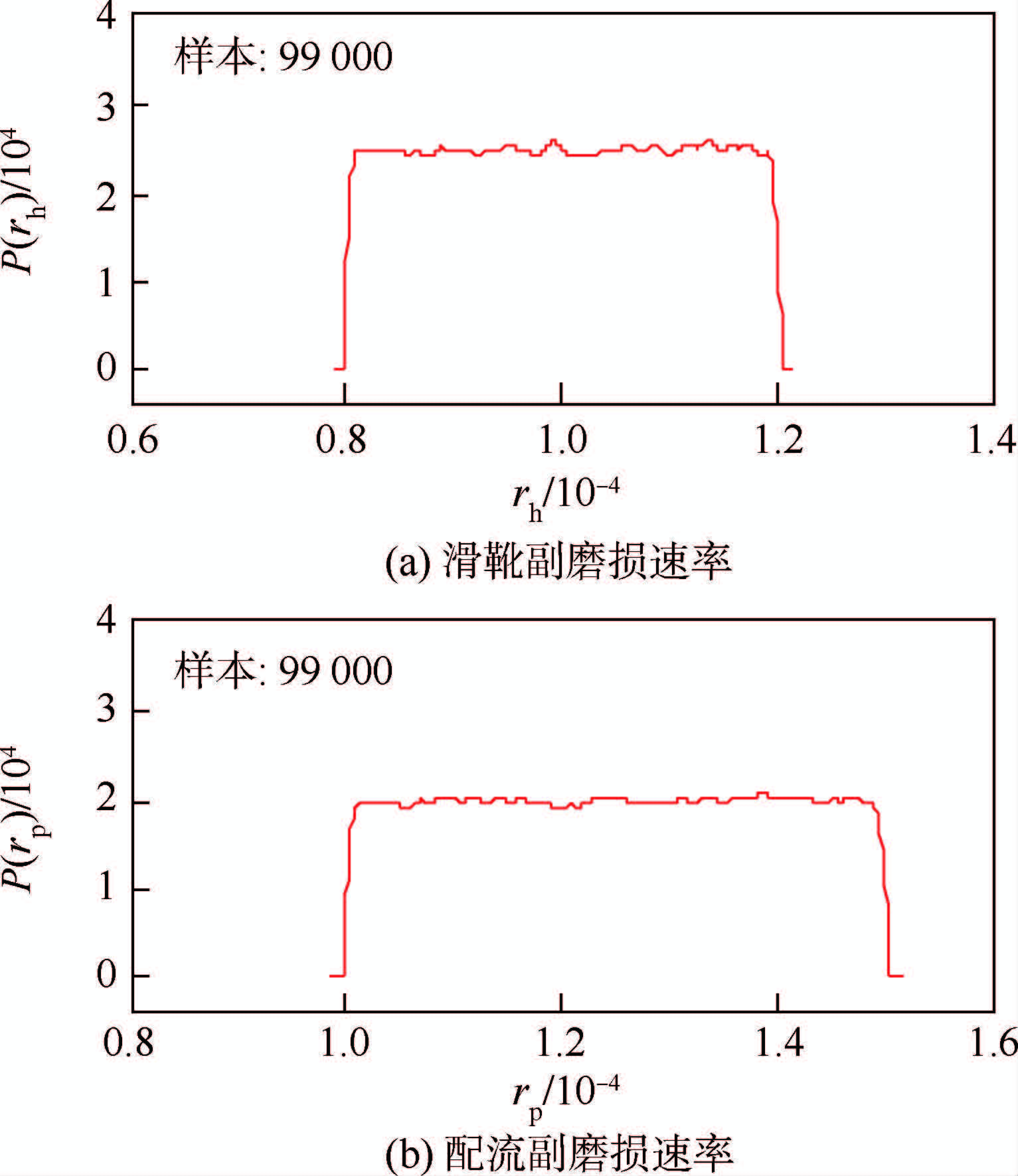 |
| 图 11 滑靴副和配流副磨损速率的后验分布Fig. 11 Posterior distribution of friction rates of slipper-swash plate and barrel-port plate |
| 图选项 |
摩擦副润滑磨损与材料属性紧密相关,计算滑靴副磨损量需要获得滑靴底座的剪切模量[19]。本案例中,柱塞泵滑靴副底座的材料是铜合金HMn61-2.5-1.0(R),剪切模量未知。合金材料成分为黄铜与锰,黄铜是铜锌合金,在其中加入锰,可显著提高合金的强度和耐蚀性,而不降低塑性。冷拔黄铜的剪切模量是34~37 GPa,轧制锰青铜的剪切模量是39 GPa。本文以此为基础,采用前述贝叶斯融合方法,获得该柱塞泵滑靴底座剪切模量的不确定性,如表 6所示。
表 6 滑靴副剪切模量的后验分布概要统计量Table 6 Summary statistics of posterior distribution of shear modulus of slipper-swash plate
| 参数名称 | 均值 | 标准差 | 5%分位点 | 中值 | 95%分位点 |
| 剪切模量/MPa | 36 500.0 | 1 440.0 | 34 260.0 | 36 500.0 | 38 750.0 |
表选项
对于模型误差E(Δ),本文假设其服从零均值正态分布,则Δ为方差σ2,以考察可靠性定量模型和试验数据差异的分散程度,取σ2服从Gamma (0.01,0.01),目的是期望二者偏差尽可能小。利用本文提出的贝叶斯融合方法,得到模型误差σ2参数的后验分布如表 7所示。图 12进一步展示了利用OpenBUGS绘制的σ2的后验分布。
表 7 模型误差参数的后验分布概要统计量Table 7 Summary statistics of posterior distribution of model error parameter
| 参数名称 | 均值 | 标准差 | 5%分位点 | 中值 | 95%分位点 |
| σ 2 | 0.219 9 | 0.130 1 | 0.093 67 | 0.187 | 0.451 7 |
表选项
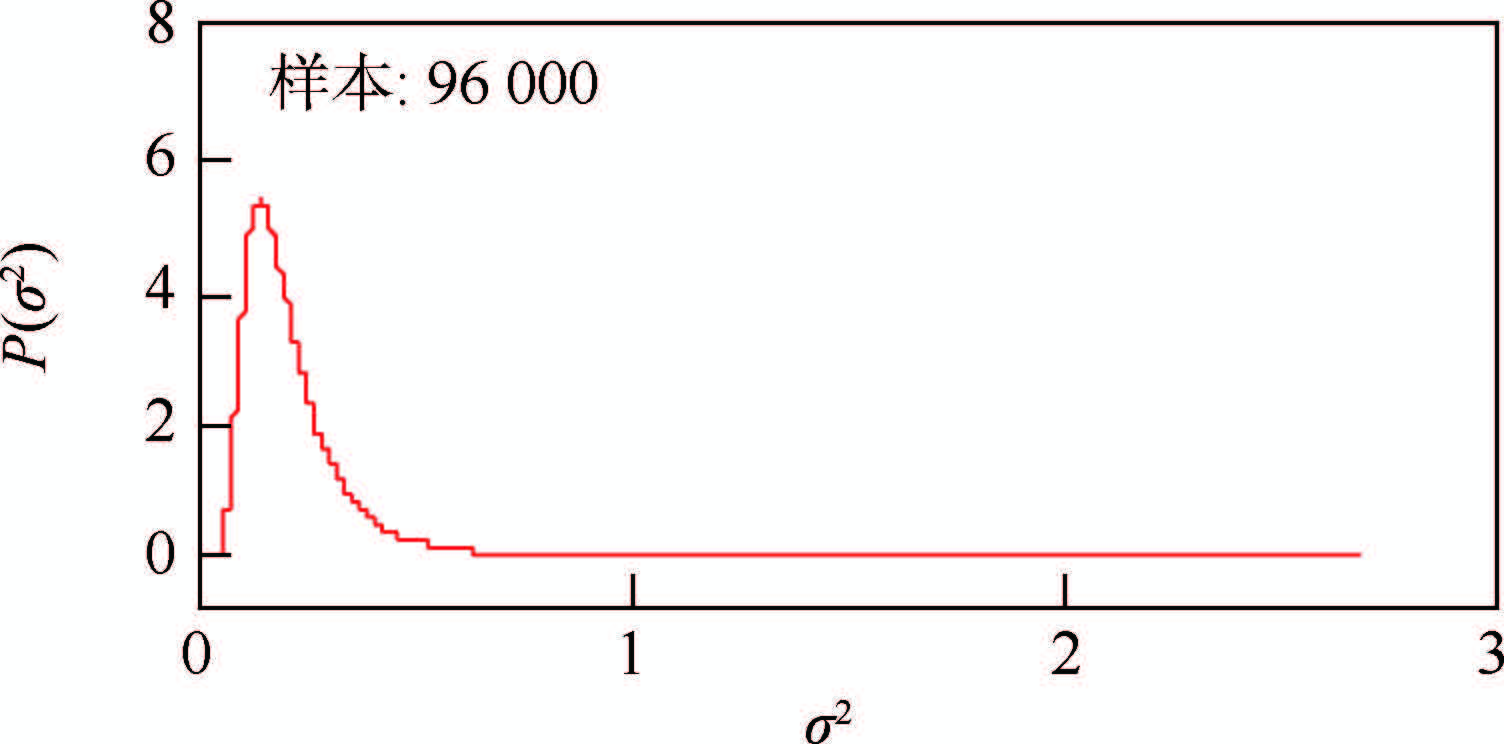 |
| 图 12 模型误差参数的后验分布Fig. 12 Posterior distribution of model error parameter |
| 图选项 |
至此,利用本文提出的贝叶斯融合方法,柱塞泵滑靴副的设计变量{d2,l,r3,r4,hh}和配流副的设计变量{R1,R2,R3,R4,hp}、常参数剪切模量m、滑靴副和配流副的磨损速率rh和rp,以及模型误差参数σ2的不确定性均得到更新。相应的,柱塞泵泄漏量仿真模型的代理模型(前2个系数的时变特征如图 13所示)和模型误差也获得更新。此时,更新的输入参数不确定性、代理模型和模型误差,共同组成可靠性定量模型,从而完成柱塞泵可靠性定量模型建模工作。
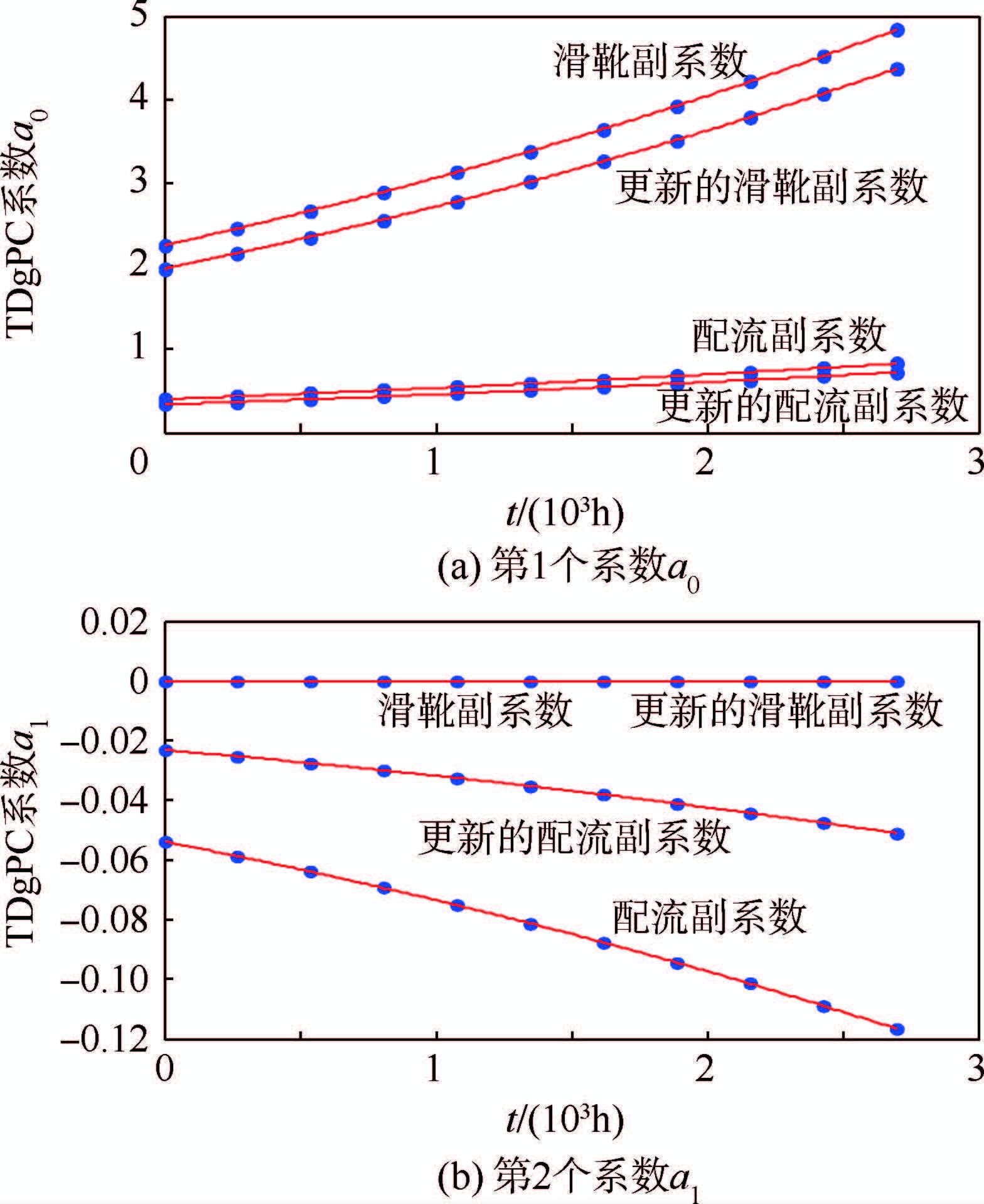 |
| 图 13 更新后摩擦副泄漏量TDgPC系数的时变特征Fig. 13 Time-varying characteristics of updated coefficients of TDgPC for friction pair leakage |
| 图选项 |
5 结论现有的可靠性定量模型建模工作主要依靠设计人员对产品对象故障规律的知识开展。但设计人员掌握的故障规律知识存在有限性和不完整性,据此建立的可靠性定量模型存在模型误差和输入参数不确定性。本文针对这一问题,提出:
1) 知识与数据融合的可靠性定量模型建模方法,量化模型误差,更新输入参数不确定性。
2) 适用于性能波动数据和性能退化数据不同特点的贝叶斯融合方法。
并通过机载轴向柱塞泵的案例,验证了:
1) 本文所提方法能够通过知识与数据的融合,更新模型误差参数不确定性,从而量化模型误差。
2) 本文所提方法能够通过知识与数据的融合,更新可靠性定量模型中设计变量、物理常参数和退化特征量等输入参数的不确定性,进而更新可靠性一体化仿真模型的代理模型。
参考文献
| [1] | SILVERMAN M,KLEYNER A.What is design for reliability and what is not[C]//Proceedings of Annual Reliability and Maintainability Symposium.Piscataway,NJ:IEEE Press,2012:1-5. |
| Click to display the text | |
| [2] | SANCHEZ L M,PAN R.An enhanced parenting process:Predicting reliability in product's design phase[J].Quality Engineering,2011,23(4):378-387. |
| Click to display the text | |
| [3] | 曾声奎.系统可靠性与性能一体化设计方法研究[D].北京:北京航空航天大学,2009:1-3. ZENG S K.Integrated design method of system reliability and performance[D].Beijing:Beihang University,2009:1-3 (in Chinese). |
| Cited By in Cnki | |
| [4] | 夏青,钱山,张士峰,等.飞行器可靠性与性能一体化设计初步研究[J].弹箭与制导学报,2009,29(1):257-259. XIA Q,QIAN S,ZHANG S F,et al.Primary study of reliability and performance incorporate design of aerocraft[J].Journal of Projectiles,Rockets,Missiles and Guidance,2009,29(1):257-259(in Chinese). |
| Cited By in Cnki (4) | Click to display the text | |
| [5] | DU X P,CHEN W.Collaborative reliability analysis under the framework of multidisciplinary systems design[J].Optimization and Engineering,2005,6(1):63-84. |
| Click to display the text | |
| [6] | XIA Q,LI M,CAO Z J,et al.The study of reliability in MDO of aircraft[J].Applied Mechanics & Materials,2012,226-228:598-601. |
| >Click to display the text | |
| [7] | 郭健彬.考虑可靠性的无人机总体设计方法及平台[D].北京:北京航空航天大学,2008:1-3. GUO J B.Study on method and platform for reliability considered UAV concept design[D].Beijing:Beihang University,2008:1-3(in Chinese). |
| Cited By in Cnki | |
| [8] | VALDEBENITO M A,SCHUËLLER G I.A survey on approaches for reliability-based optimization[J].Structural and Multidisciplinary Optimization,2010,42(5):645-663. |
| Click to display the text | |
| [9] | QIU Z P,HUANG R,WANG X J,et al.Structural reliability analysis and reliability-based design optimization:Recent advances[J].Science China Physics,Mechanics and Astronomy,2013,56(9):1611-1618. |
| Click to display the text | |
| [10] | HU Z,DU X P.Lifetime cost optimization with time-dependent reliability[J].Engineering Optimization,2014,46(10):1389-1410. |
| Click to display the text | |
| [11] | WANG Y,ZENG S K,GUO J B.Time-dependent reliability-based design optimization utilizing nonintrusive polynomial chaos[J].Journal of Applied Mathematics,2013(4):1-16. |
| Click to display the text | |
| [12] | 张义民.机械动态与渐变可靠性理论与技术评述[J].机械工程学报,2013,49(23):101-114. ZHANG Y M.Review of theory and technology of mechanical reliability for dynamic and gradual systems[J].Journal of Mechanical Engineering,2013,49(23):101-114(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [13] | 曾声奎,李霏霞,马纪明.基于响应面的系统性能可靠性优化设计方法[J].航空学报,2009,30(9):1655-1606. ZENG S K,LI F X,MA J M.Response surface-based performance reliability optimization design method[J].Acta Aeronautica et Astronautica Sinica,2009,30(9):1655-1606(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [14] | 陈云霞.性能与可靠性一体化建模[D].北京:北京航空航天大学,2004:1-2. CHEN Y X.Study on method of model and analysis for integrating performance and reliability[D].Beijing:Beihang University,2004:1-2(in Chinese). |
| Cited By in Cnki | |
| [15] | 陈云霞,曾声奎,晋严尊.飞控系统性能与可靠性一体化设计技术[J].北京航空航天大学学报,2008,34(2):210-214. CHEN Y X,ZENG S K,JIN Y Z.Integrating design of performance and reliability for flight control systems[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(2):210-214(in Chinese). |
| Cited By in Cnki (6) | Click to display the text | |
| [16] | KENNEDY M C,O'HAGAN A.Bayesian calibration of computer models[J].Journal of the Royal Statistical Society:Series B (Statistical Methodology),2001,63(3):425-464. |
| Click to display the text | |
| [17] | 杨华勇,张斌,徐兵.轴向柱塞泵/马达技术的发展演变[J].机械工程学报,2008,44(10):1-8. YANG H Y,ZHANG B,XU B.Development of axial piston pump/motor technology[J].Journal of Mechanical Engineering,2008,44(10):1-8(in Chinese). |
| Cited By in Cnki (87) | Click to display the text | |
| [18] | BERGADA J M,KUMAR S,DAVIES D L,et al.A complete analysis of axial piston pump leakage and output flow ripples[J].Applied Mathematical Modelling,2012,36(4):1731-1751. |
| Click to display the text | |
| [19] | 黄平,温诗铸.粘弹性流体动力润滑与润滑磨损[J].机械工程学报,1996,32(3):35-41. HUANG P,WEN S Z.Visco-elastohydrodynamic lubrication and lubricated wear[J].Journal of Mechanical Engineering,1996,32(3):35-41(in Chinese). |
| Cited By in Cnki (15) | Click to display the text | |
| [20] | KATO K.Abrasive wear of metals[J].Tribology International,1997,30(5):333-338. |
| Click to display the text | |
| [21] | KUMAR S.CFD analysis of an axial piston pump[D].Barcelona:Universidad Politecnica de Catalunya,2010:142-156. |
| Click to display the text | |
| [22] | 中国航空工业总公司.一般公差:HB 5800[S].北京:中国航空工业总公司,1999:2-5. Aviation Industry Corporation of China.General tolerances:HB 5800[S].Beijing:Aviation Industry Corporation of China,1999:2-5(in Chinese). |
| [23] | GERRITSMA M I,STEEN J B V D,VOS P,et al.Time-dependent generalized polynomial chaos[J].Journal of Computational Physics,2010,229(22):8333-8363. |
| Click to display the text | |
| [24] | ELDRED M,BURKARDT J.Comparison of non-intrusive polynomial chaos and stochastic collocation methods for uncertainty quantification[J].AIAA Paper,2009,976:1-20. |
| Click to display the text | |
| [25] | KELLY D,SMITH C.Bayesian inference for probabilistic risk assessment[M].London:Springer,2011:18. |
