文献[1, 2]在文献[3]的基础之上将备件保障多级库存(METRIC)理论应用到舰船装备并建立了装备多层级库存优化模型;魏曙寰等[4]以备件费用、体积为约束条件,应用边际效应法求得随船备件配置最优方案;文献[5, 6]以备件质量、费用为约束对航空航天备件配置优化进行了研究;文献[7]建立了以费效比为目标函数,以可用度、备件质量及体积为约束条件的优化模型;王乃超和康锐[8]运用拉格朗日乘子法和边际效应法,建立备件库存优化模型及算法;文献[9]通过对约束指标权重反复调整,求得备件最优库存方案;王正元等[, ]建立了基于维修能力的战时备件资源配置模型以及考虑运输时间和保障任务的均衡性,建立了仓库位置优化问题的模型并提出了求解算法;李大伟等[12]运用Bayes方法建立研制阶段备件配置初始方案;卢雷和杨江平[13]建立一种k/N(G)结构系统初始备件配置模型.从上述文献可以看出,一方面,多约束下随船备件配置方案优化问题是研究的热点也是难点;另一方面,文献[4, 5, 6, 7, 8, 9]主要从定量方面进行研究,文献[10, 11]主要从定性方面进行研究,可以看出目前研究主要集中在只有定性或定量约束问题上,而对既有定量约束又有定性约束的混合约束问题研究比较少,同时可以看出定量约束问题的解决方法不能应用于定性约束,反之亦不成立,由此可见寻找一种能够解决混合约束问题方法的重要性、必要性.
随船备件配置中一个重要问题就是如何在有限的保障费用、载荷、排水量及维修能力约束下使保障方案最优,文献[14, 15, 16, 17, 18, 19, 20]建立了不同目标函数下的最优备件配置方案,但很少有目标函数是以备件保障概率作为优化目标,上述目标函数在实际工程应用中,管理部门是难以掌控和把握的,同时备件只是其中一个影响因素,很难使随船备件保障方案具有很高的费效比.因此,本文建立了约束因素判断矩阵并进行一致性检验,运用边际效应法、归一化及拉格朗日乘子法对模型进行求解,同时,依据专家职称及经验等赋予维修能力不同的权重,提出一种系统资源约束因子确定及动态调整的方法并对模型算法进行了优化,最后通过案例分析验证了本文方法的有效性和模型的合理性.
1 单舰海上备件保障模式分析单舰海上执行任务时备件保障模式如图 1所示,其中用于故障现场可更换的备件,按所属的层次不同可分为现场可更换单元(Line-Replaceable Unit,LRU)和车间可更换单元(Shop-Replaceable Unit,SRU),本文讨论备件保障模式的背景为舰艇海上执行任务期间,对于岸上进行的备件修理不作讨论;舰上仓库存放故障现场修理所需的备件LRU及SRU;由于舰艇修理车间的修理水平相当于舰员级,其修理能力水平有限,故其作用主要是更换LRU及SRU,本文模型假设故障件修理只要更换一个LRU或SRU即可修复完好,因而故障件更换的过程可以看成是相对独立的修理过程,同时具备耗费少量人力、物力资源修复少量LRU的能力,修复完好的LRU送到舰艇仓库存起来当作库存备件供后续使用,和舰上数以万计的备件存储量相比,上述事件发生的次数可以看作是小概率事件,本文模型假设舰上所有故障件都是可以被更换的但却不能在舰艇修理车间进行修复;同时,因SRU修理需要中继级修理能力水平,所以故障的SRU件被存放在舰艇仓库,等返航后统一上报给岸上基地进行处理,具有修复价值的进行修理,修复完毕后存放在岸上仓库,没有修复价值或者不能修复的直接报废.
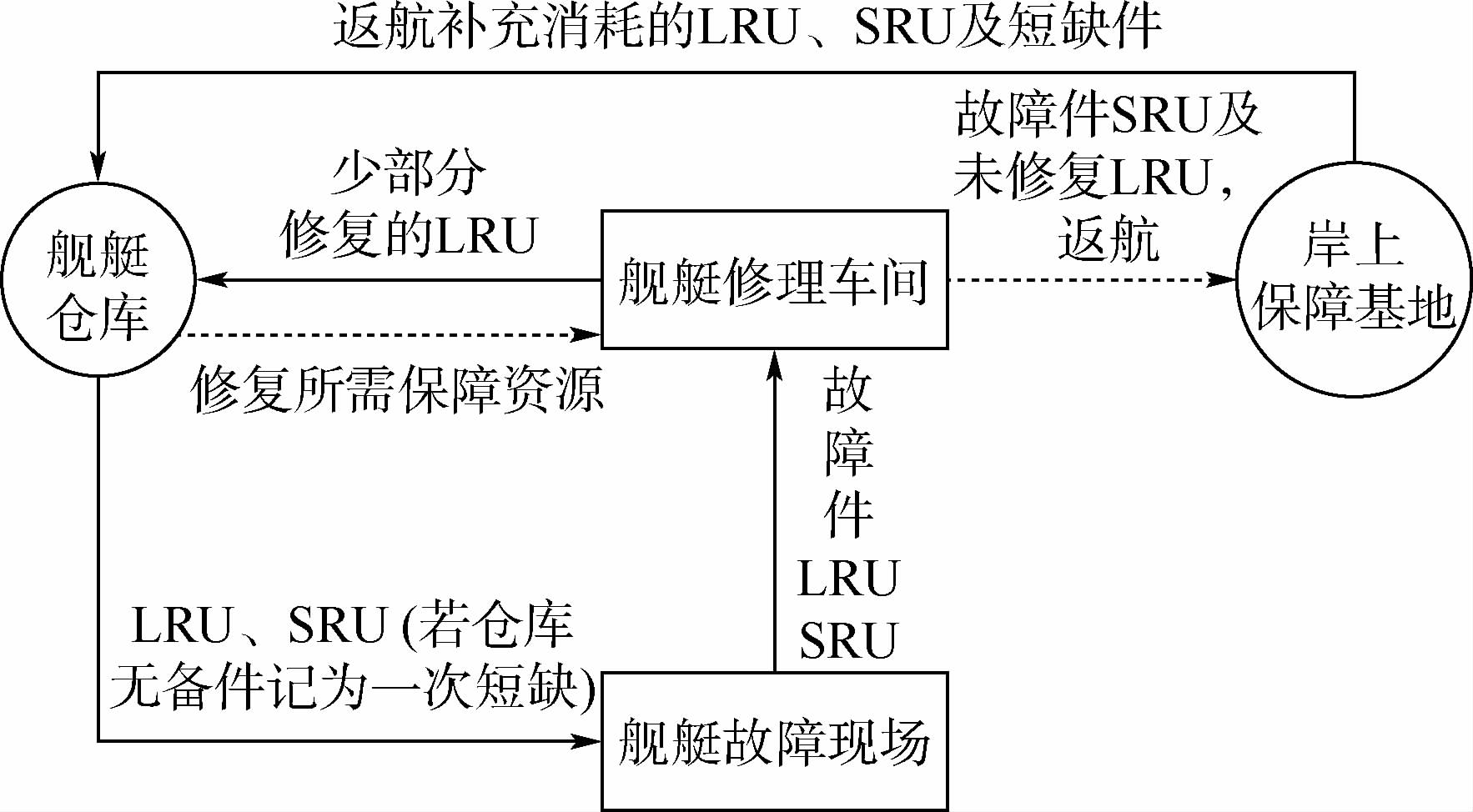 |
| 图 1 海上执行任务期间单舰备件保障模式Fig. 1 Spares support mode for single warship on sea during mission |
| 图选项 |
2 模型建立过程2.1 目标函数船上电子设备的寿命分布都服从指数分布,计算每项备件保障概率Pi是一致的,即
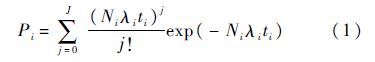
式中:Ni为第i项备件单机安装数,i为装备所属备件编号;λi为第i项备件故障率;j=0,1,…,J,为第i项备件的备件需求量;ti为第i项备件供应周期,若舰艇返航后都可以补给备件,供应周期应等于舰艇在海上执行任务时间,本文假设执行任务周期为1a.
依据LRU(SRU)的维修参数信息可以求出备件需求率,也就是备件保障概率,LRUi的故障率为
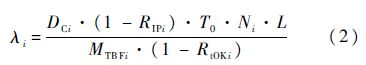
式中,DCi为占空比,表示备件i运行时间占装备运行时间的百分比,代表了备件在所属装备上的工作强度;RIPi为故障备件原位维修率;T0为装备年平均工作时间;L为舰船装备配置数量;MTBFi为备件i的平均故障间隔时间;RtOKi为备件i的重测完好率.根据装备的故障树,装备母体的故障率由其所属分备件的故障率决定,设母体LRUi的发生故障由备件SRUk(k∈(Sub(i))为LRUi的子单元SRUk的集合,Sub(i)为LRUi的集合)故障导致的概率为Pik,则SRUk的故障率为
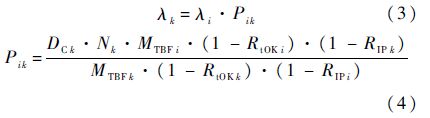
式中:Nk为分备件SRUk在其母体LRUi中的单机安装数;DCk为SRUk的占空比;RtOKk为SRUk重测完好率;RIPk为SRUk的原位维修率;MTBFk为SRUk的故障间隔时间.
把式(4)代入式(3)得
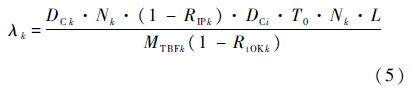
依据式(1)计算得到系统备件保障概率为

式中:psd为假定在出现备件短缺的情况下,需求的备件存放在船上且可以取到的概率;psc为需求的备件存放在船上的概率:
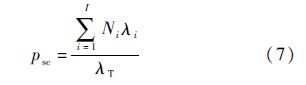
式中:λT为系统总故障率.
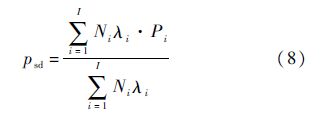
依据式(6)~式(8)计算得到系统备件保障概率,即
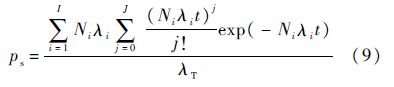
此时目标函数为

2.2 约束条件定义1 混合约束是指既含有定量约束又含有定性约束的一种复杂约束.
本文约束条件是备件质量、费用、体积及维修工时,因备件质量、费用及体积是定量约束条件,维修工时是定性约束条件,所以本文研究的约束问题为混合约束问题.
系统备件保障概率问题可以表述为在给定保障经费、维修能力、仓库空间及载荷约束条件下,通过选择不同品种及数量的备件,使其最大.
随船携带备件所占用的空间必须小于事先给定的仓库空间指标,即

式中:vi为单件LRU、SRU的体积;Vt为事先给定的仓库空间指标;si为备件i在舰艇上的存储量.
随船携带备件所需保障费用的总和必须小于事先给定的保障经费指标,即
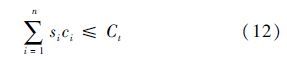
式中:ci为单件LRU、SRU的费用;Ct为事先给定的保障经费指标;
随船携带备件质量的总和必须小于事先给定的质量指标,即
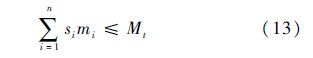
式中:mi为单件LRU、SRU的质量;Mt为事先给定的仓库质量指标.
随船更换及调试备件所需的维修能力必须小于事先给定的维修能力指标,即
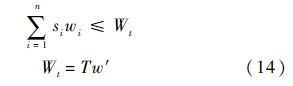
式中:wi为第i个备件从拆卸开始到测试完好结束所需要维修工时,h;Wt为事先给定的维修能力指标;w′为船上单位时间内所具有的平均维修保障能力;T为执行任务总时间.
2.3 模型建立考虑到费用、维修能力、载荷及仓库空间的限制,将上述影响因素转换为约束条件,模型建立的基本思想就是将上述限制因素转换为系统资源约束因子,运用边际效应法在满足所有指标的前提下,求出最优配置方案.所建模型为
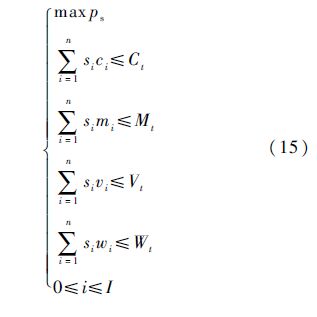
3 模型求解及算法优化3.1 模型求解步骤1 从式(9)及式(15)可以看出,随船备件保障概率模型涉及的约束和变量较多,引进系统资源约束因子,将备件质量、体积、费用及维修能力约束统一转化为系统资源约束因子,即
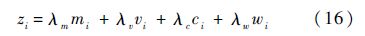
式中:zi为备件i的系统资源约束因子;λm为质量因子;λv为体积因子;λc为费用因子;λw为维修能力因子.
步骤2 将备件质量、体积、费用及维修能力约束统一转化为系统资源约束zi后,随船备件保障概率可表示为
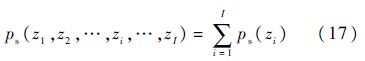
步骤3 依据凸函数叠加之后仍然是凸函数的原理,可以利用边际效应分析法求得最优库存量,当前系统资源约束组合为
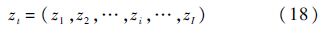
步骤4 对式(17)做一阶差分,此时,边际增量为
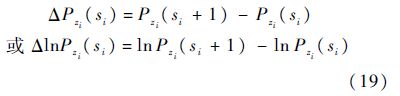
步骤5 依据式(16)~式(19),计算得到边际效应值为
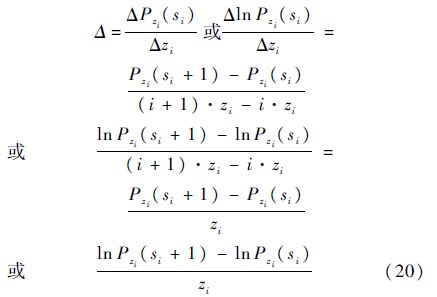
在每一列中选择Δ值最大的备件,去掉已选的Δ值,对剩下各Δ列的Δ值进行比较,选择其中Δ值最高的备件,依次类推,直到约束指标不满足要求时停止.
步骤6 重复步骤4~步骤5,直到得到可行方案时停止.
3.2 算法优化3.2.1 系统资源约束因子的确定及动态调整以wi为例进行说明.
步骤1假设共有m个LRU及n个SRU.
步骤2 依据装备故障对系统的影响程度建立评分等级,见表 1.
表 1 专家因子权重Table 1 Rating of expert factors
| 等级 | 不重要 | 一般 | 重要 | 关键 |
| 评分 | (0,4) | [4,6) | [6,8) | [8,10) |
表选项
步骤3 专家依据表 1对每个部件和式(19)因子进行打分,并进行归一化处理,见表 2及表 3.
表 2 维修能力打分Table 2 Maintenance ability scoring
| 备件名称 | LRU1 | LRU2 | … | LRUm | SRU1 | SRU2 | … | SRUn |
| 分值 | w1 | w2 | … | wm | w(m+1) | w(m+2) | … | w(m+n) |
表选项
表 3 约束因子权重Table 3 Weight of constraint factors
| 因子 | λm | λv | λc | λw |
| 权重 | wλm | wλv | wλc | wλw |
表选项
步骤4 将wi值进行两两比较,具体见表 4.
表 4 维修能力比值对照Table 4 Comparison of ratio of maintenance ability
| 备件名称 | LRU1 | LRU2 | … | LRUm | SRU1 | SRU2 | … | SRUn |
| LRU1 | w1/w1 | w1/w2 | … | w1/wm | w1/w(m+1) | w1/w(m+2) | … | w1/w(m+n) |
| LRU2 | w2/w1 | w2/w2 | … | w2/wm | w2/w(m+1) | w2/w(m+2) | … | w2/w(m+n) |
| | | | … | | | | … | |
| LRUm | wm/w1 | wm/w2 | … | wm/wm | wm/w(m+1) | wm/w(m+2) | … | wm/w(m+n) |
| SRU1 | w(m+1)/w1 | w(m+1)/w2 | … | w(m+1)/wm | w(m+1)/w(m+1) | w(m+1)/w(m+2) | … | w(m+1)/w(m+n) |
| SRU2 | w(m+2)/w1 | w(m+2)/w2 | … | w(m+2)/wm | w(m+2)/w(m+1) | w(m+2)/w(m+2) | … | w(m+2)/w(m+n) |
| | | | … | | | | … | |
| SRUn | w(m+n)/w1 | w(m+n)/w2 | … | w(m+n)/wm | w(m+n)/w(m+1) | w(m+n)/w(m+2) | … | w(m+n)/w(m+n) |
表选项
步骤5 表 4还可以通过矩阵来表示:
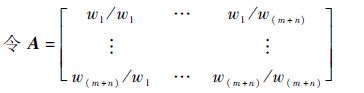
A称为约束条件判断矩阵,显然wii=1,wij=1/wji.
步骤6 矩阵A的一致性检验,具体方法为计算随机一致性比例,即
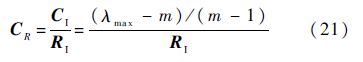
式中:CI为一致性指标;λmax为最大特征值;RI为平均随机一致性指标,它是一个经验值,1~15阶矩阵平均随机一次性比例值,见表 5.
表 5 平均随机一致性指标RITable 5 Mean random consistency index RI
| 阶数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| RI | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.32 | 1.41 |
| 阶数 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| RI | 1.45 | 1.49 | 1.52 | 1.54 | 1.56 | 1.58 | 1.59 |
表选项
若CR≤0.1,则认为矩阵A的一致性是可以接受的,否则为不可接受,需重新打分调整计算,转入步骤3.
步骤7 求出矩阵A的最大特征值对应的特征向量,即
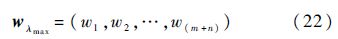
步骤8 对式(22)进行去量纲、归一化处理:

依据式(23)计算得到正规化(归一化)向量,即

步骤9 对于定性约束条件重复步骤1~步骤8,计算得到其他定性约束指标的相对值;对于定量约束条件重复步骤4~步骤8,计算得到其他定量约束指标的相对值.
步骤10 依据式(16)~式(21)及表 3~表 5计算得到系统资源约束因子的值.
3.2.2 算法优化步骤以wi为例进行说明.
步骤1针对专家打分存在主观性缺点这个问题,往往需要聘请多位综合保障领域相关专家共同打分,依据专家的职称及经验等因素确定相应的权重值,假设专家数量为x个,并对权重值进行归一化处理,见表 6.
表 6 专家权重系数Table 6 Experts weight coefficients
| 专家 | E1 | E2 | … | Ex |
| 权重系数 | wE1 | wE2 | … | wEx |
表选项
步骤2 针对式(24)中w′i,x名专家进行打分并乘以相应的权重值求,求出其均值w″i.
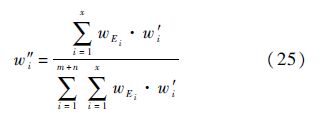
步骤3 转入步骤2重复(m+n)次,得到新的正规化向量:
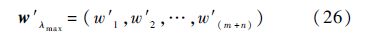
步骤4 依据式(16)~式(21)及表 3~表 6,计算得到系统资源约束因子.
步骤5 转入第3.1节步骤1~步骤6,直到得到装备最优备件携带方案时停止.
4 案例分析为达到在给定保障经费、维修能力、仓库空间及载荷约束条件下使系统备件保障概率最优,舰船在出海之前需要对随船备件配置方案进行优化.随船备件清单及相关参数见表 7,在实装数据中,该船备件清单包含400多项备件,出于对方法介绍的目的及篇幅限制,文中不能将所有备件全部列出,因此,表 7只列举了该船的一些关键性设备,并对相关属性值进行了一些适当的调整,但分析该类问题的方法是一致的.
表 7 备件多重属性Table 7 Multi-attributes of spare parts
| 备件名称 | 单机数量 | 备件属性 | ||||||
| MTBF/a | T0/a | ti/a | Ci/万元 | Mi/kg | Vi/m3 | Wi/h | ||
| LRU1 | 1 | 0.0513 | 0.4452 | 0.0836 | 1.4 | 19.6 | 0.49 | 4.7 |
| LRU2 | 1 | 0.0795 | 0.5019 | 0.1073 | 2.1 | 27.3 | 0.82 | 4.3 |
| LRU3 | 1 | 0.0878 | 0.3936 | 0.0994 | 1.5 | 21.4 | 0.64 | 3.8 |
| LRU4 | 2 | 0.0613 | 0.4871 | 0.0552 | 1.8 | 23.8 | 0.75 | 4.5 |
| SRU11 | 2 | 0.1374 | 0.3982 | 0.0976 | 0.5 | 1.47 | 0.14 | 2.6 |
| SRU12 | 1 | 0.0927 | 0.4175 | 0.0665 | 0.4 | 2.31 | 0.22 | 1.9 |
| SRU21 | 2 | 0.1219 | 0.4328 | 0.0811 | 0.9 | 1.88 | 0.38 | 2.4 |
| SRU31 | 1 | 0.1573 | 0.3264 | 0.0817 | 0.4 | 1.59 | 0.17 | 0.9 |
| SRU32 | 1 | 0.1781 | 0.2994 | 0.0907 | 0.6 | 2.37 | 0.15 | 0.7 |
| SRU33 | 2 | 0.1292 | 0.3144 | 0.0786 | 0.3 | 2.61 | 0.11 | 1.1 |
表选项
在互不影响的情况下,不同专家构建的维修能力判断矩阵可能不尽相同,分析得出的结论可能也存在差异,为了克服这个缺点,在实际工程应用中,特别是多层次、多目标、混合约束问题中,需要多领域、多部门专家共同会商、集体决定,并根据专家的职称及经验等赋予不同的权重.
依据表 7~表 9的数据,按文中模型给定的步骤进行计算,限于篇幅原因这里不再详细叙述,计算得到不同约束条件下的备件配置最优方案如表 10所示.
表 8 备件所需维修工时专家打分及专家权重系数Table 8 Maintenance per hour of spare parts for expert scoring and experts weight coefficients
| 专家编号 | 专家打分 | ||||||||||
| LRU1 | LRU2 | LRU3 | LRU4 | SRU11 | SRU12 | SRU21 | SRU31 | SRU32 | SRU33 | 权重 | |
| 1 | 4.7 | 4.3 | 3.8 | 4.5 | 2.6 | 1.9 | 2.4 | 0.9 | 0.7 | 1.1 | 0.3 |
| 2 | 4.8 | 4.5 | 3.6 | 4.7 | 2.6 | 2.0 | 2.1 | 0.7 | 0.7 | 0.9 | 0.25 |
| 3 | 4.8 | 4.4 | 3.9 | 4.7 | 2.7 | 2.1 | 2.2 | 0.8 | 0.6 | 1.2 | 0.25 |
| 4 | 4.9 | 4.4 | 3.7 | 4.8 | 2.5 | 1.8 | 2.0 | 0.8 | 0.8 | 1.1 | 0.1 |
| 5 | 4.6 | 4.2 | 3.8 | 4.3 | 2.7 | 1.9 | 2.5 | 0.9 | 0.8 | 1.0 | 0.1 |
表选项
表 9 约束条件的相对值Table 9 Relative values on constraint condition
| 备件名称 | 相对值 | ||||
| C′ | M′ | V′ | W′ | Z′ | |
| LRU1 | 0.1414 | 0.1879 | 0.1266 | 0.1768 | 0.1582 |
| LRU2 | 0.2121 | 0.2617 | 0.2119 | 0.1626 | 0.2121 |
| LRU3 | 0.1515 | 0.2051 | 0.1654 | 0.1398 | 0.1655 |
| LRU4 | 0.1818 | 0.2281 | 0.1938 | 0.1713 | 0.1938 |
| SRU11 | 0.0505 | 0.0141 | 0.0362 | 0.0975 | 0.0496 |
| SRU12 | 0.0404 | 0.0221 | 0.0568 | 0.0730 | 0.0481 |
| SRU21 | 0.0909 | 0.0180 | 0.0982 | 0.0834 | 0.0726 |
| SRU31 | 0.0404 | 0.0152 | 0.0439 | 0.0303 | 0.0325 |
| SRU32 | 0.0606 | 0.0227 | 0.0388 | 0.0258 | 0.0370 |
| SRU33 | 0.0303 | 0.0250 | 0.0284 | 0.0395 | 0.0308 |
| 注:C′,M′,V′,W′,Z′—备件费用、备件质量、备件体积、维修工时及系统资源约束因子的相对值. | |||||
表选项
表 10 不同约束条件下的最优备件携带方案Table 10 Optimal support project of carrying spare parts under different constraints
| 备件名称 | 备件携带量 | ||||
| 方案1 | 方案2 | 方案3 | 方案4 | 方案5 | |
| LRU1 | 2 | 1 | 2 | 2 | 1 |
| LRU2 | 1 | 1 | 1 | 1 | 1 |
| LRU3 | 1 | 1 | 1 | 1 | 1 |
| LRU4 | 3 | 3 | 3 | 3 | 3 |
| SRU11 | 3 | 4 | 4 | 3 | 3 |
| SRU12 | 2 | 2 | 1 | 1 | 1 |
| SRU21 | 2 | 4 | 2 | 3 | 3 |
| SRU31 | 1 | 1 | 1 | 1 | 1 |
| SRU32 | 1 | 1 | 1 | 1 | 1 |
| SRU33 | 3 | 3 | 3 | 3 | 3 |
表选项
依据给定的数据,构建备件费用、质量、体积及维修能力的判断矩阵,并对矩阵一致性进行检验,结果都满足要求(CR都为0),同时求出其归一化值,具体见表 9.
依据模型给定的算法计算得到5个方案下所对应保障概率如表 11所示.费用指标为18万元,质量指标为170kg,体积指标为6.95m3,维修能力指标为53h,在这5个方案中,依据表 11可知,方案1~方案4中都有2~3个指标超过了给定指标的值(用加粗字体表示),不满足要求,只有方案5的所有指标都满足给定的约束条件.
表 11 不同约束条件下随船备件方案结果Table 11 Results of warship spare parts project under different constraints
| 备件方案 | 备案方案结果 | |||||
| C/万元 | M/kg | V/m3 | W/h | 是否可行?(N/Y) | 保障概率/% | |
| 方案1 | 17.8 | 183.88 | 6.96 | 52.3 | N | 93.08 |
| 方案2 | 18.7 | 169.51 | 7.37 | 55.0 | N | 88.39 |
| 方案3 | 17.9 | 183.04 | 6.88 | 53.0 | N | 93.05 |
| 方案4 | 18.3 | 183.45 | 7.12 | 52.8 | N | 93.77 |
| 方案5 | 16.9 | 163.85 | 6.63 | 48.1 | Y | 91.97 |
| 注:C,M,V,W—备件费用、备件质量、备件体积及维修工时的实际值. | ||||||
表选项
从表 10和表 11可以看出:
1) 只考虑单个约束条件而不考虑其余约束条件的方案1~方案4都不满足要求,这从另一个方面验证了研究混合约束下编队备件配件优化的重要性、必要性.
2) 依据系统资源约束因子运用边际效应法求得备件最优配置方案,各项约束条件都满足给定指标要求且系统备件保障概率不是最小,从另外一个角度证明了本文方法的可行性.
不同约束条件下的备件最优配置曲线如图 2~图 6所示.
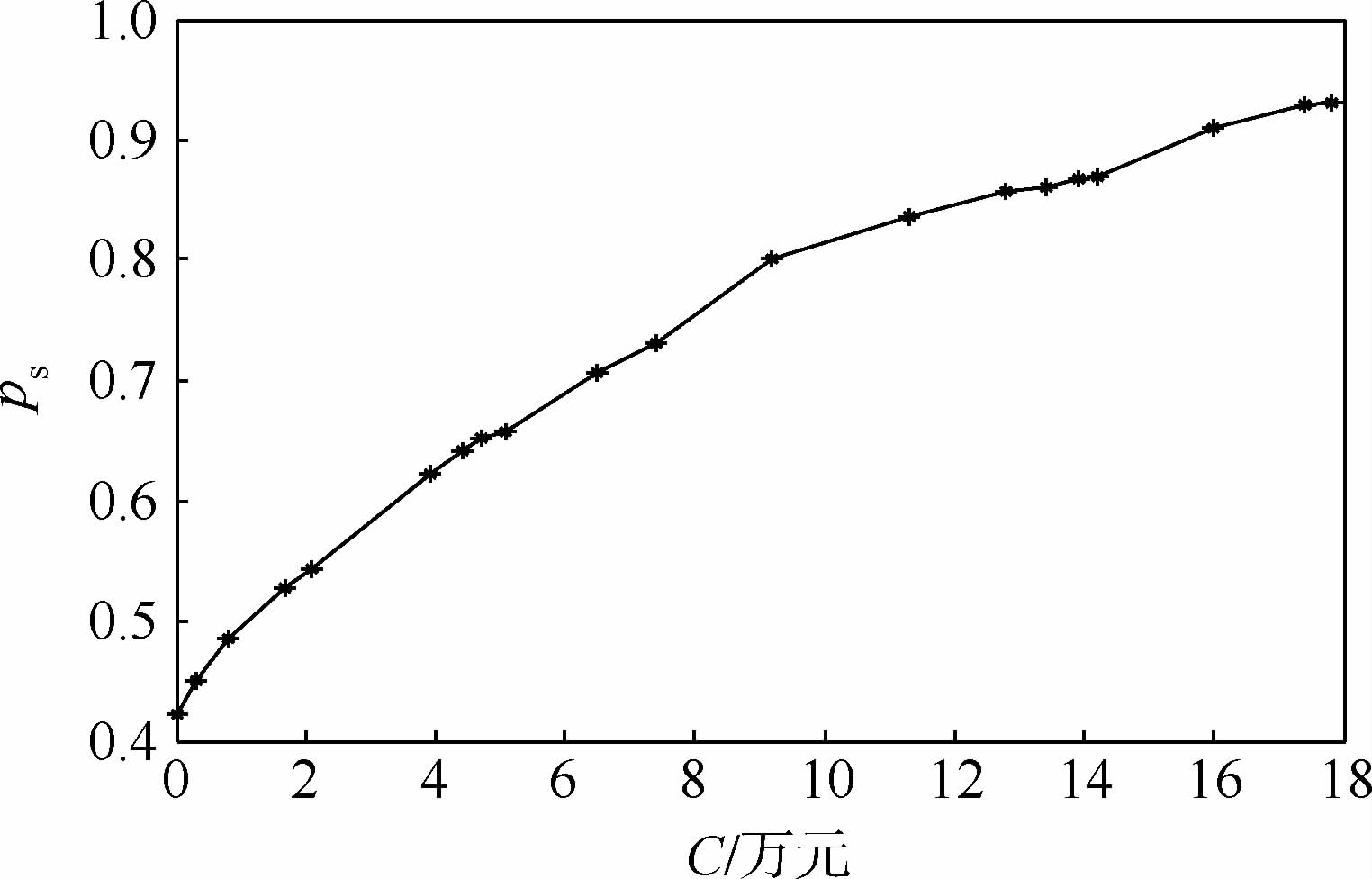 |
| 图 2 费用约束下的最优保障概率曲线Fig. 2 Optimal curve of support probability under cost constraints |
| 图选项 |
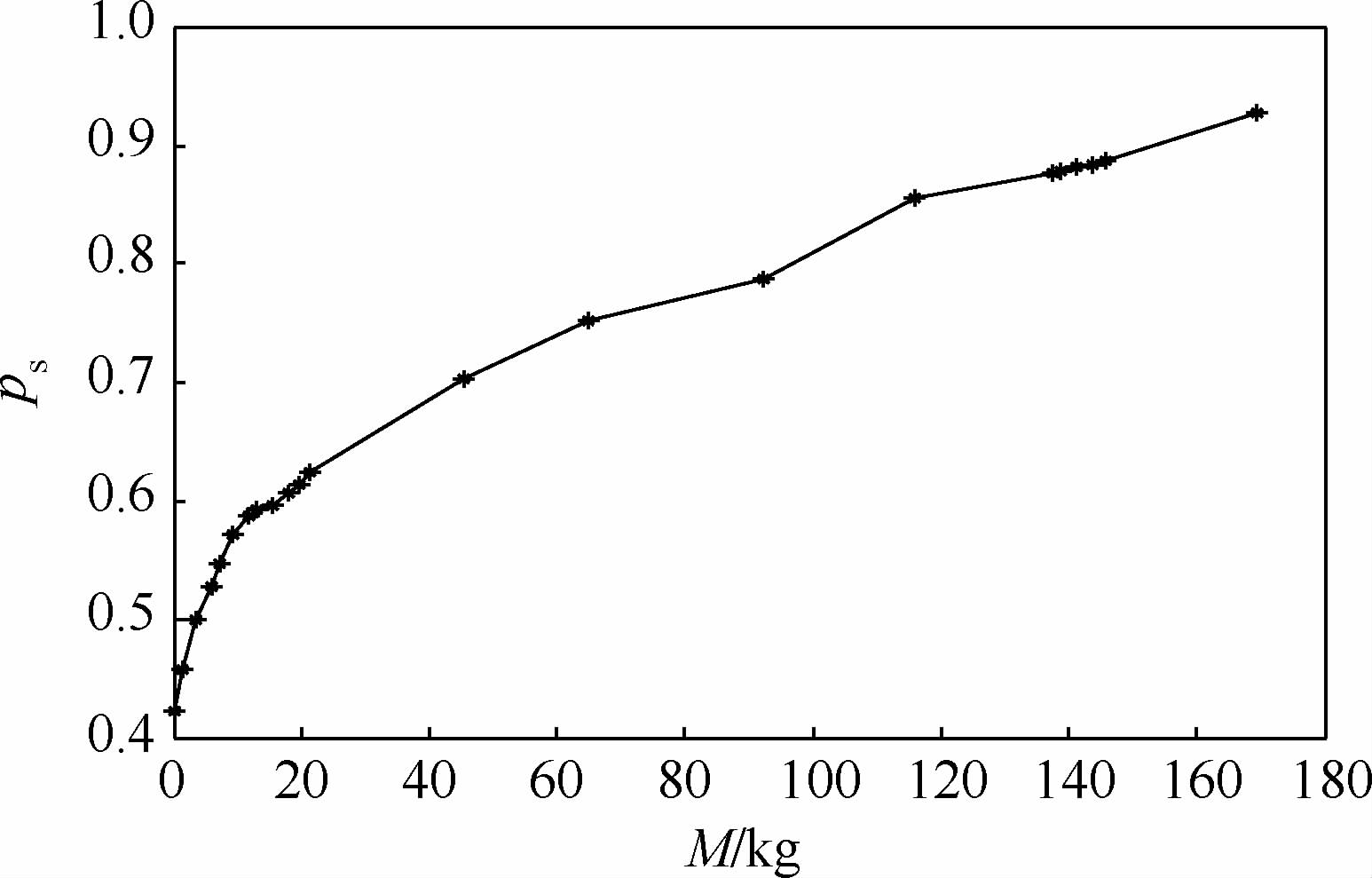 |
| 图 3 质量约束下的最优保障概率曲线Fig. 3 Optimal curve of support probability under mass constraints |
| 图选项 |
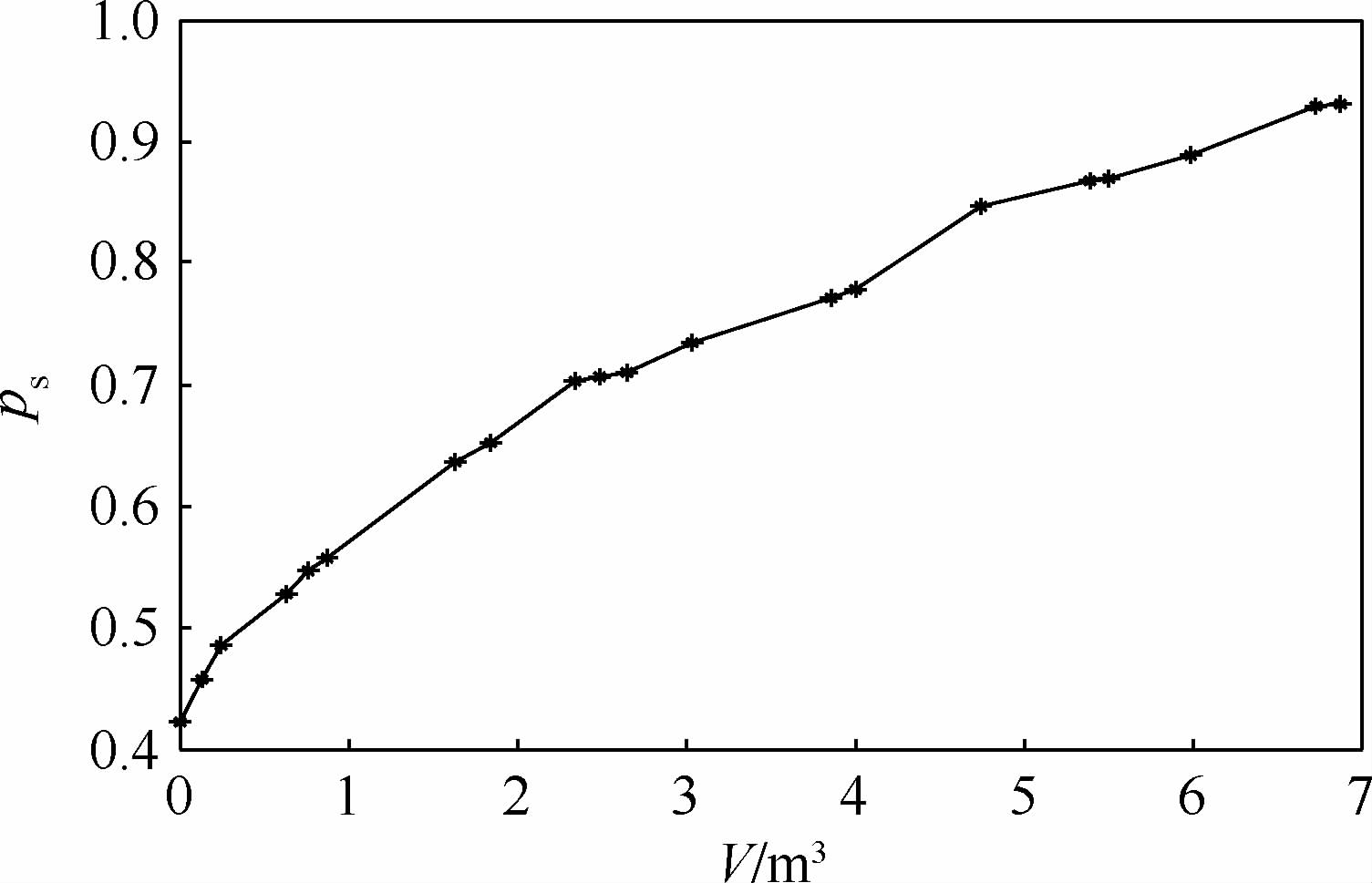 |
| 图 4 体积约束下的最优保障概率曲线Fig. 4 Optimal curve of support probability under volume constraints |
| 图选项 |
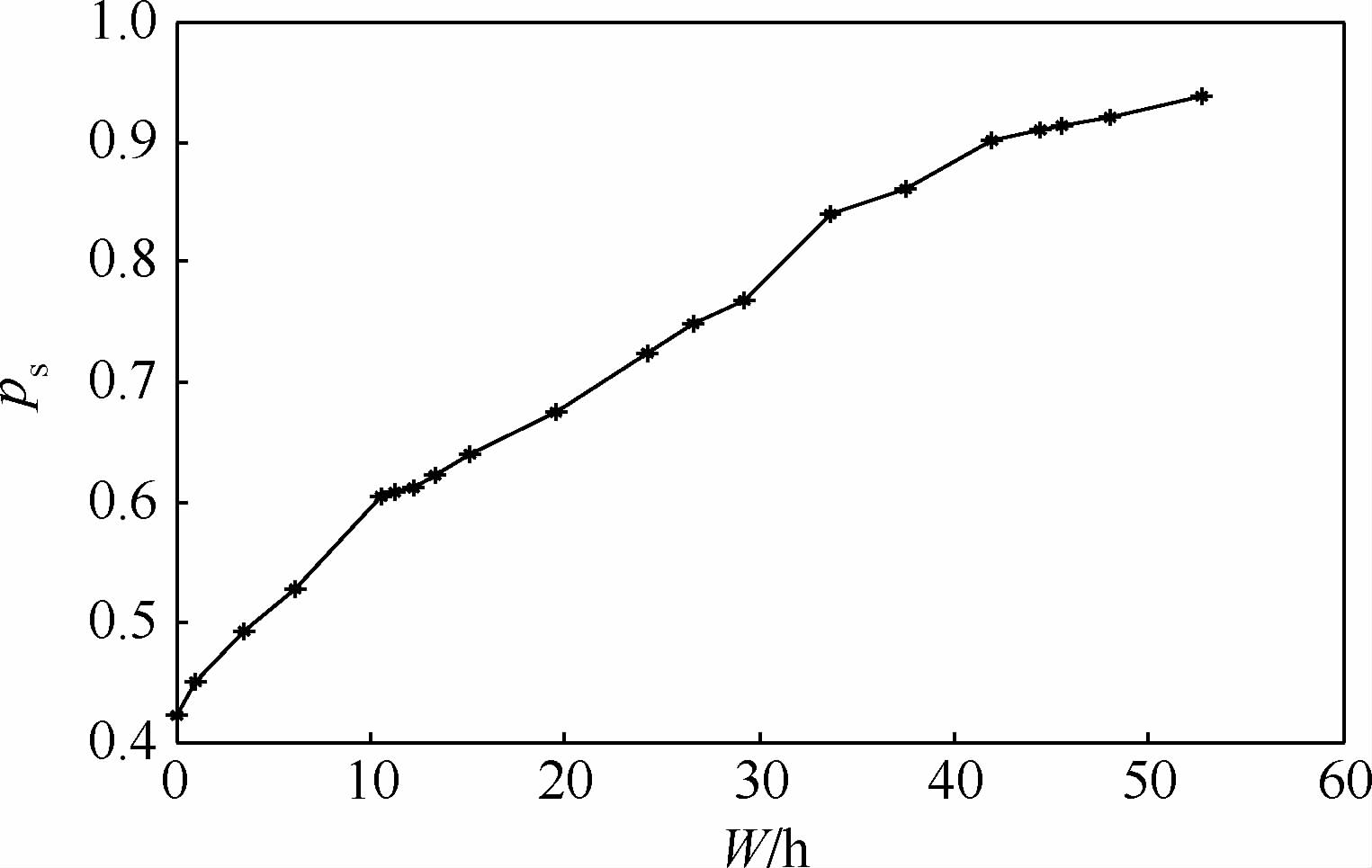 |
| 图 5 维修能力每小时约束下的最优保障概率曲线Fig. 5 Optimal curve of support probability under maintenance per hour constraints |
| 图选项 |
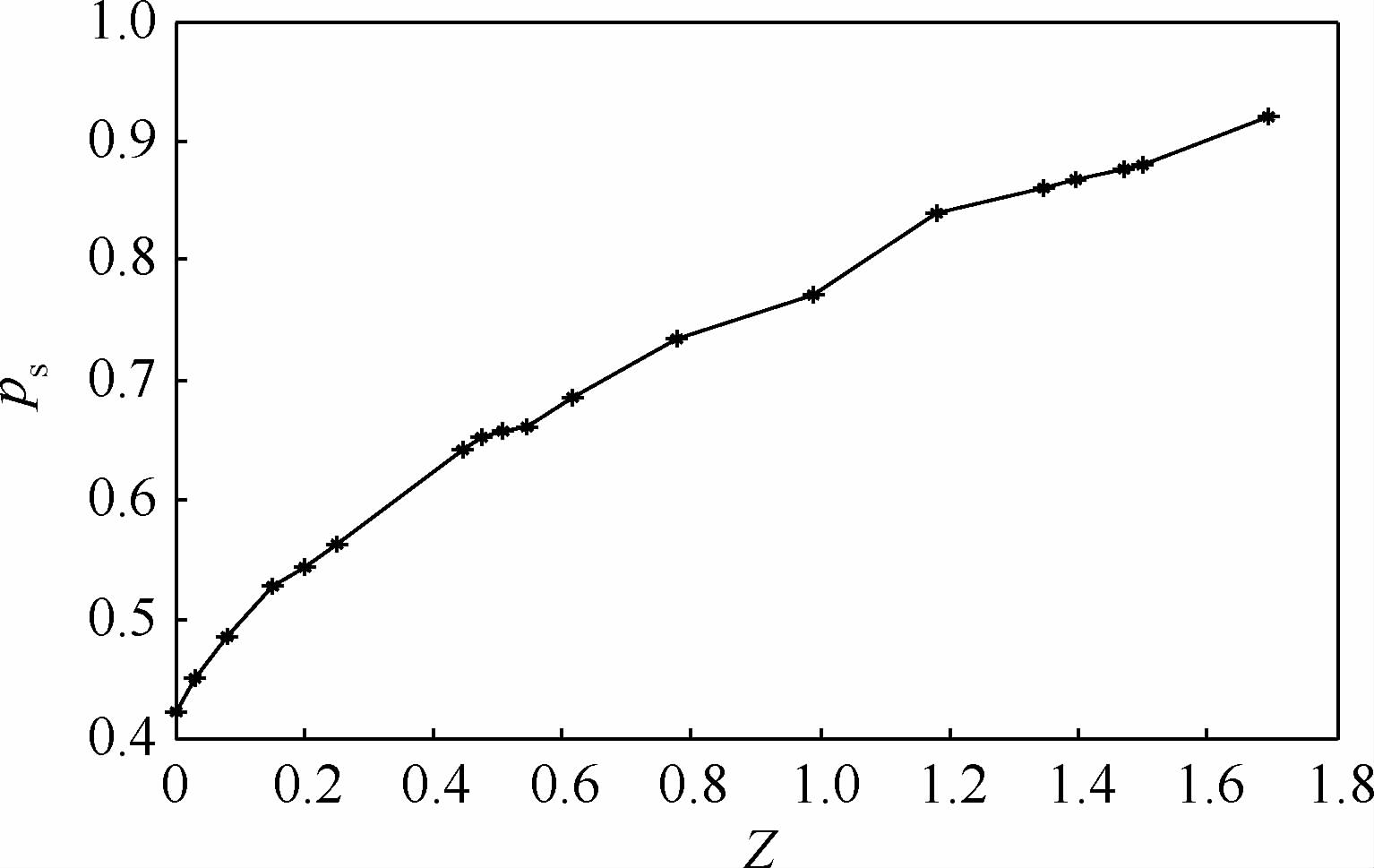 |
| 图 6 混合约束下的最优保障概率曲线Fig. 6 Optimal curve of support probability under mix-constraints |
| 图选项 |
从上述5个方案的备件保障概率曲线图可以看出:
1) 随船备件配置方案不仅受备件种类和数量的影响,同时受其各种指标条件约束.依据不同约束条件,运用边际效应法计算得到不同优化曲线.
2) 依据备件保障概率变化曲线,能够为决策者制定决策及设定各个指标范围提供依据.例如,以图 2为例,当编队备件保障概率达到87.01%时,备件总费用为14.2万元,因此,设定的费用约束必须满足C≥14.2万元,若给定的费用小于14.2万元时,必须相应降低备件保障概率指标ps来满足费用约束要求.
3) 备件保障概率关系曲线上的各个离散点是既定约束条件下的最优备件保障概率,且等同于该保障概率条件下最低指标值.
5 结 论本文在综合分析边际效应、拉格朗日乘子、归一化及专家打分的基本原理基础上提出了一种新的舰船备件配置优化算法,经案例验证表明:
1) 算法可以为解决多个定量约束和多个定性约束的混合问题提供借鉴.
2) 算法可以在满足所有约束条件的前提下,使目标函数最优.
3) 算法不仅适用于海军随船备件配置优化问题,而且对于空军装备、航空航天装备及陆军集群装备等领域同样具有一定的参考价值.
随船备件配置方案不仅与备件种类和数量有关,还与任务强度及仓库地理位置等相关,在今后的工作和学习中,还需针对上述问题进行更进一步的研究.
参考文献
| [1] | Sleptchenko A,van der Heijden M C,van Harten A.Effects of finite repair capacity in multi-echelon,multi-indenture service part supply systems[J].International Journal of Production Economics,2002,79(3):209-230. |
| Cited By in Cnki (0) |>Click to display the text | |
| [2] | Rustenburg W D,van Houtum G J,Zijm W H M.Spare parts management at complex technology-based organizations:An agenda for research[J].International Journal of Production Economics,2001,71(1):177-193. |
| Cited By in Cnki (0) |>Click to display the text | |
| [3] | Sherbrooke C C.METRIC:A multi-echelon technique for recoverable item control[J].Operations Research,1968,16(1):122-141. |
| Cited By in Cnki (0) |>Click to display the text | |
| [4] | 魏曙寰,陈砚桥,金家善.空间和费用约束条件下的随船备件配置优化方法[J].系统工程与电子技术,2013,35(12):2540-2544. Wei S H,Chen Y Q,Jin J S.Warship spare parts allotment method under space and cost constraints[J].Systems Engineering and Electronics,2013,35(12):2540-2544(in Chinese). |
| Cited By in Cnki (2) | |
| [5] | Loo H L,Ek P C,Suyna T,et al.Multi-objective simulation based evolutionary algorithm for an aircraft spare parts allocation problem[J].European Journal of Operational Research,2008,189(2):325-341. |
| Cited By in Cnki (0) |>Click to display the text | |
| [6] | Robert C K,Tovey C.Estimating spare requirements with commonality and redundancy[J].Journal of Spacecraft and Rock-ets,2007,44(4):977-984. |
| Cited By in Cnki (0) |>Click to display the text | |
| [7] | 阮旻智,李庆民,张光宇,等.多约束下舰船装备携行备件保障方案优化方法[J].兵工学报,2013,34(9):1144-1149. Ruan M Z,Li Q M,Zhang G Y,et al.Optimization method of carrying spare parts warship equipment under multi-constraints[J].Acta Armamentarll,2013,34(9):1144-1149(in Chinese). |
| Cited By in Cnki (7) | |
| [8] | 王乃超,康锐.多约束条件下备件库存优化模型及分解算法[J].兵工学报,2009,30(2):247-251. Wang N C,Kang R.An optimization model for inventory spares under multi-constraints and its decomposition algorithm[J].Acta Armamentarll,2009,30(2):247-251(in Chinese). |
| Cited By in Cnki (34) | Click to display the text | |
| [9] | Nosoohi I,Hejazi S R.A multi-objective approach to simultaneous times[J].Applied Mathematical Modeling,2011,35(3):1157-1166. |
| Click to display the text | |
| [10] | 王正元,曹继平,朱昱,等.考虑维修能力的战时备件资源配置方法研究[J].兵工学报,2014,35(5):719-724. Wang Z Y,Cao J P,Zhu Y,et al.An optimization model of wartime spare parts resource allocation on consideration of maintainability[J].Acta Armamentarll,2014,35(5):719-724(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [11] | 王正元,曹继平,朱亚红,等.可移动备件仓库设置优化方法[J].系统工程与电子技术,2013,35(11):2352-2355. Wang Z Y,Cao J P,Zhu Y H,et al.Optimization model on removable spare parts warehouse deployment[J].Systems Engineering and Electronics,2013,35(11):2352-2355(in Chinese). |
| Cited By in Cnki (1) | Click to display the text | |
| [12] | 李大伟,张志华,刘天华.基于Bayes方法的初始备件调整方法研究[J].系统工程理论与实践,2013,33(11):2967-2971. Li D W,Zhang Z H,Liu T H.A regulated method of initial spare based on the bays method[J].Systems Engineering-Theory & Practice,2013,33(11):2967-2971(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [13] | 卢雷,杨江平.k/N(G)结构系统初始备件配置方法[J].航空学报,2014,35(3):773-779. LU L,YANG J P.Initial spare allocation method for k/N(G) structure system[J].Acta Aeronautica et Astronautica Sinica,2014,35(3):773-779(in Chinese). |
| Click to display the text | |
| [14] | Ward R,Ruud T,Willem V J.A two-step method for forecasting spare parts demand using information on component repairs[J].European Journal of Operational Research,2012,220(2):386-393. |
| Click to display the text | |
| [15] | Molenaers A,Herman B,Liliane P,et al.Criticality classification of spare parts:A case study[J].International Journal of Production Economics,2012,140(2):570-578. |
| Click to display the text | |
| [16] | Francesco C,Giulio D G,Massimo T.Multi-echelon,multi-indenture spare parts inventory control subject to system availability and budget constraints[J].Reliability Engineering & System Safety,2013,119(11):95-101. |
| Click to display the text | |
| [17] | Sherbrooke C C.Optimal inventory modeling of systems:Multi-echelon techniques[M].2nd ed.New York:Springer,2004:57-71. |
| Click to display the text | |
| [18] | Famfulík J,Míková J,Lánská M,et al.A stochastic model of the logistics actions required to ensure the availability of spare parts during maintenance of railway vehicles[J].Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,2014,228(1):85-92. |
| Click to display the text | |
| [19] | Costantino F,di Gravio G,Tronci M.Multi-echelon,multi-indenture spare parts inventory control subject to system availability and budget constraints[J].Reliability Engineering & System Safety,2013,119:95-101. |
| Click to display the text | |
| [20] | Molenaers A,Baets H,Pintelon L,et al.Criticality classification of spare parts:A case study[J].International Journal of Production Economics,2012,140(2):570-578. |
| Click to display the text |
