删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于子目标进化的高维多目标优化算法

本站小编 Free考研考试/2021-12-25
当前在解决目标数超过3个的高维多目标优化问题(Many-objective Optimization Problems,MOPs)中,由于目标函数数量的增加,传统的基于Pareto占优关系生成Pareto最优解时,互不占优解的数目急剧增多,使得Pareto最优解的选择压力降低,难以有效地逼近Pareto前沿[1, 2].一些经典算法:NSGA-Ⅱ[3]、SPEA2[4]和PESA-Ⅱ[5]对于高维多目标优化问题都不能很好地适应[6, 7].Saxena和Deb[8]分别运用PCA和最大变化伸展PCA以及相关熵PCA的方法来减少冗余目标,但是多个目标函数不存在冗余时是无效的.文献[9]提出了Pareto自适应ε占优机制,结合Pareto前沿面的几何形状和前沿面的不同部分的占优强度信息,自适应地调节ε矢量中元素的值.实现了高维多目标的降维,但是这种方法会改变部分解的支配关系,求解有些高维目标优化问题时解的质量较差.文献[10]基于GDDR(Group Divided Dimensional Reduction)算法实现了多目标降维处理,虽然性能上有一定的优势,但是该方法在目标函数进行分组时具有较大的随意性,不同的分组方法将导致不同的优化结果.文献[11]应用文献[12]提出的基于聚集函数的方法,使用加权的最小最大法以及结合对偶优化的权角距离的度量方法,能用于解决MOPs问题,但是处理较低维数时效果欠佳.文献[13]提出的efficiency of order方法能够将Pareto解集中的每个解的目标向量向K维空间进行投影.该方法能够找到更逼近Pareto前沿且分布均匀的非支配解,在解决低维的多目标优化问题时有一定的优势.文献[14]利用超体积、分布度和延展度将高维多目标优化问题转化为具有3个目标函数的多目标优化问题,虽然从理论上证明了可应用于求解高维多目标优化,但是设计高性能的集合进化策略往往是十分困难的,这给此种方法的应用造成了很大的限制.
本文从缩小搜索空间入手,在理论上证明了通过子目标函数值排序进行Pareto最优解求取的可行性,能够有效减少比较次数,加快求解速度.同时,基于SPEA2(Strength Pareto Evolutionary Algorithm2)算法框架,对密度评估策略中的距离和密度计算公式进行重新定义.提出的SOEA(Sub-Object Evolutionary Algorithm)算法同文献[15, 16, 17]中的高维多目标优化算法,在测试函数DTLZ[2, 18]上关于收敛性指标[17]、覆盖率指标[19]进行比较,显示出一定的优势.
1 多目标优化相关表述n个决策变量和m个目标变量的多目标优化问题[2]可以表述为
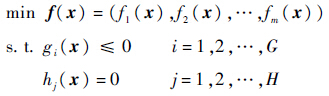
式中:x为n维决策矢量,x∈Rn;f(x)为m维目标矢量,f(x)∈Rm,f(x)定义了m个由决策空间向目标空间映射的函数；gi(x)≤0(i=1,2,…,G)定义了G个不等式约束；hj(x)=0(j=1,2,…,H)定义了H个等式约束.
定义1 Pareto占优[3].若xa,xb∈Xf是多目标优化问题的两个可行解,则称xa是比xb Pareto占优的.
1) 若对于∀i=1,2,…,m;fi(xa)≤fi(xb)且∃j=1,2,…,m;fj(xa)＜fj(xb)，则记作xa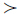sxb,也称为xa强支配xb.
2) 若对于∀i=1,2,…,m;fi(xa)≤fi(xb)记作xa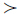xb,也称为xa弱支配xb.文中的支配概念,均是该定义下的弱支配.
2 高维优化SOEA算法2.1 理论可行性证明在证明相关命题之前,需要对Rm空间(m维欧氏空间)上的多目标优化问题,进行如下的假设:
1) 多目标优化问题的各个子目标函数在解空间上是连续的.若存在可去间断点和阶跃间断点,则利用目标函数在解空间连续的方法进行讨论,而不影响问题求解结果.
2) 解空间是Rn上的有界闭子空间.
引理1 多目标优化问题的可行解集是半序集.
证明设x1,x2∈Xf,对应的目标函数为F1=(f1(x1),f2(x1),…,fm(x1)),F2=(f1(x2),f2(x2),…,fm(x2)),F1,F2∈Rm,“≤”表示实数域条件下的小于等于含义.①对于x1,有fi(x1)≤fi(x1),i=1,2,…,m成立,由解支配的定义即得x1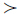x1.②对x1,x2,若有fi(x1)≤fi(x2),fi(x2)≤fi(x1),即fi(x2)=fi(x1)成立.由①的结论可得x1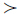x2(x2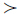x1).③对x1,x2,x3∈Xf,若有fi(x1)≤fi(x2),fi(x2)≤fi(x3),即有fi(x1)≤fi(x3)(i=1,2,…,m)成立,则x1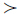x3.所以,在可行解集上定义的Pareto占优关系,即Pareto支配“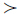”,是集合Xf上的半序.证毕
引理2 子目标的最优解集是全序集.
证明设{xp}是子目标fi(x)可行解的集合,则{xp}⊂Xf.由于Xf≠∅.对∀x1,x2∈{xp},x1≠x2,有fi(x1)≤fi(x2)或fi(x2)≤fi(x1),则{xp}是全序集.由于fi(x)是解空间上的连续函数,解空间是Rn上的有界闭子空间,故{xp}存在上界.由Zorn引理[20]可知Xf至少存在一个极大元.证毕
引理3 极大元是非支配解.
证明对于多目标优化问题的可行解集Xf,Xf已被证明为半序集.若x*是Xf的极大元,则由极大元的定义[20],对∀x∈Xf,若x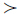x*,则x*=x.故对∀x∈Xf,有x*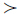x成立.也即:¬∃x∈Xf使得x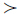x*成立,则x*是多目标优化问题的非支配解.证毕
定理1 设{f1,f2,…,fm}是优化问题的目标函数集,Xf为其解空间,x**为其Pareto非支配集;x*1,x*2,…,x*m,是使得各目标函数取得极值的解,则集合Y={x*1,x*2,…,x*m}是非支配解集,且Y是x**的子集.
证明对∀xi∈Xf,取集合Y中的任一元素x*j,由定义,x*j使得fj(·)取得极值,则由支配的定义,对∀xi∈Xf,使得fj(xi)≤fj(x*j)不成立,故xi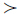x*j不成立,即x*j是极大元.由引理3知x*j是非支配解,故集合Y={x*1,x*2,…,x*m}是非支配解集.
往证,Y是x**的子集.对∀x*j∈Y,由于Y是非支配解集,故x*j∈x**.若有x*′j∈x**,则对∀xi∈Xf,∃l,l∈{1,2,…,m},使得fl(xi)≥fl(x*′j)≥fl(x*j)成立,则fl(x*′j)不是fl(·)上的极值,故x*′j∉Y,则Y⊂x**.证毕
定理2 多目标优化Pareto非支配解x**的求取,可分解为f1,f2,…,fm个子目标进行,且此种求取非支配解的方法是完备的.
证明对∀xi,xj∈Xf,若对∀l=1,2,…,m,有fil≤fjl成立,则xi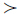xj.若fil≤fjl成立,则记F(fil,fjl)=1,否则,记R(fil,fjl)=0.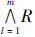(fil,fjl)=1⇔xi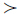xj,可见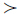关系可分解为m个子目标函数值比较结果的逻辑与关系.若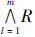(fil,fjl)=0,则xi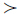xj不成立.
对于x*i(i=1,2,…,m)是使得各目标函数取得极值的解,则集合Y={x*1,x*2,…,x*m}是非支配解集,且Y是x**的子集,已由定理1得证.若x*′i是在目标函数fi(·)上取值仅次于的极值点x*i的解.由于x*i是Pareto非支配解,x*′i在目标函数fi(·)上的取值仅次于x*i,故只需比较j≠i上的fj(x*i)与fj(x*′i)的取值大小,若fj(x*′i)≤fj(x*i)成立,则x*i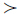x*′i不成立,由于x*i是非支配解,故x*′i也是非支配解.同理,若x*″i是在目标函数fi(·)上的取值次于x*′i的解.若有fk(x*″i)≤fk(x*′i)、 fj(x*″i)≤fj(x*i),j≠i,k≠j成立,则x*′i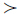x*″i,x*ix*″i不成立,则x*″i也是非支配解.继续此过程求取更多Pareto非支配解x*′″i,…,x*(n′)i,记这些非支配解构成的集合为{x*(n′)i}.
往证,完备性.对∀x∈x**,若x∈Y,则∃i∈{1,2,…,m}使得fi(x)=minfi(·),则通过子目标排序的方法一定能找到minfi(·),即能找到非支配解x.若x∈x**,x∉Y,不妨设在某子目标i∈{1,2,…,m}上有fi(x)≥fi(x*″)≥fi(x*′),由于fi(x*′)=minfi(·),故x*′必定被找到,且x*′x*″不成立,由于x*″在fi(·)上的取值仅次于x*′,故x*″必定被找到,依此法x必定被找到,则对∀x∈x**都可被找到.证毕
2.2 SOEA算法2.2.1 进化过程SOEA算法是以进化种群中子目标函数值排序为基础.根据求取的是目标函数的最大(最小)值,对子目标函数值进行排序.通过子目标值的排序,快速找出非支配解.以子目标函数f1为例,要求取目标函数的最小值.进化过程如图 1所示,通过排序,得到使f1取最小值的解空间中的点A,A为通过目标函数f1获得的第1个非支配解.继续该过程得到C、C1在f1上的函数值仅比A大,但是C、C1在子目标f2上的函数值比A小,故C、C1相对于A为非支配解.但是C支配C1,故C为非支配解.由此可见,子目标进化算法的方向性很强.
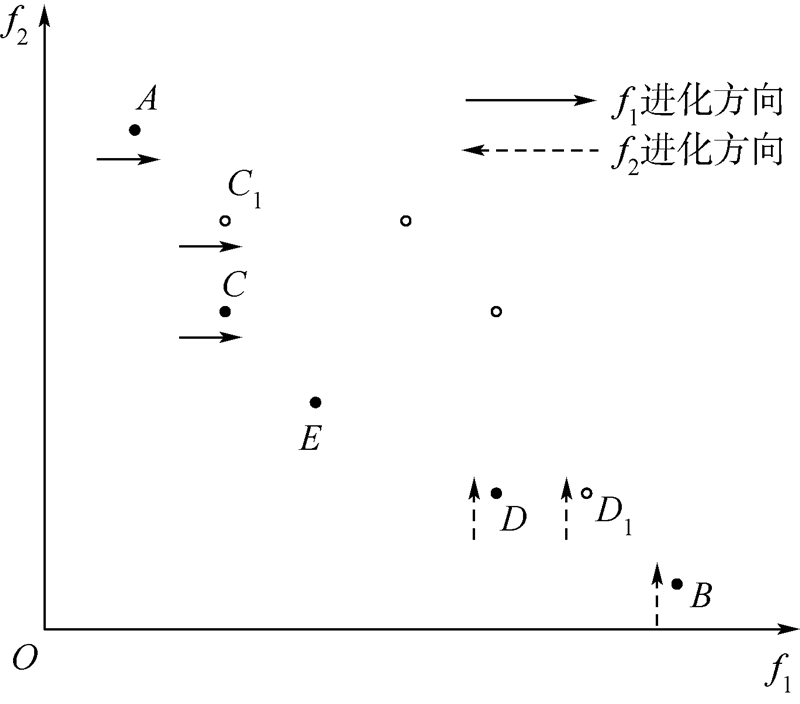图 1 进化过程示意图Fig. 1 Schematic of evolution process
图选项


SOEA算法利用了SPEA2算法的框架,与SPEA2算法不同之处有:利用子目标函数值排序,快速获得非支配解集,而不需要通过进化种群中的解之间两两比较来获得非支配解;利用归一化函数差值的Minkowski距离进行解之间的距离计算,通过“k近邻”距离来评判密度值的大小.而不是通过计算进化种群中解之间的欧氏距离.利用从外部种群中获取下一代进化的解,而不是在外部集合和进化种群中选取下一代的进化种群.
2.2.2 算法流程输入值:进化种群的大小M,外部集合的势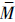,最大进化代数P.
输出值:非支配解集Unon.
第1步 初始化,产生初始种群U0,并且产生一个空的外部集合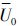=∅,设置进化代数p=0.
第2步 利用子目标优化方法求取进化种群Up中的Pareto非支配解.
第3步 将产生的非支配解加入外部集合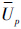,如果非支配解的个数大于外部集合的大小,则利用截断方法进行操作;如果产生的解的个数小于外部集合的大小,则利用适应度的值,选择满足条件的解进入外部集合.
第4步 如果达到最大进化代数P,则停止计算.将外部集合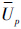中的非支配解输出到Unon中作为最终的非支配解集.
第5步 计算外部集合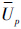中解的适应度,对外部集合利用锦标赛的方法进行选择,当被选择的解的个数等于进化种群的大小M时停止选择.
第6步 利用交叉、变异操作对进化种群中的解进行操作,产生新一代种群Up+1,转入第2步.
2.2.3 非支配解获取在求取外部集合的解时,设置一个临时集合用于存放由进化种群中选出的解,这些解在满足一定的条件时将被选入外部集合,临时集合作为求取过程中的辅助存储空间.根据外部集合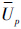的势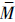=||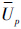,对于有m个子目标的多目标优化问题,首先由每个子目标对外部集合提供Mi=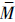/m个元素.利用子目标快速选择方法生成非支配解,生成的非支配解的数目为|Upi|,当|Upi|=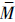/m时,暂时中止在此子目标上生成Pareto非支配解.将以上生成的非支配解加入临时集合,同时将这些非支配解从进化种群中删去.依据子目标f1,f2,…,fm依次生成非支配解集Up1,Up2,…,Upm.按最后一个子目标生成非支配解时,如果产生的非支配解的个数已经等于外部集合的大小.则依次选择进化种群中的解,按照该解中子目标的值最小(或者最大)的子目标,与临时集合中相应的非支配解进行比较,直至进化种群中所有的解比较完毕.此时,进化种群中的全部非支配解被选入临时集合.在选择非支配解进入临时集合的过程中,如果进化种群中的解选择完毕,也没有达到外部集合的个数,则利用适应度值选择支配解进入外部集合.
2.2.4 基于归一化Minkowski距离的“k近邻”方法解的选择是以适应度为准则进行评判的,解的适应度计算由解的强度和解的密度两部分组成.强度由解之间的支配关系确定;密度评估以解的距离计算为前提.密度值小,说明该解与空间中其他解的距离大,从而优先考虑被保留.关于距离的计算也有很多不同的计算方法,NSGAⅡ(Nondominated Sorting Genetic Algorithm Ⅱ)在子目标函数值排序的基础上,通过相邻的两个函数值的差值求取绝对值,归一化处理后,对每个子目标上的这些差值进行求和,从而得出个体的排挤距离.SPEA2算法中,通过计算两个非支配解之间的欧氏距离,然后对与本非支配解相关的距离进行排序,利用“k近邻”的方法,求取在排序中的第k个距离值的大小,通过第k个距离值的大小计算密度值.Pareto存档进化策略(Pareto Archived Evolution Strategy,PAES)算法利用空间超格机制来保持种群的多样性.超格的数目需要预先设定,但是当目标的数目增多时,超格的数目难以确定,并没有很好的方法可循.以上的密度评估策略应用在高维多目标优化问题上时,获得的效果并不理想.
根据以上方法的不足,提出了更为广义的基于归一化Minkowski距离的“k近邻”方法.流程如下.
第1步 对于临时集合中的解,找出每个子目标上的最大值和最小值,计算两个解的同一子目标上函数值的差值,对这一差值进行归一化处理.
第2步 利用Minkowski距离计算公式,对两个解的子目标进行归一化处理后的差值进行距离计算.
第3步 对于临时集合中的每个解,对计算所得的与其他解之间的Minkowski距离按升序进行排列.
第4步 k值取外部集合大小的方根,k=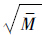.记与解Xi距离为k的解的距离为σki.密度评估按D(i)=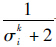计算.
子目标函数差值的归一化是对每个子目标函数fi,在临时集合中分别求取最大值fmaxi和最小值fmini,则两个解Xk、Xl在此子目标函数上的差值归一化后的形式为

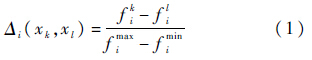
Minkowski距离计算公式为

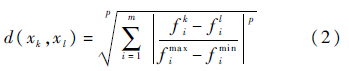
当p值较小时,对差值的影响不明显,相当于均衡考虑各个目标;当p值较大时,差值大的目标对距离的影响明显.可以看出,NSGAⅡ和SPEA2中的距离计算公式是式(2)在p取值为1和2时的特例.在高维多目标优化时,非支配解的数目增长很快,均衡的进化方法势必导致收敛到Pareto前沿的速度过慢,因此适当地增大p的取值可以加速收敛速度.本文中采用随机的p值选取方法,在[1,H]的范围内随机选取一个p值,H为某正整数,作为每一代进化的Minkowski距离计算公式中的幂次,在同一代进化中p取相同的值.
2.2.5 外部集合解的选取1) 非支配解个数小于外部集合时解的选取.
利用子目标快速选择方法中产生的非支配解的数目不足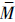时,通过计算进化种群中的支配解的适应度,选择适应度值小的支配解进入外部集合,直至满足外部集合的大小要求.适应度计算公式为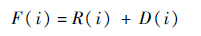

式中:

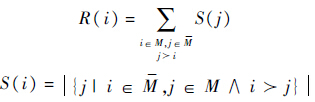
D(i)的计算按归一化Minkowski距离的“k近邻”方法进行.
2) 非支配解个数大于外部集合时解的选取.
由于此时临时集合中所有的解都是非支配解,适应度值计算公式F(i)=R(i)+D(i),退化为F(i)=D(i).将密度评估值进行升序排列,取密度值小的前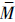个解进入外部集合.非支配解xk1、xk2到xi的距离相同时,即σk1i=σk2i.统计非支配解xk1、xk2在各个子目标函数上的差值的正负.若在fj(xk1)－fj(xk2)(j=1,2,…,m)中,取正值的子目标函数占多数,则当优化是求取最小化各目标时,选取xk2进入外部集合;反之,选取xk1.
2.2.6 时间复杂度分析对于含有m个子目标,进化种群中有M个解,外部集合的势为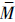的多目标进化问题.初始化的时间复杂度是O(M),求取非支配解的时间复杂度是O(KM);求取外部集合的时间复杂度是O(L2)+O(LlogL),其中,L是临时存储集合0＜L≤M;交叉、变异及种群更新时间复杂度是O(M).总的时间复杂度为:O(M)+O(KM)+O(L2)+O(LlogL)+O(M),按照时间复杂度的运算规则,最差的时间复杂度应为:max{O(KM),O(L2)}.
对于SPEA2算法,初始化的时间复杂度是O(M).非支配解求取由适应度计算决定,适应度计算包含强度和距离计算.计算强度R(i)的时间复杂度为O((M+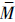)2);计算距离D(i)的时间复杂度为O((M+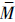)2log(M+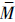)).求取外部集合的时间复杂度为O((M+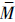)2log(M+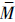));交叉、变异以及种群更新的时间复杂度为O(M).所以,SPEA2算法的平均时间复杂度为:O((M+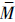)2log(M+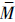)).由时间复杂度的分析可以看出,本文提出的算法在时间复杂度方面与SPEA2算法相比具有明显的优势.
解决高维多目标优化问题的基于子集覆盖实现目标减少的近似k-MOSS算法,时间复杂度为O(m3L2),其中m为子目标的个数,L为临时集合的大小.基于特征选择的目标减少算法,通过选择最拥挤的邻居群,保留该邻居群的中心,然后删除其余的目标,算法的时间复杂度为O(m2L).
3 测试结果与分析3.1 测试函数及评价指标1) 测试函数.
测试函数使用高维多目标进化领域被广泛使用的DTLZ1~DTLZ7函数,函数的具体形式可参见文献[2, 18],在此不再赘述.
2) 收敛性指标[17].
令G*={g1,g2,…,g|G*|}是理想的均匀分布的Pareto最优解集，Q={a1,a2,…,aQ}是通过进化算法得到的Pareto最优解集.则对于集合Q中的解ai,通过式(3)得到该解距离G*的最小欧氏距离:

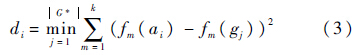
IGD评价方法用于衡量所求的Pareto前沿面到真实的Pareto前沿面的收敛程度,该指标的值越小,表明算法得到的解的收敛性越好,越接近理想Pareto前端,定义为

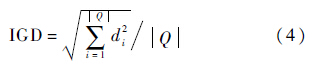
3) 覆盖率指标C[19].
E、F是优化问题的两个解集,覆盖率指标C定义为

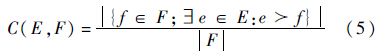
式中: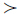表示Pareto支配(弱支配);C(E,F)=1,表示所有在F中的解均可由E中的解支配;C(E,F)∈[0, 1],C(E,F)取值越大,表示E集合中的解越优于F.
3.2 测试结果及分析设置进化种群的规模为600,外部种群的大小为200,进化代数为400代,每个算法独立运行20次,评价指标为20次运行的平均值.为了测试SOEA算法的性能,选择类似的解决高维多目标优化问题的算法进行比较,分别是由Jaimes和Coello提出的基于特征选择的算法(记为JC),以及由Brockhoff和Zitzler提出的基于最小子集覆盖的目标减少算法k-MOSS(记为BZ).利用以上3种解决高维多目标优化问题的算法对DTLZ1~DTLZ7测试函数进行计算,比对各算法对不同的测试函数的计算性能.由于以上3种算法对7个测试函数进行求解后,求解结果表现出一定的相似性,选取SOEA算法、BZ算法、JC算法对DTLZ2、DTLZ5、DTLZ7测试函数的测试结果在文中列出.
SOEA算法在进化的过程中,并没有减少目标函数的个数,所以在进化过程中解之间的支配关系不会发生变化.求得的非支配解必定是原来的多目标优化问题的Pareto最优解,从表 1中的数据也能说明这一点.可以看出SOEA算法的IGD值比BZ算法和JC算法得到的值要小,说明SOEA算法获得的Pareto前沿与最优Pareto前沿接近程度更好.JC算法由于删除了过多的目标函数,解的支配情况与BZ算法相比改变程度会大一些,得到的IGD值也比BZ算法得到的要大.
表 1 对DTLZ2的收敛性指标比较Table 1 Convergence metric comparison on DTLZ2
目标数量BZ算法JC算法SOEA算法
60.394 60.479 30.184 3
120.502 50.625 20.363 8
180.423 70.384 60.374 1
240.388 20.402 70.256 9
300.584 90.601 90.436 2

表选项


由表 2可见,当目标数为12维时,通过对获得的非支配解进行统计,得出利用SOEA算法求得的非支配解,可以支配BZ算法求得的非支配解,占BZ算法求得解的0.544 3,而BZ算法中可支配SOEA算法中的解,只占到SOEA算法求得解的0.396 2.可以得出利用SOEA算法所求得的非支配解集比BZ算法的质量要高，与JC算法比较结果的统计数据也显示出这一结论.
表 2 对DTLZ2的覆盖率指标比较Table 2 Coverage metric comparison on DTLZ2
目标
数量		C(SOEA,BZ)C(BZ,SOEA)C(SOEA,JC)C(JC,SOEA)
60.538 40.383 70.547 90.317 4
120.544 30.396 20.560 40.328 3
180.560 20.398 50.569 30.335 9
240.572 80.403 60.568 50.347 2
300.510 50.345 10.533 40.319 6

表选项


通过图 2可见,JC算法的运行时间比另两个算法占优,这是因为该算法是直接在目标函数上进行处理的,通过删除冗余的目标函数,来达到降低维数的目的,算法的时间复杂度相当于处理低维的目标优化问题.SOEA算法和BZ算法均需要进行支配关系的比较,时间复杂度与外部集合的大小相关.可以看出SOEA算法相比较于BZ算法,基本上是正比例相关的.SOEA算法在时间上要优于BZ算法.
图 2 求解DTLZ2~DTLZ7时各算法运行时间Fig. 2 DTLZ2-DTLZ7 computation time of every algorithm
图选项


通过对3个算法在测试函数DTLZ5、DTLZ7上相应值的统计结果,显示了与在DTLZ2上类似的结论,如表 3～表 6和图 2所示.
表 3 对DTLZ5的收敛性指标比较Table 3 Convergence metric comparison on DTLZ5
目标数量BZ算法JC算法SOEA算法
60.148 70.294 20.138 2
120.364 20.577 50.154 9
180.405 40.291 20.236 1
240.506 80.195 60.362 2
300.313 20.380 30.285 7

表选项


表 4 对DTLZ5的覆盖率指标比较Table 4 Coverage metric comparison on DTLZ5
目标
数量		C(SOEA,BZ)C(BZ,SOEA)C(SOEA,JC)C(JC,SOEA)
60.452 60.357 20.487 30.324 9
120.473 20.365 50.501 60.336 4
180.514 70.382 40.535 70.338 1
240.537 20.389 70.562 80.345 3
300.557 80.392 50.595 40.327 5

表选项


表 5 对DTLZ7的收敛性指标比较Table 5 Convergence metric comparison on DTLZ7
目标数量BZ算法JC算法SOEA算法
60.438 40.564 90.427 5
1218.7918.9311.48
1858.9658.3724.72
2472.4873.0636.44
3085.1587.1778.53

表选项


表 6 对DTLZ7的覆盖率指标比较Table 6 Coverage metric comparison on DTLZ7
目标
数量		C(SOEA,BZ)C(BZ,SOEA)C(SOEA,JC)C(JC,SOEA)
60.568 20.287 50.597 40.225 6
120.583 40.292 80.612 70.228 6
180.597 60.293 90.638 40.248 3
240.601 40.295 10.652 80.246 3
300.632 70.294 90.657 30.245 9

表选项


4 结 论在分析高维多目标优化问题特点和研究现有多目标优化求解算法的基础上,得出如下结论:
1) 高维多目标优化问题Pareto非支配解x*的求取,可以通过分解为f1,f2,…,fm个子目标,并在子目标函数值排序的基础上获得,且此法获得的Pareto非支配解完备.
2) 解的适应度值求取时,在基于归一化函数差值的Minkowski距离计算方法中采用随机在[1,H]范围内选取p值的方法可以加快算法的收敛速度.
3) 将本文提出的SOEA算法与BZ、JC算法比较,得出SOEA算法在收敛性和覆盖率两个指标上均优于BZ、JC算法.运行的时效性JC算法最优,SOEA算法次之,BZ算法最差.
参考文献
[1] 孔维健,丁进良,柴天佑.高维多目标进化算法研究综述[J].控制与决策,2010,25(3):321-326.Kong W J,Ding J L,Chai T Y.Survey on large-dimensional multi-objective evolutionary algorithms[J].Control and Decision,2010,25(3):321-326(in Chinese).
Cited By in Cnki (36)
[2] 公茂果,焦李成,杨咚咚,等.进化多目标优化算法研究[J].软件学报,2009,20(2):271-289.Gong M G,Jiao L C,Yang D D,et al.Evolutionary multi-objective optimization algorithm[J].Journal of Software,2009,20(2):271-289(in Chinese).
Cited By in Cnki (469)
[3] Deb K,Pratap A,Agarwal S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
Click to display the text
[4] Zitzler E,Laumanns M,Thiele L.SPEA2:Improving the strength Pareto evolutionary algorithm,TIK-Rep103[R].Lausanne:Swiss Federal Institute of Technology,2001.
Click to display the text
[5] Corne D W,Jerram N R,Knowles J D,et al.PESA-Ⅱ:Region-based selection in evolutionary multi-objective optimization[C]∥Proceeding of the Genetic and Evolutionary Computation Conference,GECCO 2001.San Francisco:Morgan Kaufmann Publishers,2001:283-290.
Click to display the text
[6] Khare V,Yao X,Deb K.Performance scaling of multi-objective evolutionary algorithms[C]∥Proceeding of the 2nd Conference on Evolutionary Multi-Criterion Optimization,EMO 2003.Berlin:Springer-Verlag,2003:376-390.
Click to display the text
[7] Bandyopadhyay S,Bhattacharya R.Solving multi-objective parallel machine scheduling problem by a modified NSGA-II[J].Applied Mathematical Modelling,2013,37(10-11):6718-6729.
Click to display the text
[8] Saxena D K,Deb K.Non-linear dimensionality reduction procedure for certain large-dimensional multi-objective optimization problems:Employing correntropy and a novel maximum variance unfolding[C]∥Proceedings of the 4th International Conference on Evolutionary Multi-Criterion Optimization.Berlin:Springer-Verlag,2007:772-787.
Click to display the text
[9] Hernández-Diaz A G,Santana-Quintero L V,Coello Coello C A,et al.Pareto-adaptiveε-dominance[J].Evolutionary Computation,2007,15(4):493-517.
Click to display the text
[10] 刘立佳,李相民,颜骥.解决高维多目标优化的分组进化算法[J].四川大学学报,2013,45(1):118-122.Liu L J,Li X M,Yan J.Group divided dimensional reduction evolutionary algorithm for multi-objective pptimization[J].Journal of Sichuan University,2013,45(1):118-122(in Chinese).
Cited By in Cnki
[11] Wagner T,Beume N,Naujoks B.Pareto-,aggregation-,and indicator-based methods in many-objective optimization[C]∥Lecture Notes in Computer Science.Berlin:Springr-Verlag,2007:742-756.
Cited By in Cnki (0) | Click to display the text
[12] Hughes E J.Multiple single objective Pareto sampling[C]∥Congress on Evolutionary Computation (CEC03).Piscataway,NJ:IEEE Press,2003:2678-2684.
Click to display the text
[13] di Piero F.Many objectives evolutionary algorithms and applications to water resources engineering[D].Exeter:University of Exeter,2006.
Click to display the text
[14] 巩敦卫,季新芳,孙晓燕.基于集合的高维多目标优化问题的进化算法[J].电子学报,2014,42(1):77-83.Gong D W,Ji X F,Sun X Y.Solving many-objective optimization problems using set-based evolutionary algorithms[J].Acta Electronica Sinica,2014,42(1):77-83(in Chinese).
Cited By in Cnki (6)
[15] Brockhoff D,Zitziler E.Are all objectives necessary? On dimensionality reduction in evolutionary multi objective optimization[C]∥Parallel Problem Solving from Nature.Berlin:Springer,2006:533-542.
Click to display the text
[16] Brockhoff D,Zitziler E.Objective reduction in evolutionary multi objective optimization:Theory and applications[J].Evolutionary Computation,2009,17(2):135-166.
Click to display the text
[17] Jaimes A L,Coello C A C,Chakraborty D,et a1.Objective reduction using a feature selection technique[C]∥Proceedings of the Genetic and Evolutionary Computation Conference(GECCO 08).Atlanta:ACM Press,2008:673-680.
Click to display the text
[18] Deb K,Thiele L,Laumanns M,et a1.Scalable multi objective optimization test problems[C]∥Congress on Evolutionary Computation(CEC02).Piscataway,NJ:IEEE Press,2002:825-830.
Click to display the text
[19] Knowles J,Corne D.On metrics for comparing non-dominated sets[C]∥Proceeding of the IEEE Congress on Evolutionary Computation.Piscataway,NJ:IEEE Press,2002:711-716.
Click to display the text
[20] 时宝,王兴平,盖明久.泛函分析引论及其应用[M].北京:国防工业出版社,2009:104-110.Shi B,Wang X P,Gai M J.Introduction to functional analysis with application[M].Beijing:National Defense Industry Press,2009:104-110(in Chinese).


相关话题/优化 计算 空间 指标 测试
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于带宽优化的载波跟踪算法
    在航天测控系统中,由于通信传输距离远及载体相对运动剧烈,使得接收信号具有低信噪比高动态的特点[1].在目前测控系统中,接收机的射频部分尚不能完全实现数字化,一般采用数字中频方案[2].载波跟踪是对频率及相位的精细估计,是决定中频接收机性能的重要环节,常见的算法有极大似然估计法(MLE)[3]、扩展卡 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于混合优化算法的空间拦截轨道优化设计
    空间拦截是空间系统的重要任务之一,而拦截轨道设计是实现空间拦截的基础,其中在拦截的初制导阶段,燃料和转移时间的优化是需要重点考虑的问题.目前,空间拦截轨道优化问题的解法主要是结合不同的优化指标要求建立轨道优化数学模型,将其转化为最优控制问题,再通过直接法或间接法求取最优解[1].其中直接法是指通过参 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 参数化产品族递进式优化设计方法
    产品族设计是实现大批量定制的有效方式[1],模块化产品族与参数化产品族是当前产品族设计领域的两大分支.模块化产品族的设计策略主要是通过模块单元的组合与变换来实现客户需求的响应,参数化产品族不改变产品的拓扑结构,通过改变影响产品性能的设计变量的取值来设计出性能差异的产品.在参数化产品族的设计与优化方法 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于自由尾迹/面元法的旋翼下洗干扰计算和直升机配平
    受旋翼涡系的影响,直升机工作在十分复杂的流场当中,旋翼的下洗流对机身振动、桨叶气动载荷和直升机的飞行性能都有十分重要的影响.长期以来,科研人员从数值计算和试验两方面对涡动力学方法进行了大量的研究[1,2,3],对旋翼/机身的复杂气动干扰的理解也愈发加深.当直升机在吊挂飞行、舰载和沙漠等复杂条件起降时 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 面铣刀正交车铣加工切屑厚度的计算方法
    在航空工业,存在着许多的回转体或是半回转体同时带有凸台、耳片或者窗口等异形特征的工件.这类工件在应用传统的方法进行加工时效率低、成本高,对工厂来说是个很大的挑战.近些年出现的车铣复合加工技术为应对这一问题提供了有效的解决途径.越来越多的研究人员开始重视这一新技术,并在许多方面对其进行了探索和研究[1 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于姿态可操作度的机械臂尺寸优化方法
    机械臂的设计有多种准则,大多数机械臂是在运动学可逆的情况下设计的.许多****,如Roth和Lee等[1,2]最早开始分析机械臂的工作空间,并将其作为机械臂设计准则.文献[1]讨论了给定结构下机械臂工作空间的形状,以及根据工作空间的形状,如何设计机械臂的结构.Bergamaschi等[3]提出了一种 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • H2O对空间站5A分子筛CO2去除性能影响
    宇航员在正常工作状态下会产生约1kg/d的CO2气体[1],为了保证宇航员在载人飞行器封闭环境下正常生存,必须配置CO2去除系统.该系统工作的可靠性和鲁棒性已成为保障载人航天任务成败的关键.CO2非再生技术已在中国得到充分发展,目前已成功应用于“神舟”系列以及空间实验室等载人航天任务中.但若要实现更 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于验前信息的测试性验证试验方案确定方法
    在工程实际中,为了判断装备的测试性设计水平是否达到了合同规定的指标要求,需要开展测试性验证试验.按照国家标准(GB5080.5—1985)所规定的测试性验证试验方案需要进行大样本试验,而复杂装备由于造价昂贵、研制经费紧张,大样本工程上一般较难实现,也不利于装备的尽早定型[1,2].Bayes方法充分 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 柔片式密封数值计算及性能分析
    柔片式密封作为一种非接触式密封,应用于高速转子系统[1],具有较好的密封性能.柔片式密封在结构上继承了刷式密封的径向柔性[2,3]特点,转子直径变化或偏移±1mm内对其性能影响很小.柔片式密封不存在“滞后效应”[4],其最大工作压差可达1MPa[5],且在较高的密封压差下仍能维持较小的质量泄漏率.优 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 航天器测试需求描述及其自动生成
    ?航天器包括卫星和飞船,其作为典型的安全苛刻系统,系统功能一旦失效将引起财产、生命等的重大损失以及环境可能遭到严重破坏[1,2].因此,其是否可信[3,4,5,6]已成为广泛关注的问题.可信性主要通过测试获取的数据进行评估和验证[7,8].随着我国航天事业飞速发展,特别是随着二代导航、军用遥感、军用 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.